A New Hybrid Prime Code for OCDMA Network Multimedia Applications
Abstract
1. Introduction
- (1)
- Maximum number of code sequences for maximum number of users, leading to an increase in the network capacity for data and multimedia applications.
- (2)
- Minimum code length to increase the user bit rate.
- (3)
- Optimal code weight for good network bit error rate (BER) performance.
- (4)
- Minimum cross-correlation values to prevent multiple access interference (MAI).
- (5)
- Reliable code parameter variation while keeping the same cross-correlation value.
- (6)
- Simplicity of code generation.
- (7)
- Minimum cost with respect to the line coding techniques in optical domain.
- (1)
- High signal integrity in the midst of interference at the receiving end.
- (2)
- Broader network capacity.
2. Literature Review
3. Code Construction
3.1. Code Construction Procedure
- (a)
- Arrange the code sequences in the first tree, row by row in one column, as shown in Table 3, column 1.
- (b)
- (c)
- Rotate the final code sequences in column 2 horizontally from right to left until the first code word in this sequence becomes the last one, as shown in Table 3, column 3.
| Column 1 | Column 2 | Column 3 | |||
|---|---|---|---|---|---|
| Code Index m | First Tree Code Sequences | Merged Code Sequences | Resultant Code Sequences | ||
| 0 | C0 | C00 | = 100001000000010000100000 | ||
| C01 | = 010000010000100000001000 | ||||
| C02 | = 010000100000100001000000 | ||||
| C03 | = 100000001000010000010000 | ||||
| 1 | C1 | C10 | = 100000100000001000010000 | ||
| C11 | = 001000010000010000000100 | ||||
| C12 | = 001000010000100000100000 | ||||
| C13 | = 010000000100001000010000 | ||||
| 2 | C2 | C20 | = 100000010000000100001000 | ||
| C21 | = 000100010000001000000010 | ||||
| C22 | = 000100001000100000010000 | ||||
| C23 | = 001000000010000100010000 | ||||
| 3 | C3 | C30 | = 100000001000000010000100 | ||
| C31 | = 000010010000000100000001 | ||||
| C32 | = 000010000100100000001000 | ||||
| C33 | = 000100000001000010010000 | ||||
| 4 | C4 | C40 | = 010000000100001000000010 | ||
| C41 | = 000001001000000010000100 | ||||
| C42 | = 001000000010010000000100 | ||||
| C43 | = 000010000100000001001000 | ||||
| 5 | C5 | C50 | = 010000000010000100000001 | ||
| C51 | = 000000101000000001000010 | ||||
| C52 | = 000100000001010000000010 | ||||
| C53 | = 000001000010000000101000 | ||||
| 6 | C6 | C60 | = 010001000000000010010000 | ||
| C61 | = 001000001000100000000001 | ||||
| C62 | = 000010010000010001000000 | ||||
| C63 | = 100000000001001000001000 | ||||
| 7 | C7 | C70 | = 001000100000000100001000 | ||
| C71 | = 000100000100010000000010 | ||||
| C72 | = 000100001000001000100000 | ||||
| C73 | = 010000000010000100000100 | ||||
| 8 | C8 | C80 | = 001000010000000010000100 | ||
| C81 | = 000010000100001000000001 | ||||
| C82 | = 000010000100001000010000 | ||||
| C83 | = 001000000001000010000100 | ||||
| 9 | C9 | C90 | = 000100001000000010000010 | ||
| C91 | = 000001000010000100000001 | ||||
| C92 | = 000010000010000100001000 | ||||
| C93 | = 000100000001000001000010 | ||||
| 10 | C10 | C100 | = 010000000100100000000001 | ||
| C101 | = 000000101000000010010000 | ||||
| C102 | = 100000000001010000000100 | ||||
| C103 | = 000010010000000000101000 | ||||
| 11 | C11 | C110 | = 001001000000100000001000 | ||
| C111 | = 000100000100100000010000 | ||||
| C112 | = 100000001000001001000000 | ||||
| C113 | = 100000010000000100000100 | ||||
| 12 | C12 | C120 | = 000100100000100000000100 | ||
| C121 | = 000010000010010000010000 | ||||
| C122 | = 100000000100000100100000 | ||||
| C123 | = 010000010000000010000010 | ||||
| 13 | C13 | C130 | = 000010010000100000000010 | ||
| C131 | = 000001000001001000010000 | ||||
| C132 | = 100000000010000010010000 | ||||
| C133 | = 001000010000000001000001 | ||||
| 14 | C14 | C140 | = 001000001000010000000001 | ||
| C141 | = 000000100100000100001000 | ||||
| C142 | = 010000000001001000001000 | ||||
| C143 | = 000100001000000000100100 | ||||
| 15 | C15 | C150 | = 000101000000010000000100 | ||
| C151 | = 000010000010100000001000 | ||||
| C152 | = 010000000100000101000000 | ||||
| C153 | = 100000001000000010000010 | ||||
| 16 | C16 | C160 | = 000010100000010000000010 | ||
| C161 | = 000001000001010000001000 | ||||
| C162 | = 010000000010000010100000 | ||||
| C163 | = 010000001000000001000001 | ||||
| 17 | C17 | C170 | = 000100010000001000000001 | ||
| C171 | = 000000100010001000000100 | ||||
| C172 | = 001000000001000100010000 | ||||
| C173 | = 001000000100000000100010 | ||||
| 18 | C18 | C180 | = 000011000000001000000010 | ||
| C181 | = 000001000001100000000100 | ||||
| C182 | = 001000000010000011000000 | ||||
| C183 | = 100000000100000001000001 | ||||
| 19 | C19 | C190 | = 000010100000000100000001 | ||
| C191 | = 000000100001010000000010 | ||||
| C192 | = 000100000001000010100000 | ||||
| C193 | = 010000000010000000100001 | ||||
- Limited cross-correlation “0” or “1”;
- Very large number of code sequences can provide a large number of simultaneous users without sacrificing performance;
- Shorter code length for the same higher bit rate transmission.
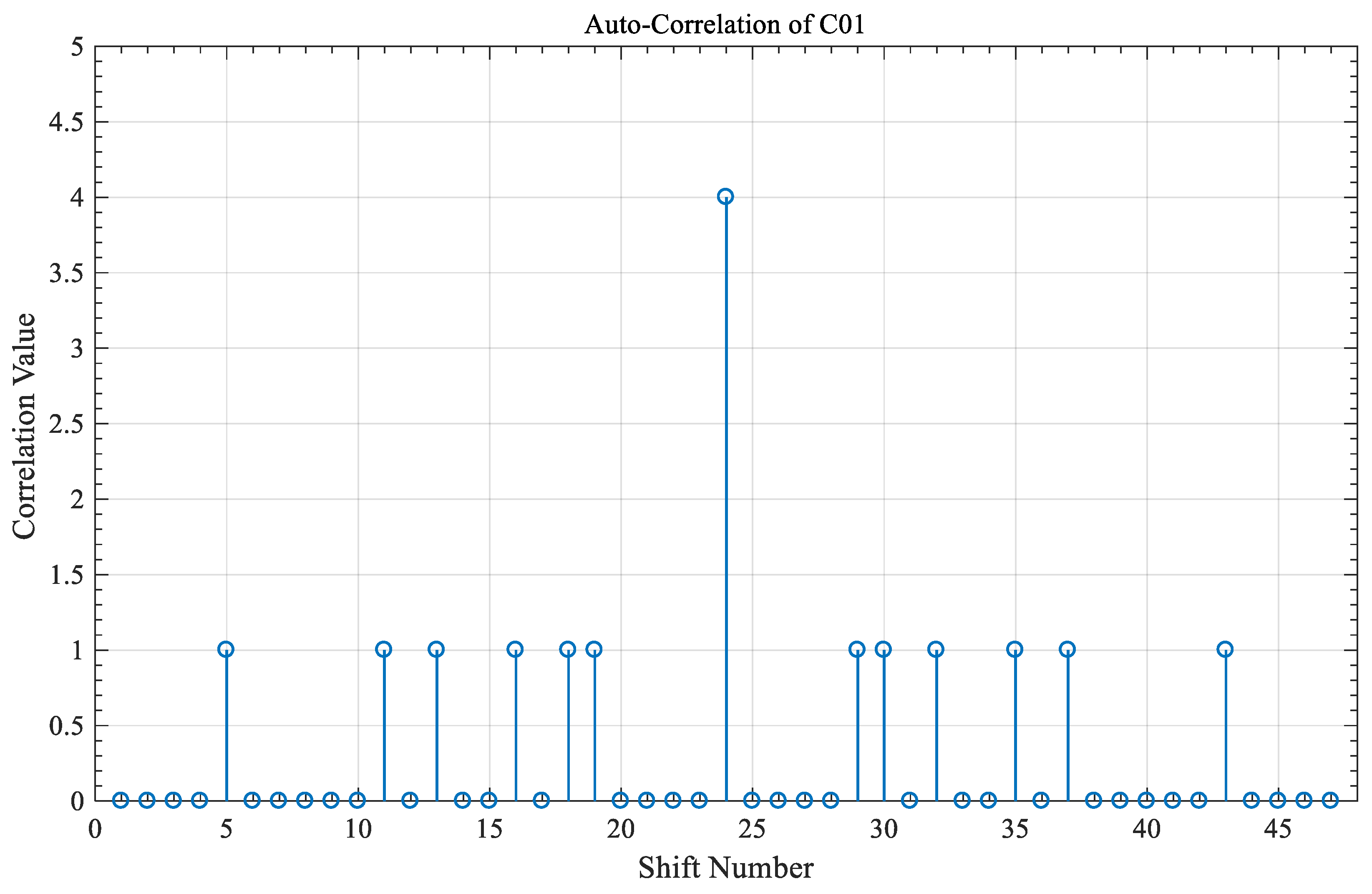
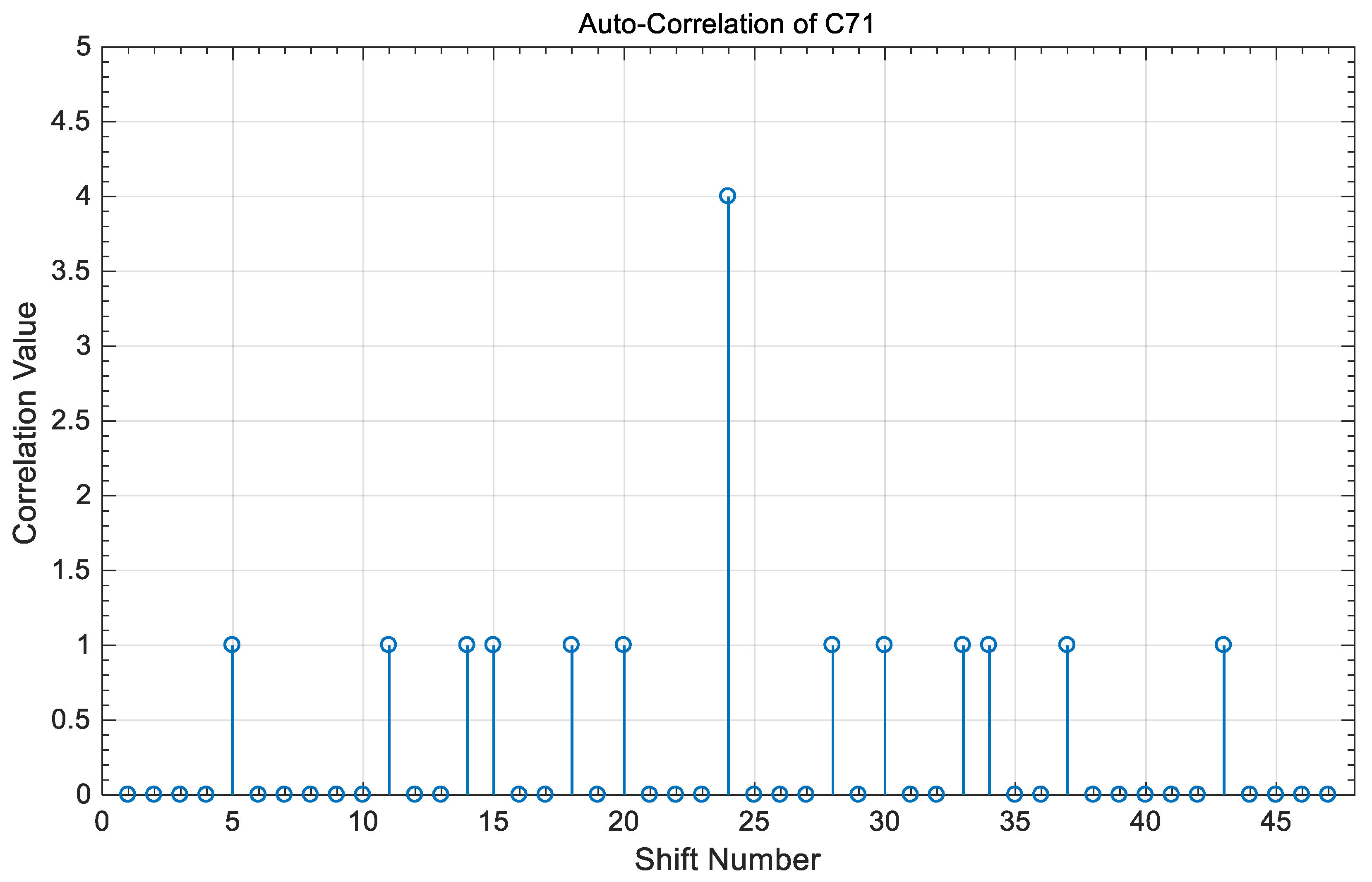
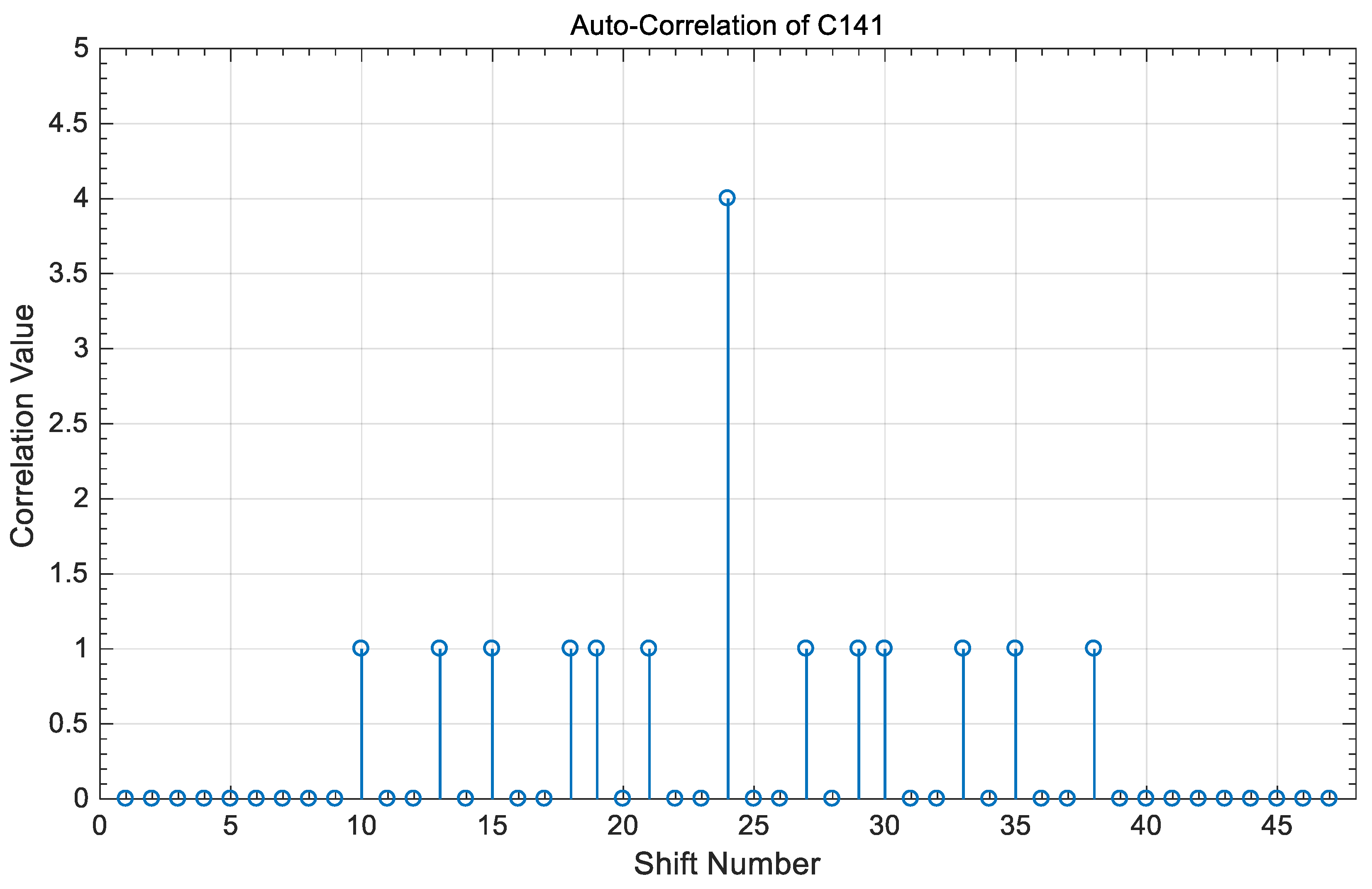
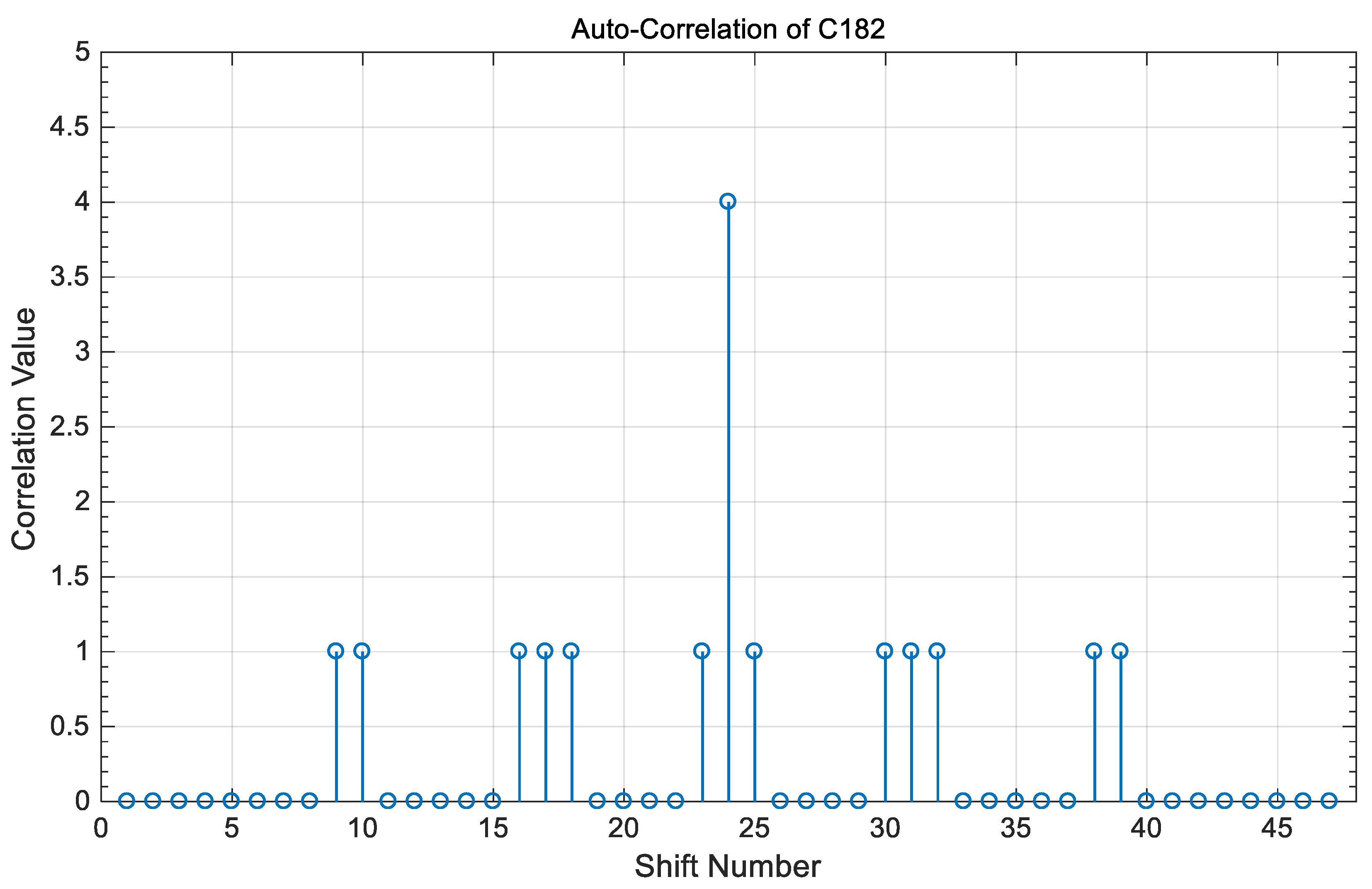
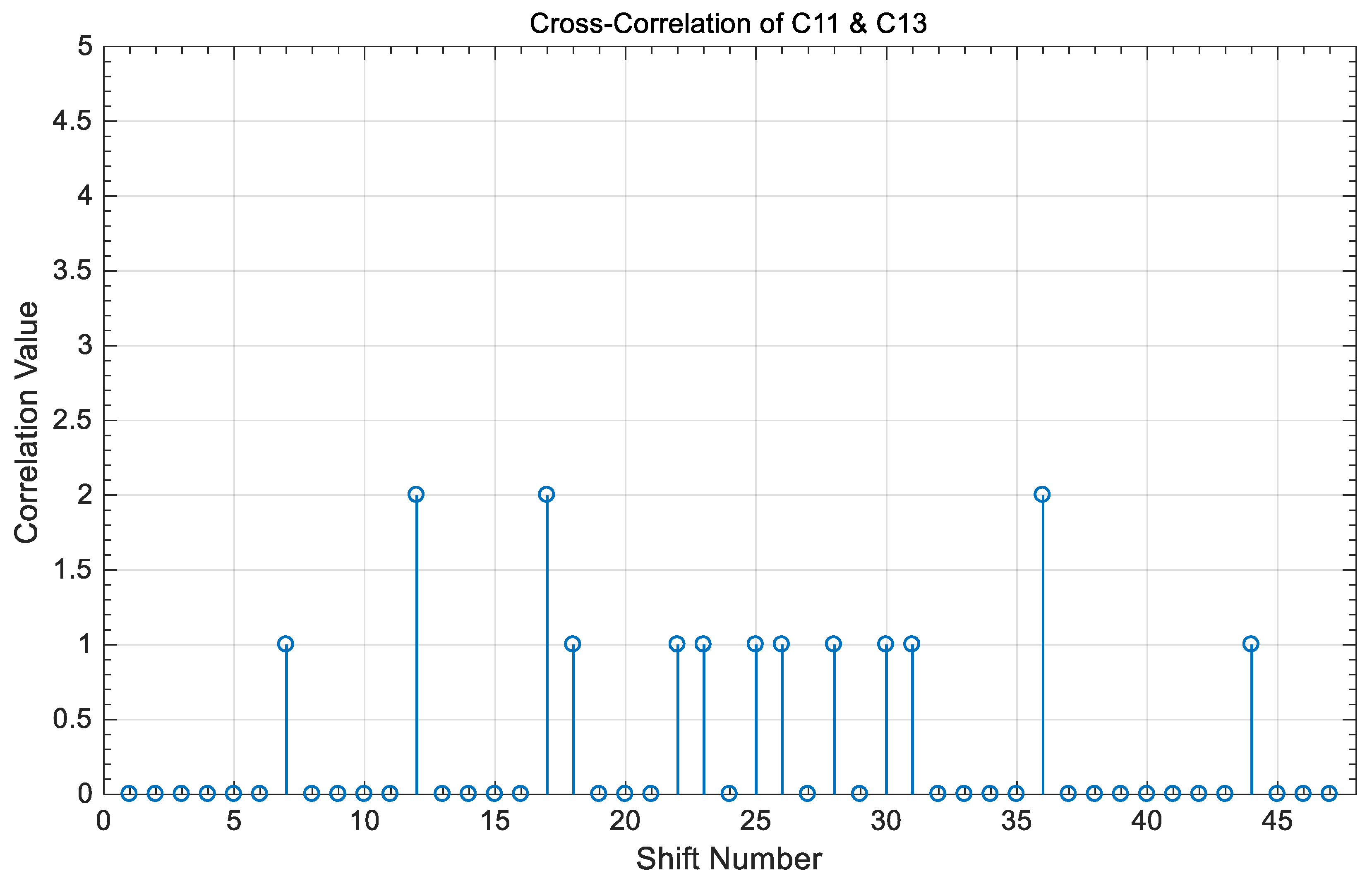
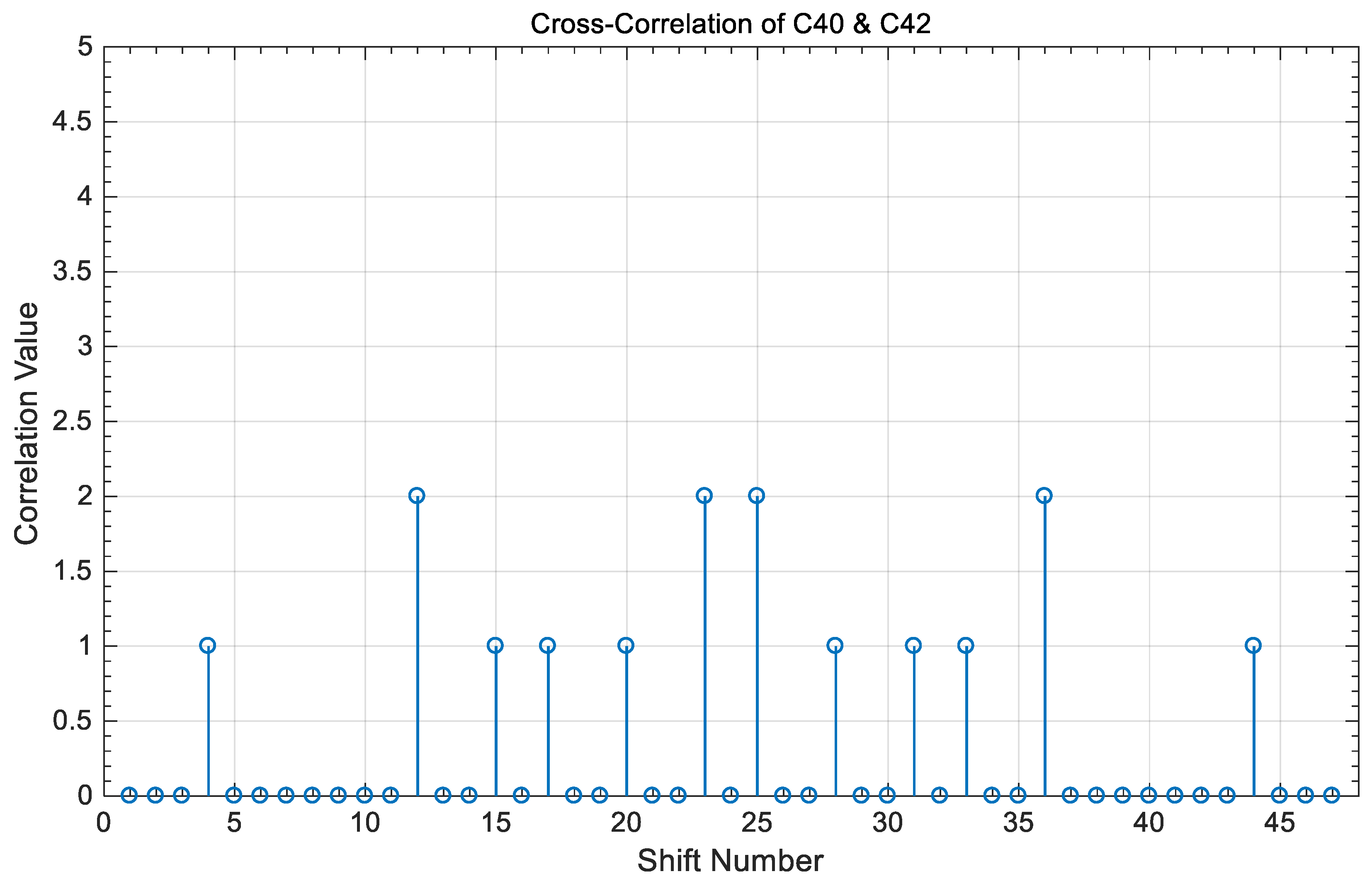
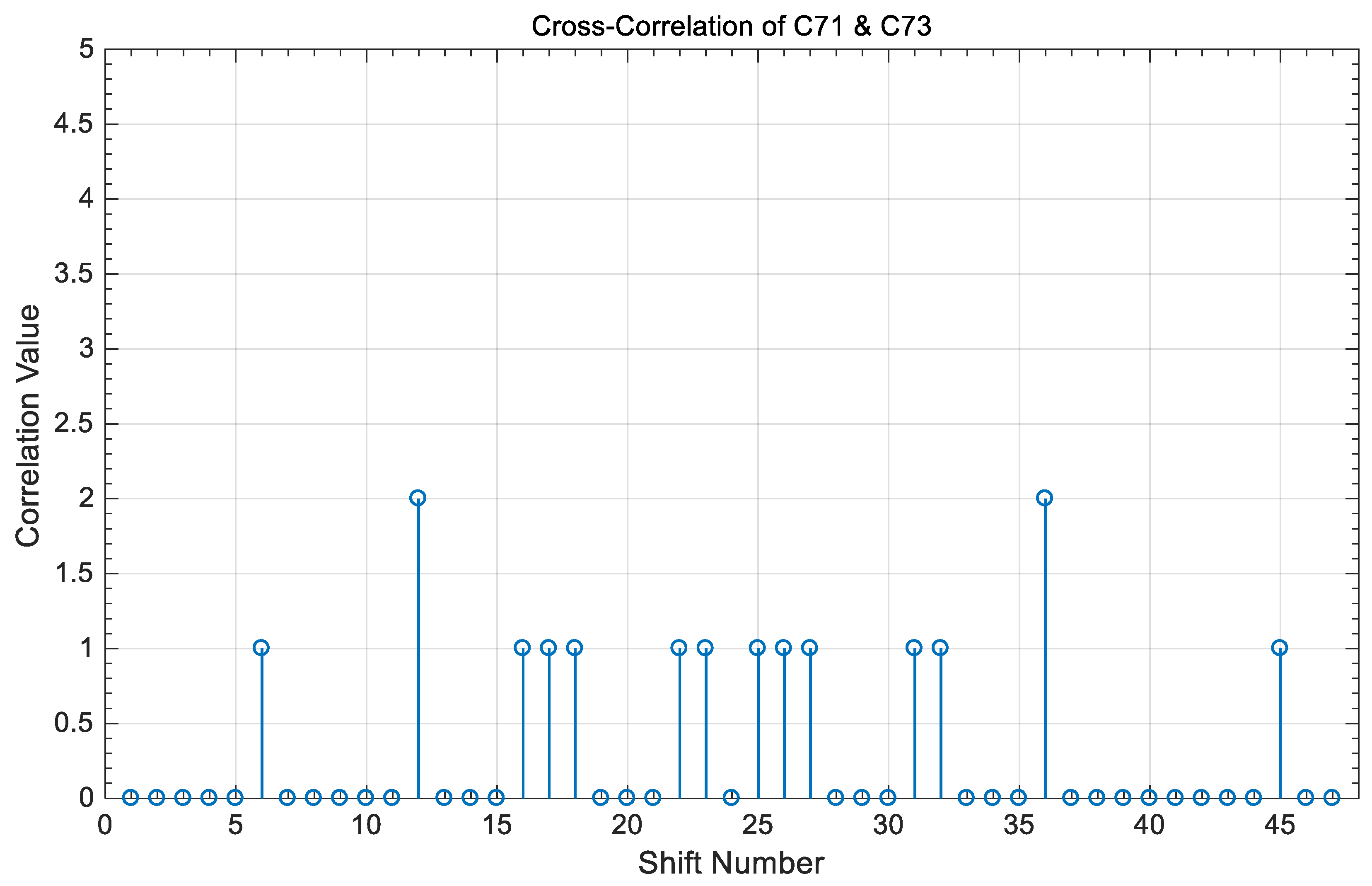
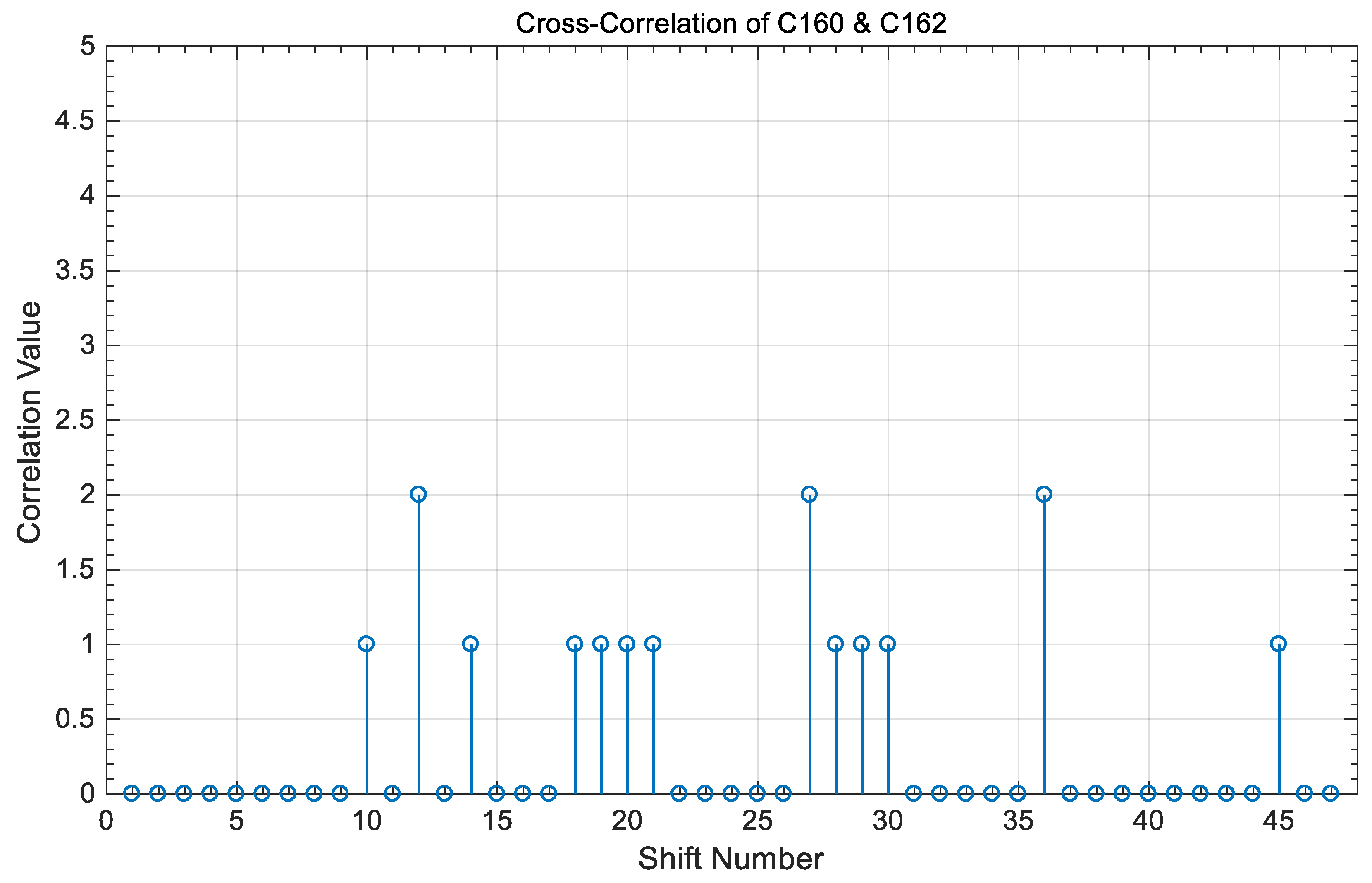
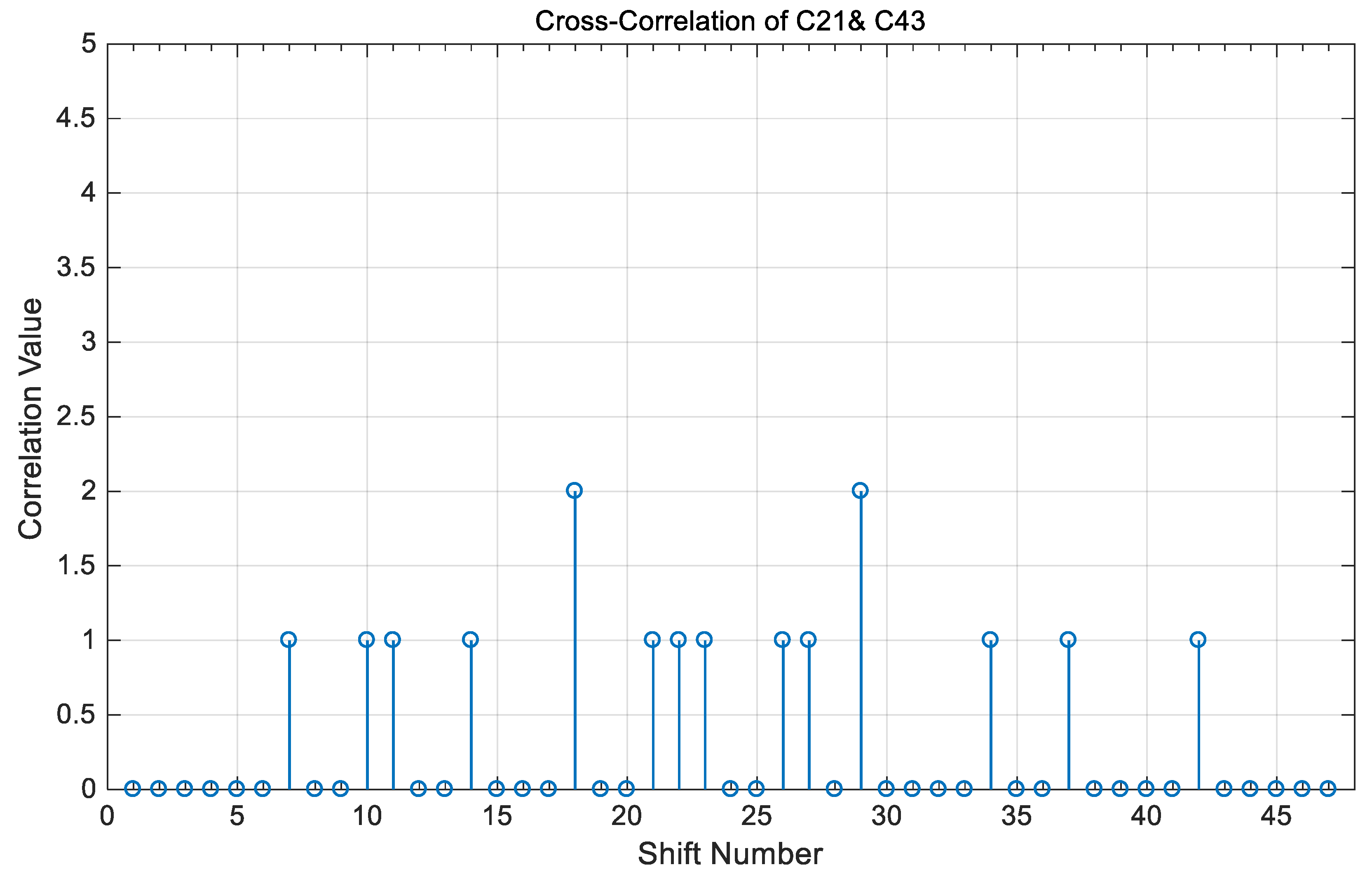
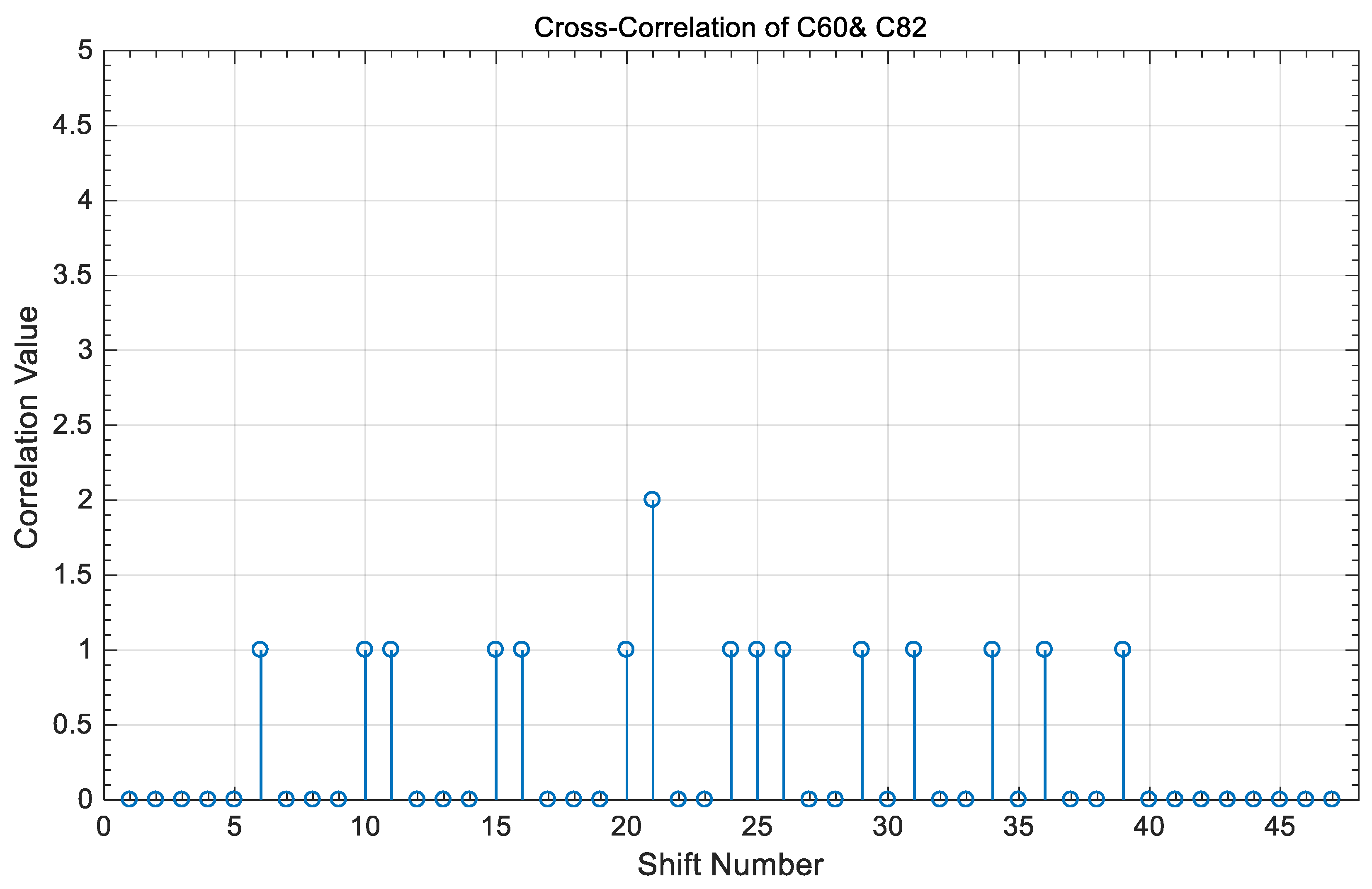
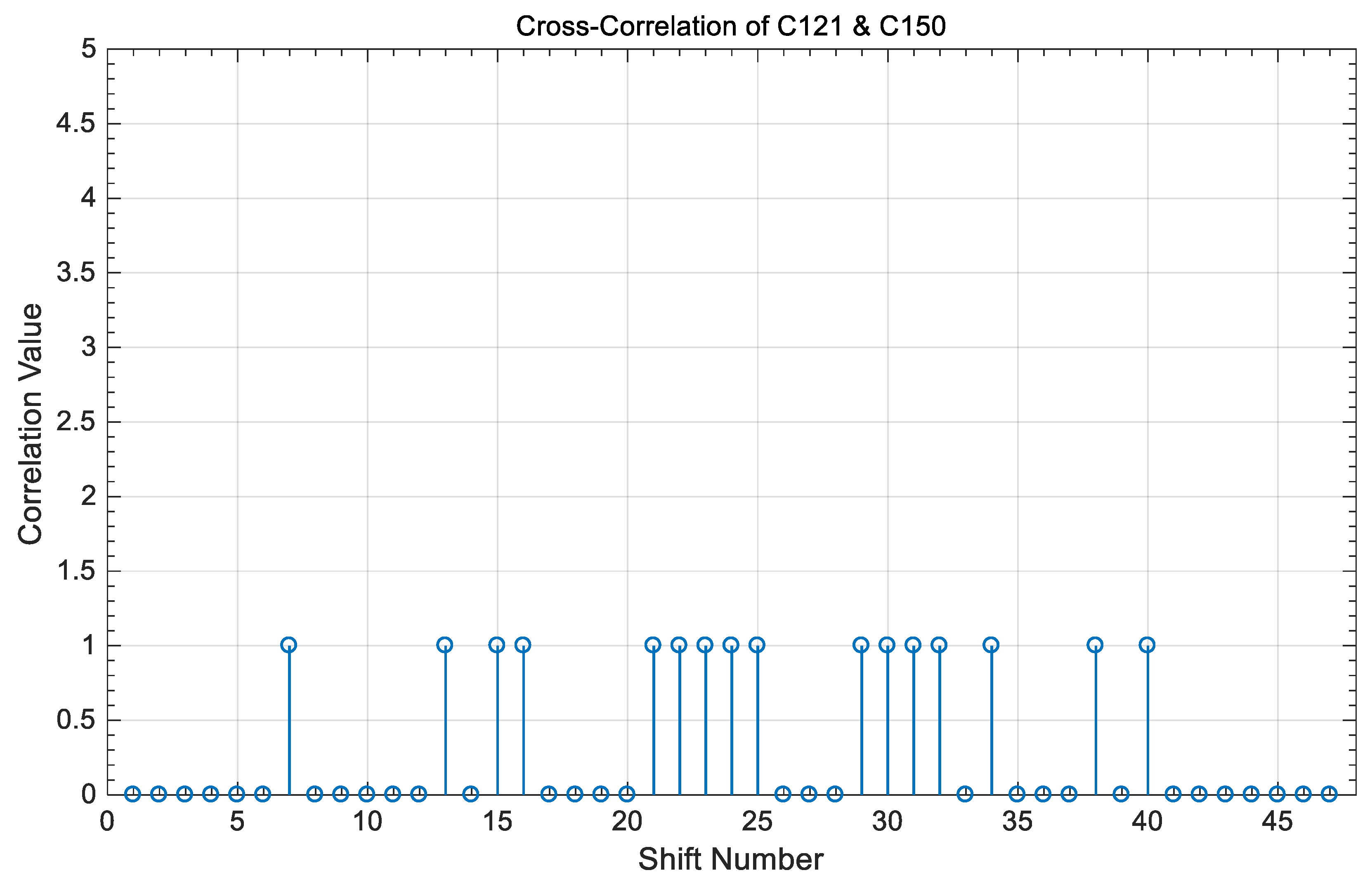
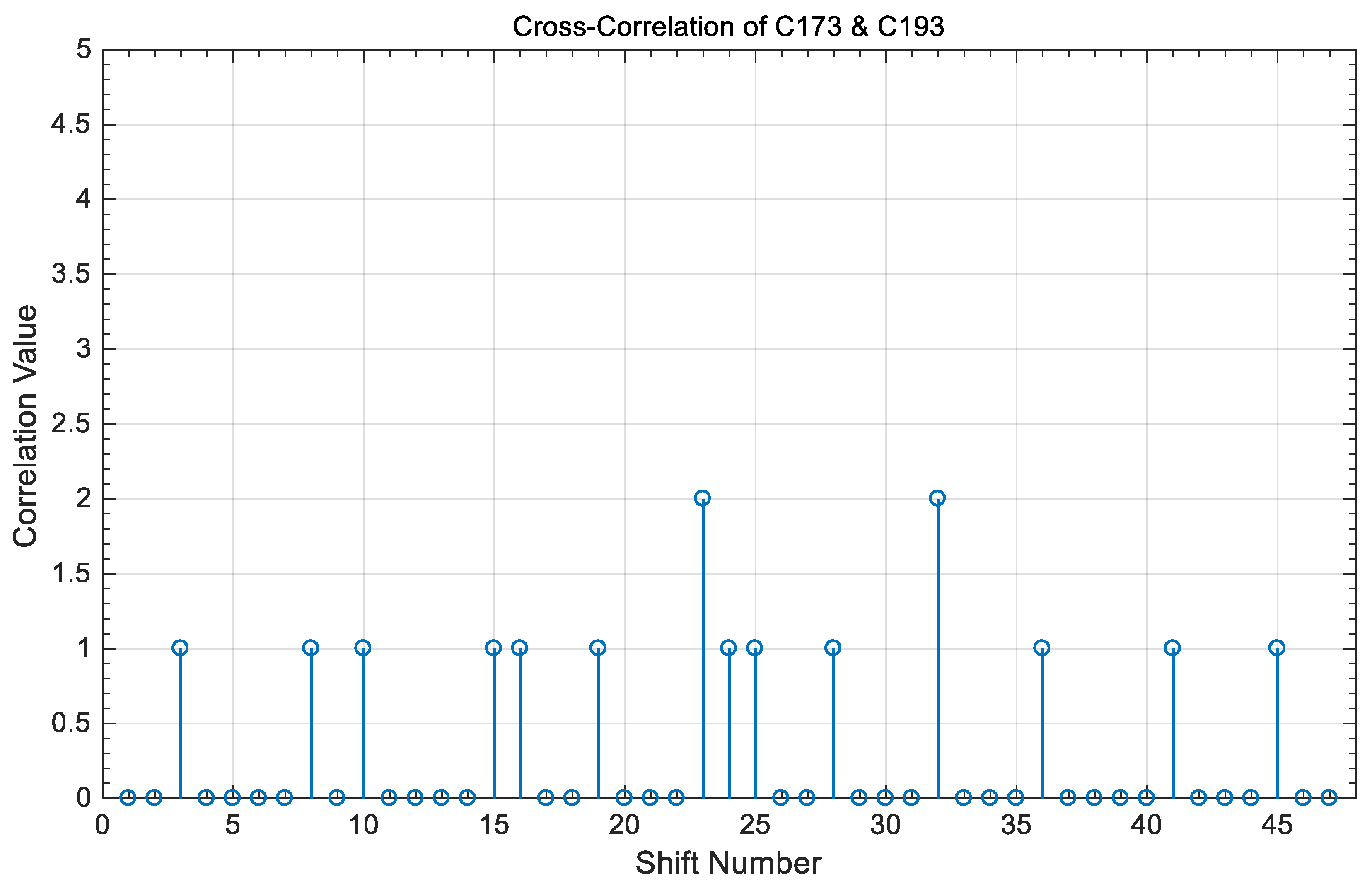
3.2. Correlation Properties
- (a)
- The peak value of the auto-correlation property is 2n, where n is an integer number equal to the number of code words used to construct the code sequence in each tree.
- (b)
- The value of the cross-correlation property is “0” or “1” between any two different code sequences in the coding of Table 3 and is independent of whether these two codes share the same code index or not.
- (c)
- and
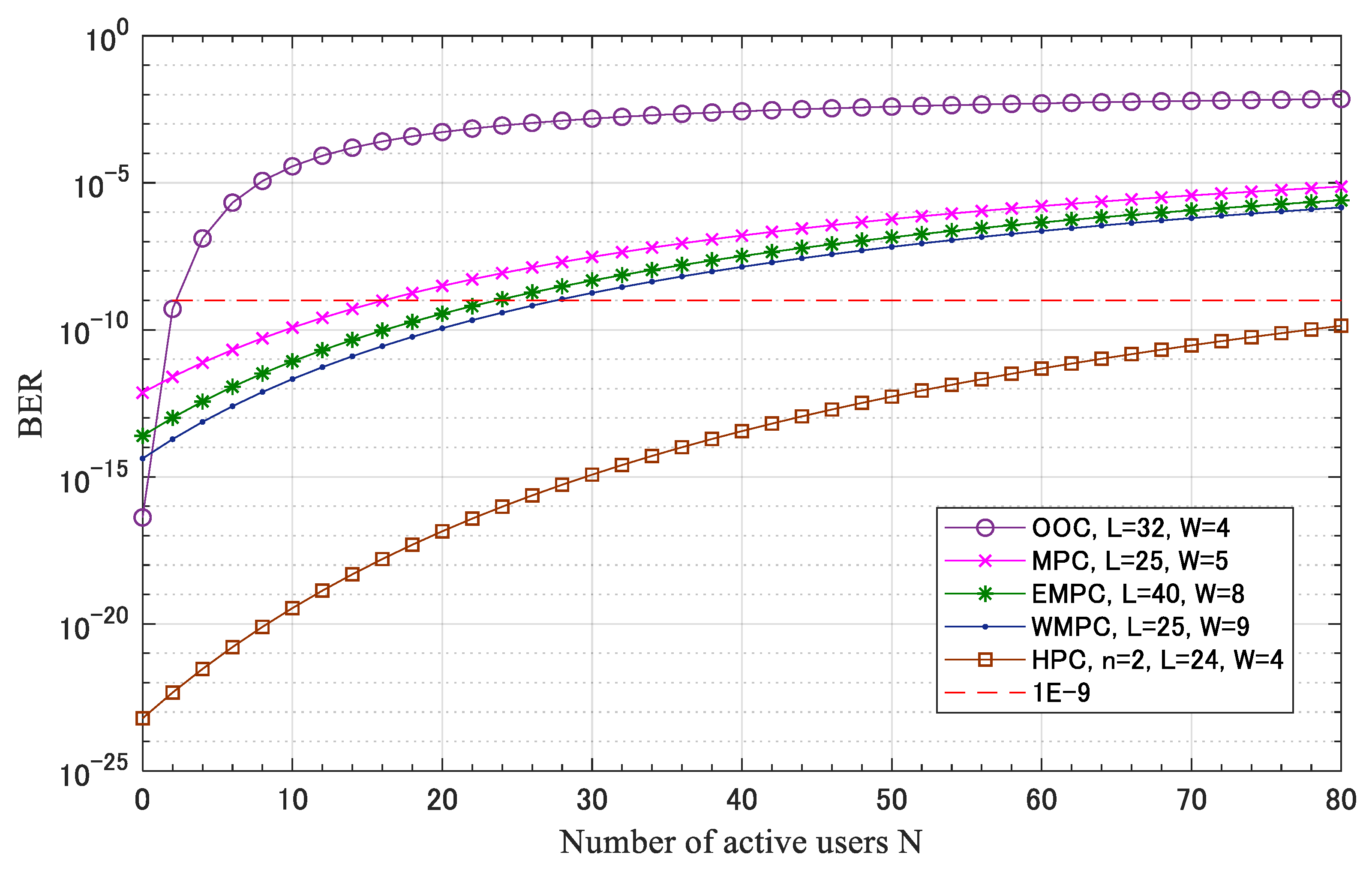
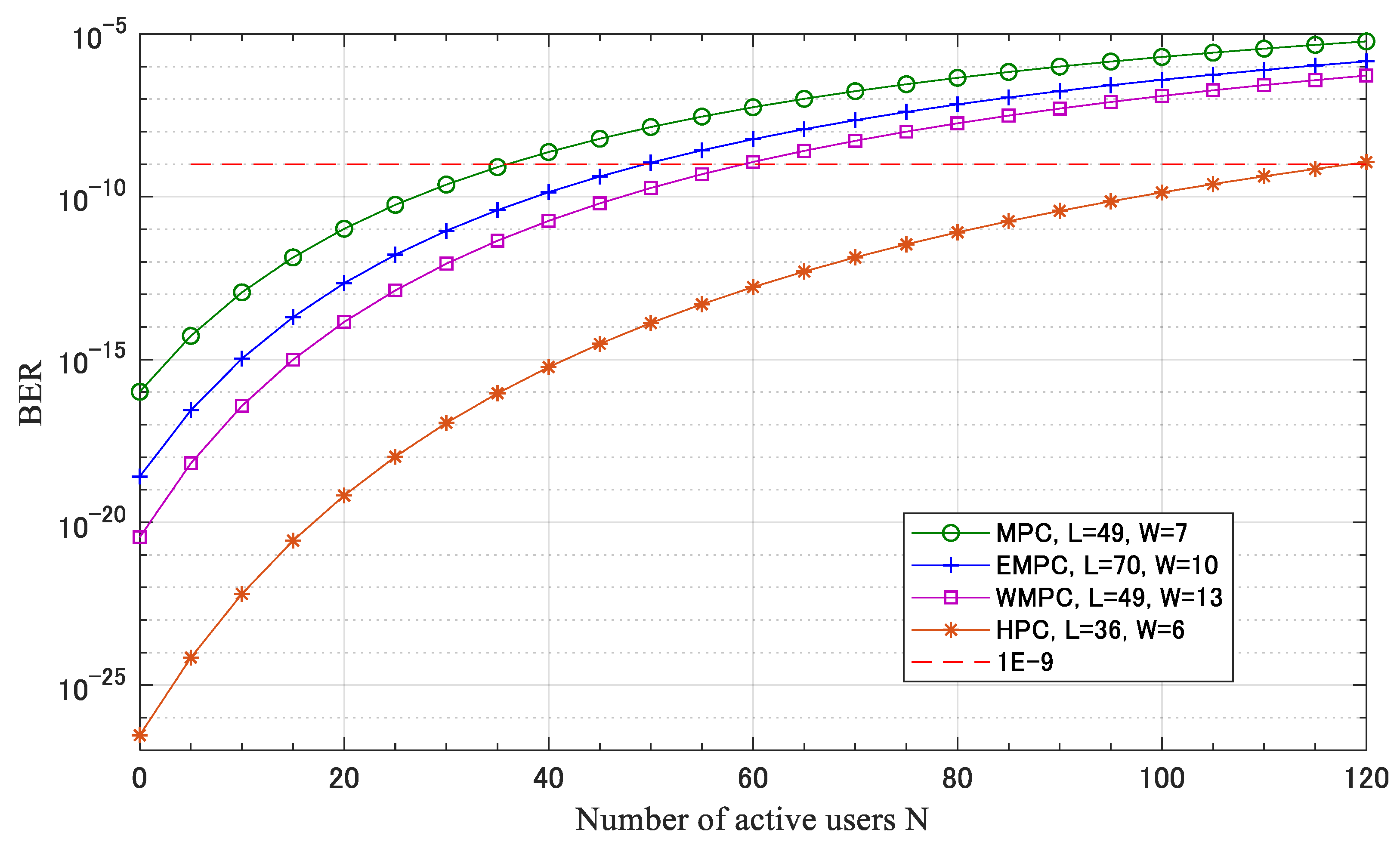
4. Correlation Results
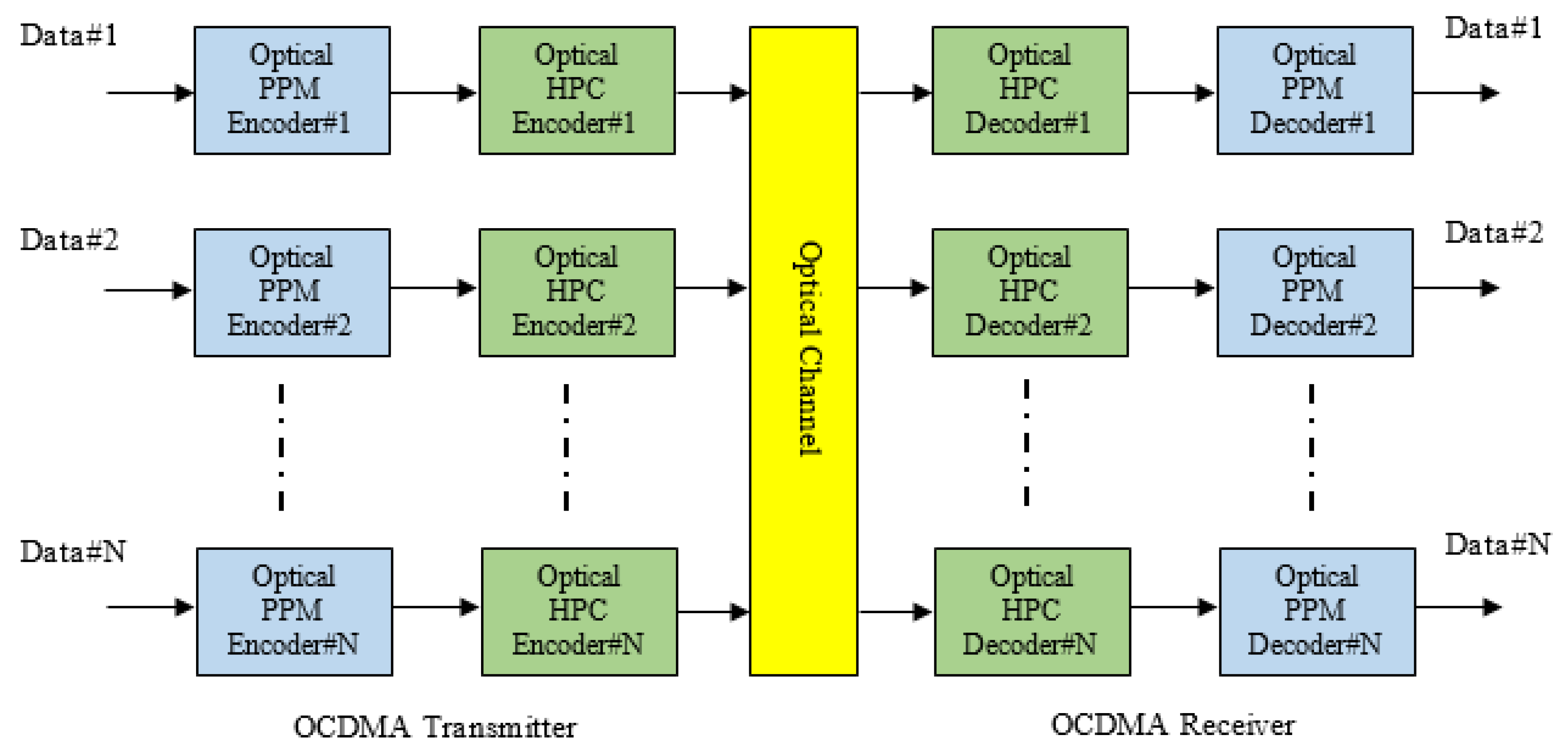
5. The Proposed OCDMA System Model
6. BER Performance Analysis
- Code length equal to , where is the prime number and n is the number of the different prime numbers used for the code construction.
7. Throughput Analysis
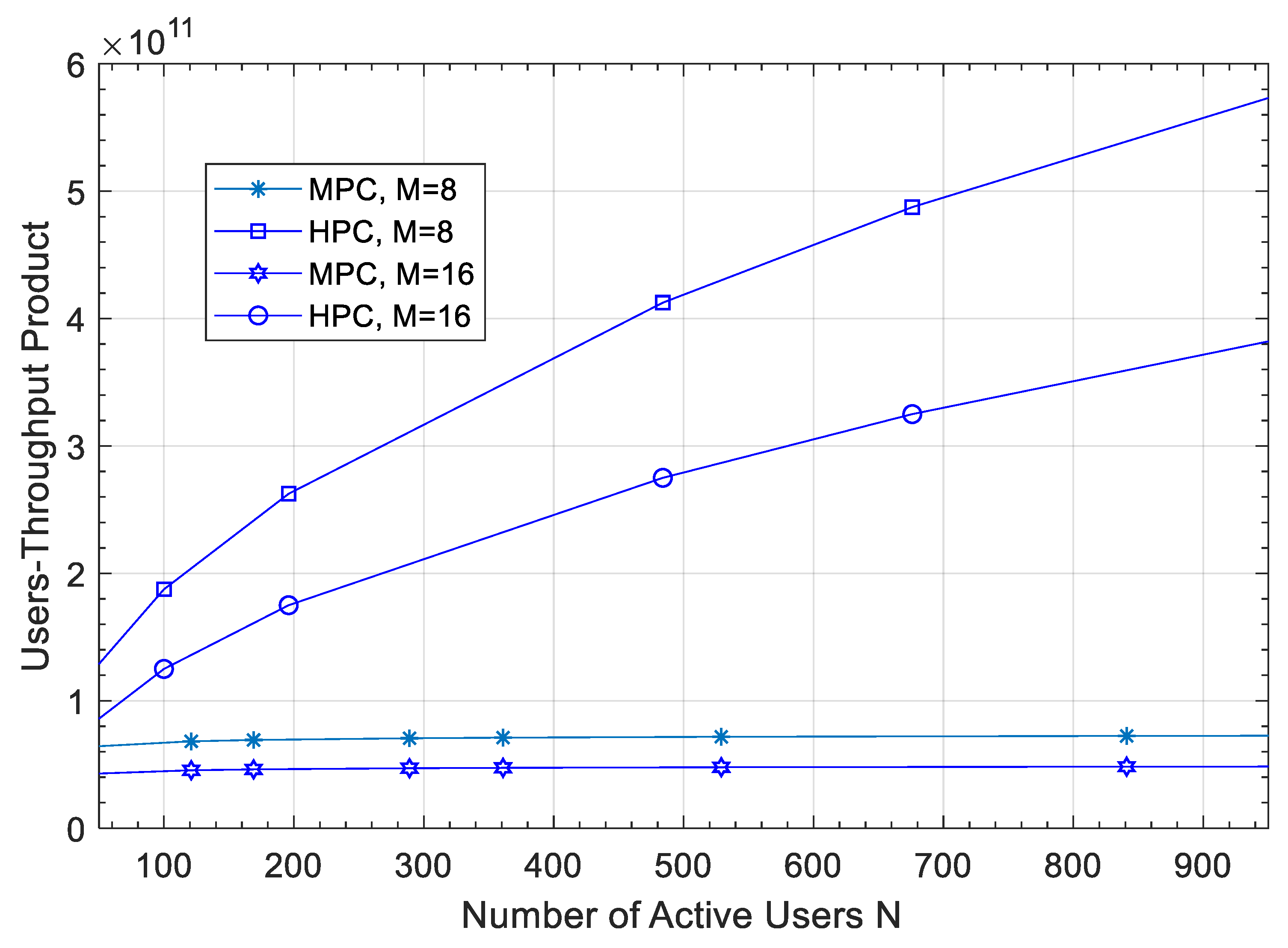
8. EVM Analysis
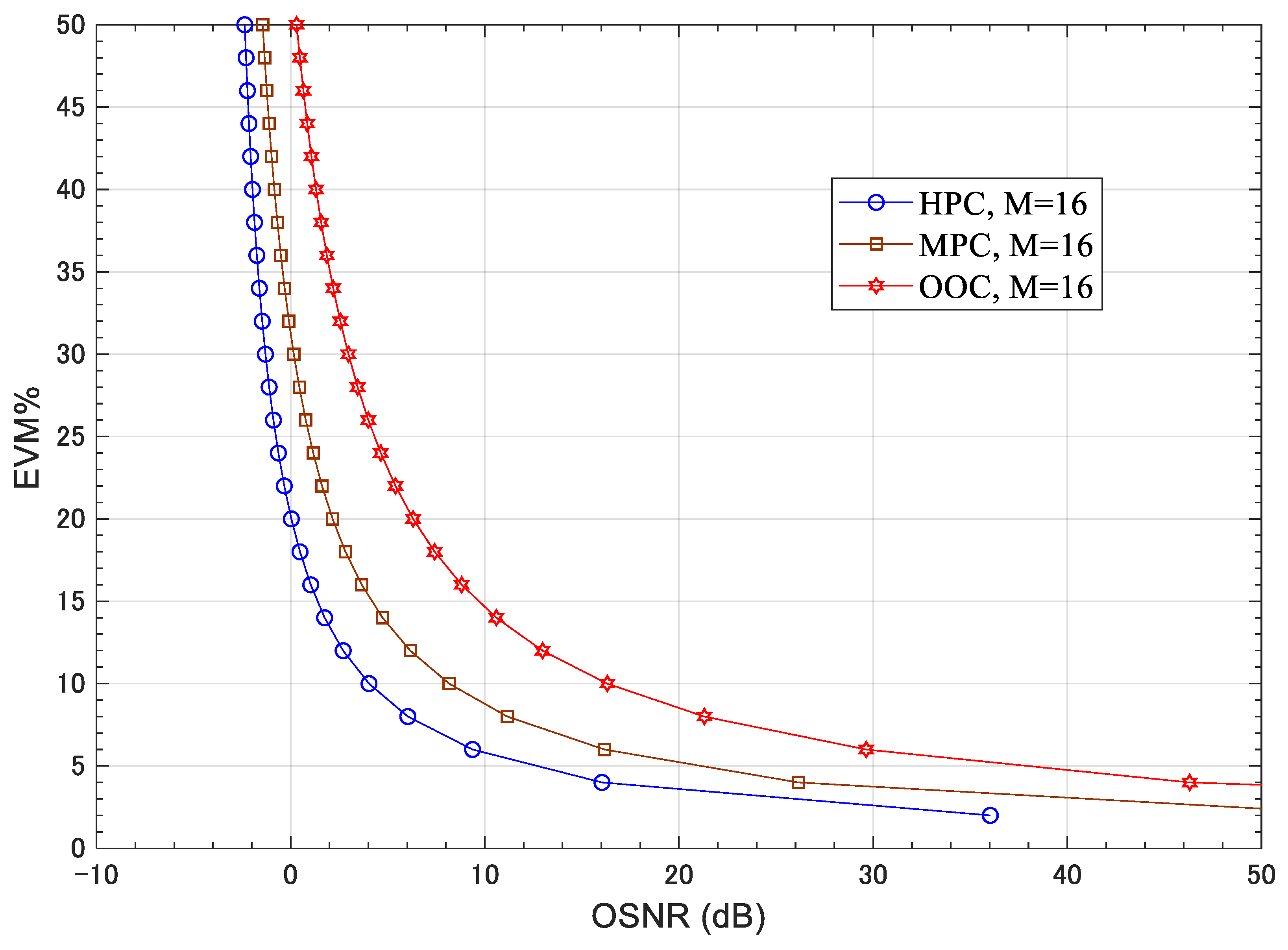
9. Simulation Results
10. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alderson, T.L. n-dimensional optical orthogonal codes, bounds and optimal constructions. Appl. Algebra Eng. Commun. Comput. 2019, 30, 373–386. [Google Scholar] [CrossRef]
- Alderson, T.L. 3-Dimensional Optical Orthogonal Codes with Ideal Autocorrelation-Bounds and Optimal Constructions. IEEE Trans. Inf. Theory 2017, 64, 4392–4398. [Google Scholar] [CrossRef]
- Feng, T.; Chang, Y. Combinatorial Constructions for Optimal Two-Dimensional Optical Orthogonal Codes With λ = 2. IEEE Trans. Inf. Theory 2011, 57, 6796–6819. [Google Scholar] [CrossRef]
- Wang, X.; Chang, Y.; Feng, T. Optimal 2-D (n × m,3,2,1)-optical Orthogonal Codes. IEEE Trans. Inf. Theory 2012, 59, 710–725. [Google Scholar] [CrossRef]
- Cai, H.; Liang, H.; Tang, X. Constructions of Optimal 2-D Optical Orthogonal Codes via Generalized Cyclotomic Classes. IEEE Trans. Inf. Theory 2014, 61, 688–695. [Google Scholar] [CrossRef]
- Chung, J.-H.; Yang, K. New Families of Optimal Variable-Weight Optical Orthogonal Codes with High Weights. IEEE Trans. Inf. Theory 2015, 61, 4511–4517. [Google Scholar] [CrossRef]
- Li, X.; Lu, L. General Construction Method of Multilength Optical Orthogonal Codes with Arbitrary Cross-Correlation Constraint for OCDMA Multimedia Network. J. Opt. Commun. Netw. 2015, 7, 156–163. [Google Scholar] [CrossRef]
- Morsy, M.A.; Hassan, K.M.; Morshed, A.H.; Elhennawy, A. Analysis of Optical Code Division Multiple Access Passive Networks for Different Encoder Delay Elements. In Proceedings of the 2006 International Conference on Computer Engineering and Systems, Cairo, Egypt, 5–7 November 2006; pp. 294–299. [Google Scholar]
- Farghal, A.E.A.; Shalaby, H.M.H.; Kato, K.; Pokharel, R.K. Performance Analysis of Multicode OCDM Networks Supporting Elastic Transmission with QoS Differentiation. IEEE Trans. Commun. 2015, 64, 741–752. [Google Scholar] [CrossRef]
- Raddo, T.; Sanches, A.L.; Monroy, I.T.; Borges, B.-H.V. Throughput Performance Evaluation of Multiservice Multirate OCDMA in Flexible Networks. IEEE Photonics J. 2016, 8, 1–15. [Google Scholar] [CrossRef]
- Liu, X.-J.; Xia, S.-T.; Fu, F.-W. Reconstruction Guarantee Analysis of Basis Pursuit for Binary Measurement Matrices in Compressed Sensing. IEEE Trans. Inf. Theory 2017, 63, 2922–2932. [Google Scholar] [CrossRef]
- Bharti, A.Y.; Kar, S.; Jain, V.K. Performance analysis of wireless OCDMA multi-user system based on new 2-D code in presence of atmospheric turbulence and various weather conditions. In Proceedings of the 9th International Conference on Communication Systems and Networks (COMSNETS), Bengaluru, India, 4–8 January 2017; pp. 109–115. [Google Scholar]
- Alderson, T.L.; Mellinger, K.E. Families of Optimal OOCs with λ = 2. IEEE Trans. Inf. Theory 2008, 54, 3722–3724. [Google Scholar] [CrossRef]
- Yang, G.-C.; Kwong, W. Performance analysis of optical CDMA with prime codes. Electron. Lett. 1995, 31, 569–570. [Google Scholar] [CrossRef]
- Karbassian, M.M.; Ghafouri-Shiraz, H. Fresh Prime Codes Evaluation for Synchronous PPM and OPPM Signaling for Optical CDMA Networks. J. Lightwave Technol. 2007, 25, 1422–1430. [Google Scholar] [CrossRef]
- Wen, J.-H.; Lin, J.-Y.; Liu, C.-Y. Modified prime-hop codes for optical CDMA systems. IEE Proc. Commun. 2003, 150, 404–408. [Google Scholar] [CrossRef]
- Huang, W.-J.; Niu, C.-T.; Lin, C.-H.; Wu, J. Spatial/Spectral OCDMA System Using Partial Modified Prime Codes and Error-Correction Codes. J. Lightwave Technol. 2008, 26, 3030–3040. [Google Scholar] [CrossRef]
- Yang, C.-C. Optical CDMA Passive Optical Network Using Prime Code with Interference Elimination. IEEE Photonics Technol. Lett. 2007, 19, 516–518. [Google Scholar] [CrossRef]
- Ding, C.; Pless, V. Cyclotomy and duadic codes of prime lengths. IEEE Trans. Inf. Theory 2002, 45, 453–466. [Google Scholar] [CrossRef]
- Ding, C. Cyclotomic Constructions of Cyclic Codes with Length Being the Product of Two Primes. IEEE Trans. Inf. Theory 2012, 58, 2231–2236. [Google Scholar] [CrossRef]
- Karbassian, M.M.; Kueppers, F. Synchronous Optical CDMA Networks Capacity Increase Using Transposed Modified Prime Codes. J. Lightwave Technol. 2010, 28, 2603–2610. [Google Scholar] [CrossRef]
- Morsy, M.A. Analysis and design of weighted MPC in incoherent synchronous OCDMA network. Opt. Quantum Electron. 2018, 50, 387. [Google Scholar] [CrossRef]
- Hong, C.-F.; Yang, G.-C. Concatenated prime codes. IEEE Commun. Lett. 1999, 3, 260–262. [Google Scholar] [CrossRef]
- Zoualfaghari, M.H.; Ghafouri-Shiraz, H. Uniform Cross-Correlation Modified Prime Code for Applications in Synchronous Optical CDMA Communication Systems. J. Lightwave Technol. 2012, 30, 2955–2963. [Google Scholar] [CrossRef]
- Yang, G.-C.; Kwong, W.C. Performance Analysis of Extended Carrier-Hopping Prime Codes for Optical CDMA. IEEE Trans. Commun. 2005, 53, 876–881. [Google Scholar] [CrossRef]
- Yang, C.-C. Optical CDMA coding scheme with a large size of code space. IEEE Commun. Lett. 2009, 13, 145–147. [Google Scholar] [CrossRef]
- Fujiwara, Y.; van den Driessche, P. Quantum Synchronizable Codes from Finite Geometries. IEEE Trans. Inf. Theory 2014, 60, 7345–7354. [Google Scholar] [CrossRef]
- Oggier, F.; Sole, P.; Belfiore, J.-C. Codes Over Matrix Rings for Space-Time Coded Modulations. IEEE Trans. Inf. Theory 2012, 58, 734–746. [Google Scholar] [CrossRef]
- Ding, C.; Kohel, D.; Ling, S. Elementary 2-group character codes. IEEE Trans. Inf. Theory 2000, 46, 280–284. [Google Scholar] [CrossRef]
- Hamarsheh, M.; Shalaby, H.; Abdullah, M. Design and analysis of a dynamic code division multiple access communication system based on tunable optical filter. J. Lightwave Technol. 2005, 23, 3959–3965. [Google Scholar] [CrossRef][Green Version]
- Yen, C.-T.; Chen, C.-M. A study of three-dimensional optical code-division multiple-access for optical fiber sensor networks. Comput. Electr. Eng. 2016, 49, 136–145. [Google Scholar] [CrossRef]
- Liu, F.; Karbassian, M.M.; Ghafouri-Shiraz, H. Novel family of prime codes for synchronous optical CDMA. Opt. Quantum Electron. 2007, 39, 79–90. [Google Scholar] [CrossRef]
- Lalmahomed, A.; Karbassian, M.; Ghafouri-Shiraz, H. Performance Analysis of Enhanced-MPC in Incoherent Synchronous Optical CDMA. J. Lightwave Technol. 2009, 28, 39–46. [Google Scholar] [CrossRef]
- Park, E.; Mendez, A.; Garmire, E. Temporal/spatial optical CDMA networks-design, demonstration, and comparison with temporal networks. IEEE Photonics Technol. Lett. 1992, 4, 1160–1162. [Google Scholar] [CrossRef]
- Yu, K.; Park, N. Design of new family of two-dimensional wavelength-time spreading codes for optical code division multiple access networks. Electron. Lett. 1999, 35, 830–831. [Google Scholar] [CrossRef]
- Mendez, A.J.; Gagliardi, R.M.; Hernandez, V.J.; Bennett, C.V.; Lennon, W.J. Design and performance analysis of wavelength/time (W/T) matrix codes for optical CDMA. J. Lightwave Technol. 2003, 21, 2524–2533. [Google Scholar] [CrossRef]
- Yang, C.-C.; Huang, J.-F. Two-dimensional M-matrices coding in spatial/frequency optical CDMA networks. IEEE Photonics Technol. Lett. 2003, 15, 168–170. [Google Scholar] [CrossRef]
- Heo, H.; Min, S.; Won, Y.; Yeon, Y.; Kim, B.; Kim, B. A New Family of 2-D Wavelength–Time Spreading Code for Optical Code-Division Multiple-Access System with Balanced Detection. IEEE Photonics Technol. Lett. 2004, 16, 2189–2191. [Google Scholar] [CrossRef]
- Gu, F.-R.; Wu, J. Construction of two-dimensional wavelength/time optical orthogonal codes using difference family. J. Lightwave Technol. 2005, 23, 3642–3652. [Google Scholar] [CrossRef]
- Lin, C.-H.; Wu, J.; Yang, C.-L. Noncoherent Spatial/Spectral Optical CDMA System with Two-Dimensional Perfect Difference Codes. J. Light Technol. 2005, 23, 3966–3980. [Google Scholar]
- Shurong, S.; Yin, H.; Wang, Z.; Xu, A. A new family of 2-D optical orthogonal codes and analysis of its performance in optical CDMA access networks. J. Lightwave Technol. 2006, 24, 1646–1653. [Google Scholar] [CrossRef]
- Morelle, M.; Goursaud, C.; Julien-Vergonjanne, A.; Aupetit-Berthelemot, C.; Cances, J.-P.; Dumas, J.-M.; Guignard, P. 2-Dimensional optical CDMA system performance with parallel interference cancellation. Microprocess. Microsyst. 2007, 31, 215–221. [Google Scholar] [CrossRef]
- Yang, C.-C.; Huang, J.-F.; Chiu, I.-M. Performance Analyses on Hybrid MQC/M-Sequence Coding Over Frequency/Spatial Optical CDMA System. IEEE Trans. Commun. 2007, 55, 40–43. [Google Scholar] [CrossRef]
- Tien, J.-H.; Yang, G.-C.; Chang, C.-Y.; Kwong, W.C. Design and Analysis of 2-D Codes with the Maximum Cross-Correlation Value of Two for Optical CDMA. J. Lightwave Technol. 2008, 26, 3632–3639. [Google Scholar] [CrossRef]
- Yeh, B.-C.; Lin, C.-H.; Yang, C.-L.; Wu, J. Noncoherent Spectral/Spatial Optical CDMA System Using 2-D Diluted Perfect Difference Codes. J. Lightwave Technol. 2009, 27, 2420–2432. [Google Scholar]
- Yin, H.; Ma, L.; Li, H.; Zhu, L. A new family of 2D wavelength/time codes with large cardinality for incoherent spectral amplitude coding OCDMA networks and analysis of its performance. Photonic Netw. Commun. 2010, 19, 204–211. [Google Scholar] [CrossRef]
- Morsy, M.A.; Alsayyari, A. BER Performance of OCDMA System Based on Optimized 2D PhC Passive Encoder. IET Commun. 2020, 14, 1268–1274. [Google Scholar] [CrossRef]
- Ismail, M.A.M.; Alsayyari, A.; Galal, O.H. Performance analysis of optical code division multiple access networks for multimedia applications using multilength weighted modified prime codes. Opt. Eng. 2019, 58, 035101. [Google Scholar] [CrossRef]
- Morsy, M.A.; Alsayyari, A.S. Multi-rate OCDMA system BER performance evaluations for different ML-code sequences. Opt. Quantum Electron. 2019, 51, 198. [Google Scholar] [CrossRef]
- Morsy, M.A.; Alsayyari, A.S. Performance analysis of incoherent PPM-OCDMA networks based on optimised modified prime code for multimedia applications. IET Commun. 2020, 14, 4014–4021. [Google Scholar] [CrossRef]
- Morsy, M.A.; Alsayyari, A.S. Performance analysis of coherent BPSK-OCDMA wireless communication system. Wirel. Netw. 2020, 26, 4491–4505. [Google Scholar] [CrossRef]
- Morsy, M.A.; Alsayyar, A.S. Performance analysis of OCDMA wireless communication system based on double length modified prime code for security improvement. IET Commun. 2020, 14, 1139–1146. [Google Scholar] [CrossRef]
- Morsy, M.A.; Alsayyari, A.S. Performance Control of Incoherent Synchronous PPM-OCDMA Networks. In Proceedings of the 2019 2nd IEEE Middle East and North Africa COMMunications Conference (MENACOMM), Manama, Bahrain, 19–21 November 2019; pp. 1–4. [Google Scholar]
- Morsy, M.A.; Hadeel, S.A.R.; Al-Obaidan, H.M. Performance of Passive OCDMA Networks for Different Encoder/Decoder Delay Lines. Int. J. Opt. Appl. 2013, 3, 19–26. [Google Scholar]
- Nebendahl, B.; Schmogrow, R.; Josten, A.; Koenig, S.; Freude, W.; Koos, C.; Meyer, J.; Dreschmann, M.; Huebner, M.; Hillerkuss, D.; et al. EVM as new quality metric for optical modulation analysis. In Proceedings of the 2013 Saudi International Electronics, Communications and Photonics Conference, Riyadh, Saudi Arabia, 27–30 April 2013; pp. 1–4. [Google Scholar]
- Schmogrow, R.; Nebendahl, B.; Winter, M.; Josten, A.; Hillerkuss, D.; Koenig, S.; Meyer, J.; Dreschmann, M.; Huebner, M.; Koos, C.; et al. Error Vector Magnitude as a Performance Measure for Advanced Modulation Formats. IEEE Photonics Technol. Lett. 2011, 24, 61–63. [Google Scholar] [CrossRef]
- Shafik, R.A.; Rahman, M.S.; Islam, A.H.M.R. On the Extended Relationships Among EVM, BER and SNR as Performance Metrics. In Proceedings of the 4th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 19–21 December 2006; pp. 408–411. [Google Scholar]







| Folded Code Sequences | Code Sequences | ||||||
|---|---|---|---|---|---|---|---|
| Folded Code Sequences | Code Sequences | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X62X02 | X02X62 | ||||||||||
| . | |||||||||||
| . | |||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morsy, M.A.; Aly, M.H. A New Hybrid Prime Code for OCDMA Network Multimedia Applications. Electronics 2021, 10, 2705. https://doi.org/10.3390/electronics10212705
Morsy MA, Aly MH. A New Hybrid Prime Code for OCDMA Network Multimedia Applications. Electronics. 2021; 10(21):2705. https://doi.org/10.3390/electronics10212705
Chicago/Turabian StyleMorsy, Morsy A., and Moustafa H. Aly. 2021. "A New Hybrid Prime Code for OCDMA Network Multimedia Applications" Electronics 10, no. 21: 2705. https://doi.org/10.3390/electronics10212705
APA StyleMorsy, M. A., & Aly, M. H. (2021). A New Hybrid Prime Code for OCDMA Network Multimedia Applications. Electronics, 10(21), 2705. https://doi.org/10.3390/electronics10212705







