Evolutionary Multiobjective Optimization with Endmember Priori Strategy for Large-Scale Hyperspectral Sparse Unmixing

Abstract

Mixed pixels inevitably appear in the hyperspectral image due to the low resolution of the sensor and the mixing of ground objects. Sparse unmixing, as an emerging method to solve the problem of mixed pixels, has received extensive attention in recent years due to its robustness and high efficiency. In theory, sparse unmixing is essentially a multiobjective optimization problem. The sparse endmember term and the reconstruction error term can be regarded as two objectives to optimize simultaneously, and a series of nondominated solutions can be obtained as the final solution. However, the large-scale spectral library poses a challenge due to the high-dimensional number of spectra, it is difficult to accurately extract a few active endmembers and estimate their corresponding abundance from hundreds of spectral features. In order to solve this problem, we propose an evolutionary multiobjective hyperspectral sparse unmixing algorithm with endmember priori strategy (EMSU-EP) to solve the large-scale sparse unmixing problem. The single endmember in the spectral library is used to reconstruct the hyperspectral image, respectively, and the corresponding score of each endmember can be obtained. Then the endmember scores are used as a prior knowledge to guide the generation of the initial population and the new offspring. Finally, a series of nondominated solutions are obtained by the nondominated sorting and the crowding distances calculation. Experiments on two benchmark large-scale simulated data to demonstrate the effectiveness of the proposed algorithm.

1. Introduction

Hyperspectral imagery, which contains a wealth of spectral information for the surface features in each pixel, has been widely used in various remote sensing applications, such as geological analysis, environmental monitoring and military reconnaissance. However, due to the low spatial resolution and the ground substances intimate mixtures, the mixed pixels inevitably appear in the hyperspectral images. To solve this problem, the spectral unmixing technique aims to extract the pure spectral signatures (also called endmembers) from hyperspectral images and estimate their corresponding proportions (also called abundances).

The spectral unmixing assumes that there is no multiple scattering between endmembers in the spectrum, each pixel is a linear combination of elements from the endmember set in the linear mixed model (LMM) [1]. Under this model, various methods such as geometry-based [2], nonnegative matrix factorization-based (NMF) [3,4,5] and statistical-based [6] have been conducted research in the hyperspectral spectral unmixing, which also obtained a very ideal unmixing effect. However, these methods suffer from poor performance when the assumption of pure pixels or the generation of virtual endmembers do not satisfy.

As an emerging spectral unmixing technology, Hyperspectral sparse unmixing aims to find the optimal subset of the true endmembers for reconstructing the mixed pixels based on the known spectral library in advance. Compared to the number of endmembers in the spectral library, the number of endmembers use for reconstructing is is relatively sparse. Mathematically speaking, it is a ${\mathit{l}}_0$ norm problem, which is highly non-convex and NP-hard [7]. The relaxation methods, such as the ${\mathit{l}}_1$ norm or the ${\mathit{l}}_{\mathit{p}}$ norm (0 < $\mathit{p}$ < 1), are some of the relatively effective solutions to deal with the ${\mathit{l}}_0$ norm problem. Bioucas-Dias et al. [8] solves the sparse unmixing problem by the alternating direction method of multipliers, but the SUnSAL [8] only focuses on the spectral information without taking the spatial structure information between different pixels into account. To take advantage of the relationship between pixels in the hyperspectral image, many strategies such as collaborative sparse regression framework [9] or spectral regularization terms [10,11] are applied in the sparse unmixing model to promote the spatial correlation.

However, these algorithms are very sensitive to parameter settings, which greatly affect the stability of unmixing algorithms. Recently, the intelligent optimization algorithms have been greatly developed. Połap et al. [12] proposed a red fox optimization algorithm by simulating the hunting behavior of fox. In [13], a polar bear optimization algorithm was proposed to simulate the hunting behavior of a polar bear into the stage of global search and the stage of local search. Khishe et al. [14] proposed a chimp optimization algorithm to further alleviate the two problems of slow convergence speed and trapping in local optima in solving high-dimensional problems. Nevertheless, in solving the NP hard problems, the multiobjective evolutionary algorithms (MOEAs) have attracted extensive attention because of the global search ability. Therefore, some excellent algorithms proposed in [15,16,17,18] have applied the multiobjective optimization to sparse unmixing. However, most of MOEA-based algorithms in sparse unmixing only focus on solving pixel by pixel efficiently without considering the spatial structure information because of the curse of dimensions. In addition, MOEA-based algorithms suffer from the problem of being time-consuming, resulting in inefficiency and impracticality. Compared with the large-scale spectral library, the number of endmembers used to reconstruct the hyperspectral image is actually sparse. Therefore, many existing MOEAs suffer from a large number of decision variables when dealing with the sparse multiobjective optimization problems, which consumes the expensive computing resources to search in a large decision space with an arbitrary initialization.

To alleviate the above problems, an evolutionary multiobjective hyperspectral sparse unmixing algorithm with endmember priori strategy (EMSU-EP) is proposed in this paper. In the proposed EMSU-EP, each decision variable is taken out separately for evaluation in the initialization, and their corresponding scores are recorded for the subsequent crossover and mutation. In the subsequent genetic operation, a new genetic operator is designed to ensure the sparsity of the offspring in a uniform interval. With the prior knowledge of the quality of each decision variable and the new genetic operators for binary variables, the proposed EMSU-EP can achieve the better convergence performance and diversity, and the result of unmixing has been greatly improved. The main contributions of the proposed EMSU-EP are summarized as follows.

(1) We propose a novel multiobjective optimization framework for sparse unmixing, which can guide the subsequent evolution of the algorithm according to the prior knowledge obtained from the spectrum library.

(2) A special initialization mechanism is designed, it is demonstrated that the proposed EMSU-EP can obtain the diverse and targeted population compare with the state-of-the-art MOEA-based sparse unmixing methods.

(3) The particular crossover and mutation operators are proposed to maintain the sparsity of the population, which can not only promote the convergence of the algorithm, but also improve the performance of sparse unmixing.

The rest of this paper is organized as follows. In Section 2, the related works are summarized. In Section 3, the framework of our proposed EMSU-EP algorithm is introduced in detail. The experimental results are presented and analyzed in Section 4. Finally, the work in this paper is concluded in Section 5.

2. Related Works

In this section, the related works on sparse unmixing and the multiobjective optimization are introduced.

2.1. Sparse Unmixing

As shown in Figure 1, sparse unmixing aims to find the optimal set of endmembers for modeling the mixed pixels from a large-scale and pre-known spectral library. Therefore, a mixed pixel ($\mathit{y}\in {\mathbb{R}}^{\mathit{L}\times 1}$) with L spectral bands can be formulated as

$$\begin{array}{c}\mathit{y}=\mathit{Ax}+\mathit{n}\hfill \end{array}$$

(1)

where $\mathit{A}\in {\mathbb{R}}^{\mathit{L}\times \mathit{D}}$ is the spectral library, $\mathit{x}\in {\mathbb{R}}^{\mathit{D}\times 1}$ represents the corresponding fractional abundance vector and $\mathit{n}\in {\mathbb{R}}^{\mathit{L}\times 1}$ is the noise term. In the absence of noise, the sparse unmixing method of the Formula (1) is mathematically expressed as

$$\begin{array}{c}\underset{\mathit{x}}{min}{∥\mathit{x}∥}_0\hfill \\ \mathit{s}.\mathit{t}.{∥\mathit{y}-\mathit{Ax}∥}_2^2\le \delta \hfill \end{array}$$

(2)

where $\delta \ge 0$ denotes the error tolerance, ${\parallel \mathit{x}\parallel }_0$ is the ${\mathit{l}}_0$ norms of $\mathit{x}$, which is highly non-convex and NP-hard. It was not well solved until Candes et al. [7] proved that ${\mathit{l}}_1$ norm can induce sparsity instead of ${\mathit{l}}_0$ norm under a certain restricted isometry property condition. In [8], the SUnSAL was proposed to solve the sparse unmixing problem of mixed pixels by establishing constrained sparse regression as

$$\begin{array}{c}\underset{\mathit{x}}{min}(1/2){∥\mathit{y}-\mathit{Ax}∥}_2^2+\lambda {∥\mathit{x}∥}_1+{\iota }_{\mathit{R}+}\left(\mathit{x}\right)+{\iota }_{\left\{1\right\}}\left({\mathbf{1}}^{\mathbf{T}}\mathit{x}\right)\hfill \end{array}$$

(3)

where ${∥\mathit{x}∥}_1$ denotes the ${\mathit{l}}_1$ norm of $\mathit{x}$, $\lambda$ is a regularization parameter that controls the relative weight of the error term and the sparse term, $\mathbf{1}$ denotes a column vector of 1’s, the ${\iota }_{\mathit{R}+}\left(\mathit{x}\right)$ and ${\iota }_{\left\{1\right\}}\left({\mathbf{1}}^{\mathbf{T}}\mathit{x}\right)$ represent the abundance non-negativity constraint (ANC) and the abundance sum-to-one constraint (ASC) [19], respectively.

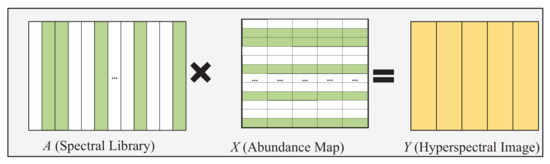
Figure 1. Illustration of the hyperspectral sparse unmixing problem, Y is the image to be unmixed, A is the large-scale spectral library, and X is the obtained abundance matrix. Only colored active endmembers participate in the reconstruction of endmembers.

However, the SUnSAL [8] only focuses on the spectral information without taking the spatial structure information between different pixels into account. In general, a hyperspectral image ($\mathit{Y}\in {\mathbb{R}}^{\mathit{L}\times \mathit{n}}$) with $\mathit{n}$ pixels structured in the matrix can be formulated as

$$\mathit{Y}=\mathit{AX}+\mathit{N}$$

(4)

where $\mathit{Y}=[{\mathit{y}}_1,{\mathit{y}}_2,\cdots ,{\mathit{y}}_{\mathit{n}}]$, ${\mathit{y}}_{\mathit{i}}$ is the $\mathit{i}$-th mixed pixel, $\mathit{X}\in {\mathbb{R}}^{\mathit{D}\times \mathit{n}}$ is the abundance matrix, and $\mathit{N}\in {\mathbb{R}}^{\mathit{L}\times \mathit{n}}$ is the corresponding error term. The formula (4) can be transformed into an optimization problem expressed as

$$\begin{array}{c}\underset{\mathit{X}}{min}{∥\mathit{X}∥}_0\hfill \\ \mathit{s}.\mathit{t}.{∥\mathit{Y}-\mathit{AX}∥}_F^2\le \delta \hfill \end{array}$$

(5)

where ${\parallel \mathit{X}\parallel }_0$ = $\left|\mathrm{supp}\right(\mathit{X}\left)\right|$, $\mathrm{supp}\left(\mathit{X}\right)=\{1\le \mathit{i}\le \mathit{D},{\mathbf{x}}_{\mathit{i}}\ne \mathbf{0}\}$, ${\mathit{x}}_{\mathit{i}}$ is $\mathit{i}$th row of $\mathit{X}$. To take advantage of the relationship between pixels in the hyperspectral image, CLSUnSAL [9] assumes that all pixels share the same active endmembers to reduce the influence of the spectral coherence between endmembers on the unmixing effect. The model is shown as follows

$$\begin{array}{c}\underset{\mathit{X}}{min}{∥\mathit{Y}-\mathit{AX}∥}_F^2+\lambda {∥\mathit{X}∥}_{2,1}+{\iota }_{\mathit{R}+}\left(\mathit{X}\right)\hfill \end{array}$$

(6)

where ${∥\mathbf{X}∥}_{2,1}={\sum }_{\mathit{k}=1}^{\mathit{m}}{∥{\mathbf{x}}^{\mathit{k}}∥}_2$ represents the $l_{2,1}$ norm, ${\iota }_{\mathit{R}+}\left(\mathit{X}\right)={\sum }_{\mathit{i}=1}^{\mathit{n}}{\iota }_{\mathit{R}+}\left({\mathbf{x}}_{\mathit{i}}\right)$ denotes the indicator function. Moreover, many spectral regularization terms, such as the total variation regularization term [10] and the non-local regularization terms [11], are integrated into the sparse unmixing model to promote the spatial correlation.

2.2. Multiobjective Optimization

The multiobjective evolutionary algorithms (MOEAs) have attracted extensive attention because of the global search ability in solving the sparse unmixing problems. In [15], Gong et al. proposed the multiobjective sparse unmixing model with a cooperative coevolutionary strategy. Jiang et al. [16] formulated the sparse unmixing problem into a two-phase multiobjective problem to estimate the endmembers and determine the abundances, respectively. In [17,18], the multiobjective evolutionary algorithm based on decomposition (MOEA/D) [20] has also been explored and applied in the sparse unmixing problem. For the multiobjective optimization problem, the mathematical form with a objectives and b decision variables can be described as

$$\begin{array}{c}minF\left(\mathit{x}\right)={(f_1\left(\mathit{x}\right),f_2\left(\mathit{x}\right),\cdots ,f_a\left(\mathit{x}\right))}^{\mathit{T}}\hfill \\ s.t.\mathit{x}={({\mathit{x}}_1,{\mathit{x}}_2,\cdots ,{\mathit{x}}_{\mathit{b}})}^{\mathit{T}}\in \mathsf{\Omega }\hfill \end{array}$$

(7)

where $\mathit{x}$ is the decision vector, F: $\mathsf{\Omega }\to {\mathbb{R}}^{\mathit{a}}$, $\mathsf{\Omega }$ is the decision space and ${\mathbb{R}}^{\mathit{a}}$ is the objective space.

In the majority of cases, there is no single solution capable of minimizing all the objectives at the same time. Instead, the best trade-off between the objectives can be defined as Pareto optimality. Therefore, in order to evaluate the pros and cons of multiple solutions, the nondominated fronts and crowding distances of the individual can be applied. If the individuals are dominated by the same number of individuals, these individuals belong to the same nondominated front. In addition, the crowding distance of an individual can be obtained by calculating the side length of the rectangle formed between two adjacent individuals that belong to the same nondominated front with the individual. Assuming that ${\mathit{p}}_1$ and ${\mathit{p}}_2$ are two individuals in the population, individual $p_2$ is preferred over $p_1$ (i.e., $p_2\succ p_1$) if any one of the following conditions holds [21], (1) ${\mathrm{NF}}_2<{\mathrm{NF}}_1$, (2) ${\mathrm{NF}}_2={\mathrm{NF}}_1$ and ${\mathrm{CD}}_2>{\mathrm{CD}}_1$, where ${\mathrm{NF}}_1$ and ${\mathrm{NF}}_2$ represent the nondominated fronts of individuals $p_1$ and $p_2$, respectively. ${\mathrm{CD}}_1$ and ${\mathrm{CD}}_2$ represent the crowding distances of individuals $p_1$ and $p_2$, respectively.

3. Proposed Method

For the sparse unmixing problem, there are two conflicting objectives to be optimized, namely the sparse endmember term and the reconstruction error term. Therefore, the multiobjective optimization problem for sparse unmixing is

$$\underset{\mathit{X}}{min}{(\parallel \mathit{X}\parallel }_0,{∥\mathit{Y}-\mathit{AX}∥}_F^2)$$

(8)

where the ${\parallel \mathit{X}\parallel }_0$ is the sparse term and the ${∥\mathit{Y}-\mathit{AX}∥}_F^2$ represents the reconstruction error. The Formula (8) can be solved with the multiobjective optimization to obtain the Pareto Front (PF) of a compromise between these two objectives. Then the knee point is selected as the final solution, which is the preferred solution on PF with the maximum marginal utility and can be obtained from the individual with the maximum angle with the two adjacent individuals. In addition, two constrains for the abundance are required by

$$\left\{\begin{array}{cc}\hfill & \mathrm{ANC}:\mathit{X}=[{\mathit{x}}_1,\cdots ,{\mathit{x}}_{\mathit{n}}]\ge \mathbf{0}\hfill \\ \hfill & \mathrm{ASC}:\forall {\mathit{x}}_{\mathit{i}}\in \mathit{X},{\mathbf{1}}^{\mathit{T}}{\mathit{x}}_{\mathit{i}}=1,\mathit{i}=1,\cdots ,\mathit{n}\hfill \end{array}\right.$$

(9)

The pseudocode of the proposed EMSU-EP is shown in Algorithm 1. First of all, in the initialization, the k-th endmember is extracted from the spectral library at a time to reconstruct the hyperspectral image ${\widehat{\mathit{Y}}}_{\mathit{k}}$ for obtaining the corresponding reconstruction error with the original image. This operation needs to run through all the endmembers in the spectral library. The reconstruction errors of all endmembers are sorted in ascending order, and the corresponding ${\mathit{Score}}_{\mathit{k}}$ represents the position order. Then the spectral library is encoded into a binary vector with dimension $\mathit{D}$, where “1” and “0” represent the selected and unselected endmembers, respectively. Then EMSU-EP randomly selects two elements from the D-dimensional decision variables each time, and uses the endmember score as the evaluation criterion to set one of to “1” with the binary tournament selection method, which is shown in Figure 2. In order to ensure the diversity of the initial population, the $\mathit{rand}\left(\right)$ operator is employed to uniformly distribute $\mathit{N}$ individuals in the sparse interval [0, D], respectively. Unlike the inefficiency of random initialization, the more likely real endmembers can be selected to form the initial population with the prior knowledge.

Algorithm 1 Pseudocode of EMSU-EP

Input: A (the spectral library), Y (the hyperspectral image), $\mathit{N}$ (population size), ${\mathit{t}}_{\mathit{max}}$ (maximum number of iterations). Output: ${\mathit{X}}^{*}$ (the estimated abundance map).  1: fork = 1 : D do  2:     Reconstruct ${\widehat{\mathit{Y}}}_{\mathit{k}}$ with the k-th endmember in A.  3: ${\mathit{ Score}}_{\mathit{k}}$←$\parallel \mathit{Y}-{\widehat{\mathit{Y}}}_{\mathit{k}}{\parallel }_{\mathit{F}}^2$  4: end for  5: Encode A as a binary vector;  6: % P ← Initialization(N)  7: fori = 1 : N do  8:    for j = 1 : rand()× D do  9:       [m, n] ← Randomly select two endmembers; 10:      if ${\mathit{Score}}_{\mathit{m}}$ < ${\mathit{Score}}_{\mathit{n}}$ then 11:         Set the m-th endmember to 1 in i-th individual; 12:      else 13:         Set the n-th endmember to 1 in i-th individual; 14:     end if 15:   end for 16: end for 17: t← 0; 18: whilet≤${\mathit{t}}_{\mathit{max}}$do 19:   C←Mutation(Crossover(P, N)); 20:   P∪C←Evaluation(P∪C, 2N); 21:   P←Selection(P∪C, N); 22:   t←t + 1; 23: end while

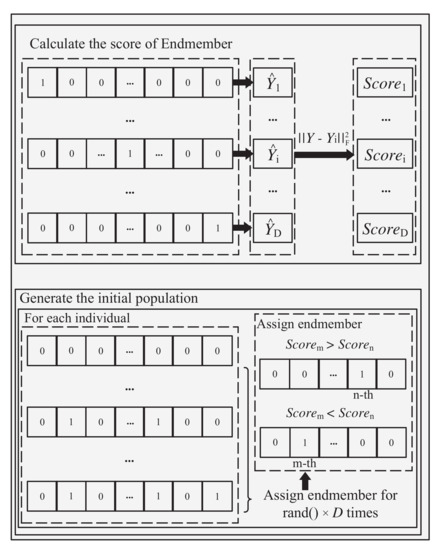
Figure 2. Obtaining the score of every endmember and generate the initial population.

With the prior knowledge of decision variables, those decision variables with higher scores should be given more attention in the subsequent genetic operations. Therefore, the genetic operators of crossover and mutation proposed in [22] are employed to generate the offspring, which are represented by Crossover() and Mutation(), respectively, in Algorithm 1. The left gray box and the the right gray box represent the Crossover() operator and the Mutation() operator, respectively, in Figure 3. Before evolution, two individuals ${\mathit{p}}_1$ and ${\mathit{p}}_2$ are randomly selected from population as the parents. There are two situations in the Crossover(). On the one hand, the original offspring $\mathit{c}$ inherits ${\mathit{p}}_1$, then two non-zero elements are randomly selected from the differential gene positions of ${\mathit{p}}_1$ and ${\mathit{p}}_2$, and one of the gene positions of $\mathit{c}$ is set to “0” based on endmember scores (the larger the better). On the other hand, two zero elements are randomly selected from the differential gene positions of ${\mathit{p}}_1$ and ${\mathit{p}}_2$, and one of the gene positions of $\mathit{c}$ is set to “1” based on endmember scores (the smaller the better). In the Mutation(), two non-zero elements are randomly selected from the offspring $\mathit{c}$, and one of the gene positions is set to “0” determined by the larger score. To the opposite, two zero elements are randomly selected from $\mathit{c}$, and set one of the gene positions is set to “1” determined by the smaller score. A zero or non-zero element in the binary vector is flipped with the same probability as shown in Figure 3. Compared with the single-point crossover (SPC) and bitwise mutation (BitM), the operators designed by the EMSU-EP select the element to be flipped according to the score of the decision variable to ensure the sparsity of the offspring.

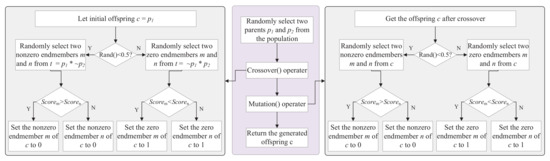
Figure 3. Illustration of the flow of crossover and mutation operators. The middle procedure represents the generation process of a offspring, the left procedure represents the crossover operation, and the right procedure represents the mutation operation.

During the evolution of the population, if too many endmembers are selected, some solutions are no longer sparse. To prevent this problem from happening, the sparsity limit $\mathit{d}$ is applied to the population evolution. When the number of selected endmembers in an individual exceeds the sparsity limit $\mathit{d}$, EMSU-EP will only retain the endmember whose endmember score sorting in the first $\mathit{d}$-th, and the rest will not be selected (i.e., set to 0).

Finally, all individuals of the parent and offspring are evaluated for nondominated sorting and crowding distance calculation [23], and the best $\mathit{N}$ individuals are selected to form the next generation population. After satisfying the end of the iteration, the knee point in the last generation population is returned [24]. The set of non-zero elements are extracted from this optimal binary vector, which also represents the corresponding endmember subset ${\mathit{A}}_{{\mathit{s}}^{*}}$ from the spectral library A. Therefore, the abundance map ${\mathit{X}}_{{\mathit{s}}^{*}}$ can be calculated according to the least square method, which is shown as follows

$${\mathit{X}}_{{\mathit{s}}^{*}}=arg\underset{{\mathit{X}}_{{\mathit{s}}^{*}}}{min}{∥\mathit{Y}-{\mathit{A}}_{{\mathit{s}}^{*}}{\mathit{X}}_{{\mathit{s}}^{*}}∥}_{\mathit{F}}.$$

(10)

According to the Formula (10), we can not only achieve dimensionality reduction of hyperspectral data, but also ensure the sparseness of unmixing solutions. After the calculation of Formula (10), the zero element is inserted into the non-zero real solution according to the original position to realize the restoration of the data dimension.

4. Experimental Results and Discussion

In this section, the effectiveness of EMSU-EP in solving large-scale sparse unmixing problems will be demonstrated. Two large-scale sparse unmixing benchmark datasets are used to validate the performance of the EMSU-EP. In order to reflect the efficiency of EMSU-EP, some advanced algorithms such as SUnSAL [8], CLSUnSAL [9], MOSU [15] and MTSR [21] will be compared with EMSU-EP.

In the experiment, the population size is set to 100, and the maximum generation Maxgen is set to 300, the population sparse limit interval $\mathit{d}$ is 50. Part of the experiment code refers to the PlatEMO platform (PlatEMO 2.8: https://github.com/BIMK/PlatEMO (accessed on 22 August 2021)) [25]. All experiments will be added with different degrees of Gaussian white noise (SNR = 20, 30 and 40 dB). All experimental results are obtained from the average of 100 independent repeated runs.

4.1. Dataset and Evaluation Indicators

4.1.1. Dataset

Data 1 is a 64 × 64 synthetic image containing 224 bands provided by Tang [26], its digital spectral library A1 is a sub-library of 498 spectral features selected from the USGS spectral library (http://speclab.cr.usgs.gov/spectral.lib06 (accessed on 22 August 2021)). These spectral signals are evenly distributed at 0.25–0.4 $\mathsf{\mu }$m. The true abundance map of all five endmembers of data 1 is shown in Figure 4. Data 2 is an image of 100 × 100 pixels and 224 bands per pixel, provided by Iordache et al. [10], its digital spectral library A2 is a sublibrary with 230 spectral signatures of the USGS spectral library. The true abundance map of all nine endmembers of data 2 is shown in Figure 5.

Figure 4. True abundance maps of five endmembers in data 1. (a) True abundance map of endmember 1. (b) True abundance map of endmember 2. (c) True abundance map of endmember 3. (d) True abundance map of endmember 4. (e) True abundance map of endmember 5.

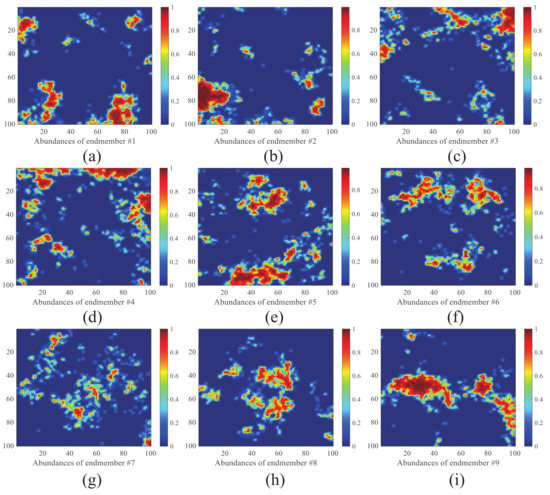
Figure 5. True abundance maps of five endmembers in data 2. (a) True abundance map of endmember 1. (b) True abundance map of endmember 2. (c) True abundance map of endmember 3. (d) True abundance map of endmember 4. (e) True abundance map of endmember 5. (f) True abundance map of endmember 6. (g) True abundance map of endmember 7. (h) True abundance map of endmember 8. (i) True abundance map of endmember 9.

To summarize, data 1 needs to accurately select five endmembers from 498 spectral signals and estimate the corresponding abundance, and data 2 needs to select nine endmembers from 230 spectral signals and estimate the corresponding abundance. Two datasets are sparse enough and difficult. Therefore, both data 1 and data 2 are large-scale sparse unmixing problems.

4.1.2. Evaluation Indicators

In order to compare the accuracy and the robustness of different sparse unmixing algorithms on large-scale hyperspectral sparse unmixing problem, two evaluation indicators are considered in the experiments.

(1) Signal-to-Reconstruction Error (SRE) can be expressed as:

$$\mathrm{SRE}\left(\mathrm{dB}\right)\equiv 10{log}_{10}\left(\frac{E\left[{∥\mathbf{X}∥}_F^2\right]}{E\left[{∥\mathbf{X}-\widehat{\mathbf{X}}∥}_F^2\right]}\right)$$

(11)

where $\mathbf{x}$ is the true fractional abundance matrix and $\widehat{\mathbf{x}}$ is the estimated fractional abundance matrix. Without loss of generality, the larger the SRE value is, the better the unmixing accuracy will be.

(2) Success Ratio (SR): If the relative error is smaller than a given threshold $\tau$, the corresponding run of this method is denoted as a successful run [27]. SR under the threshold $\tau$ is defined as:

$${\mathrm{SR}}_{\tau }\equiv \mathrm{P}\left(\frac{{∥\mathbf{X}-\widehat{\mathbf{X}}∥}_F^2}{{∥\mathbf{X}∥}_F^2}\le \tau \right)$$

(12)

The probability is the ratio of the successful runs on 100 random instances. If we set $\tau$ = 5 and arrive at ${\mathrm{SR}}_{\tau }$ = 1, this implies that the relative error of the reconstruction result is less than 5 with probability one.

The Hypervolume (HV) [28] indicator can be used to evaluate the quality of PF, which can reflect the convergence and diversity of the solutions. HV is calculated by utilizing a reference point who is 1% larger in every component than the corresponding nadir point. In this paper, we use it to evaluate the performance on large-scale sparse unmixing problem by crossover and mutation operations of EMSU-EP, traditional SPC and BitM.

4.2. Experiments on Synthetic Data

Figure 6 shows the PF of the 50-th generation population obtained by different methods on data 1 and data 2. Whether compared to the PF obtained by SPC and BitM with the initial population of EMSU-EP or the PF obtained by SPC and BitM with the random initial population, EMSU-EP obviously has better convergence and a clearer knee point area, which will be very helpful to choose the final solution later.

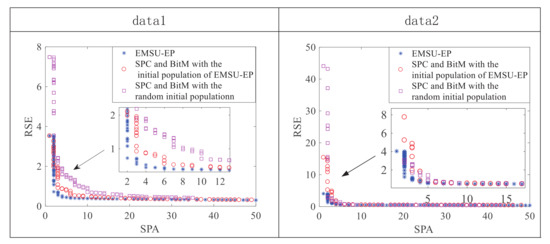
Figure 6. Illustration of the Pareto Front of the 50th generation on data 1 and data 2.

In order to reflect the advantages of EMSU-EP in each generation, Figure 7 uses the HV indicator to evaluate the PF of the first 100 generations. As shown by the red and purple curves in Figure 7, since the SPC and BitM operation has the same initial population of EMSU-EP, a higher HV value can be obtained from the first generation compared to the SPC and BitM with the random initial population, which corresponds to a better initial population quality and shows the guiding effect of endmember scores on the production of initial population. However, as shown by the blue and red curves in Figure 7, after the 20-th generation on data 1 and the 50-th generation on data 2, there are large static difference between the HV value of EMSU-EP and the HV value of the SPC and BitM operation, which shows the guiding effect of endmember scores on the evolution of the population.

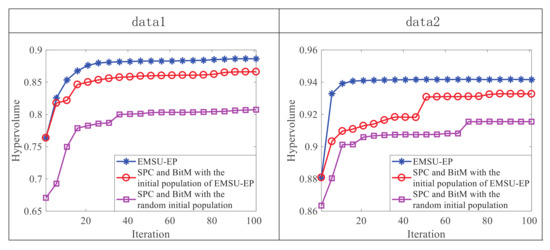
Figure 7. Illustration of the HV value of each evolution step on data 1 and data 2.

The estimated abundance maps of some endmembers obtained by different algorithms on data 1 and data 2 are shown in Figure 8 and Figure 9, respectively. These experimental results are all on the 30dB SNR. In Figure 8, the abundance maps obtained by SUnSAL, CLSUnSAL, MOSU, MTSR and EMSU-EP are exhibited from left to right, endmember 1, endmember 2 and endmember 5 of data 1 are arranged from top to bottom. In Figure 9, the abundance maps obtained by SUnSAL, CLSUnSAL, MOSU, MTSR, and EMSU-EP are exhibited from left to right, endmember 1, endmember 5 and endmember 8 of data 2 are arranged from top to bottom. As shown in Figure 8 and Figure 9, it is obvious to see that EMSU-EP always has the best performance compared to other algorithms, the unmixing maps color of EMSU-EP is the closest to the real image. Nevertheless, the performance of EMSU-EP in reducing noise is not stable enough, only the abundance map of endmember 1 has the least noise points in Figure 8, and only the abundance map of endmember 8 has the least noise points in Figure 9. Table 1 and Table 2 show the $\mathrm{SRE}\left(\mathrm{dB}\right)$ and ${\mathrm{SR}}_{\tau }$ of the unmixing results obtained by different algorithms on data1 and data 2, respectively. The two data sets are corrupted by different levels of correlated noise (SNR = 20, 30 and 40 dB). According to Table 1 and Table 2, EMSU-EP has the highest $\mathrm{SRE}\left(\mathrm{dB}\right)$ and ${\mathrm{SR}}_{\tau }$ compared to other algorithms at three SNR levels, which indicates that EMSU-EP has the best unmixing accuracy and robustness. The experimental results of two hyperspectral datasets demonstrate that the proposed EMSU-EP method can improve the performance of the sparse unmixing model by utilizing the endmember prior information.

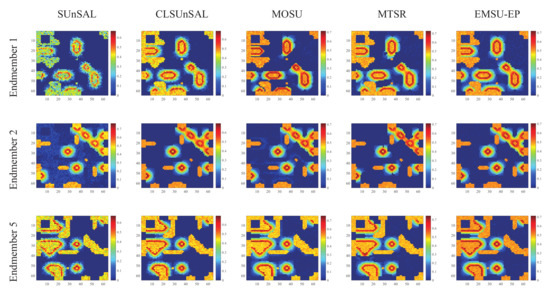
Figure 8. The estimated abundance maps of endmember 1, endmember 2 and endmember 5 for data 1 on 30 dB SNR obtained by different algorithms.

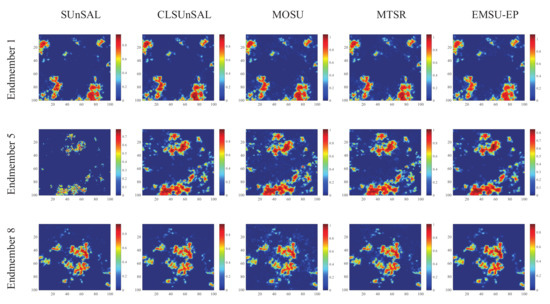
Figure 9. The estimated abundance maps of endmember 1, endmember 5 and endmember 8 for data 2 on 30 dB SNR obtained by different algorithms.

Table 1. Comparison of EMSU-EP with other algorithms on data 1. The value of $\tau$ is set to 0.15.

Method	$\mathbf{SRE} \left(\mathbf{dB}\right)$			${\mathbf{SR}}_{\mathit{\tau }}$
	20	30	40	20	30	40
SUnSAL	−4.3472	4.0704	13.8207	0.15	0.43	0.74
CLSUnSAL	8.2830	13.1349	14.3583	0.65	0.83	0.88
MOSU	7.3594	13.1434	14.4707	0.69	0.87	0.90
MTSR	10.7254	14.6143	17.6775	0.75	0.89	0.93
EMSU-EP	16.4900	19.9379	23.7559	0.78	0.91	0.95

Table 2. Comparison of EMSU-EP with other algorithms on data 2. The value of $\tau$ is set to 0.15.

Method	$\mathbf{SRE} \left(\mathbf{dB}\right)$			${\mathbf{SR}}_{\mathit{\tau }}$
	20	30	40	20	30	40
SUnSAL	−4.2856	4.0604	13.3420	0.23	0.35	0.54
CLSUnSAL	5.5443	11.5608	18.9487	0.62	0.75	0.91
MOSU	5.5623	11.1713	19.4105	0.66	0.78	0.94
MTSR	7.0496	13.7802	22.7329	0.70	0.80	1.00
EMSU-EP	7.2801	14.6303	23.1275	0.74	0.86	1.00

5. Conclusions

In this paper, we proposed an evolutionary multiobjective hyperspectral sparse unmixing algorithm with an endmember a priori strategy (EMSU-EP) to solve the large-scale hyperspectral sparse unmixing problem. EMSU-EP reconstructs the hyperspectral image by a single endmember to generate every endmember score first. Then the obtained endmember scores are used as prior knowledge to guide the generation of initial populations and new individuals. Experiments have demonstrated that the proposed EMSU-EP algorithm is effective in solving large-scale sparse unmixing problems, and EMSU-EP can maintain the superiority compared with the state-of-the-art sparse unmixing algorithms.

In the future, we will focus on reducing the noise on hyperspectral sparse unmixing problems and exploring the further improvement of EMSU-EP performance.