Abstract
This paper presents a new optimization algorithm based on the behavior of the fungi kingdom expansion (FKE) to optimize the radiation pattern of the array antenna. The immobile mass expansion of the fungi is mimicked in this work as a chaotic behavior with a sinusoidal map function, while the mobile mass expansion is realized by a linear function. In addition, the random germination of the spores is utilized for randomly distributing the variables that are far away from the best solution. The proposed FKE algorithm is applied to optimize the radiation pattern of the antenna array, and then its performance is compared with that of some well-known algorithms. The MATLAB simulation results verify the superiority of the proposed algorithm in solving 20-element antenna array problems such as sidelobe reduction with sidelobe ratio (SLR = 25.6 dB), flat-top pattern with SLR = 23.5 dB, rectangular pattern with SLR = 19 dB, and anti-jamming systems. The algorithm also results in a 100% success rate for all of the mentioned antenna array problems.
1. Introduction
In recent years, the increasing complexity and difficulty of real applications have led to more efficient metaheuristic algorithms. Most of these algorithms use random variables and can estimate the best solutions for different fields of optimization problems [1]. Metaheuristic algorithms outperform traditional algorithms due to their gradient-free techniques and avoidance of dropping in local optima [2]. During the solving process of any optimization problem, metaheuristic algorithms depend on two techniques namely intensification and diversification [3]. Intensification searches for the best solution within the local search space while diversification explores the search space globally to avoid dropping in local optima. The outstanding performance of an algorithm demands an appropriate balance between these two techniques. All collective solutions-based algorithms employ these features but with various operators and strategies [1]. Metaheuristic collective solutions-based algorithms can be grouped based on various inspiration fields into seven categories: biology, physics, chemistry, mathematics, social/human, music, and sport/games.
Biology-based algorithms are categorized into two dominant groups: evolutionary algorithms and bio-based/swarm intelligence techniques. Evolutionary algorithms are simulated Darwin’s theory of evolution. A genetic algorithm (GA) was the first evolutionary algorithm proposed by John Holland [4]. On the other hand, the second group of biology-based algorithms includes bio/swarm intelligence-based algorithms that can be sub-categorized into seven classes based on their behavior of
- Wild animals like grey wolf optimizer [5], camel algorithm [6], and wild horse optimizer [7].
- Aquatic animals such as whale optimization algorithm [1] and salp swarm search [8].
- Insects like ant colony optimization [9,10] and moth search algorithm [11].
- Birds such as particle swarm optimization (PSO) [12] which has widely been used for antenna applications in recent years [13,14], bat algorithm [15], and African vultures optimization algorithm [16].
- Plant such as plants tree growth optimization algorithm [17] and smart flower optimization algorithm [3].
- Viruses as virus colony search [18] and coronavirus herd immunity optimizer [19].
- Human body parts such as heart optimization algorithm [20] and kidney algorithm [21].
The second group of metaheuristic algorithms is the physics-based algorithms which simulate the physics rules in nature like Archimedes optimization algorithm [22] and atomic orbital search [23]. The third group that relies on chemistry in their optimization procedure such as artificial chemical reaction optimization [24] and gases Brownian motion optimization [25]. Math-based algorithms are the fourth category of metaheuristic algorithms that mimic the mathematical rules. The most common math algorithms are the sine cosine algorithm [26] and the arithmetic optimization algorithm [2]. Social/human algorithms are the fifth type of metaheuristic algorithms which include the student psychology optimization algorithm [27] and harmony search [28] which is a music-based algorithm. The last category is sports and games algorithms like football optimization algorithm [29] and billiards optimization algorithm [30].
Basically, the majority of high-gain antennas suffer from undesired sidelobe levels, and hence several approaches have been proposed to manipulate these kind of issues such as using all-metal wideband metasurface [31] and using non-uniform metallic lattice [32]. Moreover, the side lobes of the antenna radiation pattern can also be improved by manipulating the primary antenna phase [33] and placing a 3D superstructure in the nearfield [34].
In this paper, the Fungi Kingdom Expansion (FKE) behavior is utilized for optimizing the radiation pattern of the antenna array. The immobile and mobile mass expansions are emulated by a chaotic sinusoidal map function and linear deterministic function, respectively. The parameters that are far away from the best solution are randomly spread out to explore other more suitable locations. The proposed FKE algorithm is simulated using MATLAB to solve some of the array antenna beamforming problems like sidelobe reduction with SLR = 25.6 dB, flat-top pattern with SLR = 23.5 dB, rectangular pattern with SLR = 19 dB, and anti-jamming systems. After comparing the performance of the proposed algorithm with some other prominent algorithms, the results show the FKE algorithm has an almost flawless optimization performance in solving the antenna array problems.
2. Fungi Kingdom Expansion Behavior
The filamentous fungi shown in Figure 1 have a special form called mycelium [35]. Before extending their biomass, the fungi spread filament structures called (hyphae whose singular is hyphen) which begin the growth of the fungi kingdom in a form starting with the germination of spores. The expansion of the fungal colony is based on the availability of warmth and moisture within the surrounding area. The fungi extend their hyphae chaotically in different directions but within a small area to check the directions at which the amount of the moisture and warmth are suitable [35]. Subsequently, the biomass flows through tubes inside the hyphae toward the terminals of the hyphae that are oriented toward suitable conditions [35]. In concise, the materials that contribute to the fungi expansion behavior can be categorized into two types:
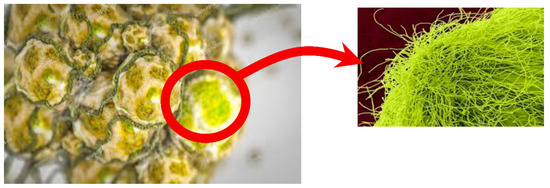
Figure 1.
Filamentous fungi.
- (a)
- Immobile biomass expansion: which represents the materials that are used to build the hyphae and the tubes inside them.
- (b)
- Mobile biomass expansion: this part represents the material flowing through the tubes of the hyphae to provide nutrition to the terminal of the hyphae.
Therefore, the aforementioned behavior can be translated into an optimization algorithm that searches for the best solution to a certain problem. It is worth mentioning that the behavior of the Fungi in [35] is mimicked as a routing algorithm. In this work, the fungi expansion behavior is exploited to form an optimization algorithm that searches for a certain optimum solution that is not related to the routing problems at all.
3. Implementation of the Fungi Kingdom Expansion (FKE) Algorithm
Consider that represents the position of the i-th fungus where , and represents the population size of the fungi kingdom. The initial population distribution can be determined by randomly () spreading spores within the maximum allowed distance () and the minimum allowed distance () as given below:
where represents the iteration number which is equal to zero at the initial step.
Based on what has been mentioned in the previous section, the authors noticed that the fungi kingdom is expanded in three different modes:
- Mode 1:Chaotic Expansion Mode
This mode represents the generation of the hyphae for the immobile biomass expansion which is equivalent to the local searching mechanism. Since the fungi spread their hyphae in different directions but within a pre-determined area, this behavior is likely to be chaotic rather than random. Let the parameter () denote the hyphen number, then the proposed Equation that describes the immobile mass expansion is given as:
where represents the immobile expansion factor and represents the chaotic function which is selected to be the sine map function in this work:
It is worth mentioning that the value of the should not be too small because that results in too short hyphae, and the optimization process will take a very large number of iterations. In contrast, the value of should not be too large in order not to lose the local searching property of this mode of expansion.
After evaluating the positions of the terminals of the hyphae, they should be applied to a certain fitness function to pick up the best local position among them () for the present iteration (), and then the mobile mass expansion will be applied.
- Mode 2:Deterministic Expansion Mode
This mode is corresponding to the mobile biomass expansion in which the nutrition of the biomass is passed through the tube of the best hyphen. The Equation that is proposed to find the new location of each fungus in the population at the present iteration depending on the past iteration () and the present best local position () is given by:
where represents the surrounding condition factor that is directly proportional to the moisture and the temperature. This factor can be evaluated from the following formula:
where denotes the Moisture-Temperature effect at the present iteration, and are the maximum and minimum Moisture-Temperature effect, respectively. can be evaluated by randomly () selecting a value between and such that:
After applying (4), (5), and (6) to the entire fungi population, the position of each of them is assessed by the fitness function to determine the global best position of the present iteration ().
- Mode 3:Random Dispersion
The random dispersion in the fungi kingdom happens when some of the population get far away from the nutrition sources. In this case, the fungi randomly germinate spores in random directions within the nutrition region bounded by the distance exactly like that in Equation (1). The resulted population is also subjected to the fitness function to determine whether the global best location of the present iteration is more preferable to the previous best location or not. Thence, the new fungi population is generated, and the next iteration () is started. This optimization sequence is repeated until the required condition is met, or the number of iterations is terminated. The pseudo-code of the proposed Fungi Kingdom Expansion (FKE) algorithm is given in Algorithm 1.
| Algorithm 1 Fungi kingdom Expansion |
| 1: Set the moisture-temperature range and the location range. |
| 2: Set the number of hyphae |
| 3: Set the fungi kingdom size and the dimension. |
| 4: Set the random dispersion number (DIS). |
| 5: Initialize the location of each fungus from Equation (1). |
| 6: Subject the locations to a certain fitness function. |
| 7: Determine the current best location. |
| 8: Apply Equation (3) for the entire population and entire iterations. |
| 9: While (iter < itermax) |
| 10: % The immobile mass expansion |
| 11: For i = 1: fungi kingdom size |
| 12: For j = 1: number of hyphae |
| 13: Apply Equation (2) with the aid of Equation (3) |
| 14: End j |
| 15: Subject the hyphae to a fitness function then pick the best hyphen only. |
| 16: % The mobile mass expansion |
| 17: Compute (MT) from Equation (6) |
| 18: Compute (cond) from Equation (5) |
| 19: Apply Equation (4) |
| 20: End i |
| 21: Subject the new locations to the fitness function |
| 22: If the new best location is better than the older one |
| 23: The new best is the global best |
| 24: End If |
| 25: Randomly spread the worst (DIS) locations |
| 26: Subject the new population to the fitness function to determine the global best. |
| 27: End While |
4. Engineering Applications: Antenna Array Beamforming
The proposed FKE algorithm is implemented using MATLAB to optimize the operation of the antenna array. Based on the no free lunch theorem [36], there is no optimization technique that can perfectly operate in all problems of optimization. However, the authors found that the FKE algorithm is quite flawless in solving the antenna array beamforming process. The structure of the M-element antenna array is illustrated in Figure 2a. The array factor of the entire array is given by:
where represents the weights vector that described the magnitude and the phase of the current that excites each element, the superscript H denotes the Hermitian transpose, and represents the steering vector of the antenna at any azimuth angle ():
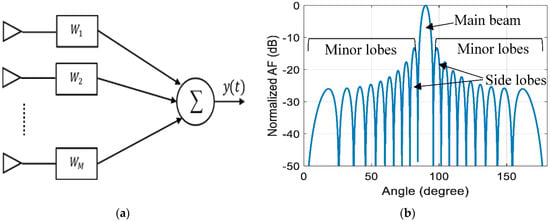
Figure 2.
Antenna array (a) structure and (b) the array factor in dB.
The symbol denotes the distance between every two adjacent elements in terms of the wavelength (), and represents the propagation phase constant:
In fact, the array factor is exactly equal to the antenna radiation pattern if the antenna elements are omnidirectional [37]. Figure 2b illustrates the general form of the array factor of an arbitrary antenna array. It is clear that the array factor consists of the main beam (major lobe) and minor lobes. The two minor lobes adjacent to the main beam are called the side lobes, and they are often with the highest level compared to the other minor lobes. To set the main beam toward the excitation phase angle between the excitation current of each antenna element should be equal to . In other words, the weights vector () has real values since the phase of this vector is set to zero in this work.
It should be noted that the optimization process is applied under the following conditions:
- Array size is 20-element.
- Fungi population size is 50.
- and .
- Immobile expansion factor .
- Number of hyphae .
- Fungi dispersion = 5.
- Number of runs = 30.
It is important to note that the immobile mass expansion requires to apply the fitness function on each hyphen, so the actual number of steps for the entire optimization is given by:
Consequently, to make a fair comparison with the other algorithms, the number of steps applied for the other algorithms will be times the number of steps of the FKE algorithm.
The antenna array can be manipulated in two ways:
- Linear Optimization: by optimizing the magnitude of the weight vector.
- Nonlinear optimization: by optimization the inter-element spacing d.
4.1. Side Lobe Reduction
This section is about optimizing the sidelobe ratio (SLR) of the antenna array which is given by:
It is well-known that decreasing the width of the main beam results in a very good concentration of electromagnetic energy toward the target, but it also results in a higher sidelobe level. It is found that the uniform distribution (equal excitation amplitudes and equal element spacing) provides the narrowest beam compared to the other distributions but with the highest side lobes [38]. The optimization problem in this subsection is concluded by: providing a beam width as narrow as that of the uniform distribution but with SLR as high as possible.
4.1.1. Side Lobe Reduction by Optimizing the Excitation Magnitude
This sub-section is about optimizing the to be larger than 22 dB under the constraint of narrow main beamwidth via optimizing the magnitude () of the excitation current (as given in Equation (7)) of the antenna element while keeping the inter-element spacing equal to . As mentioned earlier, the width of the main beam (null-to-null beam width) is chosen to be equal to that of the uniform distribution which is equal to 14°. Therefore, the fitness function is based on the following condition:
Table 1 demonstrates a comparison between the success rate of the proposed FKE algorithm with that of some other well-known optimization algorithms. The success rate is given by:

Table 1.
The success rate (SR) of the proposed FKE algorithm, PSO, and GA for the sidelobe reduction using the magnitude of the excitation current (No. of runs = 30).
It is clear that the SR of the proposed algorithm is perfect for this kind of problem. Table 2 gives the best excitation magnitude that results in with null-to-null beam width equal to 14°. Figure 3 illustrates a comparison between the normalized array factor (in dB) resulting from the FKE algorithm and that of the uniform distribution. The sidelobe reduction can clearly be seen from this figure for the same number of antenna elements.

Table 2.
The best normalized value of the magnitude of the excitation current of FKE.
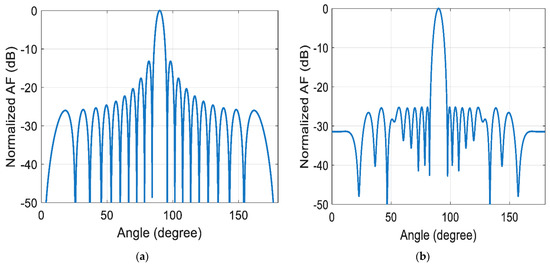
Figure 3.
The normalized array factor for 2- element array antenna (a) using uniform distribution and (b) using FKE optimization.
4.1.2. Side Lobe Reduction by Optimizing the Enter Element Spacing
Based on Equation (7), the scenario of this optimization problem is concluded by exciting the antenna elements with an equal amount of current magnitude while optimizing the inter-element spacing ( with respect to ) in order to obtain a large SLR with a narrow beam. The range of the element-spacing is chosen to be . The fitness function is exactly the same as that given in (12). The success rate of the FKE algorithm compared to some other prominent algorithms is given in Table 3, whereas the inter-element spacing corresponding to the best SLR is shown in Table 4. The success rate of the proposed algorithm for is also superior to that of the other algorithms in this type of problem. The normalized array factor corresponding to the best element spacing is shown in Figure 4 which also shows a noticeably reduced sidelobe level.

Table 3.
The success rate (SR) of the proposed FKE algorithm, PSO, and GA for the sidelobe reduction using the inter-element spacing (No. of runs = 30).

Table 4.
The best normalized value of inter-element spacing with respect to the wavelength (λ) using FKE.
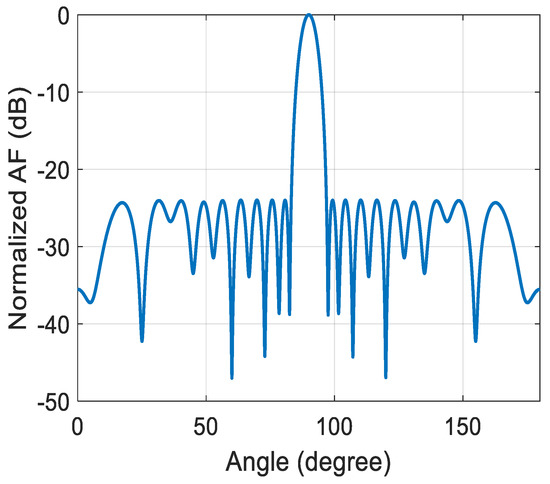
Figure 4.
The normalized array factor for 20 element array antenna by optimizing the inter-element spacing of the array antenna using FKE algorithm.
4.2. Flat-Top Pattern
This sub-section is about obtaining a wide beam with a flat-top pattern to transmit an equal amount of radiation to the intended area with the constraint of a low sidelobe level. In fact, this optimization problem is too complicated, so it is required two steps of optimization. The first step includes providing a flat top regardless of the sidelobe level by optimizing the excitation magnitude only. Thence, the optimization of the sidelobe levels starts by modifying the inter-element spacing under the constraint of the obtained flat-top pattern.
4.2.1. Step 1: Flat-Top Pattern Regardless the SLR
This pattern is obtained by optimizing the magnitude of the excitation () with . The constraint is to obtain a ripple value less than 0.5 dB within the required azimuth angle range. Therefore, the fitness function that describes this problem is given by:
where represents the maximum value of the array factor in dB which is equal to for the normalized array factor. In this work, the azimuth angle range is set to be as and . Table 5 shows the success rate of the FKE algorithm compared to some other algorithms, and the proposed algorithm surpasses the others by its 100% success rate. The weights vector that is corresponding to the best solution that the algorithm provides is listed in Table 6. The resulted normalized array factor of the optimized antenna is exhibited in Figure 5. The flat-top pattern is clearly obvious from this figure within the intended azimuth angle range, while the side lobe is quite high.

Table 5.
The success rate (SR) of the proposed FKE algorithm, PSO, and GA for the flat-top pattern. (No. of runs = 30).

Table 6.
The best normalized value of the amplitude of the excitation current and element spacing with respect to λ using FKE for flat-top pattern.
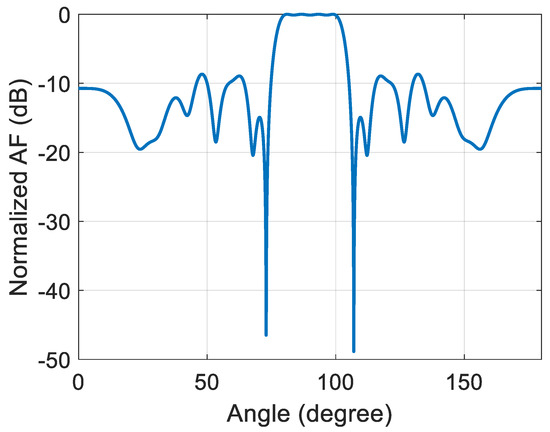
Figure 5.
The normalized flat-top array factor for 20 element array antenna by modifying the excitation amplitude of the array antenna using FKE algorithm.
4.2.2. Step 2: Flat-Top Pattern with Reduced Side Lobes
After optimizing the flatness of the main beam, SLR larger than 20 dB is achieved by modifying the inter-element spacing while keeping the excitation magnitude as given in the previous step. The fitness function consists of two parts. The first part is exactly the same as the one given in (12) but with a beam width equal to , whereas the second part is the same as the fitness condition of (14) to keep the flatness of the main beam. The success rate of the FKE algorithm is found to be 100%, and it is superior to the other algorithms as given in Table 5. On the other hand, Table 6 lists the inter-element spacing with respect to the wavelength that results in the best solution for the proposed antenna. The obtained normalized flat-top array factor with reduced side lobes is illustrated in Figure 6.
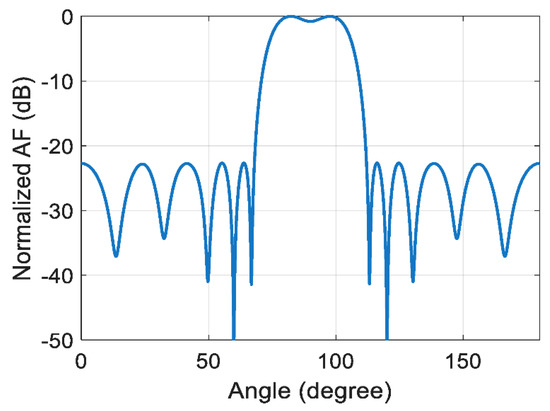
Figure 6.
The normalized array factor for 20 element array antenna by modifying the inter-element spacing of the array antenna using FKE.
4.3. Triangular Beam Pattern
This section is about obtaining a wide beam with a triangular pattern to focus the transmitted power of the radiation toward the intended area with the constraint of low sidelobe level. Therefore, it also requires two steps.
4.3.1. Step 1: Triangular Beam Regardless the Side Lobe Level
The magnitude of the excitation of the antenna elements () is optimized in this problem to obtain a triangular edge in the main beam of the radiation pattern (with ). The problem is to provide a pattern with almost a straight line with a positive slope in the range [], and another straight line with a negative slope along with the range []. Luckily, since the excitation weights are real, the pattern of the array factor is symmetric. Therefore, the optimization process deals with the angular range [], and the symmetry of the pattern has the custody of generating the other straight line within the range []. As a result, the fitness function corresponding to generating the triangular shape pattern is given by:
The success rate of the FKE algorithm versus some other well-known algorithms is demonstrated in Table 7, and the weights vector that results in the best triangular shape is given in Table 8. In this problem, FKE algorithm results in a perfect success rate equal to 100%. Figure 7 illustrates the normalized array factor with a triangular shape regardless of the value of the sidelobe level.

Table 7.
The success rate (SR) of the proposed FKE algorithm, PSO, and GA for the triangular pattern. (No. of runs = 30).

Table 8.
The best normalized value of the amplitude of the excitation current and element spacing with respect to λ using FKE for triangular pattern.
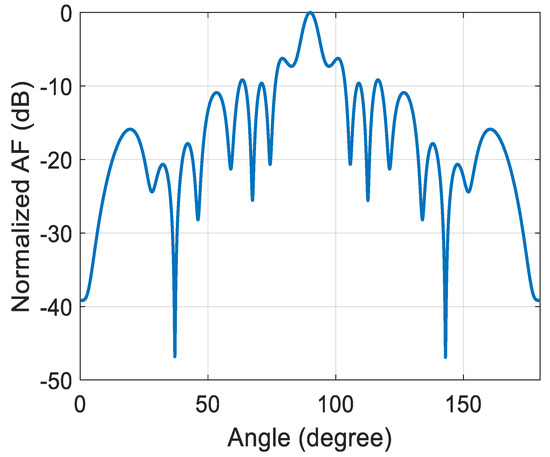
Figure 7.
The normalized triangular-shaped array factor for 20 element array antenna by modifying the excitation amplitude of the array antenna using FKE.
4.3.2. Step 2: Triangular Pattern with Reduced Side Lobes
The side lobe of the triangular pattern can also be reduced by optimizing the inter-element spacing between the antenna elements while keeping the excitation magnitude as that given in Table 8. The fitness function of this problem is also with two parts. The first part ensures the reduction of the sidelobe using (12), while the second part is a condition that maintains the triangular shape of the main beam as given in (14). The success rate (for SLR < 18 dB) of the FKE algorithm given in Table 7 is found to be 100%, and it clearly surpasses the other algorithms. On the other hand, the list of the inter-element spacing with respect to the wavelength that results in the best solution for the proposed antenna is demonstrated in Table 8. The obtained normalized triangular-shaped array factor with reduced side lobes is exhibited in Figure 8.
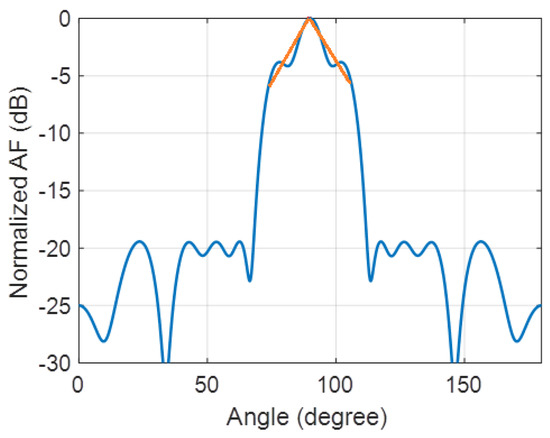
Figure 8.
The normalized triangular array factor for 20 element array antenna by modifying the inter-element spacing of the array antenna using FKE algorithm.
4.4. Anti-Jamming System
Anti-jamming smart antennas are substantial in military applications especially in those vulnerable to intentional jamming that may be transmitted by the enemies. Figure 9 reveals the parameters of M-element anti-jamming antenna system with its operation concept. The desired transmitted signal is in line of sight (LOS) with the antenna array of this system. The jamming signals are transmitted from different directions to interfere with the desired signal or to send fake information to the receiver. As shown in Figure 9, the anti-jamming antenna system should adjust its main beam in the direction of the desired signal and orient radiation nulls toward the directions of the jamming signals. The conventional beam-forming algorithms can orient its main beam toward the desired direction, but unfortunately, they can only attenuate the jamming signals especially with highly correlated jamming signals [37]. Since the jamming signals sometimes have power values higher than that of the desired signal itself, the attenuation is inefficient in these kinds of problems. In fact, FKE algorithm is independent of the correlation between signals, so it can perfectly reject the jamming signals by positioning radiation nulls toward them regardless of their amount of transmitted power. The output signal () of the anti-jamming antenna array is given by [37]:
where
where K represents the number of the received signals, the power value of each signal, and is the steering vector of each signal which is given by:
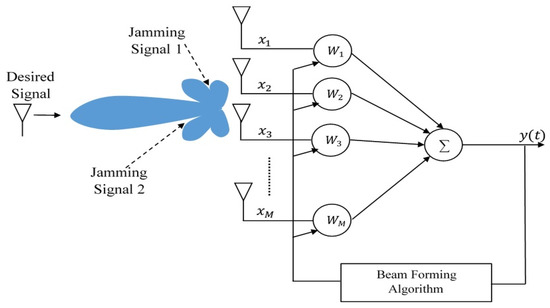
Figure 9.
Smart antenna system with M-antenna elements [39].
The problem that is wanted to be solved in this work is that there is a desired signal with signal power equal to at with the presence of eight interfering signals. The power values of the eight jamming signals are as follows: , and their angle of arrivals are as follows: , respectively. The magnitude of the excitation vector () is the parameter to be optimized with . The fitness function that is suitable for this kind of problem is given by:
Table 9 reveals the perfect success rate of FKE and all the other algorithms in solving this problem, and the optimum magnitude of excitation is given in Table 10. The resulted antenna-normalized array factor is shown in Figure 10 at which the main beam is forwarded toward the desired signal and all the jamming signals are eliminated by locating radiation nulls in their directions.

Table 9.
The success rate (SR) of the proposed FKE algorithm, PSO, and GA for the anti-jamming smart antenna system (No. of runs = 30).

Table 10.
The best normalized value of the magnitude of the excitation current using FKE algorithm for anti-jamming optimization.
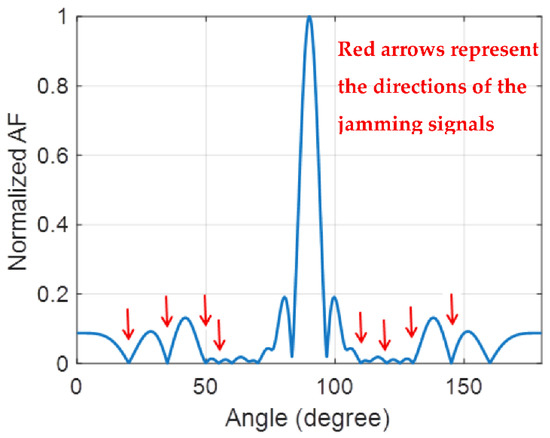
Figure 10.
The normalized array factor for 20-element anti-jamming antenna by optimizing the excitation amplitude of the array antenna using FKE algorithm.
5. Results Discussion
This section includes a comparison between the performance of the FKE algorithm and those of the PSO and GA in terms of the average CPU time, memory size, and success rate. Actually, the CPU time and the memory size were calculated for all problems discussed in the previous section, and then the resulted numbers were averaged to give a concise and clear comparison scenario. The algorithms were executed using a computer with the following specifications: Processor (Intel (R) Core(TM) i7), RAM 16 GB. Table 11 lists the CPU time average, the average memory size, and the average success rate of the FKE algorithm, PSO, and GA. As mentioned in Section 4, the immobile mass results in extending the number of hyphae, and this makes the total number of iteration of the FKE multiplied by the number of hyphae as given in Equation (10). For this reason, the memory size of FKE is larger than that of the PSO and GA. However, the average CPU time is almost the same for the three algorithms because the number of steps of the FKE algorithm should be equal to that of the PSO and GA divided by the number of hyphae (as discussed in Section 4). Nevertheless, the precision of the proposed FKE algorithm is highlighted by its perfect average success rate in solving the aforementioned antenna array problems where the average SR of the proposed algorithm is equal to 100%.

Table 11.
The average CPU time, average memory size, and the average SR of FKE algorithm compared to that of the PSO and GA.
Generally, antenna array problems are single-objective problems. Therefore, as a future work, the effectiveness of the FKE algorithm will be studied for multi-objective optimizations problems since this require completely different applications and different sets of results.
6. Conclusions
A new optimization algorithm based on the Fungi Kingdom Expansion (FKE) behavior has successfully been implemented for antenna array beamforming problems. The chaotic immobile mass expansion, deterministic mobile mass expansion, and the random dispersion of the fungi are utilized for optimizing the magnitude of the excitation and/or the inter-element spacing to attain the required shape of the antenna array factor. The algorithm is applied on a 20-element antenna array to solve the problem of the side lobe reduction, flat-top pattern, triangular pattern, and anti-jamming system. The performance of the proposed algorithm is statistically compared with some other prominent optimization algorithms, and the proposed antenna gives a 100% success rate for all of the aforementioned problems.
Author Contributions
Conceptualization, F.M.A., D.S. and Y.I.A.A.-Y.; methodology, F.M.A.; investigation, F.M.A., Y.I.A.A.-Y., D.S., R.S.A., C.H.S. and R.A.A.-A.; resources, F.M.A., D.S. and Y.I.A.A.-Y.; writing—original draft preparation, F.M.A., Y.I.A.A.-Y., D.S. and R.S.A.; writing—review and editing, F.M.A., Y.I.A.A.-Y., D.S., R.S.A., C.H.S. and R.A.A.-A.; visualization, F.M.A., Y.I.A.A.-Y., D.S., R.S.A., C.H.S. and R.A.A.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Sattar, D.; Salim, R. A smart metaheuristic algorithm for solving engineering problems. Eng. Comput. 2021, 37, 2389–2417. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Ali, R.S.; Alnahwi, F.M.; Abdullah, A.S.J.A.J.o.E.; Engineering, E. A modified camel travelling behaviour algorithm for engineering applications. Aust. J. Electr. Electron. Eng. 2019, 16, 176–186. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T.J.I.C.I.M. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Lalbakhsh, P.; Zaeri, B.; Lalbakhsh, A. An Improved Model of Ant Colony Optimization Using a Novel Pheromone Update Strategy. IEICE Trans. Inf. Syst. 2013, 96, 2309–2318. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.-G.J.M.C. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2018, 10, 151–164. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S. Design of an artificial magnetic conductor surface using an evolutionary algorithm. In Proceedings of the 2017 International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 11–15 September 2017; pp. 885–887. [Google Scholar]
- Lalbakhsh, A.; Esselle, K.P. Directivity improvement of a Fabry-Perot cavity antenna by enhancing near field characteristic. In Proceedings of the 2016 17th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM), Montreal, QC, Canada, 10–13 July 2016; pp. 1–2. [Google Scholar]
- Yang, X.S.; Hossein Gandomi, A. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef] [Green Version]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Akyol, S.; Alatas, B. Plant intelligence based metaheuristic optimization algorithms. Artif. Intell. Rev. 2017, 47, 417–462. [Google Scholar] [CrossRef]
- Li, M.D.; Zhao, H.; Weng, X.W.; Han, T. A novel nature-inspired algorithm for optimization: Virus colony search. Adv. Eng. Softw. 2016, 92, 65–88. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Alyasseri, Z.A.A.; Awadallah, M.A.; Abu Doush, I. Coronavirus herd immunity optimizer (CHIO). Neural Comput. Appl. 2021, 33, 5011–5042. [Google Scholar] [CrossRef] [PubMed]
- Hatamlou, A. Heart: A novel optimization algorithm for cluster analysis. Prog. Artif. Intell. 2014, 2, 167–173. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Alvankarian, J.; Abdullah, S. Kidney-inspired algorithm for optimization problems. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 358–369. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
- Azizi, M. Atomic orbital search: A novel metaheuristic algorithm. Appl. Math. Model. 2021, 93, 657–683. [Google Scholar] [CrossRef]
- Alatas, B. ACROA: Artificial Chemical Reaction Optimization Algorithm for global optimization. Expert Syst. Appl. 2011, 38, 13170–13180. [Google Scholar] [CrossRef]
- Abdechiri, M.; Meybodi, M.R.; Bahrami, H. Gases Brownian Motion Optimization: An Algorithm for Optimization (GBMO). Appl. Soft Comput. 2013, 13, 2932–2946. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Das, B.; Mukherjee, V.; Das, D. Student psychology based optimization algorithm: A new population based optimization algorithm for solving optimization problems. Adv. Eng. Softw. 2020, 146, 102804. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V.J.S. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Fadakar, E.; Ebrahimi, M. A new metaheuristic football game inspired algorithm. In Proceedings of the 2016 1st Conference on Swarm Intelligence and Evolutionary Computation (CSIEC), Bam, Iran, 9–11 March 2016; pp. 6–11. [Google Scholar]
- Kaveh, A.; Khanzadi, M.; Rastegar Moghaddam, M. Billiards-inspired optimization algorithm; a new meta-heuristic method. Structures 2020, 27, 1722–1739. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Hayat, T.; Esselle, K.P.; Mandal, K. All-metal wideband metasurface for near-field transformation of medium-to-high gain electromagnetic sources. Sci. Rep. 2021, 11, 9421. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S.L. Low-Cost Nonuniform Metallic Lattice for Rectifying Aperture Near-Field of Electromagnetic Bandgap Resonator Antennas. IEEE Trans. Antennas Propag. 2020, 68, 3328–3335. [Google Scholar] [CrossRef]
- Afzal, M.U.; Esselle, K.P.; Lalbakhsh, A. A Methodology to Design a Low-Profile Composite-Dielectric Phase-Correcting Structure. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1223–1227. [Google Scholar] [CrossRef]
- Hayat, T.; Afzal, M.U.; Lalbakhsh, A.; Esselle, K.P. Additively Manufactured Perforated Superstrate to Improve Directive Radiation Characteristics of Electromagnetic Source. IEEE Access 2019, 7, 153445–153452. [Google Scholar] [CrossRef]
- Bento, C.R.d.C.; Wille, E.C.G. Bio-inspired routing algorithm for MANETs based on fungi networks. Ad Hoc Networks 2020, 107, 102248. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Godara, L.C. Smart Antennas; CRC press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Balanis, C.A. Antenna Theory and Design; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Singh, J.; Pal, A. A Smart Antenna Beamforming Using LMS Adaptive Filter Algorithm. Semant. Scholar. 2014, 1, 1–3. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).