Analysis of the Dynamic Thermal Barrier in Building Envelopes
Abstract
1. Introduction
2. Current Status of Technical Solutions and Overview of Research Work in the Field of Active Thermal Protection
2.1. Inspirational Technical Solution of Our Research
2.2. Scientific and Professional Work in the Field of ATP
2.3. Scientific Works in the Field of ATP Computer Simulations
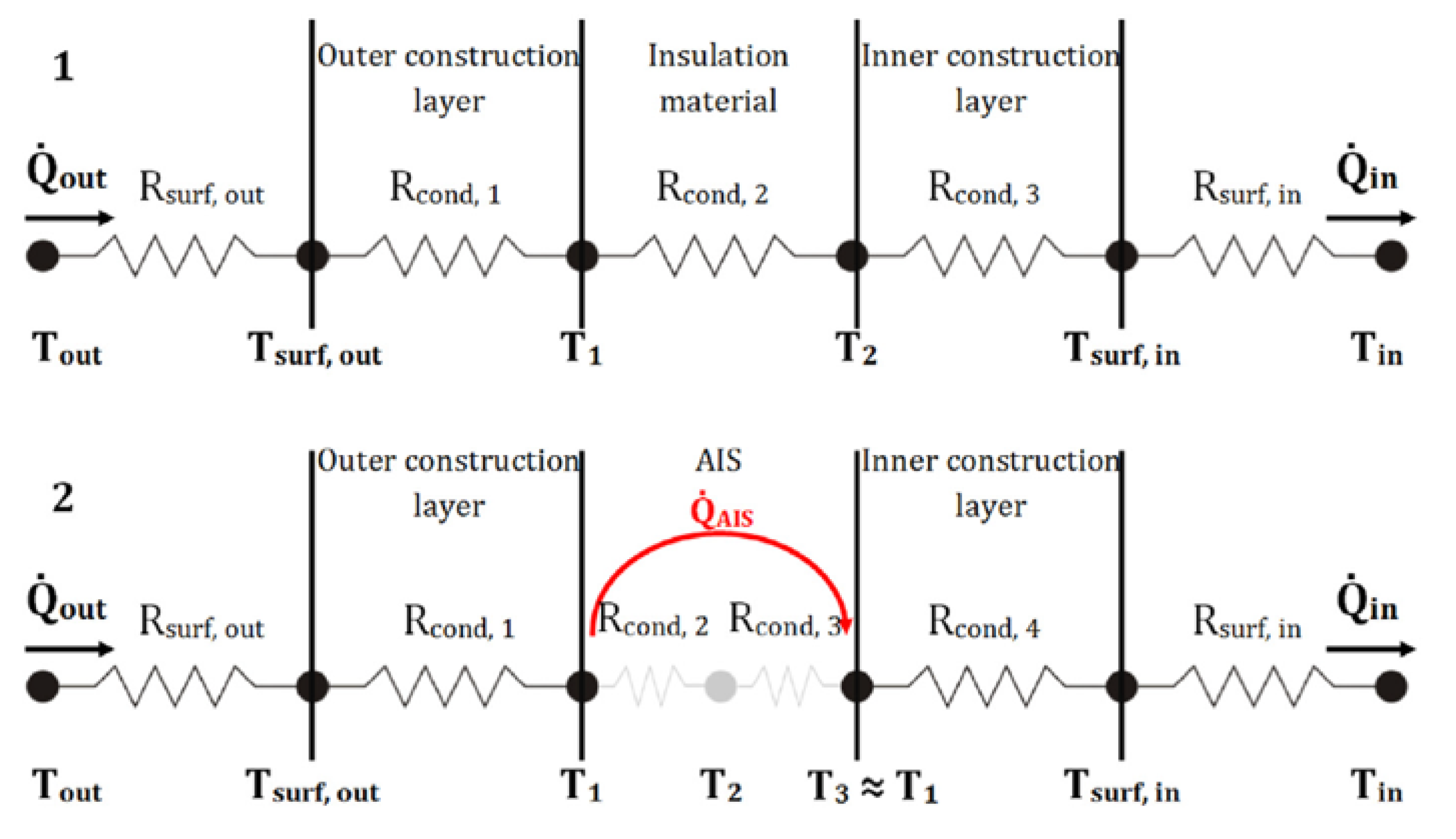
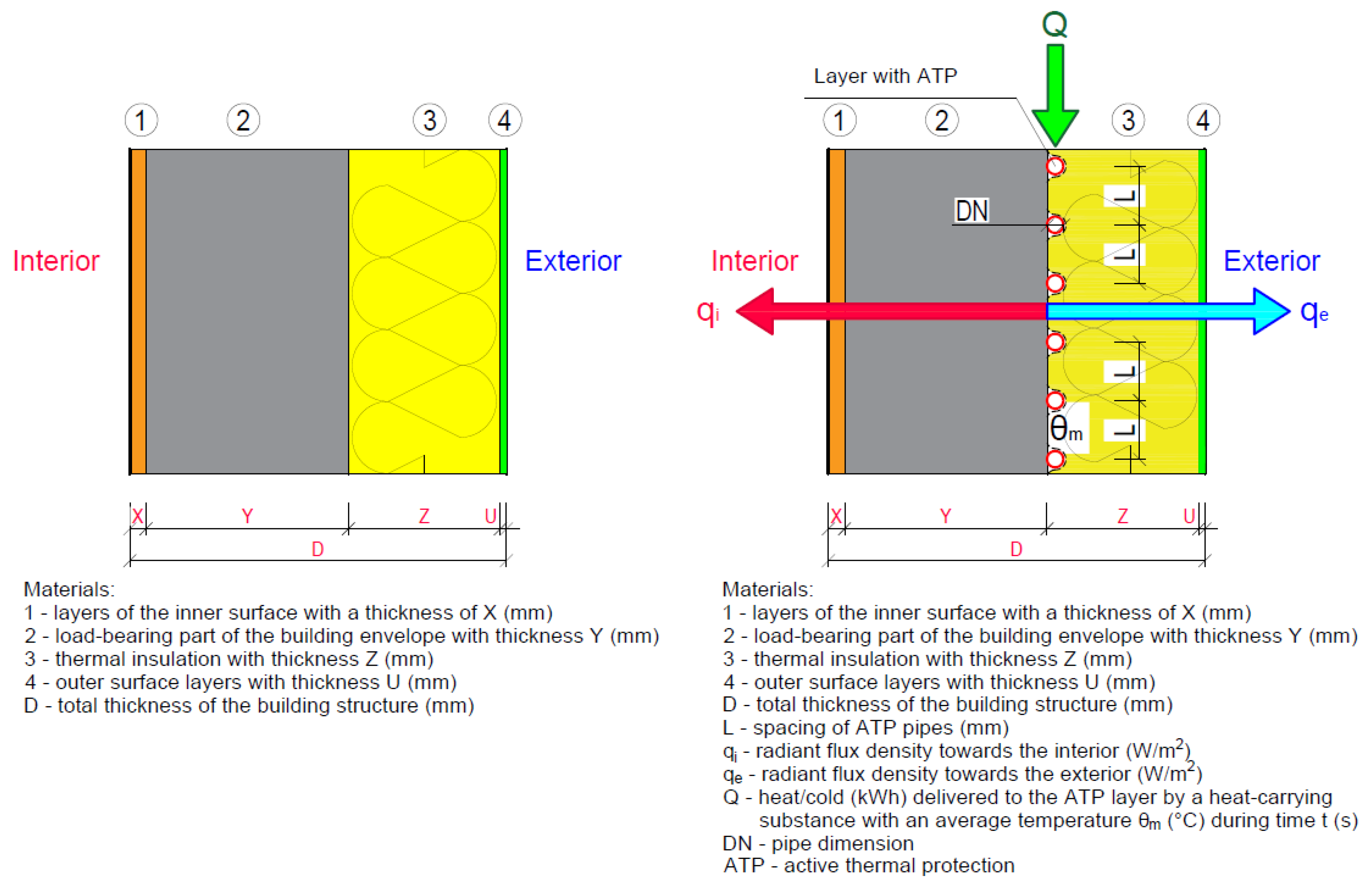
3. Methodology
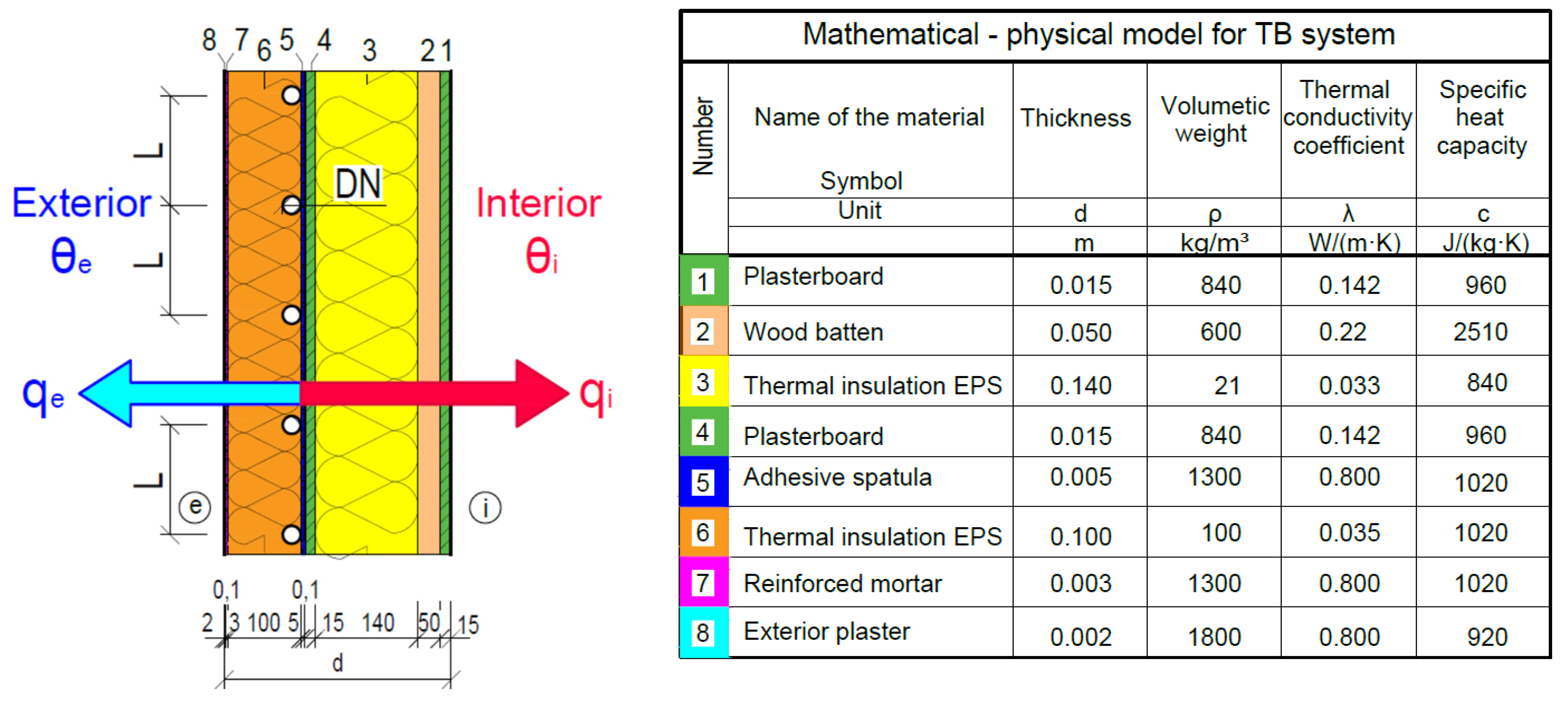
3.1. Calculation Procedure for Thermal Resistance R and Heat Transfer Coefficient U according to EN 73 0540
3.2. Calculation Procedure for Wall Heating according to EN 1264-(1–5)
- ■
- Heating pipe spacing;
- ■
- The thickness su and the thermal conductivity λE of the wall layer in front of the heating tubes towards the interior;
- ■
- The thermal resistance of the surface covering Rλ,B of the wall;
- ■
- The outer diameter of the heating tubes D = da, possibly with coating D = dM, and the thermal conductivity of the heating tubes λR or coating λM;
- ■
- The contact between the tubes and the heat pipe elements or spreading layer is characterized by the coefficient aK.
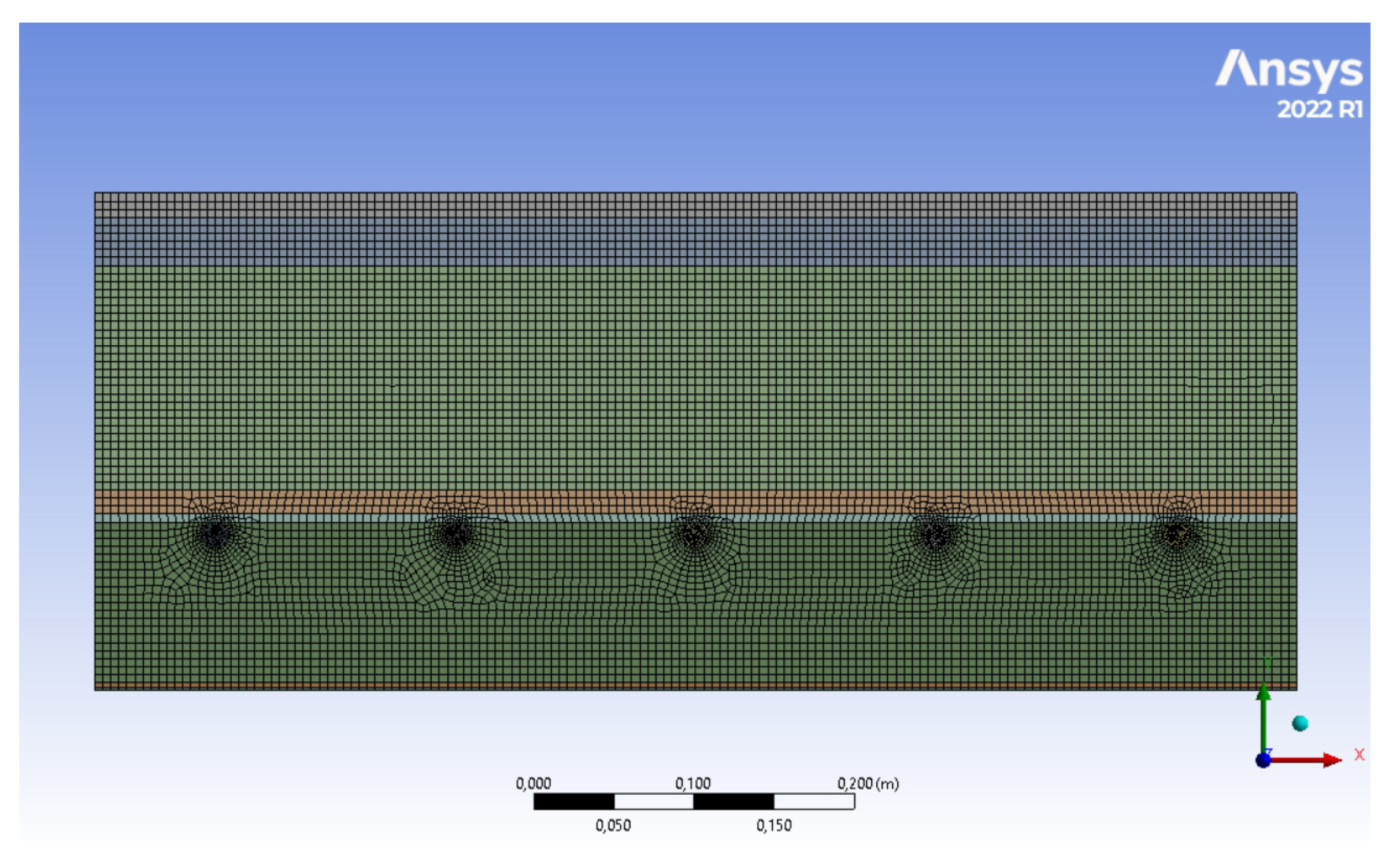
3.3. Computer Simulation Procedure—ANSYS
4. Results
- The results of a parametric study of four fragments of building envelopes;
- The results of the computer simulation of the temperature progression in the ATP layer for a fragment of the building envelope of a prefabricated timber building.
4.1. Parametric Study of Fragments of Building Envelope Structures
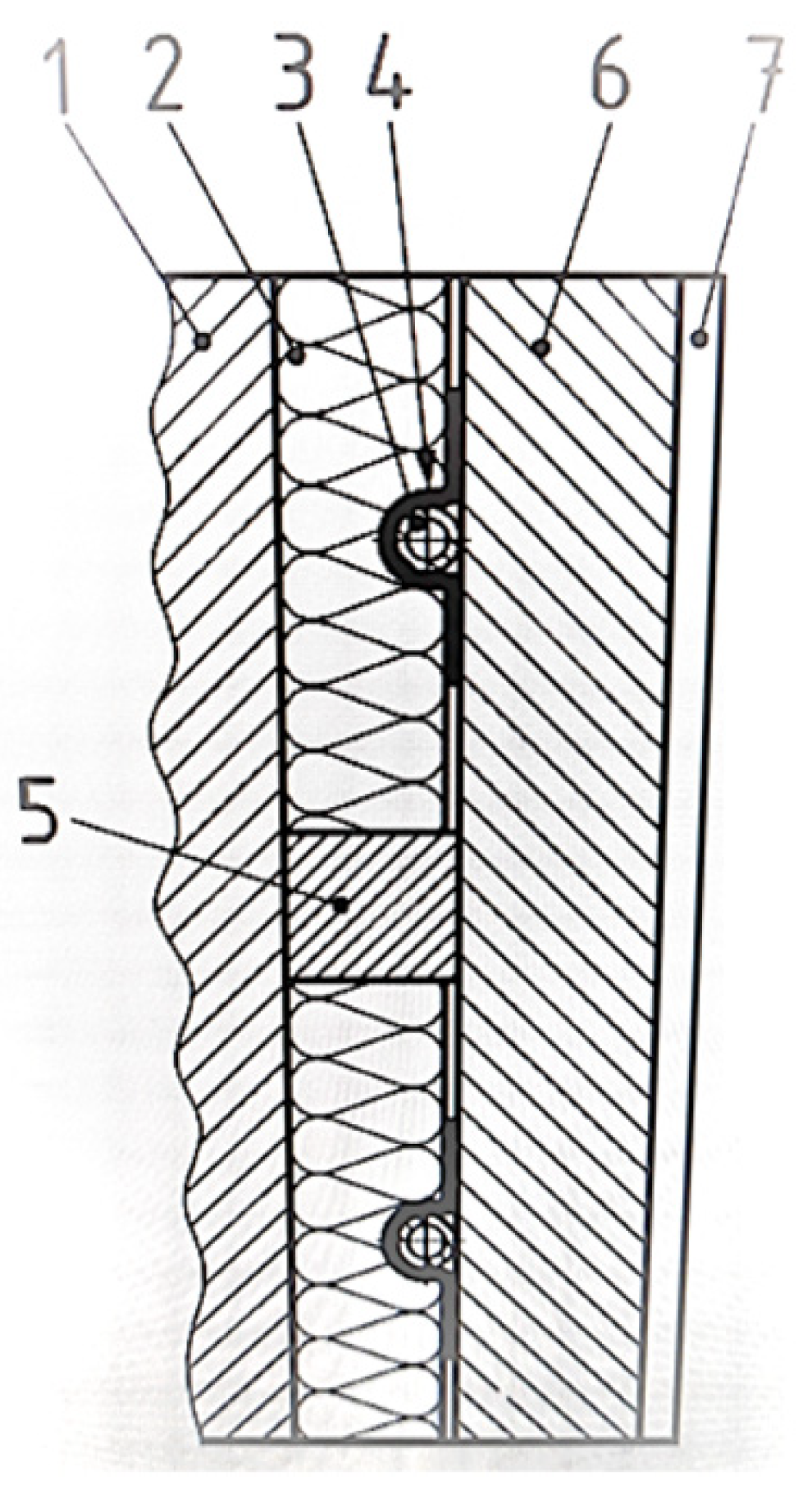
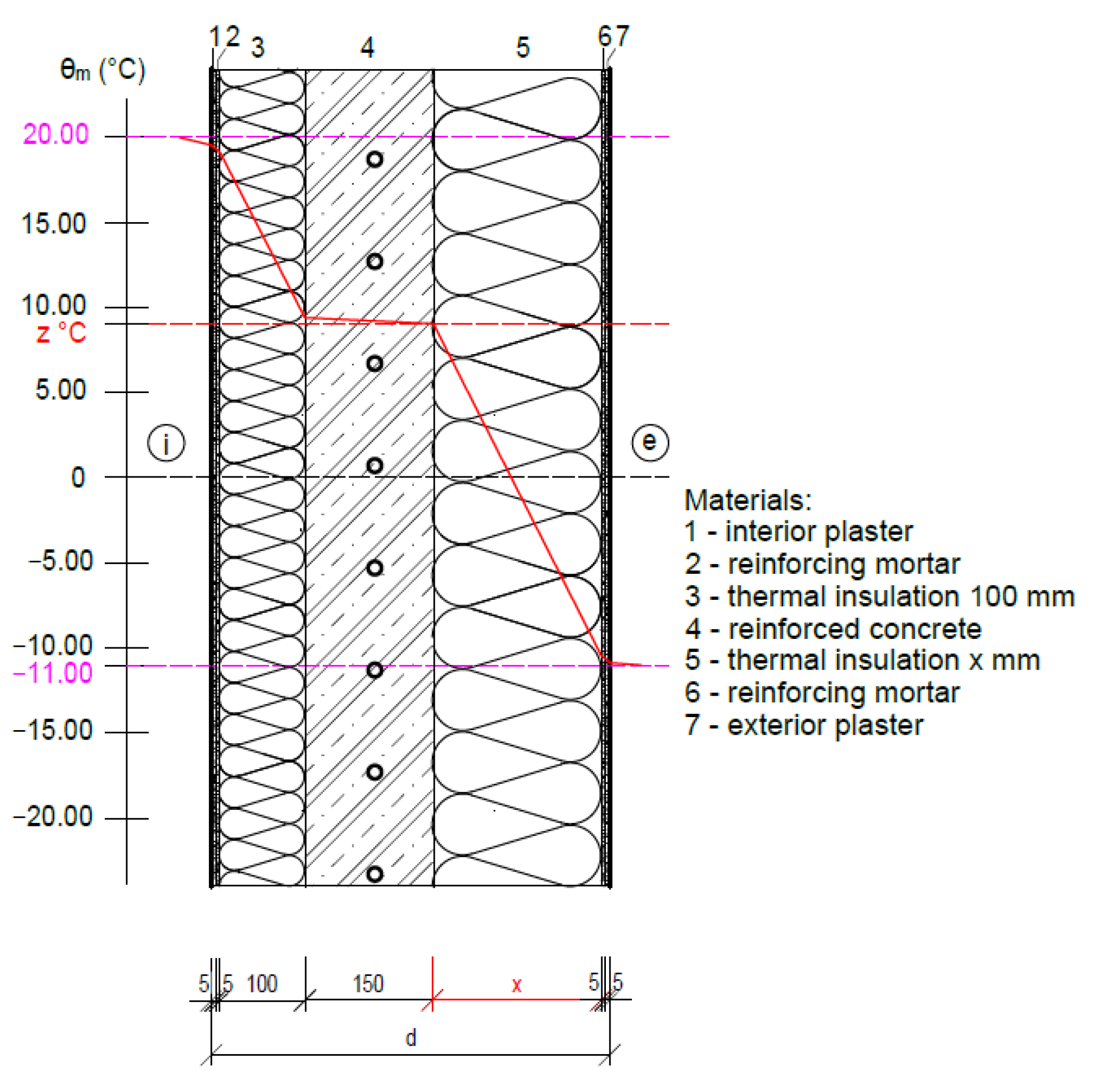
- Fragment 1—construction of the ISOMAX system perimeter wall (thermal insulation–reinforced concrete–thermal insulation);
- Fragment 2—reinforced concrete wall with thermal insulation on the exterior side;
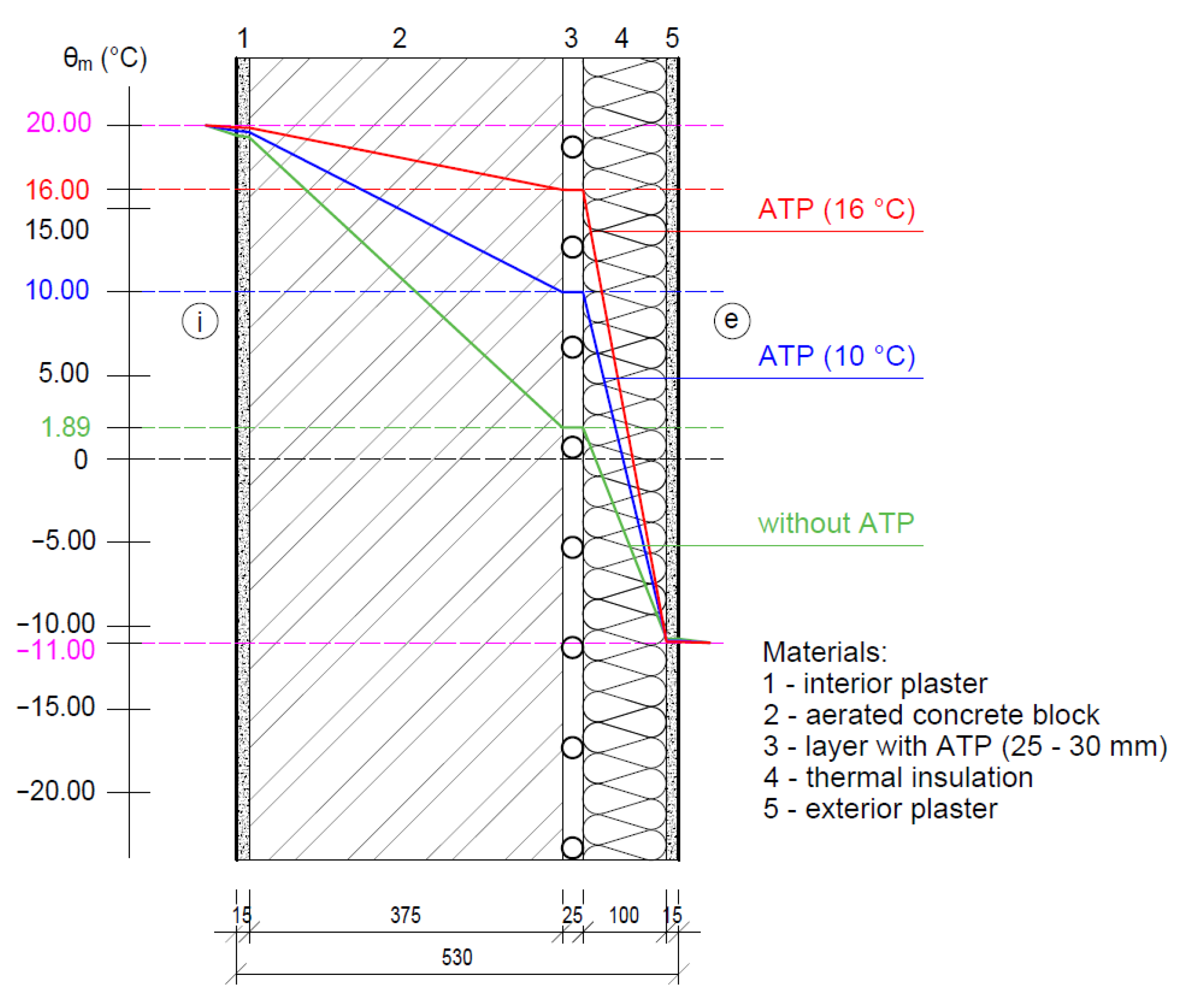
- Fragment 3—a wall made of aerated concrete blocks with thermal insulation on the exterior side;
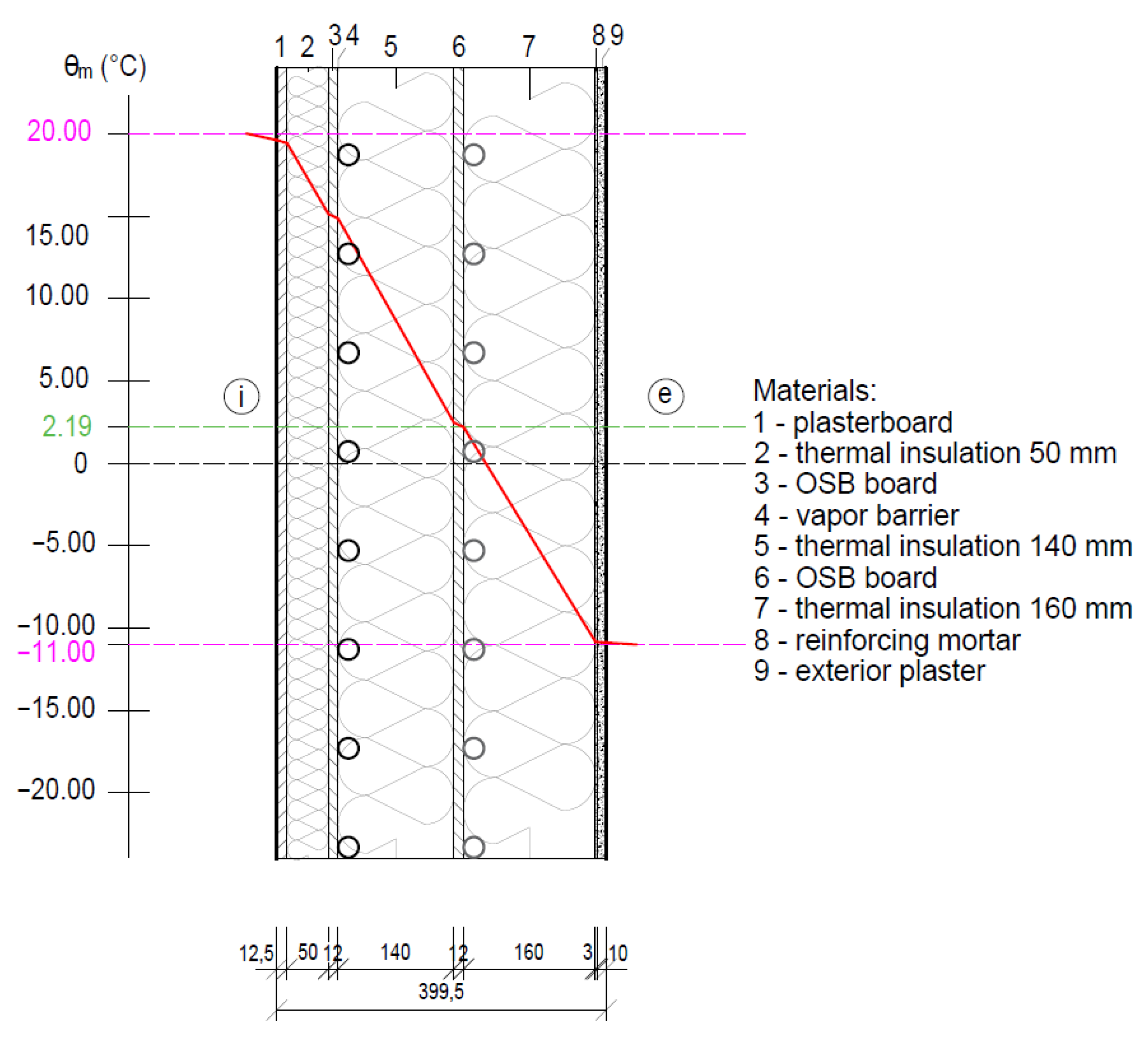
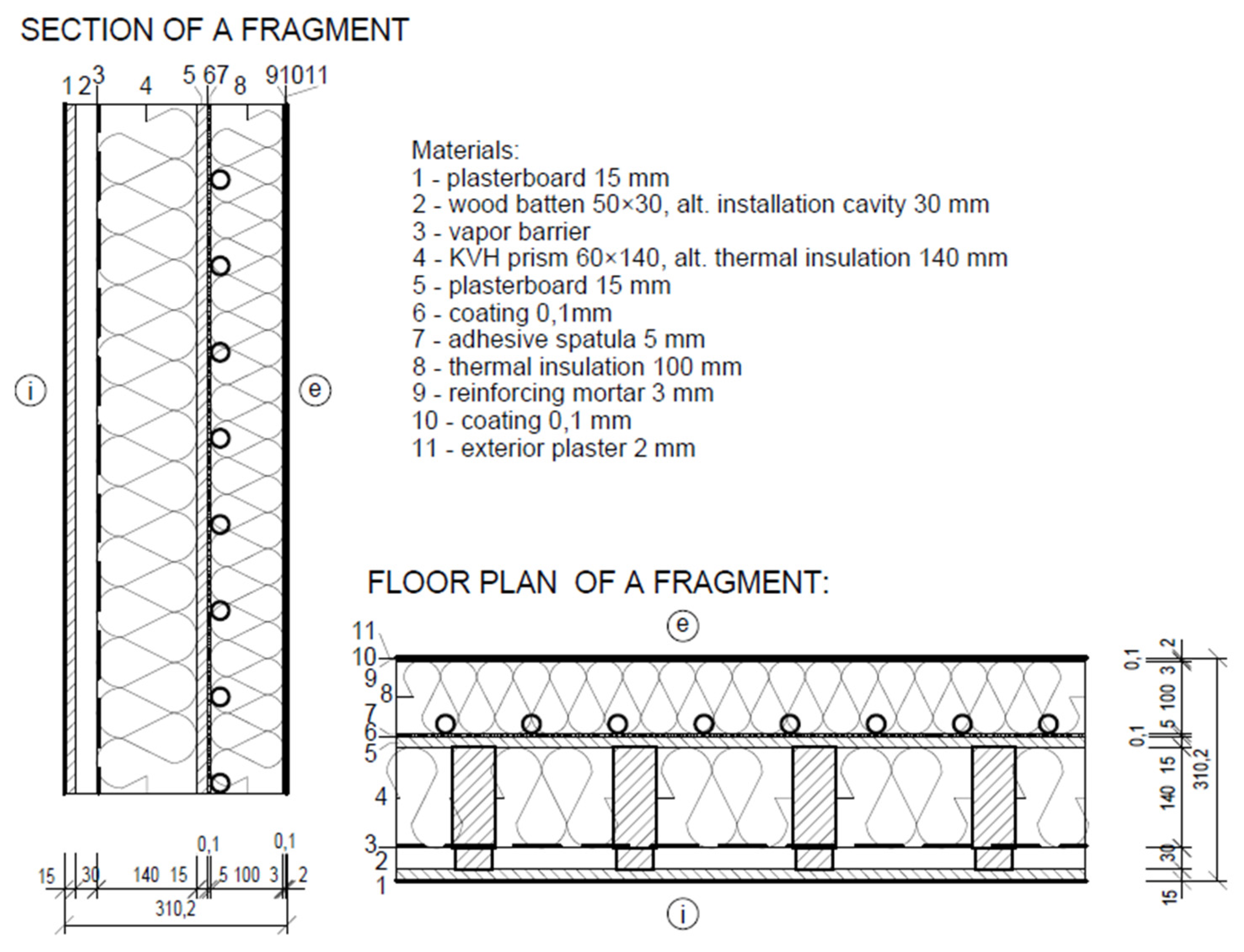
- Fragment 4—prefabricated timber building wall.
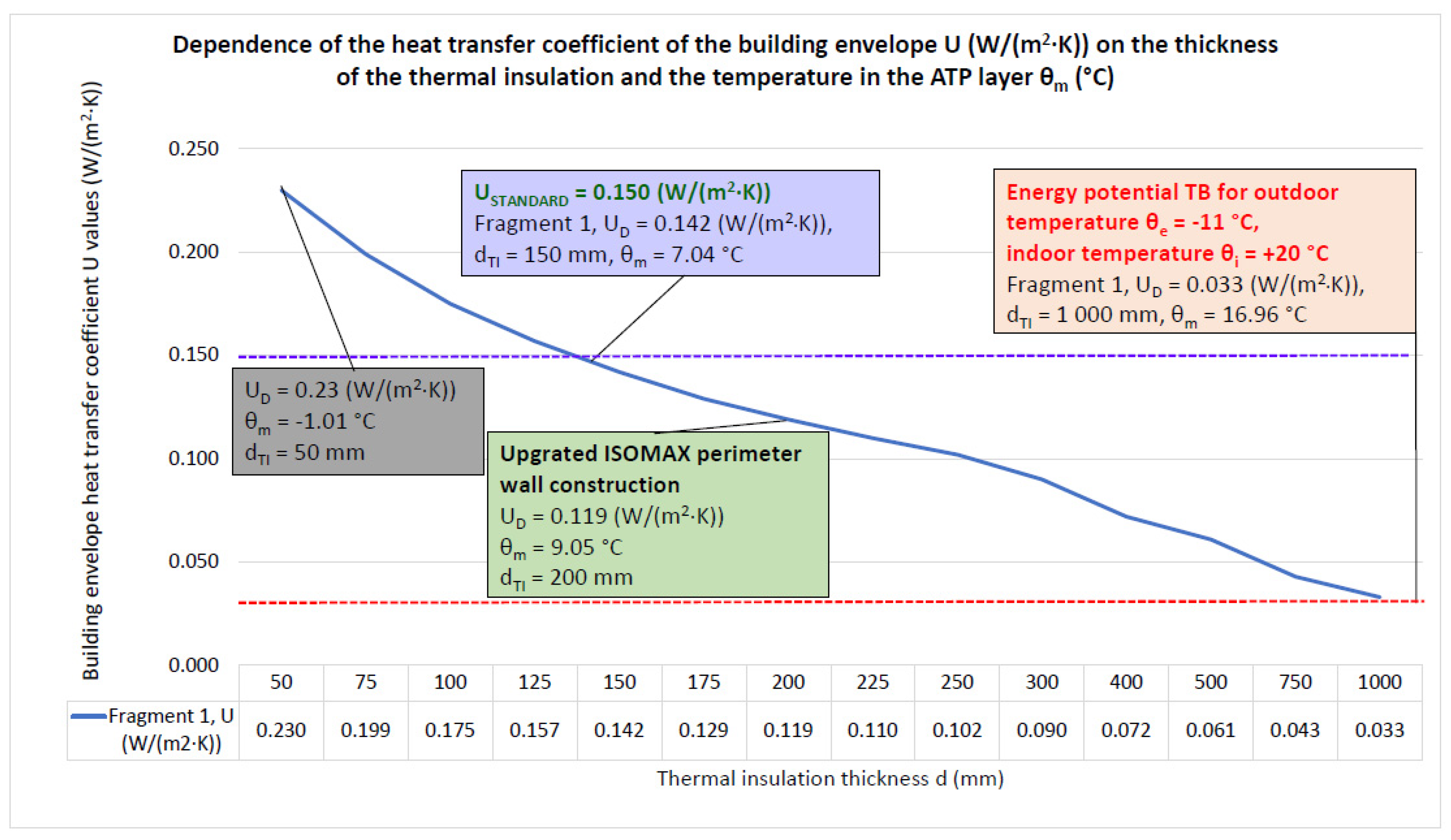
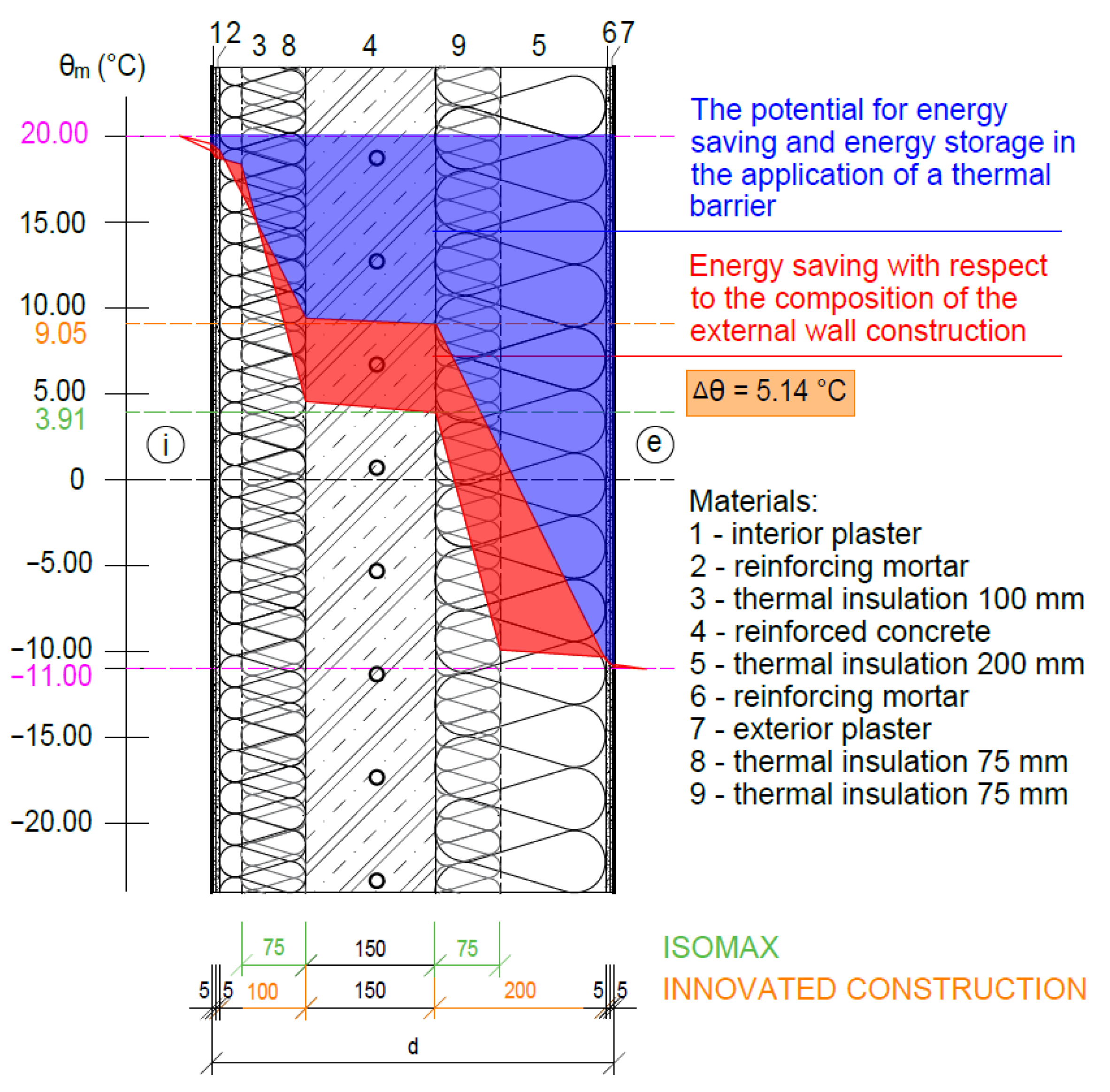
4.1.1. Fragment 1—Construction of the ISOMAX System Perimeter Wall
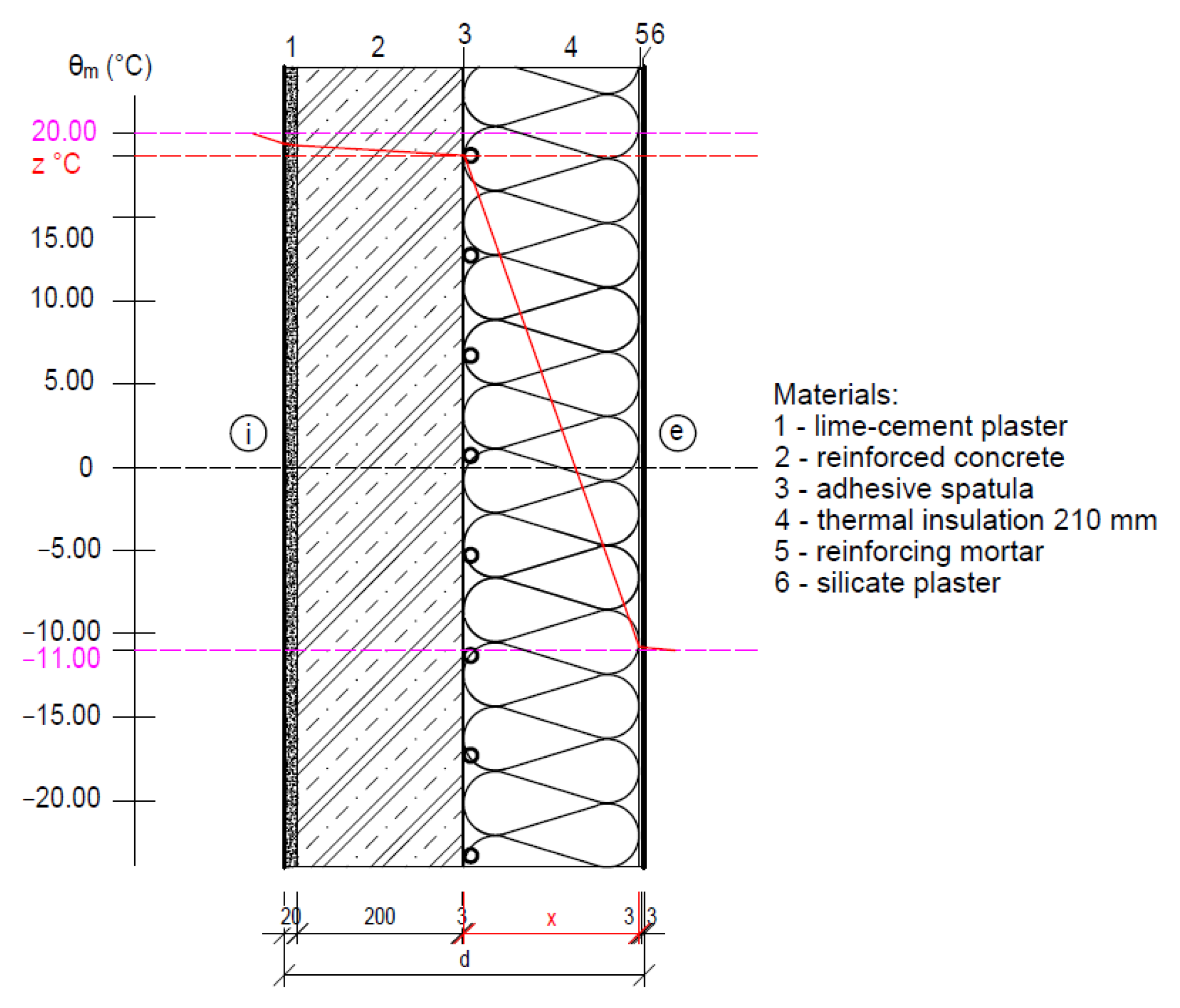
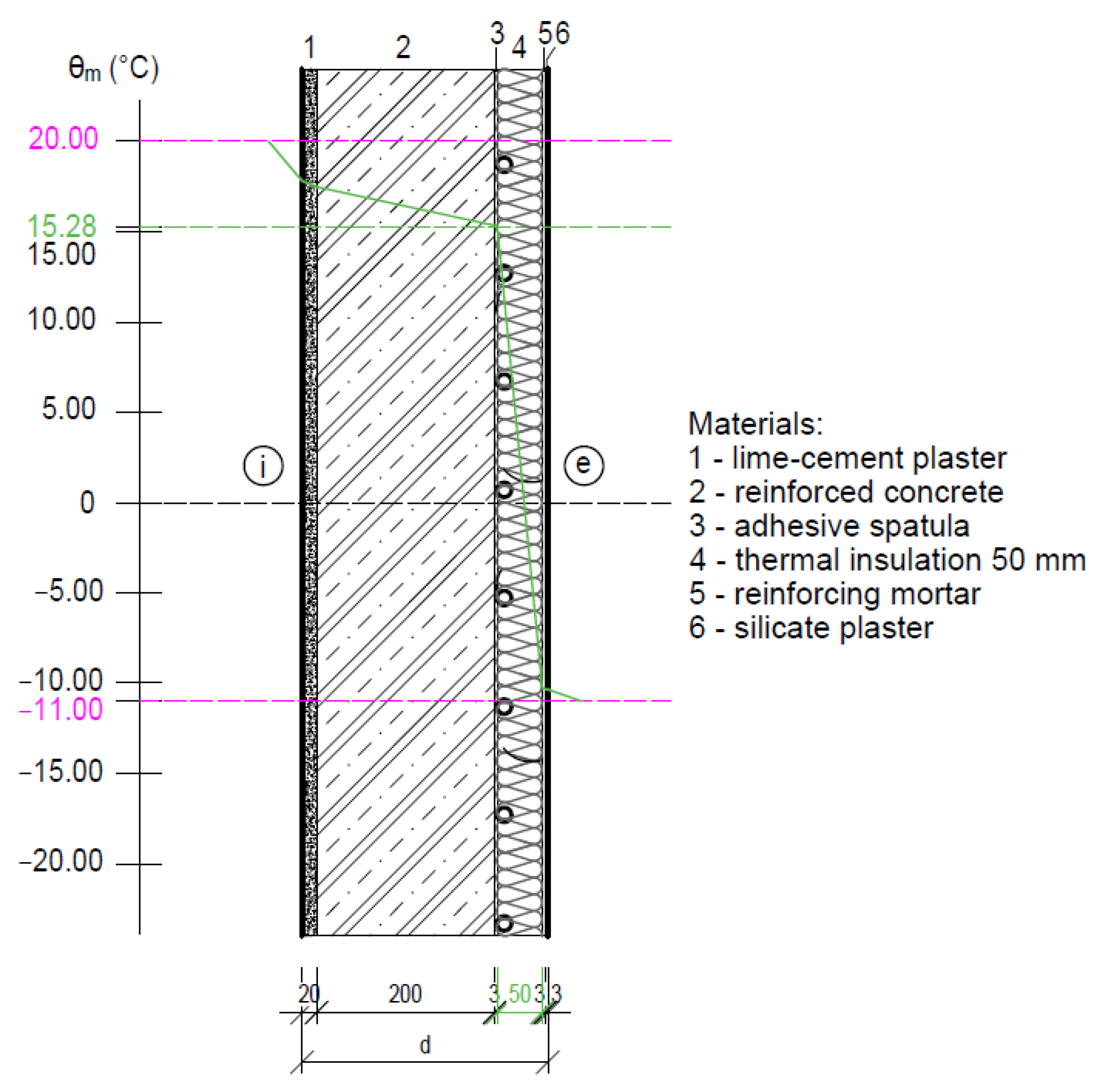
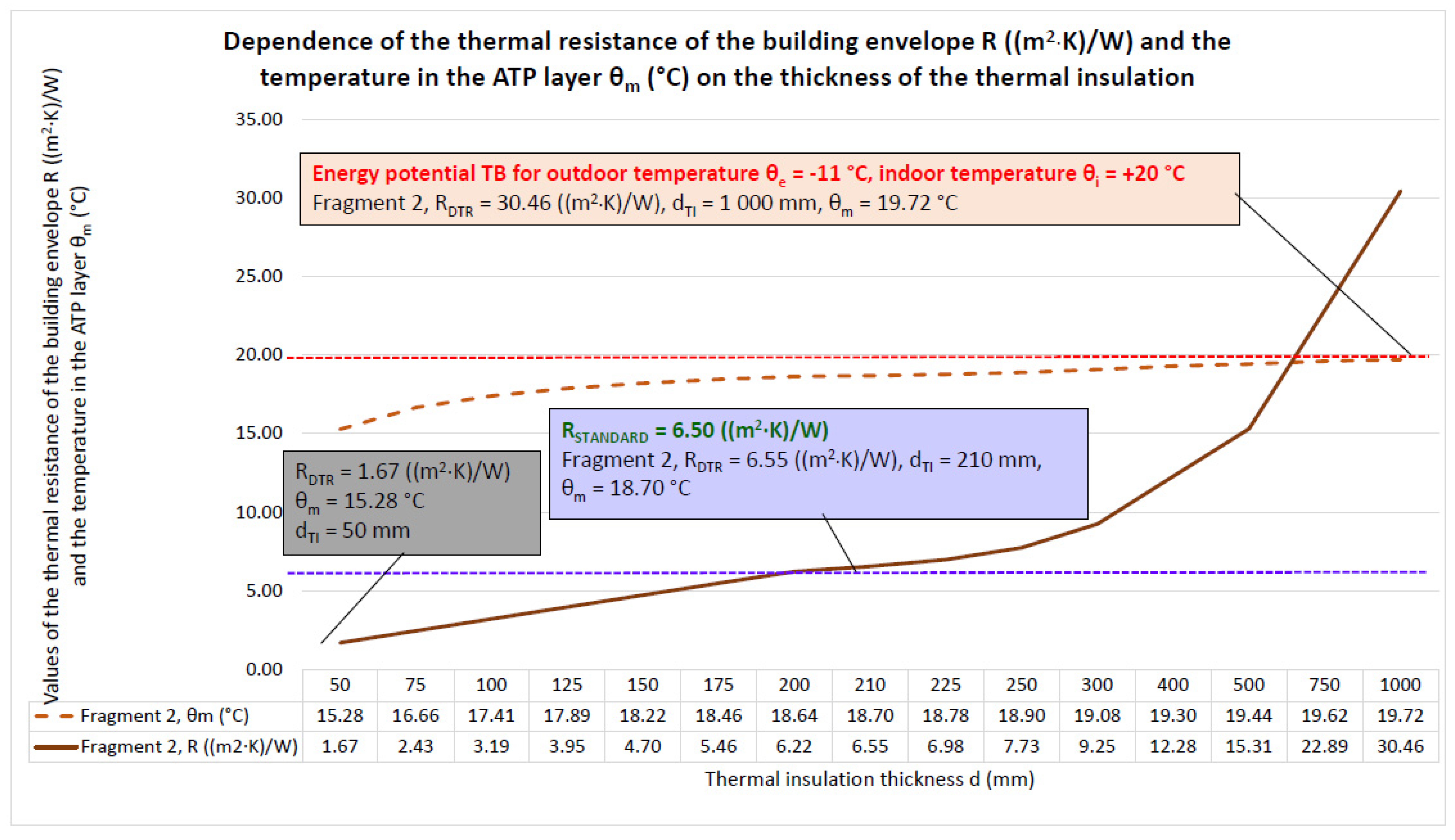
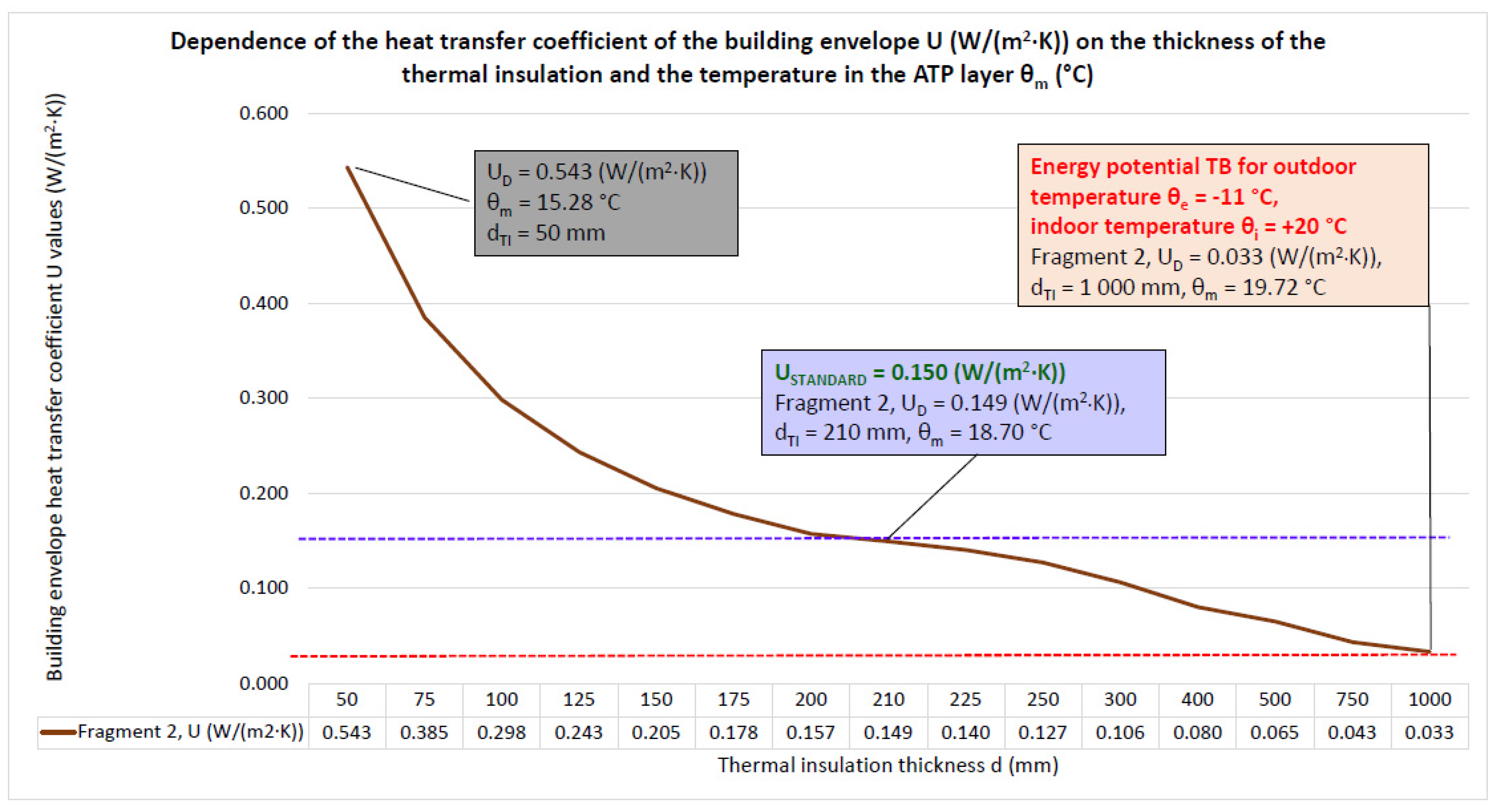
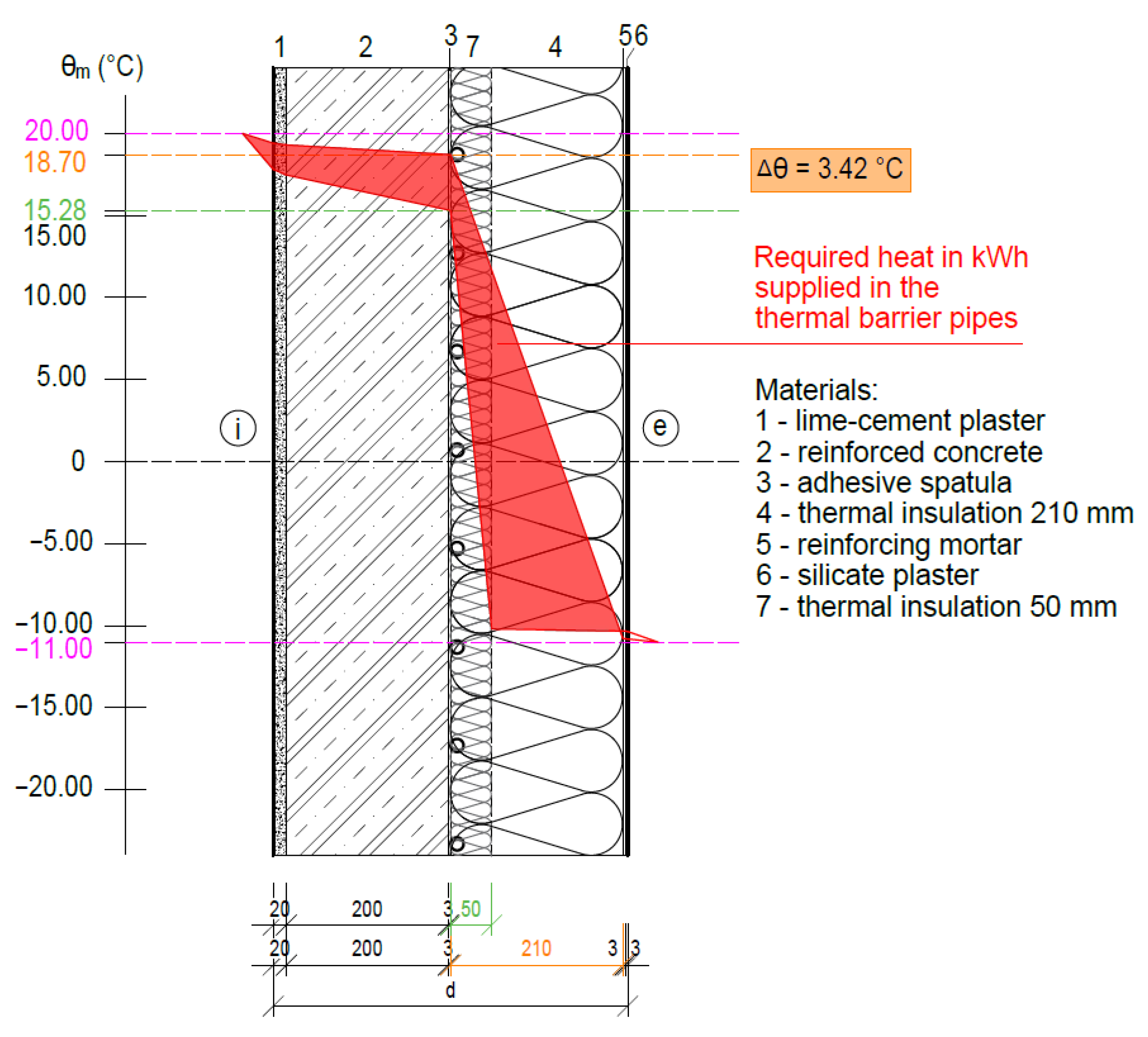
4.1.2. Fragment 2—Reinforced Concrete Wall with Thermal Insulation on the Exterior Side
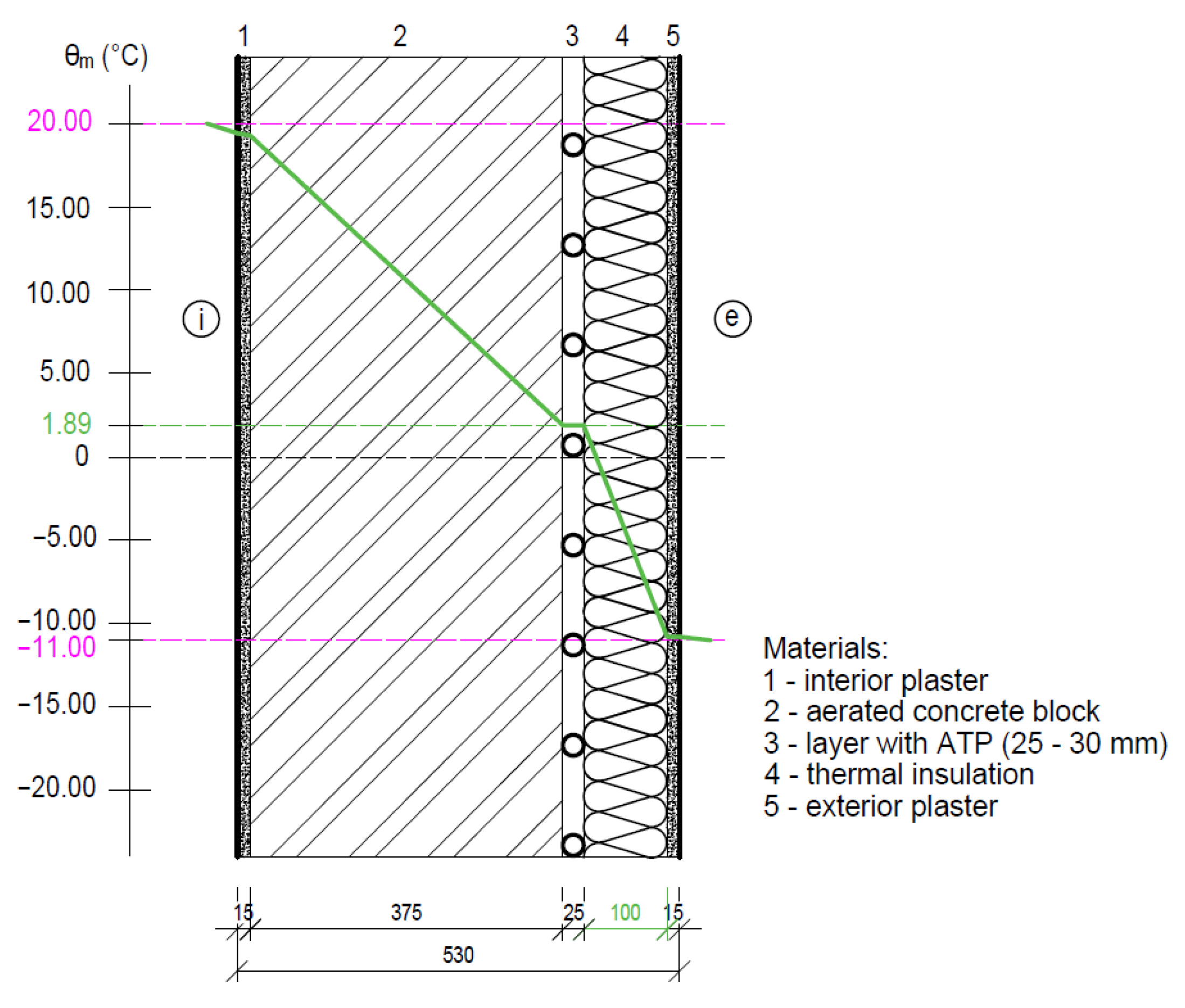
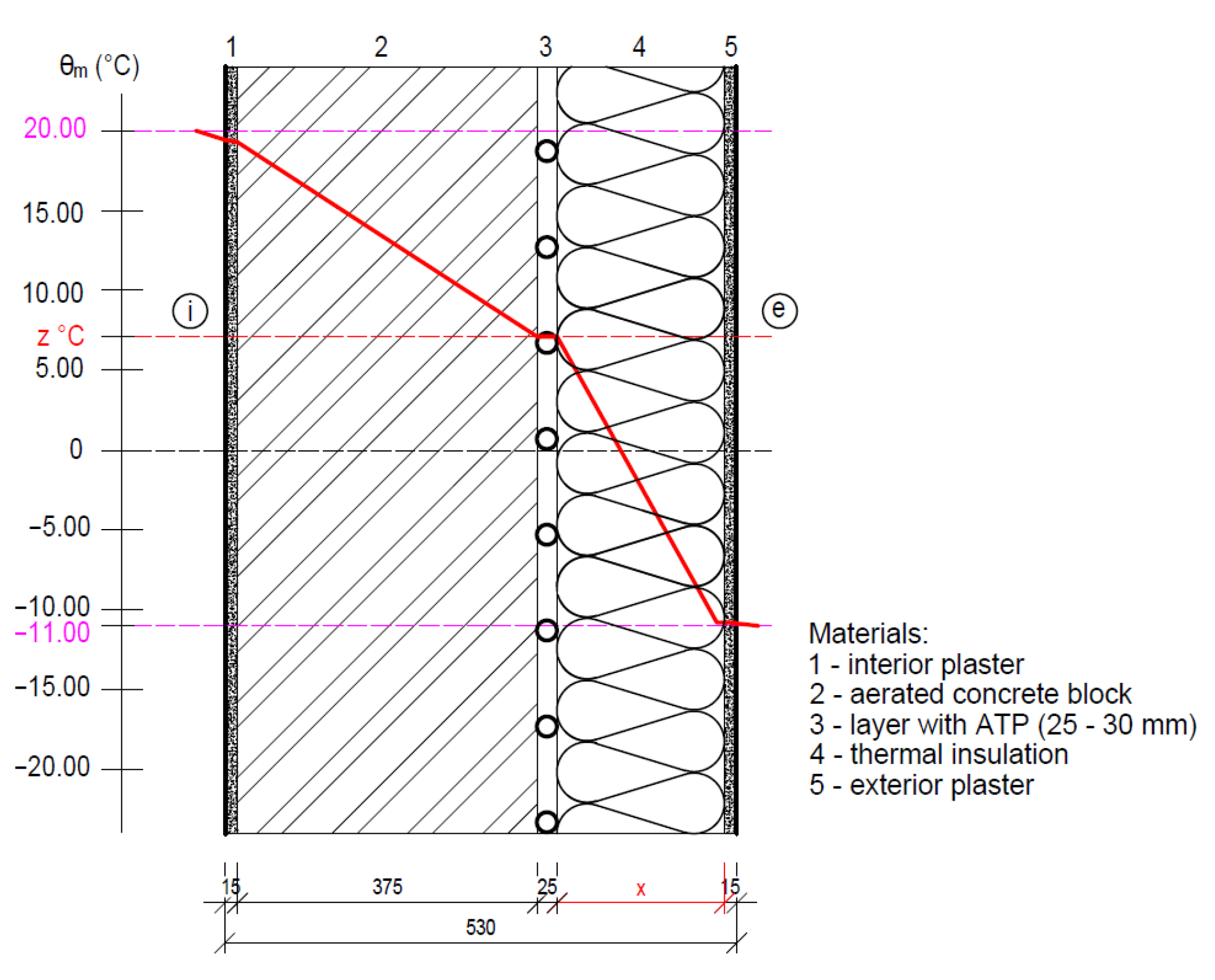
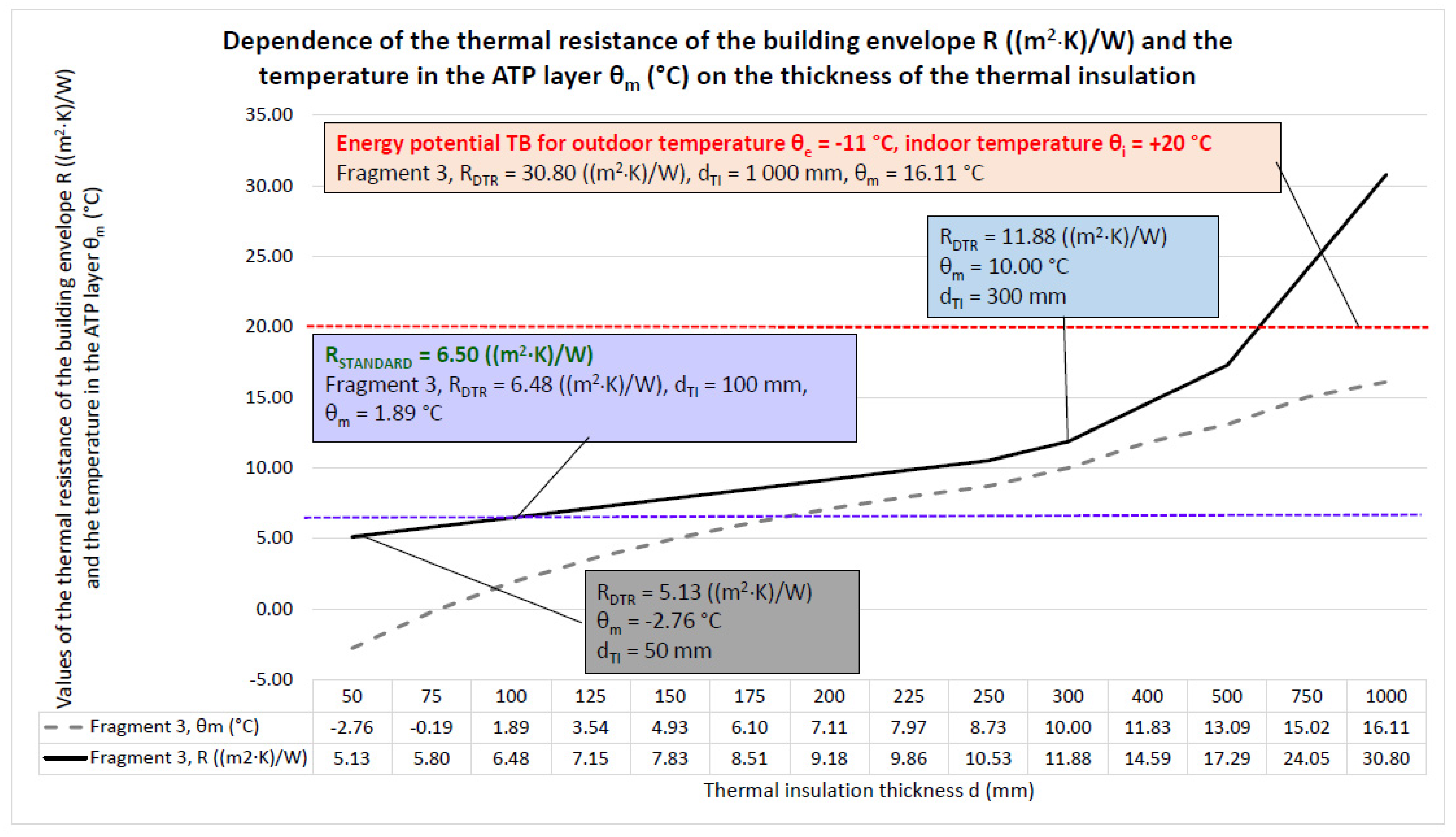
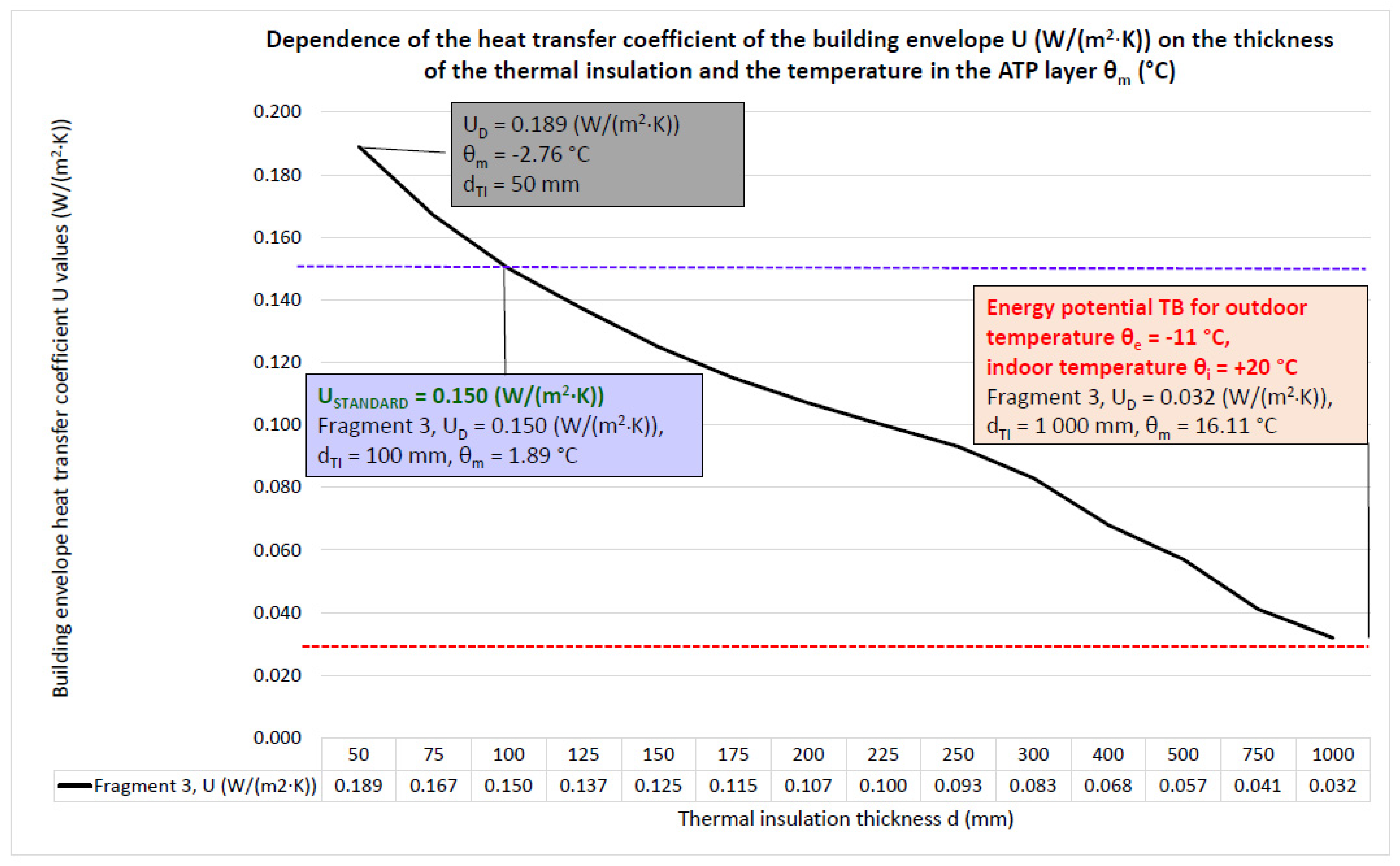
4.1.3. Fragment 3—A Wall Made of Aerated Concrete Blocks with Thermal Insulation on the Exterior Side
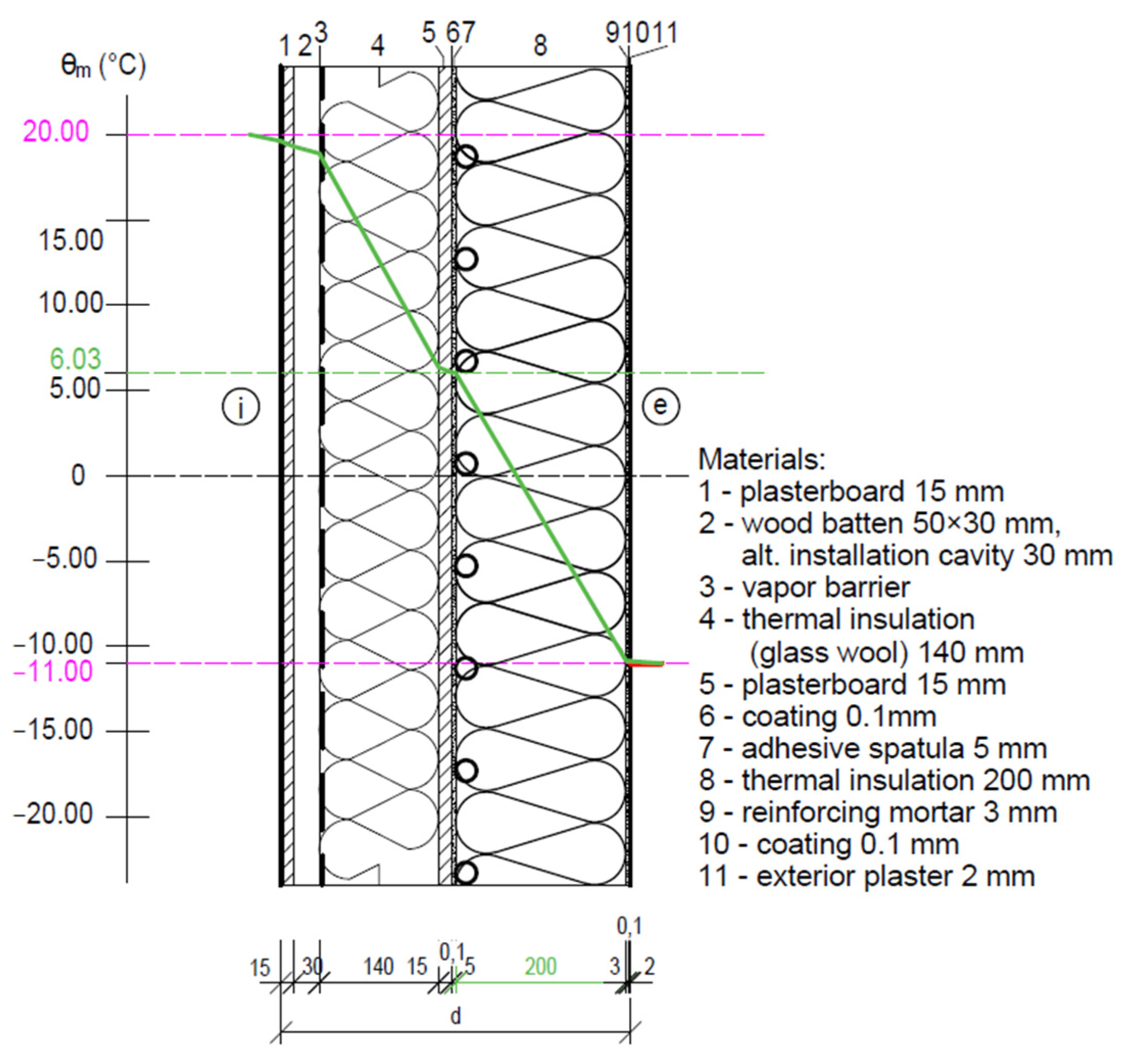
4.1.4. Fragment 4—Prefabricated Timber Building Wall
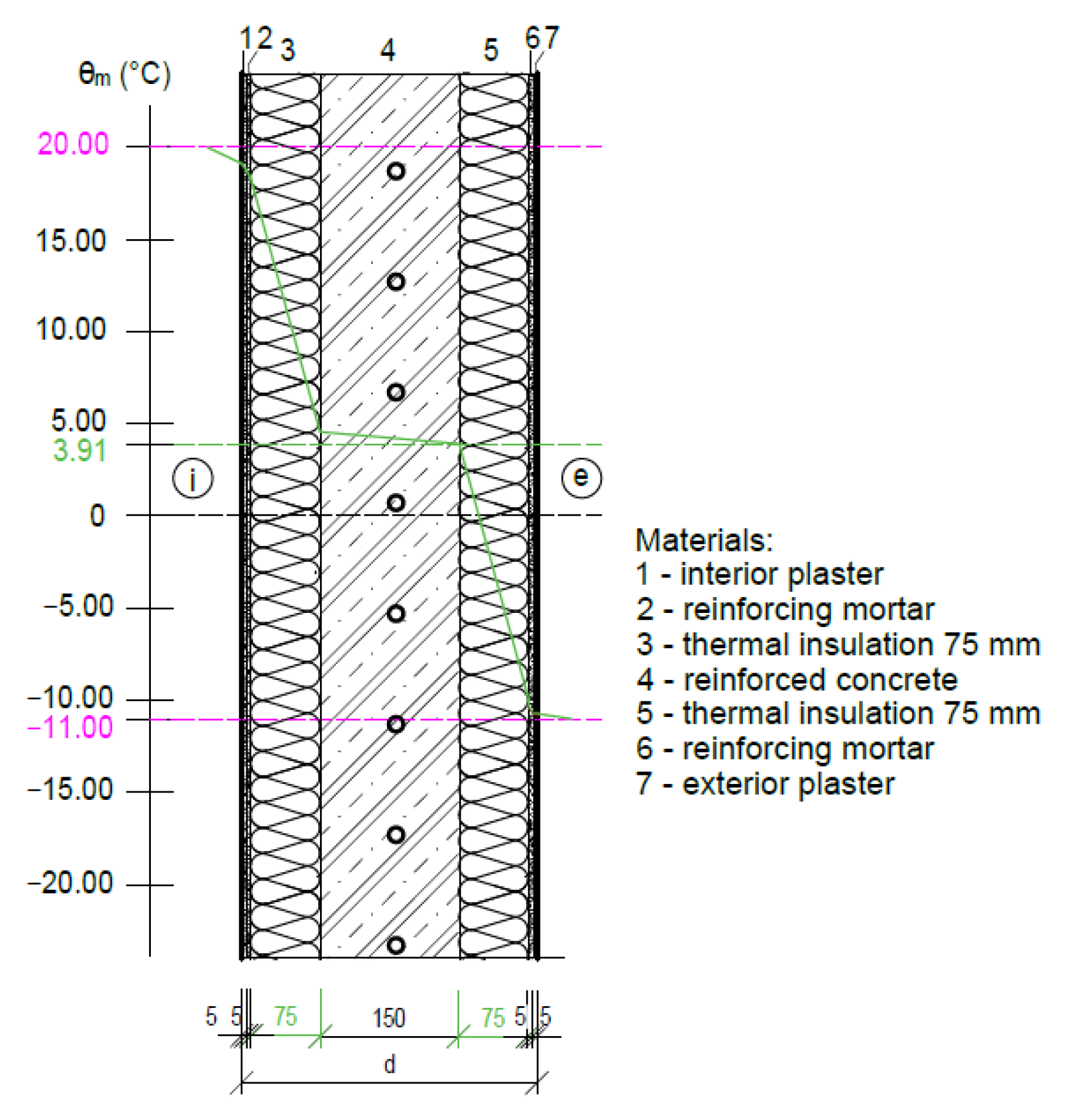
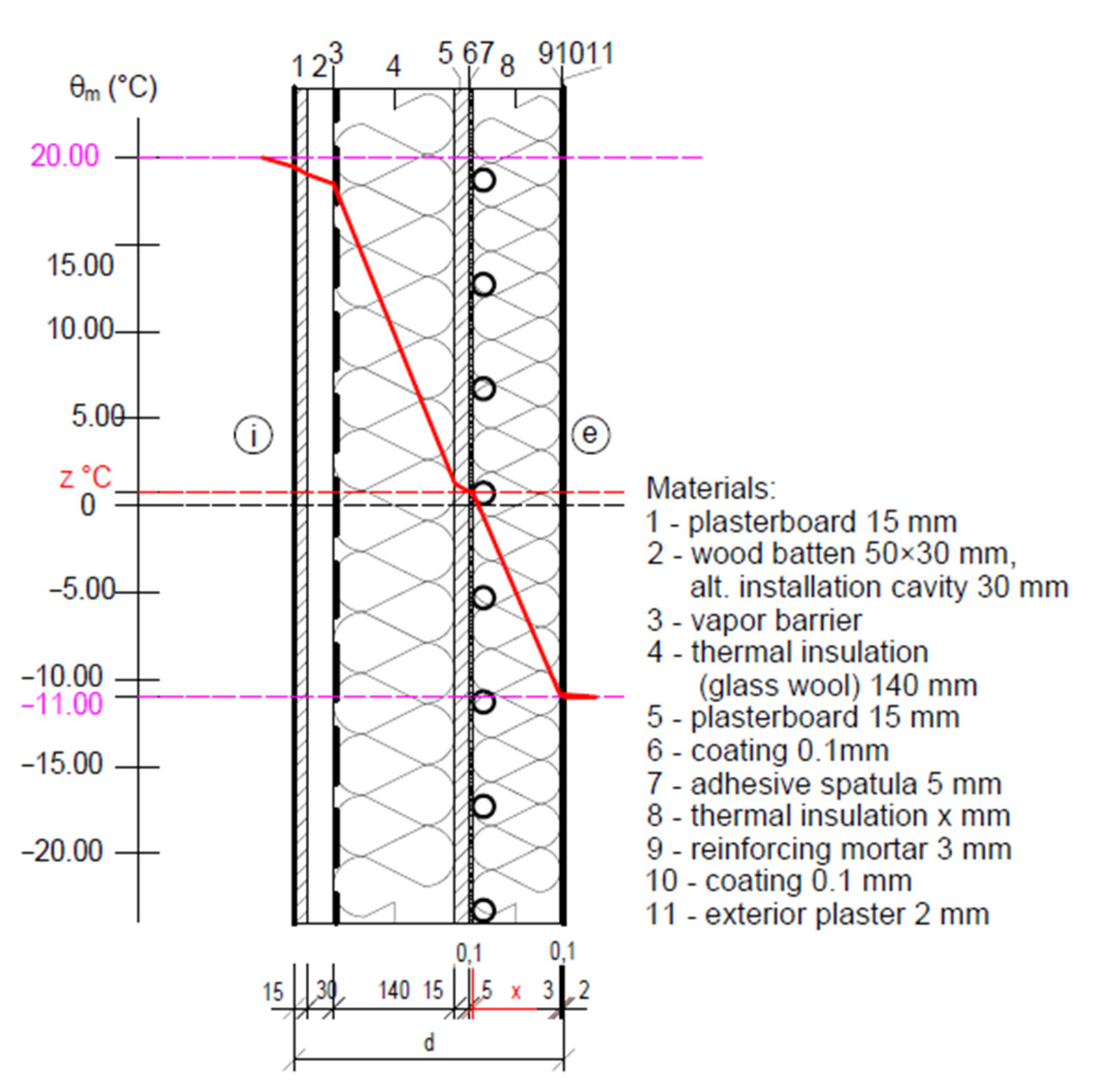
4.2. Computer Simulation of the Progression of the Temperature on a 2D Model of a Fragment of the Perimeter Wall
5. Discussion
- ■
- A comprehensive analysis of the dynamic thermal barrier for the four most applied practices and materially different fragments of the building envelope;
- ■
- The creation of mathematical-physical models for the parametric study of the individual fragments under consideration;
- ■
- The creation of a 2D model for computer simulation of temperature distribution in individual layers of the building structure of a prefabricated timber building, the results of which will be verified on a test cell;
- ■
- The development of a graphical evaluation of the dynamic thermal resistance and dynamic heat transfer coefficient as a function of the temperature of the heat transfer medium in the TB layer for the comparison of the individual fragments;
- ■
- The evaluation of the multifunctional energy potential of individual building envelope fragments (TB functions, heating, cooling, and heat storage).
6. Conclusions
- We developed mathematical-physical models for four materially different building envelope types to determine the energy saving and energy storage potential of ATP, as well as to define the dynamic thermal resistance using a parametric study;
- Due to the application of thermal insulation also on the interior side in Fragment 1, the function of the ATP for this building envelope solution is limited to the thermal barrier and heat/cool accumulation functions only;
- Because the load-bearing wall is made of porous concrete blocks, Fragment 3 has a high thermal resistance, and the function of the ATP for this building envelope solution is limited only to the functions of a thermal barrier and partial heat/cold accumulation;
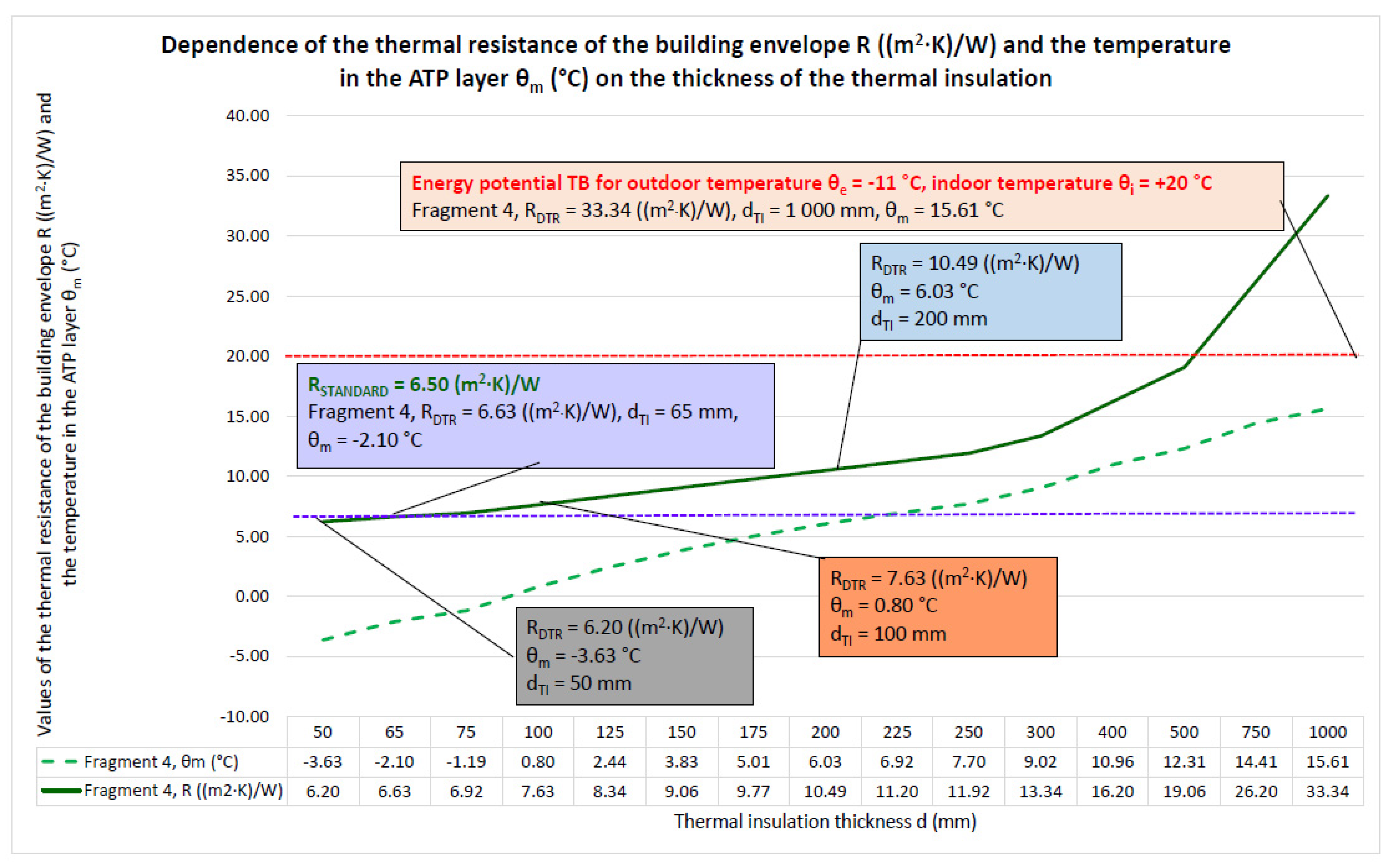
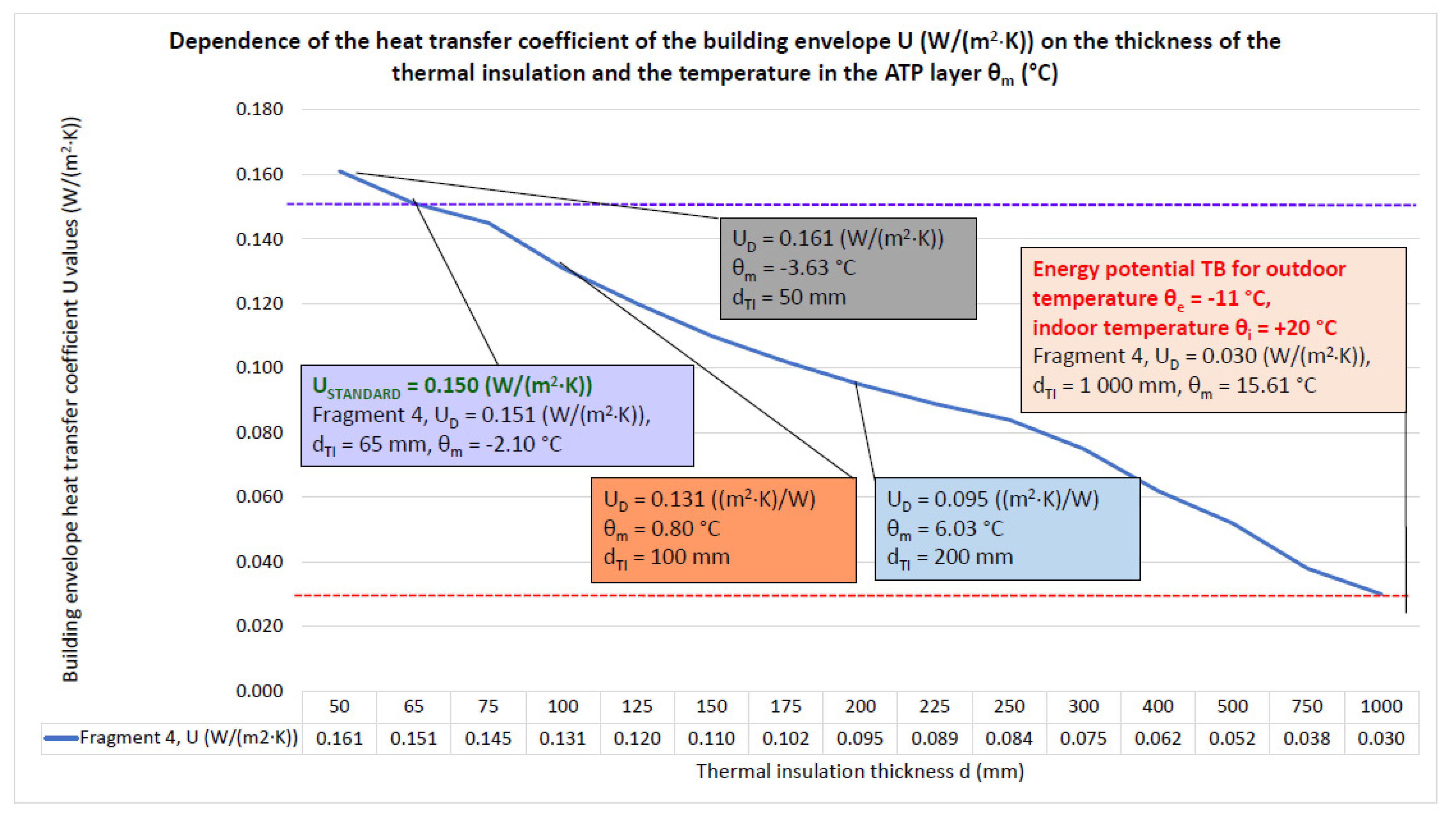
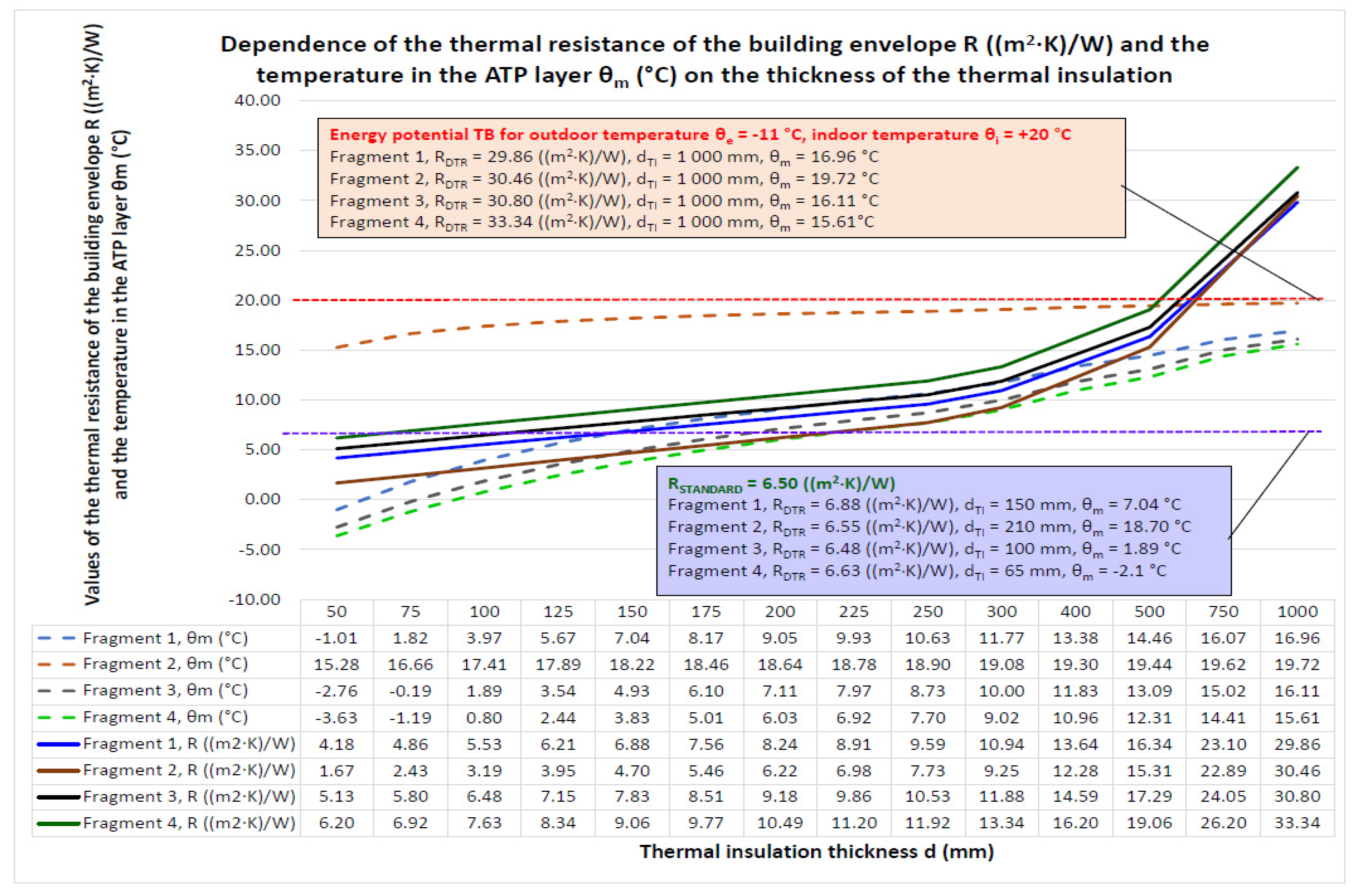
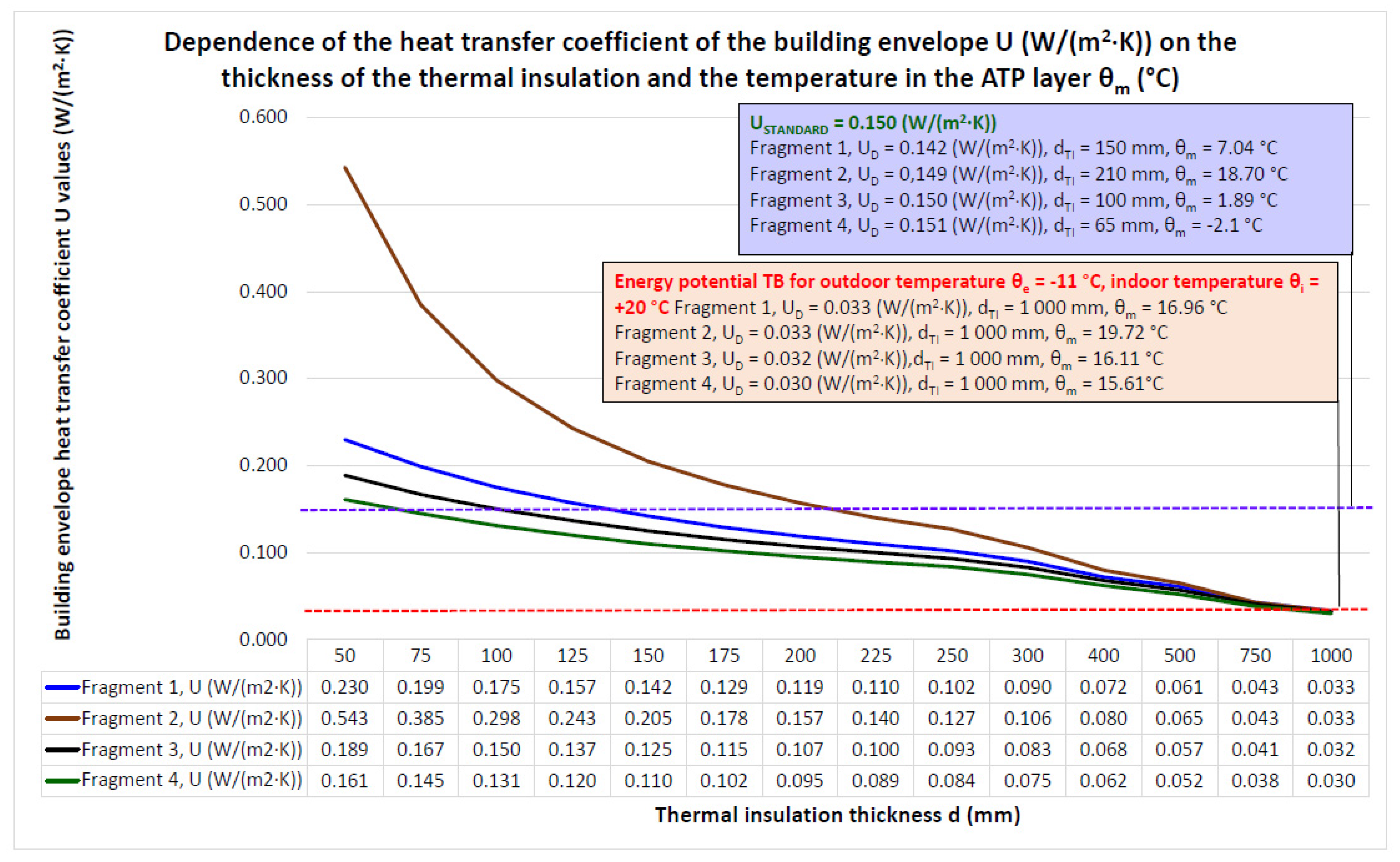
- Based on the analysis of the dynamic thermal resistance, we can conclude that in the case of the building envelope, Fragment 4, ATP is significant only as a function of TB, but at relatively low mean temperatures of the heat carrier θm = 15.61 °C, the dynamic thermal resistance has a high-value RDTR = 30.34 ((m2·K)/W), which corresponds to a static thermal insulation thickness of 1000 mm;
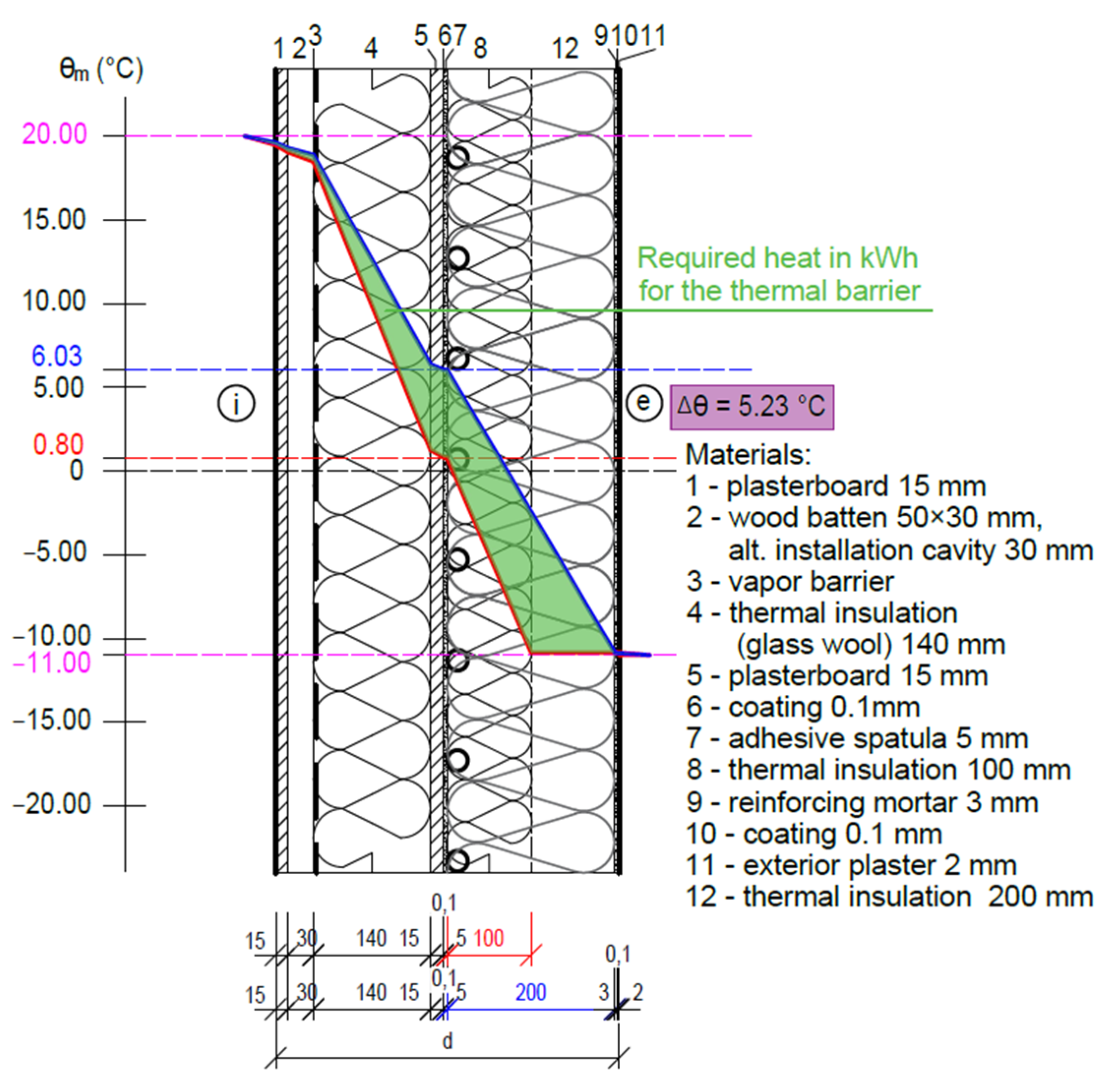
- An important result of the computer simulation is the uniform and continuous temperature distribution in the ATP heat transfer layer with a temperature θm = of about 6 °C, confirming the functionality of the TB with the achievement of a dynamic thermal resistance RDTR = 10.487 ((m2·K)/W) at a dynamic thermal insulation thickness of 100 mm, which is equal to the thermal resistance at a static thermal insulation thickness of 200 mm;
- The relatively low mean temperature of the heat transfer medium θm = 15.61 to 19.72 °C delivered to the tubes of the ATP heat transfer layer gives a dynamic thermal resistance of RDTR = 29.86 to 33.34 ((m2·K)/W) with an equivalent dynamic thermal insulation thickness of 1000 mm for the required standard resistances RSTANDARD = 6.50 ((m2·K)/W) of the individual fragments of the building envelope with static thermal insulation of 65 to 210 mm. Then, the energy potential of using TB is 455 to 513% for the increase in thermal resistance and 476 to 1.538% for the thickness of the dynamic thermal insulation;
- A mean temperature of the heat transfer medium θm (°C) delivered to the tubes of the ATP heat transfer layer equal to the interior temperature θi (°C) represents zero heat loss/gain to and from the interior;
- The energy-saving potential of using TB is undoubtedly significant in the heating season as well as in the summer season. It is increased by the use of heating/cooling from RES;
- The computer simulation was intended only for a basic analysis of the uniform and continuous temperature distribution in the ATP layer. We will continue the simulations to analyze for different changes in input parameters, the heat fluxes to the interior and exterior, the amount of heat delivered, the effect of operating time, and other physical variables affecting the dynamic thermal resistance of the individual building envelope structures.
7. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalús, D.; Koudelková, D.; Mučková, V.; Sokol, M.; Kurčová, M.; Šťastný, P. Parametric study of the energy potential of a building’s envelope with integrated energy-active elements. Acta Polytech. 2022, 62, 595–606. [Google Scholar] [CrossRef]
- Kalús, D.; Koudelková, D.; Mučková, V.; Sokol, M.; Kurčová, M.; Janík, P. Practical Experience in the Application of Energy Roofs, Ground Heat Storages, and Active Thermal Protection on Experimental Buildings. Appl. Sci. 2022, 12, 9313. [Google Scholar] [CrossRef]
- Kalús, D.; Koudelková, D.; Mučková, V.; Sokol, M.; Kurčová, M. Experience in Researching and Designing an Innovative Way of Operating Combined Building–Energy Systems Using Renewable Energy Sources. Appl. Sci. 2022, 12, 10214. [Google Scholar] [CrossRef]
- Kalús, D.; Gašparík, J.; Janík, P.; Kubica, M.; Šťastný, P. Innovative building technology implemented into facades with active thermal protection. Sustainability 2021, 13, 4438. [Google Scholar] [CrossRef]
- Isomax Technology. Available online: http://www.isomax-terrasol.eu/home.html (accessed on 9 February 2023).
- ®ISOMAX-TERRASOL Zero-Energy Building Technologies—Outer Wall Design with Thermal Barier (Climate Barier). Available online: http://www.isomax-terrasol.eu/en/technologie/isomax-technologies/isomax-temperature-barrier.html (accessed on 11 December 2021).
- Sebright, M.T.; Berg, D. Critical Look into® ISOMAX (Zero Energy Use Structures) Construction. In Proceedings of the 1st Residential Building Design & Construction Conference, Bethlehem, PA, USA, 20–21 February 2013. [Google Scholar]
- Koenders, S.J.M.; Loonen, R.C.G.M.; Hensen, J.L.M. Investigating the potential of a closed-loop dynamic insulation system for opaque building elements. Energy Build. 2018, 173, 409–427. [Google Scholar] [CrossRef]
- Krzaczek, M.; Florczuk, J.; Tejchman, J.J.A.E. Improved energy management technique in pipe-embedded wall heating/cooling system in residential buildings. Appl. Energy 2019, 254, 113711. [Google Scholar] [CrossRef]
- Kisilewicz, T.; Fedorczak-Cisak, M.; Barkanyi, T. Active thermal insulation as an element limiting heat loss through external walls. Energy Build. 2019, 205, 109541. [Google Scholar] [CrossRef]
- Fawaier, M.; Bokor, B. Dynamic insulation systems of building envelopes: A review. Energy Build. 2022, 270, 112268. [Google Scholar] [CrossRef]
- Shen, J.; Wang, Z.; Luo, Y.; Jiang, X.; Zhao, H.; Tian, Z. Performance evaluation of an active pipe-embedded building envelope system to transfer solar heat gain from the south to the north external wall. J. Build. Eng. 2022, 59, 105123. [Google Scholar] [CrossRef]
- Yan, B.; Han, X.; Malkawi, A.; Dokka, T.H.; Howard, P.; Knowles, J.; Edwards, K. Comprehensive assessment of operational performance of coupled natural ventilation and thermally active building system via an extensive sensor network. Energy Build. 2022, 260, 111921. [Google Scholar] [CrossRef]
- Junasová, B.; Krajčík, M.; Šikula, O.; Arıcı, M.; Šimko, M. Adapting the construction of radiant heating and cooling systems for building retrofit. Energy Build. 2022, 268, 112228. [Google Scholar] [CrossRef]
- Šimko, M.; Petráš, D.; Krajčík, M.; Szabó, D. Testing of a Radiant Wall Cooling System with Pipes Coupled to Aerated Blocks. Period. Polytech. Mech. Eng. 2022, 66, 59–66. [Google Scholar] [CrossRef]
- Chen, S.; Yang, Y.; Chang, T. Uncertainty and parameter ranking analysis on summer thermal characteristics of the hydronic thermal barrier for low-energy buildings. In Building Simulation; Tsinghua University Press: Beijing, China, 2023; Volume 16, pp. 27–49. [Google Scholar]
- Zhu, Q.; Xu, X.; Wang, J.; Xiao, F. Development of dynamic simplified thermal models of active pipe-embedded building envelopes using genetic algorithm. Int. J. Therm. Sci. 2014, 76, 258–272. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, J.; Olesen, B.W.; Fang, L.; Wang, F. A new simplified model to calculate surface temperature and heat transfer of radiant floor heating and cooling systems. Energy Build. 2015, 105, 285–293. [Google Scholar] [CrossRef]
- Xie, J.; Xu, X.; Li, A.; Zhu, Q. Experimental validation of frequency-domain finite-difference model of active pipe-embedded building envelope in time domain by using Fourier series analysis. Energy Build. 2015, 99, 177–188. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, A.; Xie, J.; Li, W.; Xu, X. Experimental validation of a semi-dynamic simplified model of active pipe-embedded building envelope. Int. J. Therm. Sci. 2016, 108, 70–80. [Google Scholar] [CrossRef]
- Lydon, G.P.; Caranovic, S.; Hischier, I.; Schlueter, A. Coupled simulation of thermally active building systems to support a digital twin. Energy Build. 2019, 202, 109298. [Google Scholar] [CrossRef]
- STN EN 73 0540-2+Z1+Z2; Thermal Protection of Buildings. Thermal Performance of Buildings and Components. Part 2: Functional Requirements. Úrad pre Normalizáciu, Metrológiu a Skúšobníctvo Slovenskej Republiky: Bratislava, Slovakia, 2019.
- STN EN 73 0540-3; Thermal Protection of Buildings. Thermal Performance of Buildings and Components. Part 3: Properties of Environments and Building Products. Úrad pre Normalizáciu, Metrológiu a Skúšobníctvo Slovenskej Republiky: Bratislava, Slovakia, 2012.
- Krzaczek, M.; Kowalczuk, Z. Thermal Barrier as a technique of indirect heating and cooling for residential buildings. Energy Build. 2011, 43, 823–837. [Google Scholar] [CrossRef]
- STN EN 1264-1; Water Based Surface Embedded Heating and Cooling Systems—Part 1: Definitions and Symbols. Úrad pre Normalizáciu, Metrológiu a Skúšobníctvo Slovenskej Republiky: Bratislava, Slovakia, 2021.
- STN EN 1264-2+A1; Water Based Surface Embedded Heating and Cooling Systems. Part 2: Floor Heating: Prove Methods for the Determination of the Thermal Output Using Calculation and Test Methods. Úrad pre Normalizáciu, Metrológiu a Skúšobníctvo Slovenskej Republiky: Bratislava, Slovakia, 2013.
- STN EN 1264-3; Water Based Surface Embedded Heating and Cooling Systems—Part 3: Dimensioning. Úrad pre Normalizáciu, Metrológiu a Skúšobníctvo Slovenskej Republiky: Bratislava, Slovakia, 2021.
- STN EN 1264-4; Water Based Surface Embedded Heating and Cooling Systems—Part 4: Installation. Úrad pre Normalizáciu, Metrológiu a Skúšobníctvo Slovenskej Republiky: Bratislava, Slovakia, 2021.
- STN EN 1264-5; Water Based Surface Embedded Heating and Cooling Systems—Part 5: Determination of the Thermal Output for Wall and Ceiling Heating and for Floor, Wall and Ceiling Cooling. Úrad pre Normalizáciu, Metrológiu a Skúšobníctvo Slovenskej Republiky: Bratislava, Slovakia, 2021.
- Benča, Š. Výpočtové Postupy MKP pri Riešení Lineárnych úloh Mechaniky; Vydavateľstvo STU: Bratislava, Slovakia, 2004. [Google Scholar]
- Kalús, D.; Koudelková, D.; Mučková, V.; Sokol, M.; Kurčová, M. Contribution to the Research and Development of Innovative Building Components with Embedded Energy-Active Elements. Coatings 2022, 12, 1021. [Google Scholar] [CrossRef]
- Kalús, D.; Koudelková, D.; Mučková, V.; Kurčová, M.; Sokol, M. Design, Project, and Realization of a Prototype of an Energy-efficient Prefabricated House IDA I. using Renewable Energy Sources. Period. Polytech. Civ. Eng. 2023, 67, 232–248. [Google Scholar]
- Kalús, D.; Janík, P.; Koudelková, D.; Mučková, V.; Sokol, M. Contribution to research on ground heat storages as part of building energy systems using RES. Energy Build. 2022, 267, 112125. [Google Scholar] [CrossRef]
- Kalús, D.; Mučková, V.; Koudelková, D. Energy, Economic and Environmental Assessment of Thermal Barrier Application in Building Envelope Structures. Coatings 2021, 11, 1538. [Google Scholar] [CrossRef]
- Kalús, D.; Janík, P.; Kubica, M. Experimental house EB2020–Research and experimental measurements of an energy roof. Energy Build. 2021, 248, 111172. [Google Scholar] [CrossRef]
- Kalús, D.; Straková, Z.; Kubica, M. Parametric Study of Heating and Cooling Capacity of Interior Thermally Active Panels. Period. Polytech. Mech. Eng. 2021, 65, 269–279. [Google Scholar] [CrossRef]
- UTILITY MODEL SK 5749 Y1 (UTILITY MODEL): Method of Operation of a Combined Construction-Energy System of Buildings and Equipment. Date of Entry into Force of the Utility Model: 1.4.2011. In Vestník ÚPV SR č.: 5/2011, 23p. Spôsob Prevádzky Kombinovaného Stavebno-Energetického Systému Budov a Zariadenie: Číslo Prihlášky 5027-2010, Zverejnená 8. 11. 2010 vo Vestníku ÚPV SR č. 11/2010; Úrad Priemyselného Vlastníctva Slovenskej Republiky: Banská Bystrica, Slovakia, 2011; 23p. Available online: https://wbr.indprop.gov.sk/WebRegistre/UzitkovyVzor/Detail/5027-2010 (accessed on 9 February 2023).
- UTILITY MODEL SK 5729 Y1 (UTILITY MODEL): Samonosný Tepelnoizolačný Panel pre Systémy s Aktívnym Riadením Prechodu Tepla. [Self-Supporting Thermal Insulation Panel for Systems with Active Heat Transfer Control]. Date of Entry into Force of the Utility Model: 28.2.2011. In Vestník ÚPV SR No. 4/2011, Banská Bystrica, Slovak Republic, 32 p. Samonosný Tepelnoizolačný Panel pre Systémy s Aktívnym Riadením Prechodu Tepla: Číslo Prihlášky UV 5030-2010, Zverejnená 7. 10. 2010 vo Vestníku ÚPV SR č. 10/2010; Úrad Priemyselného Vlastníctva Slovenskej Republiky: Banská Bystrica, Slovakia, 2011; 32p. Available online: https://wbr.indprop.gov.sk/WebRegistre/UzitkovyVzor/Detail/5030-2010 (accessed on 9 February 2023).
- UTILITY MODEL SK 5725 Y1 (UTILITY MODEL): Tepelnoizolačný Panel pre Systémy s Aktívnym Riadením Prechodu Tepla: Číslo Prihlášky UV 5031-2010, Zverejnená 7.10. 2010 vo Vestníku ÚPV SR č. 10/2010; Úrad Priemyselného Vlastníctva Slovenskej Republiky: Banská Bystrica, Slovakia, 2011; 63p. Available online: https://wbr.indprop.gov.sk/WebRegistre/UzitkovyVzor/Detail/5031-2010 (accessed on 9 February 2023).
- EUROPEAN PATENT EP 2 572 057 B1. Heat Insulating Panel with Active Regulation of Heat Transition. International Application Number: PCT/SK2011/000004, International Publication Number: WO 2011/146025 (24.11.2011 Gazette 2011/47). 15 October 2014. 67p. Available online: https://register.epo.org/application?number=EP11716446&tab=main&lng=en10 (accessed on 9 February 2023).
- Imbabi, M.S.E. A passive–active dynamic insulation system for all climates. Int. J. Sustain. Built Environ. 2012, 1, 247–258. [Google Scholar] [CrossRef]
- Yaegashi, A.; Hiyama, K.; Kato, S.; Tezuka, J.; Nikawa, S. Thermal performance evaluation of a dynamic insulation technology applied to a timber framework house in a real environment. J. Asian Archit. Build. Eng. 2015, 14, 213–218. [Google Scholar] [CrossRef]
- Fantucci, S.; Serra, V.; Perino, M. Dynamic insulation systems: Experimental analysis on a parietodynamic wall. Energy Procedia 2015, 78, 549–554. [Google Scholar] [CrossRef]
- Shekar, V.; Krarti, M. Control strategies for dynamic insulation materials applied to commercial buildings. Energy Build. 2017, 154, 305–320. [Google Scholar] [CrossRef]
- Gopalan, A.; Antony, A.S.M.; Suresh, R.; Sahoo, S.; Livingston, L.M.; Titus, A.; Sathyamurthy, R. Performance enhancement of building energy through the combination of dynamic insulation panels and phase changing materials. Energy Rep. 2022, 8, 945–958. [Google Scholar] [CrossRef]
- Horak, P.; Formanek, M.; Fečer, T.; Plášek, J. Evaporation of refrigerant R134a, R404A and R407C with low mass flux in smooth vertical tube. Int. J. Heat Mass Transf. 2021, 181, 121845. [Google Scholar] [CrossRef]
- Formánek, M.; Horák, P.; Diblík, J.; Hirš, J. Experimental increase in the efficiency of a cooling circuit using a desuperheater. Period. Polytech. Civ. Eng. 2016, 60, 355–360. [Google Scholar] [CrossRef]
- Jurča, J.; Horák, P. Influence of Sustainability on Comprehensive Assessment of Buildings. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 214, p. 012049. [Google Scholar]
- Park, B.; Srubar, W.V.; Krarti, M. Energy performance analysis of variable thermal resistance envelopes in residential buildings. Energy Build. 2015, 103, 317–325. [Google Scholar] [CrossRef]
- Menyhart, K.; Krarti, M. Potential energy savings from deployment of dynamic insulation materials for US residential buildings. Build. Environ. 2017, 114, 203–218. [Google Scholar] [CrossRef]
- Pflug, T.; Bueno, B.E.; Siroux, M.; Kuhn, T.E. Potential analysis of a new removable insulation system. Energy Build. 2017, 154, 391–403. [Google Scholar] [CrossRef]
- Garriga Martínez, S.; Dabbagh, M.; Krarti, M. Evaluation of dynamic insulation systems for residential buildings in Barcelona, Spain. J. Eng. Sustain. Build. Cities 2020, 1, 011002. [Google Scholar] [CrossRef]
- Rupp, S.; Krarti, M. Analysis of multi-step control strategies for dynamic insulation systems. Energy Build. 2019, 204, 109459. [Google Scholar] [CrossRef]
- Kishore, R.A.; Bianchi, M.V.A.; Booten, C.; Vidal, J.; Jackson, R. Enhancing building energy performance by effectively using phase change material and dynamic insulation in walls. Appl. Energy 2021, 283, 116306. [Google Scholar] [CrossRef]












| su/λE (m2·K)/W | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.08 | 0.10 | 0.15 | 0.18 |
|---|---|---|---|---|---|---|---|---|---|---|
| aT | 1.103 | 1.100 | 1.097 | 1.093 | 1.091 | 1.088 | 1.082 | 1.075 | 1.064 | 1.059 |
| L (m) | 0.05 | 0.075 | 0.1 | 0.15 | 0.20 | 0.225 | 0.30 | 0.375 | 0.45 |
|---|---|---|---|---|---|---|---|---|---|
| aK | 1.00 | 0.99 | 0.98 | 0.95 | 0.92 | 0.90 | 0.82 | 0.72 | 0.60 |
| D (m) | 0.022 | 0.020 | 0.018 | 0.016 | 0.014 |
|---|---|---|---|---|---|
| L (m) | aWL | ||||
| 0.05 | 0.96 | 0.93 | 0.90 | 0.86 | 0.82 |
| 0.075 | 0.80 | 0.754 | 0.70 | 0.644 | 0.59 |
| 0.10 | 0.658 | 0.617 | 0.576 | 0.533 | 0.488 |
| 0.15 | 0.505 | 0.47 | 0.444 | 0.415 | 0.387 |
| 0.20 | 0.422 | 0.40 | 0.379 | 0.357 | 0.337 |
| 0.225 | 0.396 | 0.376 | 0.357 | 0.34 | 0.32 |
| 0.30 | 0.344 | 0.33 | 0.315 | 0.30 | 0.288 |
| 0.375 | 0.312 | 0.30 | 0.29 | 0.278 | 0.266 |
| 0.450 | 0.30 | 0.29 | 0.28 | 0.264 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mučková, V.; Kalús, D.; Koudelková, D.; Kurčová, M.; Straková, Z.; Sokol, M.; Ingeli, R.; Šťastný, P. Analysis of the Dynamic Thermal Barrier in Building Envelopes. Coatings 2023, 13, 648. https://doi.org/10.3390/coatings13030648
Mučková V, Kalús D, Koudelková D, Kurčová M, Straková Z, Sokol M, Ingeli R, Šťastný P. Analysis of the Dynamic Thermal Barrier in Building Envelopes. Coatings. 2023; 13(3):648. https://doi.org/10.3390/coatings13030648
Chicago/Turabian StyleMučková, Veronika, Daniel Kalús, Daniela Koudelková, Mária Kurčová, Zuzana Straková, Martin Sokol, Rastislav Ingeli, and Patrik Šťastný. 2023. "Analysis of the Dynamic Thermal Barrier in Building Envelopes" Coatings 13, no. 3: 648. https://doi.org/10.3390/coatings13030648
APA StyleMučková, V., Kalús, D., Koudelková, D., Kurčová, M., Straková, Z., Sokol, M., Ingeli, R., & Šťastný, P. (2023). Analysis of the Dynamic Thermal Barrier in Building Envelopes. Coatings, 13(3), 648. https://doi.org/10.3390/coatings13030648






