A Computational Study on Two-Parameter Singularly Perturbed Third-Order Delay Differential Equations

Abstract

A class of third-order singularly perturbed two-parameter delay differential equations of boundary value problems is studied in this paper. Regular and singular components are used to estimate the solution’s a priori bounds and derivatives. A fitted finite-difference method is constructed to solve the problem on a Shishkin mesh. The numerical solution converges uniformly to the exact solution; it is validated via numerical test problems. The order of convergence of the numerical method is almost first-order, which is independent of the parameters $\epsilon$ and $\mu$.

1. Introduction

Third-order ordinary differential equations are crucial for modeling and forecasting phenomena in a wide range of scientific domains, including electromagnetic waves, thin-film flow, gravity-driven flows, and the propagation of sound waves in relaxing media [1,2,3,4,5], as well as in many other domains, such as biology, chemical, control engineering, celestial mechanics, and quantum mechanics.

One notable application of third-order ordinary differential equations (ODEs) is the nonlinear Genesio equation. This equation is essential for modeling jerk dynamical systems, which are systems that describe the rate of change of acceleration. The study by Umut and Yasar [6] explored the key characteristics of both regular and chaotic motion within these jerk systems. The most fundamental problem in considering such differential equations is well-posedness. The uniqueness and stability can be established via the differential inequality theorem or maximum principle theorem. For the solution existence, some regularity conditions are to be assumed. For the existence of the solution, the necessary and sufficient conditions for such a linear differential equation are discussed in [7].

Differential equations of the third order with deviating arguments are valuable tools in applied mathematics and physics. They are used to study entry-flow phenomena [8], model electrical pulse propagation in squid nerves with the Nagumo equation [9], and analyze feedback problems in nuclear reactors [10].

This paper deals with a third-order singularly perturbed delay differential equations (SPDDEs) when the diffusion and convection terms are multiplied by two parameters, $\epsilon$ and $\mu$. The solution of such a problem exhibits multi-scale behavior (when $\epsilon \to 0$), i.e., the differential equation’s order is reduced, the reduced problem’s solution does not converge uniformly to the original problem’s solution within the definition’s domain, and the boundary condition is lost in the limiting case. This type of problem exhibits boundary and interior layers. Unless an infinitely large number of mesh points are used within the domain, standard numerical methods usually fail to provide a satisfactory approximate solution on a uniform mesh because of the presence of the boundary and interior layers, as well as the propagation of discontinuity caused by the delay term. Most classical numerical methods demand a large number of uniform mesh points, which leads to a huge algebraic system that is computationally expensive and takes longer to solve. Developing a numerical method is vital for addressing this problem effectively if the method allows more mesh points inside the boundary and interior layer region. A mesh of such kind is called a piecewise uniform Shishkin mesh. A priori knowledge about the solution and its derivatives is necessary for constructing this mesh. The fitted finite-difference method, which we apply in this article to a uniform Shishkin mesh, enables us to obtain robust numerical results. This means that, regardless of the magnitude of the parameters, the accuracy and rate of convergence of the method are guaranteed for the fixed mesh point.

Numerous authors in the literature have developed numerical techniques for two-parameter second-order singularly perturbed differential equations; see [11,12,13,14,15,16,17,18,19] and the references cited therein; however, there is limited work on SPDDEs for second-order; see [20]. The analysis for two-parameter problems occurs in two cases: Case (i) $\mu \le C\sqrt{\epsilon }$ and Case (ii) $\mu \ge C\sqrt{\epsilon }.$ The first case is straightforward and aligns with a simple reaction–diffusion problem. In contrast, the analysis for the second case uses a notably different approach, reflecting the complexities of this situation. O’Malley [13] was the first to introduce the two-parameter problem, highlighting the significance of the ratio of $\mu$ to $\epsilon$, and established sufficient conditions for convergent analysis of the solution of the problem. Numerical methods for singularly perturbed third-order problems with and without deviating arguments have been extensively discussed in [21,22,23,24] and [25,26,27,28], respectively, and the references cited therein.

In the present paper, the motivation and statement of the problem are explained in Section 2. The analytical results are discussed in Section 3. In Section 4, we establish sharp bounds on the derivative estimates of the solution, effectively addressing both regular and singular components. We employ a robust barrier function and maximum principle techniques in this analysis. These sharp bounds are then decisively utilized to examine the upwind finite-difference scheme on the Shishkin mesh, as detailed in Section 5. We establish almost first-order convergence in Section 6. Section 7 examines several test problems that effectively validate our theoretical results, culminating in insightful remarks in Section 8.

Throughout this paper, C and its subscript denote a generic positive constant independent of the parameters $\epsilon ,$$\mu$, and N. Furthermore, $\Vert .\Vert$ denotes the supremum norm ${\Vert \psi \Vert }_{\omega }={sup}_{r\in \omega }\left|\psi (r)\right|.$

2. Problem Statement

The following boundary value problem (BVP) for SPDDEs is taken into consideration, inspired by the works of [11,13].

Find $\mathsf{\Phi }\in Y=C^1(\overline{\mathsf{\Omega }})\cap C^2(\mathsf{\Omega })\cap C^3({\mathsf{\Omega }}^{*})$ such that

$$\left\{\begin{array}{c}-\epsilon {\mathsf{\Phi }}^{\prime \prime \prime }(r)+\mu p(r){\mathsf{\Phi }}^{\prime \prime }(r)+q(r){\mathsf{\Phi }}^{\prime }(r)+g(r)\mathsf{\Phi }(r)+h(r){\mathsf{\Phi }}^{\prime }(r-1)=\mathcal{F}(r),r\in {\mathsf{\Omega }}^{*},\hfill \\ \mathsf{\Phi }(r)=\vartheta (r),r\in [-1,0],{\mathsf{\Phi }}^{\prime }(2)=l,\hfill \end{array}\right.$$

(1)

where $0<\epsilon$; $\mu \ll 1$; $p(r)\ge \alpha >{\alpha }_1>0$; $q(r)\ge \beta \ge {\beta }^0>0$; ${\gamma }_0\le g(r)\le \gamma \le 0$; ${\eta }_0\le h(r)\le 0$; $2\mu \alpha +5\beta +24{\gamma }_0+5{\eta }_0>0$; $\beta -(\gamma -\eta )>\alpha (\alpha +{\alpha }_1)$; and $p,q,g,h,\mathcal{F}$ are sufficiently smooth on $\overline{\mathsf{\Omega }}$. The singularly perturbed BVP (1) can be written as the following equivalent problem.

Find $\overline{\mathsf{\Phi }}=({\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2),{\mathsf{\Phi }}_1\in Y_1=C^0(\overline{\mathsf{\Omega }})\cap C^1(\mathsf{\Omega }\cup \{2\})$ and ${\mathsf{\Phi }}_2\in Y_2=C^0(\overline{\mathsf{\Omega }})\cap C^1(\mathsf{\Omega })\cap C^2({\mathsf{\Omega }}^{*})$ such that

$$\begin{array}{cc}\hfill P_1\overline{\mathsf{\Phi }}(r)& :={\mathsf{\Phi }}_1^{\prime }(r)-{\mathsf{\Phi }}_2(r)=0,r\in \mathsf{\Omega }\cup \{2\},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill P_2\overline{\mathsf{\Phi }}(r)& :=\left\{\begin{array}{c}-\epsilon {\mathsf{\Phi }}_2^{\prime \prime }(r)+p(r)\mu {\mathsf{\Phi }}_2^{\prime }(r)+q(r){\mathsf{\Phi }}_2(r)+g(r){\mathsf{\Phi }}_1(r)\hfill \\ \hfill =\mathcal{F}(r)-h(r){\vartheta }^{\prime }(r-1),r\in {\mathsf{\Omega }}^{-},\\ -\epsilon {\mathsf{\Phi }}_2^{\prime \prime }(r)+p(r)\mu {\mathsf{\Phi }}_2^{\prime }(r)+q(r){\mathsf{\Phi }}_2(r)+g(r){\mathsf{\Phi }}_1(r)\hfill \\ \hfill +h(r){\mathsf{\Phi }}_2(r-1)=\mathcal{F}(r),r\in {\mathsf{\Omega }}^{+},\end{array}\right.\hfill \end{array}$$

(3)

$${\mathsf{\Phi }}_1(0)=\vartheta (0),{\mathsf{\Phi }}_2(0)={\vartheta }^{\prime }(0),{\mathsf{\Phi }}_2(1-)={\mathsf{\Phi }}_2(1+),{\mathsf{\Phi }}_2^{\prime }(1-)={\mathsf{\Phi }}_2^{\prime }(1+),{\mathsf{\Phi }}_2(2)=l,$$

where ${\mathsf{\Phi }}_2(1-)$ and ${\mathsf{\Phi }}_2(1+)$ denote the left and right limits of ${\mathsf{\Phi }}_2$ at $r=1,$ respectively.

A layer of width $O(\epsilon )$ is expected at the right-hand boundary of the domain at $r=2$; when $\epsilon$ is small, $\mu$ is $O(1)$ and positive. If $p(r)$ is negative, a layer is anticipated at the left boundary of the domain at $r=0.$ When $0<\mu \ll 1$ (or $\mu \ne 0,1$), the above problem comprises two-parameter SPDDEs. In this case, the boundary layers may occur at both ends of the domain; the location and width of the layers depend on the magnitude of $\epsilon$ and $\mu .$

When $\mu =0$ and $\mu =1,$ the above two-parameter problem (2) and (3) is reduced to well-known singularly perturbed reaction–diffusion and convection–diffusion problems of a single parameter, respectively. When $0<\mu <1,$ the problem’s solution shows boundary layers that rely on both $\epsilon$ and $\mu .$

If the parameter satisfies the Case (i) condition $\mu \le C\sqrt{\epsilon },$ then the reduced problem of (2) and (3) is

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\upsilon }_{0,1}^{\prime }(r)-{\upsilon }_{0,2}(r)=0,r\in {\mathsf{\Omega }}^{*}\cup \{2\},\hfill \\ q(r){\upsilon }_{0,2}(r)+g(r){\upsilon }_{0,1}(r)=\mathcal{F}(r)-h(r){\vartheta }^{\prime }(r-1),r\in {\mathsf{\Omega }}^{-},\hfill \\ q(r){\upsilon }_{0,2}(r)+g(r){\upsilon }_{0,1}(r)+h(r){\upsilon }_{0,2}(r-1)=\mathcal{F}(r),r\in {\mathsf{\Omega }}^{+},\hfill \end{array}\right.\end{array}$$

with the history function defined in a suitable subdomain. Thus, a boundary layer of width $O(\sqrt{\epsilon })$ is expected in a right-hand neighborhood of $r=0,$ (if ${\mathsf{\Phi }}_2(0)\ne {\vartheta }^{\prime }(0)$) and $r=1$ and also in a left neighborhood of $r=2,$ (if ${\mathsf{\Phi }}_2(2)\ne \ell$) and in a left neighborhood of $r=1.$

If the parameter satisfies the Case (ii) condition $\mu \ge C\sqrt{\epsilon },$ then the reduced problem of (2) and (3) is again a singularly perturbed delay problem with $\mu$ as a parameter.

$$\begin{array}{cc}\hfill P_1\overline{\rho }(r):=& {\rho }_1^{\prime }(r)-{\rho }_2(r)=0,\hfill \\ \hfill P_3\overline{\rho }(r):=& \mu p(r){\rho }_2^{\prime }(r)+q(r){\rho }_2(r)+g(r){\rho }_1(r)+h(r){\rho }_2(r-1)=\mathcal{F}(r),r\in {\mathsf{\Omega }}^{*},\hfill \end{array}$$

with suitable initial conditions. In the right-hand neighborhood of $r=0$ and $r=1,$ a boundary layer of width $O(\mu )$ is anticipated. In the left-hand neighborhood of $r=1$ and $r=2$, a boundary layer of width $O({\displaystyle \frac{\epsilon }{\mu }})$ is anticipated. Since the reduced problem comprises a unit delay term, the boundary layer appears at $r=1$ in both cases.

3. Stability Result

In this section, properties of the solution of the above problem (2) and (3) are discussed. Additionally, the maximum principle is used to generate a stable solution for the same problem.

Theorem 1 

(Maximum principle). For any function $\overline{ð}=({ð}_1,{ð}_2)$ such that ${ð}_1(0)\ge 0$ and ${ð}_2(0)\ge 0,{ð}_2(2)\ge 0,$ $P_1\overline{ð}(r)\ge 0,$ $\forall r\in \mathsf{\Omega }\cup \{2\},$ $P_2\overline{ð}(r)\ge 0,$ $\forall r\in {\mathsf{\Omega }}^{*}$, and ${ð}_2^{\prime }(1+)-{ð}_2^{\prime }(1-)=\left[{ð}_2^{\prime }\right](1)\le 0$, then, ${ð}_1(r)\ge 0,{ð}_2(r)\ge 0,\forall r\in \overline{\mathsf{\Omega }},$ where ${ð}_1\in C^1(\mathsf{\Omega })\mathrm{and}{ð}_2\in C^0(\overline{\mathsf{\Omega }})\cap C^2({\mathsf{\Omega }}^{*}).$

Proof. 

See [24], Theorem 3.1. □

Corollary 1 

(Stability result). For any $\overline{\mathsf{\Phi }}=({\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2)$, ${\mathsf{\Phi }}_1\in Y_1,{\mathsf{\Phi }}_2\in Y_2,$ we have

$$\begin{array}{c}\hfill \mid {\mathsf{\Phi }}_i(r)\mid \le Cmax\{\mid {\mathsf{\Phi }}_1(0)\mid ,\mid {\mathsf{\Phi }}_2(0)\mid ,\mid {\mathsf{\Phi }}_2(2)\mid ,\underset{{\zeta }_1\in \mathsf{\Omega }\cup \{2\}}{sup}\mid P_1\overline{\mathsf{\Phi }}({\zeta }_1)\mid ,\\ \hfill \underset{{\zeta }_2\in {\mathsf{\Omega }}^{-}\cup {\mathsf{\Omega }}^{+}}{sup}\mid P_2\overline{\mathsf{\Phi }}({\zeta }_2)\mid \},\forall r\in \overline{\mathsf{\Omega }},i=1,2.\end{array}$$

(4)

Proof. 

See [24], Corollary 3.1. □

4. Derivative Estimates

A priori bounds for the solutions of (2) and (3) and their derivatives are derived in this section. The subsequent section’s error analysis strongly depends on these bounds.

Lemma 1. 

The solution $\overline{\mathsf{\Phi }}(r)$ of (2) and (3) and its derivatives ${\overline{\mathsf{\Phi }}}^{(k)}(r)$ satisfy the following estimates:

$$\begin{array}{cc}\hfill \Vert {\mathsf{\Phi }}_1^{(k)}{\Vert }_{{\mathsf{\Omega }}^{*}}\le & C\{{\epsilon }^{{\displaystyle \frac{1-k}{2}}}+{({\displaystyle \frac{\mu }{\epsilon }})}^{(k-1)}\},k=0,1,2,3,\hfill \\ \hfill \Vert {\mathsf{\Phi }}_2^{\prime }{\Vert }_{{\mathsf{\Omega }}^{*}}\le & C\{\left({\displaystyle \frac{1}{\sqrt{\epsilon }}}+{\displaystyle \frac{\mu }{\epsilon }}\right)max\{\Vert {\mathsf{\Phi }}_2\Vert ,\Vert {\mathsf{\Phi }}_1{\Vert }_{\overline{\mathsf{\Omega }}}{,\Vert \mathcal{F}\Vert }_{\overline{\mathsf{\Omega }}},\Vert {\vartheta }^{\prime }{\Vert }_{[-1,0]}\}\},\hfill \\ \hfill \Vert {\mathsf{\Phi }}_2^{\prime \prime }{\Vert }_{{\mathsf{\Omega }}^{*}}\le & C\{\left({\displaystyle \frac{1}{{(\sqrt{\epsilon })}^2}}+{\displaystyle \frac{{\mu }^2}{{(\sqrt{\epsilon })}^4}}\right)max\{\Vert {\mathsf{\Phi }}_2\Vert ,\Vert {\mathsf{\Phi }}_1{\Vert }_{\overline{\mathsf{\Omega }}}{,\Vert \mathcal{F}\Vert }_{\overline{\mathsf{\Omega }}},\Vert {\vartheta }^{\prime }{\Vert }_{[-1,0]}\}\},\hfill \\ \hfill \Vert {\mathsf{\Phi }}_2^{\prime \prime \prime }{\Vert }_{{\mathsf{\Omega }}^{*}}\le & C\{\left({\displaystyle \frac{1}{{(\sqrt{\epsilon })}^3}}+{\displaystyle \frac{{\mu }^3}{{(\sqrt{\epsilon })}^6}}\right)max\{\Vert {\mathsf{\Phi }}_2\Vert ,\Vert {\mathsf{\Phi }}_1{\Vert }_{\overline{\mathsf{\Omega }}}{,\Vert \mathcal{F}\Vert }_{\overline{\mathsf{\Omega }}},\Vert {\vartheta }^{\prime }{\Vert }_{[-1,0]}\}\}+{\displaystyle \frac{1}{\epsilon }}{\Vert {\mathcal{F}}^{\prime }\Vert }_{\overline{\mathsf{\Omega }}}.\hfill \end{array}$$

Proof. 

Let $r\in {\mathsf{\Omega }}^{-}.$ We have

$$\begin{array}{cc}\hfill & {\mathsf{\Phi }}_1(r)={\mathsf{\Phi }}_1(0)+{\int }_0^r{\mathsf{\Phi }}_2(t)dt,\hfill \\ \hfill & {\int }_0^{r}p(s){\mathsf{\Phi }}_2^{\prime }(s)ds=\left[p(r){\mathsf{\Phi }}_2(r)-p(0){\mathsf{\Phi }}_2(0)\right]-{\int }_0^r{p}^{\prime }(t){\mathsf{\Phi }}_2(t)dt.\hfill \end{array}$$

$$\begin{array}{cc}\hfill -\epsilon ({\mathsf{\Phi }}_2^{\prime }(r)-{\mathsf{\Phi }}_2^{\prime }(0))& =-{\int }_0^r\mu p(t){\mathsf{\Phi }}_2^{\prime }(t)dt-{\int }_0^r[q(t){\mathsf{\Phi }}_2(t)+g(t){\mathsf{\Phi }}_1(t)]dt\hfill \\ \hfill & +{\int }_0^r[\mathcal{F}(t)-h(t){\vartheta }^{\prime }(t-1)]dt\hfill \\ \hfill & =-\mu \left[p(r){\mathsf{\Phi }}_2(r)-p(0){\mathsf{\Phi }}_2(0)\right]+{\int }_0^r{p}^{\prime }(t){\mathsf{\Phi }}_2(t)dt\hfill \\ \hfill & -{\int }_0^r\left[q(t){\mathsf{\Phi }}_2(t)+g(t){\mathsf{\Phi }}_1(t)\right]dt+{\int }_0^r[\mathcal{F}(t)-h(t){\vartheta }^{\prime }(t-1)]dt.\hfill \end{array}$$

Let ${\mathsf{\Omega }}_{\wp }=[\wp ,\wp +\sqrt{\epsilon }];$ then, by the mean value theorem, there exists $z\in (\wp ,\wp +\sqrt{\epsilon })$ such that $\mid {\mathsf{\Phi }}_2^{\prime }(z)\mid \le {\displaystyle \frac{2}{\sqrt{\epsilon }}}\Vert {\mathsf{\Phi }}_2\Vert .$ Choose $r\in (\wp ,\wp +\sqrt{\epsilon })$ such that $r<y;$ then,

$$\begin{array}{cc}\hfill -\epsilon ({\mathsf{\Phi }}_2^{\prime }(y)-{\mathsf{\Phi }}_2^{\prime }(r))& =-{\int }_r^y\mu p(t){\mathsf{\Phi }}_2^{\prime }(t)dt-{\int }_r^y[q(t){\mathsf{\Phi }}_2(t)+g(t){\mathsf{\Phi }}_1(t)]dt\hfill \\ & +{\int }_r^y[\mathcal{F}(t)-h(t){\vartheta }^{\prime }(t-1)]dt\hfill \\ \hfill & =-\mu \left[p(y){\mathsf{\Phi }}_2(y)-p(r){\mathsf{\Phi }}_2(r)\right]+{\int }_r^y{p}^{\prime }(t){\mathsf{\Phi }}_2(t)dt\hfill \\ & -{\int }_r^y[q(t){\mathsf{\Phi }}_2(t)+g(t){\mathsf{\Phi }}_1(t)]dt+{\int }_r^y[\mathcal{F}(t)-h(t){\vartheta }^{\prime }(t-1)]dt\hfill \\ \hfill \epsilon {\mathsf{\Phi }}_2^{\prime }(r)& =\epsilon {\mathsf{\Phi }}_2^{\prime }(y)-\mu \left[p(y){\mathsf{\Phi }}_2(y)-p(r){\mathsf{\Phi }}_2(r)\right]+{\int }_r^y{p}^{\prime }(t){\mathsf{\Phi }}_2(t)dt\hfill \\ \hfill & -{\int }_r^y[q(t){\mathsf{\Phi }}_2(t)+g(t){\mathsf{\Phi }}_1(t)]dt+{\int }_r^y[\mathcal{F}(t)-h(t){\vartheta }^{\prime }(t-1)]dt.\hfill \end{array}$$

By the triangular inequality, we have

$$\begin{array}{cc}\hfill \epsilon \mid {\mathsf{\Phi }}_2^{\prime }(r)\mid & \le \epsilon \mid {\mathsf{\Phi }}_2^{\prime }(y)\mid +\mu \mid p(y)\mid \mid {\mathsf{\Phi }}_2(y)\mid +\mu \mid p(r)\mid \mid {\mathsf{\Phi }}_2(r)\mid +\mid {\int }_r^y{p}^{\prime }(t){\mathsf{\Phi }}_2(t)dt\mid \hfill \\ \hfill & +\mid {\int }_r^y[q(t){\mathsf{\Phi }}_2(t)\mid +\mid {\int }_r^{y}g(t){\mathsf{\Phi }}_1(t)]dt\mid +\mid {\int }_r^y\mathcal{F}(t)dt\mid \hfill \\ & +\mid {\int }_r^{y}h(t){\vartheta }^{\prime }(t-1)]dt\mid .\hfill \\ \hfill & \le {\displaystyle \frac{2\epsilon }{\sqrt{\epsilon }}}\Vert {\mathsf{\Phi }}_2\Vert +C\mu \Vert {\mathsf{\Phi }}_2\Vert +C\mu \Vert {\mathsf{\Phi }}_2\Vert +C\mu \sqrt{\epsilon }\Vert {\mathsf{\Phi }}_2\Vert +C\sqrt{\epsilon }\Vert {\mathsf{\Phi }}_2\Vert \hfill \\ \hfill & +C\sqrt{\epsilon }\Vert {\mathsf{\Phi }}_1\Vert +C\sqrt{\epsilon }\Vert \mathcal{F}\Vert +C\sqrt{\epsilon }{\Vert {\vartheta }^{\prime }\Vert }_{[-1,0]},\hfill \\ \hfill \mid {\mathsf{\Phi }}_2^{\prime }(r)\mid & \le C\{\left({\displaystyle \frac{1}{\sqrt{\epsilon }}}+{\displaystyle \frac{\mu }{\sqrt{\epsilon }}}+{\displaystyle \frac{\mu }{\epsilon }}\right)\Vert {\mathsf{\Phi }}_2\Vert +{\displaystyle \frac{1}{\sqrt{\epsilon }}}\left(\Vert {\mathsf{\Phi }}_1\Vert +\Vert \mathcal{F}\Vert +\Vert {\vartheta }^{\prime }\Vert \right)\}.\hfill \end{array}$$

Since ${\mathsf{\Phi }}_1,$f, and $\vartheta$ are bounded functions. Therefore,

$$\mid {\mathsf{\Phi }}_2^{\prime }(r)\mid \le C\{\left({\displaystyle \frac{1}{\sqrt{\epsilon }}}+{\displaystyle \frac{\mu }{\epsilon }}\right)max\{\Vert {\mathsf{\Phi }}_2\Vert ,\Vert {\mathsf{\Phi }}_1{\Vert }_{\overline{\mathsf{\Omega }}}{,\Vert \mathcal{F}\Vert }_{\overline{\mathsf{\Omega }}},\Vert {\vartheta }^{\prime }{\Vert }_{[-1,0]}\}\}.$$

From the Equation (3), we have

$$\begin{array}{cc}\hfill -\epsilon {\mathsf{\Phi }}_2^{\prime \prime }(r)=& \mathcal{F}(r)-\mu p(r){\mathsf{\Phi }}_2^{\prime }(r)-q(r){\mathsf{\Phi }}_2(r)-g(r){\mathsf{\Phi }}_1(r)-h(r){\mathsf{\Phi }}_2(r-1),\hfill \\ \hfill \Vert {\mathsf{\Phi }}_2^{\prime \prime }\Vert \le & C\{\left({\displaystyle \frac{1}{{(\sqrt{\epsilon })}^2}}+{\displaystyle \frac{{\mu }^2}{{(\sqrt{\epsilon })}^4}}\right)max\{\Vert {\mathsf{\Phi }}_2\Vert ,\Vert {\mathsf{\Phi }}_1{\Vert }_{\overline{\mathsf{\Omega }}}{,\Vert \mathcal{F}\Vert }_{\overline{\mathsf{\Omega }}},\Vert {\vartheta }^{\prime }{\Vert }_{[-1,0]}\}\}.\hfill \end{array}$$

Differentiating Equation (3) and using the bounds of ${\mathsf{\Phi }}_2^{\prime },$${\mathsf{\Phi }}_2^{\prime \prime },$ we obtain

$$\begin{array}{cc}\hfill \epsilon {\mathsf{\Phi }}_2^{\prime \prime \prime }(r)=& {\mathcal{F}}^{\prime }(r)-\mu p(r){\mathsf{\Phi }}_2^{\prime \prime }(r)-\mu p^{\prime }(r){\mathsf{\Phi }}_2^{\prime }(r)-q(r){\mathsf{\Phi }}_2^{\prime }(r)-q^{\prime }(r){\mathsf{\Phi }}_2(r)-g(r){\mathsf{\Phi }}_1^{\prime }(r)\hfill \\ \hfill & -g^{\prime }(r){\mathsf{\Phi }}_1(r)-h(r){\mathsf{\Phi }}_2^{\prime }(r-1)-h^{\prime }(r){\mathsf{\Phi }}_2(r-1).\hfill \\ \hfill \Vert {\mathsf{\Phi }}_2^{\prime \prime \prime }{\Vert }_{{\mathsf{\Omega }}^{*}}\le & C\{\left({\displaystyle \frac{1}{{(\sqrt{\epsilon })}^3}}+{\displaystyle \frac{{\mu }^3}{{(\sqrt{\epsilon })}^6}}\right)max\{\Vert {\mathsf{\Phi }}_2\Vert ,\Vert {\mathsf{\Phi }}_1{\Vert }_{\overline{\mathsf{\Omega }}}{,\Vert \mathcal{F}\Vert }_{\overline{\mathsf{\Omega }}},\Vert {\vartheta }^{\prime }{\Vert }_{[-1,0]}\}\}+{\displaystyle \frac{1}{\epsilon }}{\Vert {\mathcal{F}}^{\prime }\Vert }_{\overline{\mathsf{\Omega }}}.\hfill \end{array}$$

Now, let $r,y\in (\wp ,\wp +\sqrt{\epsilon })$ such that $r<y$, then

$$\begin{array}{cc}\hfill {\mathsf{\Phi }}_1(y)-{\mathsf{\Phi }}_1(r)=& {\int }_r^y{\mathsf{\Phi }}_2(t)dt\hfill \\ \hfill \mid {\mathsf{\Phi }}_1(y)\mid =& \mid {\mathsf{\Phi }}_1(r)\mid +\mid {\int }_r^y{\mathsf{\Phi }}_2(t)dt\mid \le C+O(\sqrt{\epsilon }).\hfill \end{array}$$

Subsequent differentiation yields the following estimates: $\mid {\mathsf{\Phi }}_1^{(k)}(r)\mid \le C\left({\epsilon }^{{\displaystyle \frac{(1-k)}{2}}}+{({\displaystyle \frac{\mu }{\epsilon }})}^{(k-1)}\right).$ □

4.1. Case (i): Analysis and Estimates

To obtain uniform error estimates, sharper bounds on the derivatives of the solution $\overline{\mathsf{\Phi }}(r)$ are required. We obtain these by breaking down the solution into regular and singular components.

$$\overline{\mathsf{\Phi }}(r)=\overline{\upsilon }(r)+\overline{\chi }(r),$$

where $\overline{\upsilon }=({\upsilon }_1,{\upsilon }_2),$ where ${\upsilon }_1={\overline{\upsilon }}_{0,1}+\sqrt{\epsilon }{\overline{\upsilon }}_{1,1}+\epsilon {\overline{\upsilon }}_{2,1}+{\sqrt{\epsilon }}^3{\upsilon }_{3,1}$; ${\upsilon }_2={\overline{\upsilon }}_{0,2}+\sqrt{\epsilon }{\overline{\upsilon }}_{1,2}+\epsilon {\overline{\upsilon }}_{2,2}+{\sqrt{\epsilon }}^3{\upsilon }_{3,2};$ and ${\overline{\upsilon }}_0,{\overline{\upsilon }}_1$, ${\overline{\upsilon }}_2$, and ${\overline{\upsilon }}_3$ are, in turn, defined to be the solutions of the following problems, respectively:

4.1.1. Estimation of the Smooth Component $\overline{\upsilon }$

Find ${\overline{\upsilon }}_0=({\upsilon }_{0,1},{\upsilon }_{0,2}),{\upsilon }_{0,1},{\upsilon }_{0,2}\in Y_1$ such that

$$\left\{\begin{array}{c}{\upsilon }_{0,1}^{\prime }(r)={\upsilon }_{0,2}(r),r\in {\mathsf{\Omega }}^{*}\cup \{2\},\hfill \\ q(r){\upsilon }_{0,2}(r)+g(r){\upsilon }_{0,1}(r)+h(r){\upsilon }_{0,2}(r-1)=\mathcal{F}(r),r\in {\mathsf{\Omega }}^{*}\cup \{2\},\hfill \\ {\upsilon }_{0,1}(0)=\vartheta (0),{\upsilon }_{0,2}(r)={\vartheta }^{\prime }(r),r\in [-1,0);\hfill \end{array}\right.$$

(5)

${\overline{\upsilon }}_1=({\upsilon }_{1,1},{\upsilon }_{1,2}),{\upsilon }_{1,1}\in Y_1,{\upsilon }_{1,2}\in C^0(\overline{\mathsf{\Omega }})\cap C^1({\mathsf{\Omega }}^{*}\cup \{2\})$ such that

$$\left\{\begin{array}{c}{\upsilon }_{1,1}^{\prime }(r)={\upsilon }_{1,2}(r),r\in {\mathsf{\Omega }}^{*}\cup \{2\},\hfill \\ q(r){\upsilon }_{1,2}(r)+g(r){\upsilon }_{1,1}(r)+h(r){\upsilon }_{1,2}(r-1)=\sqrt{\epsilon }{\upsilon }_{0,2}^{\prime \prime }(r)-{\displaystyle \frac{\mu }{\sqrt{\epsilon }}}a{\upsilon }_{0,2}^{\prime },r\in {\mathsf{\Omega }}^{*}\cup \{2\},\hfill \\ {\upsilon }_{1,1}(0)=0,{\upsilon }_{1,2}(r)=0,r\in [-1,0);\hfill \end{array}\right.$$

(6)

${\overline{\upsilon }}_2=({\upsilon }_{2,1},{\upsilon }_{2,2}),{\upsilon }_{2,1}\in Y_1,{\upsilon }_{2,2}\in Y_2$ such that

$$\left\{\begin{array}{c}{\upsilon }_{2,1}^{\prime }(r)-{\upsilon }_{2,2}(r)=0,r\in {\mathsf{\Omega }}^{*}\cup \{2\},\hfill \\ q(r){\upsilon }_{2,2}(r)+g(r){\upsilon }_{2,1}(r)+h(r){\upsilon }_{2,2}(r-1)=\sqrt{\epsilon }{\upsilon }_{1,2}^{\prime \prime }(r)-{\displaystyle \frac{\mu }{\sqrt{\epsilon }}}a{\upsilon }_{1,2}^{\prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {\upsilon }_{2,1}(0)=0,{\upsilon }_{2,2}(r)=0,r\in [-1,0);\hfill \end{array}\right.$$

(7)

and ${\overline{\upsilon }}_3=({\upsilon }_{3,1},{\upsilon }_{3,2}),{\upsilon }_{2,1}\in Y_1,{\upsilon }_{2,2}\in Y_2$ such that

$$\left\{\begin{array}{c}{P}_1{\overline{\upsilon }}_3:={\upsilon }_{3,1}^{\prime }(r)-{\upsilon }_{3,2}(r)=0,r\in {\mathsf{\Omega }}^{*}\cup \{2\},\hfill \\ P_2{\overline{\upsilon }}_3:=-\epsilon {\upsilon }_{3,2}^{\prime \prime }(r)+\mu p(r){\upsilon }_{3,2}^{\prime }(r)+q(r){\upsilon }_{3,2}(r)+g(r){\upsilon }_{3,1}(r)\hfill \\ +h(r){\upsilon }_{3,2}(r-1)=\sqrt{\epsilon }{\upsilon }_{2,2}^{\prime \prime }(r)-{\displaystyle \frac{\mu }{\sqrt{\epsilon }}}a{\upsilon }_{2,2}^{\prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {\upsilon }_{3,1}(0)=0,{\upsilon }_{3,2}(r)=0,r\in [-1,0],{\upsilon }_{3,2}(2)=0.\hfill \end{array}\right.$$

(8)

Thus, the smooth component $\overline{\upsilon }$ satisfies the following: Find $\overline{\upsilon }=({\upsilon }_1,{\upsilon }_2),{\upsilon }_1\in Y_1,{\upsilon }_2\in C^0(\overline{\mathsf{\Omega }})\cap C^2({\mathsf{\Omega }}^{*})$ such that

$$\left\{\begin{array}{c}{P}_1\overline{\upsilon }(r):={\upsilon }_1(r)-{\upsilon }_2(r)=0,r\in {\mathsf{\Omega }}^{*}\cup \{2\},\hfill \\ P_2\overline{\upsilon }(r):=-\epsilon {\upsilon }_2^{\prime \prime }(r)+\mu p(r){\upsilon }_2^{\prime }(r)+q(r){\upsilon }_2(r)+g(r){\upsilon }_1(r)+h(r){\upsilon }_2(r-1)=\mathcal{F}(r),r\in {\mathsf{\Omega }}^{*},\hfill \\ {\upsilon }_1(0)=\vartheta (0),{\upsilon }_2(r)=\left\{\begin{array}{c}{\vartheta }^{\prime }(r),r\in [-1,0),\hfill \\ {\upsilon }_{0,2}(0)+\sqrt{\epsilon }{\upsilon }_{1,2}(0)+{(\sqrt{\epsilon })}^2{\upsilon }_{2,2}(0)+{(\sqrt{\epsilon })}^3{\upsilon }_{3,2}(0),r=0,\hfill \end{array}\right.\hfill \\ {\upsilon }_2(1)={\upsilon }_{0,2}(1)+\sqrt{\epsilon }{\upsilon }_{1,2}(1)+{(\sqrt{\epsilon })}^2{\upsilon }_{2,2}(1)+{(\sqrt{\epsilon })}^3{\upsilon }_{3,2}(1),\hfill \\ {\upsilon }_2(2)={\upsilon }_{0,2}(2)+\sqrt{\epsilon }{\upsilon }_{1,2}(2)+{(\sqrt{\epsilon })}^2{\upsilon }_{2,2}(2).\hfill \end{array}\right.$$

(9)

Since $p(r),$ $q(r),$ $g(r),$ $h(r),$ $\mathcal{F}(r),$ and $\vartheta (r)$ are sufficiently differentiable functions and $\mu \le C\sqrt{\epsilon },$ we have $\Vert {\upsilon }_{0,1}^{(k)}{\Vert }_{\overline{\mathsf{\Omega }}}\le C,$ $\Vert {\upsilon }_{0,2}^{(k)}{\Vert }_{\overline{\mathsf{\Omega }}}\le C,$ $\Vert {\upsilon }_{1,1}^{(k)}{\Vert }_{\overline{\mathsf{\Omega }}}\le C,$ $\Vert {\upsilon }_{1,2}^{(k)}{\Vert }_{\overline{\mathsf{\Omega }}}\le C,$ $\Vert {\upsilon }_{2,1}^{(k)}{\Vert }_{\overline{\mathsf{\Omega }}}\le C,$ $\Vert {\upsilon }_{2,2}^{(k)}{\Vert }_{\overline{\mathsf{\Omega }}}\le C.$

Using Lemma 2 in [11], we have $\Vert {\upsilon }_{3,1}{\Vert }_{\overline{\mathsf{\Omega }}}\le C,$ $\Vert {\upsilon }_{3,2}{\Vert }_{\overline{\mathsf{\Omega }}}\le C.$

Using (8) and for $\mu \le C\sqrt{\epsilon },$ we have $\Vert {\upsilon }_{3,1}^{(k)}{\Vert }_{\overline{\mathsf{\Omega }}}\le C{\epsilon }^{-{\displaystyle \frac{(k-1)}{2}}},$ $\Vert {\upsilon }_{3,2}^{(k)}{\Vert }_{\overline{\mathsf{\Omega }}}\le C{\epsilon }^{-{\displaystyle \frac{k}{2}}}.$ To bound the regular component $\overline{\upsilon }(r),$ using the above bounds and their derivatives, as well as the Corollary 1, we have

$$\Vert {\upsilon }_1^{(k)}\Vert \le C(1+{\epsilon }^{{\displaystyle \frac{3-k}{2}}}),\Vert {\upsilon }_2^{(k)}\Vert \le C(1+{\epsilon }^{{\displaystyle \frac{2-k}{2}}}).$$

4.1.2. Estimates of Singular Component $\overline{\chi }(r)$

Furthermore, $\overline{\chi }$ satisfies the following problem:

find $\overline{\chi }=({\chi }_1,{\chi }_2),{\chi }_1\in Y_1,{\chi }_2\in C^0(\overline{\mathsf{\Omega }})\cap C^2({\mathsf{\Omega }}^{*})$ such that

$$\left\{\begin{array}{c}{P}_1\overline{\chi }(r):={\chi }_1^{\prime }(r)-{\chi }_2(r)=0,r\in {\mathsf{\Omega }}^{*}\cup \{2\},\hfill \\ P_2\overline{\chi }(r):=-\epsilon {\chi }_2^{\prime \prime }(r)+\mu p(r){\chi }_2^{\prime }(r)+q(r){\chi }_2(r)+g(r){\chi }_1(r)\hfill \\ +h(r){\chi }_2(r-1)=0,r\in {\mathsf{\Omega }}^{*},\hfill \\ {\chi }_1(0)=0,{\chi }_2(r)=\left\{\begin{array}{c}0,r\in [-1,0),\hfill \\ {\vartheta }^{\prime }(0)-v_2(0),r=0,\hfill \end{array}\right.\left[{\chi }_2\right](1)=-\left[{\upsilon }_2\right](1),\hfill \\ {\chi }_2^{\prime }](1)=-\left[{\upsilon }_2^{\prime }\right](1),{\chi }_2(2)=l-{\upsilon }_2(2).\hfill \end{array}\right.$$

(10)

Note that ${\upsilon }_2+{\chi }_2={\mathsf{\Phi }}_2\in Y_2.$ We further decompose $\overline{\chi }={\overline{\chi }}_L+{\overline{\chi }}_R$, where ${\overline{\chi }}_L=({\chi }_{L,1},{\chi }_{L,2})$ and ${\overline{\chi }}_R=({\chi }_{R,1},{\chi }_{R,2})$. The functions ${\overline{\chi }}_L$ and ${\overline{\chi }}_R$ satisfy the following problems, respectively:

Find ${\overline{\chi }}_L$, ${\chi }_{L,1}\in Y_1,{\chi }_{L,2}\in Y_2$ such that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_1{\overline{\chi }}_L:={\chi }_{L,1}^{\prime }(r)-{\chi }_{L,2}(r)=0,\hfill \\ P_2{\overline{\chi }}_L:=-\epsilon {\chi }_{L2}^{\prime \prime }(r)+\mu p(r){\chi }_{L,2}^{\prime }(r)+q(r){\chi }_{L,2}(r)+g(r){\chi }_{L,1}(r)+h(r){\chi }_{L,2}(r-1)=0,\hfill \\ {\chi }_{L,1}(0)=0,{\chi }_{L,2}(r)=\left\{\begin{array}{c}0,r\in [-1,0),\hfill \\ {\vartheta }^{\prime }(0)-v_2(0),r=0,\hfill \end{array}\right.\hfill \\ {\chi }_{L,2}^{\prime }](1)=-{\displaystyle \frac{1}{2}}\left[{\upsilon }_2^{\prime }\right](1),{\chi }_{L,2}(2)=0,\hfill \end{array}\right.\end{array}$$

(11)

and find ${\overline{\chi }}_R,{\chi }_{R,1}\in Y_1,{\chi }_{R,2}\in C^0(\overline{\mathsf{\Omega }})\cap C^2({\mathsf{\Omega }}^{*})$ such that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_1{\overline{\chi }}_R:={\chi }_{R,1}^{\prime }(r)-{\chi }_{R,2}(r)=0,\hfill \\ P_2{\overline{\chi }}_R:=-\epsilon {\chi }_{R,2}^{\prime \prime }(r)+\mu p(r){\chi }_{R,2}^{\prime }(r)+q(r){\chi }_{R,2}(r)+g(r){\chi }_{R,1}(r)+h(r){\chi }_{R,2}(r-1)=0,\hfill \\ {\chi }_{R,1}(0)=0,{\chi }_{R,2}(r)=0,r\in [-1,0],\left[{\chi }_{R,2}\right](1)=-\left[{\upsilon }_2\right](1),\hfill \\ {\chi }_{R,2}^{\prime }](1)=-{\displaystyle \frac{1}{2}}\left[{\upsilon }_2^{\prime }\right](1),{\chi }_{R,2}(2)=l-{\upsilon }_2(2).\hfill \end{array}\right.\end{array}$$

(12)

Using Lemma 1, ${\chi }_{R,1}(r)$ and ${\chi }_{R,2}(r)$ satisfy the following rough bounds:

$$\Vert {\chi }_{R,1}^{(k)}\Vert \le C{\epsilon }^{{\displaystyle \frac{1-k}{2}}},\Vert {\chi }_{R,2}^{(k)}\Vert \le C{\epsilon }^{{\displaystyle \frac{-k}{2}}}.$$

The following theorem gives the sharp bounds of the above.

Theorem 2. 

Let $\overline{\chi }$ be the singular components of the solution $\overline{\mathsf{\Phi }};$ for $\mu \le C\sqrt{\epsilon }$, $k=0,1,2,3,$ we have the following:

$$\begin{array}{cc}\hfill & \mid {\chi }_{L,1}^{(k)}(r)\mid \le C{\epsilon }^{{\displaystyle \frac{1-k}{2}}}\left\{\begin{array}{c}{e}^{-r\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(r-1)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},r\in {\mathsf{\Omega }}^{+},\hfill \end{array}\right.\mid {\chi }_{L,2}^{(k)}(r)\mid \le C{\epsilon }^{-{\displaystyle \frac{k}{2}}}\left\{\begin{array}{c}{e}^{-r\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(r-1)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},r\in {\mathsf{\Omega }}^{+},\hfill \end{array}\right.\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & \mid {\chi }_{R,1}^{(k)}(r)\mid \le C{\epsilon }^{{\displaystyle \frac{1-k}{2}}}\left\{\begin{array}{c}{e}^{-(1-r)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(2-r)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},r\in {\mathsf{\Omega }}^{+},\hfill \end{array}\right.\mid {\chi }_{R,2}^{(k)}(r)\mid \le C{\epsilon }^{-{\displaystyle \frac{k}{2}}}\left\{\begin{array}{c}{e}^{-(1-r)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(2-r)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},r\in {\mathsf{\Omega }}^{+}.\hfill \end{array}\right.\hfill \end{array}$$

(14)

Proof. 

Let ${\overline{ð}}^{\pm }=({ð}_1^{\pm },{ð}_2^{\pm })$ be the barrier function used to estimate the bounds of ${\chi }_{L,1}(r)$ and ${\chi }_{L,2}(r)$ in [0, 1] such that

$$\begin{array}{cc}\hfill {ð}_{L,1}^{\pm }(r)=& C_1\sqrt{\epsilon }\sqrt{\beta }\{1-e^{-r\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}}\}\pm {\chi }_{L,1}(r),r\in {\mathsf{\Omega }}^{-},\hfill \\ \hfill {ð}_{L,2}^{\pm }(r)=& C_1\{\beta e^{-r\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}}\}\pm {\chi }_{L,2}(r),r\in {\mathsf{\Omega }}^{-}.\hfill \end{array}$$

It is easy to check that ${ð}_{L,1}^{\pm }(0)\ge 0,$ and ${ð}_{L,2}^{\pm }(0)\ge 0,$ ${ð}_{L,2}^{\pm }(1)\ge 0$ and, for sufficiently large $C_1,$

$$\begin{array}{cc}\hfill P_1{\overline{ð}}^{\pm }(r)=& C\{\sqrt{\epsilon }({\displaystyle \frac{\beta }{\sqrt{\epsilon }}}{e}^{-r\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}})-(\beta e^{-r\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}})\}\pm 0\ge 0,\hfill \\ \hfill P_2{\overline{ð}}^{\pm }(r)=& C\{[\beta (q(r)-\beta )-\mu \beta p(r)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}-\sqrt{\epsilon }g(r)\sqrt{\beta }]e^{-r\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}}+g(r)\sqrt{\beta }\sqrt{\epsilon }\}\pm 0\ge 0.\hfill \end{array}$$

By [27], Theorem 2.1, we have

$$\begin{array}{cc}\hfill |{\chi }_{L,1}^{(k)}(r)|\le & C{\epsilon }^{{\displaystyle \frac{1-k}{2}}}{e}^{-r\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},r\in [0,1],k=0,1,2,3.\hfill \\ \hfill |{\chi }_{L,2}^{(k)}(r)|\le & C{\epsilon }^{-{\displaystyle \frac{k}{2}}}{e}^{-r\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},r\in [0,1],k=0,1,2,3.\hfill \end{array}$$

Let $r\in [1,2];$ thenm ${\overline{ð}}^{\pm }=({ð}_{L,1}^{\pm },{ð}_{L,2}^{\pm })$, where

$$\begin{array}{cc}\hfill {ð}_{L,1}^{\pm }(r)=& C_1\sqrt{\epsilon }\{\sqrt{\beta }-\sqrt{\beta }{e}^{-(r-1)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}}\}\pm {\chi }_{L,1}(r),r\in {\mathsf{\Omega }}^{+},\hfill \\ \hfill {ð}_{L,2}^{\pm }(r)=& C_1\{\beta e^{-(r-1)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}}\}\pm {\chi }_{L,2}(r),r\in {\mathsf{\Omega }}^{+}.\hfill \end{array}$$

Also, ${ð}_{L,1}^{\pm }(1)\ge 0,$${ð}_{L,2}^{\pm }(1)\ge 0,$${ð}_{L,2}^{\pm }(2)\ge 0$, and

$$\begin{array}{cc}\hfill P_1{\overline{ð}}_L^{\pm }(r)=& C\{\sqrt{\epsilon }({\displaystyle \frac{\beta }{\sqrt{\epsilon }}}{e}^{-(r-1)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}})-(\beta e^{-(r-1)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}})\}\pm 0\ge 0,\hfill \\ \hfill P_2{\overline{ð}}_L^{\pm }(r)=& C\{[\beta (q(r)-\beta )-\mu p(r)\beta \sqrt{{\displaystyle \frac{\beta }{\epsilon }}}-\sqrt{\epsilon }g(r)\sqrt{\beta }+h(r)\beta ]e^{-(r-1)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}}\hfill \\ \hfill & +\sqrt{\epsilon }g(r)\sqrt{\beta }+h(r)\beta e^{\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}}\}\pm 0\ge 0.\hfill \end{array}$$

Again, by using [27], Theorem 2.1, we have

$$\begin{array}{c}\hfill \mid {\chi }_{L,1}^{(k)}(r)\mid \le C{\epsilon }^{{\displaystyle \frac{1-k}{2}}}\{e^{-(r-1)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}}\},r\in [1,2],k=0,1,2,3.\\ \hfill \mid {\chi }_{L,2}^{(k)}(r)\mid \le C{\epsilon }^{-{\displaystyle \frac{k}{2}}}\{e^{-(r-1)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}}\},r\in [1,2],k=0,1,2,3.\end{array}$$

Similarly, the singular component ${\chi }_{R,1},{\chi }_{R,2}$ and its derivative bounds are estimated using the maximum principle with a suitable barrier function. □

Note: from the preceding theorem, it is clear that when $\mu \le C\sqrt{\epsilon },$ $k=1,2,$ we have

$$\begin{array}{c}\hfill \mid {\mathsf{\Phi }}_{L,k}(r)-{\upsilon }_{L,k}(r)\mid \le C{\epsilon }^{{\displaystyle \frac{2-k}{2}}}\left\{\begin{array}{cc}{e}^{-r\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},\hfill & r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(r-1)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},\hfill & r\in {\mathsf{\Omega }}^{+},\hfill \end{array}\right.\end{array}$$

(15)

$$\begin{array}{c}\hfill \mid {\mathsf{\Phi }}_{R,k}(r)-{\upsilon }_{R,k}(r)\mid \le C{\epsilon }^{{\displaystyle \frac{2-k}{2}}}\left\{\begin{array}{cc}{e}^{-(1-r)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},\hfill & r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(2-r)\sqrt{{\displaystyle \frac{\beta }{\epsilon }}}},\hfill & r\in {\mathsf{\Omega }}^{+}.\hfill \end{array}\right.\end{array}$$

(16)

4.2. Case (ii): Analysis and Estimates

The estimates of the regular and singular components for the case $\mu \ge C\sqrt{\epsilon }$ are provided in this section.

4.2.1. Estimation of the Smooth Component $\overline{\upsilon }$

Furthermore, we have the decomposition of $\overline{\upsilon }$ into $\overline{\rho }+\epsilon \overline{\psi }+{\epsilon }^2\overline{{\rm Y}}+{\epsilon }^3\overline{\phi }$ and $\overline{\upsilon }=({\upsilon }_1,{\upsilon }_2),$ where ${\upsilon }_1={\rho }_1(r,\mu )+\epsilon {\psi }_1(r,\mu )+{\epsilon }^2{{\rm Y}}_1(r,\mu )+{\epsilon }^3{\phi }_1(r,\mu ,\epsilon )$ and ${\upsilon }_2={\rho }_2(r,\mu )+\epsilon {\psi }_2(r,\mu )+{\epsilon }^2{{\rm Y}}_2(r,\mu )+{\epsilon }^3{\phi }_2(r,\mu ,\epsilon ).$

Let $\overline{\rho }=({\rho }_1,{\rho }_2)$ satisfy the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\rho }_1^{\prime }(r)-{\rho }_2(r)=0,\hfill \\ \mu p(r){\rho }_2^{\prime }(r)+q(r){\rho }_2(r)+g(r){\rho }_1(r)+h(r){\rho }_2(r-1)=\mathcal{F}(r),r\in {\mathsf{\Omega }}^{*},\hfill \\ {\rho }_1(r)=\vartheta (r),{\rho }_2(r)=\left\{\begin{array}{c}{\vartheta }^{\prime }(r),r\in [-1,0),\hfill \\ {\rho }_{0,2}(0)+\mu {\rho }_{1,2}(0)+{\mu }^2{\rho }_{2,2}(0),r=0.\hfill \end{array}\right.\hfill \end{array}\right.\end{array}$$

(17)

Let $\overline{\psi }=({\psi }_1,{\psi }_2)$ satisfy the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\psi }_1^{\prime }(r)-{\psi }_2(r)=0,\hfill \\ \mu p(r){\psi }_2^{\prime }(r)+q(r){\psi }_2(r)+g(r){\psi }_1(r)+h(r){\psi }_2(r-1)=-{\rho }_2^{\prime \prime }(r),r\in {\mathsf{\Omega }}^{*},\hfill \\ {\psi }_1(0)=0,{\psi }_2(r)=\left\{\begin{array}{c}0,r\in [-1,0),\hfill \\ {\psi }_{0,2}(0)+\mu {\psi }_{1,2}(0),r=0.\hfill \end{array}\right.\hfill \end{array}\right.\end{array}$$

(18)

Let $\overline{{\rm Y}}=({{\rm Y}}_1,{{\rm Y}}_2)$ satisfy the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{{\rm Y}}_1^{\prime }(r)-{{\rm Y}}_2(r)=0,\hfill \\ \mu p(r){{\rm Y}}_2^{\prime }(r)+q(r){{\rm Y}}_2(r)+g(r){{\rm Y}}_1(r)+h(r){{\rm Y}}_2(r-1)=-{\psi }_2^{\prime \prime }(r),r\in {\mathsf{\Omega }}^{*},\hfill \\ {{\rm Y}}_1(0)=0,{{\rm Y}}_2(r)=\left\{\begin{array}{c}0,r\in [-1,0),\hfill \\ {{\rm Y}}_{0,2}(0)+\mu {{\rm Y}}_{1,2}(0),r=0.\hfill \end{array}\right.\hfill \end{array}\right.\end{array}$$

(19)

Let $\overline{\phi }=({\phi }_1,{\phi }_2)$ satisfy the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_1\overline{\phi }(r):={\phi }_1^{\prime }(r)-{\phi }_2(r)=0,\hfill \\ P_2\overline{\phi }(r):=-\epsilon {\phi }_2^{\prime \prime }(r)+\mu p(r){\phi }_2^{\prime }(r)+q(r){\phi }_2(r)+g(r){\phi }_1(r)\hfill \\ +h(r){\phi }_2(r-1)=-{{\rm Y}}_2^{\prime \prime }(r),r\in {\mathsf{\Omega }}^{*},\hfill \\ {\phi }_1(0)=0,{\phi }_2(0)=0,r\in [-1,0),{\phi }_2(2)=0.\hfill \end{array}\right.\end{array}$$

(20)

Lemma 2 

([29]). Let $\overline{\mathsf{\Phi }}\in C^1({\mathsf{\Omega }}^{*})\times C^1({\mathsf{\Omega }}^{*})$ with ${\mathsf{\Phi }}_1(0)\ge 0,$${\mathsf{\Phi }}_2(0)\ge 0,$$P_1\overline{\mathsf{\Phi }}\ge 0$, $P_3\overline{\mathsf{\Phi }}\ge 0,\forall r\in {\mathsf{\Omega }}^{*};$ then, ${\mathsf{\Phi }}_i(r)\ge 0,\forall r\in \overline{\mathsf{\Omega }},i=1,2.$

Further decomposition of $\overline{\rho }=({\rho }_1,{\rho }_2)$ is defined below:

${\rho }_1={\rho }_{0,1}(r)+\mu {\rho }_{1,1}(r)+{\mu }^2{\rho }_{2,1}(r)+{\mu }^3{\rho }_{3,1}(r)$ and ${\rho }_2={\rho }_{0,2}(r)+\mu {\rho }_{1,2}(r)+{\mu }^2{\rho }_{2,2}(r)+{\mu }^3{\rho }_{3,2}(r,\mu ).$

Let ${\overline{\rho }}_0=({\rho }_{0,1},{\rho }_{0,2})$ satisfy the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\rho }_{0,1}^{\prime }(r)-{\rho }_{0,2}(r)=0,\hfill \\ q(r){\rho }_{0,2}(r)+g(r){\rho }_{0,1}(r)+h(r){\rho }_{0,2}(r-1)=\mathcal{F}(r),r\in {\mathsf{\Omega }}^{*},\hfill \\ {\rho }_{0,1}(0)=\vartheta (0),{\rho }_{0,2}(r)={\vartheta }^{\prime }(r),r\in [-1,0).\hfill \end{array}\right.\end{array}$$

Let ${\overline{\rho }}_1=({\rho }_{1,1},{\rho }_{1,2})$ satisfy the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\rho }_{1,1}^{\prime }(r)-{\rho }_{1,2}(r)=0,\hfill \\ q(r){\rho }_{1,2}(r)+g(r){\rho }_{1,1}(r)+h(r){\rho }_{1,2}(r-1)=-p(r){\rho }_{0,2}^{\prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {\rho }_{1,1}(0)=0,{\rho }_{1,2}(r)=0,r\in [-1,0).\hfill \end{array}\right.\end{array}$$

Let ${\overline{\rho }}_2=({\rho }_{2,1},{\rho }_{2,2})$ satisfy the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\rho }_{2,1}^{\prime }(r)-{\rho }_{2,2}(r)=0,\hfill \\ q(r){\rho }_{2,2}(r)+g(r){\rho }_{2,1}(r)+h(r){\rho }_{2,2}(r-1)=-p(r){\rho }_{1,2}^{\prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {\rho }_{2,1}(0)=0,{\rho }_{2,2}(r)=0,r\in [-1,0).\hfill \end{array}\right.\end{array}$$

Let ${\overline{\rho }}_3=({\rho }_{3,1},{\rho }_{3,2})$ satisfy the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\rho }_{3,1}^{\prime }(r)-{\rho }_{3,2}(r)=0,\hfill \\ \mu p(r){\rho }_{3,2}^{\prime }+q(r){\rho }_{3,2}(r)+g(r){\rho }_{3,1}(r)+h(r){\rho }_{3,2}(r-1)=-p(r){\rho }_{2,2}^{\prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {\rho }_{3,1}(0)=0,{\rho }_{3,2}(r)=0,r\in [-1,0],{\rho }_{3,2}(1)=0\hfill \end{array}\right.\end{array}$$

(21)

since $p(r),$$q(r),$$g(r),$$h(r),$$\vartheta (r)$, and $\mathcal{F}(r)$ are sufficiently differential functions on $\overline{\mathsf{\Omega }}$.

Hence, $\Vert {\rho }_{0,1}^{(k)}\Vert \le C,$$\Vert {\rho }_{0,2}^{(k)}\Vert \le C,$$\Vert {\rho }_{1,1}^{(k)}\Vert \le C,$$\Vert {\rho }_{1,2}^{(k)}\Vert \le C,$$\Vert {\rho }_{2,1}^{(k)}\Vert \le C,$ $\Vert {\rho }_{2,2}^{(k)}\Vert \le C.$

Using (21) and Theorem 1, it is proved that $\Vert {\rho }_{3,2}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^k}}.$

Therefore,

$$\begin{array}{c}\hfill \Vert {\rho }_1^{(k)}\Vert \le C(1+{\mu }^{-(k-4)}),\Vert {\rho }_2^{(k)}\Vert \le C(1+{\mu }^{-(k-3)}),k=0,1,2,3.\end{array}$$

(22)

Consider the further decomposition of $\overline{\psi }=({\psi }_1,{\psi }_2),$ where ${\psi }_1(r)={\psi }_{0,1}(r)+\mu {\psi }_{1,1}(r)+{\mu }^2{\psi }_{2,1}(r)$ and ${\psi }_2(r,\mu )={\psi }_{0,2}(r)+\mu {\psi }_{1,2}(r)+{\mu }^2{\psi }_{2,2}(r,\mu ).$

Let ${\overline{\psi }}_0=({\psi }_{0,1},{\psi }_{0,2}),$${\overline{\psi }}_1=({\psi }_{1,1},{\psi }_{1,2}),$ and ${\overline{\psi }}_2=({\psi }_{2,1},{\psi }_{2,2})$ be the solutions, respectively, satisfying the following problems with zero initial function:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\psi }_{0,1}^{\prime }(r)-{\psi }_{0,2}(r)=0,\hfill \\ q(r){\psi }_{0,2}(r)+g(r){\psi }_{0,1}(r)+h(r){\psi }_{0,2}(r-1)=-{\rho }_2^{\prime \prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {\psi }_{0,1}(0)=0,{\psi }_{0,2}(r)=0,r\in [-1,0),\hfill \end{array}\right.\end{array}$$

(23)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\psi }_{1,1}^{\prime }(r)-{\psi }_{1,2}(r)=0,\hfill \\ q(r){\psi }_{1,2}(r)+g(r){\psi }_{1,1}(r)+h(r){\psi }_{1,2}(r-1)=-p(r){\psi }_{0,2}^{\prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {\psi }_{1,1}(0)=0,{\psi }_{1,2}(r)=0,r\in [-1,0),\hfill \end{array}\right.\end{array}$$

(24)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\psi }_{2,1}^{\prime }(r)-{\psi }_{2,2}(r)=0,\hfill \\ \mu p(r){\psi }_{2,2}^{\prime }(r)+q(r){\psi }_{2,2}(r)+g(r){\psi }_{2,1}(r)+h(r){\psi }_{2,2}(r-1)=-p(r){\psi }_{1,2}^{\prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {\psi }_{2,1}(0)=0,{\psi }_{2,2}(r)=0,r\in [-1,0],{\psi }_{2,2}(1)=0.\hfill \end{array}\right.\end{array}$$

(25)

From (23)–(25) and Lemma 2 with suitable barrier function ${ð}_k^{\pm }=C\{s_k(x)\}\pm {\psi }_{2,k}(x),k=1,2,$ we obtain the following bounds $\mid {\psi }_{0,2}^{(k)}\mid \le C(1+{\mu }^{-(k-1)}),$$\mid {\psi }_{1,2}^{(k)}\mid \le {\displaystyle \frac{C}{{\mu }^k}},$$\mid {\psi }_{2,2}^{(k)}\mid \le {\displaystyle \frac{C}{{\mu }^{k+1}}}.$

Therefore, $\mid {\psi }_1^{(k)}\mid \le C(1+{\mu }^{-(k-2)}),$ and $\mid {\psi }_2^{(k)}\mid \le C(1+{\mu }^{-(k-1)}).$

Consider the further decomposition of $\overline{{\rm Y}}=({{\rm Y}}_1,{{\rm Y}}_2),$ where

$$\begin{array}{cc}\hfill & {{\rm Y}}_1(r)={{\rm Y}}_{0,1}(r)+\mu {{\rm Y}}_{1,1}(r)+{\mu }^2{{\rm Y}}_{2,1}(r),{{\rm Y}}_2(r,\mu )={{\rm Y}}_{0,2}(r)+\mu {{\rm Y}}_{1,2}(r)+{\mu }^2{{\rm Y}}_{2,2}(r,\mu ).\hfill \end{array}$$

Let ${\overline{{\rm Y}}}_0=({{\rm Y}}_{0,1},{{\rm Y}}_{0,2}),$${\overline{{\rm Y}}}_1=({{\rm Y}}_{1,1},{{\rm Y}}_{1,2}),$ and ${\overline{{\rm Y}}}_2=({{\rm Y}}_{2,1},{{\rm Y}}_{2,2})$ be the solutions of the following problems, respectively:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{{\rm Y}}_{0,1}^{\prime }(r)-{{\rm Y}}_{0,2}(r)=0,\hfill \\ q(r){{\rm Y}}_{0,2}(r)+g(r){{\rm Y}}_{0,1}(r)+h(r){{\rm Y}}_{0,2}(r-1)=-{\psi }_2^{\prime \prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {{\rm Y}}_{0,1}(0)=0,{{\rm Y}}_{0,2}(r)=0,r\in [-1,0),\hfill \end{array}\right.\hfill \\ \hfill & \left\{\begin{array}{c}{{\rm Y}}_{1,1}^{\prime }(r)-{{\rm Y}}_{1,2}(r)=0,\hfill \\ q(r){{\rm Y}}_{1,2}(r)+g(r){{\rm Y}}_{1,1}(r)+h(r){{\rm Y}}_{1,2}(r-1)=-p(r){{\rm Y}}_{0,2}^{\prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {{\rm Y}}_{1,1}(0)=0,{{\rm Y}}_{1,2}(r)=0,r\in [-1,0),\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{{\rm Y}}_{2,1}^{\prime }(r)-{{\rm Y}}_{2,2}(r)=0,\hfill \\ \mu p(r){{\rm Y}}_{2,2}^{\prime }(r)+q(r){{\rm Y}}_{2,2}(r)+g(r){{\rm Y}}_{2,1}(r)+h(r){{\rm Y}}_{2,2}(r-1)=-p(r){{\rm Y}}_{1,2}^{\prime },r\in {\mathsf{\Omega }}^{*},\hfill \\ {{\rm Y}}_{2,1}(0)=0,{{\rm Y}}_{2,2}(r)=0,r\in [-1,0],{{\rm Y}}_{2,2}(1)=0.\hfill \end{array}\right.\hfill \end{array}$$

(26)

Using (26) with suitable barrier function ${ð}_k^{\pm }=C\{s_k(x)\}\pm {{\rm Y}}_{2,k}(x),k=1,2,$ and Lemma 2, it is easy to see that $\mid {{\rm Y}}_1^{(k)}\mid \le {\displaystyle \frac{C}{{\mu }^k}},$$\mid {{\rm Y}}_2^{(k)}\mid \le {\displaystyle \frac{C}{{\mu }^{k+1}}}.$

Applying Theorem 1 with Equation (20), we obtain $\mid {\phi }_2\mid \le {\displaystyle \frac{C}{{\mu }^3}}$ and $\mid {\phi }_1\mid \le {\displaystyle \frac{C}{{\mu }^2}}.$

Using Lemma 1, it is easy to show that $\mid {\phi }_2^{\prime }\mid \le {\displaystyle \frac{C}{{\mu }^3}}{\displaystyle \frac{1}{\sqrt{\epsilon }}}(1+{\displaystyle \frac{\mu }{\sqrt{\epsilon }}}),$$\mid {\phi }_2^{\prime \prime }\mid \le {\displaystyle \frac{C}{{\mu }^3}}{\displaystyle \frac{1}{\epsilon }}(1+{\displaystyle \frac{{\mu }^2}{\epsilon }}).$ Since $\mu \ge C\sqrt{\epsilon },$ we obtain $\mid {\phi }_2^{(3)}\mid \le {\displaystyle \frac{C}{{\epsilon }^3}};$ then,

$$\begin{array}{c}\hfill \mid {\upsilon }_1^{(k)}\mid \le C(1+{({\displaystyle \frac{\epsilon }{\mu }})}^{-(k-4)}),\mid {\upsilon }_2^{(k)}\mid \le C(1+{({\displaystyle \frac{\epsilon }{\mu }})}^{-(k-3)}),k=0,1,2,3.\end{array}$$

4.2.2. Estimates of Singular Component $\overline{\chi }(r)$

Furthermore, $\overline{\chi }$ satisfies the following problem:

Find $\overline{\chi }=({\chi }_1,{\chi }_2),{\chi }_1\in Y_1,{\chi }_2\in C^0(\overline{\mathsf{\Omega }})\cap C^2({\mathsf{\Omega }}^{*})$ such that

$$\left\{\begin{array}{c}{P}_1\overline{\chi }(r):={\chi }_1^{\prime }(r)-{\chi }_2(r)=0,r\in {\mathsf{\Omega }}^{*}\cup \{2\},\hfill \\ P_2\overline{\chi }(r):=-\epsilon {\chi }_2^{\prime \prime }(r)+\mu p(r){\chi }_2^{\prime }(r)+q(r){\chi }_2(r)+g(r){\chi }_1(r)+h(r){\chi }_2(r-1)=0,r\in {\mathsf{\Omega }}^{*},\hfill \\ {\chi }_1(0)=0,{\chi }_2(r)=\left\{\begin{array}{c}0,r\in [0,1),\hfill \\ {\vartheta }^{\prime }(0)-{\upsilon }_2(0),r=0,\hfill \end{array}\right.\left[{\chi }_2\right](1)=-\left[{\upsilon }_2\right](1),\hfill \\ {\chi }_2^{\prime }](1)=-\left[{\upsilon }_2^{\prime }\right](1),{\chi }_2(2)=l-{\upsilon }_2(2).\hfill \end{array}\right.$$

(27)

Note that ${\upsilon }_2+{\chi }_2={\mathsf{\Phi }}_2\in Y_2.$ We further decompose $\overline{\chi }={\overline{\chi }}_L+{\overline{\chi }}_R$, where ${\overline{\chi }}_L=({\chi }_{L,1},{\chi }_{L,2})$ and ${\overline{\chi }}_R=({\chi }_{R,1},{\chi }_{R,2})$. The functions ${\overline{\chi }}_L$ and ${\overline{\chi }}_R$ satisfy the following problems, respectively:

Find ${\overline{\chi }}_L$ such that

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & P_1{\overline{\chi }}_L:={\chi }_{L,1}^{\prime }(r)-{\chi }_{L,2}(r)=0,\hfill \\ \hfill & P_2{\overline{\chi }}_L:=-\epsilon {\chi }_{L2}^{\prime \prime }(r)+\mu p(r){\chi }_{L,2}^{\prime }(r)+q(r){\chi }_{L,2}(r)+g(r){\chi }_{L,1}(r)+h(r){\chi }_{L,2}(r-1)=0,\hfill \\ \hfill & {\chi }_{L,1}(0)=0,{\chi }_{L,2}(r)=\left\{\begin{array}{c}0,r\in [0,1),\hfill \\ {\vartheta }^{\prime }(0)-{\upsilon }_2(0),r=0,\hfill \end{array}\right.{\chi }_{L,2}(2)=0,\hfill \end{array}\right.\end{array}$$

(28)

and find ${\overline{\chi }}_R$ such that

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & P_1{\overline{\chi }}_R:={\chi }_{R,1}^{\prime }(r)-{\chi }_{R,2}(r)=0,\hfill \\ \hfill & P_2{\overline{\chi }}_R:=-\epsilon {\chi }_{R,2}^{\prime \prime }(r)+\mu p(r){\chi }_{R,2}^{\prime }(r)+q(r){\chi }_{R,2}(r)+g(r){\chi }_{R,1}(r)+h(r){\chi }_{R,2}(r-1)=0,\hfill \\ \hfill & {\chi }_{R,1}(0)=0,{\chi }_{R,2}(r)=0,r\in [-1,0),\hfill \\ \hfill & \left[{\chi }_{R,2}\right](1)=-\left[{\upsilon }_2\right](1),\left[{\chi }_{R,2}^{\prime }\right](1)=-\left[{\upsilon }_2^{\prime }\right](1),{\chi }_{R,2}(2)=l-{\upsilon }_2(2).\hfill \end{array}\right.\end{array}$$

(29)

Using Lemma 1, ${\chi }_{R,1}(r)$ and ${\chi }_{R,2}(r)$ satisfy the following bounds:

$$\Vert {\chi }_{R,1}^{(k)}\Vert \le C{({\displaystyle \frac{\epsilon }{\mu }})}^{1-k},\Vert {\chi }_{R,2}^{(k)}\Vert \le C{({\displaystyle \frac{\epsilon }{\mu }})}^{-k}.$$

To bound the estimate of ${\chi }_{L,1}(r)$ and ${\chi }_{L,2}(r),$ we adopt the following procedure.

Lemma 3. 

The singular component $\overline{\chi }=({\chi }_{L1},{\chi }_{L2})$ satisfies the following bounds for $\mu \ge C\sqrt{\epsilon },$ $k=1,2,3.$: $\Vert {\chi }_{L,01}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^{k-1}}},$ $\Vert {\chi }_{L,02}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^k}}.$

Proof. 

Consider the following decomposition:

$$\begin{array}{c}\hfill {\chi }_{L,1}(r,\mu ,\epsilon )={\chi }_{L,01}(r,\mu )+\epsilon {\chi }_{L,11}(r,\mu )+{\epsilon }^2{\chi }_{L,21}(r,\mu )+{\epsilon }^3{\chi }_{L,31}(r,\mu ,\epsilon ),\\ \hfill {\chi }_{L,2}(r,\mu ,\epsilon )={\chi }_{L,02}(r,\mu )+\epsilon {\chi }_{L,12}(r,\mu )+{\epsilon }^2{\chi }_{L,22}(r,\mu )+{\epsilon }^3{\chi }_{L,32}(r,\mu ,\epsilon ),\end{array}$$

where

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{P}_1{\overline{\chi }}_{L,0}:={\chi }_{L,01}^{\prime }(r)-{\chi }_{L,02}(r)=0,\hfill \\ P_3{\overline{\chi }}_{L,0}:=\mu p(r){\chi }_{L,02}^{\prime }(r)+q(r){\chi }_{L,02}(r)+g(r){\chi }_{L,01}(r)+h(r){\chi }_{L,02}(r-1)=0,\hfill \\ {\chi }_{L,01}(0)=0,{\chi }_{L,02}(0)={\vartheta }^{\prime }(0)-{\upsilon }_2(0),r\in [-1,0),{\chi }_{L,02}(2)=0.\hfill \end{array}\right.\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{P}_1{\overline{\chi }}_{L,1}:={\chi }_{L,11}^{\prime }(r)-{\chi }_{L,12}(r)=0,\hfill \\ P_3{\overline{\chi }}_{L,1}:=\mu p(r){\chi }_{L,12}^{\prime }(r)+q(r){\chi }_{L,12}(r)+g(r){\chi }_{L,11}(r)+h(r){\chi }_{L,12}(r-1)={\chi }_{L,02}^{\prime \prime },\hfill \\ {\chi }_{L,11}(0)=0,{\chi }_{L,12}(0)=0,r\in [-1,0),{\chi }_{L,12}(2)=0.\hfill \end{array}\right.\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{P}_1{\overline{\chi }}_{L,2}:={\chi }_{L,21}^{\prime }(r)-{\chi }_{L,22}(r)=0,\hfill \\ P_3{\overline{\chi }}_{L,2}:=\mu p(r){\chi }_{L,22}^{\prime }(r)+q(r){\chi }_{L,22}(r)+g(r){\chi }_{L,21}(r)+h(r){\chi }_{L,22}(r-1)={\chi }_{L,12}^{\prime \prime },\hfill \\ {\chi }_{L,21}(0)=0,{\chi }_{L,22}(0)=0,r\in [-1,0),{\chi }_{L,22}(2)=0.\hfill \end{array}\right.\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{P}_1{\overline{\chi }}_{L,3}:={\chi }_{L,31}^{\prime }(r)-{\chi }_{L,32}(r)=0,\hfill \\ P_2{\overline{\chi }}_{L,3}:=-\epsilon {\chi }_{L,32}^{\prime \prime }(r)+\mu p(r){\chi }_{L,32}^{\prime }(r)+q(r){\chi }_{L,32}(r)+g(r){\chi }_{L,31}(r)\hfill \\ +h(r){\chi }_{L,32}(r-1)={\chi }_{L,22}^{\prime \prime },\hfill \\ {\chi }_{L,31}(0)=0,{\chi }_{L,32}(0)=0,r\in [-1,0),{\chi }_{L,32}(2)=0.\hfill \end{array}\right.\hfill \end{array}$$

(33)

Consider the barrier function $\overline{ð}=({ð}_1,{ð}_2),$ where ${ð}_1^{\pm }=C\{\mu s_1(r)-\mu e^{-{\displaystyle \frac{\alpha r}{\mu }}}\}\pm {\chi }_{L,01}(r),r\in {\mathsf{\Omega }}^{-},$ ${ð}_2^{\pm }=C\{\mu s_2(r)+e^{-{\displaystyle \frac{\alpha r}{\mu }}}\}\pm {\chi }_{L,02}(r),r\in {\mathsf{\Omega }}^{-}.$ It is easy to see that ${ð}_1(0)\ge 0,$ ${ð}_2(0)\ge 0,$ ${ð}_2(1)\ge 0$ for a suitable choice of $C\ge 0.$

$$\begin{array}{cc}\hfill P_1\overline{ð}(r)=& C\{{\displaystyle \frac{3\mu }{8}}+(\alpha -1)e^{-{\displaystyle \frac{\alpha r}{\mu }}}\}\pm P_1{\overline{\chi }}_{L,0}(r)\ge 0,\hfill \\ \hfill P_3\overline{ð}(r)=& C\{\mu \left({\displaystyle \frac{\mu p(r)}{2}}+q(r)({\displaystyle \frac{1}{8}}+{\displaystyle \frac{r}{2}})+g(r)(1+r)\right)+(-\alpha p(r)+q(r)\hfill \\ & -\mu g(r))e^{-{\displaystyle \frac{\alpha }{\mu }}r}\}\pm P_3{\overline{\chi }}_{L,0}(r)\ge 0.\hfill \end{array}$$

Then, by Lemma 2, we have $\overline{ð}(r)\ge 0,$ for $k=1,2,$

$$\Vert {\chi }_{L,01}\Vert \le C\left(\mu +\mu e^{-{\displaystyle \frac{\alpha r}{\mu }}}\right),r\in {\mathsf{\Omega }}^{-},\Vert {\chi }_{L,02}\Vert \le C\left(\mu +e^{-{\displaystyle \frac{\alpha r}{\mu }}}\right),r\in {\mathsf{\Omega }}^{-}.$$

Consider the barrier function

$${ð}_1^{\pm }(r)=C\{\mu s_1(r)-{\mu }^2{e}^{-{\displaystyle \frac{\alpha }{\mu }}(r-1)}\}\pm {\chi }_{L,01}(r),r\in {\mathsf{\Omega }}^{+},$$

$${ð}_2^{\pm }(r)=C\{\mu s_2(r)+\mu e^{-{\displaystyle \frac{\alpha }{\mu }}(r-1)}\}\pm {\chi }_{L,02}(r),r\in {\mathsf{\Omega }}^{+},$$

$$\begin{array}{cc}\hfill P_1\overline{ð}(r)=& C\{{\displaystyle \frac{3\mu }{4}}+\mu (\alpha -1)e^{-{\displaystyle \frac{\alpha }{\mu }}(r-1)}\}\pm P_1{\overline{\chi }}_{L,0}(r)\ge 0,\hfill \\ \hfill P_3\overline{ð}(r)=& C\{\mu [{\displaystyle \frac{\mu p(r)}{4}}+q(r)({\displaystyle \frac{5}{8}}+{\displaystyle \frac{r}{4}})+g(r)(1+r)+h(r)({\displaystyle \frac{r}{4}}+{\displaystyle \frac{1}{8}})]\hfill \\ & +\mu \left(-\alpha p(r)+q(r)-\mu g(r)+h(r)e^{{\displaystyle \frac{\alpha }{\mu }}}\right)e^{-{\displaystyle \frac{\alpha }{\mu }}(r-1)}\}\pm P_3{\overline{\chi }}_{L,0}(r)\ge 0.\hfill \end{array}$$

Then, by Lemma 2, we have ${\overline{ð}}^{\pm }(r)\ge 0,$ which gives the required estimate.

With the integration of (30), we obtain $\Vert {\chi }_{L,02}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^k}},$$\Vert {\chi }_{L,01}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^{k-1}}},r\in {\mathsf{\Omega }}^{*},$$k=0,1,2,3.$

Using Lemma 2 with the barrier functions

$${ð}_1^{\pm }(r)=C\{\mu s_1(r)-\mu e^{-{\displaystyle \frac{\alpha }{\mu }}r}\}\pm {\chi }_{L,11}(r),r\in {\mathsf{\Omega }}^{-},$$

$${ð}_2^{\pm }(r)=C\{\mu s_2(r)+e^{-{\displaystyle \frac{\alpha }{\mu }}r}\}\pm {\chi }_{L,12}(r),r\in {\mathsf{\Omega }}^{-}$$

and integration of (31), we obtain $\Vert {\chi }_{L,12}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^{k+2}}},$$\Vert {\chi }_{L,11}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^{k+1}}}.$

Similarly, it is easy to prove the required bounds of ${\chi }_{L,11}$${\chi }_{L,12}$ in [1, 2].

We use Lemma 2 and the barrier functions

$${ð}_1^{\pm }(r)=C\{\mu s_1(r)-\mu e^{-{\displaystyle \frac{\alpha }{\mu }}r}\}\pm {\chi }_{L,21}(r),r\in {\mathsf{\Omega }}^{-},$$

$${ð}_2^{\pm }(r)=C\{\mu s_2(r)+e^{-{\displaystyle \frac{\alpha }{\mu }}r}\}\pm {\chi }_{L,22}(r),r\in {\mathsf{\Omega }}^{-}.$$

With the integration of (32), we obtain

$$\Vert {\chi }_{L,22}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^{k+4}}},\Vert {\chi }_{L,21}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^{k+3}}}.$$

Similarly, it is easy to prove the required bounds of ${\chi }_{L,21}$ ${\chi }_{L,22}$ in [1, 2].

Consider the barrier function $\overline{ð}=({ð}_1,{ð}_2),$ where

$${ð}_1^{\pm }(r)=C\{\mu s_1(r)-\mu e^{-{\displaystyle \frac{\alpha r}{\mu }}}\}\pm {\chi }_{L,31}(r),$$

$${ð}_2^{\pm }(r)=C\{\mu s_2(r)+e^{-{\displaystyle \frac{\alpha r}{\mu }}}\}\pm {\chi }_{L,32}(r).$$

It is easy to see that ${ð}_1(0)>0,$${ð}_2(0)>0,$$P_1\overline{ð}(r)\ge 0,$$P_2\overline{ð}(r)\ge 0;$ then, by Theorem 1, we have ${ð}_1(r)\ge 0,$${ð}_2(r)\ge 0.$ Hence, $\Vert {\chi }_{L,3k}\Vert \le {\displaystyle \frac{C}{{\mu }^6}}.$ Using (33) and Lemma 1, we obtain $\Vert {\chi }_{L,32}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^6{(\sqrt{\epsilon })}^k}}(1+{\displaystyle \frac{{\mu }^K}{{\sqrt{\epsilon }}^k}}),k=1,2,$$\Vert {\chi }_{L,32}^{(3)}\Vert \le {\displaystyle \frac{C}{{\mu }^6{(\sqrt{\epsilon })}^3}}(1+{\displaystyle \frac{{\mu }^3}{{\sqrt{\epsilon }}^3}})+{\displaystyle \frac{C}{\epsilon {\mu }^7}},\Vert {\chi }_{L,31}^{(3)}\Vert \le {\displaystyle \frac{C}{{\mu }^6{(\sqrt{\epsilon })}^2}}(1+{\displaystyle \frac{{\mu }^2}{{\sqrt{\epsilon }}^2}})+{\displaystyle \frac{C}{\epsilon {\mu }^7}}.$ Therefore, for the case $\mu \ge C\sqrt{\epsilon },$ we have $\Vert {\chi }_{L,2}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^k}},$$\Vert {\chi }_{L,1}^{(k)}\Vert \le {\displaystyle \frac{C}{{\mu }^{k-1}}}.$ □

Note: the functions ${\overline{\chi }}_L$ and ${\overline{\chi }}_R$ represent the left layer component and right layer component, respectively.

Theorem 3. 

Let $\overline{\chi }$ be the singular components of the solution $\overline{\mathsf{\Phi }}$, and let $\mu \ge C\sqrt{\epsilon }$, $k=0,1,2,3.$ We have the following:

$$\begin{array}{cc}\hfill & \mid {\chi }_{L,1}^{(k)}(r)\mid \le C{\mu }^{1-k}\left\{\begin{array}{c}{e}^{-{\displaystyle \frac{\alpha }{\mu }}r},r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(r-1){\displaystyle \frac{\alpha }{\mu }}},r\in {\mathsf{\Omega }}^{+},\hfill \end{array}\right.\mid {\chi }_{L,2}^{(k)}(r)\mid \le C{\mu }^{-k}\left\{\begin{array}{c}{e}^{-{\displaystyle \frac{\alpha }{\mu }}r},r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(r-1){\displaystyle \frac{\alpha }{\mu }}},r\in {\mathsf{\Omega }}^{+},\hfill \end{array}\right.\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & \mid {\chi }_{R,1}^{(k)}(r)\mid \le C{({\displaystyle \frac{\epsilon }{\mu }})}^{(1-k)}\left\{\begin{array}{c}{e}^{-(1-r){\displaystyle \frac{\alpha \mu }{\epsilon }}},r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(2-r){\displaystyle \frac{\alpha \mu }{\epsilon }}},r\in {\mathsf{\Omega }}^{+},\hfill \end{array}\right.\mid {\chi }_{R,2}^{(k)}(r)\mid \le C{({\displaystyle \frac{\epsilon }{\mu }})}^{(-k)}\left\{\begin{array}{c}{e}^{-(1-r){\displaystyle \frac{\alpha \mu }{\epsilon }}},r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(2-r){\displaystyle \frac{\alpha \mu }{\epsilon }}},r\in {\mathsf{\Omega }}^{+}.\hfill \end{array}\right.\hfill \end{array}$$

(35)

Proof. 

By Lemma 3 and using the technique given by Gracia et al. [11] and Kalaiselvan et al. [20], it is easy to prove the estimate of the above theorem with suitable barrier function and Theorem 1. □

Note: from the preceding theorem, it is clear that when $\mu \ge C\sqrt{\epsilon },$$k=1,2,$ we have

$$\begin{array}{c}\hfill \mid {\mathsf{\Phi }}_{L,k}(r)-{\upsilon }_{L,k}(r)\mid \le C{\mu }^{2-k}\left\{\begin{array}{cc}{e}^{-{\displaystyle \frac{\alpha }{\mu }}x},\hfill & r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(r-1){\displaystyle \frac{\alpha }{\mu }}},\hfill & r\in {\mathsf{\Omega }}^{+}.\hfill \end{array}\right.\end{array}$$

(36)

$$\begin{array}{c}\hfill \mid {\mathsf{\Phi }}_{R,k}(r)-{\upsilon }_{R,k}(r)\mid \le C{({\displaystyle \frac{\epsilon }{\mu }})}^{(2-k)}\left\{\begin{array}{cc}{e}^{-(1-r){\displaystyle \frac{\alpha \mu }{\epsilon }}},\hfill & r\in {\mathsf{\Omega }}^{-},\hfill \\ e^{-(2-r){\displaystyle \frac{\alpha \mu }{\epsilon }}},\hfill & r\in {\mathsf{\Omega }}^{+}.\hfill \end{array}\right.\end{array}$$

(37)

5. Finite Difference Method

This section presents the piecewise uniform mesh (Shishkin mesh) as the mesh selection strategy, along with an upwind finite-difference scheme that involves piecewise linear interpolation on the Shishkin mesh to solve problems (2) and (3).

5.1. Shishkin Mesh

We now discuss the behavior of upwind finite-difference schemes (38) and (39) on a special type of mesh called piecewise uniform Shishkin (S-type) mesh. Based on the relation between the magnitude of the parameters $\epsilon$ and $\mu ,$ we have the transition parameters as follows:

Define the two transition mesh parameters ${\tau }_1$ and ${\tau }_2$ such that

$${\tau }_1=\left\{\begin{array}{c}min\{{\displaystyle \frac{1}{4}},{\displaystyle \frac{2\sqrt{\epsilon }}{\sqrt{\alpha }}}lnN\},\mu \le C\sqrt{\epsilon },\hfill \\ min\{{\displaystyle \frac{1}{4}},{\displaystyle \frac{2\mu }{\alpha }}lnN\},\mu \ge C\sqrt{\epsilon },\hfill \end{array}\right.{\tau }_2=\left\{\begin{array}{c}min\{{\displaystyle \frac{1}{4}},{\displaystyle \frac{2\sqrt{\epsilon }}{\sqrt{\alpha }}}lnN\},\mu \le C\sqrt{\epsilon },\hfill \\ min\{{\displaystyle \frac{1}{4}},{\displaystyle \frac{2\epsilon }{\mu \alpha }}lnN\},\mu \ge C\sqrt{\epsilon }.\hfill \end{array}\right.$$

Divide the interval $[0,2]$ into six subintervals, namely, $[0,{\tau }_1]$, $[{\tau }_1,1-{\tau }_2],$$[1-{\tau }_2,1],$$[1,1+{\tau }_1],$$[1+{\tau }_1,2-{\tau }_2],$$[2-{\tau }_2,2].$ The mesh ${\overline{\mathsf{\Omega }}}^N=\{r_0,r_1,\cdots ,r_N\}$ is defined by

$$\begin{array}{c}\hfill r_i=\left\{\begin{array}{cc}i*H_1,\hfill & 0\le i\le {\displaystyle \frac{N}{8}},\hfill \\ {\tau }_1+(i-{\displaystyle \frac{N}{8}})*H_2,\hfill & {\displaystyle \frac{N}{8}}\le i\le {\displaystyle \frac{3N}{8}},\hfill \\ 1-{\tau }_2+(i-{\displaystyle \frac{3N}{8}})*H_3,\hfill & {\displaystyle \frac{3N}{8}}\le i\le {\displaystyle \frac{N}{2}},\hfill \\ 1+(i-{\displaystyle \frac{N}{2}})*H_1,\hfill & {\displaystyle \frac{N}{2}}\le i\le {\displaystyle \frac{5N}{8}},\hfill \\ 1+{\tau }_1+(i-{\displaystyle \frac{5N}{8}})*H_2,\hfill & {\displaystyle \frac{5N}{8}}\le i\le {\displaystyle \frac{7N}{8}},\hfill \\ 2-{\tau }_2+(i-{\displaystyle \frac{7N}{8}})*H_3,\hfill & {\displaystyle \frac{7N}{8}}\le i\le N,\hfill \end{array}\right.\end{array}$$

where the step size in each subinterval is as follows: $H_1=8N^{-1}{\tau }_1,$$H_2=4N^{-1}(1-{\tau }_1-{\tau }_2)$ and $H_3=8N^{-1}{\tau }_2.$ The partition of the domain is given in the Figure 1.

Figure 1. Domain partition.

5.2. Finite-Difference Scheme

An upwind finite-difference scheme is defined on mesh ${\overline{\mathsf{\Omega }}}^N$ as follows:

$$\begin{array}{cc}\hfill & P_1^N\overline{\mathsf{\Psi }}(r_i):=D^{-}{\mathsf{\Psi }}_1(r_i)-{\mathsf{\Psi }}_2(r_i)=0,i=1(1)N,\hfill \\ \hfill & P_2^N\overline{\mathsf{\Psi }}(r_i):=-\epsilon {\delta }^2{\mathsf{\Psi }}_2(r_i)+\mu p(r_i)D^{-}{\mathsf{\Psi }}_2(r_i)+q(r_i){\mathsf{\Psi }}_2(r_i)\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & +g(r_i){\mathsf{\Psi }}_1(r_i)+h(r_i){\mathsf{\Psi }}_2^I(r_i)={\mathcal{F}}^{*}(r_i),\forall i,i\ne 0,N/2,N,\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & {\mathsf{\Psi }}_1(r_0)=\vartheta (0),{\mathsf{\Psi }}_2(r_0)={\vartheta }^{\prime }(0),D^{-}{\mathsf{\Psi }}_2(r_{N/2})=D^{+}{\mathsf{\Psi }}_2(r_{N/2}),{\mathsf{\Psi }}_2(r_N)=l,\hfill \end{array}$$

(40)

where

$$\begin{array}{cc}\hfill & {\delta }^2{\mathsf{\Psi }}_2(r_i)={\displaystyle \frac{2}{r_{i+1}-r_{i-1}}}\left[D^{+}{\mathsf{\Psi }}_2(r_i)-D^{-}{\mathsf{\Psi }}_2(r_i)\right],D^{-}{\mathsf{\Psi }}_2(r_i)={\displaystyle \frac{{\mathsf{\Psi }}_2(r_i)-{\mathsf{\Psi }}_2(r_{i-1})}{r_i-r_{i-1}}},\hfill \\ \hfill & D^{+}{\mathsf{\Psi }}_2(r_i)={\displaystyle \frac{{\mathsf{\Psi }}_2(r_{i+1})-{\mathsf{\Psi }}_2(r_i)}{r_{i+1}-r_i}},{\mathcal{F}}^{*}(r_i)=\left\{\begin{array}{c}\mathcal{F}(r_i)-h(r_i){\vartheta }^{\prime }(r_i-1),r_i\in {\mathsf{\Omega }}^{-}\cap {\overline{\mathsf{\Omega }}}^N,\hfill \\ \mathcal{F}(r_i),r_i\in {\mathsf{\Omega }}^{+}\cap {\overline{\mathsf{\Omega }}}^N,\hfill \end{array}\right.\hfill \\ \hfill & {\mathsf{\Psi }}_2^I(r_i)=\left\{\begin{array}{c}0,r_i\in {\mathsf{\Omega }}^{-}\cap {\overline{\mathsf{\Omega }}}^N,\hfill \\ {\mathsf{\Psi }}_2(r_j){\displaystyle \frac{r_{j+1}-(r_i-1)}{h_{j+1}}}+{\mathsf{\Psi }}_2(r_{j+1}){\displaystyle \frac{(r_i-1)-r_j}{h_{j+1}}},r_i\in {\mathsf{\Omega }}^{+}\cap {\overline{\mathsf{\Omega }}}^N,r_j\le r_i-1\le r_{j+1},\hfill \end{array}\right.\hfill \\ \hfill & h_i=r_i-r_{i-1},i=1(1)N.\hfill \end{array}$$

5.3. Discrete Maximum Principle and Stability Result

Lemma 4 

(Discrete maximum principle). Let $\overline{Z}(r_i)=(Z_1(r_i),Z_2(r_i))$ be mesh function satisfying $Z_1(r_0)\ge 0,$$Z_2(r_0)\ge 0,$$Z_2(r_N)\ge 0,$$P_1^N\overline{Z}(r_i)\ge 0,$$P_2^N\overline{Z}(r_i)\ge 0,$ and $\left[D\right]Z_2(r_{N/2})\le 0$. Then, $Z_1(r_i)\ge 0$ and $Z_2(r_i)\ge 0$, $r_i\in {\overline{\mathsf{\Omega }}}^N$.

Proof. 

Let us define $\overline{s}(r_i)=(s_1(r_i),s_2(r_i))$, where

$$\begin{array}{c}\hfill s_1(r_i)=1+r_i,r_i\in \overline{\mathsf{\Omega }}\cap {\overline{\mathsf{\Omega }}}^N\mathrm{and}{s}_2(r_i)=\left\{\begin{array}{c}{\displaystyle \frac{1}{8}}+{\displaystyle \frac{r_i}{2}},r_i\in [0,1]\cap {\overline{\mathsf{\Omega }}}^N,\hfill \\ {\displaystyle \frac{3}{8}}+{\displaystyle \frac{r_i}{4}},r_i\in [1,2]\cap {\overline{\mathsf{\Omega }}}^N.\hfill \end{array}\right.\end{array}$$

It is just obvious that, $s_k(r_i)>0,\forall r_i\in {\overline{\mathsf{\Omega }}}^N,k=1,2,P_1^N\overline{s}(r_i)>0,\forall r_i\in {\overline{\mathsf{\Omega }}}^N\cap \mathsf{\Omega }\cup \{2\},P_2^N\overline{s}(r_i)>0,\forall r_i\in {\overline{\mathsf{\Omega }}}^N\cap {\mathsf{\Omega }}^{*}$ and $\left[D\right]s_2(r_{N/2})<0$. Let ${\sigma }^{*}=max\left\{\underset{r_i\in {\overline{\mathsf{\Omega }}}^N}{max}\{{\displaystyle \frac{-Z_1(r_i)}{s_1(r_i)}}\},\underset{r_i\in {\overline{\mathsf{\Omega }}}^N}{max}\{{\displaystyle \frac{-Z_2(r_i)}{s_2(r_i)}}\}\right\}$. Then, there exists one $r_i^{*}\in {\overline{\mathsf{\Omega }}}^N$ such that $Z_1(r_i^{*})$$+{\sigma }^{*}{s}_1(r_i^{*})=0$ or $Z_2(r_i^{*})+{\sigma }^{*}{s}_2(r_i^{*})=0$ or both. Now, we have $Z_i(r_k)+{\sigma }^{*}{s}_i(r_k)\ge 0,r_k\in {\overline{\mathsf{\Omega }}}^N,i=1,2.$ Therefore, either $(Z_1+{\sigma }^{*}{s}_1)$ or $(Z_2+{\sigma }^{*}{s}_2)$ reaches its minimum at $r_i=r_i^{*}$.

In the case where ${\sigma }^{*}>0$, the theorem does not hold true.

Case (A). $(Z_1+{\sigma }^{*}{s}_1)$ reaches its minimum.

We have

$$\begin{array}{c}\hfill 0<P_1^N(\overline{Z}+{\sigma }^{*}\overline{s})(r_i^{*})=D^{-}(Z_1+{\sigma }^{*}{s}_1)(r_i^{*})-(Z_2+{\sigma }^{*}{s}_2)(r_i^{*})\le 0.\end{array}$$

This contradicts the theorem’s underlying assumption.

Case (B). $(Z_2+{\sigma }^{*}{s}_2)$ reaches its minimum.

Case (i). $(r_i^{*}\in {\mathsf{\Omega }}^{-}\cap {\overline{\mathsf{\Omega }}}^N)$

$$\begin{array}{cc}\hfill 0<P_2^N(\overline{Z}+{\sigma }^{*}\overline{s})(r_i^{*})=-\epsilon {\delta }^2(Z_2+{\sigma }^{*}{s}_2)(r_i^{*})& +\mu p(r_i^{*})D^{-}(Z_2+{\sigma }^{*}{s}_2)(r_i^{*})\hfill \\ \hfill +q(r_i^{*})(Z_2+{\sigma }^{*}{s}_2)(r_i^{*})& +g(r_i^{*})(Z_1+{\sigma }^{*}{s}_1)(r_i^{*})\le 0.\hfill \end{array}$$

This contradicts the theorem’s underlying assumption.

Case (ii). $(r_i^{*}\in {\mathsf{\Omega }}^{+}\cap {\overline{\mathsf{\Omega }}}^N)$

$$\begin{array}{cc}\hfill 0<P_2^N(\overline{Z}+{\sigma }^{*}\overline{s})(r_i^{*})=& -\epsilon {\delta }^2(Z_2+{\sigma }^{*}{s}_2)(r_i^{*})+\mu p(r_i^{*})D^{-}(Z_2+{\sigma }^{*}{s}_2)(r_i^{*})\hfill \\ \hfill +q(r_i^{*})(Z_2+{\sigma }^{*}{s}_2)(r_i^{*})& +g(r_i^{*})(Z_1+{\sigma }^{*}{s}_1)(r_i^{*})+h(r_i^{*})(Z_2+{\sigma }^{*}{s}_2)(r_i^{*}-r_{N/2})\le 0.\hfill \end{array}$$

This contradicts the theorem’s underlying assumption.

Case (iii). $(r_i^{*}=r_{N/2})$

$$0\le \left[D\right](Z_2+{\sigma }^{*}{s}_2)(r_i^{*})=\left[D\right]Z_2(r_i^{*})+{\sigma }^{*}\left[D\right]s_2(r_i^{*})<0.$$

This leads contrary to the theorem’s underlying assumption. Thus, the theorem’s proof is complete. □

The following discrete stability result is a consequence of the discrete maximum principle.

Lemma 5 

(Discrete stability result). For any mesh function, $\overline{\mathsf{\Psi }}(r_i)=({\mathsf{\Psi }}_1(r_i),{\mathsf{\Psi }}_2(r_i))$ such that $\overline{\mathsf{\Psi }}$ satisfies the followings:

$$\begin{array}{c}\hfill \mid {\mathsf{\Psi }}_k(r_i)\mid \le Cmax\{\mid {\mathsf{\Psi }}_1(r_0)\mid ,\mid {\mathsf{\Psi }}_2(r_0)\mid ,\mid {\mathsf{\Psi }}_2(r_N)\mid ,\underset{j\in I_N}{max}\mid P_1^N\overline{\mathsf{\Psi }}(r_j)\mid ,\\ \hfill \underset{j\in I_N\setminus \{0,N/2,N\}}{max}\mid P_2^N\overline{\mathsf{\Psi }}(r_j)\mid \},i\in I_N,k=1,2.\end{array}$$

We break down the numerical solution $\overline{\mathsf{\Psi }}(r_i)$ described by (38) and (39) as

$$\overline{\mathsf{\Psi }}(r_i)=\overline{V}(r_i)+\overline{W}(r_i),$$

(41)

which is analogous to the continuous function $\overline{\mathsf{\Phi }},$ where $\overline{V}(r_i)$ and $\overline{W}(r_i)$ satisfy the following:

$$\left\{\begin{array}{c}{P}_1^N\overline{V}(r_i):=D^{-}{V}_1(r_i)-V_2(r_i)=0,i\in I_N\setminus \{0\},\hfill \\ P_2^N\overline{V}(r_i):=-\epsilon {\delta }^2{V}_2(r_i)+\mu p(r_i)D^{-}{V}_2(r_i)+q(r_i)V_2(r_i)\hfill \\ +g(r_i)V_1(r_i)+h(r_i)V_2^I(r_i)={\mathcal{F}}^{*}(r_i),i\in I_N\setminus \{0,N/2,N\},\hfill \\ V_j(r_0)=v_j(0),\left[D\right]V_2(r_{N/2})=\left[v_2^{\prime }\right](1),V_2(r_N)=v_2(2),j=1,2,\hfill \end{array}\right.$$

(42)

and

$$\left\{\begin{array}{c}{P}_1^N\overline{W}(r_i):=D^{-}{W}_1(r_i)-W_2(r_i)=0,i\in I_N\setminus \{0\},\hfill \\ P_2^N\overline{W}(r_i):=-\epsilon {\delta }^2{W}_2(r_i)+\mu p(r_i)D^{-}{W}_2(r_i)+q(r_i)W_2(r_i)\hfill \\ +g(r_i)W_1(r_i)+h(r_i)W_2^I(r_i)=0,i\in I_N\setminus \{0,N/2,N\},\hfill \\ W_j(r_0)=w_j(0),\left[D\right]W_2(r_{N/2})=-\left[D\right]V_2(r_{N/2}),W_2(r_N)={\chi }_2(2),j=1,2.\hfill \end{array}\right.$$

(43)

An estimate for the difference between the solutions of (38), (39) and (42) is provided by the following theorem.

Theorem 4. 

At each mesh point $r_i\in {\overline{\mathsf{\Omega }}}^N,$ the difference of the numerical solution of singular component $\overline{\mathsf{\Psi }}(r_i)$ of (2) and (3) defined by (38) and (39) and the numerical solution of the regular component $\overline{V}(r_i)$ defined by (42) satisfies the following bounds: if $\delta =max\left\{\mid {\vartheta }^{\prime }(0)-V_2(r_0)\mid ,\mid {\mathsf{\Psi }}_1(r_{{\displaystyle \frac{N}{2}}})-V_1(r_{{\displaystyle \frac{N}{2}}})\mid ,\mid {\mathsf{\Psi }}_2(r_{{\displaystyle \frac{N}{2}}})-V_2(r_{{\displaystyle \frac{N}{2}}})\mid ,\mid l-V_2(r_N)\mid \right\}$ and $\mu \le C\sqrt{\epsilon },$ we have

$$\begin{array}{cc}\hfill & \mid {\mathsf{\Psi }}_k(r_i)-V_k(r_i)\mid \le C\left\{\begin{array}{cc}{N}^{-1},\hfill & i\in \{{\displaystyle \frac{N}{8}},\cdots ,{\displaystyle \frac{3N}{8}}\}\cup \{{\displaystyle \frac{5N}{8}},\cdots ,{\displaystyle \frac{7N}{8}}\},\hfill \\ N^{-1}+\delta ,\hfill & otherwise,\hfill \end{array}\right.k=1,2.\hfill \end{array}$$

Proof. 

Consider a mesh function

$$\begin{array}{cc}\hfill {\phi }_k^{\pm }(r_i)=& C_1(N^{-1}{s}_k(r_i)+{\psi }_k(r_i))\pm ({\mathsf{\Psi }}_k(r_i)-V_k(r_i)),k=1,2,\hfill \end{array}$$

where $s_1(r_i)=1+r_i,r_i\in {\overline{\mathsf{\Omega }}}^N,$ $s_2(r_i)=$$\left\{\begin{array}{c}{\displaystyle \frac{1}{8}}+{\displaystyle \frac{r_i}{2}},r_i\in {\mathsf{\Omega }}^{-}\cap {\overline{\mathsf{\Omega }}}^N,\hfill \\ {\displaystyle \frac{3}{8}}+{\displaystyle \frac{r_i}{4}},r_i\in {\mathsf{\Omega }}^{+}\cap {\overline{\mathsf{\Omega }}}^N.\hfill \end{array}\right.$ It is verified that ${\phi }_k^{\pm }(r_0)\ge 0,$$k=1,2$ and ${\phi }_2^{\pm }(r_N)\ge 0$ for large enough $C_1>0$ and

$$\begin{array}{cc}\hfill {\psi }_1(r_i)& =\left\{\begin{array}{cc}0,\hfill & i\in \{{\displaystyle \frac{N}{8}},\cdots ,{\displaystyle \frac{3N}{8}}\}\cup \{{\displaystyle \frac{5N}{8}},\cdots ,{\displaystyle \frac{7N}{8}}\},\hfill \\ r_i\delta ,\hfill & otherwise,\hfill \end{array}\right.\hfill \\ \hfill {\psi }_2(r_i)& =\left\{\begin{array}{cc}0,\hfill & i\in \{{\displaystyle \frac{N}{8}},\cdots ,{\displaystyle \frac{3N}{8}}\}\cup \{{\displaystyle \frac{5N}{8}},\cdots ,{\displaystyle \frac{7N}{8}}\},\hfill \\ ({\displaystyle \frac{r_i}{2}}+{\displaystyle \frac{1}{8}})\delta ,\hfill & i\in \{1,\cdots ,{\displaystyle \frac{N}{8}}-1\}\cup \{{\displaystyle \frac{3N}{8}}+1,\cdots ,{\displaystyle \frac{N}{2}}\},\hfill \\ ({\displaystyle \frac{r_i}{4}}+{\displaystyle \frac{3}{8}})\delta ,\hfill & i\in \{{\displaystyle \frac{N}{2}}+1,\cdots ,{\displaystyle \frac{5N}{8}}-1\}\cup \{{\displaystyle \frac{7N}{8}}+1,\cdots ,N\}.\hfill \end{array}\right.\hfill \end{array}$$

When $r_i\in (0,{\tau }_1)\cap {\overline{\mathsf{\Omega }}}^N,$

$$\begin{array}{cc}\hfill P_1^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1\{N^{-1}({\displaystyle \frac{7}{8}}-{\displaystyle \frac{{\tau }_1}{2}})+\delta ({\displaystyle \frac{7}{8}}-{\displaystyle \frac{{\tau }_1}{2}})\}\pm 0\ge 0,\hfill \\ \hfill P_2^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1\{N^{-1}[{\displaystyle \frac{\alpha \mu }{2}}+{\displaystyle \frac{\beta }{8}}+(1+{\tau }_1)\gamma ]+\delta [{\displaystyle \frac{\alpha \mu }{2}}+{\displaystyle \frac{\beta }{8}}+\gamma {\tau }_1]\}\pm 0\ge 0.\hfill \end{array}$$

When $r_i\in [{\tau }_1,1-{\tau }_2]\cap {\overline{\mathsf{\Omega }}}^N,$

$$\begin{array}{cc}\hfill P_1^N{\overline{\phi }}^{\pm }(r_i)& =C_1{N}^{-1}[1-({\displaystyle \frac{1}{8}}+{\displaystyle \frac{r_i}{2}})]\pm 0\ge C_1{N}^{-1}({\displaystyle \frac{7}{8}}-{\displaystyle \frac{1-{\tau }_2}{2}})\ge 0,\hfill \\ \hfill P_2^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1\{N^{-1}[4\alpha \mu +\beta +16\gamma +\beta -8{\tau }_2\gamma ]+\delta (0)\}\pm 0\ge 0.\hfill \end{array}$$

When $r_i\in (1-{\tau }_2,1)\cap {\overline{\mathsf{\Omega }}}^N,$

$$\begin{array}{cc}\hfill P_1^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1{N}^{-1}({\displaystyle \frac{3}{8}})+C_1\delta ({\displaystyle \frac{3}{8}})\ge 0,\hfill \\ \hfill P_2^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1\{N^{-1}[{\displaystyle \frac{\alpha \mu }{2}}+\beta ({\displaystyle \frac{1}{8}}+{\displaystyle \frac{1-{\tau }_2}{2}})+2\gamma ]\hfill \\ & +\delta [{\displaystyle \frac{\alpha \mu }{2}}+\beta ({\displaystyle \frac{1}{8}}+{\displaystyle \frac{1-{\tau }_2}{2}})+\gamma ]\}\pm 0\ge 0.\hfill \end{array}$$

When $r_i\in (1,1+{\tau }_1)\cap {\overline{\mathsf{\Omega }}}^N,$

$$\begin{array}{cc}\hfill P_1^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1{N}^{-1}({\displaystyle \frac{3}{8}}-{\displaystyle \frac{{\tau }_1}{4}})+C_1\delta ({\displaystyle \frac{3}{8}}-{\displaystyle \frac{{\tau }_1}{4}})\ge 0,\hfill \\ \hfill P_2^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1\{N^{-1}\left[{\displaystyle \frac{\alpha \mu }{4}}+{\displaystyle \frac{5\beta }{8}}+(2+{\tau }_1)\gamma +({\displaystyle \frac{3}{8}}+{\displaystyle \frac{{\tau }_1}{4}})\eta \right]\hfill \\ & +\delta [{\displaystyle \frac{\alpha \mu }{4}}+{\displaystyle \frac{5\beta }{8}}+\gamma (1+{\tau }_1)+({\displaystyle \frac{3}{8}}+{\displaystyle \frac{{\tau }_1}{4}})\eta ]\}\pm 0\ge 0.\hfill \end{array}$$

When $r_i\in [1+{\tau }_1,2-{\tau }_2]\cap {\overline{\mathsf{\Omega }}}^N,$

$$\begin{array}{cc}\hfill P_1^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1{N}^{-1}({\displaystyle \frac{1}{8}}+{\displaystyle \frac{{\tau }_2}{4}})\ge 0,\hfill \\ \hfill P_2^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1{N}^{-1}[{\displaystyle \frac{\alpha \mu }{4}}+{\displaystyle \frac{5}{8}}\beta +3\gamma +{\displaystyle \frac{5}{8}}\eta +({\displaystyle \frac{\beta {\tau }_1}{4}}-{\tau }_2\gamma -{\displaystyle \frac{{\tau }_2}{4}}\eta )]\pm 0\ge 0.\hfill \end{array}$$

When $r_i\in (2-{\tau }_2,2)\cap {\overline{\mathsf{\Omega }}}^N,$

$$\begin{array}{cc}\hfill P_1^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1\{N^{-1}({\displaystyle \frac{1}{8}})+\delta ({\displaystyle \frac{1}{8}})\}\ge 0,\hfill \\ \hfill P_2^N{\overline{\phi }}^{\pm }(r_i)& \ge C_1\{N^{-1}[{\displaystyle \frac{\alpha \mu }{4}}+({\displaystyle \frac{7}{8}}-{\displaystyle \frac{{\tau }_2}{4}})\beta +3\gamma +{\displaystyle \frac{5\eta }{8}}]\hfill \\ & +\delta [{\displaystyle \frac{\alpha \mu }{4}}+({\displaystyle \frac{7}{8}}-{\displaystyle \frac{{\tau }_2}{4}})\beta +2\gamma +{\displaystyle \frac{5\eta }{8}}]\}\pm 0\ge 0.\hfill \end{array}$$

When $r_i=r_{{\displaystyle \frac{N}{2}}}$, we have $\left[D\right]{\phi }_2^{\pm }(r_{{\displaystyle \frac{N}{2}}})=C_1{N}^{-1}(-{\displaystyle \frac{1}{4}})+C_1\delta (-{\displaystyle \frac{1}{4}})\mp \left[v_2^{\prime }\right](1)<0$ for large enough value of $C_1>0.$ Hence, the proof is complete. □

Theorem 5. 

At each mesh point $r_i\in {\overline{\mathsf{\Omega }}}^N,$ the difference of the numerical solution of singular component $\overline{\mathsf{\Psi }}(r_i)$ of (2) and (3) defined by (38) and (39) and the numerical solution of the regular component $\overline{V}(r_i)$ defined by (42) satisfies the following bounds: if $\delta =max\left\{\mid {\vartheta }^{\prime }(0)-V_2(r_0)\mid ,\mid {\mathsf{\Psi }}_1(r_{{\displaystyle \frac{N}{2}}})-V_1(r_{{\displaystyle \frac{N}{2}}})\mid ,\mid {\mathsf{\Psi }}_2(r_{{\displaystyle \frac{N}{2}}})-V_2(r_{{\displaystyle \frac{N}{2}}})\mid ,\mid l-V_2(r_N)\mid \right\}$ and if $\mu \ge C\sqrt{\epsilon },$ we have

$$\begin{array}{cc}\hfill & \mid {\mathsf{\Psi }}_k(r_i)-V_k(r_i)\mid \le C\left\{\begin{array}{cc}{N}^{-1},\hfill & i\in \{{\displaystyle \frac{N}{8}},\cdots ,{\displaystyle \frac{3N}{8}}\}\cup \{{\displaystyle \frac{5N}{8}},\cdots ,{\displaystyle \frac{7N}{8}}\},\hfill \\ N^{-1}+\delta ,\hfill & otherwise,\hfill \end{array}\right.k=1,2.\hfill \end{array}$$

6. Convergence Analysis

Theorem 6. 

The error of the regular component at each point $r_i\in {\overline{\mathsf{\Omega }}}^N$ satisfies the following estimate

$$\mid v_k(r_i)-V_k(r_i)\mid \le C{N}^{-1},i\in I_N,k=1,2,$$

where $\overline{V}(r_i)$ is the discrete solution of problem (9) defined by (42).

Proof. 

Using the truncation error argument, the derivative bounds of the regular components, and the technique given in [30], one can estimate the bounds of the above Theorem.

Thus,

$$\begin{array}{cc}\hfill P_1^N(\overline{v}(r_i)-\overline{V}(r_i))& =P_1^N\overline{v}(r_i)-P_1^N\overline{V}(r_i)=(D^{-}-{\displaystyle \frac{d}{dx}})v_1(r_i)\hfill \\ \hfill P_2^N(\overline{v}(r_i)-\overline{V}(r_i))& =-\epsilon \left({\delta }^2-{\displaystyle \frac{d^2}{d{x}^2}}\right)v_2(r_i)+\mu p(r_i)\left(D^{-}-{\displaystyle \frac{d}{dx}}\right)v_2(r_i)\hfill \\ \hfill & +h(r_i)\left\{\begin{array}{c}0,i=1,2,\cdots ,{\displaystyle \frac{N}{2}}-1,\hfill \\ v_2^I(r_i)-v_2(r_i-1),i={\displaystyle \frac{N}{2}}+1,\cdots ,N-1.\hfill \end{array}\right.\hfill \end{array}$$

$$\mid P_k^N(\overline{v}(r_i)-\overline{V}(r_i))\mid \le C{N}^{-1},i\in I_N\setminus \{0,{\displaystyle \frac{N}{2}},N\},k=1,2.$$

Using Lemma 5, we have

$$\mid v_k(r_i)-V_k(r_i)\mid \le C{N}^{-1},i\in I_N.$$

Hence, the proof is complete. □

Note: We use the following notations for better clarity of left layer and right layer functions:

$$\begin{array}{cc}\hfill & W_k=W_{L,k},W_k=W_{R,k}.\hfill \end{array}$$

Theorem 7. 

The error of the left and right layer singular component at each mesh point $r_i\in {\overline{\mathsf{\Omega }}}^N$ satisfies the following estimate:

$$\begin{array}{cc}\hfill \mid {\chi }_{L,k}(r_i)-W_{L,k}(r_i)\mid & \le \left\{\begin{array}{c}C{N}^{-1}lnN,\mathrm{if}\mu \le C\sqrt{\epsilon },\hfill \\ C{N}^{-1}lnN,\mathrm{if}\mu \ge C\sqrt{\epsilon },\hfill \end{array}\right.\hfill \\ \hfill \mid {\chi }_{R,k}(r_i)-W_{R,k}(r_i)\mid & \le \left\{\begin{array}{c}C{N}^{-1}lnN,\mathrm{if}\mu \le C\sqrt{\epsilon },\hfill \\ C{N}^{-1}{(lnN)}^2,\mathrm{if}\mu \ge C\sqrt{\epsilon },\hfill \end{array}\right.i\in I_N,k=1,2,\hfill \end{array}$$

where $\overline{W}(r_i)$ is discrete solution of the problem (10) defined by (43).

Proof. 

Let $\mu \le C\sqrt{\epsilon };$ then,

$$\mid {\chi }_{L,k}(r_i)-W_{L,k}(r_i)\mid \le \mid {\mathsf{\Phi }}_{L,k}(r_i)-{\mathsf{\Psi }}_{L,k}(r_i)\mid +\mid {\nu }_{L,k}(r_i)-V_{L,k}(r_i)\mid ,k=1,2.$$

Using (15) and by Theorems 4 and 6, we have

$$\begin{array}{cc}\hfill \mid {\mathsf{\Phi }}_{L,k}(r_i)-{\mathsf{\Psi }}_{L,k}(r_i)\mid & \le \mid {\mathsf{\Psi }}_{L,k}(r_i)-V_{L,k}(r_i)\mid +\mid v_{L,k}(r_i)-V_{L,k}(r_i)\mid \hfill \\ & +\mid {\mathsf{\Phi }}_{L,k}(r_i)-v_{L,k}(r_i)\mid \hfill \\ \hfill & \le C{N}^{-1},{\displaystyle \frac{N}{8}}\le i\le {\displaystyle \frac{N}{2}}-1.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill \mid {\chi }_{L,k}(r_i)-W_{L,k}(r_i)\mid & \le \mid {\mathsf{\Phi }}_{L,k}(r_i)-{\mathsf{\Psi }}_{L,k}(r_i)\mid +\mid v_{L,k}(r_i)-V_{L,k}(r_i)\mid ,k=1,2,\hfill \\ \hfill \mid {\chi }_{L,k}(r_i)-W_{L,k}(r_i)\mid & \le C{N}^{-1},{\displaystyle \frac{N}{8}}\le i\le {\displaystyle \frac{N}{2}}-1.\hfill \end{array}$$

(44)

For $1\le i\le {\displaystyle \frac{N}{8}}-1,$ consider a mesh function ${\overline{\phi }}^{\pm }(r_i)=({\phi }_1^{\pm }(r_i),{\phi }_2^{\pm }(r_i)),$ where

$$\begin{array}{cc}\hfill {\phi }_1^{\pm }(r_i)=& C_1{N}^{-1}\{s_1(r_i)-{\displaystyle \frac{1}{\sqrt{\epsilon }}}({\tau }_1-r_i)\}\pm ({\chi }_{L,1}(r_i)-W_{L,1}(r_i)),r_i\in [0,{\tau }_1]\cap {\overline{\mathsf{\Omega }}}^N,\hfill \\ \hfill {\phi }_2^{\pm }(r_i)=& C_1{N}^{-1}\{s_2(r_i)+{\displaystyle \frac{r_i}{\sqrt{\epsilon }}}\}\pm ({\chi }_{L,2}(r_i)-W_{L,2}(r_i)),r_i\in [0,{\tau }_1]\cap {\overline{\mathsf{\Omega }}}^N.\hfill \end{array}$$

From (44), it is straightforward to verify that ${\phi }_k^{\pm }(r_0)\ge 0,k=1,2$ and ${\phi }_2^{\pm }(r_{{\displaystyle \frac{N}{8}}})\ge 0,$ for a large enough value of $C_1>0$.

$$\begin{array}{cc}\hfill P_1^N{\overline{\phi }}^{\pm }(r_i)& =C_1{N}^{-1}[1-s_2(r_i)]+{\displaystyle \frac{1}{\sqrt{\epsilon }}}[1-r_i]\pm (P_1^N-P_1){\overline{\chi }}_L(r_i)\ge 0,\hfill \\ \hfill P_2^N{\overline{\phi }}^{\pm }(r_i)& =C_1{N}^{-1}\{\mu p(r)[{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{\sqrt{\epsilon }}}]+q(r_i)[s_2(r_i)+{\displaystyle \frac{r_i}{\sqrt{\epsilon }}}]+g(r_i)[s_1(r_i)-{\displaystyle \frac{1}{\sqrt{\epsilon }}}({\tau }_1-r_i)]\}\hfill \\ & \pm (P_2^N-P_2){\overline{\chi }}_L(r_i)\hfill \\ \hfill & \ge C_1{N}^{-1}\{{\displaystyle \frac{\mu \alpha }{2}}+{\displaystyle \frac{\beta }{8}}+\gamma (1+{\tau }_1)+{\displaystyle \frac{1}{\sqrt{\epsilon }}}(\mu \alpha )\}\mp C{N}^{-1}{\epsilon }^{-{\displaystyle \frac{1}{2}}}\ge 0.\hfill \end{array}$$

Then, by Lemma 4, we have ${\phi }_1^{\pm }(r_i)\ge 0$ and ${\phi }_2^{\pm }(r_i)\ge 0;$ therefore,

$$\mid {\chi }_{L,k}(r_i)-W_{L,k}(r_i)\mid \le C{N}^{-1}lnN,0\le i\le {\displaystyle \frac{N}{8}},k=1,2.$$

(45)

From (44) and (45), we have

$$\mid {\chi }_{L,k}(r_i)-W_{L,k}(r_i)\mid \le C{N}^{-1}lnN,0\le i\le {\displaystyle \frac{N}{2}}-1,k=1,2.$$

A similar procedure is used to show

$$\mid {\chi }_{L,k}(r_i)-W_{L,k}(r_i)\mid \le C{N}^{-1}lnN,{\displaystyle \frac{N}{2}}\le i\le N,k=1,2.$$

For $\mu \ge C\sqrt{\epsilon },$

$$\mid {\chi }_{R,k}(r_i)-W_{R,k}(r_i)\mid \le \mid {\mathsf{\Phi }}_{R,k}(r_i)-{\mathsf{\Psi }}_{R,k}(r_i)\mid +\mid v_{R,k}(r_i)-V_{R,k}(r_i)\mid ,k=1,2.$$

Then, by (15) and Theorems 5 and 6, we have

$$\begin{array}{cc}\hfill \mid {\mathsf{\Phi }}_{R,k}(r_i)-{\mathsf{\Psi }}_{R,k}(r_i)\mid & \le \mid {\mathsf{\Psi }}_{R,k}(r_i)-V_{R,k}(r_i)\mid +\mid v_{R,k}(r_i)-V_{R,k}(r_i)\mid \hfill \\ & +\mid {\mathsf{\Phi }}_{R,k}(r_i)-v_{R,k}(r_i)\mid \hfill \\ \hfill & \le C{N}^{-1}+C{N}^{-1}+C{N}^{-1}\le C{N}^{-1},i\in \left\{0,\cdots ,{\displaystyle \frac{3N}{8}}\right\}.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill \mid {\chi }_{R,k}(r_i)-W_{R,k}(r_i)\mid & \le \mid {\mathsf{\Phi }}_{R,k}(r_i)-{\mathsf{\Psi }}_{R,k}(r_i)\mid +\mid v_{R,k}(r_i)-V_{R,k}(r_i)\mid ,k=1,2,\hfill \\ \hfill \mid {\chi }_{R,k}(r_i)-W_{R,k}(r_i)\mid & \le C{N}^{-1},i\in \left\{0,\cdots ,{\displaystyle \frac{3N}{8}}\right\}.\hfill \end{array}$$

(46)

Now, consider a mesh function ${\overline{\phi }}^{\pm }(r_i)=({\phi }_1^{\pm }(r_i),{\phi }_2^{\pm }(r_i))$, where

$$\begin{array}{cc}\hfill {\phi }_1^{\pm }(r_i)=& C_1{N}^{-1}\{s_1(r_i)-{\displaystyle \frac{\mu }{\epsilon }}({\tau }_2-r_i)\}\pm ({\chi }_{R,1}(r_i)-W_{R,1}(r_i)),r_i\in [1-{\tau }_2,1]\cap {\overline{\mathsf{\Omega }}}^N,\hfill \\ \hfill {\phi }_2^{\pm }(r_i)=& C_1{N}^{-1}\{s_2(r_i)+{\displaystyle \frac{\mu }{\epsilon }}(r_i-(1-{\tau }_2))\}\pm ({\chi }_{R,2}(r_i)-W_{R,2}(r_i)),r_i\in [1-{\tau }_2,1]\cap {\overline{\mathsf{\Omega }}}^N.\hfill \end{array}$$

From (44), it is easy to verify that ${\phi }_k^{\pm }(r_{{\displaystyle \frac{3N}{8}}})\ge 0,k=1,2$ and ${\phi }_2^{\pm }(r_{{\displaystyle \frac{N}{2}}})\ge 0,$ for a suitable choice of $C_1>0$.

$$\begin{array}{cc}\hfill P_1^N{\overline{\phi }}^{\pm }(r_i)& =C_1{N}^{-1}[1-s_2(r_i)]+{\displaystyle \frac{\mu }{\epsilon }}[1-(r_i-(1-{\tau }_2))]\pm (P_1^N-P_1){\overline{\chi }}_R(r_i)\ge 0,\hfill \\ \hfill P_2^N{\overline{\phi }}^{\pm }(r_i)& =C_1{N}^{-1}\{\mu p(r_i)[{\displaystyle \frac{1}{2}}+{\displaystyle \frac{\mu }{\epsilon }}]+q(r_i)[s_2(r_i)+{\displaystyle \frac{\mu }{\epsilon }}(r_i-(1-{\tau }_2))]\hfill \\ \hfill & +g(r_i)[s_1(r_i)+{\displaystyle \frac{\mu }{\epsilon }}(r_i-{\tau }_2)]\}\pm (P_2^N-P_2){\overline{\chi }}_R(r_i)\hfill \\ \hfill & \ge C_1{N}^{-1}\{{\displaystyle \frac{\mu \alpha }{2}}+\beta [{\displaystyle \frac{5}{8}}-{\displaystyle \frac{{\tau }_2}{2}}]+2\gamma +{\displaystyle \frac{\mu }{\epsilon }}[\mu \alpha +{\beta }^0+\gamma (1-{\tau }_2)]\}\hfill \\ & \mp C{N}^{-1}{\displaystyle \frac{{\mu }^2}{\epsilon }}\ge 0.\hfill \end{array}$$

Then, by Lemma 4, we have ${\phi }_1^{\pm }(r_i)\ge 0$ and ${\phi }_2^{\pm }(r_i)\ge 0;$ therefore,

$$\mid {\chi }_{R,k}(r_i)-W_{R,k}(r_i)\mid \le C{N}^{-1}{(lnN)}^2,{\displaystyle \frac{3N}{8}}\le i\le {\displaystyle \frac{N}{2}},k=1,2.$$

(47)

From (46) and (47), we have

$$\mid {\chi }_{R,k}(r_i)-W_{R,k}(r_i)\mid \le C{N}^{-1}{(lnN)}^2,0\le i\le {\displaystyle \frac{N}{2}},k=1,2.$$

Similarly, it is easy to prove the following estimates, respectively, for $\mu \le C\sqrt{\epsilon }$ and $\mu \ge C\sqrt{\epsilon };$ we have

$$\mid {\chi }_{R,k}(r_i)-W_{R,k}(r_i)\mid \le C{N}^{-1}lnN,0\le i\le N,k=1,2.$$

$$\mid {\chi }_{L,k}(r_i)-W_{L,k}(r_i)\mid \le C{N}^{-1}lnN,0\le i\le N,k=1,2.$$

Hence, the proof is complete. □

Theorem 8. 

The maximum pointwise error satisfies the following error bounds for sufficiently large N:

$$\begin{array}{c}\hfill \mid {\mathsf{\Phi }}_k(r_i)-{\mathsf{\Psi }}_k(r_i)\mid \le \left\{\begin{array}{c}C{N}^{-1}lnN,\mathrm{if}\mu \le C\sqrt{\epsilon },\hfill \\ C{N}^{-1}{ln}^{2}N,\mathrm{if}\mu \ge C\sqrt{\epsilon },\hfill \end{array}\right.i\in I_N,k=1,2.\end{array}$$

where $\overline{\mathsf{\Psi }}(r_i)$ is the numerical problem solution of (1) defined by (38) and (39).

Proof. 

Given that ${\mathsf{\Phi }}_k=v_k+{\chi }_k,{\mathsf{\Psi }}_k=V_k+W_k$, and the preceding Theorems 6 and 7, the required estimate is obtained. □

7. Numerical Examples

The theoretical results established here are tested by considering the following problems, whose exact solutions are unknown. In all cases, the exact solutions to the test problems remain unknown. Thus, for various values of $(N,\epsilon ,\mu ),$ we estimate the error and figure out the experiment rate of convergence in our constructed solution using the double mesh principle. The maximum pointwise global two mesh differences $D_{\epsilon ,\mu }^M$ are defined as follows:

$$D_{\epsilon ,\mu }^M=\underset{0\le i\le M}{max}\mid {\mathsf{\Psi }}_i^M-{\mathsf{\Psi }}_{2i}^{2M}\mid ,$$

where ${\mathsf{\Psi }}_i^M$ and ${\mathsf{\Psi }}_{2i}^{2M}$ are the $i^{th}$ components of the numerical solutions on meshes of M and $2M$ points, respectively. We compute the uniform global error and rate of convergence as

$$D^M=\underset{\epsilon ,\mu }{max}{D}_{\epsilon ,\mu }^M\mathrm{and}{p}^M={log}_2\left({\displaystyle \frac{D^M}{D^{2M}}}\right).$$

The numerical estimates for the various perturbation parameter values are shown for the following example: $\epsilon \in \{2^{-4},2^{-5},\cdots ,2^{-23}\}$ with $\mu ={\displaystyle \frac{\sqrt{\epsilon }}{10}}$ or $\mu =2\sqrt{\epsilon }.$

Example 1. 

Consider the boundary value problem

$$\left\{\begin{array}{c}-\epsilon {\mathsf{\Phi }}^{\prime \prime \prime }(r)+10\mu {\mathsf{\Phi }}^{\prime \prime }(r)+6{\mathsf{\Phi }}^{\prime }(r)-{\displaystyle \frac{1}{2}}\mathsf{\Phi }(r)-{\displaystyle \frac{1}{4}}{\mathsf{\Phi }}^{\prime }(r-1)=1+r^2,r\in {\mathsf{\Omega }}^{-}\cup {\mathsf{\Omega }}^{+},\hfill \\ \mathsf{\Phi }(r)=1+r,r\in [-1,0],{\mathsf{\Phi }}^{\prime }(2)=2.\hfill \end{array}\right.$$

(48)

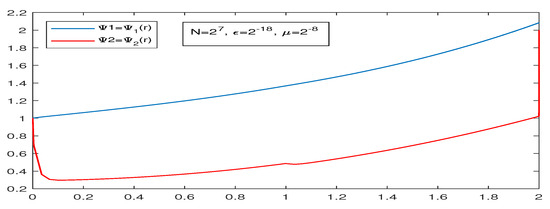
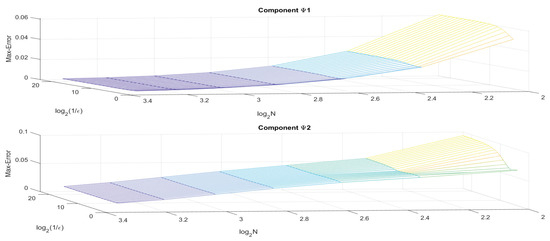
Table 1 presents the $(\epsilon ,\mu )-$ uniform error $D_k^M$ and order of convergence $p_k^M,k=1,2$, for the solution components ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2$ when $\mu >C\sqrt{\epsilon }.$ Figure 2 and Figure 3 represent the solution graph of ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2$ and the surface plot maximum pointwise error, respectively, of Example 1.

Table 1. Numerical estimates for Example 1.

	N (Number of Grid Points)
	$2^4$	$2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
$D_1^M$	6.1253 × 10−2	2.6227 × 10−2	1.4018 × 10−2	7.7693 × 10−3	4.3070 × 10−3	2.3737 × 10−3	1.4074 × 10−3
$p_1^M$	1.2237	9.0377 × 10−1	8.5145 × 10−1	8.5112 × 10−1	8.5956 × 10−1	7.5410 × 10−1	-
$D_2^M$	6.1454 × 10−2	5.4412 × 10−2	4.6333 × 10−2	3.6919 × 10−2	2.6322 × 10−2	1.7061 × 10−2	1.1023 × 10−2
$p_2^M$	1.7557 × 10−1	2.3189 × 10−1	3.2770 × 10−1	4.8805 × 10−1	6.2556 × 10−1	6.3018 × 10−1	-

Figure 2. Example 1—solution graph.

Figure 3. Example 1—surface maximum error plot.

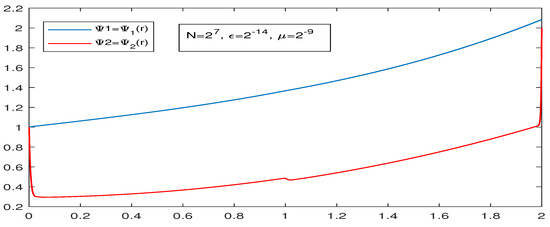
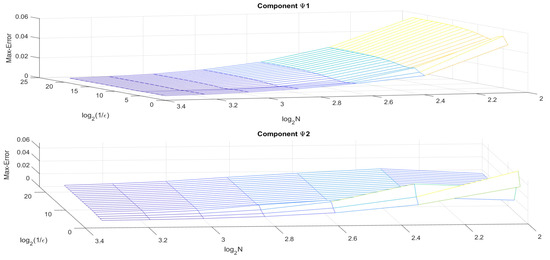
When $\mu \le C\sqrt{\epsilon }$, the values of $D_k^M$ and $p_k^M,k=1,2$, correspond to the solution components ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2,$ respectively, as shown in Table 2. Figure 4 and Figure 5 represent the solution graph of ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2$ and maximum pointwise error, respectively, of Example 1.

Table 2. Numerical estimates for Example 1.

	N (Number of Grid Points)
	$2^4$	$2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
$D_1^M$	6.7014 × 10−2	3.0316 × 10−2	1.2929 × 10−2	6.3722 × 10−3	3.1685 × 10−3	1.5794 × 10−3	7.8833 × 10−4
$p_1^M$	1.1444	1.2294	1.0208	1.0080	1.0044	1.0025	-
$D_2^M$	3.6321 × 10−2	2.9443 × 10−2	1.4043 × 10−2	1.0222 × 10−2	4.9754 × 10−3	3.1677 × 10−3	1.7172 × 10−3
$p_2^M$	3.0289 × 10−1	1.0681	4.5815 × 10−1	1.0388	6.5137 × 10−1	8.8338 × 10−1	-

Figure 4. Example 1—solution graph.

Figure 5. Example 1—surface maximum error plot.

Example 2. 

$$\left\{\begin{array}{c}-\epsilon {\mathsf{\Phi }}^{\prime \prime \prime }(r)+(10+r){\mathsf{\Phi }}^{\prime \prime }(r)+(6+exp(-r)){\mathsf{\Phi }}^{\prime }(r)-{\displaystyle \frac{1}{4}}\mathsf{\Phi }(r)\hfill \\ -r{\mathsf{\Phi }}^{\prime }(r-1)=exp(r),r\in {\mathsf{\Omega }}^{-}\cup {\mathsf{\Omega }}^{+},\hfill \\ \mathsf{\Phi }(r)=1+r^2,r\in [-1,0],{\mathsf{\Phi }}^{\prime }(2)=2.\hfill \end{array}\right.$$

(49)

Table 3 presents the $(\epsilon ,\mu )-$ uniform error $D_k^M$ and order of convergence $p_k^M,k=1,2$, for the solution components ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2,$ respectively, when $\mu >C\sqrt{\epsilon }.$ Figure 6 and Figure 7 represent the solution graph of ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2$ and the surface plot maximum pointwise error, respectively, of Example 2.

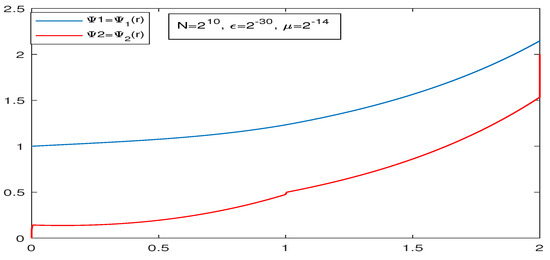
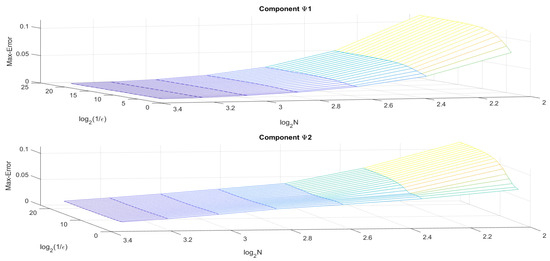
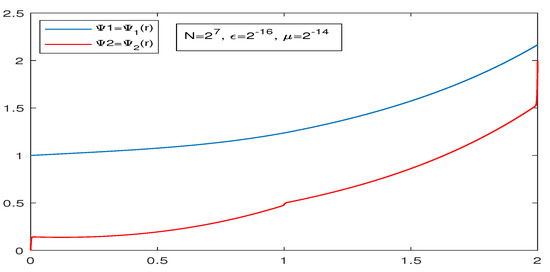
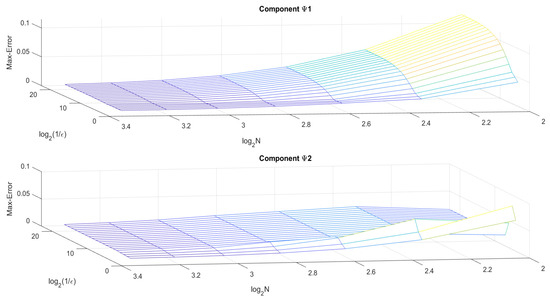
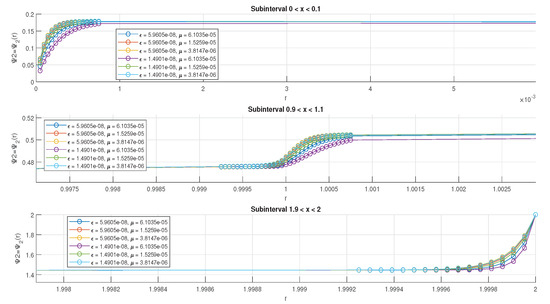
Table 3. Numerical estimates for Example 2.

	N (Number of Grid Points)
	$2^4$	$2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
$D_1^M$	9.2514 × 10−2	4.0526 × 10−2	1.8866 × 10−2	9.5490 × 10−3	5.1640 × 10−3	2.7901 × 10−3	1.6128 × 10−3
$p_1^M$	1.1908	1.1030	9.8238 × 10−1	8.8686 × 10−1	8.8819 × 10−1	7.9071 × 10−1	-
$D_2^M$	6.0392 × 10−2	5.4616 × 10−2	4.7298 × 10−2	4.0200 × 10−2	2.8992 × 10−2	1.9395 × 10−2	1.2678 × 10−2
$p_2^M$	1.4504 × 10−1	2.0753 × 10−1	2.3460 × 10−1	4.7152 × 10−1	5.7999 × 10−1	6.1335 × 10−1	-

Figure 6. Example 2—solution graph.

Figure 7. Example 2—surface maximum error plot.

When $\mu \le C\sqrt{\epsilon }.$, the values of $D_k^M$ and $p_k^M,k=1,2$, correspond to the solution components ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2,$ as shown in Table 4. Figure 8 and Figure 9 represent the solution graph of ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2$ and maximum pointwise error, respectively, of Example 2. Figure 10 represents the layer behavior of the solution component ${\mathsf{\Psi }}_2(r)$ in the subintervals $(0,0.1),(0.9,1.1)$, and $(1.9,2)$ for fixed N and different values of parameter μ and $\epsilon .$

Table 4. Numerical estimates for Example 2.

	N (Number of Grid Points)
	$2^4$	$2^5$	$2^6$	$2^7$	$2^8$	$2^9$	$2^{10}$
$D_1^M$	9.9453 × 10−2	4.6997 × 10−2	2.2824 × 10−2	1.1243 × 10−2	5.5779 × 10−3	2.7774 × 10−3	1.3855 × 10−3
$p_1^M$	1.0815	1.0420	1.0216	1.0112	1.0060	1.0033	-
$D_2^M$	2.3409 × 10−2	1.8094 × 10−2	9.0293 × 10−3	6.4286 × 10−3	3.2111 × 10−3	2.0205 × 10−3	1.0943 × 10−3
$p_2^M$	3.7157 × 10−1	1.0028	4.9010 × 10−1	1.0014	6.6836 × 10−1	8.8465 × 10−1	-

Figure 8. Example 2—solution graph.

Figure 9. Example 2—surface maximum error plot.

Figure 10. Example 2—${\mathsf{\Psi }}_2(r)$ solution graph in the layer region.

8. Conclusions

In this article, we investigate the third-order two-parameter singularly perturbed delay differential equations. The problem is transformed into a weakly coupled system of one first-order equation with non-delay terms and another second-order singularly perturbed delay differential equation with a reaction-dominant, convection-dominant, or reaction–convection-dominant problem based on the relations of the parameters $\mu$ and $\epsilon$. In [20], the boundary layer of width $O({\displaystyle \frac{\epsilon }{\mu }})$ is expected at the right of $r=0$ and right of $r=1,$ whereas the problem considered here admits the boundary layer of width $O({\displaystyle \frac{\epsilon }{\mu }})$ at the left of $r=1$ and left of $r=2$ when $\mu \ge C\sqrt{\epsilon }.$ As the problem shows that the solution component ${\mathsf{\Psi }}_2$ exhibit boundary and inner layers at $x=0,2$ and $x=1,$ respectively, we split the domain into six subdomains. The mesh points with varying mesh sizes are defined on each subdomain. Piecewise linear interpolation is used in a fitted finite difference approach on this mesh. The point $x_i-1$ does not necessarily have to be a mesh point when $i>N/2$. The interpolation must, therefore, be used to estimate $u_2(x_i-1).$ Additionally, it has been demonstrated that the method suggested here, which uses piecewise linear interpolation, yields almost linear convergence of order $O(N^{-1}{ln}^{2}N).$ For different parameter values $(\epsilon ,\mu ,N),$ the numerical solution of the problem is obtained by applying an upwind finite-difference technique to the piecewise uniform Shishkin mesh. This approach yields first-order convergence, which is consistent with the theoretical findings.