Research on the Internal Force Solution for Statically Indeterminate Structures Under a Local Trapezoidal Load

Abstract

The calculation of internal forces is a critical aspect in the design of statically indeterminate structures. Local trapezoidal loads, as a common loading configuration in practical engineering (e.g., earth pressure, uneven surcharge), make it essential to investigate how to compute the internal forces of statically indeterminate structures under such loads by using the displacement method. The key to displacement-based analysis lies in deriving the fixed-end moment formulas for local trapezoidal loads. Traditional methods, such as the force method, virtual beam method, or integral method, often involve complex computations. Therefore, this study aims to derive a general formula for fixed-end moments in statically indeterminate beams subjected to local trapezoidal loads by using the integral method, providing a more efficient and clear theoretical tool for engineering practice while addressing the limitations of existing educational and applied methodologies. The integral method is employed to derive fixed-end moment expressions for three types of statically indeterminate beams: (1) a beam fixed at both ends, (2) an an-end-fixed another-end-simple-support beam, and (3) a beam fixed at one end and sliding at the other. This approach eliminates the redundant equations of the traditional force method or the indirect transformations of the virtual beam method, directly linking boundary conditions through integral operations on load distributions, thereby significantly simplifying the solving process. Three representative numerical examples validate the correctness and universality of the derived formulas. The results demonstrate that the solutions obtained via the integral method align with software-calculated results, yet the proposed method yields analytical expressions for structural internal forces. Comparative analysis shows that the integral method surpasses traditional approaches (e.g., force method, virtual beam method) in terms of conceptual clarity and computational efficiency, making it particularly suitable for instructional demonstrations and rapid engineering calculations. The proposed integral method provides a systematic analytical framework for the internal force analysis of statically indeterminate structures under local trapezoidal loads, combining mathematical rigor with engineering practicality. The derived formulas can be directly applied to real-world designs, substantially reducing computational complexity. Moreover, this method offers a more intuitive theoretical case for structural mechanics education, enhancing students’ understanding of the mathematical–mechanical relationship between loads and internal forces. The research outcomes hold both theoretical significance and practical engineering value, establishing a solving paradigm for the displacement-based analysis of statically indeterminate structures under complex local trapezoidal loading conditions.

1. Introduction

Statically indeterminate structures have a wide range of applications in practical engineering, such as h-type anti-slide piles and row pile structures. Especially in recent years, the application of h-shaped anti-slide piles (hTPs) in slope reinforcement engineering has become increasingly widespread. However, challenges remain in their design theory and computational methods. Building on the Winkler foundation model, reference [1] proposed a novel analytical model for hTPs, which solves the internal forces and deformations of the pile through an iterative method. The study demonstrated the significant advantage of hTPs in reducing pile-top displacement (41.4% less than conventional anti-slide piles) and highlighted the critical role of pile width in displacement control. Reference [2] systematically investigated the supporting mechanism of hTPs for the first time. By comparing them with traditional structures, such as frame-type and anchor-cable piles, the study confirmed the superior stress distribution, cost-effectiveness, and construction performance of hTPs, with long-term stability further validated by monitoring data. The performance of h-shaped anti-slide piles under special geological conditions has also attracted considerable attention. Reference [3] conducted centrifugal model tests to study the mechanical behavior of h-piles in reinforcing soil–rock mixture slopes (SRMSs) under rainfall conditions. The results revealed the significant influence of rainfall duration on lateral earth pressure distribution and elucidated the dynamic evolution of soil arching effects between piles. For large-scale landslide prevention, reference [4] introduced an h-shaped prestressed anchor-cable anti-slide pile structure. By simplifying the calculation method, the study demonstrated the effectiveness of anchor cable prestressing in improving pile internal forces, particularly with double-row anchor cables, which significantly reduced bending moments and displacements. Notable progress has also been made in the study of double-row pile supporting structures. Reference [5] systematically reviewed the deformation characteristics and pile–soil interaction models of double-row piles, pointing out limitations in current research, such as the dynamic evolution of soil arching effects and applicability in complex strata, thereby providing direction for future studies. Additionally, seismic performance is a critical issue in slope engineering. Reference [6] employed the finite element method and extended finite element method to analyze the dynamic response of pile-anchor supporting structures. The study pioneered the simulation of crack initiation and propagation in anti-slide piles under seismic loads, confirming the necessity of seismic reinforcement measures near the sliding surface. For complex slope systems, reference [7] innovatively incorporated three-dimensional effects and soil suction into the analytical framework, establishing a 3D limit analysis model for stepped slopes reinforced by multi-row anti-slide piles. The study revealed the significant influence of pile height and soil type on reinforcement efficiency, providing a theoretical basis for optimizing multi-row pile systems.

The internal force solution of statically indeterminate structures is central to structural mechanics. In general, methods for solving the internal forces of statically indeterminate structures include the force, displacement, and asymptotic solution methods, as well as other methods [8]. Research on statically indeterminate structures has demonstrated significant importance in engineering practice, particularly in their analysis and optimization under complex loading conditions, material nonlinearity, or geometric nonlinearity. The development of efficient and accurate solution methods has remained a key research focus in this field. In recent years, with the increasing scale of structures and diversification of engineering requirements, traditional analytical methods have faced challenges in computational efficiency and applicability. This has prompted scholars to propose various improved approaches. In the static analysis of statically indeterminate structures, several innovative methods have been proposed. For instance, an approximate reanalysis method based on system reduction and iterative solving [9] significantly enhances computational efficiency for high-rank structural modifications through pseudo-force concepts and spectral decomposition techniques, making it suitable for complex scenarios such as functionally graded materials. For computing elastic curves of variable-cross-section beams, a novel numerical method achieves high accuracy by employing an equivalent cantilever beam model and the principle of virtual displacements [10]. Additionally, the Green’s function method provides an analytical solution for deformation, internal force, and stability analysis of statically indeterminate single-span beams, overcoming the complexity of traditional Krylov functions [11]. In solving internal forces under locally distributed moments, the integral method offers a simplified approach for displacement-based analysis [12]. For flexible structures and precision engineering, research on statically indeterminate symmetric flexure structures (SISs) demonstrates their advantages in eliminating parasitic motion and improving positioning accuracy [13]. In the field of construction mechanics, a force feedback method based on phased temperature measurements integrates real-time data with the matrix displacement method, substantially reducing errors in simulating the construction process of statically indeterminate steel structures under non-uniform temperature fields [14]. Furthermore, the layered force method optimizes internal force calculations for highly statically indeterminate structures by decomposing the problem into hierarchical subproblems, avoiding the need for solving simultaneous equations as in traditional force methods [15].

Many researchers have studied methods for solving the internal forces of statically indeterminate structures [16,17,18], but these studies typically consider common loads such as concentrated forces, concentrated force couples, or uniformly distributed loads. There have been few studies on the solution of internal forces in statically indeterminate structures under a local trapezoidal load; such loads are often involved in practical engineering. For example, in the design of plant structures, the loads transmitted to the main beam through secondary beams and floor slabs can form trapezoidal loads [19]. In contrast to other methods, the displacement method has a fixed solution approach and is easy to grasp. When using this method to solve for the internal forces in a statically indeterminate structure under a local trapezoidal load, it is necessary to know the fixed-end moment formulas for the three common types of single-span statically indeterminate beams (a beam fixed at both ends, an an-end-fixed another-end-simple-support beam, and a beam fixed at one end and sliding at the other) under local trapezoidal loads. In general, fixed-end moment formulas can be derived using methods such as the force virtual beam, the energy, and load equivalence methods [20,21]. These methods make it relatively easy to derive the fixed-end moment formulas for single concentrated forces and full-span uniformly distributed loads. However, using these methods to derive the fixed-end moment formula for local trapezoidal loads is highly challenging. In fact, a distributed load q(x) can be regarded as being composed of numerous concentrated loads, q(x) dx. Therefore, the integral method can be used, transforming the derivation of the fixed-end moment formula under the action of local trapezoidal loads into the process of solving a definite integral where the integrand is a polynomial function, using the fixed-end moment formula under the action of a single concentrated force. This approach can greatly simplify the derivation of the fixed-end moment formula under local trapezoidal loads.

In this study, to solve the internal forces of statically indeterminate structures under a local trapezoidal load, the integral method was used to derive the fixed-end moment formulas under the action of local trapezoidal loads for two different working conditions, based on the fixed-end moment formula under the action of a single concentrated force. In this way, the aforementioned problem can be solved. In addition, examples of solving the internal forces of statically multi-span beams and rigid frames with and without sidesway are given to verify the formulas derived in this study, which are significant for engineering applications and teaching.

In this paper, $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ denote the fixed-end moments at the A and B ends of the beam, respectively. Both are considered positive when oriented clockwise around the bar. l is the span of the beam, F_p is the concentrated force, and a, b, c, and d are the lengths (see the relevant figures for details).

The remainder of this paper is organized as follows: Section 2, Section 3 and Section 4 describe the derivation of the fixed-end moment formulas for the three studied types of statically indeterminate beams. Section 5 provides examples to validate the proposed approach. Finally, Section 6 concludes this paper.

2. Derivation of the Fixed-End Moment Formulas for Beams Fixed at Both Ends

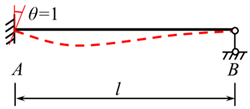
To obtain the fixed-end moment formulas for beams fixed at both ends and subjected to trapezoidal loads, it is necessary to utilize the fixed-end moment formulas given in Equations (1) and (2) for a beam fixed at both ends and subjected to a concentrated force, as illustrated in Figure 1 [8].

$$M_{AB}^{\mathrm{F}}=-{\displaystyle \frac{F_{\mathrm{P}}a{b}^2}{l^2}}$$

(1)

$$M_{BA}^{\mathrm{F}}={\displaystyle \frac{F_{\mathrm{P}}{a}^{2}b}{l^2}}$$

(2)

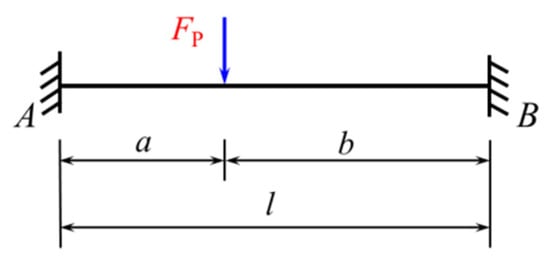
Figure 1. Beam fixed at both ends and subjected to a single concentrated force.

2.1. Loading Condition 1

To derive the fixed-end moment formulas under the action of the trapezoidal load shown in Figure 2, the integral method can be used to substitute F_P, a, and b in Equations (1) and (2) as follows: $a\to x$, $b\to l-x$, $F_{\mathrm{P}}\to q_0{\displaystyle \frac{x-a}{b}}dx(a\le x\le a+b)$, $F_{\mathrm{P}}\to q_{0}dx(a+b\le x\le a+b+c)$, $F_{\mathrm{P}}\to q_0{\displaystyle \frac{(a+b+c+d)-x}{d}}dx(a+b+c\le x\le a+b+c+d)$. Then, Equations (3) and (4) for $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ under the loading condition shown in Figure 2 can be obtained.

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}={\displaystyle {\int }_a^{a+b}-\frac{q_0\frac{x-a}{b}dx\cdot x\cdot {(l-x)}^2}{l^2}+{\displaystyle {\int }_{a+b}^{a+b+c}-\frac{q_{0}dx\cdot x\cdot {(l-x)}^2}{l^2}}}+{\displaystyle {\int }_{a+b+c}^{a+b+c+d}-\frac{q_0\frac{(a+b+c+d)-x}{d}dx\cdot x\cdot {(l-x)}^2}{l^2}}\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_0}{b{l}^2}}{\displaystyle {\int }_a^{a+b}\left[x^4-(a+2l)x^3+(l^2+2al)x^2-a{l}^{2}x\right]dx}-{\displaystyle \frac{q_0}{l^2}}{\displaystyle {\int }_{a+b}^{a+b+c}(x^3-2l{x}^2+l^{2}x)dx}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{d{l}^2}}{\displaystyle {\int }_{a+b+c}^{a+b+c+d}\left\{x^4-(a+b+c+d+2l)x^3+\left[2l(a+b+c+d)+l^2\right]x^2-(a+b+c+d)l^{2}x\right\}}dx\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_0}{b{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b)}^5-a^5\right]-{\displaystyle \frac{a+2l}{4}}\left[{(a+b)}^4-a^4\right]+{\displaystyle \frac{l^2+2al}{3}}\left[{(a+b)}^3-a^3\right]-{\displaystyle \frac{a{l}^2}{2}}\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{q_0}{l^2}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b+c)}^4-{(a+b)}^4\right]-{\displaystyle \frac{2l}{3}}\left[{(a+b+c)}^3-{(a+b)}^3\right]+{\displaystyle \frac{l^2}{2}}\left[{(a+b+c)}^2-{(a+b)}^2\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{d{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b+c+d)}^5-{(a+b+c)}^5\right]-{\displaystyle \frac{a+b+c+d+2l}{4}}\left[{(a+b+c+d)}^4-{(a+b+c)}^4\right]\right.\\ \left.\hspace{1em}\hspace{1em} +{\displaystyle \frac{2l(a+b+c+d)+l^2}{3}}\left[{(a+b+c+d)}^3-{(a+b+c)}^3\right]-{\displaystyle \frac{(a+b+c+d)l^2}{2}}\left[{(a+b+c+d)}^2-{(a+b+c)}^2\right]\right\}\end{array}$$

(3)

$$\begin{array}{l}{M}_{BA}^{\mathrm{F}}={\displaystyle {\int }_a^{a+b}\frac{q_0\frac{x-a}{b}dx\cdot x^2\cdot (l-x)}{l^2}+{\displaystyle {\int }_{a+b}^{a+b+c}\frac{q_{0}dx\cdot x^2\cdot (l-x)}{l^2}}}+{\displaystyle {\int }_{a+b+c}^{a+b+c+d}\frac{q_0\frac{(a+b+c+d)-x}{d}dx\cdot x^2\cdot (l-x)}{l^2}}\\ \hspace{1em}\hspace{1em}={\displaystyle \frac{q_0}{b{l}^2}}{\displaystyle {\int }_a^{a+b}\left[-x^4+(a+l)x^3-al{x}^2\right]dx}+{\displaystyle \frac{q_0}{l^2}}{\displaystyle {\int }_{a+b}^{a+b+c}(-x^3+l{x}^2)dx}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{d{l}^2}}{\displaystyle {\int }_{a+b+c}^{a+b+c+d}\left\{x^4-(a+b+c+d+l)x^3+l(a+b+c+d)x^2\right\}}dx\\ \hspace{1em}\hspace{1em}={\displaystyle \frac{q_0}{b{l}^2}}\left\{-{\displaystyle \frac{1}{5}}\left[{(a+b)}^5-a^5\right]+{\displaystyle \frac{a+l}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{al}{3}}\left[{(a+b)}^3-a^3\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{l^2}}\left\{-{\displaystyle \frac{1}{4}}\left[{(a+b+c)}^4-{(a+b)}^4\right]+{\displaystyle \frac{l}{3}}\left[{(a+b+c)}^3-{(a+b)}^3\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{d{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b+c+d)}^5-{(a+b+c)}^5\right]-{\displaystyle \frac{a+b+c+d+l}{4}}\left[{(a+b+c+d)}^4-{(a+b+c)}^4\right]\right.\\ \left.\hspace{1em}\hspace{1em} +{\displaystyle \frac{l(a+b+c+d)}{3}}\left[{(a+b+c+d)}^3-{(a+b+c)}^3\right]\right\}\end{array}$$

(4)

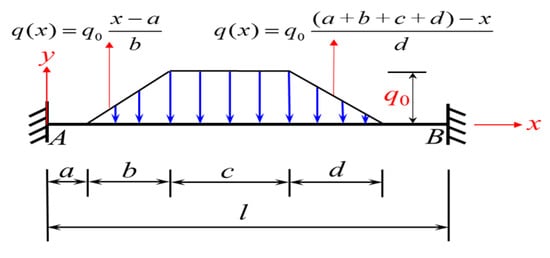
Figure 2. Beam fixed at both ends and subjected to a local trapezoidal load (loading condition 1).

If the trapezoidal load is distributed across the full span (Figure 3), then it is only necessary to set a = 0 in Equations (3) and (4), and then substitute b, c, and d in Equations (3) and (4) as follows: b → a, c → b, d → c. Then, Equations (5) and (6) for $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ under the loading condition shown in Figure 3 can be obtained.

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}=-{\displaystyle \frac{q_0}{l^2}}({\displaystyle \frac{1}{5}}{a}^4-{\displaystyle \frac{l}{2}}{a}^3+{\displaystyle \frac{l^2}{3}}{a}^2)-{\displaystyle \frac{q_0}{l^2}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{2l}{3}}\left[{(a+b)}^3-a^3\right]+{\displaystyle \frac{l^2}{2}}\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{c{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[l^5-{(a+b)}^5\right]-{\displaystyle \frac{3l}{4}}\left[l^4-{(a+b)}^4\right]\right.\left.+l^2\left[l^3-{(a+b)}^3\right]-{\displaystyle \frac{l^3}{2}}\left[l^2-{(a+b)}^2\right]\right\}\end{array}$$

(5)

$$\begin{array}{l}{M}_{BA}^{\mathrm{F}}={\displaystyle \frac{q_0}{l^2}}(-{\displaystyle \frac{1}{5}}{a}^4+{\displaystyle \frac{l}{4}}{a}^3)+{\displaystyle \frac{q_0}{l^2}}\left\{-{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]+{\displaystyle \frac{l}{3}}\left[{(a+b)}^3-a^3\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{c{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[l^5-{(a+b)}^5\right]-{\displaystyle \frac{l}{2}}\left[l^4-{(a+b)}^4\right]\right.\left.+{\displaystyle \frac{l^2}{3}}\left[l^3-{(a+b)}^3\right]\right\}\end{array}$$

(6)

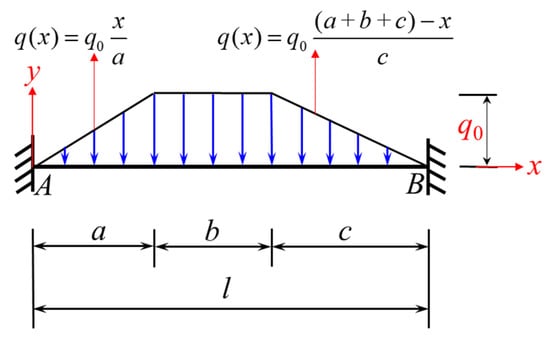
Figure 3. Beam fixed at both ends and subjected to a full-span trapezoidal load (loading condition 1).

2.2. Loading Condition 2

The fixed-end moment formulas under the action of trapezoidal distributed loads in different directions will be different, so they should be derived separately for cases in which the trapezoidal load rises from left to right and those in which it descends from left to right. The meanings of $M_{AB}^{\mathrm{F}}$, $M_{BA}^{\mathrm{F}}$, l, a, b, c, and d in the following equations are the same as in the previous equations. q₁ and q₂ are the minimum and maximum load intensities of the trapezoidal load, respectively.

2.2.1. Trapezoidal Loads Rising from Left to Right

To derive the fixed-end moment formula for the trapezoidal load shown in Figure 4, the integral method can be used by substituting F_p, a, and b in Equations (1) and (2) as follows: $F_{\mathrm{P}}\to \left[q_1+{\displaystyle \frac{q_2-q_1}{b}}(x-a)\right]dx(a\le x\le a+b)$, $a\to x$, and $b\to l-x$. In this way, Equations (7) and (8) for $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ under the loading condition shown in Figure 4 can be obtained.

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}={\displaystyle {\int }_a^{a+b}-\frac{\left[q_1+\frac{q_2-q_1}{b}(x-a)\right]dx\cdot x\cdot {(l-x)}^2}{l^2}}\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_1}{l^2}}{\displaystyle {\int }_a^{a+b}(x^3-2l{x}^2+l^{2}x)dx}-{\displaystyle \frac{q_2-q_1}{b{l}^2}}{\displaystyle {\int }_a^{a+b}\left[x^4-(a+2l)x^3+(l^2+2al)x^2-a{l}^{2}x\right]dx}\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_1}{l^2}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{2l}{3}}\left[{(a+b)}^3-a^3\right]+{\displaystyle \frac{l^2}{2}}\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{q_2-q_1}{b{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b)}^5-a^5\right]-{\displaystyle \frac{a+2l}{4}}\left[{(a+b)}^4-a^4\right]+{\displaystyle \frac{l^2+2al}{3}}\left[{(a+b)}^3-a^3\right]-{\displaystyle \frac{a{l}^2}{2}}\left[{(a+b)}^2-a^2\right]\right\}\end{array}$$

(7)

$$\begin{array}{l}{M}_{BA}^{\mathrm{F}}={\displaystyle {\int }_a^{a+b}\frac{\left[q_1+\frac{q_2-q_1}{b}(x-a)\right]dx\cdot x^2\cdot (l-x)}{l^2}}\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_1}{l^2}}{\displaystyle {\int }_a^{a+b}(x^3-l{x}^2)dx}-{\displaystyle \frac{q_2-q_1}{b{l}^2}}{\displaystyle {\int }_a^{a+b}\left[x^4-(a+l)x^3+al{x}^2\right]dx}\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_1}{l^2}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{l}{3}}\left[{(a+b)}^3-a^3\right]\right\}\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{q_2-q_1}{b{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b)}^5-a^5\right]-{\displaystyle \frac{a+l}{4}}\left[{(a+b)}^4-a^4\right]+{\displaystyle \frac{al}{3}}\left[{(a+b)}^3-a^3\right]\right\}\end{array}$$

(8)

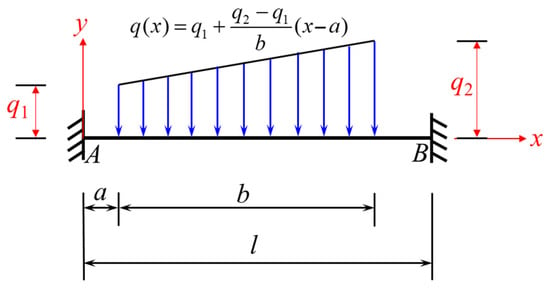
Figure 4. Beam fixed at both ends and subjected to a local trapezoidal load rising from left to right (loading condition 2).

If the trapezoidal load is distributed across the full span (Figure 5), then Equations (9) and (10) for $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ under the loading condition shown in Figure 5 can be obtained by simply setting a = 0 and b = l in Equations (7) and (8).

$$M_{AB}^{\mathrm{F}}=-({\displaystyle \frac{q_1}{20}}+{\displaystyle \frac{q_2}{30}})l^2$$

(9)

$$M_{BA}^{\mathrm{F}}=({\displaystyle \frac{q_1}{30}}+{\displaystyle \frac{q_2}{20}})l^2$$

(10)

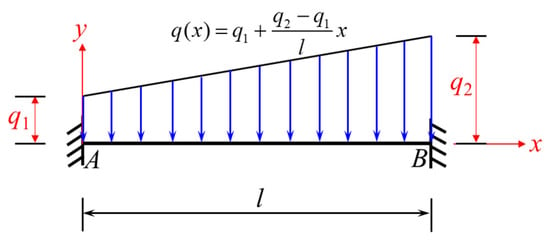
Figure 5. Beam fixed at both ends and subjected to a full-span trapezoidal load rising from left to right (loading condition 2).

2.2.2. Trapezoidal Loads Descending from Left to Right

The formulas for the loads shown in Figure 4 and Figure 6 indicate that to obtain the fixed-end moment formula for the beam shown in Figure 6, it is only necessary to replace q₁ in the first terms of Equations (7) and (8) with q₂, and add a negative sign to the second terms to obtain the corresponding Equations (9) and (10).

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}=-{\displaystyle \frac{q_2}{l^2}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{2l}{3}}\left[{(a+b)}^3-a^3\right]+{\displaystyle \frac{l^2}{2}}\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_2-q_1}{b{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b)}^5-a^5\right]-{\displaystyle \frac{a+2l}{4}}\left[{(a+b)}^4-a^4\right]+{\displaystyle \frac{l^2+2al}{3}}\left[{(a+b)}^3-a^3\right]-{\displaystyle \frac{a{l}^2}{2}}\left[{(a+b)}^2-a^2\right]\right\}\end{array}$$

(11)

$$\begin{array}{l}{M}_{BA}^{\mathrm{F}}=-{\displaystyle \frac{q_2}{l^2}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{l}{3}}\left[{(a+b)}^3-a^3\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_2-q_1}{b{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b)}^5-a^5\right]-{\displaystyle \frac{a+l}{4}}\left[{(a+b)}^4-a^4\right]+{\displaystyle \frac{al}{3}}\left[{(a+b)}^3-a^3\right]\right\}\end{array}$$

(12)

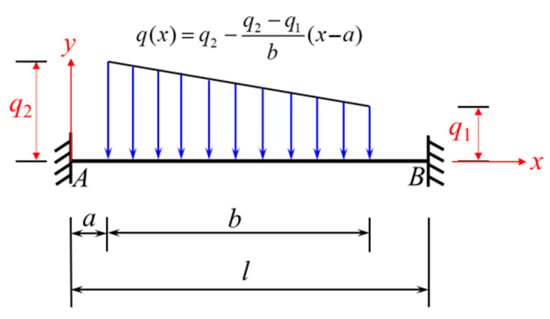
Figure 6. Beam fixed at both ends and subjected to a local trapezoidal load descending from left to right (loading condition 2).

If the trapezoidal load is distributed across the full span (Figure 7), then Equations (13) and (14) for $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ under the loading condition shown in Figure 7 can be obtained by simply setting a = 0 and b = l in Equations (11) and (12).

$$M_{AB}^{\mathrm{F}}=-({\displaystyle \frac{q_1}{30}}+{\displaystyle \frac{q_2}{20}})l^2$$

(13)

$$M_{BA}^{\mathrm{F}}=({\displaystyle \frac{q_1}{20}}+{\displaystyle \frac{q_2}{30}})l^2$$

(14)

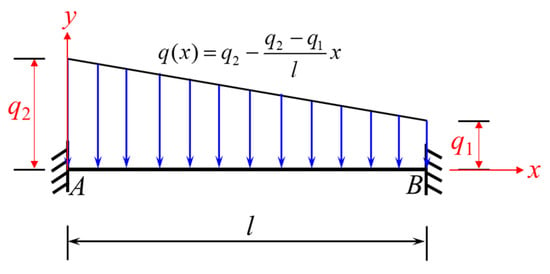
Figure 7. Beam fixed at both ends and subjected to a full-span trapezoidal load descending from left to right (loading condition 2).

3. Derivation of the Fixed-End Moment Formula for An-End-Fixed Another-End-Simple-Support Beam

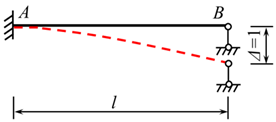
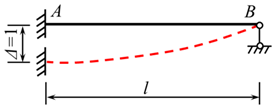
In order to obtain the fixed-end moment formula for the an-end-fixed another-end-simple-support beam subjected to a trapezoidal load, it is necessary to utilize the fixed-end moment Formula (15) for the an-end-fixed another-end-simple-support beam subjected to a concentrated force, as shown in Figure 8 [4].

$$M_{AB}^{\mathrm{F}}=-{\displaystyle \frac{F_{\mathrm{P}}ab(l+b)}{2l^2}}$$

(15)

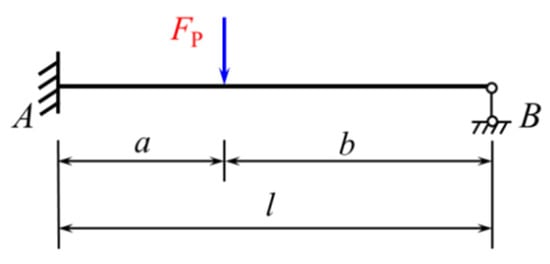
Figure 8. An-end-fixed another-end-simple-support beam subjected to a single concentrated force.

3.1. Loading Condition 1

To derive the fixed-end moment formula under the action of the trapezoidal load shown in Figure 9, the integral method can be used by applying the same transformation used in Section 2.1 for FP, a, and b to Equation (15) to obtain Equation (16) for $M_{AB}^{\mathrm{F}}$ under the loading condition shown in Figure 9.

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}={\displaystyle {\int }_a^{a+b}-\frac{q_0\frac{x-a}{b}dx\cdot x\cdot (l-x)\left[l+(l-x)\right]}{2l^2}+{\displaystyle {\int }_{a+b}^{a+b+c}-\frac{q_{0}dx\cdot x\cdot (l-x)\left[l+(l-x)\right]}{2l^2}}}\\ \hspace{1em}\hspace{1em} +{\displaystyle {\int }_{a+b+c}^{a+b+c+d}-\frac{q_0\frac{(a+b+c+d)-x}{d}dx\cdot x\cdot (l-x)\left[l+(l-x)\right]}{2l^2}}\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_0}{2b{l}^2}}{\displaystyle {\int }_a^{a+b}\left[x^4-(a+3l)x^3+(2l^2+3al)x^2-2a{l}^{2}x\right]dx}-{\displaystyle \frac{q_0}{2l^2}}{\displaystyle {\int }_{a+b}^{a+b+c}(x^3-3l{x}^2+2l^{2}x)dx}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{2d{l}^2}}{\displaystyle {\int }_{a+b+c}^{a+b+c+d}\left\{x^4-(a+b+c+d+3l)x^3+\left[3l(a+b+c+d)+2l^2\right]x^2-2l^2(a+b+c+d)x\right\}}dx\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_0}{2b{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b)}^5-a^5\right]-{\displaystyle \frac{a+3l}{4}}\left[{(a+b)}^4-a^4\right]+{\displaystyle \frac{2l^2+3al}{3}}\left[{(a+b)}^3-a^3\right]-a{l}^2\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{q_0}{2l^2}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b+c)}^4-{(a+b)}^4\right]-l\left[{(a+b+c)}^3-{(a+b)}^3\right]+l^2\left[{(a+b+c)}^2-{(a+b)}^2\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{2d{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b+c+d)}^5-{(a+b+c)}^5\right]-{\displaystyle \frac{a+b+c+d+3l}{4}}\left[{(a+b+c+d)}^4-{(a+b+c)}^4\right]\right.\\ \left.\hspace{1em}\hspace{1em} +{\displaystyle \frac{3l(a+b+c+d)+2l^2}{3}}\left[{(a+b+c+d)}^3-{(a+b+c)}^3\right]-l^2(a+b+c+d)\left[{(a+b+c+d)}^2-{(a+b+c)}^2\right]\right\}\end{array}$$

(16)

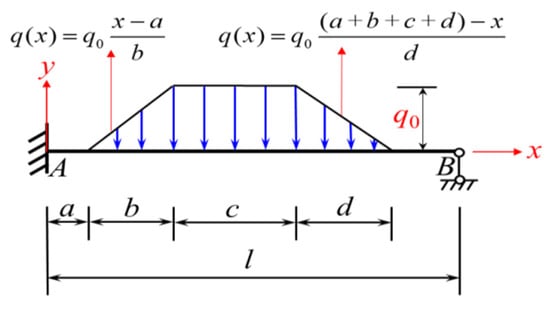
Figure 9. An-end-fixed another-end-simple-support beam subjected to a local trapezoidal load (loading condition 1).

If the trapezoidal load is distributed across the full span (Figure 10), then it is only necessary to set a = 0 in Equation (16); then, substituting b, c and d in Equation (16) as follows: b → a, c → b, d → c, Equation (17) for $M_{AB}^{\mathrm{F}}$ under the loading condition shown in Figure 10 can be obtained.

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}=-{\displaystyle \frac{q_0}{2l^2}}({\displaystyle \frac{1}{5}}{a}^4-{\displaystyle \frac{3l}{4}}{a}^3+{\displaystyle \frac{2l^2}{3}}{a}^2)\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{q_0}{2l^2}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-l\left[{(a+b)}^3-a^3\right]+l^2\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{2c{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[l^5-{(a+b)}^5\right]-l\left[l^4-{(a+b)}^4\right]\right.\left.+{\displaystyle \frac{5l^2}{3}}\left[l^3-{(a+b)}^3\right]-l^3\left[l^2-{(a+b)}^2\right]\right\}\end{array}$$

(17)

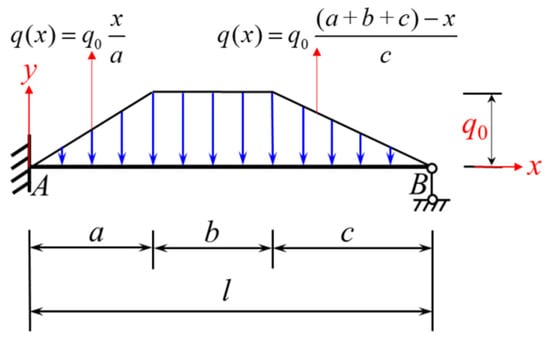
Figure 10. An-end-fixed another-end-simple-support beam subjected to a full-span trapezoidal load (loading condition 1).

3.2. Loading Condition 2

3.2.1. Trapezoidal Loads Rising from Left to Right

To derive the fixed-end moment formula under the action of the trapezoidal load shown in Figure 11, the integral method can be used by applying the same transformation used in Section 2.2.1. for F_P, a, and b to Equation (15) to obtain Equation (18) for $M_{AB}^{\mathrm{F}}$ under the loading condition shown in Figure 11.

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}={\displaystyle {\int }_a^{a+b}-\frac{\left[q_1+\frac{q_2-q_1}{b}(x-a)\right]dx\cdot x\cdot (l-x)\left[l+(l-x)\right]}{2l^2}}\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_1}{2l^2}}{\displaystyle {\int }_a^{a+b}(x^3-3l{x}^2+2l^{2}x)dx}-{\displaystyle \frac{q_2-q_1}{2b{l}^2}}{\displaystyle {\int }_a^{a+b}\left[x^4-(a+3l)x^3+(2l^2+3al)x^2-2a{l}^{2}x\right]dx}\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_1}{2l^2}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-l\left[{(a+b)}^3-a^3\right]+l^2\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{q_2-q_1}{2b{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b)}^5-a^5\right]-{\displaystyle \frac{a+3l}{4}}\left[{(a+b)}^4-a^4\right]+{\displaystyle \frac{2l^2+3al}{3}}\left[{(a+b)}^3-a^3\right]-a{l}^2\left[{(a+b)}^2-a^2\right]\right\}\\ \end{array}$$

(18)

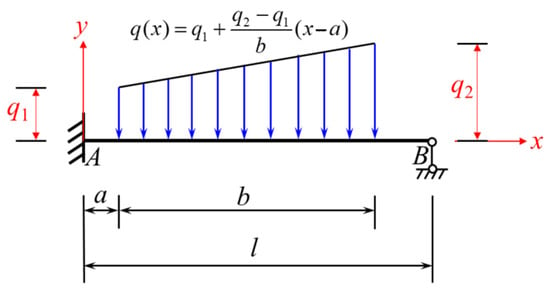
Figure 11. An-end-fixed another-end-simple-support beam subjected to a local trapezoidal load rising from left to right (loading condition 2).

If the trapezoidal load is distributed across the full span (Figure 12), then Equation (19) for $M_{AB}^{\mathrm{F}}$ under the loading condition shown in Figure 12 can be obtained by simply setting a = 0 and b = l in Equation (18).

$$M_{AB}^{\mathrm{F}}=-({\displaystyle \frac{q_1}{15}}+{\displaystyle \frac{7q_2}{120}})l^2$$

(19)

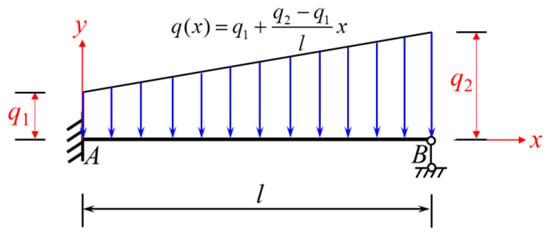
Figure 12. An-end-fixed another-end-simple-support beam subjected to a full-span trapezoidal load rising from left to right (loading condition 2).

3.2.2. Trapezoidal Loads Descending from Left to Right

The formulas for the loads in Figure 11 and Figure 13 indicate that to obtain the fixed-end moment formula for the beam shown in Figure 13, it is only necessary to replace q₁ in the first term of Equation (18) by q₂ and add a negative sign to the second term to obtain the corresponding Equation (20) for $M_{AB}^F$.

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}=-{\displaystyle \frac{q_2}{2l^2}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-l\left[{(a+b)}^3-a^3\right]+l^2\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_2-q_1}{2b{l}^2}}\left\{{\displaystyle \frac{1}{5}}\left[{(a+b)}^5-a^5\right]-{\displaystyle \frac{a+3l}{4}}\left[{(a+b)}^4-a^4\right]+{\displaystyle \frac{2l^2+3al}{3}}\left[{(a+b)}^3-a^3\right]-a{l}^2\left[{(a+b)}^2-a^2\right]\right\}\end{array}$$

(20)

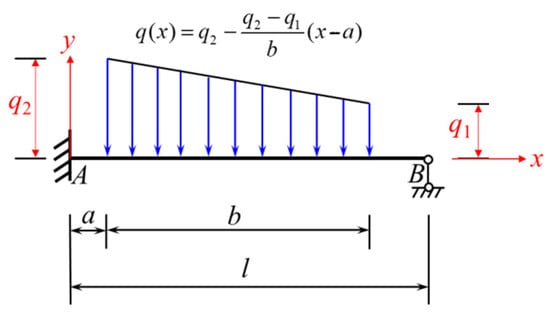
Figure 13. An-end-fixed another-end-simple-support beam subjected to a local trapezoidal load descending from left to right (loading condition 2).

If the trapezoidal load is distributed across the full span (Figure 14), then Equation (21) for $M_{AB}^{\mathrm{F}}$ under the loading condition shown in Figure 14 can be obtained by simply setting a = 0 and b = l in Equation (20).

$$M_{AB}^{\mathrm{F}}=-({\displaystyle \frac{q_2}{15}}+{\displaystyle \frac{7q_1}{120}})l^2$$

(21)

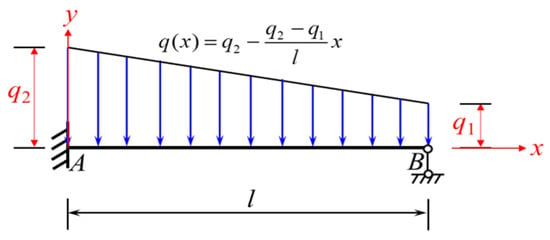
Figure 14. An-end-fixed another-end-simple-support beam subjected to a full-span trapezoidal load descending from left to right (loading condition 2).

4. Derivation of the Fixed-End Moment Formula for a Beam Fixed at One End and Sliding at the Other

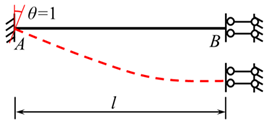
To obtain the fixed-end moment formula for a beam fixed at one end and sliding at the other and subjected to a trapezoidal load, it is necessary to utilize the fixed-end moment formulas given in Equations (22) and (23) for the same beam subjected to a concentrated force, as shown in Figure 15 [4].

$$M_{AB}^{\mathrm{F}}=-{\displaystyle \frac{F_{\mathrm{P}}a(l+b)}{2l}}$$

(22)

$$M_{BA}^{\mathrm{F}}=-{\displaystyle \frac{F_{\mathrm{P}}{a}^2}{2l}}$$

(23)

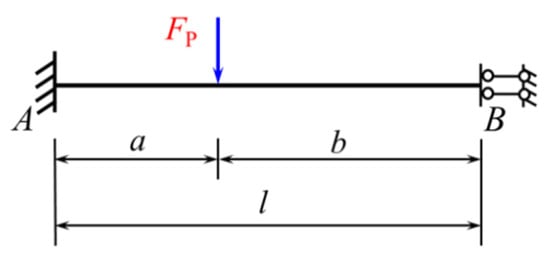
Figure 15. A beam fixed at one end and sliding at the other and subjected to a single concentrated force.

4.1. Loading Condition 1

To derive the fixed-end moment formulas under the action of the trapezoidal load shown in Figure 16, the integral method can be used by applying the same transformations used in Section 2.1. for F_P, a, and b to Equations (22) and (23); then, Equations (24) and (25) for $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ under the loading condition shown in Figure 16 can be obtained.

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}={\displaystyle {\int }_a^{a+b}-\frac{q_0\frac{x-a}{b}dx\cdot x\cdot \left[l+(l-x)\right]}{2l}+{\displaystyle {\int }_{a+b}^{a+b+c}-\frac{q_{0}dx\cdot x\cdot \left[l+(l-x)\right]}{2l}}}\\ \hspace{1em}\hspace{1em} +{\displaystyle {\int }_{a+b+c}^{a+b+c+d}-\frac{q_0\frac{(a+b+c+d)-x}{d}dx\cdot x\cdot \left[l+(l-x)\right]}{2l}}\\ \hspace{1em}\hspace{1em}={\displaystyle \frac{q_0}{2bl}}{\displaystyle {\int }_a^{a+b}\left[x^3-(a+2l)x^2+2alx\right]dx}+{\displaystyle \frac{q_0}{2l}}{\displaystyle {\int }_{a+b}^{a+b+c}(x^2-2lx)dx}\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{q_0}{2dl}}{\displaystyle {\int }_{a+b+c}^{a+b+c+d}\left\{x^3-(a+b+c+d+2l)x^2+2l(a+b+c+d)x\right\}}dx\\ \hspace{1em}\hspace{1em} ={\displaystyle \frac{q_0}{2bl}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{a+2l}{3}}\left[{(a+b)}^3-a^3\right]+al\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{2l}}\left\{{\displaystyle \frac{1}{3}}\left[{(a+b+c)}^3-{(a+b)}^3\right]-l\left[{(a+b+c)}^2-{(a+b)}^2\right]\right\}\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{q_0}{2dl}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b+c+d)}^4-{(a+b+c)}^4\right]-{\displaystyle \frac{a+b+c+d+2l}{3}}\left[{(a+b+c+d)}^3-{(a+b+c)}^3\right]\right.\\ \left.\hspace{1em}\hspace{1em} +l(a+b+c+d)\left[{(a+b+c+d)}^2-{(a+b+c)}^2\right]\right\}\end{array}$$

(24)

$$\begin{array}{l}{M}_{BA}^{\mathrm{F}}={\displaystyle {\int }_a^{a+b}-\frac{q_0\frac{x-a}{b}dx\cdot x^2}{2l}+{\displaystyle {\int }_{a+b}^{a+b+c}-\frac{q_{0}dx\cdot x^2}{2l}}}+{\displaystyle {\int }_{a+b+c}^{a+b+c+d}-\frac{q_0\frac{(a+b+c+d)-x}{d}dx\cdot x^2}{2l}}\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_0}{2bl}}{\displaystyle {\int }_a^{a+b}(x^3-a{x}^2)dx}-{\displaystyle \frac{q_0}{2l}}{\displaystyle {\int }_{a+b}^{a+b+c}{x}^{2}dx}+{\displaystyle \frac{q_0}{2dl}}{\displaystyle {\int }_{a+b+c}^{a+b+c+d}\left[x^3-(a+b+c+d)x^2\right]}dx\\ \hspace{1em}\hspace{1em}=-{\displaystyle \frac{q_0}{2bl}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{a}{3}}\left[{(a+b)}^3-a^3\right]\right\}-{\displaystyle \frac{q_0}{6l}}\left[{(a+b+c)}^3-{(a+b)}^3\right]\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_0}{2dl}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b+c+d)}^4-{(a+b+c)}^4\right]-{\displaystyle \frac{a+b+c+d}{3}}\left[{(a+b+c+d)}^3-{(a+b+c)}^3\right]\right\}\end{array}$$

(25)

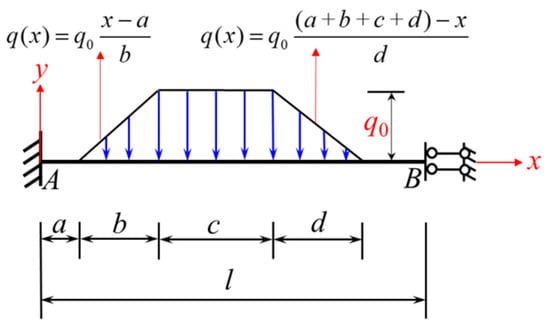
Figure 16. A beam fixed at one end and sliding at the other and subjected to a local trapezoidal load (loading condition 1).

If the trapezoidal load is distributed across the full span (Figure 17), then it is only necessary to set a = 0 in Equations (22) and (23), and then substitute b, c, and d in Equations (22) and (23) as follows: b→a, c→b, and d→c; then, Equations (26) and (27) for $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ under the loading condition shown in Figure 17 can be obtained.

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}={\displaystyle \frac{q_0}{2l}}({\displaystyle \frac{1}{4}}{a}^3-{\displaystyle \frac{2l}{3}}{a}^2)+{\displaystyle \frac{q_0}{2l}}\left\{{\displaystyle \frac{1}{3}}\left[{(a+b)}^3-a^3\right]-l\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{q_0}{2cl}}\left\{{\displaystyle \frac{1}{4}}\left[l^4-{(a+b)}^4\right]-l\left[l^3-{(a+b)}^3\right]\right.\left.+l^2\left[l^2-{(a+b)}^2\right]\right\}\end{array}$$

(26)

$$M_{BA}^{\mathrm{F}}=-{\displaystyle \frac{q_0}{8l}}{a}^3-{\displaystyle \frac{q_0}{6l}}\left[{(a+b)}^3-a^3\right]+{\displaystyle \frac{q_0}{2cl}}\left\{{\displaystyle \frac{1}{4}}\left[l^4-{(a+b)}^4\right]-{\displaystyle \frac{l}{3}}\left[l^3-{(a+b)}^3\right]\right\}$$

(27)

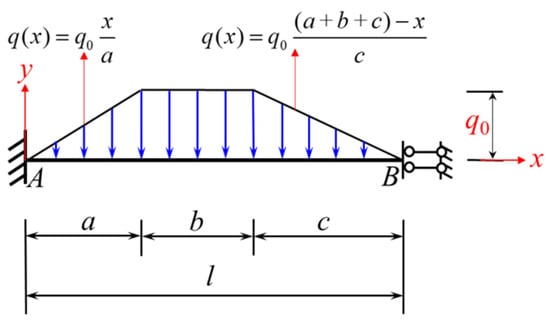
Figure 17. A beam fixed at one end and sliding at the other and subjected to a full-span trapezoidal load (loading condition 1).

4.2. Loading Condition 2

4.2.1. Trapezoidal Loads Rising from Left to Right

To derive the fixed-end moment formula under the action of the trapezoidal load shown in Figure 18, the integral method can be used by applying the same transformations used in Section 2.2.1. for F_P, a, and b to Equations (22) and (23); then, Equations (28) and (29) for $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ under the loading condition shown in Figure 18 can be obtained.

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}={\displaystyle {\int }_a^{a+b}-\frac{\left[q_1+\frac{q_2-q_1}{b}(x-a)\right]dx\cdot x\cdot \left[l+(l-x)\right]}{2l}}\\ \hspace{1em}\hspace{1em} ={\displaystyle \frac{q_1}{2l}}{\displaystyle {\int }_a^{a+b}(x^2-2lx)dx}+{\displaystyle \frac{q_2-q_1}{2bl}}{\displaystyle {\int }_a^{a+b}\left[x^3-(a+2l)x^2+2alx\right]dx}\\ \hspace{1em}\hspace{1em} ={\displaystyle \frac{q_1}{2l}}\left\{{\displaystyle \frac{1}{3}}\left[{(a+b)}^3-a^3\right]-l\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} +{\displaystyle \frac{q_2-q_1}{2bl}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{a+2l}{3}}\left[{(a+b)}^3-a^3\right]+al\left[{(a+b)}^2-a^2\right]\right\}\end{array}$$

(28)

$$\begin{array}{l}{M}_{BA}^{\mathrm{F}}={\displaystyle {\int }_a^{a+b}-\frac{\left[q_1+\frac{q_2-q_1}{b}(x-a)\right]dx\cdot x^2}{2l}}=-{\displaystyle \frac{q_1}{2l}}{\displaystyle {\int }_a^{a+b}{x}^{2}dx}-{\displaystyle \frac{q_2-q_1}{2bl}}{\displaystyle {\int }_a^{a+b}(x^3-a{x}^2)dx}\\ \hspace{1em}\hspace{1em} =-{\displaystyle \frac{q_1}{6l}}\left[{(a+b)}^3-a^3\right]-{\displaystyle \frac{q_2-q_1}{2bl}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{a}{3}}\left[{(a+b)}^3-a^3\right]\right\}\end{array}$$

(29)

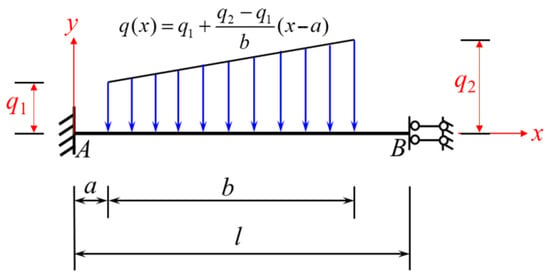
Figure 18. A beam fixed at one end and sliding at the other and subjected to a local trapezoidal load rising from left to right (loading condition 2).

If the trapezoidal load is distributed across the full span (Figure 19), then Equations (30) and (31) for $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ under the loading condition shown in Figure 19 can be obtained by simply setting a = 0 and b = l in Equations (28) and (29).

$$M_{AB}^{\mathrm{F}}=-({\displaystyle \frac{q_1}{8}}+{\displaystyle \frac{5q_2}{24}})l^2$$

(30)

$$M_{BA}^{\mathrm{F}}=-({\displaystyle \frac{q_1}{24}}+{\displaystyle \frac{q_2}{8}})l^2$$

(31)

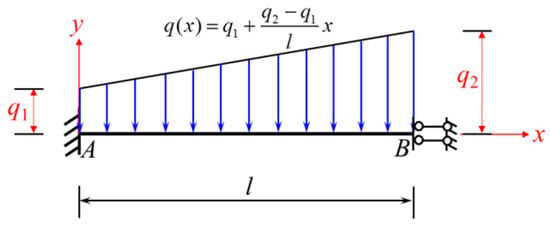
Figure 19. A beam fixed at one end and sliding at the other and subjected to a full-span trapezoidal load rising from left to right (loading condition 2).

4.2.2. Trapezoidal Loads Descending from Left to Right

The formulas for the loads shown in Figure 18 and Figure 20 indicate that to obtain the fixed-end moment formulas for the beam shown in Figure 20, it is only necessary to replace q₁ in the first terms of Equations (28) and (29) by q₂, and add a negative sign to the second terms to obtain the corresponding Equations (32) and (33).

$$\begin{array}{l}{M}_{AB}^{\mathrm{F}}={\displaystyle \frac{q_2}{2l}}\left\{{\displaystyle \frac{1}{3}}\left[{(a+b)}^3-a^3\right]-l\left[{(a+b)}^2-a^2\right]\right\}\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{q_2-q_1}{2bl}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{a+2l}{3}}\left[{(a+b)}^3-a^3\right]+al\left[{(a+b)}^2-a^2\right]\right\}\end{array}$$

(32)

$$M_{BA}^{\mathrm{F}}=-{\displaystyle \frac{q_2}{6l}}\left[{(a+b)}^3-a^3\right]+{\displaystyle \frac{q_2-q_1}{2bl}}\left\{{\displaystyle \frac{1}{4}}\left[{(a+b)}^4-a^4\right]-{\displaystyle \frac{a}{3}}\left[{(a+b)}^3-a^3\right]\right\}$$

(33)

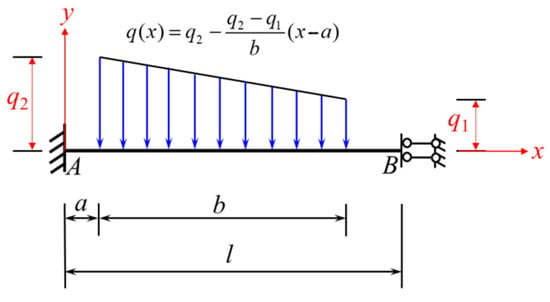
Figure 20. A beam fixed at one end and sliding at the other and subjected to a local trapezoidal load descending from left to right (loading condition 2).

If the trapezoidal load is distributed across the full span (Figure 21), then Equations (34) and (35) for $M_{AB}^{\mathrm{F}}$ and $M_{BA}^{\mathrm{F}}$ under the loading condition shown in Figure 21 can be obtained by simply setting a = 0 and b = l in Equations (32) and (33).

$$M_{AB}^{\mathrm{F}}=-({\displaystyle \frac{5q_1}{24}}+{\displaystyle \frac{q_2}{8}})l^2$$

(34)

$$M_{BA}^{\mathrm{F}}=-({\displaystyle \frac{q_1}{8}}+{\displaystyle \frac{q_2}{24}})l^2$$

(35)

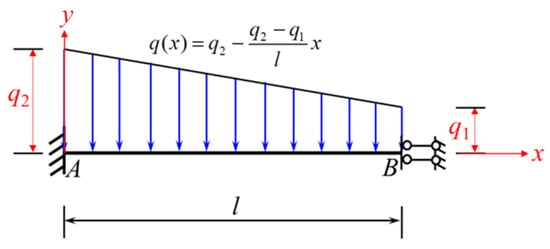
Figure 21. A beam fixed at one end and sliding at the other and subjected to a full-span trapezoidal load descending from left to right (loading condition 2).

5. Derivation of Bar End Moment Formulas Induced by Bar End Displacements

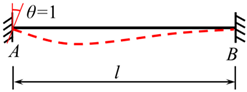
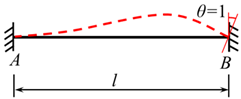
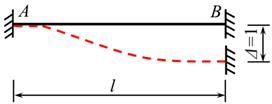
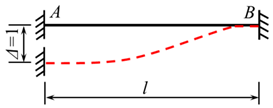
The displacement method analyzes statically indeterminate structures by discretizing the system into individual bars. The total bar end moment of each bar comprises two components: the fixed-end moments induced by external loads, and the end moments caused by bar end displacements. Section 2, Section 3 and Section 4 previously derived fixed-end moment formulas for various local trapezoidal load configurations. For completeness, Table 1 below systematically summarizes the end moment formulas induced by bar end displacements [8].

Table 1. Bar end moments induced by bar end displacements.

Types of Beams	Number	Calculation Diagram	MAB	MBA
A beam fixed at both ends	1		$4i$	$2i$
	2		$2i$	$4i$
	3		$-6{\displaystyle \frac{i}{l}}$	$-6{\displaystyle \frac{i}{l}}$
	4		$6{\displaystyle \frac{i}{l}}$	$6{\displaystyle \frac{i}{l}}$
An-end-fixed another-end-simple-support beam	5		$3i$	0
	6		$-3{\displaystyle \frac{i}{l}}$	0
	7		$3{\displaystyle \frac{i}{l}}$	0
A beam fixed at one end and sliding at the other	8		$i$	$-i$

In Table 1, for the term *$i={\displaystyle \frac{EI}{l}}$* EI represents the bending stiffness of the bar AB and *l* denotes the length of the bar AB.

6. Validation with Examples

Figure 22a displays a small bridge in a park, which is analytically represented as a continuous beam in the computational model shown in Figure 22b. Figure 23a illustrates the supporting structure of an aqueduct. Given the structural uniformity along its longitudinal direction, the analysis can be simplified by considering a single frame (highlighted in red in Figure 23a), with its corresponding computational model depicted as a statically indeterminate rigid frame in Figure 23b. Similarly, Figure 24a presents a crane girder support system, where an individual frame (marked in red in Figure 24a) is modeled as the statically indeterminate rigid frame shown in Figure 24b. These examples demonstrate that statically indeterminate structures are prevalent in both civil engineering projects and everyday structures.

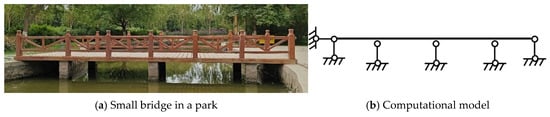
Figure 22. A small bridge in a park and its computational model.

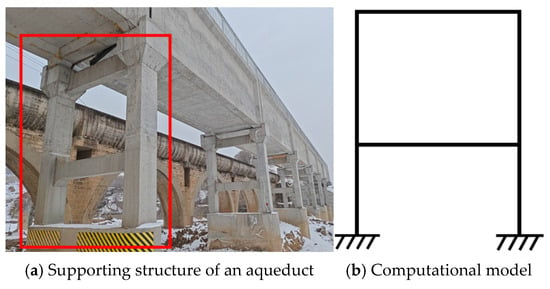
Figure 23. A supporting structure of an aqueduct and its computational model.

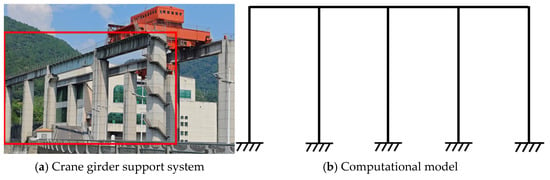
Figure 24. A crane girder support system and its computational model.

To verify the fixed-end moment formulas derived in this paper for the three types of statically indeterminate beams under two different trapezoidal load conditions, the following internal force verification is illustrated using the examples of a statically indeterminate beam, a rigid frame without sidesway, and a rigid frame with sidesway.

6.1. Example of a Statically Indeterminate Beam

The statically indeterminate beam subjected to a trapezoidal load is shown in Figure 25. The bending stiffness of each bar is EI. Its bending moment diagram was made.

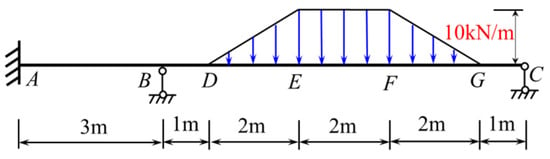
Figure 25. A statically indeterminate beam subjected to a trapezoidal load.

The detailed solving procedure is as follows:

(1)

Determine the basic unknowns: the angular displacement θ_B of the B node.

(2)

Calculate the fixed-end moment of each bar caused by the load.

No external load is applied to the AB bar, so the fixed-end moment is 0. The BC bar falls into the case where the beam is fixed at the B end, simply supported at the C end, and subjected to a local trapezoidal load. The fixed-end moment at the C end is 0. To solve for the fixed-end moment at the B end, $q_0=10 \mathrm{kN}/\mathrm{m}$, $l=8 \mathrm{m}$, $a=1 \mathrm{m}$, $b=2 \mathrm{m}$, $c=2 \mathrm{m}$, and $d=2 \mathrm{m}$ can be substituted into Equation (16) to obtain $M_{BC}^F=-53.75 \mathrm{kN}\cdot \mathrm{m}$.

(3)

Calculate the bending moment at the end of each bar caused by the load and the displacement at the end of the bar.

The linear stiffness of the AB bar is $i_{AB}={\displaystyle \frac{EI}{3}}$, and the linear stiffness of the AB bar is $i_{BC}={\displaystyle \frac{EI}{8}}$. Then, the bending moment at the end of each bar is calculated as follows:

AB bar: $M_{AB}=2i_{AB}{\theta }_B={\displaystyle \frac{2}{3}}EI{\theta }_B$; $M_{BA}=4i_{AB}{\theta }_B={\displaystyle \frac{4}{3}}EI{\theta }_B$.

BC bar: $M_{BC}=-53.75+3i_{BC}{\theta }_B=-53.75+{\displaystyle \frac{3}{8}}EI{\theta }_B$.

(4)

Establish the equation for the displacement method.

Considering the equilibrium of the B node (Figure 26), i.e., $\Sigma M_B=0$, we obtain $M_{BA}+M_{BC}=0$, which leads to ${\theta }_B={\displaystyle \frac{1290}{41EI}}$.

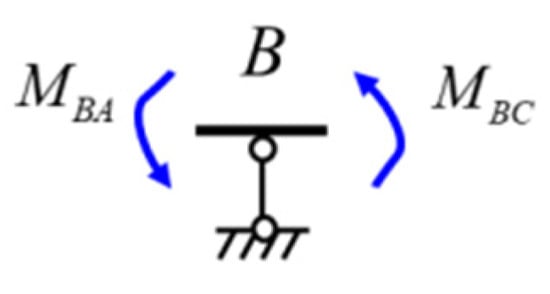
Figure 26. Free-body diagram of the B node.

(5)

Solve for the bending moment at the end of each bar and plot the bending moment diagram.

Substituting ${\theta }_B={\displaystyle \frac{1290}{41EI}}$ into the formulas for the bending moments at the end of each bar in step (3) yields the following: $M_{AB}=20.98 \mathrm{kN}\cdot \mathrm{m}$; $M_{BA}=41.95 \mathrm{kN}\cdot \mathrm{m}$; and $M_{BC}=-41.95 \mathrm{kN}\cdot \mathrm{m}$. The superposition principle was applied to create a bending moment diagram, shown in Figure 27 (in which the unit of the bending moment is kN·m).

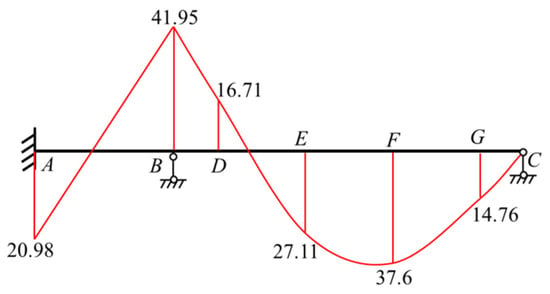
Figure 27. The bending moment diagram of the beam shown in Figure 25.

A structural mechanics solver is a computer-aided analysis and calculation program for teachers, students, and engineers based on the matrix displacement method [22,23]. The bending moment diagram shown in Figure 27 agrees with the bending moment diagram obtained using the structural mechanics solver.

6.2. Example of a Statically Indeterminate Rigid Frame Without Sidesway

The statically indeterminate rigid frame without sidesway subjected to a trapezoidal load is shown in Figure 28, and the linear stiffness of each bar is i. The effect of axial deformation is not considered, and the bending moment diagram of the beam was made.

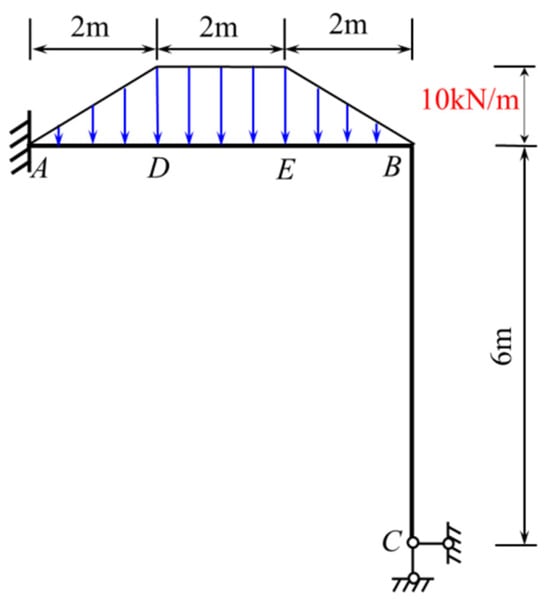
Figure 28. A statically indeterminate rigid frame without sidesway subjected to a trapezoidal load.

The detailed solving procedure is as follows:

(1)

Determine the basic unknowns: the angular displacement θ_B of the B node.

(2)

Calculate the fixed-end moment of each bar caused by the load.

For the AB bar, the beam is fixed at both ends and subjected to a full-span trapezoidal load. To solve for the fixed-end moment, $q_0=10 \mathrm{kN}/\mathrm{m}$, $a=2 \mathrm{m}$, $b=2 \mathrm{m}$, and $c=2 \mathrm{m}$ can be substituted into Equations (5) and (6) to obtain $M_{AB}^F=-24.44 \mathrm{kN}\cdot \mathrm{m}$; $M_{BA}^F=24.44 \mathrm{kN}\cdot \mathrm{m}$. No load is applied to the BC bar, so its fixed-end moment is zero.

(3)

Calculate the bending moment at the end of each bar caused by the load and the displacement at the end of the bar.

AB bar: $M_{AB}=2i{\theta }_B-24.44$; $M_{BA}=4i{\theta }_B+24.44$.

BC bar: $M_{BC}=3i{\theta }_B$.

(4)

Establish the equation for the displacement method.

Considering the equilibrium of the B node (Figure 29), i.e., $\Sigma M_B=0$, we obtain $M_{BA}+M_{BC}=0$, which leads to ${\theta }_B={\displaystyle \frac{24.44}{7i}}$.

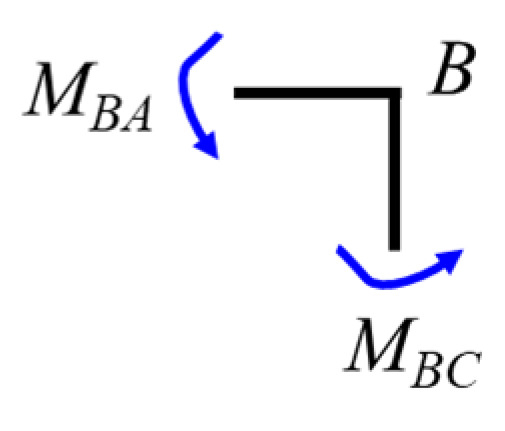
Figure 29. Free-body diagram of the B node.

(5)

Solve for the bending moment at the end of each bar and plot the bending moment diagram.

Substituting ${\theta }_B=-{\displaystyle \frac{24.44}{7i}}$ into the formulas for the bending moments at the end of each bar in step (3) yields the following: $M_{AB}=-31.42 \mathrm{kN}\cdot \mathrm{m}$; $M_{BA}=10.47 \mathrm{kN}\cdot \mathrm{m}$; and $M_{BC}=-10.47 \mathrm{kN}\cdot \mathrm{m}$. The superposition principle was applied to create a bending moment diagram, shown in Figure 30 (in which the unit of the bending moment is kN·m).

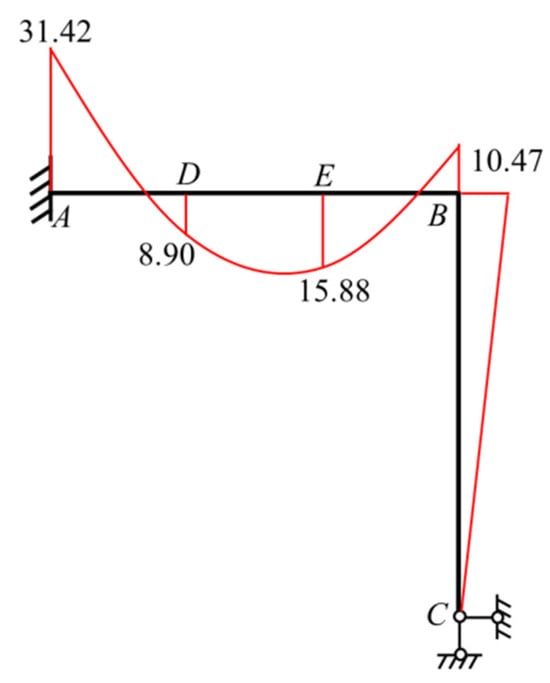
Figure 30. The bending moment diagram of the frame shown in Figure 25.

The bending moment diagram shown in Figure 30 agrees with the bending moment diagram obtained using the structural mechanics solver.

6.3. Example of a Statically Indeterminate Rigid Frame with Sidesway

The statically indeterminate rigid frame with sidesway subjected to a trapezoidal load is shown in Figure 31, and the bending stiffness of each bar is EI. The effect of axial deformation is not considered, and the bending moment diagram of the beam was made.

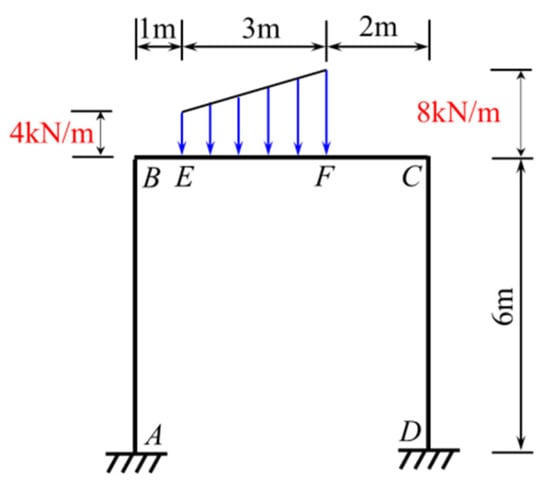
Figure 31. A statically indeterminate rigid frame with sidesway subjected to a trapezoidal load.

The detailed solving procedure is as follows:

(1)

Determine the basic unknowns: the angular displacement θ_B of the B node; the angular displacement θ_C of the C node; the angular displacement θ_B of the B node; and the same horizontal displacement Δ at the B end of the AB bar as that at the C end of the CD bar.

(2)

Calculate the fixed-end moment of each bar caused by the load.

No external load is applied to the AB or CD bars, so their fixed-end moment is 0. For the BC bar, the beam is fixed at both ends and subjected to a trapezoidal load that rises from left to right. To solve for the fixed-end moment, $q_1=4 \mathrm{kN}/\mathrm{m}$, $q_2=8 \mathrm{kN}/\mathrm{m}$, $l=6 \mathrm{m}$, $a=1 \mathrm{m}$, and $b=3 \mathrm{m}$ can be substituted into Equations (7) and (8) to obtain the following: $M_{BC}^F=-13.3 \mathrm{kN}\cdot \mathrm{m}$, $M_{CB}^F=11.2 \mathrm{kN}\cdot \mathrm{m}$.

(3)

Calculate the bending moment at the end of each bar caused by the load and the displacement at the end of the bar.

To facilitate the calculation, we set EI = 6; then, the linear stiffness of each bar is i_AB = i_BC = i_CD = 1, so the bending moment at the end of each bar is calculated as follows:

AB bar: $M_{AB}=2i_{AB}{\theta }_B-{\displaystyle \frac{6i_{AB}}{l_{AB}}}\Delta =2{\theta }_B-\Delta$; $M_{BA}=4i_{AB}{\theta }_B-{\displaystyle \frac{6i_{AB}}{l_{AB}}}\Delta =4{\theta }_B-\Delta$.

BC bar: $M_{BC}=4i_{BC}{\theta }_B+2i_{BC}{\theta }_C+M_{BC}^F=4{\theta }_B+2{\theta }_C-13.3$; $M_{CB}=2i_{BC}{\theta }_B+4i_{BC}{\theta }_C+M_{CB}^F=2{\theta }_B+4{\theta }_C+11.2$.

CD bar: $M_{CD}=4i_{CD}{\theta }_C-{\displaystyle \frac{6i_{CD}}{l_{CD}}}\Delta =4{\theta }_C-\Delta$; $M_{DC}=2i_{CD}{\theta }_C-{\displaystyle \frac{6i_{CD}}{l_{CD}}}\Delta =2{\theta }_C-\Delta$.

(4)

Establish the equations for the displacement method and solve for the basic unknowns.

Considering the equilibrium of the B node (Figure 32), i.e., $\Sigma M_B=0$, we obtain $M_{BA}+M_{BC}=0$, which leads to the following equilibrium equation:

$$8{\theta }_B+2{\theta }_C-\Delta -13.3=0$$

(36)

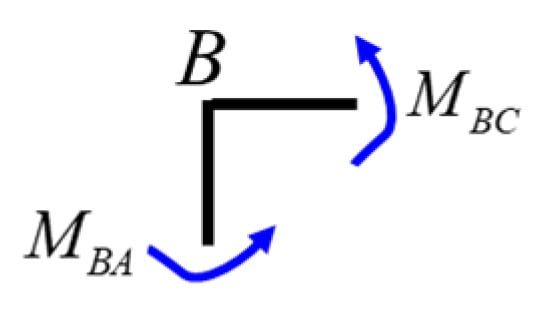
Figure 32. Free-body diagram of the B node.

Considering the equilibrium of the C node (Figure 33), i.e., $\Sigma M_C=0$, we obtain $M_{CB}+M_{CD}=0$, which leads to the following equilibrium equation:

$$2{\theta }_B+8{\theta }_C-\Delta +11.2=0$$

(37)

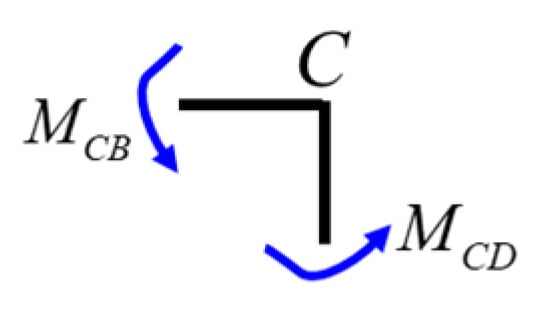
Figure 33. Free-body diagram of the C node.

Cutting off the top of the column by the section and considering the equilibrium of the BC portion of the beam above the top of the column (Figure 34), i.e., $\Sigma F_x=0$, we obtain $F_{\mathrm{Q}BA}+F_{\mathrm{Q}CD}=0$.

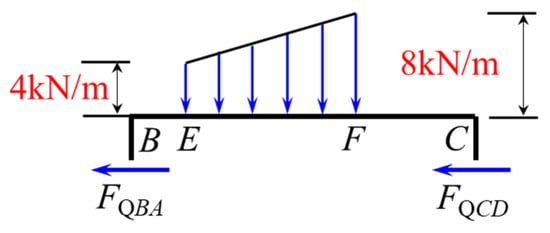
Figure 34. Free-body diagram of the BC crossbeam.

Then, considering the equilibrium of the column AB and column CD (Figure 35), we calculate F_QBA and F_QCD. That is, $F_{\mathrm{Q}BA}=-{\displaystyle \frac{M_{AB}+M_{BA}}{l_{AB}}}$ can be determined from $\Sigma M_A=0$, $F_{\mathrm{Q}CD}=-{\displaystyle \frac{M_{CD}+M_{DC}}{l_{CD}}}$ can be determined from ${\displaystyle \sum M_D=0}$, and thus the equilibrium equation for the crossbeam BC becomes as follows:

$$3{\theta }_B+3{\theta }_C-2\Delta =0$$

(38)

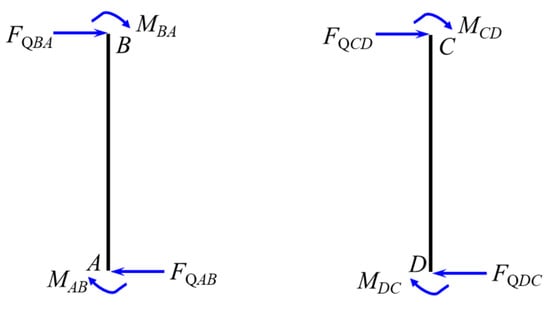
Figure 35. Free-body diagram of the columns AB and CD.

Combining Equations (36)–(38) yields the following results: ${\theta }_B=2.19$, ${\theta }_C=-1.89$, and $\Delta =0.45$.

(5)

Solve for the bending moment at the end of each bar and plot the bending moment diagram.

Substituting ${\theta }_B=2.19$, ${\theta }_C=-1.89$, and $\Delta =0.45$ into the formulas in step (3) for the bending moments at the end of each bar yields the following: $M_{AB}=3.93 \mathrm{kN}\cdot \mathrm{m}$, $M_{BA}=8.32 \mathrm{kN}\cdot \mathrm{m}$, $M_{BC}=-8.32 \mathrm{kN}\cdot \mathrm{m}$, $M_{CB}=8.02 \mathrm{kN}\cdot \mathrm{m}$, $M_{CD}=-8.02 \mathrm{kN}\cdot \mathrm{m}$, and $M_{DC}=-4.23 \mathrm{kN}\cdot \mathrm{m}$. Using the cross-section method and the principle of superposition, a bending moment diagram was created, as shown in Figure 36 (in which the unit of the bending moment is kN·m).

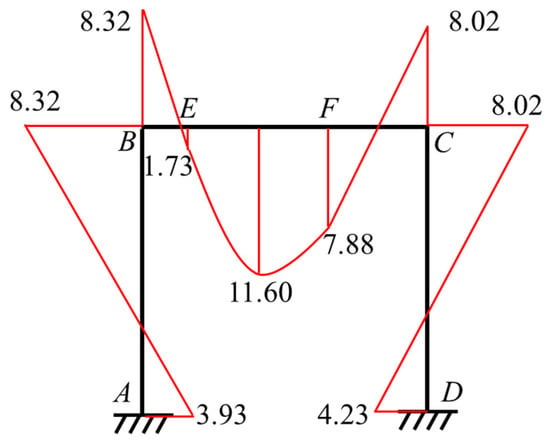
Figure 36. The bending moment diagram of the frame shown in Figure 28.

The bending moment diagram shown in Figure 36 agrees with the bending moment diagram obtained using the structural mechanics solver.

7. Discussion

In current structural mechanics textbooks, ready-made calculation formulas for fixed-end moments under various load types are typically provided in tabulated forms. However, these formulas are generally only applicable when trapezoidal loads are fully distributed across the entire beam element. For calculating fixed-end moments of three types of single-span statically indeterminate beams under partial loading, separate derivations are usually required. Some structural calculation manuals present solutions using the virtual beam method, yet the computational effort remains substantial. Theoretically, the force method could also be employed, but for local trapezoidal load—which represents complex loading conditions—the force method involves prohibitively large computation. This paper derives fixed-end moment formulas for three types of single-span statically indeterminate beams under partial trapezoidal loading using the integration method. Compared with traditional approaches like the force method and virtual beam method, the proposed technique demonstrates superior clarity in physical concepts and computational efficiency.

Furthermore, while existing structural mechanics solvers and certain finite element software can only provide numerical solutions for internal forces under specific loads, the present method yields analytical formulas for internal forces in statically indeterminate structures subjected to local trapezoidal load. Future work could employ substructure concepts to derive fixed-end moment formulas for common substructures under local trapezoidal load, thereby facilitating internal force solutions for specific types of statically indeterminate structures.

8. Conclusions

(1) The integral method can be used with the fixed-end moment formula under the action of a single concentrated force, transforming the derivation of the fixed-end moment formula under the action of a trapezoidal load into the problem of solving a definite integral in which the integrand is a polynomial function. Compared with the force, virtual beam, and energy methods, this derivation is faster and easier. Moreover, the more complicated the distribution form of the load (e.g., quadratic and multi-order parabolic distribution loads), the more obvious the advantage of the integral method.

(2) In this paper, the fixed-end moment formulas of three types of basic statically indeterminate beams under the action of two different trapezoidal load conditions were derived; in this way, we addressed the problem of solving the internal forces of statically indeterminate structures subjected to trapezoidal loads by using the displacement method. Three examples were provided to illustrate the solutions.

(3) The findings of this paper can greatly assist with the task of solving the internal forces of statically indeterminate structures under trapezoidal loads, which is highly significant for engineering practice and teaching.