Abstract
Milled peat must be dried for the production of peat fuel briquettes. The current trend in the creation of drying technologies is the intensification of the dehydration process while obtaining a high-quality final product. An increase in the temperature of the drying agent, above 300 °C, significantly accelerates the reaching of the final moisture content of the peat. In the final stage, it is also accompanied by partial thermal decomposition of the solid phase. Its first stage, which is the decomposition of hemicellulose, contributes to a decrease in weight and an increase in the caloric content of the dry residue. The development of high-temperature drying modes consists of determining the temperature and velocity of the drying agent, wherein the duration of the material reaching the equilibrium moisture content will be minimal and the temperature of the material will not rise above the second-stage decomposition temperature of cellulose. This problem can be solved by the mathematical modeling of the dynamics of peat particles drying in the flow. The article presents a mathematical model of heat and mass transfer, phase transitions, and shrinkage during the dehydration of milled peat particles. The equations of the mathematical model were built based on the differential equation of mass transfer in open deformable systems, which, in the absence of deformations, turns into the known equation of state. A numerical method for implementing a mathematical model has been developed. The adequacy of the mathematical model is confirmed by comparing the results of numerical modeling with known experimental data.
1. Introduction
Most modern solid fuel boilers are able to combust peat briquettes. The use of peat for obtaining solid fuel has great potential in the renewable energy of the countries of Central and Northern Europe. Despite the high initial moisture content and lower calorific value than coal, peat has several advantages. The cost of energy obtained from combustion and gasification plants with high efficiency is lower than the cost of energy obtained from gas and oil. Moreover, the content of sulfur and harmful non-combustible impurities is insignificant compared to coal, fuel oil, and shale. An important part of the technological process of manufacturing fuel briquettes from peat, which determines their quality and cost, is drying. The initial moisture content of peat, which is determined by the ratio of the mass of water held in the pores to the mass of the wet sample, can reach 90%. For the production of high-quality briquettes, their moisture content should be 8–10%. Several methods of drying milled peat are known. The least expensive way is in the open ground under the influence of solar radiation. Such drying is seasonal, as evidenced by the experimental data presented in [1]. Its intensity significantly depends on weather conditions and the thickness of the peat layer, the duration is significant even for a 4 mm layer, and it is not possible to dry the peat to a low equilibrium moisture content. In [2], the advantages of filtration drying are demonstrated. The main advantage is the possibility of mechanical displacement of moisture (due to pressure gradient) from peat immediately after mining and its environmental friendliness. Dehydration is carried out in a dense layer through which the gas flow moves with temperature Td.a. = 60–100 °C towards the perforated partition, the space below which is connected to the air suction fan. The power of the fan limits the thickness of the layer of wet material and, accordingly, the productivity of the dryer.
In practice, peat drying is carried out in two stages: after extraction under natural conditions to a moisture content of 45–50%, followed by drying to the final moisture content in aerodynamic or drum-type dryers using a mixture of flue gases and air. The choice of drying temperature depends on the size of the peat particles, their initial moisture content and thermophysical properties, as well as the technical capabilities of the dryer. At the same time, a moderately intensive course of the process (flow temperature Td.a. = 120–170 °C), and a highly intensive course (Td.a. = 300–500 °C) can be ensured. In the latter case, flue gases are involved as a drying agent. The high-temperature drying of milled peat particles can be accompanied by the thermal decomposition of the solid phase. The temperature interval at the beginning of the thermal destruction of peat is 160–210 °C [3]. At the same time, the decomposition of hemicellulose begins with the release of oxygen-containing gases and pyrogenetic moisture, which helps to reduce the weight and increase the caloric content of the dry residue [4,5,6,7]. The next two stages are characterized by the decomposition of cellulose and lignin and begin [3] in the temperature ranges of 260–340 °C and 315–400 °C, respectively. In the presence of air, the processes of the second and third stages of decomposition are exothermic, accompanied by a rapid increase in temperature and a significant loss of the combustible component of peat; these are undesirable in obtaining quality peat briquettes.
The selection of operating parameters of the drying agent, at which the temperature at any point of the particle will stay below the temperature of the beginning of cellulose decomposition, will ensure effective high-temperature drying. The possibilities of experimental methods for researching transfer processes during the drying of porous materials are limited by determining the average values of their moisture content and temperature. The development of an adequate mathematical model of the dynamics of the milled peat particle drying must account for all the determining factors and the method of its implementation. In this case, it allows studying the range of temperature and concentrations of the components of the bound substance to determine optimal process conditions.
In the mathematical description of interrelated processes of heat and mass transfer and phase transitions in theories of drying, a unified phenomenological approach has not yet been formed [8,9,10,11,12,13,14,15,16,17,18,19]. Differences in mathematical models are related to the number of involved equations and approaches used to determine the IV intensity function of phase transitions between the liquid and vapor phases in the internal points of the porous body. In general, the number of transfer equations in a mathematical model is determined by the number of system state parameters to be determined, as well as interphase interaction parameters, in particular the IV.
In [9], a mathematical model of the low-temperature drying of a peat layer in the soil is presented, assuming that the temperatures in the thin layer of the peat and the surrounding air are the same. The peat layer is considered as a multi-component system containing a solid base, a liquid, and a gas phase. Vapor and air phases are not considered separately. The system of equations contains the mass transfer equation of the gas phase, which considers the filtration transfer and the intensity of the formation of the vapor phase. The filtration rate is determined by Darcy’s law, whereas, for the correct determination of the pressure change in the gas phase, it is necessary to have information on the change in the volume fraction of vapor in the vapor-air mixture. The energy transfer equation takes into account the influence of thermal conductivity, filtration movement in the pores of the gas phase, and the thermal effect of liquid evaporation on the porous peat layer’s temperature state. However, in the micropores, there is diffusion transfer of both gas and liquid phases. The liquid phase transfer equation is written under the assumption that the change in liquid concentration occurs only due to evaporation, whereas the expression for the evaporation rate contains the volume concentration of the liquid phase. The article does not contain information about the mathematical model’s method of numerical implementation. In addition, filtration transfer, as a rule, is not manifested in drying processes of moderate intensity [10]. In [11], a mathematical model of low-temperature drying of capillary-porous material in sludge is presented. The model is written for the case of diffusion-filtration heat and mass transfer and includes equations of energy transfer and mass transfer of the liquid phase. To determine the effective values of the thermophysical properties of wet sludge, the diffusion coefficient, and the intensity of phase transitions, semi-empirical equations are used. Obtaining these requires a significant amount of experimental information. The effective diffusion coefficient is represented by a polynomial function of the sixth order relative to the mass content of the liquid phase. It is known that the intensity of diffusion processes significantly depends on the temperature [12], which is indirectly taken into account in the presented dependence.
In the mathematical model of drying in a fluidized bed of processed pumpkin pulp [13], the one-hour efficiency of the apparatus for dry product Π per volume unit V of the drying chamber is considered as the desired value. The calculated dependence Π(W,T,V) and the empirical equation for the drying rate dW/dt are presented based on experimental data on the drying kinetics. Using the proposed approach to obtain results for other dispersed materials requires new experiments.
In [14], a mathematical model of heat and mass transfer during drying in a fluidized bed of spherical particles of baker’s yeast was built, which includes equations of energy transfer and filtration transfer of vapor and liquid phases. The intensity of phase transitions IV is determined by differentiating the sorption equation. With this approach, the IV for the case of stationary heat and mass transfer is zero, while during stationary processes, the value of IV can be of the same order as for non-stationary processes.
In [15], a mathematical model of the dynamics of filtration drying of vegetable raw materials in the period of decreasing velocity was built. This model includes the kinetic equation of mass transfer. It characterizes the velocity of movement of the moisture front inside the particle, the equation for the boundary condition of the third kind at the boundary between the solid body and the heating agent, and the equation for the change in the moisture content of the heating agent along the height of the material layer. For its conclusion, empirical equations were obtained by summarizing experimental data. This allows us to evaluate the interconnection between the moisture content of the material and the gas flow.
The mathematical model of drying dynamics of A.V. Luikov [10,16] for the case of a high-intensity process contains three differential equations—energy, moisture mass transfer, and filtration. The IV function is determined through the phase transition criterion. It represents the ratio of the change in moisture content of the material due to evaporation to the total change in moisture content due to mass transfer and phase transitions. However, these processes can take place independently of each other. That is why such a technique is represented by the introduction of an additional unknown function, the estimation of which requires conducting physical experiments. It should be noted that the model of A.V. Luikov is quite widely used for the theoretical description of the drying process [17,18,19,20,21,22]. Therefore, the phase transition criterion is defined for a sufficiently wide range of materials. In [17,18,19,20,21], the solution of the differential equations system of heat and mass transfer is carried out by an analytical method under several assumptions. In [22,23], the expediency of using numerical methods for the simultaneous solution of nonlinear differential transfer equations included in the mathematical model of the drying dynamics of porous materials is demonstrated.
In [24], a mathematical model of the kinetics of high-temperature peat drying is presented. It includes the thermal conductivity equation for a porous particle written in a linear form and the Stefan boundary condition for heat transfer problems with moving boundaries due to phase transitions. At the same time, it is assumed that the change in moisture content W occurs only due to evaporation. The phase transition boundary divides the volume of the particle into a dry region (without the liquid phase) and a wet region (where the moisture content does not change and remains equal to the initial one). Such assumptions are quite controversial from a physical point of view. However, they allow us to use the quasi-stationary method of Leibenzon [25] to solve the problem and obtain curves of changes in the average moisture content.
The paper [23] describes the molecular radiation theory of heat and mass transfer. It is mainly based on the law of particle spectral-radiation intensity by N.I. Nikitenko, which made it possible to mathematically describe the activation processes of evaporation [26] and diffusion transfer [12]. This made it possible to build closed mathematical models of the drying dynamics of consolidated and dispersed capillary-porous materials and colloidal capillary-porous materials and solved several practical problems [8,27,28].
This work presents a mathematical model of high-temperature drying of milled peat. In the final stage, it is accompanied by the initial stage of thermal destruction. The mathematical model includes differential equations of energy and mass transfer of liquid, vapor, and air phases. They are built based on the differential equation of substance transfer (mass, energy, and momentum) for the deformable bodies [23,28]. The mathematical model includes also the following additional equations:
- Darcy’s law for calculating the filtration velocities of the phases;
- the equation of state for calculating the pressures of the gas phase components;
- the expression for the capillary pressure of the liquid;
- the formula for the contact surface area of the liquid and gas phases in the pores of the body;
- the thermal-concentration deformation equation;
- the formulas for the intensity of the phase transitions on the outer and inner surfaces of peat particles and the diffusion coefficients of the liquid and gas phases.
During the drying process, under the action of heating when a certain temperature is reached, the process of thermal decomposition of peat begins. In [5,7], the activation nature of the thermal decomposition of the milled peat solid phase is experimentally proved. Processing of the derivatographic studies results [6] of the thermal properties of the milled peat solid residue, using the kinetic model of A.A. Broido [29], made it possible to determine the numerical values of the effective activation energy, Aef, of the bound substance particles. The Aef value [6] for crushed milled peat was included in the mathematical model. A numerical method for calculating a mathematical model has been developed. It allows for the determination of the dynamics of changes in temperature and volume concentrations of the bound substance components in a porous particle, depending on its thermophysical, structural, and geometric characteristics, as well as the parameters of the drying agent. The development of drying modes of porous materials is based on specific calculations. They ensure a reduction in the time of the process and, accordingly, energy resources for its implementation while maintaining the high quality of the final product.
2. Materials and Methods
2.1. Mathematical Model
In a wet state, milled peat is a heterogeneous system that includes a base, in the pores of which liquid, vapor, and air phases are kept. When the system is heated, each component of the substance bound to the base begins to change its concentration as a result of diffusion and filtration mass transfer. This also happens as a result of the phase transition of a liquid to vapor. Peat belongs to the class of colloidal capillary-porous materials [10], the volume of which can decrease several times upon drying. Material shrinkage, in turn, significantly affects the dynamics of transfer processes [8,10,20,23,27,28,30,31]. Particles of milled peat when crushed have a shape close to spherical [24]. In a drum-type or aerodynamic dryer, the uniform runaround of particles with a flow is achieved. The parameters of the flow along the length of the drying chamber will be kept unchanged. In this case, the mathematical model of diffusion–filtration heat and mass transfer, phase transitions, and deformation during high-temperature drying of milled peat particles is represented by a system of differential Equations (1)–(4):
Here, T—temperature; Ufl, Uv and Uai—volume concentrations of liquid, steam, and air; t—time; cef—effective specific volumetric heat capacity of a peat particle, , cb, cfl, cv and cai—specific mass heat capacities of the solid phase, water, steam and air, ρb and Ψb—density and volume fraction of the solid phase; λef—effective thermal conductivity: ; Dfl, Dv and Dai—diffusion coefficients of liquid, vapor and air phases; IV—the intensity of phase transitions in the body pores; L—latent heat of phase transitions; —relative volumetric strain; —effective rate of filtration of the bound substance along the coordinate r, , where wflr, wgr i—filtration rates of liquid and gas phases.
The diffusion coefficient of the liquid phase is determined by the formula of N.I. Nikitenko [12]: , where Ru—universal gas constant, AD—activation energy of diffusion transfer, γDfl—diffusion coefficient. This formula is present in boundary cases, when it becomes the empirical Arrhenius formula for solid bodies, and, when it becomes the Einstein formula for liquid medium. Diffusion coefficients for gas phase components are found according to the well-known formula [32]: , where Pg—gas phase pressure, γDfl—diffusion coefficient.
The filtration rates of the liquid wfl and gas wg phases are proportional to the pressure gradients of the corresponding phase and can be calculated with Darcy’s Equation (5):
Here, K0—total permeability of the medium; Kψ—relative permeability of the phase ψ; ηψ—dynamic viscosity coefficient of the phase ψ.
The pressures of the liquid Pfl and gas Pg phases are calculated through functions Ufl, Uv, Uai, and T. For this, the volume fractions of the body Ψb, liquid Ψfl, and gas Ψg in the material are determined according to the following relations: Ψb = 1 − Π, Ψfl = Ufl/ρfl and Ψg = 1 − Ψb − Ψfl, where Π—peat porosity and ρfl—liquid phase density. The partial densities of steam and air are equal, ρv = Uv/Ψg and ρai = Uai/Ψg, respectively. Partial pressures are found using the equation of state for diluted gases Pv = ρvRuT/μv and Pai = ρaiRuT/μai. The pressure of the gas mixture will be Pg = Pv + Pai. Liquid phase pressure will be Pfl = Pg + Pcap, where the capillary pressure Pcap is calculated [8,23] as the average capillary pressure of the liquid. The volume of liquid dV(r), contained in capillaries with a radius from r to r + dr in a unit volume of the body is proportional to the differential function f(r) of the capillary size distribution and the volume fraction θ(r) of the capillary, which is occupied by liquid: dV(r) = θ(r)f(r)dr. Then, the average value of the capillary pressure at a given point of the body is represented by an expression similar to the Laplace Equation (6):
where rmin, rmax—minimum and maximum pores radius and r*—characteristic parameter of pore size dispersion.
The function θ(r,t) in a capillary of radius r at time t is determined by the expression obtained as the ratio of the cross-sectional area of the capillary occupied by liquid to its total cross-sectional area . Where δ is the thickness of the liquid layer on the walls of partially-filled capillaries. It was obtained by the formula for the equilibrium thickness of the condensate layer on a solid surface obtained in [26], Equation (7):
Here, φ—degree of saturation of the steam and gas mixture at a given temperature, φ = PΠ/PH(T); δ*—the average displacement length of an activated particle in the liquid layer, . Where A is activation energy at which a liquid particle can move, const—coefficient of resistance to the particle movement to the free surface of the body, n—density of evaporating molecules, , μ—molar mass, NA—the Avogadro number; when and when . The value δ* can be considered as the thickness of the boundary layer. It is adjacent to the free surface of a rather massive, condensed body in which the evaporation process takes place.
The saturation pressure was calculated according to the formula of N.I. Nikitenko [26], Equation (8):
The values of A and NP can be found as a result of the solution of the system of two equations obtained by writing Equation (8) for two points on the saturation line. They correspond to the values of T1, Ps1 and T2, Ps2 in the table of saturated steam and water, respectively. Formula (8) is valid for liquids of various natures and is quite accurate. This is the case when dividing the temperature interval of the existence of water into two areas 0 < T < 100 °C and 100 < T < 374 °C. The maximum errors of calculated and tabular data were: Πmax = 3.4% when A’ = 0.4206 × 108 J/mol and N = 0.4361 × 1010 kg/(m·s2·K0.5) for the first interval, and Πmax = 2.6% when A’ = 0.3689 × 108 and N = 0.8514 × 109 for the second interval. Here is A’ = ANA.
The intensity of liquid evaporation on the outer surface of thorium particles is found as the resulting flow of evaporating and condensing particles [23,26] according to the Formula (9):
Here, γc—coefficient of evaporation from the surface, ; —coefficient of evaporation; φb—moisture content of the body, which can be considered as the relative moisture content of the steam and gas mixture, which, according to the sorption isotherm, corresponds to the volume concentration of the liquid (7): .
The intensity of evaporation in the pores of the body is found by the formula that follows from (9) under the condition of local thermodynamic equilibrium of coexisting phases:
Here, S is the contact area of the liquid and gas phases in the pores of the body unit volume that are not completely filled with liquid. The function S varies from zero, in the case of capillaries completely filled with liquid, to the value of the specific surface of the pores Smax [33] freed from the liquid. This function can be determined based on the equation of the sorption isotherm [23]. According to the equation φ = fφ(Ufl) the relative moisture content of the air φ is found, which corresponds to the volume concentration of the liquid Ufl at the considered point of the porous body. Formula (7) determines the average thickness δ of the condensate layer on the surfaces of partially-filled capillaries. During the time interval dt, as a result of the processes of evaporation and heat and mass transfer, the thickness δ will change by the value dδ. This value is found when differentiating (7): . The volume concentration of the liquid will change in the same period of time to . Here, the expression for the contact area of the phases S is represented by the Equation (11):
The derivative ∂Ufl/∂φb is determined by differentiating the desorption isotherm equation. For wood peat, the results on the equilibrium moisture content [10] are rather well-approximated by the equation .
The relative volume deformation εV is based on the differential equation of the thermal-concentration deformation [23]. In spherical coordinates, for the case of uniform blowing of the body, when there is axial symmetry of the deformation and the radial displacement ur depends only on the radius r, and there are no displacements uφ, uθ in the directions of φ and θ, the thermal-concentration deformation equation is represented in the following form (12):
Here, G, G1—Lamé coefficients, , ; —Poisson’s ratio; —modulus of elasticity; N—thermal-concentration function [34,35], which determines the change in the specific volume of a body during its free expansion caused by the processes of thermal conductivity, diffusion, filtration, phase, and chemical transition, . There and are average coefficients of thermal and concentration expansion in the intervals of temperature [T, T0] and mass concentration of the component ψ [ωψ, ωψ0]. The function εV is related to the normal components εrr, εφφ, εθθ of the deformation tensor εij (i = 1, 2, 3) by the relation , where εrr = dur/dr, εφφ = εθθ = ur/r. If the body is capillary-porous, its shrinkage during drying can be neglected, and εV = 0.
The influence of the thermal decomposition of peat on the dynamics of drying is accounted for, given that the processes of thermal destruction, diffusion, and evaporation are activational [3,4,5,6,7,23]. Pyrogenetic water is removed together with the remains of free water and the one bound to the solid phase of peat. As was studied in [5], the beginning of the thermal decomposition stage in the process of milled peat dehydration is characterized by a noticeable decrease in the effective activation energy of moving microparticles. This means there is a diffusion transfer of molecules of a pyrogenetic water mixture, which begins to be released during the thermal decomposition of hemicellulose, and the remains of natural water contained in the peat pores. This transfer will occur when they reach a lower energy level than the activation energy of microparticles of bound water. It has been considered that A.V. Luikov’s kinetic equation of drying [10,16] and the kinetic equation of thermal conversion by A.A. Broido [29] have the same structure. This means that the differential equations of substance transfer can be used to adequately describe the dynamics of compatible drying processes and the first stage of thermal decomposition. Thus, the data on the temperature Tt of the beginning of the thermal decomposition of peat and the values of the effective energy of activation Aef are obtained. Thus, in the process of calculating the dynamics of high-temperature drying based on the mathematical model (1)–(4), as the temperature Tt is reached in individual points of the peat particles, the values of Aef should be included in the formulas for Dfl, Ps, Iv and I.
2.2. Single-Valued Condition
While modeling drying processes, it can be assumed that the milled peat was in equilibrium with the surrounding environment before the initial moment of time. Its initial temperature T0 and pressure Pg of the steam and gas mixture in the internal points of the body are equal to the environmental temperature Te.m. and pressure Pe.m., respectively.
The conditions of heat and mass transfer at the boundary r = 0 represent the conditions of symmetry of the temperature fields and volume concentrations of the bound substance components, Equation (13):
At the outer boundary r = R, there are conditions of the third kind, Equations (14)–(17):
Expression (16) is obtained from [23] considering the following conditions: when the system enters the equilibrium state t → ∞, parameters ρv = ρv,e.m., .
The formula for heat transfer in a fluidized bed can be used to determine the heat transfer coefficient α [36]: Nu = 0.03Pr0.33Re. The similarity criteria Nu and Re include a diameter of the peat particle that depends on time due to shrinkage.
2.3. Numerical Method of Solution
The system of differential Equations (1)–(4) under boundary conditions (13)–(17), closed by relations (5)–(12), is essentially nonlinear. Its implementation is possible using a numerical method. Equations (1)–(4) contain convective terms, and for their solution, it is advisable to use the explicit three-layer scaling difference circuit of N.I. Nikitenko. [22]. An advantage of this circuit is [27] the simplicity characteristic of all explicit circuits, and, similar to the known implicit circuits, it allows the choosing of arbitrary time steps without deteriorating the accuracy of the solution. In addition, mass transfer Equations (2)–(4) contain terms related to peat shrinkage. To take into account its influence on the required functions, the procedure of splitting the algorithm by physical factors is involved. The difference approximations of the differential Equations (1)–(4) are built on the non-uniform difference grid ri = ih, (i = 0, 1, …, IK; h ≠ const), tn = nl (n = 0, 1, …, l > 0). There, h is the spatial coordinate step, and l is the time step. At the initial time, the following applies: h = d/(2∙IK), where d is the peat particle diameter (Figure 1).
Figure 1.
View of the computational domain.
Per the mentioned approach, the difference approximation of the liquid phase transfer Equation (2) is represented by the Equations (18)–(20):
Equations (3) and (4) are approximated similarly. The differential approximation of the energy Equation (1) based on an explicit scaling difference circuit is represented by two Equations (21) and (22):
The boundary condition (15) for the surface r = R is represented by the finite difference Equation (23):
Similar difference equations approximate the boundary conditions (14), (16), and (17). The approximation error of differential Equations (1)–(4) by difference equations of the form (18)–(20) has the order of O(). The weight parameter Ωψ (ψ = T, fl, v, ai) allows to increase in the time step, Ωψ ≥ 0. The necessary conditions for the stability of the difference equations, obtained based on the method of a conditional set of some required functions of the system [22], have the form of inequality (24):
where wr = wefr, νψ = λef/cef, Ωψ = ΩT when ψ = T; wr = wflr, νψ = Dfl, Ωψ = Ωfl when ψ = fl; wr = wgr, νψ = Dv, Ωψ = Ωv when ψ = v; wr = wgr, νψ = Dai, Ωψ = Ωai when ψ = ai. The calculated time step for the solution of the system (1)–(4) is selected from the condition . In accordance with (24), ΩT, Ωfl, Ωv and Ωai are determined after the optional sampling of the difference grid h steps.
2.4. Approbation
To confirm the adequacy of the mathematical model (1)–(4) and the effectiveness of the numerical method, a comparison was made. It consisted of the results of the calculation of the dynamics and kinetics of lowland peat particles drying in the airflow and the results of an experimental study of the peat particles drying kinetics under the same initial conditions. The particles were placed on a mesh surface made of aluminum and evenly blown with atmospheric air with a temperature of Te.m. = 120 °C, at velocity of we.m. = 1 m/s and moisture content of de.m. = 10 g/kg of dry air. The shape of the particles was close to spherical with a diameter of 7 mm, the initial temperature was T0 = 291 K, the initial moisture content—W0 = 0.97 kg/kg, the porosity—Π = 0.6, the specific surface area Smax = 8 × 105 m2/kg. For the calculation, thermophysical parameters of peat were taken [37]: λb = 0.08 W/(m·K); cb = 1970 J/(kg·K); ρb = 700 kg/m3. The activation energy was A = AD = 0.4350 × 108 J/kmol [5]. The constants used in the calculation are presented in Table 1. The constants for the coefficients of diffusion and evaporation from surface are determined by the experimental verification.

Table 1.
Values of refined constants.
Figure 2 shows the curves of changes over time in the average moisture content of a peat particle, obtained by numerical and physical experiments. It also presents the results of calculating the change in the average temperature of the particle and the temperature on its outer surface. The maximum error of the difference of the values does not exceed 4%. This indicates the possibility of using the developed mathematical model and calculation method to study the dynamics of peat drying in a dispersed state in the aerodynamic layer.
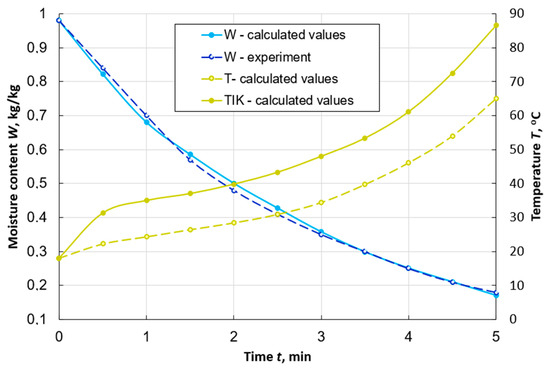
Figure 2.
Graphs of changes in the average values of moisture content W and temperature T, as well as the temperature on the surface TIK of a spherical particle of peat with a diameter of d = 7 mm during its drying with the flow uniform washing with the following parameters: Te.m. = 120 °C, we.m. = 1 m/s, de.m. = 10 g/kg of dry air.
Figure 3 shows the time dependencies of coordinates of spatial nodal points along the peat particle radius. At the beginning of the drying process, the most significant changes in the liquid phase volume concentration, Ufl, take place at the outer boundary. Due to shrinkage, the surface area of the external forces tends to decrease. The inner layers of the particle, in which the volume concentration changes more slowly under the action of compressive forces, somewhat reduce their area. At the same time, they increase in their thickness in such a way that their volume is practically unchanged. As the equilibrium moisture content is approached, a more uniform displacement of the coordinates of the nodal points along the radius of the particle is observed. The shrinkage of the particle was 28%, which corresponds to the data given in [10].
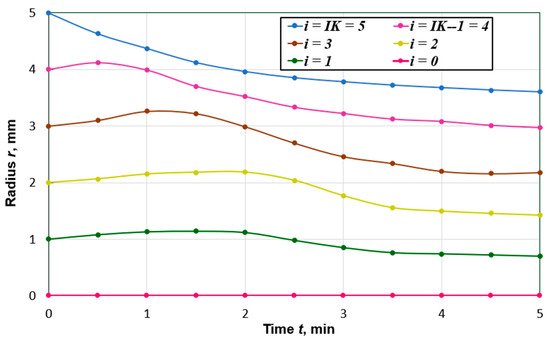
Figure 3.
Curves of changes in time of nodal points coordinates along the radius of the particle, which at the initial moment of time had the value , (i = 0, 1, …, IK; IK = 5).
The temperature of thermal decomposition of peat (lowland peat with average degree of decomposition) was taken [5] as 175 °C. The activation energy of the movement of the bound substance particles, when peat is heated above the temperature of the thermal destruction beginning, is lower than that of the physically and chemically bound water [5] in the temperature range of 28–175 °C and is equal to Aef = 0.370 × 108 J/kmol. Accordingly, the intensity of reaching the final peat moisture content with the simultaneous thermal decomposition process will increase. In order to account for the influence of thermal destruction on the dynamics of peat particle dehydration, the calculation program assumed the condition of a local change in the activation energy. The program itself was developed on the basis of the mathematical model (1)–(4) and the numerical method (18)–(22). The abovementioned means that when a temperature of 175 °C is reached at this nodal point of the particle at the given moment of time, in expressions (8)–(10), and for Dfl, the value of the activation energies A and AD changed to the effective Aef. The results of calculating the change over time in the average values of temperature and moisture content of the particle are presented in Figure 4, Figure 5 and Figure 6. Figure 4, Figure 5 and Figure 6 also show the results of calculating the temperature change of the surface in contact with the high-temperature flow without taking into account thermal decomposition and taking into account its effect on the duration of dehydration. To exclude the self-ignition of particles, there was a flow of flue gases. When conducting numerical experiments, the temperature of the flow Te.m. and particle size were varied. The flue gases flow velocity was we.m. = 4 m/s.
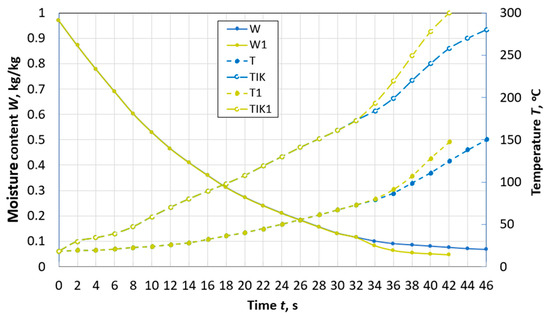
Figure 4.
Changes over time in the average moisture content W and temperature T, temperature TIK on the surface of a spherical particle of peat with a diameter of d = 10 mm during drying with and without taking into account thermal destruction (W1, T1, TIK1) in the flow of flue gases with the parameters: Te.m. = 300 °C, we.m. = 4 m/s, de.m. = 12 g/kg of dry gas.
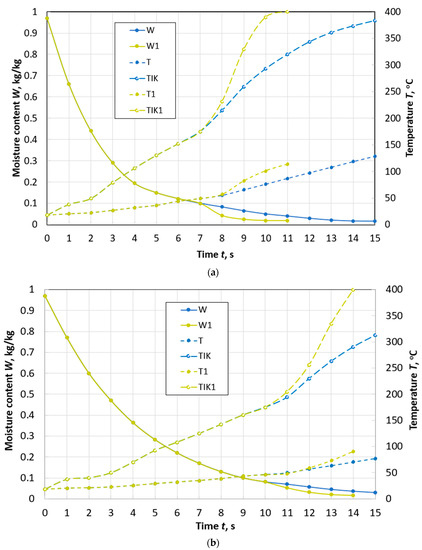
Figure 5.
Changes over time in the average values of moisture content W and temperature T, temperature TIK on the surface of a spherical particle of peat with a diameter of d = 10 mm (a) and a diameter of d = 13 mm (b) during drying with and without taking into account thermal destruction (W1, T1, TIK1) in the flow of flue gases with parameters: Te.m. = 400 °C, we.m. = 4 m/s, de.m. = 12 g/kg of dry gas.
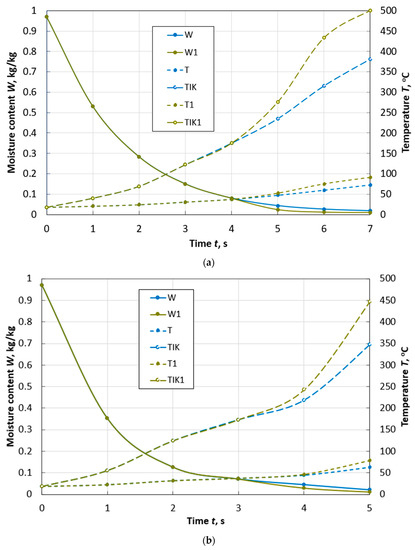
Figure 6.
Changes over time in the average values of moisture content W and temperature T, temperature TIK on the surface of a spherical particle of peat with a diameter of d = 10 mm (a) and a diameter of d = 13 mm (b) during drying with and without taking into account thermal destruction (W1, T1, TIK1) in the flow of flue gases with parameters: Te.m. = 500 °C, we.m. = 4 m/s, de.m. = 12 g/kg of dry gas.
At a flow temperature of 300 °C, in a particle with a diameter of 10 mm (Figure 4), thermal destruction begins when its moisture content W is 12%. The time of reaching the moisture content of 8%, accounting for the effect of thermal decomposition, is 27% less than in cases neglecting this process. In addition, an important point in the development of high-temperature drying technologies is the completion of the process before the beginning of the second stage of thermal decomposition. The second stage can begin already at a temperature of 260 °C, and a particle achieves it faster due to the decomposition of hemicellulose.
When the temperature of the drying agent is increased by 100 °C for a particle of the same size, thermal decomposition begins at a moisture content of W = 10% and the time to reach W = 8% is reduced by almost 3 times (Figure 5a). At the same time, the effect of thermal destruction becomes even more noticeable. The time of the first stage of decomposition is limited to an interval of 1.5 s, and for a particle with a diameter of 13 mm—to an interval of 2 s (Figure 5b).
At a flow temperature of 500 °C, dehydration occurs so quickly (Figure 6) that the temperature of the thermal destruction’s beginning is reached by peat particles of the adopted sizes when they reach a final moisture content of 8%.
The temperature and velocity of the drying agent should be selected based on a number of conditions. Among them, there is the productivity of the technological line for the production of peat briquettes, the technical characteristics of the dryer, the dispersed composition of milled peat, its initial humidity, and the moisture content of the drying agent. The presented mathematical model and the method of its calculation, which are the basis of the computer program, make it possible to account for the influence of all the specified factors and to choose rational parameters of the flow.
3. Discussion
In the technological chain of processing peat into fuel briquettes, the process of dehydration is the most energy-consuming and most decisive for fuel quality. The organization of high-temperature drying of milled peat contributes to solving the issue of energy saving and increasing the calorific value of fuel under the condition of passing the first stage of thermal decomposition [5,6,7]. The development of effective modes of high-temperature peat drying is possible on the basis of mathematical modeling of the dynamics of heat and mass transfer, phase transitions, and shrinkage under the appropriate conditions of the process. In addition, it is possible when there is information about the kinetic characteristics of thermal destruction in a wide temperature range. The attempt to calculate drying and thermal destruction together was justified by the activation nature of the processes of diffusion, evaporation, and thermal decomposition [3,4,5,6,7,23]. The mathematical model (1)–(4) presented in the work includes the formulas for the diffusion coefficient Dfl of the liquid phase, the intensity of evaporation on the outer and inner surfaces of peat particles, and for the saturation pressure. The formulas take into account the dependence of these parameters on temperature and activation energy at each spatial and temporal calculation step. The first stage of thermal destruction is the decomposition of hemicellulose. It is accompanied by the removal of oxygen-containing gases and pyrogenetic moisture and is characterized by a sharp change in the effective activation energy. When peat particles are in contact with a high-temperature flow, the temperature of their outer surface can reach the temperature of thermal decomposition. However, the internal pores will still contain a liquid phase. In this case, the removal of bound water will occur together with pyrogenetic water. This allows us to consider that the proposed approach, when the mathematical model takes into account the simultaneous processes of drying and thermal destruction of peat by means of a local change in the activation energy at the nodal points of the particles, is physically justified.
4. Conclusions
A mathematical model and a numerical method for calculating the dynamics of diffusion–filtration heat and mass transfer, phase transitions, and shrinkage during the dehydration of spherical capillary-porous colloidal peat particles have been developed. This allows the determination of the temperature fields, volume concentrations, and partial pressures of the liquid, vapor, and air phases in the body. Additionally, this allows us to determine the drying time depending on the temperature, moisture content, and velocity of the drying agent, geometric and thermophysical characteristics of the wet body. Physical and numerical experiments were conducted in order to confirm the adequacy of the developed mathematical model and the possibility of its application for the development of peat drying modes. The approach, where the mathematical model takes into account the simultaneous processes of drying and thermal destruction of peat, is proposed. When developing modes of high-temperature peat drying, this allows us to observe the conditions for passing the first stage of thermal destruction and completing the drying process when the particles reach the temperature at the beginning of the second stage of destruction. This increases the calorific value of fuel peat briquettes.
Author Contributions
Conceptualization, N.S.; methodology, N.S. and M.V.; software, N.S.; validation, N.S. and Y.K.; formal analysis, M.V.; investigation, N.S., M.V. and Y.K.; resources, Y.P. and M.V.; data curation, Y.P.; writing—original draft preparation, N.S.; writing—review and editing, M.V.; visualization, M.V. and Y.K.; supervision, N.S.; project administration, Y.P. and M.V.; and funding acquisition, M.V. and Y.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stolbikova, G.E.; Kuporova, A.V. Milled peat drying in case of different size of feed and conditions. Gorn. Inf. Anal. Byulleten 2018, 5, 65–73. Available online: https://cyberleninka.ru/article/n/osobennosti-sushki-frezernogo-torfa-razlichnoy-udelnoy-zagruzki-i-rezhimov-sushki/viewer (accessed on 12 November 2022). (In Russian). [CrossRef]
- Kindzera, D.P.; Khanyk, Y.a.M.; Atamanyuk, V.M.; Duleba, V.P. Kinetic of filtration drying of peat. NU Lviv. Polytech. Chem. Technol. Subst. Appl. 2002, 447, 179–182. Available online: https://ena.lpnu.ua:8443/server/api/core/bitstreams/10659275-4d3c-4960-baf9-d8ae59a11013/content (accessed on 13 November 2022).
- Smolyaninov, S.I.; Lozbin, V.I.; Ikryn, V.M.; Bblichmaer, Y.A. Features of thermal decomposition of peat according to derivatographic data. Bull. Tomsk. Polytech. Univ. Geo Assets Eng. 1976, 274, 56–60. Available online: https://cyberleninka.ru/article/n/osobennosti-termicheskogo-razlozheniya-torfa-po-derivatograficheskim-dannym (accessed on 1 December 2022).
- Mykhailyk, V.A.; Snezhkin, Y.u.F.; Oranska, O.I.; Korinchevska, T.V.; Korinchuk, D.M. Study of the thermal properties of solid residues of milled peat after the humus substances extraction. Ind. Heat Eng. 2015, 37, 54–64. (In Ukrainian) [Google Scholar] [CrossRef]
- Korinchuk, D. Non-isothermal analysis of components of composite fuels based on peat and biomass. Energy Autom. 2018, 1, 56–71. Available online: http://nbuv.gov.ua/UJRN/eia_2018_1_8 (accessed on 1 December 2022). (In Russian). [CrossRef]
- Leroy-Cancellieri, V.; Cancellieri, D.; Leoni, E.; Filkov, A.I.; Simeoni, A. A global mechanism for the thermal degradation of peat. In Proceedings of the 4th Fire Behavior and Fuels Conference, St. Petersburg, Russia, 1–4 July 2013; International Association of Wildland Fire: Missoula, MT, USA, 2013. [Google Scholar]
- Chen, W.-H.; Kuo, P.-C. Isothermal torrefaction kinetics of hemicellulose, cellulose, lignin and xylan using thermogravimetric analysis. Energy 2011, 36, 6451–6460. [Google Scholar] [CrossRef]
- Nikitenko, N.I.; Snezhkin, Y.F.; Sorokovaya, N.N. Mathematical simulation of heat and mass transfer, phase conversions, and shrinkage for optimization of the process of drying of thermolabile materials. J. Eng. Phys. Thermophys. 2005, 78, 75–89. [Google Scholar] [CrossRef]
- Fil’kov, A.I.; Gladkii, D.A. Mathematical modeling of low-temperature drying of a peat layer. Tomsk. State Univ. J. 2012, 3, 93–106. (In Russian) [Google Scholar]
- Luikov, A.V. Drying Theory; Energy: Moscow, Russia, 1968; p. 472. Available online: https://www.twirpx.com/file/1241798/ (accessed on 10 December 2022). (In Russian)
- Wang, Z.; Wang, Q.; Lai, J.; Liu, D.; Hu, A.; Xu, L.; Chen, Y. Numerical Simulation of Heat and Mass Transfer in Sludge Low-Temperature Drying Process. Entropy 2022, 24, 1682. [Google Scholar] [CrossRef]
- Nikitenko, N.I. Problems of the radiation theory of heat and mass transfer in solid and liquid media. J. Eng. Phys. Thermophys. 2000, 73, 840–848. [Google Scholar] [CrossRef]
- Aleksanyan IYu Titova, L.M.; Nugmanov, A.K. Simulation of the process of drying a dispersed material in a fluidized bed. Tech. Technol. Food Prod. 2014, 3, 96–102. Available online: https://cyberleninka.ru/article/n/modelirovanie-protsessa-sushki-dispersnogo-materiala-v-kipyaschem-sloe/viewer (accessed on 15 November 2022). (In Russian).
- Strumillo, C.; Grinchik, N.N.; Kuts, P.S.; Akulich, P.V.; Zbicinski, I. Numerical modeling of nonisothermal moisture transfer in biological colloidal porous materials. J. Eng. Phys. Thermophys. 1994, 66, 181–190. [Google Scholar] [CrossRef]
- Huzova, I.O.; Atamanyuk, V.M. Dynamics of drying processes of plant raw material in the period of decreasing speed. J. Chem. Technol. 2022, 30, 419–430. Available online: http://chemistry.dnu.dp.ua/article/view/259694 (accessed on 9 December 2022).
- Luikov, A.V. Heat and Mass Transfer in Capillary Porous Bodies; Pergamon Press: Oxford, UK, 1966; pp. 233–303. [Google Scholar] [CrossRef]
- Akulich, P.V. Thermohydrodynamic Processes in Drying Technique; ITMO: Minsk, Belarus, 2002; p. 268. [Google Scholar]
- Kotov, B.I.; Bandura, V.N.; Kalinichenko, R.A. Mathematical modeling and identification of heat and mass transfer in plant dispersed material during drying and heating by an ultra-high frequency electromagnetic field. Energy Autom. 2018, 6, 35–50. Available online: http://nbuv.gov.ua/UJRN/eia_2018_6_6 (accessed on 3 December 2022).
- Akulich, P.V.; Slizhuk, D.S. Heat and Mass Transfer in a Dense Layer during Dehydration of Colloidal and Sorption Capillary-Porous Materials under Conditions of Unsteady Radiation-Convective Energy Supply. Theor. Found. Chem. Eng. 2022, 56, 152–161. [Google Scholar] [CrossRef]
- Rudobashta, S.P.; Kartashov, E.M.; Zueva, G.A. Mathematical modeling of convective drying of materials with taking into account their shrinking. Inzh. Fiz. Zh. 2020, 93, 1394–1401. [Google Scholar] [CrossRef]
- Rudobashta, S.P.; Dmitriev, V.M. Investigation of the Diffusion Properties of Plant Capillary-Porous Colloidal Materials with Regard to Their Shrinkage. J. Eng. Phys. Thermophys. 2022, 95, 1357–1365. [Google Scholar] [CrossRef]
- Narang, H.; Wu, F.; Mohammed, A.R. An Efficient Acceleration of Solving Heat and Mass Transfer Equations with the First Kind Boundary Conditions in Capillary Porous Radially Composite Cylinder Using Programmable Graphics Hardware. J. Comput. Commun. 2019, 7, 267–281. [Google Scholar] [CrossRef]
- Nikitenko, N.I.; Snezhkin, Y.u.F.; Sorokovaya, N.N.; Kolchik Yu, N. Molecular Radiation Theory and Methods for Calculating Heat and Mass Transfer; Naukova Dumka: Kyiv, Ukraine, 2014; p. 744. Available online: http://ittf.kiev.ua/wp-content/uploads/2016/12/nikitenko.pdf (accessed on 3 December 2022). (In Russian)
- Sneszkin, Y.F.; Korinchuk, D.N. Modeling of high-temperature drying of peat and biomass in biofuel production technologies. Sci. Work. 2017, 81, 125–130. Available online: https://sciworks.ontu.edu.ua/en/site/archives/81-1?page=2 (accessed on 15 January 2023). (In Russian).
- Leibenzon, L.S. Variational Methods for Solving Problems in the Theory of Elasticity; Gostekhizdat: Moscow, Russia, 1943; p. 286. (In Russian) [Google Scholar]
- Nikitenko, N.I. Investigation of dynamics of evaporation of condensed bodies on the basis of the law of spectral-radiation intensity of particles. Inzh. Fiz. Zh. 2002, 75, 128–134. [Google Scholar] [CrossRef]
- Sorokovaya, N.N.; Snezhkin, Y.F.; Shapar, R.A.; Sorokovoi, R.Y. Mathematical Simulation and Optimization of the Continuous Drying of Thermolabile Materials. J. Eng. Phys. Thermophys. 2019, 92, 1180–1190. [Google Scholar] [CrossRef]
- Sorokova, N.; Didur, V.; Variny, M. Mathematical Modeling of Heat and Mass Transfer during Moisture–Heat Treatment of Castor Beans to Improve the Quality of Vegetable Oil. Agriculture 2022, 12, 1356. [Google Scholar] [CrossRef]
- Broido, A. A Simple, sensitive graphical method of treating thermogravimetric analysis data. J. Polym. Sci. Part B Polym. Phys. 1969, 7, 1761–1773. [Google Scholar] [CrossRef]
- Oostindie, K. A Simulation Model for the Calculation of Water Balance, Cracking and Surface Subsidence of Clay Soils; Rep. 47; Winand Staring Centre for Integrated Land, Soil and Water Research: Wageningen, The Netherlands, 1992; p. 65. Available online: https://books.google.com.ua/books/about/FLOCR.html?id=D39jHAAACAAJ&redir_esc=y (accessed on 12 January 2023).
- Garnier, P.; Perrier, E.; Angulo, A.J.; Baveye, P. Numerical model of 3-dimensional anisotropic deformation and water flow in welling soil. Soil Sci. 1997, 162, 410–420. [Google Scholar] [CrossRef]
- Rudobashta, S.P. Mass Transfer in Systems with a Solid Phase; Chemistry: Moscow, Russia, 1980; p. 248. Available online: https://www.libex.ru/detail/book796756.html (accessed on 11 January 2023). (In Russian)
- Keltsev, N.V. Fundamentals of Sorption Technology, 2nd ed.; Chemistry: Moscow, Russia, 1984; p. 590. (In Russian) [Google Scholar]
- Nikitenko, N.I. A method for calculating the temperature field by the data of measurement of the deformation of a body. Inzh. Fiz. Zh. 1980, 39, 281–285. [Google Scholar]
- Nikitenko, N.I. Radiation heat conduction mikromechanism. In Proceedings of the First International Conference on Transport Phenomena in Processing, Lancaster, PA, USA, 22–26 March 1992; pp. 1580–1588. [Google Scholar]
- Kutateladze, S.S. Fundamentals of the Theory of Heat Transfer; Atomizdat: Moscow, Russia, 1979; p. 416. (In Russian) [Google Scholar]
- Voznyuk, S.T.; Moshinsky, V.S.; Klymenko, M.O.; Lyko, D.V.; Gneushev, V.O.; Lagodnyuk, O.A.; Voznyuk, N.M.; Kucherova, A.V. Peat Land Resource of the North-Western Region of Ukraine; NUWEE: Rivne, Ukraine, 2017; p. 117. Available online: http://ep3.nuwm.edu.ua/id/eprint/7506 (accessed on 11 October 2022). (In Ukrainian)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).