Digital Microfluidic Droplet Path Planning Based on Improved Genetic Algorithm
Abstract
1. Introduction
2. Droplet Driving Principles in Digital Microfluidic Systems
3. Problem Description and Spatial Modelling
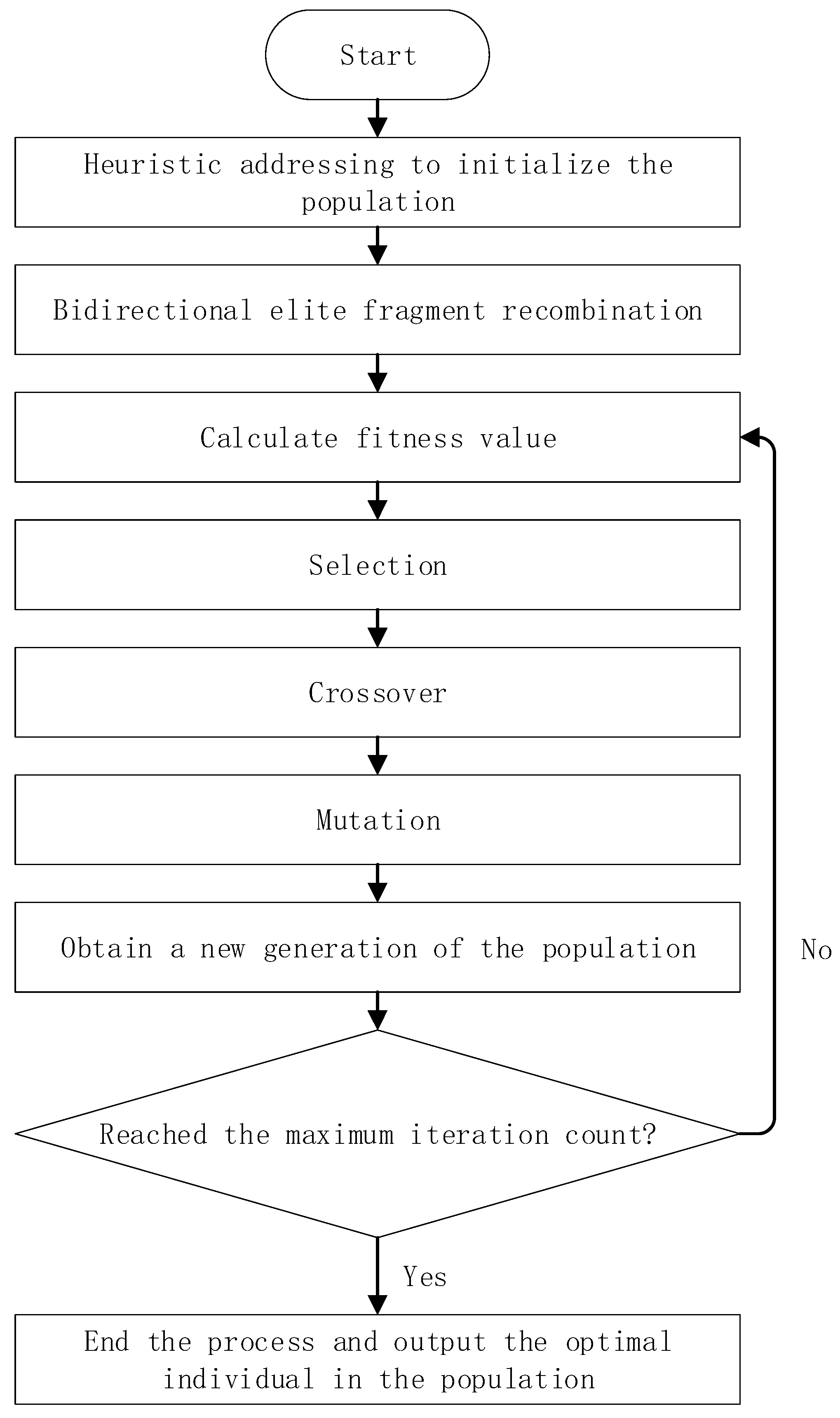
4. Heuristic-Elite Genetic Algorithm
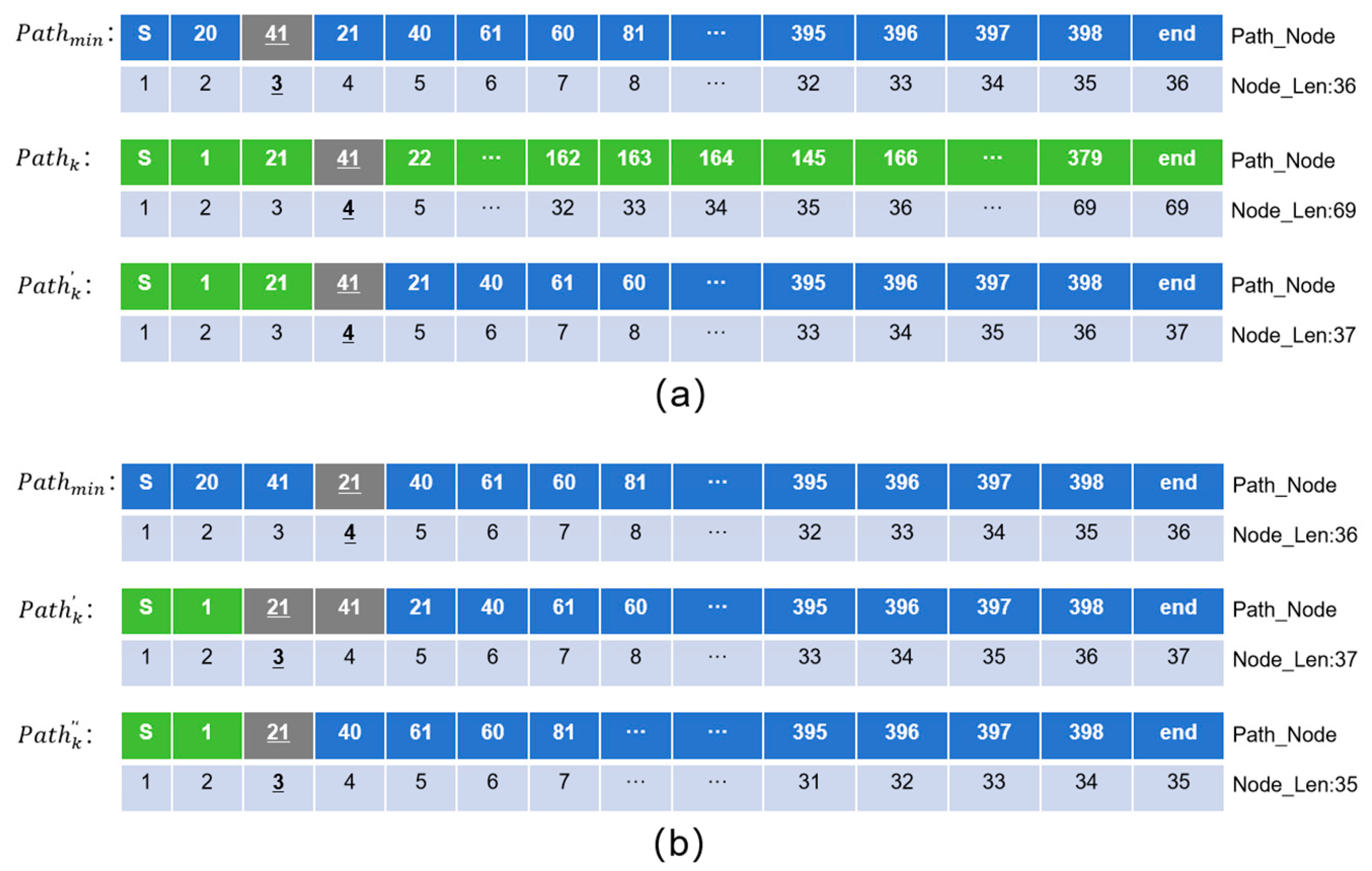
4.1. Population Initialization
4.2. Fitness Function
4.3. Genetic Operations
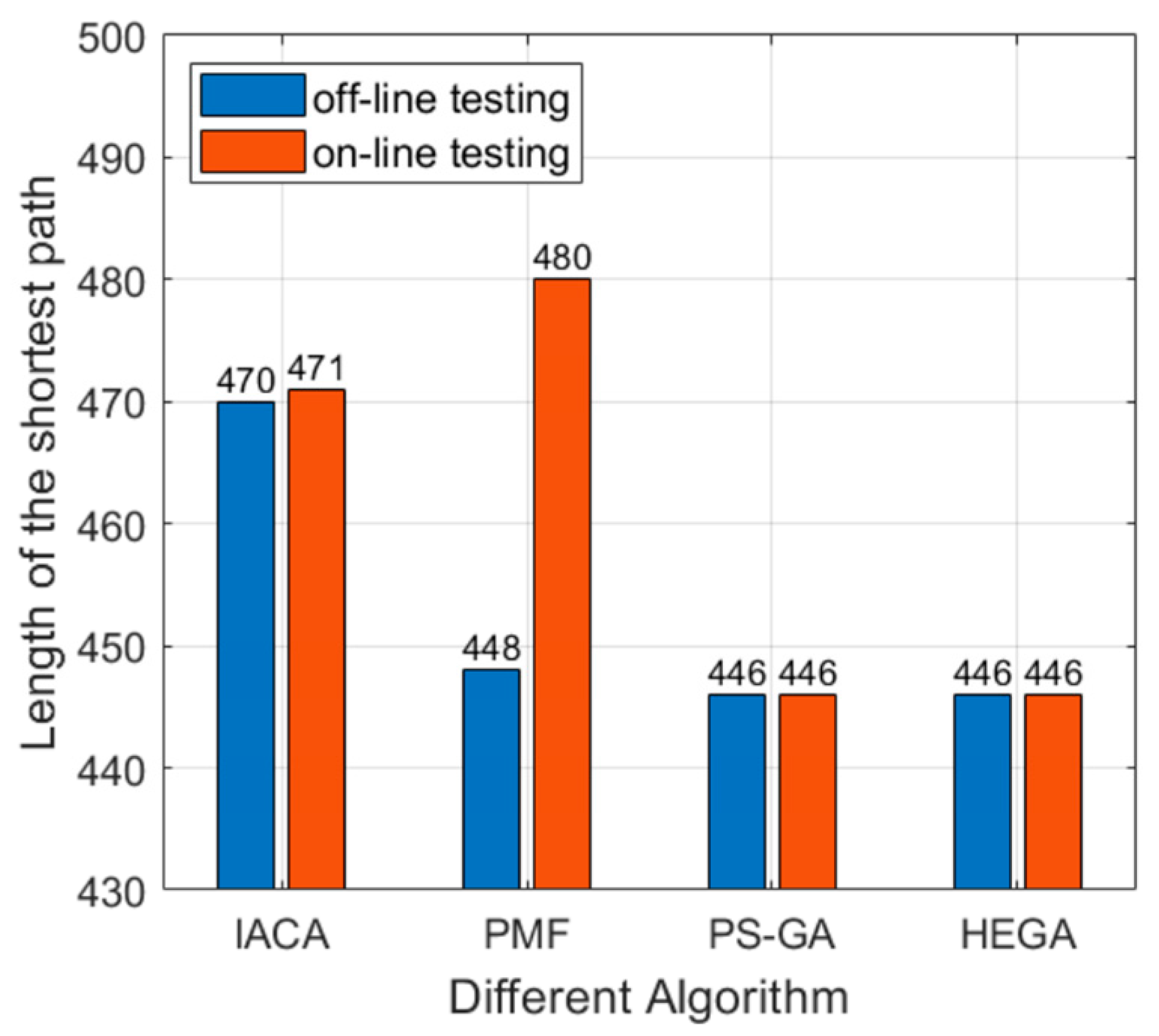
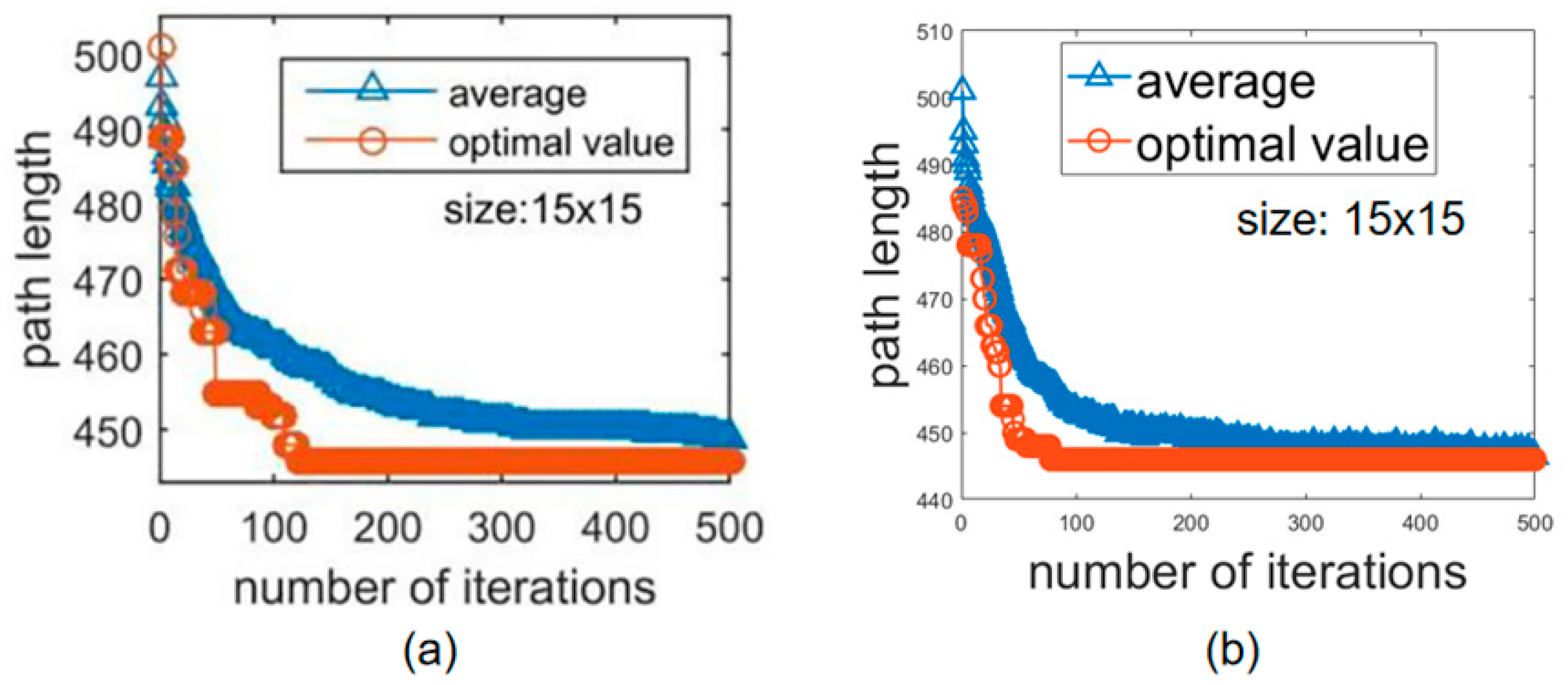
5. Simulation Validation
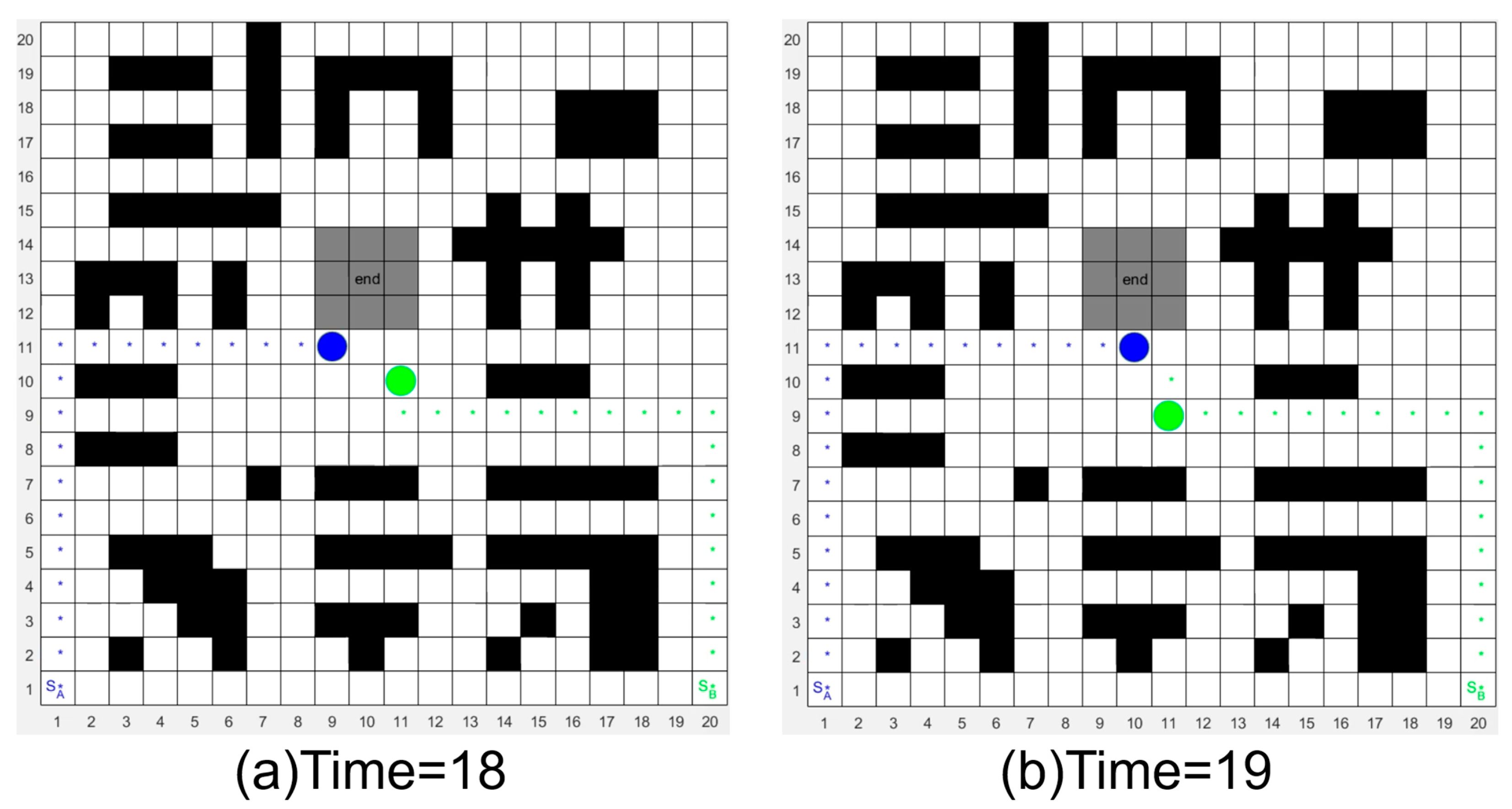
5.1. Single Droplet Path Planning for EWOD Devices
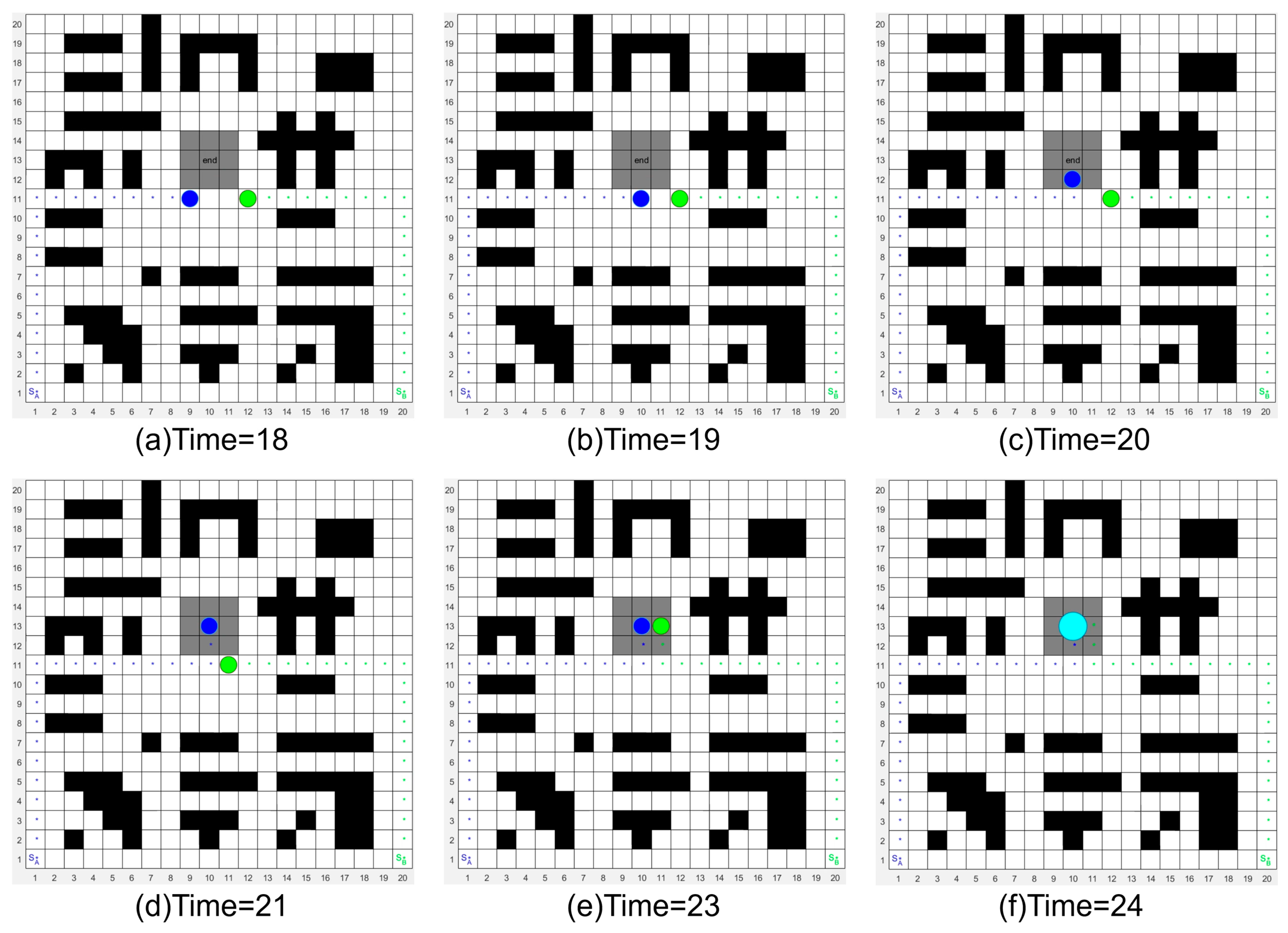
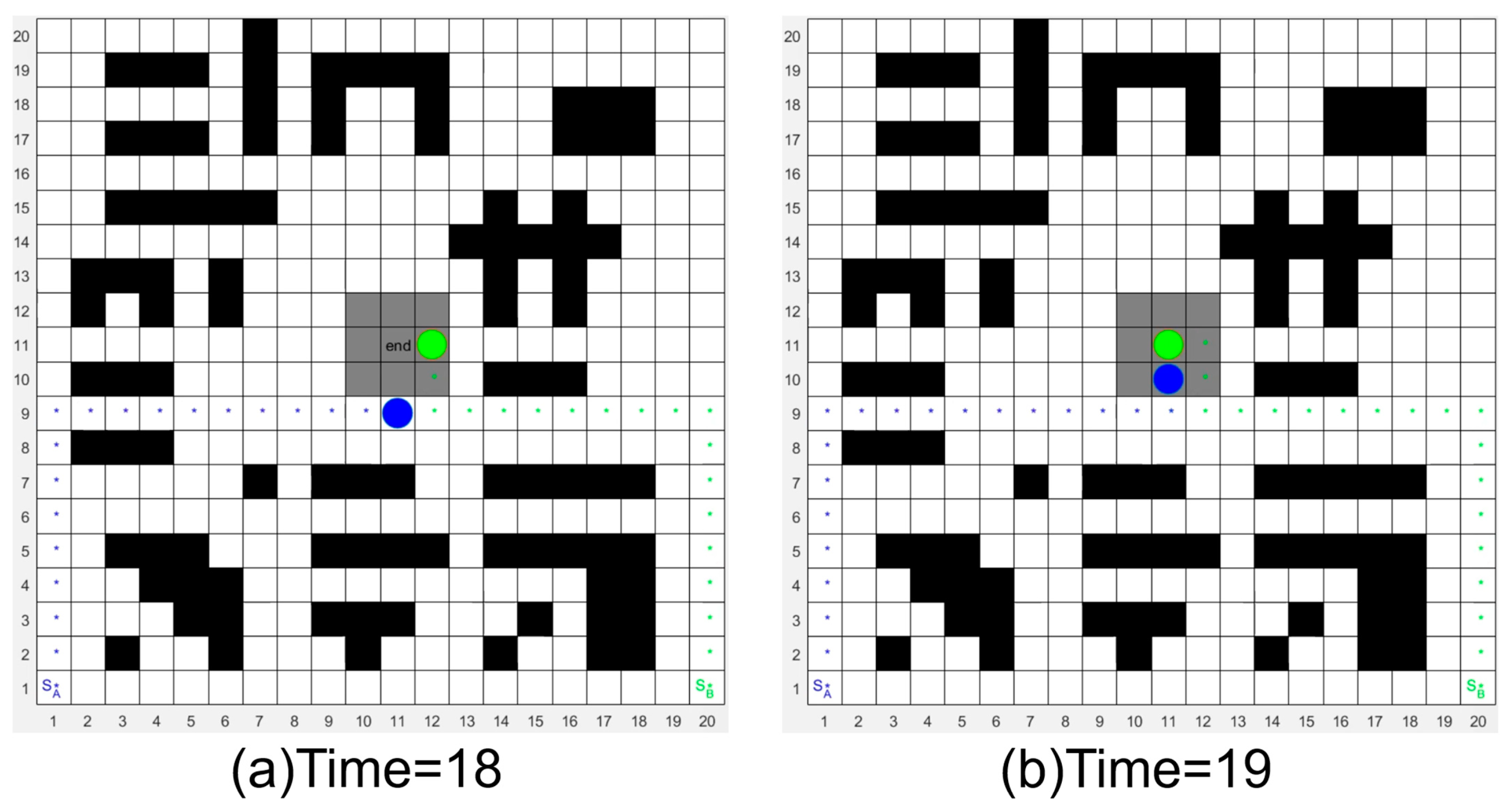
5.2. Collision Avoidance Strategies for Multiple Droplets in EWOD Devices
5.2.1. Collision Avoidance Strategy 1: Lower-Priority Droplet Remains Stationary
5.2.2. Collision Avoidance Strategy 2: Retraction of the Secondary Priority Droplet
5.2.3. Collision Avoidance Strategy 3: Droplet Priority Switching
5.3. Test Droplet Path Planning for EWOD Devices
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thorsen, T.; Maerkl, S.J.; Quake, S.R. Microfluidic Large-Scale Integration. Science 2002, 298, 580–584. [Google Scholar] [CrossRef]
- Mugele, F.; Baret, J.C. Electrowetting: From basics to applications. J. Phys. Condens. Matter 2005, 17, R705–R774. [Google Scholar] [CrossRef]
- Teh, S.Y.; Lin, R.; Hung, L.H.; Lee, A.P. Droplet microfluidics. Lab Chip 2008, 8, 198–220. [Google Scholar] [PubMed]
- Jebrail, M.J.; Wheeler, A.R. Let’s get digital: Digitizing chemical biology with microfluidics. Curr. Opin. Chem. Biol. 2010, 14, 574–581. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.N. Design of a Digital Microfluidic-Based cTnl Imunoassay System. Ph.D. Thesis, Shandong Normal University, Jinan, China, 2023. [Google Scholar]
- Dong, C.; Li, F.; Sun, Y.; Long, D.; Chen, C.; Li, M.; Wei, T.; Martins, R.; Chen, T.; Mak, P.-I. A syndromic diagnostic assay on a macrochannel-to-digital microfluidic platform for automatic identification of multiple respiratory pathogens. Lab Chip 2024, 24, 3850–3862. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Gan, X.; Zeng, Y.; Xu, Z.; Xu, L.; Hu, C.; Ma, H.; Chai, B.; Hu, S.; Chai, Y. Advanced design and applications of digital microfluidics in biomedical fields: An update of recent progress. Biosens. Bioelectron. 2023, 242, 115723. [Google Scholar]
- Lu, G.; Lin, D.J.; Wang, X.D. Progress of electrowetting applications in micro-nano energy conversion and utilization systems. Chin. Sci. Bull. 2017, 62, 799–811. (In Chinese) [Google Scholar] [CrossRef]
- Wang, S.; Ying, Y.; Fan, X. Chip cooling model and path optimization based on digital microfluidics. J. Northwestern Polytech. Univ. 2019, 37, 107–113. [Google Scholar] [CrossRef]
- Torabinia, M.; Dakarapu, U.S.; Asgari, P.; Jeon, J.; Moon, H. Electrowetting-on-dielectric (EWOD) digital microfluidic device for in-line workup in organic reactions: A critical step in the drug discovery work cycle. Sens. Actuators B Chem. 2021, 330, 129252. [Google Scholar] [CrossRef]
- Huang, X.J. Test Path Optimization of Digital Microfluidic Biochip Based on Intelligent Algorithm. Ph.D. Thesis, Guilin University of Electronic Technology, Guilin, China, 2023. [Google Scholar]
- Xu, C.P.; Cai, Z.; Hu, C. On-line test path optimization for digital microfluidic biochips based on ant colony algorithm. Chin. J. Sci. Instrum. 2014, 35, 1417–1424. [Google Scholar]
- Xu, C.P.; Liu, H.; Wan, C.T.; Mo, W. Route optimization of contamination removal in digital microfluidic biochips based on chaos particle swarm optimization. J. Electron. Meas. Instrum. 2018, 32, 46–52. [Google Scholar]
- Zheng, W.; Shi, J.; Wang, A.; Fu, P.; Jiang, H. A Routing-Based Repair Method for Digital Microfluidic Biochips Based on an Improved Dijkstra and Improved Particle Swarm Optimization Algorithm. Micromachines 2020, 11, 1052. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, R.; Sarkar, A.; Roy, P. An Intelligent Path Estimation Technique for Transportation of Heterogeneous Droplets in Digital Micro Fluidic Biochips (DMFB). In Applications of Artificial Intelligence in Engineering; Gao, X.Z., Kumar, R., Srivastava, S., Soni, B.P., Eds.; Algorithms for Intelligent Systems; Springer: Singapore, 2021. [Google Scholar]
- Kawakami, T.; Shiro, C.; Nishikawa, H.; Kong, X.; Tomiyama, H.; Yamashita, S. A Deep Reinforcement Learning Approach to Droplet Routing for Erroneous Digital Microfluidic Biochips. Sensors 2023, 23, 8924. [Google Scholar] [CrossRef] [PubMed]
- Juárez, J.; Brizuela, C.A.; Martínez Pérezal, I.M. An Evolutionary Multi-objective Optimization algorithm for the routing of droplets in Digital Microfluidic Biochips. Inf. Sci. 2018, 429, 130–146. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.; Wei, W. An Initialization Method of Genetic Algorithm for Robot Path Planning Based on Directed Acyclic Graph and Effective Obstacles. In Proceedings of the 2024 IEEE International Conference on Industrial Technology (ICIT), Bristol, UK, 25–27 March 2024; pp. 1–7. [Google Scholar]
- Chang, Y.X. Research on the Droplet Movement in Electrowetting on Dielectric Based Ditigal Microfluidic System. Ph.D. Thesis, Hebei University of Technology, Tianjin, China, 2014. [Google Scholar]
- Luo, Z.J.; Huang, Z.T.; Peng, C.L.; Pan, Z.; Liu, S.; Cao, L.; Yin, H. Research on droplet path planning of digital microfluidic system based on improved A* algorithm. Electron. Meas. Technol. 2021, 44, 56–63. [Google Scholar]
- Luo, Z.J.; Xu, J.Z.; Pan, Z.Y.; Huang, A.Q.; He, J.Y.; Cao, L.; Liu, S.Y. Accurate Droplet Generation and Splitting in Digital Microfluidic System Based on Electrowetting on Dielectric. Micro-Nanoelectron. Technol. 2021, 58, 818–826. [Google Scholar]
- Xu, X.W.; Sun, L.N.; Zhang, Y.L.; Jiang, H. Mechanism of Droplets from Stationary to Moving on Electrowetting on dielectric Chips. China Mech. Eng. 2018, 29, 2905–2911. [Google Scholar]
- Su, F.; Chakrabarty, K.; Fair, R.B. Microfluidics-based biochips: Technology issues, implementation platforms, and design automation challenges. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2006, 25, 211–223. [Google Scholar] [CrossRef]
- Su, F.; Hwang, W.; Mukherjee, A.; Chakrabarty, K. Testing and diagnosis of realistic defects in digital microfluidic biochips. J. Electron. Test. 2007, 23, 219–233. [Google Scholar] [CrossRef]
- Zheng, W.; Yu, H.; Feng, L.; Fu, P.; Jiang, H. Single droplet on-line testing path optimization for digital microfluidic biochips based on the improved ant colony algorithm. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference, Turin, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar]
- Huang, X.; Xu, C.; Zhang, L. An Efficient Algorithm for Optimizing the Test Path of Digital Microfluidic Biochips. J. Electron. Test. 2020, 36, 205–218. [Google Scholar] [CrossRef]





| Algorithm | Average Shortest Paths | Mean Turning Points for Shortest Paths | Execution Time/s |
|---|---|---|---|
| Basic ant colony algorithm | 58 | 10.27 | 13.8533 |
| HEGA of this study | 58 | 8.5 | 1.0255 |
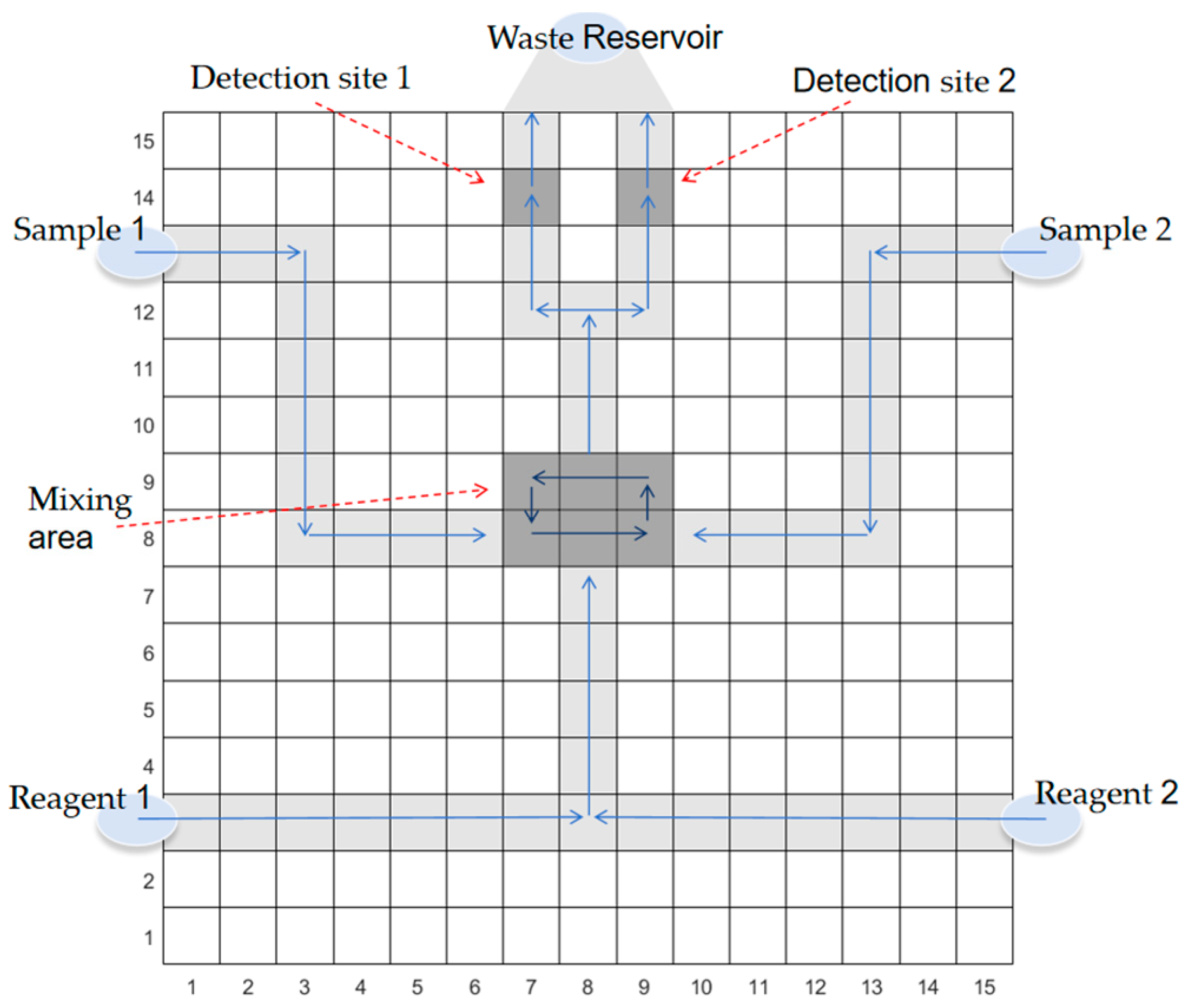
| Time/s | Operation |
|---|---|
| 0 | Sample 2 and reagent 2 move towards the mixing area |
| 0.8 | Sample 2 and reagent 2 start mixing in the mixing area |
| 6.0 | Sample 1 and reagent 1 move towards the mixing area & Sample 2 and reagent 2 continue to mix |
| 6.8 | Sample 2 and reagent 2 are mixed and moved to the testing area 2 & Sample 1 and reagent 1 start mixing in the mixing area |
| 12.8 | Sample 1 and reagent 1 are mixed and moved to the testing area 1 & Mixture 2 continues to be tested in the testing area |
| 19.8 | Mixture 2 has been tested and is moving to the waste reservoir & Mixture 1 continues to be tested |
| 25.8 | Mixture 1 is tested and moved to the waste reservoir, and the experiment is over |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Long, W.; Chen, R.; Wu, J.; Huang, A.; Zheng, J. Digital Microfluidic Droplet Path Planning Based on Improved Genetic Algorithm. Information 2025, 16, 103. https://doi.org/10.3390/info16020103
Luo Z, Long W, Chen R, Wu J, Huang A, Zheng J. Digital Microfluidic Droplet Path Planning Based on Improved Genetic Algorithm. Information. 2025; 16(2):103. https://doi.org/10.3390/info16020103
Chicago/Turabian StyleLuo, Zhijie, Wufa Long, Rui Chen, Jianhao Wu, Aiqing Huang, and Jianhua Zheng. 2025. "Digital Microfluidic Droplet Path Planning Based on Improved Genetic Algorithm" Information 16, no. 2: 103. https://doi.org/10.3390/info16020103
APA StyleLuo, Z., Long, W., Chen, R., Wu, J., Huang, A., & Zheng, J. (2025). Digital Microfluidic Droplet Path Planning Based on Improved Genetic Algorithm. Information, 16(2), 103. https://doi.org/10.3390/info16020103






