UAVs for Medicine Delivery in a Smart City Using Fiducial Markers
Abstract
1. Introduction
2. Related Works
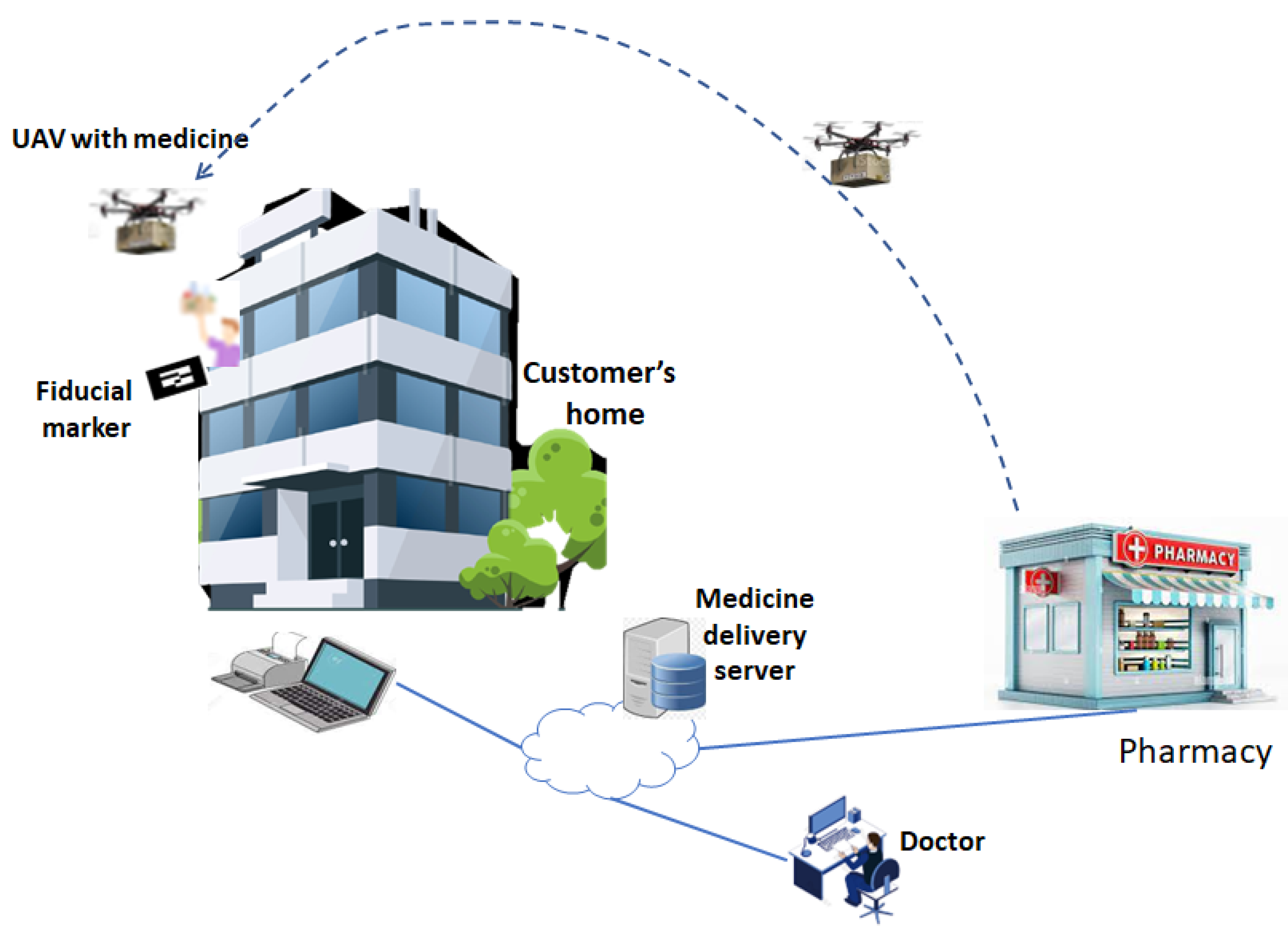
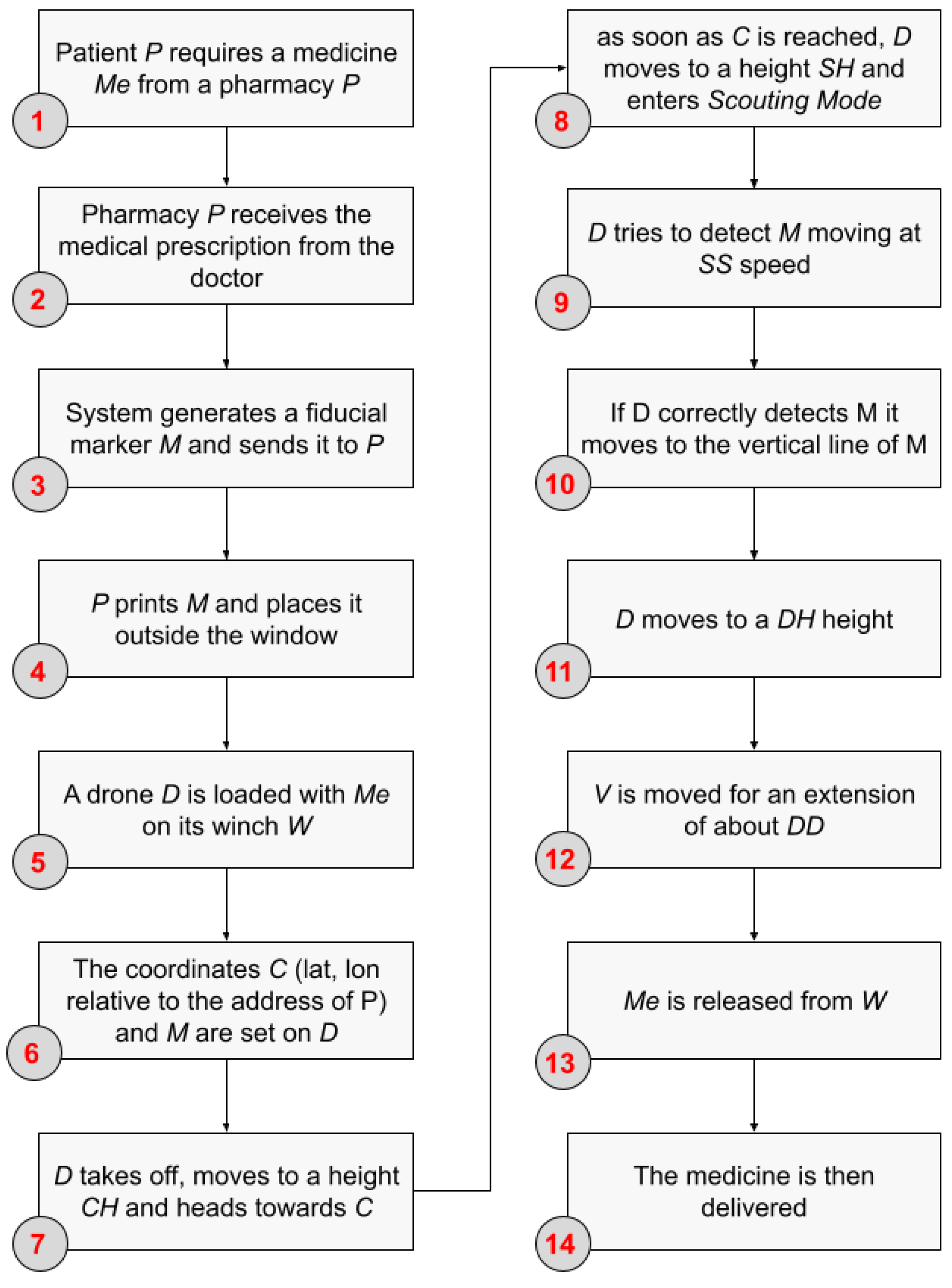
3. System Description
3.1. System Architecture
3.2. Fiducial System Comparison
3.3. Fiducial System and Related Issues
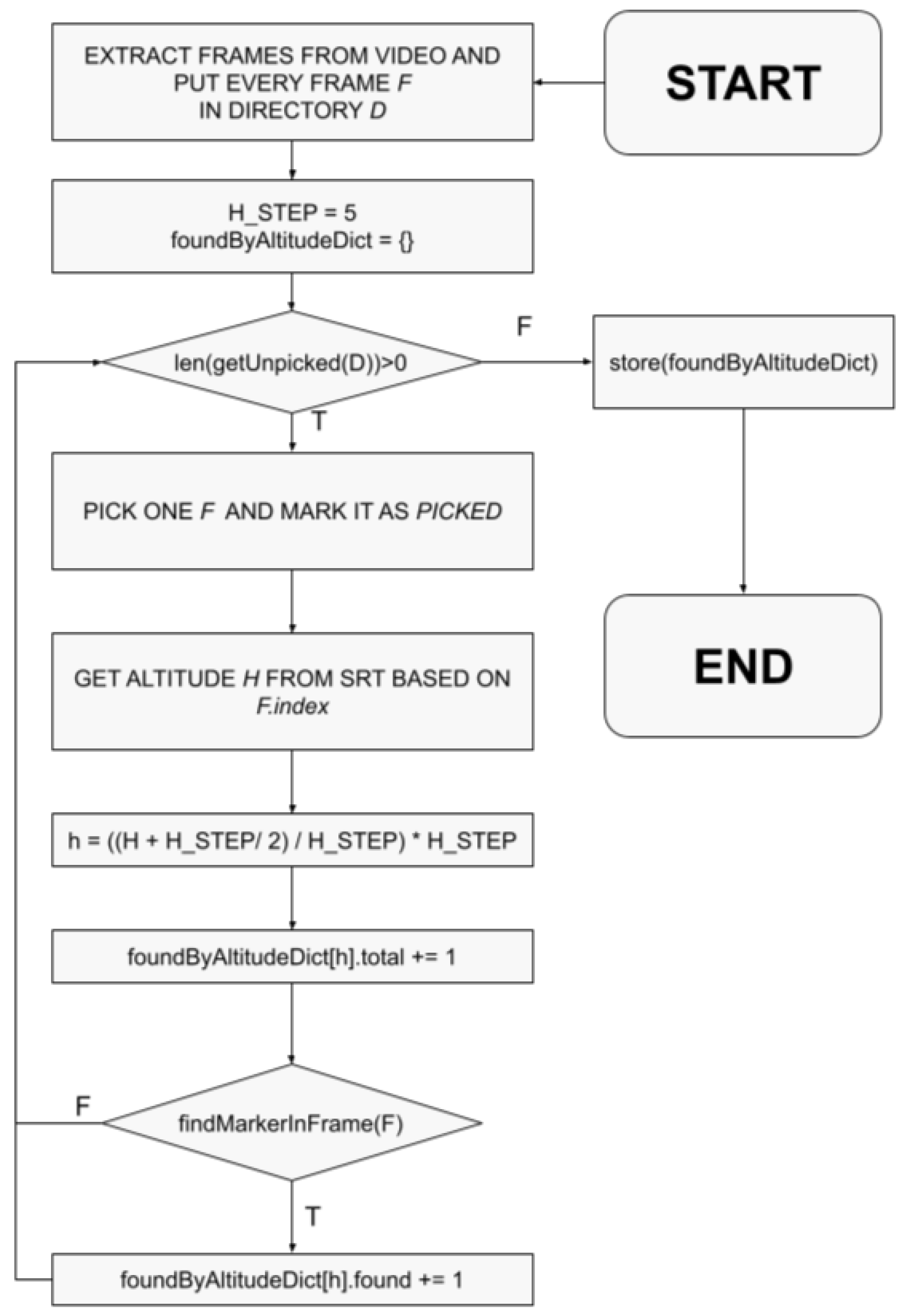
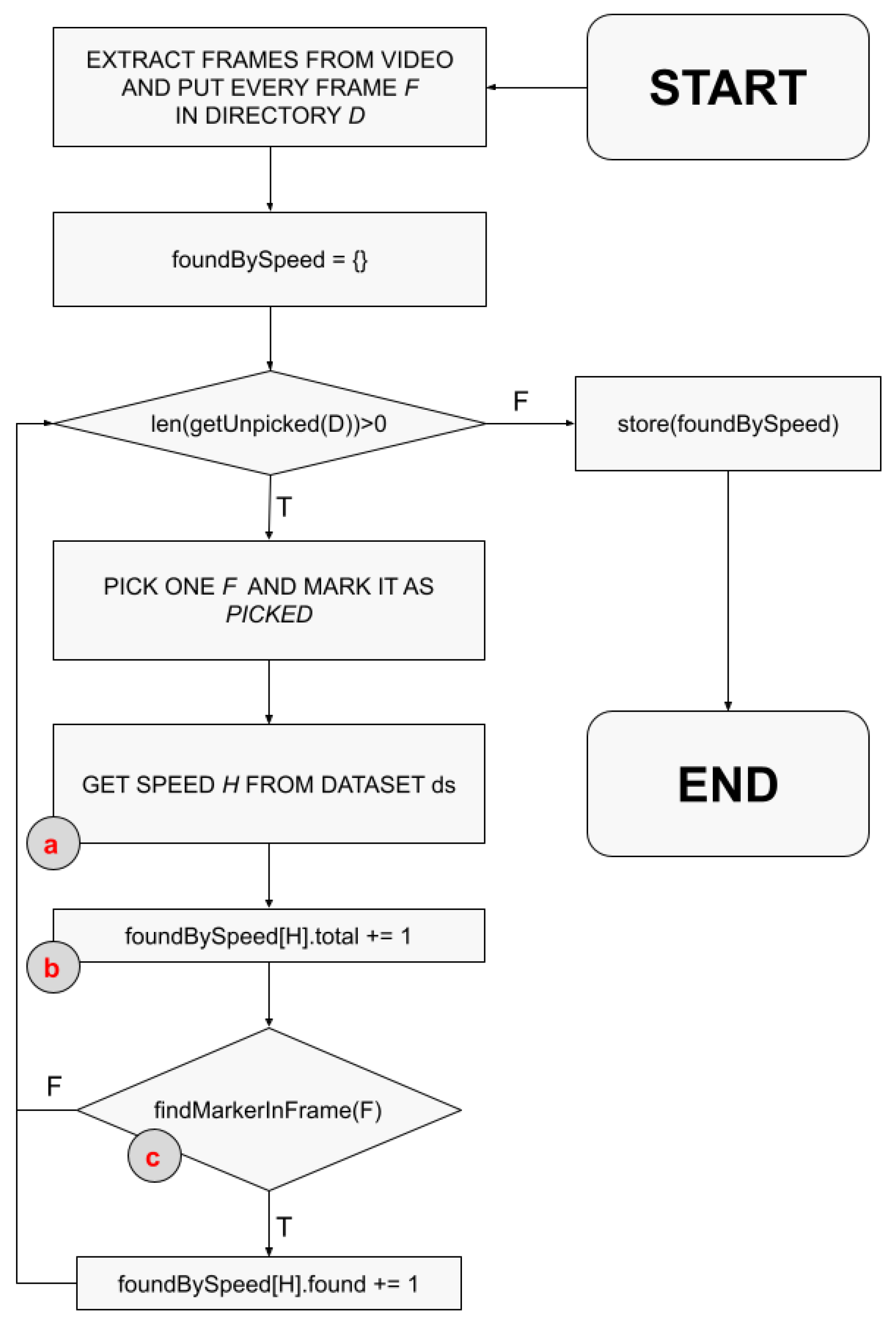
4. Testbed Description and Dataset Creation
- In seq #1, we acquired samples during a sunny day using the 0.15 m printed tag version of each fiducial family/system, setting the camera focal length at 24 mm (no zoom).
- In seq #2, we acquired samples during a sunny day using the 0.26 m printed tag version of each fiducial family/system, setting the camera focal length at 24 mm (no zoom).
- In seq #3, we acquired samples during a sunny day using the 0.15 m printed tag version of each fiducial family/system, setting the camera focal length at 48 mm (2× zoom).
- In seq #4, we acquired samples during a sunny day using the 0.26 m printed tag version of each fiducial family/system, setting the camera focal length at 48 mm (2× zoom).
- Sequences #5, #6, #7 and #8 are set up to be equivalent to sequences #1, #2, #3 and #4 except for the weather and light conditions; we acquired these sequences during a cloudy day.
- Sequence #9 was acquired during a sunny day using the 0.26 m printed tag version of each fiducial family/system, setting the camera focal length at 48 mm (2× zoom).
5. Evaluation
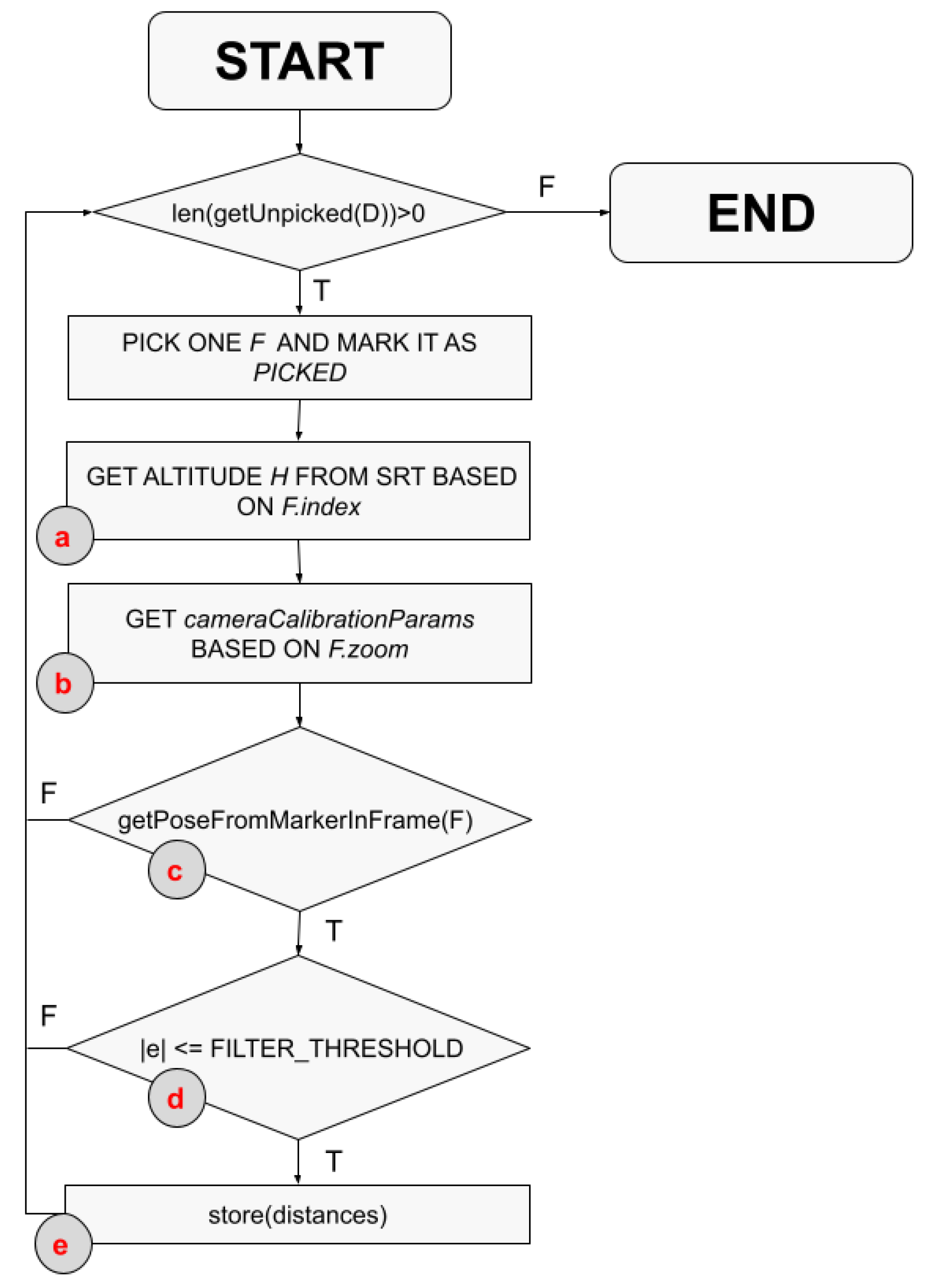
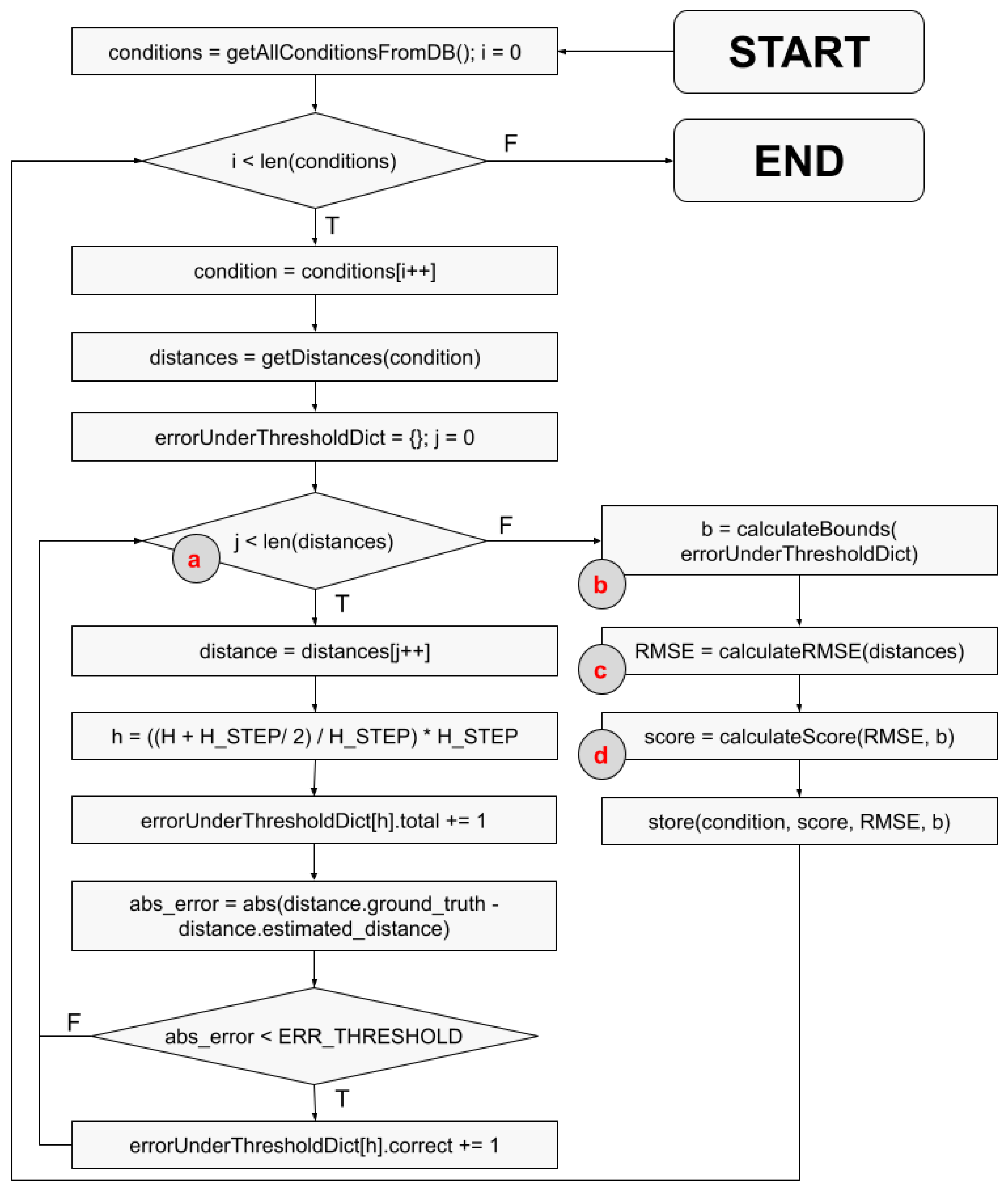
5.1. Definitions
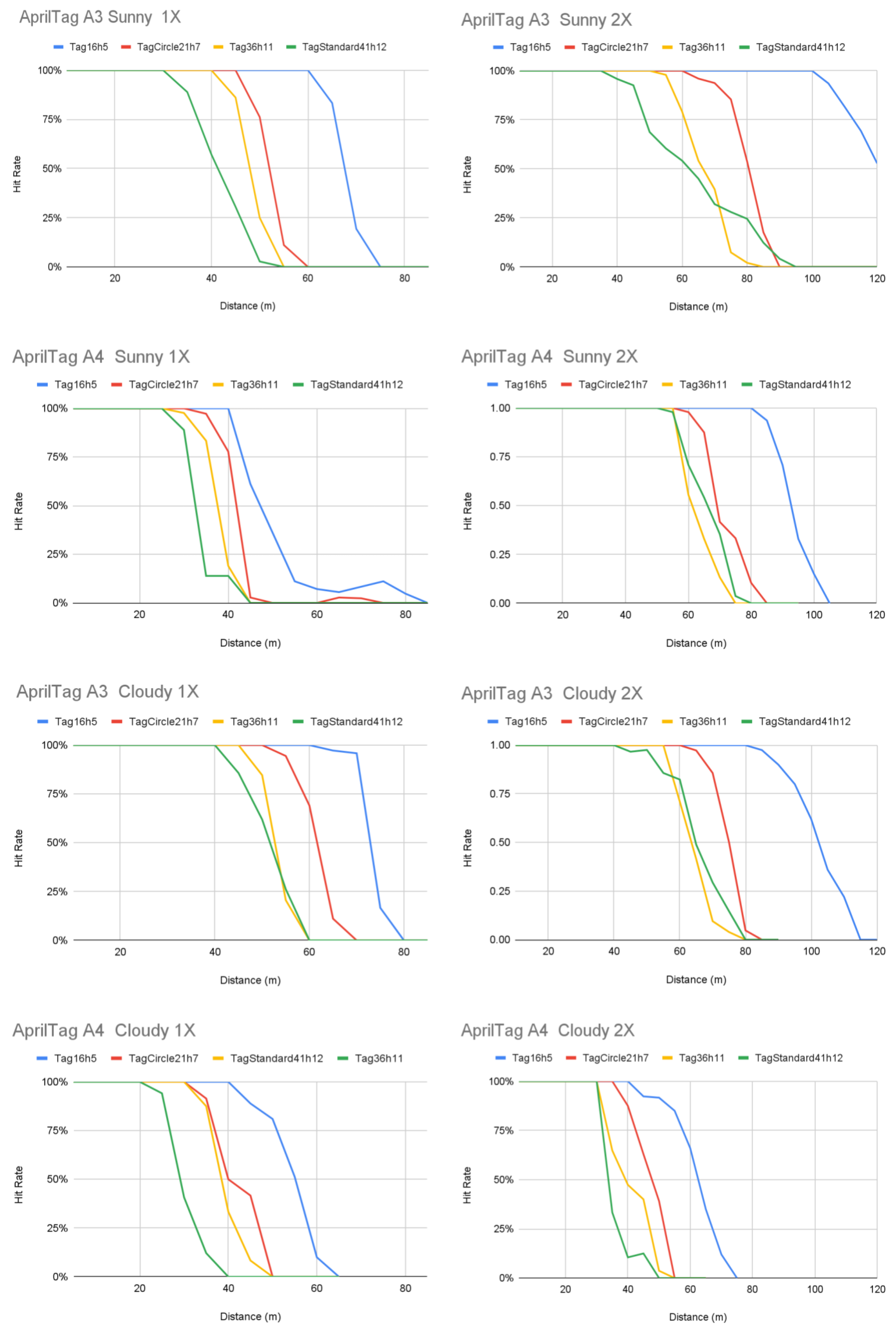
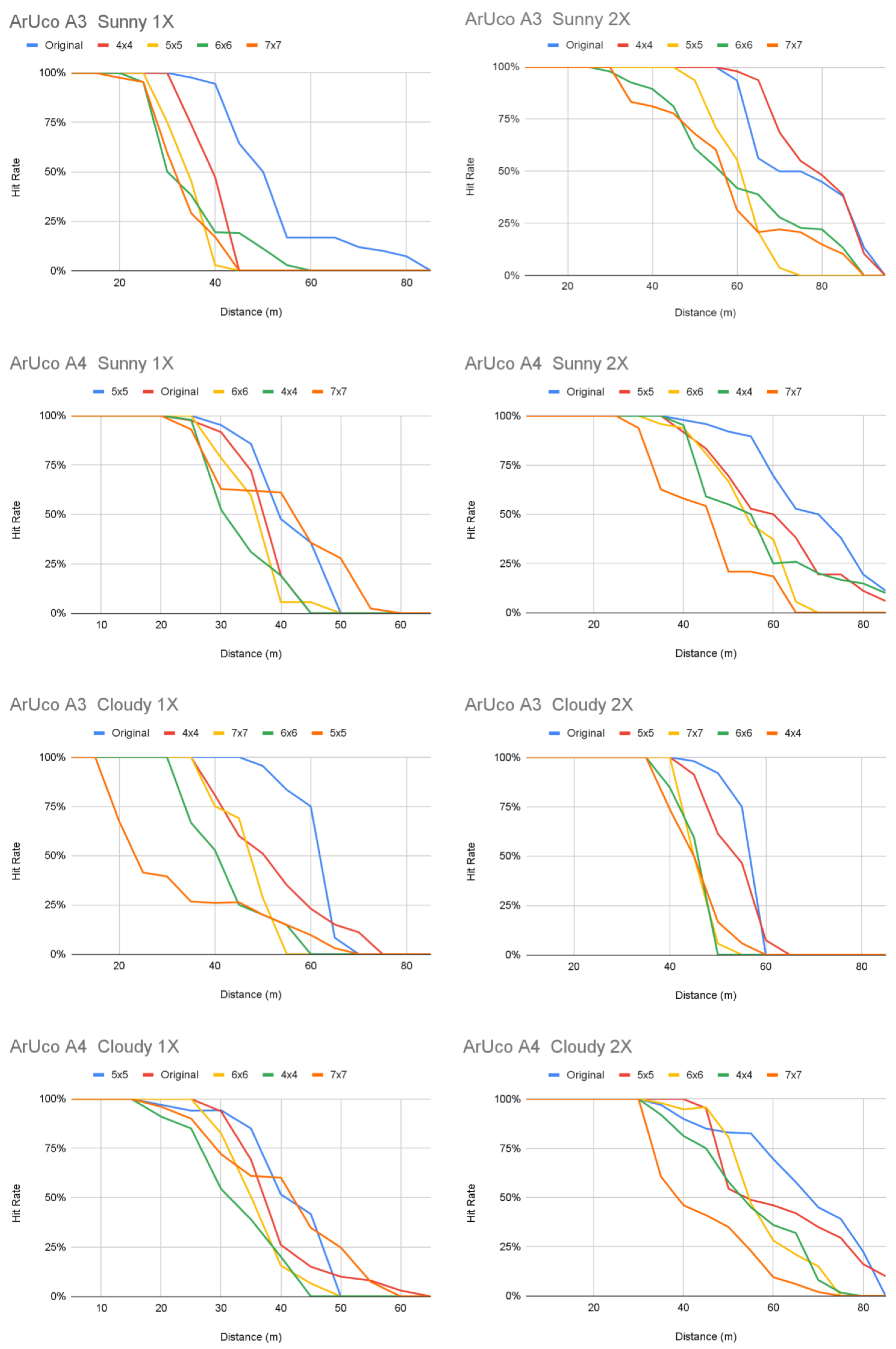
5.2. Results
6. Metrics and Results
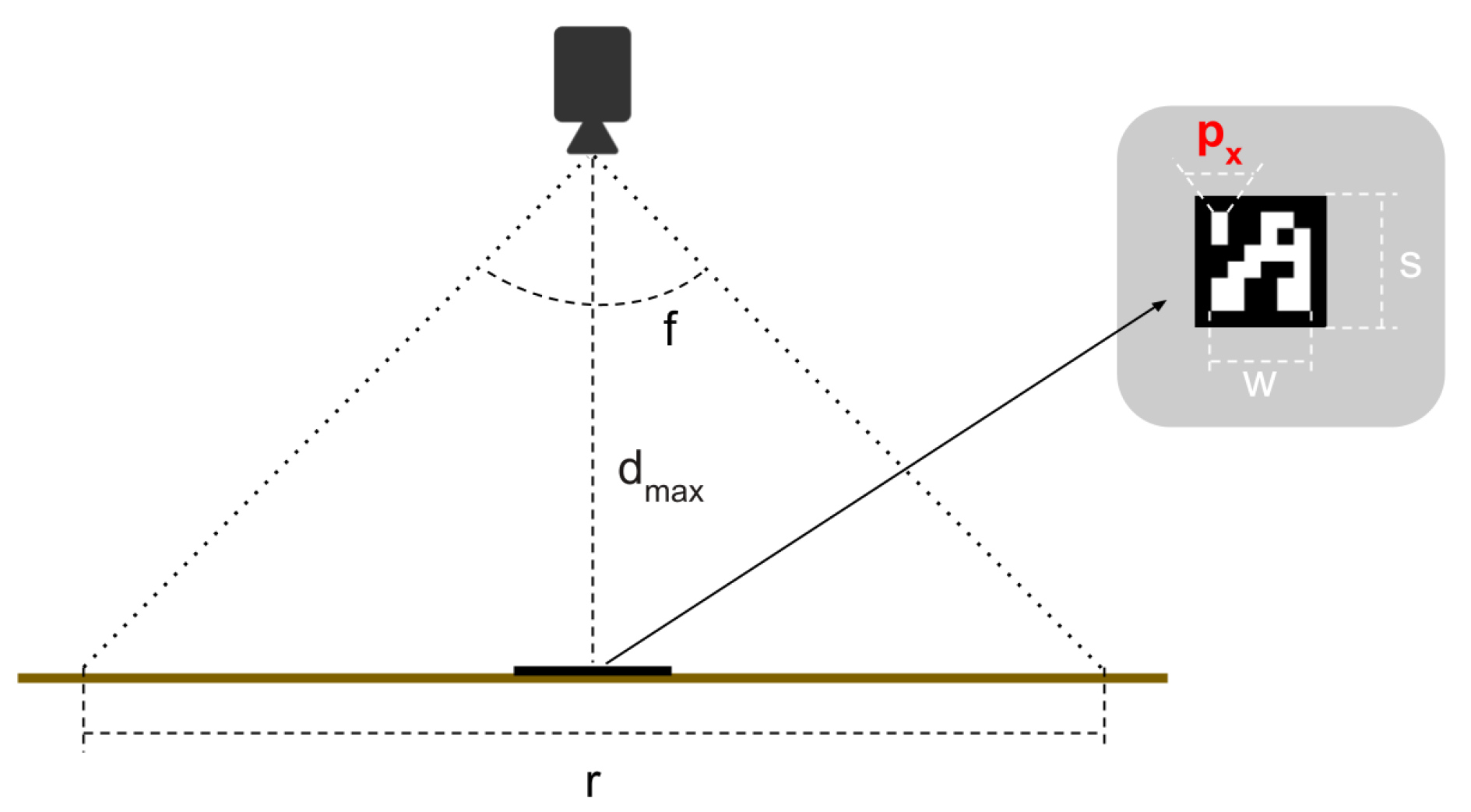
6.1. Maximum Detection Distance
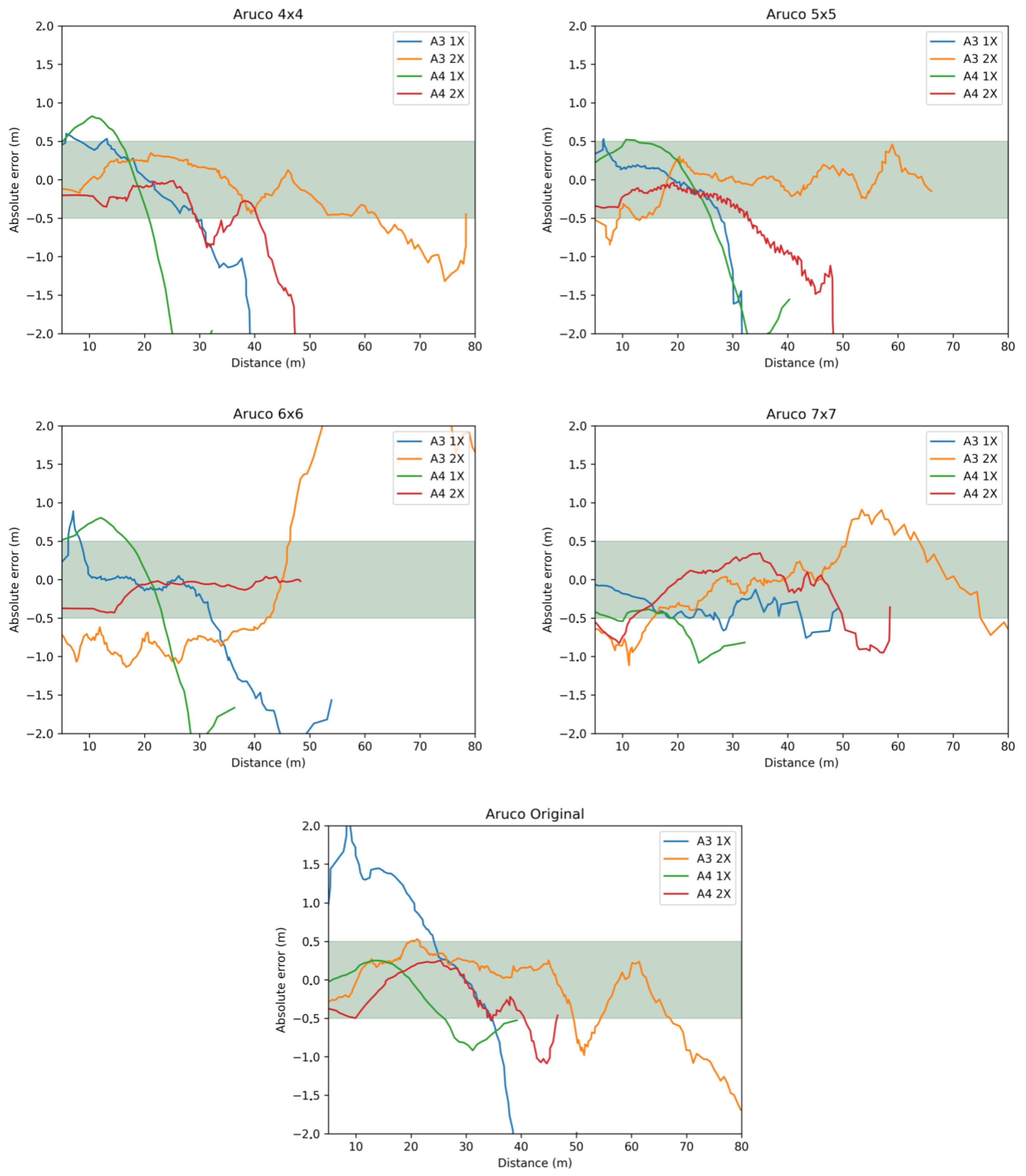
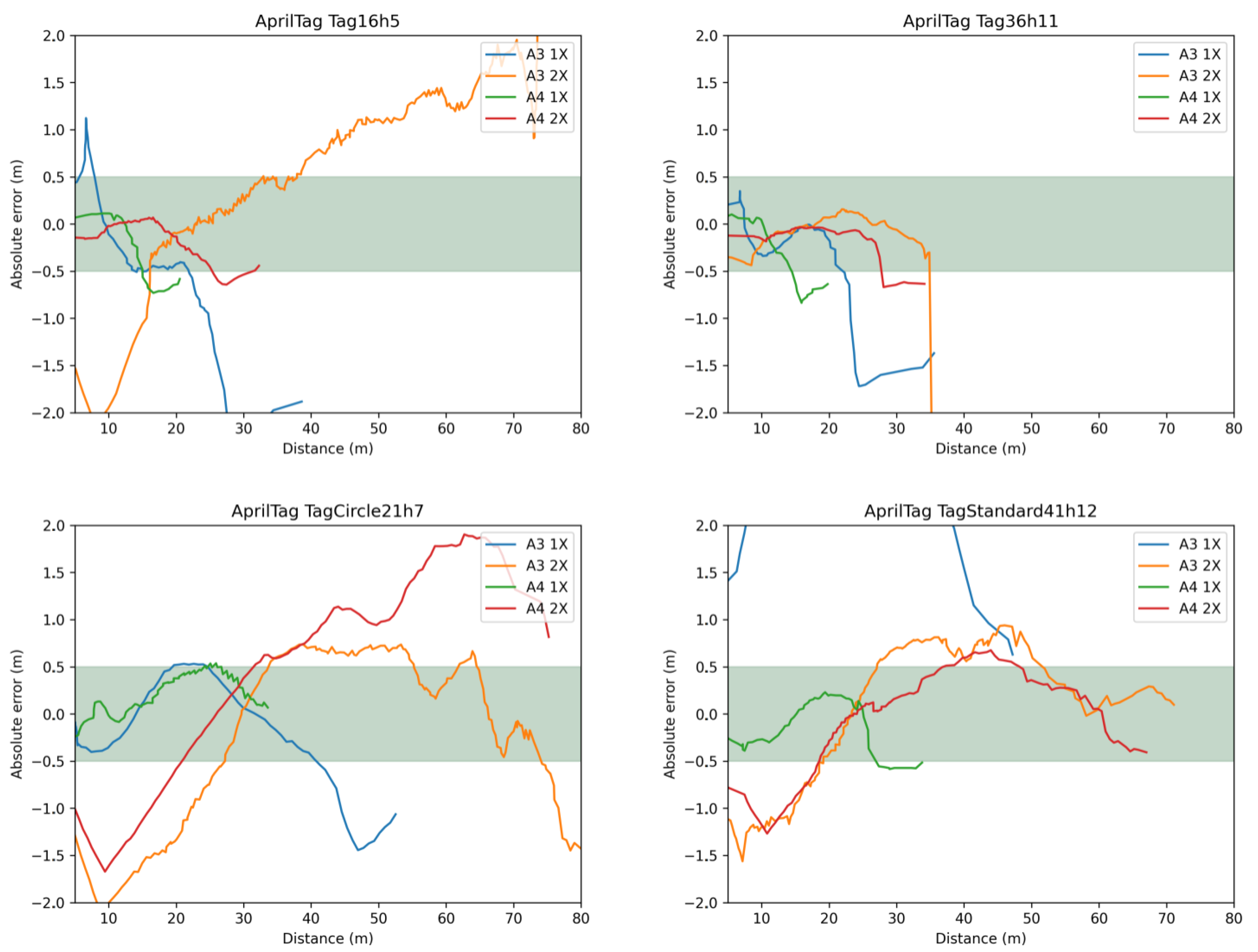
6.2. Pose Estimation Error
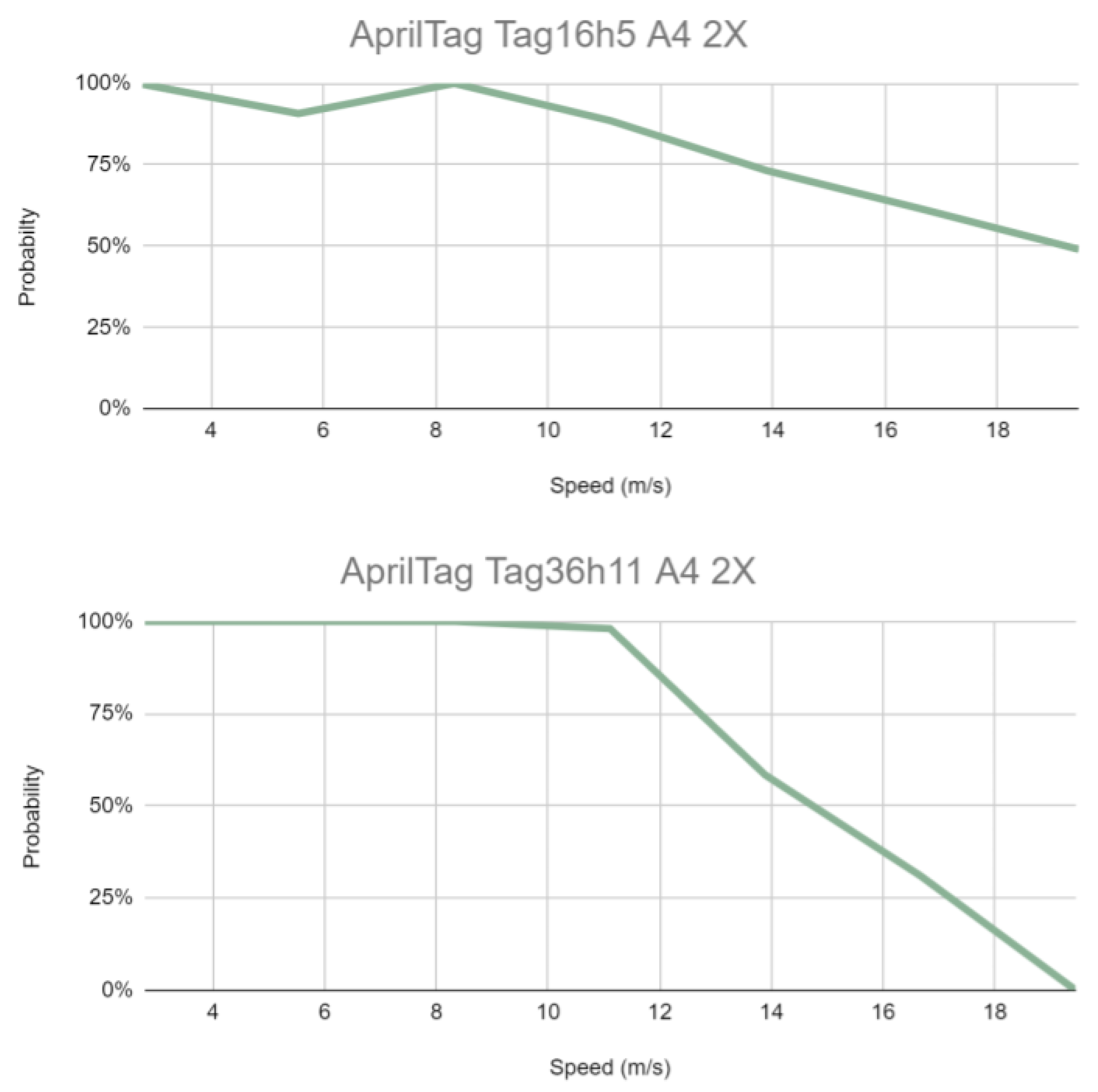
6.3. Maximum Detection Speed
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reis, J.; Marques, P.A.; Marques, P.C. Where Are Smart Cities Heading? A Meta-Review and Guidelines for Future Research. Appl. Sci. 2022, 12, 8328. [Google Scholar] [CrossRef]
- Esashika, D.; Masiero, G.; Mauger, Y. An investigation into the elusive concept of smart cities: A systematic review and meta-synthesis. Technol. Anal. Strateg. Manag. 2021, 33, 957–969. [Google Scholar] [CrossRef]
- De Nicola, A.; Villani, M.L. Smart City Ontologies and Their Applications: A Systematic Literature Review. Sustainability 2021, 13, 5578. [Google Scholar] [CrossRef]
- Giuliano, R. The Next Generation Network in 2030: Applications, Services, and Enabling Technologies. In Proceedings of the 2021 8th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), Semarang, Indonesia, 20–21 October 2021; pp. 294–298. [Google Scholar]
- Košťák, M.; Slabý, A. Designing a Simple Fiducial Marker for Localization in Spatial Scenes Using Neural Networks. Sensors 2021, 21, 5407. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.L.; Chen, Y.; Gillai, B.; Rammohan, S. Technological disruption and innovation in last-mile delivery. Value Chain. Innov. Initiat. 2016, 1–26. Available online: https://www.gsb.stanford.edu/faculty-research/publications/technological-disruption-innovation-last-mile-delivery (accessed on 12 October 2022).
- Singireddy, S.R.R.; Daim, T.U. Technology Roadmap: Drone Delivery—Amazon Prime Air. In Infrastructure and Technology Management; Springer: Cham, Switzerland, 2018; pp. 387–412. [Google Scholar]
- Lohn, A.J. What’s the Buzz? The City-Scale Impacts of Drone Delivery; Tech. Rep.; RAND Corporation: Santa Monica, CA, USA, 2017. [Google Scholar]
- Murray, C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Ha, Q.; Deville, Y.; Pham, Q.D.; Hà, M. On the mincost traveling salesman problem with drone. Transp. Res. Part C Emerg. Technol. 2018, 86, 597–621. [Google Scholar] [CrossRef]
- Tavana, M.; Khalili-Damghani, K.; Santos-Arteaga, F.J.; Zandi, M.H. Drone shipping versus truck delivery in a cross-docking system with multiple fleets and products. Expert Syst. Appl. 2017, 72, 93–107. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle routing problems for drone delivery. IEEE Trans. Syst. Man, Cybern.—Part A Syst. Humans 2016, 47, 70–85. [Google Scholar] [CrossRef]
- Stolaroff, J.K.; Samaras, C.; O’Neill, E.R.; Lubers, A.; Mitchell, A.S.; Ceperley, D. Energy use and life cycle greenhouse gas emissions of drones for commercial package delivery. Nat. Commun. 2018, 9, 1–13. [Google Scholar]
- Joerss, M.; Schrder, A.; Neuhaus, F.; Klink, C.; Mann, A.F.T. Parcel Delivery: The Future of the Last Mile; Tech. Rep. on Travel, Transport and Logistics; McKinsey & Company: New York, NY, USA, 2016. [Google Scholar]
- Guerrero, M.E.; Mercado, D.A.; Lozano, R.; García, C.D. Passivity based control for a quadrotor UAV transporting a cable-suspended payload with minimum swing. In Proceedings of the 54th IEEE Conference on Decision and Control, Osaka, Japan, 15–18 December 2015; pp. 6718–6723. [Google Scholar]
- Gatteschi, V.; Lamberti, F.; Paravati, G.; Sanna, A.; Demartini, C.; Lisanti, A.; Venezia, G. New frontiers of delivery services using drones: A prototype system exploiting a quadcopter for autonomous drug shipments. In Proceedings of the 39th IEEE Annual Computer Software and Applications Conference, Taichung, Taiwan, 1–5 July 2015; pp. 920–927. [Google Scholar]
- Brunner, G.; Szebedy, B.; Tanner, S.; Wattenhofer, R. The Urban Last Mile Problem: Autonomous Drone Delivery to Your Balcony. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 1005–1012. [Google Scholar]
- Walsh, R.; Falesch, A.J. Landing Pad for Unmanned Aerial Vehicle Delivery. U.S. Patent No. 11,117,680, 14 September 2021. [Google Scholar]
- Wheeler, D.; Wilkinson, C. From calm to storm: The origins of the Beaufort wind scale. Mar. Mirror 2004, 90, 187–201. [Google Scholar] [CrossRef]
- Alyassi, R.; Khonji, M.; Karapetyan, A.; Chau, S.C.-K.; Elbassioni, K.; Tseng, C.-M. Autonomous Recharging and Flight Mission Planning for Battery-Operated Autonomous Drones. IEEE Trans. Autom. Sci. Eng. 2022, 1–13. [Google Scholar] [CrossRef]
- Yu, G.; Hu, Y.; Dai, J. TopoTag: A Robust and Scalable Topological Fiducial Marker System. IEEE Trans. Vis. Comput. Graph. 2021, 27, 3769–3780. [Google Scholar] [CrossRef] [PubMed]
- Gu, J.; Ramamoorthi, R.; Belhumeur, P.; Nayar, S. Removing image artifacts due to dirty camera lenses and thin occluders. ACM Trans. Graph. 2009, 28, 1–10. [Google Scholar] [CrossRef]
- ArUco Marker Detection. opencv.org. Available online: https://docs.opencv.org/4.x/d9/d6a/group__aruco.html (accessed on 13 March 2022).
- Python Bindings for Apriltags v3. pupil-labs.com. Available online: https://package.wiki/pupil-apriltags (accessed on 13 March 2022).
- Kurimo, E.; Lepistö, L.; Nikkanen, J.; Grén, J.; Kunttu, I.; Laaksonen, J. The Effect of Motion Blur and Signal Noise on Image Quality in Low Light Imaging. In Proceedings of the 16th Scandinavian Conference of Image Analysis, Oslo, Norway, 15–18 June 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 81–90. [Google Scholar]

| Fiducial System | Open-Source | Language | Last Release | Families | Min. Bit |
|---|---|---|---|---|---|
| AprilTag | Y | C, Python, Matlab | 29 November 2021 | 9 | 16 |
| ARTag | N | - | - | 1 | 36 |
| ARToolKit | Y | C, Python | 21 August 2020 | 1 | - |
| ArUco | Y | C, Python | 22 December 2021 | 16 | 16 |
| BlurTag | N | - | - | 1 | - |
| CALTag | Y | Matlab | 10–21 October 2019 | 1 | 64 |
| RuneTag | Y | C | 15 March 2017 | 1 | 43 |
| System | Family | # Samples | |||
|---|---|---|---|---|---|
| Aruco | 4 × 4 | 3130 | 1908 | 95 | 1222 |
| Aruco | 5 × 5 | 3485 | 2240 | 0 | 1245 |
| Aruco | 6 × 6 | 3609 | 1855 | 0 | 1754 |
| Aruco | 7 × 7 | 3307 | 1721 | 0 | 1586 |
| Aruco | Original | 3037 | 2165 | 339 | 872 |
| AprilTag | Tag16h5 | 4722 | 4265 | 4070 | 457 |
| AprilTag | Tag36h11 | 5346 | 3252 | 0 | 2094 |
| AprilTag | TagCircle21h7 | 4712 | 3299 | 1153 | 1413 |
| AprilTag | TagStandard41h12 | 4743 | 2757 | 0 | 1986 |
| System | Family | Precision, | Recall, | Accuracy, | F-Score |
|---|---|---|---|---|---|
| Aruco | 4 × 4 | 0.95 | 0.61 | 0.59 | 0.74 |
| ArUco | 5 × 5 | 1.00 | 0.64 | 0.64 | 0.78 |
| ArUco | 6 × 6 | 1.00 | 0.51 | 0.51 | 0.68 |
| ArUco | 7 × 7 | 1.00 | 0.52 | 0.52 | 0.68 |
| ArUco | Original | 0.86 | 0.71 | 0.64 | 0.78 |
| AprilTag | Tag16h5 | 0.51 | 0.90 | 0.49 | 0.65 |
| AprilTag | Tag36h11 | 1.00 | 0.61 | 0.61 | 0.76 |
| AprilTag | TagCircle21h7 | 0.74 | 0.70 | 0.56 | 0.72 |
| AprilTag | TagStandard41h12 | 1.00 | 0.58 | 0.58 | 0.74 |
| Dataset_id | Distance (m) | Total | Found | Probability |
|---|---|---|---|---|
| 3 | 85 | 21 | 8 | 38.10% |
| 3 | 80 | 54 | 25 | 46.29% |
| 3 | 75 | 48 | 29 | 60.42% |
| 3 | 70 | 48 | 34 | 70.83% |
| 3 | 65 | 48 | 39 | 81.25% |
| 3 | 60 | 47 | 44 | 93.62% |
| 3 | 55 | 48 | 48 | 100.00% |
| 3 | 50 | 48 | 48 | 100.00% |
| Expected Value | Detected Value | Difference % | |
|---|---|---|---|
| 2×/1× ratio | 2 | 1.45 | −27.50% |
| Cloudy/Sunny ratio | 1 | 0.98 | −2.00% |
| A3/A4 ratio | 1.28 | −9.48% |
| System | Fiducial Family | Best Zoom | Best Size | (m) | |
|---|---|---|---|---|---|
| AprilTag | Tag16h5 | 2× | A3 | 106.49 | 2.26 |
| AprilTag | Tag36h11 | 2× | A3 | 57.11 | 2.74 |
| AprilTag | TagCircle21h7 | 2× | A3 | 73.64 | 1.81 |
| AprilTag | TagStandard41h12 | 2× | A3 | 71.10 | 1.81 |
| Aruco | 4 × 4 | 2× | A3 | 59.70 | 5.09 |
| Aruco | 5 × 5 | 2× | A3 | 50.82 | 4.78 |
| Aruco | 6 × 6 | 2× | A4 | 48.32 | 3.33 |
| Aruco | 7 × 7 | 2× | A3 | 81.66 | 5.26 |
| Aruco | Original | 2× | A3 | 66.94 | 4.02 |
| Family | Zoom | Size | Distance | Total | Correct | Probability |
|---|---|---|---|---|---|---|
| Original | 2× | A4 | 10 | 54 | 38 | 70.37% |
| Original | 2× | A4 | 15 | 53 | 51 | 96.23% |
| Original | 2× | A4 | 20 | 54 | 43 | 79.63% |
| Original | 2× | A4 | 25 | 48 | 26 | 54.17% |
| Original | 2× | A4 | 30 | 68 | 28 | 41.18% |
| Original | 2× | A4 | 35 | 90 | 19 | 21.11% |
| Original | 2× | A4 | 40 | 51 | 18 | 35.29% |
| Original | 2× | A4 | 45 | 70 | 17 | 24.29% |
| Expected Value | Detected Value | Difference % | |
|---|---|---|---|
| 2×/1× ratio | 2 | 2.22 | +11.00% |
| A3/A4 ratio | 1.59 | +12.43% |
| Zoom | Upper Bound (m) | (m) |
|---|---|---|
| 1× | 8.21 | 37.19 |
| 2× | 18.23 | 52.53 |
| Fiducial System | Family | Best Zoom | Best Size | Lower Bound | Upper Bound |
|---|---|---|---|---|---|
| AprilTag | Tag16h5 | 2× | A3 | 5.00 | 37.91 |
| AprilTag | Tag36h11 | 2× | A3 | 5.00 | 34.86 |
| AprilTag | TagCircle21h7 | 2× | A3 | 27.29 | 33.64 |
| AprilTag | TagStandard41h12 | 2× | A3 | 19.16 | 24.10 |
| ArUco | 4 × 4 | 2× | A3 | 5.00 | 59.70 |
| ArUco | 5 × 5 | 2× | A3 | 9.52 | 50.82 |
| ArUco | 6 × 6 | 2× | A4 | 5.00 | 48.32 |
| ArUco | 7 × 7 | 2× | A3 | 15.90 | 51.66 |
| ArUco | Original | 2× | A3 | 5.00 | 48.94 |
| Fiducial System | Fiducial Family | Conditions | (m) | Height (m) |
|---|---|---|---|---|
| AprilTag | Tag16h5 | Zoom 2×, A4 | 85.79 | 78.37 |
| AprilTag | Tag36h11 | Zoom 2×, A4 | 57.11 | 52.17 |
| Dataset_id | Speed (m/s) | Total | Found | Probability |
|---|---|---|---|---|
| 72 | 19.44 | 22 | 0 | 0.00% |
| 73 | 16.66 | 29 | 9 | 31.03% |
| 74 | 13.88 | 48 | 28 | 58.33% |
| 75 | 11.11 | 51 | 50 | 98.04% |
| 76 | 8.33 | 61 | 61 | 100.00% |
| 77 | 5.55 | 83 | 83 | 100.00% |
| 78 | 2.77 | 361 | 361 | 100.00% |
| 79 | 19.44 | 23 | 11 | 47.83% |
| 80 | 16.66 | 31 | 19 | 61.29% |
| 81 | 13.88 | 56 | 41 | 73.21% |
| 82 | 11.11 | 61 | 54 | 88.52% |
| 83 | 8.33 | 131 | 131 | 100.00% |
| 84 | 5.55 | 151 | 137 | 90.73% |
| 85 | 2.77 | 351 | 350 | 99.72% |
| AprilTag Tag16h5 | AprilTag Tag36h11 | |
|---|---|---|
| Family Size | 30 | 587 |
| Best Zoom | 2× | 2× |
| Maximum Shutter Time | 1/500 s | 1/500 s |
| Best Marker Size | A3 | A3 |
| Maximum Detection Distance | 106.49 m | 57.11 m |
| Pose Estimation Upper Bound | 37.91 m | 34.86 m |
| Maximum Detection Speed | 10.75 m/s | 11.67 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Innocenti, E.; Agostini, G.; Giuliano, R. UAVs for Medicine Delivery in a Smart City Using Fiducial Markers. Information 2022, 13, 501. https://doi.org/10.3390/info13100501
Innocenti E, Agostini G, Giuliano R. UAVs for Medicine Delivery in a Smart City Using Fiducial Markers. Information. 2022; 13(10):501. https://doi.org/10.3390/info13100501
Chicago/Turabian StyleInnocenti, Eros, Giacomo Agostini, and Romeo Giuliano. 2022. "UAVs for Medicine Delivery in a Smart City Using Fiducial Markers" Information 13, no. 10: 501. https://doi.org/10.3390/info13100501
APA StyleInnocenti, E., Agostini, G., & Giuliano, R. (2022). UAVs for Medicine Delivery in a Smart City Using Fiducial Markers. Information, 13(10), 501. https://doi.org/10.3390/info13100501








