Abstract
In the present work, an integrated coastal engineering numerical model is presented. The model simulates the linear wave propagation, wave-induced circulation, and sediment transport and bed morphology evolution. It consists of three main modules: WAVE_L, WICIR, and SEDTR. The nearshore wave transformation module WAVE_L (WAVE_Linear) is based on the hyperbolic-type mild slope equation and is valid for a compound linear wave field near coastal structures where the waves are subjected to the combined effects of shoaling, refraction, diffraction, reflection (total and partial), and breaking. Radiation stress components (calculated from WAVE_L) drive the depth averaged circulation module WICIR (Wave Induced CIRculation) for the description of the nearshore wave-induced currents. Sediment transport and bed morphology evolution in the nearshore, surf, and swash zone are simulated by the SEDTR (SEDiment TRansport) module. The model is tested against experimental data to study the effect of representative coastal protection structures and is applied to a real case study of a coastal engineering project in North Greece, producing accurate and consistent results for a versatile range of layouts.
1. Introduction
Nowadays, numerical models are the main tool for engineers involved in the design of coastal and marine structures. There are numerous examples in relevant literature of more or less advanced models, covering various aspects of wave-, hydro-, and morpho-dynamics from deep water to the nearshore, at different scales and at varying levels of detail [1,2,3,4,5,6,7,8]. However, coastal engineering practice requires robust integrated models that are able to represent in a reliable way the full range of processes governing coastal dynamics, including the effect of the presence of structures, while maintaining the computational effort needed at reasonable levels. Model versatility should also be considered as an essential requirement, since such models should be able to be adapted to a wide range of design layouts and perform satisfactorily for an equally wide range of field conditions.
For a long time, the design of coastal protection structures was essentially based on engineering experience and empirical rules. Such approaches were gradually replaced by models of varying complexity, focusing on the structures’ effects on wave dynamics, circulation patterns, and morphological evolution in coastal areas. Morphodynamic processes are among the most complex ones to accurately reproduce, since they depend on the combined effect of waves and currents, whose interaction becomes increasingly complicated when moving within the breaker zone and towards the swash. Morphological evolution modelling has indeed come a long way throughout the years, from simple conceptual models to fully 3D ones, currently encompassing a series of improvements in our understanding of the involved processes. Regarding relevant literature (on the more advanced 2D horizontal, quasi-3D, and 3D models), one may indicatively refer to: pioneering [9] and more recent works [10,11,12] on bed morphology evolution due to the presence of detached breakwaters, studies on the morphological effects of groins and groin systems [13,14], and more complete/inclusive works on modelling coastal morphodynamics in the presence of coastal structures [15,16,17,18]. Focusing on the main features that separate similar integrated modelling attempts, one could refer to: (a) Model capabilities to represent the effects of various types of structures on coastal dynamics; (b) the representation of swash zone dynamics; and (c) the approaches and formulae used to calculate bed load and suspended load sediment transport.
In this work, an integrated coastal engineering numerical model—developed by the authors—is presented and described in detail. The model consists of three main modules that simulate: linear wave propagation (i.e., WAVE_L), wave-induced circulation (i.e., WICIR), and sediment transport along with bed morphology evolution (i.e., SEDTR). The model is capable of simulating the presence of various types of structures (vertical structures; groins and groin systems; emerged, submerged, and floating breakwaters) and includes a novel approach for the representation of swash zone hydrodynamics, while sediment transport is modelled based on the formula proposed by Camenen and Larson [19,20]. The model is tested against experimental data to study the effect of representative coastal protection structures [21,22], and—given the good agreement between calculated results and measured data—is afterwards applied to a real case study of a coastal engineering project in North Greece (combination of submerged breakwaters and beach nourishment).
2. Model Description
2.1. Nearshore Wave Transformation Module–WAVE_L
Linear wave propagation is simulated by applying a mild-slope model [23,24], derived without the assumption of progressive waves. The module WAVE_L is based on the hyperbolic-type mild slope equation and is valid for a compound wave field near coastal structures where waves are subjected to the combined effects of shoaling, refraction, diffraction, reflection (total and partial), and breaking. The module consists of the following pair of equations [23,24]:
where η is the surface elevation; Uw is the mean velocity vector Uw = (Uw, Vw); d is the depth, Qw = Uwhw = (Qw, Pw); hw is the total depth (hw = d + η); c is the celerity; and cg is the group velocity (cg = (gd)0.5). The term νh is a horizontal eddy viscosity coefficient introduced in order to include breaking effects based on the formulation of [25]:
In Equation (3), D is the dissipation of wave energy expressed as:
where Hm is the maximum wave height; ρ is the water density; f is the wave frequency; and Qb is the probability of a wave breaking at a certain depth, expressed as (1 − Qb)/(lnQb) = (Hrms/Hm)2 according to [26]. The mean square wave height Hrms is calculated from Hrms = 2(<2η2>)1/2, with the brackets denoting a time-mean quantity. It should be noted that—since linear wave models are not capable of describing waves in the swash zone—in WAVE_L, the water depth from the rundown point (i.e., depth equal to R/4; R is the runup height) and up to the runup point (i.e., depth equal to −R) is considered to be constant and equal to R/4.
WAVE_L is adapted for engineering applications based on the following:
- The input wave is introduced at a line inside the computational domain according to [27],[28].
- A sponge layer boundary condition is used to absorb the outgoing waves at the four sides of the domain [27].
- The presence of vertical structures is incorporated by introducing a total reflection boundary condition (Uw = (Uw. Vw) = 0 normal to the boundary, where Uw is the mean velocity vector; for a rectilinear grid, the above is equivalent to Uw = 0 or Vw = 0).
- Partial reflection is also simulated, by introducing an artificial eddy viscosity coefficient νh. The values of νh are estimated from the method developed by Karambas and Bowers [29], using the reflection coefficient values proposed by Bruun [30].
- The presence of submerged structures is incorporated as in [31].
- The presence of floating structures is incorporated as in [32].
The numerical solution is based on the well-documented explicit second order finite difference staggered scheme using a mid-time method [24].
2.2. Wave-Induced Circulation Module—WICIR
The depth and shortwave-averaged 2D continuity and momentum equations are used for simulating nearshore currents in the coastal zone. They are expressed as:
where Sxx, Syy, and Sxy are the radiation stresses; h = d + ζ (ζ being the mean water elevation); U and V are the depth-averaged current velocities; and τbx and τby are the bottom shear stresses. Based on linear wave theory, Copeland [33] derived the equations for radiation stresses (Sij) without the typical assumption of progressive waves, expressed as:
where k is the wave number and the brackets denote time-mean quantities.
In nearshore circulation models, the treatment of the bottom stress is critical. The bottom shear stresses τb = (τbx, τby) in WICIR are calculated based on the formulae proposed by Kobayashi et al. [34]:
where fb is the bottom friction factor, σT is the standard deviation of the oscillatory horizontal velocity, and |U| = (U2 + V2)0.5.
Since it acts as the “link” between WAVE_L and SEDTR in the framework of the proposed integrated model, it is important for WICIR to be able to reproduce a number of processes that are essential for the realistic description of sediment transport.
Regarding the surf zone, it should be noted that the existence of the undertow (i.e., the current directed offshore) cannot be directly predicted by depth-averaged models; nonetheless, its representation is essential in the aforementioned context. In WICIR, quasi-3D effects are introduced by adopting the analytical expression for the vertical distribution of the cross-shore flow below the wave trough level proposed by Stive and Wind [35], expressed as:
where νu is the undertow velocity in the direction normal to the shore, ξ = z/(h − ζt), h = d + ζ (ζ being the mean water elevation), ζt is the wave trough level, dR/dy = 0.14ρgdh/dy, τs is the shear stress at the wave trough level, M is the wave mass flux above trough level (including surface roller effects), Θ is the direction of wave propagation (Θ = arctan[(<Qw2>/<Pw2>)1/2]), and ντ is the eddy viscosity coefficient according to De Vriend and Stive [36]:
Regarding the swash zone, an essential process for shoreline evolution is longshore sediment transport. For obliquely incident waves, the trajectory of the bore-front follows a parabolic movement in the swash, in the direction of the net longshore flow per wave period. The mean longshore transport velocity VR at the shoreline is determined according to Baba and Camenen [37] as:
where R is the runup height (R = 1.6H0ξ0, where H0 is the deep water wave height and ξ0 is the Iribarren number) and Θ is the wave direction near the rundown point at depth d = R/4. The longshore velocity VR is presumed constant within the swash zone, the width of which is considered as extending from d = R/4 (i.e., the rundown point) to d = −R. The above velocity is indirectly introduced in the model by increasing the radiation stresses in the swash zone, based on the rationale described in the following. Longshore velocity can be expressed analytically by:
where γ is the breaking index, and db and αb are the water depth and incident wave angle at the breaking point, respectively. Assuming a linear variation of , the velocity at the shoreline can be approximated as:
where ds is the water depth at the shoreline. A comparison of Equation (20) to Equation (22) shows that the square of the ratio does not deviate significantly from an empirical factor, as, expressed as:
where ξ0 is the Iribarren number, and H0 and L0 are the wave height and wavelength, respectively, for deep water conditions. Accordingly, the aforementioned increase in radiation stresses in the swash zone is achieved by multiplying them by the factor as.
Finally, regarding flooding due to wave setup, in WICIR, this process is simulated using the “dry bed” boundary condition which, according to Militello et al. [38], can be written as the following set of pairs of conditions for any given grin point (i,j):
- if (d + ζ)i,j > hcr and (d + ζ)i − 1,j ≤ hcr and Ui,j > 0 → Ui,j = 0
- if (d + ζ)i,j > hcr and (d + ζ)i,j − 1 ≤ hcr and Vi,j > 0 → Vi,j = 0
- if (d + ζ)i,j ≤ hcr and (d + ζ)i − 1,j ≤ hcr → Ui,j = 0
- if (d + ζ)i,j ≤ hcr and (d + ζ)i,j − 1 ≤ hcr → Vi,j = 0
- if (d + ζ)i,j ≤ hcr and (d + ζ)i − 1,j > hcr and Ui,j < 0 → Ui,j = 0
- if (d + ζ)i,j ≤ hcr and (d + ζ)i,j − 1 > hcr and Vi,j < 0 → Vi,j = 0
where ζ is the mean water surface elevation and hcr is a terminal depth below which drying is assumed to occur (e.g., in WICIR this depth is set to hcr = 0.001 m).
The numerical solution in WICIR is also (as in WAVE_L) based on the explicit second order finite difference staggered scheme using a mid-time method [24].
2.3. Sediment Transport Module—SEDTR
The mode of sediment movement on the coast is usually divided into bed load, suspended load, and sheet flow transport. Different model concepts are being presently used for the prediction of each one, which range from empirical transport formulae to more sophisticated bottom boundary layer models. In the present work, bed load transport (qb) is estimated with a quasi-steady, semi-empirical formulation, developed by Camenen, and Larson [19,20] for an oscillatory flow combined with a superimposed current under an arbitrary angle:
where the subscripts w and n correspond, respectively, to the wave direction and the direction normal to the wave direction; s (= ρs/ρ) is the relative density between the sediment (ρs) and water (ρ); g is the acceleration due to gravity; d50 is the median grain size; aw, an, and b are empirical coefficients; θcw,m and θcw are the mean and maximum Shields parameters due to the wave-current interaction, respectively; θcn is the current-related Shields parameter in the direction normal to the wave direction, and θcr is the critical Shields parameter for the inception of transport. The net Shields parameter θcw,net in Equation (24) is given by:
where θcw,on and θcw,off are the mean values of the instantaneous Shields parameter over the two half “periods” Twc (crest-onshore) and Twt (trough-offshore), αpl,b is a coefficient for the phase-lag effects [19], and αα is a coefficient for the acceleration effects [39]. The Shields parameter θcw is defined by:
with Ucw being the wave and current velocity and fcw the friction coefficient taking into account the wave and current interaction, while the subscript j should be replaced either by onshore or offshore. In the above formulation (since linear wave theory cannot be used), the estimation of nonlinear time-varying near-bottom wave velocities is also needed. For the incorporation of nonlinear velocity characteristics (i.e., skewness and asymmetry) in SEDTR, the parameterisation proposed by Isobe and Horikawa [40] is adopted.
The incorporation of the suspended sediment transport rate in SEDTR is done by solving the depth-integrated transport equation for suspended sediment [41,42]:
where h is the total mean depth, C is the depth-averaged volumetric sediment concentration, cR is the reference concentration at the bottom [19], ws is the sediment fall velocity, and βd is a coefficient calculated based on [20] by:
with ε being the sediment diffusivity (related to the eddy viscosity coefficient), estimated by [36]:
Cross-shore sediment transport in the swash zone in SEDTR is calculated according to [43], while for the longshore sediment transport, only the increased mean velocity is taken into account, as described in Section 2.2.
These sediment transport rates are then used for the simulation of the coastal bathymetry changes by the module SEDTR. The methodology adopted for the series of model applications can be encoded into the steps described in the following. First, the initial bathymetry is inserted into the wave and wave-induced circulation modules (WAVE_L and WICIR, respectively) in order to estimate the wave and current fields. These fields are afterwards used by the sediment transport module SEDTR to calculate the sediment transport rates. Finally, bathymetry is updated by SEDTR solving the equation of the conservation of sediment transport (for the previously calculated transport rates; [44]). The procedure is repeated for a user-specified time period or until a state of morphologic equilibrium is reached. The aforementioned repetitions take place after bottom change in the order of 10–15% is observed in the field, so that the changes in wave and wave-induced current fields calculated by WAVE_L and WICIR for the updated bathymetry are significant.
3. Model Applications
3.1. Comparison with Experimental Data
The integrated numerical model was set-up and applied in order to reproduce the small-scale laboratory experiments of: (a) Ming and Chiew [21], who studied the shoreline changes caused by the presence of a detached breakwater under the influence of pure wave action; and (b) Badiei et al. [22], who studied the morphological effects of groins on an initially straight beach exposed to oblique irregular waves.
The experiments of Ming and Chiew [21] were conducted in a 10 m long, 5 m wide, and 0.7 m high wave basin. A plunger-type wavemaker was used to generate monochromatic waves and sponge was placed behind the wavemaker in order to minimize wave reflection. The 6 m long beach consisted of uniformly distributed sand with a median grain size of d50 = 0.25 mm. The duration of the tests was approximately 15 h (which was the duration needed for the beach to reach an equilibrium state). Three different cases were reproduced numerically and are presented in the following, for normally incident waves of H0 = 0.05 m deep water wave height and T = 0.85 s wave period. The test cases, presented in Table 1, differed in breakwater length (B) and breakwater distance from the initial shoreline (X), in order to cover a wide range of B/X ratios resulting in both tombolo and salient formation behind the breakwaters.

Table 1.
Test conditions for the numerically reproduced experiments of Ming and Chiew [21].
Baidei et al. [22] employed a series of mobile bed process models (according to [45]) in order to investigate the impact of groins on nearshore morphology under the attack of obliquely incident random waves. Two series of tests were carried out at the Queen’s University Coastal Engineering Laboratory (QUCERL) and the Hydraulic Laboratory of the National Research Council of Canada (NRCC). The physical model regarded an initially plane sloping beach (1:10 slope), composed of D50 = 0.12 mm sand grains. The beach—without the presence of the groins—was exposed to wave action for a duration of 4 h until the formation of a nearly stable bathymetry (clear offshore bar trough/step formation). The installation of the groins followed, and the tests continued thereafter in 2 h cycles. In this work, the case of a single groin was modelled, exposed to waves of Hs0 = 0.08 m deep water significant wave height, Tp = 1.15 s peak period, and θ0 = 11.6° deep water incident wave angle, for a total duration of 12 h after groin installation (Test NT2, NRCC test series).
3.2. Application to Paralia Katerinis Beach (Greece)—Coastal Protection with Submerged Breakwaters
Following its validation for laboratory experiments, the presented integrated model was applied to a real case study of a coastal engineering project regarding the protection of a beach by using detached submerged breakwaters. The study area is located in the Region of Central Macedonia, Greece, at a sandy beach north of the fishing port of Katerini (Figure 1). The area has been facing coastal erosion problems for well over 30 years, which started after the construction of the harbour seen in the left part of Figure 1 (1980–1984). As a result, and due to the prevailing SE winds, the coastal zone south of the fishing port showed strong accretion, while the coast north from the port was eroded, with a shoreline retreat in the order of 20 m; the erosive phenomena stretched over a zone of 800 m north from the port. In order to reverse erosion, a groin field consisting of 13 rubble mount groins was constructed (1990–1997). The project not only failed to further protect the beach—since additional erosion occurred in between the constructed groins—but it also transferred coastal retreat northwards. Furthermore, the semi-closed basins that formed between the constructed groins (being in the non-tidal Mediterranean Sea) caused significant environmental problems regarding water quality due to the limited renewal rates. In 2010, a new coastal protection project was designed and constructed; the groin field was replaced by a set of three 200 m long submerged breakwaters placed at a distance of approximately 200 m from the coast, and the gaps between the structures were approximately 110 m. The breakwaters were designed to have transmission coefficients in the order of 0.4 (Kt ≈ 0.4). In addition, a beach nourishment project was also designed and applied to restore the beach to its previous condition. Bathymetry measurement data for the area are available for the period right after the completion of coastal works (beach nourishment and construction of the submerged breakwaters), as well as for three years later [46].

Figure 1.
Location and satellite image of the study area at Paralia Katerinis, Greece ([47]; privately processed).
The integrated model was applied to simulate coastal morphodynamics after the realization of the coastal protection project. Since wave data were not available for the area, hindcast data were used. The main incident wind directions are: NE, E, and SE-S. The model was run by applying three representative waves (i.e., three equivalent wave heights on an annual basis; see Table 2). The workflow for the coupled module runs can be summed-up in the following. Starting with the initial bathymetry, WAVE_L, WICIR and SEDTR modules were run in sequence for the characteristics of the first representative wave and taking into account its annual frequency of occurrence for the simulation of morphology evolution. The updated bed morphology was then used to run the integrated model for the second representative wave (in the same way) and the morphology at the end of this second run for the third representative wave. The aforementioned simulation steps were repeated until the total duration of the wave action was reached.

Table 2.
Characteristics of the three representative waves used for the Paralia Katerinis beach runs.
4. Results and Discussion
4.1. Comparison with Experimental Data
Figure 2 shows the initial wave-induced current velocity field and the comparison between the computed and measured shoreline evolution data for Test 11 of Ming and Chiew [21]. The presence of the breakwater leads to the formation of two opposing eddies in the area behind it, as currents move towards the sheltered area along the foreshore from both sides of the structure. A secondary cause of the observed circulation pattern is the mean sea level gradient between the illuminated and sheltered areas due to diffraction effects, while the representation of swash zone hydrodynamics by the model should also be highlighted (see also Section 2.2). Regarding morphology evolution, the model results are in good agreement with the measured data of Ming and Chiew [21], satisfactorily representing the formation of the tombolo in Test 11 (Figure 2b), as well as the formation of the tombolo and salient in Tests 3 (Figure 3a) and 10 (Figure 3b), respectively.
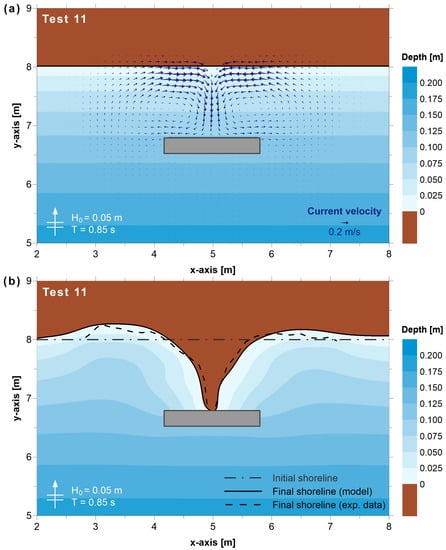
Figure 2.
(a) Initial wave-induced current velocity field (contours represent the initial bathymetry) and (b) comparison between the computed and measured shoreline evolution (contours represent the final computed bathymetry) for Test 11 of Ming and Chiew [21].
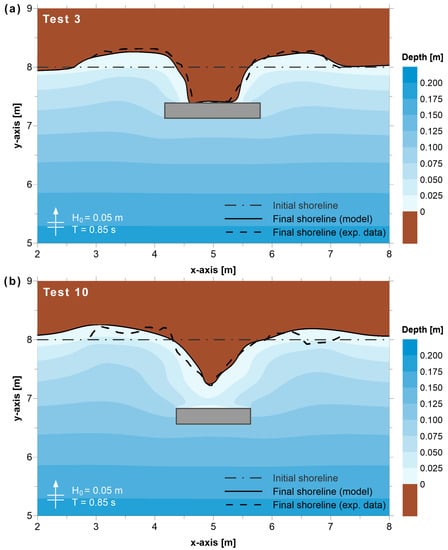
Figure 3.
Comparison between the computed and measured shorelines evolution (contours represent the final computed bathymetry) for: (a) Test 3 and (b) Test 10 of Ming and Chiew [21].
Figure 4 shows the initial breaking wave-induced current velocity field and the comparison between the computed and measured shoreline evolution for the single groin test (Test NT2) of Baidei et al. [22]. The sediment accretion updrift of the groin-type structure results in an advance of the shore, while the lack of sediments at the lee of the groin leads to a retreat of the shore; shoreline evolution is well-reproduced, with model results and measurement lines practically overlapping.
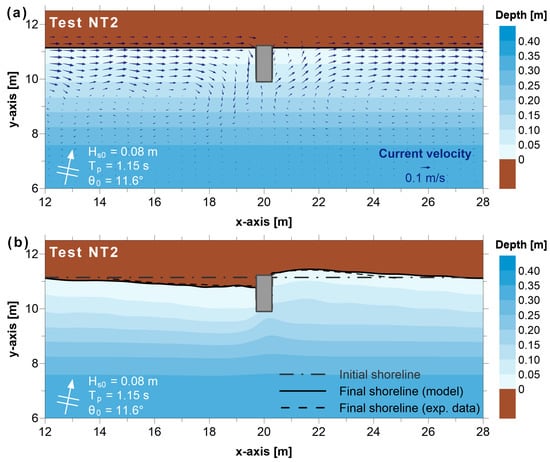
Figure 4.
(a) Initial breaking wave-induced current velocity field (contours represent the initial bathymetry) and (b) comparison between the computed and measured shoreline evolution (contours represent the final computed bathymetry) for Test NT2 of Baidei et al. [22].
In general, the integrated model results in smooth but consistent (considering also test runs that are not presented in this work) bathymetries behind detached breakwaters and in the vicinity of groin-type structures, while it appears to be smoothing in a close-to-natural way eventual local shoreline irregularities which, on the other hand, are present in the experimental results.
4.2. Application to Paralia Katerinis Beach (Greece)—Coastal Protection with Submerged Breakwaters
Figure 5 shows the breaking wave-induced current field for the prevailing SE-S waves. The submerged breakwaters allow some wave transmission and overtopping that cause an additional supply of water behind the structures, which is taken into account by the circulation module and affects the current field. This net transport of water into the lee zone causes a water level rise and is balanced mainly by outgoing currents at the heads of the structures. Consequently, the main flow pattern is characterized by an onshore flow over the submerged breakwaters, an offshore flow at the gaps between them (eroding rip currents), and nearshore eddies similar to those formed in the case of emerged breakwaters (although with lower relative intensity). The first two flow patterns do not exist in the latter case, while the third flow pattern is not extended up to the structures, where onshore flow leads to the formation of—more intense—opposite direction eddies.
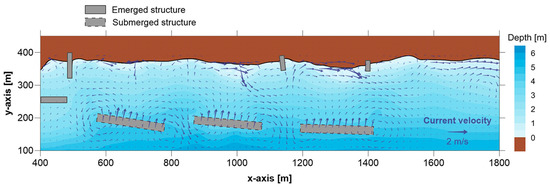
Figure 5.
Breaking wave-induced current field for the prevailing SE waves at Paralia Katerinis beach (Greece) after the construction of the detached submerged breakwaters.
Figure 6 shows the initial bed morphology of Paralia Katerinis beach and the comparison between the computed and measured bed morphology evolution, along with the satellite image of the same area (2016). The workflow for the coupled module runs is described in Section 3.2. The model results are in close agreement with the measurements (respective lines are practically overlapping), with the integrated model succeeding in reproducing all morphological patterns behind the breakwaters and up to the shoreline, under the presence of both permanent structures (emerged groins) and the realized beach nourishment project there.
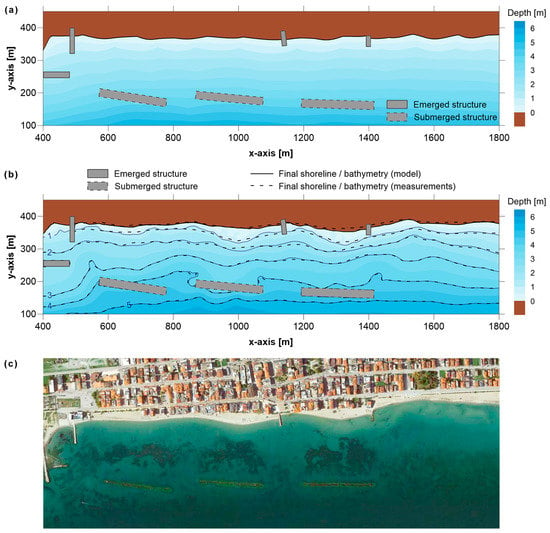
Figure 6.
(a) Initial bed morphology of Paralia Katerinis beach, (b) comparison between the computed and measured bed morphology evolution, and (c) satellite image of the same area ([47]; privately processed).
4.3. General Discussion
Elaborating further on the integrated model’s performance in simulating the morphological effects of the presence of coastal protection structures, particular insights can be drawn by the discussion in the following.
Model setup was based on the successful model calibration for the experimental data presented in this work (see Section 3.1 and Section 4.1), along with specific modelling choices based on extensive experience in morphological modelling for both research and engineering applications. The calibration process of the presented model mainly refers to: (a) swash zone incorporation, i.e., the introduction of coefficient as (see Equation (23)) and the region of its application (i.e., the swash zone as defined in Section 2.2); (b) the use of the bottom friction formulae proposed by Kobayashi et al. [34]; and (c) the use of the Camenen and Larson [19,20] formulae for the calculation of bed and suspended load (instead of other approaches).
The satisfactory agreement between model predictions and experimental/field data should be mainly attributed to the above choices, which are deemed to distinguish the presented model from relevant work. The novelty of incorporating swash zone hydrodynamics using a linear wave model and a nonlinear wave-induced circulation model particularly allows for the simulation of swash zone morphodynamics which play an essential role in nearshore morphology evolution. The above, keeping in mind that the objective of this work was to present an integrated model that could be adapted to a wide range of design layouts and perform satisfactorily for an equally wide range of field conditions, while maintaining the computational effort needed at reasonable levels, an aspect that usually limits the applicability of more complex models in engineering applications.
5. Conclusions
This work presents an integrated coastal engineering numerical model that simulates linear wave propagation, wave-induced circulation, sediment transport, and bed morphology evolution. The model consists of three main modules: The nearshore wave transformation model WAVE_L, properly adapted for the simulation of compound linear wave fields near coastal structures; the wave-induced circulation module WICIR, which includes a novel approach for the representation of swash zone hydrodynamics; and the sediment transport and bed morphology evolution module SEDTR.
The model is tested against experimental data to study the effect of representative coastal protection structures, such as detached breakwaters (data from [21]) and groins (data from [22]). Given the good agreement between model results and laboratory measurements, the model was also successfully applied to a real case study of a coastal engineering project in North Greece (combination of submerged breakwaters and beach nourishment). The model is deemed to constitute a suitable tool for the design and evaluation of the morphological influence of harbour and coastal protection works, being able to deliver results in a fast and seamless way at all times for a wide range of design layouts.
Acknowledgments
The authors would like to thank the anonymous reviewers for their constructive comments and suggestions.
Author Contributions
T.V.K. and A.G.S. collaboratively developed the presented integrated numerical model, conceived and designed this work, performed the numerical simulations for the model runs, and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References and Note
- Rakha, K.A. A Quasi-3D phase-resolving hydrodynamic and sediment transport model. Coast. Eng. 1998, 34, 277–311. [Google Scholar] [CrossRef]
- Karambas, T.V.; Koutitas, C. Surf and swash zone morphology evolution induced by nonlinear waves. J. Waterw. Port Coast. Ocean Eng. 2002, 128, 102–113. [Google Scholar] [CrossRef]
- Karambas, T.V.; Karathanassi, E.K. Longshore sediment transport by nonlinear waves and currents. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 277–286. [Google Scholar] [CrossRef]
- Karambas, T.V. Prediction of sediment transport in the swash-zone by using a nonlinear wave model. Cont. Shelf Res. 2006, 26, 599–609. [Google Scholar] [CrossRef]
- Karambas, T.V.; Samaras, A.G. Soft shore protection methods: The use of advanced numerical models in the evaluation of beach nourishment. Ocean Eng. 2014, 92, 129–136. [Google Scholar] [CrossRef]
- Gallerano, F.; Cannata, G.; De Gaudenzi, O.; Scarpone, S. Modeling bed evolution using weakly coupled phase-resolving wave model and wave-averaged sediment transport model. Coast. Eng. J. 2016, 58, 58. [Google Scholar] [CrossRef]
- Gallerano, F.; Cannata, G.; Lasaponara, F. A new numerical model for simulations of wave transformation, breaking and long-shore currents in complex coastal regions. Int. J. Numer. Methods Fluids 2016, 80, 571–613. [Google Scholar] [CrossRef]
- Klonaris, G.T.; Memos, C.D.; Drønen, N.K.; Deigaard, R. Boussinesq-type modeling of sediment transport and coastal morphology. Coast. Eng. J. 2017, 59, 59. [Google Scholar] [CrossRef]
- Watanabe, A.; Maruyama, K.; Shimizu, T.; Sakakiyama, T. Numerical prediction model of three-dimensional beach deformation around a structure. Coast. Eng. J. 1986, 29, 179–194. [Google Scholar]
- Nicholson, J.; Broker, I.; Roelvink, J.A.; Price, D.; Tanguy, J.M.; Moreno, L. Intercomparison of coastal area morphodynamic models. Coast. Eng. 1997, 31, 97–123. [Google Scholar] [CrossRef]
- Zyserman, J.A.; Johnson, H.K. Modelling morphological processes in the vicinity of shore-parallel breakwaters. Coast. Eng. 2002, 45, 261–284. [Google Scholar] [CrossRef]
- Postacchini, M.; Russo, A.; Carniel, S.; Brocchini, M. Assessing the hydro-morphodynamic response of a beach protected by detached, impermeable, submerged breakwaters: A numerical approach. J. Coast. Res. 2016, 32, 590–602. [Google Scholar] [CrossRef]
- Roelvink, J.A.; Uittenbogaard, R.E.; Liek, G.J. Morphological modelling of the impact of coastal structures. In Coastal Structures ‘99, Proceedings of the International Conference Coastal Structures ‘99, Santander, Spain, June 1999; Losada, I.J., Balkema, A.A., Eds.; CRC Press: Boca Raton, FL, USA, 2000; pp. 865–871. [Google Scholar]
- Johnson, H.K. Coastal area morphological modelling in the vicinity of groins. In Proceedings of the 29th International Conference on Coastal Engineering, Lisbon, Portugal, 19–24 September 2004; pp. 2646–2658. [Google Scholar]
- Ding, Y.; Wang, S.Y.; Jia, Y. Development and validation of a quasi-three-dimensional coastal area morphological model. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 462–476. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, S.S.Y. Development and application of a coastal and estuarine morphological process modeling system. J. Coast. Res. 2008, 127–140. [Google Scholar] [CrossRef]
- Leont’yev, I.O. Modelling of morphological changes due to coastal structures. Coast. Eng. 1999, 38, 143–166. [Google Scholar] [CrossRef]
- Nam, P.T.; Larson, M.; Hanson, H.; Hoan, L.X. A numerical model of beach morphological evolution due to waves and currents in the vicinity of coastal structures. Coast. Eng. 2011, 58, 863–876. [Google Scholar] [CrossRef]
- Camenen, B.; Larson, M. A Unified Sediment Transport Formulation for Coastal Inlet Application; ERDC/CH: CR-07-1; US Army Corps of Engineers, Engineering Research and Development Center: Vicksburg, MS, USA, 2007; p. 247. [Google Scholar]
- Camenen, B.; Larson, M. A general formula for noncohesive suspended sediment transport. J. Coast. Res. 2008, 24, 615–627. [Google Scholar] [CrossRef]
- Ming, D.; Chiew, Y. Shoreline changes behind detached breakwater. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 63–70. [Google Scholar] [CrossRef]
- Badiei, P.; Kamphuis, J.; Hamilton, D. Physical experiments on the effects of groins on shore morphology. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; pp. 1782–1796. [Google Scholar]
- Copeland, G.J.M. A practical alternative to the “mild-slope” wave equation. Coast. Eng. 1985, 9, 125–149. [Google Scholar] [CrossRef]
- Watanabe, A.; Maruyama, K. Numerical modelling of nearshore wave field under combined refraction, diffraction and breaking. Coast. Eng. Japan 1986, 29, 19–39. [Google Scholar]
- Battjes, J.A. Modelling of turbulence in the surf zone. In Proceedings of the Symposium on Modelling Techniques, San Francisco, CA, USA, 3–5 September 1975; ASCE: San Francisco, CA, USA, 1975; pp. 1050–1061. [Google Scholar]
- Battjes, J.A.; Janssen, J.P.F.M. Energy loss and set-up due to breaking of random waves. In Proceedings of the 16th International Conference on Coastal Engineering, Hamburg, Germany, 27 August–3 September 1978; pp. 569–587. [Google Scholar]
- Larsen, J.; Dancy, H. Open boundaries in short wave simulations—A new approach. Coast. Eng. 1983, 7, 285–297. [Google Scholar] [CrossRef]
- Lee, C.; Suh, K.D. Internal generation of waves for time-dependent mild-slope equations. Coast. Eng. 1998, 34, 35–57. [Google Scholar] [CrossRef]
- Karambas, T.V.; Bowers, E.C. Representation of partial wave reflection and transmission for rubble mound coastal structures. WIT Trans. Ecol. Environ. 1996, 12, 415–423. [Google Scholar]
- Bruun, P. Design and Construction of Mounds for Breakwaters and Coastal Protection; Elsevier: Amsterdam, The Netherland, 1985; Volume 37. [Google Scholar]
- Kriezi, E.; Karambas, T. Modelling wave deformation due to submerged breakwaters. Marit. Eng. Proc. Inst. Civ. Eng. 2010, 163, 19–29. [Google Scholar] [CrossRef]
- Koutandos, E.V.; Karambas, T.V.; Koutitas, C.G. Floating breakwater response to waves action using a Boussinesq model coupled with a 2DV elliptic solver. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 243–255. [Google Scholar] [CrossRef]
- Copeland, G.J.M. Practical radiation stress calculations connected with equations of wave propagation. Coast. Eng. 1985, 9, 195–219. [Google Scholar] [CrossRef]
- Kobayashi, N.; Agarwal, A.; Johnson, B.D. Longshore current and sediment transport on beaches. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 296–304. [Google Scholar] [CrossRef]
- Stive, M.J.F.; Wind, H.G. Cross-shore mean flow in the surf zone. Coast. Eng. 1986, 10, 325–340. [Google Scholar] [CrossRef]
- De Vriend, H.J.; Stive, M.J.F. Quasi-3D modelling of nearshore currents. Coast. Eng. 1987, 11, 565–601. [Google Scholar] [CrossRef]
- Baba, Y.; Camenen, B. Importance of the Swash Longshore Sediment Transport in Morphodynamic Models. In Proceedings of the Coastal Sediments ‘07 6th International Symposium on Coastal Engineering and Science of Coastal Sediment Process, Louisiana, LA, USA, 13–17 May 2007; Kraus, N.C., Rosati, J.D., Eds.; ASCE: San Francisco, CA, USA, 2012. [Google Scholar]
- Militello, A.; Reed, C.W.; Zundel, A.K.; Kraus, N.C. Two-Dimensional Depth-Averaged Circulation Model M2D: Version 2.0, Report 1, Technical Documentation and User’s Guide; ERDC/CHL TR-04-2; US Army Corps of Engineers, Engineering Research and Development Center: Vicksburg, MS, USA, 2004; p. 134. [Google Scholar]
- Camenen, B.; Larson, M. Phase-lag effects in sheet flow transport. Coast. Eng. 2006, 53, 531–542. [Google Scholar] [CrossRef]
- Isobe, M.; Horikawa, K. Study on water particle velocities of shoaling and breaking waves. Coast. Eng. Japan 1982, 25, 109–123. [Google Scholar]
- Kobayashi, N.; Tega, Y. Sand Suspension and Transport on Equilibrium Beach. J. Waterw. Port Coast. Ocean Eng. 2002, 128, 238–248. [Google Scholar] [CrossRef]
- Nam, P.T.; Larson, M.; Hanson, H.; Hoan, L.X. A numerical model of nearshore waves, currents, and sediment transport. Coast. Eng. 2009, 56, 1084–1096. [Google Scholar] [CrossRef]
- Larson, M.; Wamsley, T.V. A formula for longshore sediment transport in the swash. In Proceedings of the Coastal Sediments ‘07 6th International Symposium on Coastal Engineering and Science of Coastal Sediment Process, Louisiana, LA, USA, 13–17 May 2007; Kraus, N.C., Rosati, J.D., Eds.; ASCE: Reston, VA, USA, 2007; pp. 1924–1937. [Google Scholar]
- Leont’yev, I.O. Numerical modelling of beach erosion during storm event. Coast. Eng. 1996, 29, 187–200. [Google Scholar] [CrossRef]
- Kamphuis, J.W. Physical Modeling. In Handbook of Coastal and Ocean Engineering; Herbich, J., Ed.; Gulf Publishing Company: Huston, TX, USA, 1991; Volume 2, pp. 1049–1066. [Google Scholar]
- Christopoulos, S. Coastal Protection Works of Paralia Katerinis; Technical Report; Municipality of Katerini: Katerini, Greece, 2014.
- Google Earth, Image ©2017 TerraMetrics, Data SIO, NOAA, U.S. Navy, NGA, GEBCO. 2017.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).