Integration of the CEL and ML Methods for Landing Safety Prediction and Optimization of Full-Scale Track Design in a Deep-Sea Mining Vehicle
Abstract
1. Introduction
2. FEM Method for Obtaining the DSMV Sinking Process
2.1. CEL Numerical Method
2.2. A Constitutive Soil Model That Integrates Strain Softening and Strain Rates
2.3. Numerical Model of the Track–Soil Sinkage Interaction
2.4. Sensitivity Analyses of Mesh Parameters
3. Results and Discussion
3.1. Effect of the Sediment Undrained Shear Strength
3.2. Effect of the Softening Effect Parameter
3.3. Effect of the Dynamic Parameter Situation
3.4. Interplay Between Strain-Softening and Rate Effects
4. Prediction Model Using the Random Forest Algorithm
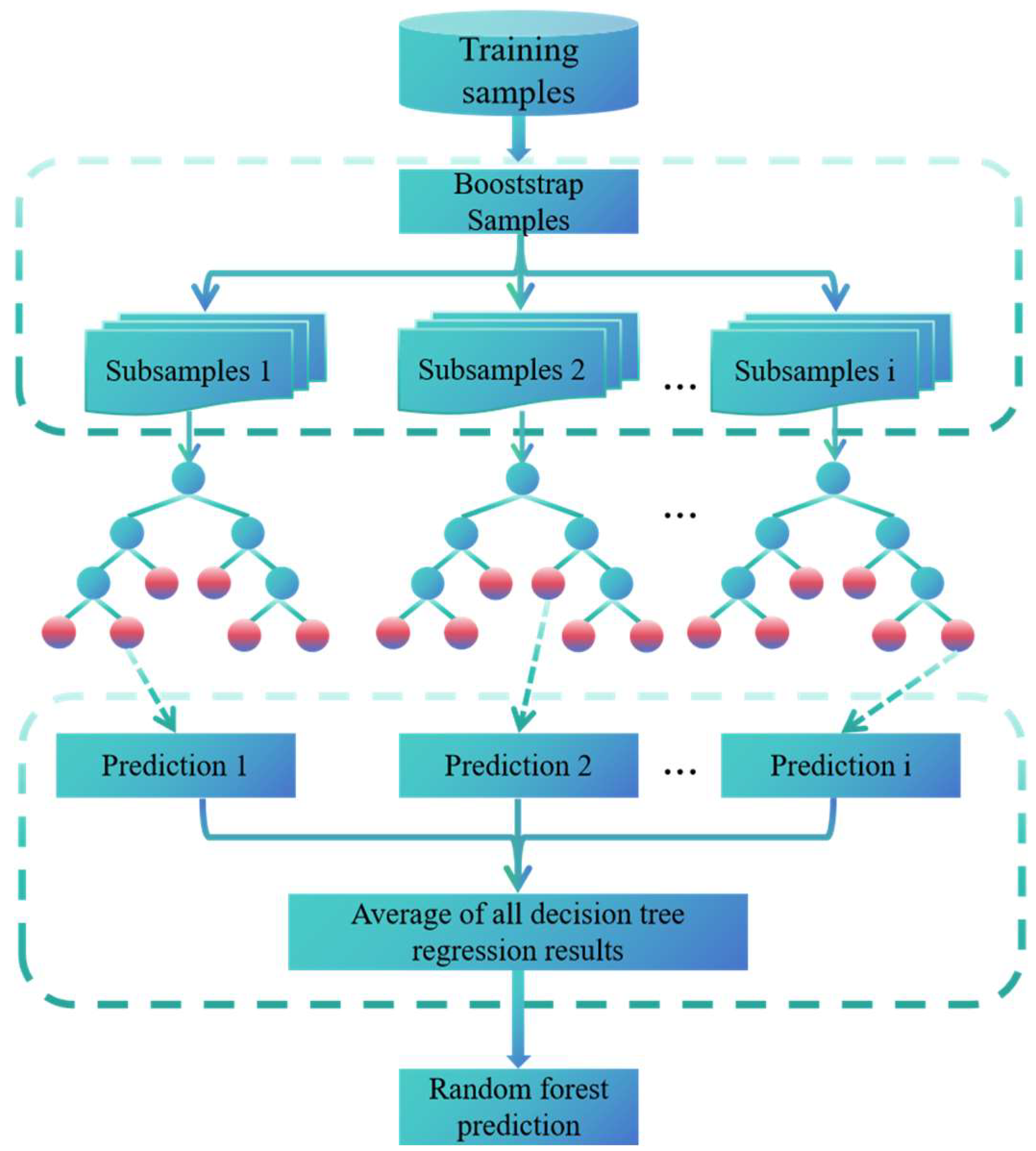
4.1. Random Forest Approach
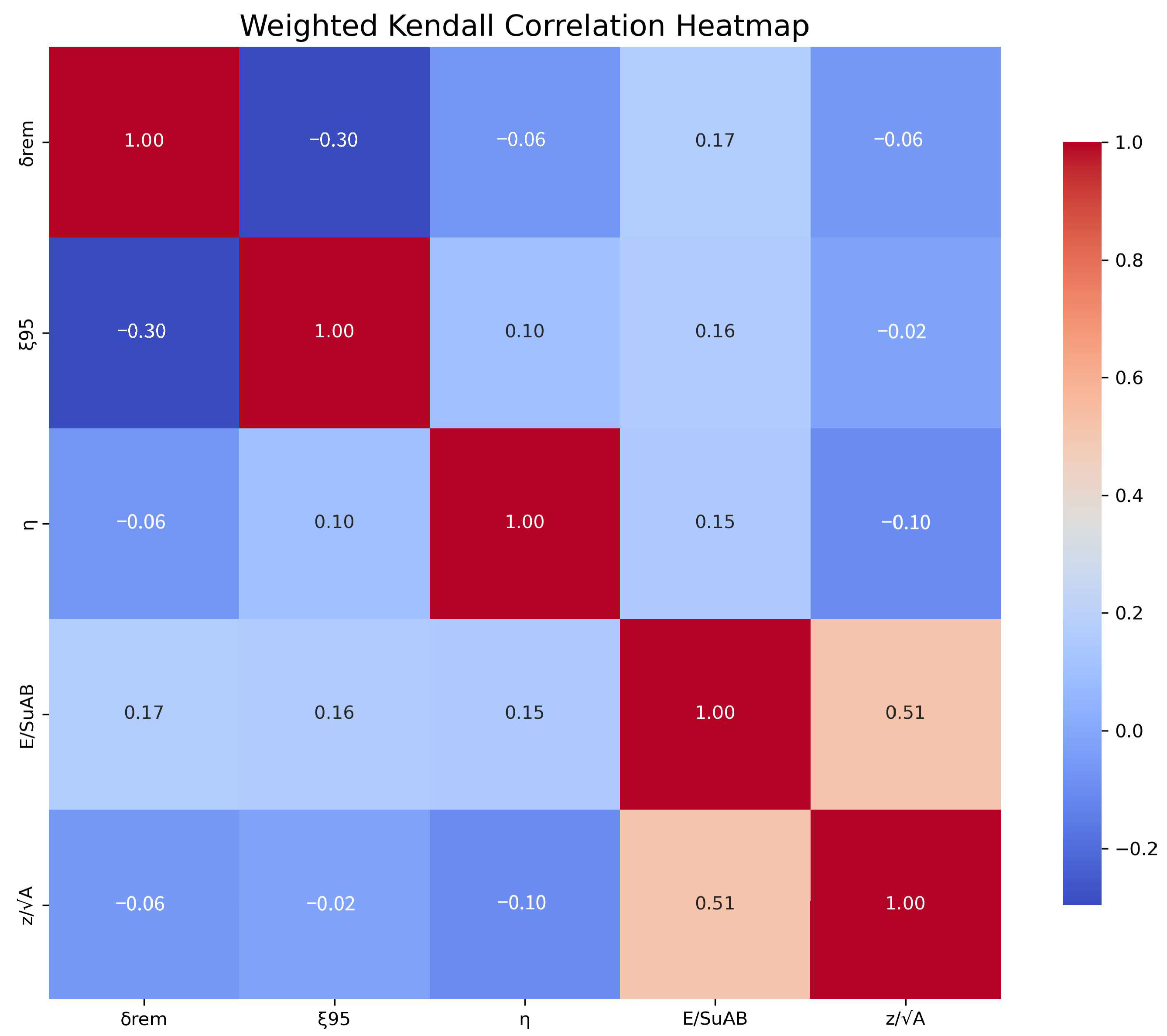
4.2. Dimensionless Sinkage Depth
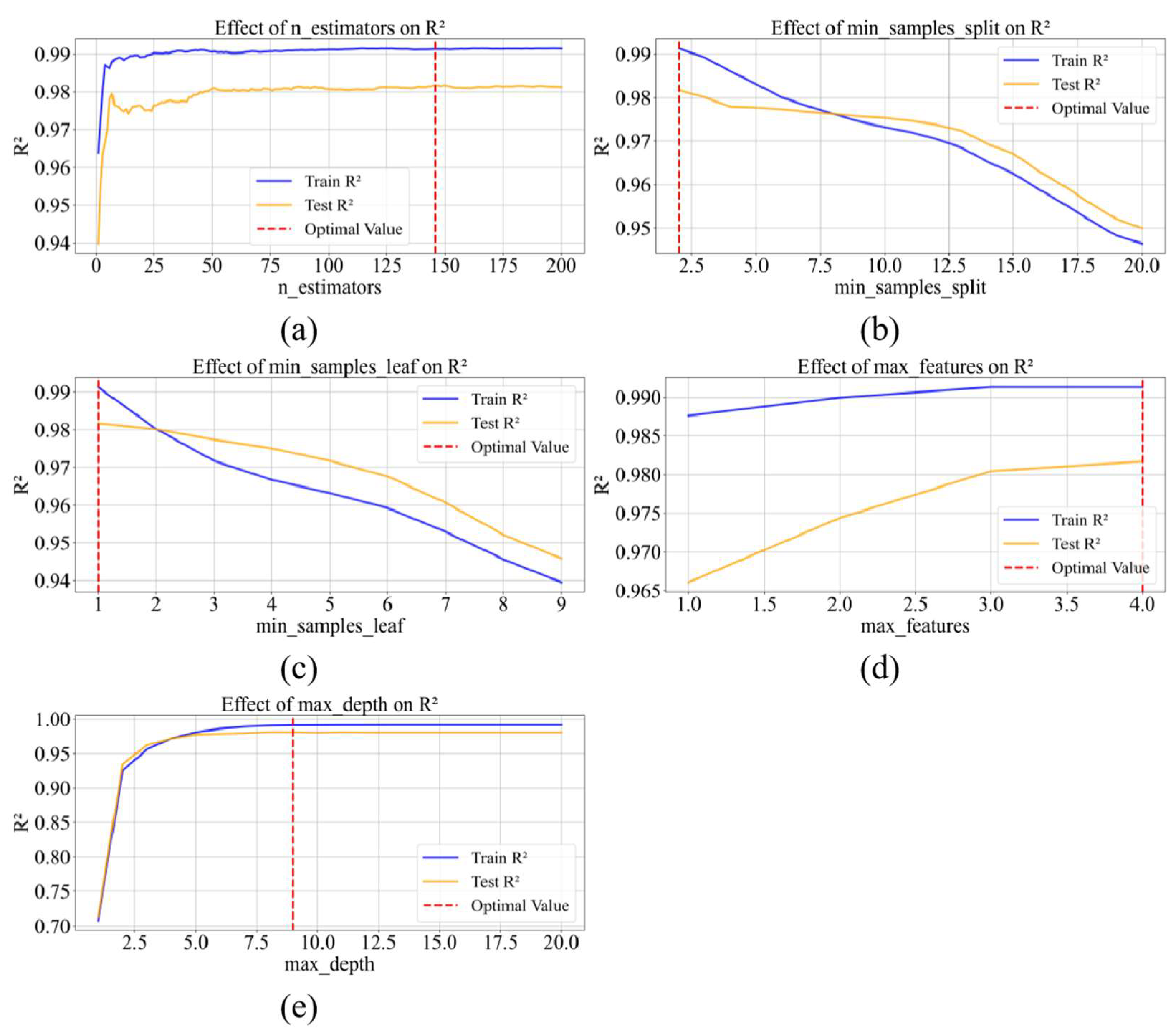
4.3. Establishment of the Prediction Model
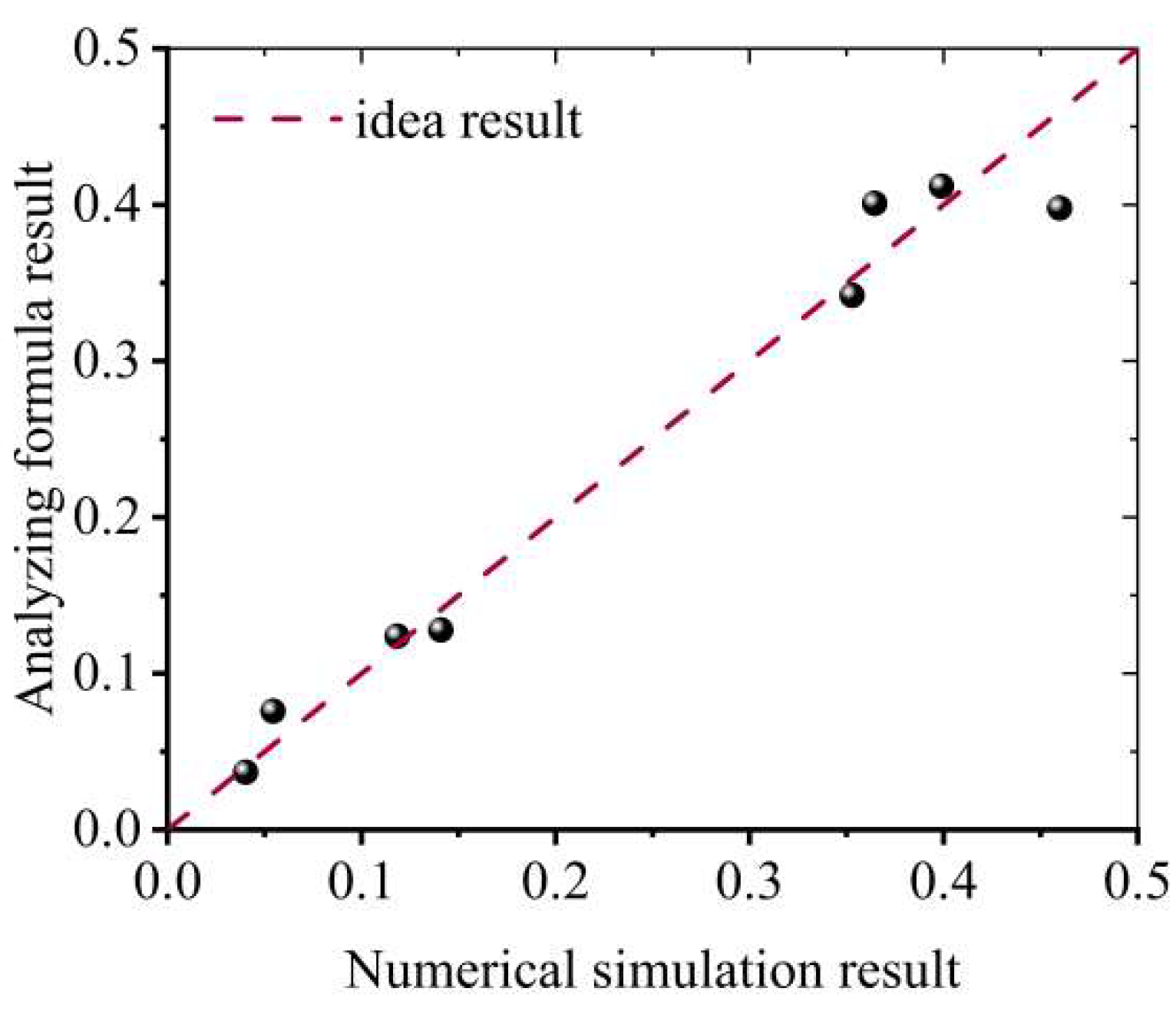
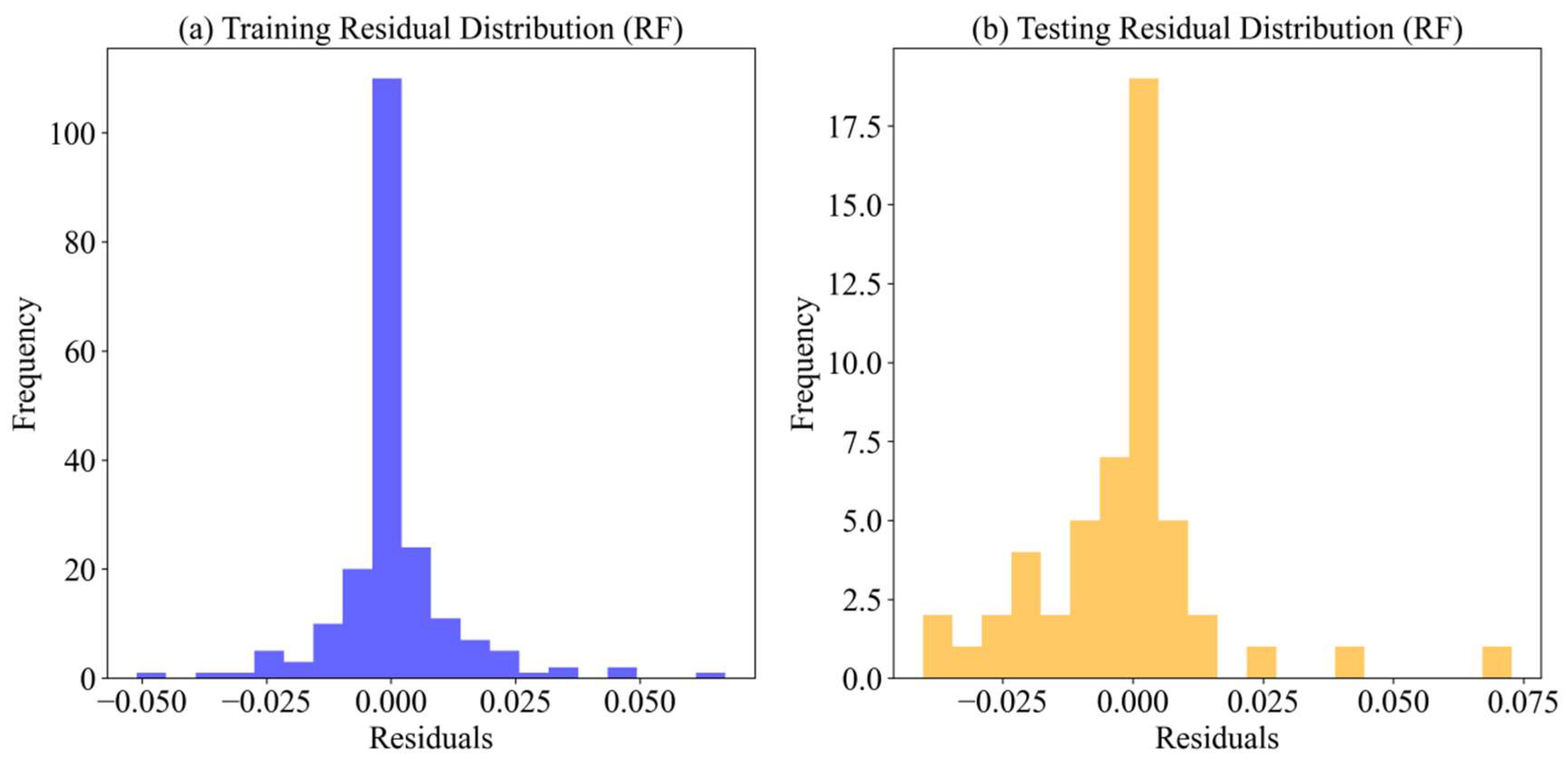
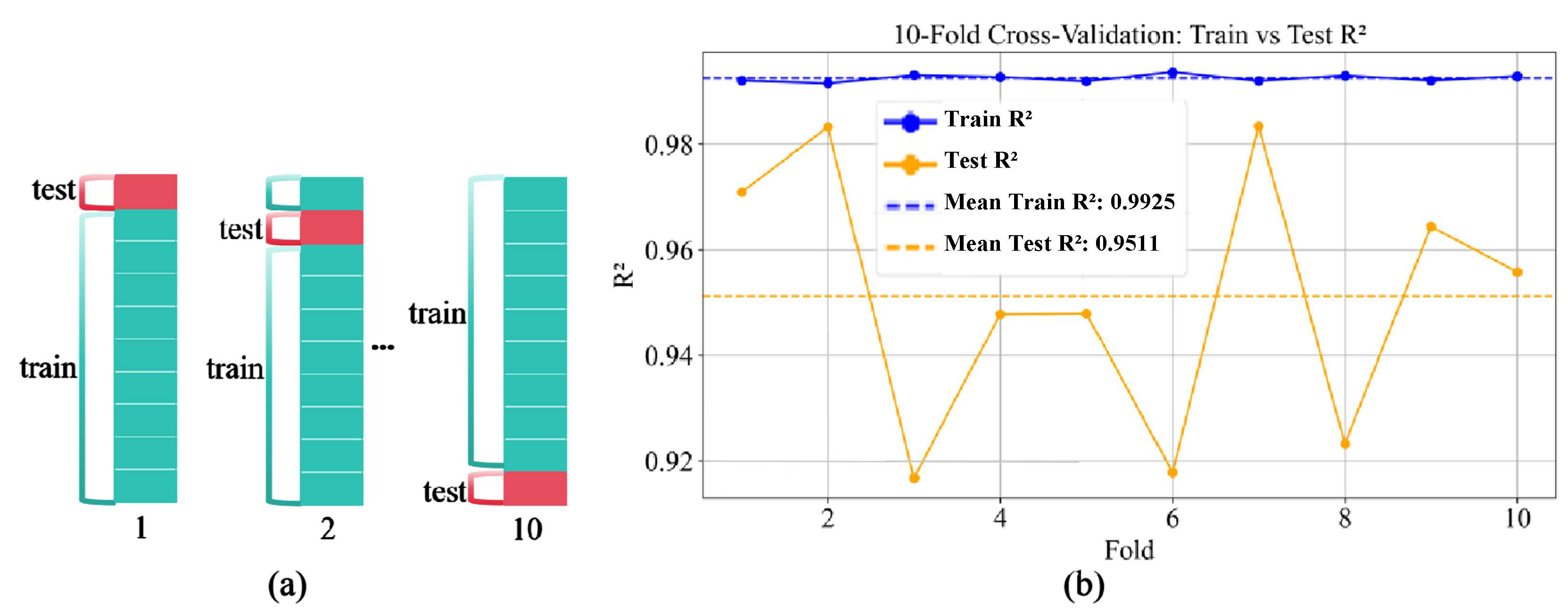
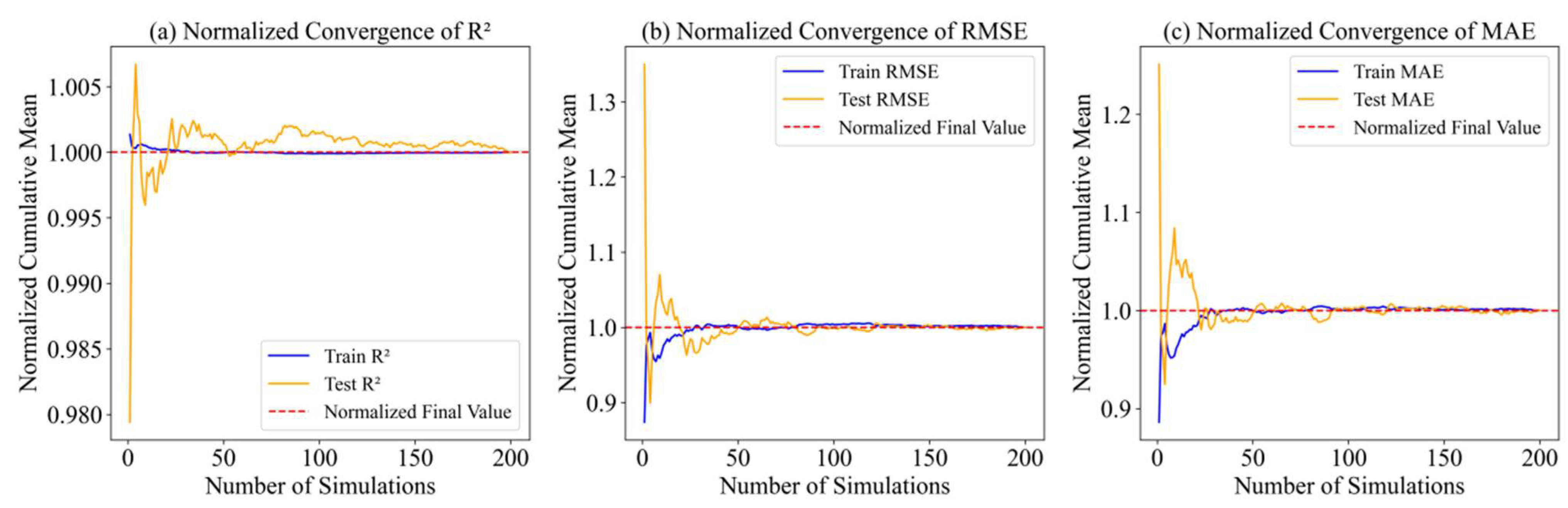
4.4. Evaluation of the Prediction Model
5. Conclusions
6. Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, K.; Xi, W.; Huang, S.; Zhou, J. Deep-sea mineral resource mining: A historical review, developmental progress, and insights. Miner. Metall. Explor. 2024, 41, 173–192. [Google Scholar] [CrossRef]
- Sha, F.; Xi, M.; Chen, X.; Liu, X.; Niu, H.; Zuo, Y. A recent review on multi-physics coupling between deep-sea mining equipment and marine sediment. Ocean Eng. 2023, 276, 114229. [Google Scholar] [CrossRef]
- Sharma, R. Deep-sea mining and the water column: An introduction. In Deep-Sea Mining and the Water Column: Advances, Monitoring and Related Issues; Springer: Cham, Switzerland, 2024; pp. 3–40. [Google Scholar]
- Zhang, N.; Zhai, W.K.; Yin, S.Y.; Chen, X.G.; Xia, J.X.; Luan, L.B.; Zhai, A.S. Deep-sea soft soil and deep-sea mining vehicle interaction: From soil properties to locomotion performance. Appl. Ocean Res. 2025, 154, 104372. [Google Scholar] [CrossRef]
- Atmanand, M.; Janardhanan, K.; Amuda, K.; Gnanaraj, A.; Rajesh, S.; Muthuvel, P.; Kuttikrishnan, G.; Ramadass, G. Contemporary technological progress in deepsea mining. In Deep-Sea Mining and the Water Column: Advances, Monitoring and Related Issues; Springer: Cham, Switzerland, 2024; pp. 67–89. [Google Scholar]
- Leng, D.; Shao, S.; Xie, Y.; Wang, H.; Liu, G. A brief review of recent progress on deep sea mining vehicle. Ocean Eng. 2021, 228, 108565. [Google Scholar] [CrossRef]
- Wu, Q.; Yang, J.; Lu, H.; Lu, W.; Liu, L. Effects of heave motion on the dynamic performance of vertical transport system for deep sea mining. Appl. Ocean Res. 2020, 101, 102188. [Google Scholar] [CrossRef]
- Shen, Y.J.; Chen, M.F.; Du, Y.L.; Li, M. Key mechanical issues and technical challenges of deep-sea mining development system. Mech. Eng. 2022, 44, 1005–1020. [Google Scholar]
- Liu, S.J.; Chang, L.; Yu, D. Status and progress on researches and developments of deep ocean mining equipments. Chin. J. Mech. Eng. 2014, 50, 8–18. [Google Scholar] [CrossRef]
- Zhao, H.L.; Sun, Y.F.; Jia, C.; Wei, R.C.; Deng, H.; Wu, T. The sinkage by mining car traveling on deep-sea soft bottom based on Burger’s creep model. Mar. Geol. Quat. Geol. 2024, 44, 179–190. [Google Scholar] [CrossRef]
- Hong, S.; Kim, H.W.; Yeu, T.; Choi, J.S.; Lee, T.H.; Lee, J.K. Technologies for safe and sustainable mining of deep-seabed minerals. In Environmental Issues in Deep-Sea Mining: Impacts, Consequences and Policy Perspectives; Springer: Cham, Switzerland, 2019; pp. 95–143. [Google Scholar]
- Kang, Y.J.; Liu, S.J. The development history and latest progress of deep-sea polymetallic nodule mining technology. Minerals 2021, 11, 1132. [Google Scholar] [CrossRef]
- Rauf, O.; Yang, N.; Chen, M.; Ma, H.X. Evaluation of ground pressure, bearing capacity, and sinkage in rigid-flexible tracked vehicles on characterized terrain in laboratory conditions. Sensors 2024, 24, 1779. [Google Scholar] [CrossRef]
- Laughery, S.; Gerhart, G.; Goetz, R. Bekker’s Terramechanics Model for Off-Road Vehicle Research; US Army TARDEC: Hammond, WI, USA, 1990. [Google Scholar]
- Bekker, M.G. Introduction to Terrain-Vehicle Systems; University of Michigan Press: Ann Arbor, MI, USA, 1969. [Google Scholar]
- Bekker, M.G.; Kitano, M.; Kumagai, K. Theory of Land Locomotion; University of Michigan Press: Ann Arbor, MI, USA, 1969. [Google Scholar]
- Agarwal, S.; Senatore, C.; Zhang, T.G.; Kingsbury, M.; Iagnemma, K.; Goldman, D.I.; Kamrin, K. Modeling of the interaction of rigid wheels with dry granular media. J. Terramechanics 2019, 85, 1–14. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X.G.; Li, Z.G.; Liu, X.L.; Liu, X.X.; Wang, L.Z.; Yang, W.D. Analysis of traction performance of deep-sea tracked mining vehicles under different grouser pitch-to-height ratios and traveling speeds. Ocean Eng. 2024, 297, 117112. [Google Scholar] [CrossRef]
- Kim, Y.H.; Hossain, M.S. Dynamic installation of OMNI-Max anchors in clay: Numerical analysis. Géotechnique 2015, 65, 1037–1096. [Google Scholar] [CrossRef]
- Kim, Y.H.; Hossain, M.S.; Wang, D. Effect of strain rate and strain softening on embedment depth of a torpedo anchor in clay. Ocean Eng. 2015, 108, 704–715. [Google Scholar] [CrossRef]
- Kim, Y.H.; Hossain, M.S.; Wang, D.; Randolph, M.F. Numerical investigation of dynamic installation of torpedo anchors in clay. Ocean Eng. 2015, 108, 820–832. [Google Scholar] [CrossRef]
- Zhao, J.; Jang, B.; Duan, M. On spudcan deep penetration using Eulerian finite element in multi-layer sediments: Soil plug mechanism. Ships Offshore Struct. 2017, 12, 715–721. [Google Scholar] [CrossRef]
- Dai, X.; Xu, T.; Chen, J. Physical and mechanical properties of deep oceanic sediments cored from the bottom of Challenger Deep, Mariana Trench. Geofluids 2021, 2021, 9109132. [Google Scholar] [CrossRef]
- Li, L.; Li, S.L. Simulation and mechanical characteristics of terramechanics of the surface soil on deep-sea bed. Eng. Mech. 2010, 13, 213–220. [Google Scholar]
- Su, Q.; Lv, H.; Yang, J.M.; Sun, P.F. Analysis of the walking performance of tracked deep-sea mining vehicle on soft sediment. Ocean Eng. 2022, 2, 162–168. [Google Scholar]
- Einav, I.; Randolph, M.F. Combining upper bound and strain path methods for evaluating penetration resistance. Int. J. Numer. Meth. Eng. 2005, 63, 1991–2016. [Google Scholar] [CrossRef]
- Benson, D.J. Computational methods in Lagrangian and Eulerian hydrocodes. Comput. Methods Appl. Mech. Eng. 1992, 99, 235–394. [Google Scholar] [CrossRef]
- Wang, J.Y.; Cao, W.G.; Zhai, Y.C. Experimental study of interaction between deep-sea sediments and tracks. Rock Soil Mech. 2011, S2, 274–278. [Google Scholar]
- Zhang, W.; Cassidy, M.J.; Tian, Y. Practical large-deformation finite-element method for 3D geotechnical problems involving free surface deformations. Int. J. Geomech. 2020, 20, 04020064. [Google Scholar] [CrossRef]
- Liu, M.; Huang, W.X.; Yuan, W.H.; Zhang, W. Modelling the large deformation failure behaviour of unsaturated porous media with a two-phase fully-coupled smoothed particle finite element method. SSRN Electron. J. 2023, 427, 117013. [Google Scholar] [CrossRef]
- Yuan, W.; Zhu, J.; Wang, N.; Zhang, W.; Dai, B.; Jiang, Y.; Wang, Y. A dynamic large-deformation particle finite element method for geotechnical applications based on Abaqus. J. Rock Mech. Geotech. Eng. 2023, 15, 1859–1871. [Google Scholar] [CrossRef]
- Huang, C.; Qian, J. FEM-BEM modeling of dynamic responses of a fluid-filled lined tunnel under a water hammer. J. Eng. Mech. 2024, 150, 04022045. [Google Scholar] [CrossRef]
- Janarthanan, C.; Kuttikrishnan, G.; Sundaramoorthi, V.; Chandran, V.; Ramadass, G.A. Deep Sea Soil Sinkage Simulation and Experimental Studies for Development of Deep Water Mining Machine. Mar. Technol. Soc. J. 2022, 56, 72–82. [Google Scholar] [CrossRef]
- Amudha, K.; Reshma, K.V.; Ramesh, N.R.; Deepak, C.R.; Ramadass, G.A.; Atmanand, M.A. Estimation of sinkage and breakout forces for tracked vehicle for soft soils. In Proceedings of the OCEANS 2014—TAIPEI, Taipei, Taiwan, 7–10 April 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Janarthanan, C.; Muruganandhan, R.; Gopkumar, K. Design and multi-body dynamic analysis of inline and offset track configuration in deep-sea mining vehicles for enhanced traction in soft seabed. J. Terramechanics 2024, 116, 100999. [Google Scholar] [CrossRef]
- Sun, P.; Lu, H.; Yang, J.; Deng, L.; Liu, M.; Li, S. Numerical study on multiple parameters of sinkage simulation between the track plate of the deep-sea mining vehicle and the seafloor soil. J. Mar. Sci. Eng. 2022, 10, 1680. [Google Scholar] [CrossRef]
- Sun, P.; Lu, H.; Yang, J.; Xu, Z. A numerical investigation on the sinkage of the deep-sea mining vehicle based on a modified constitutive soil model. ASME J. Offshore Mech. Arct. Eng. 2025, 147, 022101. [Google Scholar] [CrossRef]
- Luan, L.; Chen, X.; Kouretzis, G.; Ding, X. Dynamic seabed stresses due to moving deep-sea mining vehicles. Comput. Geotech. 2023, 157, 105356. [Google Scholar] [CrossRef]
- Xia, M.; Lu, H.; Yang, J.; Sun, P. Multi-Body Dynamics Modeling and Straight-Line Travel Simulation of a Four-Tracked Deep-Sea Mining Vehicle on Flat Ground. J. Mar. Sci. Eng. 2023, 11, 1005. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Wan, Z.; Quan, D.G.; Liu, Y.F.; Jia, Y.G.; Zhu, N. Analysis of bearing capacity of consolidated clay under the track load of deep-sea mining vehicle. Mar. Georesour. Geotechnol. 2024, 43, 508–523. [Google Scholar] [CrossRef]
- Tho, K.K.; Leung, C.F.; Chow, Y.K.; Swaddiwudhipong, S. Eulerian finite-element simulation of spudcan–pile interaction. Can. Geotech. J. 2013, 50, 595–608. [Google Scholar] [CrossRef]
- Gonzalez, R.; Iagnemma, K. DeepTerramechanics: Terrain classification and slip estimation for ground robots via deep learning. arXiv 2018, arXiv:1806.07379. [Google Scholar] [CrossRef]
- Chavez-Garcia, R.O.; Guzzi, J.; Gambardella, L.M.; Giusti, A. Learning ground traversability from simulations. IEEE Robot. Autom. Lett. 2018, 3, 1695–1702. [Google Scholar] [CrossRef]
- Zhang, N.; Zhai, W.; Yin, S.; Song, Y.; Chen, X.; Guo, C.; Ma, Y. Study of the tractive performance of a deep-sea mining vehicle based on the soil failure mode. Int. J. Geomech. 2025, 25, 04025013. [Google Scholar] [CrossRef]
- Zande, M.; Smith, J.; Thompson, R. Coupled numerical–experimental framework for track–soil interaction in planetary rovers. J. Terramechanics 2024, 101, 35–43. [Google Scholar] [CrossRef]
- White, D.; Randolph, M. Seabed characterisation and models for pipeline-soil interaction. Int. J. Offshore Polar Eng. 2007, 17, 193–204. [Google Scholar]
- Xiao, Z.; Fu, D.F.; Zhou, Z.F.; Lu, Y.; Yan, Y. Effects of strain softening on the penetration resistance of offshore bucket foundation in nonhomogeneous clay. Ocean Eng. 2019, 193, 106594. [Google Scholar] [CrossRef]
- Xie, Q.; Xu, Q.; Xiu, Z.; Liu, L.; Du, X.; Yang, J.; Liu, H. Convenient method for large-deformation finite-element simulation of submarine landslides considering shear softening and rate correlation effects. J. Mar. Sci. Eng. 2024, 12, 81. [Google Scholar] [CrossRef]
- Guo, X.; Liu, Z.; Zheng, J.; Luo, Q.; Liu, X. Bearing capacity factors of T-bar from surficial to stable penetration into deep-sea sediments. Soil Dyn. Earthq. Eng. 2023, 165, 107671. [Google Scholar] [CrossRef]
- Pham, B.T.; Hoang, T.A.; Nguyen, D.M.; Bui, D.T. Prediction of shear strength of soft soil using machine learning methods. Catena 2018, 166, 181–191. [Google Scholar] [CrossRef]
- Phoon, K.K.; Zhang, W.G. Future of machine learning in geotechnics. Georisk 2023, 17, 7–22. [Google Scholar] [CrossRef]
- Nguyen, M.; Pham, B.; Tuyen, T.; Yen, H.; Prakash, I.; Vu, T.; Chapi, K.; Shirzadi, A. Development of an artificial intelligence approach for prediction of consolidation coefficient of soft soil: A sensitivity analysis. Open Constr. Build. Technol. J. 2019, 13, 178–188. [Google Scholar] [CrossRef]
- Shahani, N.M.; Kamran, M.; Zheng, X.G.; Liu, C.C.; Guo, X.W. Application of gradient boosting machine learning algorithms to predict uniaxial compressive strength of soft sedimentary rocks at Thar Coalfield. Adv. Civ. Eng. 2021, 2021, 2565488. [Google Scholar] [CrossRef]
- Shao, W.; Yue, W.H.; Zhang, Y.; Zhou, T.X.; Zhang, Y.T.; Dang, Y.B.; Wang, H.Y.; Feng, X.H. The application of machine learning techniques in geotechnical engineering: A review and comparison. Mathematics 2023, 11, 3976. [Google Scholar] [CrossRef]
- Guo, X.S.; Meng, X.S.; Han, F.H.; Zhang, H.; Liu, X.L. Assessing the strength of deep-sea surface ultrasoft sediments with T-bar penetration: A machine learning approach. Eng. Geol. 2024, 338, 107632. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Yin, J.N.; Li, N. Ensemble learning models with a Bayesian optimization algorithm for mineral prospectivity mapping. Ore Geol. Rev. 2022, 145, 104916. [Google Scholar] [CrossRef]
- Zhang, D.M.; Zhang, J.Z.; Huang, H.W.; Qi, C.C.; Chang, C.Y. Machine learning-based prediction of soil compression modulus with application of 1D settlement. J. Zhejiang Univ. Sci. A 2020, 21, 430–444. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2021, 45, 5–32. [Google Scholar] [CrossRef]
- Graw, J.H.; Wood, W.T.; Phrampus, B.J. Predicting global marine sediment density using the random forest regressor machine learning algorithm. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020135. [Google Scholar] [CrossRef]
- Benson, D.J.; Okazawa, S. Contact in a multi-material Eulerian finite element formulation. Comput. Methods Appl. Mech. Eng. 2004, 193, 4277–4298. [Google Scholar] [CrossRef]
- Li, T.; Tang, X.W.; Wang, Z. Experimental Study on Unconfined Compressive and Cyclic Behaviors of Mucky Silty Clay with Different Clay Contents. Int. J. Civ. Eng. 2019, 17, 841–857. [Google Scholar] [CrossRef]
- Aubeny, C.P.; Shi, H. Effect of rate-dependent soil strength on cylinders penetrating into soft clay. IEEE J. Ocean. Eng. 2007, 32, 49–56. [Google Scholar] [CrossRef]
- Zhou, H.; Randolph, M.F. Computational techniques and shear band development for cylindrical and spherical penetrometers in strain-softening clay. Int. J. Geomech. 2007, 7, 287–295. [Google Scholar] [CrossRef]
- Zhou, H.; Randolph, M.F. Numerical investigations into cycling of full-flow penetrometers in soft clay. Géotechnique 2009, 59, 801–812. [Google Scholar] [CrossRef]
- Zhu, H.; Randolph, M.F. Numerical analysis of a cylinder moving through rate-dependent undrained soil. Ocean Eng. 2010, 38, 943–953. [Google Scholar] [CrossRef]
- Boukpeti, N.; White, D.J.; Randolph, M.F.; Low, H.E. Strength of fine grained soils at the solid-fluid transition. Géotechnique 2012, 62, 213–226. [Google Scholar] [CrossRef]
- Biscontin, G.; Pestana, J.M. Influence of peripheral velocity on vane shear strength of an artificial clay. Geotech. Test. J. 2001, 24, 423–429. [Google Scholar] [CrossRef]
- Randolph, M.F. Characterisation of soft sediments for offshore applications. In Proceedings of the 2nd International Conference on Site Characterization, Rotterdam, The Netherlands, 19–22 September 2004; pp. 209–232. [Google Scholar]
- Dutta, S.; Hawlader, B.; Phillips, R. Finite element modeling of partially embedded pipelines in clay seabed using coupled Eulerian-Lagrangian method. Can. Geotech. J. 2015, 52, 58–72. [Google Scholar] [CrossRef]
- Dutta, S.; Hawlader, B. Pipeline soil-water interaction modelling for submarine landslide impact on suspended offshore pipelines. Géotechnique 2019, 69, 29–41. [Google Scholar] [CrossRef]
- Hansbo, S. A new approach to the determination of the shear strength of clay by the fall-cone test. Proc. Swed. Geotech. Inst. 1957, 14, 1–46. [Google Scholar]
- Uddin, M.F.; Lee, J.; Rizvi, S.; Hamada, S. Proposing Enhanced Feature Engineering and a Selection Model for Machine Learning Processes. Appl. Sci. 2018, 8, 646. [Google Scholar] [CrossRef]
- O’Loughlin, C.D.; Richardson, M.D.; Gaudin, C.; Randolph, M.F. Penetration of dynamically installed anchors in clay. Géotechnique 2013, 63, 909–919. [Google Scholar] [CrossRef]
- Wei, M.D.; Meng, W.Z.; Dai, F.; Wu, W. Application of machine learning in predicting the rate-dependent compressive strength of rocks. J. Rock Mech. Geotech. Eng. 2022, 14, 1356–1365. [Google Scholar] [CrossRef]
- Zhang, W.G.; Wu, C.Z.; Zhong, H.Y.; Li, Y.Q.; Wang, L. Prediction of undrained shear strength using extreme gradient boosting and random forest based on Bayesian optimization. Geosci. Front. 2021, 12, 469–477. [Google Scholar] [CrossRef]
- Abdi, Y.; Momeni, E.; Armaghani, D.J. Elastic modulus estimation of weak rock samples using random forest technique. Bull. Eng. Geol. Environ. 2023, 82, 185. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.G.; Armaghani, D.J.; Zhang, W.G.; Li, C.Q.; Zhu, S.L.; Tarinejad, R. Predicting TBM penetration rate in hard rock condition: A comparative study among six XGB-based metaheuristic techniques. Geosci. Front. 2021, 12, 101093. [Google Scholar] [CrossRef]
- Yan, T.; Shen, S.L.; Zhou, A.N.; Chen, X.S. Prediction of geological characteristics from shield operational parameters by integrating grid search and K-fold cross validation into stacking classification algorithm. J. Rock Mech. Geotech. Eng. 2022, 14, 1292–1303. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.Y.; Jin, Y.F.; Chan, T.H. A novel hybrid surrogate intelligent model for creep index prediction based on particle swarm optimization and random forest. Eng. Geol. 2020, 265, 105328. [Google Scholar] [CrossRef]
- Ly, H.B.; Nguyen, T.A.; Pham, B.T. Estimation of soil cohesion using machine learning method: A random forest approach. Adv. Civ. Eng. 2021, 2021, 8873993. [Google Scholar] [CrossRef]



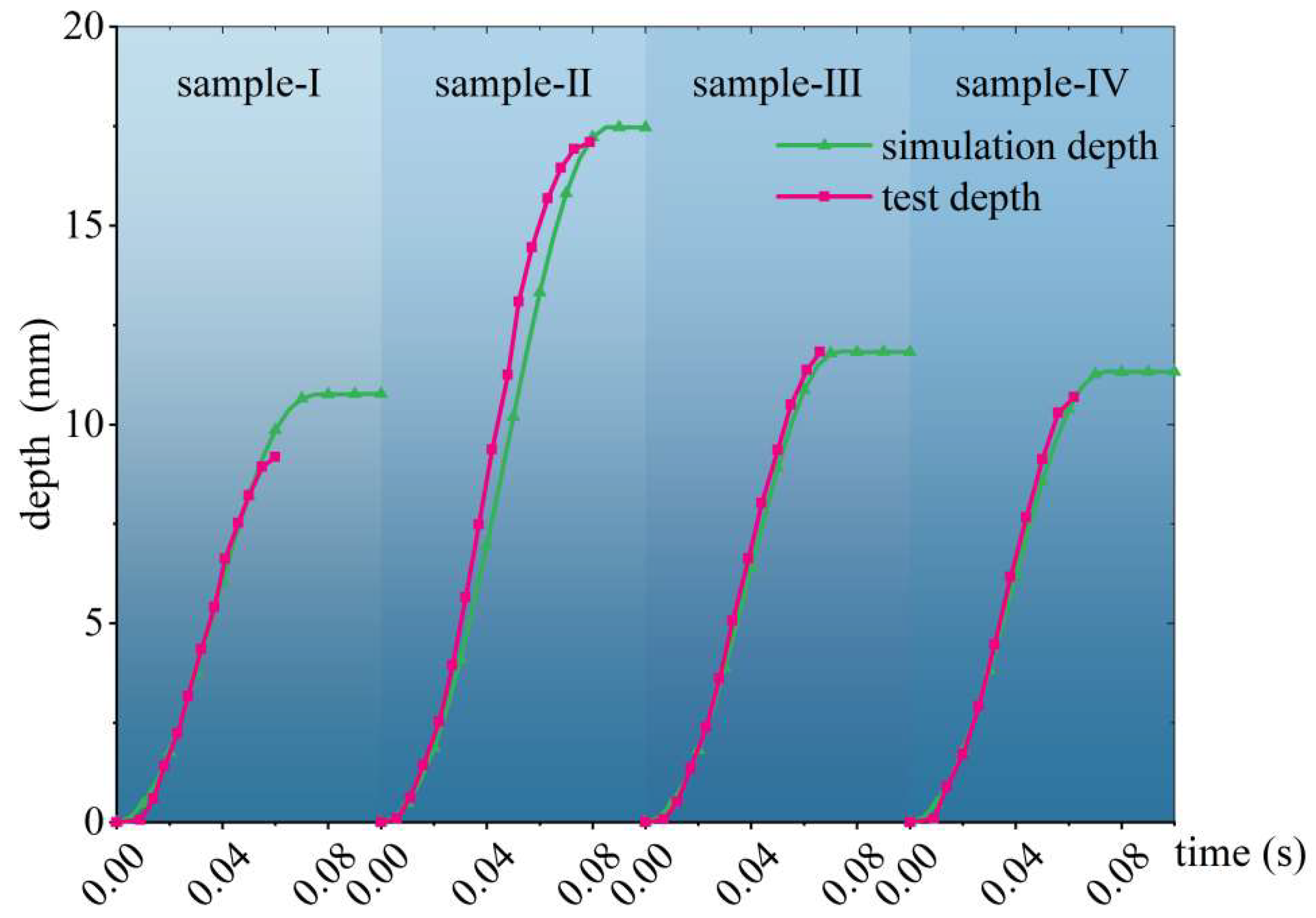
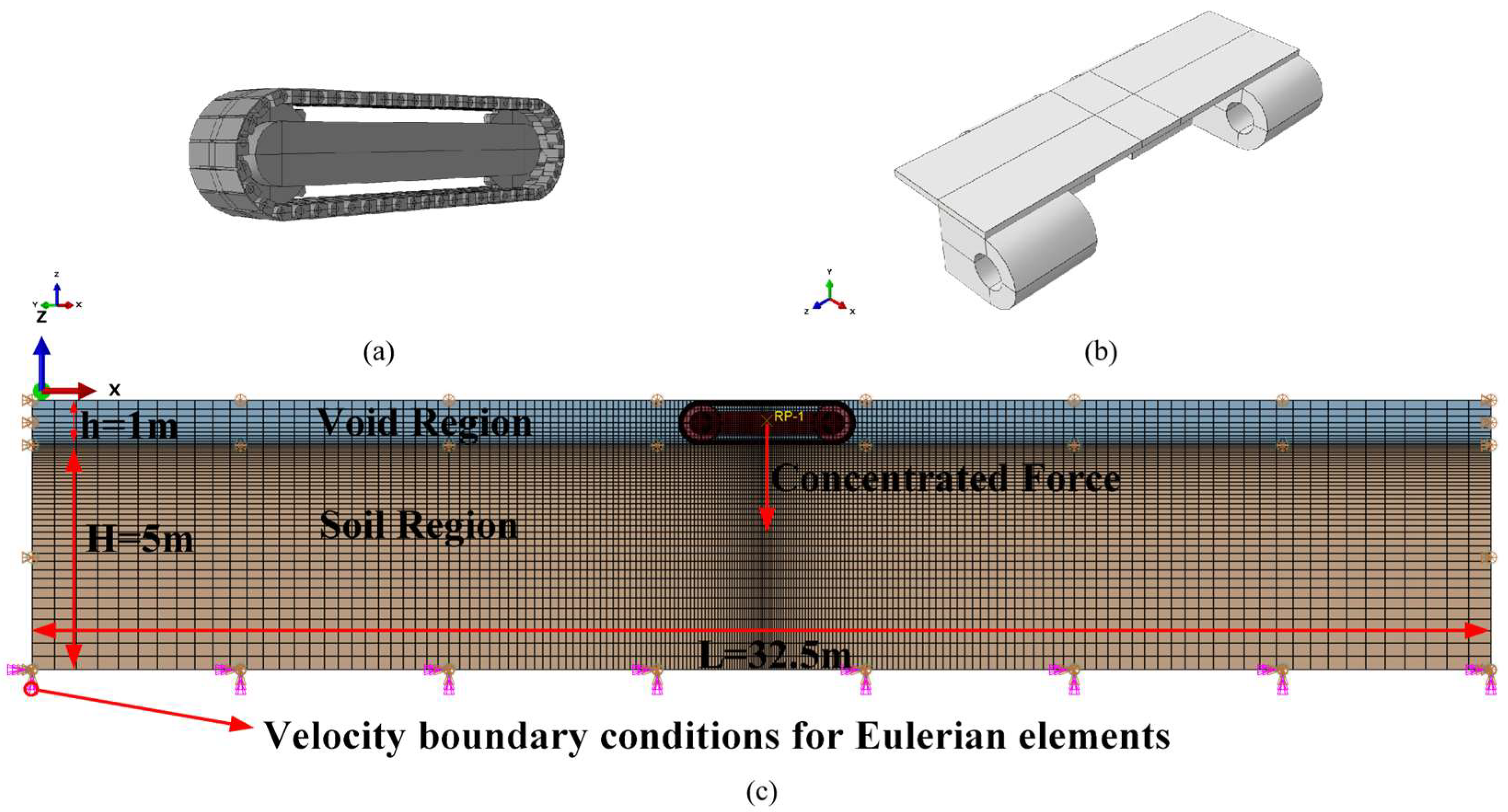
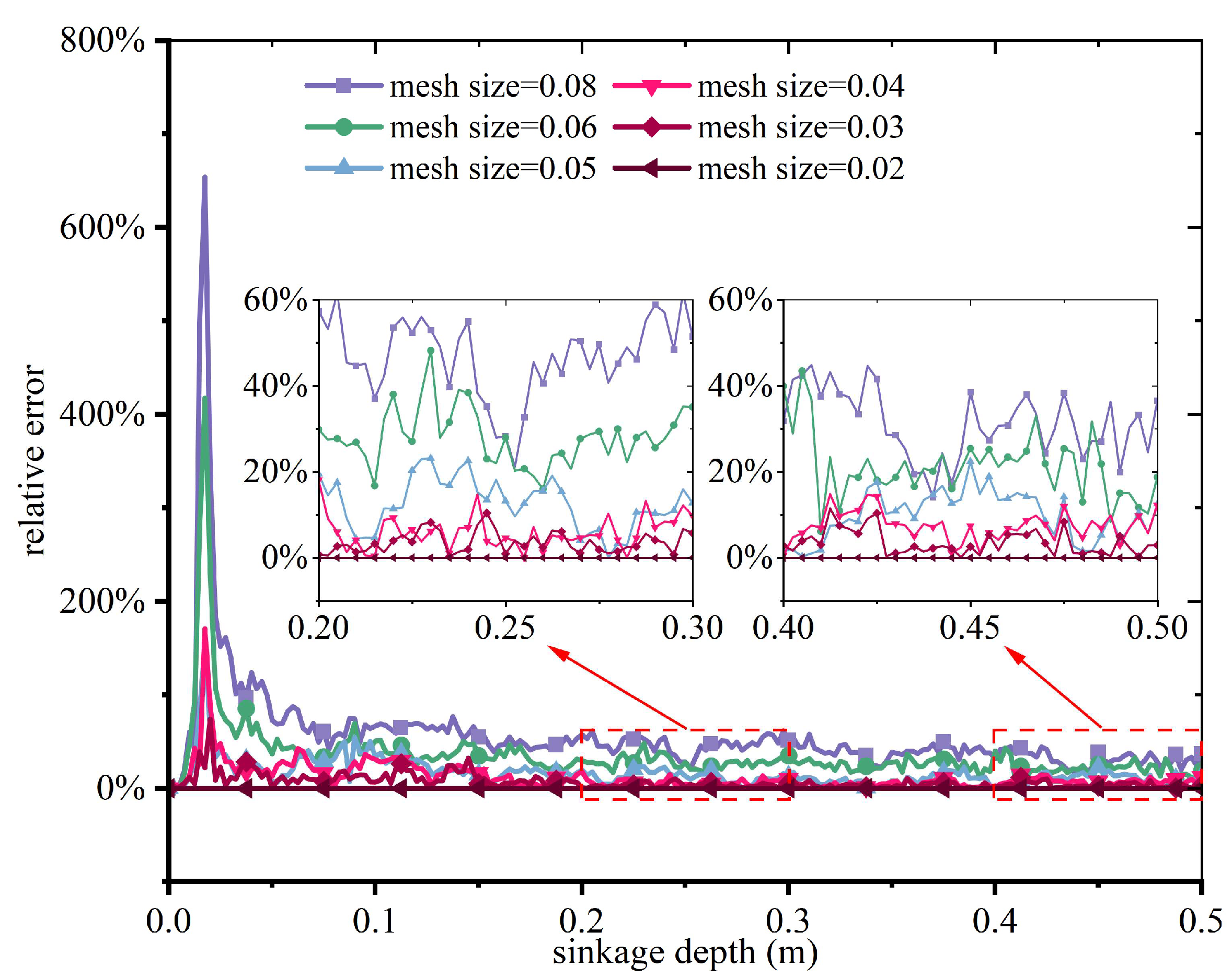
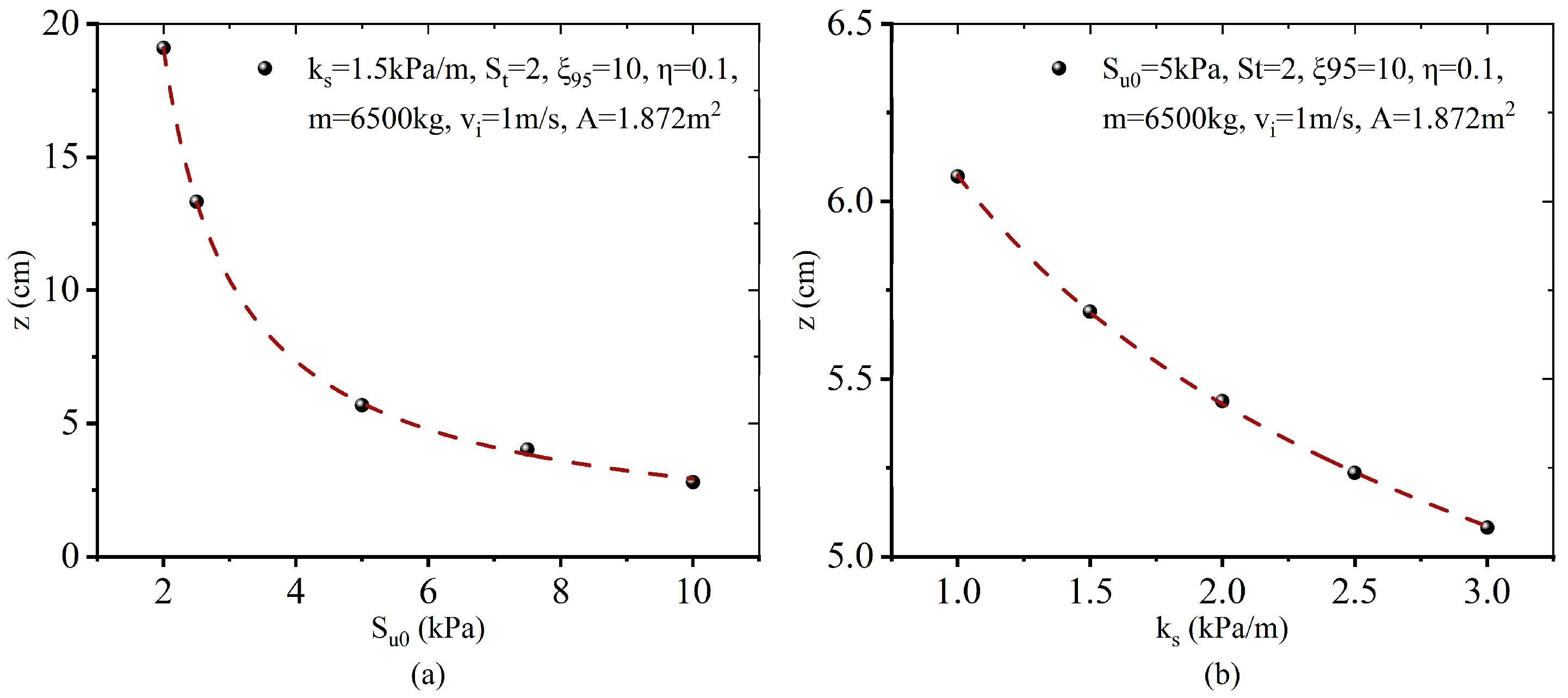
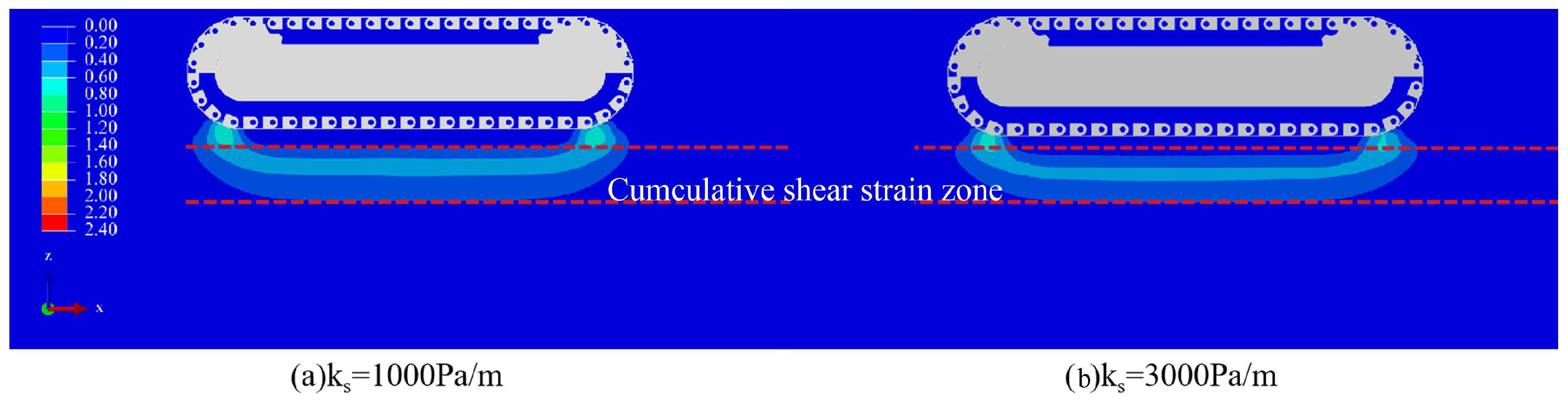
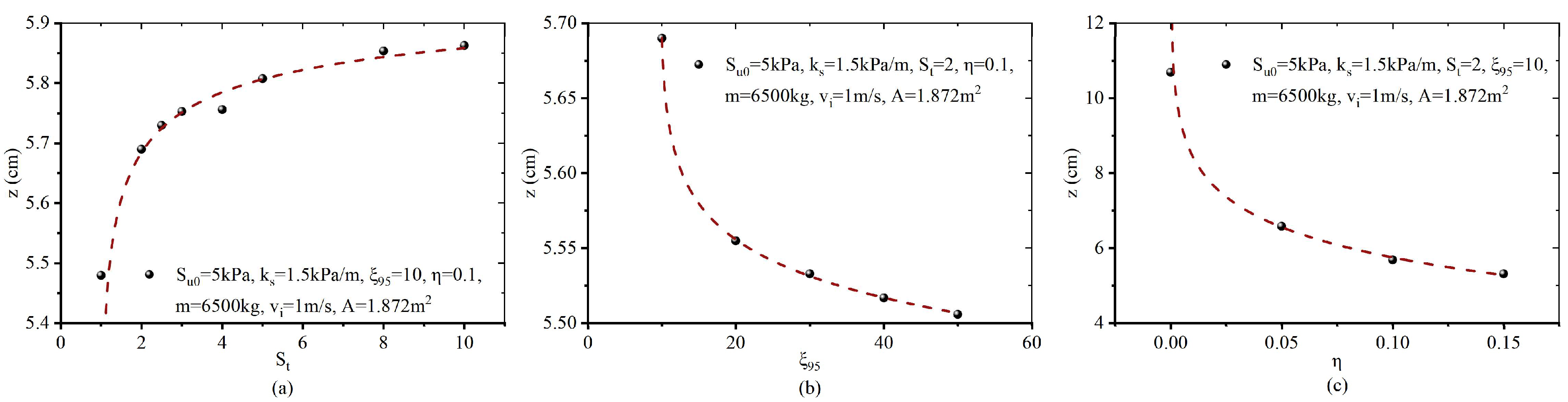

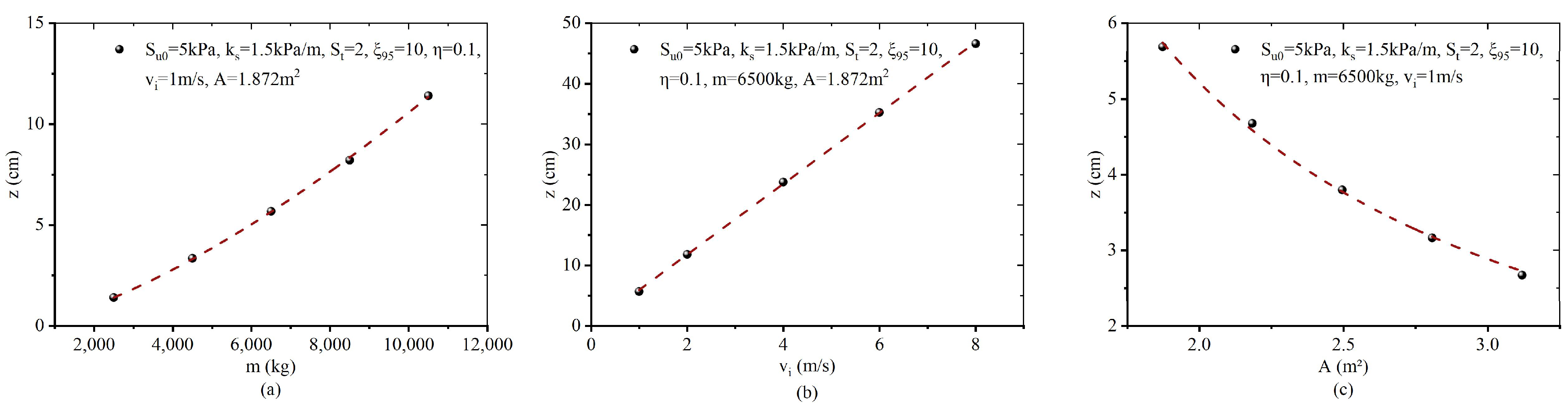
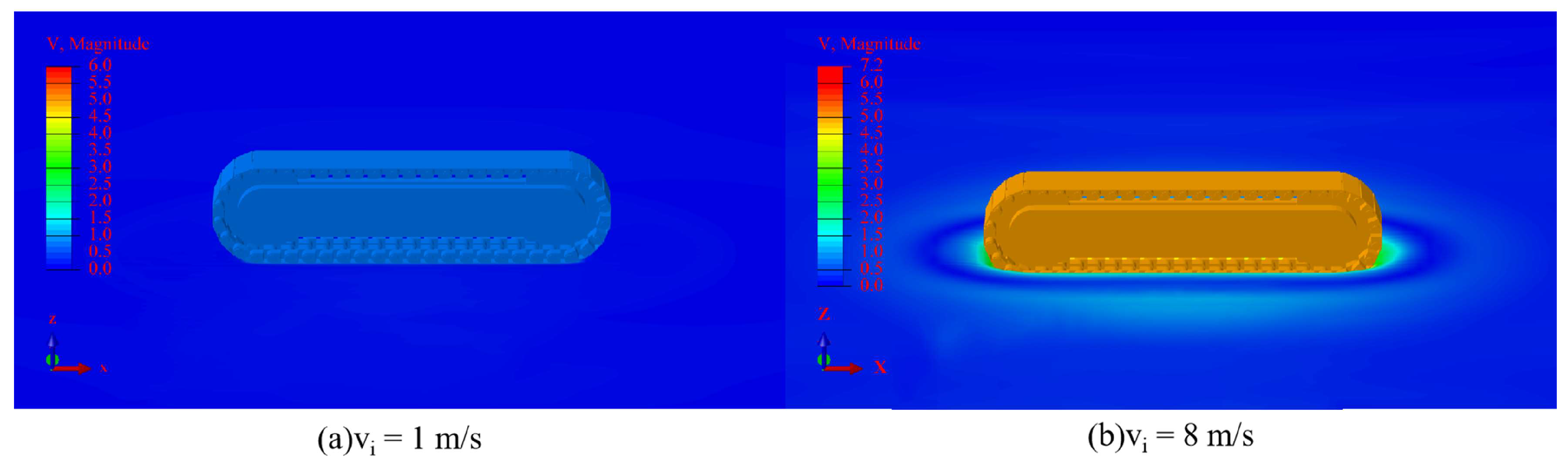

| Sample No. | Submerged Density (kg/m3) | Cohesion (kPa) | Elastic Modulus (MPa) | Soil Sensitivity | Poission’s Ratio |
|---|---|---|---|---|---|
| I | 590 | 15 | 7.5 | 10 | 0.49 |
| II | 520 | 4.2 | 2.1 | 42 | 0.49 |
| III | 660 | 8.2 | 4.1 | 16.4 | 0.49 |
| IV | 180 | 11 | 5.5 | 8.5 | 0.49 |
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | |
|---|---|---|---|---|---|---|
| Center region | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.08 |
| Edge region | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| Number of elements | 1,905,120 | 1,503,663 | 1,248,912 | 1,091,475 | 940,212 | 787,626 |
| Stable time increment (s) | 4.89 × 10−5 | 7.34 × 10−5 | 9.78 × 10−5 | 1.22 × 10−4 | 1.47 × 10−4 | 1.96 × 10−4 |
| m (kg) | A (m2) | vi (m/s) | η | St | ξ95 | Su0 (Pa) | K (Pa/m) |
|---|---|---|---|---|---|---|---|
| 2500 | 1.87 | 1 | 0 | 1 | 10 | 2000 | 0 |
| 3000 | 2.18 | 2 | 0.01 | 2 | 15 | 2500 | 1000 |
| 4500 | 2.5 | 3 | 0.04 | 2.5 | 20 | 3000 | 2000 |
| 6500 | 2.81 | 4 | 0.05 | 3 | 25 | 5000 | 2500 |
| 8500 | 3.12 | 5 | 0.1 | 3.33 | 30 | 6000 | 3000 |
| 9000 | 6 | 0.15 | 4 | 40 | 7500 | ||
| 10,500 | 7 | 5 | 50 | 9000 | |||
| 8 | 8 | 10,000 | |||||
| 10 |
| Parameters | N_Estimators | Max_Depth | Min_Samples_Split | Min_Samples_Leaf | Max_Features |
|---|---|---|---|---|---|
| Value | 146 | 9 | 2 | 1 | 4 |
| Evaluation Metrics | R2 | MSE | MAE | RMSE |
|---|---|---|---|---|
| Training set | 0.9914 | 0.0001 | 0.0066 | 0.0120 |
| Testing set | 0.9807 | 0.0003 | 0.0104 | 0.0173 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Xiu, Z.; Liu, L.; Xie, Q.; Sun, Y.; Yang, J.; Guo, X. Integration of the CEL and ML Methods for Landing Safety Prediction and Optimization of Full-Scale Track Design in a Deep-Sea Mining Vehicle. J. Mar. Sci. Eng. 2025, 13, 1584. https://doi.org/10.3390/jmse13081584
Zeng Y, Xiu Z, Liu L, Xie Q, Sun Y, Yang J, Guo X. Integration of the CEL and ML Methods for Landing Safety Prediction and Optimization of Full-Scale Track Design in a Deep-Sea Mining Vehicle. Journal of Marine Science and Engineering. 2025; 13(8):1584. https://doi.org/10.3390/jmse13081584
Chicago/Turabian StyleZeng, Yifeng, Zongxiang Xiu, Lejun Liu, Qiuhong Xie, Yongfu Sun, Jianghui Yang, and Xingsen Guo. 2025. "Integration of the CEL and ML Methods for Landing Safety Prediction and Optimization of Full-Scale Track Design in a Deep-Sea Mining Vehicle" Journal of Marine Science and Engineering 13, no. 8: 1584. https://doi.org/10.3390/jmse13081584
APA StyleZeng, Y., Xiu, Z., Liu, L., Xie, Q., Sun, Y., Yang, J., & Guo, X. (2025). Integration of the CEL and ML Methods for Landing Safety Prediction and Optimization of Full-Scale Track Design in a Deep-Sea Mining Vehicle. Journal of Marine Science and Engineering, 13(8), 1584. https://doi.org/10.3390/jmse13081584






