Optimizing Underwater Image Restoration and Depth Estimation with Light Field Images

Abstract

Methods based on light field information have shown promising results in depth estimation and underwater image restoration. However, improvements are still needed in terms of depth estimation accuracy and image restoration quality. Previous work on underwater image restoration employed an image formation model (IFM) that overlooked the effects of light attenuation and scattering coefficients in underwater environments, leading to unavoidable color deviation and distortion in the restored images. Additionally, the high blurriness and associated distortions in underwater images make depth information extraction and estimation very challenging. In this paper, we refine the light propagation model and propose a method to estimate the attenuation and backscattering coefficients of the underwater IFM. We simplify these coefficients into distance-related functions and design a relationship between distance and the darkest channel to estimate the water coefficients, effectively suppressing color deviation and distortion in the restoration results. Furthermore, to increase the accuracy of depth estimation, we propose using blur cues to construct a cost for refocusing in the depth direction, reducing the impact of high signal-to-noise ratio environments on depth information extraction, and effectively enhancing the accuracy and robustness of depth estimation. Finally, experimental comparisons show that our method achieves more accurate depth estimation and image restoration closer to real scenes compared to state-of-the-art methods.

1. Introduction

Underwater image restoration and depth estimation are crucial research areas that have broad applications in underwater scene reconstruction, heritage conservation, and seabed surveying, among others. However, underwater optical imaging is often compromised by water quality and lighting conditions, which can lead to color distortion and image blurring. To address these challenges, numerous solutions have been explored, including the use of polarization [1], light fields (LF), and stereoscopic imaging techniques [2]. Among these, light field applications in underwater imaging have garnered attention due to the micro-lens array of light field cameras, which can capture sufficient spatial and angular information in a single shot. This capability makes it possible to extract accurate depth information from a single viewpoint, significantly enhancing the quality of restoration in underwater environments.

A considerable amount of research has utilized light field data to enhance underwater image restoration [3,4,5,6]. These algorithms typically rely on the Image Formation Model (IFM) proposed by Narasimhan and Nayar [7], which assumes constant and identical attenuation and scattering coefficients. However, in real underwater environments, the attenuation coefficient varies with distance and differs from the scattering coefficient, leading to inaccuracies in the IFM that result in noticeable color biases in the restored images.

In the field of underwater depth estimation, the clarity of target scenes is often compromised by backscatter from dense water bodies, leading to blurred images. This effect renders most traditional refocusing algorithms that rely on correlation cues and methods using the dark channel prior for long-range depth estimation ineffective, especially in areas with significant backscatter noise. Recently, researchers like Lu [5] and Huang [8] have proposed using deep neural networks to estimate underwater image depth. However, like all methods that employ deep learning for underwater depth estimation, they face challenges due to the scarcity of adequate paired training data. Consequently, these methods perform poorly in underwater environments where no training data pairs are available.

In this paper, we introduce a method for estimating intrinsic parameters of an underwater image formation model and propose a depth estimation method for underwater light field images based on blur cues. Inspired by [9], we use distance as a cue to estimate the inherent parameters of the water body. However, compared to [9], our method further simplifies the parameters required by the model while maintaining accuracy. Furthermore, leveraging the positive correlation between underwater image depth and blurriness, we propose using blur cues as a cost component for light field depth refocusing, effectively enhancing the accuracy of depth estimation in underwater scenes. As illustrated in Figure 1, our approach achieves higher accuracy in depth estimation and improves image restoration outcomes in underwater settings. The contributions of this paper are outlined as follows:

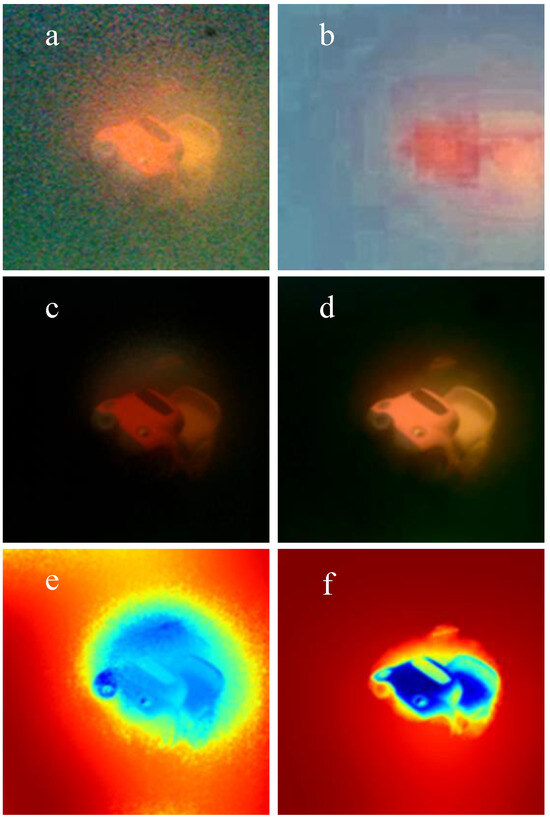
Figure 1. Comparison of Depth Estimation and Image Restoration. (a) Central view of an underwater light field image captured with a light field camera. (b) Restored image using Huang’s deep learning-based method [8]. (c) Restored image using Tian’s light field refocusing method [3]. (d) Restored image using our method. (e) Depth estimation by Tian [3]. (f) Depth estimation image using our method.

• We have introduced an underwater light propagation model for image restoration and developed a method to estimate water body attenuation parameters and backscatter;
• We proposed a method for underwater image depth estimation that utilizes the relationship between blurriness and scene depth as one of the clues for estimating the depth of underwater light field images, thereby improving the accuracy of underwater scene depth estimation;
• In an experimental water tank environment, we demonstrated through extensive experimental data that our method achieves higher depth estimation accuracy and better restoration effects compared to previous methods.

2. Related Work

The problem of underwater image degradation has been approached from various research angles, such as hardware-based and software-based restoration techniques. Image distortions caused by forward attenuation are generally addressed using software approaches, including the establishment of attenuation functions [10,11,12], image enhancement [13], or deep learning methods [8]. However, software solutions face limitations in handling information loss caused by scattering noise, and deep learning approaches struggle to acquire high-quality data pairs for training.

To mitigate backscatter noise, Schechner and Karpel [1] utilized the polarization properties of light in the medium, capturing images at different angles with polarizers to retrieve effective image information. Hitam et al. [14] explored range-gated imaging, using pulsed lasers and fast-gated cameras to precisely control the imaging process and reduce backscatter. Additionally, Roser and colleagues [2] employed stereoscopic imaging techniques to determine object distances by comparing the disparity between images captured from different angles. These methods have achieved notable results, but harsh underwater conditions can significantly reduce the imaging quality, thus impacting the performance of traditional sensors and environmental sensing accuracy.

In recent years, as light field cameras have entered the consumer market, the field of light field imaging has garnered increased attention. Compared to traditional imaging, light field cameras can capture not only the intensity of light but also its angular information, allowing for far superior estimation accuracy in image depth. Tao and others [15] combined digital refocusing blur cues with corresponding cues to estimate scene depth. Georgiev [16] further applied this to super-resolution imaging.

However, there has been limited research on using light field cameras for underwater image restoration. Tian [3] and Lu [4] were the first to attempt applying light field methods to underwater image restoration, combining the dark channel prior (DCP) [17] method and digital refocusing cues to estimate depth maps and restore images, which showed better robustness and restoration effects compared to monocular image strategies. Skinner [18] applied 2D defogging methods to each sub-aperture image and processed them using guided image filtering, resulting in 4D defogged underwater light field images. Feng [19] established an underwater imaging system based on Mie scattering theory for underwater 3D reconstruction and image restoration. Additionally, Lu [20] introduced depth convolutional neural fields in image restoration tasks to address the desaturation problem in light field images. To tackle the challenge of obtaining underwater image data, Ye [21] proposed a deep learning-based method to transform images taken in air into underwater images. However, due to limited training data, the effectiveness of deep learning methods was not satisfactory. While these methods have achieved good results, they have neglected the impact of light imaging model parameters in the restoration process. Moreover, the accuracy of light field depth estimation methods needs improvement due to the noise caused by backscattering.

Despite the superior performance of light field cameras compared to traditional cameras, there remain significant limitations. In this paper, we employ blur cues from light field refocusing combined with traditional priors to achieve more accurate depth maps. We then introduce a refined underwater optical imaging model and estimate more precise parameters for light attenuation and scattering to improve the quality of underwater image restoration.

The remainder of this paper is organized as follows. In Section 3, we describe the proposed method. In Section 4, we set up the experiments and conduct extensive performance comparisons of the results. In Section 5, we provide some discussions and conclusions. Specifically, in Section 3.1, we describe the image restoration model and its related parameters, and the subsequent subsection details the solving process for these parameters. In Section 3.2, we explain the methods and processes for solving the scattering and attenuation coefficients in the model. In Section 3.3, we present our proposed underwater light field depth estimation method. In Section 3.4, we describe the refocusing restoration process for light field images.

3. Method

3.1. Underwater Image Formation Model

Figure 2 depicts the underwater image formation model, where the camera captures underwater image information comprising attenuated direct signals and scattered signals from the water body. The imaging model is represented as follows:

$$I_c\left(x\right)=D_c\left(x\right)+B_c\left(x\right),$$

(1)

where $c\in \{R,G,B\}$ represents the color channels, $I_c$ is the distorted image captured by the camera, $D_c$ is the target information attenuated during propagation through the water, and $B_c$ is the scattering signal from light reflected off particles suspended in the water, which degrades and blurs the image.

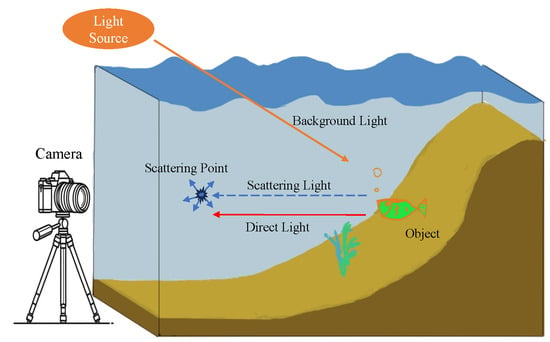
Figure 2. Schematic diagram of underwater imaging and light propagation in Scattering media.

The extended form of Equation (1) is given as follows [9]:

$$I_c\left(x\right)=J_c\left(x\right)e^{-{\beta }_c^{D}z}+B_c^{\infty }\left(1-e^{-{\beta }_c^{B}z}\right),$$

(2)

where z denotes the distance from the camera to the target, $B_c^{\infty }$ represents the external input light source, $J_c$ represents the undegraded scene image, ${\beta }_c^D$ is the beam attenuation coefficient, and ${\beta }_c^B$ is the backscattering coefficient of the water body.

The attenuation coefficient ${\beta }_c^D$ in the attenuation term $D_c\left(x\right)$ depends on wavelength $\lambda$, depth d, and distance z. Similarly, the scattering coefficient ${\beta }_c^B$ is related to the wavelength and the background light $B_c$. These coefficients can be expressed as follows [22]:

$$\begin{array}{cc}\hfill & {\beta }_c^D=ln\left[\frac{{\int }_{{\lambda }_1}^{{\lambda }_2}{S}_c\left(\lambda \right)\rho \left(\lambda \right)E(d,\lambda )e^{-\beta \left(\lambda \right)z}d\lambda }{{\int }_{{\lambda }_1}^{{\lambda }_2}{S}_c\left(\lambda \right)\rho \left(\lambda \right)E(d,\lambda )e^{-\beta \left(\lambda \right)(z+\Delta z)}d\lambda }\right]/\Delta z\hfill \\ \hfill & {\beta }_c^B=ln\left[1-\frac{{\int }_{{\lambda }_1}^{{\lambda }_2}{S}_c\left(\lambda \right)B^{\infty }\left(\lambda \right)(1-e^{-\beta \left(\lambda \right)z})d\lambda }{{\int }_{{\lambda }_1}^{{\lambda }_2}{B}^{\infty }\left(\lambda \right)S_c\left(\lambda \right)d\lambda }\right]/z,\hfill \end{array}$$

(3)

where $\rho$ represents the reflectance of the object’s surface, $E(d,\lambda )$ is the intensity of the incident light at depth d, $S_c$ is the spectral response of the camera, $\beta$ is the physical attenuation coefficient, and ${\lambda }_1$ and ${\lambda }_2$ represent the visible wavelength range (400 to 700 nm).

The background light $B_c^{\infty }$ is the sum of the light received at the position where the distance $z\to \infty$, represented by the following:

$$B_c^{\infty }={\int }_{{\lambda }_1}^{{\lambda }_2}{B}^{\infty }\left(\lambda \right)S_c\left(\lambda \right)d\lambda .$$

(4)

3.2. Coefficients Estimation

According to Equation (2), to effectively restore underwater images, it is essential to determine or estimate the parameters associated with light attenuation and scattering during propagation. As mentioned in Equation (3), (${\beta }_c^D$) and (${\beta }_c^B$) depend on the parameters $\{z,\rho ,E\left(d\right),S_c,\beta \}$ and $\{E\left(d\right),S_c,\beta \}$, respectively. The parameters $\beta$, $E\left(d\right)$ (defined by the optical water type), the depth d at which photos are taken, the reflectance $\rho$ of each target in the scene, and the camera response $S_c$ are considered constants once determined at the time of capture. These parameters are seldom known precisely at the time an underwater photo is taken. ${\beta }_c^D$ is significantly influenced by the distance z, and ${\beta }_c^B$ is highly correlated with the type of water body and illumination. Here we detail the methods for estimating these coefficients.

3.2.1. ${\beta }_c^B$ and $B_c^{\infty }$ Estimation

To estimate the backscattering parameters, it is crucial to isolate other influencing factors. Inspired by He’s [23] dark channel prior method, where the minimum RGB values in a hazy image’s dark channel represent the relative distance between the camera and the target and the maximum values indicate the background light region, our approach differs in that we know the target distance range rather than estimating it.

From Equations (1) and (2):

$$B_c\left(x\right)=J_c\left(x\right)e^{-{\beta }_c^{D}z}+I_c\left(x\right).$$

(5)

It is evident that the backscatter part is related to distance z and reflectance $\rho$, and tends to the captured distorted image as distance increases or target reflectance decreases. Therefore, for reflectance $\rho \to 0$ or $E_d\to 0$ (in shadow regions), the captured target pixel intensity tends toward the backscatter pixel intensity $B_c\left(x\right)\to I_c\left(x\right)$. This is similar to the DCP method, but here we look for the lowest 1% of RGB triplets in the image area represented as $\mathsf{\Omega }$ where ${\rho }_c\approx 0$ or $E_d\approx 0$, hence ${\widehat{B}}_c\left(\mathsf{\Omega }\right)\approx I_c\left(\mathsf{\Omega }\right)$. Concurrently, to obtain a more accurate scattering parameter relative to distance, we take the target distance as a known parameter. Thus, the backscatter in the region $\mathsf{\Omega }$ can be further expressed as follows:

$${\widehat{B}}_c\approx B_c^{\infty }(1-e^{-{\beta }_c^B{z}_i})+J_c^{\prime }{e}^{-{\beta }_c^{D^{\prime }}{z}_i},$$

(6)

where $z_i$ is the known distance variable and $J_c^{\prime }{e}^{-{\beta }_c^{D^{\prime }}{z}_i}$ represents a minor residual amount, retained due to dense scattering conditions in water. Using nonlinear least squares, we then estimate parameters $B_c^{\infty }$, ${\beta }_c^B$, $J_c^{\prime }$, ${\beta }_c^{D^{\prime }}$. Note that since the forward signal is minimal, ${\beta }_c^{D^{\prime }}$ can be temporarily considered constant.

3.2.2. ${\beta }_c^D\left(z\right)$ Estimation

According to [9], ${\beta }_c^D$ is strongly related to distance z, and its dependency on any range z is described using a dual-exponential form:

$${\beta }_c^D\left(z\right)={\alpha }_{1}exp\left({\alpha }_{2}z\right)+{\alpha }_{3}exp\left({\alpha }_{4}z\right),$$

(7)

where ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, and ${\alpha }_4$ are constants.

Assuming $B_c^{\infty }$ and ${\beta }_c^B$ have been obtained, $B_c$ can be removed from the original image $I_c$, and ${\beta }_c^D\left(z\right)$ can be estimated by processing the direct signal $D_c$. According to Equations (2) and (3), the restored image can be expressed as follows:

$${\widehat{J}}_c\left(x\right)=(I_c\left(x\right)-B_c)e^{{\beta }_c^D\left(z\right)·z}.$$

(8)

In our experimental setup, where absolute distances are not extensive, we assume the corresponding image captured in clear water undergoes minimal scattering and attenuation, using it as a reference image for restoration effects set as ${\widehat{J}}_c\left(x\right)$. Rewriting the formula, we obtain the following:

$$\tilde{z}=\frac{ln{\widehat{J}}_c\left(x\right)}{I_c\left(x\right)-B_c}/e^{{\beta }_c^D\left(z\right)}.$$

(9)

By minimizing this expression, we obtain discrete ${\beta }_c^D$ data related to range z.

$$\underset{{\beta }_c^D\left(z\right)}{min}\parallel \tilde{z}-z\parallel$$

(10)

Combining with Equations (7) and (9), we derive constants ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, ${\alpha }_4$ for ${\beta }_c^D$.

3.3. Depth Estimation

In densely scattering media such as water, the random scattering of light during propagation leads to restored images with relatively low signal-to-noise ratios, causing traditional defocus and correspondence cues to perform poorly. To address this, we propose using blur cues and incorporating a depth threshold method to reduce the influence of noise on depth estimation, thereby improving accuracy. Below, we detail our approach.

3.3.1. Construction of Blur Clue Cost

We utilize a parallel plane parameterization to represent the four-dimensional light field $L_F(x,y,u,v)$, where $(x,y)$ and $(u,v)$ correspond to spatial and angular coordinates, respectively. Following Ng et al. [24], we segment the light field data at different depths as follows:

$$L_{\alpha }(x,y,u,v)=L_F\left(x+u\left(1-\frac{1}{\alpha }\right),y+v\left(1-\frac{1}{\alpha }\right),u,v\right),$$

(11)

where $\alpha$ represents the current focus depth ratio and $L_{\alpha }$ is the refocused light field image at the depth ratio $\alpha$, with the central view located at coordinates $(u,v)=(0,0)$.

Considering that the further the distance of a target pixel due to attenuation, the greater its blurriness, and that the blurriness of a target pixel after light field refocusing is inversely proportional to its true distance, we choose to use blurriness as a cost clue for depth estimation. We employ a local frequency analysis method using the Discrete Cosine Transform (DCT) [25] to analyze the characteristics of the area around a pixel. By evaluating the absence of high-frequency components, we can quantify the image’s blurriness. The DCT representation for the area $\mathsf{\Omega }$ around a clue point $(x,y)$ is given as follows:

$$T(p,q)=c\left(p\right)c\left(q\right)\sum _{x=0}^{N-1}\sum _{y=0}^{N-1}\mathsf{\Omega }(x,y)cos\left[\frac{\pi (2x+1)p}{2N}\right]cos\left[\frac{\pi (2y+1)q}{2N}\right],$$

(12)

where $p,q$ are frequency variables ranging from 0 to $N-1$, $\mathsf{\Omega }(x,y)$ are the pixel values in an $N\times N$ area, and $c\left(p\right),c\left(q\right)$ are normalization factors defined as follows:

$$c\left(p\right)=\left\{\begin{array}{cc}\frac{1}{\sqrt{N}}\hfill & \mathrm{if}p=0\hfill \\ \sqrt{\frac{2}{N}}\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

(13)

The blurriness at that location is then expressed as follows:

$$M_{\alpha }(x,y)=\sum _{p=1}^{N-1}\sum _{q=1}^{N-1}{\left|T(p,q)\right|}^2.$$

(14)

For the refocused light field image at depth ratio $\alpha$, the cost clue is represented as follows:

$$C_{\alpha }^M(x,y)=\frac{1}{N}\sum _{u,v}{M}_{\alpha }(x,y,u,v).$$

(15)

This method systematically utilizes the inherent blurriness of the underwater images caused by scattering to establish a robust depth estimation framework. By integrating blur as a quantitative measure into the cost function for depth estimation, we can enhance the accuracy of light field-based depth estimation in challenging underwater conditions.

3.3.2. Single Image Preprocessing

Given the initial high blurriness of underwater images, it is crucial to obtain more texture detail information through preprocessing before depth estimation. As discussed in Section 3.2, having acquired the parameters of the light propagation model, we now only need an initial depth estimate to retrieve more detailed textures from underwater images.

Inspired by the methods of Peng [11] and Carlevaris-Bianco [26], we combine the characteristics of these two approaches for our image preprocessing depth estimation.

First, considering the relationship between imaging distance and blurriness in the captured images, Peng [11] introduced an image formation model based on blurriness prior, where the pixel blurriness related to depth distance is represented as follows:

$$F\left(x\right)=\underset{y\in \mathsf{\Omega }\left(x\right)}{max}\left\{\frac{1}{n}\sum _{i=1}^n\left|I_{\mathrm{grey}}\left(y\right)-G\left(I_{\mathrm{grey}}\left(y\right)\right)\right|\right\},$$

(16)

where $I_{\mathrm{grey}}$ is the grayscale version of the input image $I_c$, G is a spatial filter of size $h\times h$ with variance ${\sigma }^2$, set as $h=2^{i+n+1}$, with n set to 4. $\mathsf{\Omega }\left(x\right)$ is a local patch centered at x.

Next, we estimate depth distances based on the absorption rate differences of light at various wavelengths in the medium, where attenuation of red wavelengths is greater than that of blue and green wavelengths. Carlevaris-Bianco [26] suggested using the difference between the maximum intensities of the red channel and the green and blue channels as depth cues, represented as follows:

$$Q\left(x\right)=\underset{y\in \mathsf{\Omega }\left(x\right)}{max}{I}_r\left(y\right)-\underset{y\in \mathsf{\Omega }\left(x\right)}{max}\{I_g\left(y\right),I_b\left(y\right)\}.$$

(17)

We combine the distance cues from Equations (16) and (17) to estimate an initial depth map, expressed as follows:

$$\begin{array}{cc}\hfill {\tilde{z}}_F& =1-N_{\mathrm{norm}}\left(F\left(x\right)\right)\hfill \\ \hfill {\tilde{z}}_Q& =1-N_{\mathrm{norm}}\left(Q\left(x\right)\right)\hfill \end{array},$$

(18)

where $N_{\mathrm{norm}}$ is a stretching normalization function. Then, depending on the input’s average red channel value, we choose between light absorption-based or image blurriness-based methods to estimate the underwater scene depth:

$${\tilde{z}}_{\mathrm{init}}={\tilde{d}}_F+(1-\theta ){\tilde{d}}_Q,$$

(19)

where $\theta =S(\mathrm{avg}\left(I_r\right),0.1)$, $avg$ is the mean function, and S is the sigmoid function defined as follows:

$$S(a,b)=\frac{1}{1+e^{-s(a-b)}},$$

(20)

where s controls the slope of the activation function, thereby controlling the amplitude of the output change when the input values have slight differences. We experimented with different values and found that the model performs best when $s=32$.

Finally, based on Equation (19), we can obtain the initial depth estimation map. By substituting the depth results into the process described in Section 3.1, we can obtain the preliminary restored underwater image.

3.3.3. Depth Cue Fusion and Depth Estimation

After obtaining the blur-based depth cues to enhance the robustness of depth estimation, we also introduce Tao’s [15] defocus cost as a supplementary metric. The spatial point defocus cost response is represented as follows:

$$C_{\alpha }^F(x,y)=\frac{1}{|W_F|}\sum _{x^{\prime },y^{\prime }\in W_F}\left|\Delta {\overline{L}}_{\alpha }(x^{\prime },y^{\prime })\right|,$$

(21)

where $W_F$ is the window size around the current pixel, $\Delta$ is the Laplacian operator in both horizontal and vertical directions, and ${\overline{L}}_{\alpha }(x,y)$ is the mean of all angular positions for that pixel, expressed as follows:

$${\overline{L}}_{\alpha }(x,y)=\frac{1}{N}\sum _{u,v}{L}_{\alpha }(x,y,u,v).$$

(22)

Combining the depth cost clues from Equations (15) and (21), the depth relationship is finally established as follows:

$$z_{{\alpha }^{\ast }}(x,y)=arg\underset{\alpha }{min}\left\{C_{\alpha }^F(x,y)+C_{\alpha }^M(x,y)\right\}.$$

(23)

By inputting the restored light field image into this formula, we obtain the depth estimation map for the underwater light field image. This comprehensive approach effectively merges various depth cues to produce a more accurate and robust estimation of underwater depths.

3.4. Underwater LF Image Restoration

Although attenuation and scattering effects have been removed in light field imaging, the random scattering of light by particles in water often still results in noise in the restored images, especially in waters with high turbidity. To address this, we take into account that the noise patterns and their distributions formed at the same object point across different sub-apertures vary. By averaging multiple light field views through a light field refocusing algorithm, we can further suppress noise and reduce the impact of backscatter noise.

4. Experimental Results

This section introduces the experimental setup, displays results from our experimental apparatus, compares them against various state-of-the-art algorithms, and discusses the limitations of our approach.

4.1. Experimental Methodology

In this study, we conducted experiments in a dark environment using a water tank with dimensions of 0.7 × 0.4 × 0.4 m. All sides of the tank, except the shooting face, were covered with opaque black film to prevent external light reflections. We used white LED lights as the light source. The Lytro Illum camera was positioned 2 cm away from the tank. Figure 3 illustrates this experimental setup. Note that the selection of the tank size was based on the physical space constraints of the laboratory and the practical feasibility of operations. Ideally, a larger water tank would better simulate the light propagation paths in real environments. However, due to the limitations of our laboratory conditions, we could only use the available size of the water tank for our experiments.

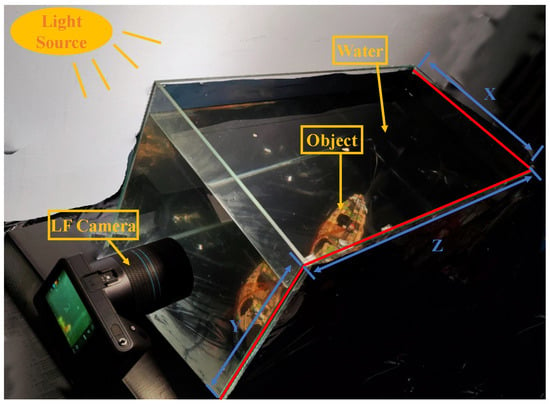
Figure 3. Our experimental setup.

In the experiment, we gradually added milk to the water tank, totaling 4 mL. This incremental addition method allowed us to precisely control the turbidity of the water, thereby simulating different levels of scattering effects.

We chose milk as the scattering medium because it can evenly disperse in water, providing consistent optical scattering effects. Although other studies have used substances like red wine, milk is more suitable for simulating suspended particles and turbidity in water. Additionally, milk is easy to control and measure, and its optical properties better meet the requirements of our experiment.

4.2. Results Comparisons

In this experiment, we evaluated the performance of our proposed method against the latest techniques in image restoration and depth estimation. We selected prior-based single image methods for depth estimation and restoration [11,27], light field (LF)-based methods [3], and deep learning-based methods [8,28] for comparison. It should be noted that the LF-based methods were not optimized specifically for this task during replication, leading to discrepancies between their replication results and practical outcomes. Note that the methods selected above all have publicly available source code or authors willing to provide the code. This allows us to accurately reproduce the results of these methods and make fair comparisons.

The original image data used in Figure 4 and Figure 5, labeled LF1 to LF5, were collected in a medium turbidity environment created by adding 4ml of milk. To verify robustness to distance, the targets in these five scenes were randomly placed at different positions in the water tank, with designs including both single target and varying positions of front and back targets.

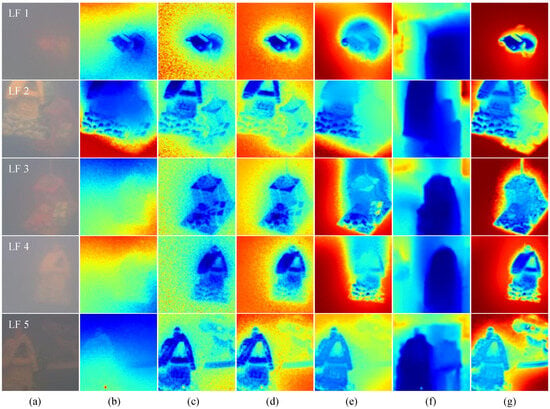
Figure 4. Comparison of depth estimation results. (a) Original image. (b) UDCP [27]. (c) ULAP [10]. (d) IBLA [11]. (e) Tian’s method [3]. (f) UW-Net [28]. (g) Our method.

Figure 5. Comparison of restoration results. (a) Original image. (b) UDCP [27]. (c) ULAP [10]. (d) IBLA [11]. (e) Tian’s method [3]. (f) Semi-UIR [8]. (g) Our method.

Figure 4 presents a comparison of depth estimation results between our method and other methods, corresponding to the original images in column (a). In columns (b–c) of Figure 4, methods based on blur and light attenuation priors show relatively stable performance but are significantly affected by high blur in the background regions. In column (d), the light field-based depth estimation method performs well in blurred background regions, second only to our method. However, it exhibits poor robustness in the halo regions caused by light scattering around the target. Column (e) shows good detail in the target area but performs poorly in noisy regions. Column (f) has the worst performance due to the limited generalization capability caused by the underwater image data constraints. Column (g) of our method exhibits more target depth details and smoother, more accurate results in noisy background regions. From a subjective evaluation perspective, our method exhibits certain advantages over other methods in terms of depth estimation accuracy in areas with background light noise interference and target details.

Figure 5 provides a comparison of restoration effects between our method and other methods based on the original images shown in column (a). Columns (b–c) in Figure 5 show that prior-based methods result in noticeable red color casts in the restored images. Additionally, due to incorrect depth map estimation, the target blur remains significant. Columns (d) and (f) display a certain degree of blue-green cast, and the image in column (f) is relatively blurred. Column (e) performs well in the background region but still exhibits some red color cast in the target area. Column (g) of our method effectively removes backscatter from both the target and background, reducing noise. Additionally, light field refocusing brings about better clarity, and the colors are more aligned with human visual perception. Therefore, from a subjective evaluation perspective, our method demonstrates better restoration effects compared to the other methods.

Underwater images have various objective evaluation methods. The underwater color image quality evaluation (UCIQE) [29] is the most widely used set of criteria, providing a no-reference metric specifically for assessing underwater image quality by analyzing color, saturation, and contrast. This standard addresses image quality degradation caused by light attenuation, scattering, and color shifts. A higher score indicates better image quality. Table 1 presents the evaluation scores for Figure 5. It can be observed that the image restoration results of our method achieve better overall performance across the five different image scenes compared to other methods.

Table 1. Comparison of restoration results using the UCIQE scores corresponding to Figure 5.

Method	LF1	LF2	LF3	LF4	LF5	Average
UDCP	20.32	20.75	21.16	19.07	20.44	20.34
ULAP	25.09	32.43	23.89	25.11	22.03	25.31
IBLA	18.35	14.38	10.02	10.12	9.447	12.86
Tian’s method	26.11	28.72	21.88	19.43	30.09	25.24
Semi-UIR	16.72	25.13	24.64	21.16	19.43	21.01
Our method	27.21	27.99	30.27	28.42	37.24	30.22

The best result is shown in Red.

Furthermore, We also tested the robustness of our method in environments with varying degrees of turbidity. We evaluated the restoration performance of our approach in waters of different turbidity levels using the underwater color image quality evaluation (UCIQE) and the structural similarity index (SSIM) [30] as quality metrics. SSIM, which mimics the human visual system to measure the structural similarity between two images, is a widely used reference-based index. We used images captured in clear water as the real image reference. The restoration results, as shown in Figure 6 and Figure 7, demonstrate that our method outperforms others across various turbidity levels. However, our method has limitations; when the water reaches a certain level of turbidity, the quality of our restored images rapidly deteriorates.

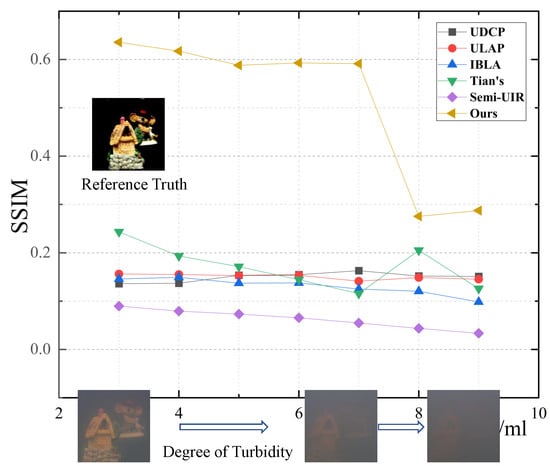
Figure 6. Comparison of restoration results across various turbidity levels using the SSIM index. For better display, our data begins recording from the third addition of an equal amount of milk. Note that aside from our results and Tian’s results, all other views are from the LF’s central perspective. Note that all images are from the same original target with turbidity being the only variable.

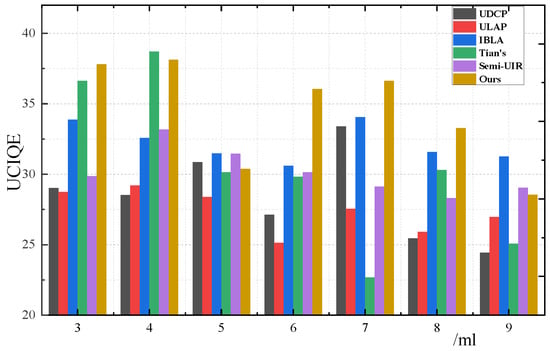
Figure 7. Comparison of restoration effects across various turbidity levels using the UCIQE index. Note that all image data is the same as in Figure 6.

In summary, we subjectively compared the latest methods with our proposed approach in terms of depth maps and image restoration. Our method demonstrates better accuracy and image texture details in the depth maps compared to other methods. Additionally, due to the full-focus characteristics of the light field, our method significantly outperformed single image approaches in controlling noise in the final restored images. Objectively, we used the reference-free UCIQE to compare the restoration effects of different models and the reference-based SSIM to assess the restoration performance under various turbidity levels. The results conclusively showed that our method performed better than existing methods in both respects.

5. Discussion and Conclusions

In this paper, we proposed a method for underwater depth estimation and image restoration in near-field illumination environments. Our contributions include introducing a novel approach that utilizes blurriness and backscatter as depth estimation cues, proposing an image restoration scheme based on state-of-the-art underwater imaging models in near-field illumination and dense scattering environments, and a method to improve the accuracy of light field depth estimation in dense noisy environments. Through comparisons with existing methods, our approach demonstrates improved accuracy in depth estimation, image restoration, and stability compared to color prior-based methods and several state-of-the-art light field-based restoration methods. However, our results also have some errors and limitations, such as inaccuracies in depth estimation in shadow regions and a significant decline in restoration performance in highly turbid water. Future research will further optimize our method and validate its effectiveness under more experimental conditions. Our next step is to establish a database of underwater light field images to analyze the impact of different lighting conditions and water parameters on imaging.