Available-Maneuvering-Margins-Based Ship Collision Alert System

Abstract

The timing of a ship taking evasive maneuvers is crucial for the success of collision avoidance, which is affected by the perceived risk by the navigator. Therefore, we propose a collision alert system (CAS) based on the perceived risk by the navigator to trigger a ship’s evasive maneuvers in a timely manner to avoid close-quarters situations. The available maneuvering margins (AMM) with ship stability guarantees are selected as a proxy to reflect the perceived risk of a navigator; hence, the proposed CAS is referred to as an AMM-based CAS. Considering the dynamic nature of ship operations, the non-linear velocity obstacle method is utilized to identify the presence of collision risk to further activate this AMM-based CAS. The AMM of a ship are measured based on ship maneuverability and stability models, and the degree to which they violate the risk-perception-based ship domain determines the level of collision alert. Several typical encounter scenarios are selected from AIS data to demonstrate the feasibility of this AMM-based CAS. The promising results suggest that this proposed AMM-based CAS is applicable in both ship pair encounter and multi-vessel encounter scenarios. Collision risk can be accurately detected, and then a collision alert consistent with the risk severity is issued. This proposed AMM-based CAS has the potential to assist autonomous ships in understanding the risk level of the encounter situation and determining the timing for evasive maneuvers. The advantages and limitation of this proposed method are discussed.

1. Introduction

Although many advanced methods and technologies have been applied in the maritime field, ship collisions still occur frequently, posing a threat to maritime transportation safety [1,2,3,4,5]. Ship collision alert systems (CAS) are widely applied to prevent ship collision by alerting the navigators to take evasive maneuvers in a timely manner to eliminate the existing collision risk [6,7,8,9,10,11,12,13,14,15]. Some limitations or simplifications of these methods make it challenging to put them into practical use. One is the inadequate consideration paid to the dynamic nature of ship maneuvers. This can be proven by the most widely used blind sailing hypothesis that when there is a risk of collision, the ship is assumed to sail in a straight line with a constant speed. As a matter of fact, the ship will normally take evasive maneuvers for collision avoidance [16,17]. The second limitation is the neglect of the risk resolution. The existing research mainly utilized the danger level of approaching ships as a basis to quantify risk severity. The risk resolution of a ship reflects her capability to eliminate the existing danger, which is critical to the success of collision avoidance. Under the same circumstances, a ship with a higher risk resolution is more likely to eliminate the risk, so the risk is relatively low. Therefore, risk measures independent of conflict resolution may lead to inaccurate detection of actual danger [18]. Third, these methods are mainly designed for ship pair encounters without considering traffic conditions [10]. The traffic complexity increases the likelihood of serious encounters [19,20,21], so the applicability of these methods in complicated multi-vessel encounters has not been confirmed.

Many methods have been proposed to alert the navigator of imminent danger, including the last time to maneuver [22], the minimum distance to collision [23], the last line of defense [16] and critical safety area [24]. A projected collision can still be avoided if the navigator takes evasive maneuvers before reaching the critical condition. “Action too late” is the primary cause of collisions [25]. However, these methods cannot provide an optimal solution for starting evasive maneuvers to avoid serious encounters, such as close-quarters situations and imminent danger.

Our previous work proposes a risk-perception-based ship domain [26]. This ship domain reveals the general strategy of a ship determining the timing for taking evasive maneuvers. The boundary of the risk-perception-based ship domain is quantified by statistically analyzing the perceived risk of a navigator when the first evasive maneuvers started over a large sample of vessel encounters taken from AIS data. A non-linear velocity obstacle (NLVO) algorithm is adopted to detect collision risk with the dynamic nature of ship maneuvers considered. Available maneuvering margins (AMM) are utilized as a proxy to measure the perceived collision risk by the navigator, so the risk resolution of a ship is considered. Although this risk-perception-based ship domain considers the dynamic nature of ship operations and risk resolution, this risk-perception-based ship domain cannot be directly used to define when a ship should maneuver for collision avoidance in practical applications. The constraint of ship stability is not considered. Some drastic maneuvers leading to the success of collision avoidance can create risk of the ship capsizing. The neglect of ship stability leads to an inaccurate estimation of ship’s capability to eliminate the collision risk.

Therefore, the principal aim of this work is to construct a CAS based on the perceived risk by the navigator, which is applicable in encounter scenarios with various traffic complexities, including both ship pair encounters and multi-vessel encounters. The available maneuvering margins (AMM) with ship stability guarantees are selected as a proxy to reflect the perceived risk of a navigator, hence this proposed CAS is referred to as AMM-based CAS. The existence of collision risk activates this AMM-based CAS, whereas the degree of the violation of this risk-perception-based ship domain determines the level of collision alert. To be clear, our work alerts the ship of a collision in a timely manner and supports in determining the timing for taking evasive maneuvers rather than directly proposing collision avoidance maneuvers. This ship collision alert system intends to further contribute to the development of maritime autonomous surface ships (MASS), particularly in assisting their strategizing for collision avoidance.

The remainder of this paper is organized as follows. Section 2 reviews the related literature. Section 3 focuses on the proposal of the AMM-based CAS, including framework construction and methodology development. Section 4 presents the case study to demonstrate the feasibility of this proposed method. Discussion and conclusions are addressed in Section 5.

2. Related Work

The CAS proposed in this work alerts users to the presence of hazards with specific risk levels and reminds them to be prepared for the response rather than providing them with solutions. Two important components in establishing CAS are collision risk identification and risk level quantification. A large amount of research work has been conducted on these two topics [27].

For ship collision risk identification, distance to closest point of approach (DCPA) and time to closest point of approach (TCPA) are two typical risk indicators [28]. Collision risk is evaluated based on the combination of DCPA and TCPA to assess the collision risk in the Yangtze River [29] and in the Madura Strait [30]. Another popular approach is based on ship domain theory, originally intended to determine the capacity of waterways and further developed to support collision avoidance [31]. The shapes and dimensions of the ship domain have been significantly modified and developed to suit various application scenarios, see a detailed review in [32]. Additonally, the concepts of probability of collision [33], collision threat parameter area (CTPA) [34], velocity obstacle (VO) [35] and fuzzy collision danger domain are introduced to detect collision risk [36]. With the development of methods for collision risk identification, more and more scholars have realized that ignoring the dynamic nature of ship behavior reduces the accuracy of risk detection [37]. For instance, the non-linear velocity of obstacle method has been introduced and developed to accurately detect the presence of collision risk [18].

For risk level quantification, Zhang et al. developed vessel conflict ranking operator (VCRO) to divide the risk severity of near misses into three levels [38,39]. The frequency or probability of ship collision is adopted to separate the serious encounter with non-serious encounters. The degree of domain violation (DDV) and time to domain violation (TDV) are proposed to quantify risk severity to further support real-time collision avoidance decision [40]. Weng et al. proposed an ordered probit model to analyze the severity of two-ship collisions and found that ship size and visibility affect the probability of serious accidents [41]. A risk hierarchy prewarning (RHP) model based on the violation detection of a ship domain is proposed to determine risk level [42]. These methods help to enhance the understanding of the evolution of collision risk and provide a reference for a ship deciding her maneuvering strategy for collision avoidance in real time. However, most existing collision risk measures are independent of conflict resolution, so a high risk does not indicate whether a collision is inevitable or not. This could over/under-estimate the collision risk [27]. Our previous work introduced the concept of available maneuvering margins (AMM) to measure risk resolution when determining the risk level, but as the ship stability constraint is not considered, the risk resolution of a ship is overestimated [14]. In addition, these methods are mainly designed for ship pair encounters without considering traffic conditions [10]. A very limited number of methods consider multi-vessel encounters but divide them into several ship pair encounters. This simplified division ignores the interactions between ship behaviors, leading to an underestimation of the collision risk levels.

Several typical works related to CAS published in recent years are listed in Table 1. Goerlandt et al. proposed a risk-informed CAS based on fuzzy expert rules to divide the alert level into safe, caution, warning, and alarm in accordance with IMO recommendations [8]. The dynamic nature of ship actions and ship resolution are considered by adopting proximity indicators, such as reaction time and turning action, but this method is only applied in ship pair encounters. Baldauf. et al. focused specifically on the critical last phase of an encounter [16]. The last line of defense has been defined and indicates that the available maneuvers leading to the success of collision avoidance are extremely limited. The ship resolution is considered when calculating the last line of defense. Cheng et al. proposed an early warning system based on coordinated collision avoidance actions and applied it in inland waters [43]. DCPA, TCPA, and the coordination degree of collision avoidance actions of the two considered ships are the risk indicators, and this method could effectively reduce false alerts. Du et al. proposed a ship collision alert system for a stand-on ship by quantifying the action obligation of a stand-on ship as specified in the International Regulations for Preventing Collisions at Sea (COLREG) [14]. The non-linear velocity obstacle is employed to detect collision risk, and the available maneuvering margins of a ship are introduced to measure her risk resolution. When measuring the risk resolution of a ship, the impact of traffic complexity is considered, and the constraint of ship stability is ignored. Szlapczynski and Szlapczynska proposed a collision alert system based on five parameters derived from the ship domain concept [10]. The impact of late maneuvers and surrounding traffic are considered. However, one limitation is that the maneuverability of the ship is not available from the AIS data, so the risk resolution of a ship cannot be measured, which makes it difficult to directly inform the timing of the ship’s evasive maneuvers to avoid a collision. Qin et al. proposed a risk hierarchy prewarning (RHP) model based on the violation detection of a ship domain [42]. Two layers of protection are constructed based on the ship domain and the possible collision domain (PCD), and the violation of each of them will activate the lower and higher alarms, respectively. The violation of inner protective layer PCD means the collision between this ship pair cannot be avoided by any maneuvers. The traffic conditions and the dynamic nature of ship actions must be considered to increase the adaptability of this model in different waters.

Table 1. Several typical works related to CAS published in recent years.

Research Work	Risk Identification	Risk Level Quantification
	Action Dynamics	Ship Resolution	Traffic Condition	Ship Stability
Goerlandt et al., 2015	+	+	−	−
Baldauf et al., 2017	−	+	−	−
Cheng et al., 2020	+	−	−	−
Du et al., 2020	+	+	+	−
Szlapczynski and Szlapczynska, 2021	+	−	+	−
Qin et al., 2021	−	+	−	−

3. Methodology

3.1. Conceptual Framework

When two ships are approaching each other, a collision risk analysis will be conducted at the onset of the encounter. If there is no collision risk, both involved ships shall carefully check and remain vigilant until the other ships have passed safely. If collision risk occurs, the ship must prepare for evasive maneuvers based on the actual encounter. The determination of timing for taking evasive maneuvers is one crucial step. COLREGs provides guidance. A give-way ship should take early and substantial action to keep well clear if possible, see Rule 16. A stand-on ship is permitted to take evasive maneuvers if the give-way ship is evidently not maneuvering properly and effectively, as specified in Rule 17. In addition to these rules in COLREGs, the ship resolution that reflects the capability of a ship to eliminate the existing collision directly affects a navigator’s decision regarding the timing to perform evasive maneuvers for collision avoidance. Our previous work has observed that the maneuvering timing is affected by a ship’s COLREGs identity (a give-way ship or a stand-on ship) and her risk resolution [26].

Based on this collision avoidance process, an AMM-based CAS for ship collision avoidance is proposed to help determine the timing for a ship taking evasive maneuvers, which contains three main steps (see Figure 1), including the collision candidate detection (Step I), determination of timing for evasive maneuvers (Step II), and collision alert based on timing for evasive maneuvers (Step III). Specifically, collision candidate detection is to check whether the collision risk exists between this targeted ship pair. If a collision risk exists, Step II and Step III are activated to determine the alert level. The determination of the timing for evasive maneuvers is to quantify when the ship should take evasive maneuvers (Step II). The difference of a ship with a different COLREGs identity (a give-way ship or a stand-on ship) in determining the action timing is reflected based on the proposed risk-perception-based ship domain. Last is to determine the collision alert level based on the degree of violation of this risk perception-based ship domain (Step III). Here, we consider the ship risk resolution and ship stability limit. The methodologies for measuring these three steps are elaborated upon in Section 3.2 respectively.

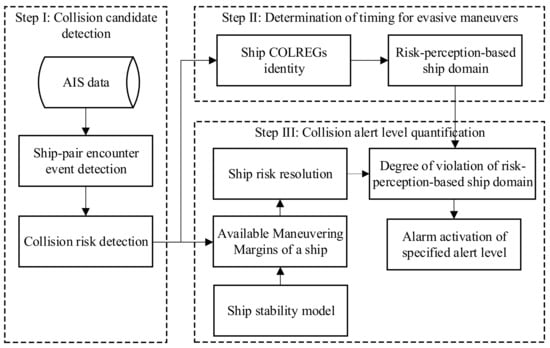
Figure 1. The conceptual framework of AMM-based ship collision alert system.

3.2. Methods Development

3.2.1. Collision Candidate Detection

To consider the dynamic nature of ship maneuvers during collision avoidance, the NLVO algorithm is adopted for collision risk detection [37], which is Step I for the construction of this AMM-based CAS, see Figure 1. By utilizing the NLVO algorithm, the collision risk for each ship pair can be detected by checking whether one ship’s velocity falls into the velocity obstacle zone ($S_{NL\_VO}$), see Figure 2.

$$IC(t)=\left\{\begin{array}{l}1, if V_{TS}(t)\cap S_{NL\_VO}(t)\ne \varnothing \\ 0, \mathrm{else}\end{array}\right.$$

(1)

where is the index of ship conflict. $V_{TS}$ is the velocity of the target ship (TS). $S_{NL\_VO}$ is the collection of all conflicting velocities that lead to ship collision. In Figure 2, collision risk exists for $V_{TS1}$, while there is no collision risk for $V_{TS2}$.

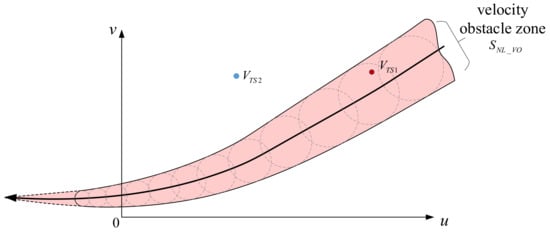
Figure 2. Ship collision risk detection based on NLVO algorithm.

3.2.2. Determination of Timing for Evasive Maneuvers

Step II is to determine the timing for evasive maneuvers, which is affected by ship COLREGs identity and the risk perceived by the navigator.

COLREGs identity is the identity of the ship during the collision avoidance process as specified in the COLREGs. It is classified as a stand-on ship (SO) or a give-way ship (GW) in terms of its action obligation for collision avoidance. As specified in Rules 16 and 17 in COLREGs, a ship with a different COLREGs identity has a diverse strategy. The ship’s COLREGs identity can be determined based on their relative heading and relative bearing.

The timing of a ship taking evasive maneuvers is primarily affected by the risk perceived by the navigator [44]. AMM is selected as a proxy to reflect the risk perceived by the navigator [26]. AMM is measured based on the proportion of maneuvers of all the available maneuvers by which a ship can eliminate potential conflicts. The assumption that a ship only changes her course to avoid collision is adopted. Therefore, AMM is determined by its turning ability.

$$\left\{\begin{array}{l}AMM(t)=\frac{{\displaystyle \sum {\delta }_s(t)}}{{\delta }_a(t)}, if \exists V(t)\in RV({\delta }_s(t),t_{ob}):V(t)\cap S_{NL\_VO}(t)=\varnothing \\ t_{ob}=\max (TCPA,5)\end{array}\right.$$

(2)

where $AMM$ is the value of AMM when the ship maneuvers at time t. ${\delta }_s$ is the adopted rudder angle that can eliminate the existing collision risk. ${\delta }_a$ is all the available rudder angles of a ship. $RV$ is the OS’s reachable velocity after steering with a demanded rudder angle. $\varnothing$ is an empty set. $t_{ob}$ is the observation time window, which is determined by the time to the closest point of approach (TCPA).

Next, the risk-perception-based ship domain is defined to determine the timing for evasive maneuvers. Specifically, by statistically analyzing when ships started to take evasive maneuvers under different encounter situations over a large sample of ship encounters from AIS data, the general practice of determining the timing for a ship taking evasive maneuvers is obtained in [45], see Table 2. The lengths of small-size ships, medium-size ships, and large-size ships are 100 m or less, 100 m to 200 m, and 200 m or more, respectively. $AM{M}_1$ and $AM{M}_2$ are the upper limit and lower limit of AMM, respectively.

Table 2. The value of AMM at the boundary of risk-perception-based ship domain.

Ship Type	COLREGs Status	$\mathbf{AMM} \mathbf{Threshold} (\mathit{A}\mathit{M}{\mathit{M}}_1$$/\mathit{A}\mathit{M}{\mathit{M}}_2)$
		Small-Size	Medium-Size	Large-Size
Passenger Ship	GW	0.986/0.586	0.914/0.486	0.814/0.343
	SO	0.943/0.443	0.786/0.314	0.729/0.229
Tanker	GW	0.871/0.471	0.829/0.314	0.8/0.229
	SO	0.857/0.371	0.629/0.214	0.486/0.186
Cargo Ship	GW	0.9/0.4	0.886/0.343	0.871/0.257
	SO	0.729/0.314	0.5/0.243	0.486/0.157

3.2.3. Collision Alert Level Quantification

The final step, Step III, is quantifying the collision alert level (Figure 1). The collision alert will be activated if collision risk exists and the degree of the violation of risk-perception-based ship domain determines the alert level. Violation of this risk-perception-based ship domain means that the ship’s behavior is abnormal and may lead to a danger, as most ships (about 90% of ships sailing in this area) would maneuver before this moment. The degree of the violation of risk-perception-based ship domain can be measured based on ship risk resolution.

The risk resolution of a ship $AMMs$ can be measured by her available maneuvering margins with stability guarantees. A ship will heel to the opposite direction of course change when turning for collision avoidance. If the ship’s heeling angle $\theta$ exceeds its threshold value ${\theta }_c$, the ship will be in danger of capsizing. The ship’s heeling angle can be expressed as:

$$\tan \theta =\frac{V\cdot r\cdot GB}{g\cdot GM}$$

(3)

where $\theta$ is the ship’s heeling angle. $V$ is the ship speed. $r$ is the yaw rate of ship steering. $GB$ is the distance between the center of ship gravity and the center of ship buoyancy. $GM$ is metacentric height, a vertical distance from the center of gravity to the metacenter. $g$ is gravitational acceleration.

The yaw rate of ship steering $r$ can be measured based on Nomoto model when the rudder angle is determined.

$$r=K\delta (1-e^{-t/T})$$

(4)

where $\delta$ is the rudder angle. Turning ability index K and turning lag index T vary with ship length and velocity.

Then, the ship risk resolution $AMMs$ can be modeled as follows:

$$\left\{\begin{array}{l}AM{M}_s(t)=\frac{{\displaystyle \sum {\delta }_s(t)}}{{\delta }_a(t)}, if \exists V(t)\in RV({\delta }_s(t),t_{ob}):V(t)\cap S_{NL\_VO}(t)=\varnothing \\ {\delta }_s(t)\le \frac{\tan {\theta }_c\cdot g\cdot GM}{V\cdot K\cdot GB\cdot (1-e^{-t/T})}\\ t_{ob}=\max (TCPA,5)\end{array}\right.$$

(5)

In terms of the degree of violation of this risk-perception-based ship domain, the collision alert is divided into three levels, ranging from low risk to medium risk and high risk.

$$CAL(t)=\left\{\begin{array}{l}L,if IC(t)=1\&AMMs(t)\ge AM{M}_1\\ M, if IC(t)=1\&AM{M}_1>AMMs(t)\ge AM{M}_2\\ H, if IC(t)=1\&AMMs(t)<AM{M}_2\end{array}\right.$$

(6)

where $CAL$ is collision alert level. $CAL$ is low if collision risk exists but the $AMMs$ of a ship is higher than the upper limit $AM{M}_1$. When collision risk exists and the $AMMs$ of a ship is lower than the lower limit $AM{M}_2$, $CAL$ is in the high level. For other situations when the risk exists, $CAL$ is medium. $AM{M}_1$ and $AM{M}_2$ mean that 90% and 99% of the ship starts an evasive action with a higher AMM than this, respectively [19].

4. Case Study

Three typical encounter scenarios are selected from AIS data to demonstrate the feasibility of this proposed AMM-based CAS. Specifically, the first two scenarios are ship pair encounters, and the last one is a multi-vessel encounter. The ship attributes are shown in Table 3. The encounter process lasts for 30 min. A maritime mobile service identity (MMSI) uniquely identifies ship stations and is masked in Table 3 to ensure vessel can be anonymous. The encounter processes are illustrated in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.

Table 3. Ship attributes in two typical encounter scenarios.

Encounter Scenarios	Ship Identity	MMSI	Type	Length (m)	Width (m)
Scenario 1	OS	27335XXXX	Cargo ship	84	15
	TS	27343XXXX	Tanker	126	16
Scenario 2	OS	27333XXXX	Passenger ship	56	11
	TS	20544XXXX	Cargo ship	182	28
Scenario 3	OS	21352XXXX	Cargo ship	92	18
	TS1	21107XXXX	Cargo ship	110	14
	TS2	26125XXXX	Cargo ship	185	32

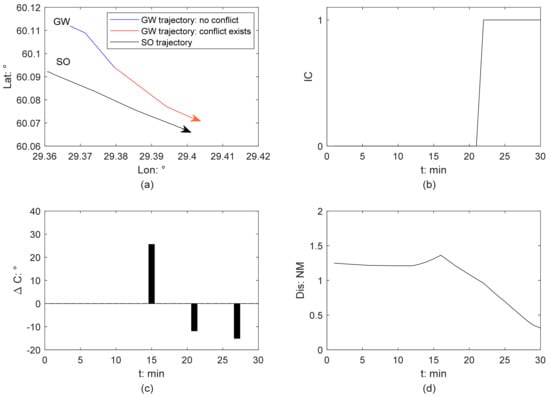
Figure 3. Ship collision detection from GW perspective in Scenario 1: (a) ship trajectory; (b) ship collision risk identification; (c) course change of a GW; (d) relative distance between this ship pair.

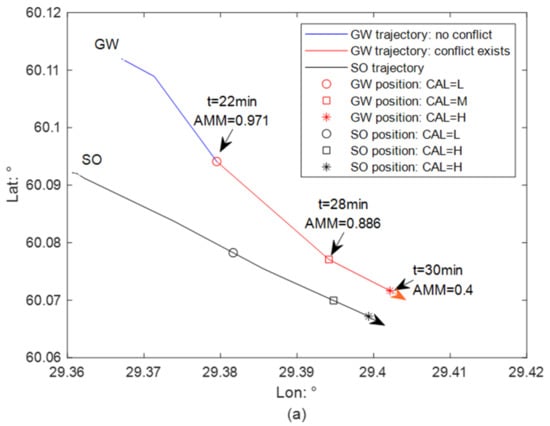
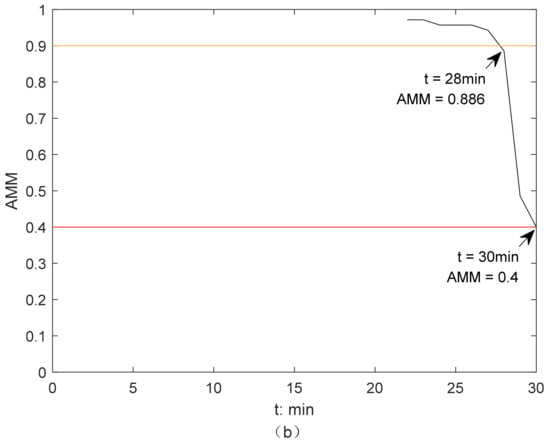
Figure 4. Illustration of the activation of AMM-based CAS from GW perspective in Scenario 1, without ship stability considered: (a) collision alert level determination; (b) the change of AMM of a GW.

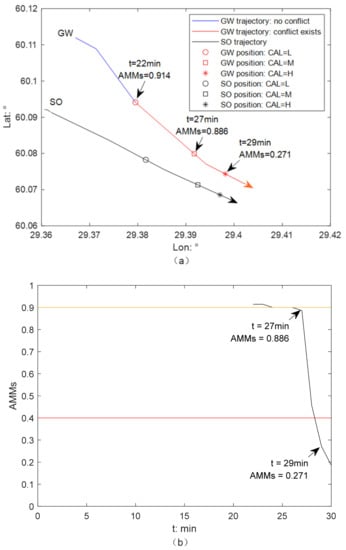
Figure 5. Illustration of the activation of AMM-based CAS from GW perspective in Scenario 1, with ship stability considered: (a) collision alert level determination; (b) the change of AMM of a GW.

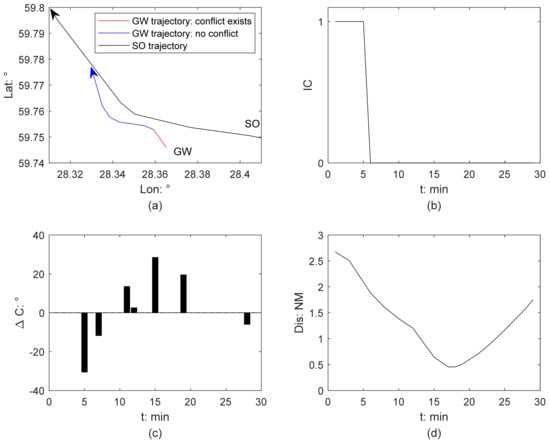
Figure 6. Ship collision detection from GW perspective in Scenario 2 (a) ship trajectory; (b) ship collision risk identification; (c) course change of a GW; (d) relative distance between this ship pair.

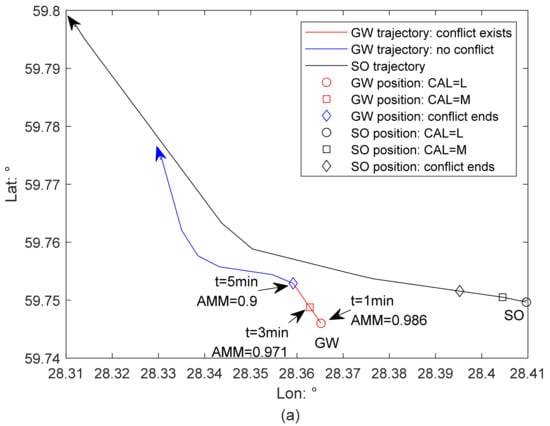
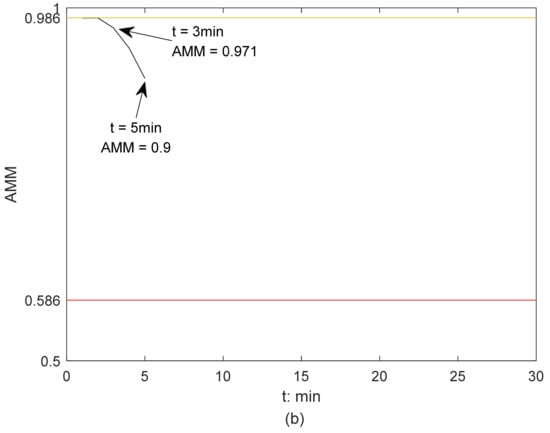
Figure 7. Illustration of the activation of AMM-based CAS from GW perspective in Scenario 2, without ship stability considered: (a) collision alert level determination; (b) the change of AMM of a GW.

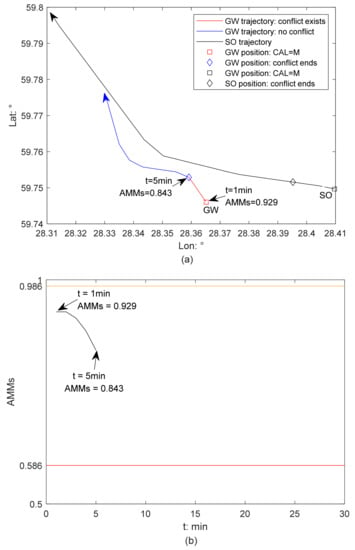
Figure 8. Illustration of the activation of AMM-based CAS from GW perspective in Scenario 2, with ship stability considered: (a) collision alert level determination; (b) the change of AMM of a GW.

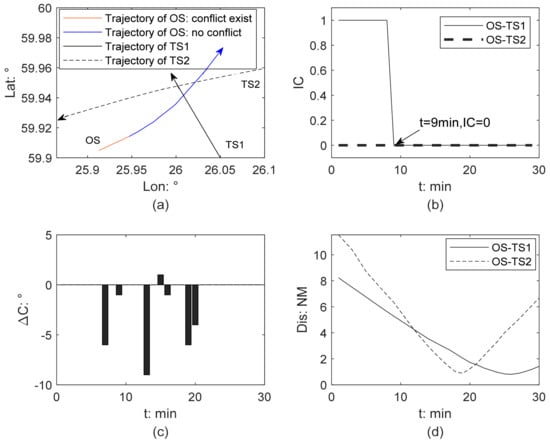
Figure 9. Ship collision detection from GW perspective in Scenario 3 (a) ship trajectory; (b) ship collision risk identification; (c) course change of a GW; (d) relative distance between each two ships.

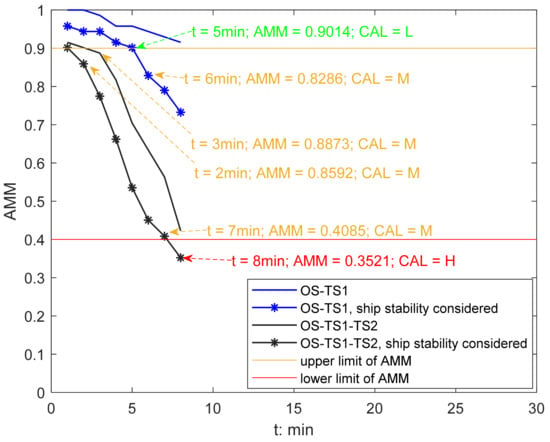
Figure 10. Illustration of the activation of AMM-based CAS from GW perspective in Scenario 3.

4.1. Ship Pair Encounter Scenarios

Figure 3 and Figure 6 present the results of ship collision detection in Scenarios 1 and 2, respectively. According to their relative positions and relative bearings, the ship COLREGs provide the basis for determining whether a ship is a give-way (GW) or a stand-on ship (SO). The trajectory of the stand-on ship is a black line. In Figure 3a and Figure 6a, the GW’s trajectory is marked in color, in which blue and red present safe and dangerous, respectively. The arrow indicates the direction in which the ship moves forward. Figure 3b and Figure 6b displays the change of IC, and IC = 1 means that collision risk exists, while IC = 0 means there is no collision risk. Figure 3c and Figure 6c present the course change of a give-way ship. If ΔC is positive, it means that a ship turns to starboard, while ΔC being negative means that a ship turns to port. Figure 3d and Figure 6d show the relative distance (Dis) between two ships.

Figure 4, Figure 5, Figure 7 and Figure 8 illustrate how the AMM-based CAS from the GW perspective is activated and developed without or with the ship’s stability considered, respectively.

4.1.1. Scenario 1

The cargo ship is a give-way ship because the cargo ship approaches the tanker from the tanker’s port side. Figure 3 presents the result of Scenario 1 from a GW perspective. This give-way ship is regarded as own ship (OS) and the tanker is target ship (TS). The GW is a small-size cargo ship, so two limit values—$AM{M}_1$ and $AM{M}_2$—are 0.9 and 0.4, respectively, from Table 2. When measuring the stability of GW, the value of $GM$ is set to 4.2 times the value of $GB$. The maximum value of ship’s heeling angle ${\theta }_c$ is set as 35 degrees.

There is no collision risk between this ship pair at the beginning, see Figure 3b. GW’s turn to portside at 21 min generates the collision risk (Figure 3b,c). From 22 min, the collision risk occurs. Afterward, the relative distance between two ships keeps decreasing, see Figure 3d,e. GW’s turns to port at 28 min are not effective, as the collision hazard remains (Figure 3a,c).

Figure 4 illustrates the activation of the AMM-based CAS from the GW perspective in Scenario 1 without ship stability considered. From 22 min, collision risk occurs when the AMM of GW is 0.971 (Figure 4). Afterward, the AMM of GW continues to decrease, see Figure 4b. Before 27 min, the AMM of GW is larger than 0.9. Therefore, the CAS is activated, and CAL is low. GW’s turns to port at 28 min are not effective for collision avoidance, which can be attested by the dramatic drop in her AMM from that point. From 28 min, the CAS is activated, and CAL is medium. The AMM of GW drops to 0.4 at 30 min, which reaches the lower limit $AM{M}_2$. Therefore, the CAS is activated, and CAL increases to medium from 28 min to 30 min. From 30 min, the CAS is activated, and CAL is high, as AMM of GW is less than 0.4.

Figure 5 illustrates the determination of the collision alert level from the GW perspective in Scenario 1 with ship stability considered. The CAS is activated from 22 min, when its risk resolution (AMMs) is 0.914. The CAL is low, as AMMs are larger than the upper limit value $AM{M}_1$. Afterwards, the AMMs of a GW continue to reduce (Figure 5b). From 27 min, the CAL changes to medium, as the AMMs of this GW are lower than the upper limit $AM{M}_1$ but still larger than the lower limit $AM{M}_2$. With ship stability considered, the time of the CAL mutating from low to medium was advanced by 1 min. The GW does not maneuver properly and effectively, and collision risk develops. The AMMs of the GW drops and is lower than the lower limit $AM{M}_2$ from 29 min, and therefore, the CAL increases to high. This mutation time is 1 min earlier than that when the constraint of ship stability is ignored.

4.1.2. Scenario 2

According to the relative position and relative bearing of this ship pair, GW is a small-sized passenger ship. Figure 6 presents the result of Scenario 2 from a GW perspective. This GW is regarded as OS. From Table 2, $AM{M}_1$ and $AM{M}_2$ are 0.986 and 0.586, respectively. When measuring the stability of GW, the value of $GM$ is set to 1.5 times the value of $GB$. The maximum value of ship’s heeling angle ${\theta }_c$ is set as 35 degrees.

The collision risk arises from the beginning (Figure 6a,b). GW does not take maneuvers from 3 min to 5 min (Figure 6c), so the relative distance between this ship pair reduces (Figure 6d). At 5 min, GW turns approximately 30° to port, which is sufficient to eliminate the existing collision risk. After that, there is no risk of collision; the GW turns several times to maintain a sufficient passing distance and then returns to her planned trajectory.

Figure 7 illustrates how the AMM-based CAS from the GW perspective in Scenario 2 is activated without ship stability being considered. The collision risk emerges from the beginning (Figure 6b). The AMM of the GW is 0.986 at 1 min and remains before 3 min (Figure 7b). Therefore, the CAS is activated, and CAL is low during this period. At 3 min, the AMM of the GW drops to 0.971, which is lower than the upper limit $AM{M}_1$, and the CAL changes to medium. From 3 min to 5 min, the GW sails with a constant speed and course, and her AMM continues to reduce but is still higher than the lower limit $AM{M}_2$. The CAL remains at medium level before 5 min. Due to the GW’s positive and effective evasive maneuvers, there is no collision risk, and therefore, the CAS is deactivated afterwards.

Figure 8 presents the results of the activation of CAS and determination of CAL from the GW perspective in Scenario 2 with ship stability considered. At 1 min, the AMM of this GW is 0.929, which is lower than the upper limit $AM{M}_1$, and therefore the CAS is activated; the CAL is medium 2 min earlier than that with ship stability ignored. During the next five minutes, the severity of collision risk develops as the GW does not maneuver as required for collision avoidance. The AMM of the GW reduces but remains larger than the lower limit $AM{M}_2$, the CAS is activated, and CAL is medium. The CAS is deactivated since 5 min as the collision risk is eliminated due to the GW’s evasive maneuvers.

4.2. Multi-Vessel Encounter Scenario

Figure 9 shows the results of the ship collision detection in Scenario 3, which is a multi-vessel encounter involving three ships, whose basic information is described in Table 3. Figure 9a displays the trajectory of three ships. Figure 9b shows that the collision risk exists only between own ship (OS) and target ship 1 (TS1) from the beginning. According to their relative positions and relative bearings, OS is a give-way ship. OS’s trajectory is marked in color, in which blue and red present safe and dangerous, respectively.

Before 9 min, OS sails with constant course and speed (Figure 9c), so the collision risk remains (Figure 9b), and the relative distances between OS and other two ships continue to decrease (Figure 9d). The collision risk between OS and TS1 is eliminated from 9 min due to OS’s turning to port (Figure 9c), which is proven to be positive and effective. Afterwards, there is no collision risk in this multi-vessel encounter. At 19 min, OS and TS2 reached their CPA at a distance of 0.9 nm. At 26 min, the relative distance between OS and TS1 drops to a minimum of 0.8 nm.

Figure 10 illustrates how the AMM-based CAS from the GW perspective is activated and how the CAL is developed. The GW is a small-sized cargo ship, so the upper and lower limits of AMM are 0.9 and 0.4, respectively, as shown in Table 2. The impacts of ship stability and traffic conditions on quantifying collision risk severity and collision alert level are analyzed. Four sets of experiments were conducted.

The first group neither considers the effects of ship stability nor the surrounding traffic conditions, and the experimental result is a blue line. During the period in which collision risk exists, the AMM of GW continues to reduce but is always larger than the upper limit, and therefore, the CAS is activated and the CAL is determined as low.

In the second group, only the effect of ship stability is considered, and the result is shown as a blue line with stars marked. The AMM of GW shows a steady decreasing trend and is smaller than that in Group 1 at the same moment. At 5 min, the AMM of GW is 0.9014. Prior to this, CAS is activated, and the CAL remains at a low level. At 6 min, GW’s AMM violates its upper limit, dropping to 0.8286, which increased CAL from a low to a medium level. Before the collision risk is eliminated, the CAL remains at a medium level.

In the third group, only the surrounding traffic is considered, and the result is a black line. Although the surrounding ship TS2 does not directly threaten the navigation of GW, it limits the GW’s risk resolution. The AMM of the GW decreases from 0.9155 at 1 min to 0.8873 at 3 min and 0.4225 at 8 min. Therefore, the CAS is activated during this period, and the CAL increases from low to medium level at 4 min.

In the fourth group, the impacts of both ship stability and surrounding traffic are considered, and the result is the black line with stars marked. At the beginning, the AMM of the GW is 0.9014, which is higher than its upper limit. The CAS is activated, and the CAL is at a low level. At 2 min, the AMM of the GW dropped to 0.8592, which lies between its upper and lower limits. The AMM of the GW continuously drops to 0.4085 at 7 min. The CAL remains at medium level from 2 min to 7 min. At 8 min, the AMM of the GW drops below its lower limit. The severity of the risk becomes severe, and at this moment, CAL escalates to high. The collision risk is eliminated since 9 min as the GW adopted effective evasive maneuvers.

4.3. Remarks

In comparison to the results of CAL determination in Scenarios 1 and 2, this proposed AMM-based CAS considering ship stability can more accurately quantify the collision risk level. Even though some extreme maneuvers, such as adopting full-rudder steering, can lead the own ship to pass safely with target ships, this full-rudder steering may lead to the capsizing of the own ship under certain environmental and loading conditions. The neglect of ship stability may lead to overestimation of the risk resolution of a ship, thus leading to an underestimation of collision risk.

This proposed AMM-based CAS is applicable in both ship pair encounters and multi-vessel encounters. Regarding a multi-vessel encounter as a linear superposition of multiple ship pair encounters could underestimate the collision risk as possible interaction effects between all ships operating nearby are ignored. In this AMM-based CAS, the impact from other ships nearby on the own ship’s risk resolution is well explained. In Figure 10, the comparison of the experimental results between the first two groups and the latter two groups reveals that the AMM of the GW is relatively lower in the latter two groups. This is because the latter two groups argue that the presence of the surrounding vessel TS2 directly reduces the GW’s capability of collision avoidance as some of her available operations could generate a new collision risk with TS2. The severity of the collision risk can be more accurately quantified by taking into account the complexity of traffic that caused by other vessels in the vicinity.

5. Discussion and Conclusions

This paper proposes an available maneuvering margins (AMM)-based collision alert system to alert the navigator to take evasive maneuvers timely for safe passing. This AMM-based CAS contains two main parts. The first part is the detection of collision risk. Instead of assuming the ship retains her speed and course under the threat of collision risk, the non-linear velocity obstacle (NLVO) algorithm is adopted to detect the collision risk by considering the encounter as a process. This considers the dynamic nature of ship maneuvering, so the accuracy of collision risk detection is improved. The second part is the determination of the alert level. The alert level is divided into three levels in terms of the degree of violation of risk-perception-based ship domain, which can be measured based on ship risk resolution. A ship’s risk resolution is quantified by her available maneuvering margins with stability guarantees.

Three typical encounter scenarios are selected from AIS data to demonstrate the feasibility of this AMM-based CAS, and the results are promising. This proposed AMM-based CAS is applicable in both ship pair encounter and multi-vessel encounter scenarios. The collision risk can be accurately detected for these cases. It can further accurately quantify the risk level and activate the corresponding level of risk warning. Therefore, this AMM-based CAS has the potential to be applied for various purposes in complicated encounter scenarios. First, it can support the navigator to formulate a strategy for collision avoidance. Second, it could contribute to enable the safety of autonomous ships if the CAS is further developed to lay at the basis of an automatic collision avoidance system or if it is used in a shore control center. Having sufficient information on navigational safety, including the severity of collision risk and the timing for performing evasive maneuvers, is essential for both autonomous vessels and conventional ships to take the proper actions to ensure safe passage.

Nonetheless, this AMM-based CAS can be improved in the following aspects. First, this work assumes that a ship only changes course to avoid collisions. The consideration of the reduction of ship speed and course change during collision avoidance helps to improve the computational accuracy of a ship’s AMM, which is one direction for our next research. Second, environmental disturbance, which directly decreases the ship’s maneuverability and ship stability, must be considered in future studies. The consideration of the impact of environmental disturbance could expand the applicability of this method. Third, to the method of developing an optimal collision avoidance strategy after receiving a collision alert requires future work. Safety, economy, and comfort will be considered simultaneously. Finally, this AMM-based CAS has demonstrated its reasonableness and feasibility only in a limited test scenario, so further testing (additional scenarios of encounter cases occurring in different waters, in bridge simulators, and onboard vessels) is required before it can be used in practical contexts. Considering the difference between open waters and restricted waters, more tests in restricted waters are necessary to check whether this AMM-based CAS is still effective under such encounters.