Spectral Analysis of Flow around Single and Two Crossing Circular Cylinders Arranged at 60 and 90 Degrees

Abstract

Two modal decomposition techniques, including proper orthogonal decomposition (POD) and dynamic mode decomposition (DMD), were used to identify the wake patterns past single and two crossing cylinders in 60° and 90° arrangements with gap ratio G = 4. The flow was simulated using direct numerical simulations (DNS) for Reynolds numbers Re = 100. From modal analysis, the flow’s spatial scale decreased with increasing modal frequency. Two main modes were identified in the wake of the cylinders, namely spatially antisymmetric and symmetric modes. Antisymmetric and symmetric modes were related to the cylinders’ vortex shedding and shedding vortices’ shift motion, respectively, whose frequencies were odd and even multiples of the cylinders’ lift force frequency. In addition, a low-frequency mode concerning the shadowing effect of the downstream cylinder (DC) in 90° arrangement was found in the wake of the DC centre.

1. Introduction

Vortex-induced vibration (VIV) of a circular cylinder has always been of interest to researchers due to its engineering applications [1,2]. In particular, if the self-oscillation frequency of a downstream structure is close to the vortex shedding frequency from the upstream circular cylinder, the structure will be destroyed by resonance [3,4,5]. Therefore, the relationship between wake morphologies and flow frequencies is worth studying.

The vortex shedding from a single circular cylinder is dependent on the flow direction [1,2] and Reynolds number Re. Different arrangements of multiple circular cylinders also affect the morphologies of the wake vortices. For two circular cylinders, parallel (including tandem, side-by-side, and staggered) and crossing arrangements make the flow past the cylinders more complex [4,5,6,7,8,9,10]. For instance, if two circular cylinders are perpendicular to each other, i.e., the so-called cruciform arrangement, the morphologies of the gap flow between two cylinders and vortex shedding are determined by the flow direction, gap-to-diameter ratio (defined as G), and Reynolds number Re [8].

Flows around circular cylinders are spatiotemporally coupled results, and it is not easy to separate the single-frequency flows from them. Modal decomposition technologies [10], including proper orthogonal decomposition (POD, [11]) and dynamic mode decomposition (DMD, [12]) have been proved to be powerful methods for solving this problem and have been widely used to analyse single cylinder wake obtained via particle image velocimetry (PIV) experiments [13,14,15] and numerical simulations [16,17,18,19,20,21].

For multiple cylinders in different arrangements, Zhang et al. [22] conducted a comprehensive comparison on identifying coherent structures in wake flow behind two side-by-side circular cylinders of different diameters obtained by PIV. Sakai et al. [23] employed POD and DMD to analyse the experimental and numerical flow around two circular cylinders in tandem and side-by-side arrangements. Sirisup and Tomkratoke [24] performed POD on the flow around two staggered circular cylinders obtained by using direct numerical simulations (DNS). Wang et al. [25] analysed the flow around two square cylinders in tandem arrangement with different G spacing ratios based on POD and DMD. Noack et al. [26] proposed a variant DMD algorithm, called recursive DMD (RDMD), to analyse the wake past three rotating cylinders in staggered arrangements calculated by DNS, and the modal results were compared with those obtained by original POD and DMD methods.

The above investigations mainly employed POD and DMD in analysing the parallel cylinder flows. However, little attention was paid to the modal patterns around the crossing point of two crossing cylinders, and the physical relevance between POD and DMD modes’ spatial patterns and cylinders’ lift force is not clear. Therefore, the main objective of our study was to explore the relationship between flow morphologies and their corresponding frequencies. To this end, we employ POD and DMD to analyse the wake past a single circular cylinder and two crossing circular cylinders with the crossing angles β = 60° and 90° and G = 4 (see Figure 1). This study can provide a reference for VIV in standard three-dimensional cylinder configurations (for example, heat exchanger pipes, underwater trusses, etc.).

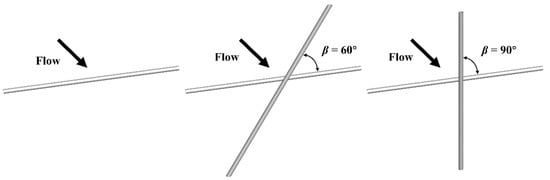
Figure 1. Sketch of single- and two-crossing circular cylinders configurations.

The paper is organised as follows. Section 2 presents the numerical simulation methodology, and Section 3 studies the lift force coefficient of cylinders, and cylinder wake’s spatial and spectral features. The modal analysis of the wake is presented in Section 4. Finally, the crucial results are summarised in Section 5.

2. Overview of Numerical Simulation

The governing equations for simulating the incompressible viscous fluid flow are the three-dimensional continuity and Navier–Stokes (NS) equations:

$$\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }{x}_i}=0,$$

(1)

$$\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }t} + u_j\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }{x}_j} = -\frac{\mathrm{\partial }p}{\mathrm{\partial }{x}_i}+\frac{1}{\mathit{Re}}\frac{{\mathrm{\partial }}^2{u}_i}{\mathrm{\partial }{x}_j\mathrm{\partial }{x}_j},$$

(2)

where x_i (x₁ = x, x₂ = y, x₃ = z) represents the Cartesian coordinates, u_i is the fluid velocity in the x_i direction (u₁ = U_x, u₂ = U_y, u₃ = U_z), t is time, and p is pressure. The Reynolds number Re is defined as Re = U_∞D/ν, where ν is the kinematic viscosity of the fluid. In this study, the fluid velocity was U_∞ = 1 m/s in the x direction, the cylinder diameter was D = 1 m, the fluid kinematic viscosity was chosen as ν = 0.01 m²/s, and the Reynolds number was Re = 100. All cases are summarized in Table 1.

Table 1. Cases in the study.

Case	Objective
Single cylinder	For spectral analysis
β = 60°, G = 4, Re = 100	For spectral analysis
β = 90°, G = 4, Re = 100	For spectral analysis
β = 90°, G = 0.5, Re = 500	For comparison only

The computational domain was a rectangular box with a length of 42D and a width and height of 40D (see Figure 2a,b). The length of the cylinders spanned the entire computational domain. The non-dimensional gap between the two crossing cylinders was defined as G = S/D, where S is the spacing between two cylinders (see Figure 2c,d). The upstream cylinder (UC) is a transversal cylinder with the centre of (0, 0, 0) for the studied three configurations. For the crossing configurations, the centre of the downstream cylinder (DC) was (5, 0, 0), and the crossing angle β was defined as DC’s inclination angle concerning the line of (x/D, z/D) = (5, 0).

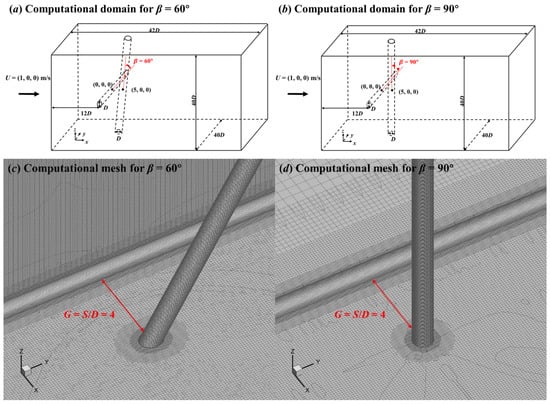
Figure 2. Rectangular computational domain and computational mesh for the two crossing circular cylinders in 60° (a,c) and 90° (b,d) arrangements with G = 4.

The boundary conditions of the computational domain were specified as follows. A uniform velocity was given on the left boundary, and the pressure gradient in the streamwise direction was zero. On the right boundary, the velocity gradient in the streamwise direction and the pressure were set to zero. To avoid the influence from two ends of the cylinders, the velocity component and the pressure gradient in the normal direction of the other four boundaries were set to zero. Moreover, no-slip boundary condition was applied on the cylinder surfaces.

The effect of the mesh density on the numerical results was investigated by performing the simulations on three meshes of different densities for two cylinders in cruciform arrangement (β = 90°) with G = 0.5 at Re = 500. The computational domain was discretised by the snappyHexMesh mesh generator. Figure 2 shows the computational mesh near the cylinders. The mesh information is listed in Table 2, and the comparisons of mean drag coefficient $\overline{C}$_D within |L/D| < 3 (L is cylinder length) and mean streamwise velocity $\overline{U}$_x (averaged over time) along the x axis from x/D = 2 to 12 between coarse, medium, and fine meshes are present in Figure 3.

Table 2. Coarse, medium, and fine mesh used for mesh convergence analysis.

	Mesh Number	Thickness of First Layer Mesh	Number of Boundary Layer Nodes
Coarse	9 million	0.004D	48
Medium	14 million	0.002D	96
Fine	22 million	0.001D	192

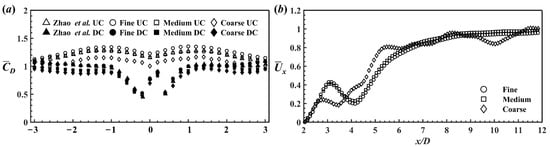
Figure 3. Comparison of mean drag coefficient (a) and mean streamwise velocity along the x axis (b) between the coarse, medium, and fine meshes.

The sectional drag coefficient was defined as C_D = 2F_D/(ρD$U_{\infty }^2$dL), where F_D is the sectional drag force calculated by integrating the pressure and shear stress along the section circumference parallel to the inflow direction. Each cylinder was divided into 400 blocks along the cylinder’s spanwise direction, so that dL was the cylinder length divided by 400. It is clear from Figure 3a that the $\overline{C}$_D of UC calculated by the medium mesh and that of DC calculated by the fine mesh was closer to the results obtained from Mesh 1 in [8]. For the wake region, the $\overline{U}$_x obtained from the medium mesh was similar to that of the fine mesh (Figure 3b).

Although the two largest meshes showed similar convergence, we still picked up the highest-density one as the target mesh to ensure accuracy. Finally, the mesh numbers were 18 million, 22 million, and 22 million for the cases of single cylinder and two crossing cylinders in 60° and 90° arrangements with G = 4, respectively. Based on the DNS, the time step of the simulation was set to dt = 0.005 s.

3. Numerical Results

The numerical results in this section focus on the lift coefficients, wake morphologies, and their spectra.

3.1. Lift Force Coefficient

Figure 4 shows the contours of sectional lift force coefficient C_L = 2F_L/(ρD$U_{\infty }^2$dL) along the cylinders, where F_L is the sectional lift force and its direction is perpendicular to the inflow direction. For the single cylinder, the lift force oscillated with time, and there was no time shift of the lift force along the spanwise direction of the cylinder (Figure 4a). While, for the two crossing cylinders, the lift force at the UC centre was always ahead of that at two sides of the UC centre, and the amplitude of the lift force at the UC centre was higher than that at two sides of the UC centre (see Figure 4b,c).

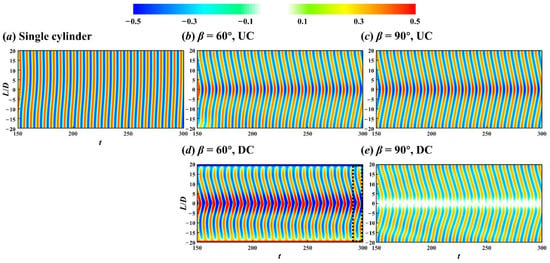
Figure 4. Contours of sectional lift coefficient along the single cylinder (a), and UC (b,c) and DC (d,e) for two crossing cylinders in 60° (middle) and 90° (right) arrangements.

For the DC in 60° arrangement, in addition to the increased lift force amplitude around the DC centre, the lift force on two sides of DC centre had an insignificant time shift, which can be seen in the dashed box in Figure 4d. However, for the DC in 90° arrangement, the lift force at the DC centre was almost zero under the influence of UC. The lift force characteristics of DC in 90° arrangement in the present work agree well with that of DC in cruciform arrangement for Re = 150 [8], both of which are in the laminar regime.

A fast Fourier transform (FFT) was further performed on the sectional lift force coefficient to calculate lift force’s power spectral density (PSD), and the contours of the Strouhal number St_L = f_LD/U_∞ determined by the frequency of lift force f_L is shown in Figure 5. It is clear from Figure 5 that the lift force frequency is St_L = 0.16 and was not related to the inclination angle of DC. For the DC in 60° arrangement, there was a second high frequency of St_L = 0.32 at the cylinder centre.

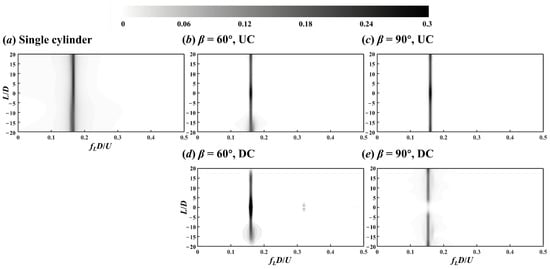
Figure 5. Contours of PSD calculated by sectional lift coefficient along the single cylinder (a), and UC (b,c) and DC (d,e) in 60° (middle) and 90° (right) arrangements.

3.2. Flow Field

Since the lift force is related to the vortex shedding from the cylinders [7,8], the wake morphologies of the single and two crossing cylinders are presented by the λ₂ iso-surfaces [27] in Figure 6. λ₂ is the second eigenvalue of the tensor Ψ²+ Ω², where Ψ and Ω are the symmetric and the anti-symmetric parts of the velocity-gradient tensor, respectively.

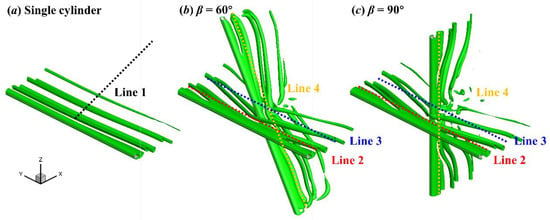
Figure 6. Instantaneous flow around the single cylinder (a) and two-crossing cylinders in 60° (b) and 90° (c) arrangements. Iso-surfaces λ₂ = −0.2.

For the single cylinder of finite length, the lift force along the cylinder oscillated simultaneously (Figure 4a), and the flow around the single cylinder was a two-dimensional phenomenon [7]. From a global perspective, the wake vortices shedding from the single cylinder were parallel to the cylinder, which is called parallel (P) mode (see Figure 6a).

For the crossing cylinders, although the gap ratio between the two cylinders was G = 4, the DC still affected UC’s flow patterns. Under the influence of the DC, the vortex shedding near the centre of each cylinder lagged the vortex shedding from two sides of the centre of the cylinder, forming inclined vortex morphology, i.e., K mode (see Figure 6b,c). The flow field of two crossing cylinders had a typical three-dimensionality.

The vorticity magnitude |ω| = |$▽$×U| = (${\omega }_x^2{+\omega }_y^2{+\omega }_z^2$)^1/2 contours on the xz and xy planes are presented in Figure 7 and Figure 8, respectively. For the gap flow, the gap ratio G was sufficiently large in this study and the vortex shedding was also generated in the gap between two crossing cylinders (Figure 7b,c and Figure 8). However, the front surface of DC delayed the vortex shedding from UC, and this delay resulted in the K mode wake vortices.

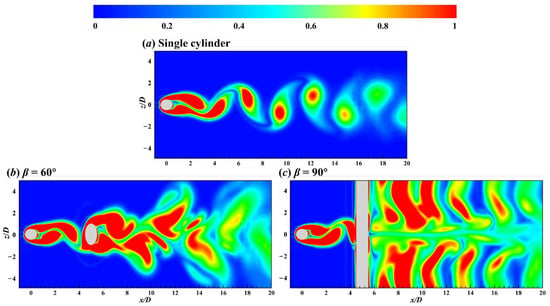
Figure 7. Contours of instantaneous vorticity magnitude on the xz plane for the flow around the single cylinder (a) and two crossing cylinders in 60° (b) and 90° (c) arrangements. The vorticity is normalized by U_∞/D.

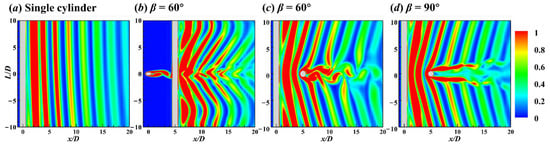
Figure 8. Contours of instantaneous vorticity magnitude on the xy plane for the flow around the single (a) and two crossing cylinders in 60° (b,c) and 90° (d) arrangements. The angle between the plane shown in (b) and xy plane is 60°, and the plane is parallel to DC in 60° arrangement. The vorticity is normalized by U_∞/D.

For the 60° arrangement, the wake vortices from UC centre interacted with DC and cause an asymmetric circulation distribution on the surface of the DC centre due to DC’s inclination (Figure 7b). As a result, the lift force of DC centre increased (Figure 4d), and the vortex shedding intensity near the DC centre was significantly higher than that of DC ends (Figure 8b). Although there was a time shift in lift force (Figure 4d) and wake vortices (Figure 8b) between two sides of DC in 60° arrangement, lift force and wake vortices of DC were continuous along the DC.

For the DC in 90° arrangement, the lift force of DC centre was almost zero (Figure 4e) and DC’s wake vortices were discontinuous at DC centre (Figure 7c). The symmetric wake vortices around the DC centre in Figure 8d are related to the UC wake and DC’s blockage effect [8].

A series of probes spaced at 1D interval were inserted in the wake field to record the wake velocity, as shown by lines 1 (y/D = 0, z/D = 0), 2 (x/D = 3, z/D = 0), 3 (x/D = 8, z/D = 0), 4 (x/D = 8, z/y = tan60° for β = 60° case and x/D = 8, y/D = 0 for β = 90° case) in Figure 6. Based on the wake velocity, the kinetic energy KE = 0.5($U_x^2$+${ U}_y^2$+${ U}_z^2$) in the wake is obtained and the PSD of KE was calculated through FFT. Figure 9 presents the energy evolution in the wake of the single cylinder along the x axis from x/D = 1 to 30, and Figure 10 shows the flow frequencies along the spanwise direction of each cylinder at different streamwise positions.

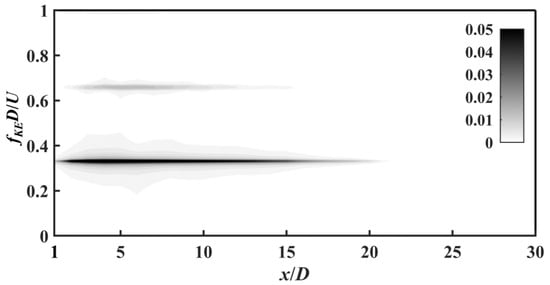
Figure 9. Contour of PSD calculated by the KE along line 1 in the wake of the single cylinder.

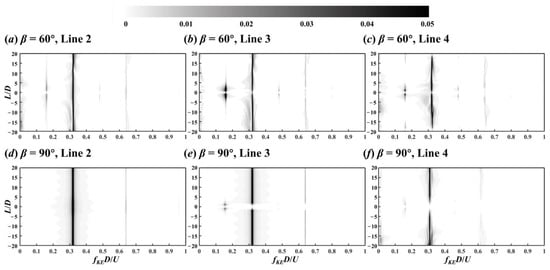
Figure 10. Contour of PSD calculated by the KE along lines 2, 3, and 4 in the wake of the two crossing cylinders in 60° (a–c) and 90° (d–f) arrangements.

It is clear from Figure 9 that there were two distinct spectral peaks of St_KE = f_KED/U_∞ = 0.32 and 0.64, which were two and four times the lift force frequency St_L = 0.16 in Figure 5a, respectively. The free shear layers generated the shedding vortices on left and right boundaries of a cylinder. Since the vortex shedding on one side corresponds to the peak lift force and the next vortex shedding on the other side corresponds to the valley lift force, there were two vortex shedding phenomena in one lift force period, i.e., St_KE = 0.32 = 2St_L. A complete vortex shedding period T was approximately 6.25 s.

Similarly, multiple spectral peaks could also be found in the wake of two crossing cylinders, i.e., St_KE = 0.16, 0.32, 0.48, and 0.64, where St_KE = 0.16 and 0.48 are significant only near the crossing point. However, the spectra and flow field cannot resolve the flow morphologies corresponding to the above characteristic frequencies. Therefore, modal decomposition methods were employed to solve this problem.

4. Modal Analysis

4.1. Methodology

The aim of reduced order model (ROM) is to identify the dominant modes in a dynamic system. As data-driven analysis methods, POD [11] and DMD [12] allow us to extract the domainant spatial and temporal features in the flow based on spatial orthogonality and frequency independence, respectively. The algorithms of these methods are introduced as follows.

4.1.1. POD

For a snapshot matrix X = [x₁, …, x_m], where the snapshot data x_i with n meshes are arranged as column vectors, the goal of POD is to seek m optimal basis u_i that best represent the flow field data. In a discrete dynamic system, the above problem is ultimately transformed into a problem of solving the eigenvalues of spatial correlation matrix, namely covariance matrix R = XX^T of the snapshot matrix X. Finally, the eigenvalue decomposition (EVD) of matrix R is equivalent to dealing with the singular value decomposition (SVD) of the snapshot matrix X in the sense of least squares [28]:

X = UΣV^T,

(3)

where U = [u₁, u₂, …, u_m] is POD mode matrix, Σ = diag(σ₁, σ₂, …, σ_m) is energy matrix, and V = [v₁, v₂, …, v_m] is time evolution matrix. In addition, both mode vectors u_i and time vectors v_i are unitary. Each mode’s time coefficient a_i(t) (i = 1, 2, …, m) can then be calculated by multiplying its singular values σ_i with the time vectors v_i:

a_i(t) = σ_iv_i^T,

(4)

Modal energy σ_i is related to the contribution of each orthogonal mode (basis) to the wake dynamic, namely each POD mode is ranked according to the degree to which it captures the spatial features of the flow field. The relative energy of each mode and the cumulative energy up to the ith modes are defined as

$$E_i=\frac{{\mathsf{\sigma }}_i}{{{\displaystyle \sum }}_{j=1}^m{\mathsf{\sigma }}_j}{, E}_i^{\mathrm{cum}}={{\displaystyle \sum }}_{k=1}^i{E}_k.$$

(5)

4.1.2. DMD

In a discrete-time dynamic system, DMD assumes a constant linear operator A between adjacent snapshots x_i and x_i+1, which can be denoted as

X′ =AX,

(6)

where X = [x₀, x₁, …, x_m−1] and X′ = [x₁, x₂, …, x_m] are snapshot matrices. The best-fit operator A is given by

A= X′X^†,

(7)

where X^† denotes the Moore–Penrose pseudoinverse of matrix X. Equation (7) is equivalent to minimising the error of ||X′ − AX^†||_F, where ||·||_F is the Frobenius norm.

Since the high-dimensional matrix A is generally too large (n × n), a projection algorithm proposed by Tu et al. [29] is used to reduce the computational cost. Let X = UΣV^T, then the low-rank matrix à can be obtained

à = U^TAU = U^TXVΣ⁻¹

(8)

If the eigenvector and eigenvalue matrix of matrix à are W and Λ, the DMD mode matrix Φ is given by

Φ = UW,

(9)

and the DMD eigenvalues are given by Λ. Each DMD mode’s growth/decay rate g_i and frequency f_i can then be obtained based on the eigenvalue λ_i as

g_i = In(Re(λ_i))/Δt_s,

(10)

f_i = In(Im(λ_i))/(2πΔt_s).

(11)

The initial amplitude (energy) α_i can be calculated by projecting the initial snapshot x₀ onto a low-rank subspace, as shown in Kutz et al. [28]:

α = [α₁, α₂, …, α_m]^T = Φ^†·x₀,

(12)

The original flow field data x_j (j = 0, 1, …, m) can be reconstructed by r modes as

$$x_j \approx {\tilde{y}}_j={{\displaystyle \sum }}_{i=1}^r{\varphi }_i{a}_i{(t}_j),$$

(13)

where $a_i\left(t_j\right)$ is the time coefficient of DMD mode ϕ_i at time j.

4.2. Raw Data

In this paper, the vorticity magnitude was selected for modal decomposition. In addition, the time-averaged vorticity was retained in the snapshot dataset because the removal of mean flow would reduce the DMD to the temporal discrete Fourier transform (DFT), which may lead to each mode being distributed at a constant frequency interval.

As seen from Figure 4, the lift force remained stable from 200 s onwards, and thus vorticity data in the last 100 s (from 200 to 300 s, around sixteen vortex shedding periods) were chosen for modal decomposition. The snapshot data were output at the time interval of Δt = 2 dt = 0.01 s, corresponding to the maximum sampling frequency of f_max = 1/Δt = 100 Hz.

4.3. Modal Convergence Analysis

The modal convergence is dependent on dataset’s sampling time interval Δt_s and the coverage period T_s. According to the Nyquist–Shannon criterion [30], the sampling frequency f_s should be at least two times the flow frequency f to capture flow features in the range of 0 to f, i.e.,

f_s = 1/Δt_s ≥ 2f.

(14)

The modal convergence is determined by the root mean square error (RMSE) between the snapshot data and DMD reconstruction result at time m + 1, i.e., the L₂ norm of $x_{m+1} - {\tilde{y}}_{m+1}$:

$$||x_{m+1} - {\tilde{y}}_{m+1}||{}_2=\sqrt{{{\displaystyle \sum }}_{i=1}^n{{(x}_{i, m+1} - {\tilde{y}}_{i, m+1})}^2}.$$

(15)

If all significant modes are contained, DMD can predict the next time flow field with high accuracy.

In this study, different sampling time intervals Δt_s = 3, 4, 5Δt = 0.03, 0.04, 0.05 s (capturing the modes in the frequency range of 0 ≤ St = fD/U_∞ ≤ 33.3, 12.5, 10, respectively) and coverage periods T_s = 1, 2, 3, 4, 5T = 6.25, 12.5, 18.75, 25, 31.25 s (covering 1 to 5 vortex shedding periods, respectively) were set to investigate the effect of sampling time interval and coverage period on modal convergence. Figure 11 illustrates the RMSE between the snapshot data and the DMD reconstruction result for the single cylinder case. The reconstruction error decreased with increasing coverage periods and the decreasing sampling interval. For Δt_s = 3Δt, the error reached a plateau for T_s = 4T, after which it did not change significantly. Hence, we considered the snapshot number m = 1042 (Δt_s = 0.03 s, T_s = 5.0016 s) for this study.

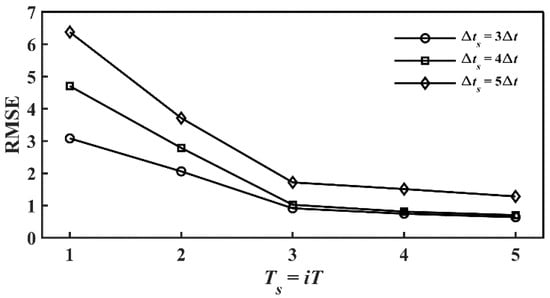
Figure 11. RMSE of the DMD reconstruction as a function of sampling interval with coverage period.

4.4. Modal Energy and Spectrum Statistics

POD provides modal energy and time coefficient (see Equation (4)), and its spectral information can be obtained by calculating the time coefficient’s PSD. DMD provides modal eigenvalue λ_i, frequency f_i and amplitude α_i (see Equations (9), (11) and (12)). Statistics on these important parameters are given as follows.

4.4.1. POD Modes

Figure 12 illustrates the relative energy of the first 25 POD modes and their cumulative energy. Overall, the energy of each mode decreased with increasing modal order. For the flow around the single and two crossing cylinders in 60° and 90° arrangements, the first mode had 84.55%, 81.82% and 81.29% of total energy, respectively. In addition, the first 3, 3, and 5 modes were needed to reach 90% of total energy, and the first 31, 29, 71 modes were needed to reach 99% of total energy, respectively. Statistics on modal energy show that the presence or absence of DC and DC’s arrangement significantly affected the convergence of the modal energy.

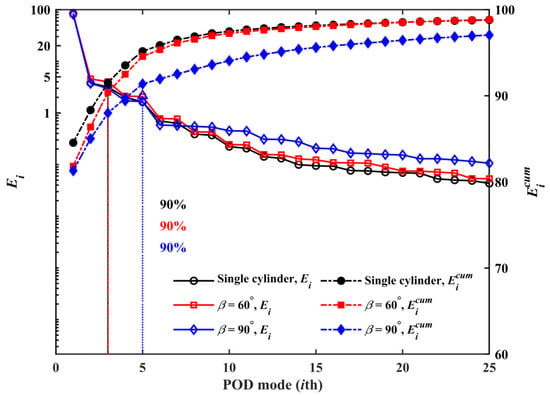
Figure 12. Relative and cumulative energy of the POD modes.

The spectral peak distribution of the first 25 POD modes are further demonstrated in Figure 13, where the spectral peak value of each mode was normalized by its maximum value. Although most POD modes appear as multi-frequency coupling forms, the modal frequency peaks (black pixels) followed a linear function with modal order, and the frequency peaks of adjacent modes were the same in pairs. However, for the two crossing cylinders in 90° arrangement case, the linear relationship between modal order and frequency peaks was not as pronounced as the other two cases. For the studied three cases, these modes’ frequency peaks were approximately integer multiples of St = 0.16.

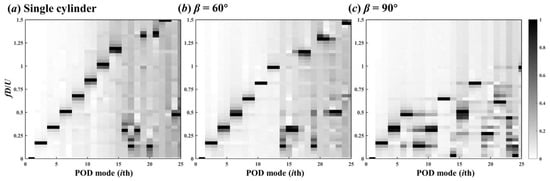
Figure 13. Frequency peak distribution of POD modes for the cases of the single cylinder (a) and two crossing cylinders in 60° (b) and 90° (c) arrangements.

4.4.2. DMD Modes

For DMD modes, a normalized dynamic factor d_i = |α_i| × |λ_i|^m−1/max(|α_i| × |λ_i|^m−1) was defined to exclude spurious mode with a high amplitude and a high decay rate, consistent with the approach in Shi et al. [31]. Each DMD mode was ranked according to its dynamic factor, and the leading modes were expected to make a prominent contribution to the wake dynamics. The distribution of important modes are shown in Figure 14, where zero-frequency mean flow modes are not considered and the leading 15 modes are colored in red.

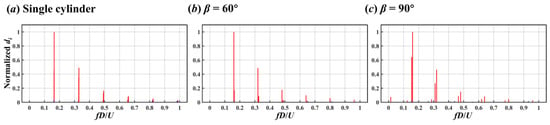
Figure 14. Spectral distribution of DMD modes for the cases of the single cylinder (a) and two crossing cylinders in 60° (b) and 90° (c) arrangements.

The spectra of DMD modes demonstrate that the modal contribution to the wake dynamics decreased with increasing modal frequency, and that the contribution of modes with St > 1 was negligible. Similar to the POD modes’ spectra in Figure 13, the frequencies of the crucial DMD mode are integer multiples of St = 0.16. However, more than one DMD mode existed around integer multiples of St = 0.16, especially for two crossing cylinder cases.

4.5. Modal Results

This section focuses on the relationship between modal spatial patterns and frequencies. Note that the vorticity magnitude in the three-dimensional flow field is the quantity being analysed in this study, and only the spatial results on the y = 0 and z = 0 slices are shown below.

4.5.1. Single Cylinder

The spatial patterns, time coefficients, and PSDs of some important POD modes for the flow around the single cylinder are shown in Figure 15, Figure 16 and Figure 17. Since adjacent POD modes have the same spectral peak (Figure 13), and their spatial flow patterns and time information are similar (not shown here for conciseness), the first 18 POD modes are presented at intervals. In addition, the norm of each spatial mode is one (Equations (3) and (9)), and the colors in the contours are used only to show flow patterns.

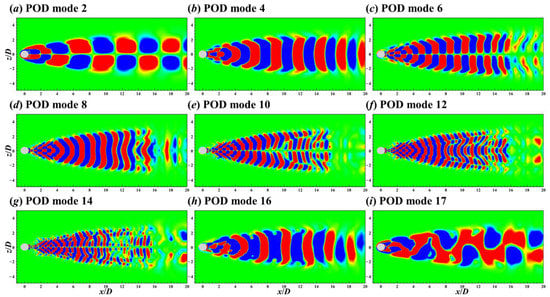
Figure 15. Contours of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 17th (i) POD modes on the xz plane for the flow around the single cylinder.

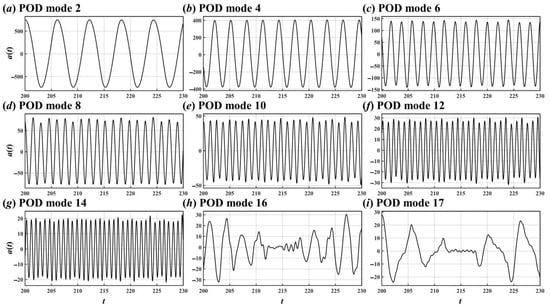
Figure 16. Time coefficients of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 17th (i) POD modes for the flow around the single cylinder.

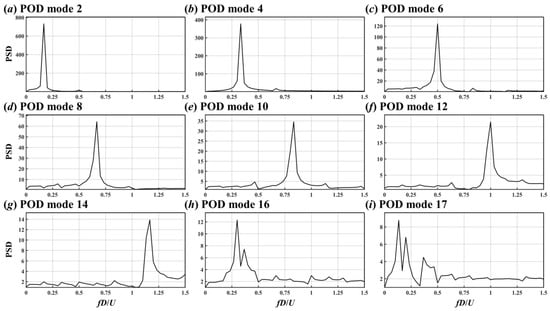
Figure 17. PSDs of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 17th (i) POD modes for the flow around the single cylinder.

It is clear from Figure 17 that the 2nd, 4th, 6th, 8th, 10th, 12th, and 14th POD modes had a relatively prominent spectral peak, corresponding to St = 0.16, 0.32, 0.48, 0.64, 0.8, 0.96, and 1.12, respectively. For the 16th and 17th modes, there were substantial fluctuations in their time coefficients (Figure 16h,i) and these two modes had multiple spectral peaks (Figure 17h,i).

The combination of Figure 15 and Figure 17 shows that spatial patterns of the modes with a spectral peak of odd multiples of St = 0.16 (St = i × 0.16, i = 1, 3, 5, 7) were antisymmetric in space and those with a spectral peak of even multiples of St = 0.16 (St = i × 0.16, i = 2, 4, 6) were spatially symmetric.

Because the vortex shedding frequency was calculated by lift coefficient is St_L = 0.16 (see Figure 5a), the antisymmetric mode with a spectral peak of St = 0.16 is related to the vortex shedding from the cylinder. Similar to the decomposition results of rotating flows [31,32], the antisymmetric modes with a higher frequency peak (St = 0.48, 0.8, 1.12) differ only on spatial scale with respect to the mode with a low-frequency peak of St = 0.16. These antisymmetric patterns with no flow along the central axis of (y/D, z/D) = (0, 0) explain the absence of the St = 0.16, 0.48 signals in the KE spectrum of Figure 9.

The symmetric patterns are associated with the shift motion of shedding vortices during downstream evolution, and their flow signals are monitored in the KE spectrum of Figure 9. Similar to antisymmetric modes, the spatial scale of symmetry modes decreased with increasing frequency.

Although the 16th and 17th modes also represent the shedding vortices’ shift motion and vortex shedding phenomena, respectively, their flow patterns were irregular in both space (Figure 15h,i) and time (Figure 16h,i), and they had multi-frequency characteristics (Figure 17h,i).

DMD modes are sorted according to their corresponding dynamic factors (see Figure 14a), and Figure 18 and Figure 19 show the first nine DMD modes and their corresponding time coefficients, respectively. Unlike POD modes, DMD modes did not fluctuate in time, and their time coefficients increased or decreased exponentially (Equation (10)) or remained constant over time (see Figure 19).

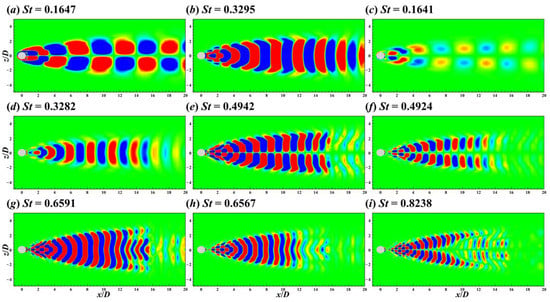
Figure 18. Contours of the St = 0.1647 (a), 0.3295 (b), 0.1641 (c), 0.3282 (d), 0.4942 (e), 0.4924 (f), 0.6591 (g), 0.6567 (h), and 0.8238 (i) DMD modes on the xz plane for the flow around the single cylinder.

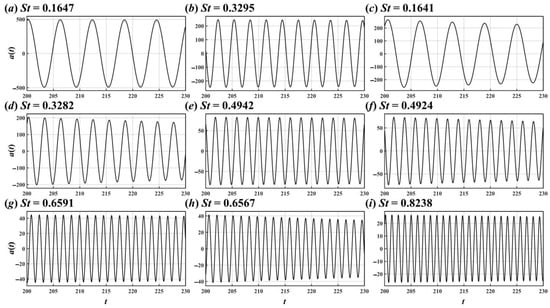
Figure 19. Time coefficients of the St = 0.1647 (a), 0.3295 (b), 0.1641 (c), 0.3282 (d), 0.4942 (e), 0.4924 (f), 0.6591 (g), 0.6567 (h), and 0.8238 (i) DMD modes for the flow around the single cylinder.

Two DMD modes with close frequencies occurred in pairs around St = 0.165, 0.33, 0.49, and 0.66 (i.e., St = 0.1647 and 0.1641, 0.3295 and 0.3282, 0.4942 and 0.4924, and 0.6591 and 0.6567), and the spatial characteristics between the two modes were similar. Considering the three-dimensional numerical simulation results, when a cylinder is long, there is a small frequency difference between the vortex shedding from two ends of the cylinder. Because DMD is sensitive in identifying flow phenomena with a single-frequency characteristic, similar DMD modes emerged in pairs in the three-dimensional flow around the single cylinder in this study, while this phenomenon did not occur in the two-dimensional flow case [28].

The spatial patterns of DMD modes were consistent with those of POD modes, and higher-frequency DMD modes are no longer shown here.

4.5.2. Two Crossing Cylinders in 60° Arrangement

For the two crossing cylinder cases, in addition to the modal contours on the xz plane, the contours of modes on the xy plane are also presented to show the global wake patterns of UC. The first 18 POD modes for the case of two crossing cylinders in 60° arrangement are shown at intervals in Figure 20, Figure 21, Figure 22 and Figure 23.

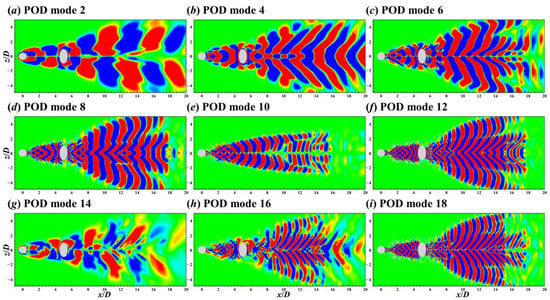
Figure 20. Contours of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 18th (i) POD modes on the xz plane for the flow around the two crossing cylinders in 60° arrangement.

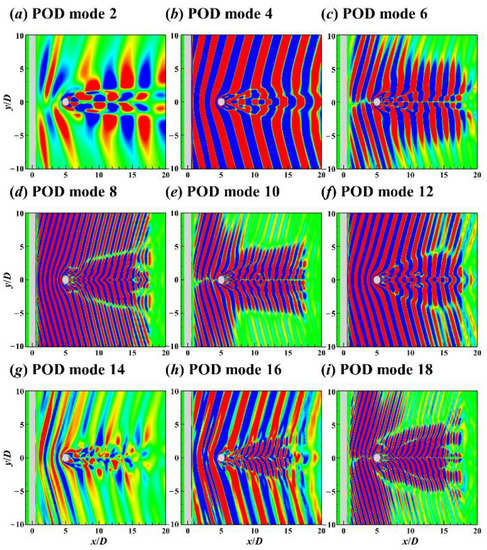
Figure 21. Contours of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 18th (i) POD modes on the xy plane for the flow around the two crossing cylinders in 60° arrangement.

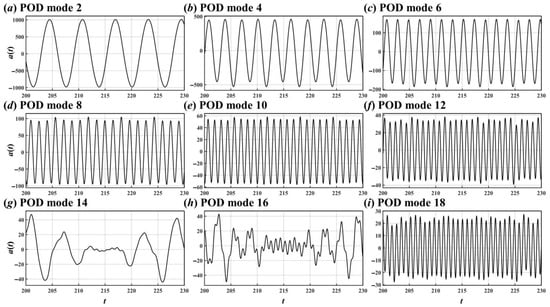
Figure 22. Time coefficients of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 18th (i) POD modes for the flow around the two crossing cylinders in 60° arrangement.

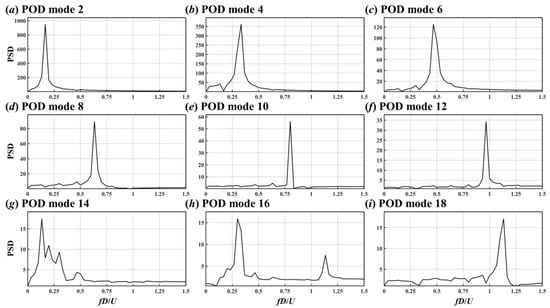
Figure 23. PSDs of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 18th (i) POD modes for the flow around the two crossing cylinders in 60° arrangement.

For the flow around the UC, it can be seen from the 2nd, 4th, 6th, 8th, 10th, 12th, and 18th POD modes in Figure 20 that the modal patterns in the range of 0.5 < x/D < 4.5 were the same as those of the corresponding modes in the single cylinder case (Figure 15). When the shedding vortices from UC centre encountered the DC, these modes’ symmetry and anti-symmetry remained unchanged (see Figure 20 and Figure 21). Furthermore, because the cross section of the DC arranged at 60° on the xz plane is an ellipse, diffraction of the flow caused the DC wake to expand in the z direction (Figure 20).

As can be seen from Figure 20a and Figure 21a, for the mode with a spectral peak of St = 0.16, its pattern was always antisymmetric on both xz and xy planes, corresponding to the unchanged lift force frequency along the spanwise direction of UC and DC (Figure 5b,d). As for the KE spectra in Figure 10b,c, the spectral peaks of St = 0.16 and 0.48 around the crossing point of lines 3 are caused by the antisymmetric flow patterns from DC centre, and those of lines 4 are caused by the antisymmetric patterns from UC centre.

The spatial and temporal results of DMD modes are shown in Figure 24, Figure 25 and Figure 26, where the spatial patterns of DMD modes are similar to those of POD modes but DMD modes have a single-frequency characteristic. Interestingly, three similar DMD modes appeared around St = 0.32, and their frequencies were St = 0.3204, 0.3258, and 0.3227 (see Figure 24b,f,h and Figure 25b,f,h). In addition to the frequency difference between the vortex shedding from two ends of the cylinder explained above, the difference in vortex shedding frequency between UC and DC caused by three-dimensionality is responsible for the appearance of more than two similar DMD modes.

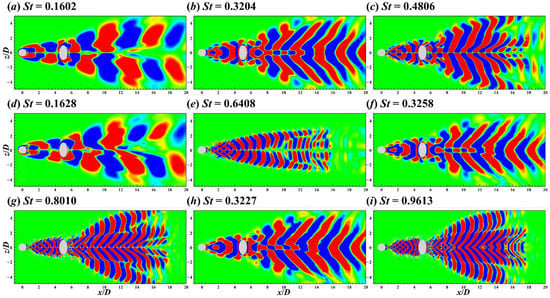
Figure 24. Contours of the St = 0.1602 (a), 0.3204 (b), 0.4806 (c), 0.1628 (d), 0.6408 (e), 0.3258 (f), 0.8010 (g), 0.3227 (h), and 0.9613 (i) DMD modes on the xz plane for the flow around the two crossing cylinders in 60° arrangement.

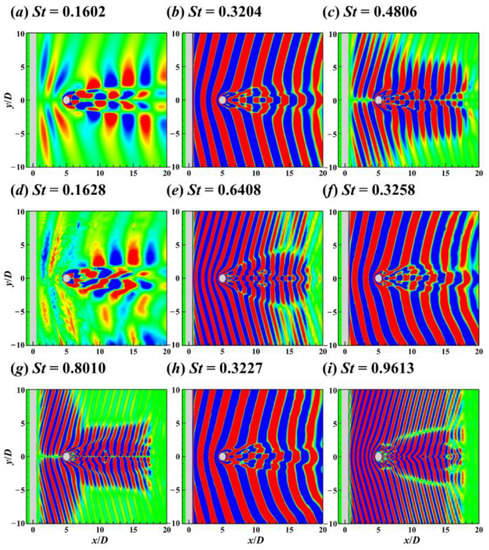
Figure 25. Contours of the St = 0.1602 (a), 0.3204 (b), 0.4806 (c), 0.1628 (d), 0.6408 (e), 0.3258 (f), 0.8010 (g), 0.3227 (h), and 0.9613 (i) DMD modes on the xy plane for the flow around the two crossing cylinders in 60° arrangement.

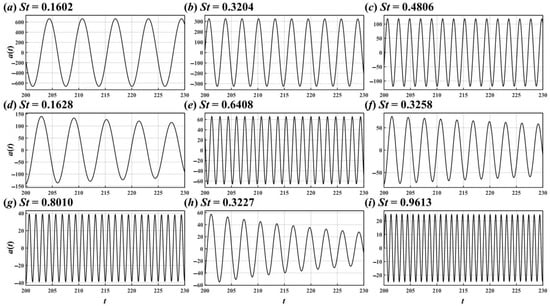
Figure 26. Time coefficients of the St = 0.1602 (a), 0.3204 (b), 0.4806 (c), 0.1628 (d), 0.6408 (e), 0.3258 (f), 0.8010 (g), 0.3227 (h), and 0.9613 (i) DMD modes for the flow around the two crossing cylinders in 60° arrangement.

4.5.3. Two Crossing Cylinders in 90° Arrangement

The first 18 POD modes in the two crossing cylinders in 90° arrangement case are shown at intervals in Figure 27, Figure 28, Figure 29 and Figure 30. The POD modes’ multi-frequency couplings were more severe than that of the other two cases (Figure 30). Enhanced multi-frequency coupling and slow energy convergence (Figure 12) were caused by the blockage of DC on the shedding vortices from UC and the resulting vortex breakdown. In other words, when encountering DC in 90° arrangement, large-scale wake vortices from UC centre broke down into numerous small-scale vortices, which is not conducive for POD to decompose the flow field.

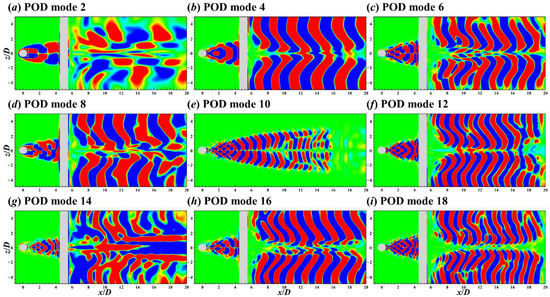
Figure 27. Contours of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 18th (i) POD modes on the xz plane for the flow around the two crossing cylinders in 90° arrangement.

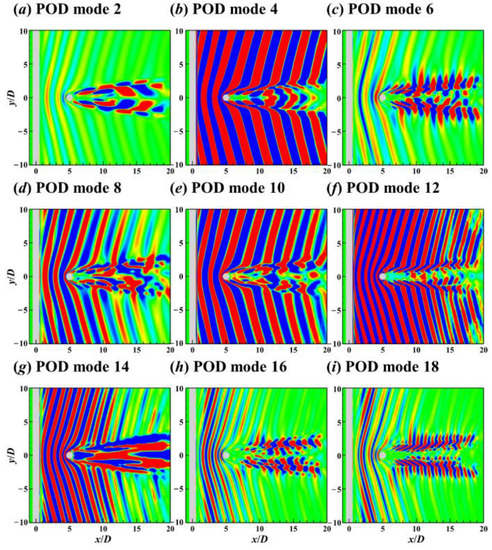
Figure 28. Contours of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 18th (i) POD modes on the xy plane for the flow around the two crossing cylinders in 90° arrangement.

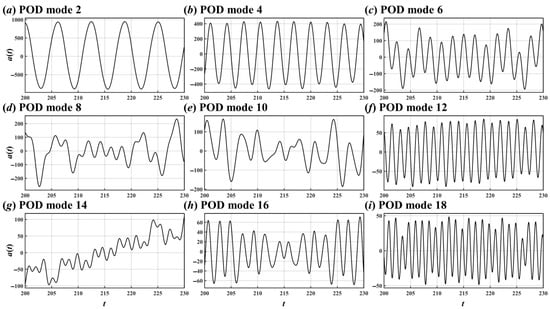
Figure 29. Time coefficients of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 18th (i) POD modes for the flow around the two crossing cylinders in 90° arrangement.

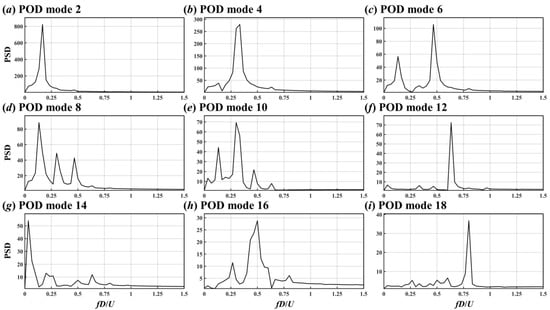
Figure 30. PSDs of the 2nd (a), 4th (b), 6th (c), 8th (d), 10th (e), 12th (f), 14th (g), 16th (h), and 18th (i) POD modes for the flow around the two crossing cylinders in 90° arrangement.

Figure 31, Figure 32 and Figure 33 show the first nine DMD modes of flow around two cylinders in 90° arrangement. Compared with POD, DMD is a practical tool in the severe destabilisation case due to its single-frequency characteristic. For the flow around the crossing point, the flow patterns of symmetric modes were distinctive on both xy and xz planes, e.g., St = 0.3101 DMD mode (see Figure 31d and Figure 32d). However, for the antisymmetric modes, the distinctive flow patterns of the wake vortices from UC and DC appeared on different planes. For instance, for the St = 0.1600 DMD mode, the antisymmetric flow pattern of the UC wake was significant on the xz plane (see Figure 27a), but that of the DC wake was significant on the xy plane (see Figure 28a).

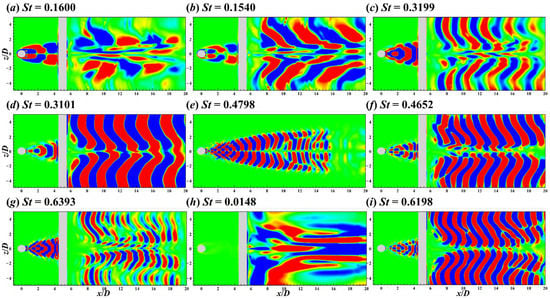
Figure 31. Contours of the St = 0.1600 (a), 0.1540 (b), 0.3199 (c), 0.3101 (d), 0.4798 (e), 0.4652 (f), 0.6393 (g), 0.0148 (h), and 0.6198 (i) DMD modes on the xz plane for the flow around the two crossing cylinders in 90° arrangement.

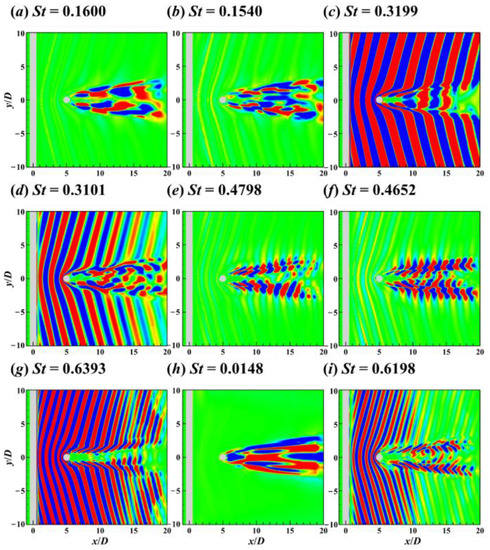
Figure 32. Contours of the St = 0.1600 (a), 0.1540 (b), 0.3199 (c), 0.3101 (d), 0.4798 (e), 0.4652 (f), 0.6393 (g), 0.0148 (h), and 0.6198 (i) DMD modes on the xy plane for the flow around the two crossing cylinders in 90° arrangement.

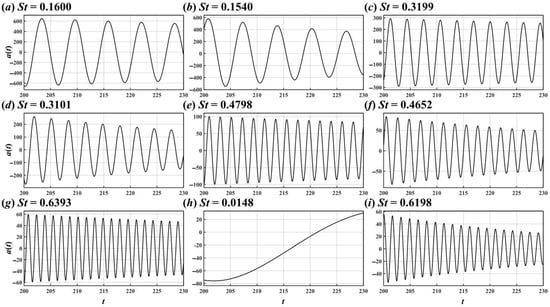
Figure 33. Time coefficients of the St = 0.1600 (a), 0.1540 (b), 0.3199 (c), 0.3101 (d), 0.4798 (e), 0.4652 (f), 0.6393 (g), 0.0148 (h), and 0.6198 (i) DMD modes for the flow around the two crossing cylinders in 90° arrangement.

Although UC wake’s induction and DC’s blockage effect [8] caused the flow around DC centre to move downstream along approximately |L/D| = 1 (Figure 8c), the antisymmetric vortex shedding modes and symmetric shift motion modes still existed.

For the antisymmetric mode with St = 0.1600 (Figure 32a), the flow around the DC centre became narrower in the y direction due to UC wake’s induction and DC’s blockage effect. For the symmetric mode with St = 0.3199 (Figure 31c and Figure 32c), symmetric flow patterns were not found on the central axis (y/D = 0, z/D = 0) in the range of x/D = 5.5–9 due to the blockage of DC. In addition, there was a low-frequency flow pattern in the wake of the DC centre (see Figure 31h and Figure 32h). The low-frequency mode is related to the low-speed flow under the shadowing effect of DC.

5. Summary

This study employed modal decomposition techniques, including POD and DMD, to investigate the wake patterns past single and two crossing cylinder configurations at Re = 100. The two crossing cylinders were arranged at 60° and 90° with a gap ratio G = 4. The numerical simulation was conducted using DNS.

We focused on the effect of DC’s arrangement on the wake patterns around the crossing point. For the DC in 60° arrangement, the shedding vortices from UC centre underwent diffraction after passing through the DC. However, for the DC in 90° arrangement, due to the DC’s blockage effect, the wake vortices from UC centre broke down when encountering the DC.

POD and DMD have their own advantages. For the stable flow, i.e., flow around the single and two crossing cylinders in 60° arrangement, POD can successfully extract the modes that contribute most to the wake dynamics, and these modes have a single, prominent spectral peak. Due to the frequency sensitivity, DMD may capture the single-frequency modes with similar frequencies, temporal information, and spatial patterns. This is caused by the three-dimensionality of flow, i.e., the frequency difference between the vortex shedding from two ends of the cylinder, and the frequency difference between the wake of UC and DC. For the severely destabilised flow, i.e., flow around two crossing cylinders in 90° arrangement, POD is not practical for analysis due to the enhanced multi-frequency coupling.

Both POD and DMD identified spatially antisymmetric and symmetric wake patterns for the studied three cases. Antisymmetric modes are associated with the vortex shedding phenomenon in the flow field, and these modes’ frequencies are odd multiples of cylinders’ lift force frequency. Symmetric modes are associated with the shift motion of shedding vortices during downstream evolution, and these modes’ frequencies are even multiples of cylinders’ lift force frequency. The spatial scale of the above modes decreased with increasing frequency.

For the flow around the DC in 90° arrangement, both symmetric and antisymmetric modes had significant deformation due to the interference of the UC wake and the blockage effect of DC. In addition, a low-frequency mode was found in the wake of DC centre, which is related to the shadowing effect of DC.

For the three-dimensional flow, the cylinder length seemed to affect the DMD analysis, and in the next work we will focus on this subject.