Distributed Robust Fast Finite-Time Formation Control of Underactuated ASVs in Presence of Information Interruption

Abstract

To adapt to complex navigation conditions, this paper addresses the coordination formation of autonomous surface vehicles (ASVs) with the constraint of information interruption. For this purpose, a distributed robust fast finite-time formation control algorithm is proposed by fusion of the directed graph and neural network method. In the strategy, the graph theory is utilized for the channel of information transmission to maintain the stability of the formation system. In addition, the radial basic function (RBF) neural network is employed to approximate the structure uncertainty. Due to the merits of the robust neural damping technique, only two adaptive parameters are designed to compensate the perturbation from the model uncertainty and external environmental. Furthermore, an improved dynamic surface control (DSC) technology is developed for constituting the exponential term of the Lyapunov function. It is proven that the proposed scheme is able to achieve consensus tracking in finite time quickly, and the errors rapidly approach a small region around the origin. Finally, the feasibility and effectiveness of the algorithm are verified by two numerical simulations.

1. Introduction

In the past decades, there has been increased attention aimed at the development of autonomous surface vehicles (ASVs) in the field of marine cybernetics [1]. This attention primarily originates from the practical applicability of ASVs in various civilian and military missions, e.g., the emergency search and rescue, the offshore supply and the cooperative transportation [2]. The formation control is a class of effective solutions to implement the coordinated and compensated operation of ASVs. In the existing work, the control protocols almost entirely use uniformly ultimately-bounded convergence performance. In practice, the possible delay or tardiness may cause the inaccuracy of the attitude of ASV and even lead to invalidation of the whole engineering operation. Therefore, the investigation of the formation control of ASVs, with consideration to the fast response and information loss, requires more efforts and holds significance in the marine industry.

The research on vehicle formation has been developed to some extent [3,4,5,6]. Its control objective is to drive a group of ASVs converged to an anticipated geometric formation with a desired heading angle. To obtain the predefined formation, the mainstream formation control methods in the existing literature are the leader-follower approach [7,8], the virtual structure approach [9], the behavioral-based approach [10] and the graph theory-based approach [11]. In addition, the above formation methods present a mixed development state in recent years, which effectively promote the further development of formation control. In [12], novel sliding mode control laws are proposed to control multiple surface vehicles with arbitrary formations. Xiang et al. [13] developed a nonlinear controller for formation coordination to avoid collision with a certain formation. Moreover, a leader-follower formation tracking approach with limited torque was developed for tackling actuator saturation. Considering accurate formation in [14], Xiao et al. [15] designed a novel disturbance estimation scheme for the formation controller based on a terminal sliding mode observer. In [4], a practical coordinated path-following algorithm was presented for a group of underactuated surface vehicles to achieve and maintain the desired formation pattern. For the multi-input and multi-output system, a traditional adaptive control approach was designed in the presence of the amplitude and rate saturation in [9].

Aside from the proposed formation control methods, the consensus control for multi-agent system (MAS) is also a method to solve the vehicle formation coordination problem. It has the superiorities of autonomy, distribution, coordination and certain autonomous learning ability. Moreover, it holds strong robustness to the external influence and high tolerance to the fault of internal single agent. The consensus problem for MAS is a basic research direction in multi-agent cooperation; it makes each individual reach a common state. The existing papers on consensus control are mainly divided into two general categories, e.g., leader-following consensus problem and leaderless consensus problem. Especially, leader-following consensus problem (also called distributed tracking control) has already become an active research area owing to its dependability. The leader is an individual different from a follower. On the one hand, the state information of the leader can be directly or indirectly transmitted to all followers, and affects the behaviors of followers. On the other hand, the leader can be a virtual, ideal individual which is not affected by external disturbance. Based on these proposed advantages, the consensus control of MAS has been widely used with the development of vehicle formation control, such as in papers [11,16]. Based on a modular design approach, a new cooperative control scheme is proposed for the dynamic positioning of multiple offshore vessels. In [16], the paper designs a leader-follower cooperative formation control algorithm for ASV with uncertain dynamics and external disturbances.

The control algorithms mentioned above deal with the asymptotic consensus for the system. Each system state can reach the equilibrium only when the time tends to infinity theoretically. Moreover, the convergence speed is an important performance index, which affects the real-time performance of formation systems. In the existing literature, there is little fast finite-time stability theory applied to the formation control of ASVs. Actually, the fast finite time stability analysis is used in [17,18,19,20] to achieve rapid stability. In [17], a tracking control scheme for the first-order MAS is proposed in the sense of finite time convergence. The works in [18] address the tracking control of second-order MASs, and the tracking control strategies are developed, which guarantee the achievement of fast tracking in finite time. Subsequently, a fast finite-time consensus proposal with a virtual leader is presented for heterogeneous MASs in [19]. In [20], the leader-follower consensus tracking problems are discussed for high-order MASs.

Motivated by the aforementioned discussions, an improved distributed fast finite-time formation of ASVs control scheme is developed for ASVs with information interruption. The objective is to propose a consensus formation control proposal for underactuated ASVs based on fast finite-time stability criterion; the main contributions are summarized as follows:

(1)

Considering the possible information interruptions during the navigation, the directed theory has been adopted to improve the fault-tolerant performance of the vehicle formation. Unlike the traditional leader-follower method, the proposed distributed control algorithm is designed to communicate between the networked underactuated vehicles which only required the information of partial neighbors, which can effectively enhance the robustness and reduce the over-dependence on the leader vehicle.

(2)

In this paper, the proposed formation control scheme is firstly developed for the underactuated ASVs based on the fast finite-time stable criterion and an improved DSC technique. Different from the existing finite time protocols, the proposed strategy has the superiority of a faster convergence rate and higher control accuracy. Moreover, the convergence time of the errors has been independent with the initial condition, and is only related to the design parameters, which are more in accordance with the practical requirements.

2. Problem for Formulation and Preliminaries

Throughout the paper, $h$ is a constant with $h=\frac{4z-1}{4z+1}(z\in Z_{+})$. $\widehat{(\cdot )}$ is the estimate of $(\cdot )$, and the estimation error $\widetilde{(\cdot )}=\widehat{(\cdot )}-(\cdot )$. The variables $u$ and $r$ are represented by $\varsigma$.

2.1. The Mathematical Model for Underactuated ASVs

In this paper, the control plant is the underactuated vehicle with h propellers and rudders for surge and yaw motions only. Based on the Newtonian and Lagrangian mechanics, the mathematical dynamic model of ASVs is given as Equations (1) and (2), following [21].

$$\{\begin{array}{l}{\dot{x}}_i=u_i\cos \left({\psi }_i\right)-v_i\sin \left({\psi }_i\right)\\ {\dot{y}}_i=u_i\sin \left({\psi }_i\right)+v_i\cos \left({\psi }_i\right)\\ {\dot{\psi }}_i=r_i\\ {\dot{u}}_i=\frac{m_v}{m_u}{v}_i{r}_i-f_u\left(u_i\right)+\frac{1}{m_u}{\tau }_{ui}+d_{wui}\\ {\dot{v}}_i=-\frac{m_u}{m_v}{u}_i{r}_i-f_v\left(v_i\right)+d_{wvi}, \\ {\dot{r}}_i=\frac{m_u-m_v}{m_r}{u}_i{v}_i-f_u\left(u_i\right)+\frac{1}{m_r}{\tau }_{ri}+d_{wri}\end{array}$$

(1)

with

$$\{\begin{array}{l}{f}_u(u_i)=\frac{d_u}{m_u}{u}_i+\frac{d_{u2}}{m_u}\left|u_i\right|u_i+\frac{d_{u3}}{m_u}{u}_i^3\\ f_v(v_i)=\frac{d_v}{m_v}{v}_i+\frac{d_{v2}}{m_v}\left|v_i\right|v_i+\frac{d_{v3}}{m_v}{v}_i^3\\ f_r(r_i)=\frac{d_r}{m_r}{r}_i+\frac{d_{r2}}{m_r}\left|r_i\right|r_i+\frac{d_{r3}}{m_r}{r}_i^3\end{array}$$

(2)

where $x_i$, $y_i$ ${\psi }_i$ denote the position and heading angle of the ith vehicle based on the earth centered fixed coordinate frame. $u_i, v_i, r_i$ are the vehicle velocities in surge, sway and yaw in the body-fixed frame. $d_{wui}, d_{wvi}, d_{wri}$ are the interference effect of marine environment on vehicles, such as wind, wave and ocean current. ${\tau }_u{}_i, {\tau }_{ri}$ are control input of vehicle model on surge and yaw. $m_u,m_v,m_r,d_u,d_v,d_r,d_{u2},d_{v2},d_{r2},d_{u3},d_{v3},d_{r3}$ are all considered as unknown parameters, and described as the vehicle’s inertia, hydrodynamic damping and nonlinear damping terms. $f_u\left(u_i\right),f_v\left(v_i\right),f_r\left(r_i\right)$ denote the high-order hydrodynamic effects.

2.2. Directed Graph Theory

In a formation system with $M$ ASVs, each ASV can be regarded as the node of the directed graph $G$, and the channel among ASVs can be regarded as the edge of the directed graph $G$. $v=\{v_1,v_2,\cdots ,v_M\}$ is called the vertex set of graph $G$, and its elements are nodes; $e=\{e_1,e_2,\cdots ,e_M\}$ is called the edge set of graph $G$, whose elements are edges. The M-order matrix $A$ is called adjacency matrix with the elements $a_{ij}=1$, representing the adjacency relationship between the nodes of the whole system. When $a_{ij}=1$, it means that the information flow can be directly transmitted from jth vehicle to ith vehicle; when $a_{ij}=0$, it means that there is no direct connection between the two agents. Diagonal matrix $D=diag(d_1,d_2,\cdots ,d_M)$ is the in-degree matrix of graph $G$, with $d_i={\displaystyle \sum _{j=1}^M{a}_{ij}}$. When the autonomous vehicle sent a message to the jth vehicle (called its neighbor), thus, the neighbor set of jth vehicle is expressed as $N_j=\left\{v_k\right|(v_k,v_j)\}$. Taking the leader into consideration, the augmented graph $\overline{G}$ is used to denote the communication topology of the leader-following system for ASVs.

2.3. RBF NNs

Based on the existing results [22,23], the neural networks and fuzzy logic systems are effective approximation tools to model the model uncertainty and extraneous disturbances. This paper adopts the radial basis function neural networks (RBF NNs) to address the uncertainty of the above mathematical model.

Lemma 1

([24]). For any real continuous function $f(x)$ with $f(0)=0$, there is always one result like Equation (3)

$$f\left(x\right)=S\left(x\right)A(x)+\epsilon$$

(3)

where $S(x)=[s_1,s_2,\cdots ,s_n]$ with $s_i(x)$ is called the basis function and chosen as in Gaussian form:

$$s_i=\frac{1}{\sqrt{2\pi }{\eta }_i}\exp (-\frac{{(x-{\mu }_i)}^{\mathrm{T}}(x-{\mu }_i)}{2{\eta }_i}),i=1,2,\cdots ,l$$

(4)

$l$ is the node number of NNs, $\epsilon$ is the approximation error with unknown upper bound $\overline{\epsilon }$, $n$ is the dimension number of $\overline{x}$, and

$$\mathit{A}=\left[\begin{array}{cccc}{w}_{11}& w_{12}& \cdots & w_{1n}\\ w_{21}& w_{22}& \cdots & w_{1n}\\ ⋮& ⋮& \ddots & ⋮\\ w_{l1}& w_{l2}& \dots & w_{ln}\end{array}\right]$$

is an optimal weight matrix.

Assumption 1.

The formation system consists of a leader and its followers, and each follower just communicates with its neighbors. Thus, a directed graph$\overline{G}$is formed mathematically from the cooperative formation, contained a directed spanning tree when the leader is considered as the root.

Remark 1.

As for directed graph$\overline{G}$, if only the Laplacian matrix$\mathit{L}=\mathit{D}-\mathit{A}$has only one zero eigenvalue and other eigenvalues have positive real parts, then the directed graph is strongly connected or has a directed spanning tree. That is, all the control information is available for every agent.

Assumption 2.

Assume that the unstructured uncertainty terms satisfy$d_{wui}\le d_{u\max }$$d_{wvi}\le d_{v\max },d_{wri}\le d_{r\max }$, where$d_{u\max },d_{v\max },d_{r\max }$are unknown positive constants.

Assumption 3.

The leader is an ideal vehicle with no inertia and damping, it is not affected by the marine environmental disturbance. $x_0,y_0,{\psi }_0$represent its status information, the reference path of leader is generated by following Equation (5).

$$\{\begin{array}{l}{\dot{x}}_0=u_0\cos {\psi }_0\\ {\dot{y}}_0=u_0\sin {\psi }_0\\ {\dot{\psi }}_0=r_0\end{array}$$

(5)

where$u_0$ and$r_0$ are set values according to the needs.

Lemma 2

([25]). Supposing a continuous function $V(x,t)$ satisfies $V$is positive define.

There exist scalars $\beta >0,\gamma >0,0<\alpha <1,0<\rho <\infty$ and an open neighborhood $\mathsf{\Omega }$ of origin such that $\dot{V}(x,t)\le -\beta V{(x,t)}^{\alpha }-\gamma V(x,t)+\rho ,x\in \mathsf{\Omega }$. Then there exists a finite time $T,0<\eta <\gamma$ such that for any $t\ge T,$ one has $V(x,t)\le \frac{\rho }{\gamma -\eta },$ where $T=\frac{1}{\eta (1-\alpha )}\ln \left(\frac{\frac{\beta }{\eta }+V{(0)}^{1-\alpha }}{\frac{\beta }{\eta }+{\left(\frac{\rho }{\gamma -\eta }\right)}^{1-\alpha }}\right)$.

Lemma 3.

For$s_l\in R,l=1,2,\cdots ,k,0<\mu \le 1,$ the following inequality is correct.

$${({\displaystyle \sum _{l=1}^k\left|s_l\right|})}^{\mu }\le {\displaystyle \sum _{l=1}^k{\left|s_l\right|}^{\mu }}\le k^{1-\mu }{({\displaystyle \sum _{l=1}^k\left|s_l\right|})}^{\mu }$$

3. Roust Fast Finite-Time Controller Design

As shown in Figure 1, the purpose of this paper is to provide an algorithm such that the vehicle formation would converge to the desired planning trajectory in a predetermined geometric pattern. In this part, the algorithm for vehicle formation is fully explained and proved through mathematical derivation and theoretical analysis.

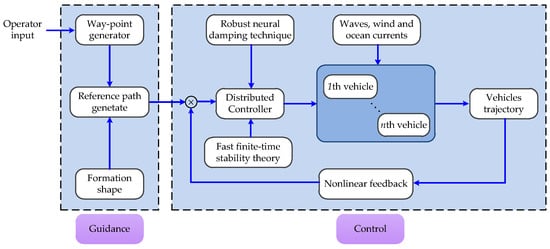
Figure 1. Conceptual signal flow box diagram for guidance, and control.

3.1. Distributed Robust Fast Finite-Time Controller Design

In this paper, the vehicle formation consists of a virtual leader and its followers. The function of the leader is to guide the vehicle formation to navigate along the planned path. The ith vehicle in the formation system just communicates with its neighbors or leader according to the designed directed graph. Based on the information from its own and other vehicles, the robust fast finite-time formation controller of ith ASV is designed by a backstepping approach and directed graph theory. In this part, the construction method of the controller is described in the following two steps.

Step 1: According to the relative position of the vehicles in Figure 2, the position errors of ith are defined based on directed graph as Equations (6) and (7).

$$x_{ei}={\displaystyle \sum _{j=1}^M{a}_{ij}(x_i-x_j-\Delta x_{ij})}+b_i(x_i-x_0)$$

(6)

$$y_{ei}={\displaystyle \sum _{j=1}^M{a}_{ij}(y_i-y_j-\Delta y_{ij})}+b_i(y_i-y_0)$$

(7)

where $\Delta x_{ij},\Delta y_{ij}$ are constants maintained the geometry for vehicle formation.

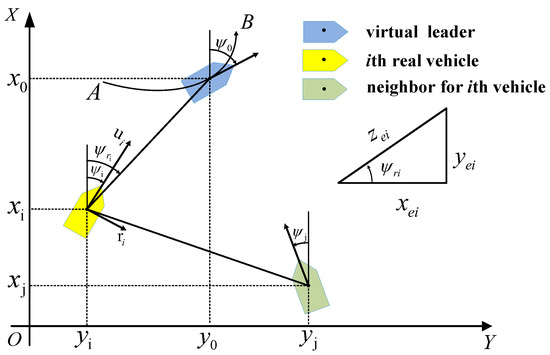
Figure 2. The schematic diagram of the proposed control principle.

Remark 2.

$B={[b_1,b_2,\cdots ,b_M]}^{\mathrm{T}}$is a column of vectors, which is used to describe the existence of information connectivity between ith vehicle and leader. When the ith vehicle can receive the information from the leader, $b_i=1$, otherwise $b_i=0$. Here, the leader and vehicles in the formation are constructed into a directed graph$\overline{G}$.

Based on the geometrical relation between the current position of ith vehicle and the reference signal in Figure 2, the error $z_{ei}$ and ${\psi }_{ei}$ are calculated as Equation (8).

$$\begin{array}{l}{z}_{ei}=\sqrt{x_{ei}^2+y_{ei}^2}\\ {\psi }_{ei}={\psi }_i-{\psi }_{ri}\end{array}$$

(8)

Note that ${\psi }_{ri}\in (-\pi ,\pi )$ is the expected angle of the ith ship, which can be calculated as Equation (9).

$${\psi }_{ri}=0.5[1-\mathrm{sign}(x_{ei})]\mathrm{sign}(y_{ei})\pi +\arctan (\frac{y_{ei}}{x_{ei}})$$

(9)

The mathematical relationship between position errors is calculated according to the trigonometric function as Equation (10).

$$x_{ei}=z_{ei}\cos {\psi }_{ri},{\mathrm{y}}_{ei}=z_{ei}\sin {\psi }_{ri}$$

(10)

In view of the Equations (1) and (2), the time derivative of $x_{ei}$ and $y_{ei}$ are calculated as follows:

$$\begin{array}{l}{\dot{x}}_{ei}=(d_i+b_i)(u_i\cos {\psi }_i-v_i\sin {\psi }_i)-{\displaystyle \sum _{i=1}^M{a}_{ij}(u_j\cos {\psi }_j-v_j\sin {\psi }_j+\Delta {\dot{x}}_{ij})-b_i{\dot{x}}_0}\\ {\dot{y}}_{ei}=(d_i+b_i)(u_i\sin {\psi }_i+v_i\cos {\psi }_i)-{\displaystyle \sum _{i=1}^M{a}_{ij}(u_j\sin {\psi }_j+v_j\cos {\psi }_j+\Delta {\dot{y}}_{ij})-b_i{\dot{y}}_0}\end{array}$$

(11)

Combining Equations (8)–(11), we can simplify the time derivation of $z_{ei}$ as

$$\begin{array}{ll}{\dot{z}}_{ei}& ={\dot{x}}_{ei}\cos {\psi }_{ri}+{\dot{y}}_{ei}\sin {\psi }_{ri}\\ & =(d_i+b_i)[u_i\cos {\psi }_{ei}-v_i\sin {\psi }_{ei}]-{\displaystyle \sum _{j=1}^M{a}_{ij}\xi -b_i\cos {\psi }_{ri}{\dot{x}}_0-b_i\sin {\psi }_{ri}{\dot{y}}_0}\end{array}$$

(12)

with $\xi =u_j\cos ({\psi }_j-{\psi }_{rj})+v_j\sin ({\psi }_j-{\psi }_{rj})$.

According to the Equations (2) and (8), the time derivative of the heading angle error ${\psi }_{ei}$ is calculated as (13).

$${\dot{\psi }}_{ei}={\dot{\psi }}_i-{\dot{\psi }}_{ri}=r_i-{\dot{\psi }}_{ri}$$

(13)

To stabilize the kinematic error dynamics (8), the virtual control laws ${\alpha }_{ui}$ and ${\alpha }_{ri}$ can be respectively designed for $u_i$ and $r_i$ as Equation (14).

$$\begin{array}{ll}{\alpha }_{ui}& ={[(d_i+b_i)\cos {\psi }_{ei}]}^{-1}[-k_{z1}{z}_{ei}-k_{z2}{z}_{ei}^{2h-1}+(d_i+b_i)v_i\sin {\psi }_{ei}\\ & +{\displaystyle \sum _{i=1}^M{a}_{ij}\xi +b_i\cos {\psi }_{ri}{\dot{x}}_0+b_i\sin {\psi }_{ri}{\dot{y}}_0}]\\ {\alpha }_{ri}& =-k_{\psi 1}{\psi }_{ei}-k_{\psi 2}{\psi }_{ei}^{2h-1}+{\dot{\psi }}_{ri}\end{array}$$

(14)

where $k_{z1},k_{z2},k_{\psi 1},k_{\psi 2}$ are positive design parameters.

Remark 3.

For control law Equation (14), note that${\alpha }_{ui}$is not defined at${\psi }_{ei}=\pm 0.5\pi$, thus, we assume in the control design that$\left|{\psi }_{ei}<0.5\pi \right|$, and conceive that if ${\psi }_{ei}=\pm 0.5\pi$, then${\psi }_{ei}=0.5\pi \mp 0.01\pi$. Moreover, in the algorithm, the real vehicle follows a certain route generated by a virtual vehicle, and the heading angle error${\psi }_{ei}$will not be equal to$0.5\pi$owing to the small tracking error.

In this part, we introduce a novel DSC technology by applying first-order nonlinear filter ${\beta }_{ui}$ and ${\beta }_{ri}$ instead of the traditional first-order linear filter to avoid repeatedly differentiating ${\alpha }_{\zeta i}$ as Equation (15). This effectively simplifies the process of controller design and solves the problem of the so-called “explosion of complexity”.

$${\epsilon }_{\zeta i}{\dot{\beta }}_{\zeta i}=sig{({\alpha }_{\zeta i}-{\beta }_{\zeta i})}^{2h-1}+sig({\alpha }_{\zeta i}-{\beta }_{\zeta i})$$

(15)

where ${\epsilon }_{\zeta i}$ are time constants, $sig{(\cdot )}^{\kappa }={|\cdot |}^{\kappa }sig(\cdot )$.

Defining the errors of filters as Equation (16).

$$q_{ui}={\beta }_{ui}-{\alpha }_{ui},q_{ri}={\beta }_{ri}-{\alpha }_{ri}$$

(16)

From the above result, $q_{\zeta i}{\dot{q}}_{\zeta i}$ can be simplified as Equation (17)

$$\begin{array}{ll}{q}_{\zeta i}{\dot{q}}_{\zeta i}& =q_{\zeta i}({\dot{\beta }}_{\zeta i}-{\dot{\alpha }}_{\zeta i})=-\frac{1}{{\epsilon }_{\zeta i}}{q}_{\zeta i}^{2h}-\frac{1}{{\epsilon }_{\zeta i}}{q}_{\zeta i}^2-q_{\zeta i}{\dot{\alpha }}_{\zeta i}\\ & \le -\frac{1}{{\epsilon }_{\zeta i}}{q}_{\zeta i}^{2h}-\frac{1}{{\epsilon }_{\zeta i}}{q}_{\zeta i}^2+q_{\zeta i}^2+\frac{1}{4}{\eta }_{\zeta i}^2(\cdot )\end{array}$$

(17)

where ${\eta }_{\zeta i}(\cdot )\ge \left|-{\dot{\alpha }}_{\zeta i}\right|$ is a nonnegative continuous function.

Step 2: At this step, the control inputs ${\tau }_{{\varsigma }_i}$ and the derivative of adaptive laws ${\dot{\hat{\lambda }}}_{{\varsigma }_i}$ for the ith vehicle are obtained according to the deduction of kinetic errors. In addition, the RBF NNs is used to approximate the model uncertainty part, which effectively enhances the stability of the system.

Firstly, one defines the kinetic errors as Equation (18).

$$\begin{array}{ll}{u}_{ei}\hfill & =u_i-{\beta }_{ui} \hfill \\ r_{ei}\hfill & =r_i-{\beta }_{ri}\hfill \end{array}$$

(18)

The time derivative of $u_{ei}$ and $r_{ei}$ can be calculated along Equations (2) and (18) as Equation (19).

$$\begin{array}{ll}{\dot{\mathrm{u}}}_{\mathrm{ei}}\hfill & ={\dot{u}}_i-{\dot{\beta }}_{ui}=\frac{m_v}{m_u}{v}_i{r}_i-f_u(u_i)+\frac{1}{m_u}{\tau }_{ui}+d_{wui}-{\dot{\beta }}_{ui}\hfill \\ {\dot{\mathrm{r}}}_{\mathrm{ei}}\hfill & ={\dot{r}}_i-{\dot{\beta }}_{ri}=\frac{m_u-m_v}{m_r}{u}_i{v}_i-f_r(r_i)+\frac{1}{m_r}{\tau }_{ri}+d_{wri}-{\dot{\beta }}_{ri}\hfill \end{array}$$

(19)

Here, $f_{\varsigma }({\varsigma }_i)$ is an unknown smooth function in vehicle model which is used to describe hydrodynamic effects. According to Lemma 1, it can be approximated by NNs as

$$\begin{array}{ll}{f}_{\varsigma }({\varsigma }_i)& =S_{{\varsigma }_i}(\varsigma )A_{{\varsigma }_i}{\varsigma }_i+{\epsilon }_{{\varsigma }_i}\\ & =S_{{\varsigma }_i}(\varsigma )A_{{\varsigma }_i}{\beta }_{{\varsigma }_i}+S_{{\varsigma }_i}(\varsigma )A_{{\varsigma }_i}{\varsigma }_{ei}+{\epsilon }_{\varsigma i}\\ & =S_{{\varsigma }_i}(\varsigma )A_{{\varsigma }_i}{\beta }_{{\varsigma }_i}+b_{{\varsigma }_i}{S}_{{\varsigma }_i}{W}_{{\varsigma }_i}+{\epsilon }_{{\varsigma }_i}\end{array}$$

(20)

where $b_{\varsigma }=\left|\right|A_{\varsigma }\left|\right|,A_{\varsigma }^m=(A_{\varsigma }/b_{\varsigma }), W_{\varsigma }=A_{\varsigma }^m{\varsigma }_e=(A_{\varsigma }/b_{\varsigma }){\varsigma }_e,b_{\varsigma }{W}_{\varsigma }=A_{\varsigma }{\varsigma }_e$.

According to Equation (20), the simplified ${\dot{u}}_{ei}$ and ${\dot{r}}_{ei}$ can be obtained as Equation (21).

$$\begin{array}{l}{\dot{u}}_{ei}={\upsilon }_{ui}-b_{ui}{S}_{ui}{W}_{ui}+\frac{1}{m_u}{\tau }_{ui}-{\dot{\beta }}_{ui}\\ {\dot{r}}_{ei}={\upsilon }_{ri}-b_{ri}{S}_{ri}{W}_{ri}+\frac{1}{m_r}{\tau }_{ri}-{\dot{\beta }}_{ri}\end{array}$$

(21)

To promote the understanding, one defines the variables ${\upsilon }_{{\varsigma }_i},{\vartheta }_{{\varsigma }_i}$ and ${\phi }_{{\varsigma }_i}$ to describe simplistically the controller construction.

$$\begin{array}{ll}{\upsilon }_{ui}=& \frac{m_v}{m_u}{v}_i{r}_i-S_{\mathrm{ui}}{A}_{ui}{\beta }_{ui}+d_{wui}-{\epsilon }_{ui}\\ & \le d_u\frac{v_i^2+r_i^2}{2}+S_{\mathrm{ui}}{A}_{ui}{\beta }_{ui}{+\mathrm{d}}_{\mathrm{u} \max }+{\overline{\epsilon }}_{ui}\\ & \le \max \{\Vert A_{ui}{\beta }_{ui}\Vert ,d_u,{\mathrm{d}}_{\mathrm{u} \max }+{\overline{\epsilon }}_{ui}\}\left(1+\Vert S_{ui}(u)\Vert +\frac{v_i^2+r_i^2}{2}\right)\\ & \le {\vartheta }_{ui}{\phi }_{ui}\end{array}$$

(22)

where ${\vartheta }_{ui}=\max \{\Vert A_{ui}{\beta }_{ui}\Vert ,d_u,{\mathrm{d}}_{\mathrm{u} \max }+{\overline{\epsilon }}_{ui}\}$ and ${\phi }_{ui}=\left(1+\Vert S_{ui}(u)\Vert +\frac{v_i^2+r_i^2}{2}\right)$

Similar to the previous process, we can obtain

$${\upsilon }_{ri}\le {\vartheta }_{ri}{\phi }_{ri}$$

(23)

where ${\vartheta }_{ri}=\max \{\Vert A_{ri}{\beta }_{ri}\Vert ,d_r,{\mathrm{d}}_{\mathrm{r} \max }+{\overline{\epsilon }}_{ri}\}$ and ${\phi }_{ri}=\left(1+\Vert S_{ri}(r)\Vert +\frac{u_i^2{+\mathrm{v}}_i^2}{2}\right)$, with $d_u$ and $d_{\mathrm{r}}$ are an unknown positive constant.

Now, the controller inputs of ${\tau }_{ui},{\tau }_{ri}$ and parameter update laws ${\dot{\hat{\lambda }}}_{ui},{\dot{\hat{\lambda }}}_{ri}$ are designed as follows Equations (24) and (25).

$$\begin{array}{l}{\tau }_{ui}=m_u{\dot{\beta }}_{ui}-{\hat{\lambda }}_{\mathrm{ui}}{\mathsf{\Phi }}_{ui}(\cdot )u_{ei}-k_{u1}{u}_{ei}-k_{u2}{u}_{ei}^{2h-1}\\ {\tau }_{ri}=m_r{\dot{\beta }}_{ri}-{\hat{\lambda }}_{\mathrm{ri}}{\mathsf{\Phi }}_{ri}(\cdot )r_{ei}-k_{r1}{r}_{ei}-k_{r2}{r}_{ei}^{2h-1}\end{array}$$

(24)

$$\begin{array}{l}{\dot{\hat{\lambda }}}_{ui}={\mathsf{\Gamma }}_{ui}\left[{\mathsf{\Phi }}_{ui}(\cdot )u_{ei}^2-{\delta }_{u1}({\hat{\lambda }}_{\mathrm{ui}}-{\hat{\lambda }}_{ui}^0)-{\delta }_{u2}{({\hat{\lambda }}_{\mathrm{ui}}-{\hat{\lambda }}_{ui}^0)}^{2h-1}\right]\\ {\dot{\hat{\lambda }}}_{ri}={\mathsf{\Gamma }}_{ri}\left[{\mathsf{\Phi }}_{ri}(\cdot )r_{ei}^2-{\delta }_{r1}({\hat{\lambda }}_{\mathrm{ri}}-{\hat{\lambda }}_{ri}^0)-{\delta }_{r2}{({\hat{\lambda }}_{\mathrm{ri}}-{\hat{\lambda }}_{ri}^0)}^{2h-1}\right]\end{array}$$

(25)

with

$$\begin{array}{c}{\mathsf{\Phi }}_{{\varsigma }_i}(\cdot )=(S_{{\varsigma }_i}(\varsigma )S_{{\varsigma }_i}{(\varsigma )}^{\mathrm{T}}/(4{\gamma }_{i1}^2))+({\phi }_{{\varsigma }_i}^2/(4{\gamma }_{{\varsigma }_2}^2)\\ {\lambda }_{\varsigma }=m_{\varsigma }max\{b_{\varsigma }^2,{\vartheta }_{\varsigma }^2\} \varsigma =u,r\end{array}$$

where $k_{{\varsigma }_1},k_{{\varsigma }_2},{\mathsf{\Gamma }}_{{\varsigma }_i},{\delta }_{{\varsigma }_1},{\delta }_{{\varsigma }_2}$ are positive parameters for controller. ${\hat{\lambda }}_{{\varsigma }_i}$ is the estimate of ${\lambda }_{\varsigma }$, and ${\hat{\lambda }}_{\varsigma }^0$ is the initial value of ${\hat{\lambda }}_{\varsigma }$.

3.2. Distributed Robust Fast Finite-Time Control Algorithm Stability Analysis

In this section, the stability analysis for the vehicle formation system, which is equipped with the proposed distributed robust fast finite-time controller, is carried out based on the Lemma 2 and Lyapunov approach.

The main result is summarized as Theorem 1.

For any $B_1>0$ and $B_2>0$, the sets

$$\begin{array}{l}{\mathsf{\Pi }}_1:=\{(x_0,{\dot{x}}_0,{\ddot{x}}_0,y_0,{\dot{y}}_0,{\ddot{y}}_0,{\dot{\psi }}_0,{\ddot{\psi }}_0) :x_0^2+{\dot{x}}_0^2+{\ddot{x}}_0{}^2+y_0^2+{\dot{y}}_0^2+{\ddot{y}}_0^2+{\dot{\psi }}_0^2+{\ddot{\psi }}_0^2\le B_1\}\\ {\mathsf{\Pi }}_2:=\{z_{ei},{\psi }_{ei},u_{ei},r_{ei},q_{ui},q_{ri},{\tilde{\lambda }}_{ui},{\tilde{\lambda }}_{ri}:z_{ei}^2+{\psi }_{ei}^2+u_{ei}^2+r_{ei}^2+q_{ui}^2+q_{ri}^2+{\tilde{\lambda }}_{ui}^2+{\tilde{\lambda }}_{ri}^2\le B_2\}\end{array}$$

Therefore, the nonnegative continuous function ${\eta }_{{\varsigma }_i}(\cdot )$ has a maximum value $M_{{\varsigma }_i}$ on compact set Π₁ × Π.

Theorem 1.

Assume the close-loop system consists of the vehicle dynamic (1) satisfied Assumption 2, the virtual controllers (14), the distributed robust controllers (24) and the adaptive laws (25). The proposed algorithm for the closed-loop will guarantee that: 1. all signals remain bounded uniformly; 2. the tracking errors converge to a small region in finite time T.

Proof. 

To make the reasoning process clear, we divide it into the four steps according to the system state.

Step 1: Defining the Lyapunov function $V_1=\frac{1}{2}{z}_{ei}^2$, we can get the derivative of $V_1$ as Equation (26) according to Equations (12), (16) and (18).

$$\begin{array}{ll}{\dot{V}}_1=& z_{ei}\{(d_i+b_i)[(q_{ui}+{\alpha }_{ui}+u_{ei})\cos {\psi }_{ei}-v_i\sin {\psi }_{ei}]\\ & -{\displaystyle \sum _{j=1}^M{a}_{ij}\zeta }-b_i\cos {\psi }_{ri}{\dot{x}}_0-b_i\sin {\psi }_{ri}{\dot{y}}_0\}\end{array}$$

(26)

On account of Young’s inequality, the time derivative of $V_1$ is derived along (14) and (26) as Equation (27)

$$\begin{array}{ll}\dot{V}& \le -k_{z1}{z}_{ei}^2-k_{z2}{z}_{ei}^{2h}+(d_i+b_i)cos{\psi }_{ei}(q_{ui}+u_{ei})z_{ei}\\ & \le -\left[k_{z1}-\frac{1}{2}(d_i+b_i)\right]z_{ei}^2-k_{z2}{z}_{ei}^{2h}\\ & +(d_i+b_i)q_{ui}^2+(d_i+b_i)u_{ei}^2\end{array}$$

(27)

Step 2: Constructing the Lyapunov function $V_2=\frac{1}{2}{\psi }_{ei}^2$, one can obtain the ${\dot{V}}_2$ by substituting (13), (16) and (18).

$${\dot{V}}_2={\psi }_{\mathrm{ei}}(q_{ri}+{\alpha }_{ri}+r_{ei}-{\dot{\psi }}_r)$$

(28)

Substituting the virtual law ${\alpha }_{ri}$ (14) into (28), ${\dot{V}}_2$ can be simplified as

$$\begin{array}{ll}{\dot{V}}_2& \le -k_{\psi 1}{\psi }_{ei}^2-k_{\psi 2}{\psi }_{ei}^{2h}+q_{ri}{\psi }_{ei}+r_{ei}{\psi }_{ei}\\ & \le -(k_{\psi 1}-\frac{1}{2}){\psi }_{ei}^2-k_{\psi 2}{\psi }_{ei}^{2h}+q_{ri}^2+r_{ei}^2\end{array}$$

(29)

Step 3: In order to stabilize kinetic errors ${\varsigma }_{ei}$ and adaptive parameters ${\lambda }_{{\varsigma }_i}$, here we allow

$$V_3=\frac{1}{2}{\varsigma }_{ei}^2+\frac{1}{2m_{\varsigma }}{\mathsf{\Gamma }}_{{\varsigma }_i}^{-1}{\tilde{\lambda }}_{{\varsigma }_i}^2+\frac{1}{2}{q}_{{\varsigma }_i}^2$$

(30)

The time derivative of $V_3$ can be derived by invoking from Equations (21) and (17) as Equation (31)

$$\begin{array}{ll}{\dot{V}}_3& ={\varsigma }_{ei}({\upsilon }_{{\varsigma }_i}-b_{{\varsigma }_i}{S}_{{\varsigma }_i}{W}_{{\varsigma }_i}+\frac{1}{m_{\varsigma }}{\tau }_{{\varsigma }_i}-{\dot{\beta }}_{{\varsigma }_i})+\frac{{\mathsf{\Gamma }}_{{\varsigma }_i}^{-1}}{m_{\varsigma }}{\tilde{\lambda }}_{{\varsigma }_i}{\dot{\widehat{\lambda }}}_{{\varsigma }_i}+q_{{\varsigma }_i}{\dot{q}}_{{\varsigma }_i}\\ & \le {\upsilon }_{{\varsigma }_i}{\varsigma }_{ei}-b_{{\varsigma }_i}{S}_{{\varsigma }_i}{W}_{{\varsigma }_i}{\varsigma }_{ei}+\frac{1}{m_{\varsigma }}{\tau }_{{\varsigma }_i}{\varsigma }_{ei}-{\dot{\beta }}_{{\varsigma }_i}{\varsigma }_{ei}+\frac{{\mathsf{\Gamma }}_{{\varsigma }_i}^{-1}}{m_{\varsigma }}{\widehat{\lambda }}_{{\varsigma }_i}{\dot{\widehat{\lambda }}}_{{\varsigma }_i}\\ & -\frac{{\mathsf{\Gamma }}_{{\varsigma }_i}^{-1}}{m_{\varsigma }}{\lambda }_{{\varsigma }_i}{\dot{\widehat{\lambda }}}_{{\varsigma }_i}-\frac{1}{{\epsilon }_{{\varsigma }_i}}{q}_{{\varsigma }_i}^{2h}-\frac{1}{{\epsilon }_{{\varsigma }_i}}{q}_{{\varsigma }_i}^2+q_{{\varsigma }_i}^2+\frac{1}{4}{M}_{{\varsigma }_i}^2\end{array}$$

(31)

Based on Young’s inequality, one simplifies the partial variables of Equation (31).

$$\begin{array}{l}{\upsilon }_{{\varsigma }_i}{\varsigma }_{ei}-b_{{\varsigma }_i}{S}_{{\varsigma }_i}{W}_{{\varsigma }_i}{\varsigma }_{ei}\\ \le \frac{b_{{\varsigma }_i}^2{S}_{{\varsigma }_i}^T{S}_{{\varsigma }_i}{\varsigma }_{ei}^2}{4{\gamma }_{{\varsigma }_1}^2}+{\gamma }_{{\varsigma }_1}^2{W}_{{\varsigma }_i}^T{W}_{{\varsigma }_i}+\frac{{\phi }_{{\varsigma }_i}^2{\vartheta }_{{\varsigma }_i}^2{\varsigma }_{ei}^2}{4{\gamma }_{{\varsigma }_2}^2}+{\gamma }_{{\varsigma }_2}^2\\ \le (\frac{S_{{\varsigma }_i}^T{S}_{{\varsigma }_i}}{4{\gamma }_{{\varsigma }_1}^2}+\frac{{\phi }_{{\varsigma }_{\mathrm{i}}}^2}{4{\gamma }_{{\varsigma }_2}^2})m_{\varsigma }max\{b_{{\varsigma }_i}^2,{\vartheta }_{{\varsigma }_i}^2\}\frac{1}{m_{\varsigma }}{\varsigma }_{ei}^2+{\gamma }_{{\varsigma }_1}^2{W}_{{\varsigma }_i}^T{W}_{{\varsigma }_i}+{\gamma }_{{\varsigma }_2}^2\\ \le \frac{1}{m_{\varsigma }}{\lambda }_{{\varsigma }_i}{\mathsf{\Phi }}_{{\varsigma }_i}{\varsigma }_{ei}^2+{\gamma }_{{\varsigma }_1}^2{\varsigma }_{ei}^2+{\gamma }_{{\varsigma }_2}^2\end{array}$$

(32)

with

$$\begin{array}{l}{W}_{{\varsigma }_i}=A_{{\varsigma }_i}^{\mathrm{m}}{\varsigma }_{ei}=\frac{A_{{\varsigma }_i}}{\Vert A_{{\varsigma }_i}\Vert }{\varsigma }_{ei}=\frac{1}{\Vert A_{{\varsigma }_i}\Vert }\left[\begin{array}{c}{w}_{{\varsigma }_1}{\varsigma }_e\\ w_{{\varsigma }_2}{\varsigma }_e\\ ⋮\\ w_{{\varsigma }_l}{\varsigma }_e\end{array}\right]\\ W_{{\varsigma }_i}^T{W}_{{\varsigma }_i}=\frac{1}{\Vert A_{{\varsigma }_i}\Vert }(w_{{\varsigma }_1}^2+w_{{\varsigma }_2}^2++w_{{\varsigma }_L}^2){\varsigma }_{{\varsigma }_i}^2={\varsigma }_{{\varsigma }_i}^2\end{array}$$

Then, ${\dot{V}}_3$ is calculated by virtue of Equation (32).

$$\begin{array}{ll}{\dot{V}}_3\hfill & \le \frac{1}{m_{\varsigma }}{\mathsf{\Phi }}_{{\varsigma }_i}{\lambda }_{{\varsigma }_i}{\varsigma }_{ei}^2+{\gamma }_{{\varsigma }_1}^2{\varsigma }_{ei}^2+{\gamma }_{{\varsigma }_2}^2+\frac{1}{m_{\varsigma }}{\tau }_{{\varsigma }_i}{\varsigma }_{ei}-{\dot{\beta }}_{{\varsigma }_i}{\varsigma }_{ei}\hfill \\ \hfill & +\frac{{\mathsf{\Gamma }}_{{\varsigma }_i}^{-1}}{m_{\varsigma }}{\widehat{\lambda }}_{{\varsigma }_i}{\dot{\widehat{\lambda }}}_{{\varsigma }_i}-\frac{{\mathsf{\Gamma }}_{{\varsigma }_i}^{-1}}{m_{\varsigma }}{\lambda }_{{\varsigma }_i}{\dot{\widehat{\lambda }}}_{{\varsigma }_i}-\frac{1}{{\epsilon }_{{\varsigma }_i}}{q}_{{\varsigma }_i}^{2h}-\frac{1}{{\epsilon }_{{\varsigma }_i}}{q}_{{\varsigma }_i}^2+q_{{\varsigma }_i}^2+\frac{1}{4}{M}_{{\varsigma }_i}^2\hfill \\ \hfill & \le \frac{{\varsigma }_{ei}}{m_{\varsigma }}({\mathsf{\Phi }}_{{\varsigma }_i}{\widehat{\lambda }}_{{\varsigma }_i}{\varsigma }_{ei}-m_{\varsigma }{\dot{\beta }}_{{\varsigma }_i}+{\tau }_{{\varsigma }_i})+\frac{{\tilde{\lambda }}_{{\varsigma }_i}}{{\mathrm{m}}_{\varsigma }}({\mathsf{\Gamma }}_{{\varsigma }_i}^{-1}\dot{\widehat{\lambda }}-{\mathsf{\Phi }}_{{\varsigma }_i}{\varsigma }_{ei}^2)\hfill \\ \hfill & -\frac{1}{{\epsilon }_{{\varsigma }_i}}{q}_{{\varsigma }_i}^{2h}-\frac{1}{{\epsilon }_{{\varsigma }_i}}{q}_{{\varsigma }_i}^2+q_{{\varsigma }_i}^2+\frac{1}{4}{M}_{{\varsigma }_i}^2+{\gamma }_{{\varsigma }_1}^2{\varsigma }_{ei}^2+{\gamma }_{{\varsigma }_2}^2\hfill \end{array}$$

(33)

Substituting control inputs Equation (24) and adaptive laws (25) into Equation (33), one can get

$$\begin{array}{ll}{\dot{V}}_3\hfill & \le -\frac{k_{{\varsigma }_1}}{m_u}{\varsigma }_{ei}^2-\frac{k_{{\varsigma }_2}}{m_u}{\varsigma }_{ei}^{2h}-\frac{{\delta }_{{\varsigma }_1}}{m_{\mathrm{u}}}{\tilde{\lambda }}_{{\varsigma }_i}({\widehat{\lambda }}_{{\varsigma }_i}-{\widehat{\lambda }}_{{\varsigma }_i}^0)\hfill \\ \hfill & -\frac{{\delta }_{{\varsigma }_2}}{m_u}{\tilde{\lambda }}_{{\varsigma }_i}{({\widehat{\lambda }}_{{\varsigma }_i}-{\widehat{\lambda }}_{{\varsigma }_i}^0)}^{2h-1}+\frac{1}{4}{\eta }_{{\varsigma }_i}^2-\frac{1}{{\epsilon }_{{\varsigma }_i}}{q}_{{\varsigma }_i}^{2h}\hfill \\ \hfill & -(\frac{1}{{\epsilon }_{{\varsigma }_i}}-1)q_{{\varsigma }_i}^2+{\gamma }_{{\varsigma }_1}^2{\varsigma }_{ei}^2+{\gamma }_{{\varsigma }_2}^2\hfill \end{array}$$

(34)

where

$$\begin{array}{ll}\hfill & -{\tilde{\lambda }}_{{\varsigma }_i}{({\widehat{\lambda }}_{{\varsigma }_i}-{\widehat{\lambda }}_{{\varsigma }_i}^0)}^{2h-1}\hfill \\ \hfill & =-{\tilde{\lambda }}_{{\varsigma }_i}{({\widehat{\lambda }}_{{\varsigma }_i}-{\lambda }_{{\varsigma }_i}+{\lambda }_{{\varsigma }_i}-{\widehat{\lambda }}_{{\varsigma }_i}^0)}^{2h-1}\hfill \\ \hfill & =-{\left[{\tilde{\lambda }}_{{\varsigma }_i}^{\frac{2h}{2h-1}}+{\tilde{\lambda }}_{{\varsigma }_i}^{\frac{1}{2h-1}}({\lambda }_{{\varsigma }_i}-{\widehat{\lambda }}_{{\varsigma }_i}^0)\right]}^{2h-1}\hfill \\ \hfill & \le -{\left[{\tilde{\lambda }}_{{\varsigma }_i}^{\frac{2h}{2h-1}}-\frac{1}{2h}{\tilde{\lambda }}_{{\varsigma }_i}^{\frac{2h}{2h-1}}-\frac{2h-1}{2h}{({\lambda }_{{\varsigma }_i}-{\widehat{\lambda }}_{{\varsigma }_i}^0)}^{\frac{2h}{2h-1}}\right]}^{2h-1}\hfill \\ \hfill & \le -{\left(\frac{2h-1}{2h}{\tilde{\lambda }}_{{\varsigma }_i}^{\frac{2h}{2h-1}}\right)}^{2h-1}-{\left[-\frac{2h-1}{2h}{({\lambda }_{{\varsigma }_i}-{\widehat{\lambda }}_{{\varsigma }_i}^0)}^{\frac{2h}{2h-1}}\right]}^{2h-1}\hfill \\ \hfill & \le -a{\tilde{\lambda }}_{{\varsigma }_i}^{2h}+a{({\lambda }_{{\varsigma }_i}-{\widehat{\lambda }}_{{\varsigma }_i}^0)}^{2h}\hfill \end{array}$$

(35)

with $a={(\frac{2h-1}{2h})}^{2h-1},-{\tilde{\lambda }}_{{\varsigma }_i}({\hat{\lambda }}_{{\varsigma }_i}-{\hat{\lambda }}_{{\varsigma }_i}^0)\le -\frac{1}{2}{\tilde{\lambda }}_{{\varsigma }_i}^2+\frac{1}{2}{({\lambda }_{{\varsigma }_i}-{\hat{\lambda }}_{{\varsigma }_i}^0)}^2$, when $h=1$.

Step 4: Based on the above argument, we construct the Lyapunov function $V$ for5the close-loop control system.

$$\begin{array}{ll}V\hfill & =V_1+V_2+V_3\hfill \\ \hfill & =\frac{1}{2}{z}_{ei}^2+\frac{1}{2}{\psi }_{ei}^2+\frac{1}{2}{\varsigma }_{ei}^2+\frac{1}{2m_{\varsigma }}{\mathsf{\Gamma }}_{{\varsigma }_i}^{-1}{\tilde{\lambda }}_{{\varsigma }_i}^2+\frac{1}{2}{q}_{{\varsigma }_i}^2\hfill \end{array}$$

(36)

By combining (27), (29), (34) and (35), the time derivative of $V$ can be derived as Equation (37)

$$\begin{array}{ll}\dot{V}& =z_{ei}{\dot{z}}_{ei}+{\psi }_{ei}{\dot{\psi }}_{ei}+{\varsigma }_{ei}{\dot{\varsigma }}_{ei}+\frac{{\mathsf{\Gamma }}_{{\varsigma }_i}^{-1}}{m_{\varsigma }}{\tilde{\lambda }}_{{\varsigma }_i}{\dot{\widehat{\lambda }}}_{{\varsigma }_i}+q_{{\varsigma }_i}{\dot{q}}_{{\varsigma }_i}\\ & \le -\left[k_{z1}-\frac{1}{2}(d_i+b_i)\right]z_{ei}^2-\left(k_{\psi 1}-\frac{1}{2}\right){\psi }_{ei}^2\\ & -\left[\frac{k_{\varsigma 1}}{m_{\varsigma }}-{\gamma }_{{\varsigma }_1}^2-(d_i+b_i)\right]{\varsigma }_{ei}^2-\left[\frac{1}{{\epsilon }_{ui}}-1-(d_i+b_i)\right]q_{ui}^2\\ & -\left[\frac{1}{{\epsilon }_{ri}}-2\right]q_{ri}^2-\frac{{\delta }_{{\varsigma }_1}}{2m_{\varsigma }}{\tilde{\lambda }}_{{\varsigma }_i}^2-k_{z2}z{e}_{ei}^{2h}-k_{\psi 2}{\psi }_{ei}^{2h}\\ & -\frac{k_{{\varsigma }_2}}{m_{\varsigma }}{\varsigma }_{ei}^{2h}-\frac{1}{{\epsilon }_{{\varsigma }_i}}{q}_{{\varsigma }_i}^{2h}-\frac{a{\delta }_{{\varsigma }_2}}{m_{\varsigma }}{\tilde{\lambda }}_{{\varsigma }_i}^{2h}+\rho \end{array}$$

(37)

with

$$\rho =\frac{{\delta }_{{\varsigma }_1}}{2m_{\varsigma }}{({\lambda }_{{\varsigma }_i}-{\widehat{\lambda }}_{{\varsigma }_i}^0)}^2+\frac{a{\delta }_{{\varsigma }_2}}{m_{\varsigma }}{({\lambda }_{{\varsigma }_i}-{\hat{\lambda }}_{{\varsigma }_i}^0)}^{2h}+{\gamma }_{{\varsigma }_2}^2+\frac{1}{4}{M}_{{\varsigma }_i}^2$$

Now we can choose

$$\begin{array}{ll}\gamma \hfill & =\min \{2k_{z1}-(d_i+b_i),2k_{{\psi }_1}-1,\frac{2k_{\varsigma }}{m_{\varsigma }}-{\gamma }_{{\varsigma }_1}^2-2(d_i+b_i),\hfill \\ \hfill & \frac{2}{{\epsilon }_{ui}}-1-(d_i+b_i),\frac{2}{{\epsilon }_{ri}}-4,\frac{{\delta }_{{\varsigma }_1}}{{\mathsf{\Gamma }}_{{\varsigma }_i}}\}\hfill \\ \beta \hfill & =\min \left\{2k_{z2},2k_{\psi 2},\frac{k_{2{\varsigma }_2}}{m_{\varsigma }},\frac{2}{{\epsilon }_{{\varsigma }_i}},\frac{a{\delta }_{{\varsigma }_2}}{{\mathsf{\Gamma }}_{{\varsigma }_i}}\right\}\hfill \end{array}$$

(38)

then $\dot{V}\le -\gamma V-\beta V^h+\rho$. □

Remark 4.

By applying Lemma 2, this inequality implies that all the signals in the formation of ASVs are bounded uniformly. Moreover,$V(x)\le \frac{\rho }{\gamma -\eta }$always holds for$t>T$, with$\alpha =h$according to the proof process of Lemma 2 in [25]. Compared with the system satisfied$\dot{V}\le -\alpha V+\rho$or$\dot{V}\le -\alpha V^{\alpha }+\rho$, the proposed control strategy is with the merits of fast convergence and practicability.

4. Numerical Simulation

In this section, two examples are given to verify the performance and feasibility of the proposed distributed robust fast finite-time control scheme. The simulation plant are the underactuated vehicles (length of 38 m, mass of $118\times {10}^3$ kg), which is the same as it in [26], and model parameters of simulation vehicles as follows: $m_u=120\times {10}^3$ kg,$m_v=177.9\times {10}^3$ kg, $m_r=636\times {10}^5$ kg. Moreover, the personal computer (the PC (Ryzen 7 4700U CPU @2GHz RAM:16GB)) was chosen to simulate the proposed algorithm.

4.1. Search and Rescue Formation in Presence of Partial Information Interruption

In the field of maritime search and rescue, we expect that the task should be conducted with the advantages of a wide search range and high efficiency, hence multi-vehicle cooperative formations are more suitable for this task. In this part, we suppose the vehicle formation consists of a virtual leader and three analogous followers. They are arranged horizontally to carry out the search task under the disturbance of ocean environment. The processes of information communication between vehicles are designed as Figure 3.

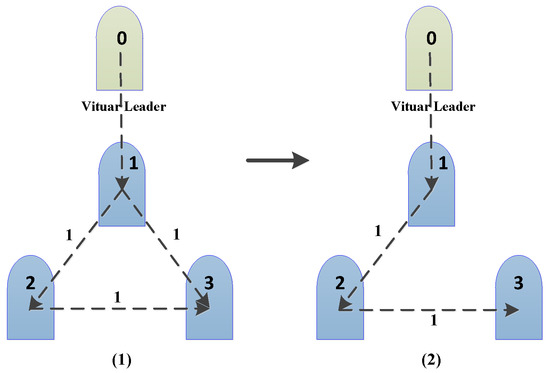
Figure 3. The augmented graph of information transfer in the ASVs.

Considering the possible delay or information interruption, the experiment simulates the interruption of a message during navigation by invalidating one of the information transmission channels at 600 s. Moreover, this above situation is described by graph theory as: the corresponding adjacency matrix and Laplacian matrix are expressed in the topological relationship of the vehicle formation, respectively,

$$\begin{array}{l}A=\left[\begin{array}{ccc}0& 0& 0\\ 1& 0& 0\\ 1& 1& 0\end{array}\right]\to \left[\begin{array}{ccc}0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\end{array}\right],\\ L=\left[\begin{array}{ccc}0& 0& 0\\ -1& 1& 0\\ -1& -1& 2\end{array}\right]\to \left[\begin{array}{ccc}0& 0& 0\\ -1& 1& 0\\ 0& -1& 1\end{array}\right].\end{array}$$

Remark 5.

Before or after the information channel interruption, the Laplacian matrix L from graph always satisfies the condition in Assumption 1, and the information needed to achieve control tasks is always globally accessible, hence the result of formation control will not be affected by the interruption of a specific signal.

Additionally, $B=\left[1,0,0\right]$ is a used to describe the communication ability between the vehicle and leader; following Remark 2, the leader’s path is composed of path planning based on waypoints, with details such as in article [26]. The geometric formation is constructed by the distances in X and Y directions between vehicles, and the relative distances between vehicles are given as $\Delta x_{21}=-1, \Delta y_{21}=299$; $\Delta x_{32}=-1,\Delta y_{32}=299$; $\Delta x_{31}=-2,\Delta y_{31}=598$. Moreover, the initial positions and orientations of the three ASVs are designed as Equation (39).

$$\left[\begin{array}{c}{x}_i(0)\\ y_i(0)\\ {\psi }_i(0)\end{array}\right]=\left[\begin{array}{ccc}-1m& -1m& -1m\\ 0m& -300m& -600m\\ 0^{°}& 0^{°}& 0^{°}\end{array}\right]$$

(39)

The RBF NNs for $f_u(u_i)$ and $f_r(r_i)$ include 32 nodes, $l=35$, the centers spaced in [−10 m/s, 10 m/s] for $f_u(u_i)$ and [−2.5 rad/s, 2.5 rad/s] for $f_r(r_i)$ and widths ${\eta }_j=3(j=1,2,\dots ,l)$. For the external disturbances, the ASVs inevitably encounter the disturbance of wind and wind-generated waves in the course of navigation. This paper adopts a physical-based mathematical model to reflect the actual environment. The NORSOK wind and the JONSWAP wave spectrums are adapted to produce these two disturbances, which have been defined as an International Towing Tank Conference standard. Figure 4 describes the wind conditions (e.g., the speed is about 12.25 m/s and the direction is about 45 deg) and wind-generated waves in the simulation experiment. As for the current perturbation, the speed $v_{vurrent}=0.8$ m/s and the direction ${\psi }_{current}={60}^{\circ }$. These disturbances exert influence on the underactuated ASVs through a certain mechanism, and the detailed descriptions of the impact method are illustrated in book [27]. For adjusting the parameters more conveniently in the application, the three ASVs in this simulation use the same set of controller parameters. The main controller parameters adjusted properly are selected as Table 1.

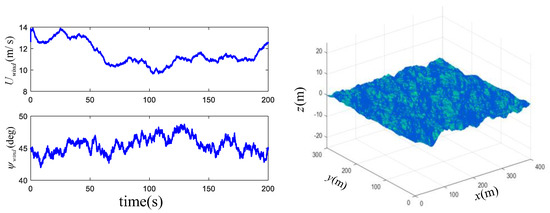
Figure 4. The simulated environment with physical-based mathematical model.

Table 1. Controller parameters for the controller.

Indexes	Items
Control gains	$\begin{array}{l}{k}_{z1}=5,k_{z2}=0.9,k_{\psi 1}=1.2,k_{\psi 2}=10,\\ k_{u1}=8.6\times {10}^5,k_{u2}=20,\\ k_{r2}=1.52\times {10}^9,k_{r2}=20.\end{array}$
Other parameters	$\begin{array}{l}{\delta }_{u1}=4.5,{\delta }_{u2}=4.5,{\delta }_{r1}=4.5,{\delta }_{r2}=4.5,\\ {\gamma }_{u1}=1.2,{\gamma }_{u2}=4.3,{\gamma }_{r1}=1.2,{\gamma }_{r2}=4.3,\\ {\mathsf{\Gamma }}_{u1}=8.5,{\mathsf{\Gamma }}_{u2}=9.0,{\mathsf{\Gamma }}_{r1}=8.5,{\mathsf{\Gamma }}_{r2}=10.0,\\ {\mathsf{\Gamma }}_u=0.08,{\mathsf{\Gamma }}_r=0.08,{\epsilon }_u=0.01,{\epsilon }_r=0,01.\end{array}$

Based on the above configuration, the numerical simulation results are shown in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. Figure 5 is the navigation chart of ASVs formation under the proposed control scheme. The navigation path for ASVs formation is expanded by concentric square, the circles (with a radius of 150 m) in figure is the search radius. Figure 6 demonstrates the tracking errors $x_{ei}$, $y_{ei}$ and ${\psi }_{ei}$, the fluctuation of the errors curve in the figure is caused by the turning of the ASVs formation. When the information is interrupted at 600 s, the positions errors $x_{e3}$ and $y_{e3}$ have a sudden change, which is consistent with the description of Equation (6) combined with the ASVs’ position at 600 s in Figure 5. In Figure 6, other places are continuous except that the error at the signal interrupt is discontinuous. During the turning, the surge speed of the vehicle outside the circle is larger than that of the inner circle to achieve the formation turning behavior; the action is described in Figure 7. In addition, there exists a decline in the surge velocity of second and third vehicles at the time 180 s, which is different from at 600 s. For Figure 8, we can see that one of the changes in the adaptive parameters related to surge and yaw velocity, and the fluctuation time is the same as that of surge and yaw velocity, which is reasonable for this phenomenon to appear in the course of a formation system turning. Figure 9 shows the control efforts ${\tau }_u$ and ${\tau }_r$ of the three ASVs with the proposed algorithm.

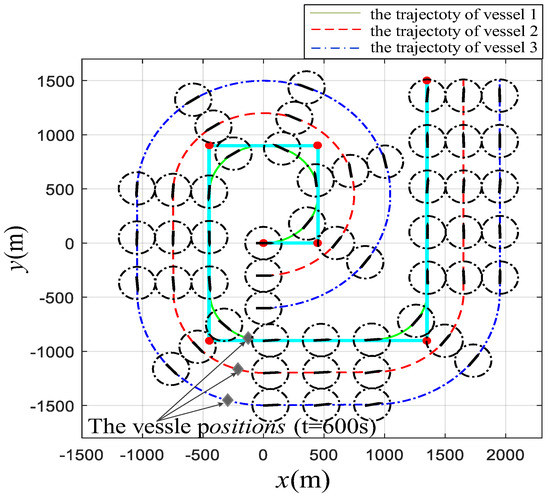
Figure 5. The position and orientation errors for the formation.

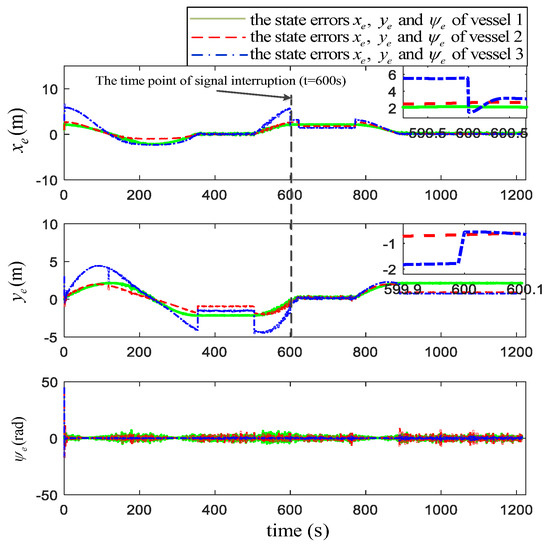
Figure 6. The position and orientation errors for the formation.

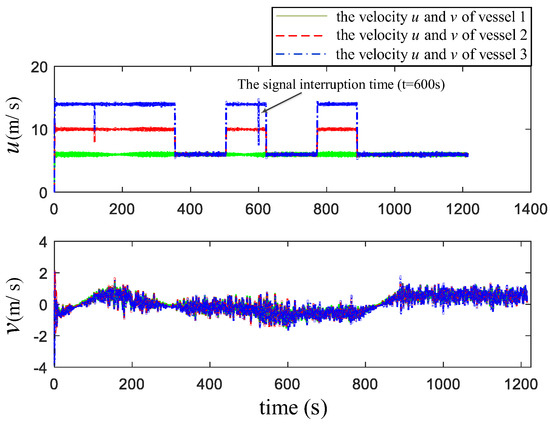
Figure 7. The change in surge velocity and sway velocity in vehicle navigation.

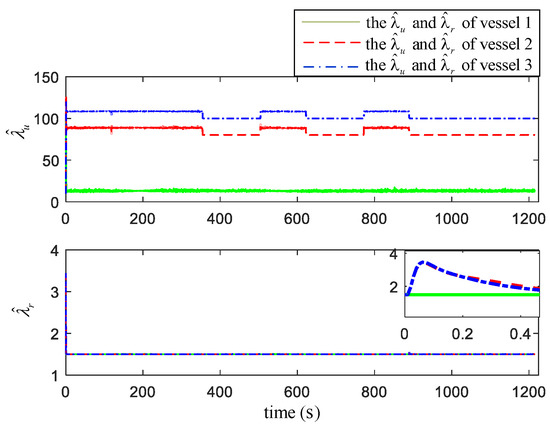
Figure 8. The changes in adaptive laws ${\lambda }_u$ and ${\lambda }_r$ during simulation.

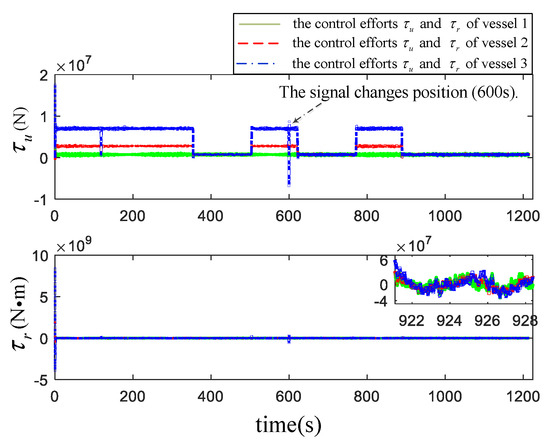
Figure 9. The control inputs ${\tau }_u$ and ${\tau }_r$ for ASVs.

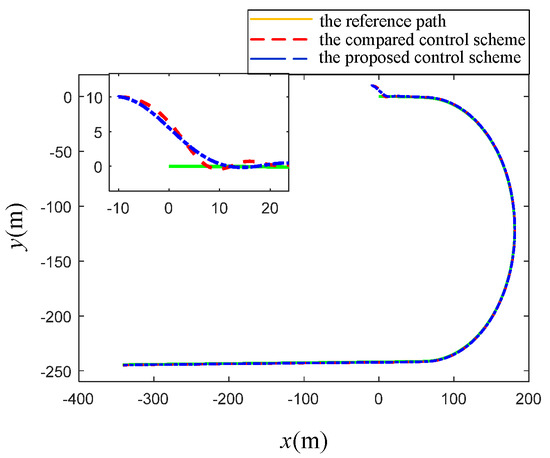
Figure 10. Comparison of the tracking path: the proposed scheme (dot dash line) and the result in [28] (dashed line).

4.2. Comparison Simulation for Individual Ship

In this section, a comparative experiment is given to demonstrate the superiority of the proposed robust fast finite-time control algorithm with a single ship. The proposed approach is compared with the finite-time path-following control algorithm in [28]. The vehicle model used in this experiment are same as above simulation, and the time-varying disturbances in the comparison simulation are as follows:

$$\begin{array}{l}{d}_{wu}=(11/22)(1+0.35\sin (0.2t)+0.15\cos (0.5t))\\ d_{wv}=(26/17.79)(1+0.3\cos (0.4t)+0.2\sin (0.1t))\\ d_{wr}=-(950/636)(1+0.3\cos (0.3t)+0.1\sin (0.5t))\end{array}$$

The reference path is generated by a virtual vehicle, as shows in Equation (40).

$$r_d=\{\begin{array}{cc}-\exp (\frac{0.005t}{300}),& 0s\le t<10s\\ -0.05,& 10s\le t<72s\\ 0,& t\ge 72.\end{array}$$

(40)

$$\begin{array}{l}MAE=\frac{1}{t_{\infty }-t_0}{\displaystyle {\int }_{t_0}^{t_{\infty }}|}e(t)|dt\\ MAI=\frac{1}{t_{\infty }-t_0}{\displaystyle {\int }_{t_0}^{t_{\infty }}|}\tau (t)|dt\end{array}$$

(41)

Figure 10, Figure 11 and Figure 12 and Table 2 show the results of the comparison simulation. To better reflect the comparison results, three performance indexes in Table 2 are employed to display the advantages and disadvantages of the two algorithms, e.g., the mean absolute error (MAE), the mean absolute control input (MAI) and the adjustment time (AT). MAE is used for evaluating the control accuracy of control algorithm. MAI is for properties of energy consumption and smoothness; the two indicators are calculated as Equation (41). In addition, AT represents the time from the initial state to the steady state of the errors, which can directly reflect the convergence performance.

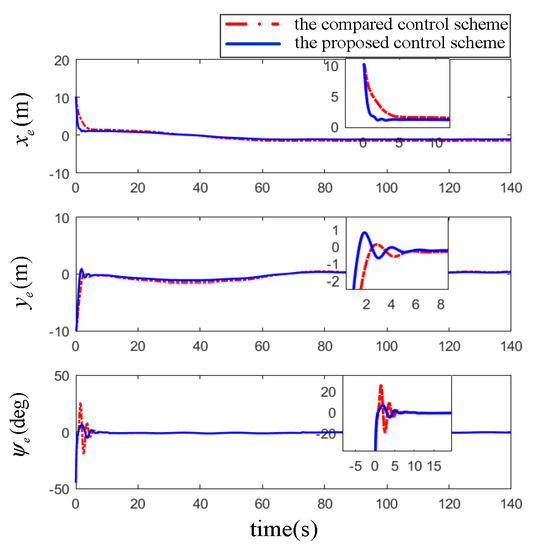
Figure 11. The error $x_e,y_e,{\psi }_e$ of comparison experiment: the proposed scheme (solid line) and the result in [28] (dot dash line).

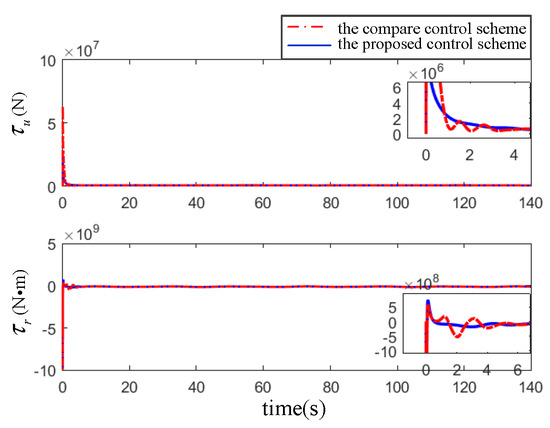
Figure 12. The control inputs ${\tau }_u$ and ${\tau }_r$ of comparison experiment: the proposed scheme (solid line) and the result in [28] (dot dash line).

Table 2. The main comparison results for two algorithms.

Indexes	Items	The Proposed Approach	The Scheme in [28]
MAE	$x_e(m)$	0.6129	0.5000
	$y_e(m)$	0.2712	0.3748
	${\psi }_e(\mathrm{deg})$	0.0084	0.0479
MAI	${\tau }_u(N)$	$6.4942\times {10}^5$	$7.0622\times {10}^5$
	${\tau }_r(N\cdot m)$	$9.4191\times {10}^7$	$9.4224\times {10}^7$
AT	$x_e(s)$	2.25	3.86
	$y_e(s)$	4.82	5.26
	${\psi }_e(s)$	6.42	6.87

5. Conclusions

In this paper, a fast finite-time robust adaptive control method-based directed graph theory is proposed for underactuated vehicle formation, which has a superior faster convergence rate and better robust performance. In addition, the effectiveness of the algorithm mentioned above has been verified through the simulation results. It is meaningful for improving the coordination performance of vehicle formation. However, the proposed strategy of vehicle formation is suitable for the ideal sea area, which has limitations on areas with restricted formation deployment. In navigation, it is expected that the formation shape can be adjusted according to the changes in obstacles or coast. Hence, we will spend more energy on the research of variable vehicle formation of in the following research.