Abstract
The site-specific nutrient management (SSNM) strategy provides guidelines for effective nitrogen, phosphorus and potassium management to help farmers make better decisions on fertilizer input and output levels in rice (Oryza sativa) production. The SSNM fertilizer recommendations are based on the yield goal approach, which has been frequently cited in empirical studies. This study evaluates the assumptions underlying the SSNM strategy for rice in the top rice-producing countries around the world, including India, Indonesia, the Philippines, Thailand, and Vietnam. Using a generalized quadratic production function, I explore whether major nutrients are substitutes as inputs and if there are complementarities between inorganic fertilizer and soil organic matter (SOM). The results suggest the relationships among major nutrients vary across sites—some inputs are complements, some are substitutes, and some are independent. The SOM also significantly affects the nitrogen fertilizer uptake. I conclude by suggesting that the SSNM strategy can be made to be more adaptive to farmer’s fields if these relationships are accounted for in the fertilizer recommendation algorithm.
JEL codes:
Q10; Q12; Q16
1. Introduction
Irrigated rice grown under favorable tropical conditions requires essential nutrients such as nitrogen (N), phosphorus (P), and potassium (K) (often abbreviated as NPK) that are typically not present in the soil in sufficient amounts to meet crop needs. Nitrogen is the most important nutrient because it significantly affects tillering, leaf area growth, biomass production, and grain yield [1]. To ensure that N and other essential plant nutrients are provided optimally and are readily available during crop growth periods, it is critical to define and establish an appropriate fertilization rate, which is the foundation to science-based nutrient management [2]. Crop production requires appropriate fertilization strategies, which is a recurrent challenge for the farmer before and during each cropping period.
The International Rice Research Institute (IRRI) develops the site-specific nutrient management (SSNM) strategy for rice in Asia. SSNM is an “alternative approach for dynamic management of nutrients to optimize supply and demand of a nutrient within a specific field in a particular cropping season”, as compared to other fertilizer recommendation algorithms that are often derived from factorial fertilizer trials conducted across multiple locations [3]. The underlying premise of SSNM is that if nutrients are applied to crops at appropriate times and rates, then the use of indigenous and applied nutrients will be optimized. SSNM strategy offers proper timing and splitting patterns for fertilizer applications using a location-specific nutrient splitting scheme or tools such as a leaf color chart. It defines the optimal amounts of N and other essential plant nutrients as the amounts that maximize yield. It is practiced in Bangladesh, China, India, Indonesia, Philippines, and West Africa [4] using the Nutrient Manager for Rice (NMR). NMR is a computer and mobile phone-based application that provides farmers with fertilizer advice matching their particular farming conditions. In 2013, the IRRI converted NMR into web-based Rice Crop Manager (RCM) [5], which provides advice on crop management practices, in addition to nutrient management.
The SSNM fertilizer recommendations are based on the “yield goal” approach. Yield-goal-based recommendations are N fertilizer recommendations that are based on the farmer’s “target yield” or the anticipated yield gain, i.e., “yield potential” or the yield that the farmer “hopes to achieve” on their field in a specific production unit, with additional adjustments in some areas for soil organic matter (SOM) or other soil characteristics [6,7]. The yield-goal-based approach makes economic sense if the crop response function takes on the von Liebig functional form, i.e., there is a kink in the function, so that input and output prices do not affect the (interior) solution to the profit maximization problem [8]. This reflects the “law of the minimum” [9], whereas crop growth is constrained by the level of the scarcest nutrient, exhibiting zero elasticity of factor substitution. Crop scientists consider N the most “yield-limiting” agent in almost all soils [10,11]. The deficiency of any one nutrient will impair the crop uptake and utilization of the other nutrients, i.e., these nutrients are “technical complements”. Many authors have interpreted this as an assumption of Leontief technology [12]. By assuming the von Liebig response function, fertilizer recommendations are made simple. Most commonly, these assumptions are not stated explicitly in the SSNM research. The von Liebig function is only used as a starting point to test the validity of the SSNM strategy. It is not necessarily the correct production function.
However, there are no studies on SSNM to date that have confirmed if there are indeed von Liebig-type complementarities among the major soil nutrients, NPK. There are studies that assess the impacts of SSNM strategy in rice in terms of economic profitability and environment impacts. Very few assess its scope for improving irrigated rice production. While published reports on SSNM tend to be optimistic, their proposed framework does not explicitly consider nutrient interactions as the driving force behind plant uptake. To my knowledge, no studies have critically discussed and investigated some of the assumptions underlying the SSNM strategy, its current NPK fertilizer recommendation algorithm, and its scope for improving irrigated rice management.
The objective of this study is to discuss and evaluate the principles of SSNM research. By estimating a quadratic production function, I investigate two research questions:
- Is there evidence of complementary, von Liebig-type relationships among N, P, and K fertilizers?
- Does yield response to N fertilizer application depend on the initial state of the soil?
A focus on agronomically optimal nutrient application rates can be misleading if it fails to note the importance of interaction between inputs and whether inputs are substitutes, complements, or independent. Understanding nutrient interactions may provide an explanation as to why farmers over- or underapply nutrients. Therefore, determining the correct level of fertilizer application is an important issue. These issues are also critical in the decision-making processes of policymakers from the top rice producing countries in the world. The path that these countries choose to take on fertilizer policy has significant implications for food security through the global market for rice.
2. Background, Data Description and Empirical Model
2.1. The SSNM Strategy for Rice
The SSNM strategy for rice requires information on a farmer’s yield goal; indigenous supply of N, P, and K; and the crop nutrient requirements. Season-specific yield goals are set in the range of 70–80% of potential yield. Crop nutrient requirements for a specific yield goal are quantified using the empirical modeling approach in the quantitative evaluation of the fertility of tropical soils (QUEFTS) [13]. The QUEFTS principles can be expressed in an equation as
where X is one of the three macronutrients N, P, or K; (kg per ha) is the fertilizer nutrient requirement to achieve a specified yield target; is the predicted optimal nutrient uptake requirement for the specified yield target (kg per ha); is the indigenous nutrient supply; and is the agronomic efficiency of fertilizer X. The indigenous nutrient supplies of N, P, and K are each defined as the total amount of that nutrient available to the crop from the soil during a cropping cycle when other nutrients are non-limiting. This is estimated by measuring plant nutrient uptake in an omission plot. For example, the indigenous N supply can be measured as plant N uptake at harvest in a small 0-N plot located in a farm field, where P, K, and other nutrients are supplied in sufficient amounts so that plant growth is limited only by the indigenous N supply. This is one distinct characteristic of the SSNM approach, i.e., use of crop-based estimates of the indigenous nutrient supply instead of relying on soil tests. Hence, Equation (1) can be expressed using a yield-gain-based approach algorithm:
where reflects the total amount of N, P, or K nutrient that must be taken up by the crop to achieve the yield goal or target yield; is the X-nutrient-limited yield or grain yield attainable from the indigenous supply of X nutrient; (a constant) is the optimal plant nutrient uptake requirement of N, P, K, or to produce a ton of grain; and is the agronomic efficiency of fertilizer X. The nutrient requirement is only a constant if the yield goals that are chosen are equal to or lower than 70–80% of the potential yield. Location-specific fertilizer requirements can be calculated for most irrigated rice areas based on the expected yield increase over the respective omission plot and using certain assumptions of plant nutrient requirements and the fertilizer efficiency of applied fertilizer nutrients. The QUEFTS model predicts a linear increase in grain yield if nutrients are taken up in balanced amounts of 14.7 kg for N, 2.6 kg for P, and 14.5 kg for K (, Equation (2)) per one ton of grain yield produced, until the yield reaches about 70–80% of the potential yield [14]. This algorithm is simple, with minimal characterization or interviewing of farmers for each field, ensuring rapid, cost-effective delivery of field-specific guidelines to millions of small-scale farmers [15].
Since Equation (2) suggests that input and output prices and input substitution will not affect the amount of fertilizer that is recommended, the von Liebig functional form is implied. If nutrients exhibit a von Liebig-type relationship, the isoquants of the crop production function, as shown in Figure 1a, will have vertical and horizontal legs that join at right angles and the Liebig production function when charted as dependent on N (with other inputs held constant) will be kinked, as shown in Figure 1b. An isoquant is a locus of points (curve or line) representing the various combinations of two inputs that can be combined to produce the same output. If N is yield-limiting, its marginal physical product (MPP) is constant, while if N is no longer yield-limiting, its MPP is zero. In economics, the MPP of an input (factor of production) is the change in output resulting from employing an additional unit of a particular input. In this context, the MPP is the change in rice yield when the amount of N fertilizer is increased by one unit.
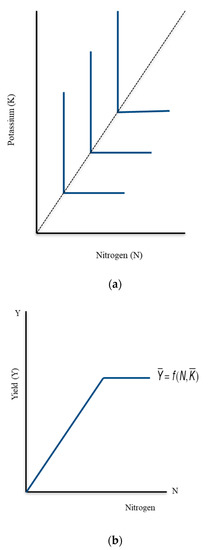
Figure 1.
Isoquants under Leontief technology (a); Yield response under Leontief technology (b).
The yields will be unresponsive to increases in K (or P), as is the case for a Leontief production function. In this case allocations under profit maximization, relative input and output prices can be ignored in the fertilizer algorithm. Farmer can maximize profits by finding the lowest level of N fertilizer at which the response function reaches its plateau height. The economic optimal N rate is the minimum N rate at which the yield reaches its plateau. This supposes that a given level of yield can be attained only by use of a single combination of inputs. Any change in the ratios of input prices does not affect the fixed proportion in which inputs are optimally combined in the production process. Any price ratio between inputs will always go through where the kink is. The two inputs are technical complements, and if they are to be used at all they should be used in the single combination.
Input and output prices, however, affect farmers’ production decisions [16]. The declining yield growth rates in double- and triple-crop rice monocropping systems were partly due to lower rice prices [17]. When farmers are faced with cash constraints and if there are differences in the availability and price of a single fertilizer due to differential subsidy levels, they tend to buy and use mostly N fertilizers [10]. If N fertilizer is applied alone, P becomes a yield-limiting element after a few years of intensive cultivation with high doses of N and P [10]. If P becomes yield-limiting in the soil, and if indeed N and P are complements, adding more N fertilizer will not be beneficial for crops.
Moreover, the existing SSNM algorithm does not consider the possible relationship of N fertilizer application and SOM, as reflected in soil carbon (C) contents, which is recognized as the single best summary statistic for soil fertility status associated with SOM stocks [18]. This is probably because indigenous N supply (INS) is quite variable among fields and not related to SOM content and farmers’ fertilizer N rate [19]. The organic amendments when used as a complement to inorganic NPK increase yields, but these increased yields are due to increased nutrient supply (N, P, K, or other nutrients under conditions of deficient soil nutrient supply) and not the “organic matter effect” [20].
However, a few studies have shown that increasing the SOM makes fertilizer application of N more effective and can improve crop yields (e.g., [20,21]). Soil organic matter contributes to soil quality and ecosystem function through its influence on soil physical stability, soil microbial activity, nutrient storage and release, and environmental quality [22]. The INS increases if the soil organic C content of the rice paddy soil increases [23]. Increasing organic C content in SOM reduces soil erosion and degradation, improves surface water quality, and increases soil productivity. SOM content either (i) increases under inorganic fertilization (e.g., [24,25]), especially for inorganic N fertilizers; (ii) decreases under inorganic fertilization (e.g., [26,27,28]); or (iii) does not change (e.g., [29,30]).
As such, I hypothesize that the MPP, and hence the profitability, of N fertilizer application depends on soil C stocks, which may vary systematically in farmers’ fields. As an initial test, I use kernel-weighted local polynomial regression to check if rice yields are strongly and directly associated with soil C stocks. (Figures are available from the author upon request. Weighted least squares regression is used to fit linear or quadratic functions of the predictors at the centers of neighborhoods [31].)
Generally, there is clear evidence that the grain yield increases as SOM increases. Quantifying the role of SOM, particularly the soil C stocks, in relation to the crop output response to N fertilizer in irrigated rice systems would be relevant. The complementarity between SOM and N fertilizer application might mean that N fertilizer application becomes unprofitable in soils depleted of SOM [21]. Poor soil fertility might actually be a cause, not merely a consequence, of low rates of fertilizer use [32]. If this is the case, then ex ante soil conditions matter a lot to the return on investments in fertilizer policies [21]. In cases where soil degradation has become severe, provision of temporary fertilizer subsidies or cost shares might not be an appropriate policy.
This paper contributes to the literature by providing a broader scope of analysis of SSNM in the irrigated rice systems by exploring whether there are indeed interactions among essential nutrients N, P, and K, and between the SOM and applied N fertilizer.
2.2. Data Description
The data on irrigated rice production and input use come from the IRRI project on Reversing Trends of Declining Productivity in Intensive Irrigated Rice Systems (RTDP), carried out in eight locations in five countries across tropical and subtropical environments in Asia (Table 1). Three of the experimental sites are located in India (Aduthurai, Thanjavur, and Uttar Pradesh), one site in Indonesia (Sukamandi in West Java), one site in the Philippines (Nueva Ecija), one site in Thailand (Suphan Bari), and two sites in Vietnam (Can Tho and Ha Noi). In each of the five countries, the data originate from both nutrient omission and fertilizer evaluation trials conducted in farmers’ fields [33]. The treatments used in the study were: (1) no fertilizer applied (0 N, 0 P, 0 K); (2) PK applied, 0 N applied; (3) SSNM; and (4) farmer’s field practice (FFP) with no interference by IRRI. All data are for irrigated rice, whereby water rarely limited plant growth. The 0-N plots received 30 kg P fertilizer and 50 kg K fertilizer per hectare. The 0-N, 0-P, and 0-K treatments were separated from the surrounding fields by bunds and were moved to a different location after each crop grown to avoid residual effects caused by nutrient depletion. Each experiment in the five countries was run for three to five years. Due to data availability, I only used data for one year in some areas (1996–1998) and two years (1995–1996) in other areas. Each treatment contained two to three replicate sampling plots per farm. Comparable methodologies for plant sampling, yield determination, and analysis for plant nutrients were used for collected data across countries and experiments [14]. Soil data were collected at the single field or single treatment level, i.e., only for the field used for the agronomic research. Two 6 m × 6 m plots were sampled for each treatment and the samples were processed separately. The total organic C levels of soil samples taken at 0–0.2 meter depth from 0-N plots were determined [34].

Table 1.
Study area, RTDP, IRRI.
The sample farmers and sites were selected based on the following criteria: (1) their sites represented the most common soil types in the region; (2) their sites represented the most typical cropping systems and farm management practices in the region; (3) their sites represented a range of socioeconomic conditions (small to large farms, poor to rich farmers); (4) their sites allowed reasonable accessibility for frequent field visits; (5) the farmers were interested in participating in the project over a longer term. Socioeconomic data were collected at the whole-farm level, i.e., including the field used for the agronomic research, as well as other fields belonging to the same farmer.
2.3. The Empirical Model
The rice production function for each experimental site can be defined by using a generalized quadratic specification [35]:
Here, is grain yield; is the vector of independent variables (N applied, P applied, K applied, and soil C stocks, age of farmers, farm area harvested, and dummy variable for high-yield season (HYS)), and the vector comprises the parameter estimates of interest, where , and e is an iid N(0, σ2) error term. The N, P, and K fertilizer application by farmers could be endogenous given the unobserved factors that affect yields. There were no good instruments available to address endogeneity concerns regarding the production function estimation. In the presence of heterogeneity, the polynomial and linear plus plateau approximations essentially converge, making the quadratic a viable alternative to the von Liebig and linear response plateau models [36]. Moreover, von Liebig models generally do not fit the data well and the actual estimation does not yield the right-angle isoquants described in its derivation [37].
To explore the systematic relationship among fertilizer NPK application and ex ante soil fertility in each experimental site, I tested the null hypothesis that N, P, and K fertilizers do not significantly interact with each other and that soil C content has no indirect effects on yields through N fertilizer application:
A Wald test was performed to test the joint significance of parameters in Equation (3) for each study site. If H0 cannot be rejected, then it indicates the independence of and . The marginal productivity of is not affected by changes in the level of If, however, is rejected, then nutrient interaction between and is present. If , then and are technically complementary. The marginal product of increases as increases. If , then and are technically substitutes. Increasing reduces the marginal productivity of . Table 2 and Table 3 present the definition and summary of the statistics, respectively, for the regression variables.

Table 2.
Description of variables.

Table 3.
Descriptive statistics.
I also employed the non-nested hypothesis framework proposed by Davidson and MacKinnon [38] to determine the correct crop nutrient model. A previous study [38] provides a detailed discussion of the non-nested hypothesis framework. I contrasted the quadratic model (), Equation (3), against three alternative hypotheses (: linear von Liebig model, non-linear von Liebig model, and the square-root model). The linear von Liebig model is defined by
where M is the plateau yield. The non-linear von Liebig model is defined by
The square-root model is defined by
3. Results and Discussion
Two variations of my basic model were estimated. For model 1, the nutrients (N, P, and K) and organic C content only were used as controls for the production function. For model 2, a high-yield season dummy (HYS) and farm size variable were added to model 1. The addition of these two controls proved to be statistically significant when included in the regression. Hence, I favored the second model over the first for all study sites and discussed only those results.
There was good reason to believe that some important variables in determining the yield are often unobserved (e.g., the skill level of farmers). Hence, I also ran a farmer fixed effects to correct for unaccounted farmer specific factors that may affect the level of fertilizer applied using the data (i.e., farmer’s age and education) only from farmers’ field practice. I also favored model 2 over this model because of its greater precision. Other factors such as pests and diseases can also influence yield, but there were no available data to account for them. Table 4, Table 5 and Table 6 report the OLS regression results from Equation (3) by study site. Across all sites, there are significant coefficient estimates that do not have the expected signs in the first-order term. For example, the expected rice yield is decreasing in soil organic C content in Can Tho, Vietnam. It is possible that large amounts of organic materials repeatedly applied to soil with lower buffering capacity and high reducible iron content may cause an acceleration in the reduction of the soil redox potential, and therefore in the potential iron toxicity in rice [39]. Plants suffering from iron toxicity may cover large contiguous areas, such as in the Mekong Delta in Vietnam [40]. Single parameter point estimates, however, are of limited usefulness here, because it is impossible to vary only one term at a time in Equation (3).

Table 4.
Production function estimates using two versions of the quadratic model in India.

Table 5.
Production function estimates using two versions of the quadratic model in Indonesia, Philippines, and Thailand.

Table 6.
Production function estimates using two versions of the quadratic model in Vietnam.
3.1. Marginal Physical Product and Output Elasticity
Using the regression results reported in Table 4, Table 5 and Table 6, I estimated the MPP and output elasticity at the mean level for each variable for the entire sample plots in all locations (Table 7, Table 8 and Table 9). Except in Thanjavur and Uttar Pradesh in India and Can Tho in Vietnam, the average MPP value for N (MPPN) fertilizer application was positive and the output elasticity value was less than one; both results were significant at the 1% level. The additional N fertilizer use had a significant positive influence on the yield in most plots in the sample. Henceforth, in this section, the term “N” refers to “N fertilizer applied” and “N fertilizer.” Similar interpretations are used for “P” and “K.” Nitrogen fertilizer application increases the height of leaves [41,42], the number of tillers/m2 [41,43,44], and both the number and size of grain [45,46,47].

Table 7.
Marginal physical product (MPP) and output elasticity values at the mean level in India.

Table 8.
Marginal physical product (MPP) and output elasticity at the mean level in Indonesia, Philippines, and Thailand.

Table 9.
Marginal physical product (MPP) and output elasticity at the mean level in Vietnam.
The MPPN is decreasing in Aduthurai (India) (Figure 2), Sukamandi (Indonesia) (Figure 3), Nueva Ecija (Philippines) (Figure 4), and Ha Noi (Vietnam) (Figure 5), but increasing in Suphan Buri (Thailand) at all N rates (Figure 6). The increasing MPPN suggests a deficiency in N on most plots in the sample areas. Hence, use of an additional fertilizer could exert a positive influence on the yield. The maximum yield will be achieved at N rate where the MPPN = 0. These rates are 139 kg per ha in Aduthurai, 135 kg per ha in Sukamandi, 160 kg per ha in Nueva Ecija, and 100 kg per ha in Ha Noi. In Aduthurai, applying 139 kg per ha will result in almost 6 tons per ha of grain yield, given all the other factors are constant at the mean level. If more than 139 kg per ha is applied, MPPN will be negative. This is because excessive N promotes lodging and plants become more attractive to insects and diseases.
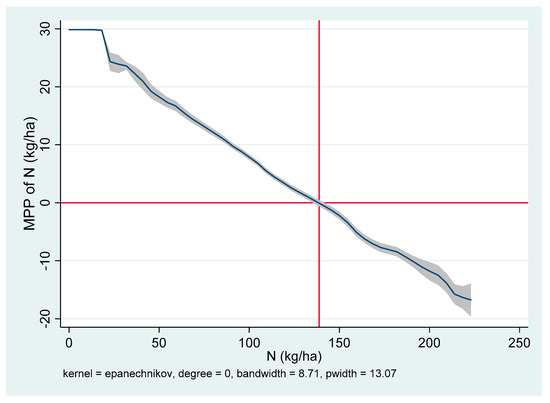
Figure 2.
Marginal physical product of N (MPPN) at the mean level in Aduthurai, India.
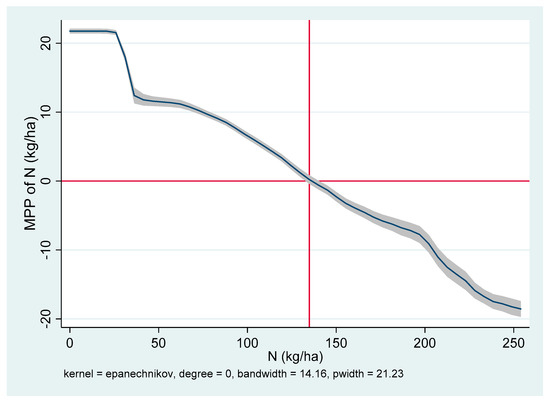
Figure 3.
Marginal physical product of N (MPPN) at the mean level in Sukamandi, West Java, Indonesia.
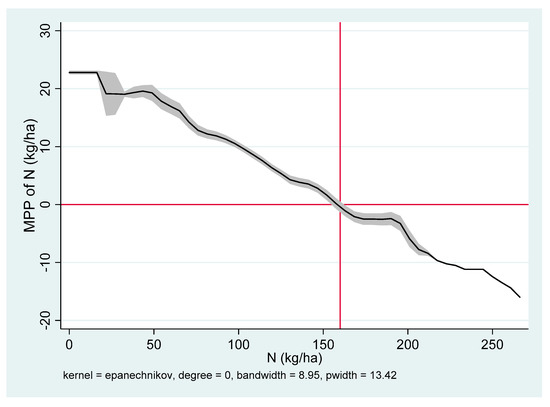
Figure 4.
Marginal physical product of N (MPPN) at the mean level in Nueva Ecija, Philippines.
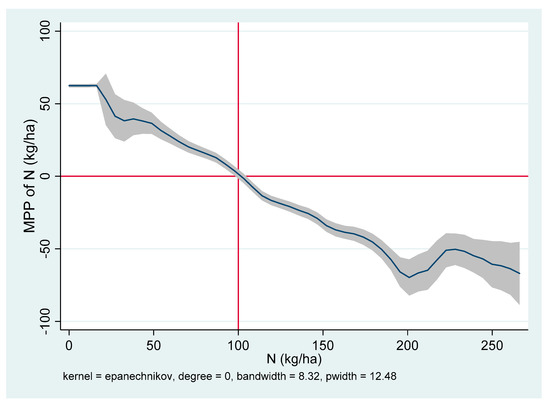
Figure 5.
Marginal physical product of N (MPPN) at the mean level in Ha Noi, Vietnam.
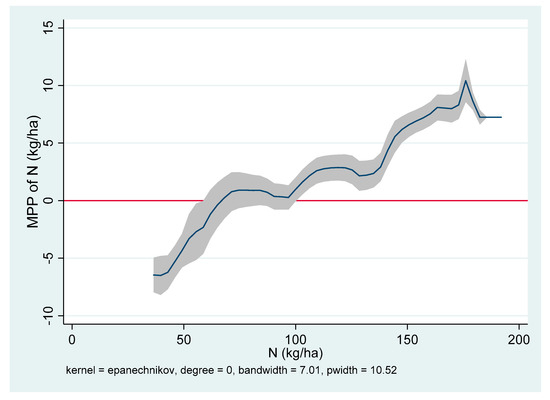
Figure 6.
Marginal physical product of N (MPPN) at the mean level in Suphan Buri, Thailand.
Meanwhile, the marginal contribution of a kilogram of P (MPPP) was positive but the output elasticity is greater than one in Uttar Pradesh (India) (Table 7). The MPPP was positive and output elasticity was less than one in Sukamandi (Table 8), Can Tho (Vietnam), and Ha Noi (Table 9) at 1% significance level. The magnitude of the estimated coefficients of P reveals the significance of this nutrient in rice production, specifically in Vietnam. For example, a kilogram increase in P increases the yield by 136 kg per ha in Ha Noi.
In contrast, the estimated MPPP and output elasticity at the mean level were negative in Nueva Ecija and Suphan Buri (Table 8), with both being statistically significant at 1% level. There is a possibility that most of the rice straw was retained in the field, and hence those soils were often saturated with P due to continuous P fertilizer application. The extractable Olsen-P level was relatively high for all farms in the sample areas [4]. No additional amount of P fertilizer is required to replenish the P removed with grain and straw. The additional P fertilizer application might result in overapplication. The overapplication of P fertilizer does not necessarily lead to environmental damage, but the ability of the soil to retain P is limited.
As with the P fertilizer, the MPP of K fertilizer (MPPK) varied across sites. The MPPK was positive and output elasticity was less than one at the mean level in Suphan Buri (Table 8). Potassium plays a key role in many metabolic processes in the plant. Meanwhile, a negative MPPK was observed in Can Tho (Table 9). With the current SSNM fertilizer algorithm, the doses of mineral fertilizers, including N-P-K fertilizers, are determined based on the target yield and the required nutritional needs of the plants. The K requirement of rice is sometimes supplied from plant residues that have been turned under and from K in irrigation water [48]. The SSNM approach takes into account the amount of K recycled from straw yield and the straw management level in the previous season when calculating K fertilizer requirements to avoid excessive K fertilizer use. However, it does not consider the abundance of digestible nutrients in the soil. The water from the Mekong River Delta has high contents of sediments that provide nutrients for crop. Additional K fertilizer would not be beneficial here and could result in overfertilization or negative MPPK. When fertilizer is overapplied, this may result in the formation of an excess of soluble fertilizer components in the soil and their increased leaching. This would burden the natural environment with a given nutrient, and at the same time reduce the effectiveness of the component application.
3.2. Evidence of Complementarity Among N-P-K Fertilizers
The main aim of this paper was to explore the relationships among major nutrients of NPK and N fertilizers with soil fertility, as reflected by the soil organic C content (Table 10). The relationship of N, P, and K varied across sites—some inputs were complements, some were substitutes, and some were independent. This may be due to the plant’s biological processes.

Table 10.
Results of hypothesis testing.
The Wald test statistics for the interaction of N and P were not statistically significant in Thanjavur, Uttar Pradesh, Nueva Ecija, and Suphan Bari. This indicates that there was no interaction between N and P, , in the model. If this is the case, the N and P requirements of the crops can be estimated independently and can be applied without each other. However, previous studies have reported that N and P are complements, , [49] such as the case in Sukamandi (Indonesia), whereby increasing the application of P increases the marginal revenue (MR) of N . Note that the price of paddy rice was set at IDR 3300 and the N price was IDR 794. Phosphorus enhances the root activities of rice crops, and when N fertilizer is applied to a rice crop that has a healthy, active root system, the fertilizer efficiency will be high—the N will be absorbed before it can be transformed or lost. Moreover, the movement of N within the plant depends largely upon transport through cell membranes, which requires energy to oppose the forces of osmosis. Here, ATP and other high-energy P compounds provide the needed energy. In addition, when rice is grown with heavy N application, a decline in the ratio of filled grains is frequently observed [50,51]. The only way to further increase the yield is to improve the photosynthesis and biomass production of the rice [52] through P fertilizer application.
It is also possible that N might already be yield-limiting in the soil and that adding more P would not contribute to the crop growth, so . Typically, the ratio of N to P is lower in manure than that required by crops. If farm manure is used to satisfy the N requirements of crops, overapplication of P might be possible. Given that N and P are complements, plants require these inputs at a fixed ratio.
There was also no significant interaction between P and K,, in Aduthurai, Uttar Pradesh, Nueva Ecija, Can Tho, and Ha Noi. In Aduthurai and Nueva Ecija, P and K both had no significant effect on yield (Table 7 and Table 8). In Uttar Pradesh (Table 7) and in both locations in Vietnam (Table 9), P and K had opposite effects on yield, i.e., and . Similar to the previous results, one of the nutrients might already be yield-limiting. The MPP levels of P and K were very low or even negative. If farmers practice selective fertilizer application, i.e., only applying P, application of K fertilizer to the soil will be yield-limiting in the long run. Adding more K will have no effect on yield.
In contrast, there was clear evidence of input substitution between N and P in Aduthurai and in both study sites in Vietnam. Figure 7, Figure 8 and Figure 9 display the kernel-weighted local polynomial smoothing of the estimated marginal value product (MVP; the marginal revenue from multiplying MPP by the price of rice) of N against P, along with the cost of N and P fertilizer inputs (red horizontal line). Note that a kilo of rice was INR 24 in India and VND 8000 in Vietnam. The input cost of N fertilizer was INR 30 in India and VND 5600 in Vietnam.
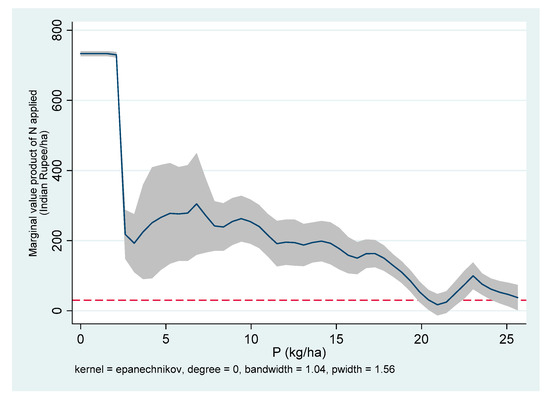
Figure 7.
Marginal value product of N (MVPN) and P applied in Aduthurai, India.
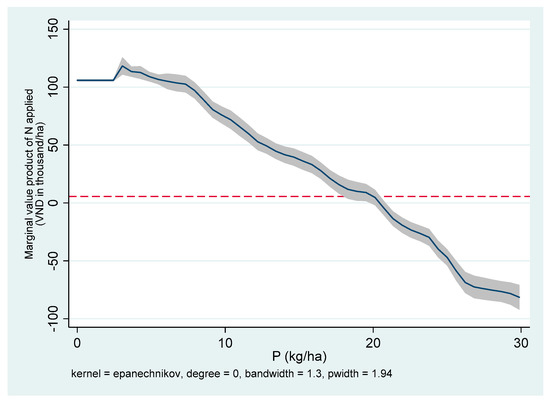
Figure 8.
Marginal value product of N (MVPN) and P applied in Can Tho, Vietnam.
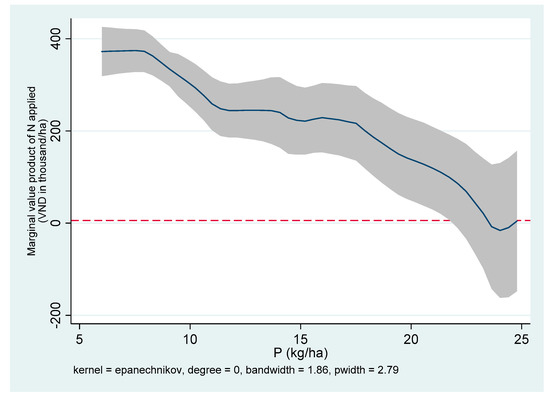
Figure 9.
Marginal value product of N (MVPN) and P applied in Ha Noi, Vietnam.
If two nutrients are substitutes, increasing the application of one nutrient will reduce the MR of the other nutrient. In all three areas, only N had a positive and statistically significant effect on yield, (Table 4). In this case, it makes sense to prefer the application of N than P. The was higher than the cost of N at almost all levels of P in Aduthurai (Figure 7) and Ha Noi (Figure 9). In Can Tho, the was less than the price of N when the P applied was beyond 20 kg/ha (Figure 8). This supports the farmers’ practice of selective application of nutrients. Compared to phosphate and potash fertilizer, N fertilizer is heavily subsidized in India. Hence, this adversely affects the consumption of P and K fertilizers.
On the other hand, N and K are found to be complements in Uttar Pradesh (Table 10). As with P, K plays an important role in the physiological process for rice and contributes to greater canopy photosynthesis and crop growth. Potassium also increases the number of spikelets per panicle (flowers per grain bunch) and the percentage of filled grain. Individually, N and K significantly decrease yield, and , while significantly increasing the marginal product of N, (Table 4). A positive relationship between yield and K can occur only if the positive effect of K on the MPPN is higher in absolute value than the direct effect of K on yield. Potassium must not be applied alone, but rather in combination with N. Given this, selective application of fertilizer, i.e., only applying N or K when farmers are faced with cash constraints, might cause more harm than good to the crop. The Wald test failed to reject the null hypothesis that there is no interaction between N and K fertilizers in Aduthurai, Thanjavur, Sukamandi, Nueva Ecija, Can Tho, and Ha Noi.
In Thailand, the resulting estimates are intuitive but quite inconsistent. Nitrogen fertilizer can be substituted for P , while P can be substituted for K (Table 10). Hence, by transitivity, N and K are substitutes as well. Interestingly, the results suggest otherwise, i.e., N and K are complements , implying an increased yield due to the positive effect of K on the marginal product of N (Table 5). With all other factors held constant, an extra kilogram of K is associated with an almost two kilogram increase in yield to a kilogram of N. Given that K is not usually applied in Thailand, a deficiency of K will not be a problem because nearly all rice straw (which is high in K) is left on the ground after harvest (Moya et al. 2004).
3.3. Is Yield Response to N Fertilizer Dependent on the Ex Ante State of Soil?
I also hypothesized that the yield response to N fertilizer is dependent on the ex ante soil condition. The Wald test rejects the hypothesis that the interaction of N and soil C contents is jointly zero, . implying complementarity between soil fertility and N in Sukamandi, Nueva Ecija, and Ha Noi (Table 10).
Figure 10, Figure 11 and Figure 12 display the kernel-weighted local polynomial smoothing of the estimated MVP of N against the plots’ soil organic C contents for Sukamandi, Nueva Ecija, and Ha Noi, respectively. There exists a positive relationship between the N fertilizer yield response and soil C content. The exceeded the price of N fertilizer in both locations at all levels of a plot’s soil organic content. The N fertilizer price was IDR 794 per kilogram in Indonesia, PHP 13.30 per kilogram in the Philippines, and VND 5600 per kilogram in Vietnam, respectively. In Sukamandi, Indonesia, the MVPN was invariant to a C content level of approximately 13g/kg, at which point the MVPN increased up to a C content level of approximately 21 g/kg, after which the MVPN flattened out, with no further statistically significant growth in rice yield response to N fertilizer beyond that soil fertility level. On the other hand, the MVPN is rapidly increasing in all Philippine sample plots (Figure 11). The figure also suggests that a farmer with 15 g/kg of C content would get about PHP 84 (approximately USD 2) more profit than a farmer with 5 g/kg of C content, given that they apply the same level of N fertilizer at the mean level. The maximum yield will be achieved at the N rate where the MPPOrgCN = 0. The in Ha Noi did not vary up to a C content level of approximately 17 g/kg, then it increased at an increasing rate up to a C content level of approximately 22 g/kg, after which it increased at a decreasing rate (Figure 12). If further investments are devoted to increasing the soil C content in Vietnam, N fertilizer application is expected to be profitable.
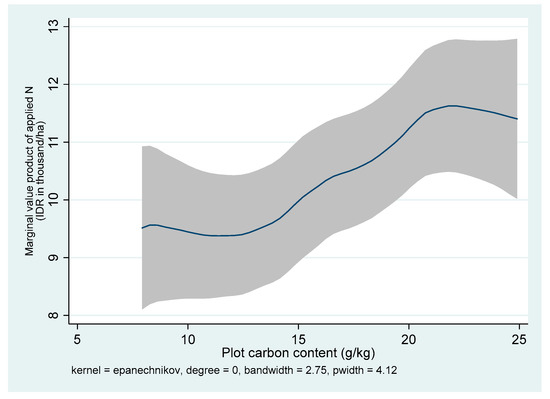
Figure 10.
Marginal value product of N (MVPN) based on the plot’s carbon content in Sukamand, Indonesia.
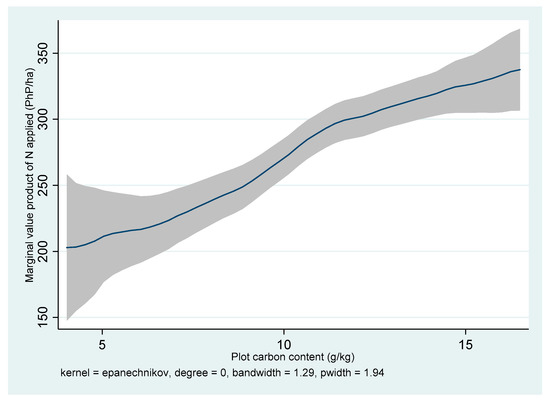
Figure 11.
Marginal value product of N (MVPN) based on the plot’s carbon content in Nueva Ecija, Philippines.
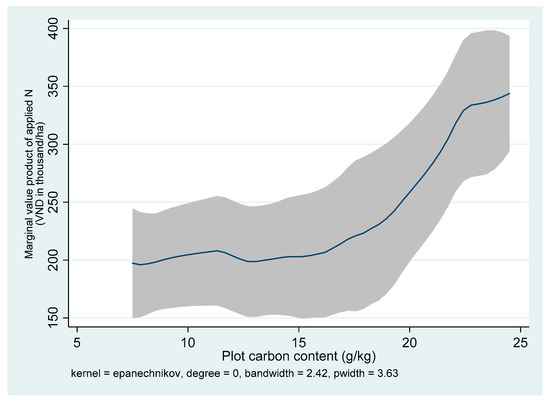
Figure 12.
Marginal value product of N (MVPN) based on the plot’s carbon content in Ha Noi, Vietnam.
While the Wald test failed to reject the hypothesis that the interaction term of N and soil C content are jointly zero in all three sites in India, Can Tho, and Suphan Bari, soil C contents in these areas might already be yield-limiting, whereby adding more N would not contribute to crop growth. For example, at more than around 8 g/kg carbon content, the marginal revenue of N fertilizer started to increase in Aduthurai. On average, the soil C content in Aduthurai was only 9 g/kg (Figure 13).
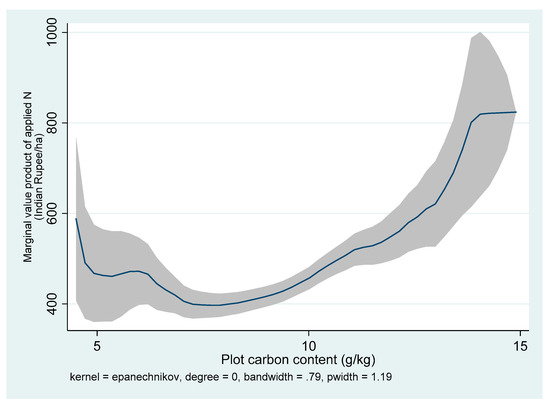
Figure 13.
Marginal value product of N (MVPN) based on the plot’s carbon content in Aduthurai, India.
3.4. Non-Nested Hypothesis Test Results
The non-nested hypothesis tests rejected the linear von Liebig model specification, except in Aduthurai (Table 11). The quadratic model outperformed all of the rival specifications, both in a pairwise comparison as well as in a collective test against all of the alternatives. In the case of a quadratic functional form, profit maximization requires information for input and output prices and the marginal product of each increment of fertilizer. The economic optimal fertilizer rate is attained when the marginal product of the fertilizer is equal to the ratio of input and output prices. Given a non-zero price ratio, there is a difference between the yield-maximizing and profit-maximizing input levels. Rising fertilizer prices are a particular problem for poor farmers who cannot afford sufficient amounts of fertilizers.

Table 11.
Non-nested hypothesis test results.
4. Conclusions and Policy Implications
There is clear evidence that the interactions among major nutrients matter in terms of making fertilizer recommendations for farmers. The relationships among N, P, and K varied across sites—some inputs were complements, some were substitutes, and some were independent. SOM, which is manifested in soil C stocks, significantly affected the economic returns on N fertilizer inputs in some areas. The marginal product of N was low in soils with low C content. In other areas, SOM did not have an effect in N fertilizer application.
Accounting for the nutrient interactions and the relationship between N fertilizer and SOM can make the SSNM strategy more adaptive to farmers’ fields and will allow the integration of nutrient management techniques of maximum benefit to rice producers. In addition, input and output prices are important considerations in the SSNM algorithm, given that the quadratic model specification of the crop response outperformed linear von Liebig model. The major challenge for SSNM will be to retain the simplicity of the approach, which is understandable to producers and extension agents, while accounting for the relationship between NPK and soil organic matter.
The results of this study could stimulate IRRI scientists and policymakers to review the existing fertilizer policies in the study countries. To ensure the effectiveness of fertilizer policies, they must be targeted not only to match the needs, preferences, and resources of farmers, but also the interactions of production inputs. The substitutability, complementarity, and independence of major nutrients and SOM are also critical in the decision-making processes of policymakers from the study countries. Government, more often than not, focuses on policies that are conducive to increased availability and consumption of fertilizers. If major nutrients such as N and P are substitutes, input and output prices are important in the determination of the economic optimal fertilizer rate. The decisions of farmers regarding which fertilizer to use depend on which fertilizers are cheapest to obtain and apply. If major nutrients are complements, then direct subsidies for these nutrients must be considered. For example, if N and P are complements, low subsidized prices for N fertilizers matched by similar levels for P fertilizers will reduce the probability of farmers practicing selective application when they are faced with cash constraints.
Fertilizer subsidies or distribution schemes might not be appropriate ways of supporting rice production, however, in areas where soils have limited organic matter content. The yield response of rice to N depends on the initial state of the soil. Although IRRI scientists strongly encourage farmers to use organic fertilizers such as farmyard manure in their rice fields, this does not discount the need to explicitly incorporate the interaction of the soil C content and N in the SSNM algorithm. In order for farmers to reap significant economic returns from N fertilizer application, there needs to be an adequate amount of SOM. In such cases, government interventions might be considered, putting greater emphasis on integrated soil fertility management and adoption of soil conservation technologies. Organic sources of nutrients (e.g., farmyard manure, crop residues carried over) can be promoted as a response to increasing prices for commercial manufactured fertilizers and as a basis for increasing productivity. Extension agencies and others can potentially encourage further adoption of the use of organic fertilizers by emphasizing to farmers the benefit of organic materials on the physical properties of rice soils.
The results of this paper also suggest that nutrient interactions among major nutrients and soil organic matter tend to vary from site to site. However, there are two caveats to keep in mind when interpreting these results. First, while the substitution of N and P in some areas might be justified on economic grounds, this relationship requires further research or studies that can support it from a biological viewpoint. Most of the previous studies suggest that N and P are complementary inputs. The second caveat is that the results from this study only pertain to one to two years of experimentation. If the crop response function to major nutrients and SOM varies from year to year, the results are only representative for a given state of nature observed at a certain point in time. A multiyear analysis would be an interesting extension of this study. This demonstrates a frontier where agricultural economists and agronomists can work together.
Funding
This research received no external funding. The APC was funded by the Norwegian Institute of Bioeconomy Research.
Acknowledgments
I thank David S. Bullock, Amy Ando, Donald G. Bullock, Charles Nelson, and Nicholas Paulson for their valuable comments and suggestions for my research. I also want to thank Roland Buresh, Achim Doberman, and Grant Singleton for allowing me to use their data sets and for the support. I also thank the three anonymous reviewers for their helpful comments.
Conflicts of Interest
The author declares no conflict of interest.
References
- Yang, W.H. Using leaf color charts to estimate leaf nitrogen status of rice. Agronomy 2003, 95, 212–217. [Google Scholar]
- Chuan, L.; He, P.; Pampolino, M.F.; Johnston, A.M.; Jin, J.; Xu, X.; Zhao, S.; Qiu, S.; Zhou, W. Establishing a scientific basis for fertilizer recommendations for wheat in China: Yield response and agronomic efficiency. Field Crops Res. 2013, 140, 1–8. [Google Scholar] [CrossRef]
- Dobermann, A.; Witt, C.; Dawe, D. (Eds.) Increasing Productivity of Intensive Rice Systems through Site-Specific Nutrient Management; Science Publishers, Inc.: Enfield, NH, USA; International Rice Research Institute (IRRI): Los Baños, Philippines, 2004; p. 410. [Google Scholar]
- IRRI. International Rice Research Institute. 2020. Available online: http://www.irri.org/about/about.asp (accessed on 10 June 2020).
- Buresh, R.J.; Castillo, R.L.; Dela Torre, J.C.; Laureles, E.V.; Samson, M.I.; Sinohin, P.J.; Guerra, M. Site-specific nutrient management for rice in the Philippines: Calculation of field-specific fertilizer requirements by Rice Crop Manager. Field Crops Res. 2019, 239, 56–70. [Google Scholar] [CrossRef]
- Lory, J.A.; Scharf, P.C. Yield goal versus delta yield for predicting fertilizer nitrogen need in corn. Agron. J. 2003, 95, 994–999. [Google Scholar] [CrossRef]
- Vanotti, M.B.; Bundy, L.G. An alternative rationale for corn nitrogen fertilizer recommendations. J. Prod. Agric. 1994, 7, 243–248. [Google Scholar] [CrossRef]
- Rodriguez, D.G.P.; Bullock, D.S.; Boerngen, M.A. The origins, implications, and consequences of yield-based nitrogen fertilizer management. Agron. J. 2019, 111. [Google Scholar] [CrossRef]
- Paris, Q. The von Liebig hypothesis. Am. J. Agric. Econ. 1992, 74, 1019–1028. [Google Scholar] [CrossRef]
- Balasubramanian, V. Farmer adoption of improved nitrogen management technologies in rice farming: Technical constraints and opportunities for improvement. Nutr. Cycl. Agroecosyst. 1998, 53, 93–101. [Google Scholar] [CrossRef]
- Ishii, S.; Ikeda, S.; Minamisawa, K.; Senoo, K. Nitrogen cycling in rice paddy environments: Past achievements and future challenges. Microbes Environ. 2011, 26. [Google Scholar] [CrossRef]
- Grimm, S.S.; Paris, Q.; Williams, W.A. A von Liebig model for water and nitrogen crop response. West. J. Agric. Econ. 1987, 12, 182–192. [Google Scholar]
- Janssen, B.H.; Guiking, F.C.T.; van der Eijk, D.; Smaling, E.M.A.; Wolf, J.; van Reuler, H. A system for quantitative evaluation of the fertility of tropical soils (QUEFTS). Geoderma 1990, 46. [Google Scholar] [CrossRef]
- Witt, C.; Dobermann, A.; Abdulrachman, S.; Gines, H.C.; Guanghuo, W.; Nagarajan, R.; Satawatananont, S.; Thuc Son, T.; Sy Tan, P.; Van Tiem, L.; et al. Internal nutrient efficiencies of irrigated lowland rice in tropical and subtropical Asia. Field Crops Res. 1999, 63. [Google Scholar] [CrossRef]
- Buresh, R.; Pampolino, M.; Witt, C. Field-specific potassium and phosphorus balances and fertilizer requirements for irrigated rice-based cropping systems. Plant Soil 2010, 335, 35–64. [Google Scholar] [CrossRef]
- Silberberg, E. The Structure of Economics: A Mathematical Analysis; McGraw-Hill Book Company: New York, NY, USA, 1978. [Google Scholar]
- Dawe, D. Reenergizing the Green Revolution in Rice. Am. J. Agric. Econ. 1998, 80, 948–953. [Google Scholar] [CrossRef]
- Manlay, R.J.; Feller, C.; Swift, M.J. Historical evolution of soil organic matter concepts and their relationships with the fertility and sustainability of cropping systems. Agric. Ecosyst. Environ. 2007, 119, 217–233. [Google Scholar] [CrossRef]
- Cassman, K.; Dobermann, A.; Cruz, P. Soil organic matter and the indigenous nitrogen supply of intensive irrigated rice systems in the tropics. Plant Soil 1996, 267–278. [Google Scholar] [CrossRef]
- Tiessen, H.; Cuevas, E.; Chacon, P. The Role of Soil Organic Matter in Sustaining 785 Soil Fertility. Nature 1994, 371, 783–785. [Google Scholar] [CrossRef]
- Marenya, P.P.; Barrett, C.B. State-conditional fertilizer yield response on Western Kenyan Farms. Am. J. Agric. Econ. 2009, 91, 991–1006. [Google Scholar] [CrossRef]
- Herrick, J.E.; Wander, M.M. Relationships between soil organic carbon and soil quality in cropped and rangeland soils: The importance of distribution, composition, and soil biological activity. In Soil Processes and the Carbon Cycle; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Espe, M.B.; Kirk, E.; van Kessel, C.; Horwath, W.H.; Linquist, B.A. Indigenous Nitrogen Supply of Rice Is Predicted by Soil Organic Carbon. Soil Sci. Soc. Am. J. 2015, 79. [Google Scholar] [CrossRef]
- Majumder, B.; Mandal, B.; Bandyopadhyay, P.K.; Gangopadhyay, A.; Mani, P.K.; Kundu, A.L.; Mazumdar, D. Organic Amendments Influence Soil Organic Carbon Pools and Rice-Wheat Productivity. Soil Sci. Soc. Am. J. 2008, 72. [Google Scholar] [CrossRef]
- Reid, D.K. Comment on “The Myth of Nitrogen Fertilization for Soil Carbon Sequestration”, by S.A. Khan et al. in the Journal of Environmental Quality 36:1821–1832. J. Environ. Qual. 2008, 37. [Google Scholar] [CrossRef]
- Manna, M.C.; Swarup, A.; Wanjari, R.H.; Singh, Y.V.; Ghosh, P.K.; Singh, K.N.; Tripathi, A.K.; Saha, M.N. Soil Organic Matter in a West Bengal Inceptisol after 30 Years of Multiple Cropping and Fertilization. Soil Sci. Soc. Am. J. 2006, 70, 121. [Google Scholar] [CrossRef]
- Khan, S.A.; Mulvaney, R.L.; Ellsworth, T.R.; Boast, C.W. The Myth of Nitrogen Fertilization for Soil Carbon Sequestration. J. Environ. Qual. 2007, 36. [Google Scholar] [CrossRef] [PubMed]
- Li, J.T.; Zhang, B. Paddy Soil Stability and Mechanical Properties as Affected by Long-Term Application of Chemical Fertilizer and Animal Manure in Subtropical China. Pedosphere 2007, 17. [Google Scholar] [CrossRef]
- López-Bellido, R.J.; Fontán, J.M.; López-Bellido, F.J.; López-Bellido, L. Carbon sequestration by tillage, rotation, and nitrogen fertilization in a mediterranean vertisol. Agron. J. 2010, 102. [Google Scholar] [CrossRef]
- Luo, L.; Lin, H.; Schmidt, J. Quantitative Relationships between Soil Macropore Characteristics and Preferential Flow and Transport. Soil Sci. Soc. Am. J. 2010, 74. [Google Scholar] [CrossRef]
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979, 74. [Google Scholar] [CrossRef]
- Morris, M.; Kelly, V.A.; Kopicki, R.J.; Byerlee, D. Fertilizer Use in African Agriculture: Lessons Learned and Good Practices; World Bank: Washington, DC, USA, 2007. [Google Scholar]
- Doberman, A. Site-specific nutrient management for intensive rice cropping systems in Asia. Field Crops Res. 2002, 74, 37–66. [Google Scholar] [CrossRef]
- Walkley, A. A critical examination of a rapid method for determining organic carbon in soils: Effect of variations in digestion conditions and of inorganic soil constituents. Soil Sci. 1947, 63, 251–263. [Google Scholar] [CrossRef]
- Chambers, R.G. Applied Production Analysis: A Dual Approach; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Berck, P.; Helfand, G. Reconciling the von Liebig and Differentiable Crop Production Functions. Am. J. Agric. Econ. 1990, 72, 985–996. [Google Scholar] [CrossRef]
- Berck, P.; Geoghegan, J.; Stohs, S. A strong test of the von Liebig hypothesis. Am. J. Agric. 2000, 82, 948–955. [Google Scholar] [CrossRef]
- Davidson, R.; MacKinnon, J.G. Testing the specification of multivariate models in the presence of alternative hypotheses. J. Econom. 1983, 23. [Google Scholar] [CrossRef]
- Ponnamperuma, F.N. The Chemistry of Submerged Soils. Adv. Agron. 1972, 24. [Google Scholar] [CrossRef]
- Becker, M.; Asch, F. Iron toxicity in rice—Conditions and management concepts. J. Plant Nutr. Soil Sci. 2005, 168, 558–573. [Google Scholar] [CrossRef]
- Chaturvedi, I. Effect of nitrogen fertilizers on growth, yield and quality of hybrid rice (Oryza sativa). J. Cent. Eur. Agric. 2006, 6, 611–618. [Google Scholar]
- Mandal, N.N.; Chaudhry, P.P.; Sinha, D. Nitrogen, phosphorus and potash uptake of wheat (var. Sonalika). Environ. Ecol. 1993, 10, 297. [Google Scholar]
- Rajput, M.K.K.; Ansari, A.H.; Mehdi, S.; Hussain, A.M. Effect of N and P fertilizers alone and in combination with OM on the growth and yield of Toria. Sarhad J. Agri. Res. 1988, 4, 3–6. [Google Scholar]
- Yoshida, S. Tropical Climate and Its Influence on Rice; International Rice Research Institute: Los Baños, Philippines, 1978; Volume 20. [Google Scholar]
- Rupp, D.; Hubner, H. Influence of Nitrogen fertilization on the mineral content of apple leaves. Erwerbsobstbau 1995, 37, 29–31. [Google Scholar]
- Jamieson, P.D.; Martin, R.J.; Francis, G.S. Drought influences on grain yield of barley, wheat and maize. N. Z. J. Crops Hortic. Sci. 1995, 23, 55–66. [Google Scholar] [CrossRef]
- Fisher, R.A.; Aguilar, I.; Laing, D.R. Post-anthesis sink size in a high-yielding dwarf wheat: Yield response to grain number. Aust. J. Agric. Res. 1977, 28, 165–175. [Google Scholar] [CrossRef]
- De Datta, S.K. Principles and Practice of Rice Production; John Wiley and Sons: Singapore, 1981; pp. 348–419. [Google Scholar]
- Sheriff, G. Efficient Waste? Why Farmers over-Apply Nutrients and the Implications for Policy Design. Appl. Econ. Perspect. Policy 2005, 27, 542–557. [Google Scholar] [CrossRef]
- Mae, T.; Inaba, A.; Kaneta, Y.; Masaki, S.; Sasaki, M.; Aizawa, M.; Okawa, S.; Hasegawa, S.; Makino, A. A large-grain rice cultivar, Akita-63, exhibits high yields with high physiological N-use efficiency. Field Crops Res. 2006, 97, 227–237. [Google Scholar] [CrossRef]
- Matsushima, S. Researches on the requirements for achieving high yields in rice. In Science of the Rice Plant: Physiology; Matsuo, T., Ishii, R., Ishihara, K., Hirata, H., Eds.; Food and Agriculture Policy Research Center: Nobunkyo, Tokyo, 1993; Volume 2, pp. 737–747. [Google Scholar]
- Makino, A. Photosynthesis, Grain Yield, and Nitrogen Utilization in Rice and Wheat. Plant Physiol. 2011, 155, 125–129. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).