Featured Application
This study presents the experimental results of the shear strength of reinforced concrete (RC) “real” beams extracted from an old RC building in Rome, built in 1929. The concrete strength is very small as in the case of many existing old RC structures. These results about “real” beams are innovative in the literature because the beams are usually built purposely to be retrofitted and tested. The data presented in this paper improve the literature database giving original data about the measured concrete strength variation along the beams, the stiffness, the deflections, and the strengths of the beams before and after retrofitting, and the Carbon FRP U-Strips strains. The shear strengths of these “real” beams, together with the ones obtained in other experimental studies, are in good agreement with the predicted strengths by design code equations.
Abstract
In recent years, old reinforced concrete (RC) buildings have increasingly been protected as historic symbols in Italy. The conversion of these buildings can resolve the increasing need for new structures, reducing much social, economic, and environmental impact. Retrofitting solutions by carbon fiber reinforced polymer (CFRP) reinforcements are very common nowadays. Code predictions present uncertainties due to the brittle behavior and the debonding of CFRP strips resulting from concrete cracking. Therefore, especially in the case of old beams, experimental validation is necessary. This paper deals the experimental evaluation of the shear strength of two beams extracted from an old RC building in Rome built in 1929 with modest-quality concrete. Preliminary tests were carried out to evaluate the beam elastic response and the material characteristics. These beams were tested until failure (three-point load shear/bending tests) after strengthening for shear by CFRP U-jacketing and for bending by new steel rebars. The results obtained, together with the extensive data taken from the literature, were compared with the predictions by design code equations. The influence of construction details on beam shear strength and the experimental maximum CFRP strain were also analyzed. Code predictions can be effective to estimate the shear strength of the retrofitted beams.
1. Introduction
In seismic countries as Italy, many reinforced concrete (RC) buildings were built from the beginning of the 20th century. The existing buildings designed by old design codes can be very vulnerable to the medium-high seismic hazard of Italy [1,2,3,4]. Furthermore, Italy has extremely high exposure due to population density and its artistic, historical, and monumental heritage. During recent years, old artistic, industrial or civil RC buildings have increasingly been protected as historic symbols through carefully planned interventions [5,6]. The conversion of these buildings, their rehabilitation, and their reuse for modern activities may assure their protection and represent a solution for the increasing need for new structures, assuring modest social, economic, and environmental impacts. For that reason, the attention of the construction industry increasingly moves from new constructions to maintenance, repair and/or retrofitting and rehabilitation of existing structures [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].
In this context, this paper focuses on the study of retrofitting solutions to improve the load-carrying capacity of existing old RC beams by Externally Bonded Fiber-Reinforced Polymer (EB-FRP) reinforcement much used in construction. In particular, many researchers have extensively studied and tested the shear strengthening of RC beams by EB-FRP reinforcement [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43] but the behavior of these beams is still much discussed in the literature [29,31,44,45,46]. The main discussion issues are regarding: the shear interaction between the different contributions for the shear strength [47,48,49], the influence of the beam size [50] of the shear span-to-depth ratio [30] and the contribution of the shear FRP reinforcement to the beam resistance in proportion to the FRP thickness [51].
Regarding the first issue, the experimental results have shown that not all steel stirrups crossed by shear cracks yield [32,38,39,40,45,46,47,52,53,54,55], and so the steel shear reinforcement contribution may not be fully mobilized [48] especially in the case of FRP reinforcement debonding. For that reason, the shear strength value predicted by well-known models may be not safe [44,48,49].
Furthermore, many research efforts are still necessary for resolving some critical issues about FRP reinforcement such as: the brittle failure mode of retrofitted RC members due to sudden failure or debonding of the FRP reinforcement [56]; the effects of wet-dry cycles and freeze-thaw conditions on the FRP fabric that produce deterioration of the FRP mechanical properties; the reduction of the strength of the FRP reinforcement due to improper installation procedures, the lack of proper bond strength models and the need for efficient anchorage systems when it is not possible to provide a correct anchorage length or in the case of inevitable strip debonding [57].
These research studies were usually performed on beams purposely built in the lab to be retrofitted and tested, that did not present material deterioration phenomena (corrosion of rebar, concrete carbonatation or surface peeling) [58,59], poor concrete quality, improper reinforcement detail and uncertainties about steel and concrete mechanical characteristics and rebar configuration typical of “real” old RC structures [60,61]. For that reason, the experimental tests are necessary to evaluate the shear strength, the failure mode, and the strain of the FRP reinforcement for “real” beams.
The present paper investigates the shear strength of two “real” retrofitted beams extracted by an old RC structure built with poor-quality concrete in Rome in 1929.
The two beams were removed during retrofitting of the building (Figure 1) and brought to ‘the Proof testing and Research in Structures and Materials Laboratory (PRiSMa)’ of the Roma Tre University (Rome, Italy) (§2). The results of the survey on the beams geometries and steel reinforcement configuration are given in §2.1. The variation of the compressive strength of concrete was investigated by numerous non-destructive tests (sonic and rebound tests) along each beam in §2.2. These evaluations were corrected by means of the results of destructive tests on some material specimens: compression tests on concrete cores and tension tests on steel rebar parts extracted after the failure tests on the retrofitted beams. The description of the retrofitting intervention to improve the beam shear strength by EB-CFRP reinforcement (U-jacketing) and the beam flexural strength at midspan by new bottom longitudinal steel rebars, is given in §3.

Figure 1.
Beams DB1 (a) and DB2 (b) in the RC building at the basement floor (c).
Three-point load shear/bending tests were carried out on the beam before the retrofitting and after retrofitting (§4). The preliminary elastic tests on the extracted beams were performed to evaluate the stiffness of each beam before retrofitting (§4.2). The failure tests on the retrofitted beams (§4.3) were carried out to evaluate the shear strength, the failure mode and deflections of the beams (§4.3.1), the beam damage (§4.3.2), the CFRP U-strips strains (§4.3.3) and the contribution of the steel reinforcement, the CFRP reinforcement and the concrete to the beam shear resistance (§4.3.4). The code design equations used to predict the shear strength for the beam before and after retrofitting are given in §5. The results obtained for the tested beams, together with the experimental data available from the literature for many beams retrofitted by EB-CFRP reinforcement, were compared to the one predicted by codes in §6. The comparisons between predicted and measured values were performed for: 1. the beam shear strength before retrofitting assuming different inclination angle for the shear cracks (§6.1); 2. the beam shear strength after retrofitting considering or not the concrete contribution (§6.2); 3. the shear strength contribution of the CFRP reinforcement (§6.3).
A discussion about the research conclusions and the possible future research development starting from the given experimental data analysis is given in §7. The code equation results are able to estimate the shear strength of the “real” retrofitted beams but the uncertainties due to the brittle behavior of CFRP and to the premature debonding of strips resulting from concrete cracking should be closely considered by the designer. Both beams failed in shear because of improper design of the construction details (insufficient new longitudinal rebar anchorage) resulting in a complete debonding of the CFRP strips that reduced the beam strength. Finally, experimental measures showed a significant variation of the concrete compressive strength in adjacent beams as well as in different portion of each beam. This uncertainty about the compressive strength should be closely considered by a designer to define properly the beam capacity [60,61].
2. Extracted Beams
Two “real” RC beams were extracted from an old RC building in Rome to insert new RC walls during building retrofitting. The structure was built in 1929 with concrete that had small compressive strength (<15 MPa) as in the case of many old RC buildings. The structural system is a space frame with four floors (75 × 36 m2 plan dimension) and many columns and beams (Figure 1a–c). The two extracted secondary beams were located very close to each other on the basement floor (Figure 1c) and were probably built by the same concrete cast. The beams were labeled as DB1 and DB2, were cut by means of a diamond wire at two sections very close to the ends and were brought to the Proof testing and Research in Structures and Materials Laboratory (PRiSMa) of the Roma Tre University (Rome, Italy).
After the survey of the beam concrete geometries and steel reinforcement configuration, tests on the beam materials were performed to evaluate the variation of the concrete compressive strength along each beam and the steel rebar strength.
2.1. Concrete Geometries and Steel Reinforcement Configuration
The extracted RC beams DB1 and DB2 had concrete geometries and the steel reinforcement configurations given in Figure 2a,b. The cross-section of the beams was rectangular, and the steel reinforcement was realized by smooth rebars protected by a thin concrete cover (5–30 mm) with some rebars partially exposed at some points. The location of the rebars embedded in the concrete was determined by means of a pachometer device. This non-destructive test (NDT) permitted identification of the direction, the length, the number and the spacing of longitudinal and transverse steel rebars for each beam (Figure 2a,b). The steel stirrups were realized by ϕ 6 mm rebars with irregular spacing. The pachometer survey showed that the stirrup spacing was more irregular along each beam. This is frequent in existing RC beams when the stirrups are not well fixed before the concrete cast and so they move during concrete casting. There were not regions with a constant value of spacing: the spacing ranged randomly from 150 mm to 300 mm in the case of the beam DB1 and from 150 mm to 320 mm in the case of the beam DB2.
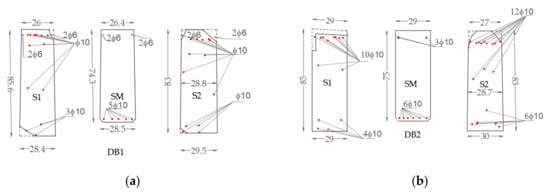
Figure 2.
Beams DB1 (a) and DB2 (b); concrete geometries and steel reinforcement configuration for the sections at the beam ends (S1, S2) and at the beam midspan (SM); rebar diameter [mm]; concrete geometries [cm].
2.2. Mechanical Characteristics of the Beam Materials
2.2.1. Compressive Strength of Concrete
NDTs were carried out on the two beams DB1 and DB2 to evaluate the variation of the compressive strength of concrete along the beams. Measurements of ultrasonic pulse velocities and rebound index values were conducted on the beam surface at 18 and 25 test stations located along the beams DB1 and DB2 (U points in Figure 3a). A rebound hammer was used to measure the rebound index as indicated in UNI EN 12504-2:2001 [62] after surface preparation to remove the more external deteriorated concrete parts. A digital portable detector (50 kHz probes; Low frequency) was used to carry out transparent velocity measurement as indicated in UNI EN 12504-4:2005 [63]. The NDT results were combined and correlated with the cubic compressive strength of concrete (R) by the combined method SonReb to compensate for the limits and the uncertainties of the two NDTs. The cubic compressive strength (R) was obtained by means of Equation (1) in RILEM guideline [64]:
in which N is the rebound index and V the ultrasonic velocity measured by the NDTs.
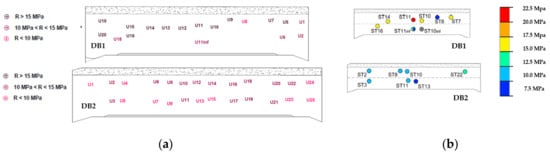
Figure 3.
Beams DB1 and DB2: cubic concrete compressive strength values (R) along the beams obtained by (a) the corrected non-destructive tests at U test stations or (b) by destructive tests on concrete cores (ST).
This strength is usually different with respect to the one obtained by destructive tests (DT) on concrete cores extracted by a beam especially in the case of old concretes. The uncertainties in the evaluation of concrete strength by NDT depend on different factors: concrete composition and ages, effect of admixture, water/cement ratio, non-homogeneous concrete structure, and surface deterioration.
The compressive strength values obtained by DT on concrete cores extracted from beams are less uncertain than the ones by NDTs. For that reason, DTs were conducted on 8 and 7 concrete cores (diameter 94 mm, height/diameter ratio equal to 2) extracted from the beams DB1 and DB2 at the ST points in Figure 3b after the failure tests (§4.3) on the retrofitted beams (§3). The cores were extracted predominantly at some NDT stations to compare the DT and the NDT results. The choice of the stations, where to perform the core extractions, was determined by the local conditions of the beams after the beam collapse (regions in tension or in compression during the tests without evident damage), selecting the points that represented better the distribution of the compressive strength of concrete measured by means of the NDTs. A diamond core drill (water cooled) was used for the core drilling made with constant and modest velocity to avoid excessive stresses on the concrete core.
The cylindrical compressive strength (fc) values obtained by the DTs on the concrete cores were converted in the cubic compressive strength values (R) in Figure 3b and Table 1 by means of Equation (2). This conversion permits comparison of the DT compressive strength values directly with the ones obtained by NDTs using Equation (1) which gives the cubic compressive strength values.

Table 1.
Cubic concrete compressive strength (R) by compressive tests on cores (ST) and steel yield stress (f0.2%) by tensile tests on steel rebar pieces (RT); [MPa].
The mean cubic compressive strength values (Rm) are 14.7 MPa and 10.9 MPa for the beam DB1 and DB2 whereas the coefficient of variation (CoV) values are 0.28 and 0.12 for the beam DB1 and DB2. The concretes show a wide scatter of the compressive strength values especially along the beam DB1.
The comparison between the values of the cubic compressive strength obtained by NDT and DT tests at the same points permitted estimation of the strength correction factor to correct the compressive strength evaluated by NDTs only at each U-test station. The corrected cubic compressive strength values are given in Figure 3a. The concrete of the beam DB1 was on average of better quality with respect to the one of the beam DB2 even if the two beams were very close in the structure (Figure 1c) but the concrete of the beam DB1 had a wider scatter of strength values. Furthermore, the compressive strength at the top part of each beam was greater than the one at the bottom part. This is probably due to two main aspects: 1. Concrete segregation after the concrete cast that is typical of old concretes; 2. The adopted load scheme produces compression at the beam extrados and tension at the beam intrados; Even if the concrete cores were extracted where damage was modest, inevitable concrete cracking may affect the concrete mechanical characteristics.
Similar compressive strength values were observed for the cores extracted at the beam end and at the beam midspan extrados (ST7, ST10, ST14 for the beam DB1; ST2, ST8 and ST10 for the beam DB2).
It seems that eventual preexisting cracking at the beam regions in tension, when the beam was in the structure (extrados at the beam ends and intrados at the beam midspan), did not affect the mechanical properties of concrete.
These experimental results should be investigated better by further experimental research on “real” existing beams and closely considered to assess the beam strength and deformation capacity [60,61].
2.2.2. Test on Steel Rebar
The mechanical properties of the beam reinforcement were evaluated by DT performed on rebar pieces extracted by the retrofitted beams after the failure tests (§4.3). These rebars had smooth surfaces and mechanical properties comparable to the ones of Italian Steel grade rebar with yield stress of 430 MPa. 14 rebar specimens (RT) were taken from the two-beam reinforcement to be tested in tension (Table 1): 8 rebar specimens with diameter ϕ 6 mm (3 from stirrups of DB1 and 5 from stirrups of DB2) and 6 rebar specimens with diameter ϕ 10 mm (3 from longitudinal reinforcement of DB1 and 3 from longitudinal reinforcement of DB2). The yield stresses values (f0.2%) obtained by these tests are shown in Table 1. The existing rebar extracted by the beams were carefully chosen to be without any sign of yielding, after the beam failure tests. This was confirmed by tensile tests during which no plastic deformation seemed to preexist.
The mechanical properties of the steel rebars used to improve the flexural strength of the extracted beams at the midspan (§3), were also tested. 4 rebar pieces with diameter ϕ 20 mm, Italian Steel grade with the yield stress of 430 MPa and ribbed surface were tested under monotonic tensile load until failure. In Table 2, the mean value (mean) and the CoV of yield (f0.2%) and the maximum stresses (fsu) are given considering groups of rebars with the same diameter. The results obtained for the ribbed rebars used for retrofitting, showed very small values for the CoV whereas the results of the smooth rebars were wide scattered, especially in the case of the ϕ6 mm rebars.

Table 2.
Beams DB1 and DB2: existing and new strengthening bars diameter (ϕ), yield stress at strain of 0.2% (f0.2%); maximum stress (fsu) [mm, MPa].
3. Beams Retrofitting
The beams DB1 and DB2 were strengthened in bending by the addition of new bottom longitudinal ribbed rebars and in shear by EB-CFRP reinforcement (U-jacketing) and were labeled as DB1-R and DB2-R beams. The retrofitting interventions consist of (Figure 4a–d): 1. the mechanical removal of the concrete cover from each beam side; 2. the cleaning of the original rebars surface and the application of anticorrosive protection; 3. the addition of 3 bottom longitudinal steel rebars with diameter ϕ20 mm (§2.2.2); 4. the concrete cover restoration by a thixotropic hydraulic anti-shrinkage mortar with synthetic fibers (mean cubic compressive strength Rm = 35 MPa); 5. the construction of a concrete groove with transverse section 20 mm × 20 mm along the entire beam length to anchor the CFRP strips; and 6. the application of epoxy mortar on beam surface to fix the CFRP strips.

Figure 4.
Beam retrofitting: (a) rebars cleaning and protection, addition of new bottom rebars for beam flexural strengthening; (b) concrete cover restoration; (c) CFRP U-jacketing application for beam shear strengthening; (d) Details of U-jacketing anchorage by pultruded composite bar.
The application of the EB-CFRP reinforcement was performed on the two beam sides and on the intrados of the beams (U-jacketing). The CFRP shear reinforcement was realized by 3 U-strips for each beam end (Figure 4c). Each U-strip was built by two strips of CFRP fabric, one for beam side at 45° orientation, with spacing of 200 mm that crossed on the beam intrados (Figure 4d). In addition, 3 U-strips built by one single strip of CFRP fabric were applied at midspan vertically oriented, with spacing of 200 mm to restrain the new bottom longitudinal rebar (Figure 4c). The strips were realized by unidirectional CFRP fabric with weight equal to 300 g/m2, tensile modulus of 240 GPa, tensile strength of 3500 MPa, thickness of 0.167 mm and width of 100 mm. Each U-strip end was anchored to the beam surface by an improved anchorage system. This anchorage system was realized for the following steps: 1. bending the CFRP fabric in the groove realized the beam web; 2. inserting a 150 mm long composite bar in the groove on the bended fabric; and 3. fixing the bar in the groove by an epoxy mortar that fills the groove (Figure 4d).
4. Test on Beams
In general, experimental results available from the literature on RC beams retrofitted by means of EB-CFRP are based on simply supported beam specimens under point loads. Then, the obtained results are analytically and/or numerically elaborated to take into consideration more realistic static behavior given in the case of framed structures.
In the present research, a three-point loading scheme (simply supported beam) was selected to test the extracted beams before and after retrofitting. In this way, it is possible to compare the results of the “real” beams with the ones given in the literature.
The existing steel reinforcement in the extracted beams was designed considering a frames/continuous beam configuration (the beam in the structure) with negative moments at beam ends and positive moments at beam midspan. This steel reinforcement configuration is different with respect to the one obtained considering a simply supported beam. However, elastic three-point loading tests were performed on the extracted beams before retrofitting to compare the deflection and stiffness of two beams with very similar rebar configurations and the same design materials. This is interesting because:
- The material mechanical characteristics showed variability along the beams (§2);
- The preexisting concrete cracking may be different for the two beams.
Finally, failure of three-point loading tests were carried out after the addition of new longitudinal rebars along the beam intrados, which increased the flexural strength at midspan and assured the beam failure due to shear at the beam ends. In fact, the moment values increase at the beam intrados when the beam is tested considering a simply supported beam with respect to the ones of the beam in the structure.
4.1. Test Apparatus
Three-point loading tests were performed on the beams DB1 and DB2 before retrofitting and on the beams DB1-R and DB2-R after retrofitting. Each beam was simply supported by a steel hinge support H and by a steel roller support R (Figure 5a,b). The span length (L) measured between the supports was 280 cm and 310 cm for the beams DB1 and DB2.
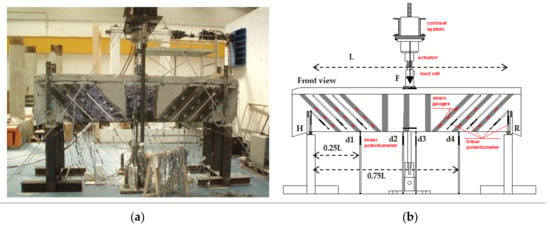
Figure 5.
Three-points loading test apparatus: (a) photo and (b) scheme of the system to apply the loads and to measure deformation of the beam and strain of the CFRP U-strips (frontal view).
The three-point loading test was carried out applying a vertical load (F) at the beam midspan by means of a 1000 kN hydraulic actuator supported by a vertical steel frame. This force produced two vertical reactions at the two beam supports. Vertical steel plates were added at the supports to avoid the beam torsion and lead plates regularized the contact surface between the beam intrados and the steel supports (Figure 5a). The apparatus setup is shown in Figure 5b and measured: the applied vertical load of a 1000 kN load cell placed between the actuator and a thick steel plate on the beam extrados at the midspan; the vertical deformations of each beam support by two vertical potentiometers (one for each beam side); the vertical beam deflections by 4 potentiometers at 0.25 L, 0.5 L (2 at the beam midspan) and 0.75 L for each beam side; 3 diagonal displacements along the potential shear cracks by 3 potentiometers for each beam side at each beam end (Figure 5b); the local axial strains of the CFRP fabric at bottom, middle and top position along each U-strip side at each beam end. The beams deflections measured along each beam were corrected considering the vertical deformations at the supports.
4.2. Elastic Tests on the Extracted Beams
Before retrofitting, elastic tests (three-point loading tests) were performed on the extracted beams DB1 and DB2 to measure their deformation shapes and stiffness values. The maximum load applied during the elastic tests should guarantee the elastic behavior of the beam during the tests. This load was calculated for each beam considering about half of the load value that produces a moment at section SM in Figure 1 equal to the section resisting moment. The section resisting moments were calculated considering the steel reinforcement and the beam geometries given in §2.1 and the steel yield stress indicated in §2.2 for each beam. The resulting maximum loads were 156 kN and 172 kN for the beams DB1 and DB2. The applied elastic loads on the beams were 92 kN and 72 kN for the beam DB1 and DB2. The load/deflection curves at different points along each beam (at 0.25L, at two points near 0.5L and at 0.75L, Figure 5b) are shown in Figure 6a. The beam stiffness (load/deflection) values were essentially constant at each measurement point during the test on each beam: this confirms that the beam behavior was elastic.
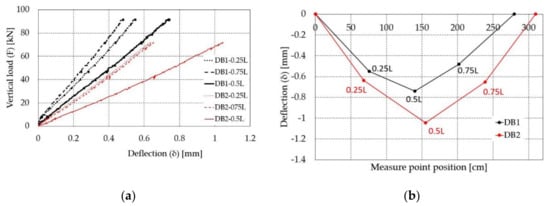
Figure 6.
Extracted beam DB1 and DB2: (a) load-deflection curves and (b) maximum beam deflections during the elastic tests (L is the beam length).
The beam deformation shapes corresponding to the maximum applied load are given in Figure 6b where the maximum beam deflections at midspan are −0.74 mm and −1.04 mm for the beam DB1 and DB2. The beam stiffness values calculated by the beam load-deflection curve at midspan (Figure 6a), were 124.3 kN/mm and 69.2 kN/mm for the beam DB1 and DB2: the stiffness of DB1 was 80% greater than the one of DB2.
Stiffness of beams depends on the Young’s modulus of concrete and steel, the beam length, and the area moment of inertia of section. Cracking is expected in section of RC members subjected to load with reduction of the area moment of inertia with respect to the one of the gross sections before cracking. The values of Young’s modulus of concrete can be estimated by Equation (3) in [65]:
where fcm is the mean compressive cylindrical strength of concrete. The values of fcm can be obtained by means of the mean compressive cubic strength given in §2.2.1 for each beam. The Young’s modulus values are 23.3 GPa and 21.3 GPa for the beam DB1 and DB2. The elastic beam deflections at midspan for a given applied load can be calculated by the elastic curve equation considering the concrete gross section (pre-cracking stage) properties, the beam length, and the calculated Young’s moduli of concrete. Based on these results, the beam stiffness values before cracking at midspan are 500.0 kN/mm and 349.7 kN/mm for the beams DB1 and DB2. From the beginning of the elastic tests, the experimental stiffness values are smaller than the ones calculated considering the gross section and therefore the beam sections were already cracked before these tests. This is expected because the beams were extracted from a building subjected to loads.
The experimental flexural rigidity (EcIexp) can be evaluated by Equation (4) based on the elastic curve equation.
where Femax and δemax are the maximum load and the corresponding beam deflection at midspan during the elastic test.
The experimental flexural rigidity is included in the range with:
- The lower limit equal to the fully cracked flexural rigidity (EcIII) calculated by Equation (5);
- The upper lit equal to the uncracked flexural rigidity (EcI0) calculated by Equation (6)in which I0 is the area moment inertia of the uncracked section, III the area moment of inertia of the full cracked section, b is the section width, h is the section height, yc is the compression zone height, Es is the steel elastic modulus (200,000 MPa), As is the tension reinforcement area and d is the distance between the reinforcement and the top of the cross-section.
The experimental (EcIexp), uncraked (EcI0), and fully cracked (EcIII) flexural rigidity values are given for each beam in Table 3. The effective depth for flexure (d) was about 72 mm for each beam.

Table 3.
Extracted beams DB1 and DB2: experimental (EcIexp), fully cracked (EcIII) and uncraked (EcI0) flexural rigidity [kNm2].
In Table 3, the comparison between the ratios EcIexp/EcI0 and EcIII/EcI0 shows that the beams DB1 and DB2 presented a significant cracking of the section before the elastic test.
These results show that the prediction of the deflection for a “real beam” may be more uncertain because the variability of the concrete properties may be high (§2.2.1) and the preexisting cracks in the section may be significant.
4.3. Failure Tests on the Retrofitted Beams
After retrofitting, the beams were tested until there was failure to estimate the failure mode, the shear strength, the deflections, the CFRP reinforcement strain and the contribution to the shear resistance of the transverse steel reinforcement, the concrete, and the CFRP reinforcement.
4.3.1. Beam Deflections
Beam deflections (δ) were measured at 0.25 L, 0.75 L and at two points near 0.5 L (Figure 5b) during the application of the vertical load (F). The vertical load-deflection curves are given for each measurement point in Figure 7a,b. Deflection at each point was calculated as the mean value of measurements taken on both sides of beam (§4.1). The deflection d1 and d4 were measured at 0.25 L and 0.75 L whereas the deflections d2 and d3 were taken at the point on the left and the one on the right of the midspan (0.5 L) (Figure 7a). The maximum vertical load values at failure were 427.5 kN and 425.5 kN for the beams DB1-R and DB2-R and the corresponding midspan deflection values were 6.48 mm and 7.25 mm.
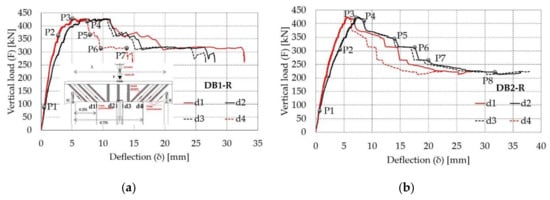
Figure 7.
Retrofitted beams: load-deflection responses along the beams DB1-R (a) and DB2-R (b).
4.3.2. Retrofitted Beam Failure Mechanism and Damage
Each beam showed brittle failure with diagonal shear cracks and CFRP reinforcement debonding probably due to insufficient anchorages of the new bottom longitudinal rebars close to the beam supports H and R (Figure 8a,b). The anchorages of the new bottom rebars used to improve the beam flexural strength at the midspan, were interrupted close to the beam supports in the case of the beam DB1-R and at the supports for the beam DB2-R. This interruption is not correct because Mörsch’s truss physical model requires the contribution of continuous bottom rebars along the beam length with efficient anchorages at beam ends. The beam failure mechanism was triggered by concrete cracks at beam intrados close to the support H (Figure 8a,b). These cracks were due probably to the slip of the new bottom rebars at anchorages or to detachment of the new bottom concrete parts (the RC slab built to insert the new bottom rebars) not connected properly to the beam by means of connectors (Figure 4a). The extension of these cracks caused the detachment of the new concrete cover and the CFRP reinforcement debonding from the beam sides.

Figure 8.
Damage on the beam DB1-R (a) and DB2-R (b) at support H after failure tests (back view).
Both strengthened beams collapsed for shear in correspondence to a large diagonal crack and the failure occurred with a complete debonding of the U-strips (Figure 8a,b) at about the same load (F ≈ 425.5 ~ 427.5 kN).
Since the beam spans and the bottom reinforcement area at the midspan are different in both beams (Figure 2), different capacities are expected if a flexure failure happens. However, the shear failure was observed at the end of the experimental tests and therefore the beam span and longitudinal reinforcement did not affect the peak force.
The failure of the beam DB1-R started from the hinge support H (Figure 8a) where a wide diagonal crack crossed the closer U-strip. The experimental behavior of this beam can be described along the load-deflection curve showed in Figure 7a. Along the initial branch of the curve (until point 1, Figure 7a), the DB1-R presented about 12% greater stiffness than the DB1 beam before retrofitting based on the measured midspan deflection: the mean deflection values for F = 92 kN were 0.66 mm and 0.74 mm for the beam DB1-R and DB1. Around the vertical load value of 370 kN (point 2, Figure 7a), the U-strips on the left of the midspan close to the support H started to debond locally. When the vertical load increased from 400 kN to 425 kN, the strips debonding became more evident proceeding until failure (point 3, Figure 7a). Deflection at the midspan increased and diagonal shear cracks, already wide at 400 kN, continued to grow becoming very large. A noticeable difference between the diagonal displacement along the U-strips near the hinge support (H, Figure 5b) and the ones near the roller support (R, Figure 5b) was evident with the displacement values close to the support H 4–5 times greater than those near the support R. When the beam was loaded up to failure, the beam shear collapse mechanism concentrated near the hinge support H. After the maximum vertical load, the beam behavior was characterized by decreasing of the load-carrying capacity due to the subsequent debonding of the remaining U-strips (point 4–7, Figure 7a) starting from the ones closer to the H support. The loss of the beam carry capacity was sudden along the load-deflection curves at each U-strips debonding from the maximum load 425 kN to the ultimate load 310 kN (point 7, Figure 7a). The rupture sequence involved four strips within a couple of seconds: each sudden fall of force along the curve (Figure 7a) represents the detachment of a strip. When the load is about 310 kN, all the U-strips broke, and the diagonal shear cracks became larger and larger until the beam failure occurred (point 7, Figure 7a).
The beam DB2-R behaved similarly to DB1-R (Figure 7a,b): shear failure started near the H hinge support with a first wide diagonal crack at about a quarter of the beam span and a second diagonal crack near the H support (Figure 8b). The shear failure of DB2-R occurred at about the same load value measured for the beam DB1-R, but the failure mode was different because the anchorages of the new bottom longitudinal rebars were extended over the supports of the beam DB2-R. This longer rebar anchorage anchored better the new rebars with respect to the one in the beam DB1-R. The new bottom reinforcement gave a better contribution to resist the force due to the shear at support and therefore the shear cracks moved toward the beam midspan (the crack located at about a quarter of the beam span from the support H).
The experimental behavior of this beam can be described along the load versus displacement curve shown in Figure 7b. Along the initial branch of the curve, the beam DB2-R presented about 14% greater stiffness than the DB2 beam before retrofitting based on the midspan deflection: the mean deflection values for F = 72 kN were 0.92 mm and 1.04 mm for the beam DB2-R and DB2 (point 1, Figure 7b). When the load is 300 kN, the CFRP U-strips started to debond locally (point 2, Figure 7b). The same phenomenon was observed also by Carolin et al. 2005 [53,54] during the beam loading at two-thirds of the failure load. The beam failure was abrupt without other significant warning signals with a main diagonal crack that grew up to failure. When the load is F = 350 kN, diagonal shear cracks close to the support H became evident and the new concrete cover started to detach at 400 kN. The U-strips debonding became more evident and the strips started to break (point 3, Figure 7b) at 425 kN. The diagonal displacements close to the support H were still small, about 2 mm, and the ones near the support R were smaller than 1 mm. Post-peak behavior was characterized by a subsequent detachment of the remaining strips starting from the H support up to the beam midspan until the applied load was equal to 270 kN (point 4–7, Figure 7b). The diagonal CFRP strips close to the support H and to the midspan together with the adjacent vertical ones gradually came off within 11 seconds. The failure of each strip corresponds to a loss of load along the curve in Figure 7b. Finally, the increasing of the load produced the rupture of all strips and the beam collapsed (point 8, Figure 7b).
After the CFRP reinforcement rupture, the shear resistance is guaranteed by the transverse steel and the concrete contribution (aggregate interlock, longitudinal rebar dowel effect, etc.). The CFRP reinforcement reduced the transverse steel contribution because plastic force distribution was limited along the transverse steel and the shear cracks angle was about 45°: the number of the stirrups that gave a contribution to the shear resistance was modest. However, the CFRP reinforcement reduced the width of the shear cracks improving the aggregate interlock and contrasted the cover spalling improving the dowel effect of the longitudinal rebars.
4.3.3. Experimental Strains of the CFRP Reinforcement
Strains of the CFRP U-strips were monitored during the beam failure test by means of three strain gauges at bottom, middle and top position along each U-strip side (Figure 9a). In Figure 9, the strains measured by the strain gauges on the diagonal CFRP strips FRP-U1, FRP-U2 and FRP-U3 (Figure 9b–d) near the support H of the DB1-R beam are plotted for five different values of the vertical load (F). These five load values are smaller than the maximum vertical load (Fmax) applied on the beam and are: F = 0.25Fmax (107 kN), the load that produced the beam flexural cracking (F =0.24Fmax, on average from the literature); F = 0.50Fmax (212 kN); F = 2/3Fmax (285 kN), that usually corresponds to the onset of strips debonding [53,54]; F = 0.85Fmax (360 kN) and F = 0.95Fmax (400 kN). The strains measured at Fmax (425 kN) are not included in Figure 9 because the strips detached from the beam surface and so the strain gauge measurement is not interesting at complete debonding of strips. The strains measured before complete debonding for F = 0.95Fmax were about equal to 0.3% (Figure 9b–d).
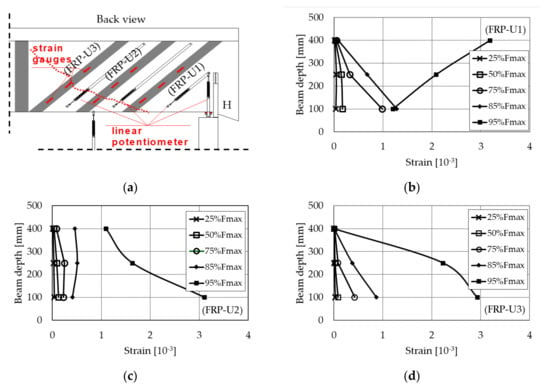
Figure 9.
Retrofitted beam DB1-R: strips locations on the beam side (a); strains distribution along the diagonal CFRP U-strips FRP-U1 (b), FRP-U2 (c) and FRP-U3 (d).
Given the linear elastic behavior of CFRP fabric, CFRP stress can be obtained directly by the measured strain and the Young’s modulus of the CFRP fabric (Ef = 240 GPa). The stress value corresponding to the maximum strain is 720 MPa. The CFRP effective strength (ffed) that produces debonding of the CFRP reinforcement is 695 MPa by Equation (18) in CNR-DT 200 R1/2013 [66]. This stress is function of the debonding strength (ffdd) calculated by Equation (23) in CNR-DT 200 R1/2013 [66] that is equal to 715 MPa assuming the tensile strength of the CFRP fabric equal to 2400 MPa, the mean cubic compressive strength of the restored concrete cover equal to 35 MPa and the unit value for the partial safety coefficients in [66]. The experimental CFRP stress at the strips debonding is very similar to the predicted value by the code equations [66].
The behavior of the CFRP strips of the beam DB2-R was similar to the one observed for the beam DB1-R. The strains measured before complete debonding for F = 0.95Fmax were about equal to 0.2–0.3%, except for one U-strip close to the midspan that showed locally strain values of 0.3–0.4%. A modest strain of about 0.1% was measured on the CFRP fabric region close to the beam extrados at top and middle positions along the U-strips, where strips debonding due to concrete cracking started to propagate. The applied load was about 2/3 of Fmax and this behavior was already observed by Carolin et al. 2005 [53,54].
The CFRP strains values measured at the beam failure due to strip debonding were smaller than the maximum values given on the CFRP fabric datasheet or obtained by direct coupon tests on CFRP specimen.
Furthermore, the experimental evidence showed that the maximum CFRP strain at strip debonding was smaller than the design one indicated in many design guidelines [66,67,68,69]. Design guidelines limit the value of the maximum CFRP strain to assure the integrity of concrete and prevent aggregate interlock failure. The value of the maximum strain is 0.005 and 0.006 in CNR-DT 200 R1/2013 [66] and fib Bulletin 14 [67], and is 0.004 in ACI 440.2R-08 [68] and TR 55 [69].
However, it is important to underline that the experimental measurement of the maximum FRP strain is difficult because strain gauges measurement gives the local value of strain. For that reason, the maximum strain can arise in a point along the strip, where strain is not measured during the test.
For that reason, the maximum CFRP strain can be a few greater that the measured one.
4.3.4. Experimental Contributions to the Beam Shear Resistance
The experimental contributions to the beam shear resistance due to the transverse steel reinforcement (), the CFRP reinforcement () and the concrete (), were estimated for the tested beams DB1-R and DB2-R in Table 4 when the maximum experimental shear was recorded.

Table 4.
Experimental contribution to the shear resistance of the transverse steel reinforcement ( ), the CFRP reinforcement ( ) and the concrete ( ) [kN].
The shear crack with an inclination angle ϴ equal to about 45° extended along each beam for about 800 mm (Figure 8a,b).
The experimental transverse steel contribution was evaluated by Equation (7):
in which nsw is the number of the stirrups crossing the shear crack, Asw is the cross-section area of the stirrups and f0.2%,m is the mean value of the yield stress of the stirrups from the data in Table 1.
The spacing of the stirrups was irregular along each beam (§2.1) and therefore nsw was calculated by the ratio between the length of the beam part crossed by the shear crack (800 mm) and the mean spacing of the stirrups. The values of nsw were 3.5 and 3.4 for the beam DB1-R and DB2-R.
The CFRP reinforcement contribution was estimated by Equation (8):
where nf,strips is the number of the CFRP strips crossing the shear crack, tf is the CFRP fabric thickness, bf is the CFRP strip width, Ef is the CFRP fabric Young’s modulus and is the strain measured on the CFRP U-strips at beam failure (§4.3.3). The CFRP fabric characteristics and the strip geometries are given in §3. The evaluation of the number of the U-strips, which gave a contribution to the shear resistance, is not simple because debonding of the strips was evident and the brittle failure of the CFRP reinforcement did not permitted plastic force distribution. However, nf,strips equal to 3 is used to evaluate the CFRP contribution in Table 4 because this is the number of the strips crossing the shear crack in Figure 8a,b for each beam. The value of the experimental CFRP strain was about equal to 0.3% for the beam DB1-R (Figure 9) and 0.25% for the beam DB2-R.
The experimental concrete contribution was obtained by the subtraction of the experimental shear contribution of the CFRP and the steel reinforcements from the maximum experimental shear recorded on the retrofitted beams (Figure 7a,b).
After the CFRP reinforcement failure, the experimental shear was about 157 kN and 114 kN for the beam DB1-R and DB2-R (Figure 7a,b). The beams could sustain these shear forces thanks to the transverse steel reinforcement and the concrete contributions. In fact, the sum of the transverse steel reinforcement and the concrete contributions in Table 4 is equal to 142 kN and 153 kN for the beams DB1-R and DB2-R: these values are very similar to the ones recorded after CFRP reinforcement failure.
However, the evaluation of the steel contribution is uncertain because: 1. The stirrups spacing was irregular; 2. The plastic force distribution was reduced by the CFRP reinforcement and so some stirrups could give a smaller contribution; 3. The CFRP reinforcement limited the crack width and the stress in the stirrups could be smaller than the yield stress depending on the actual steel strain. For the tested beams, the experimental strain measured on the CFRP strips were about 0.3% (§4.3.3) and therefore the stirrups more probably yielded because the steel yield strain is 0.2%.
The evaluation of the CFRP contribution is also uncertain because: 1. The number of the strips, that gave a contribution at the same time, is uncertain; 2. the actual strain of the CFRP fabric could be greater than the one measured locally where strain gauges were placed (Figure 9).
The uncertainties about the experimental steel and the CFRP reinforcement contributions make uncertain also the evaluation of the concrete contribution in Table 4. This contribution is not considered in the modern code equations that predict the retrofitted beam shear strength [66].
It is interesting to calculate the concrete contribution by Equation (12) in Eurocode 2 [70] considering the mean cubic concrete strengths given in §2.2.1 and the beams geometries and steel reinforcement showed in §2.1 for each beam. This contribution is equal to 74.3 kN for the beam DB1-R and it is equal to 72.8 kN for the beam DB2-R without considering the new bottom longitudinal rebars added in each beam. These values are similar to the experimental ones in Table 4. This means that the new bottom rebars, which had insufficient anchorages at the section where ρl (the reinforcement ratio for the longitudinal reinforcement) in Equation (12) is evaluated, did not give a contribution to the shear resistance. In fact, the concrete contribution calculated for each beam considering also the contribution of the new bottom rebar (§3) is 111.7 kN for the beam DB1-R and 105.0 kN for the beam DB2-R; values greater than the experimental ones in Table 4.
5. Design Equations for the Shear Strength of RC Beams
5.1. Strength of RC Beams before and after Retrofitting
The shear strength of beam with shear steel reinforcement only (VRd) can be evaluated by the two methods proposed in Eurocode 2 [70]:
- The Standard Method (Equation (9)) that considers the steel (VRd,s) and the concrete contribution (VRd,c); The truss model has the compressive strut inclination angle (ϴ) equal to 45°.
- The Variable Inclination Method (Equation (10)) not containing the concrete contribution; The truss model has a variable compressive strut inclination angle (ϴ) lower than 45°
The design value of the shear force, which can be sustained by the yielding shear reinforcement (VRd,s), can be calculated by Equation (11).
where fywd, Asw and s are the design yield stress, the cross-sectional area and the spacing of the shear steel reinforcement.
The design shear resistance of the member without shear steel reinforcement (VRd,c) can be calculated by Equation (12) assuming member axial load equal to zero.
in which is the partial factory, ρl is the reinforcement ratio for the longitudinal reinforcement, bw is the smallest width of the cross-section in the tensile area, fck is the characteristic compressive cylinder strength of concrete at 28 days and the parameter may be found in Country National Annex.
The term VRd,max is the maximum shear capacity of the section calculated by Equation (13) that depends on the compressive strength of the concrete strut (Mörsch’s truss analogy model).
in which the coefficients αcw and υ1 for use in a Country may be found in its National Annex, fcd is the design value of concrete compressive strength and α is the angle between shear reinforcement and the beam axis perpendicular to the shear force.
From a physical point of view, the Standard Method is unsatisfactory because the concrete contribution is empirical and includes different resisting mechanisms (compressed concrete zone contribution, aggregate interlock, and dowel action of the longitudinal rebars crossing the shear cracks) difficult to estimate. Furthermore, the experimental evidence shows a redistribution of the forces in the beam web, which results in compressive concrete strut inclination angles smaller than 45°. The number of stirrups crossed by the shear cracks can be greater and more stirrups can contribute to the beam shear strength. This redistribution is considered by the Variable Inclination Method that does not contain the uncertain concrete contribution. The recommended limits for the variable angle ϴ are given by Equation (14).
The shear strength of the retrofitted beam by means of EB-CFRP reinforcement (VRd,r) can be predicted by Equation (15) in fib Bulletin 14 [67] or by Equation (16) in CNR-DT 200 R1/2013 [66].
in which VRd,f is the CFRP U-jacket contribution to shear resistance given in §5.2.
The main difference between the two code Equations (15) and (16) is that fib Bulletin 14 [67] guideline considers also the concrete term VRd,c. The angle ϴ should be assumed equal to 45° in each equation to limit the value of the VRd,s (cot ϴ = 1). In fact, the plastic redistribution of the force in the transverse steel reinforcement could be limited by the CFRP reinforcement.
5.2. CFRP U-Jacket Contribution to Shear Resistance
The guidelines CNR-DT 200 R1/2013 [66] and fib Bulletin 14 [67] assume that the EB-FRP reinforcement behaves like the transverse steel reinforcement. The contribution of CFRP shear reinforcement (VRd,f) is calculated by Equation (17) in CNR-DT 200 R1/2013 [66] based on the Mörsch’s truss analogy model. This is the same equation used to evaluate the steel shear contribution (VRd,s) in Eurocode 2 [70] considering the cross-section area (Af = bf∙tf where bf and tf are the width and the thickness of CFRP strips), the spacing (pf) and the effective strength of CFRP strips (ffed) instead of the steel cross-section area (Asw), the spacing (s) and the yield stress of the steel rebar (fy).
ϴ is the inclination of the concrete crack to the beam axis, β is the inclination of CFRP strips to the beam axis, d is the distance from the extreme compression fiber to the centroid of tension steel reinforcement and ϒRd = 1.2 is the partial factory.
The effective design strength of the CFRP shear reinforcement (ffed) is usually governed by debonding according Equation (18):
where ffdd is the design debonding strength of FRP, hw the web depth completely impregnated with U-wrap and led the design effective bond length.
The design debonding strength ffdd at failure is evaluated from the maximum transmissible force by the anchorage (Pmax) given by Equation (19).
The value of Pmax can be measured by tests or alternatively obtained according to Wu et al. 2002 [71] using the following interface law (Equation (20)):
in which Ef is the Young’s modulus of elasticity of FRP reinforcement and Γfd is the fracture energy that characterizes the bond interface between the FRP sheet and concrete calculated by Equation (21) considering wet lay-up FRP.
where fcm is the mean value of concrete compressive strength, fctm is the mean value of concrete tensile strength, FC is the factor of confidence and kb is the scale coefficient defined by Equation (22)
in which b is the width of the beam. Through Equations (21), (22) and (23), it is possible to obtain the design debonding strength (ffdd).
where Υfd is the partial safety factor depending on the application of the FRP sheet. The design optimal bond length can be calculated by Equation (24) in fib Bulletin 14 [67].
The contribution of the FRP shear reinforcement calculated by Equation (17) is not completely correct. Differently from the steel reinforcement, the CFRP reinforcement does not activate any Mörsch’s truss resisting mechanism with plastic force redistribution [52]. Therefore, the effective design strength of the CFRP shear reinforcement should not be used like the yield stress for the transverse steel reinforcement. Furthermore, it is possible that the CFRP reinforcement strain at failure is smaller than the yield strain of the transverse steel and so the steel shear contribution should be closely considered [52].
6. Shear Strength of the Beams Tested in Lab
This chapter collects the experimental results regarding the RC beams retrofitted by EB-CFRP reinforcement or not retrofitted that were tested in Monti et al. 2007 [38], Pellegrino et al. 2002 [39], Carolin et al. 2005 [54], Bousselham et al. 2009 [72], Barros et al. 2006 [73], and Zhang et al. 2005 [74]. The experimental shear strength values measured for these beams and the ones measured for the two beams DB1-R and DB2-R tested in this study were compared with the predicted values obtained by the code design equations described in §5.
The retrofitted beams collapsed due to the shear failure with debonding of the CFRP reinforcement and brittle rupture of CFRP fabric. The beams tested in the literature were purposely designed and built with insufficient transverse steel reinforcement to be reinforced by EB-CFRP reinforcement. The beams DB1-R and DB2-R are the only ones removed from a “real” existing building. The beam geometries, the material mechanical characteristics (steel, concrete and FRP) and the configurations of the steel and the FRP reinforcements for each beam are given in Table A1 and Table A2 (Appendix A).
6.1. Shear Strength of the Beams before Retrofitting
The shear strength of the RC beams with steel shear reinforcement before retrofitting selected in §6 was predicted by Equation (10) in Eurocode 2 [70] assuming the partial factors are equal to one. The material mechanical characteristics, the beam concrete geometries and the reinforcement configurations are given in Table A1 and Table A2 for each beam.
Two different values for the inclination angle of the concrete compressive strut (ϴ) were selected:
- A fixed value of ϴ equal to 45°
- A variable value of ϴ smaller than 45° calculated by the variable inclination angle method in §5.1.
These two values of ϴ permit consideration of the minimum (cotϴ = 1) and the maximum (1 ≤ cotϴ ≤ 2.5) transverse steel contribution to the shear resistance (VRd,s) in Equation (10). In fact, if the inclination angle of the cracks (ϴ) is smaller than 45°, the number of internal stirrups crossing the crack and the resulting shear carried by the stirrups may be higher, up to the maximum value defined by cotϴ = 2.5.
The experimental shear strength (VRd,exp) of the selected beams is given by the authors (§6) that tested these beams.
In Figure 10, each point gives information about the predicted and the experimental shear strength values for the beams considering the two angles ϴ. The line “m” indicates the perfect correspondence between the predicted and the measured shear strength values.
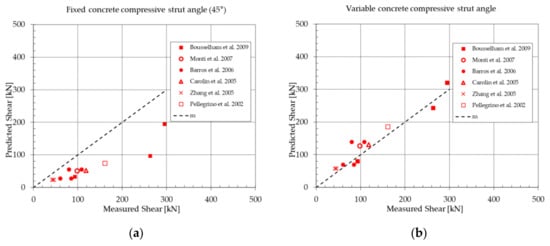
Figure 10.
Beam before retrofitting: experimental and predicted shear strength values considering (a) the fixed or (b) the variable inclination angle of the concrete compressive strut.
The data points are below the straight line “m” when the fixed inclination angle is used (Figure 10a) and so this prediction underrates the real shear strength of the beam before retrofitting. The data points are closer to the straight line “m” when the variable inclination angle is used (Figure 10b) and therefore the predictions of the shear strength are more realistic. In Figure 10b, there are some points above the line “m” for which the predicted shear strength using the variable angle is a little greater than the experimental one but the application of the partial factors may assure safe design.
The statistical values of the ratio VRd,exp/VRd for each beam in Figure 10a,b, are given in Table 5.

Table 5.
Statistical values of the predictions: mean, Standard deviation, Coefficient of Variation, max, min, 5% and 95% percentile of the ratio VRd,exp/VRd.
The prediction of the beam strength using the fixed value of ϴ equal to 45° gives, on average, values equal to 47% of the experimental ones. The inclination angle of the shear cracks in a beam before retrofitting is usually smaller than 45° and so the number of internal stirrups crossing the crack is greater. The steel reinforcement plastic strains increase the shear cracks width and therefore the concrete contribution (aggregate interlock, dowel effect, etc.) can be much reduced. For that reason, it may be neglected in Equation (10).
6.2. Shear Strength of the Beams after Retrofitting by CFRP Reinforcement
For the beams retrofitted by means of EB-CFRP reinforcement, the transverse steel and the CFRP contributions to the shear resistance should be calculated using the angle of the concrete compressive strut (ϴ) equal to 45°. In fact, the plastic force redistribution in the shear steel reinforcement is limited by the CFRP reinforcement that is characterized by a brittle failure, and the angle ϴ does not reduce much with respect to 45°.
The predicted shear strength values were calculated by Equation (15) or (16) for the retrofitted beams indicated in §6 with steel and FRP shear reinforcement, and for the beams DB1-R and DB2-R assuming the partial factors are equal to one; the angle ϴ is equal to 45°; the material mechanical characteristics, the beam concrete geometries and the reinforcement configurations given in Table A1 and Table A2. The effective depth for flexure is about 750 mm for the beams DB1-R and DB2-R.
The experimental shear strength (VRd,r exp) of the selected beams is given by the authors (§6) that tested these beams.
In Figure 11, each point gives information about the predicted and the experimental shear strength values for each tested beam. The line “m” indicates the perfect correspondence between the predicted and the measured shear strength values.
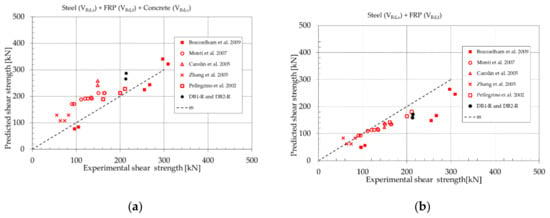
Figure 11.
Beam after retrofitting: experimental and predicted shear strength values including (a) or not including (b) the concrete contribution (VRd,c).
Figure 11a shows a model with large scatter. The shear strength values predicted by Equation (15), in which the contribution of the concrete is added to the ones of the CFRP and the transverse steel reinforcements, overestimate the experimental shear strength values for many tested beams.
This happens despite the assumption of the angle ϴ equal to 45° that underrates the transverse steel contribution (§6.1). Partial factors should be considered to properly reduce the prediction of the Equation (15) to consider the scatter, but this is not investigated in this study.
Alternatively, Figure 11b shows a large scatter but the predicted values by Equation (16), that do not consider the concrete contribution, are safer because many points are below the line “m”. The partial factors may improve the safety of the prediction for the a few points above the line “m” in Figure 11b.
The statistical values of the ratio VRd,r exp/VRd,r calculated by Equation (15) or Equation (16) for each beam, are given in Table 6.

Table 6.
Statistical values of the predictions: mean, Standard deviation, Coefficient of Variation, max, min, 5% and 95% percentile of the ratio VRd,r exp/VRd,r.
The predicted value of the retrofitted beam shear strength is, on average, 82% of the experimental one if the contribution of concrete is not considered. For that reason, the concrete contribution, which is uncertain, should be not considered in the prediction equation. The application of the two models (Equation (15) or (16)) on the “real” beams DB1-R and DB2-R gives result similar to the ones obtained for the beam tested in the literature.
6.3. Experimental FRP Reinforcement Contribution to the Shear Resistance
The experimental shear contribution of the CFRP reinforcement () can be obtained through subtraction of the experimental beam shear strength before retrofitting () from the experimental shear strength measured for the retrofitted beam () by Equation (25).
The experimental for the beam DB1-R and DB2-R was evaluated in Table 4 based on the experimental data.
The predicted values of the CFRP reinforcement contribution () were evaluated by Equation (17) considering: the partial factors are equal to 1.2, the fixed angle ϴ is equal to 45° and the beam concrete geometries and the FRP reinforcement details given in Table A1 and Table A2.
In Figure 12, each point gives information about the predicted and the experimental Vrd,f values for the tested beams selected in §6 and for the beams DB1-R and DB2-R. The line “m” indicates the perfect correspondence between the predicted and the measured shear strength values. One should note that the strength predicted by Equation (17) may be quite unsafe because many points are above the line “m”.
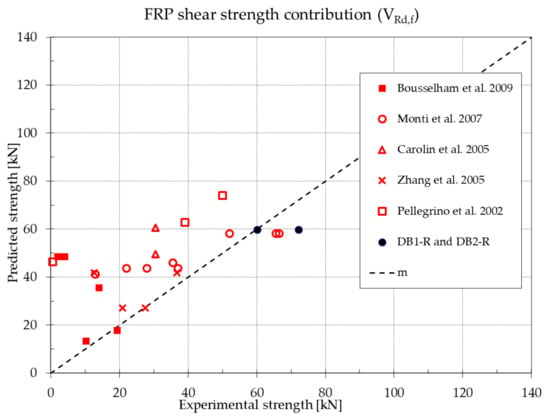
Figure 12.
Experimental and predicted values for the CFRP reinforcement contribution to the shear resistance.
The statistical values of the ratio VRd,f exp/VRd,f for each beam are given in Table 7.

Table 7.
Statistical values of the predictions: mean, Standard deviation, Coefficient of Variation, max, min, 5% and 95% percentile of the ratio VRd,f exp/VRd,f.
The prediction by Equation (17) is, on average, 1.47 times greater than the experimental one.
However, the experimental FRP contribution result may be smaller than the predicted one (Figure 12) because the brittle behavior of FRP does not permit the plastic distribution of the force along the FRP reinforcement and so a few FRP strips only can contribute to the FRP reinforcement shear resistance at the same time. Furthermore, the maximum stress may be different between the strips. This uncertainness should be considered to develop a new predictive model.
Finally, the experimental CFRP contribution obtained by Equation (25) requires some critical considerations. The transverse steel reinforcement and the concrete contributions to the beam shear strength are different in a beam before and after retrofitting (§6.1, §6.2). For that reason, Equation (25) could not properly evaluate the experimental FRP contribution. The possible variation of these two contributions before and after retrofitting, should be further investigated by experimental tests to evaluate properly the experimental FRP contribution.
7. Conclusions and Discussion
Two beams (DB1, DB2) extracted from an old RC structure, were strengthened for shear by an EB- CFRP reinforcement and for bending by new bottom longitudinal rebars to be tested in the lab until failure. The case at hand is the only one with “real” old RC beams built with modest-quality concrete and transverse steel rebar distributed randomly along the beam, as in the case of many existing beams. Experimental tests on materials showed a wide scatter of the concrete compressive strength values and the concrete of the beam DB1 was, on average, of better quality with respect to the one of the beam DB2 even if the two beams were located very close in the structure. Furthermore, the concrete compressive strength at the beam top part was greater than the one at the bottom part along each beam; this is probably due to cracking of the beam region in tension and to concrete segregation. The experimental initial beam stiffness was up to 4–5 times smaller than the theoretical one calculated considering the uncracked gross section. This is expected because the beams were extracted from a building subjected to loads and therefore the beam sections were already cracked. Consequently, the “real” beam capacity in terms of strength and deformation should be closely considered by designers because the CFRP reinforcement can modestly restore the beam stiffness by up to 12–14%.
From the experimental tests, the brittle failure mechanism of each beam was characterized by the propagation of concrete diagonal cracks and by the delamination of CFRP reinforcement as soon as the CFRP-concrete bond interface started to crack. The experimental transverse steel reinforcement, CFRP reinforcement and concrete contributions to the shear resistance were calculated based on the experimental measurements when the maximum shear was recorded on the beams.
After the CFRP reinforcement failure, the sum of the experimental transverse steel reinforcement and concrete contributions are similar to the residual shear value recorded on each beam. This means that the aggregate interlock, the dowel effects of the longitudinal rebars and the other “concrete” resisting mechanisms gave a contribution to the shear resistance of the retrofitted beam.
However, this concrete contribution is uncertain because it is obtained starting from the retrofitted beam maximum shear and from the experimental steel and CFRP reinforcement contributions that are uncertain.
The evaluation of the steel contribution is uncertain because:
- The stirrup spacing was irregular;
- The plastic force distribution was reduced by the CFRP reinforcement and so some stirrups could give a smaller contribution;
- The CFRP reinforcement limited the crack width and so the stress in the stirrups could be smaller than the yield stress depending on the actual steel strain;
- The scatter of the steel yield and of the maximum steel stresses were wide (§2.2).
For the tested beams, the experimental strain measured on the CFRP strips were about 0.3% (§4.3.3) and so the stirrups more probably yielded because the steel yield strain is 0.2%.
The evaluation of the CFRP contribution is also uncertain because:
- The number of the strips, that gave a contribution at the same time, is uncertain;
- The actual strain of the CFRP fabric could be greater than the one measured locally where strain gauges were placed (Figure 9).
For that reason, the retrofitted beam shear strength evaluated without considering the concrete contribution by the modern design code seems safer.
Finally, the concrete contribution predicted by Eurocode 2 [70] without considering the new bottom longitudinal rebars, is similar to the experimental one for each beam. This means that the new bottom rebars, which had insufficient anchorages, did not give a contribution to the beam shear resistance. However, the new bottom rebars avoided flexural failure according the test design target. For that reason, retrofitting construction details should be closely considered by designers.
Finally, the experimental shear strength of these beams, together with the ones provided by many authors in the literature, were compared to the predicted values calculated by the code equations in Eurocode 2 [70], CNR-DT 200/2013 [66] and fib bulletin 14 [67] that provide two different design approaches. The results of these comparisons have showed that:
- Before retrofitting, the Variable Angle Method [70] gives values of the shear strength that result in good agreement with the experimental results. The shear carried by the stirrups, considering the real shear crack angle, may be 2.12 times greater than the one estimated considering an inclination angle of 45°.
- After CFRP retrofitting, the experimental beam shear strength is, on average, 1.21 times greater than the predicted one assuming a crack inclination angle of 45° without considering the concrete contribution (CNR-DT 200/2013 [66]). The predictive model capacity should be improved considering the uncertainties about each shear strength contribution.
- The concrete contribution predicted by code equation [70] is similar to the experimental one for the tested beam DB1-R and DB2-R. Further research efforts should be undertaken because the steel and CFRP reinforcement contributions are uncertain.
- The CFRP reinforcement contribution to the shear resistance could be overestimated by the design model [66]. This resisting model seems improper for evaluating the FRP contribution because: i. The brittle failure of the CFRP shear reinforcement does not permit plastic force redistribution; ii. The number of CFRP strips that contribute efficiently to the shear resistance is uncertain; iii. The maximum FRP fabric deformation is still uncertain.
- The experimental CFRP strain can be modest and comparable to the yield strain of the steel reinforcement. In this case, the transverse steel contribution to the shear resistance can be smaller than the one predicted by code equation [70].
Further research efforts are needed in order to understand better:
- The effect of the material property variability on the capacity of “real” beams
- The strength of the “real” beam retrofitted with proper new rebar anchorages
- The resisting mechanism of the retrofitted beams based on physical assumptions.
Author Contributions
D.L. makes substantial contributions to conception and design, acquisition of data, analysis and interpretation of data, analytical elaborations, writing the article and revising it critically for each content. He gives final approval of the version to be submitted and any revised version. C.N. makes substantial contributions to conception and design, analysis and interpretation of data, revising the paper critically for important intellectual content. He gives final approval of the version to be submitted and any revised version. S.S. makes substantial contributions to conception and design, acquisition of data, analysis and interpretation of data, analytical elaborations, writing the article and revising it critically for each content. She gives final approval of the version to be submitted and any revised version.
Funding
The authors gratefully acknowledge the funding by “The Laboratories University Network of seismic engineering” (ReLUIS) thanks to the research project ReLUIS/DPC 2015-2018.
Acknowledgments
The authors wish to express their gratitude to Interbau s.r.l. for providing CFRP sheet and adhesive for the specimens. They also thank the Italian Ministry of Public Works and The Italian State Property Office. The writers would also like to express their appreciation for the technical support given by the staff at the Proof testing and Research in Structures and Materials Laboratory (PRiSMa) of the Roma Tre University (Rome, Italy).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The symbols used in Table A1 and Table A2 represent: base, depth and span length of the beam; Asw/s is the ratio area steel stirrups/spacing; fc is the compressive strength of concrete; fy is the yield stress of stirrups; bf/pf is the FRP ratio width/spacing; thick is the thickness of the FRP fabric; angle is the inclination angle of FRP strips; Ef is the Young’s modulus of the FRP.

Table A1.
Geometrical and mechanical properties of the selected RC beams and FRP strengthening; the “ref” beams are the ones without FRP retrofitting [38,39,54,72,73,74,75,76,77].
Table A1.
Geometrical and mechanical properties of the selected RC beams and FRP strengthening; the “ref” beams are the ones without FRP retrofitting [38,39,54,72,73,74,75,76,77].
| Ref. | Specimens | Base (mm) | Depth (mm) | Span (m) | Geom Ratio | Asw/s | fc Mean (MPa) | fy Mean (MPa) | bf/pf | Thick (mm) | Angle | Ef (GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DB1 | 285 | 750 | 3.47 | 0.006 | 0.26 | 12.2 | 497 | 0.25 | 0.165 | 45° | 240 | |
| DB2 | 290 | 750 | 3.89 | 0.006 | 0.22 | 9.0 | 497 | 0.25 | 0.165 | 45° | 240 | |
| Bouss 2009 | ED1-S1-0L (ref) | 152 | 350 | 4.52 | 0.037 | 0.57 | 25.0 | 538 | ||||
| ED1-S1-1L | 152 | 350 | 4.52 | 0.037 | 0.57 | 25.0 | 538 | 1.00 | 0.107 | 90° | 231 | |
| ED1-S1-2L | 152 | 350 | 4.52 | 0.037 | 0.57 | 25.0 | 538 | 1.00 | 0.214 | 90° | 231 | |
| ED1-S2-0L (ref) | 152 | 350 | 4.52 | 0.037 | 1.15 | 25.0 | 538 | |||||
| ED1-S2-1L | 152 | 350 | 4.52 | 0.037 | 1.15 | 25.0 | 538 | 1.00 | 0.107 | 90° | 231 | |
| ED1-S2-2L | 152 | 350 | 4.52 | 0.037 | 1.15 | 25.0 | 538 | 1.00 | 0.214 | 90° | 231 | |
| ED2-S1-0L (ref) | 95 | 175 | 3 | 0.036 | 0.39 | 25.0 | 538 | |||||
| ED2-S1-1L | 95 | 175 | 3 | 0.036 | 0.36 | 25.0 | 538 | 1.00 | 0.066 | 90° | 231 | |
| ED2-S1-2L | 95 | 175 | 3 | 0.036 | 0.36 | 25.0 | 538 | 1.00 | 0.132 | 90° | 231 | |
| Garcez 2008 | CB (ref) | 150 | 300 | 3 | 0.005 | 0.89 | 41.4 | 578 | ||||
| CFB_01 | 150 | 300 | 3 | 0.005 | 0.89 | 41.4 | 578 | 0.22 | 0.165 | 90° | 227 | |
| CFB_02 | 150 | 300 | 3 | 0.005 | 0.89 | 41.4 | 578 | 0.22 | 0.23 | 90° | 227 | |
| Monti 2007 | REF (ref) | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | ||||
| US90 | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | 0.50 | 0.22 | 90° | 390 | |
| US60 | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | 0.50 | 0.22 | 60° | 390 | |
| USVA | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | 0.50 | 0.22 | 45° | 390 | |
| USVA+ | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | 0.50 | 0.22 | 45° | 390 | |
| US45+ | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | 0.50 | 0.22 | 45° | 390 | |
| US90(2) | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | 0.50 | 0.22 | 90° | 390 | |
| US45++ | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | 0.50 | 0.22 | 45° | 390 | |
| US45++D | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | 0.67 | 0.22 | 45° | 390 | |
| US45++E | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | 0.67 | 0.22 | 45° | 390 | |
| US45++F | 250 | 450 | 2.8 | 0.011 | 0.25 | 11.0 | 500 | 0.67 | 0.22 | 45° | 390 | |
| Barros 2006 | A10_C (ref) | 150 | 300 | 1.5 | 0.007 | 37.6 | 549 | |||||
| A10_S (steel) | 150 | 300 | 1.5 | 0.007 | 0.19 | 37.6 | 549 | |||||
| A10_M (cfrp) | 150 | 300 | 1.5 | 0.007 | 37.6 | 549 | 0.13 | 0.334 | 90° | 390 | ||
| A12_C (ref) | 150 | 300 | 1.5 | 0.010 | 37.6 | 549 | ||||||
| A12_S (steel) | 150 | 300 | 1.5 | 0.010 | 0.38 | 37.6 | 549 | |||||
| A12_M (cfrp) | 150 | 300 | 1.5 | 0.010 | 37.6 | 549 | 0.26 | 0.334 | 90° | 390 | ||
| B10_C (ref) | 150 | 150 | 0.9 | 0.014 | 49.5 | 549 | ||||||
| B10_S (steel) | 150 | 150 | 0.9 | 0.014 | 0.38 | 49.5 | 549 | |||||
| B10_M (cfrp) | 150 | 150 | 0.9 | 0.014 | 49.5 | 549 | 0.31 | 0.334 | 90° | 390 | ||
| B12_C (ref) | 150 | 150 | 0.9 | 0.020 | 49.5 | 549 | ||||||
| B12_S (steel) | 150 | 150 | 0.9 | 0.020 | 0.75 | 49.5 | 549 | |||||
| B12_M (cfrp) | 150 | 150 | 0.9 | 0.020 | 49.5 | 549 | 0.63 | 0.334 | 90° | 390 |

Table A2.
Geometrical and mechanical properties of the selected RC beams and FRP strengthening: the “ref” beams are the ones without FRP retrofitting; glass and cfrp the FRP material types [38,39,54,72,73,74,75,76,77].
Table A2.
Geometrical and mechanical properties of the selected RC beams and FRP strengthening: the “ref” beams are the ones without FRP retrofitting; glass and cfrp the FRP material types [38,39,54,72,73,74,75,76,77].
| Ref. | Specimens | Base (mm) | Depth (mm) | Span (m) | Geom Ratio | Asw/s | fc Mean (MPa) | fy Mean (MPa) | bf/pf | Thick (mm) | Angle | Ef (GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Guadagn 2006 | SB40 (ref) | 150 | 250 | 2.3 | 0.012 | 0.00 | 42.8 | 500 | 90° | |||
| SB40R (glass) | 150 | 250 | 2.3 | 0.012 | 0.00 | 42.8 | 500 | 0.25 | 0.11 | 90° | 65 | |
| SB41 (ref) | 150 | 250 | 1.8 | 0.012 | 0.00 | 42.8 | 500 | 90° | ||||
| SB41R (glass) | 150 | 250 | 1.8 | 0.012 | 0.00 | 42.8 | 500 | 0.25 | 0.11 | 90° | 65 | |
| SB42 (ref) | 150 | 250 | 1 | 0.012 | 0.00 | 42.8 | 500 | 90° | ||||
| SB42R (glass) | 150 | 250 | 1 | 0.012 | 0.00 | 42.8 | 500 | 0.50 | 0.206 | 90° | 65 | |
| Carolin 2005 | Type B R (ref) | 180 | 400 | 3.5 | 0.033 | 0.28 | 45.6 | 515 | ||||
| Type B 290 | 180 | 400 | 3.5 | 0.033 | 0.28 | 45.6 | 515 | 1.00 | 0.11 | 90° | 210 | |
| Type B 390 | 180 | 400 | 3.5 | 0.033 | 0.28 | 45.6 | 515 | 1.00 | 0.17 | 90° | 210 | |
| Zhang 2005 | ZC4 (ref) | 152.4 | 228.6 | 1.22 | 0.012 | 0.28 | 43.8 | 400 | ||||
| Z4-90 (cfrp) | 152.4 | 228.6 | 1.22 | 0.012 | 0.28 | 43.8 | 400 | 0.39 | 1 | 90° | 165 | |
| Z4-45 (cfrp) | 152.4 | 228.6 | 1.22 | 0.012 | 0.28 | 43.8 | 400 | 0.39 | 1 | 45° | 165 | |
| ZC6 (ref) | 152.4 | 228.6 | 1.83 | 0.012 | 0.28 | 43.8 | 400 | |||||
| ZC6(2) (ref) | 152.4 | 228.6 | 1.83 | 0.012 | 0.28 | 43.8 | 400 | |||||
| Z6-90 (cfrp) | 152.4 | 228.6 | 1.83 | 0.012 | 0.28 | 43.8 | 400 | 0.39 | 1 | 90° | 165 | |
| Z6-45 (cfrp) | 152.4 | 228.6 | 1.83 | 0.012 | 0.28 | 43.8 | 400 | 0.39 | 1 | 45° | 165 | |
| Adhikary 2004 | B-1 (ref) | 150 | 200 | 2.6 | 0.010 | 0.00 | 34.0 | 389 | ||||
| B-8 | 150 | 200 | 2.6 | 0.010 | 34.0 | 389 | 1.00 | 0.167 | 90° | 226 | ||
| Pellegr 2002 | TR30D1 (ref) | 150 | 300 | 2.7 | 0.010 | 0.50 | 31.4 | 548 | ||||
| TR30D2 (3- plies) | 150 | 300 | 2.7 | 0.010 | 0.50 | 31.4 | 548 | 1.00 | 0.495 | 90° | 236 | |
| TR30D3 (1 ply) | 150 | 300 | 2.7 | 0.010 | 0.50 | 31.4 | 548 | 1.00 | 0.165 | 90° | 236 | |
| TR30D4 (2 plies) | 150 | 300 | 2.7 | 0.010 | 0.50 | 31.4 | 548 | 1.00 | 0.33 | 90° | 236 | |
| Khalifa 2000 | BT1 (ref) | 150 | 405 | 3.05 | 0.011 | 0.00 | 35.0 | 410 | ||||
| BT2 (1-ply) | 150 | 405 | 3.05 | 0.011 | 35.0 | 410 | 1.00 | 0.165 | 90° | 228 | ||
| BT3 (2-plies) | 150 | 405 | 3.05 | 0.011 | 35.0 | 410 | 1.00 | 0.33 | 90° | 228 | ||
| BT4 (90 strip) | 150 | 405 | 3.05 | 0.011 | 35.0 | 410 | 0.25 | 0.165 | 90° | 228 | ||
| BT5 (90 strip) | 150 | 405 | 3.05 | 0.011 | 35.0 | 410 | 0.25 | 0.165 | 90° | 228 | ||
| BT6 (sheet) | 150 | 405 | 3.05 | 0.011 | 35.0 | 410 | 1.00 | 0.165 | 90° | 228 |
References and Notes
- Vanzi, I.; Marano, G.C.; Monti, G.; Nuti, C. A synthetic formulation for the Italian seismic hazard and code implications for the seismic risk. Soil Dyn. Earthq. Eng. 2015, 77, 111–122. [Google Scholar] [CrossRef]
- Braga, F.; Gigliotti, R.; Monti, G.; Morelli, F.; Nuti, C.; Salvatore, W.; Vanzi, I. Post-seismic assessment of existing constructions: Evaluation of the shakemaps for identifying exclusion zones in Emilia. Earthq. Struct. 2015, 8, 37–56. [Google Scholar] [CrossRef]
- Nuti, C.; Rasulo, A.; Vanzi, I. Seismic safety of network structures and infrastructures. Struct. Infrastruct. Eng. 2010, 6, 95–110. [Google Scholar] [CrossRef]
- Fiorentino, G.; Forte, A.; Pagano, E.; Sabetta, F.; Baggio, C.; Lavorato, D.; Nuti, C.; Santini, S. Damage patterns in the town of Amatrice after August 24th 2016 central Italy earthquakes. Bull. Earthq. Eng. 2018, 16, 1399–1423. [Google Scholar] [CrossRef]
- Decreto 22 gennaio 2004. Codice dei beni culturali e del paesaggio, ai sensi dell’articolo 10 della legge 6 luglio 2002, n. 137. Gazzetta Ufficiale della Repubblica Italiana. n.45 del 24-2-2004—Suppl. Ordinario n. 28. (In Italian)
- Aveta, A. Conservazione E Valorizzazione Del Patrimonio Culturale. Indirizzi E Norme Per Il Restauro Architettonico; Arte Tipografica Editrice: Napoli, Italy, 2005. [Google Scholar]
- Nuti, C.; Vanzi, I. To retrofit or not to retrofit? Eng. Struct. 2003, 25, 701–711. [Google Scholar] [CrossRef]
- Braga, F.; Gigliotti, R.; Monti, G.; Morelli, F.; Nuti, C.; Salvatore, W.; Vanzi, I. Speedup of post earthquake community recovery: The case of precast industrial buildings after the Emilia 2012 earthquake. Bull. Earthq. Eng. 2014, 12, 2405–2418. [Google Scholar] [CrossRef]
- Lavorato, D.; Bergami, A.V.; Nuti, C.; Briseghella, B.; Xue, J.; Tarantino, A.M.; Marano, G.C.; Santini, S. Ultra-high-performance Fibre-reinforced Concrete Jacket for the Repair and the Seismic Retrofitting of Italian and Chinese RC Bridges. In Proceedings of the 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June 2017; Volume I, pp. 2149–2160. [Google Scholar]
- Lavorato, D.; Nuti, C. Pseudo-dynamic tests on reinforced concrete bridges repaired and retrofitted after seismic damage. Eng. Struct. 2015, 94, 96–112. [Google Scholar] [CrossRef]
- Albanesi, T.; Lavorato, D.; Nuti, C.; Santini, S. Experimental program for pseudodynamic tests on repaired and retrofitted bridge piers. Eur. J. Environ. Civ. Eng. 2009, 13, 671–683. [Google Scholar] [CrossRef]
- Lavorato, D.; Nuti, C.; Santini, S.; Briseghella, B.; Xue, J. A repair and retrofitting intervention to improve plastic dissipation and shear strength of Chinese RC bridges. In Proceedings of the IABSE Conference, Geneva, Switzerland, 23–25 September 2015; pp. 1762–1767. [Google Scholar]
- Lavorato, D.; Nuti, C. Seismic response of repaired bridges by pseudodynamic tests. In Proceedings of the 5th International Conference on Bridge Maintenance, Safety and Management, Philadelphia, PA, USA, 11–15 July 2010; Frangopol, D., Sause, R., Kusko, C., Eds.; CRC Press: Boca Raton, FL, USA, 2010. ISBN 978-0-415-89137-0. [Google Scholar]
- Lavorato, D.; Nuti, C. Pseudo-dynamic testing of repaired and retrofitted RC bridges. In Proceedings of the fib Symposium 2011 in PRAGUE: Concrete Engineering for Excellence and Efficiency, Praha, Czech Republic, 8–10 June 2011; Volume 1, pp. 451–454. [Google Scholar]
- Zhou, Z.; Lavorato, D.; Nuti, C.; Marano, G.C. A model for carbon and stainless steel reinforcing bars including inelastic buckling for evaluation of capacity of existing structures. In Proceedings of the 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, 25–27 May 2015; pp. 876–886. [Google Scholar]
- Zhou, Z.; Nuti, C.; Lavorato, D. Modeling of the Mechanical Behavior of Stainless Reinforcing Steel. In Proceedings of the 10th fib International PhD Symposium in Civil Engineering, Québec, QC, Canada, 21–23 July 2014; pp. 515–520. [Google Scholar]
- Imperatore, S.; Lavorato, D.; Nuti, C.; Santini, S.; Sguerri, L. Numerical modeling of existing RC beams strengthened in shear with FRP u-sheets. In Proceedings of the 6th International Conference on FRP Composites in Civil Engineering, CICE 2012, Rome, Italy, 13–15 June 2012. [Google Scholar]
- Imperatore, S.; Lavorato, D.; Nuti, C.; Santini, S.; Sguerri, L. Shear behavior of existing RC t-beams strengthened with CFRP. In Proceedings of the Assessment, Upgrading and Refurbishment of Infrastructures (IABSE 2013), Rotterdam, The Netherlands, 6–8 May 2013. [Google Scholar]
- Imperatore, S.; Lavorato, D.; Nuti, C.; Santini, S.; Sguerri, L. Shear Performance of Existing Reinforced Concrete T-Beams Strengthened with FRP. In Proceedings of the 6th International Conference on FRP Composites in Civil Engineering, CICE 2012, Rome, Italy, 13–15 June 2012. [Google Scholar]
- Lavorato, D.; Bergami, A.V.; Fiorentino, G.; Fiore, A.; Santini, S.; Nuti, C. Experimental tests on existing RC beams strengthened in flexure and retrofitted for shear by C-FRP in presence of negative moments. Int. J. Adv. Struct. Eng. 2018. [Google Scholar] [CrossRef]
- Pelliciari, M.; Marano, G.C.; Cuoghi, T.; Briseghella, B.; Lavorato, D.; Tarantino, A.M. Parameter identification of degrading and pinched hysteretic systems using a modified Bouc-Wen model. Struct. Infrastruct. Eng. 2018. [Google Scholar] [CrossRef]
- Marano, G.C.; Pelliciari, M.; Cuoghi, T.; Briseghella, B.; Lavorato, D.; Tarantino, A.M. Degrading Bouc-Wen Model Parameters Identification under Cyclic Load. Int. J. Geotech. Earthq. Eng. 2017, 8, 60–81. [Google Scholar] [CrossRef]
- Bergami, A.V.; Forte, A.; Lavorato, D.; Nuti, C. Proposal of a incremental modal pushover analysis (IMPA). Earthq. Struct. 2017, 13, 539–549. [Google Scholar] [CrossRef]
- Bergami, A.V.; Nuti, C. A design procedure of dissipative braces for seismic upgrading structures. Earthq. Struct. 2013, 4, 85–108. [Google Scholar] [CrossRef]
- Fiorentino, G.; Lavorato, D.; Quaranta, G.; Pagliaroli, A.; Carlucci, G.; Nuti, C.; Sabetta, F.; Monica, G.D.; Piersanti, M.; Lanzo, G.; et al. Numerical and experimental analysis of the leaning tower of Pisa under earthquake. Procedia Eng. 2017, 199, 3350–3355. [Google Scholar] [CrossRef]
- Fiorentino, G.; Nuti, C.; Squeglia, N.; Lavorato, D.; Stacul, S. One-Dimensional Nonlinear Seismic Response Analysis Using Strength-Controlled Constitutive Models: The Case of the Leaning Tower of Pisa’s Subsoil. Geosciences 2018, 8, 228. [Google Scholar] [CrossRef]
- Fiore, A.; Spagnoletti, G.; Greco, R. On the Prediction of Shear Brittle Collapse Mechanisms Due to the Infill-Frame Interaction in RC Buildings under Pushover Analysis. Eng. Struct. 2016, 121, 147–159. [Google Scholar] [CrossRef]
- Resta, M.; Fiore, A.; Monaco, P. Non-Linear Finite Element Analysis of Masonry Towers by Adopting the Damage Plasticity Constitutive Model. Adv. Struct. Eng. 2013, 16, 791–803. [Google Scholar] [CrossRef]
- Bousselham, A.; Chaallal, O. Shear Strengthening Reinforced Concrete Beams with Fiber-Reinforced Polymer: Assessment of Influencing Parameters and Required Research. Struct. J. 2004, 101, 219–227. [Google Scholar]
- Bousselham, A.; Chaallal, O. Effect of Transverse Steel and Shear Span on the Performance of RC Beams Strengthened in Shear with CFRP. Compos. Part B Eng. 2006, 37, 37–46. [Google Scholar] [CrossRef]
- Bousselham, A.; Chaallal, O. Behaviour of RC T beams strengthened in shear with CFRP: An experimental study. ACI Struct. J. 2006, 103, 339–347. [Google Scholar]
- Bousselham, A.; Chaallal, O. Mechanism of Shear Resistance of Concrete Beams Strengthened in Shear with Externally Bonded FRP. J. Compos. Construct. 2008, 12, 499–512. [Google Scholar] [CrossRef]
- Chen, J.F.; Teng, J.G. Shear Capacity of FRP-Strengthened RC Beams: FRP Debonding. Construct. Build. Mater. 2003, 17, 27–41. [Google Scholar] [CrossRef]
- Chen, J.F.; Teng, J.G. Shear capacity of fiber reinforced polymer- strengthened reinforced concrete beams: Fiber reinforced polymer rupture. J. Struct. Eng. 2003, 129, 615–625. [Google Scholar] [CrossRef]
- Islam, M.R.; Mansur, M.A.; Maalej, M. Shear Strengthening of RC Deep Beams Using Externally Bonded FRP Systems. Cem. Concr. Compos. 2005, 27, 413–420. [Google Scholar] [CrossRef]
- Khalifa, A.; Nanni, A. Improving Shear Capacity of Existing RC T-Section Beams Using CFRP Composites. Cem. Concr. Compos. 2000, 22, 165–174. [Google Scholar] [CrossRef]
- Khalifa, A.; Nanni, A. Rehabilitation of Rectangular Simply Supported RC Beams with Shear Deficiencies Using CFRP Composites. Construct. Build. Mater. 2002, 16, 135–146. [Google Scholar] [CrossRef]
- Monti, G.; Liotta, M. Tests and Design Equations for FRP-Strengthening in Shear. Construct. Build. Mater. 2007, 21, 799–809. [Google Scholar] [CrossRef]
- Pellegrino, C.; Modena, C. Fiber reinforced polymer shear strengthening of reinforced concrete beams with transverse steel reinforcement. J. Compos. Construct. 2002, 6, 104–111. [Google Scholar] [CrossRef]
- Pellegrino, C.; Modena, C. Fiber-Reinforced Polymer Shear Strengthening of Reinforced Concrete Beams: Experimental Study and Analytical Modeling. Struct. J. 2006, 103, 720–728. [Google Scholar]
- Taljsten, B. Strengthening concrete beams for shear with CFRP sheets. Construct. Build. Mater. 2003, 17, 15–26. [Google Scholar] [CrossRef]
- Chen, W.; Pham, T. M.; Sichembe, H.; Chen, L.; Hao, H. Experimental Study of Flexural Behaviour of RC Beams Strengthened by Longitudinal and U-Shaped Basalt FRP Sheet. Compos. Part B Eng. 2018, 134, 114–126. [Google Scholar] [CrossRef]
- Triantafillou, T.C. Shear Strengthening of Reinforced Concrete Beams Using Epoxy-Bonded FRP Composites. Struct. J. 1998, 95, 107–115. [Google Scholar]
- Chen, G.M. Shear Behaviour and Strength of RC Beams Shear-Strengthened with Externally Bonded FRP Reinforcement. Ph.D. Thesis, Department of Civil and Structural Engineering, The Hong Kong Polytechnic University, Hong Kong, China, 2010. [Google Scholar]
- Teng, J.G.; Chen, J.F.; Smith, S.T.; Lam, L. FRP-Strengthened RC Structures; John Wiley and Sons: Chichester, UK, 2002. [Google Scholar]
- Chen, J.F.; Teng, J.G. 5-Shear Strengthening of Reinforced Concrete (RC) Beams with Fibre-Reinforced Polymer (FRP) Composites. In Strengthening and Rehabilitation of Civil Infrastructures Using Fibre-Reinforced Polymer (FRP) Composites; Woodhead Publishing Series in Civil and Structural Engineering; Woodhead Publishing: Cambridge, UK, 2008; pp. 141–157. [Google Scholar]
- Mohamed Ali, M.S.; Oehlers, D.J.; Seracino, R. Vertical Shear Interaction Model between External FRP Transverse Plates and Internal Steel Stirrups. Eng. Struct. 2006, 28, 381–389. [Google Scholar] [CrossRef]
- Chen, G.M.; Teng, J.G.; Chen, J.F.; Rosenboom, O.A. Interaction between Steel Stirrups and Shear-Strengthening FRP Strips in RC Beams. J. Compos. Construct. 2010, 14, 498–509. [Google Scholar] [CrossRef]
- Teng, J.G.; Chen, J.F. Mechanics of Debonding in FRP-Plated RC Beams. Proc. Inst. Civ. Eng. Struct. Build. 2009, 162, 335–345. [Google Scholar] [CrossRef]
- Leung, C.K.Y.; Chen, Z.; Lee, S.; Ng, M.Y.M.; Xu, M.; Tang, J. Effect of Size on the Failure of Geometrically Similar Concrete Beams Strengthened in Shear with FRP Strips. J. Compos. Construct. 2007, 11, 487–496. [Google Scholar] [CrossRef]
- Panda, K.C. Behavior of Reinforced Concrete T-Beams Strengthened in Shear with Glass Fiber Reinforced Polymer. ACI Struct. J. 2006, 103, 339. [Google Scholar]
- Li, W.; Hu, C.; Pan, Z.; Peng, W.; Yang, Y.; Xing, F. A Proposed Strengthening Model Considering Interaction of Concrete-Stirrup-FRP System for RC Beams Shear-Strengthened with EB-FRP Sheets. J. Reinf. Plast. Compos. 2018, 37, 685–700. [Google Scholar] [CrossRef]
- Carolin, A.; Taljsten, B. Theoretical Study of Strengthening for Increased Shear Bearing Capacity. J. Compos. Construct. 2005, 9, 497–506. [Google Scholar] [CrossRef]
- Carolin, A.; Taljsten, B. Experimental Study of Strengthening for Increased Shear Bearing Capacity. J. Compos. Construct. 2005, 9, 488–496. [Google Scholar] [CrossRef]
- Li, A.; Diagana, C.; Delmas, Y. Shear Strengthening Effect by Bonded Composite Fabrics on RC Beams. Compos. Part B Eng. 2002, 33, 225–239. [Google Scholar] [CrossRef]
- Chen, G.M.; Teng, J.G.; Chen, J.F. Process of Debonding in RC Beams Shear-Strengthened with FRP U-Strips or Side Strips. Int. J. Solids Struct. 2012, 49, 1266–1282. [Google Scholar] [CrossRef]
- Grelle, S.V.; Sneed, L.H. Review of Anchorage Systems for Externally Bonded FRP Laminates. Int. J. Concr. Struct. Mater. 2013, 7, 17–33. [Google Scholar] [CrossRef]
- Wang, L.; Dai, L.; Zhang, X.; Zhang, J. Concrete Cracking Prediction Including the Filling Proportion of Strand Corrosion Products. Materials 2016, 10, 6. [Google Scholar] [CrossRef] [PubMed]
- Bossio, A.; Monetta, T.; Bellucci, F.; Lignola, G.P.; Prota, A. Modeling of Concrete Cracking Due to Corrosion Process of Reinforcement Bars. Cem. Concr. Res. 2015, 71, 78–92. [Google Scholar] [CrossRef]
- Forte, A.; Santini, S.; Fiorentino, G.; Lavorato, D.; Bergami, A.V.; Nuti, C. Influence of materials knowledge level on the assessment of the shear strength characteristic value of existing RC beams. In Proceedings of the 12th fib International PhD-Symposium in Civil Engineering, Prague, Czech Republic, 29–31 August 2018. [Google Scholar]
- Lavorato, D.; Bergami, A.V.; Forte, A.; Quaranta, G.; Nuti, C.; Monti, G.; Santini, S. Influence of Materials Knowledge Level on the Assessment of the Characteristic Value of the Shear Strength of Existing RC Beams. In Proceedings of Italian Concrete Days 2016; Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2016; pp. 535–547. [Google Scholar]
- UNI EN 12504-2:2001. Testing Concrete in Structures—Non-Destructive Testing—Determination of Rebound Number; BSI: London, UK, 2001.
- UNI EN 12504-4:2005. Testing Concrete—Part 4: Determination of Ultrasonic Pulse Velocity; Italian Standards: Rome, Italy, 2005.
- RILEM NDT 4 Recommendation for In Situ Concrete Strength Determination by Nondestructive Combined Methods; Compendium of RILEM Technical Recommendations; E&FN Spon: London, UK, 1993.
- NTC 2018. Decreto 17 gennaio 2018. Aggiornamento delle «Norme tecniche per le costruzioni». Gazzetta Ufficiale della Repubblica Italiana. Serie Generale n.42 del 20-02-2018—Suppl. Ordinario n. 8. (In Italian)
- National Research Council. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures; CNR-DT 200 R1/2013; National Research Council: Roma, Italy, 2014. [Google Scholar]
- Féderation Internationale du Béton (FIB). Design and Use of Externally Bonded FRP Reinforcement (FRP-EBR) for Reinforced Concrete Structures; Fib Bulletin 14: Lausanne, Switzerland, 2001. [Google Scholar]
- American Concrete Institute (ACI). ACI440.2R-02 Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 2002. [Google Scholar]
- TR 55. Design Guidance for Strengthening Concrete Structures Using Fibre Composite Materials, 3rd ed.; Technical Report No. 55; The Concrete Society: Lone, UK, 2012. [Google Scholar]
- Eurocode2 Design of Concrete Structures—Part1-1: General Rules and RUles for Buildings; ENV 1992-1-1; European Standards: Brussels, Belgium, 1992.
- Wu, Z.; Yuan, H.; Niu, H. Stress transfer and fracture propagation in different kinds of adhesive joints. J. Eng. Mech. 2002, 128, 562–573. [Google Scholar] [CrossRef]
- Bousselham, A.; Chaallal, O. Maximum Shear Strength of RC Beams Retrofitted in Shear with FRP Composites. J. Compos. Construct. 2009, 13, 302–314. [Google Scholar] [CrossRef]
- Barros, J.A.O.; Dias, S.J.E. Near Surface Mounted CFRP Laminates for Shear Strengthening of Concrete Beams. Cem. Concr. Compos. 2006, 28, 276–292. [Google Scholar] [CrossRef]
- Zhang, Z.; Hsu, C.T.T. Shear Strengthening of Reinforced Concrete Beams Using Carbon-Fiber-Reinforced Polymer Laminates. J. Compos. Construct. 2005, 9, 158–169. [Google Scholar] [CrossRef]
- Guadagnini, M.; Pilakoutas, K.; Waldron, P. Shear Resistance of FRP RC Beams: Experimental Study. J. Compos. Construct. 2006, 10, 464–473. [Google Scholar] [CrossRef]
- Adhikary, B.B.; Mutsuyoshi, H. Behavior of concrete beams strengthened in shear with carbon-fiber sheets. J. Compos. Construct. 2004, 8, 258–264. [Google Scholar] [CrossRef]
- Garcez, M.; Meneghetti, L.; da Silva Filho, P.; Carlos, L. Structural Performance of RC Beams Post strengthened with Carbon, Aramid, and Glass FRP Systems. J. Compos. Construct. 2008, 12, 522–530. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).