Numerical Analysis for Thermal Performance of a Photovoltaic Thermal Solar Collector with SiO₂-Water Nanofluid

Abstract

Numerical analysis of a photovoltaic-thermal (PV/T) unit with SiO${}_2$-water nanofluid was performed. The coupled heat conduction equations within the layers and convective heat transfer equations within the channel of the module were solved by using the finite volume method. Effects of various particle shapes, solid volume fractions, water inlet temperature, solar irradiation and wind speed on the thermal and PV efficiency of the unit were analyzed. Correlation for the efficiencies were obtained by using radial basis function neural networks. Cylindrical shape particles were found to give best performance in terms of efficiency enhancements. Total efficiency enhances by about 7.39% at the highest volume fraction with cylindrical shape particles. Cylindrical shape particle gives 3.95% more enhancement as compared to spherical ones for the highest value of solid particle volume fraction. Thermal and total efficiency enhance for higher values of solid particle volume fraction, solar irradiation and lower values of convective heat transfer coefficient and inlet temperature. The performance characteristics of solar PV-thermal unit with radial basis function artificial neural network are found to be in excellent agreement with the results obtained from computational fluid dynamics modeling.

1. Introduction

Nanofluids are composed of base fluid such as water, ethylene glycol or mineral oil and added solid nano-sized particles. They have been extensively used in different thermal engineering applications [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. The nano-sized particle could be metallic or non-metallic such as Cu, Ag, CuO, Al${}_2$O${}_3$, TiO${}_2$, SiO${}_2$ with average particle size less than 100 nm. Higher thermal conductivity of the nanoparticles increase the thermal conductivity of the heat transfer fluid and enhances the thermal performance. Size, shape and type of the particles are effective for the thermal conductivity enhancement of nanofluids. Thermophysical properties are derived from theoretical or experimental studies for nanofluids containing various particle types, shapes and sizes for different temperatures. Generally, a small amount of particle addition of the base fluid results in higher heat transfer enhancements. Application of the nanofluids for the thermal engineering systems are diverse such as in refrigeration, microelectromechanical systems (MEMs), cooling of nuclear reactors, thermal management of fuel cells, cooling of hydrogen storage, heat exchangers and many others. In the refrigeration application, nano additives are added to compressor oil to increase the coefficient of performance. In some applications, solid nano particles are added to the refrigerants. In heat exchanger design, more compact and lightweight structures can be designed when heat transfer fluid has a higher thermal conductivity with the addition of nanoparticles.

Application of nanotechnology in the field of renewable energy is growing. There are many studies related to the nanofluids application in solar power. A review for the application of the nanofluid in solar energy was presented in the study by Mahian et al. [15]. Using nanofluids in solar collectors and solar water heaters and their impacts on the efficiency and environmental effects were also discussed. Mahian et al. [16] performed analytical study for the performance of a solar collector with various types of nanofluids such as Cu/water, Al${}_2$O${}_3$/water, TiO${}_2$/water, and SiO${}_2$/water nanofluids with particle size of 25 nm. System with Cu/water nanofluid has lowest entropy generation rate whereas Al${}_2$O${}_3$/water nanofluid has the highest heat transfer coefficient as compared to other nanofluids. In the study by Meibodi et al. [17], an experimental investigation was performed for a flat plate solar collector with SiO${}_2$/ethylene glycol (EG-water nanofluid. Various mass flow rates and particle volume fraction up to 1% were tested. It was observed that, despite the low conductivity of SiO${}_2$ nanoparticles, solar collector efficiency was found to be enhanced with nanofluid. Chen et al. [18] studied the effects of inclusion of Au nanoparticles for the photo-thermal conversion performance numerically and experimentally for various solar intensities and particle volume fractions. The absorption efficiency was found to increase with higher nanoparticle volume fractions. Effects of SiO${}_2$ nanoparticles in solar collector tubes were numerically and experimentally studied by Yan et al. [19]. Heat transfer rate was found to be higher for nanofluid and, due to nanofluid agglomeration, the heat transfer rate deteriorates for longer operation times.

In the Photovoltaic/Thermal modules (PV/T), heat and electricity are produced by using photovoltaic and heat extraction units. A review study for the application of nanofluids in PV/T systems and discussions about effective parameters and effectiveness of nanofluids were presented in [20]. Al-Waeli et al. [21] performed an experimental study for the determination of effective thermophyscial properties of water containing SiC nanoparticles that was used as a cooler for PV/T system. It was observed that thermal conductivity enhancements are about 8.2% for the temperature range of 25–60 ${}^{\circ }$C. The electrical efficiency with 3 wt % of SiC nanofluid results in electrical efficiency enhancements of 24.1% and it was observed that the nanofluids were stable for long use. In the study by Hassani et al. [22], a new cascade PV/T module was proposed with separate channels. Two nanofluids were used to enhance the electrical and thermal performance of the PV/T module. Jing et al. [23] investigated the effects of silica/water nanofluids on the efficiency of PV/T module. Various sizes of nanoparticles, concentrations and flow velocity were considered. Optimum operational parameters for the economical considerations were also obtained.

In the present study, efficiency of a PV/T module with SiO${}_2$-water nanofluid was numerically investigated for nanoparticle properties (shape, volume fraction) and for different operating conditions. Despite the low conductivity of SiO${}_2$ nanoparticles as compared to other particles, its low cost, favorable physical and chemical properties makes it attractive for usage with water. Artificial neural networks with radial basis functions are used to obtain the correlations for efficiencies of PV-thermal module.

2. Mathematical Modeling

Figure 1 shows a schematic representation of a PV-thermal module which is composed of several layers and a channel in which SiO${}_2$-water nanofluid is flowing throughout. Thermophysical properties of the layers in the PV-thermal module is given in Table 1.

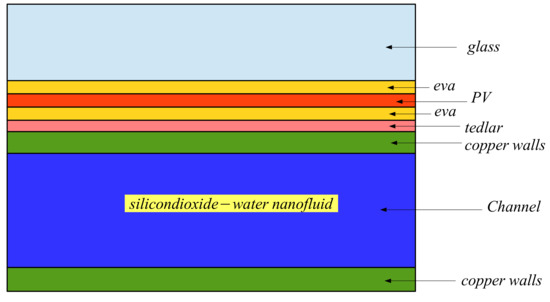
Figure 1. Schematic representation of the layers in the PV-thermal module.

Table 1. Thermophysical properties of layers of the PV-thermal module.

Name	Thickness (mm)	Density (kg/m${}^3$)	Thermal Conductivity (W/m K)	Heat Capacity (J/kg K)
glass	3.2	2515	0.98	820
eva	0.45	960	0.31	2090
PV	0.2	2330	150	712
tedlar	0.35	1162	0.23	1465
aluminum	1	2700	160	900

An energy balance between the solar irradiance and heat transfer to the heat transfer fluid with nanoparticles is considered. Within the layers of the PV-module, the heat conduction equation is used.

Within the layers of the PV-thermal module steady state, the heat conduction equation is valid and is given by the following equation:

$$\nabla .\left(k_{layer}\nabla T\right)=0.$$

(1)

Navier–Stokes and energy equations for the fluid flow and heat transfer in the channel are given by the following equations:

$$\nabla .\left(\mathbf{u}\right)=\mathbf{0},$$

(2)

$$\rho \mathbf{u}.\nabla \mathbf{u}=-\nabla p+\mu {\nabla }^2\mathbf{u},$$

(3)

$$\rho c_p\mathbf{u}.\nabla T=\nabla .\left(k\nabla T\right).$$

(4)

The PV cell electrical efficiency is given by the following equation:

$${\eta }_{pv}={\eta }_{T_{ref}}\left[1-{\beta }_{ref}\left(T_{pv}-T_{ref}\right)\right].$$

(5)

Thermal efficiency is defined as the ratio of the energy gained by the collector divided by the total incident energy

$${\eta }_{th}=\frac{\dot{m}{c}_p\left(T_{out}-T_{in}\right)}{G}.$$

(6)

• For the upper surface, the heat flux boundary condition with incident radiation and convective heat loss due to wind (heat transfer coefficient h and wind speed are related) is considered:
  $q^{\prime }=q-hA(T_{upper}-T_{\infty }).$
• Among the layers of of the PV-module, heat flux continuity is utilized, $q_{layer,n+1}=q_{layer,n}.$
• At the inlet of the channel, temperature and velocity are uniform, $u=u_0,v=0,T=T_c$.
• At the exit of the channel, gradients in the x-direction are set to zero, $\frac{\partial u}{\partial x}=0,\frac{\partial v}{\partial x}=0,\frac{\partial T}{\partial x}=0.$

2.1. Nanofluid Thermophysical Properties

SiO${}_2$-water nanofluid was used in this study and the thermo-physical properties are given in Table 2 [24]. The effective density, specific heat, thermal expansion coefficient of the nanofluid are given by the following formulas:

$${\rho }_{nf}=(1-\varphi ){\rho }_f+\varphi {\rho }_p,$$

(7)

$${\left(\rho c_p\right)}_{nf}=(1-\varphi ){\left(\rho c_p\right)}_f+\varphi {\left(\rho c_p\right)}_p,$$

(8)

$${\left(\rho \beta \right)}_{nf}=(1-\varphi ){\left(\rho \beta \right)}_f+\varphi {\left(\rho \beta \right)}_p,$$

(9)

where the subscripts f, $nf$ and p denote the base fluid, nanofluid and solid particle, respectively.

Table 2. Thermophysical properties of base fluid and SiO${}_2$ nanoparticle [28].

Property	Water	SiO${}_2$
$\rho (\mathrm{kg}/{\mathrm{m}}^3)$	998.2	2200
${\mathrm{c}}_p(\mathrm{J}/\mathrm{kg}\mathrm{K})$	4812	703
$\mathrm{k}(\mathrm{W}/\mathrm{mK})$	0.61	1.2
$\mu (\mathrm{N}\mathrm{s}/{\mathrm{m}}^2)$	0.001003	-

The effective thermal conductivity of the nanofluid includes the effect of Brownian motion. In this model, the effects of particle size, particle volume fraction and temperature dependence are taken into account and it is given by the following formula [25]:

$$k_{nf}=k_{st}+k_{Brownian},$$

(10)

where $k_{st}$ is the static thermal conductivity as given by [26]

$$k_{st}=k_f\left[\frac{(k_p+2k_f)-2\varphi (k_f-k_p)}{(k_p+2k_f)+\varphi (k_f-k_p)}\right].$$

(11)

The interaction between the nanoparticles and the effect of temperature are included in the models as

$$k_{Brownian}=5\times {10}^4\times 1.9526\times {\left(100\varphi \right)}^{-1.4594}\varphi {\rho }_f{c}_{p,f}\sqrt{\frac{{\kappa }_{b}T}{{\rho }_p{d}_p}}{f}^{\prime }(T,\varphi ),$$

(12)

where the function $f^{\prime }$ is given in [25].

The effective viscosity model of the nanofluid was given in [27]

$${\mu }_{nf}={\mu }_f\frac{1}{\left(1-34.87{\left(\frac{d_p}{d_f}\right)}^{-0.3}{\varphi }^{1.03}\right)},$$

(13)

where the average particle size of the fluid is given as [27]:

$$d_f={\left(\frac{6M}{N\pi {\rho }_f}\right)}^{1/3},$$

(14)

with M and N denoting the molecular weight and Avogadro number.

2.2. Nanoparticle Shape Effect

The above given correlations in Equations (10)–(14) are used for the description of effective thermal conductivity for spherical particles. The effective thermal conductivity and viscosity of the nanofluid using non-spherical nanoparticle shape are defined using the following formulas:

$$k_{nf}=k_f\left(1+C_k\varphi \right),{\mu }_{nf}={\mu }_f\left(1+A_1\varphi +A_2{\varphi }^2\right),$$

(15)

where the constant coefficients for different nanoparticle shapes are defined as in Table 3 [28,29].

Table 3. Constant coefficients for the effect of nanoparticle shape to the thermal conductivity and viscosity of the nanofluid [28,29].

Nanoparticle Type	C${}_{\mathit{k}}$	A${}_1$	A${}_2$
cylindrical	3.95	13.5	904.4
bricks	3.37	1.9	471.4
blades	2.74	14.6	123.3

2.3. Solution Method

The finite volume method was used to solve the governing equations along with the boundary conditions. A general convection-diffusion equation for a scalar transport variable $\mathsf{\Psi }$ has the following form:

$$\nabla .\left(\rho \mathbf{u}\mathsf{\Psi }\right)=\nabla .\left(\Gamma \nabla \mathsf{\Psi }\right)+b$$

(16)

for velocity $\mathit{u}$, source term b and diffusion coefficient $\Gamma$. Integration of the PDE over a control volume and using Gauss divergence theorem yields:

$${\int }_A\left(\mathbf{n}\right).\left(\rho \mathbf{u}\mathsf{\Psi }\right)dA={\int }_A\left(\mathbf{n}\right).\left(\Gamma \nabla \mathsf{\Psi }\right)dA+{\int }_{CV}bdV.$$

(17)

After using suitable discretization schemes for convective and diffusion terms, the resulting algebraic equation at the node point p surrounded by neighboring relevant nodes (subscript n) is written as:

$$a_p{\varphi }_p=\sum a_n{\varphi }_n+s.$$

(18)

A QUICK scheme is used to discretize the convective terms in the momentum and energy equations while a SIMPLE algorithm is used for velocity–pressure coupling. The resulting system of algebraic equations was solved using the Gauss–Siedel point-by-point iterative method and algebraic multigrid method. The normalized residual is calculated as:

$$R^{\varphi }=\frac{{\sum }_{allcells}|a_p{\varphi }_p-a_n{\varphi }_n-s|}{{\sum }_{allcells}\left|a_p{\varphi }_p\right|}.$$

(19)

When the residuals for all dependent variables become less than 10${}^{-5}$, an iterative solution is stopped. Under-relaxation factors are used to enhance the converge speed of the solution and the under-relaxation parameters for u, v, and T are all set to 0.6, whereas the under-relaxation parameter for pressure correction is set to 0.32.

2.4. Grid Independence and Code Validation

The grid independent test for various numbers of elements was performed. High gradients in the boundary layers are resolved by using finer meshes near the walls.Thermal efficiency and PV efficiency for different number of elements are demonstrated in Table 4. G3 with 66,056 triangular elements are used in the subsequent computations. Validation of the present code is performed by using the numerical results of [30]. Forced convection in a cavity was considered at Reynolds number of 500. The comparison results for the local Nusselt number distribution along the walls of the cavity are shown in Figure 2.

Table 4. Grid independence test (q = 1000 W/m${}^2$, h = 5 W/m${}^2$K, $\varphi =0.05$, $T_{i}n$ = 30 ${}^{\circ }$C).

Grid Name	Number of Elements	Thermal Efficiency (%)	PV Efficiency (%)
G1	10,816	50.32	12.52
G2	19,457	48.25	12.50
G3	66,056	47.20	12.49
G4	144,934	47.13	12.49

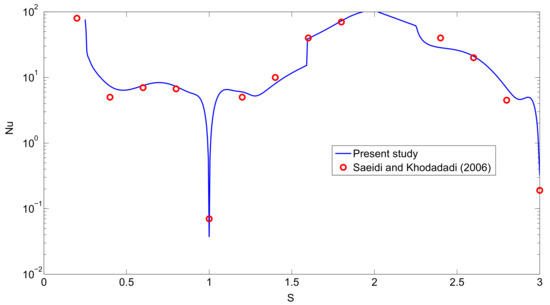
Figure 2. Code validation study.

3. Results and Discussion

Effects of nanoparticle addition to the water in the channel of a PV-thermal module on the thermal and PV-efficiency was numerically investigated. SiO${}_2$ nanoparticles different shapes and solid particle volume fractions were used. Figure 3 shows the velocity and temperature distribution in the PV-module. In the channel, a laminar velocity profile is developed and its maximum value is seen in the mid of the channel which has a value of 0.025 m/s for the fixed value of (q = 1000 W /m${}^2$, h = 5 W /m${}^2$ K, $\varphi =0.02$ with cylindrical shape particles). For this flow velocity, Reynolds number remains less than 2100 in the channel. Thermal gradients are seen in the layers of the PV module, which is due to the different thicknesses and thermal conductivities of these layers.

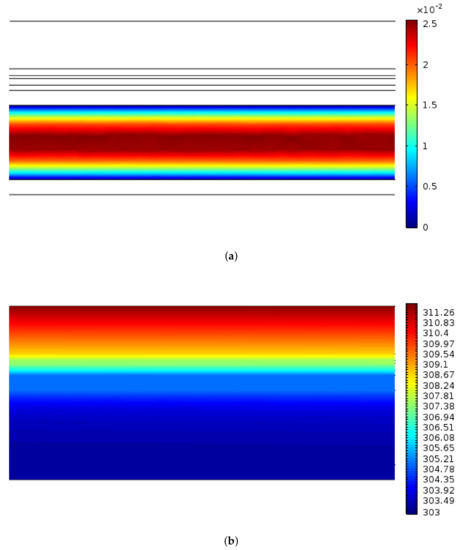
Figure 3. Velocity field (a) and temperature (b) in the Photovoltaic-thermal module module, (q = 1000 W/m${}^2$, h = 5 W/m${}^2$K, $\varphi =0.02$, cylindrical shape).

Figure 4 shows the effects of nanoparticle volume fraction ($\varphi$) and particle type on the variation of thermal and total efficiency of the PV-thermal module. Both efficiencies enhance with higher $\varphi$ values. Among different particle shapes, cylindrical ones perform best. Discrepancy between cylindrical shape and other shapes increases for higher particle volume fractions. Total efficiency increases by about 7.39% at the highest volume fraction ($\varphi =0.05$) with cylindrical shape particles. As compared to spherical shape particle, cylindrical ones gives 3.95% more enhancement in the total efficiency for the highest particle volume fraction.

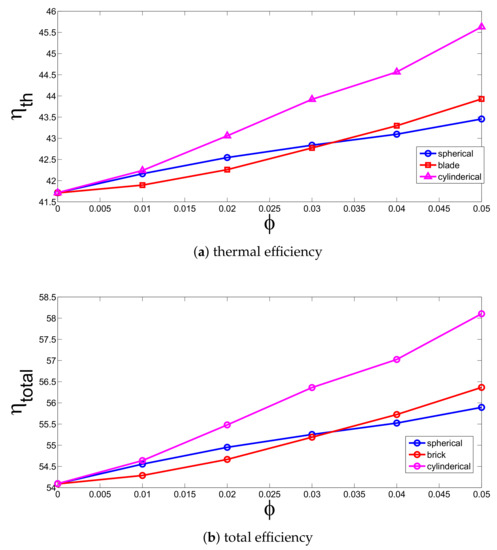
Figure 4. Effects of the particle shape and solid volume fraction on the variation of efficiencies (q = 1000 W/m${}^2$, h = 5 W/m${}^2$K, $T_{i}n$ = 30 ${}^{\circ }$C)

As the inlet temperature of water-SiO${}_2$ nanofluid increases, thermal and total efficiency deteriorate as shown in Figure 5. The rate of deterioration is higher for the thermal efficiency and up to 40% in the reduction of the efficiency is seen when nanofluid temperature is increased from 10 ${}^{\circ }$C to 50 ${}^{\circ }$C.

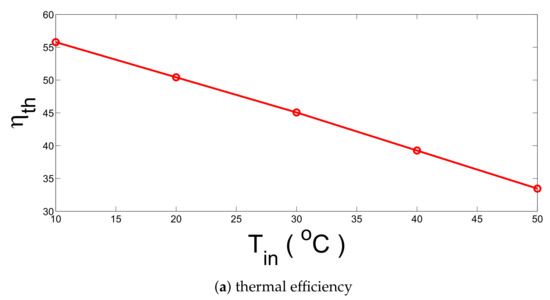
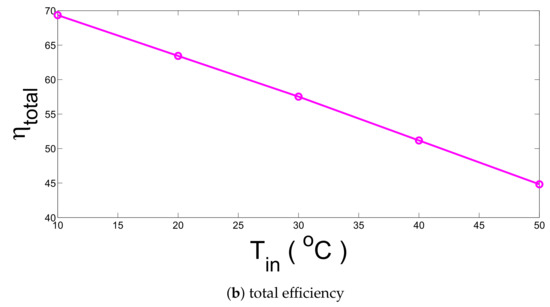
Figure 5. Effects of the inlet temperature on the variation of efficiencies (q = 1000 W/m${}^2$, h = 5 W/m${}^2$K, $\varphi =0.02$, cylindrical shape).

Figure 6 demonstrates the effects of solar irradiation and solid nanoparticles volume faction on the variation of efficiencies (h = 5 W /m${}^2$ K, T${}_{in}$ = 30 ${}^{\circ }$C with cylindrical shape particles). Thermal efficiency increases with higher values of solar irradiation while the PV-efficiency decreases and higher efficiency values are achieved for higher $\varphi$ values. Higher surface temperature is obtained for higher values of solar irradiation and PV-efficiency decreases, which are defined in Equation (5). Thermal efficiency increases by about 9.17% and 9.82% for water and for nanofluid with highest volume fraction. There is a negligible effect of the particle addition on the PV-efficiency enhancements.

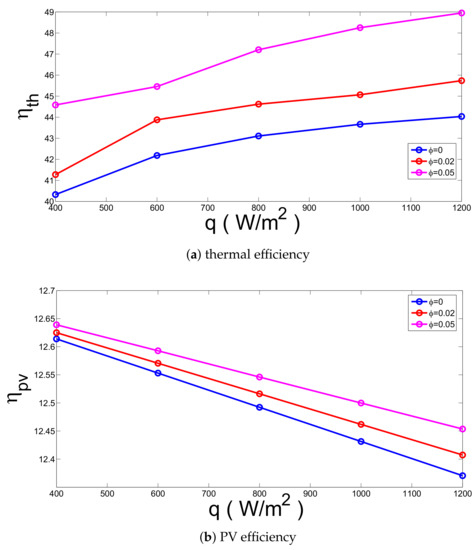
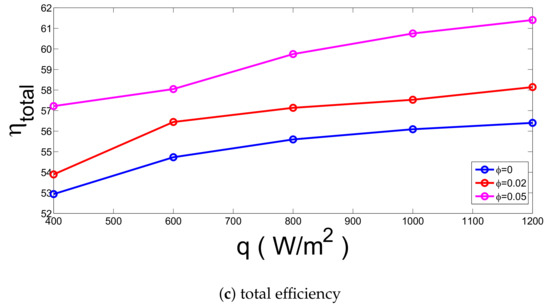
Figure 6. Effects of the solar radiation on the variation of efficiencies for various solid particle volume fraction (h = 5 W/m${}^2$K, $T_{i}n$ = 30 ${}^{\circ }$C, cylindrical shape ).

Convective loss is characterized by the convective heat transfer coefficient dependent upon the wind speed v. As the value of heat transfer coefficient enhances, thermal efficiency decreases as it is shown in Figure 7 and Figure 8. However, PV-efficiency enhances with higher h values since the PV-layer surface temperature decreases, but the rate of enhancement is not significant.The discrepancy between thermal efficiency for heat transfer coefficient of h = 5 W /m${}^2$ K and h = 10 W /m${}^2$ K is 12.5% and 9.28% for water and for nanofluid with $\varphi =0.05$. Adding nanoparticle results in higher thermal efficiency enhancement for the highest value of heat transfer coefficient, which is 11.11% with the highest volume fraction of cylindrical particles.

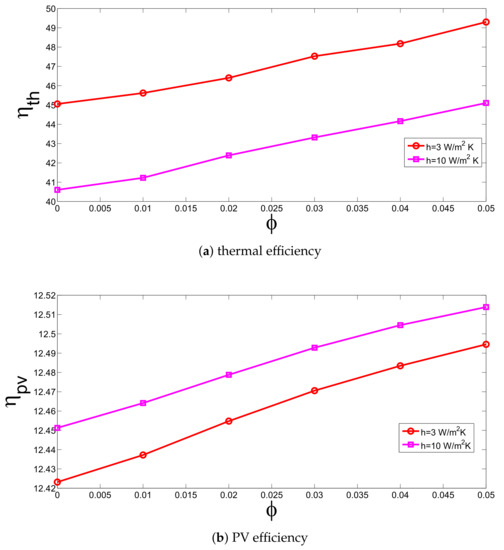
Figure 7. Efficiency versus solid particle volume fraction for two values of external heat transfer coefficient (q = 1000 W/m${}^2$, $T_{in}$ = 30 ${}^{\circ }$C, cylindrical shape).

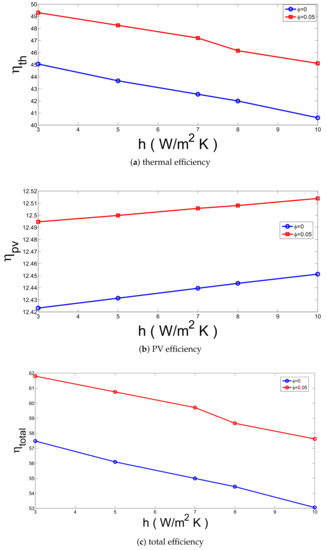
Figure 8. Efficiency versus external heat transfer coefficient for two values of nanoparticle volume concentration (q = 1000 W/m${}^2$, $T_{in}$ = 30 ${}^{\circ }$C, cylindrical shape).

3.1. Efficiency Correlation with Artificial Neural Networks

Artificial neural networks (ANN) or other practical prediction methods can be used to obtain the correlations for efficiencies of PV-thermal module or thermal engineering systems [31,32,33,34,35,36,37,38,39,40,41]. Radial basis function networks consist of three-layer network structures that include input, hidden and output layers. The hidden layer nodes are radial basis functions. The outputs are calculated by a weighted average sum of the radial basis functions, which can be given as [37]:

$$y\left(x_i\right)=\sum _{k=1}^N{w}_k\mathsf{\Psi }\left(\left|\right|x_i-d_k\left|\right|\right)+b.$$

(20)

Radial basis function response decreases monotonically from a center point with distance. Gaussian function is a radial basis function which has central point c and smoothness parameter $\sigma$ which controls the shape of the function. It is given in the following form:

$$f\left(x\right)=e^{\left(-{(x-c)}^2/{\sigma }^2\right)}.$$

(21)

A schematic representation of network topology is given in Figure 9 with three inputs: (solid particle volume fraction ($\varphi$), convective heat transfer coefficient (h) and solar irradiation (q)) and two outputs (thermal and PV-efficiency).

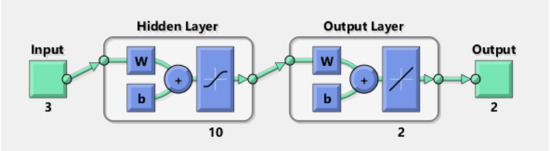
Figure 9. Schematic representation of the layers in the PV-thermal module.

In order to evaluate the performance of trained networks, different error measures can be used. Mean square error (MSE) and coefficient of determination ($R^2$) performance parameters can be given as:

$$\mathrm{MSE}=\frac{1}{N}\sum _{k=1}^N{(y^{CFD}-y_k^{ANN})}^2,$$

(22)

$$R^2=1-\frac{{\sum }_{k=1}^N{(y_k^{CFD}-y_k^{ANN})}^2}{{\sum }_{k=1}^N{(y_k^{CFD}-\overline{y})}^2},$$

(23)

where $y_k^{ANN}$, $y_k^{CFD}$, N and $\overline{y}$ represent the predicted value form ANN, CFD value, sample number and the mean value of CFD values, respectively.

The MATLAB Neural Network Toolbox (Version 2010, The Mathworks, Natick, USA) was used to select the number of hidden layers, number of neurons in each layer, training algorithm [42]. Feed-forward network structure with one hidden layer and a linear output layer was selected. The number of the neurons of ANN model was taken as 10. The feed-forward network structure with hidden layers and the linear output layer was selected and Levenberg–Marquardt back-propagation was used as the training algorithm. The random data division property of MATLAB is used and $70\%$ of the data was used for estimation while $15\%$ was used for validation and $15\%$ of the data was used for testing purposes. Table 5 shows the number of samples for training, validation and testing, mean squared error (MSE) values and regression R values. A higher R value denotes a higher correlation between the outputs and target values.

Table 5. Number of samples, mean square error (MSE) and correlation coefficients in the artificial neural network (ANN) modeling.

	Number of Samples	MSE	R
Training	378	3.89 $\times {10}^{-6}$	0.99992
Validation	81	4.60 $\times {10}^{-6}$	0.99991
Testing	81	3.53 $\times {10}^{-6}$	0.99993

Table 6 represents the comparison results of CFD data between the predicted data by artificial neural networks for various values of pertinent parameters. The difference between the actual CFD data and established artificial neural network model is very small. This modeling strategy with ANN is useful for this system in order to obtain the performance predictions of a PV-thermal module in a fast and cheap way as compared to a high fidelity CFD computation, but it still requires some of the data from CFD computations for training.

Table 6. Performance predictions of solar PV-thermal module with ANN.

$\mathit{\varphi }$	h (W/m${}^2$K)	q (W/m${}^2$)	${\mathit{\eta }}_{\mathit{thermal}}$ (CFD)	${\mathit{\eta }}_{\mathit{thermal}}$ (ANN)	${\mathit{\eta }}_{\mathit{PV}}$ (CFD)	${\mathit{\eta }}_{\mathit{PV}}$ (ANN)
0	3	400	41.716	41.953	12.609	12.594
0	3	800	44.497	44.436	12.485	12.444
0	3	1200	45.424	45.31	12.361	12.408
0	4	700	43.305	43.281	12.519	12.507
0	4	1100	44.497	44.576	12.397	12.417
0	5	600	42.18	41.973	12.553	12.557
0	5	1000	43.663	43.636	12.431	12.454
0	6	500	40.604	40.399	12.586	12.593
0	6	900	42.952	42.708	12.465	12.479
0	7	400	38.24	38.28	12.619	12.63
0	7	800	41.716	41.797	12.499	12.491
0	7	1200	42.875	42.967	12.38	12.417
0	8	700	40.524	40.696	12.532	12.527
0	8	1100	42.222	42.148	12.414	12.427
0.015	3	400	42.47	42.85	12.617	12.606
0.015	3	800	45.365	45.387	12.503	12.478
0.015	3	1200	46.33	46.291	12.389	12.379
0.015	4	700	44.124	44.235	12.535	12.529
0.015	4	1100	45.629	45.532	12.421	12.427
0.015	5	600	43.113	42.926	12.566	12.568
0.015	5	1000	44.786	44.604	12.454	12.46
0.015	6	500	41.697	41.235	12.596	12.601
0.015	6	900	43.757	43.674	12.485	12.477
0.015	7	400	38.609	38.995	12.626	12.634
0.015	7	800	42.47	42.634	12.516	12.513
0.015	7	1200	43.757	43.799	12.406	12.424
0.015	8	700	41.367	41.526	12.547	12.539
0.015	8	1100	43.172	42.991	12.437	12.44
0.02	3	600	44.62	44.91	12.565	12.555
0.02	3	1000	46.404	46.344	12.455	12.428
0.02	4	500	43.727	43.395	12.595	12.589
0.02	4	900	45.611	45.438	12.486	12.479
0.02	5	400	41.273	41.261	12.625	12.623
0.02	5	800	44.62	44.356	12.516	12.52
0.02	5	1200	45.363	45.515	12.408	12.421
0.02	6	700	43.345	43.185	12.546	12.56
0.02	6	1100	44.62	44.647	12.438	12.434
0.02	7	600	41.645	41.829	12.576	12.579
0.02	7	1000	43.727	43.765	12.469	12.456
0.02	8	500	40.158	39.914	12.605	12.598
0.02	8	900	42.637	42.828	12.499	12.493
0.025	3	400	44.038	43.705	12.624	12.61
0.025	3	800	45.981	46.237	12.516	12.501
0.025	3	1200	47.06	47.149	12.409	12.386
0.025	4	700	45.148	45.11	12.546	12.551
0.025	4	1100	46.158	46.375	12.44	12.443
0.025	5	600	44.038	43.801	12.575	12.583
0.025	5	1000	45.593	45.517	12.47	12.464
0.025	6	500	42.484	42.021	12.604	12.608
0.025	6	900	44.326	44.522	12.499	12.495
0.025	7	400	40.153	39.743	12.632	12.639
0.025	7	800	43.391	43.495	12.528	12.526
0.025	7	1200	44.902	44.648	12.425	12.435
0.025	8	700	42.188	42.4	12.557	12.542
0.025	8	1100	43.803	43.829	12.454	12.458
0.035	3	400	45.282	44.557	12.629	12.617
0.035	3	800	47.023	47.139	12.528	12.527
0.035	3	1200	48.184	48.136	12.427	12.414
0.035	4	700	45.779	46.11	12.556	12.573
0.035	4	1100	47.498	47.371	12.455	12.447
0.035	5	600	45.282	44.79	12.583	12.592
0.035	5	1000	46.675	46.538	12.484	12.479
0.035	6	500	43.192	42.898	12.61	12.614
0.035	6	900	45.669	45.523	12.512	12.514
0.035	7	400	40.057	40.62	12.637	12.642
0.035	7	800	44.411	44.556	12.539	12.532
0.035	7	1200	45.862	45.682	12.441	12.452
0.035	8	700	42.794	43.424	12.566	12.545
0.035	8	1100	44.965	44.845	12.469	12.475
0.04	3	600	46.84	46.837	12.582	12.58
0.04	3	1000	48.178	48.229	12.483	12.472
0.04	4	500	44.966	45.202	12.609	12.608
0.04	4	900	47.286	47.305	12.511	12.528
0.04	5	400	42.156	42.872	12.636	12.641
0.04	5	800	46.171	46.335	12.538	12.558
0.04	5	1200	47.509	47.53	12.441	12.434
0.04	6	700	44.737	45.254	12.565	12.563
0.04	6	1100	46.718	46.678	12.469	12.467
0.04	7	600	44.163	43.741	12.591	12.572
0.04	7	1000	45.769	45.72	12.496	12.501
0.04	8	500	41.755	41.638	12.617	12.596
0.04	8	900	44.61	44.85	12.523	12.524
0.045	3	400	46.023	45.272	12.634	12.622
0.045	3	800	48.324	48.05	12.537	12.549
0.045	3	1200	49.092	49.222	12.441	12.43
0.045	4	700	47.338	47.102	12.564	12.579
0.045	4	1100	48.534	48.38	12.468	12.454
0.045	5	600	46.023	45.742	12.59	12.595
0.045	5	1000	47.864	47.522	12.495	12.499
0.045	6	500	44.182	43.729	12.616	12.617
0.045	6	900	46.023	46.579	12.521	12.526
0.045	7	400	41.421	41.485	12.641	12.641
0.045	7	800	46.023	45.646	12.548	12.536
0.045	7	1200	46.79	46.784	12.455	12.466
0.045	8	700	44.708	44.436	12.574	12.549
0.045	8	1100	46.023	45.908	12.481	12.495
0.05	3	600	47.203	47.64	12.589	12.58
0.05	3	1000	49.301	49.157	12.495	12.499
0.05	4	500	46.154	45.935	12.614	12.613
0.05	4	900	47.786	48.193	12.521	12.538
0.05	5	400	44.581	43.556	12.639	12.647
0.05	5	800	47.203	47.351	12.547	12.554
0.05	5	1200	48.078	48.497	12.454	12.449
0.05	6	700	46.454	46.239	12.572	12.558
0.05	6	1100	47.68	47.661	12.48	12.488
0.05	7	600	45.455	44.587	12.597	12.573
0.05	7	1000	47.203	46.745	12.506	12.518
0.05	8	500	41.959	42.418	12.622	12.602
0.05	8	900	45.455	45.935	12.531	12.531

4. Conclusions

In this study, a numerical simulation of a PV-thermal module with SiO${}_2$-water nanofluid was performed. It was observed that cylindrical shape particles give the best performance in terms of efficiency enhancement. Total PV/T module efficiency enhances by about 7.39% at the highest volume fraction with cylindrical shape particles. As compared to spherical ones, up to 4% more in the efficiency enhancement was observed with cylindrical shape particles. Thermal and total efficiency increase for higher solid particle volume fraction, higher values of solar irradiation, lower values of convective heat transfer coefficient and inlet temperature. Adding nanoparticles is advantageous for the case where convective heat transfer coefficient is high. Finally, correlation based on radial basis artificial neural networks was obtained for thermal and PV-efficiency of the PV-thermal module. The performance characteristics of solar PV-thermal module with ANN are compared with those obtained using the CFD modeling and have been to be in excellent agreement.