Featured Application
high mobility transistors.
Abstract
The metal-insulator transition (MIT) in two-dimension (2D) was discovered by Kravchenko et al. more than two decades ago in strongly interacting 2D electrons residing in a Si-metal-oxide-semiconductor field-effect transistor (Si-MOSFET). Its origin remains unresolved. Recently, low magnetic field reentrant insulating phases (RIPs), which dwell between the zero-field (B = 0) metallic state and the integer quantum Hall (QH) states where the Landau-level filling factor υ > 1, have been observed in strongly correlated 2D GaAs hole systems with a large interaction parameter, rs, (~20–40) and a high purity. A new complex phase diagram was proposed, which includes zero-field MIT, low magnetic field RIPs, integer QH states, fractional QH states, high field RIPs and insulating phases (HFIPs) with υ < 1 in which the insulating phases are explained by the formation of a Wigner crystal. Furthermore, evidence of new intermediate phases was reported. This review article serves the purpose of summarizing those recent experimental findings and theoretical endeavors to foster future research efforts.
1. Introduction
Tremendous knowledge from more than fifty years of research has been accumulated regarding the transport behavior of electrons in a variety of two-dimension (2D) materials and systems. It has regained strong interest in the field of physics and material science due to the recent discoveries of topological insulators [2] and new 2D materials [3].
With different types and strengths of interactions, many fascinating phenomena can emerge at various temperatures and energy scales, such as the Fermi liquid, the Wigner crystal [4], the integer quantum Hall (QH) effect [5], and the fractional QH effect [6]. The scaling theory of localization for noninteracting 2D systems [7] predicts that the electronic states are localized while the temperature T approaches zero. In a low density and high mobility Si-metal-oxide-semiconductor field-effect transistor (Si-MOSFET), however, a metal-insulator transition (MIT) was observed by Kravchenko [1]. This implies that strong correlation effects play a key role in the MIT [8,9], as the value of rs (the ratio between the Coulomb energy and the kinetic energy, is the effective Bohr radius) is much greater than one.
In this brief review, we will first introduce and focus on the recently discovered low magnetic field reentrant insulating phases (RIPs) in high quality GaAs 2D systems [10,11,12,13] with a new phase diagram, which connects the zero-field MIT with RIPs, integer QH states, fractional QH states, and high magnetic field insulating phases [14]. Resistivity, capacitance and inductance measurements exploring the RIPs and phase diagram are presented and discussed in the context of the transition between a 2D electron liquid and a Wigner crystal (WC), an ordered solid phase of electrons or holes whose formation is driven by the minimization of strong Coulomb interactions in an electronic system with a high enough rs. Secondly, experimental observations of a possible Wigner crystal melting and new intermediate phases are shown and examined. Finally, relevant theoretical models that try to explain the MIT are briefly discussed.
2. New Reentrant Insulating Phases at Low Magnetic Fields
Perpendicular magnetic field induced insulating phases in 2D electron systems were intensively studied back in the 1990’s [14]. While many of these early studies reported insulating phases at a Landau-level filling factor υ < 1 (mainly in GaAs based 2D systems [14]), insulating phases at υ > 1 were also reported in Si-MOSFETs [15]. Recently, a new reentrant insulating phase at a Landau-level filling factor υ > 1 was discovered by Qiu et al. [10,11] in ultra clean GaAs quantum well samples with low carrier densities and it was suggested that this RIP at υ > 1 evolved from the RIPs at υ < 1 in the GaAs samples with higher carrier densities as reported in the 1990’s [14]. Figure 1 is taken from Reference [10], which shows the observed phase diagram at 150, 80 and 50 mK.
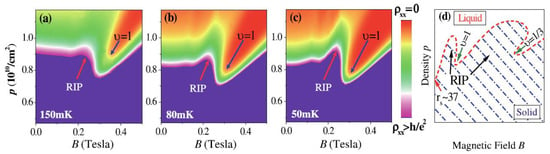
Figure 1.
Longitudinal resistivity map plotted for the density (p)—magnetic field (B) plane at T = 150 (a), 80 (b) and 50 (c) mK for dilute 2D holes in a 10 nm wide high mobility GaAs quantum well. The reentrant insulating phases (RIP) phase () becomes more prominent at a lower temperature. (d) The proposed phase diagram includes the metal-insulator transition (MIT), RIP, integer and fractional quantum Hall (QH) states. Figure was adapted from Reference [10].
The formation of a WC was widely believed to be the origin of the high field insulating phases (HFIP) and RIPs where the Landau-level filling factor υ < 1 [14]. Experiment evidence was given from transport, thermodynamic compressibility, and microwave transmission measurements [14]. In a recent study, Reference [16] observed a tunneling resonance feature that was attributed to the vibrations of a WC. However, theoretically, a liquid-WC transition was predicted to appear both at B = 0 and υ > 1 around rs ~ 30–40 [17,18], which had not been shown in experimental measurements until the study in Reference [10]. Therefore, the observation of the new RIP in Reference [10] provided a phase diagram consistent with the theory [18], which further suggested that the zero-field MIT is a liquid-WC transition.
Later, the existence of low field RIPs (υ > 1) was confirmed by Knighton [12,13], see Figure 2 adopted from Reference [12]. Moreover, three RIPs were observed, which are seen between υ = 1, 2, 3 and 4. This observation implies a phase diagram in which the 2D WC or low field RIP can alternate between integer QH states to take a lower energy down to low fields where ν >1.
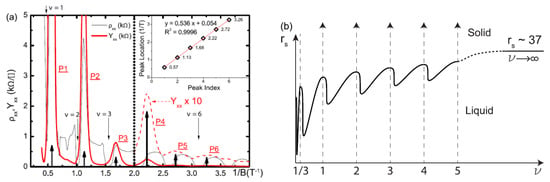
Figure 2.
(a) Observation of multiple RIPs between Landau-level filling factors 1, 2, 3 and 4 in a dilute 2D hole system in GaAs with rs~20. (b) The modified phase diagram with multiple RIPs. Figure is taken from Reference [12].
The reported resistance, capacitance and inductance characteristics of the RIPs are discussed below.
2.1. Resistivity
Both Qiu et al. [10,11] and Knighton [12,13] reported clearly the insulating behavior () of the RIPs that are far stronger than the Shubnikov-de Haas oscillation amplitude. The resistivity values of the RIPs between ν = 1 and 2 are all above the quantum resistivity . However, there are some discrepancies in the amplitude and temperature dependency, which could be caused by differences in the sample structure and quality. Figure 3 presents the results from Reference [10], which used the thermal activation model () to fit the temperature dependence of the RIP peak resistance. On the other hand, Knighton et al. [12,13] fitted the data to the Efros-Shklovskii variable-range-hopping model . Figure 4 shows their data and fitting results. It is worth to point out that the resistivity value of the RIPs at ν > 2 in Knighton’s work was much lower than h/e2 (Figure 4a) and the data do not have a high dynamic range to warrant a reliable fitting to the model. Therefore, the mechanism (thermal activation vs. variable-range-hopping) of the temperature dependent resistivity in the RIPs remains to be seen.
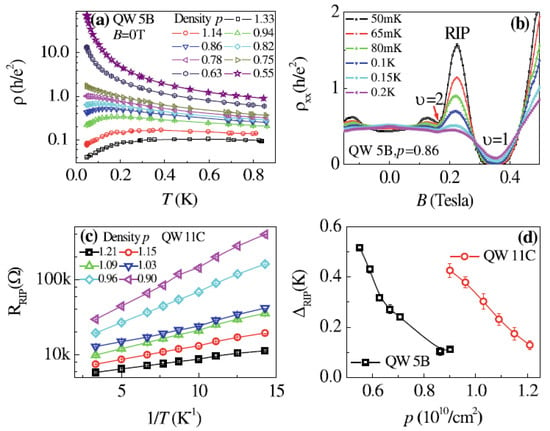
Figure 3.
(a) 2D MIT at a zero magnetic field in a dilute 2D hole system in a 10 nm wide GaAs quantum well, . (b) with . (c) Arrhenius plot of the RIP peak resistance at various hole densities. (d) The fitted thermal activation gap. Figure from Reference [10].
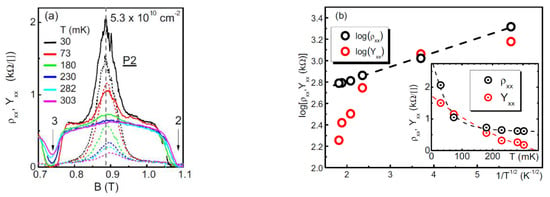
Figure 4.
(a) Real (solid) and imaginary (dashed) parts of the magnetoresistance for a RIP between υ = 2 and 3 for 2D holes in a 20 nm wide GaAs quantum well. (b) Real and imaginary components of the magnetoresistance plotted on a semi-log scale. Figure from Reference [12].
2.2. Capacitance Measurement
Qiu et al. [10,11] also reported a thermodynamic compressibility study through capacitance measurements in the RIP, shown in Figure 5. It was found that the RIP tended to be incompressible, like the zero-field insulating phase and the HFIP. The phase diagram from the capacitance measurements matched well with that from the transport measurement. This observation suggests the possibility of the same origin for them, i.e., the liquid-WC transition. We also point out that in the capacitance measurement of a 2D heterostructure with a single-gate configuration, the geometric gate capacitance usually dominates over the 2D system’s quantum capacitance, which is related to the compressibility. It is only when the 2D system becomes very incompressible and the 2D system’s quantum capacitance is greatly reduced, that the measured gate capacitance starts to show an observable deviation from the geometric capacitance. More intricate methods such as penetration field measurements in 2D structures with both a top and bottom gate [19] will be desirable to further study the compressibility of RIPs and their connection or competition with the zero-field MIT or integer QHs to enable better precision.
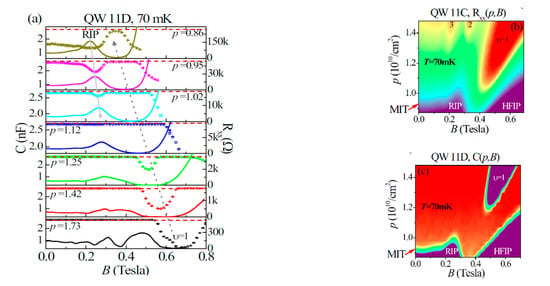
Figure 5.
(a) Capacitance (symbol) and resistance (line) vs. perpendicular magnetic field at several hole densities in a 10 nm wide GaAs quantum well system. (b) The phase diagram viewed in the longitudinal resistance map at 70 mK. (c) The phase diagram viewed in the capacitance map at 70 mK. Figure from Reference [10].
2.3. Inductance
The inductance of 2D systems is a rarely studied topic. Knighton [12,13] reported the inherent inductive behavior of the RIPs, illustrated in Figure 6. The inductance behavior is different between RIPs at a low magnetic field with υ > 1 and the RIPs at a high magnetic field where υ < 1. There have not been many (or any) theoretical studies on the inductive behavior of correlated 2D electron systems. Thus, the understanding of these anomalous inductance observations is limited and awaits further theoretical investigation.
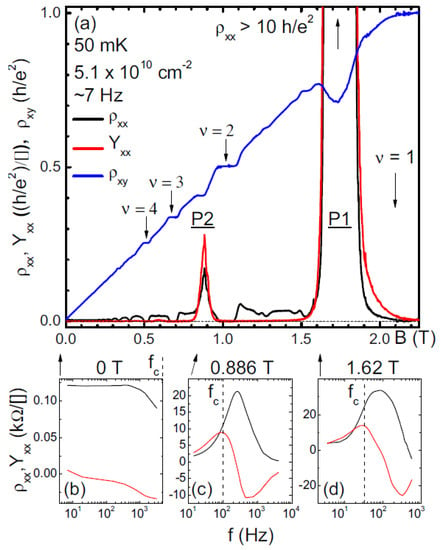
Figure 6.
(a) Magnetoresistance of 2D holes in GaAs showing two RIPs at ν > 1 (labeled as P1 and P2). (b) mechanism (thermal activation vs. variable-range-hopping) (d) The longitudinal resistivity ρxx and inductive signal Yxx vs. frequency at various magnetic fields, showing the clear inductive effect of the RIPs. Figure taken from Reference [12].
In summary, all of the measured properties of the RIPs indicate that the RIPs share the same origin with the zero-field insulating phase and the RIPs at a higher magnetic field υ < 1. The phase diagram of 2D p-GaAs systems with a very high mobility and a high rs in the density-perpendicular magnetic field plane is consistent with the liquid-WC transition phase diagram in clean 2D systems.
3. Possible Transport Evidence for Intermediate Phases and Wigner Crystal Melting
Since the discovery of the RIPs at a lower magnetic field υ > 1 implies a liquid to Wigner crystal transition in clean 2D systems with high rs, then an important question arises: What type of phase transitions are experimentally observed for a 2D metallic liquid to insulator transition (whereas the insulator is either the zero-field insulator or the RIPs at a low magnetic fields). Given the well-known theoretical results that there is no long-range order in a 2D solid and the possible existence of various phases intermediate between a 2D WC and a liquid [20,21,22,23,24,25,26,27,28,29,30,31,32,33], is there any experimental evidence for intermediate phases when a WC melts into liquid?
Evidence of intermediate phases has been presented by several groups [34,35,36]. Qiu et al. studied how the low field RIP is suppressed by either increasing the temperature or carrier density and found evidence for the 2D holes in p-GaAs transforming into a mixed state of an incipient RIP and a metallic liquid [34]. Other researchers took a different approach and used an increasing voltage (or electric field) applied to the sample to probe the breakdown of a presumed 2D WC deep in the insulating state where the resistivity is very high. In such a state where the WC is presumably well formed, Brussarski [35] and Knighton [36] found non-linear I-V curves at low temperatures, shown in Figure 7 and Figure 8. Different threshold voltages were seen, suggesting a two-stage phase transition instead of a direct phase transition, although different explanations were given by the two groups. More experimental data and theoretical models are needed to further elucidate the situation.
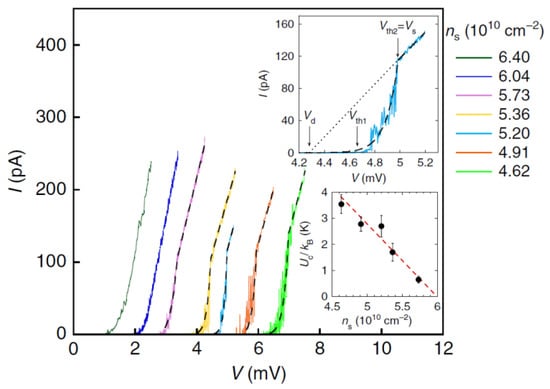
Figure 7.
Voltage-current characteristics of 2D electrons in a Si-metal-oxide-semiconductor field-effect transistor (Si-MOSFET) in a possible Wigner crystal (WC) state. V-I curves of different electron densities are shown to show the depinning of the WC. Figure taken from Reference [35].
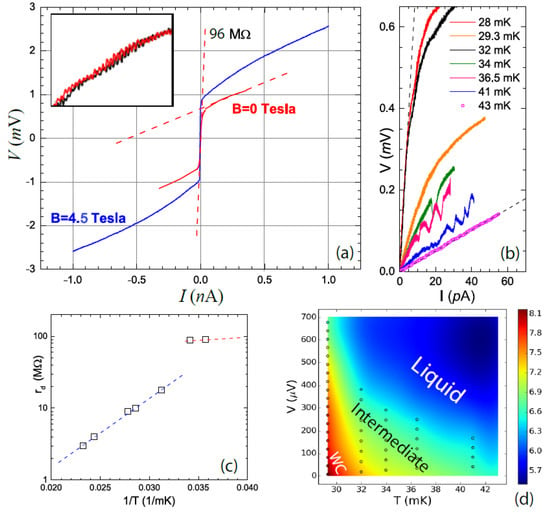
Figure 8.
Voltage-current characteristics of 2D holes in GaAs in a possible WC state to show the two-stage melting of the WC. (a) dc IV at 28 mK. (b) IVs at different temperatures. (c) Temperature dependence of (d) Suggested phase diagram. Figure from Reference [36].
4. Discussion and Outlook
Although various recent transport experiments and findings point to the existence of a 2D Wigner crystal and the relevance of a liquid-WC transition in the observed RIPs and peculiar voltage-current characteristics in strongly correlated 2D carrier systems, due to the limitations of transport data and the various challenging aspects of the experiments (ultra-low temperatures, low noise-low level measurements, and stringent sample quality requirements), information about how the 2D Wigner crystal transforms into a metallic liquid and the nature of the intermediate phase are still limited and further experiments are required to obtain an in-depth understanding.
On the theoretical side, from the beginning of the discovery of 2D MIT, a number of weak-interaction based models were proposed to explain the metal-insulator transition or cross-over behavior of the electrical resistivity such as screening, potential fluctuation, and percolation [37,38,39]. In these theories, conventional Anderson localization (weak-localization in the metal-side and strong localization in the insulator side of the MIT) is still relevant. From extensive prior studies on the Anderson insulator to 2D QH transition, it is expected that the zero-field insulator would directly transition to an integer QH state upon the application of perpendicular magnetic fields [40]. This is in stark contrast to the observation of low field RIPs between the zero-field insulator and integer QH state [10,11,12]. It appears that it is difficult to use weak-interaction based models to reconcile the observations of various RIP, QH and HFIP states and their connection to the liquid-WC transition when the behavior of strongly interacting high rs 2D systems is examined beyond the zero magnetic field to finite perpendicular magnetic fields. In contrast to weak interaction theories, many other theories emphasize the importance of strong correlations and relevance of WC physics in the systems showing a 2D MIT [9,26,27,33] and therefore, may be further compared with the experimental results. These theories are based on a number of different approaches: Analytical mean-field models [26,27], quantum Monte Carlo simulations [30], or dynamic mean field theory (DMFT) [32,33]. In the mean-field theories by Kivelson and Spivak [26,27], the various spectacular transport behavior in the correlated 2D systems showing an MIT are attributed to the Fermi liquid to WC transition where intermediate states are unavoidable [31]. In the intermediate ‘micro-emulsion’ states (e.g., WC bubbles in a Fermi liquid background), it is the interplay or transformation between a Fermi liquid and the WC components tuned by the temperature or a magnetic field that dictates the transport behavior and gives rise to the resistivity change of the system. It seems that the most relevant micro-emulsion phase to the experimentally observed RIPs and intermediate phases is the scenario where WC bubbles co-exist in a Fermi liquid. Whether other micro-emulsion states (Fermi liquid bubbles in WC, 1D ordered stripes) exist in experiments requires further research and more theoretical developments are desired to establish more quantitative predictions on the experimental systems. New theoretical approaches, based on hydrodynamics, seem quite promising and are currently being developed [41,42]. In addition to the mean-field models by Kivelson and Spivak, a strong interaction and Wigner-Mott transition based theoretical studies, led by Dobrosavljevic and collaborators [32,33], may also be relevant to the experimental findings. Modern DMFT was applied to study the MIT in 2D carriers with a high rs and the early approaches of Wigner and Mott were reconciled. Based on this ‘Wigner-Mott’ transition scenario, DMFT calculations are able to explain many detailed behaviors in the electrical transport and charge ordered intermediate phases similar to a charge density wave (CDW) predicted to form before the system enters a WC. It is worth noting that in the DMFT theory, both metallic CDW and insulating CDW are found [33]. It will be very interesting to see whether such CDW states exist in experiments.
On the experimental side, besides the previously mentioned compressibility and inductance measurements that require further advancements and understanding, other striking effects found in the zero-field 2D MIT are very worth exploring in relation to the RIPs. One particular case is the effect of an in-plane magnetic field. In the zero-field MIT, it was established that an in-plane magnetic field causes large positive magneto-resistance and drives the system toward the insulating phase [8,9,43,44]. Recent in-plane field magneto-transport experiments have revealed that the resistivity of dilute 2D electrons in Si-MOSFET in the insulating state is the same for the zero-field and in the presence of an in-plane field that polarizes the spins [45], a behavior different from the metallic phase of the 2D MIT [8,9,43]. Thus, t would be very insightful to study the effect of in-plane magnetic field induced spin-polarization on the RIPs and examine how the in-plane field affects the transition between the RIPs and a metallic liquid. In addition to the spin-polarization effect, understanding the physics of correlated 2D systems at ‘high temperatures’ comparable with the Fermi temperature is also an interesting topic. In this ‘semi-quantum’ regime, the correlated electron fluid is expected to show unique behavior in viscosity [27]. While many experiments have been carried out at low temperatures, transport studies in this ‘semi-quantum’ regime where T~TF are limited and worth exploring further [46]. In addition to transport, new techniques such as thermopower measurements are strongly desired to shed new light on the RIPs. For instance, diverging thermopower observed for strongly interacting 2D electrons in Si-MOSFET [47] revealed the critical nature of the zero-field MIT, complementing the views from critical behavior in resistance or effective mass [48]. Such critical behavior in thermopower or effective mass has generated theoretical interest and analogy to other strongly correlated materials like high Tc cuprate may be made [49]. Finally, although this review is focused on strongly interacting 2D systems with an ultra-high purity/mobility and the effect of the impurities or disorder is not discussed much, understanding the effect of disorder on a 2D MIT has elicited rich physics [50] and thus we expect the disorder effect on the RIPs and RIP to liquid transition to be an interesting outstanding issue.
In summary, the recent observations of RIPs in low magnetic fields where ν > 1 and the connections between low field RIPs and high field RIPs and HFIPs with ν < 1 point to the formation of a WC as the origin of the low field RIP and the 2D MIT being driven by the liquid-WC transition. There is also transport evidence for possible new intermediate phases when the insulating phase (either the insulator in a zero-field or the RIPs at low magnetic fields) is destroyed by an increasing voltage, temperature or carrier density. Further experimental and theoretical progress in these fronts is needed and is expected to yield many more exciting new insights on the long-standing problems of the 2D WC-liquid transition and MIT.
Author Contributions
R.L.J.Q. and X.P.A.G. conceived the overall outline of the manuscript and all the authors contributed to the writing and revision of the paper.
Funding
This research was funded by NSF grant number DMR-0906415 and DMR-1607631.
Acknowledgments
We thank Vladimir Dobrosavljevic and Jian Huang for helpful discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kravchenko, S.V.; Kravchenko, G.V.; Furneaux, J.E.; Pudalov, V.M.; D’Iorio, M. Possible metal-insulator transition at B=0 in two dimensions. Phys. Rev. B 1994, 50, 8039–8042. [Google Scholar] [CrossRef]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- Butler, S.Z.; Hollen, S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutiérrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F.; et al. Progress, Challenges, and Opportunities in Two-Dimensional Materials Beyond Graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef] [PubMed]
- Wigner, E. On the Interaction of Electrons in Metals. Phys. Rev. 1934, 46, 1002–1011. [Google Scholar] [CrossRef]
- Klitzing, K.V.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494–497. [Google Scholar] [CrossRef]
- Tsui, D.C.; Stormer, H.L.; Gossard, A.C. Two-Dimensional Magnetotransport in the Extreme Quantum Limit. Phys. Rev. Lett. 1982, 48, 1559–1562. [Google Scholar] [CrossRef]
- Abrahams, E.; Anderson, P.W.; Licciardello, D.C.; Ramakrishnan, T.V. Scaling Theory of Localization: Absence of Quantum Diffusion in Two Dimensions. Phys. Rev. Lett. 1979, 42, 673–676. [Google Scholar] [CrossRef]
- Abrahams, E.; Kravchenko, S.V.; Sarachik, M.P. Metallic behavior and related phenomena in two dimensions. Rev. Mod. Phys. 2001, 73, 251–266. [Google Scholar] [CrossRef]
- Spivak, B.; Kravchenko, S.V.; Kivelson, S.A.; Gao, X.P.A. Colloquium: Transport in strongly correlated two dimensional electron fluids. Rev. Mod. Phys. 2010, 82, 1743–1766. [Google Scholar] [CrossRef]
- Qiu, R.L.J.; Gao, X.P.A.; Pfeiffer, L.N.; West, K.W. Connecting the Reentrant Insulating Phase and the Zero-Field Metal-Insulator Transition in a 2D Hole System. Phys. Rev. Lett. 2012, 108, 106404. [Google Scholar] [CrossRef] [PubMed]
- Qiu, R.L.J.; Gao, X.P.A. Qiu and Gao Reply. Phys. Rev. Lett. 2013, 110, 249702. [Google Scholar] [CrossRef] [PubMed]
- Knighton, T.; Wu, Z.; Tarquini, V.; Huang, J.; Pfeiffer, L.N.; West, K.W. Reentrant insulating phases in the integer quantum Hall regime. Phys. Rev. B 2014, 90, 165117. [Google Scholar] [CrossRef]
- Knighton, T.; Tarquini, V.; Wu, Z.; Huang, J.; Pfeiffer, L.; West, K. Large intrinsic inductance in strongly correlated GaAs two-dimensional holes in the integer quantum hall regime. Appl. Phys. Lett. 2014, 104, 193109. [Google Scholar] [CrossRef]
- Shayegan, M. Case for the Magnetic-Field-Induced Two-Dimensional Wigner Crystal. In Perspectives in Quantum Hall Effects; Das Sarma, S., Pinczuk, A., Eds.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- D’Iorio, M.; Pudalov, V.M.; Semenchinsky, S.G. Magnetic field induced transitions between quantized hall and insulator states in a dilute 2D electron gas. Phys. Lett. A 1990, 150, 422. [Google Scholar] [CrossRef]
- Jang, J.; Hunt, B.M.; Pfeiffer, L.N.; West, K.W.; Ashoori, R.C. Sharp tunneling resonance from the vibrations of an electronic Wigner crystal. Nat. Phys. 2017, 13, 340–344. [Google Scholar] [CrossRef]
- Tanatar, B.; Ceperley, D.M. Ground state of the two-dimensional electron gas. Phys. Rev. B 1989, 39, 5005. [Google Scholar] [CrossRef]
- Zhu, X.; Louie, S.G. Variational quantum Monte Carlo study of two-dimensional Wigner crystals: Exchange, correlation, and magnetic-field effects. Phys. Rev. B 1995, 52, 5863. [Google Scholar] [CrossRef]
- Dultz, S.C.; Jiang, H.W. Thermodynamic Signature of a Two-Dimensional Metal-Insulator Transition. Phys. Rev. Lett. 2000, 84, 4689. [Google Scholar] [CrossRef] [PubMed]
- Mermin, N.D.; Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Brazovskii, S.A. Phase transition of an isotropic system to a nonuniform state. Sov. Phys. JETP 1975, 41, 85. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 1973, 6, 1181. [Google Scholar] [CrossRef]
- Strandburg, K.J. Two-dimensional melting. Rev. Mod. Phys. 1988, 60, 161. [Google Scholar] [CrossRef]
- Halperin, B.I.; Nelson, D.R. Theory of two-dimensional melting. Phys. Rev. Lett. 1978, 41, 121. [Google Scholar] [CrossRef]
- Young, A.P. Melting and the vector Coulomb gas in two dimensions. Phys. Rev. B 1979, 19, 1855. [Google Scholar] [CrossRef]
- Spivak, B.; Kivelson, S.A. Phases intermediate between a two-dimensional electron liquid and Wigner crystal. Phys. Rev. B 2004, 70, 155114. [Google Scholar] [CrossRef]
- Spivak, B.; Kivelson, S.A. Transport in two dimensional electronic micro-emulsions. Ann. Phys. 2006, 321, 2071. [Google Scholar] [CrossRef]
- Falakshahi, H.; Waintal, X. Hybrid phase at the quantum melting of the Wigner crystal. Phys. Rev. Lett. 2005, 94, 046801. [Google Scholar] [CrossRef] [PubMed]
- Drummond, N.D.; Needs, R.J. Phase diagram of the low-density two-dimensional homogeneous electron gas. Phys. Rev. Lett. 2009, 102, 126402. [Google Scholar] [CrossRef] [PubMed]
- Clark, B.K.; Casula, M.; Ceperley, D.M. Hexatic and mesoscopic phases in a 2D quantum Coulomb system. Phys. Rev. Lett. 2009, 103, 055701. [Google Scholar] [CrossRef] [PubMed]
- Jamei, R.; Kivelson, S.A.; Spivak, B. Universal aspects of Coulomb-frustrated phase separation. Phys. Rev. Lett. 2005, 94, 056805. [Google Scholar] [CrossRef] [PubMed]
- Dobrosavljevic, V.; Tanaskovic, D. Chapter 1: Wigner-Mott quantum criticality: From 2D-MIT to 3He and Mott organics. In Strongly Correlated Electrons in Two Dimensions, 1st ed.; Kravchenko, S., Ed.; Pan Stanford Publishing Pte. Ltd.: Singapore, 2017; ISBN 9789814745376. [Google Scholar]
- Camjayi, A.; Haule, K.; Dobrosavljevic, V.; Kotliar, G. Coulomb correlations and the Wigner-Mott transition. Nat. Phys. 2008, 4, 932–935. [Google Scholar] [CrossRef]
- Qiu, R.L.J.; Goble, N.J.; Serafin, A.; Yin, L.; Xia, J.S.; Sullivan, N.S.; Pfeiffer, L.N.; West, K.W.; Gao, X.P.A. Evidence for a New Intermediate Phase in a Strongly Correlated 2D System near Wigner Crystallization. Available online: arXiv:1509.07463 [cond-mat] (accessed on 12 October 2018).
- Brussarski, P.; Li, S.; Kravchenko, S.V.; Shashkin, A.A.; Sarachik, M.P. Transport evidence for a sliding two-dimensional quantum electron solid. Nat. Commun. 2018, 9, 3803. [Google Scholar] [CrossRef] [PubMed]
- Knighton, T.; Wu, Z.; Huang, J.; Serafin, A.; Xia, J.S.; Pfeiffer, L.N.; West, K.W. Evidence of two-stage melting of Wigner solids. Phys. Rev. B 2018, 97, 085135. [Google Scholar] [CrossRef]
- Das Sarma, S.; Hwang, E.H.; Li, Q. Two-dimensional metal-insulator transition as a potential fluctuation driven semiclassical transport phenomenon. Phys. Rev. B 2013, 88, 155310. [Google Scholar] [CrossRef]
- Das Sarma, S.; Hwang, E.H. Two-dimensional metal-insulator transition as a strong localization induced crossover phenomenon. Phys. Rev. B 2014, 89, 235423. [Google Scholar] [CrossRef]
- Das Sarma, S.; Hwang, E.H.; Kechedzhi, K.; Tracy, L.A. Signatures of localization in the effective metallic regime of high-mobility Si MOSFETs. Phys. Rev. B 2014, 90, 125410. [Google Scholar] [CrossRef]
- Jiang, H.W.; Johnson, C.E.; Wang, K.L.; Hannahs, S.T. Observation of magnetic-field-induced delocalization: Transition from Anderson insulator to quantum Hall conductor. Phys. Rev. Lett. 1993, 71, 1439. [Google Scholar] [CrossRef] [PubMed]
- Andreev, A.V.; Kivelson, S.A.; Spivak, B. Hydrodynamic Description of Transport in Strongly Correlated Electron Systems. Phys. Rev. Lett. 2011, 106, 256804. [Google Scholar] [CrossRef] [PubMed]
- Levchenko, A.; Xie, H.Y.; Andreev, A.V. Viscous magnetoresistance of correlated electron liquids. Phys. Rev. B 2017, 95, 121301. [Google Scholar] [CrossRef]
- Gao, X.P.A.; Boebinger, G.S.; Mills, A.P.; Ramirez, A.P.; Pfeiffer, L.N.; West, K.W. Spin-polarization-induced tenfold magnetoresistivity of highly metallic two-dimensional holes in a narrow GaAs quantum well. Phys. Rev. B 2006, 73, 241315. [Google Scholar] [CrossRef]
- Dolgopolov, V.T.; Shashkin, A.A.; Kravchenko, S.V. Spin polarization and exchange-correlation effects in transport properties of two-dimensional electron systems in silicon. Phys. Rev. B 2017, 96, 075307. [Google Scholar] [CrossRef]
- Li, S.; Sarachik, M.P. Resistivity of the insulating phase approaching the two-dimensional metal-insulator transition: The effect of spin polarization. Phys. Rev. B 2017, 95, 041301. [Google Scholar] [CrossRef]
- Qiu, R.L.J.; Gao, X.P.A.; Pfeiffer, L.N.; West, K.W. Degenerate versus semidegenerate transport in a correlated two-dimensional hole system. Phys. Rev. B 2011, 83, 193301. [Google Scholar] [CrossRef]
- Mokashi, A.; Li, S.; Wen, B.; Kravchenko, S.V.; Shashkin, A.A.; Dolgopolov, V.T.; Sarachik, M.P. Critical Behavior of a Strongly Interacting 2D Electron System. Phys. Rev. Lett. 2012, 109, 096405. [Google Scholar] [CrossRef] [PubMed]
- Shashkin, A.A.; Kravchenko, S.V.; Dolgopolov, V.T.; Klapwijk, T.M. Sharp increase of the effective mass near the critical density in a metallic two-dimensional electron system. Phys. Rev. B 2002, 66, 073303. [Google Scholar] [CrossRef]
- Kim, H.T. Analysis of the diverging effective mass in YaBa2Cu3O6+x for high-Tc mechanism and pairing symmetry. Int. J. Mod. Phys. B 2018, 32, 1840031. [Google Scholar] [CrossRef]
- Popovic, D. Chapter 5. Metal-insulator transition in correlated two-dimensional systems with disorder. In Strongly Correlated Electrons in Two Dimensions, 1st ed.; Kravchenko, S., Ed.; Pan Stanford Publishing Pte. Ltd.: Singapore, 2017; ISBN 9789814745376. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).