Remote Servo Tuning System for Multi-Axis CNC Machine Tools Using a Virtual Machine Tool Approach

Abstract

Servo systems affect the performances of machining in accuracy and surface quality for high speed and precision machine tools. This study introduces an efficient servo tuning technique for Computer Numerical Control (CNC) feed drive systems using particle swarm optimization (PSO) algorithm by virtual machine tool approach. The proposed approach contained a system identification phase and a servo tuning phase based on the same bandwidth for all axes feed drive systems. The PSO algorithm was adopted to obtain the system parameters and maximize the corresponding bandwidth. An efficient two-step servo tuning method based on gain and phase margins was proposed for high speed and precision requirements. All feed drive systems controller gains were optimized simultaneously for synchronization. A remote system called Machine Dr. was established for servo tuning and monitoring. Simulation and experimental results were introduced to illustrate the effectiveness of the proposed approach.

1. Introduction

Computer numerical control (CNC) machine tools have been widely used in high speed and precision machining, such as curved surface, gears, aerospace materials, integrated circuit (IC) parts, and precision components, etc. This is why machine tool has been focused on how to accomplish high-speed and high-precision machining. Accurate control is required for machine tools to follow the desired contours. With increasing requirements for precision operations, many control strategies have been proposed [1,2,3,4,5,6,7,8,9,10,11]. For industrial applications, the proportional-integral-derivative (PID) controllers of each axis are used for feed drive systems, therefore the tuning method for multi-axis synchronization for precision results are required. However, system dynamic parameters may be uncertain or vary with time. Thus, the system identification of feed drive systems should be done before tuning parameters. Some literature introduce virtual machine tools, including virtual CNC, servo models, and mechanical dynamics of feed drive systems, for treating the problem [11,12,13,14,15,16,17,18,19].

Feed drive systems may have unstable results or poor performance when servo parameters are not designed properly [20,21]. Conventionally, the control gains of position and velocity controller are set as high as possible, under the condition that the stability and robustness of the closed loop system is secured with some stability margins [21,22]. In general, each commercial CNC machine tool guides the user for tuning parameters step-by-step according to expert experience. In this study, we propose an intelligent and efficient method for the servo tuning problem to improve synchronization.

In order to employ the intelligent efficient method, this study developed a virtual CNC feed drive system via system identification technology using Heidenhain TNCopt software. This can obtain the characteristics of the system and the mathematical models which we can use in numerical simulations; therefore, we were able to implement this intelligent and efficient method by an optimization algorithm, e.g., a genetic algorithm, particle swarm optimization (PSO), evolutionary algorithm, electromagnetism-like algorithm, etc. [23,24,25,26,27,28,29,30]. In this study, the PSO was adopted for solving optimization problems. As a result, combined with feed system signals processing and spectrum analysis, the servo system with mechanical dynamics was established. The intelligent algorithm was used to automatically generate a set of suitable servo parameters for the current machine tool. After optimization, performance and processing quality would be better than the original. The proposed approach contained a system identification phase and a servo tuning phase based on the same bandwidth for all axes feed drive systems. The particle swarm optimization algorithm was adopted to obtain the system parameters and maximize the corresponding bandwidth. An efficient two-step servo tuning method based on gain and phase margins was proposed for high speed and precision requirements. All feed drive systems controller gains were optimized simultaneously for synchronization. Finally, the cloud computing system, called Machine Dr., was established for system identification, servo tuning, and monitoring.

This organization of this paper is introduced as follows. Section 2 introduces the preliminaries, including the modeling of feed drive systems, specification of machine tools, and the particle swarm optimization algorithm. The proposed system identification based on PSO is introduced in Section 3. Section 4 introduces the intelligent servo tuning technique by two-step PSO. The corresponding simulation, experimental results, and the Machine Dr. system are shown in Section 3 and Section 4. Finally, the conclusion is given.

2. Preliminaries

This section introduces the preliminaries including feed drive system modeling, specifications of five-axis machine tools, and the particle swarm optimization algorithm.

2.1. Feed Drive Systems

Machine tool feed drive servo control systems are designed to accomplish a task, that is, to control the positions and velocities of machine tool axes in follow the commons generated by CNC controller. In general, the feed drive system contains two major parts. The first one is the electronic control system or servo control system. The second one is the mechanical system such as the lead screw, bearing, motor, and worktable, etc. The servo system consists of plant, actuator, controller, and sensor. The control system with feedback is a closed-loop system, and without feedback is an open-loop system. The most common structure of servo control is closed loop, which belonging to passive control, and it has multiple loop characteristics and each loop has close relationships.

Many feed drive models have been proposed for system identification and controller design [2,3,6,16,31,32]. Literature [31] proposes a virtual simulation model, the model contains the influence of the cutting force, friction and backlash nonlinear phenomenon. However, it assumes that the lead-screw is a rigid body, and the table mass and damping ratio were not considered. These reduce the accuracy and response of feed drive system. Figure 1 shows the dynamic model of the single-axis feed drive system with mechanical vibration, where J_m: rotary inertia (kg·m²), B_m: damping coefficient of the rotary motion (Ns/m), M_t: table mass (kg), C_t: damping coefficient of the lead-screw (Ns/m), T: motor torque(Nm), K: stiffness coefficient of the lead-screw (N/m), θ_m: motor rotation angle (rad), x_t: table position (m), R: transform ratio from motor rotation angle to table position (mm/rad) ($R=p/2\pi$), p is the lead-screw pitch (mm). The dynamic equation of this model can be expressed as:

$$\left[\begin{array}{cc}{J}_m& 0\\ 0& M_t\end{array}\right]\left[\begin{array}{c}{\ddot{\theta }}_m\\ {\ddot{x}}_t\end{array}\right]+\left[\begin{array}{cc}{B}_m& 0\\ 0& M_t\end{array}\right]\left[\begin{array}{c}{\dot{\theta }}_m\\ {\dot{x}}_t\end{array}\right]+\left[\begin{array}{cc}{R}^{2}K& -RK\\ -RK& K\end{array}\right]\left[\begin{array}{c}{\theta }_m\\ x_t\end{array}\right]=\left[\begin{array}{c}T\\ 0\end{array}\right]$$

(1)

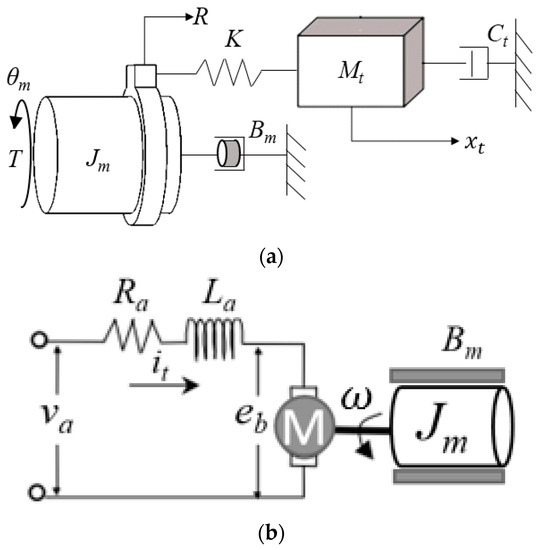
Figure 1. Dynamic model of single-axis feed drive system; (a) mechanical dynamics, (b) motor dynamics.

The schematic diagram for a motor is shown on Figure 1b, where $v_a$ is separate input voltage (V), $i_t$ is the circuit current (A) generated by the motor equivalent circuit impedance, $R_a$ is motor equivalent resistance (Ω), $L_a$ is motor inductance (H), $e_b$ is total voltage (V) induced in the armature, and ω is motor velocity (rad/s). Therefore, we have

$$\frac{\omega (s)}{v_a(s)}=\frac{K_t}{(J_{m}s+B_m)(L_{a}s+R_a)+K_e{K}_t}$$

(2)

The corresponding block diagram of the feed drive system is shown in Figure 2; Figure 2a–c show the servo motor system, feed mechanical dynamic systems, and the overall closed-loop systems, respectively. The proportional (P) or proportional-integral (PI) or proportional-integral-derivative (PID) controller are typically used to control the servo systems of machine tools. In general, current and velocity loops are usually part of the PI controller and the position loop is in the P controller [13,22,31].

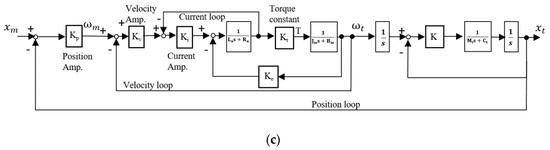
Figure 2. Block diagram of feed drive system; (a) Servo motor system; (b) Mechanical system; and (c) Closed-loop systems.

From Figure 2c, the closed-loop consists of a current loop, velocity loop and position loop. The current loop has a high-frequency response and the bandwidth is higher than processing. The typical values of bandwidths of the current, velocity, and position loops are 100–3000 Hz, 10–100 Hz, and 1–50 Hz, respectively. Since the control target of the milling application is the position control and the current loop gain is at unity in the low frequency band, therefore, the current loop can be bypassed in the applications of milling. Thus, the transfer function is:

$$G_p(s)=\frac{x_t(s)}{x_m(s)}=\frac{\left(K_p{K}_t{K}_{vp}K\right)s+K_p{K}_t{K}_{vi}K}{a_5{s}^5+a_4{s}^4+a_3{s}^3+a_2{s}^2+a_{1}as+a_0}$$

(3)

where a₅ = J_mM_t, a₄ = C_tJ_m + B_mM_t + K_tK_vpM_t, a₃ = J_mK + B_mC_t + C_tK_tK_vp + K_tK_viM_t, a₂ = B_mK + C_tK_tK_vi, a₁ = K_pK_tK_vpK, and a₀ = K_pK_tK_viK.

2.2. Specifications of the Machine Tool System

In this study, the proposed approach was applied in the Microcut-MCU-5X five-axis machine tool (shown in Figure 3) at National Chung Hsing University, Taiwan. Its major specifications are shown in Table 1. The CNC controller of the machine tool is TNC640, published by Heidenhain Co. (Schaumburg, IL, USA) [22]. By using TNC640, we could obtain table position by linear scales, spindle speed, speed or acceleration of each axis, etc.

Figure 3. Five-axis machine tool MCU-5X in National Chung Hsing University (NCHU).

Table 1. Major specifications of the machine tool (MCU-5X).

Specifications	Values
X/Y/Z Axis Travel (mm)	600/600/500
Tilting Axis A (degree)	+120/−120
Rotary C (degree)	360
Rapid Traverse X/Y/Z (mm/min)	36,000/36,000/36,000
Max. Speed A/C (rpm)	16.6/90
Spindle Speed Range (rpm)	12,000 (std)/15,000 (opt)
Type of Position Control	Full-closed control

2.3. Particle Swarm Optimization

Within optimization problems, the objective is to find extreme values of objective function. In this section we introduce the particle swarm optimization (PSO) algorithm, an evolutionary computation technique proposed by Kennedy & Eberhart [23]. It was developed by research on the social behavior of animals, e.g., bird flocking. Like Genetic Algorithms, PSO is initialized with a population of random solutions. It has been applied on optimization problems such as neural network learning, fuzzy control, and evolutionary algorithms [24,25,26,27,28,29,30]. Compared with other evolutionary algorithms [24,25,26,27,28,29,30], PSO has less selected parameters to provide efficiency. At first, the optimization problem is formulated as

minimize f(X)

$$\mathrm{subject}\mathrm{to}X=\left\{x_1,x_2,...,x_N\right\}\in S,$$

(4)

where f(X) is the objective function, X are the tuning parameters, U_B and L_B are the corresponding upper and lower bound vectors, respectively, D is the problem dimension, and constraint denotes the optimization constraints. Herein, each individual (or particle) X represents a solution agent. Thus, we have:

$$V(k+1)=wV(k)+c_1{\varphi }_1[p_{best}-X(k)]+c_2{\varphi }_2[g_{best}-X(k)]$$

(5a)

$$X(k+1)=X(k)+V(k+1)$$

(5b)

where V denotes the velocity (update) for the particle X, w is the inertia weight, c₁, c₂ > 0, and ${\varphi }_1$, ${\varphi }_2$ are random number in [0, 1], $p_{best}$ is the best solution of this particle in current iteration and $g_{best}$ is the best solution for the overall particle. Based on (5), the population of particles tended to cluster together with others after optimization. The flow chart of the PSO algorithm is introduced in Figure 4. In this study, the PSO was adopted for system identification and servo tuning. Other heuristic evolutionary algorithms can be used for optimization.

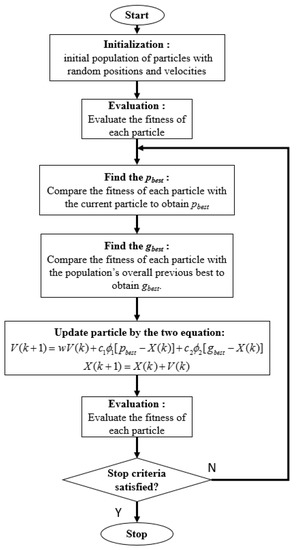
Figure 4. The flow chart of the particle swarm optimization (PSO) algorithm.

3. System Identification

3.1. Frequency Domain System Identification by PSO

In this paper, the system identification results were based on sine chirp approach. The outputs (red line) of velocity and position loops corresponds to chirp sine signals were obtained from the linear scale shown in Figure 5, and input (blue line) was generated by TNCopt. To enhance the efficiency of identification, a two-stage approach for frequency domain was proposed; at first the velocity loop was considered to obtain motor parameters (J_m, B_m), and then the position loop identification was done for lead-screw and table parameters (K, M_t, C_t). The procedure can be summarized as follows.

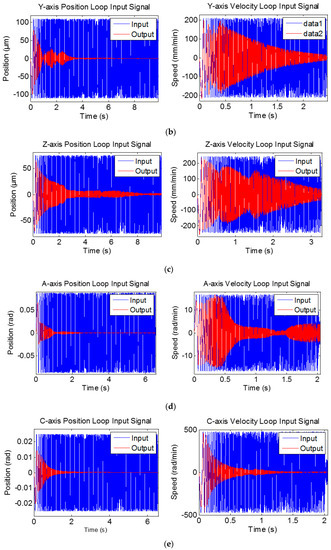
Figure 5. Sine chirp input signals and the corresponding outputs for system identification. (a) X-axis (b) Y-axis (c) Z-axis (d) A-axis (e) C-axis.

Procedure 1: System Identification

• (Step 1) Data Acquisition:
      Obtain corresponding data (velocity and positon results) from chirp sine response.
• (Step 2) Data Transformation:
      Convert data to get the corresponding frequency responses [gain versus frequency, (A_i, ω_i)]
• (Step 3) Estimation of J_m and B_m:
      Velocity Loop Identification via PSO:

  $$\begin{array}{l}\underset{J_m,B_m}{\min }E={\displaystyle \sum _i{[|G_v(j{\omega }_i)|-|{\widehat{G}}_v(j{\omega }_i)|]}^2}\\ \mathrm{s}.\mathrm{t}.J_m,B_m>0\end{array}$$

  where $\left|{\widehat{G}}_v(j{\omega }_i)\right|$ denotes the corresponding estimation of velocity gain at ω_i.
• (Step 4) Estimation of K, M_t, and C_t:
      Position Loop Identification via PSO:

  $$\begin{array}{l}\underset{K,M_t,C_t}{\min }E={{\displaystyle \sum _i(|G_p(j{\omega }_i)|-|{\widehat{G}}_p(j{\omega }_i)|)}}^2\\ \mathrm{s}.\mathrm{t}.K,M_t,C_t>0\end{array}$$

  where $\left|{\widehat{G}}_p(j{\omega }_i)\right|$ denotes the corresponding estimation of position gain at ω_i.

As above, Steps 3 and 4 used the PSO technique for finding system parameters (J_m, B_m) and (M_t, C_t, K). The PSO was adopted to minimize the square error of estimated frequency response function (FRF). Subsequently, application of the velocity loop resulted in a position loop with unknown parameters (M_t, C_t, K). The same optimization process by PSO could find the parameters (M_t, C_t, K). In order to improve the efficiency of the calculation, the stop criterion was an iteration with a number greater than 4000 and with a particle number of 35, according our experience. Small values of the iteration number and population size resulted in worse optimization results, large values had the problem of complexity and computation effort. The overall identification process is shown in the Figure 6.

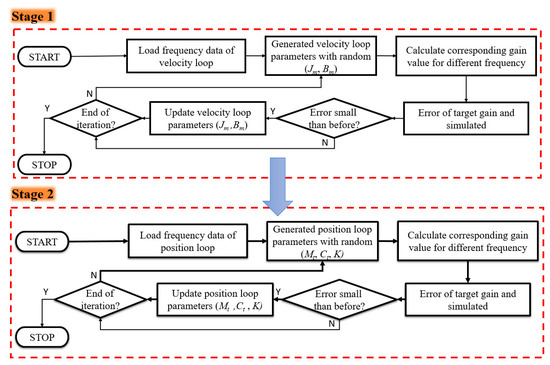
Figure 6. Two-stage approach for system identification.

3.2. Identification Results

Herein, the identification results of MCU-5X are introduced by our approach. We obtained system parameters (J_m, B_m, M_t, C_t, K) of axes feed drive systems and the corresponding transfer function in form of (3). For the velocity loop, the corresponding frequency responses of the actual system and estimation system are shown in Figure 7 (solid-line: experimental results; dotted-line: identification model). From Figure 7a,c,e, we observed that there existed an identification error in the high frequency region due to the identified results in the form of an ideal model which showed as Figure 7b. For servo tuning, we focused on the bandwidth; therefore, it was adopted to obtain the equivalent inertia and viscosity coefficient of the motor, respectively. This identification results were valid as long as they fit low-frequency characteristics and maintained the actual velocity loop system characteristics.

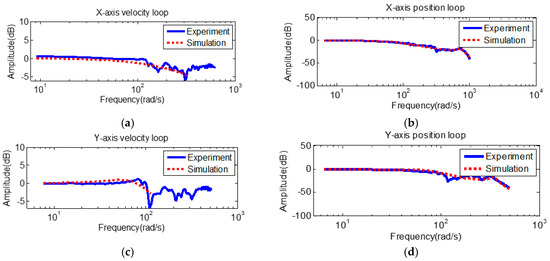
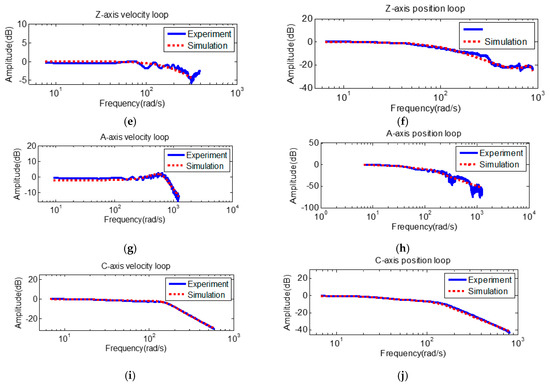
Figure 7. Frequency responses of velocity loop and position loop. (a) X-axis: velocity loop. (b) X-axis: position loop. (c) Y-axis: velocity loop. (d) Y-axis: position loop. (e) Z-axis: velocity loop. (f) Z-axis: position loop. (g) A-axis: velocity loop. (h) A-axis: position loop. (i) C-axis: velocity loop. (j) C-axis: position loop.

Subsequently, the results of the velocity loop coefficients J_m and B_m were set (as obtained from the above process) for identifying the position loop. The FRF of the actual system and estimation results are shown in Figure 7. Obviously, the estimation results were suitable, and the corresponding frequency response and dynamic properties were almost the same. In summary, the parameters for velocity and position loop were identified and listed in Table 2. Herein, a time domain test where the input signal was generated by TNCOPT, was performed to demonstrate the identification results. The root mean square error (RMSE) of outputs corresponding to sine chirp signals are introduced in Table 3.

Table 2. The results of identification for each axis.

Parameters	X-Axis	Y-Axis	Z-Axis	A-Axis	C-Axis
Jm $(\mathrm{kg}\cdot {\mathrm{m}}^2)$	$0.0477$	$0.1777$	$0.0359$	$52.4890$	$1.8186$
Bm $\left(\mathrm{Ns}/\mathrm{m}\right)$	$5.3104$	$6.5080$	$3.4831$	$83.6643$	0
Mt $\left(\mathrm{kg}\right)$	$250.8211$	$625.8345$	$132.1592$	---	---
Ct $(\mathrm{Ns}/\mathrm{m})$	$5.2196\times {10}^4$	$3.2294\times {10}^4$	$2.7773\times {10}^4$	---	---
K $(\mathrm{N}/\mathrm{m})$	$2.2847\times {10}^8$	$7.0270\times {10}^7$	$9.6864\times {10}^7$	---	---
Bandwidth (Hz)	$9.3771$	$7.2411$	$10.6631$	$4.5$	$9.4743$
Resonance frequency (Hz)	$114.0283$	$55.0414$	$126.0036$	---	---

Table 3. Root mean square error (RMSE) of each axis for time responses.

Error\Axis	X-Axis	Y-Axis	Z-Axis	A-Axis	C-Axis
RMSE	3.4791 ($\mathsf{\mu }\mathrm{m}$)	6.5061 ($\mathsf{\mu }\mathrm{m}$)	4.3310 ($\mathsf{\mu }\mathrm{m}$)	0.0005 (rad)	0.0002 (rad)

To verify the model obtained from system identification, another illustration example was introduced. We changed the servo parameters K_pp, K_vi, and K_vp to have the FRF of the actual experimental results (machine tool results) and the identified results. Figure 8 shows the identification results of the X-axis, Y-axis, Z-axis, A-axis, and C-axis, respectively. The blue line in Figure 8a–e are the FRF of default servo parameters, which we employed in system identification. The black line in Figure 8a–e are the FRF of changed servo parameters which were obtained by MCU-5X. Both dotted red lines represent the simulation FRF of the default and change servo parameters. It was confirmed that the system identification process was reliable.

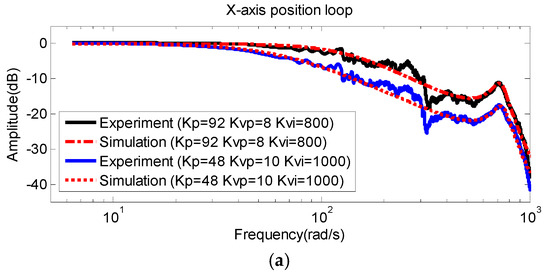
Figure 8. FRF comparison results of experiment and simulation. (a) X-axis, (b) Y-axis, (c) Z-axis, (d) A-axis, (e) C-axis.

4. Intelligent Servo Tuning Cloud System: Machine Dr.

4.1. Servo Tuning Method by PSO

In this study, an intelligent servo tuning method was proposed to adjust the servo parameters of each axis for synchronization. This approach was a two-step adjustment method; the velocity loop control parameters (K_vp, K_vi) were first designed, and then the position loop K_pp was chosen to enhance the bandwidth at several constraints. Figure 8 shows the flow chart of the proposed method, it contains data acquisition, system identification, virtual servo system setup, parameters optimization of velocity loop, and parameters optimization of the position loop. After data analysis and system identification, we established the virtual system of the feed drive. By using the virtual model, the PSO was adopted to optimize velocity controllers of five axes in the same bandwidth for synchronization. In this procedure, velocity loop servo parameters (K_vp, K_vi) of each axis were obtained by PSO with constraints.

• Maximize BW_vel.
• Subject to $\mathrm{Max}\left|G_v(iw)\right|\le 1$
•      Gain margin (GM) > 10 dB
•      Phase margin (PM) > 45°.

where BW_vel. denotes the bandwidth of velocity loop. According our experience, excessive gain of FRF may result unstable and vibrations. We used this Constraint 1 to ensure that the system was stable and vibration was low. Constraints 2 and 3 related to gain margin (GM) and phase margin (PM). GM and PM are widely used to confirm system stability and robustness. Herein, for the initialization of PSO, the default values were assigned to be for initial particles; thus, the tuning method would ensure that bandwidth would not decrease. By this method, we obtained velocity controller parameters with better bandwidth. After updating the velocity servo parameters, we then optimized the position controller (K_pp). Similar to velocity loop, we have:

• Maximize BW_pos..
• Subject to $\mathrm{Max}\left|G_p(iw)\right|\le 1$
•      Gain margin (GM) > 15 dB
•      Phase margin (PM) > 45°
•      ${\mathrm{BW}}_{pos.}<\frac{{\mathrm{BW}}_{vel.}}{3}$

where BW_pos. denotes the bandwidth of the position loop.

Note that Constraint 4, ${\mathrm{BW}}_{pos.}<\frac{{\mathrm{BW}}_{vel.}}{3}$, ensured system stability and only a small overshoot of the time response [33].

4.2. Comparison Results-One and Two Steps Optimization

Herein, we had a comparison of results of illustration for our approach. The tuning parameters (K_vp, K_vi, K_pp) were optimized simultaneously and by two-step optimization. Our approach was a two-step method, where the velocity loop control parameter (K_vp, K_vi) were first designed, and then the position loop K_pp was chosen to enhance the bandwidth, shown in Figure 9. Table 4 shows the comparison results of tuning results between one-step and two-steps. We found that the computation effort was reduced by our approach. An almost 50% improvement in computation time was saved. In summary, the two-step was better than the one-step in various aspects.

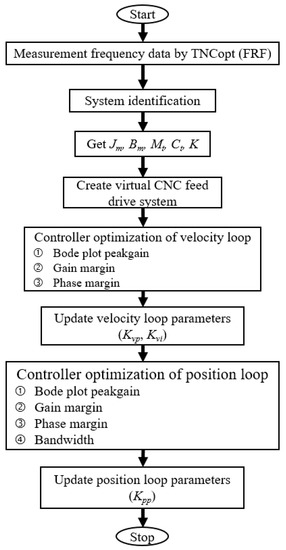
Figure 9. Intelligent tuning servo system flowchart.

Table 4. Comparison results of tuning results between one-step and two-steps.

Two-Step	1	2	3	4	5	6
Time (s)	199.9	210.8	323.5	344.4	513.3	501.9
Bandwidth (rad/s)	81.23	82.95	82.95	84.55	84.55	84.55
Particle (PSO)	25	30	30	35	35	40
Iteration (PSO)	200	200	500	500	600	600
One-Step	1	2	3	4	5	6
Time (s)	371.7	440.5	687.2	712.9	833.4	904.2
Bandwidth (rad/s)	42.58	27.33	41.14	43.64	42.74	79.18
Particle (PSO)	25	30	30	35	35	40
Iteration (PSO)	200	200	500	500	600	600

4.3. Machine Dr. System Development

We developed a platform to implement remote connection with machine tools, where the user could connect the machine tools and obtain the status of machines via the internet, called Machine Dr.; the functions illustration is shown in Figure 10. It is based on system identification, intelligent tuning servo systems, database processing, and cloud computing. Figure 10b illustrates the communication between machine tools and users. After receiving system identification data, Machine Dr. calculates the associated information of the machine and establishes corresponding data in the cloud, and then Machine Dr. also provides identification results and suggested P-PI controller parameters with the corresponding bandwidth. The Vendor can also get these information and supply services when needed. Thus, the vendor and users can reduce the maintenance duration and increase the efficiency of the machine tools.

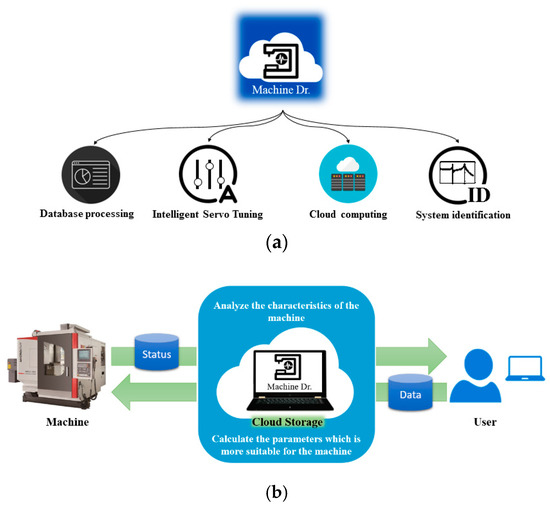
Figure 10. Illustration of the cloud platform—Machine Dr. system; (a) functions illustration; (b) communication between the user and the cloud servo system.

In addition, when the machine tools have already been in use for some time, and the stiffness of the structure may have changed, Machine Dr. recommends suitable parameters to enhance the bandwidth. Figure 11a shows the results of using the Machine Dr. The current system parameters obtained by system identification are shown in the right column and the suggested controller parameters are listed as below. Furthermore, Machine Dr. also provides the function of remote monitoring, since communication has already been established between the user and the CNC machine tools though the platform. When a user operates the software to survey the machine, the information of the machine is stored in the cloud, which is shown in Figure 11b. As the result, both the user and vendor can monitor the machine operation status, servo parameters, tuning history, etc. by their personal computer (PC) remotely.

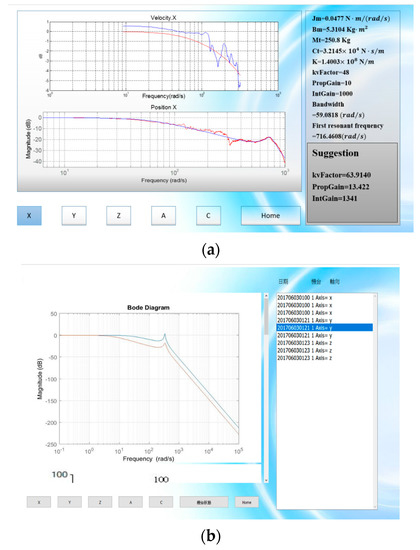
Figure 11. Operation illustration of the Machine Dr. (a) Auto-tuning screen; (b) Operation history data screen.

In summary, Machine Dr. combines cloud computing with knowledge of CNC machine tools to develop additional features for CNC machine tools. Machine Dr. provides customers and vendors a more easy method of controlling and obtaining information on machine tools. The vendor can also receive these data from the platform. As the result, the vendor can keep track the condition of CNC machine tools which are sold, and then services can be easily offered. In addition to this, if problems occur with the machine tools, the vendor may obtain the causes of the problems from the data stored in the cloud. Consequently, downtime and customers’ service time can be reduced.

5. Intelligent Servo Tuning Results

Table 5 shows the PI controller parameters and bandwidth of before and after optimization. A large and almost the same bandwidth of five axes feeding the drive systems, were obtained for synchronization. To verify the effectiveness of the intelligent servo tuning approach for MCU-5X CNC machine tools, there are some tests which are conducted with different parameter settings. The virtual feed drive system of the CNC machine tools is able to estimate the performance, and the tendency of simulation results are representative. The simulation and experimental results are introduced to illustrate our approach.

Table 5. Proportional-integral (PI) controller parameters and bandwidth values.

Before Optimization
Parameters	X-axis	Y-axis	Z-axis	A-axis	C-axis
Kpp	48	32	55	32	32
Kvp	10	10	8	12	200
Kvi	1000	1000	800	1400	20,000
Bandwidth (Hz)	9.3771	7.2411	10.6631	4.500	9.4743
After Optimization by PSO
Parameters	X-axis	Y-axis	Z-axis	A-axis	C-axis
Kpp	$63.914$	$48.532$	$65.1669$	$55.533$	$68.7714$
Kvp	$13.422$	$12.147$	$9.866$	$23$	$397.9897$
Kvi	$1341$	$1211$	$987$	$2305$	$41211$
Bandwidth (Hz)	$12.8667$	$12.2543$	$12.6139$	$11.1301$	$12.9859$

5.1. Simulation Results

We established the model with the optimized servo parameters with values shown in Table 5, and a spiral trajectory, shown in Figure 12, with high feed rate generated to evaluate the efficacy of intelligent servo tuning. From Table 6, we observed that both tracking error and contouring error were decreased.

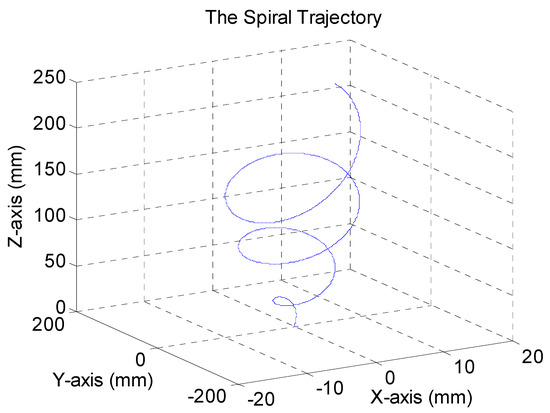
Figure 12. Spiral trajectory.

Table 6. Simulation result of spiral trajectory.

Tracking Error	X-Axis	Y-Axis	Z-Axis	Contouring Error
Before optimization	0.0017	0.0299	0.0027	0.0173
After optimization	0.0013	0.0197	0.0023	0.0164
improvement	23.53%	34.11%	14.81%	5.20%

There is another simulation for rotation axes, which is the harmonic movement of the A-axis and C-axis. We generated a sine wave with a particular frequency, which was treated as the desired reference. As shown in Table 7, the tracking error was lower than both the A-axis and C-axis. It was explicated that the servo parameters obtained from intelligent servo tuning took effect on the rotation axes.

Table 7. Simulation result of rotation axes.

Tracking Error	A-Axis	C-Axis
Before optimization	$1.65\times {10}^{-4}$	$2.53\times {10}^{-4}$
After optimization	$0.99\times {10}^{-5}$	$1.23\times {10}^{-4}$
improvement	40.28%	51.38%

The next simulation was the circular test, with a reference command consisting of 8 Hz angular frequency and a 1 mm radius circular path. Any two of the three axes would follow the command and the simulation results are shown in Figure 13, where Figure 13a,c,e are results of before optimization and Figure 13b,d,f are results of after optimization. The circular motion test illustrated that the performance of machine tool would be improved by an intelligent tuning servo approach. The reason why we selected 8 Hz as the reference command was that this frequency was near the bandwidth, and if the bandwidth increased, the system performance would be obviously improved. Compared to the frequency within the bandwidth, the optimized FRF showed that 8 Hz had an obvious rise. As shown in Table 8, there was a significant improvement in both contouring errors and tracking errors.

Figure 13. Simulation result of circular motion tests. (a) Before optimization (X-Y), (b) After optimization (X-Y), (c) Before optimization (X-Z), (d) After optimization (X-Z), (e) Before optimization (Y-Z), (f) After optimization (Y-Z).

Table 8. Contour error and tracking error RMSE of circular motion.

Simulation Result of Circular Motion
Axes\Errors		Contouring Error		Tracking Error
		RMSE (mm)	Max. (mm)	RMSE (mm)	Max. (mm)
X-Y Axes	Default	0.2566	0.2637	1.1497	1.1567
	Our approach	0.2079	0.2136	1.1362	1.1418
	Improvement	18.98%	19.00%	1.17%	1.29%
X-Z Axes	Default	0.2253	0.2617	1.1402	1.1772
	Our approach	0.1984	0.2061	1.1330	1.1407
	Improvement	11.94%	21.25%	0.63%	3.10%
Y-Z Axes	Default	0.2315	0.2743	1.1411	1.1852
	Our approach	0.2027	0.2159	1.1342	1.1476
	Improvement	12.44%	21.29%	0.60%	3.17%

5.2. Experiment Results

The corresponding experimental results are introduced in Figure 14, Figure 14a,c,e are results before optimization and Figure 14b,d,f are results after optimization. Due to the limitations of the mechanism, the maximum value of angular frequency was about 3–4Hz. Here, the reference command was 3 Hz. As shown in the Table 9, we observed our approach results had smaller contour errors, especially since the reference 3 Hz was within the bandwidth, and the reference frequency was at a distance from the bandwidth. In other words, the reference was located at a flat interval, which meant that the frequency had slight variations in the range. As Figure 14 shows, the experimental results still showed that our intelligent servo tuning method was effective.

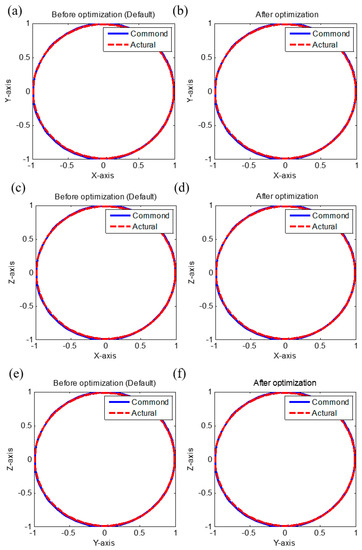
Figure 14. Experiment result of circular tests. (a) X-Y axis (default setting), (b) X-Y axis (optimized setting), (c) X-Z axis (default setting), (d) X-Z axis (optimized setting), (e) Y-Z axis (default setting), (f) Y-Z axis (optimized setting).

Table 9. Contour error and tracking error RMSE of circular test.

Experiment Result of Circular Motion
		Contouring Error		Tracking Error
		RMSE (mm)	Max. (mm)	RMSE (mm)	Max. (mm)
X-Y Axes	Default	0.0087	0.0326	0.2483	0.7863
	Our approach	0.0076	0.0284	0.2478	0.7808
	Improvement	12.64%	12.88%	0.201%	0.700%
X-Z Axes	Default	0.004	0.0142	0.2526	0.7753
	Our approach	0.0036	0.0132	0.2525	0.7745
	Improvement	10.00%	7.04%	0.04%	0.103%
Y-Z Axes	Default	0.0065	0.0196	0.2475	0.7790
	Our approach	0.0060	0.0181	0.2474	0.7748
	Improvement	7.69%	7.65%	0.04%	0.54%

6. Conclusions

This study has introduced an intelligent tuning technique for CNC servo systems using a PSO algorithm with constraints. The proposed approach contained a system identification phase and a servo tuning phase based on the same bandwidth for all axes feed drive systems. The PSO algorithm was adopted to obtain the controller parameters and maximize the corresponding bandwidth. An efficient two-step servo tuning method based on gain/phase margins was proposed for high speed and precision requirements. All feed drive systems controller gains were optimized simultaneously for synchronization. Eventually, these techniques and our research results were integrated into an intelligent cloud computing software, Machine Dr. In this paper, the machine tool MCU-5X was used to demonstrate the effectiveness and performance of intelligent tuning. Simulation and experimental results were introduced to illustrate the effectiveness of the proposed approach. Furthermore, Machine Dr. combined the cloud computing with the knowledge of CNC machine tools to develop additional features for CNC machine tools. Machine Dr. provides customers and vendor with greater ease of controlling and obtaining information on machine tools.