Abstract
The existence, stability, and dynamics of bound pairs of symbiotic matter waves in the form of dark-bright soliton pairs in two-component mixtures of atomic Bose–Einstein condensates is investigated. Motivated by the tunability of the atomic interactions in recent experiments, we explore in detail the impact that changes in the interaction strengths have on these bound pairs by considering significant deviations from the integrable limit. It is found that dark-bright soliton pairs exist as stable configurations in a wide parametric window spanning both the miscible and the immiscible regime of interactions. Outside this parameter interval, two unstable regions are identified and are associated with a supercritical and a subcritical pitchfork bifurcation, respectively. Dynamical manifestation of these instabilities gives rise to a redistribution of the bright density between the dark solitons, and also to symmetry-broken stationary states that are mass imbalanced (asymmetric) with respect to their bright soliton counterpart. The long-time dynamics of both the stable and the unstable balanced and imbalanced dark-bright soliton pairs is analyzed.
1. Introduction
After the experimental realization of Bose–Einstein condensates (BECs) in ultracold atoms, a plethora of studies has been devoted to examining and understanding the coherent structures that arise in them [1,2,3,4]. Among these structures, the formation, interactions and dynamics of matter wave dark [5,6,7] and bright solitons [2,8,9] have been a central focus of research both from the experimental and from the theoretical side. Such nonlinear waves were experimentally generated in single-component BECs over a decade ago [10,11,12,13,14]. The nature of nonlinear matter waves that can be created in a BEC background depends on the type of the interatomic interactions. Namely, dark solitons can be created in BECs with atom–atom repulsion resulting from a positive scattering length, while bright solitons exist in single-component settings with attractive interatomic interactions resulting from a negative scattering length.
In addition to the above single-component context, soliton states can arise also in multi-component settings. Such condensates have been created as mixtures of different spin states of Rb [15,16] and Na [17], and triggered numerous theoretical studies involving soliton complexes. A prototypical example of the latter is a coupled dark-bright (DB) soliton state in a highly elongated (quasi-one-dimensional) condensate cloud, consisting of a dark soliton in one component and a bright soliton in the second component of a binary BEC featuring intra- and inter-species repulsion. Since bright solitons are not self-sustained structures in repulsive (self-defocusing) media, DB solitons are often called symbiotic, that is, the dark soliton can be thought of as acting as an effective potential well trapping the bright soliton [18,19,20,21,22]. Such symbiotic entities were first observed and theoretically studied in the context of nonlinear optics [23,24,25,26,27,28,29,30,31,32]. However, their experimental realization in the atomic realm [33] opened a new and highly controllable direction towards a deeper understanding of the dynamics and interactions of these states both with each other as well as with external traps [34,35,36,37,38].
Additionally, current state-of-the art experiments offer the possibility of manipulating in a controllable fashion the nonlinear interactions via the well-established technique of Feshbach resonances [39,40,41,42,43,44,45]. This motivated recent theoretical activities where the static and dynamical properties of dark-bright symbiotic matter waves have been investigated on the level of mean field theory. Mathematically, tuning the interactions corresponds to deviating from the integrable limit [46,47,48] of the relevant nonlinear Schrödinger system, where nonintegrability is introduced when considering arbitrary nonlinearity (i.e., interaction) coefficients. The latter nonintegrable setting forms also the main focus of the present effort. In this context, despite the nonintegrability, analytical expressions of specific single-DB soliton states and lattices thereof have been obtained in [49]. Adding a parabolic trapping potential, it was revealed how the effective restoring force acting on the DB soliton depends on the inter-atomic interactions [49], verifying that the particle-like nature [34] of the symbiotic soliton is preserved. In the same spirit, the dependence of the binding energy of a DB soliton on the inter-species interactions was found analytically in [22], where, moreover, a proper bound on a phase imprinted in the bright soliton constituent was obtained (i.e., considering also moving single DB states), above which a breaking of the symbiotic entity was observed.
In our previous work [50], the interactions between DB matter waves and the consequent formation of bound states for out-of-phase (anti-symmetric) bright soliton components has been studied. Based on a two-soliton ansatz of the hyperbolic type [37,49], the full analytical expressions for the interaction energies between two DB solitons were obtained for arbitrary nonlinear coefficients, and in the absence of a confining potential. Furthermore, the key intuition that repulsion mediated by the dark solitons at short distances, and attraction mediated by anti-symmetric bright solitons at longer distances, would be counterbalanced, leading in turn to a bound state formation, has been enriched by taking into account the significant role of the cross-component interaction energy term. The crucial dependence of the latter on the inter-species interaction coefficient has been analyzed. It was shown that anti-symmetric stationary states exist and remain robust for a wide parametric window of inter-species repulsions. Importantly, an exponential instability of the anti-symmetric states was identified upon crossing a critical inter-species repulsion. The latter was found to be associated with a subcritical pitchfork bifurcation, giving rise to asymmetric stationary states with mass imbalanced bright soliton counterparts.
In the present work, we extend the aforementioned findings of [50] upon considering significant deviations from the integrable limit. By this, we mean that we always utilize a more realistic selection of the nonlinear inter- and intra-species repulsion coefficients motivated by Rb (see details in Section 3), under which it is never possible that all coefficients are equal (which would represent the integrable limit). In our analysis, we vary the inter-species repulsion towards both the immiscible (i.e., dominated by inter-species repulsion and thus phase separated in the ground state) regime, but also towards the miscible (i.e., dominated by intra-species repulsion) regime. To this end, we investigate the stability and dynamics of the anti-symmetric states, the so-called “solitonic gluons” [24], as well as the above-mentioned asymmetric modes covering both the miscible and immiscible parameter regime. In particular, the full excitation spectrum of these symbiotic states is explored in detail by means of a Bogolyubov–de Gennes linearization analysis [1]. It is found that, for the asymmetric modes, the linearization spectrum is strongly affected when crossing the immiscibility-miscibility threshold, which is, in turn, directly connected with a rapid change of their density profiles as observed already in [50]. As a next step, the stability and dynamics of the anti-symmetric DB pairs are explored past the immiscibility-miscibility threshold. It is found that, in addition to the destabilization in the immiscible regime reported in [50], a second critical point occurs deep in the miscible regime, rendering the anti-symmetric state unstable once more. This instability scenario is found to be associated with a supercritical pitchfork bifurcation, giving rise to another family of mass imbalanced (asymmetric) symbiotic structures which are found to be stable. As the inter-species repulsion is decreased, the miscible character of this regime alters the bright soliton component, resulting into asymmetric pairs with the bright solitons ”living” on top of a finite background. Comparing and contrasting the instability mechanisms in the different parameter regimes, the long-time evolution of the asymmetric and anti-symmetric states is performed numerically at different interaction ratios.
The presentation is structured as follows. In Section 2, a description of the theoretical model and prior results regarding the existence of the anti-symmetric DB soliton pairs are provided. Furthermore, we briefly comment on the methods to be used for the numerical analysis of our findings. Section 3 contains the results regarding both the stability and the dynamics of asymmetric and anti-symmetric DB soliton pairs beyond the integrable limit. Finally, in Section 4, we summarize our findings and discuss future perspectives.
2. Setup and Prior Background
2.1. Model and Theoretical Considerations
The system of interest is a two-component BEC strongly elongated along the x-direction, subject to a tight transverse harmonic trap of frequency . Such a mixture can e.g., be composed of two different hyperfine states of the same alkali isotope, like Rb. Within mean field theory and after integrating out the frozen transverse degrees of freedom, this mixture is described by the following two coupled (1+1)-dimensional Gross–Pitaevskii equations (GPEs) [51,52]:
In the above equation, denote the mean-field wave functions of the two components normalized to the numbers of atoms , while m and are the atomic mass (identical for both components) and chemical potentials, respectively. The effective one-dimensional coupling constants are given by , where denote the three s-wave scattering lengths that account for collisions between atoms belonging to the same () or different () species. We restrict our considerations to purely repulsive interactions, i.e., all , and consider an idealized homogeneous setting with no longitudinal trapping potential along the x-axis.
By measuring densities , length, time and energy in units of , , , , respectively, and in a second step rescaling space-time coordinates as , , and the densities , the system of Equation (1) can be written in the following dimensionless form:
In the above system of equations, we slightly changed the notation, using and , indicating this way that the component 1 (2) will be supporting dark (bright) solitons. Furthermore, is the rescaled chemical potential, while the interaction coefficients are normalized to the scattering length , i.e., , and . The system of Equations (2) and (3) conserves the total energy, E, the rescaled total number of atoms in each component ( and , respectively) and the rescaled total number of atoms N, where:
2.2. Interactions of Symbiotic Matter Waves beyond the Integrable Limit
In the special case where the nonlinear coefficients are all equal to each other, i.e., , the system of Equations (2) and (3) admits exact single-DB-soliton solutions of the form [34]:
subject to the boundary conditions , and for . In the aforementioned solutions, is the so-called soliton’s phase angle, which fixes the “grayness” of the dark soliton, while denotes the amplitude of the bright component. Furthermore, and D correspond to the soliton’s center and inverse width, respectively, while is the wave-number of the bright soliton, associated with the speed of the DB soliton, and is its phase.
While such a general exact expression can only be obtained in the integrable limit, one can utilize an approximate ansatz based on the expressions given in Equations (6) and (7) and depart from the integrable limit. Such a method was employed in our very recent work of Ref. [50] in order to analyze effective interactions between symbiotic matter waves in the general case of different inter-atomic repulsion strengths within each and between the species. Our aim in what follows is to briefly comment on the key results obtained there, in order to be connected with the numerical findings that will be presented below. In particular, a pair of two equal-amplitude dark-bright solitons travelling in opposite directions was considered having the approximate form:
In these expressions where is the distance between the two DB solitons, while is the relative phase between the bright solitons. If , the bright solitons are in-phase (IP), while if , the bright solitons are out-of-phase (OP) or anti-symmetric. Within a Hamiltonian variational approach [3,7,37,49], the approximate ansatz of Equations (8) and (9) is substituted into the total energy of the system given by Equation (4), and the relevant integrations are performed under the assumption that the soliton velocity is sufficiently small (, ). Full analytical results for all the integrals contributing to E were obtained in [50]. At large distances between the solitons, , simplified asymptotic expressions can be derived by expanding with respect to (see also the earlier findings for the integrable case [37]). The total energy can be decomposed as , where corresponds to the energy of a single DB soliton, contributing twice to the total energy, while the remaining three terms, namely, , and , account for the interaction between: the two dark solitons, the two bright solitons, and the cross-interaction of a dark soliton in the first component with the bright soliton of the second component, respectively.
Figure 1 illustrates our key findings regarding the interaction energy of two out-of-phase DB solitons as a function of their distance. Here and throughout this work, the chemical potential and the intra-species interaction coefficients are fixed to and [53,54], respectively, while the interatomic interaction coefficient is left to widely vary. In panels (a)–(c) both the full and the approximate asymptotic, i.e., expanded to second order with respect to , forms of the variationally obtained total interaction energy, , are shown with solid green and dashed yellow lines, respectively. As it can be seen in all cases, the two results coincide at large distances as they should. Strikingly, in all three cases, a pronounced local energy maximum is identified. The identification of this extremum suggests, if we further take into account the effective negative mass of the DB soliton [7], the existence of an effective stable (with respect to variations in ) fixed point, thus a bound state for the two OP dark-bright solitons. Such an anti-symmetric two-DB soliton bound state can indeed be identified also in the full Gross–Pitaevskii system (for the numerical methods used, we refer the reader to the following section). The predictive strength of the variational approximation is directly checked by comparing with the full numerical computation of the respective equilibria on the level of Equations (2) and (3), and the outcome is illustrated in panel (d), showing good agreement.
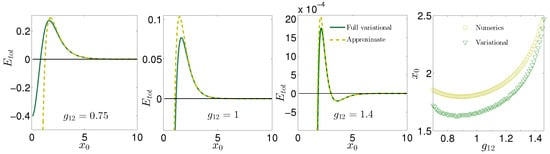
Figure 1.
Variational estimate of the total interaction energy between two OP dark-bright solitons. From left to right in panels (a–c), the value of the inter-species interaction coefficient is increased from to , while and throughout. In all cases, both the full and the asymptotic (valid for large ) expressions are shown with solid green and dashed yellow lines, respectively. The equilibrium separation of the stationary DB soliton pair as a function of is shown in panel (d). In this latter panel, circles in yellow correspond to the equilibrium distance obtained by numerically solving the GPE system of Equations (2) and (3), while triangles in green denote the variational prediction of the equilibrium, i.e., the respective maximum of .
It is worth mentioning at this point that, in order to evaluate the energy functional, we need as input the width D and amplitude occurring in Equations (8) and (9). These are obtained by numerically identifying the exact single-DB state at the given and fitting to it the profile known from the integrable limit, i.e., Equations (6) and (7). There are thus two main sources of error of this scheme, namely: (i) the imperfect fit of the - profile (strictly valid only in the integrable limit) to the single DB soliton mode and (ii) the limited accuracy of the two-DB soliton ansatz of Equations (8) and (9), especially at small separations . For details regarding this and also a discussion of the case of in-phase bright solitons, we refer the interested reader to Ref. [50]. We note also that as increases (while and are kept fixed), the norm of the bright species is increasingly suppressed and eventually vanishes [50], beyond which point there is no bound two-soliton state anymore, since the presence of the bright component is a necessary ingredient for holding the dark solitons together [24,37]. This suppression of the bright norm is compatible with the overall decrease of the total energies from panel (a) towards (b) and (c) in Figure 1.
Having variationally predicted and numerically confirmed the existence of anti-symmetric stationary dark-bright soliton bound states for a large interval of values of the inter-species interaction parameter (typically, we study in the present work), our main goal in the following is to address their stability and (where applicable) decay dynamics.
2.3. Numerical Methods
In this section, we briefly comment on the numerical methods to be used so as to obtain stationary symbiotic states consisting of two dark-bright solitons and to determine their stability and time evolution. In the numerical computations that follow, we initially obtain stationary solutions of the system of Equations (2) and (3) in the form of and by means of a fixed-point numerical iteration scheme [55]. The linear stability of the latter is adressed by using the Bogolyubov–de Gennes (BdG) analysis [7,52]. Particularly to assess the stability of the obtained fixed points, we substitute the following ansatz into Equations (2) and (3):
In the above equations, the asterisk denotes complex conjugation while is the amplitude of infinitesimal perturbations. The resulting system of equations is then linearized, by keeping only terms of order , and the eigenvalue problem for the eigenfrequencies and eigenmodes is solved numerically. Note that an instability occurs if modes with purely imaginary or complex eigenfrequencies are identified [1]. Since the linearization spectrum is invariant under and , only results in the first quadrant of the complex plane will be shown below. For the simulation of the time evolution based on Equations (2) and (3), a fourth order Runge–Kutta algorithm is employed and a second-order finite differences method is used for the spatial derivatives. The grid spacing is fixed to , while the time step used is . In all cases, the numerical computations are performed on a spatial grid in the presence of an almost hard-wall super-Gaussian potential [50] that is chosen wide enough for boundary effects to be negligible on the small and intermediate time scales considered herein.
3. Numerical Results
Having verified that stationary anti-symmetric pairs of symbiotic matter waves can be found in a wide range of values of the inter-species repulsion coefficient , a natural next step is to consider the fate of these solutions under small perturbations, providing information on their stability in the different regions of existence. The latter is explored by using the BdG linearization analysis discussed in Section 2.3. For the presentation of our results, we will distinguish the miscible () and immiscible () regimes, separated by the miscibility–immiscibility threshold [56] for our choice of .
In Figure 2, the BdG spectrum of the anti-symmetric stationary two dark-bright soliton states is shown as a function of . In particular, both the real and the imaginary parts of the eigenfrequencies are depicted in the top (a) and middle (b) panels, respectively. Panels (c) and (d) depict profiles of the dark and bright wave functions at selected values of in the miscible and immiscible regime, respectively. Two general comments can be made before examining in detail the excitation spectrum. The most significant one is that, within the background spectrum denoted with blue circles, there exist two distinguished modes. The trajectories of the latter are illustrated with red stars. These modes are the so-called anomalous modes since they possess a so-called negative Krein signature K [57], which, for the two-component system considered herein, is defined as:
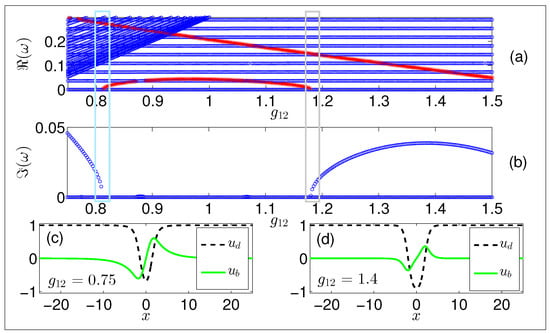
Figure 2.
Full BdG spectrum of anti-symmetric two-DB soliton states, upon varying the inter-species interaction coefficient within the interval . (a) real part, , of the eigenfrequencies as a function of . The corresponding imaginary part, , is shown in panel (b). Upon increasing there exist two critical values, , and , indicated with light blue and gray boxes, respectively, below and above which the anti-symmetric branch destabilizes. The trajectories of the two anomalous modes (see text) appearing in the spectrum are shown with red stars. (c,d) profiles of the anti-symmetric states for , and , i.e., deep in the miscible and immiscible regime, respectively.
The sign of this quantity is a topological property associated with the excited nature of this state, and the eigenvectors of such anomalous modes result in a variation of the solitary waves (as opposed to a variation of the system’s background). Furthermore, we note in passing that each continuous symmetry of the system corresponds to a pair of zero modes, , in the BdG spectrum. Thus, we expect three pairs of such modes related, respectively, with the conservation of the particle number (or the gauge invariance) in each of the two components, and with the translation invariance due to the absence of a confining potential. This is confirmed in the numerical data.
Just by inspecting the trajectories of the two anomalous modes that appear in the spectrum, their very different behavior becomes apparent. As it is observed in panel (a) of Figure 2, the higher frequency mode decreases almost monotonically upon increasing . We were able not only to identify this mode but also to relate it with an out-of-phase vibration of the bound DB soliton pair around its equilibrium distance. The latter can be done by adding the corresponding BdG eigenvector, which turns out to be localized in the vicinity of the DB pair, to the relevant stationary anti-symmetric state (results not shown here). Next, and also in the same panel of Figure 2, let us closely follow the trajectory of the lower-lying anomalous mode. The trajectory of this mode is more complicated than the former one. In particular, starting from the aforementioned reference point, , and increasing the interspecies interactions towards the immiscible regime, i.e., for , it can be seen that there exists a critical point where this mode destabilizes. This destabilization corresponds to an eigenvalue zero crossing and signals the instability of the anti-symmetric configuration deep in the immiscible regime. Notice the non-zero imaginary part that appears past this critical point shown in panel (b) of Figure 2. The existence and destabilization of this mode was found to be related with a symmetry breaking of the bright soliton component, being linked, in turn, to other stationary states that are mass imbalanced with respect to their bright soliton counterpart. The identification of these asymmetric states which exist below and collide with the anti-symmetric branch at in a subcritical pitchfork bifurcation was established in [50]. It is worth mentioning, at this point, that such asymmetric states were also analytically obtained in [31] in the integrable limit of the theory. However, to the best of our knowledge, the stability of such states has not been addressed. The following paragraphs will be devoted to a discussion of these asymmetric two-DB solutions, before we then return to an analysis of the BdG spectrum of the anti-symmetric pair, Figure 2, at small values of .
As mentioned above, the asymmetric and the anti-symmetric two-DB states coincide at the bifurcation point . Below this critical , the anti-symmetric state is stable and there are two symmetry-broken asymmetric solutions which are unstable (as is characteristic of a subcritical pitchfork bifurcation). Indeed, these asymmetric branches can themselves be continued towards much smaller values of and exist both in the immiscible and the miscible regime (see the profiles shown in Figure 3c,d). In both panels, dashed black lines denote the wavefunction of the dark soliton component, while solid green lines depict the corresponding bright soliton counterpart. To gain further insight regarding the nature of the instability of these asymmetric states, their full BdG spectrum is illustrated in Figure 3a,b. Once more, both the real and the imaginary parts of the eigenfrequencies are shown as a function of the interspecies interaction. As expected from the above discussion, only one of the anomalous modes appears in the excitation spectrum of these mass imbalanced states and is depicted with stars in red. Replacing the second anomalous mode, there is now throughout a purely imaginary frequency signaling the instability of the asymmetric branch. Remarkably, as the immiscibility-miscibility threshold is crossed, the growth rate of the instability is drastically decreased, rendering these states only weakly unstable for . This latter observation is in close contact with the change in the spatial character of these asymmetric states, and also in line with our previous findings [50]. Namely, as the interspecies interactions decrease towards the miscible region, the asymmetric states change gradually from only weakly asymmetric (i.e., weakly mass imbalanced with respect to their bright amplitudes), to maximally asymmetric (i.e., almost purely dark/dark-bright bound states). The difference is clearly seen in the profiles provided in panels (c) and (d) of Figure 3. The existence of such maximally asymmetric bound states can be intuitively understood as follows. We have found in [50] that the effective interaction between dark solitons () is repulsive while the interaction between OP bright solitons () with fixed and is attractive. Furthermore, the cross term effective interaction () is also attractive within the interval considered herein (again, we refer the reader to the relevant analytical expressions obtained in [50]). Thus, in the limiting case of maximal asymmetry, while the bright-bright interaction is absent, the dark-bright one is still present. It is this latter cross term attraction that counterbalances the dark-dark repulsion, leading in turn to the observed bound state formation.
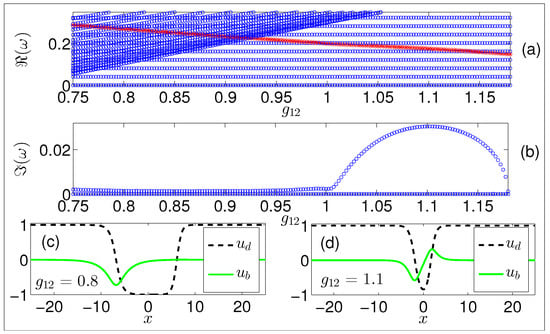
Figure 3.
BdG spectrum for the asymmetric two-DB soliton states. (a) real part, , of the eigenfrequencies as a function of . The corresponding imaginary part, , is shown in panel (b). Notice in this case the significant modification of the stability properties (i.e., a nearly vanishing imaginary part of the eigenfrequency in panel (b)), as the miscibility-immiscibility threshold is crossed. (c,d) profiles of the asymmetric states for , and , i.e., in the miscible and immiscible regime, respectively.
Having identified the unstable linearization eigenmodes, we now turn to the associated decay dynamics. In particular, Figure 4 shows the long-time dynamics of the above-obtained stationary asymmetric states for different values of the nonlinear coefficient . Panels (a)–(d) correspond to the dark soliton component while the respective bright wave functions are depicted in panels (e)–(h). For shown in panels (a)–(c) and (e)–(g), respectively, it is observed that, as a result of the instability, the solitons move towards each other forming breathing-like structures. This is accompanied by a redistribution of the bright “filling” component between the two dark solitons, in the form of almost complete tunneling back and forth. For parameter values slightly above , as e.g., the one depicted in panels (c) and (g), a strong beating phenomenon is observed, clearly evident in the dark soliton component, with the solitons oscillating around a fixed distance from each other forming an almost stationary breather that persists until the end of the propagation. Below the above-mentioned threshold and towards the miscible region, the picture becomes progressively more dramatic. The beating gets much more pronounced with the solitons experiencing more frequent collisions as shown in panels (b) and (f). Finally, when entering even deeper into the miscible side illustrated in panels (a) and (e), eventually the bound pair fully splits into an essentially empty dark and a dark-bright soliton that are released (i.e., are no longer bound by each other) and propagate towards the outer parts of the simulation domain (where they are ultimately reflected by the boundaries). However, for , i.e., upon increasing towards the immiscible side depicted in panels (d) and (h) of Figure 4, a rather different picture is painted by the symbiotic entities when compared to the asymmetric states presented above. In particular, slightly after the beginning of the propagation, where the asymmetric entity looked quite robust, a dramatic redistribution of the bright soliton’s mass occurs. The latter results in a strong repulsion between the single DB soliton formed and the almost empty dark one, leading in turn to their subsequent separation. Note that a similar decaying mechanism was also observed in [50] but for the unstable anti-symmetric states (see also later on in the text).
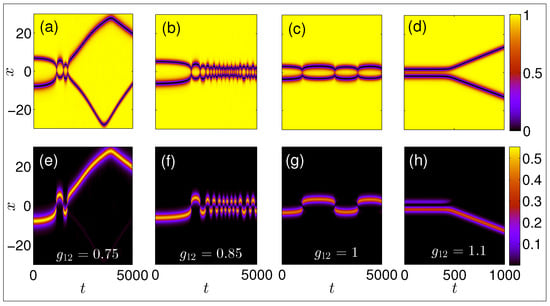
Figure 4.
Space-time evolution of the unstable asymmetric two-DB soliton state for different values of the inter-species interaction coefficient . From left to right, the interaction is increased from to , while panels (a–d) ((e–h)) correspond to the densities () of the dark (bright) component.
We have now characterized the branch of asymmetric two-DB soliton modes, which were seen to bifurcate from the anti-symmetric two-DB soliton branch in a subcritical pitchfork bifurcation in the immiscible regime, at . Let us now return to the anti-symmetric branch itself and study its fate in the miscible regime. This regime is also covered in the full excitation spectrum depicted in Figure 2, with a typical profile of the state being shown in panel (c). Departing from towards the miscible regime, and in particular by following once again the lower-lying anomalous BdG mode, we observe that as decreases a second critical point that exists deep within the miscible side. The eigenvalue zero crossing occurs at , and is indicated by the solid light blue box. We note here that this latter critical point was not discussed in our previous work [50], where only larger values of were studied. The destabilization of the aforementioned mode suggests the existence of a second pitchfork bifurcation. This is, once again, related with a symmetry breaking of the bright soliton component, resulting in mass imbalanced (i.e., asymmetric) two DB states. Indeed, we were able to identify these new pairs. In contrast to the previous instability scenario, these mass imbalanced states exist past the critical point but are stable, i.e., the pitchfork deep in the miscible domain is found to be supercritical. The corresponding bifurcation diagram is shown in panel (a) of Figure 5. In order to obtain this diagram, we measure the relative bright imbalance defined as upon varying . Notice that four branches are identified, i.e., three stable ones consisting of two asymmetric and an anti-symmetric branch all denoted by solid blue lines, and one unstable anti-symmetric branch illustrated with a dashed green line. To further demonstrate the stability of the new asymmetric symbiotic pairs in panels (b)–(d), the BdG spectra are shown for different values of the inter-species interactions below the associated critical point . Two anomalous modes appear in the linearization spectra of these asymmetric states illustrated with red stars. The respective stationary wave profiles are depicted in panels (e)–(g), where the dark (bright) soliton wavefunction is shown with a dashed black (solid green) line. We observe, that upon decreasing the asymmetry between the bright solitons increases, as was also the case for the respective asymmetric but unstable states found in the immiscible regime. Furthermore, for , a background gradually builds up for the bright solitons as is evident in the stationary state shown in panel (e) of Figure 5, revealing the miscible character of the regime supporting these states. Our detailed BdG analysis indicates that, for all values within the miscible regime that we have checked, the asymmetric states exist as stable configurations and should remain dynamically robust. This result is verified and highlighted in panels (h)–(m) of Figure 5, where we use as initial condition the stationary asymmetric states depicted in panels (e)–(g). We note that, in all three cases, panels (h)–(j) ((k)–(m)) show the evolution of the dark (bright) soliton component. Having studied both the static and the dynamical properties of the new asymmetric structures that bifurcate from the OP dark-bright states, we now turn our attention to the dynamics of the anti-symmetric DB waveforms.
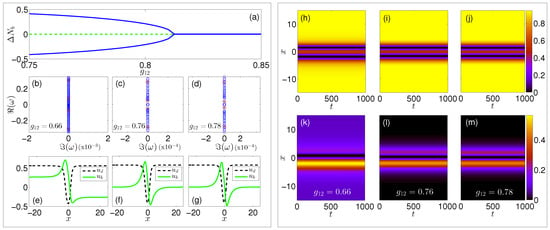
Figure 5.
(a) bifurcation diagram obtained by measuring the relative bright imbalance as a function of the inter-species interaction coefficient . The stable anti-symmetric and asymmetric branches are denoted with solid blue lines, while the unstable anti-symmetric one is shown with a dashed green line. Notice that the asymmetric branches exist before the critical point, , but are stable verifying the supercritical nature of the bifurcation. (b–d) BdG spectra at three different values of showcasing the stability of the asymmetric states. In all cases, the anomalous modes are illustrated with red stars. The associated stationary DB profiles are depicted in panels (e–g). (h–m) spatio-temporal evolution of the stationary asymmetric states shown in panels (e–g) showing the dynamical stability of these symbiotic structures. Panels (h–j) ((k–m)) correspond to the dark (bright) soliton component.
In particular, we explore the long time evolution of the OP DB states so as to reveal the decay mechanisms that such a pair suffers from. The dynamics at different values of are summarized in Figure 6, all initiated at equilibrium. As before, the upper row of panels (a)–(d) shows the spatio-temporal evolution of the dark soliton counterpart, while panels (e)–(h) depict the corresponding bright component. From the stability analysis presented above, it is expected that for all values of the interspecies interaction coefficient the anti-symmetric two dark-bright soliton states exist as stable configurations, and as such should be robust throughout the propagation. This latter result is confirmed in panels (c) and (g) of Figure 6, for which is slightly above the lower critical point. However, and as anticipated, a very different picture is found below the critical point depicted in panels (b) and (f), (a) and (e), respectively. Starting with the former, we observe that slightly below the initial stationary state quickly decays and in (b) and (f) we observe periodic tunneling of the bright component between the two dark solitons, while the dark solitons are only relatively weakly affected here. It is worth mentioning that similar tunneling dynamics have been identified and interpreted in terms of a bosonic Josephson junction model in [58], but with the crucial difference that the soliton pair was further supported by the restoring force of a harmonic trap in that work, while, in our present setup, there is no external potential that would keep the dark solitons in place. Remarkably, in this regime, despite the mass exchange, the bound soliton pair does not disintegrate. Further decreasing in panels (a) and (e), the effects of the instability are more drastic. The time scale of the bright component oscillations decreases and the dark solitons vibrate more strongly. After some time of almost periodic oscillations, a more irregular type of motion sets in, with both dark solitons (one filled by most of the bright component, the other almost empty) eventually moving towards positive x while separating and recolliding in the process, suggesting still a kind of effective attractive interaction between them. This decay mechanism deep in the miscible regime is to be contrasted to the unstable dynamics in the immiscible regime above . In panels (d) and (h), we show the time evolution of the anti-symmetric two-DB soliton state at . While initially almost no dynamics are visible in the densities, especially no oscillations within the bright component, on intermediate time scales, a strong asymmetry in the bright filling builds up (see again [50] for a more detailed discussion) and subsequently the filled and the empty dark soliton split, showing no sign of effective attraction. Notice that the above described decaying mechanism is rather similar to the one observed for the unstable asymmetric states for (see panels (d) and (h) of Figure 4).
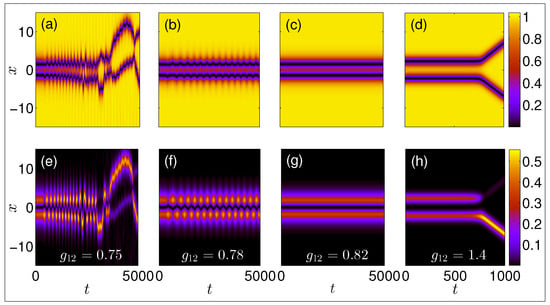
Figure 6.
Space-time evolution of the anti-symmetric stationary two-DB state for different values of the inter-species interaction coefficient . From left to right, the interaction is increased from to and then to . Panels (a–d) ((e–h)) correspond to the densities () of the dark (bright) component.
4. Discussion
In the present contribution, we investigated in detail the stability and dynamics of bound pairs of dark-bright symbiotic solitons, which arise as nonlinear matter wave excitations in mixtures of Bose–Einstein condensates featuring inter-atomic repulsion. In particular, we explored the scenario of differently weighted inter- and intra-species interaction coefficients, breaking the integrability of the relevant nonlinear Schrödinger model. It was argued by means of a recently proposed variational approach [50] and shown numerically that, upon departing from the integrable limit, bound states of such symbiotic entities exist for anti-symmetric bright soliton counterparts, the so-called solitonic gluons. These anti-symmetric states were found to be robust within a bounded interval of the inter-species repulsion coefficient , limited by critical points both in the miscible and in the immiscible regime of the model, associated with a supercritical and a subcritical pitchfork bifurcation, respectively. Below and above these boundaries, i.e., deep in the miscible and the immiscible regime, respectively, the anti-symmetric pair becomes unstable. Long-time propagation revealed differences, but also common characteristics of the decay mechanisms in the two domains of instability. Specifically, a striking common feature is the relevance of bright mass transfer between the two dark-bright solitons. In particular, in the miscible domain, we identified new stationary asymmetric states that bifurcate from the anti-symmetric ones in a supercritical pitchfork. The stability of the new asymmetric states was also dynamically confirmed. Moreover, it was shown that a further decrease of the interspecies repulsion results in asymmetric states with the bright solitons living on top of a finite BEC background, highlighting in this way the miscible character of such bound pairs. In contrast to the above picture, upon entering the immiscible regime, we had found in our recent work [50] that the destabilization of the anti-symmetric dark-bright soliton pair is caused by a subcritical pitchfork bifurcation involving an unstable stationary, mass-imbalanced dark-bright soliton pair mode. In the present work, we further explored the range of existence and stability of this asymmetric branch, demonstrating its overall instability and its substantial deformation upon entering the miscible regime.
There are many directions that are worth considering in the future along the lines of this work. In particular, by fixing the intra-species interactions in this work, we have not addressed the fate of the dark-bright soliton pair states when actually approaching the integrable limit, which would require . In this respect, it would be particularly interesting to see if the asymmetric state fully stabilizes upon restoring integrability or maintains its weakly unstable nature. Towards this direction, and since in the integrable limit exact solutions are available [31,59], one could link the anti-symmetric and asymmetric states obtained here with the exact families of dark-bright soliton solutions known in the integrable case. Establishing a possible connection of this type would also open a new direction of exploration and understanding of the symbiotic soliton pairs, since, in such a case, one could depart once more from the integrable limit, but having at hand exact analytical expressions for the two-soliton problem rather than the approximate ones constructed only from the single soliton solution, as used in our present work. Furthermore, and also in this direction, in the integrable model, exact closed form expressions exist not only for static symbiotic states like the ones considered here, but also for moving and scattering ones. Based on these, one could hope to get insights into the collisional dynamics of symbiotic entities at least in the vicinity of the integrable limit, paving the way for a detailed understanding of features like the breathing state formation observed here. Studies along these lines are left for future work.
5. Conclusions
In the present work, the existence, stability, and dynamics of symbiotic matter wave solitons that exist as nonlinear excitations in -dimensional repulsively interacting mixtures of BECs has been investigated. Significant deviations from the integrable limit of the theory were considered, by utilizing a more realistic selection of the inter- and intra- species repulsion coefficients. In particular, by fixing the latter while varying the former thus examining the aforementioned system mono-parametrically, bound pairs consisting of two DB solitons have been identified for OP bright soliton counterparts. Our detailed stability analysis revealed that such anti-symmetric states exist as stable configurations in a wide window of inter-species repulsions that spans both the miscible and the immiscible regime of interactions. Below and above this domain, the anti-symmetric pair destabilizes giving rise to new symmetry-broken states that are asymmetric (mass imbalanced) with respect to their bright soliton counterpart. In particular, the destabilization of the OP pair deep in the miscible side was found to be connected with a supercritical pitchfork bifurcation resulting in stable asymmetric bound pairs. Deep in the immiscible regime of interactions, asymmetric states have been also identified, but were found to bifurcate from the anti-symmetric ones in a subcritical pitchfork bifurcation, and as such are unstable. In all cases our stability analysis results were verified by considering the long-time dynamics of both the stable and unstable anti-symmetric and asymmetric soliton pairs.
Acknowledgments
P. S. gratefully acknowledges financial support by the Deutsche Forschungsgemeinschaft (DFG) in the framework of the grant SCHM 885/26-1. P.G.K. gratefully acknowledges the support of NSF-PHY-1602994, the Alexander von Humboldt Foundation, the Stavros Niarchos Foundation via the Greek Diaspora Fellowship Program and the ERC under FP7, Marie Curie Actions, People, International Research Staff Exchange Scheme (IRSES-605096).
Author Contributions
G.C.K. performed the analytical and numerical computations; G.C.K., J.S. and P.G.K. conducted the interpretation of the results; P.S. conceived the idea of the present work; and all authors contributed to the writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kevrekidis, P.G.; Frantzeskakis, D.J. Solitons in coupled nonlinear Schrödinger models: A survey of recent developments. Rev. Phys. 2016, 1, 140–153. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-González, R. Emergent Nonlinear Phenomena in Bose–Einstein Condensates: Theory and Experiment; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Carretero-González, R.; Kevrekidis, P.G.; Frantzeskakis, D.J. Nonlinear waves in Bose–Einstein condensates: Physical relevance and mathematical techniques. Nonlinearity 2008, 21, R139–R202. [Google Scholar] [CrossRef]
- Abdullaev, F.K.; Gammal, A.; Kamtchatnov, A.M.; Tomio, L. Dynamics of matter wave bright solitons in a Bose–Einstein condensate. Int. J. Mod. Phys. B 2005, 19, 3415–3473. [Google Scholar] [CrossRef]
- Weller, A.; Ronzheimer, J.P.; Gross, C.; Esteve, J.; Oberthaler, M.K.; Frantzeskakis, D.J.; Theocharis, G.; Kevrekidis, P.G. Experimental Observation of Oscillating and Interacting Matter Wave Dark Solitons. Phys. Rev. Lett. 2008, 101, 130401-1–130401-4. [Google Scholar] [CrossRef] [PubMed]
- Theocharis, G.; Weller, A.; Ronzheimer, J.P.; Gross, C.; Oberthaler, M.K.; Kevrekidis, P.G.; Frantzeskakis, D.J. Multiple atomic dark solitons in cigar-shaped Bose–Einstein condensates. Phys. Rev. A 2010, 81, 063604-1–063604-15. [Google Scholar] [CrossRef]
- Frantzeskakis, D.J. Dark solitons in atomic Bose–Einstein condensates: From theory to experiments. J. Phys. A 2010, 43, 213001-1–213001-68. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Matter-wave solitons in nonlinear optical lattices. Phys. Rev. E 2005, 72, 046610. [Google Scholar] [CrossRef] [PubMed]
- Borovkova, O.V.; Kartashov, Y.V.; Torner, L.; Malomed, B.A. Bright solitons from defocusing nonlinearities. Phys. Rev. E 2011, 84, 035602(R)-1–035602(R)-5. [Google Scholar] [CrossRef] [PubMed]
- Burger, S.; Bongs, K.; Dettmer, S.; Ertmer, W.; Sengstock, K.; Sanpera, A.; Shlyapnikov, G.V.; Lewenstein, M. Dark Solitons in Bose–Einstein Condensates. Phys. Rev. Lett. 1999, 83, 5198–5201. [Google Scholar] [CrossRef]
- Denschlag, J.; Simsarian, J.E.; Feder, D.L.; Clark, C.W.; Collins, L.A.; Cubizolles, J.; Deng, L.; Hagley, E.W.; Helmerson, K.; Reinhardt, W.P.; et al. Generating Solitons by Phase Engineering of a Bose–Einstein Condensate. Science 2000, 287, 97–101. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.P.; Haljan, P.C.; Regal, C.A.; Feder, D.L.; Collins, L.A.; Clark, C.W.; Cornell, E.A. Watching Dark Solitons Decay into Vortex Rings in a Bose–Einstein Condensate. Phys. Rev. Lett. 2001, 86, 2926–2929. [Google Scholar] [CrossRef] [PubMed]
- Khaykovich, L.; Schreck, F.; Ferrari, G.; Bourdel, T.; Cubizolles, J.; Carr, L.D.; Castin, Y.; Salomon, C. Formation of a Matter-Wave Bright Soliton. Science 2002, 296, 1290–1293. [Google Scholar] [CrossRef] [PubMed]
- Strecker, K.E.; Partridge, G.B.; Truscott, A.G.; Hulet, R.G. Formation and propagation of matter-wave soliton trains. Nature 2002, 417, 150–153. [Google Scholar] [CrossRef] [PubMed]
- Myatt, J.C.; Burt, E.A.; Ghrist, R.W.; Cornell, E.A.; Wieman, C.E. Production of Two Overlapping Bose–Einstein Condensates by Sympathetic Cooling. Phys. Rev. Lett. 1997, 78, 586–589. [Google Scholar] [CrossRef]
- Hall, D.S.; Matthews, M.R.; Ensher, J.R.; Wieman, C.E.; Cornell, E.A. Dynamics of Component Separation in a Binary Mixture of Bose–Einstein Condensates. Phys. Rev. Lett. 1998, 81, 1539–1542. [Google Scholar] [CrossRef]
- Stamper-Kurn, D.M.; Andrews, M.R.; Chikkatur, A.P.; Inouye, S.; Miesner, H.-J.; Stenger, J.; Ketterle, W. Optical Confinement of a Bose–Einstein Condensate. Phys. Rev. Lett. 1998, 80, 2027–2030. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Frantzeskakis, D.J.; Kevrekidis, P.G.; Malomed, B.A.; Carretero-González, R. Bright-dark soliton complexes in spinor Bose–Einstein condensates. Phys. Rev. A 2008, 77, 033612-1–033612-12. [Google Scholar] [CrossRef]
- Yan, D.; Chang, J.J.; Hamner, C.; Hoefer, M.; Kevrekidis, P.G.; Engels, P.; Achilleos, V.; Frantzeskakis, D.J.; Cuevas, J. Beating dark-dark solitons in Bose–Einstein condensates. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 115301-1–115301-11. [Google Scholar] [CrossRef]
- Achilleos, V.; Yan, D.; Kevrekidis, P.G.; Frantzeskakis, D.J. Dark-bright solitons in Bose–Einstein condensates at finite temperatures. New J. Phys. 2012, 14, 055006-1–055006-23. [Google Scholar] [CrossRef]
- Pérez-García, V.M.; Beitia, J.B. Symbiotic Solitons in Heteronuclear Multicomponent Bose–Einstein condensates. Phys. Rev. A 2005, 72, 033620-1–033620-5. [Google Scholar] [CrossRef]
- Majed, O.; Alotaibi, D; Carr, L.D. Dynamics of Vector Solitons in Bose–Einstein Condensates. arXiv, 2016; arXiv:1607.00108v2. [Google Scholar]
- Chen, Z.; Segev, M.; Coskun, T.H.; Christodoulides, D.N.; Kivshar, Y.S. Coupled photorefractive spatial-soliton pairs. J. Opt. Soc. Am. B 1997, 14, 3066–3077. [Google Scholar] [CrossRef]
- Ostrovskaya, E.A.; Kivshar, Y.S.; Chen, Z.; Segev, M. Interaction between vector solitons and solitonic gluons. Opt. Lett. 1999, 24, 327–329. [Google Scholar] [CrossRef] [PubMed]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Christodoulides, D.N. Black and white vector solitons in weakly birefringent optical fibers. Phys. Lett. A 1988, 132, 451–452. [Google Scholar] [CrossRef]
- Afanasjev, V.V.; Kivshar, Y.S.; Konotop, V.V.; Serkin, V.N. Dynamics of coupled dark and bright optical solitons. Opt. Lett. 1989, 14, 805–807. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Turitsyn, S.K. Vector dark solitons. Opt. Lett. 1993, 18, 337–339. [Google Scholar] [CrossRef] [PubMed]
- Radhakrishnan, R.; Lakshmanan, M. Bright and dark soliton solutions to coupled nonlinear Schrödinger equations. J. Phys. A Math. Gen. 1995, 28, 2683–2692. [Google Scholar] [CrossRef]
- Buryak, A.V.; Kivshar, Y.S.; Parker, D.F. Coupling between dark and bright solitons. Phys. Lett. A 1996, 215, 57–62. [Google Scholar] [CrossRef]
- Sheppard, A.P.; Kivshar, Y.S. Polarized dark solitons in isotropic Kerr media. Phys. Rev. E 1997, 55, 4773–4782. [Google Scholar] [CrossRef]
- Park, Q.H.; Shin, H.J. Systematic construction of multicomponent optical solitons. Phys. Rev. E 2000, 61, 3093–3106. [Google Scholar] [CrossRef]
- Becker, C.; Stellmer, S.; Soltan-Panahi, P.; Dörscher, S.; Baumert, M.; Richter, E.-M.; Kronjäger, J.; Bongs, K.; Sengstock, K. Oscillations and interactions of dark and dark-bright solitons in Bose–Einstein condensates. Nat. Phys. 2008, 4, 496–501. [Google Scholar] [CrossRef]
- Busch, T.; Anglin, J.R. Dark-Bright Solitons in Inhomogeneous Bose–Einstein Condensates. Phys. Rev. Lett. 2001, 87, 010401-1–010401-4. [Google Scholar] [CrossRef] [PubMed]
- Hamner, C.J.; Chang, J.; Engels, P.; Hoefer, M.A. Generation of Dark-Bright Soliton Trains in Superfluid-Superfluid Counterflow. Phys. Rev. Lett. 2011, 106, 065302-1–065302-4. [Google Scholar] [CrossRef] [PubMed]
- Middelkamp, S.; Chang, J.J.; Hamner, C.; Carretero-González, R.; Kevrekidis, P.G.; Achilleos, V.; Frantzeskakis, D.J.; Schmelcher, P.; Engels, P. Dynamics of dark-bright solitons in cigar-shaped Bose–Einstein condensates. Phys. Lett. A 2011, 375, 642–646. [Google Scholar] [CrossRef]
- Yan, D.; Chang, J.J.; Hamner, C.; Kevrekidis, P.G.; Engels, P.; Achilleos, V.; Frantzeskakis, D.J.; Carretero-González, R.; Schmelcher, P. Multiple dark-bright solitons in atomic Bose–Einstein condensates. Phys. Rev. A 2011, 84, 053630-1–053630-10. [Google Scholar] [CrossRef]
- Álvarez, A.; Cuevas, J.; Romero, F.R.; Hamner, C.; Chang, J.J.; Engels, P.; Kevrekidis, P.G.; Frantzeskakis, D.J. Scattering of atomic dark-bright solitons from narrow impurities. J. Phys. B 2013, 46, 065302-1–065302-11. [Google Scholar] [CrossRef]
- Inouye, S.; Andrews, M.R.; Stenger, J.; Miesner, H.-J.; Stamper-Kurn, D.M.; Ketterle, W. Observation of Feshbach resonances in a Bose–Einstein condensate. Nature 1998, 392, 151–154. [Google Scholar] [CrossRef]
- Roberts, J.L.; Claussen, N.R.; Burke, J.P., Jr.; Greene, C.H.; Cornell, E.A.; Wieman, C.E. Resonant Magnetic Field Control of Elastic Scattering in Cold 85Rb. Phys. Rev. Lett. 1998, 81, 5109–5112. [Google Scholar] [CrossRef]
- Donley, E.A.; Claussen, N.R.; Cornish, S.L.; Roberts, J.L.; Cornell, E.A.; Wieman, C.E. Dynamics of collapsing and exploding Bose–Einstein condensates. Nature 2001, 412, 295–299. [Google Scholar] [CrossRef] [PubMed]
- Thalhammer, G.; Barontini, G.; de Sarlo, L.; Catani, J.; Minardi, F.; Inguscio, M. Double Species Bose–Einstein condensate with Tunable Interspecies Interactions. Phys. Rev. Lett. 2008, 100, 210402-1–210402-4. [Google Scholar] [CrossRef] [PubMed]
- Papp, S.B.; Pino, J.M.; Wieman, C.E. Tunable Miscibility in a Dual-Species Bose–Einstein condensate. Phys. Rev. Lett. 2008, 101, 040402-1–040402-4. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225–1286. [Google Scholar]
- Nguyen, J.H.V.; Dyke, P.; Luo, D.; Malomed, B.A.; Hulet, R.G. Collisions of matter-wave solitons. Nat. Phys. 2014, 10, 918–922. [Google Scholar]
- Manakov, S.V. On the theory of two-dimensional stationary self-focusing of electromagnetic waves. Sov. Phys. JETP 1974, 38, 248–253. [Google Scholar]
- Gerdzhikov, V.S.; Kulish, P.P. Multicomponent nonlinear Schrödinger equation in the case of nonzero boundary conditions. J. Sov. Math. 1983, 85, 2261–2269. [Google Scholar]
- Prinari, B.; Ablowitz, M.J.; Biondini, G. Inverse scattering transform for the vector nonlinear Schrödinger equation with nonvanishing boundary conditions. J. Math. Phys. 2006, 47, 063508-1–063508-33. [Google Scholar] [CrossRef]
- Yan, D.; Tsitoura, F.; Kevrekidis, P.G.; Frantzeskakis, D.J. Dark-bright solitons and their lattices in atomic Bose–Einstein condensates. Phys. Rev. A 2015, 91, 023619-1–023619-12. [Google Scholar] [CrossRef]
- Katsimiga, G.C.; Stockhofe, J.; Kevrekidis, P.G.; Schmelcher, P. Dark-bright soliton interactions beyond the integrable limit. Phys. Rev. A 2017, 95, 013621-1–013621-11. [Google Scholar]
- Pitaevskii, L.P.; Stringari, S. Bose–Einstein Condensation; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-González, R. The Defocusing Nonlinear Schrödinger Equation; SIAM: Philadelphia, PA, USA, 2015. [Google Scholar]
- Mertes, K.M.; Merrill, J.W.; Carretero-González, R.; Frantzeskakis, D.J.; Kevrekidis, P.G.; Hall, D.S. Non-Equilibrium Dynamics and Superfluid Ring Excitations in Binary Bose–Einstein Condensates. Phys. Rev. Lett. 2007, 99, 190402-1–190402-4. [Google Scholar] [CrossRef] [PubMed]
- Egorov, M.; Opanchuk, B.; Drummond, P.; Hall, B.V.; Hannaford, P.; Sidorov, A.I. Measurement of s-wave scattering lengths in a two-component Bose–Einstein condensate. Phys. Rev. A 2013, 87, 053614-1–053614-10. [Google Scholar] [CrossRef]
- Kelley, C.T. Solving Nonlinear Equations with Newton’s Method; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1995. [Google Scholar]
- Ao, P.; Chui, S.T. Binary Bose–Einstein condensate mixtures in weakly and strongly segregated phases. Phys. Rev. A 1998, 58, 4836–4840. [Google Scholar]
- Skryabin, D.V. Instabilities of vortices in a binary mixture of trapped Bose–Einstein condensates: Role of collective excitations with positive and negative energies. Phys. Rev. A 2000, 63, 013602-1–013602-10. [Google Scholar] [CrossRef]
- Karamatskos, E.T.; Stockhofe, J.; Kevrekidis, P.G.; Schmelcher, P. Stability and tunneling dynamics of a dark-bright soliton pair in a harmonic trap. Phys. Rev. A 2015, 91, 043637-1–043637-10. [Google Scholar] [CrossRef]
- Garrett, D.; Klotz, T.; Prinari, B.; Vitale, F. Dark-dark and dark-bright soliton interactions in the two-component defocusing nonlinear Schrödinger equation. Appl. Anal. 2013, 92, 379–397. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).