Fatigue Life Estimation of Medium-Carbon Steel with Different Surface Roughness

Abstract

Medium-carbon steel is commonly used for the rail, wire ropes, tire cord, cold heading, forging steels, cold finished steel bars, machinable steel and so on. Its fatigue behavior analysis and fatigue life estimation play an important role in the machinery industry. In this paper, the estimation of fatigue life of medium-carbon steel with different surface roughness using established S-N and P-S-N curves is presented. To estimate the fatigue life, the effect of the average surface roughness on the fatigue life of medium-carbon steel has been investigated using 75 fatigue tests in three groups with average surface roughness (R_a): 0.4 μm, 0.8 μm, and 1.6 μm, respectively. S-N curves and P-S-N curves have been established based on the fatigue tests. The fatigue life of medium-carbon steel is then estimated based on Tanaka-Mura crack initiation life model, the crack propagation life model using Paris law, and material constants of the S-N curves. Six more fatigue tests have been conducted to validate the presented fatigue life estimation formulation. The experimental results have shown that the presented model could estimate well the mean fatigue life of medium-carbon steel with different surface roughness.

1. Introduction

Medium-carbon steel is usually referred to as the carbon steel that contains approximately 0.30–0.60% carbon content. It balances ductility and strength, and has good wear resistance [1]. It is commonly used for rails, wire ropes, tire cord, cold heading, forging steels, cold finished steel bars, machinable steel, and so on [2]. Its fatigue behavior analysis and fatigue life estimation play an important role in the safety and reliability in the machinery industry. From a raw steel piece to a part meeting the design requirements, a manufacturing process must be used. The surface roughness of a part as a result of the manufacturing process plays a major role in determining the fatigue behavior of the part [3]. To ensure the high safety and reliability of the part of medium-carbon steel in service, it is important to investigate S-N curve, P-S-N curve, and fatigue life of medium-carbon steel with different surface roughness.

A method has been reported where the effect of the surface roughness on fatigue behavior was commonly considered by using surface condition modification factor, which was:

$$k_a=b_1{S}_{ut}^{b_1}$$

(1)

where S_ut was the minimum tensile strength, b₁ and b₂ are statistical values and determined by the material and the machining method such as ground, machined or cold-drawn, hot-rolled, and as-forged [4]. Then, the endurance limit S_e at the critical location of a machine part in the geometry and condition of use is proportional to the product of $k_a$ and $S_e^{\prime }$:

$$S_e\propto k_a\stackrel{`}{S_e}$$

(2)

where $\stackrel{`}{S_e}$ is the rotary-beam test specimen endurance limit. However, it is very difficult for this method to estimate the fatigue life of the given material with the different surface roughness. Other methods have also been proposed. For example, the surface groove due to the manufacturing process was considered to result in stress concentration similar to a notch. The fatigue stress concentration factor K_f was used for describing the effect of the surface roughness on the fatigue limit. It was the function of the stress concentration factor K_t which can be estimated by the finite element method [5,6] or the empirical formula including the average geometric parameters of surface roughness [7,8]. A method has been also reported to estimate the fatigue life by:

$$N_f=N_i+N_p$$

(3)

where N_f, N_i, and N_p were fatigue life (the number of cycles to failure), crack initiation life, and crack propagation life, respectively. The fatigue life can be computed as:

$$N_i=\beta {\left(K_{t}S\right)}^{\alpha }$$

(4)

where $\beta$ and $\alpha$ are determined by plotting N_i as a function of the stress amplitude S. The crack propagation life could be estimated by iterative numerical integration of Paris’ law where the surface fatigue crack propagation threshold is multiplied by K_t and the fatigue crack propagation threshold in depth is not affected [5]. For the large surface roughness, the stress concentration due to the surface groove might be obvious and the methods of estimating the fatigue life based on the stress concentration factor might have high accuracy. However, the stress concentration factor might be very close to 1 for small surface roughness. Moreover, accurately computing the stress concentration factor is a time-consuming and complex process. Therefore, the method has been reported where the surface groove due to machining was considered to be an initial micro-defect. The analytic formulation of the crack initiation life N_i can be estimated based on the dislocation dipole accumulation model [9,10,11] and the crack propagation life N_p can calculated using the analytic solution of Paris’ law integral [12,13,14]. Since the reported method has been validated by six types of ultra-high strength steel [11] and high-strength martensitic stainless steel [12], it will be employed to estimate the fatigue life of medium-carbon steel with the different surface roughness in this paper.

The remainder of this paper is organized as follows: In Section 2, the material, the specimen geometry, and the testing apparatus will be described, the scatterplot of the fatigue experiment results shown, and the mean fatigue life of the specimens with different average surface roughness contrasted. In Section 3, S-N and P-S-N curves will be established and their curve-fitting parameters listed. In Section 4, the formulation for estimating the mean fatigue life of medium-carbon steel with different average surface roughness will be explained along with its validation. The conclusions are, finally, drawn in Section 5.

2. Material and Experimental Results

2.1. Material and Testing Apparatus

The material investigated in this work is the medium-carbon steel and its composition and mechanical properties are presented in Table 1 and Table 2, respectively. The raw material is a hot rolled steel bar and is machined into the funnel specimen. The geometry of the specimen is shown in Figure 1. The specimens were polished to the specified average surface roughness. To investigate the effect of the different surface roughness of the specimens on the fatigue life, specimens were machined into three groups with average surface roughness (R_a): 0.4 μm, 0.8 μm, and 1.6 μm, respectively. The rotating bending fatigue tests were performed. The testing apparatus is shown in Figure 2. The cycle frequency was 25 Hz.

Table 1. Chemical composition of the medium-carbon steel.

Element	C	Cr	Mo	Si	Mn	S	P	Ni
Weight (%)	0.44	0.04	0.02	0.23	0.57	0.016	0.024	0.002

Table 2. Mechanical properties of the medium carbon steel.

Tensile Strength (MPa)	Yield Strength (MPa)	Elongation at Break (%)
710	490	19.17

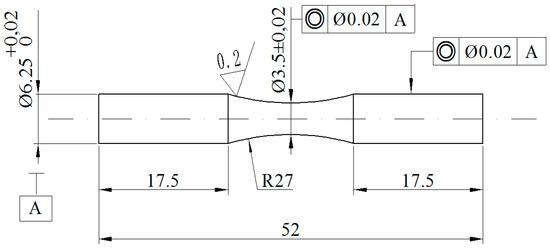
Figure 1. Fatigue specimen geometry (dimensions in mm).

Figure 2. The testing apparatus.

2.2. Experimental Results

In this work, 75 fatigue tests were conducted. They were divided into three groups with average surface roughness (R_a) of 0.4 μm, 0.8 μm, and 1.6 μm, respectively. The stress amplitudes of the first group (R_a = 0.4 μm) included 550, 500, 450, 400, and 380 MPa, and those of other two groups included 500, 450, 400, 380, and 360 MPa. A total of five fatigue tests were performed under each stress amplitude. The scatterplot of all the experimental results is shown in Figure 3. Under each stress amplitude, it can be seen that the fatigue life has the conspicuous dispersion. The means of fatigue life with different average surface roughness and stress amplitude are compared in Figure 4. The average surface roughness is clearly effective in reducing mean of fatigue life for medium-carbon steel. In high stress amplitude (for example 500 MPa), there is about 15% decrease while there is about 30% decrease in low stress amplitude (for example 380 MPa) when the average surface roughness increased from 0.4 μm to 0.8 μm or from 0.8 μm to 1.6 μm. This could confirm that the surface roughness plays a vital role in the fatigue life of medium-carbon steel.

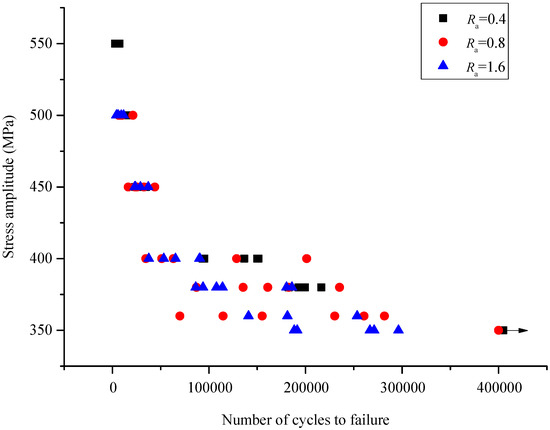
Figure 3. Scatterplot of the 75 fatigue tests.

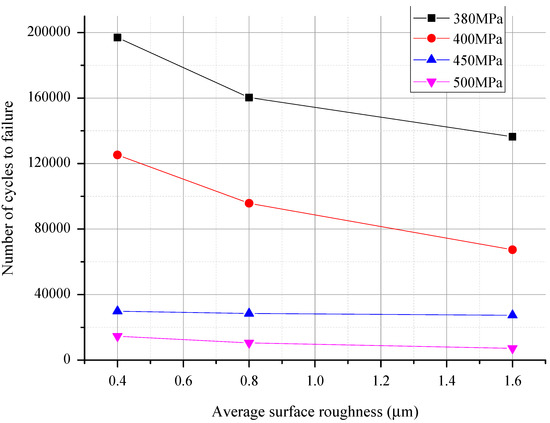
Figure 4. Contrast of mean fatigue life with R_a = 0.4 μm, R_a = 0.8 μm, and R_a = 1.6 μm.

3. S-N Curves and P-S-N Curves

The S-N curves with the different average surface roughness are shown in Figure 5. The input data points of the curve fitting were obtained by taking the logarithm of the means of the fatigue life data and stress amplitudes. The material constants were estimated by the least square method and are listed in Table 3. The material constants satisfy the logarithmic Basquin equation $\lg N_f=\lg c-n\lg S$, where S is the stress amplitude. As shown in Figure 5, (1) the mean of the fatigue life with R_a = 0.4 μm is very close to that with R_a = 0.8 μm or R_a = 1.6 μm when the stress amplitude is very high; and (2) the mean of the fatigue life with R_a = 0.8 μm is very close to that with R_a = 1.6 μm, while the mean of the fatigue life with R_a = 0.4 μm is significantly different from that with R_a = 0.8 μm or R_a = 1.6 μm when the stress amplitude is low. This phenomenon can be explained as surface damage due to machining not being the key factor of fatigue crack initiation and development of medium-carbon steel at higher-stress amplitudes than the endurance limit. It might be concluded that the mean of the fatigue life of the medium-carbon steel cannot be observably decreased when the average surface roughness is increased from R_a = 0.8 μm to R_a = 1.6 μm or even high at the low-stress amplitude.

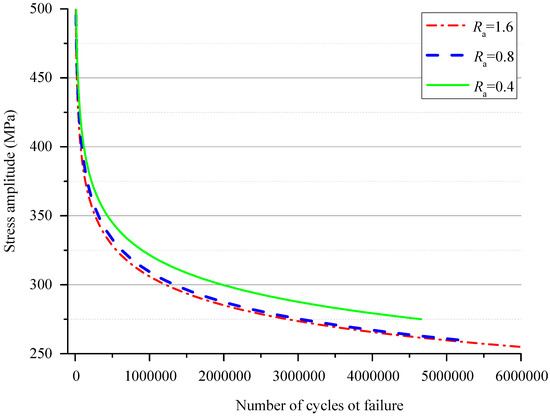
Figure 5. The S-N curves with R_a = 0.4 μm, R_a = 0.8 μm, and R_a = 1.6 μm.

Table 3. Material constants with the different average surface roughness.

Average Surface Roughness (μm)	n	c
Ra = 0.4	9.84	4.56 × 1030
Ra = 0.8	9.44	3.16 × 1029
Ra = 1.6	9.80	2.32 × 1030

The P-S-N curves with R_a = 0.4 μm, R_a = 0.8 μm, and R_a = 1.6 μm are shown in Figure 6, Figure 7 and Figure 8, respectively. R is the survival probability. The data point (pink inverted triangle, blue triangle, red dot and black square) is the confidence lower limit which is calculated by [13]:

$$x_{RL}=\overline{x}+h{\sigma }_x$$

(5)

where $\overline{x}$ and ${\sigma }_x$ are the mean and the standard deviation of the experimental fatigue life, h is the one-sided tolerance factor which is calculated by:

$$h=u_R\xi -t_{\gamma }\sqrt{\frac{1}{n_s}+u_R^2\left({\xi }^2-1\right)}$$

(6)

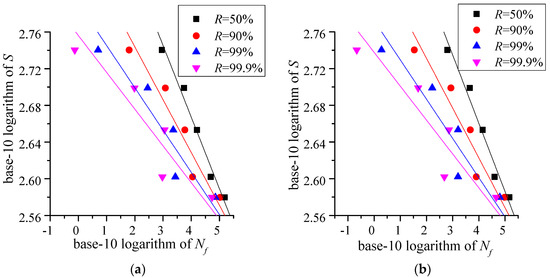
Figure 6. The P-S-N curves with R_a = 0.4 μm and confidence level (a) $\gamma =95\%$; and (b) $\gamma =99\%$

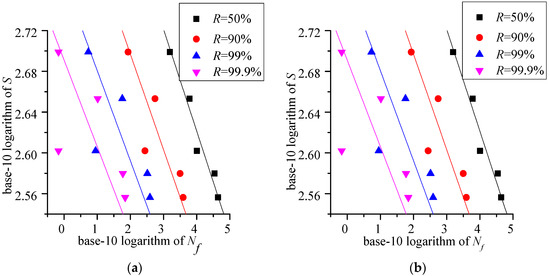
Figure 7. The P-S-N curves with R_a = 0.8 μm and confidence level (a) $\gamma =95\%$; and (b) $\gamma =99\%$

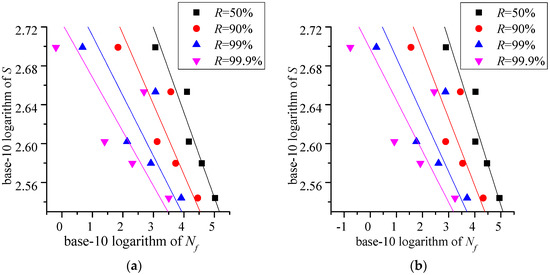
Figure 8. The P-S-N curves with R_a = 1.6 μm and confidence level (a) $\gamma =95\%$; and (b) $\gamma =99\%$

In Equation (6), $u_R={\mathsf{\Phi }}^{-1}\left(R\right)$,${\mathsf{\Phi }}^{-1}(\divideontimes )$ is the inverse function of the standard normal distribution function, $\xi$ the correction factor, $t_{\gamma }={\mathrm{T}}^{-1}\left(\gamma \right)$, ${\mathrm{T}}^{-1}(\divideontimes )$ the inverse function of the distribution function of Student’s t-distribution with n_s − 1 degrees of freedom, and n_s the sample size. When the survival probability R and the confidence level $\gamma$ are given, the confidence lower limit can be calculated by Equation (5). Then, the P-S-N curve is described by the similar logarithmic Basquin equation $\lg \left(N_f\right)=a_1-a_2\text{lg S}$, where parameters a₁ and a₂ are estimated by the least square method with R_a = 0.4 μm, R_a = 0.8 μm, and R_a = 1.6 μm shown in Table 4, Table 5 and Table 6, respectively.

Table 4. Parameters of P-S-N curves with R_a = 0.4 μm.

	R (%)	50	90	99	99.9	Parameters
$\mathit{\gamma }$ (%)
95		40.7137	54.1796	66.9757	76.5668	a1
		−13.9865	−19.3591	−24.4740	−28.3078	a2
99		42.5752	57.2561	71.7960	82.7595	a1
		−14.7206	−20.5889	−26.4008	−30.7832	a2

Table 5. Parameters of P-S-N with R_a = 0.8 μm.

	R (%)	50	90	99	99.9	Parameters
$\mathit{\gamma }$ (%)
95		28.6827	29.3268	29.9388	30.3976	a1
		−9.4241	−10.1261	−10.7931	−11.2931	a2
99		28.7717	29.4739	30.1694	30.6938	a1
		−9.5212	−10.2864	−11.0444	−11.6159	a2

Table 6. Parameters of P-S-N curves with R_a = 1.6 μm.

	R (%)	50	90	99	99.9	Parameters
$\mathit{\gamma }$ (%)
95		34.0511	39.5910	44.8554	48.8012	a1
		−11.4174	−13.8578	−16.1769	−17.9151	a2
99		34.8170	40.8567	46.8385	51.3489	a1
		−11.7547	−14.4154	−17.0504	−19.0374	a2

4. Fatigue Life Estimation

The fatigue life N_f is composed of the crack initiation life N_i and the crack propagation life N_p and can be calculated by Equation (3). The analytic formulation of the crack initiation life N_i was presented by Tanaka and Mura [9,10] and was based on the dislocation dipole accumulation model. It was extended to estimate the crack initiation life N_i of the specimen with the different surface roughness by Wang et al. [12]. It is [9,10,11,12]:

$$N_i=\frac{9\Delta K_{th}^2\mathrm{G}}{\mathrm{E}{\left(\mathrm{S}-{\mathrm{S}}_{\mathrm{e}}\right)}^2\mathsf{\pi }\left(1-\mathsf{\upsilon }\right)a_0}$$

(7)

here $\Delta K_{th}$ is the threshold of stress intensity factor, G is the shear modulus, E is the elastic modulus, S_e is the endurance limit, $\upsilon$ is the Poisson’s ratio, and a₀ is the equivalent initial micro-defect size. a₀ could be estimated as [12,14]:

$$a_0=2.97R_{\mathrm{a}}$$

(8)

The number of cycles necessary to grow the crack from the initial micro-defect size to failure can be described by Paris’ law as:

$${\frac{\mathrm{d}a}{\mathrm{d}N}}_0=C{\left(\Delta K\right)}^n$$

(9)

where $\Delta K$ is the amplitude of stress intensity factor, C the material constant, and a the crack size. The crack propagation life N_p can be calculated by the analytic solution of Paris’ law integral as [12,15,16]:

$$N_p=\frac{a_0^{\left(1-\frac{n}{2}\right)}-a_{\mathrm{sc}}^{\left(1-\frac{n}{2}\right)}}{C{S}^n{\beta }_1^n{\pi }^{\frac{n}{2}}\left(\frac{n}{2}-1\right)}+\frac{a_{\mathrm{sc}}^{\left(1-\frac{n}{2}\right)}-a_{\mathrm{f}}^{\left(1-\frac{n}{2}\right)}}{C{S}^n{\beta }_2^n{\pi }^{\frac{n}{2}}\left(\frac{n}{2}-1\right)}$$

(10)

where: a_sc is the critical crack size for identifying long and short cracks, a_f the crack size of final failure, ${\beta }_1=0.5\sqrt{\pi }$ and ${\beta }_{12}=1$. Generally, the number of crack growth cycles from a₀ to a_sc is much greater than the cycles needed to grow from a_sc to a_f. Then N_p can be taken as [17]:

$$N_p=\frac{a_0^{\left(1-\frac{n}{2}\right)}}{C{S}^n{\beta }_1^n{\pi }^{\frac{n}{2}}\left(\frac{n}{2}-1\right)}$$

(11)

It can be written by:

$$S^n{N}_p=\mathrm{c}$$

(12)

where:

$$c=\frac{a_0^{\left(1-\frac{n}{2}\right)}}{C{\beta }_1^n{\pi }^{\frac{n}{2}}\left(\frac{n}{2}-1\right)}$$

(13)

By taking logarithms in Equation (12), then:

$$\lg N_p=\lg c-n\lg S$$

(14)

The material constant n in Equation (12) is the same as n in the S-N curves. The material constant C can be solved by Equation (13). n and c have been listed in Table 3 in Section 3. The material constants C and n in Equation (11) are listed in Table 7.

Table 7. Material constants C and n in Equation (11) with different average surface roughness.

Average Surface Roughness (μm)	n	C
Ra = 0.4	9.84	4.11 × 10−34
Ra = 0.8	9.44	4.81 × 10−34
Ra = 1.6	9.80	3.02 × 10−36

Then, the fatigue life N_f of medium-carbon steel is computed as:

$$N_f=\frac{9\Delta K_{th}^2\mathrm{G}}{\mathrm{E}{\left(\mathrm{S}-{\mathrm{S}}_{\mathrm{e}}\right)}^2\mathsf{\pi }\left(1-\mathsf{\upsilon }\right)a_0}+\frac{a_0^{\left(1-\frac{n}{2}\right)}}{C{S}^n{\beta }_1^n{\pi }^{\frac{n}{2}}\left(\frac{n}{2}-1\right)}$$

(15)

where the shear modulus G is 79.40 GPa, the elastic modulus E is 206.00 GPa, and the threshold of stress intensity factor $\Delta K_{th}$ is 6.26. Substituting the material constants C and n in Table 7 into Equation (12), the mean fatigue life N_f of the medium-carbon steel with different average surface roughness is:

$$N_f=\{\begin{array}{cc}\begin{array}{c}\frac{9\times {6.26}^2\times 79.4}{206\times {\left(\mathrm{S}-275\right)}^2\times \mathsf{\pi }\times \left(1-0.27\right)\times 1.188\times {10}^{-3}}\\ +\frac{{1.188}^{\left(1-\frac{9.835}{2}\right)}}{4.11\times {10}^{-34}\times S^{9.835}\times {\left(0.5\sqrt{\pi }\right)}^{9.835}{\pi }^{\frac{9.835}{2}}\left(\frac{9.835}{2}-1\right)}\end{array}& ,⟺R_{\mathrm{a}}=0.4 \mathsf{\mu }\mathrm{m}\\ \begin{array}{c}\frac{9\times {6.26}^2\times 79.4}{206\times {\left(\mathrm{S}-260\right)}^2\times \mathsf{\pi }\times \left(1-0.27\right)\times 2.376\times {10}^{-3}}\\ +\frac{{2.376}^{\left(1-\frac{9.436}{2}\right)}}{4.81\times {10}^{-34}\times S^{9.436}\times {\left(0.5\sqrt{\pi }\right)}^{9.436}{\pi }^{\frac{9.436}{2}}\left(\frac{9.436}{2}-1\right)}\end{array}& ,⟺R_{\mathrm{a}}=0.8 \mathsf{\mu }\mathrm{m}\\ \begin{array}{c}\frac{9\times {6.26}^2\times 79.4}{206\times {\left(\mathrm{S}-255\right)}^2\times \mathsf{\pi }\times \left(1-0.27\right)\times 4.752\times {10}^{-3}}\\ +\frac{{4.752}^{\left(1-\frac{9.802}{2}\right)}}{3.02\times {10}^{-36}\times S^{9.802}\times {\left(0.5\sqrt{\pi }\right)}^{9.802}{\pi }^{\frac{9.802}{2}}\left(\frac{9.802}{2}-1\right)}\end{array}& ,⟺R_{\mathrm{a}}=1.6 \mathsf{\mu }\mathrm{m}\end{array}$$

(16)

When the average surface roughness is 0.4, 0.8, and 1.6, respectively, the mean fatigue life curves of medium-carbon steel calculated by Equation (16) are shown in Figure 9. It can be seen that the fatigue life estimation model agrees with the experiment value well. To validate the presented formulation for estimating the mean fatigue life of medium-carbon steel, six more fatigue tests were conducted and the experimental results are shown in Table 8. The stress amplitude was 420 MPa and was not equal to any stress amplitude in the previous experiments. The maximum and minimum estimation errors are 15.83% and 1.99%, respectively. Therefore, it is obvious that the presented model for estimating the mean fatigue life of medium-carbon steel gives good results for roughness R_a = 0.4 μm, R_a = 0.8 μm, and R_a = 1.6 μm.

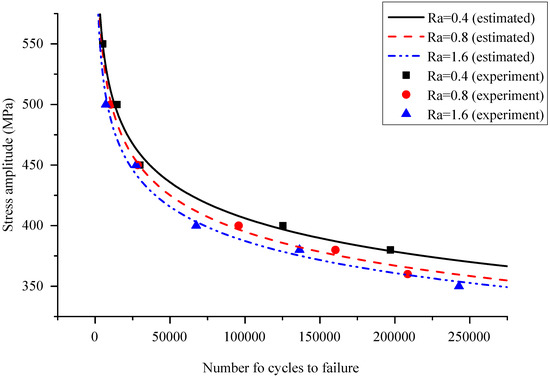
Figure 9. Estimated mean fatigue life curves and the experiment values.

Table 8. Validation experiment results.

Average Surface Roughness (μm)	Stress Amplitude	Estimated Fatigue Life	Experimental Fatigue Life	Mean of Experimental Fatigue Life	Error
Ra = 0.4	420 MPa	72,420	70,569	73,863	1.99%
			77,156
Ra = 0.8		56,060	57,824	51,120	8.81%
			44,416
Ra = 1.6		45,190	66,174	52,345	15.83%
			38,516

5. Conclusions

To estimate the fatigue life of medium-carbon steel specimen, the effect of the average surface roughness on the fatigue life has been investigated in this paper using 75 fatigue tests in three groups with average surface roughnesses of (R_a): 0.4 μm, 0.8 μm, and 1.6 μm, respectively. S-N curves and P-S-N curves were established based on the fatigue tests. It was shown that there is about 15% decrease of the mean fatigue life in high stress amplitude (for example, 500 MPa), while there is about 30% decrease in low stress amplitude (for example, 380 MPa) when the average surface roughness increased from 0.4 μm to 0.8 μm or from 0.8 μm to 1.6 μm. Then, one new method was presented to estimate the fatigue life of the medium-carbon steel with different average surface roughness (R_a). The experiment results show that the maximum estimation error of the mean fatigue life by the presented model is less than 16%.