Abstract
Surface reconstruction for freehand 3D ultrasound is used to provide 3D visualization of a VOI (volume of interest) during image-guided tumor ablation surgery. This is a challenge because the recorded 2D B-scans are not only sparse but also non-parallel. To solve this issue, we established a framework to reconstruct the surface of freehand 3D ultrasound imaging in 2011. The key technique for surface reconstruction in that framework is based on variational interpolation presented by Greg Turk for shape transformation and is named Variational Surface Reconstruction (VSR). The main goal of this paper is to evaluate the quality of surface reconstructions, especially when the input data are extremely sparse point clouds from freehand 3D ultrasound imaging, using four methods: Ball Pivoting, Power Crust, Poisson, and VSR. Four experiments are conducted, and quantitative metrics, such as the Hausdorff distance, are introduced for quantitative assessment. The experiment results show that the performance of the proposed VSR method is the best of the four methods at reconstructing surface from sparse data. The VSR method can produce a close approximation to the original surface from as few as two contours, whereas the other three methods fail to do so. The experiment results also illustrate that the reproducibility of the VSR method is the best of the four methods.
1. Introduction
In recent years, image-guided percutaneous tumor ablation has become more and more widespread in clinical applications because of its minimally invasive characteristics [1,2,3]. Three imaging modalities are commonly used for guidance of intra-operative tumor ablation: computed tomography (CT), magnetic resonance imaging (MRI), and ultrasound imaging (US). CT and MRI provide large or adequate fields of view, and good contrast and resolution, but they are limited by costs, the need to adapt equipment for a magnetic field, availability, and radiation doses in clinical applications. US can provide the unique advantages of low cost, real-time monitoring, and a lack of ionizing radiation, but lacks a large field of view and adequate resolution at increasing lesion depth [4,5,6]. It is clear that no single modality is superior in all areas, and in fact, the modalities are often complementary to each other. However, because image-guided tumor ablation is usually performed using physical tools, such as forceps, it would be ideal for the imaging system to clearly and accurately image those tools as they move inside the patient. US can accomplish this task, but other modalities with poor real-time imaging are not as effective.
Conventional two-dimensional (2D) US is extensively used for a variety of clinical applications in tumor ablation surgery. Although conventional 2D US is a highly flexible imaging modality, its images represent only 2D thin planes of the patient’s three-dimensional (3D) anatomy, and the physician must mentally integrate many 2D images to form an impression of the 3D anatomy and pathology. This practice is inefficient, and may lead to inconsistency and incorrect diagnoses and treatment. This problem can be solved by using 3D US. Through 3D US, arbitrarily oriented planes within the patient, including planes inaccessible by 2D US, can be viewed. In addition, 3D US also allows a 3D volume-rendering or surface-rendering view and 3D segmentations of the VOI (Volume of Interest). In recent years, many researchers have attempted to reconstruct 3D volumes or surfaces from conventional 2D ultrasound data. Among the several currently developed 3D ultrasound techniques, freehand 3D ultrasound may easily gain widespread clinical acceptance because it allows physicians to move the ultrasound probe unrestrictedly [7,8,9].
1.1. Freehand 3D Ultrasound Imaging
Freehand 3D ultrasound imaging adopts conventional ultrasound technology to build up 3D volumes or surfaces from a number of 2D B-scans acquired in succession (see Figure 1). It consists of tracking a standard 2D ultrasound probe using a 3D spatial localizer (magnetic, mechanical, or optical). The localizer is attached to the probe, and can continuously measure the 3D position and orientation of the probe while the physician moves the probe slowly and steadily over a particular anatomical region of the patient. The measured outputs of the 3D position and orientation are used for the localization of B-scans in the coordinate system of the spatial localizer. In order to establish the transformation between the B-scan coordinates and the 3D position and orientation of the probe, a calibration procedure is necessary [10,11,12].
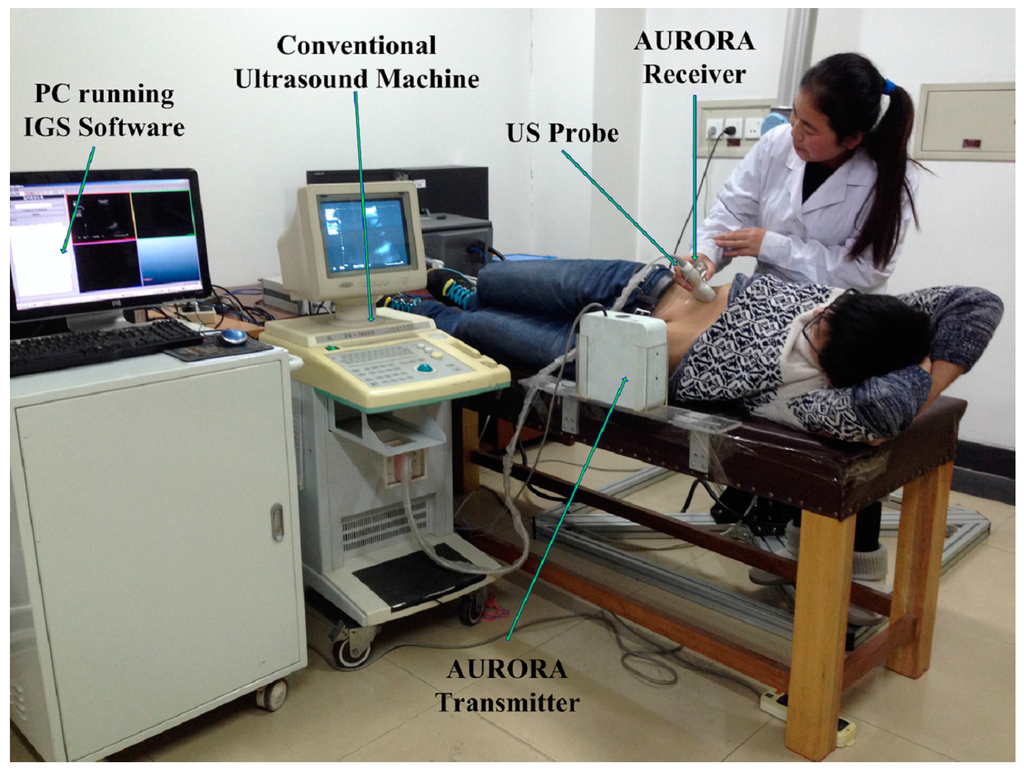
Figure 1.
Freehand 3D US system. This is also the setup for the experiments. The spatial localizer is an electromagnetic tracking device called AURORA from Northern Digital Inc. (Waterloo, ON, Canada). IGS (image-guided surgery) software serves as the 3D surface reconstruction and visualization program.
In order to obtain a 3D volume or surface model of the VOI (e.g., the lesion to be ablated), the 2D B-scans of the VOI should be acquired first, and a 3D reconstruction method should be applied to these B-scans.
Freehand 3D ultrasound has a noteworthy characteristic: the recorded B-scans of freehand 3D ultrasound are non-parallel and may intersect mutually, because the movement of the ultrasound probe is free and unrestricted in space. These non-parallel B-scans are different from the parallel slices of CT or MRI imaging. When the B-scans are segmented into contours, the contours are also non-parallel, which increases the difficulty of 3D reconstruction for freehand 3D ultrasound.
Presently, the 3D reconstruction methods for freehand 3D ultrasound can be divided into two categories: volume reconstruction and surface reconstruction.
1.2. Volume Reconstruction for Freehand 3D Ultrasound Imaging
Volume reconstruction methods interpolate the input data to a regular 3D array (voxel array) to obtain the 3D volume model of the VOI. Please refer to [13,14] for a review of freehand 3D US volume reconstruction algorithms. The different volume reconstruction algorithms have been classified into three groups in [13]: Voxel-Based Methods (VBM), Pixel-Based Methods (PBM), and Function-Based Methods (FBM). More papers about volume reconstruction methods can be found in references [15,16,17,18].
Because the volume reconstruction is performed without segmentation of the 2D US images in a prerequisite step, it is not able to display the VOI distinct from the rest of the reconstructed volume. This can only be achieved by surface reconstruction of the VOI. In order to achieve this goal, a 3D segmentation step followed by a triangulation algorithm (e.g., the Marching Cubes algorithm proposed by Lorensen and Cline [19,20]) should be performed. Because the 3D volume model is in a regular 3D voxel array, it is somewhat similar to the voxel lattice in CT or MRI imaging. If the reconstructed 3D volume is dense enough (i.e., no holes or gaps in between), many segmentation methods could be used to segment the VOI from the rest of the volume in the same way as they are used in CT or MRI imaging, such as level sets [21], 3D live-wire [22], image-adaptive radial basis functions [23], Random Walker [24], and Graph Cuts [25]. However, due to the wave interference phenomenon inherent in any coherent imaging process, US will suffer from speckle noise that makes the segmentation of US difficult, whether it is carried out by humans or using automatic segmentation methods. Moreover, if the input data are sparse, all the volume reconstruction methods cannot reconstruct a volume efficiently without introducing geometrical artifacts or distorting the images, which may lead to incorrect segmentation of the VOI by automatic segmentation methods. In clinical applications, manual segmentation is still the only universally reliable method for ultrasound data [9].
1.3. Surface Reconstruction for Freehand 3D Ultrasound Imaging
To avoid a voxel-based intermediate step, i.e., volume reconstruction, we can reconstruct the 3D surface of the VOI directly from contours (cross-sections) segmented from the original 2D B-scans in a prerequisite step. Because the contours are non-parallel, a method that does not assume parallel contours is required. Such reconstruction methods are scarce.
Moreover, because manual segmentation is still the only universally reliable method for ultrasound data in clinical applications [9], it is one of the most time-consuming processes during a tumor ablation surgery. It would be preferable to reconstruct surfaces from only a few ultrasound contours, which would be valuable in a clinical setting as it reduces manual work and reduces time spent on manual segmentation. Therefore, only a small number of B-scans are recorded and manually segmented to guarantee short segmentation time in clinical applications. However, a small number of contours provide only sparse input data to surface reconstruction. Thus, a surface reconstruction method that can handle both non-parallel and sparse contours is necessary. These two requirements (i.e., non-parallel and sparse) make the surface reconstruction of freehand 3D US a challenging task.
Candidate surface reconstruction methods for freehand 3D US usually fall into two groups: contour-based methods, and point-based methods. Contour-Based methods try to construct a triangle mesh directly from the segmented ultrasound contours and are usually ineffective when applied on non-parallel contours. Point-based methods first convert all contours into a point cloud and then construct triangle meshes from this point cloud. Hence, point-based methods can address non-parallel contours, but they are still ineffective when applied on sparse input data.
Cook et al. [26] proposed an algorithm for volume estimation based on polyhedral approximation, and several researchers [27] made use of this method for surface reconstruction. Two contours were sampled as a set of lines joining boundary points, and then the volume was calculated from these points by forming tetrahedra with a common central point on each plane. The surface was formed by triangulating each boundary point in turn between the contours. This would only be accurate for fairly similar contours; the contours are not allowed to intersect each other.
Hodges et al. [28] used a CAD package to triangulate between cross sections of saphenous vein phantoms. The cross sections were nearly parallel or nearly circular, and consequently the resulting surface was conical or cylindrical.
Liu et al. [29] proposed a method to reconstruct non-parallel contours. It was performed directly in the triangle-mesh domain and required dense contours for input. It resulted in disconnected geometry when the projections of the curves were not overlapping between planes; thus, it is incapable of reconstructing sparse data in our case.
Most of the above surface reconstruction methods could not address arbitrarily oriented contours. The orientation of each contour was typically restricted so that the contours were nearly parallel or did not intersect mutually. In fact, methods that can handle mutually intersected contours are uncommon. Although the method by Liu et al. [29] could handle non-parallel contours, it could not tackle sparse data.
After the conversion of contours to a 3D point cloud, the orientation of the contours becomes irrelevant and we can disregard the non-parallel contours. Currently, there are many surface reconstruction methods that can be used to reconstruct a surface from point clouds [30,31,32,33,34,35,36]. In this paper, we have chosen three well-known and widely accepted methods: the Ball Pivoting Algorithm [37], Power Crust [38], and Poisson reconstruction [39]. These are also representative of three types of point cloud reconstruction methods. The Ball-Pivoting Algorithm (BPA) directly forms a triangle mesh from a given point cloud. The Power Crust method uses the medial axis transform (MAT) of the object to be reconstructed and an inverse MAT to produce the surface of the object. Poisson reconstruction is an implicit-function-based method; it casts the surface reconstruction from oriented points as a spatial Poisson problem. After finding an implicit function by solving the spatial Poisson problem, the reconstructed surface is obtained by extracting an appropriate iso-surface from the implicit function.
Deng et al. [40] provided a surface reconstruction method for freehand 3D US, which is an implicit-function-based method similar to Poisson reconstruction. The surface reconstruction method was based on variational interpolation, which was used by Greg Turk for shape transformation [41]; hence, it was named the variational surface reconstruction (VSR) method. The VSR method can effectively address both sparse and mutually intersected contours. Variational interpolation is commonly used in the surface reconstruction of dense point clouds from ranger scanners [42,43,44,45], and also in the segmentation of medical data [46], but has not been used in the surface reconstruction of freehand 3D US. Although [46] was focused on the 3D segmentation of medical images, the variational interpolation technique used was the same as that in [40]. Because this paper was not dedicated to ultrasound imaging, the specific characteristics of surface reconstruction in freehand 3D US were not addressed.
However, there are three drawbacks to the previous VSR work [40]. First, the experiments were simplistic, as they only used the VSR method to reconstruct a seashell and a plastic apple. Second, the quality of the reconstructed surface was assessed by visual inspection and two simple metrics: area difference and volume difference between the reconstructed surface and the original surface. Third, the VSR method was not compared with other surface reconstruction methods. These three drawbacks make the conclusions regarding the prior VSR work [40] less convincing.
1.4. Contribution and Structure of this Paper
The three drawbacks to the work by Deng et al. [40] are ameliorated in this paper. More experiments are conducted, quantitative metrics are introduced to assess the quality of surface reconstruction, and the surface reconstruction quality of the VSR method is compared with three other methods. The major contribution of this paper is that it provides many quantitative metrics, such as the Hausdorff distance, to evaluate the quality of surface reconstruction using four methods, especially in cases where the input data are extremely sparse point clouds from freehand 3D ultrasound.
The rest of the paper is organized as follows: Section 2 describes the framework of the surface reconstruction for freehand 3D US using the VSR method. Section 3 describes the VSR method and three other methods. Section 4 introduces the quantitative metrics used to assess the quality of surface reconstruction. Section 5 describes the four experiments conducted. Finally, Section 6 summarizes the conclusions of the paper.
2. Framework of Surface Reconstruction for Freehand 3D US Using VSR
The framework of surface reconstruction for freehand 3D ultrasound using the VSR method [40] is shown in Figure 2.
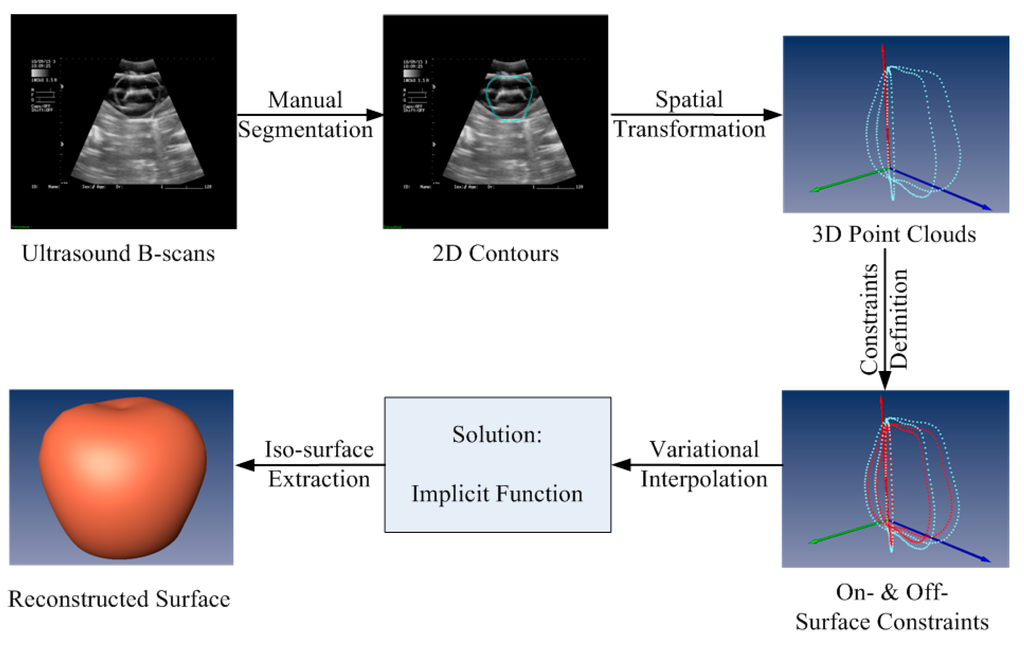
Figure 2.
Framework of surface reconstruction of freehand 3D US using VSR.
First, we perform a spatial transformation to convert the 2D pre-segmented ultrasound contours into a 3D point cloud. Thus the orientation of the contours will become irrelevant and the non-parallel contours can be disregarded.
Second, we define constraint conditions for the surface reconstruction. All the boundary points of the contours are defined as on-surface constraints. Moreover, additional off-surface constraints are defined to indicate which points should be located inside the surface.
Third, the variational interpolation is invoked to find a function that has the minimum bending energy and satisfies the defined constraints. The solution to the variational interpolation is a single 3D implicit function and is at least C1-continuous, i.e., smooth.
Finally, we perform an iso-surface extraction step using the Marching Cubes algorithm proposed by Lorensen et al. [19]. The implicit function of VSR is then evaluated to extract the zero-valued surface as the reconstruction result.
To assess the quality of the reconstructed surface, an extra assessment step is performed. Quantitative metrics [47], e.g., the Hausdorff distance, are calculated to compare the quality of reconstructed surface by four point-based surface reconstruction methods: Ball Pivoting, Power Crust, Poisson, and VSR.
3. Four Methods of Surface Reconstruction from Point Clouds
3.1. VSR
In the framework described in Section 2, the VSR method consisted of two steps: constraint definition and variational interpolation.
The mathematics about the VSR method was previously explained by [40]. Here, only the step-by-step process of constraint definition and variational interpolation without explanation are described.
3.1.1. Constraint Definition
- Step 1:
- Begin with the first contour. Mark it as the current contour.
- Step 2:
- For each point of the current contour, assign a scalar value 0 to . After the assignment, becomes an on-surface constraint .
- Step 3:
- For each point of the current contour, calculate its corresponding off-surface constraint according to Equations (1) and (2).
- Step 4:
- When all the points of the current contour are finished, go to the next contour. Mark it as the current contour.
- Step 5:
- Loop from step 2 to step 4 until all contours are finished.
3.1.2. Variational Interpolation
- Step 1:
- For any pair of constraints and , calculate
- Step 2:
- After all pairs of and are calculated, form the coefficient matrix A in Equation (3):
- Step 3:
- Calculate vector B using Equation (4). Each denotes the corresponding value assigned to the constraint point .
- Step 4:
- Solve Equation (5). The solution vector v contains the weights dj of and the coefficients of .
3.2. Ball Pivoting
The Ball-Pivoting Algorithm (BPA) [37] directly forms a triangle mesh from a given point cloud. Its principle is very simple: starting with a seed triangle, a ball of a user-specified radius pivots around an edge of the seed triangle until it reaches another point. The edge and the new point form another triangle to start with. The process continues until all reachable edges have been finished, and then starts from another seed triangle, until all points have been considered.
BPA is intuitive, flexible, efficient, and robust. If given sufficiently dense input data, it is capable of reconstructing a surface homeomorphic to and within a bounded distance from the original manifold.
However, BPA cannot necessarily reconstruct a closed surface from a sparse point cloud.
3.3. Power Crust
The Power Crust method [38] is divided into two stages: First, the medial axis transform (MAT) of the object to be reconstructed is approximated from the point cloud. Then, an inverse transform is invoked to produce the surface from the MAT.
The Power Crust method does not depend on the quality of the input point sample. It can produce watertight surfaces when the input sample is sufficiently dense. When the sample is not sufficiently dense, the Power Crust method may not produce a perfect manifold surface but its output is watertight.
However, the Power Crust method may fail if the noise of the input data is above a certain threshold.
3.4. Poisson Reconstruction
Poisson reconstruction [39] casts the surface reconstruction from oriented points as a spatial Poisson problem: The computed Laplace operator of the scalar function is equal to the divergence of a vector field , as follows:
where the vector field is defined by the oriented points and is a 3D indicator function. After finding by solving Equation (9), the reconstructed surface is obtained by extracting an appropriate iso-surface from .
The time and space complexities of Poisson reconstruction are proportional to the size of the reconstructed model, and it is highly resilient to data noise.
One drawback of Poisson reconstruction is that it requires oriented normal vectors at the input points to define the vector field .
4. Quantitative Metrics for Assessment of Surface Reconstruction
In most papers about 3D surface reconstruction, the quality of the reconstructed surface is assessed by visual inspection, rather than quantitative assessment, for two reasons. First, the original 3D surface model of VOI is unavailable before the reconstruction. Second, there is a lack of proper quantitative metrics for assessing surface reconstruction.
In this paper, we prepare two types of original surface models to assess the quality of surface reconstruction. The first type is synthetic data (such as an acorn model). The second type is original surface models gained by other image modalities of the same VOI, e.g., we prepare a kidney surface model from dense and parallel contours of CT imaging, and then compare it with its reconstructed ultrasound surface model.
For the quantitative metrics, we compute several distances between the original surface and the reconstructed surface. For each vertex of a surface, we compute its distance to the closest point on another surface. From the histogram of these values the following metrics are computed:
- mean distance (mean)
- standard deviation from the mean distance (std)
- root mean square distance (rms)
- maximum distance (Hausdorff)
- medial distance (median).
These metrics measure the shape difference between two triangulated surfaces, and their meanings are self-explanatory and intuitive. For example, the Hausdorff distance measures the maximum difference between two triangulated surfaces, and std and rms detail statistical information about the difference between the two triangulated surfaces. Moreover, we also compute the area difference and volume difference between the original and the reconstructed surfaces. For these metrics, a greater value indicates a greater difference between the original and the reconstructed surface.
For a set and a point , let denote the Euclidean distance of from , i.e.,
The Hausdorff distance [48] between two sets is given by
5. Experiments
Four experiments were conducted to evaluate the quality of surface reconstruction. The first experiment used the synthetic data as the original surface model. The second experiment used the CT data to extract the original surface model. The third experiment used the real ultrasound data of two liver tumors, without the original surface model of the tumors. The fourth experiment assessed the reproducibility of the VSR method and three other methods using the kidney data in Experiment 2 and the first liver tumor data in Experiment 2.
For ultrasound image acquisition, we used a ZK-3000 ultrasound machine with a 3.5 MHz conventional 2D ultrasound probe (Beijing Zhongke-Tianli Tech. Co., Ltd., Beijing, China). The electromagnetic tracking device was the AURORA from Northern Digital Inc. (Waterloo, ON, Canada). The digital ultrasound image was acquired through an image-grabbing card. As noted previously, the position and orientation of the ultrasound probe was also recorded simultaneously using the tracking device. The experiment system setup is shown in Figure 1.
The 3D image reconstruction and visualization were performed using a personal computer with a 2.66 GHz Intel Core2™ quad CPU (Lenovo, Beijing, China). We developed an IGS (image-guided surgery) software for microwave and radio-frequency ablation of hepatic tumors [2,3] (Figure 3), which was used as the surface reconstruction and visualization program.
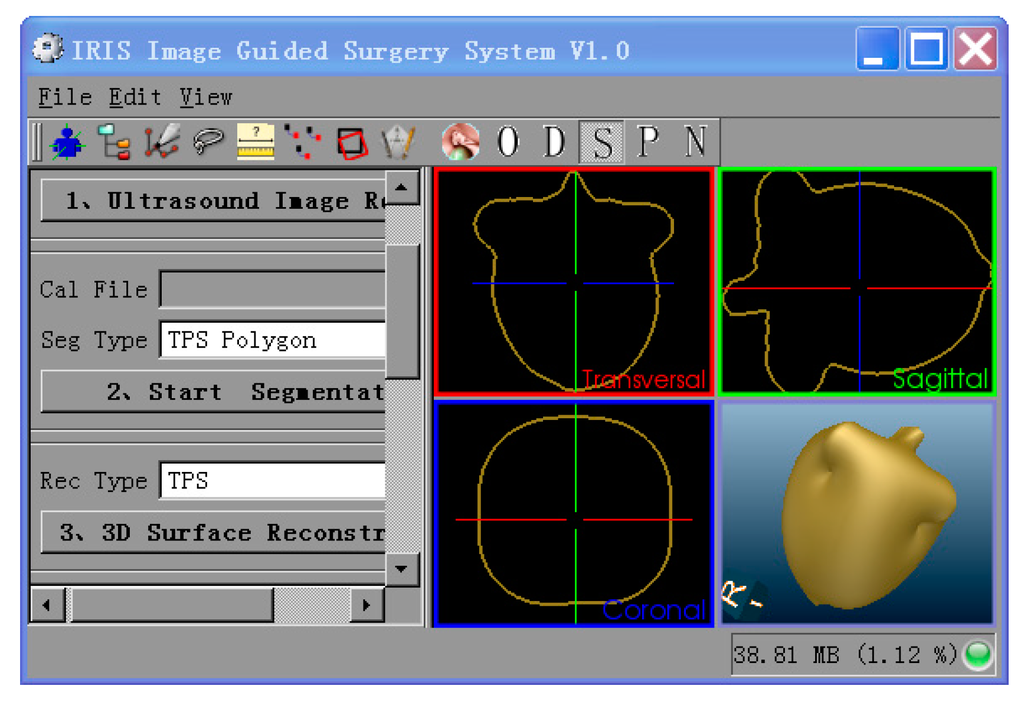
Figure 3.
Reconstruction and visualization software.
5.1. Experiment 1—Reconstruction of Acorn
In Experiment 1, we reconstructed an acorn from several non-parallel contours. The original 3D surface model was from the Amira Demos 3.1 CD (version 3.1, FEI Corporate, Hillsboro, OR, USA, 2005). Between two and seven mutually intersected contours were re-sampled from the original surface model and were used to reconstruct the acorn surface. The experiment results are shown in Figure 4 and Figure 5 and Table 1.

Figure 4.
Surface reconstruction of an acorn by four methods. For each row, from left to right: the contours used, the original surface, the surface reconstructed by BPA, the surface reconstructed by Power Crust, the surface reconstructed by Poisson, and the surface reconstructed by VSR.
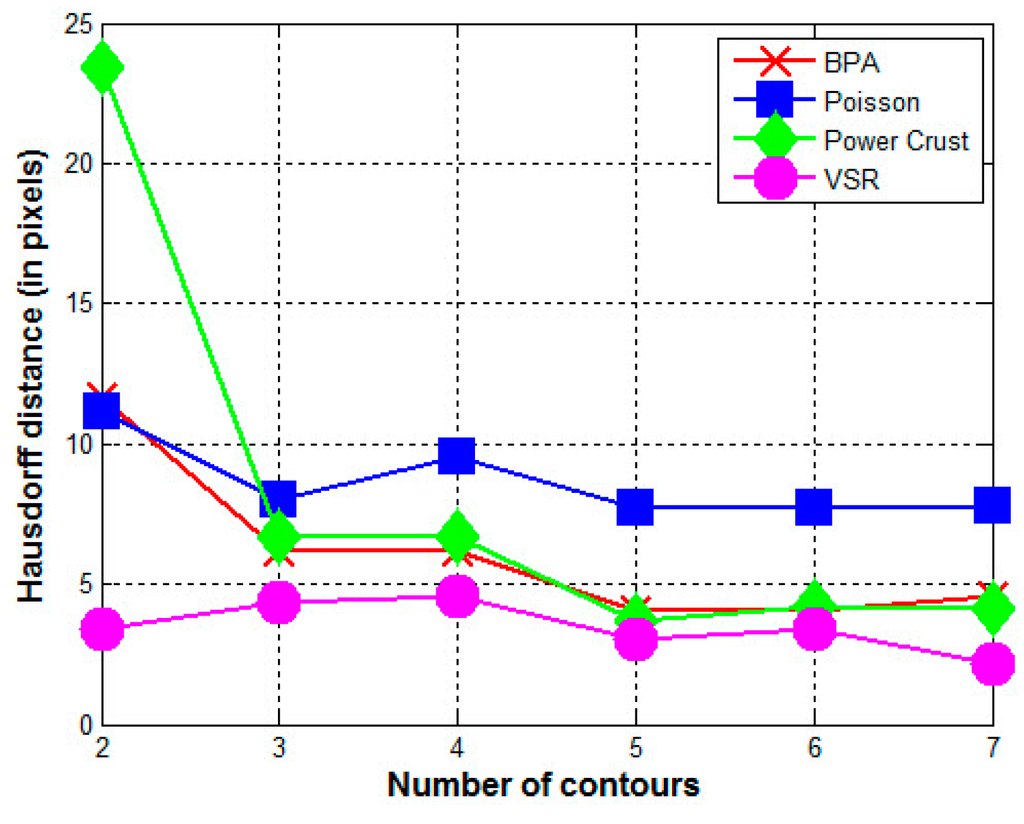
Figure 5.
Hausdorff distance between the reconstructed surface and the original surface (ACORN).

Table 1.
Difference between the reconstructed surface and the original surface (ACORN).
In Figure 4, each row shows the results of surface reconstruction by four methods: BPA, Power Crust, Poisson, and VSR, respectively. From left to right, each row shows the contours used, the original surface, the surface reconstructed by BPA, the surface reconstructed by Power Crust, the surface reconstructed by Poisson, and the surface reconstructed by VSR.
Table 1 shows the quantitative differences between the original surface and the reconstructed surface using the metrics we described in Section 4. Figure 5 is the same Hausdorff distance shown in Table 1 but expressed graphically.
All the contours used in this experiment are non-parallel to each other and intersected mutually. VSR’s performance is excellent when the input data are sparse, such that two contours can lead to a close approximation to the original surface. This indicates that the VSR method can process both arbitrarily oriented and sparse contours.
We can conclude that:
- In all cases, the surface reconstructed by the VSR method best visually resembles the original surface compared with the other methods. Most metrics show that the VSR-reconstructed surface shows fewer differences from the original surface compared with the other methods. The only exception is observed in volume difference for four contours, where the Poisson method produces a volume that is more similar to the original surface than that of the VSR method.
- For the other three methods, the quality of the reconstructed surfaces drops dramatically as the number of contours decreases (as seen for two or three contours in Figure 4 and Figure 5). However, as the number of contours decreases, both the quality and the Hausdorff distance for the VSR method show little variation. Even with only two contours, the VSR surface reconstruction closely approximates the original surface.
- Visually and quantitatively, the Poisson method performs the worst, except when reconstructed with two contours. Although Poisson and VSR are implicit-function-based methods, the Poisson method fails to reconstruct a satisfactory surface in all cases.
- Although the Power Crust method claims to be capable of producing watertight surfaces, it fails to do so when it is performed on two contours. This makes it the worst method for surface reconstruction with only two contours.
- As an intuitive and efficient method, BPA succeeds in constructing a triangle mesh for all cases. When the input data are dense (i.e., seven contours), it can produce a satisfactory surface of the acorn. However, its performance decreases dramatically as the number of contours decreases.
5.2. Experiment 2—Reconstruction of Human Kidney
In Experiment 2, we reconstructed a human kidney from non-parallel contours re-sampled from an original surface model of the kidney. The original surface model of the kidney was created from its CT counterpart as follows: First, CT images of a volunteer were acquired in our cooperative hospital. Second, the kidney was segmented slice by slice from the CT image data, using the semi-automatic segmentation function in Amira software (version 3.1, FEI Corporate, Hillsboro, OR, USA, 2005) [49], which was based on Active Contour Model. Third, the Amira software was used to reconstruct the surface of the segmented kidney to produce the original surface model of this experiment.
The differences between the four reconstructed surfaces and the original surface are illustrated in Figure 6 and Figure 7 and Table 2.
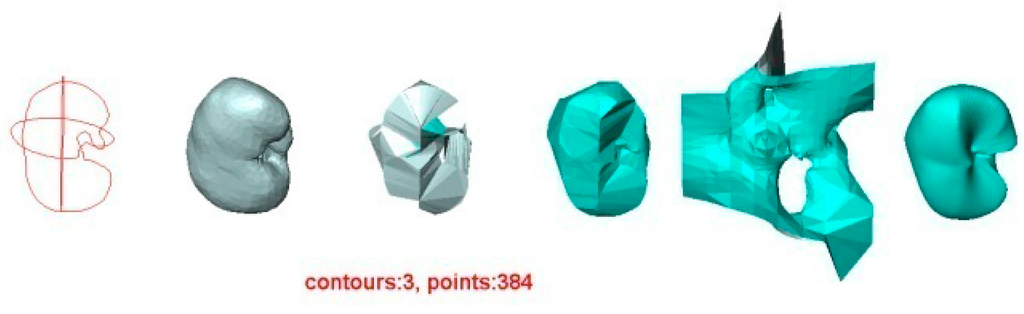
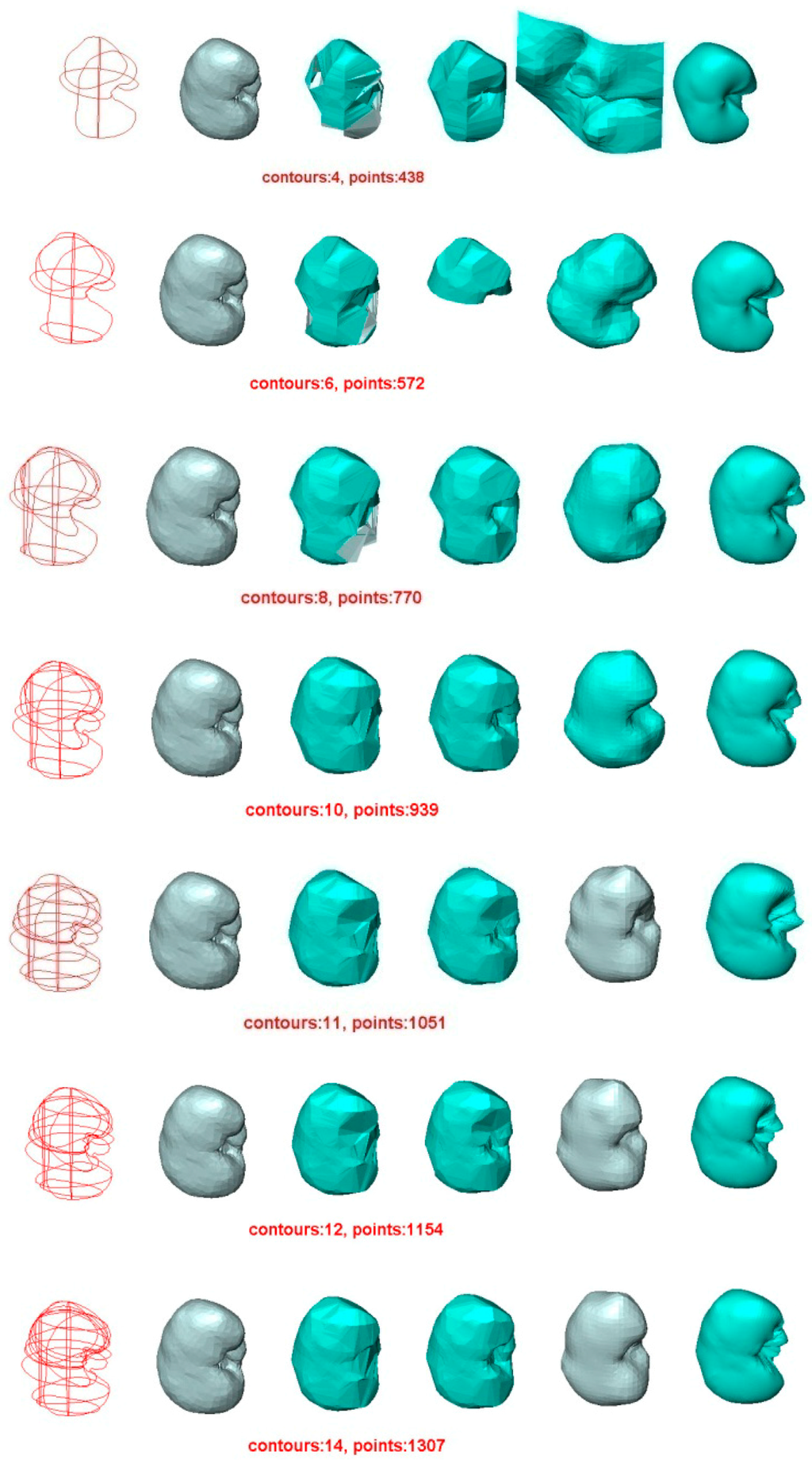
Figure 6.
Surface reconstruction of a human kidney by four methods. For each row, from left to right: the contours used, the original surface, the surface reconstructed by BPA, the surface reconstructed by Power Crust, the surface reconstructed by Poisson, and the surface reconstructed by VSR.
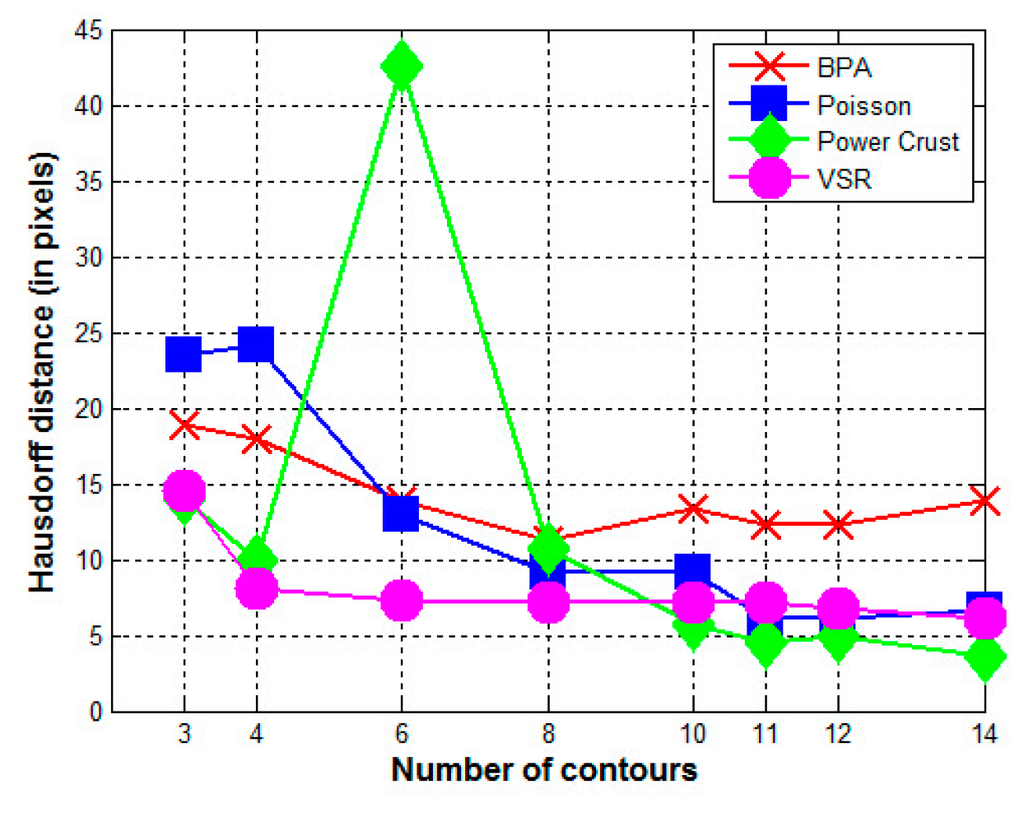
Figure 7.
Hausdorff distance between the reconstructed surface and the original surface (HUMAN KIDNEY).

Table 2.
Difference between the reconstructed surface and the original surface (HUMAN KIDNEY).
The results of this experiment conformed to those of Experiment 1. When the input data were dense enough (i.e., 14 or 12 contours), all four methods obtained satisfactory surfaces. All the quantitative differences between the reconstructed surfaces and original surface were small for all four methods. However, even with a dense point cloud, the VSR method still remained the best whether evaluated visually or quantitatively. Although the Hausdorff distance of the Power Crust method was slightly less than that of the VSR method when the number of used contours was greater than 10, it behaved poorly when the number of contours used decreased.
For the BPA, Power Crust, and Poisson methods, the quality of the reconstructed surface dropped dramatically when the number of contours used decreased. However, the performance of the VSR method was still excellent, both visually and quantitatively. Even when six, four, and three contours were used, the VSR reconstruction was a close approximation to the original surface, while the other three methods failed to create complete or closed surfaces.
The BPA method was the worst when reconstructions were produced with more than six contours, as seen in Table 2. When the input data were extremely sparse (i.e., six, four, and three contours), the Poisson method performed worst.
5.3. Experiment 3—Reconstruction of Liver Tumor
In Experiment 3, we reconstructed two human liver tumors from real ultrasound data. In this case, we did not have the original surface model for comparison. We could not perform a quantitative assessment of the reconstructed surface, and thus we inspected the visual differences instead.
The visual differences between the reconstructed surfaces and the original surface are illustrated in Figure 8 and Figure 9. As we did not have the original surface, the reconstructions are as follows, from left to right: the contours used, the surface reconstructed by BPA, the surface reconstructed by Power Crust, the surface reconstructed by Poisson, and the surface reconstructed by VSR.
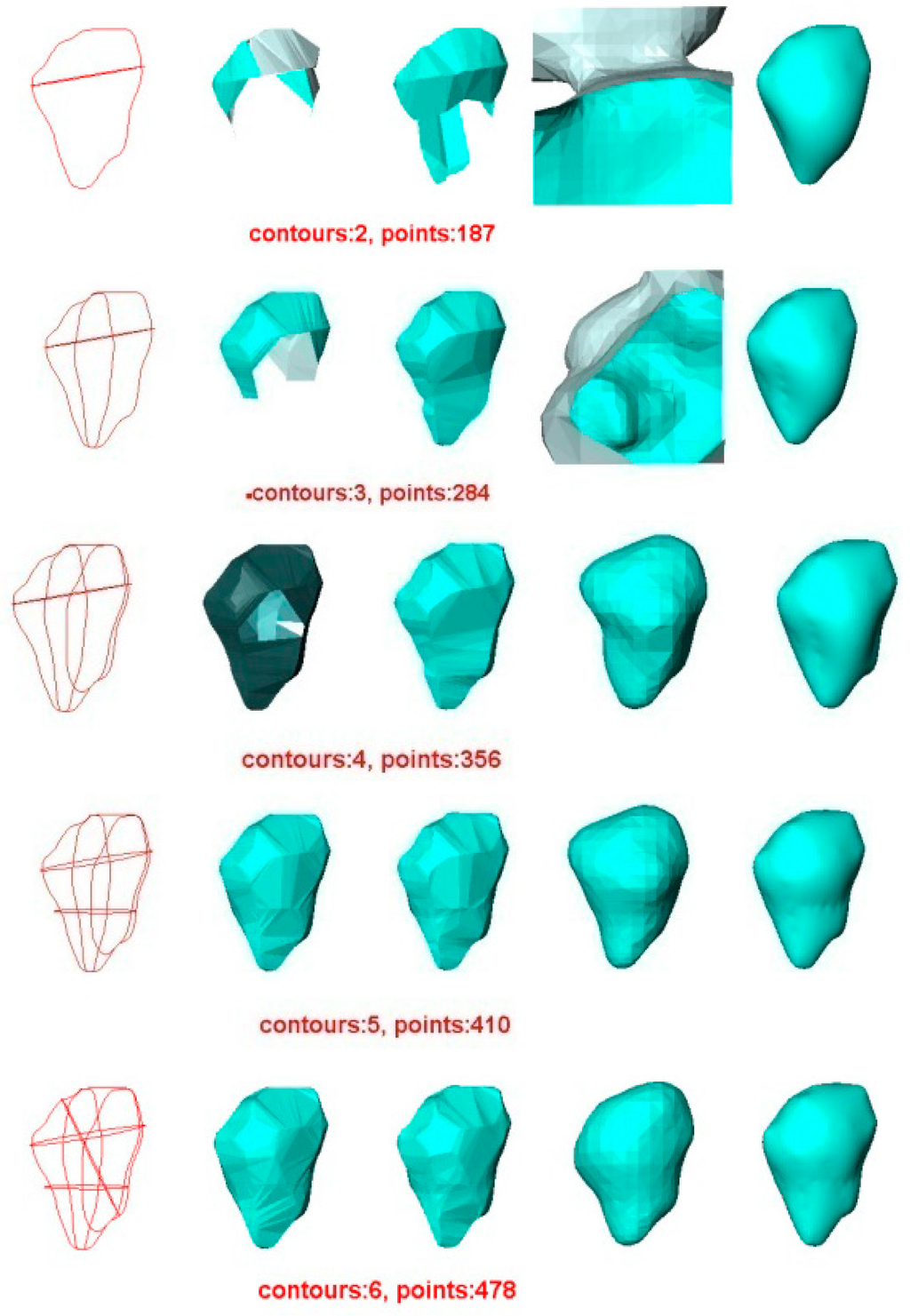
Figure 8.
Surface reconstruction of one human liver tumor using four methods. For each row, from left to right: the contours used, the surface reconstructed by BPA, the surface reconstructed by Power Crust, the surface reconstructed by Poisson, and the surface reconstructed by VSR.
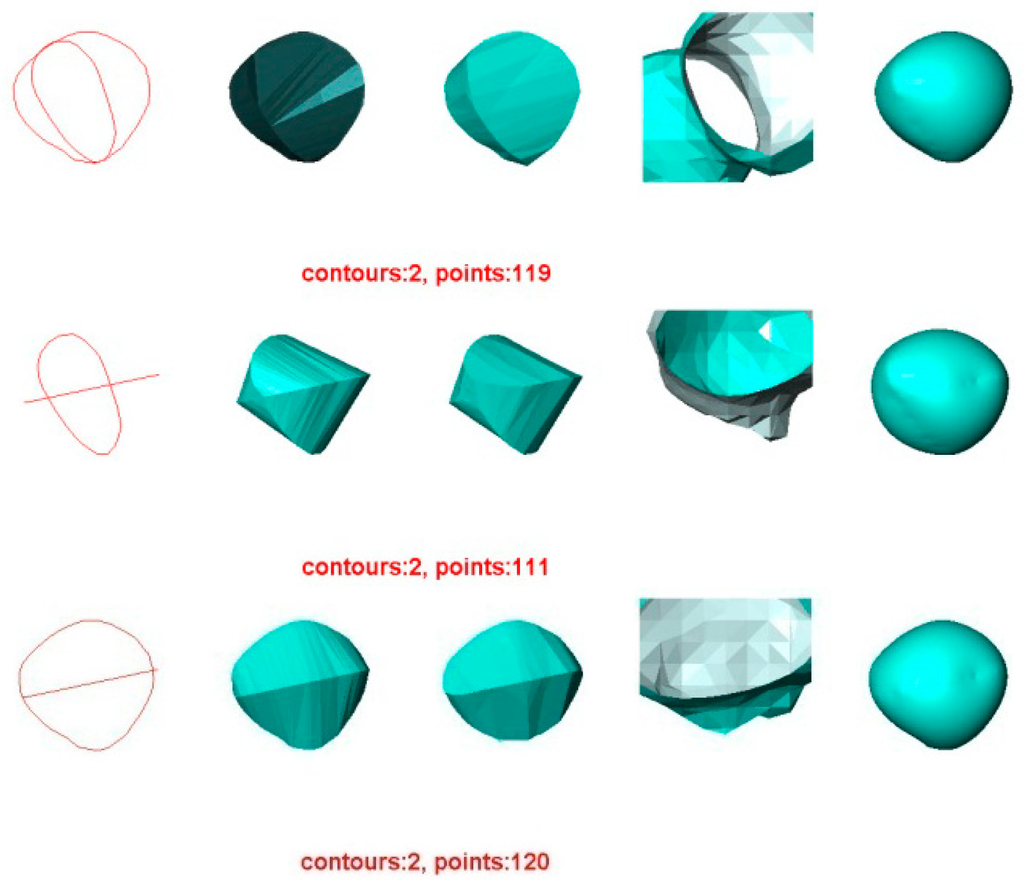
Figure 9.
Surface reconstruction of another human liver tumor by four methods. For each row, from left to right: the contours used, the surface reconstructed by BPA, the surface reconstructed by Power Crust, the surface reconstructed by Poisson, and the surface reconstructed by VSR.
Figure 8 also indicated that VSR was the best compared to three other methods, similar to the results of Experiment 1 and Experiment 2. When two contours were used, the VSR method still reconstructed a satisfactory surface while the other three methods failed to create closed surfaces.
In Figure 9, only two contours were used to reconstruct the surface of another hepatic tumor. Visually, this figure also indicated that VSR was the best method compared with the other methods, consistent with the results of the previous experiments.
5.4. Experiment 4—Assessing the Reproducibility of Four Methods
Finally, we investigated the reproducibility of the four methods. Four different users drew the same number but different contours from the kidney in Experiment 2 and the first hepatic tumor in Experiment 3, and surfaces were reconstructed from these contours and the quality of the reconstructed surfaces were evaluated.
In the case of the kidney in Experiment 2, each user drew four different contours from the original surface model of the kidney. The differences between the four reconstructed surfaces and the original surface are illustrated in Figure 10 and Figure 11 and Table 3.
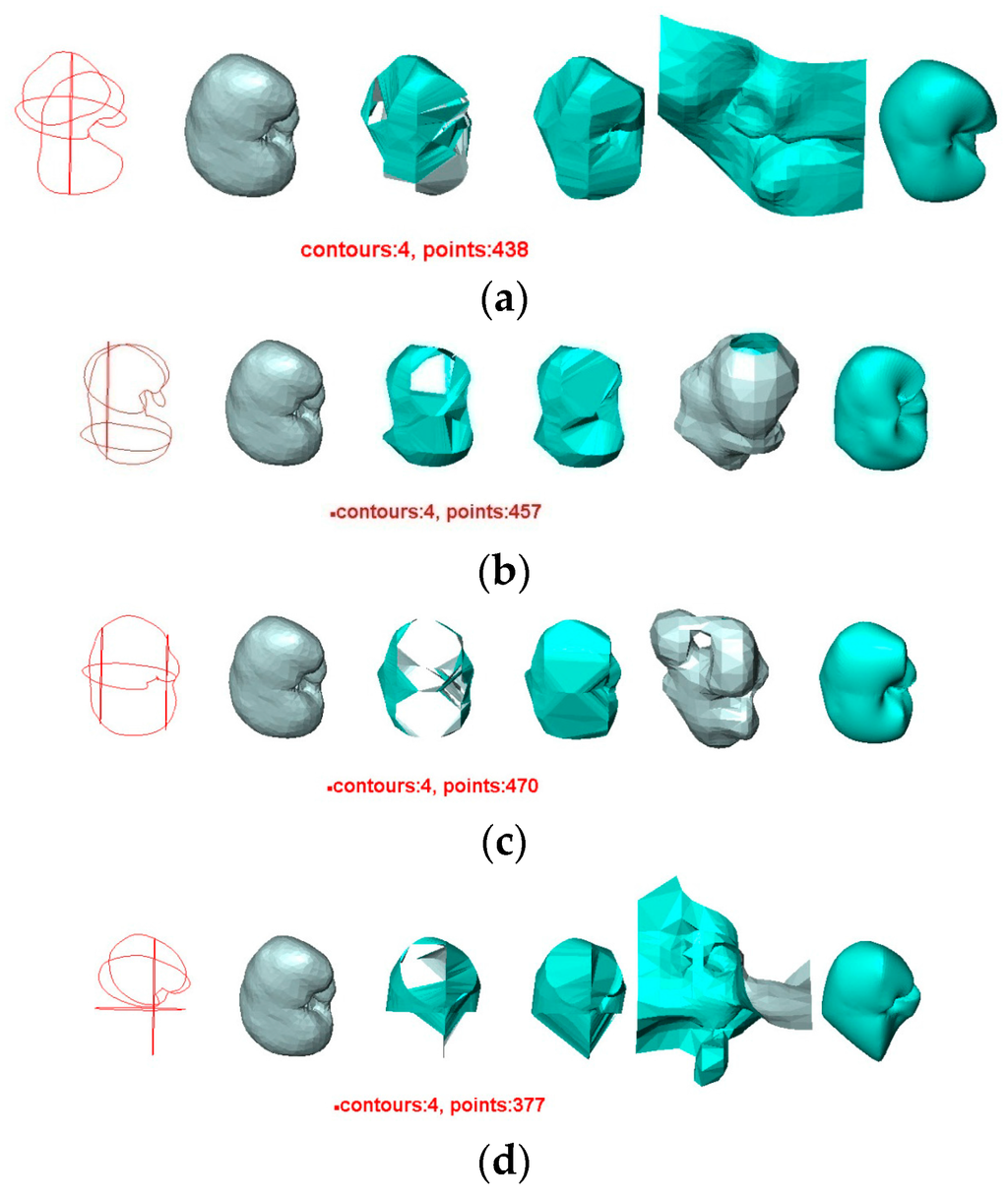
Figure 10.
Surface reconstruction of a human kidney by four methods. The number of contours are the same in different rows, but the contours were drawn by different users: (a) User 1; (b) User 2; (c) User 3; (d) User 4. For each row, from left to right: the contours used, the original surface, the surface reconstructed by BPA, the surface reconstructed by Power Crust, the surface reconstructed by Poisson, and the surface reconstructed by VSR.
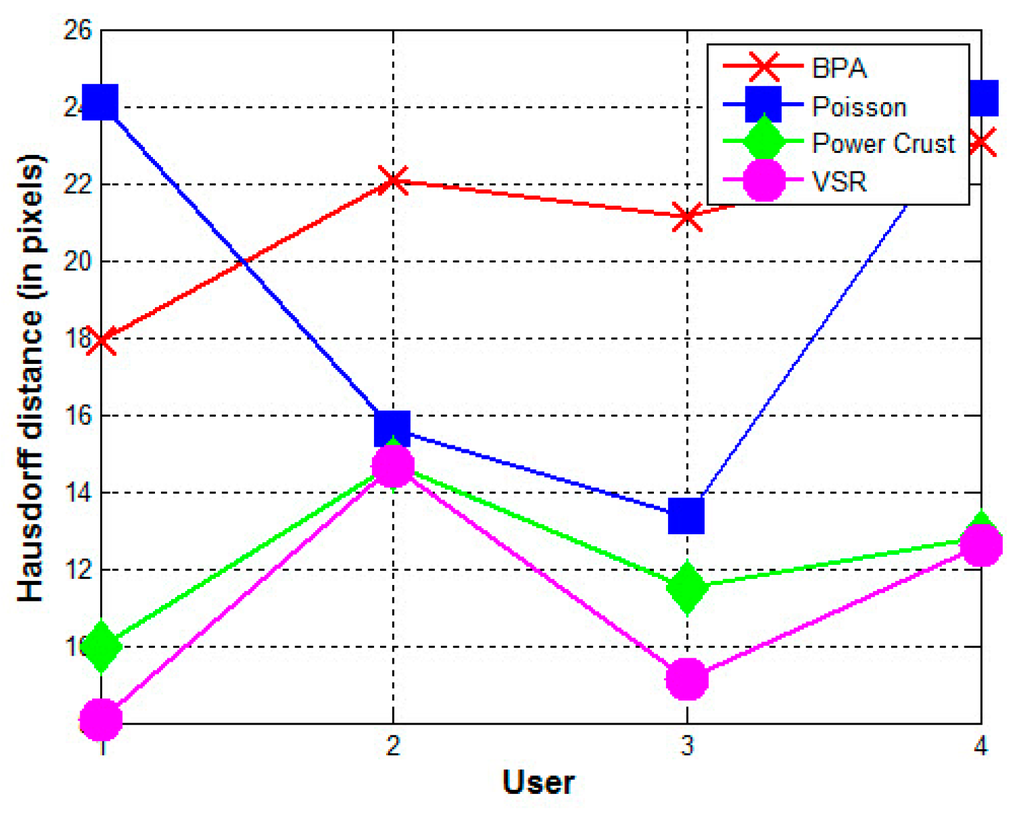
Figure 11.
Hausdorff distances between the reconstructed surfaces and the original surface (HUMAN KIDNEY). The contours were drawn by four different users.

Table 3.
Difference between the reconstructed surface and the original surface (HUMAN KIDNEY; the contours were drawn by different users).
We can conclude that:
- The contours used greatly affect the quality of the reconstructed surfaces by all four methods. Visually, the contours drawn by User 3 produce the best approximation to the original surface, and the contours drawn by User 4 produce the poorest. Figure 11 confirms this conclusion graphically. This result indicates that the sparse input contours should cover the key contours of the original surface to produce a close approximation to it.
- In all cases, the surface reconstructed by the VSR method best visually resembles the original surface compared with the other methods. All metrics show that the VSR-reconstructed surface shows fewer differences from the original surface compared with the other methods, which indicates that the reproducibility of the VSR method is the best of the four methods.
In the case of the first hepatic tumor in Experiment 3, each user manually segmented four different contours from the freehand ultrasound data of the tumor. The reconstructed surfaces are illustrated in Figure 12. As we did not have the original surface of the hepatic tumor, in order to evaluate the reproducibility of each method, the reconstructed surface from the contours drawn by user 1 using that method was temporarily taken as the original surface to evaluate the quality of surface reconstruction from the contours drawn by Users 2, 3, and 4, e.g., the quantitative assessment of the quality of the reconstructed surfaces from the contours drawn by Users 2, 3, and 4 using the VSR method were performed based on the reconstruction from the contours drawn by User 1 using the VSR method. The quantitative differences are shown in Figure 13 and Table 4.
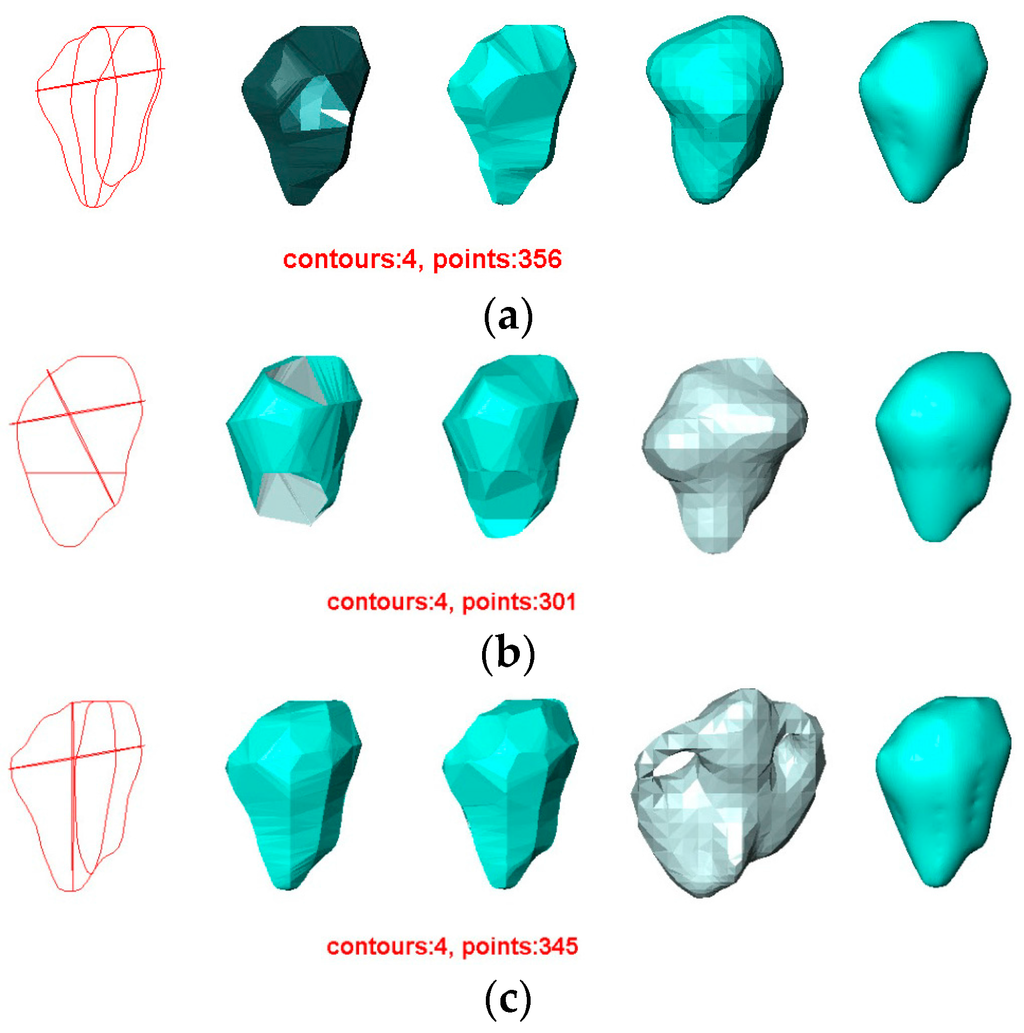
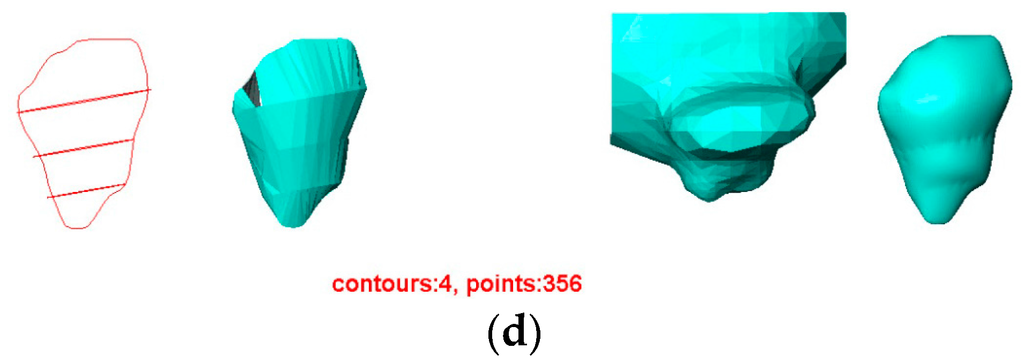
Figure 12.
Surface reconstruction of a hepatic tumor by four methods. The numbers of contours are the same in different rows, but the contours were drawn by different users: (a) User 1; (b) User 2; (c) User 3; (d) User 4. For each row, from left to right: the contours used, the surface reconstructed by BPA, the surface reconstructed by Power Crust, the surface reconstructed by Poisson, and the surface reconstructed by VSR.
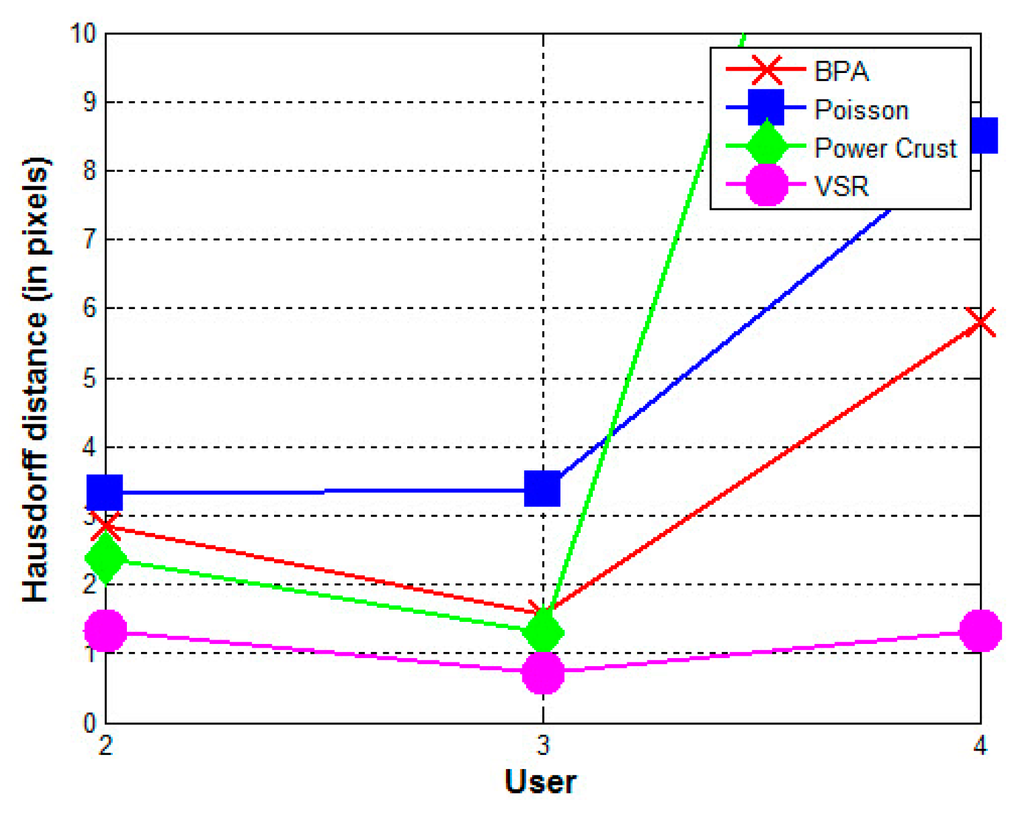
Figure 13.
Hausdorff distances between the reconstructed surfaces from the contours drawn by Users 2, 3, and 4 and the reconstructed surface from the contours drawn by User 1 (LIVER TUMOR). The contours were drawn by four different users.

Table 4.
Difference between the reconstructed surfaces from the contours drawn by Users 2, 3, and 4 and the reconstructed surface from the contours drawn by User 1 (LIVER TUMOR).
The results of this experiment conform to those of the previous reproducibility experiment, so we can conclude that:
- The contours used greatly affect the quality of the reconstructed surfaces by all four methods. Visually, the contours drawn by User 3 produce the best approximation to the reconstructed surface from the contours drawn by User 1 using the BPA, Power Crust, and VSR methods. The contours drawn by User 4 produce the poorest approximation, especially when the Power Crust method is used; it fails to produce a surface. Figure 13 confirms this conclusion graphically. It should be noted that the Hausdorff distance of the Power Crust method is missing in Figure 13 since its value is much greater than that of the other methods.
- In all cases, the surface reconstructed by the VSR method best visually resembles the original surface compared with the other methods. All metrics show that the VSR-reconstructed surfaces show fewer differences from the surface reconstructed from the contours drawn by User 1 compared with the other methods, which indicates that the reproducibility of the VSR method is the best of four methods.
6. Discussion
The main goal of this paper is to evaluate the quality of surface reconstruction from point clouds using four point-based methods, especially when the inputs are extremely sparse point clouds from freehand 3D ultrasound.
The BPA method is intuitive and robust. If given sufficiently dense input data, it is capable of reconstructing a satisfactory surface from the original manifold. However, the BPA method failed to produce a closed surface from sparse point clouds, as observed in Experiment 2 and Experiment 3. In Experiment 2, the BPA method was the worst method when more than six contours were used.
The Power Crust method produced watertight surfaces when the input sample was sufficiently dense. However, when the input data were extremely sparse, as in Experiment 2 and Experiment 3 (i.e. two contours), it failed completely.
The Poisson method also created satisfactory surfaces when given sufficiently dense input data. However, the Poisson method required oriented normal vectors at the input points to define the vector field. When the input data were extremely sparse, the vector field could not be correctly defined, and the Poisson method failed to reconstruct the correct surfaces. Hence, the Poisson method was the worst of the four methods in all experiments when reconstructed from extremely sparse contours.
In all cases, the surface reconstructed by the VSR method showed the greatest visual resemblance to the original surface, compared with the other three methods. In most cases, the metrics also indicated that the quantitative differences between the VSR reconstructed surface and the original surface were the smallest. Even given extremely sparse input data, the VSR method could reconstruct a close approximation to the original surface.
Therefore, the strengths of the VSR method were as follows: (1) the VSR method could reconstruct satisfactory surfaces from sparse data; (2) the surfaces reconstructed by the VSR method were smooth; (3) although the VSR and Poisson methods were both implicit-function-based methods, the VSR method did not need to compute the oriented normal vectors at the input point clouds to define a vector field.
However, the second strength of VSR was also a weakness. Because the reconstructed surfaces by VSR method were smooth, the reconstruction of objects with high curvature might fail if the surface was sampled too sparsely, i.e., with not enough contours.
The VSR method has another limitation concerning contradictory inputs as shown by Heckel et al. [46], i.e., contours that define different surfaces, although they should be located on the same surface. This issue was demonstrated in Figure 14. In Figure 14, we used three same contours of the kidney as in the first row of Figure 6, except that the horizontal contour was edited manually to form contradictory contours. In row (a) of Figure 14, we could see that the original horizontal contour (yellow) should intersect with the vertical contour (blue), but the edited version of the horizontal contour (red) did not intersect with the vertical contour (blue). The quantitative assessments of the quality of surface reconstruction from the contradictory contours are shown in Table 5.
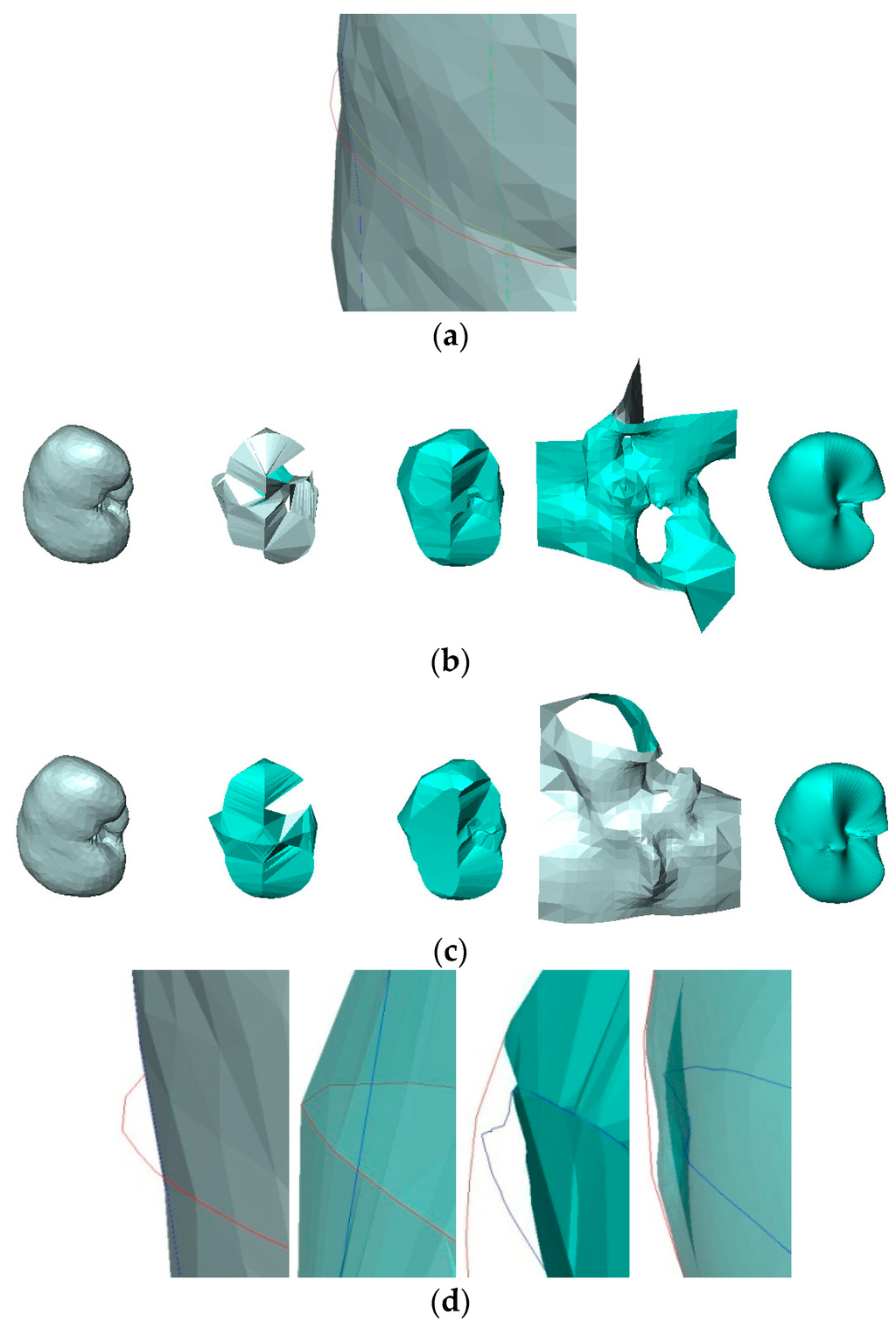
Figure 14.
Surface reconstruction of contradictory contours of the kidney. (a) Contradictory contour: the original horizontal contour (yellow) should intersect with the vertical contour (blue), but the edited version of the horizontal contour (red) did not intersect with the vertical contour (blue); (b) surface reconstruction from the original contours; (c) surface reconstruction from the contradictory contours. For row b and c, from left to right: the original surface of the kidney, the surface reconstructed by BPA, the surface reconstructed by Power Crust, the surface reconstructed by Poisson, and the surface reconstructed by VSR. (d) Detail of the surface reconstruction near the intersection of the contradictory contours. From left to right: the original surface of the kidney and the contradictory contours, the surface reconstructed by BPA, the surface reconstructed by Power Crust, the surface reconstructed by Poisson, and the surface reconstructed by VSR.

Table 5.
Difference between the reconstructed surfaces from contradictory contours and the original surface (HUMAN KIDNEY).
As seen in row (d) of Figure 14, most methods had some problems dealing with the contradictory contours. The surface reconstructed by the BPA method lay on the outer red contour, which led to a bump on the reconstructed surface, while the original surface of the kidney should lie on the inner blue contour. There was a concave near the contradictory contours on the surface reconstructed by the Power Crust method, which indicated that it could not produce a correct surface from contradictory contours. The surface reconstructed by the VSR method lay between the outer read contour and the inner blue contour, which was a better result than the BPA and Power Crust methods. The surface reconstructed by the Poisson method lay on the inner blue contour correctly, indicating that it was the best method for dealing with contradictory contours.
Because contradictory contours usually come from inconsistencies in the input data, they can be compensated for by an additional preprocessing step that solves such inconsistencies before the surface reconstruction. They can also be slightly compensated for when using approximation instead of interpolation. The results of Figure 14 may suggest a new way of combining the VSR and Poisson methods to solve the problem. We will investigate this in future work.
Moreover, the VSR method was computationally expensive and needed considerable memory. Computation times were slow for a large number of constraints. This problem could be solved by reducing the constraints, using GPU-based parallel computing strategies, and using a fast computing algorithm such as the fast multipole method, which was suggested by Carr et al. [50].
7. Conclusions
Three experiments were conducted to compare the performance of the VSR method with three other methods, i.e., BPA, Power Crust, and Poisson, when reconstructing a surface from sparse freehand 3D ultrasound contours. The research results show that VSR performed the best of the tested methods. Compared with the three other methods, the VSR method showed the best visual resemblance and the least quantitative differences to the original surface, especially when the data were very sparse. The VSR method closely approximated the original surface even with two contours, whereas the other algorithms failed to do so. The reconstructed surface produced by VSR appeared smooth and natural.
The experiments’ results show that the reproducibility of the VSR method is also the best of the tested methods.
Acknowledgments
This work was supported by the Key Projects in the National Science & Technology Pillar Program under the grant 2013BAI01B01. Their financial support was greatly appreciated.
Author Contributions
Drafting of manuscript: Shuangcheng Deng and Yunhua Li. Experiments: Shuangcheng Deng and Ping Liang. Analysis and interpretation of data: Shuangcheng Deng. Planning and supervision of the research: Yunhua Li and Lipei Jiang.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, W.P.; Han, Z.Y.; Zhang, J.; Liang, P. A retrospective comparison of microwave ablation and high intensity focused ultrasound for treating symptomatic uterine fibroids. Eur. J. Radiol. 2015, 84, 413–417. [Google Scholar] [CrossRef] [PubMed]
- Livaghi, T.; Goldberg, S.N.; Lazzaroni, S.; Meloni, F.; Ierace, T.; Solbiati, L.; Gazelle, G.S. Hepatocellular carcinoma: Radio-frequency ablation of medium and large lesions. Radiology 2000, 214, 761–768. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.Y.; Yu, X.L.; Liang, P.; Cheng, Z.G.; Han, Z.Y.; Dong, B.W.; Zhang, X.H. Microwave ablation assisted by a real-time virtual navigation system for hepatocellular carcinoma undetectable by conventional ultrasonography. Eur. J. Radiol. 2012, 81, 1455–1459. [Google Scholar] [CrossRef] [PubMed]
- Reis, J.; Butani, D. Tumor Ablation: Ultrasound versus CT. Ultrasound Clin. 2013, 8, 171–183. [Google Scholar] [CrossRef]
- Reis, J.; Butani, D. Ultrasound Guidance in Tumor Ablation. Ultrasound Clin. 2014, 9, 67–79. [Google Scholar] [CrossRef]
- Huang, X.; Hill, N.A.; Peters, T.M. Ultrasound-based technique for intrathoracic surgical guidance. In Proceedings of the Medical Imaging 2005: Visualization, Image-Guided Procedures, and Display, San Diego, CA, USA, 12 February 2005.
- Fenster, A.; Downey, D.B. 3-D ultrasound imaging—A review. IEEE Eng. Med. Biol. Mag. 1996, 15, 41–51. [Google Scholar] [CrossRef]
- Fenster, A.; Downey, D.B.; Cardinal, H.N. Three-dimensional ultrasound imaging. Phys. Med. Biol. 2000, 46, R67–R99. [Google Scholar] [CrossRef]
- Gee, A.; Prager, R.; Treece, G.; Berman, L. Engineering a freehand 3D ultrasound system. Pattern Recognit. Lett. 2003, 24, 757–777. [Google Scholar] [CrossRef]
- Mercier, L.; Langø, T.; Lindseth, F.; Collins, L.D. A review of calibration techniques for freehand 3-D ultrasound systems. Ultrasound Med. Biol. 2005, 31, 143–165. [Google Scholar] [CrossRef] [PubMed]
- Rousseau, F.; Hellier, P.; Barillot, C. Confhusius: A robust and fully automatic calibration method for 3D freehand ultrasound. Med. Image Anal. 2005, 9, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Rao, Y.; Li, X.X.; Jiang, L.P.; Deng, S.C.; Cao, Y.Y.; Yao, P.; Li, X.H.; Liu, S.Q. 3-D calibration method for freehand ultrasound image with high precision based on string-beads phantom. In Proceedings of the Industrial Mechatronics and Automation (ICIMA), 2010 2nd International Conference on, Wuhan, China, 30–31 May 2010.
- Solberg, O.V.; Lindseth, F.; Torp, H.; Blake, R.E.; Hernes, T.A.N. Freehand 3D Ultrasound Reconstruction Algorithms—A Review. Ultrasound Med. Biol. 2007, 33, 991–1009. [Google Scholar] [CrossRef] [PubMed]
- Rohling, R.; Gee, A.; Berman, L. A comparison of freehand three-dimensional ultrasound reconstruction techniques. Med. Image Anal. 1999, 3, 339–359. [Google Scholar] [CrossRef]
- Prager, R.; Gee, A.; Treece, G.; Berman, L. Freehand 3D ultrasound without voxels: Volume measurement and visualisation using the Stradx system. Ultrasonics 2002, 40, 109–115. [Google Scholar] [CrossRef]
- Sherebrin, S.; Fenster, A.; Rankin, R.N.; Spence, D. Freehand three-dimensional ultrasound: Implementation and applications. In Proceedings of the Medical Imaging 1996: Physics of Medical Imaging, Toronto, ON, Canada, 10 February 1996; pp. 296–303.
- Barry, C.D.; Allott, C.P.; John, N.W.; Mellor, P.M.; Arundel, P.A.; Thomson, D.S.; Waterton, J.C. Three dimensional freehand ultrasound: Image reconstruction and volume analysis. Ultrasound Med. Biol. 1997, 8, 1219–1224. [Google Scholar] [CrossRef]
- Scheipers, U.; Koptenko, S.; Falco, T.; Remilinger, R.; Lachaine, M. 3-D Ultrasound Volume Reconstruction Using the Direct Frame Interpolation Method. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2460–2470. [Google Scholar] [CrossRef] [PubMed]
- William, L.; Harvey, E.C. Marching cubes: A high resolution 3-d surface construction algorithm. Comput. Gr. 1987, 4, 163–169. [Google Scholar]
- Newman, T.S.; Yi, H. A survey of the marching cubes algorithm. Comput. Gr. 2006, 30, 854–879. [Google Scholar] [CrossRef]
- Suri, J.S.; Liu, K.; Singh, S.; Laxminarayan, S.N.; Zeng, X.; Reden, L. Shape recovery algorithms using level sets in 2-D/3-D medical imagery: A state-of-the-art review. IEEE Trans. Inf. Technol. Biomed. 2002, 6, 8–28. [Google Scholar] [CrossRef] [PubMed]
- Poon, M.; Hamarneh, G.; Abugharbieh, R. Efficient Interactive 3D Livewire Segmentation of Objects with Arbitrarily Topologies. Comput. Med. Imaging Gr. 2008, 32, 639–650. [Google Scholar] [CrossRef] [PubMed]
- Mory, B.; Ardon, R.; Yezzi, A.; Thiran, J.-P. Non-Euclidean Image-Adaptive Radial Basis Functions for 3D Interactive Segmentation. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 787–794.
- Grady, L. Random Walks for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1768–1783. [Google Scholar] [CrossRef] [PubMed]
- Boykov, Y.; Funka-Lea, G. Graph Cuts and Efficient N-D Image Segmentation. Int. J. Comput. Vis. 2006, 70, 109–131. [Google Scholar] [CrossRef]
- Cook, L.T.; Cook, P.N.; Lee, K.R.; Batnitzky, S.; Wong, B.Y.S.; Fritz, S.L.; Ophir, J.; Dwyer, S.J.; Bigongiari, L.R.; Templeton, A.W. An algorithm for volume estimation based on polyhedral approximation. IEEE Trans. Biomed. Eng. 1980, 9, 493–500. [Google Scholar] [CrossRef] [PubMed]
- King, D.L.; Gopal, A.S.; Keller, A.M.; Sapin, P.M.; Schröder, K.M. Three-dimensional echocardiography: Advances for measurement of ventricular volume and mass. Hypertension 1994, 1, I172–I179. [Google Scholar] [CrossRef]
- Hodges, T.C.; Detmer, P.R.; Burns, D.H.; Beach, K.W.; Strandness, D.E., Jr. Ultrasonic three-dimensional reconstruction: In vitro and in vivo volume and area measurement. Ultrasound Med. Biol. 1994, 20, 719–729. [Google Scholar] [CrossRef]
- Liu, L.; Bajaj, C.; Deasy, J.O.; Low, D.A.; Ju, T. Surface reconstruction from non-parallel curve networks. Comput. Gr. Forum 2008, 2, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Cazals, F.; Giesen, J. Delaunay Triangulation Based Surface Reconstruction: Ideas and Algorithms. Eff. Comput. Geom. Curves Surf. 2006, 231–276. [Google Scholar] [CrossRef]
- Seng, P.L.; Haron, H. Surface reconstruction techniques: A review. Artif. Intell. Rev. 2012, 42, 59–78. [Google Scholar]
- Ni, T.G.; Ma, Z.H. A fast surface reconstruction algorithm for 3D unorganized points. In Proceedings of the 2010 2nd International Conference on Computer Engineering and Technology (ICCET), Chengdu, China, 16–18 April 2010; pp. V7-15–V7-18.
- Nagai, Y.; Ohtake, Y.; Suzuki, H. Tomographic surface reconstruction from point cloud. Comput. Gr. 2015, 46, 55–63. [Google Scholar] [CrossRef]
- Moriconi, S.; Scalco, E.; Broggi, S.; Avuzzi, B.; Valdagni, R.; Rizzo, G. High quality surface reconstruction in radiotherapy: Cross-sectional contours to 3D mesh using wavelets. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 4222–4225.
- Rostami, M.; Michailovich, O.V.; Wang, Z. Surface Reconstruction in Gradient-Field Domain Using Compressed Sensing. IEEE Trans. Image Process. 2015, 24, 1628–1638. [Google Scholar] [CrossRef] [PubMed]
- Duan, J.; Haines, B.; Ward, W.O.C.; Bai, L. Surface Reconstruction from Point Clouds Using a Novel Variational Model. In Research and Development in Intelligent Systems XXXII; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Bernardini, F.; Mittleman, J.; Rushmeier, H.; Silva, C.; Taubin, G. The Ball-Pivoting Algorithm for Surface Reconstruction. IEEE Trans. Vis. Comput. Gr. 1999, 4, 349–359. [Google Scholar] [CrossRef]
- Amenta, N.; Choi, S.; Kolluri, T.K. The power crust, union of balls, and the medial axis transform. Comput. Geom. 2001, 19, 127–153. [Google Scholar] [CrossRef]
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson surface reconstruction. Symp. Geom. Process. 2006, 61–70. Available online: http://research.microsoft.com/en-us/um/people/hoppe/proj/poissonrecon/ (accessed on 16 April 2016). [Google Scholar]
- Deng, S.; Jiang, L.; Cao, Y.; Zhang, J.; Zheng, H. Variational approach to reconstruct surface from sparse and nonparallel contours in freehand 3D ultrasound imaging. In Proceedings of the 2012 International Workshop on Image Processing and Optical Engineering, Harbin, China, 15 November 2011.
- Turk, G.; Dinh, H.Q.; O’Brien, J.F.; Yngve, G. Implicit surfaces that interpolate. In Proceedings of the International Conference on Shape Modeling and Applications, Genova, Italy, 7–11 May 2001; pp. 62–71.
- Ohtake, Y.; Belyaev, A.; Seidel, H.P. 3D scattered data interpolation and approximation with multilevel compactly supported RBFs. Gr. Models 2005, 3, 150–165. [Google Scholar] [CrossRef]
- Walder, C.; Schölkopf, B.; Chapelle, O. Implicit surface modelling with a globally regularized basis of compact support. Comput. Gr. Forum 2006, 25, 635–644. [Google Scholar] [CrossRef]
- Morse, B.S.; Yoo, T.S.; Rheingans, P.; Chen, D.T.; Subramanian, K.R. Interpolating implicit surfaces from scattered surface data using compactly supported radial basis functions. In Proceedings of the 2001 International Conference on Shape Modeling and Applications (SMI 2001), Genoa, Italy, 7–11 May 2001; pp. 89–98.
- Süßmuth, J.; Meyer, Q.; Greiner, G. Surface reconstruction based on hierarchical floating radial basis functions. Comput. Gr. Forum 2010, 6, 1854–1864. [Google Scholar] [CrossRef]
- Heckel, F.; Konrad, O.; Hahn, H.K.; Peitgen, H.-O. Interactive 3D Medical Image Segmentation with Energy-Minimizing Implicit Functions. Comput. Gr Vis. Comput. Biolo. Med. 2011, 35, 275–287. [Google Scholar] [CrossRef]
- Pazinato, D.V.; Stein, B.V.; de Almeida, W.R.; Werneck, R.O.; Júnior, P.R.M.; Penatti, O.A.B.; Torres, R.S.; Menezes, F.H.; Rocha, A. Pixel-Level Tissue Classification for Ultrasound Images. IEEE J. Med. Health Inform. 2015, 20, 256–267. [Google Scholar] [CrossRef] [PubMed]
- Dey, T.K. Curve and Surface Reconstruction, 1st ed.; Cambridge University Press: New York, NY, USA, 2007; p. 10. [Google Scholar]
- FEI Coporate. Amira 3D Software for Life Sciences. Available online: http://www.amira.com (accessed on 15 April 2016).
- Carr, J.C.; Beatson, R.K.; Cherrie, J.B.; Mitchell, T.J.; Fright, W.R.; McCallum, B.C.; Evans, T.R. Reconstruction and representation of 3D objects with radial basis functions. In Proceedings of the SIGGRAPH‘01 Proceedings of the 28th annual conference on Computer graphics and interactive techniques, Los Angeles, CA, USA, 12–17 August 2001; pp. 67–76.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).