PSO-Based Voltage Control Strategy for Loadability Enhancement in Smart Power Grids

Abstract

This paper proposes a new voltage control methodology using the particle swarm optimization (PSO) technique for smart grid loadability enhancement. The goal of this paper is to achieve reliable and efficient voltage profile/stability regulation in power grids. This methodology is based on the decouple power flow equations and the worst-case design technique. Specifically, the secondary voltage control (SVC) problem is formulated as an L-infinity norm minimization problem which considers overall load voltage deviations in electrical power systems as an objective model, and the PSO technique is employed to determine a robust control action which aims to improve voltage profile and to enlarge transmission grid loadability by optimal coordinated control of VAR sources. The methodology was successfully tested on several IEEE benchmark systems.

1. Introduction

Voltage instability has always been an important issue for grid engineers during the past few decades [1]. Nowadays, renewable generation, energy storage, demand response, and electric vehicles add complexities to power system operation. These factors present more challenges in maintaining voltage stability in a prevailingly open access environment.

The grid components such as system loads, transmission networks, and generators may contribute to voltage instability [2]. When system voltage drops dramatically, it endangers the integrity of the system. Therefore, it is imperative that system operators be provided with good information regarding the system voltage stability [3,4,5]. Indeed, when voltage instability is detected (i.e., the computed value of voltage stability margin is less than or equal to the predefined security margin), appropriate remedial actions should be initiated to prevent the system from possible voltage collapse. For a bulk power system, however, just relying on grid operators to manually adjust many widely dispersed reactive power resources in real-time is an un-realistic and uneconomic way. Thus, the effectiveness and robustness of the control systems are always expected.

To address this issue, the coordinated automatic voltage control (AVC) has been developed. It is organized as a hierarchical structure with three levels: the tertiary, secondary, and primary voltage control, in which tertiary is the highest level and primary is the lowest level. Each higher control level commands the voltage set point for the lower level. In recent years, many research studies have focused on the secondary level for the achievement of the stability and security operation in smart grids [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. The secondary voltage control (SVC) method was first established in France [6], and has been applied in several countries, such as some European countries [6,7,8,9,10], Brazil [11], South Africa [12], US [13,14], and China [15].

On the other hand, the particle swarm optimization (PSO) technique, which is the family of the evolutionary computation algorithms, has attracted a lot of attention in many research areas [28,29,30]. Indeed, PSO is a heuristic optimization technique, inspired by the social behavior of bird flocks and fish schools. With flexibility and well-balanced mechanism, PSO has the abilities to enhance the global and local search [31]. Due to the simplicity of the concept and implementation, PSO has been effectively applied to various optimization problems in smart grids [32]. For example, PSO based methods were used to solve the problem regarding the optimization in the distribution networks [33,34].

This research is mainly devoted to the protection of any disturbances that may result in power grid voltage collapse. The main contribution is the development of a new voltage stability enhancement methodology for safe power grid operations. To this end, a PSO-based optimal voltage control methodology, which enables achieving reliable and efficient voltage profile/stability regulation in power grids, is proposed. The remainder of this paper is organized as follows: Section 2 gives a brief review of the related work. The basic concept of voltage stability is introduced in Section 3. In Section 4, the problem formulation of power gird Q-V control is stated. Section 5 proposes an optimal voltage control algorithm using particle swarm optimization. Test results are presented in Section 6. The paper finishes with some concluding remarks in Section 7.

2. Related Work

Voltage control has been recognized as an important issue in power grid operation during the past few years. Secondary voltage control (SVC), the structure of which is shown in Figure 1, is able to reduce the possibility of voltage instability. Indeed, a lot of approaches for the design of secondary voltage controllers have been reported in the literature [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27], some of which have been proven to be effective methods to guarantee the stability and security operation in some electric power industries [6,7,8,9,10,11,12,13,14,15]. The basic operation principle of the SVC is summarized in the following: when voltage violations occur at certain key load buses which are designated as pilot nodes, the SVC will be enabled to keep the scheduled voltage profiles by optimal coordinated control of reactive power sources. Furthermore, the potential benefit that can be gained from the secondary voltage control is the improvement of system security and power quality.

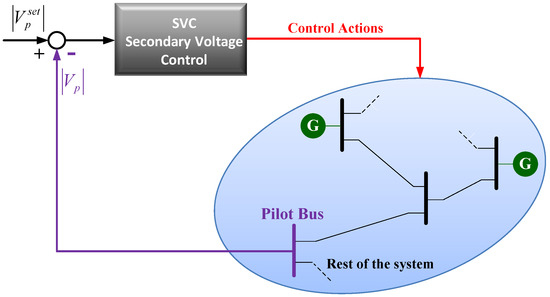
Figure 1. Secondary voltage control (SVC) in a power grid.

In recent years, some worst-case design based methods [24,25,26,27], which ensure that the largest load voltage deviation remains within the specified limit after control, have been proposed to design SVC. In general, the reactive power resources should be adjusted based on their capabilities in order to gain more reactive power margin. However, without taking reactive power generation limits into account, the control outputs provided by the methods [24,25] have high risk to exceed the VAR capacities of the generating units. Recently, a method [26] considering generator reactive power limits for practical applications was proposed to design SVC. An extension of the method in [26] was proposed in [27]. Indeed, the work [27] is a two-stage method with two optimization problems in the control algorithm. In the first stage, system load disturbances are estimated by applying the least-norm technique. With the estimated system load disturbances, a set of optimal control actions can be determined by applying the worst-case design technique in the second stage. For a bulk power network, however, it is difficult and is a time-consuming task for approximating system load disturbances due to the requirement of matrix inversion in the computation. In other words, a two-stage method may require a large amount of computation time to determine optimal control actions. To address these difficulties, a more flexible method to voltage control using the PSO technique for the achievement of the stability and security operation in power grids is developed in this paper. The performance comparison between the proposed PSO-based method and some worst-case design based methods is illustrated and discussed in Section 6.2.2.

3. Basic Concepts of Voltage Stability

3.1. Voltage Stability Margin (VSM)

Voltage instability problems usually occur when the system is heavily loaded, especially under cases with insufficient transmission or generation enhancements. In view of this, the concept of VSM, as shown in Figure 2, has been proposed.

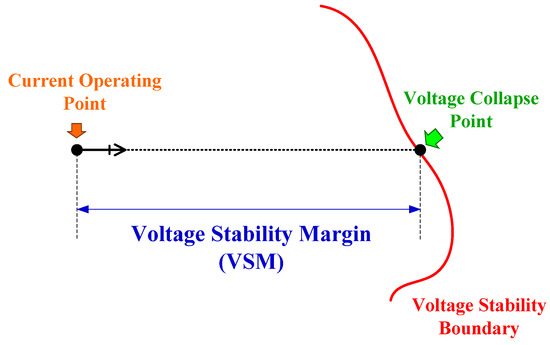
Figure 2. Illustration of Voltage Stability Margin (VSM).

Indeed, voltage stability is related to saddle-node bifurcation that coincides with the maximum loading point [2]. When the generation-transmission system is unable to supply the continuous increase of load demand, voltage instability and even voltage collapse situations are more likely to take place. Accordingly, the load power margin is extended to the VSM. In fact, a number of methods proposed (e.g., [4,5]) utilize this kind of measure as a monitoring index of voltage stability.

3.2. P-V Curve Analysis

To determine load power margin P_margin under a certain load level, the electric utility industry depends largely on the P-V curve analysis at selected load buses, as shown in Figure 3. When the P_max is determined, the P_margin can be expressed as

$$P_{\mathrm{margin}}=P_{\max }-P_{current}$$

(1)

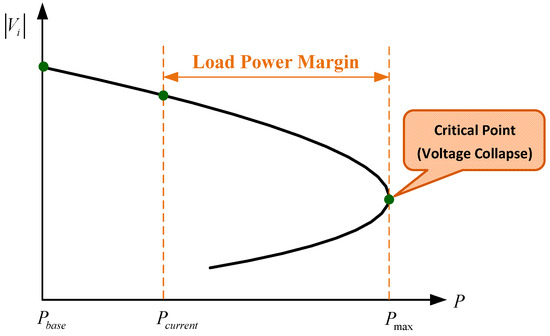
Figure 3. Typical P-V curve.

Generally, the P-V curve is generated by means of a series of power-flow solutions at different load levels. However, successive computation by the use of the traditional power-flow approach may encounter a divergence problem near the voltage stability boundary. Thus, the continuation power flow (CPFLOW) based methods were used to cope with the numerical difficulties caused by the singularity of the power-flow Jacobian matrix at and around the critical point [4]. Using CPFLOW, the VSM, which is defined by the percentage of the P_margin, can be computed as

$$VSM=\frac{P_{\mathrm{margin}}}{P_{current}}\times 100\%$$

(2)

4. Problem Statement

4.1. Power Grid Q-V Control

The steady-state model of power grid Q-V control can be considered as

$$\left[\Delta Q\right]=B\left[\Delta V\right]$$

(3)

where B is the system susceptance matrix, and ΔQ and ΔV are the vector of reactive power variation and vector of voltage magnitude variation, respectively. Expending Equation (3) gives

$$\left[\begin{array}{c}\Delta Q_G\\ \Delta Q_L\end{array}\right]=\left[\begin{array}{cc}{B}_{GG}& B_{GL}\\ B_{LG}& B_{LL}\end{array}\right]\left[\begin{array}{c}\Delta V_G\\ \Delta V_L\end{array}\right]$$

(4)

where the subscripts L denotes the load buses and G denotes the generator buses. Next, let $q=\Delta Q_L$ and $u=\Delta Q_G$, then substitute for q and u in Equation (4) yields

$$\left[\begin{array}{c}u\\ q\end{array}\right]=\left[\begin{array}{cc}{B}_{GG}& B_{GL}\\ B_{LG}& B_{LL}\end{array}\right]\left[\begin{array}{c}\Delta V_G\\ \Delta V_L\end{array}\right]$$

(5)

In the above equation, $\Delta V_G$ and q can be expressed as

$$\Delta V_G=B_{GG}^{-1}u-B_{GG}^{-1}{B}_{GL}\Delta V_L$$

(6)

$$q=B_{LG}\Delta V_G+B_{LL}\Delta V_L$$

(7)

Substituting for $\Delta V_G$ in Equation (7) yields

$$q=B_{LG}{B}_{GG}^{-1}u-B_{LG}{B}_{GG}^{-1}{B}_{GL}\Delta V_L+B_{LL}\Delta V_L$$

(8)

Equation (8) can be rearranged as

$$\Delta V_L=J_{1}q-J_{2}u$$

(9)

where

$$\begin{array}{l}{J}_1={\left(B_{LL}-B_{LG}{B}_{GG}^{-1}{B}_{GL}\right)}^{-1}\\ J_2=J_1\left(B_{LG}{B}_{GG}^{-1}\right)\end{array}$$

(10)

Note that $J_1$ and $J_2$ are the matrices with respect to system configurations. In this case, $J_{1}q$ in Equation (9) represents uncontrolled $\Delta V_L$ in response to q, while $J_{2}u$ represents the impacts of control outputs u on $\Delta V_L$.

4.2. Linear Feedback Control Design

In this study, a linear feedback control, which utilizes monitored voltages as control inputs and produces control actions as control outputs, is employed to develop a secondary voltage controller. Furthermore, it must be stressed that only pilot-bus voltage data are available to control devices. If there are sufficient measurement units at all load buses, voltage changes $J_{1}q$ will be the control inputs. In practical applications, however, only partial load buses are pilot buses. That is, the monitored voltage deviations $\Delta V_p$ can be expressed as

$$\Delta V_p=J_{p}q$$

(11)

where $J_p$ is the rows of $J_1$ relating to the selected pilot buses. Indeed, $\Delta V_p$ are only some entries of the vector $J_{1}q$. In this case, linear control vector u is given by

$$u=K\Delta V_p=K\left(J_{p}q\right)$$

(12)

where K denotes the control gain matrix that needs to be determined. Replacing the second term of Equation (9) with the control outputs u in Equation (12) results in

$$\begin{array}{ll}\Delta V_L& =J_{1}q-J_{2}K\Delta V_p\\ & =J_{1}q-J_{2}K\left(J_{p}q\right)\\ & =\left(J_1-J_{2}K{J}_p\right)q\end{array}$$

(13)

4.3. Objective Function

In this research, the worst-case design is employed to determine the optimal control gain matrix $K^{\ast }$ in Equation (13). Thus, the problem is to minimize ${\Vert \Delta V_L\Vert }_{\infty }$. Suppose that q is within a certain limit $\mathsf{\gamma }$ in a practical power system; i.e.,

$${\Vert q\Vert }_{\infty }\le \mathsf{\gamma }$$

(14)

Thus, the objective function is expressed as

$$\underset{K^{\ast }}{\min }\underset{{\Vert q\Vert }_{\infty }\le \mathsf{\gamma }}{\max }{\Vert \left(J_1-J_2{K}^{\ast }{J}_p\right)q\Vert }_{\infty }$$

(15)

Due to the fact that

$$\begin{array}{l}{\Vert \left(J_1-J_2{K}^{\ast }{J}_p\right)q\Vert }_{\infty }\le {\Vert \left(J_1-J_2{K}^{\ast }{J}_p\right)\Vert }_{\infty }{\Vert q\Vert }_{\infty }\\ \le \mathsf{\gamma }{\Vert \left(J_1-J_2{K}^{\ast }{J}_p\right)\Vert }_{\infty }\end{array}$$

(16)

The minimization problem in Equation (15) is also equivalent to

$$\underset{K^{\ast }}{\min }{\Vert J_1-J_2{K}^{\ast }{J}_p\Vert }_{\infty }$$

(17)

From the preceding equation, one can see that the optimal robust gain matrix $K^{\ast }$ depends entirely on system configurations on pilot-point locations. In other words, $K^{\ast }$ remains the same regardless of any unexpected load disturbance. Once $K^{\ast }$ is obtained, the optimal control action u can be computed by $u^{\ast }=K^{\ast }\Delta V_p$. Note that it must be within the bounds of control variables.

5. Solution Method

5.1. Particle Swarm Optimization (PSO)

PSO, which was first introduced in [29,30], is a population-based stochastic optimization tool. It was originally developed via the simulation of the simplified social models. PSO has been found to be simple, robust, and computationally efficient in solving optimization problems.

Suppose that there are n particles, denoted by $\left\{X_i|i=1,2,\cdots ,n\right\}$, in a population. Each $X_i$ represents a potential solution to the problem. Let x and v be the position and velocity of the particle coordinates in an m-dimensional search space, in which m denotes the number of optimized parameters. Thus, the ith particle $X_i$ and its velocity $V_i$ can be expressed as $X_i={\left[x_{i1},x_{i2},\cdots ,x_{im}\right]}^T$ and $V_i={\left[v_{i1},v_{i2},\cdots ,v_{im}\right]}^T$, which are two real-valued vectors. In a PSO algorithm, particles move via the feasible solution space. For the search process, each particle in the swarm updates its position according to the inertia weight $\omega$, the personal best pbest, and the global best gbest. At time step t, the velocity and position of the ith particle corresponding to the dth dimension are modified by

$$v_{id}^{t+1}=\mathsf{\omega }{v}_{id}^t+c_1{r}_1\left(pbes{t}_{id}^t-x_{id}^t\right)+c_2{r}_2\left(gbes{t}_d^t-x_{id}^t\right)$$

(18)

$$x_{id}^{t+1}=x_{id}^t+v_{id}^{t+1}$$

(19)

Notice that $c_1$ and $c_2$ in Equation (18) denote learning coefficients, and $r_1$ and $r_2$ denote random values from uniform distribution in the range of [0, 1]. To ensure the convergence of the PSO algorithm, a constriction factor proposed in [35] is added in Equation (18) yielding

$$v_{id}^{t+1}=\mathsf{\psi }\left[v_{id}^t+c_1{r}_1\left(pbes{t}_{id}^t-x_{id}^t\right)+c_2{r}_2\left(gbes{t}_d^t-x_{id}^t\right)\right]$$

(20)

with

$$\mathsf{\psi }=2/\left(\left|2-c-\sqrt{c^2-4c}\right|\right)$$

(21)

where $c=c_1+c_2$ and $c>4$. In general, both $c_1$ and $c_2$ are set to 2.05, resulting in $c=4.1$ and $\mathsf{\psi }=0.729$. More details on the comparison of inertia weight and constriction factors in particle swarm optimization can be found in [36].

5.2. Proposed Algorithm

In this study, the PSO technique is applied to solve the optimization problem in Equation (17). The aim is to determine the feasible control actions to the participating control devices in power grids. The search procedures for the proposed PSO-based control algorithm is described below:

Step 1:

Input branch parameters and bus data.

Step 2:

Input pilot-bus measured voltages.

Step 3:

If the measured voltages are not within the specified limits, the proposed PSO-based control algorithm will be activated automatically.

Step 4:

Form the matrices $J_1$, $J_2$, and $J_p$.

Step 5:

PSO Initialization.

(1)

Set iteration counter $t=0$ and maximum iteration $t_{\max }$.

(2)

Set population size.

(3)

Set learning coefficients $c_1$ and $c_2$, and $\mathsf{\psi }$ in Equation (21).

(4)

Initialize $x_i^0$ and $v_i^0$ according to the constraints of the control variables.

(5)

Initialize pbest and gbest.

Step 6:

Update iteration counter $t$.

Step 7:

For each $x_i^t$, evaluate the objective function in Equation (17), i.e., measure the fitness value for each particle (pbest) and store the particle with the best fitness (gbest) value.

Step 8:

Update $v_i^t$ using Equation (20).

Step 9:

Update $x_i^t$ using Equation (19).

Step 10:

If t reaches $t_{\max }$, then go to Step 11. Otherwise, go back to Step 6.

Step 11:

Print out the latest gbest which is the optimal control strategy.

6. Numerical Examples and Results

The proposed PSO-based voltage control algorithm is applied to two sample test systems: IEEE 9-bus and IEEE 118-bus. The grid data involving branch parameters and bus information are given in [37]. In this research, the PSO settings are selected as below:

(1)

population size = 100;

(2)

maximum iteration = 200;

(3)

learning coefficients: $c_1=2.05$ and $c_2=2.05$;

(4)

$\mathsf{\psi }$ in Equation (21) is set to 0.729.

Suppose that there are n load buses in the test system, the performance of the control strategy is measured through the root-mean-square (RMS) defined as

$$y^{RMS}=\sqrt{\frac{{\displaystyle \sum _{i=1}^m{\left(y_i^a-y_i^b\right)}^2}}{n}}$$

(22)

where $y_i^b$ and $y_i^a$ for each $i=1,2,\cdots ,n$ are the load bus voltage before and after control, respectively. Note that smaller $y^{RMS}$ gives better performance. In order to illustrate the system loadability enhancement after the proposed control strategy, the open-source software PSAT [38] is used to generate the P-V curves for calculating the VSM.

6.1. IEEE 9-Bus

The first test system is concerned with IEEE 9-bus system that consists of three generators, three loads, and nine branches, as shown in Figure 4. Furthermore, it is simply assumed that the phasor measurement units (PMUs) are installed at bus 5 and bus 6 (i.e., bus 5 and bus 6 are chosen as pilot buses). In other words, only the voltage magnitudes at bus 5 and bus 6 are used as control inputs.

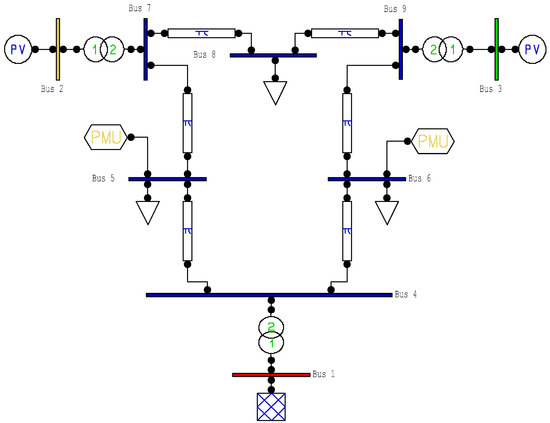
Figure 4. One-line diagram of IEEE 9-bus system with phasor measurement units (PMUs). PV: PV generaotr bus (voltage-controlled bus).

To confirm the effectiveness of the proposed control algorithm, comprehensive simulations including different load bus variations, different load levels, and different branch outage contingencies have been studied. Among those experiments, only the results listed below are discussed.

• Case 1: All load bus variations and light load conditions.
• Case 2: Single load bus variation and peak load condition.
• Case 3: Several load bus variations, peak load conditions, and line outage contingencies.

Case 1

In the first test case, all load bus variations are simulated. The test system is operated at a light load condition, where the voltage magnitudes obtained from the PMUs are V₅ = 0.8866 p.u. and V₆ = 0.9902 p.u.

In this case, low voltage violation occurs at bus 5 since V₅ = 0.8866 p.u. is less than the predetermined value of 0.9 p.u. This will activate the proposed method, and the effect of the control strategy is shown in Figure 5. From the shown figure, one can see that the voltage magnitude of bus 5 is improved from 0.8866 to 0.9974 p.u. Also, the maximum load power is increased from 3.94 to 4.47 p.u.

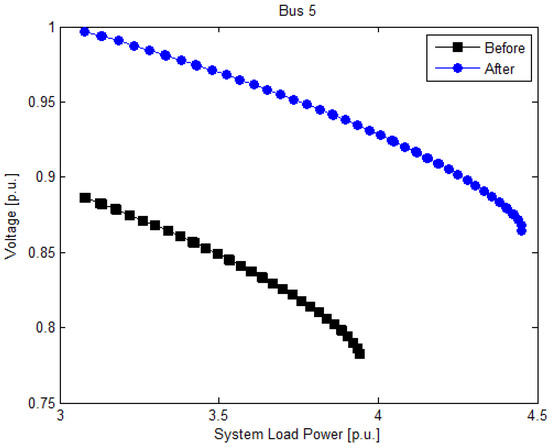
Figure 5. Simulation result of Case 1 for IEEE 9-bus.

Case 2

Single load bus variation is considered in this case. During the simulation, we raise load disturbance at bus 6. The test system is investigated under peak load conditions and is operated in the dangerous region. The measured voltages without control actions are V₅ = 0.9801 p.u. and V₆ = 0.8707 p.u.

Figure 6 illustrates the simulation result, indicating that the maximum load power is greatly enhanced from 3.77 to 4.29 p.u., and V₆ improved from 0.8707 to 1.0404 p.u.

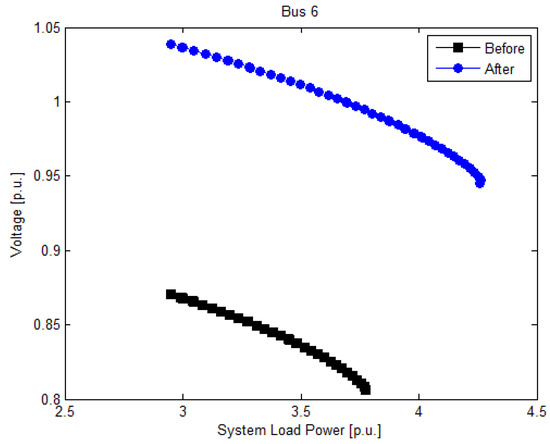
Figure 6. Simulation result of Case 2 for IEEE 9-bus.

Case 3

In the third simulation, several load bus variations are simulated. The test system is investigated under stressed conditions, and the line #7-8 is studied under branch outage contingency condition. The system is operating in the dangerous region, which could result in V₅ = 0.8773 p.u. and V₆ = 0.8687 p.u. before control actions performed. Since the system has poor voltage level, the proposed methodology will be activated to prevent imminent voltage collapse. Figure 7 shows the simulation result. In Figure 7, it is clearly seen that system voltage stability is considerably improved after the proposed methodology.

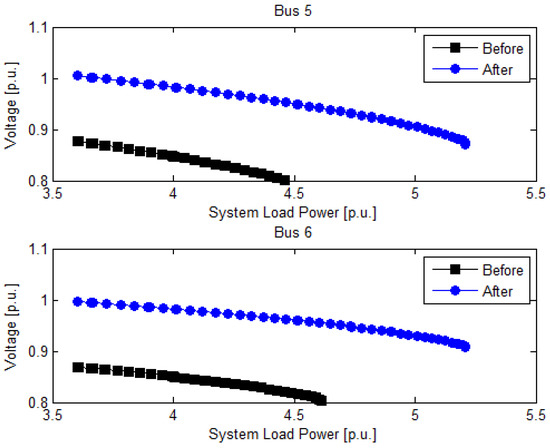
Figure 7. Simulation result of Case 3 for IEEE 9-bus.

The results in terms of $y^{RMS}$ and VSM for the above three cases are summarized in Table 1, showing that the performance of the power grid is significantly enhanced. This means that the control decisions provided by the proposed scheme are efficient and effective for the improvement of overall power grid voltage stability.

Table 1. Summary of the results for IEEE 9-bus. VSM, Voltage Stability Margin.

Test Case	yRMS (p.u.)		VSM (%)
	Before	After	Before	After
1	0.0598	0.0337	27.95	42.43
2	0.0441	0.0304	10.03	29.86
3	0.0795	0.0401	9.46	30.08

6.2. IEEE 118-Bus

To demonstrate the applicability of the proposed algorithm to large-scale power grids, the IEEE 118-bus is utilized as an example. This test model is composed of 54 generators, 64 loads, and 186 transmission lines [37].

A series of simulations including different load bus variations, different load levels, and different branch outage contingencies has been conducted. Among those investigated tests, some selected cases listed are presented below.

• Case 1: Several load bus variations and peak load conditions.
• Case 2: All load bus variations, peak load conditions, and line outage contingencies.

The simulation results are shown in Figure 8 and Figure 9. From the shown figures, one can see that the load bus voltage magnitudes after the proposed control strategy are all at the acceptable level.

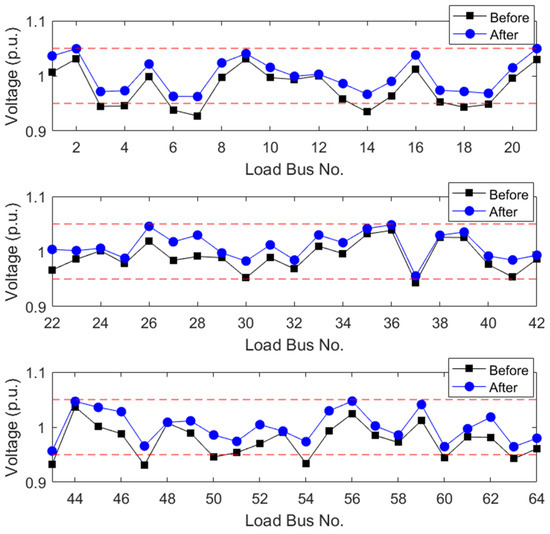
Figure 8. Load bus voltage profile of Case 1 for IEEE 118-bus.

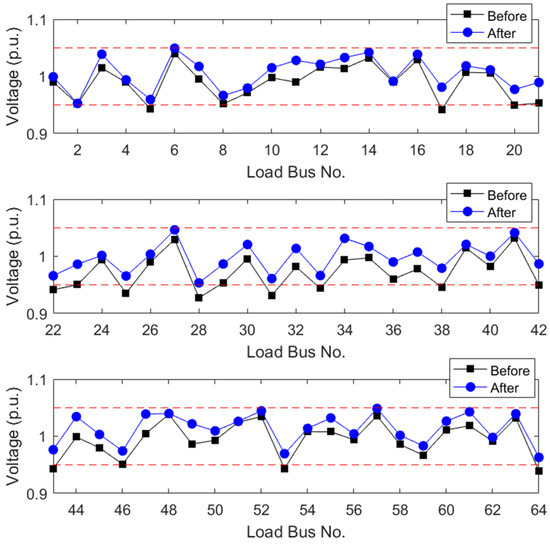
Figure 9. Load bus voltage profile of Case 2 for IEEE 118-bus.

6.2.1. Effects of Different Pilot-Bus Selections

To illustrate the effect of different pilot-bus selections on control performance, a series of simulations has been performed. Some selected cases are listed in Table 2. The simulation results are depicted in Figure 10, showing that $y^{RMS}$ and VSM are considerably enhanced after the proposed control algorithm.

Table 2. Selected scenarios for IEEE 118-bus.

Case	Load Level 1	Load Pattern	Load Variation	Pilot-Bus Selection
1	${\mathsf{\lambda }}_0=0.3$	Single	15%	Pilot_One 2
2	${\mathsf{\lambda }}_0=0.6$	Single	15%	Pilot_One 2
3	${\mathsf{\lambda }}_0=0.9$	Single	15%	Pilot_One 2
4	${\mathsf{\lambda }}_0=0.3$	Several	25%	Pilot_Even 3
5	${\mathsf{\lambda }}_0=0.6$	Several	25%	Pilot_Even 3
6	${\mathsf{\lambda }}_0=0.9$	Several	25%	Pilot_Even 3
7	${\mathsf{\lambda }}_0=0.3$	All	35%	Pilot_Odd 4
8	${\mathsf{\lambda }}_0=0.6$	All	35%	Pilot_Odd 4
9	${\mathsf{\lambda }}_0=0.9$	All	35%	Pilot_Odd 4

¹ Load Level: ${\mathsf{\lambda }}_0$ denotes initial load level; ² Pilot_One: Given the pilot bus at a specific load bus; ³ Pilot_Even: Given the pilot buses at even load buses; ⁴ Pilot_Odd: Given the pilot buses at odd load buses.

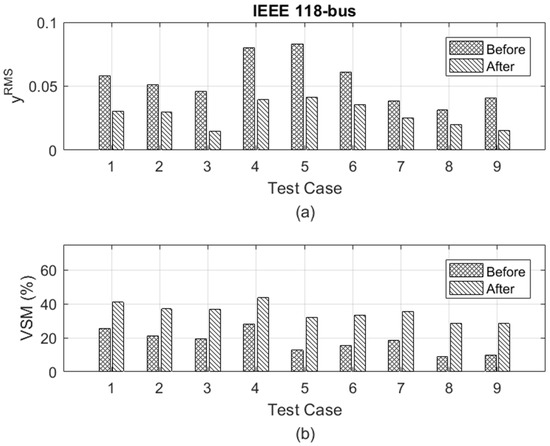
Figure 10. Results of IEEE 118-bus. (a) Results in terms of $y^{RMS}$; (b) Results in terms of VSM.

6.2.2. Comparison with Worst-Case Design Based Methods

A performance comparison study of the proposed method with some worst-case design based methods [25,27] for IEEE 118-bus system is carried out. Let $N_{lb}$ be the number of load buses in the test system, $N_{pb}$ be the number of pilot buses used in the control algorithm, and $N_{sr}$ be the number of simulation runs. The measure for performance evaluation under different $N_{pb}$ can be expressed as

$${\overline{y}}_{N_{pb}}^{RMS}=\frac{1}{N_{sr}}{\displaystyle \sum _{k=1}^{N_{sr}}{y}_k^{RMS}},N_{pb}=1,2,\cdots ,N_{lb}$$

(23)

The performance evaluation between the compared methods under the selected cases for the IEEE 118-bus system is demonstrated in Table 3. In addition, the average computation time $T_{avg}$ for each $N_{sr}$ is provided. In Table 3, it can be observed that the results in terms of ${\overline{y}}_{N_{pb}}^{RMS}$ given by the proposed method are much smaller than the results provided by the method [25], and are very close to the results provided by the method [27]. However, the results in terms of $T_{avg}$ obtained by the proposed method are the smallest ones. In other words, the proposed method is able to significantly reduce the computation time in comparison with both method [25] and method [27]. In summary, the proposed method is superior over both method [25] and method [27].

Table 3. Result comparison for IEEE 118-bus.

${\mathit{N}}_{\mathit{p}\mathit{b}}$	${\mathit{N}}_{\mathit{s}\mathit{r}}$	${\overline{\mathit{y}}}_{{\mathit{N}}_{\mathit{p}\mathit{b}}}^{\mathit{R}\mathit{M}\mathit{S}}$ (p.u.)			${\mathit{T}}_{\mathit{a}\mathit{v}\mathit{g}}$ (ms)
		Method [25]	Method [27]	Proposed	Method [25]	Method [27]	Proposed
1	640	0.0866	0.0698	0.0689	406	52	29
2	1000	0.0828	0.0664	0.0667	619	120	74
3	1000	0.0817	0.0656	0.0658	724	135	86
4	1000	0.0783	0.0579	0.0561	873	272	183
5	1000	0.0762	0.0551	0.0544	959	281	198

7. Conclusions

In this paper, a new voltage control methodology using the PSO technique for the achievement of the stability and security operation in smart grids was developed. The developed methodology is based on the normal form of voltage-var control model. Considering the worst-case design of overall load voltage deviations in electrical power systems, this methodology determines an optimal set of robust control actions by utilizing a PSO-based l-infinity norm minimization algorithm to eliminate voltage violations in smart transmission grids. With the proposed methodology, the overall network voltage levels can be improved and voltage stability margin can be enlarged as well by an appropriate reactive power management against voltage instability. The proposed methodology was applied in some standard IEEE test systems. The results of the proposed methodology are promising.