Abstract
An integration of deep learning and classical filtering techniques has been developed for achieving an accurate and robust positioning system. Despite significant technological advances, positioning systems often face fundamental challenges such as signal obstruction, multipath interference, and error drift. Although 3D map matching techniques using LiDAR sensors can mitigate these challenges, their practical implementation is limited by high costs, computational burdens, and dependency on pre-modeled environments. In response, recent research has increasingly focused on enhancing positioning systems through deep learning–based sensor fusion and adaptive filtering methods, emphasizing improvements in accuracy and operational robustness. In this paper, a seamless hierarchical context-aware intelligent positioning system (SH-CAIPS) is proposed by integrating sensor fusion, two-stage outlier mitigation gates, and deep reinforcement learning (DRL)-based noise scaling with an innovation-based adaptive Kalman filter (IAKF). As a result, the proposed positioning system can enhance robustness by adaptively adjusting measurement noise and dynamically updating the position based on the confidence score between model predictions and sensor measurements. From simulation results, it is confirmed that the positioning performances can be significantly improved based on the proposed SH-CAIPS compared with conventional positioning systems.
1. Introduction
Mechatronics engineering has been widely applied in various fields such as transport, logistics, and autonomous navigation [1]. In mechatronics and robotics, the integration of artificial intelligence has enabled advanced functionalities [2]. This integration facilitates higher-level recognition, planning, and control tasks which enable autonomous vehicles and robots to operate effectively in complex environments [3]. To perform the task effectively, precise and robust seamless positioning systems have been highlighted by estimating the position of the moving platform with respect to its surroundings from sensor measurements and correction filtering methods [4].
A variety of filtering approaches with multiple sensors have been employed in position systems for reducing positioning error. Estimation methods based on filtering techniques such as the Kalman filter (KF) [5], extended KF (EKF) [6], adaptive Kalman filter (AKF), and an innovation-based adaptive Kalman filter (IAKF) [7] have been widely used for positioning calibration. The IAKF is employed to adapt measurement and process noise covariances from innovation statistics, enabling robust and consistent updates under nonstationary noise and outliers [7]. In [8], a kernel density estimation-based outlier removal and dilution of precision-based AKF have been proposed to mitigate the effects of non-line-of-sight (NLOS) environments. However, conventional filtering-based positioning systems can be challenged by strong nonlinearity, heavy sensor noise, and rapid environmental changes.
In order to achieve precise and robust positioning, sensor fusion has emerged as the mainstream approach for positioning estimation and calibration. To enhance positioning accuracy, high-cost sensors such as LiDAR and stereo cameras, along with 3D map-matching techniques, have been extensively utilized. However, operating the positioning system that relies on such expensive sensors for extreme high-level precision is often impractical in terms of cost-efficiency, deployment, and maintenance. In response, a deep learning-based positioning system has been developed to facilitate the modeling of intricate data distributions and patterns, thereby improving positioning accuracy while providing enhanced adaptability [9,10].
A convolutional neural network (CNN)-based method has been used to convert low-precision inertial measurement unit (IMU) data into high-precision references, but its drift correction remains unclear [11]. A method for improving the accuracy of inertial-based position estimation has been proposed by correcting for runtime errors of the accelerometer and gyroscope of an inertial measurement unit using a deep IMU online calibration method [12]. To address GNSS and IMU errors, deep learning-based KF [13] and self-learning KF [14] have been proposed. Furthermore, a context-aware integrated navigation system (CAINS) has been developed to facilitate seamless positioning by combining layers of situational awareness and state estimation [15]. However, the conventional approaches have been designed to rely on fixed parameters, and their limited interpretability hinders the effective mitigation of error drift.
Deep reinforcement learning (DRL) has been adopted to attain precision while maintaining robustness in dynamic environments in positioning systems [16]. To improve positioning accuracy, a variety of DRL-based methods have been investigated, and their robustness has been demonstrated [17,18,19,20]. These methods highlight the ability of the DRL to handle complex scenarios and environmental variability. A deep deterministic policy gradient-based AKF scheme is proposed to obtain accurate and robust positioning estimation by learning the optimal process-noise covariance [21]. In [22], a KF’s state covariance is adaptively tuned by an actor–critic DRL, and error propagation in cooperative positioning is suppressed via a multi-trajectory information-matrix fusion that aggregates inverse covariances. However, applications of the DRL-based positioning system remain challenging due to the stochastic, high-dimensional observation spaces, and the unavailability of ground-truth data for setting ranges of corrections. In particular, setting the correction range and designing a stable reward function without ground truth are inherently difficult, often leading to unstable learning behavior and inconsistent updates. To address these issues, an adaptive outlier-aware mechanism can be incorporated into the DRL framework to enable effective learning in the absence of ground-truth corrections.
In this paper, a seamless hierarchical context-aware intelligent positioning system (SH-CAIPS) is proposed by integrating sensor fusion, two-stage outlier mitigation gates, and DRL-based noise scaling with the IAKF. The proposed SH-CAIPS is designed to ensure stable and ground-truth-free updates. The proposed framework integrates adaptive gating and DRL-based IAKF to adapt dynamically to changing environments. In adaptive gating, short- and long-term outliers are mitigated by adjusting measurement noise covariance. For short-term outlier mitigation, a per-channel measurement trust is dynamically computed from innovation statistics via an adaptive measurement noise covariance scaling gate, which can suppress spikes and track error drifts. A normalized innovation squared (NIS)-based adaptive gate is designed to handle long-term outliers by evaluating sliding-window consistency and identifying axis-concentrated faults and system-level mismatches. Overall, the proposed system can provide precise and robust positioning against error drift. The main contributions of this paper are summarized as follows:
- The proposed DRL-based context-aware framework is designed to manage updates to the IAKF by adaptively adjusting noise covariances that adjust for measurement and model uncertainties rather than directly correcting the position. Unlike conventional methods, time-varying uncertainties are addressed through a learning process without reliance on ground-truth data for supervision. By adaptively regulating these uncertainties, the proposed positioning system can mitigate error accumulation, thereby improving positioning accuracy and error drift.
- A two-stage outlier-aware gating scheme is developed to address channel-specific outliers and global inconsistencies, considering both short- and long-term gating. Through the integration of a short-term adaptive measurement noise scaling gate with a long-term NIS-based update gate, error drifts can be effectively suppressed.
- An integrated SH-CAIPS architecture that couples DRL-based IAKF with outlier mitigation, achieving robust and accurate positioning using cost-effective sensors such as GPS, IMU, and wheel odometry without environment-specific prior knowledge.
The rest of this paper is organized as follows: in Section 2, the system description is provided to help understand the overall proposed context-aware intelligent positioning system. The proposed SH-CAIPS is described in Section 3. Simulation results are shown in Section 4. Finally, the conclusions and future work are presented in Section 5.
2. System Model
The DRL-based GNNS/IMU-integrated positioning systems have gained attention for their ability to adjust model uncertainties [22]. In this study, enhanced positioning performance is pursued by employing a cost-efficient sensor configuration consisting of GNSS, IMU, and wheel odometry. High-cost sensors, such as LiDAR and camera sensors, are excluded to prioritize cost-effectiveness and computational efficiency. Through this configuration, hardware costs and processing burdens can be minimized, facilitating scalability to resource-constrained edge devices. To ensure precision with a cost-effective solution, the DRL-based IAKF framework and a two-stage outlier mitigation gate are integrated. Consequently, sensor reliability and measurement uncertainty can be adjusted in real-time, enabling robust and context-aware positioning without reliance on prior environmental maps.
The proposed SH-CAIPS framework is designed to operate flexibly in both centralized processing systems, where sensor measurements are transmitted to an external computation unit, and onboard processing environments such as drones and mobile ground units. In centralized deployments, the proposed framework can be executed on a remote server or edge-computing platform while receiving synchronized measurements from the ground unit. In the onboard configuration, the update can be performed directly on the embedded processor, enabling low-latency and self-contained positioning. Although this study evaluates the system using a ground-vehicle dataset, the proposed architecture can be extended to unmanned ground vehicle platforms with minimal modifications.
2.1. Positioning System Operation
The proposed positioning system is designed to provide precise and adaptive positioning estimation in both LOS and NLOS scenarios. The system model for the context-aware intelligent positioning is shown in Figure 1. The proposed SH-CAIPS is designed by the DRL-based IAKF that incorporates sensor fusion and two-stage outlier mitigation gates within the DRL framework. For the implementation of realistic positioning environments, multiple heterogeneous measurements are aligned with a common positioning frame and then integrated into a single equivalent observation.
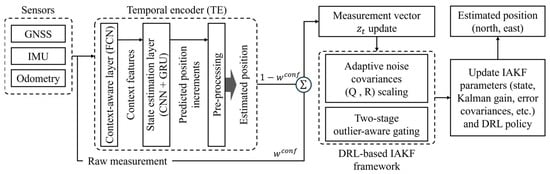
Figure 1.
System model of the context-aware intelligent positioning.
At the measurement level, the proposed positioning system is set by combining raw sensor measurements and temporally encoded features which are extracted from sequential sensor measurement data for effective context-aware learning. The proposed system primarily utilizes GPS, IMU, and wheel odometry sensors. However, the GPS measurements are treated as noisy and potentially unreliable observations rather than ground-truth positions, especially under NLOS and multipath conditions. The proposed DRL-based IAKF is designed to adaptively adjust the noise covariances and fuse these heterogeneous measurements to improve robustness and reduce long-term error drift. Although LiDAR can further enhance spatial accuracy, its heavy computational and resource requirements limit its practicality for resource-constrained positioning systems. The TE is implemented using a fully convolutional network-based context-aware layer and a state estimation layer composed of CNN and gated recurrent unit (GRU) modules to extract representative spatiotemporal features. A pre-processing stage is conducted using dynamic time warping to align sampling rates and extract the estimated position.
At the model-learning level, the DRL agent adaptively scales the noise covariances by estimating model and measurement uncertainties through the accumulated reward mechanism at each time step. Furthermore, the two-stage outlier-aware gating process is employed to address measurement uncertainty for the adaptive IAKF update. Subsequently, the parameters of the IAKF and the DRL policy are updated, and the final positions in the north and east directions are estimated.
2.2. IAKF Formulation
The IAKF improves the adaptability and reliability of the filter by updating the model using the difference between the predicted and measured values in the conventional KF. The state vector of the global frame is given as follows:
where , , , and are position and velocity of north and east directions, respectively. And denotes heading angle which is measured from IMU sensor.
In the prediction stage of IAKF, the state vector can be represented as,
where is the predicted state vector at time given measurements up to and is the state-transition matrix. The predicted error covariance matrix is expressed as,
where is the process noise covariance related to model uncertainty.
In the update stage of IAKF, the innovation and predicted innovation covariance are expressed as,
where is the innovation representing the measurement residual, is the predicted innovation covariance, is the measurement vector, is the observation matrix that maps the state vector to the measured position and velocity components in the north and east, is the white Gaussian noise at time , and is the measurement noise covariance related to measurement uncertainty.
In this paper, a new measurement vector update rule is proposed to maintain robustness in environments with frequent outliers, whereas conventional approaches directly utilize the measurement vector as the sensor reading. The measurement vector has been modified to alleviate the outlier, as follows:
where denotes the confidence-based weight by moving average over a window of 50-time steps, and are the raw sensor measurements and temporal encoded measurement, respectively. To implement temporal encoder, the GRU is used to maintain real-time operation and lower the number of parameters while capturing temporal dependencies such as drift trends and short NLOS conditions [15]. The Kalman gain and the state estimation are updated as follows:
To ensure numerical robustness for long-term stable filtering in complex dynamic environments, the Joseph-form is applied. The estimated error covariance matrix with Joseph-form is given by,
3. SH-CAIPS Architecture and Operation
The structure of the proposed SH-CAIPS is shown in Figure 2. Raw GNSS, IMU, and odometry streams are encoded and pre-processed to extract temporal features that serve as inputs to the DRL agent. Within the agent, noise covariances are adaptively scaled using innovation statistics and contextual features. Measurement noise covariances are updated for outlier mitigation through a two-stage gating pipeline consisting of an adaptive measurement-noise scaling gate and an NIS-based adaptive update gate. The gated measurements are then fed into the update stage of the IAKF. After the update process, DRL rewards are computed, and the DRL policy is refined to achieve robust and context-aware positioning.
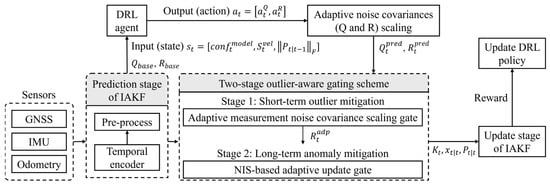
Figure 2.
Schematic diagram of the proposed SH-CAIPS.
3.1. DRL-Based Adaptive Noise Covariances Scaling
The DRL agent interacts with the environment to learn a policy that maximizes rewards for real-time optimal decision-making to achieve specific objectives. Markov decision process [23] model is defined by the tuple (), where represents the state space, is the action space, and the state transition probability, is the reward function, is the discount factor, and is the distribution of the initial state. The goal of DRL is to learn a policy that maximizes the cumulative reward.
A proximal policy optimization (PPO) algorithm is widely recognized for its capability to balance the exploration-exploitation trade-off, guarantee stability, and accomplish both computational efficiency and ease of implementation [24]. The proposed position system employs the PPO algorithm, which is a policy-based, model-free, online, and on-policy DRL algorithm. The PPO algorithm is structured within an actor–critic framework, enabling stable policy updates by simultaneously learning both the actor’s policy and the critic’s value function, thereby improving learning stability and accelerating convergence. The PPO algorithm limits the difference between the current and newly updated policies by clipping the objective function on agent-obtained samples. The objective function of the PPO is given by the clipped surrogate objective as follows:
where is the clipped surrogate objective, denotes the estimated advantage function for action taken at time step , and is the hyperparameter that controls the extent of policy update. The adaptive noise covariances scaling policy is learned using the PPO algorithm to ensure learning stability even under significant environmental changes.
In the proposed SH-CAIPS, the state is defined as
where is the state of DRL at time step , is the confidence score of the model by using the difference between the temporal encoder and GNSS measurements, is the innovation covariance of velocity by the IMU sensor, and is the Frobenius norm of predicted position covariance. In the proposed SH-CAIPS, the reward is defined as
where is the reward of DRL at time step , is the NIS value, is the penalty weight for preventing excessive conservation set to be , is set to be for numerical stability, and is the identity matrix. Unlike conventional DRL-based positioning systems that require true positions in computing reward [21,22], the proposed SH-CAIPS is trained to minimize innovation inconsistency rather than true position error. Although the utilization of ground-truth data might theoretically yield higher precision, it is recognized that such dependence contradicts the fundamental nature of the positioning system where the true position is unknown. Furthermore, by excluding true position from the reward design, the risk of the model overfitting to specific training trajectories can be effectively mitigated. Therefore, the reward in the proposed positioning system is derived from NIS and innovation covariance, which quantify the agreement between the filter’s prediction and incoming sensor measurements. These states are available in real time without requiring ground-truth. As a result, the agent can learn to regulate noise covariances based on sensor-model consistency, allowing training and deployment in realistic environments where ground truth is not accessible.
In the proposed SH-CAIPS, the action is defined as
where is the action of the DRL at time step , and are the scale factors of and , respectively. Applying the DRL action to the noise covariances of SH-CAIPS is given by
where and are the predicted process and measurement noise covariances by DRL at time step , and and are the base process and measurement noise covariances, respectively.
3.2. Adaptive Measurement Noise Covariance Scaling Gate for Short-Term Outlier Mitigation
To mitigate short-term outliers, the adaptive measurement noise scaling is proposed. Whitening innovation through the Cholesky factorization method [7] of innovation covariance is expressed as
where the Cholesky factorization of the innovation covariance is represented as . And is the lower triangular matrix obtained from the Cholesky decomposition of . The internal state variables of the exponentially weighted moving average (EWMA) of the whitening innovation energy of each channel are expressed as
where is the EWMA memory and is set to 0.98. The is dimensionless energy which is a scalar value that equals one under nominal conditions and increases when outliers or noise are present, leading to an increase in the corresponding measurement noise covariance corresponding to the channel. The adaptive noise covariance scaling factor is expressed as
where and denote the minimum and the maximum values of the scale range, and they are set to be 0.5 and 4.0, respectively, in the experimental setup. The noise covariance reflecting the adaptive noise covariance scaling factor is expressed as
When the measured value deviates significantly from the predicted value, the measurement noise covariance is increased with , indicating lower measurement reliability. Conversely, when the measured value closely matches the predicted value, is decreased with , indicating higher measurement reliability.
3.3. NIS-Based Adaptive Update Gate for Long-Term Outlier Mitigation
To mitigate long-term outliers, the NIS-based adaptive update gate is proposed. For channels exhibiting significant deviations from the measurement readings, channel-wise thresholds are applied to increase the corresponding value. To detect outliers, the chi-squared threshold with one degree of freedom for each channel is set as . If the whitened innovation exceeds the threshold, the corresponding channel’s value is inflated by up to a decuple. Adaptive thresholding employs a sliding-window technique with 100 historical NIS values to dynamically adjust thresholds based on past statistics, ensuring robust operation. To obtain an appropriate threshold, the optimal empirical value was derived by varying it within the range of 0.8 to 0.99 in increments of 0.01. A quantile-based threshold of 0.95 is applied, with the clipped upper and lower bounds accordingly. The adaptive threshold is given by
where is the quantile at probability 0.95 of the sample sets of NIS. The final adaptive threshold through EWMA smoothing is given by
In the update stage of IAKF, if , the Kalman gain matrix, the state estimation, and the estimated error covariance matrix are updated by Equations (8)–(10), respectively. However, if , the updates of the state estimate, measurement noise covariance, and the error covariance matrix are skipped as and . The training process of the SH-CAIPS model is summarized in Algorithm 1.
| Algorithm 1: Training process of the proposed SH-CAIPS |
| 1: Input: Sensor streams (GNSS, IMU, Odometry), measurement vector, pre-traine parameters and model |
| 2: Initialize filter, gate, and PPO parameters |
| 3: Pre-processing: Sensors synchronized and mapped to a common positioning frame |
| 4: Training Loop: |
| 5: for epoch = 1 to do |
| 6: for time step = 1 to do |
| 7: Context-aware sensor fusion and Prediction stage update by Equations (1)–(7) |
| 8: Update noise covariances , by PPO policy action by Equations (11)–(17) |
| 9: Perform adaptive measurement noise covariance scaling by Equations (18)–(21) |
| 10: Perform NIS-based adaptive update gating by Equations (22) and (23) |
| 11: Perform update stage of IAKF by Equations (8)–(10) |
| 12: Update PPO reward |
| 13: end for |
| 14: Update PPO policy |
| 15: end for |
4. Simulation Results
4.1. Simulation Settings
The simulations have been performed by utilizing the open dataset from the University of Michigan North Campus Long-Term (NCLT) [25] into train and test portions to evaluate the positioning system’s performance. The NCLT dataset is a large-scale dataset collected from 27 sessions collected over 15 months on a Segway platform traversing indoor–outdoor campus routes across diverse terrains, seasons, and weather conditions. A Segway-based platform provided synchronized multi-sensor measurements. This evaluation dataset allows the generalizability and adaptability of the proposed positioning correction to be assessed across diverse scenarios.
The data was collected using Velodyne HDL-32E LiDAR, Ladybug3 Omnidirectional Vision, MicroStrain GX3 IMU, KVH Fiber Optic Gyro, Segway Wheel Odometry, and both Standard and RTK GPS sensors from Trimble. To achieve cost-effective and robust position correction, the proposed system utilizes GPS, IMU, and wheel odometry. The configurations of the GPS, IMU, and odometer streams were sampled at 5 Hz, 37 Hz, and 47 Hz, respectively. All sensor streams were time-synchronized by interpolating them onto a common time axis. To extract temporal features in sequence models, the GRU input window size of 7 was adopted, aligned to the IMU sampling rate. In the simulation, all methods are initialized from the same initial state and are evaluated in a common global frame without positional offset correction or trajectory alignment techniques.
4.2. Performance Evaluations
In order to ensure the model’s generalization, the 24 sessions collected in 2012, which cover all seasonal variations, were utilized for model training, whereas the remaining 3 sessions from 2013 were employed for testing. Three distinct datasets from the NCLT dataset [25], collected on 10 January 2013, 23 February 2013, and 5 April 2013, are used for performance evaluation and are referred to as dataset 1, dataset 2, and dataset 3, respectively. The datasets 1, 2, and 3 consist of 3263 steps over approximately 17 min, 16,871 steps over approximately 79 min, and 13,544 steps over approximately 69 min, respectively. The performance of the proposed SH-CAIPS is evaluated against baseline methods, including EKF, IAKF, median filter (MF), and CAINS [15]. To evaluate the positioning performance, a root mean square error (RMSE), maximum error, and standard deviation are used. In a median filter, each output sample is obtained by sorting the values within a sliding window and selecting the median.
In this paper, the PPO algorithm was employed with the following hyperparameters: the clipping ratio , discount factor , generalized advantage estimation parameter , number of training epochs, batch size, and learning rate for both the actor and critic networks are set to be 0.2, 0.99, 0.95, 1000, 64, and , respectively. In the hidden layers, we use ReLU activation functions and the Adam optimizer. The window size is set to 15, allowing the filter to effectively suppress impulse noise while preserving sharp transitions and edge details. In this simulation, the IAKF was configured conservatively to ensure stable positioning correction. A measurement noise covariance was adjusted based on deviation and limited to 0.3 to 4.0 times its baseline, while process noise covariance was adjusted from the median innovation and constrained to 0.5 to 3.0 times its baseline. The parameters were selected empirically through simulations and sensitivity analysis. For each parameter, multiple candidate values were tested over a reasonable range, and the experimental values were chosen as a representative value within typical operating ranges, considering trade-off among positioning accuracy, stability, and convergence behavior.
A comparison of trajectories with five different positioning methods is presented in Figure 3. The RMSE, maximum error, standard deviation, average drift rate, and inference time for each method are summarized in Table 1, Table 2 and Table 3. In addition, the computing time is measured to assess the real-time feasibility of the proposed positioning system. Typically, the computing time is measured using the inference time. Since the PPO algorithm of the proposed SH-CAIPS does not employ replay memory, its computing time is constituted only by action inference. A higher computational load is incurred by the proposed SH-CAIPS compared to conventional methods. However, the average inference time per sample of the proposed SH-CAIPS is measured at approximately 0.44 ms, confirming that real-time processing capabilities can be maintained within the sensor sampling interval.
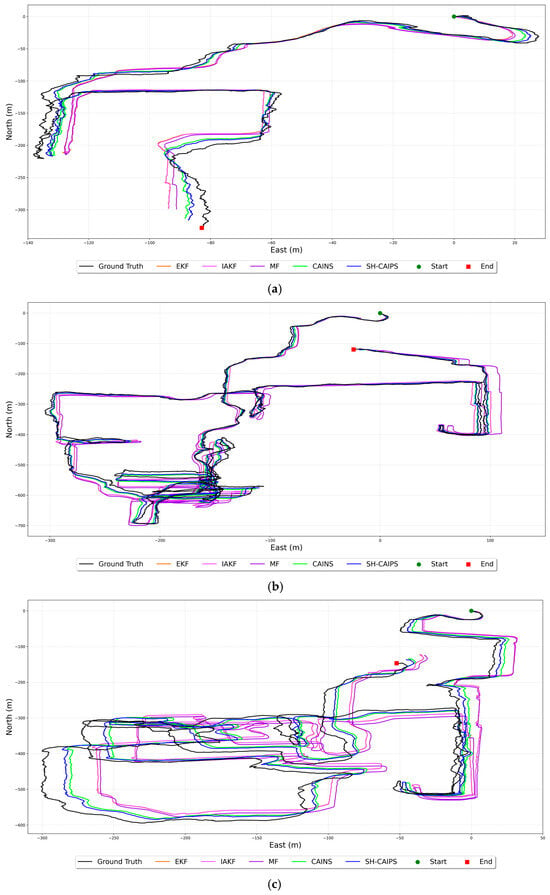
Figure 3.
Trajectory comparison of proposed SH-CAIPS across three distinct datasets: (a) dataset 1, (b) dataset 2, and (c) dataset 3.

Table 1.
Positioning statistics for positioning systems on the dataset 1.

Table 2.
Positioning statistics for positioning systems on the dataset 2.

Table 3.
Positioning statistics for positioning systems on the dataset 3.
The proposed SH-CAIPS yields the lowest RMSE, maximum error, and standard deviation, indicating enhanced positioning stability and reduced error drift over time. The RMSE of the proposed SH-CAIPS can be reduced by up to 60%, 61%, 61%, and 23%, respectively, compared to EKF, IAKF, MF, and CAINS. Furthermore, the maximum error can be decreased by up to 60%, 60%, 60%, and 21% relative to the same methods. Compared to the EKF and IAKF, which exhibit similar error statistics due to their shared linear Gaussian assumptions, SH-CAIPS achieves a substantial reduction in RMSE, reflecting the effectiveness of its adaptive and outlier-aware updating mechanism. The MF partially mitigates abrupt spikes but does not effectively capture temporal error drift, leading to limited performance improvement, particularly in long-duration sequences. In contrast, CAINS offers better robustness by leveraging context-aware sensor fusion; however, its reliance on fixed noise parameters results in performance degradation under varying measurement conditions.
The proposed SH-CAIPS further improves upon CAINS by integrating hierarchical short- and long-term gating and DRL-based IAKF. The adaptive measurement-noise covariance scaling gate suppresses sensor spikes, while the NIS-based adaptive update gate detects persistent or axis-concentrated inconsistencies over sliding windows. As a result, positioning estimator divergence can be effectively prevented, and error drift remains gradual even in extended trajectories. Overall, it is confirmed that both short- and long-term outliers can be effectively mitigated in the proposed SH-CAIPS without reliance on ground-truth supervision.
A longstanding challenge in positioning systems is the error drift and accumulation of estimation errors over time. In Table 1, Table 2 and Table 3, the average drift rate is calculated by dividing the accumulated positioning error by the elapsed time in minutes. This metric is derived by averaging the error growth over the entire trajectory, normalized to a one-minute interval. The lowest average drift rate is consistently achieved by SH-CAIPS across all datasets, demonstrating superior stability compared to EKF, IAKF, MF, and CAINS. Consequently, it is confirmed that long-term error accumulation can be effectively suppressed by the proposed method, maintaining the slowest error growth per minute. The error drift is presented in Figure 4 by the test dataset, where larger error drifts are observed to be produced by longer sequences. The average drift rate of the SH-CAIPS can be reduced by up to 62%, 62%, 62%, and 25%, respectively, compared to EKF, IAKF, MF, and CAINS. While conventional methods exhibit high sensitivity to outliers and abrupt environmental changes, the proposed SH-CAIPS can effectively suppress outliers and maintain a lower error variance throughout the sequence. These results demonstrate that large and abrupt performance degradations can be effectively mitigated even during extended operation.
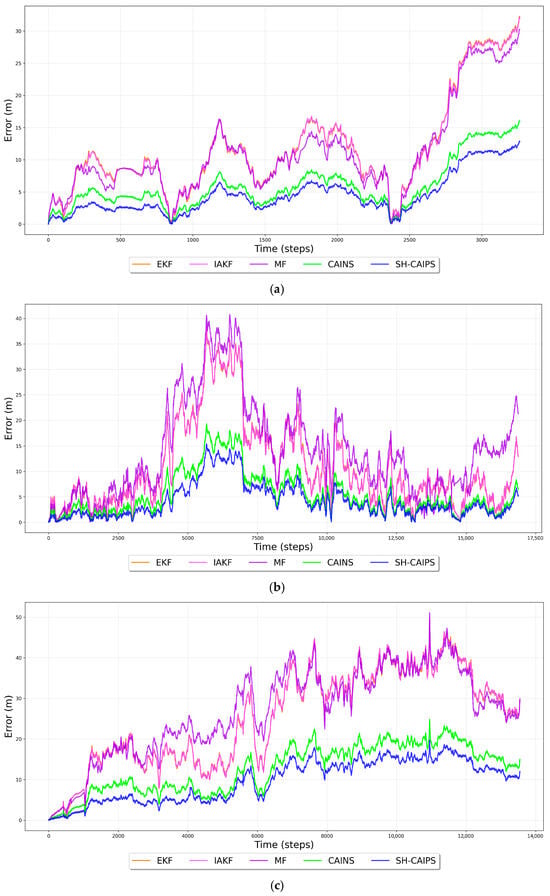
Figure 4.
Error drift comparison of proposed SH-CAIPS across three distinct datasets: (a) dataset 1, (b) dataset 2, and (c) dataset 3.
Through an ablation study presented in Table 1, Table 2 and Table 3, the benefit of the two-stage outlier gating scheme is demonstrated. It is observed that the RMSE and maximum error are reduced by approximately 20% and the average drift rate is further suppressed when the two-stage outlier gating mechanism is applied, confirming that the outliers and error drifts are effectively mitigated without increasing the inference time. The isolated efficacy of the DRL can be quantified by comparing the SH-CAIPS without two-stage outlier gating with the IAKF. As shown in Table 1, Table 2 and Table 3, the positioning performances are improved by approximately 50% through the application of the DRL. This improvement indicates that the context-aware adjustment of model and measurement uncertainties by the DRL is more effective than the standalone adaptive filter.
Consequently, the enhanced performance of the proposed SH-CAIPS, attributable to its integration of sensor fusion, DRL-based noise scaling, and hierarchical outlier-aware gating with the IAKF, enables more reliable positioning estimation in dynamic environments. It can be expected to provide a flexible and comprehensive solution for seamless context-aware intelligent positioning.
4.3. Discussions on Experimental Results
In practical positioning scenarios, GNSS measurements are often heavily affected by NLOS conditions, multipath propagation, and intermittent outages. Under these conditions, conventional filter configurations that are statically tuned for measurements are prone to residual error drift in the absence of context awareness. GNSS measurements are often characterized by nonstationary uncertainties, requiring adaptive adjustments within the system to ensure their reliability. In the proposed positioning system, the DRL-based approach that exploits innovation statistics is trained to adaptively adjust the noise covariances of IAKF so that unreliable GNSS updates are down-weighted, while IMU and wheel odometry information are prioritized when GNSS quality declines. As a result, the DRL-based positioning system is particularly advantageous in long-term, real-world operations where GNSS availability and quality are inherently inconsistent.
Although the proposed SH-CAIPS demonstrates improved positioning accuracy and robustness against error drift compared to conventional methods, several limitations and issues remain. First, the integration of the DRL-based noise covariance adaptation and the temporal encoding for feature extraction introduces additional computational overhead. Second, the proposed system was validated on a ground-vehicle platform equipped with a specific configuration of GPS, IMU, and wheel odometry. Training and inference were conducted offline using logged data from the NCLT dataset. Although the NCLT dataset, which was obtained from real-world measured data, was utilized in the validation of the proposed system, real-time constraints such as latency, offline processing, and energy consumption issues were not fully profiled. The scalability of the proposed method to other platforms remains to be verified, particularly where sensor characteristics or vehicle dynamics differ from the training distribution. Third, while the NCLT dataset encompasses seasonal variations and indoor–outdoor transitions, the model has not been tested in extreme environments such as urban canyons and fully GNSS-denied tunnels.
Future work will address these limitations by optimizing computational efficiency for embedded deployment, evaluating the system’s generalizability across diverse platforms, and extending the framework to handle challenging environmental conditions. Furthermore, a sensitivity analysis incorporating GNSS outages and sensor bias injection will be conducted to verify the system’s resilience under extreme component failure scenarios.
5. Conclusions
In this paper, a novel seamless hierarchical context-aware positioning system is proposed to improve positioning accuracy and robustness in both LOS and NLOS scenarios while ensuring cost-effectiveness. The proposed framework integrates sensor fusion and two-stage outlier mitigation gates within the DRL-based framework. By combining a short-term adaptive measurement noise covariance scaling gate with a long-term NIS-adaptive update gate, outliers and nonstationary noise can be effectively mitigated without resorting to high-cost sensors or pre-mapped environments. Moreover, the PPO-based noise scaling policy, which modulates process and measurement noise covariances, is implemented with IAKF. As a result, the proposed SH-CAIPS can significantly improve the positioning performance using only GPS, IMU, and odometry sensors. The proposed SH-CAIPS is observed to be more stable with its error drift bounded within a small range, effectively suppressing error spikes and maintaining a lower error variance. Consequently, the proposed positioning system can be regarded as a promising solution for enabling seamless and precise positioning and facilitating the development of autonomous navigation.
In future work, the applicability of the positioning system is planned to be extended to extreme scenarios with real-time embedded implementation in resource-constrained environments. In addition, mechanisms for reconfiguring sensor usage in the presence of abnormal sensor behavior and for improving scalability in large-scale deployments can be explored. Finally, the generalization capability of the positioning system is scheduled for validation on heterogeneous platforms, including unmanned aerial vehicles and robots, to verify robustness under varying dynamic characteristics.
Author Contributions
Conceptualization, S.L. and B.H.; methodology, S.L.; software, S.L., B.H., J.S. and J.K. (Jinwook Kim); validation, J.S. and S.K.; formal analysis, J.K. (Jeongho Kim); investigation, S.L., B.H. and K.K.; resources, S.L., B.H. and K.K.; data curation, B.H. and M.L.; writing—original draft preparation, S.L.; writing—review and editing, S.L., B.H., J.S., K.K., S.K. and Y.S.; visualization, B.H., S.K., J.S. and M.L.; supervision, J.K. (Jinyoung Kim); project administration, J.K. (Jinyoung Kim). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://robots.engin.umich.edu/nclt/, accessed on 15 October 2025.
Acknowledgments
This work was supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government(MSIT) (No. 2021-0-00892-005, Research on advanced physical layer technologies of LEO(low-earth orbit) satellite communication systems for ubiquitous intelligence in space) and supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (RS-2025-23524307).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AKF | Adaptive Kalman filter |
| DRL | Deep reinforcement learning |
| EKF | Extended Kalman filter |
| GNSS | Global navigation satellite system |
| IAKF | Innovation-based adaptive Kalman filter |
| IMU | Inertial measurement unit |
| KF | Kalman filter |
| LOS | Line-of-sight |
| MF | Median filter |
| NIS | Normalized innovation squared |
| NLOS | Non-line-of-sight |
| PPO | Proximal policy optimization |
| RMSE | Root mean square error |
| SH-CAIPS | Seamless hierarchical context-aware intelligent positioning system |
References
- Nnodim, T.C.; Arowolo, M.O.; Agboola, B.D.; Ogundokun, R.O.; Abiodun, M.K. Future trends in mechatronics. IAES Int. J. Robot. Autom. 2021, 1, 24. [Google Scholar] [CrossRef]
- Zaitceva, I.; Andrievsky, B. Methods of intelligent control in mechatronics and robotic engineering: A survey. Electronics 2022, 11, 2443. [Google Scholar] [CrossRef]
- Plasencia-Salgueiro, A.d.J. Deep reinforcement learning for autonomous mobile robot navigation. In Artificial Intelligence for Robotics and Autonomous Systems Applications; Springer: Berlin/Heidelberg, Germany, 2023; pp. 195–237. [Google Scholar]
- Asaad, S.M.; Maghdid, H.S. A comprehensive review of indoor/outdoor localization solutions in IoT era: Research challenges and future perspectives. Comput. Netw. 2022, 212, 109041. [Google Scholar] [CrossRef]
- Auger, F.; Hilairet, M.; Guerrero, J.M.; Monmasson, E.; Orlowska-Kowalska, T.; Katsura, S. Industrial applications of the Kalman filter: A review. IEEE Trans. Ind. Electron. 2013, 60, 5458–5471. [Google Scholar] [CrossRef]
- Giannitrapani, A.; Ceccarelli, N.; Scortecci, F.; Garulli, A. Comparison of EKF and UKF for spacecraft localization via angle measurements. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 75–84. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Kim, K.; Lee, S.; Hwang, B.; Kim, J.; Seon, J.; Kim, S.; Sun, Y.; Kim, J. Enhanced 3D outdoor positioning method based on adaptive Kalman filter and kernel density estimation for 6G wireless system. Electronics 2024, 13, 4623. [Google Scholar] [CrossRef]
- Chen, C.; Pan, X. Deep learning for inertial positioning: A survey. IEEE Trans. Intell. Transp. Syst. 2024, 25, 10506–10523. [Google Scholar] [CrossRef]
- Jwo, D.J.; Biswal, A.; Mir, I.A. Artificial neural networks for navigation systems: A review of recent research. Appl. Sci. 2023, 13, 4475. [Google Scholar] [CrossRef]
- Chen, H.; Aggarwal, P.; Taha, T.M.; Chodavarapu, V.P. Improving inertial sensor by reducing errors using deep learning methodology. In Proceedings of the IEEE National Aerospace & Electronics Conference (NAECON), Dayton, OH, USA, 23–25 July 2018; pp. 197–202. [Google Scholar]
- Liu, H.; Wei, X.; Perusquía-Hernández, M.; Isoyama, N.; Uchiyama, H.; Kiyokawa, K. DUET: Improving inertial-based odometry via deep IMU online calibration. IEEE Trans. Instrum. Meas. 2023, 72, 1–13. [Google Scholar] [CrossRef]
- Hosseinyalamdary, S. Deep Kalman filter: Simultaneous multi-sensor integration and modelling; a GNSS/IMU case study. Sensors 2018, 18, 1316. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Zhang, Y.; Guo, X.; Chen, X.; Cao, H.; Tang, J.; Li, J.; Liu, J. Seamless GPS/Inertial navigation system based on self-learning square-root cubature Kalman filter. IEEE Trans. Ind. Electron. 2021, 68, 499–508. [Google Scholar] [CrossRef]
- Hwang, B.; Lee, S.; Kim, K.; Kim, S.; Seon, J.; Kim, J.; Kim, J.; Sun, Y.; Kim, J. Context-aware integrated navigation system based on deep learning for seamless localization. Sensors 2024, 24, 7678. [Google Scholar] [CrossRef] [PubMed]
- Zhu, K.; Zhang, T. Deep reinforcement learning based mobile robot navigation: A review. Tsinghua Sci. Technol. 2021, 26, 674–691. [Google Scholar] [CrossRef]
- Nobre, F.; Heckman, C. Learning to calibrate: Reinforcement learning for guided calibration of visual–inertial rigs. Int. J. Robot. Res. 2019, 38, 1388–1402. [Google Scholar] [CrossRef]
- Øvereng, S.S.; Nguyen, D.T.; Hamre, G. Dynamic positioning using deep reinforcement learning. Ocean Eng. 2021, 235, 109433. [Google Scholar] [CrossRef]
- Sun, Y.G.; Kim, S.H.; Kim, D.I.; Kim, J.Y. Area-selective deep reinforcement learning scheme for wireless localization. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2025; early publication (accepted). [Google Scholar]
- Wu, Z.; Yao, Z.; Lu, M. Deep-reinforcement-learning-based autonomous establishment of local positioning systems in unknown indoor environments. IEEE Internet Things J. 2022, 9, 13626–13637. [Google Scholar] [CrossRef]
- Gao, X.; Luo, H.; Ning, B.; Zhao, F.; Bao, L.; Gong, Y.; Xiao, Y.; Jiang, J. RL-AKF: An Adaptive Kalman Filter Navigation Algorithm Based on Reinforcement Learning for Ground Vehicles. Remote Sens. 2020, 12, 1704. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, Q.; Sun, M.; Zhu, X. A Kalman Filter-Based Localization Calibration Method Optimized by Reinforcement Learning and Information Matrix Fusion. Entropy 2025, 27, 821. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Del Rio, A.; Jimenez, D.; Serrano, J. Comparative analysis of A3C and PPO algorithms in reinforcement learning: A survey on general environments. IEEE Access 2024, 12, 146795–146806. [Google Scholar] [CrossRef]
- Carlevaris-Bianco, N.; Ushani, A.K.; Eustice, R.M. University of Michigan north campus long-term vision and LiDAR dataset. Int. J. Robot. Res. 2016, 35, 1023–1035. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).