Abstract
This study focuses on determining stress distribution in elastic continuous beam foundations subjected to large eccentricities primarily induced by the overturning moments generated when horizontal forces, like those from earthquakes and wind, act on the superstructure. Traditional linear static solutions provide an incorrect stress distribution when a foundation loses partial contact with the ground, as they erroneously calculate tensile stress in the uplifted regions. This research aims to formulate a mathematical model that accurately calculates the corrected stress distribution. An optimization problem is defined to minimize the discrepancy between the external effects (loads and moments) from the superstructure and the internal resistance effects from the redistributed base stress under the condition of partial foundation uplift. To solve this, meta-heuristic optimization methods, including Artificial Bee Colony (ABC), Tree Seed Algorithm (TSA), and Biogeography-Based Optimization (BBO), are employed to derive accurate mathematical formulas. The performance of these methods is evaluated under varying soil conditions and loading scenarios. The Tree Seed Method has consistently delivered the most accurate results, with near-zero optimization errors. The findings provide the applicability of algorithmic methods and their potential for improving stress distribution modeling in elastic foundations.
1. Introduction
Structures, especially high-rise buildings, are subjected to significant horizontal forces caused by external effects such as seismic events and wind conditions. Continuous beam foundations are a widely used structural element designed to distribute these forces safely to the ground [1,2]. Horizontal effects acting on the superstructure generate considerable overturning moments at the foundation level. Furthermore, the combination of this high moment with axial loads can result in high eccentricity, potentially leading to partial separation of the foundation from the ground. Within a linear structural analysis, this eccentricity causes both compressive and tensile stress to develop. While the tensile stress appears in the analysis due to uplift, no such interaction occurs in reality, as soil cannot exert a remarkable tensile force on the foundation. Traditional design calculations often focus solely on compressive stress distribution, disregarding tensile stresses. In order to maintain structural integrity, the total stress must be immediately redistributed over the remaining contact area. This process, however, frequently increases the maximum stress and complicates the determination of the final stress distribution.
A prevalent approach is to represent continuous beam foundations with a frame element using a series of discrete elastic springs, but this increases the model’s intricacy by introducing non-linear behavior (such as variable stiffness or compression-only constraints) that makes it difficult to identify and redistribute the resulting stresses [3,4].
While foundation modeling includes various methods, two primary approaches are rigid and elastic. Many studies on tensile soil stresses concentrate on rigid foundation models [5,6,7], which assume a simplified linear stress distribution. This assumption, however, fails to capture the complex, non-linear stress behavior of elastic foundations, particularly under high eccentricity. When eccentricity is significant, rigid models often require extra empirical formulas [5,6] that may overlook tensile stress or oversimplify the solution. These traditional methods can be unrealistic, highlighting the need for more accurate models that better reflect the actual stress distribution beneath the foundation.
The stress response in elastic foundations is fundamentally different and more challenging to analyze. The current literature [8,9,10] addresses many advanced aspects of soil–structure interaction. However, it lacks comprehensive studies that incorporate the unique behavior of tensile stresses in elastic foundations, which presents a significant optimization problem. This study aims to address this gap by developing a mathematical model and algorithm that are capable of determining the redistribution of tensile stress under continuous beam foundations exhibiting non-linear behavior.
In the initial stage, an equation is developed to capture this complex situation by applying multiple correction factors to the classical deflection expression proposed by Hetényi [11], which is related to the behavior of an elastic beam on the Winkler soil model [12]. These correction factors are optimized to minimize the difference between the internal and external effects during the stress distribution under the foundation changes. This challenging error minimization problem is well-suited for meta-heuristic optimization techniques. Although it involves only four variables, the objective function is non-linear, non-convex, and discontinuous due to the conditional elimination of tensile stresses. These characteristics render it unsuitable for traditional gradient-based solvers, thereby justifying the use of robust global search methods.
To enhance the robustness and reliability of the results, meta-heuristic methods, which are proven to be effective in complex engineering optimization problems, are employed to calculate the correction factors. Using multiple methods allows for a comparison of the results, which helps to ensure the optimality and accuracy of the correction factors. This validation process confirms that the factors accurately represent non-linear and tensile stress conditions, thereby increasing the precision of the stress distribution models.
The correction factors are found to vary depending on parameters such as the total external load (), eccentricity (), flexural stiffness (), foundation length (ℓ), and the bedding coefficient (). These parameters play a crucial role in influencing stress distribution in continuous foundations, and the correction factors adjust accordingly to account for the non-linear behavior and the specific conditions of each foundation system.
In order to validate the proposed optimization methods, the Finite Element Method (FEM) is conducted the SAP2000 [13] structural analysis software. In the modeling approach using frame elements, linear analysis (L) with standard tension/compression springs, and non-linear analysis (NL) incorporating contact effects with compression-only springs to model foundation uplift are employed. The non-linearity in FEM analysis is confined exclusively to contact non-linearity at the base. Thus, the changing boundary conditions are redefined as the foundation loses and regains contact with the support springs. In addition, the material models for the foundation body remain linearly elastic.
The remainder of this study is structured as follows: Section 2 provides a literature review, discussing previous studies relevant to this work. In Section 3, the fundamental concepts of foundations are presented, along with an overview of stress distribution in rigid and elastic foundations, the equation employed in this study, and the optimization methods used to determine the coefficients within the equation. The results obtained from the analysis are presented in Section 4. Section 5 provides an interpretation of the results and a discussion of the findings.
2. Related Studies
The classical analytical solutions for beams on an elastic foundation were systematically established by Hetényi [11] in his 1946 publication, “Beams on Elastic Foundation.” This text is widely regarded as the definitive resource on the topic, providing a comprehensive suite of analytical solutions for a variety of loading and boundary conditions. Hetényi’s entire theoretical work is built upon the Winkler soil model [12], an idealization proposed in 1867 that represents the foundation as a series of independent, linear-elastic springs. Consequently, the governing differential equation in his analysis is derived directly from Winkler’s core assumption: that the reactive pressure from the foundation at any given point is directly proportional to the deflection of the beam at that point alone. The governing stress and deformation behavior of an elastic beam on the Winkler soil model is described with a classical analytical solution by Hetényi, which forms the basis of the considered formulation in this study.
The Section 2 of this article addresses the interdisciplinary nature of the research, which integrates aspects of stress distribution in foundations and the application of meta-heuristic optimization methods. Given the complexity of this study, the literature review is divided into two main focus areas. The first area explores existing research on stress distribution in foundations, emphasizing both traditional and advanced methods used to address non-linear and tensile stress behaviors. The second area examines recent meta-heuristic applications for geotechnical structures and the use of specific meta-heuristic optimization methods—namely, Artificial Bee Colony (ABC) [14,15,16,17,18,19,20,21,22], Biogeography-Based Optimization (BBO) [23,24,25,26,27,28], and Tree Seed Algorithm (TSA) [29,30,31,32,33]—in contexts similar to the present study. This study reveals a clear opportunity: to bridge the gap in geotechnical analysis by applying the proven power of these meta-heuristic algorithms to the problem of stress redistribution in highly eccentric-loaded elastic foundations.
The literature includes numerous studies on foundations with large eccentricities. Koseoglu [34] demonstrated a calculation of base stresses under biaxial bending, while Algin [35,36] proposed studies on a practical algebraic formula for dimensioning a rectangular foundation subjected to biaxial bending. Recent studies have focused on the refinement of foundation models. Moreno-Landeros et al. [37] proposed a novel model to determine the optimal area for rectangular footings with eccentric columns under partial ground compression, achieving a significant reduction in footing size. Tabsh and Al-Shawa [3] modeled the foundation using the FEM, incorporating springs with varying bedding coefficients. Loukidis and Tamiolakis [4] examined the spatial variation in the Winkler spring stiffness constants required for spring mattress modeling to replicate slab deflections and bending moment diagrams obtained from FEM analysis. Additionally, studies incorporating the Winkler soil model into structural analyses have been conducted to evaluate the interaction between beams and elastic supports [38,39]. However, a common limitation in these studies [38,39] is that the redistribution of tensile stresses—and the resulting concentration of compressive stress—is often overlooked, leading to models that do not satisfy force and moment equilibrium once uplift occurs.
Aydoğdu [5] and Özmen [6] developed iterative methods for determining base stresses in rectangular rigid foundations, but their approaches, while innovative for rigid-body assumptions, are not extended to the more complex deformation-dependent stress patterns found in elastic foundations. Bellos and Bakas [7] generated an eccentricity diagram to map the deformations and compression zones of the foundation in a rectangular rigid foundation. Moffitt [40] conducted an examination of the stress distribution behavior of single foundations under the effects of uniaxial and biaxial overturning. While these studies considered tensile stress distribution, the foundation behavior is modeled as a rigid body. The study presented by Adrian [41] explores the distribution of pressure under eccentrically loaded rectangular footings on elastic soils, addressing key challenges in the field of geotechnical engineering. By employing mathematical models, the research aims to improve the accuracy of pressure predictions and footing design under various loading conditions.
Collectively, these advancements underscore a critical, persistent gap in the literature. While methods have been proposed for rigid foundations [5,6,7,40] and the complexities of elastic–soil interaction have been explored [8,9,10,41], a comprehensive framework that directly addresses the non-linear redistribution of tensile stress in elastic continuous foundations remains underdeveloped. Prior studies often either model the foundation as rigid, which oversimplifies the stress distribution, or, when using elastic models, do not fully resolve the equilibrium imbalance that occurs when tensile stresses are justifiably removed. This specific challenge—correcting the stress profile in elastic foundations to restore equilibrium under large eccentricity—forms the central motivation for the present research.
Recent advancements underscore the continued relevance of the elastic Winkler approach in soil–structure interaction modeling. For example, Gan et al. [8] investigated the random responses of shield tunnels, while Lu et al. [9] examined settlement deformation in buried pipelines—both demonstrating the applicability of Winkler-based models to contemporary engineering problems. Yu et al. [42] further extended this approach by developing an analytical method to predict the response of a strip-foundation building to shallow tunneling. Enhancing predictive accuracy, Zhen et al. [43] employed Physics-Informed Neural Networks to infer beam displacement on foundations with high fidelity, even from limited data. Additionally, Muhammad et al. [10] proposed simulation-based P-multipliers for laterally loaded pile groups in granular soils, reflecting ongoing efforts to refine soil modeling techniques.
The application of meta-heuristic optimization in geotechnical engineering has expanded considerably, underscoring the relevance of the techniques adopted in this study. For instance, Varga et al. [44] developed a reliability-based optimization model to determine the optimal embedment depth of retaining walls; Dong et al. [45] proposed a GA–BP neural network to predict optimal design parameters for reinforced soil embankments; and Li et al. [46] demonstrated that machine learning can effectively predict key soil compaction parameters from index properties, thereby enhancing design efficiency. Khajehzadeh et al. [47] successfully applied an adaptive salp swarm algorithm to optimize the design of geotechnical structures, demonstrating the efficiency of bio-inspired methods in foundation engineering tasks involving non-linear conditions. Similarly, Moayedi et al. [48] utilized four meta-heuristic optimizers, including MFO and LCA, to train neural models for predicting the bearing capacity of shallow foundations on layered soils. Their work underscores the effectiveness of bio-inspired methods for solving the complex, non-linear problems inherent in foundation engineering.
There are numerous studies on the application of the meta-heuristic methods selected for this study, particularly the Artificial Bee Colony (ABC) algorithm, developed by Karaboga [14]. This method, inspired by the foraging behaviors of bee colonies, is first applied to multivariate function optimization [15]. In subsequent work, Karaboga and Basturk [16] compared the ABC with other algorithms such as the Genetic Algorithm (GA), Particle Swarm Algorithm (PSA), and Particle Swarm-Inspired Evolutionary Algorithm (PS-EA). Further comparisons demonstrated the ABC algorithm’s effectiveness against Differential Evolution (DE), Particle Swarm Optimization (PSO), and the Evolutionary Algorithm (EA) for multidimensional numerical problems [17]. The global best (Gbest)-guided ABC (GABC) algorithm, which enhances the exploitation capability of ABC by incorporating global best solution information into the search equation, showed notable results in numerical function optimization [18]. Additionally, the ABC algorithm, with a hybrid search strategy for structural damage detection, highlighted its versatility in structural engineering applications [19]. Various modifications have been proposed to enhance the convergence speed and solution accuracy of the ABC algorithm, such as integrating the Firefly algorithm strategy to improve exploration and exploitation capabilities [20] and applying an improved ABC method in clustering algorithms for higher search accuracy and efficiency [49]. These references support the applicability and effectiveness of the ABC algorithm and similar meta-heuristic methods for optimization tasks relevant to this study on stress distribution in continuous foundations. The Artificial Bee Colony (ABC) algorithm has been widely utilized across various engineering domains; for instance, the ABC algorithm for route planning in unmanned aerial vehicles [50]. They similarly applied the ABC method to model and optimize reservoir capacity, comparing it with alternative models using the Koprucay example [22]. Additionally, several heuristic algorithms, including ABC, Cuckoo Search, and Teacher–Learner Optimization, have been developed and applied for the optimal design of reinforced concrete single foundations with minimal costs [51]. These applications underscore the versatility and effectiveness of the ABC algorithm in solving complex optimization problems in engineering [21].
The Biogeography-Based Optimization (BBO) method, developed by Simon [23], is a biodiversity-inspired, population-based meta-heuristic optimization technique. This method has been extensively applied in various engineering domains. The authors of [24] evaluated the performance of the BBO algorithm with enhancements, focusing on population distribution and elitism. The authors of [23] introduced a constrained blended BBO algorithm, comparing it with the Steady-State Genetic Algorithm (SGA) and the standard Particle Swarm Optimization (PSO) methods. Several improvements have been proposed to enhance the algorithm’s exploration and convergence efficiency, including modifications such as an improved migration operator and local search mechanisms to strengthen exploration capabilities [25], as well as integrating Cauchy mutation and cosine migration models for adaptive control applications, which improve both accuracy and search speed [27]. For instance, the BBO algorithm is applied to the design and economic optimization of shell-and-tube heat exchangers, aiming to minimize costs [28]. The BBO algorithm is employed to efficiently determine the electrical equivalent circuit parameters of asynchronous motors, with its performance compared to that of the Genetic Algorithm (GA) [52]. The BBO is used to optimize real-sized complex steel space frame structures [53]. Additionally, BBO is utilized for optimizing fire image segmentation, thereby demonstrating its versatility in image-processing applications [26]. Hybrid intelligence approaches have also proven successful in related civil and geotechnical problems. For instance, Sharafati et al. [54] employed a hybrid meta-heuristic model to predict scoring depth downstream of weirs, demonstrating the capability of such models in solving non-linear hydraulic and soil–structure interaction challenges.
The Tree Seed Algorithm (TSA), introduced by Kiran [31], has been extensively studied and applied to optimization problems. In his seminal work, Kiran [31] compared the TSA with 32 other optimization methods, including the Artificial Bee Colony (ABC), Particle Swarm Optimization (PSO), Harmony Search (HS), and Firefly Algorithm (FA), demonstrating its competitive performance in continuous optimization problems. In a subsequent study, he addressed the pressure vessel design (PVD) problem using TSA, comparing its effectiveness with state-of-the-art methods such as ABC and PSO [33]. The TSA is further enhanced by incorporating Deb’s rules to address constrained optimization problems; then, its performance is compared with that of various other optimization approaches [30]. Improvements are introduced to the TSA, and its performance is evaluated against that of the original algorithm [32]. Additionally, a parallel version of the Tree Seed Algorithm is developed on the Compute Unified Device Architecture (CUDA) platform, thereby expanding its applicability to large-scale optimization problems [29].
The use of these three algorithms, each incorporating stochastic elements, allows for a comprehensive evaluation of their performance. By comparing these methods, this study aims to leverage their distinct strengths and capabilities to achieve a more accurate and effective solution for optimization problems associated with stress distribution in continuous foundations. This multi-algorithm approach provides a more robust analysis than relying on a single method, ensuring a well-rounded understanding of their relative performances.
This research contributes a comprehensive mathematical model and algorithm for continuous foundations with non-linear stress behavior under high eccentricity, specifically focusing on the often-neglected issue of tensile stress redistribution. While previous studies [5,6] concentrated on rigid foundations, this work extends the analysis to elastic foundations for a more complete understanding of stress behavior on the Winkler soil model [12]. A novel methodological method is introduced by incorporating correction factors into a classical analytical solution for elastic beam deflection, shortly defined as CAS for this study, described by Hetényi [11] and utilizing multiple meta-heuristic optimization techniques (ABC, BBO, TSA). To the authors’ knowledge, this combination of techniques to determine stress distribution, particularly concerning tensile stresses in continuous foundations, is unprecedented. By filling this gap, the study provides both theoretical advancements and practical engineering solutions, supported by a computational tool for optimization problems in foundation engineering.
3. Materials and Methods
3.1. Optimization Problem to Determine Base Stress Redistribution in Continuous Foundations
High and unpredictable horizontal forces, or a large load eccentricity, can cause a foundation to partially uplift, resulting in a loss of contact and redistribution of the base stress. In such cases, determining the base stress distribution by simple linear static analysis leads to a significant calculation fault, such as unrealized tensile base stress. Since no remarkable tensile interaction occurs between the base and the foundation surface, only the redistribution of compressive stress will take place. This situation indicates that the analysis must be performed with non-linear methods. Figure 1 provides a comprehensive description of this case under the effect of any number of superstructural loads. The value δ is defined as the distance between two points: the actual contact point and the theoretical zero-stress point from the linear analysis. The distance from the foundation edge to this contact point is the non-contact length (Δ). Additionally, the contact point also indicates the start of the redistributed compressive stress.
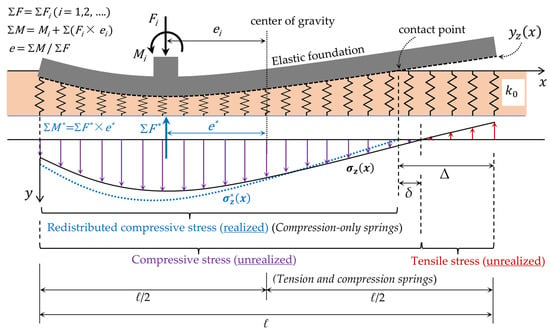
Figure 1.
Description of base stress redistribution under an elastic foundation.
In Figure 1, is a function of the compressive and tensile base stress calculated by traditional linear analysis, represents the redistributed compressive base stress that in reality occurs under the foundation and is attempted to be determined by non-linear optimization methods, is the total external load, is the total external bending moment at the center of gravity of the foundation, is the total base force obtained by the redistributed compressive base stress, is the total base bending moment at the center of gravity, considering redistributed compressive base stress. Figure 1 contrasts two different interpretations of a foundation on Winkler springs: the classical linear-elastic model, and a more realistic, non-linear “compression-only” model requiring an optimization approach. In this context, Hetenyi’s [11] deflection expression is considered in defining the elastic baseline. While Hetényi’s linear solution provides the mathematical foundation, a direct application of this is insufficient for cases with significant uplift of foundation. In order to enforce a “compression-only” condition, it is necessary to make a modification, which leads to the crucial phenomenon of stress redistribution over the actual contact area.
Winkler’s spring approach [12] is one of the most common methods used to model the linear distribution of base stresses. According to the Winkler soil model, base stress in the foundation is calculated by multiplying the deflection values by the soil stiffness per unit foundation width, as shown below.
In Equation (1), considering a foundation with a fixed width , represents the vertical deflection per unit length, while denotes the bedding coefficient, which varies according to soil type. The deflection of a beam foundation under various loads and boundary conditions, and supported along its entire length by an elastic medium is defined by Hetényi [11] as below:
Equation (2), expressed by Hetényi [11], provides the vertical deflection at any point x along the elastic beam. Conceptually, the solution is a superposition of effects from four primary components: (1) the initial deflection () and rotation () at the beam’s origin, which are captured by the terms with functions and ; (2) the bending moment () and shear force () at = 0, represented by the terms and ; (3) the effect of any intermediate concentrated moments (); and (4) the effect of any intermediate concentrated vertical loads ().
The key parameters in this equation are defined as follows:
- : Initial values for subsidence, rotation, bending moment, and shear force at the beam’s origin ( = 0).
- , : The elastic modulus and moment of inertia of the beam, respectively, defining its flexural stiffness ().
- : A characteristic parameter of the system, defined as which relates the foundation stiffness to the beam stiffness.
- : Magnitudes of concentrated moments and loads applied along the beam.
- , : Distances from the origin to the point of application for each concentrated moment and load.
- to Shape functions, which are combinations of trigonometric and hyperbolic terms describing the damped wave-like deformation of the beam. These terms are given in Appendix A.
The soil stresses obtained by Equation (2) are calculated according to the springs’ working conditions in both tension and compression, and the equilibrium conditions are calculated accordingly. While tensile stress values may arise for high eccentricity cases, these are not physically meaningful as no stress exists on surfaces that are not in contact with the base. Therefore, these tensile values should be set to zero; however, this adjustment does not satisfy the equilibrium conditions between external forces and base stresses, leading to Equations (3)–(5).
Under certain loading conditions, a foundation can partially uplift, rendering the general stress formulation in Equation (2) invalid because soil cannot sustain remarkable tensile stress. In this case, integrating only the compressive stresses from the original formula would not balance the total external load () and moment (), thus violating the equilibrium conditions expressed in Equations (4) and (5). To resolve this and ensure equilibrium is satisfied, the compressive base stresses must be redistributed over the reduced contact area. Therefore, this study addresses the issue by proposing four correction factors to be applied to the primary components of Hetényi’s [11] classical deflection formulation, Equation (2). The choice of four factors directly corresponds to the four fundamental components of the solution to the fourth-order differential equation governing a beam on an elastic foundation. Specifically, these components relate to the effects of initial deflection (), initial rotation (), initial bending moment (), and initial shear force (), along with the effects of concentrated loads. To restore this equilibrium, the original formulation is modified by introducing four correction factors (). The modified expression for the redistributed compressive base stress is obtained as follows:
Equation (6) is the proposed formulation for the redistributed base stress. This equation adapts the structure of Hetényi’s classical deflection approach [11] for an elastic beam on the Winkler soil model [12] by incorporating the four dimensionless correction factors . Each factor scales a primary component of the original solution, allowing the meta-heuristic algorithm to systematically adjust the stress profile until it correctly balances the external loads and moments. Equation (6) must be determined to satisfy the equilibrium conditions described in Equations (3)–(5). Due to the non-linearity of stress redistribution, this determination is challenging. Previous methods [5,6] that assume linear stress distribution are ineffective in this context. Finding the best-fit coefficients under these non-linear constraints is fundamentally an optimization problem. Consequently, an optimization process is proposed to identify the most suitable correction factors, transforming the problem into the optimization model defined as follows:
In this model, the goal is to minimize the function representing the absolute relative differences between total force and moment values generated by redistributed compressive base stresses, ensuring they align with the total external force and moment.
3.2. Optimization Methods
To address the challenge of accurately determining stress distributions in continuous foundations with significant eccentricity, this study employs meta-heuristic optimization techniques, including Artificial Bee Colony (ABC), Biogeography-Based Optimization (BBO), and Tree Seed Algorithm (TSA). These methods are utilized to refine the correction factors essential for the mathematical model developed, aiming to enhance the precision of stress distribution predictions under complex, non-linear conditions.
3.2.1. Artificial Bee Colony (ABC) Method
The Artificial Bee Colony (ABC) method, introduced by Karaboga [14], emulates the foraging behavior of honeybee colonies to optimize solutions. In this approach, food sources represent potential solutions, and the amount of nectar corresponds to the fitness value of these solutions. Bees are categorized into explorer and observer bees. Explorer bees randomly search for new food sources, while observer bees remain in the hive, selecting food sources based on information communicated through the waggle dance, a mechanism that conveys the quality of the discovered food sources.
The algorithm initializes with random food sources, each associated with a worker and an observer bee. The search space represents the environment around the hive where the bees search for food. The algorithm proceeds with the exploration and exploitation of food sources by the bees until a stopping criterion, typically the maximum number of iterations, is met.
The process involves the following key steps:
- Initialization: Food sources are randomly generated within the defined search space, and fitness values are calculated.
- Worker Bee Phase: Each worker bee explores neighboring food sources and updates its position if a better solution is found.
- Observer Bee Phase: Observer bees select food sources based on their fitness values, with a preference for higher-quality sources, determined probabilistically.
- Scout Bee Phase: If a food source is abandoned, the corresponding worker bee becomes a scout and searches for a new food source.
- Termination: The best solution is retained in memory, and the process repeats until the stopping criterion is satisfied.
The ABC algorithm’s primary advantage lies in its balance between exploration and exploitation, making it suitable for complex optimization problems.
3.2.2. Biogeography-Based Optimization (BBO)
The Biogeography-Based Optimization (BBO) method, developed by Simon [23], is inspired by the distribution and migration of species across different habitats. Each potential solution or “habitat” is characterized by a Habitat Suitability Index (HSI), which reflects the quality of the solution. Migration and mutation processes are applied to modify these solutions.
In the BBO algorithm, solutions share information based on their emigration and immigration rates, which depend on the habitat’s HSI. Higher-quality solutions (those with a high HSI) tend to share their attributes with other solutions, improving the overall quality of the population. Additionally, mutation introduces diversity by randomly altering some of the solution’s parameters.
The BBO algorithm follows these steps:
- Initialization: Habitats (solutions) are randomly initialized, and their suitability is evaluated.
- Migration: Solutions migrate based on their emigration and immigration rates, updating their parameters accordingly.
- Mutation: Random mutations are applied to maintain diversity in the population.
- Selection: The best solutions are retained, and the process is repeated until the termination criterion is met.
3.2.3. Tree Seed Algorithm (TSA)
The Tree Seed Algorithm (TSA), introduced by Kiran [31], is inspired by the natural process of tree seed dispersal. In this method, trees (solutions) scatter seeds (new solutions) based on a search tendency coefficient, which determines the balance between exploration and exploitation.
Seeds are generated using two equations, with the choice depending on the search tendency parameter. If a seed outperforms the tree that generated it, the seed replaces the tree, leading to improved solutions over iterations. The algorithm continues until the stopping criterion is met, usually defined by the maximum number of iterations.
The TSA can be summarized as follows:
- Initialization: Random trees are generated in the optimization problem’s search space.
- Seed Generation: Seeds are scattered based on the search tendency coefficient, which controls the degree of exploration and exploitation.
- Selection: If a seed performs better than its parent tree, it replaces the tree.
- Termination: The process repeats until the stopping criterion is reached, and the best solution is identified.
3.3. Optimization Implementation and Parameter Determination
The meta-heuristic algorithms (ABC, BBO, and TSA) are implemented in the MATLAB R2024b [46] environment. To ensure a fair and robust comparison, a sensitivity analysis is conducted to determine the optimal parameters for each algorithm. This analysis consists of two main phases: first, establishing an appropriate search space for the correction factors, and second, fine-tuning the optimization algorithm control parameters. This tuning process is repeated for each example and is efficiently managed using a custom-developed MATLAB tool [55,56] created for this study. The results of applying these tuned algorithms to comprehensive cases are presented in Section 4. The detailed methodology for the parameter tuning itself is provided in Appendix B (Determination of Search Space for Correction Factors) and Appendix C (Algorithm Control Parameter Tuning).
3.4. Implementation Workflow of the Proposed Model
To clarify how the proposed optimization model can be practically applied to solve for the base stress distribution in a continuous foundation with large eccentricity, the following step-by-step computational workflow is provided:
- Define Problem Inputs:
- Foundation properties: Length (ℓ), flexural stiffness (), and width ().
- Soil properties: Bedding coefficient ().
- External loads: Total vertical load (ΣF) and total overturning moment (ΣM) at the foundation’s center of gravity. Calculate the initial eccentricity ().
- Establish the Optimization Framework:
- Objective function: Define the goal, which is to minimize the equilibrium error (Err) as formulated in Equation (7). This function quantifies the difference between external loads and the internal stresses from the foundation base.
- Design variables: The four correction factors are the unknown variables that the optimization algorithm will solve for.
- Search space: Determine the upper and lower bounds for the design variables. This is performed using the dynamic eccentricity-dependent model. First, calculate the offset value κ using Equation (A2), then define the bounds [LB, UB] for each factor using Equations (A3) and (A4).
- Execute the Meta-Heuristic Optimization:
- Algorithm selection: Choose a suitable meta-heuristic algorithm. Based on the findings of this study, the Tree Seed Algorithm (TSA) is recommended for its superior accuracy and reliability.
- Parameter configuration: Set the control parameters for the chosen algorithm (e.g., population size, search tendency) as specified in Table A2.
- Run optimization: Execute the algorithm. The solver will iteratively search for the combination of through that minimizes the objective function (Err). The process terminates when a stopping criterion (e.g., maximum iterations or negligible error) is met.
- Calculate and Interpret the Final Results:
- Obtain optimal factors: The output of the optimization is the set of optimal correction factors .
- Determine corrected stress distribution: Substitute these optimal factors into the modified stress equation, Equation (6), to calculate the redistributed base stress profile, .
- Finalize the stress profile: As a final physical correction, set any remaining (negligible) tensile stress values in the profile to zero. The result is the final, physically realistic compressive stress distribution on the foundation. The very low Err value from the optimization confirms that this final distribution is in equilibrium with the external loads.
4. Findings and Discussion
This section presents the results of the stress distribution analysis conducted on continuous foundations. Initially, foundation cases are analyzed using the conventional linear approach. Then, the efficacy of the proposed optimization model in accurately determining the stress distribution in cases of large eccentricity is evaluated. To facilitate these calculations, a MATLAB [55]-based computational tool is developed for stress determination, with the source code available in the reference [56]. The results are verified by those of the Finite Element Method (FEM). For this purpose, linear (L) and non-linear (NL) analyses are performed with the SAP2000 V20 [13] structural analysis software, modeling the beam foundation using frame elements. In a standard linear analysis using SAP2000, spring elements exhibit both compression and tension behavior. However, to model the foundation’s compression-only response, a non-linear analysis case must be utilized. In addition, the classical analytical solution proposed by Hetényi [11] for solving a specific problem of an elastic beam deflection on Winkler soil is abbreviated as “CAS” in all figures and tables.
Before presenting the final stress distribution results, it is essential to establish robust parameters for our optimization model. The process for determining these parameters is detailed in the appendices and demonstrated through the two main cases in this section. Case 1 (Section 4.1) is used to illustrate the initial sensitivity analysis for a fixed eccentricity, which helps define an optimal baseline search space for the correction factors (detailed in Appendix B). Subsequently, Case 2 (Section 4.2) demonstrates the development of the dynamic, eccentricity-dependent model, which generalizes the search space for varying loads. The tuning of the specific meta-heuristic algorithm control parameters is also performed as part of this process (detailed in Appendix C). This preliminary analysis is performed to establish the optimal parameters for each algorithm prior to their evaluation in the main cases. The custom MATLAB tool [55,56] developed for this study efficiently manages these preparatory analyses.
4.1. Determination of Stress Distributions for a Continuous Foundation (Case 1)
4.1.1. Example 1: Continuous Foundation with Axial Loads
The example problem presented by Keskinel and Kumbasar [57] investigates a continuous beam with a length (ℓ) of 22 m, flexural stiffness (EI) of 1.89 × 106 t-m2, foundation width (b) of 1.73 m, and a soil bedding coefficient () of 4000 t/m3 (Figure 2). The foundation is subjected to the total external load () of 160 t and moment () of 640 t-m, resulting in eccentricity () of 4.0 m from the center of gravity. As presented in Appendix B.1, the search space for the correction factors using the fixed eccentricity method is determined as [0.995, 1.005].
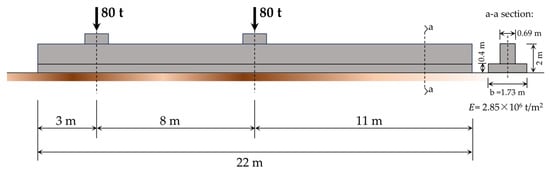
Figure 2.
Side view and section details for Case 1, Example 1.
In order to simulate the linear and non-linear soil–foundation interaction in SAP2000 [13], compression/tension and compression-only spring elements are utilized at 0.5 m intervals. Additionally, for use in a frame model, the dimensions of the cross-section and material properties are adjusted to align with a typical T-shaped beam foundation while maintaining the flexural stiffness (EI), as given in the example (Figure 2).
Initially, a verification check is performed to confirm that the foundation is operating under conditions of large eccentricity. The applied eccentricity value of 4.0 m exceeds the limit of the core region (ℓ/6 or 3.67 m). This indicates that part of the foundation will tend to lift, resulting in tensile stress in linear analysis and requiring non-linear stress redistribution. Then, a linear analysis is performed using CAS. This approach yields a solution in which tensile stresses appear. Simply ignoring these stresses in the design would result in a violation of the equilibrium conditions between the external loads and the total base stresses. In accordance with the findings of the linear analysis, the equilibrium imbalance resulting from the uncorrected stress distribution is presented quantitatively in Table 1. To correct this, the optimization models proposed in this study are applied. The ABC, BBO, and TSAs are used to find the correction factors () that minimize the equilibrium error defined in Equation (7). As shown in Table 1, a performance comparison is presented of the proposed optimization methods against both the linear analysis results of the CAS and FEM (L).

Table 1.
The optimized correction factors and the results for Example 1.
Err is the error value of the objective function defined in Equation (7), representing the total relative difference between the calculated internal forces/moments and the external loads. Suitable coefficient values are obtained using the computational tool [56] developed with ABC, BBO, and TSA optimization methods. The results in Table 1 demonstrate the effectiveness of the proposed optimization approach. All three meta-heuristic methods successfully converged to solutions that satisfy the equilibrium conditions, with error values below 0.025%. The total base force () and moment () obtained from all the non-linear (NL) analyses are almost the same as the total external load () of 160 t and the moment () of 640 t-m, respectively. The Tree Seed Algorithm (TSA) yielded the most precise result, with an error approaching zero.
Crucially, the results obtained from the proposed optimization models consistently align with those from the FEM (NL) analysis, providing an independent validation of the models. In contrast, the linear analysis results of CAS and FEM (L), which do not redistribute stress, show a significant equilibrium error. This error arises because simply removing the tensile region leaves a compressive stress distribution that does not balance the external loads. This comparison underscores the inadequacy of simplified linear assumptions and confirms the necessity of the proposed non-linear redistribution model for achieving an accurate and physically meaningful solution. The stress curves generated by the ABC, BBO, and TSA optimization methods are in good agreement with the results of FEM non-linear (NL) analysis (Figure 3), providing strong validation for the proposed optimization models.
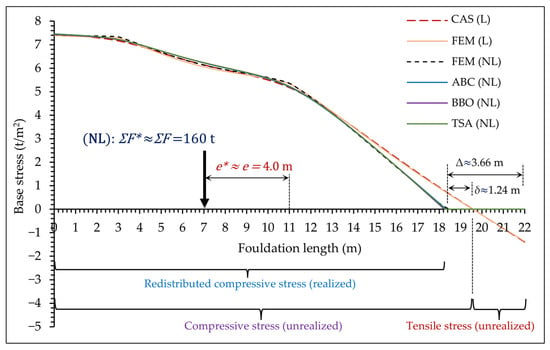
Figure 3.
Comparison of base stress distributions for Case 1, Example 1.
As seen in Figure 3, a significant finding of this study is the difference in the soil–foundation contact area between the linear and non-linear models. While the maximum stress values are comparable, the linear analyses predict a significantly longer contact length. In contrast, the non-linear methods accurately identify that the foundation lifts off the soil, resulting in a smaller contact area. This reduction in contact area is a critical consideration for design, as it more accurately represents the physical behavior and the concentration of load.
Figure 4 shows the detailed deformation shapes and the corresponding spring force distributions obtained from the FEM analyses. This clearly illustrates the uplift at the right end of the foundation and the resulting compressive stress field over the reduced contact length.
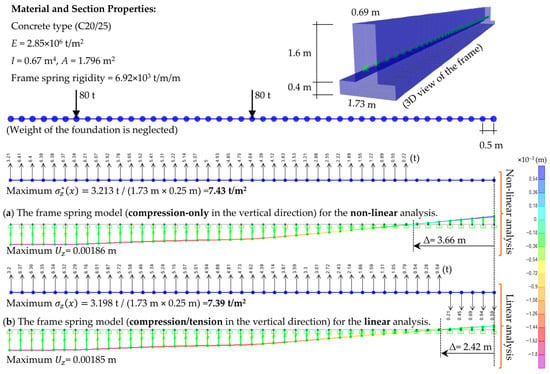
Figure 4.
Frame model: (a) compression only; (b) compression/tension for Case 1, Example 1.
The convergence histories for the ABC, BBO, and TSAs are presented in Figure 5. The Biogeography-Based Optimization (BBO) algorithm shows a strong initial convergence but tends to stagnate in later iterations. The Artificial Bee Colony (ABC) algorithm exhibits a more gradual but steady convergence rate in comparison. The Tree Seed Algorithm (TSA) demonstrates a balanced convergence behavior, effectively reducing the error throughout the optimization process and consistently achieving the most accurate solution. Notably, all three algorithms reached a stable solution plateau early in the process, typically within the first 250 iterations. This confirms that the maximum iteration limit of 1000 is sufficient for all methods to achieve convergence for this problem.
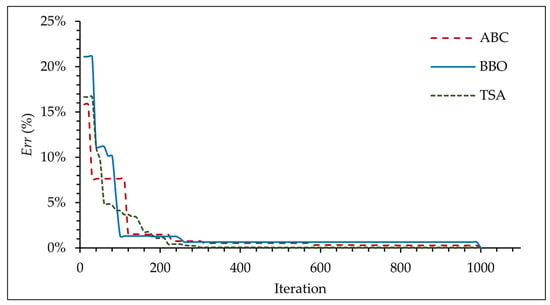
Figure 5.
Convergence histories of the optimization algorithms for Case 1, Example 1.
4.1.2. Example 2: Continuous Foundation with Axial Loads and Bending Moment
In the second example, the foundation parameters (ℓ, EI, b, and ) remain the same as in the first. The loading is modified to further test the proposed method. In addition to the existing loads, an external moment of 64 t-m is added at the center of gravity, based on the example by Keskinel and Kumbasar [57]. In this way, the foundation is subjected to the total external load () of 160 t and a moment () of 704 t-m, resulting in eccentricity () of 4.4 m from the center of gravity. The external force and moment loading conditions for this example are illustrated in Figure 6.
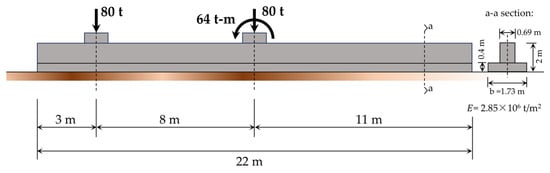
Figure 6.
Loading situation for Case 1, Example 2.
With an external load eccentricity of 4.4 m, the foundation’s critical core limit (ℓ/6 or 3.667 m) is exceeded, indicating that partial uplift will occur. As in the previous example, this condition requires a non-linear stress redistribution to achieve an accurate, equilibrium-compliant solution. The eccentricity (e = 4.4 m) is close to the value used for the initial tuning (e = 4.0 m). Therefore, the same fixed search space of [0.995, 1.005], as determined in Appendix B.1, is deemed appropriate and also utilized for this analysis to maintain consistency. Consistent with the first example, the results in Table 2 confirm the accuracy and reliability of the proposed optimization model. All three optimization methods produced solutions with equilibrium errors below 0.06%, successfully balancing the external loads (160 t and 704 t-m), and accurately calculating the applied eccentricity (4.4 m). Among the methods, TSA once again provided the solution with the lowest error value.

Table 2.
The optimized correction factors and the results for Example 2.
The optimized solutions are validated by the FEM (NL) using SAP2000 [13]. The significant output parameters, including resultant force and eccentricity, align closely with the FEM (NL) results. In contrast, the linear approaches, CAS and FEM (L), result in a significantly large equilibrium error of 8.44%. This significant discrepancy highlights the limitations of linear methodologies in accurately modeling the behavior of the foundation under conditions of large eccentricity. Linear methodologies give physically inconsistent results for internal forces and predict an overly optimistic soil–foundation contact area.
Figure 7 summarizes the results for Case 1, Example 2. Stress values confirm the findings from Table 2. The distributions predicted by the ABC, BBO, and TSA methods are virtually identical to the results from the benchmark non-linear FEM (NL) analysis, providing strong visual validation for the proposed model. Furthermore, the close agreement between CAS and the FEM (L) curves confirms the correct implementation of the linear models for comparison. The most significant insight from Figure 7 is the difference in the predicted soil–foundation contact area. While the maximum stress values are similar across the methods, the linear analyses predict a non-contact length (Δ) of approximately 2.98 m from the right end. In contrast, the non-linear solutions correctly capture the foundation uplift, resulting in a larger and more critical non-contact area of around 4.80 m in length. This discrepancy underscores a significant deficiency in linear models, as underestimating foundation uplift can lead to an unconservative assessment of the foundation’s behavior.
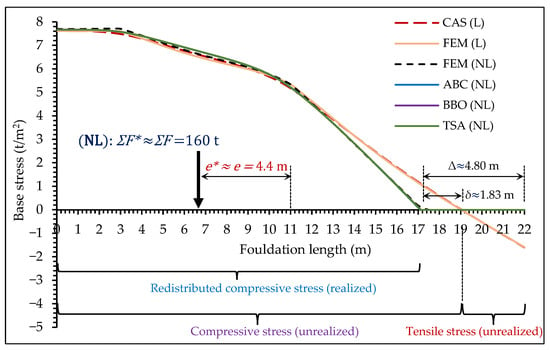
Figure 7.
Comparison of base stress distributions for Case 1, Example 2.
Additionally, detailed deformation profiles and the corresponding spring force distributions from the FEM analyses are presented in Figure 8.
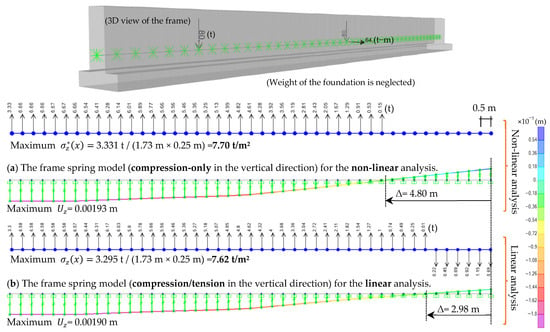
Figure 8.
Frame model: (a) compression only; (b) compression/tension for Case 1, Example 2.
The convergence histories for the second example are shown in Figure 9. The plot highlights distinct behaviors among the algorithms. All algorithms demonstrated efficient and stable convergence, reaching their final, low-error solutions within the first 200 iterations. The TSA presented the fastest convergence rate.
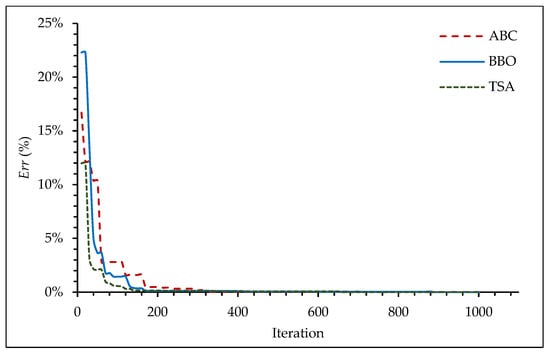
Figure 9.
Convergence histories of the optimization algorithms for Case 1, Example 2.
4.1.3. Numerical Comparison of Stress and Non-Contact Parameters
This section presents a numerical comparison of the major output parameters to provide a consolidated view of the findings. Table 3 summarizes the maximum base stress () and the soil–foundation non-contact length (Δ) for both examples across all evaluated methods. These include the reference value from the literature by Keskinel and Kumbasar [57], the linear analysis results of the CAS, the proposed non-linear optimization methods (ABC, BBO, TSA), and the linear FEM (L) and non-linear FEM (NL) results by SAP2000 [13] software. The Keskinel and Kumbasar value is derived using a classical influence-line chart method, which relies on manual table interpolation.

Table 3.
Maximum base stress () and non-contact length (Δ) values.
According to Table 3, there is strong agreement within the linear and non-linear groups. The CAS and FEM (L) results are very similar, confirming that the baseline models are consistent. Likewise, the solutions from the three optimization algorithms align closely with the FEM (NL) benchmark, with deviations in stress and contact length generally falling below 1%. This validates the accuracy of the proposed optimization work.
The most significant insight is the difference between the linear and non-linear analyses. In Example 2, the non-linear analysis predicts a maximum stress that is slightly higher (approximately 0.8%) than the linear solution. Moreover, it reveals a non-contact length that is over 8% of the total foundation length. This reduction in contact area, which concentrates the load on a smaller portion of the foundation, is a crucial design consideration that is completely missed by linear models and can lead to an unconservative design.
Finally, the table shows a discrepancy of approximately 5% between the value from Keskinel and Kumbasar [57] and the other linear solutions. This difference likely illustrates the potential for small inaccuracies inherent in older, manual methods that rely on chart interpolation for highly non-linear functions.
4.2. Parametric Study on the Effect of Eccentricity (Case 2)
An example is conducted to parametrically investigate the influence of external load eccentricity (e) on the foundation’s behavior. A foundation model with a length (ℓ) of 20 m, flexural stiffness (EI) of 1.9 × 106 t/m2, foundation width (b) of 2 m, and soil bedding coefficient () of 5000 t/m3 is analyzed under a constant vertical load of 100 t. As seen in Figure 10, the eccentricity varied across five levels: 0.20 ℓ, 0.25 ℓ, 0.30 ℓ, 0.35 ℓ, and 0.40 ℓ. Because eccentricity varies significantly in this case, it is crucial to use an adaptive search space for optimization. Therefore, as detailed in Appendix B.2, the bounds for the correction factors are determined for each eccentricity level using the dynamic, eccentricity-dependent model. Applying this model, the offset values (κ) for each of the five eccentricity situations are calculated using Equation (A2) as 0.00418, 0.01265, 0.03825, 0.115679, and 0.349837, respectively. The specific algorithm control parameters used for this analysis are detailed in Appendix C.
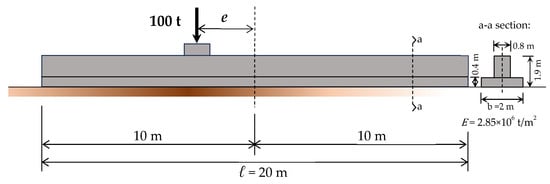
Figure 10.
Loading situation for different eccentricity conditions in a foundation.
The diagrams in Figure 11 show discrete spring forces, which are a modeling tool used in SAP2000 [13]. In reality, a foundation is supported by continuous base stress, and the transition between these concepts is necessary for design. To find the average base stress over that patch, the spring force is divided by the area it represents. Figure 11 also illustrates the critical differences between linear and non-linear models when analyzing a foundation under an eccentric load. A linear analysis can be misleading for foundations with significant eccentricity, as it fails to capture the uplift phenomenon and the resulting high-stress concentrations predicted by the more accurate non-linear model.
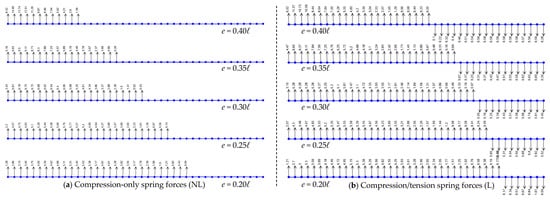
Figure 11.
The discrete spring forces for varying eccentricity levels in SAP2000 [13]: (a) non-linear analysis using compression-only springs; (b) linear analysis using compression/tension springs.
The zero-force point (contact point) is the exact location on the foundation where contact with the soil is no longer sustained. To the left of this point, the soil is in compression; to the right, there is a physical gap (zero stress). By definition, the base stress at the zero-force point is exactly zero. As observed in Figure 11a, as the load eccentricity increases, the zero-force point moves progressively to the left. This means that the total length of the foundation in contact with the soil becomes smaller. This has a critical consequence. The foundation must support the same total vertical load regardless of the contact area. When the contact area shrinks (as the zero-force point moves inward), the average and maximum compressive stresses on the remaining area must increase significantly to maintain equilibrium. This is why the arrows on the far left of Figure 11a become much larger as eccentricity increases. Consequently, the load being resisted by the smaller area results in a notable rise in stress.
The significant numerical results are presented in Table 4. These include the base stress at the loaded end (), the maximum base stress () along the entire beam, and the non-contact length (Δ) at the soil–foundation interface. Furthermore, Figure 12 shows the resulting base stress distributions for each eccentricity level, allowing for a comparison of all linear and non-linear methods.

Table 4.
Main results for the parametric example on eccentricity.
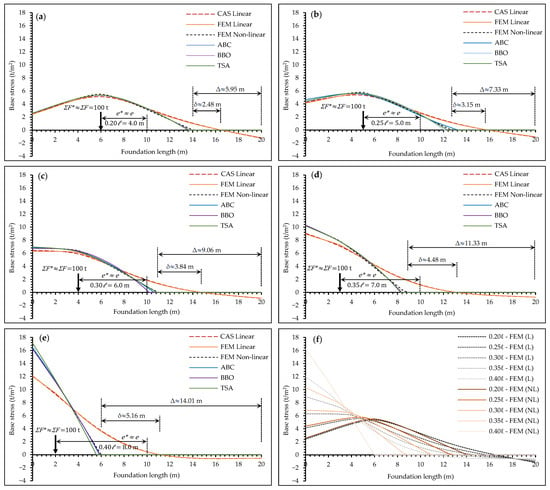
Figure 12.
Stress distribution for varying eccentricities: (a) 0.20 ℓ; (b) 0.25 ℓ; (c) 0.30 ℓ; (d) 0.35 ℓ; (e) 0.40 ℓ; (f) FEM.
The results from the parametric study demonstrate several important trends. First, there is high consistency within analytical groups. The proposed optimization methods (ABC, BBO, and TSA) produce results that are nearly identical to the FEM (NL) across all eccentricities. Likewise, CAS and FEM (L) results are in close agreement, which validates the correct implementation of both the linear and non-linear models.
As eccentricity increases, the soil–foundation non-contact length (Δ) expands across all models, with the effect being much more pronounced in non-linear analyses. The difference in non-contact length between the linear and non-linear approaches (δ) rises from about 12.4% at 0.20 ℓ to 25.8% at 0.40 ℓ. At the same time, the maximum stress () also increases with eccentricity, with the rate of increase being substantially higher in the non-linear models at larger eccentricities.
This highlights the most critical finding: the divergence between linear and non-linear models becomes more severe as eccentricity increases. At 0.20 ℓ, the difference in maximum stress between the two approaches is minimal. However, at the largest eccentricity of 0.40 ℓ, the non-linear analysis predicts a maximum stress that is over 30% greater than the linear prediction. This significant underestimation of stress by linear models, coupled with their overestimation of the contact area, underscores the importance of using a non-linear approach for the safe and accurate design of foundations under large eccentricity.
4.2.1. Reliability and Consistency of Optimization Methods
In order to assess the reliability and consistency of the meta-heuristic algorithms, each method was run ten times, with different random seeds for every eccentricity level. The statistical results of the final equilibrium error (Err%), including the standard deviation, mean, maximum, and minimum values, are presented in Table 5. This analysis helps evaluate how robust each algorithm is to the stochastic nature of its search process.

Table 5.
Statistical analysis of the equilibrium error (%) from ten independent runs.
As can be seen from the statistical results in Table 5, the optimization problem becomes more challenging, leading to a general increase in the mean error and standard deviation for all algorithms. However, clear performance differences emerge. The BBO algorithm consistently shows the highest mean error and a wider spread between its minimum and maximum results, indicating that it is the least reliable for this problem.
Both the ABC and TSA methods perform well, but TSA demonstrates superior consistency. At the most difficult situation (e = 0.40 ℓ), TSA not only achieves a significantly lower mean error (0.69%) compared to ABC (1.76%) and BBO (2.68%) but its standard deviation is also less than half that of the other methods. This indicates that TSA is not only more accurate on average but also more robust, providing consistently high-quality solutions regardless of the initial random seed. This makes it the most suitable algorithm among the three for this application.
4.2.2. Behaviors of Correction Factors
The behaviors of the four correction factors are analyzed as a function of eccentricity to provide insight into the model’s inner workings. The suitable ranges for correction factors are determined according to the “dynamic eccentricity-dependent model” explained (see Appendix B.2). Figure 13 shows the distribution of the optimal factor values found by each algorithm (ABC, BBO, and TSA) for the different eccentricity levels. It is important to note that stress distribution is highly sensitive to these factors, meaning even small adjustments can produce the correct equilibrium state.
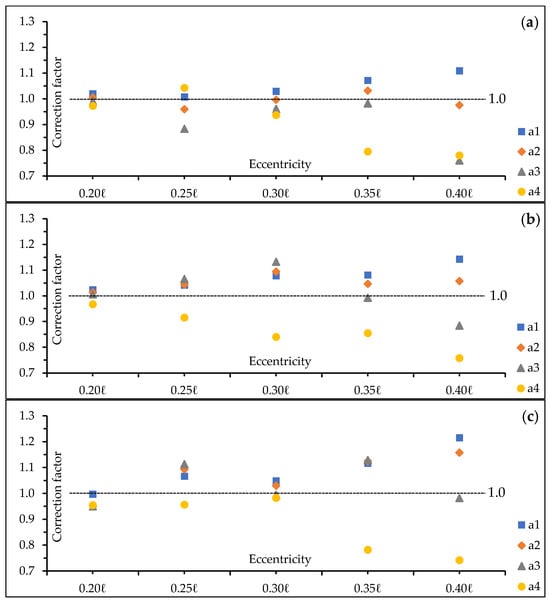
Figure 13.
Distribution of optimal correction factors (a1 to a4) as a function of eccentricity: (a) ABC; (b) BBO; and (c) TSA.
Examination of the graphs presented in Figure 13 yields several meaningful results. At lower eccentricities, the correction factors for all algorithms tend to cluster within a narrow range around the 1.0 value. As eccentricity increases, the spread between the factor values widens, indicating that more significant adjustments to the modified stress equation are necessary to handle the increased non-linearity.
More specifically, a clear relationship with eccentricity is visible for two of the factors. Across all algorithms, generally trends upward and trends downward as eccentricity increases from 0.20 ℓ to 0.40 ℓ. This suggests a systematic adjustment is being made to the terms associated with the initial deflection and the concentrated loads. In contrast, the a2 and a3 factors exhibit more fluctuating behavior without a simple monotonic trend, implying that their role in the correction is more complex and adaptive to the specific shape of the stress distribution at each step. This nuanced behavior, which was not apparent in the original analysis, indicates that while a single predictive formula for all four factors may be elusive, their adjustment by the optimization model is not random but follows discernible patterns to maintain equilibrium.
5. Conclusions
This study addressed the critical challenge of determining stress distribution in elastic continuous foundations under large eccentricities. The research introduced and validated a novel computational method that integrates meta-heuristic optimization with the Winkler soil model [12] to correct for non-physical tensile stresses and ensure force and moment equilibrium. By optimizing a set of four correction factors applied to Hetényi’s analytical solution [11], the developed model successfully produces a realistic and accurate representation of the foundation’s behavior, as validated against benchmark non-linear finite element analyses [13].
A principal finding is that conventional linear analysis, which ignores tensile stress redistribution, leads to significant and potentially unsafe design errors. This parametric study revealed that as eccentricity increases, the discrepancy between linear and non-linear models becomes severe. At the largest eccentricity tested (0.40 ℓ), the non-linear analysis predicted a maximum base stress over 30% higher and a soil–foundation contact area nearly 50% smaller than the linear model suggested. This demonstrates that simplified methods can dangerously underestimate peak stresses while overestimating the effective bearing area, highlighting the importance of a non-linear approach for ensuring structural safety.
The methodological contribution of this work lies in demonstrating the suitability of meta-heuristic optimization for this complex structural mechanics problem. The successful application of the Artificial Bee Colony (ABC), Biogeography-Based Optimization (BBO), and Tree Seed Algorithm (TSA) validates their use as robust global search tools. While all three algorithms converged to viable solutions, a statistical analysis of repeated runs showed that the TSA consistently exhibited superior performance, achieving the lowest mean error and the smallest standard deviation, proving it to be the most accurate and reliable method for this application.
Despite its success, this study has limitations that open avenues for future research. The correction factors are determined on a case-by-case basis through optimization. While the analysis revealed clear trends in some factors, a comprehensive correlation study or the application of machine learning techniques could lead to a generalized predictive model, eliminating the need for optimization in every case. The examples, while realistic, did not include foundation self-weight or extreme dynamic moments from seismic events; future studies should test the method on real-world design problems. Furthermore, the model could be extended from a one-dimensional beam to a two-dimensional plate to analyze more complex raft foundations, which are common in structures with large overturning moments. Finally, the chosen algorithms could be benchmarked against newer, state-of-the-art optimizers to explore potential improvements in efficiency.
In conclusion, this research presents novel and practical computational work for a challenging problem in foundation engineering. It not only advances the theoretical understanding of stress redistribution under large eccentricity but also provides a valuable and validated tool that can help engineers design safer and more efficient continuous foundations. Commonly employed Finite Element Method (FEM) software can address the contact non-linearity using built-in iterative procedures, but this research proposes a novel and distinct alternative. Instead of relying on numerical FEM solvers, we introduce a semi-analytical framework that integrates powerful meta-heuristic optimization techniques. The introduced method offers several advantages: it provides a transparent, equation-based solution, it offers a computationally efficient alternative for this specific problem, and the resulting correction factors provide direct physical insight into how the classical theory should be modified to restore equilibrium.
Author Contributions
Conceptualization, methodology, software, validation, writing—original draft preparation, writing—review and editing, S.T., İ.A. and E.E.; supervision, project administration, İ.A. and E.E.; data curation, S.T. and İ.A.; visualization, S.T. and E.E.; formal analysis, investigation, S.T.; resources, funding acquisition, İ.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request. The MATLAB (The Mathworks Inc., Natick, MA, USA, 2024) code required to replicate results is available at [56].
Acknowledgments
The authors gratefully acknowledge the support provided by The Scientific and Technological Research Council of Turkey (TUBITAK) and The Scientific Research Projects Units of Akdeniz University. During the preparation of this manuscript, the authors used AI tools (Google AI Studio-Gemini 2.5 Pro; ChatGPT-5; DeepL-25.9.1) for the purpose of eliminating grammatical errors and enhancing the language quality, clarity, and overall readability of the text, ensuring it meets high standards of understandability. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations and symbols are used in this manuscript:
| Width | Superstructural moment | ||
| Height | Superstructural axial force | ||
| Thickness | Initial deflection value | ||
| Eccentricity | Initial rotation value | ||
| Foundation length | Initial bending moment value | ||
| Elastic modulus | Initial shear force value | ||
| Flexural stiffness | Characteristics of the system | ||
| Bedding coefficient | Relative stiffness | ||
| κ | Offset for the correction factors | Δ | Non-contact length of the base |
| Base stress | Vertical deflection | ||
| Redistributed base stress | Coordinate value along the length | ||
| ABC | Artificial Bee Colony | BBO | Biogeography-Based Optimization |
| TSA | Tree Seed Algorithm | FEM | Finite Element Method |
| L | Linear | NL | Non-linear |
| CAS | Classical Analytical Solution by Hetényi [11] for elastic beam deflection on Winkler soil model [12] | ||
| Distance from the initial point to the point of application of the external moment | |||
| Distance from the initial point to the point of application of the external load | |||
Appendix A. Shape Functions of Classical Analytical Solution
Appendix B. Determination of Search Space for Correction Factors
A critical step in the optimization setup is defining the search space for the correction factors (). While a wide search space can find solutions with low mathematical errors, it does not guarantee a physically plausible stress distribution. Therefore, a detailed investigation is conducted where 16 different search intervals are tested using the TSA. This process is described in two stages, depending on whether the eccentricity values are fixed or dynamic.
Appendix B.1. Initial Sensitivity Analysis for a Fixed Eccentricity
The considered eccentricity value for the tuning of correction factors is = 4 m (≈0.18 ℓ). At this point, the ranges of solutions for the values are gradually narrowed down, and the boundary values that produce consistent results in line with the benchmark FEM (NL) are identified. The results, summarized in Table A1 and illustrated in Figure A1, are evaluated based on both the equilibrium error (Err) and the resulting stress profile, validated against the non-linear FEM analysis. Figure A1 also presents the base stress curve provided by Hetényi’s [11] linear approach. The main finding is that while wide intervals like [0.001, 5] produce low error, they result in stress distributions and soil–foundation contact lengths that are inconsistent with the FEM (NL) results. In contrast, as the search space narrowed around a central value of 1.0, the solutions demonstrated increasing consistency with this benchmark analysis. The optimal balance is achieved with the search space [0.995, 1.005]. This interval not only resulted in the lowest error (0.00008%) but, more importantly, produced a stress distribution that most closely matched the behavior predicted by the FEM (NL). Therefore, this search space is adopted for all subsequent analyses.

Table A1.
Sensitivity analysis for the search space bounds of correction factors ().
Table A1.
Sensitivity analysis for the search space bounds of correction factors ().
| Upper Bound (UB) | Lower Bound (LB) | Search Space | Error (Err) (%) | Contact Length (m) | Δ (m) | (t/m2) | (t/m2) |
|---|---|---|---|---|---|---|---|
| 1.0000 | −1.0000 | [−1, 1] | 0.01981 | 14.34 | 7.66 | 4.35 | 8.39 |
| 5.0000 | 0.0010 | [0.001, 5] | 0.00505 | 13.78 | 8.22 | 3.39 | 9.20 |
| 2.0000 | 0.0001 | [0.0001, 2] | 0.00110 | 13.81 | 8.19 | 3.43 | 9.16 |
| 1.5000 | 0.5000 | [0.5, 1.5] | 0.00165 | 14.01 | 7.99 | 3.80 | 8.86 |
| 1.4000 | 0.6000 | [0.6, 1.4] | 0.01032 | 14.37 | 7.63 | 4.40 | 8.35 |
| 1.3000 | 0.7000 | [0.7, 1.3] | 0.02149 | 14.82 | 7.18 | 5.04 | 7.81 |
| 1.2000 | 0.8000 | [0.8, 1.2] | 0.00245 | 15.42 | 6.58 | 5.74 | 7.22 |
| 1.1500 | 0.8500 | [0.85, 1.15] | 0.00112 | 15.82 | 6.18 | 6.13 | 6.92 |
| 1.1200 | 0.8800 | [0.88, 1.12] | 0.00086 | 16.12 | 5.88 | 6.38 | 6.84 |
| 1.1100 | 0.8900 | [0.89, 1.11] | 0.00223 | 16.22 | 5.78 | 6.45 | 6.85 |
| 1.1000 | 0.9000 | [0.9, 1.1] | 0.00258 | 17.47 | 4.53 | 7.17 | 7.18 |
| 1.0500 | 0.9500 | [0.95, 1.05] | 0.00570 | 18.29 | 3.71 | 7.45 | 7.45 |
| 1.0100 | 0.9900 | [0.99, 1.01] | 0.00168 | 18.07 | 3.93 | 7.39 | 7.39 |
| 1.0050 | 0.9950 | [0.995, 1.005] | 0.00008 | 18.37 | 3.63 | 7.44 | 7.44 |
| 1.0010 | 0.9990 | [0.999, 1.001] | 0.11631 | 18.36 | 3.64 | 7.46 | 7.46 |
| 1.0000 | 1.0000 | [1, 1] | 19.2507 | 19.58 | 2.42 | 7.44 | 7.44 |
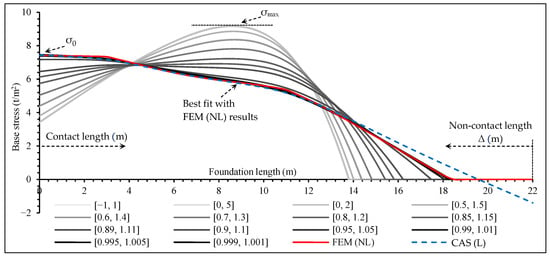
Figure A1.
Comparison of soil stress distributions obtained using different search space bounds.
Appendix B.2. Development of a Dynamic Eccentricity-Dependent Model
While the initial analysis confirms that a narrow and symmetrical range is the correct approximation, it raises the question of whether there is a single, constant range for all eccentricities. In order to address this, the investigation is extended using results from the parametric study detailed in Section 4.2. In the case considered, the optimization process is performed for five distinct eccentricity levels (from 0.20 ℓ to 0.40 ℓ), and the optimal search space, defined as [1−κ, 1+κ], is determined for each eccentric situation. To provide data for this search, an initial sensitivity analysis is performed separately for each eccentricity situation, as explained above. The results showed a strong and clear correlation: as eccentricity (e) increases, the optimal search space width represented by the offset value (κ) must also increase. To generalize this finding into a predictive tool, an exponential regression analysis is performed. This yielded a mathematical model to calculate the ideal offset for any given eccentricity in Equation (A2):
Therefore, instead of adopting a single fixed range, this study employs a dynamic eccentricity-dependent search space. For any given analysis with eccentricity, the optimal bounds [LB, UB] for the correction factors are calculated using Equations (A3) and (A4):
Appendix C. Algorithm Control Parameter Tuning
After defining the search space, the significant control parameters for each meta-heuristic algorithm are tuned to optimize performance. The selected parameters for comparative studies are summarized in Table A2. These parameters, tuned using the representative ‘Case 1, Example 1’, are found to be robust and effective for all subsequent analyses presented in this study. This is because the underlying structure of the optimization problem—four design variables, an unconstrained search space, and a single objective function—remains consistent across all cases, even as the search space boundaries and loading conditions vary. The consistent and high-quality performance of the algorithms in all examples, as detailed in the Results Section, validates the suitability of these parameters.

Table A2.
Summary of optimized control parameters used for the algorithms.
Table A2.
Summary of optimized control parameters used for the algorithms.
| Algorithm | Parameter | Notation | Selected Value |
|---|---|---|---|
| ABC | Population size | NFS | 50 |
| Limit | Limit | 50 | |
| BBO | Population size | NH | 100 |
| Mutation probability | MP | 0.01 | |
| TSA | Population size | NT | 30 |
| Search tendency | ST | 0.5 |
In Table A2, the Number of Food Sources (NFS) and the “limit” parameter are tuned for the ABC algorithm. A combination of NFS (50) and limit (50) is selected to provide the most robust solutions. For the BBO algorithm, the Number of Habitats (NH) and Mutation Probability (MP) are tested. Values of NH (100) and MP (0.01) are chosen as the best balance solution accuracy with computational cost. For the TSA, after tuning the Number of Trees (NT) and Search Tendency (ST), the combination of NT (30) and ST (0.5) is adopted as it yielded the most precise results. For all algorithms, the optimization process is terminated after a maximum of 1000 iterations or if the error function’s value remains negligible over 50 consecutive generations.
References
- Bowles, J.E. Foundation Analysis and Design, 5th ed.; The McGraw-Hill Companies, Inc.: Singapore, 1997; ISBN 0-07-118844-4. [Google Scholar]
- Das, B.M.; Sivakugan, N. Principal of Foundation Engineering, 9th ed.; Cengage Learning: Boston, MA, USA, 2018; ISBN 0357158725. [Google Scholar]
- Tabsh, S.W.; Raouf Al-Shawa, A. Effect of Spread Footing Flexibility on Structural Response. Pract. Period. Struct. Des. Constr. 2005, 10, 109–114. [Google Scholar] [CrossRef]
- Loukidis, D.; Tamiolakis, G.P. Spatial Distribution of Winkler Spring Stiffness for Rectangular Mat Foundation Analysis. Eng. Struct. 2017, 153, 443–459. [Google Scholar] [CrossRef]
- Aydoğdu, İ. New Iterative Method to Calculate Base Stress of Footings under Biaxial Bending. Int. J. Eng. Appl. Sci. 2016, 8, 40. [Google Scholar] [CrossRef][Green Version]
- Özmen, G. Eğik Eğilme Etkisi Altındaki Dikdörtgen Tekil Temellerde Taban Gerilmelerinin Hesabı. İMO Tek. Dergi 2011, 22, 5659–5674. (In Turkish) [Google Scholar][Green Version]
- Bellos, J.; Bakas, N. Complete Analytical Solution for Linear Soil Pressure Distribution under Rigid Rectangular Spread Footings. Int. J. Geomech. 2017, 17, 04017005. [Google Scholar] [CrossRef]
- Gan, X.; Liu, N.; Bezuijen, A.; Gong, X. Random Responses of Shield Tunnel to New Tunnel Undercrossing Considering Spatial Variability of Soil Elastic Modulus. Appl. Sci. 2024, 14, 3949. [Google Scholar] [CrossRef]
- Lu, Y.; He, J.; Jing, Y.; Chen, X. A Simplified Mechanical Model and Analysis for the Settlement Deformation of Buried Pipelines Caused by Open-Cut Excavation. Appl. Sci. 2023, 13, 10356. [Google Scholar] [CrossRef]
- Muhammad, B.A.; Muhammad, A.J.; Muhammad, A.; Duhee, P. Development of Simulation Based P-multipliers for Laterally Loaded Pile Groups in Granular Soil Using 3D Nonlinear Finite Element Model. Appl. Sci. 2021, 11, 26. [Google Scholar] [CrossRef]
- Hetényi, M. Beams on Elastic Foundation: Theory with Applications in the Fields of Civil and Mechanical Engineering; University of Michigan Press: Ann Arbor, MI, USA, 1946; Volume 16. [Google Scholar]
- Winkler, E. Die Lehre von der Elastizität und Festigkeit; Dominicius: Prague, Czech Republic, 1868. [Google Scholar]
- SAP2000® Version 20 Integrated Software for Structural Analysis and Design; Computers and Structures, Inc.: Walnut Creek, CA, USA; New York, NY, USA, 2017.
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report TR06; Erciyes University: Kayseri, Turkey, 2005. [Google Scholar]
- Karaboga, D.; Basturk, B. A Powerful and Efficient Algorithm for Numerical Function Optimization: Artificial Bee Colony (ABC) Algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the Performance of Artificial Bee Colony (ABC) Algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A Comparative Study of Artificial Bee Colony Algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Zhu, G.; Kwong, S. Gbest-Guided Artificial Bee Colony Algorithm for Numerical Function Optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
- Ding, Z.H.; Huang, M.; Lu, Z.R. Structural Damage Detection Using Artificial Bee Colony Algorithm with Hybrid Search Strategy. Swarm Evol. Comput. 2016, 28, 1–13. [Google Scholar] [CrossRef]
- Panniem, A.; Puphasuk, P. A Modified Artificial Bee Colony Algorithm with Firefly Algorithm Strategy for Continuous Optimization Problems. J. Appl. Math. 2018, 2018, 1237823. [Google Scholar] [CrossRef]
- Du, C.; Zhao, W.; Jiang, S.; Deng, X. Dynamic XFEM-Based Detection of Multiple Flaws Using an Improved Artificial Bee Colony Algorithm. Comput. Methods Appl. Mech. Eng. 2020, 365, 112995. [Google Scholar] [CrossRef]
- Saplıoglu, K.; Senel, F.A.; Topcu, F. Yapay Arı Kolonisi Ile Hazne Kapasitesinin Optimizasyonu: Köprüçay Örneği. Harran Univ. J. Eng. 2017, 2, 101–108. (In Turkish) [Google Scholar]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Simon, D.; Ergezer, M.; Du, D. Population Distributions in Biogeography-Based Optimization Algorithms with Elitism. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 991–996. [Google Scholar]
- Feng, Q.; Liu, S.; Wu, Q.; Tang, G.; Zhang, H.; Chen, H. Modified Biogeography-Based Optimization with Local Search Mechanism. J. Appl. Math. 2013, 2013, 960524. [Google Scholar] [CrossRef]
- Topbas, B.; Hanbay, D.; Yeroglu, C. Separation of Fire Images with Biogeography-Based Optimization. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; pp. 1–5. [Google Scholar]
- Dong, F.; Liu, D.; Wu, J.; Cen, B.; Wang, H.; Song, C.; Ke, L. Design of SVC Controller Based on Improved Biogeography-Based Optimization Algorithm. J. Appl. Math. 2014, 2014, 939326. [Google Scholar] [CrossRef]
- Hadidi, A.; Nazari, A. Design and Economic Optimization of Shell-and-Tube Heat Exchangers Using Biogeography-Based (BBO) Algorithm. Appl. Therm. Eng. 2013, 51, 1263–1272. [Google Scholar] [CrossRef]
- Çınar, A.C.; Kıran, M.S. A parallel implementation of tree-seed algorithm on CUDA-supported graphical processing unit. J. Fac. Eng. Archit. Gazi Univ. 2018, 33, 1397–1409. [Google Scholar] [CrossRef]
- Babalik, A.; Cinar, A.C.; Kiran, M.S. A Modification of Tree-Seed Algorithm Using Deb’s Rules for Constrained Optimization. Appl. Soft Comput. 2018, 63, 289–305. [Google Scholar] [CrossRef]
- Kiran, M.S. TSA: Tree-Seed Algorithm for Continuous Optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]
- Aslan, M.; Beskirli, M.; Kodaz, H.; Kıran, M.S. An Improved Tree Seed Algorithm for Optimization Problems. Int. J. Mach. Learn. Comput. 2018, 8, 20–25. [Google Scholar] [CrossRef]
- Kıran, M.S. An Implementation of Tree-Seed Algorithm (TSA) for Constrained Optimization. In Proceedings of the Intelligent and Evolutionary Systems, the 19th Asia Pacific Symposium, IES 2015, Bangkok, Thailand, 22–25 November 2015; pp. 189–197. [Google Scholar]
- Köseoğlu, S. Temeller: Statiği ve Konstruksiyonu, 3rd ed.; Şahsi Yayınlar Press: İstanbul, Turkey, 1987; ISBN 6055230313. (In Turkish) [Google Scholar]
- Algin, H.M. Practical Formula for Dimensioning a Rectangular Footing. Eng. Struct. 2007, 29, 1128–1134. [Google Scholar] [CrossRef]
- Algin, H.M. Interlock Mechanism of Concrete Block Pavements. J. Transp. Eng. 2007, 133, 318–326. [Google Scholar] [CrossRef]
- Moreno-Landeros, V.M.; Luévanos-Rojas, A.; Santiago-Hurtado, G.; López-León, L.D.; Diaz-Gurrola, E.R. Optimal Area for a Rectangular Isolated Footing with an Eccentric Column and Partial Ground Compression. Appl. Sci. 2024, 14, 6453. [Google Scholar] [CrossRef]
- Machalová, J.; Netuka, H. Solution of Contact Problems for Nonlinear Gao Beam and Obstacle. J. Appl. Math. 2015, 2015, 420649. [Google Scholar] [CrossRef]
- Limkatanyu, S.; Prachasaree, W.; Damrongwiriyanupap, N.; Kwon, M.; Jung, W. Exact Stiffness for Beams on Kerr-Type Foundation: The Virtual Force Approach. J. Appl. Math. 2013, 2013, 626287. [Google Scholar] [CrossRef]
- Moffitt, C.J. Footing Soil Pressure from Biaxial Loading. Civil. Eng. J. 2019, 5, 2423–2440. [Google Scholar] [CrossRef]
- Adrian, I. Pressures Distribution for Eccentrically Loaded Rectangular Footings on Elastic Soils. In Proceedings of the 2010 International Conference on Mathematical Models for Engineering Science (MMES’10), Tenerife, Spain, 30 November–2 December 2010; pp. 213–216. [Google Scholar]
- Yu, L.; Zhang, D.; Fang, Q.; Li, Y.; Wang, G.; Cao, L. Analytical Prediction of Strip Foundation Building Response to Shallow Tunneling Considering the Tunneling Process. Appl. Sci. 2022, 12, 4656. [Google Scholar] [CrossRef]
- Zhen, B.; Xu, C.; Ouyang, L. Physics-Informed Neural Networks-Based Wide-Range Parameter Displacement Inference for Euler–Bernoulli Beams on Foundations under a Moving Load Using Sparse Local Measurements. Appl. Sci. 2025, 15, 6213. [Google Scholar] [CrossRef]
- Varga, R.; Žlender, B.; Jelušič, P. Optimization of Embedded Retaining Walls under the Effects of Groundwater Seepage Using a Reliability-Based and Partial Factor Design Approach. Appl. Sci. 2024, 14, 11135. [Google Scholar] [CrossRef]
- Dong, Y.; Yang, J.; Qin, Y. Prediction of Optimal Design Parameters for Reinforced Soil Embankments with Wrapped Faces Using a GA–BP Neural Network. Appl. Sci. 2024, 14, 6910. [Google Scholar] [CrossRef]
- Li, B.; You, Z.; Ni, K.; Wang, Y. Prediction of Soil Compaction Parameters Using Machine Learning Models. Appl. Sci. 2024, 14, 2716. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Iraji, A.; Majdi, A.; Keawsawasvong, S.; Nehdi, M.L. Adaptive Salp Swarm Algorithm for Optimization of Geotechnical Structures. Appl. Sci. 2022, 12, 6749. [Google Scholar] [CrossRef]
- Moayedi, H.; Bui, D.T.; Ngo, P.T.T. Neural Computing Improvement Using Four Metaheuristic Optimizers in Bearing Capacity Analysis of Footings Settled on Two-Layer Soils. Appl. Sci. 2019, 9, 5264. [Google Scholar] [CrossRef]
- Jing, H. Application of Improved K-Means Algorithm in Collaborative Recommendation System. J. Appl. Math. 2022, 2022, 2213173. [Google Scholar] [CrossRef]
- Çavuş, V.; Tuncer, A. İnsansız Hava Araçları Için Yapay Arı Kolonisi Algoritması Kullanarak. Karaelmas Sci. Eng. J. 2017, 7, 259–265. (In Turkish) [Google Scholar]
- Öztürk, H.T. Cost Optimum Design of Spread Footing under Uniaxial Combined Bending According to TS500 via Various Metaheuristic Algorithms. Pamukkale Univ. J. Eng. Sci. 2018, 24, 1030–1036. [Google Scholar] [CrossRef]
- Saraçoğlu, B.; Güvenç, U.; Dursun, M.; Poyraz, G.; Duman, S. Biyocağrafya Tabanlı Optimizasyon Metodu Kullanarak Asenkron Motor Parametre Tahmini. J. Adv. Technol. Sci. 2013, 2, 46–54. (In Turkish) [Google Scholar]
- Carbas, S.; Tunca, O. Numerical Design Optimization of Real Size Complex Steel Space Frame Structures Using a Novel Adaptive Cuckoo Search Method. Int. J. Numer. Methods Eng. 2024, 125, e7386. [Google Scholar] [CrossRef]
- Sharafati, A.; Haghbin, M.; Asadollah, S.B.H.S.; Tiwari, N.K.; Al-Ansari, N.; Yaseen, Z.M. Scouring Depth Assessment Downstream of Weirs Using Hybrid Intelligence Models. Appl. Sci. 2020, 10, 3714. [Google Scholar] [CrossRef]
- MATLAB (R2024b) Software, The MathWorks Inc.: Natick, MA, USA, 2024.
- Turan, S. MATLAB Code for Det. of Base Stress Distribution in E_C_F (2.0.0). Available online: https://www.mathworks.com/matlabcentral/fileexchange/176858-matlab-code-of-det-of-base-stress-distribution-in-e_c_f (accessed on 15 August 2025).
- Keskinel, F.; Kumbasar, N. Sürekli Temeller ve Dönel Kabuklar: Sonlu Kiriş Tesir Çizgileri İle Çözüm; İstanbul Technical University Press: İstanbul, Turkey, 1967. (In Turkish) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).