On Mathematical Models Based on Delay Differential Equations in Epidemiology

Abstract

This paper examines solutions to mathematical models based on functional-differential equations, which have applications in immunology. This new approach allows us to study discontinuous solutions that more accurately depict real-world phenomena. It also enables us to exploit the information contained in the initial function. We discuss immunology models by generalizing existing impulsive delay differential equation models to the proposed form. The new phase space introduced here enables a unified approach to continuous and impulsive solutions that were previously studied, as well as the development of new properties that depend on the initial function. To illustrate our work, we present extensions of current immunological models and demonstrate some applications in fields beyond immunology. This paper focuses on establishing the theoretical basis for modifying models based on delayed differential equations, which are not limited to immunology. It also provides some examples.

1. Introduction

As in other fields of applied science, mathematical models in epidemiology are developed to find solutions that align with observations. For example, changes have been introduced to dynamic models based on differential equations to derive bounded solutions or equilibrium points in systems. This may introduce nonlinearity into the equations. Additionally, delays between a phenomenon and its effect on the model solution (or the actual phenomenon) and oscillating processes are sometimes observed. These naturally lead to delay differential equations (or, more generally, functional differential equations). These equations require consideration of the initial conditions and the functions describing the past states of the modeled processes (initial functions).

The version of the model adopted also affects certain properties of solutions. To change these properties, the model itself must be altered. Current models described by differential equations with delay demonstrate this concept by showing how to obtain continuous solutions regardless of the initial function, even when it is discontinuous. Any expected discontinuities are described by special conditions in the form of difference equations—equations with impulses. However, this results in the loss of information stored in the initial function, and the discontinuities are described as predetermined moments in time, or state-dependent fixed moments.

Note that initial functions are sometimes described as being responsible only for the future dynamics of the system, and not for its past state, for $t\in [-\tau ,0]$. Consider the abstract form of the delay differential equation:

$$x^{\prime }\left(t\right)=f(t,x(t-\tau )),x\left(s\right)=\psi \left(s\right)\mathrm{for} s\in [-\tau ,0]$$

for $t\in [0,T]$. However, the solutions are functions defined on the interval $[-\tau ,T]$, and the values of the solutions in the interval $[0,\tau ]$ are identified with the values of the initial function.

Are these approaches to understanding the initial function contradictory? In this paper, we will demonstrate that they are not. Furthermore, we will incorporate impulsive differential equations into a new model that unifies continuous and discontinuous solutions. Any information about the system’s past state can be used to construct a future solution. Interestingly, the current model has the property of smoothing solutions over successive time intervals and propagating discontinuities to successive points $t_k=k·\tau$ (cf. [1,2]). Using examples of certain epidemiological models, we will demonstrate what to expect from solution discontinuities and how to obtain them. It is surprising that a process described as discontinuous in the past cannot maintain these discontinuities in the future. We will demonstrate how to modify this. Although this requires changes to the mathematical model, it does not affect the interpretation of practical data or the stability analysis of solutions. We should not mistakenly equate the effects of using current models, which have continuous solutions for $t>0$ (sometimes, integral averaging is even used in distributed delay models to achieve this), with the real-world effects we want to model. If we observe discontinuities, such as impulses, we can expect them in the future. We will modify the models to reflect this.

This paper introduces modifications to mathematical epidemiological models, allowing for a unified approach to models with continuous solutions, models with impulses, and their extensions. Using this approach, we can study discontinuous solutions with information about the system’s known state and initial function. We will present selected models and the proposed modifications, along with justifications for the changes.

First, we will present basic models that consider discontinuous solutions, such as those related to vaccination waves. Next, we will introduce the mathematical principles for adapting these models. This requires new mathematical tools that allow for the formal construction of modified models. Finally, we will propose a new approach to the topic in relation to certain existing models and their generalizations. This approach enables us to derive similar models in situations where discontinuous solutions are reasonable. This applies to population models [2,3], engineering [4,5], and economics [6], i.e., basically any applied science that uses delay differential equation models. We will study and analyze mathematical models based on delayed equations to determine the need for modification, using examples from epidemiology. However, we emphasize from the outset that our focus will be on the mathematical aspects. Thus, the results obtained can—and, in our opinion, should—be applied to many practical situations in which lagged models yield more realistic results. A compilation of these models will supplement the results of this paper.

Consider the example of vaccinations against certain diseases to justify the existence of discontinuous solutions. On a large scale, successive vaccination groups can be considered part of a continuous process. However, introducing new mandatory vaccines (e.g., for the novel coronavirus) can suddenly increase the number of vaccinated people. In other words, over a certain time period, $\tau >0$, there is a jump in the number of immunized people. Of course, other impulse factors and models can be considered.

As claimed in [7], a common assumption of the infectious model with a vaccination strategy is that immunization activities occur continuously. However, this is not how things actually are. Generally, immunization occurs at regular intervals. Consequently, continuous human intervention is removed from the system and replaced by an impulsive perturbation. Thus, mathematical models with impulsive vaccination have been proposed and investigated, as have models with discontinuous solutions. Note that individuals immunized against one dengue virus, either through infection or vaccination, can still be infected by another dengue virus. Therefore, designing a vaccination regimen that effectively controls dengue infection while considering vaccination intensity and frequency is an interesting problem. This means the model must consider previous vaccination periods and predict future impulses. As we will demonstrate, this restricts the application of models with piecewise continuous solutions. We will replace these models with regulated functions that have finite limits at every point. Thus, we must redefine the concept of a solution. For instance, we should examine the properties of the history mapping $t\mapsto x(t-\tau )$.

We would like to emphasize that the goal of this paper is not to create a new mathematical model based on functional-differential equations. Rather, the goal is to modify the equations to account for the possibility of discontinuous solutions and the influence of discontinuous functions that describe the initial state of the process on the results. We will demonstrate through several examples that this approach more accurately reflects the real situation. This approach has already been justified in [1,2,8], but a suitable phase space consisting of discontinuous functions and an integer form suitable for study has yet to be chosen.

The main focus will be on two elements. First, we will consider the possibility and necessity of accounting for potential discontinuities in both the function itself and the history function, which describes the state of the process in the past. Second is the well-known and appreciated effect of including delays in the equations (cf. [1]). These effects appear to be important when including modeled factors, yet they have not been studied together. Thus, we permit the study of discontinuous processes in the past, i.e., potentially discontinuous solutions. Therefore, the absence of such studies is not due to the limitations of viable models. After all, why would the onset of observation at $t=0$ account for the immediate derivation of continuous processes? Rather, it is due to the limitations of previous methods. In classical cases, discontinuous solutions were obtained using equations with impulses. However, this is an entirely different approach than using functions, and it also has its limitations.

The second limitation is the unintended smoothing of solutions within each period. For example, the step method sometimes abandons discontinuous initial functions entirely. However, as discussed in [1], Baker and Paul were the first to demonstrate the feasibility and validity of this solution in delayed models. Subsequently, in the paper [9] it is proposed to preserve past discontinuities using a different type of integral, either the Riemann–Stieltjes integral or one of its generalizations. The epidemiological models discussed in the paper illustrate the possibilities offered by the proposed problem formulation. In addition to the examples discussed, we point out others that can and should be studied in the same way. However, this is beyond the scope of the paper. We recommend that interested readers see what such modifications to the models will yield.

In this paper, we will build upon previous results by presenting the complete theory and demonstrating its practical application. We will use a model from epidemiology to illustrate the advantages of our method. However, as previously mentioned, the theory can be applied anywhere that models are based on lag equations and allow for discontinuities in the past or future.

2. Mathematical Models in Epidemiology

From the perspective of applying mathematical methods to obtain properties of solutions, we will briefly review subsequent steps in constructing epidemiological models. In the subsequent sections of this paper, we will present a method to transfer the properties of the initial function to the solutions. Then, we will review nonlinear models and the introduction of delays (which are crucial to our paper) and discontinuities through impulse models.

In this section, we will briefly discuss selected epidemiological models in which both the need for modeling using delay equations and, above all, the need to include discontinuous solutions in models have already been recognized. As a rule, the first step was to take impulses into account. We will show what limitations this has. The following chapters of this paper will be devoted to constructing an extension of the mathematical apparatus used, so as not only to include existing models in a common approach (Section 3), but also to obtain their generalizations, useful in modeling (Section 4).

Let us begin with a simple motivation for both the study of retarded differential equations with discontinuous initial functions (and solutions), and to find a suitable phase space consisting of discontinuous functions. First, we will focus on a well-defined approach to models using impulse equations. However, we will also demonstrate their limitations. We will present the main steps in developing such models in epidemiology and note what can increase their realism. After introducing the mathematical foundations (Section 3), we will explain how to advance this theory by considering how information is preserved from the initial function, particularly the solution pulses (Section 4.4).

One of the earliest attempts to mathematically describe the spread of an infectious disease was made by Kermack and McKendrick [10,11]. In 1927, they introduced the Susceptible-Infectious-Removed (SIR) model. The SIR model describes the dynamics of a fixed population divided into three compartments: S represents the susceptible compartment and counts individuals who are susceptible but not yet infected by the disease. The infectious compartment, I, counts the number of infectious individuals. R is the removed compartment. The dynamics are described by the system of ordinary differential equations

$$\left\{\begin{array}{c}{\displaystyle \frac{dS}{dt}}=-\beta {\displaystyle \frac{SI}{N}},\hfill \\ {\displaystyle \frac{dI}{dt}}=\beta {\displaystyle \frac{SI}{N}}-\gamma I,\hfill \\ {\displaystyle \frac{dR}{dt}}=\gamma I,\hfill \end{array}\right.$$

where $N=S+I+R$, $\beta$ is the transmission rate, $\gamma$ is recovery rate.

This model has undergone several modifications, including (SIRS), which allows loss of immunity ($R\to S$), (SEIR) which adds an Exposed (E) compartment for latent infections or age-structured SIR, which incorporates age-dependent transmission (see, for example, [3,12]).

Here, we will not propose a modification of the entire model or versions that consider more factors than the SIR model. Instead, we will propose a mathematical modification that allows us to study processes with discontinuous initial functions and solutions, such as those involving impulses. In particular, we pay attention to the values that the delay equations provide and, more importantly, the information that discontinuous solutions offer. We explain how to achieve this within the framework of mathematical methods modified for such models, including epidemiology, of course. The proposed treatment of the topic also has natural applications in a number of practical fields.

2.1. Models with Delays

The first significant modification to SIR models was the incorporation of delays. This allows for the modeling of oscillatory solutions and better describes real situations. We describe and modify the SIR model with demography (births and deaths) and a time delay [3,11,13].

The impact of including delays in epidemiological models is well-known (see the discussion in [14]). Simulating situations in which discontinuities may appear in model solutions can be dangerous. Mathematically, we can exercise control by ensuring the sum of jumps is finite. This can be achieved by selecting the appropriate phase space, $Z_G^L$, which is described later in this paper.

Containment may fail dramatically if testing capacities are limited because such combined countermeasures drastically change the rules of the epidemic transition. Instead of being continuous, the response to countermeasures becomes discontinuous. Rather than following conventional exponential growth, an initially strongly suppressed outbreak eventually accelerates and grows faster than exponentially during an explosive growth period. Consequently, containment measures either suffice to stop the outbreak at low total case numbers or fail catastrophically if they are even slightly too weak. This implies large uncertainties in reliably estimating overall epidemic dynamics during initial phases and second wave scenarios [14].

Mathematical models are instrumental in understanding and mitigating the spread of infectious diseases. To accurately capture disease transmission dynamics, key epidemiological factors must be incorporated, including: the time delay between latent infection and the onset of infectiousness, the infectious age, defined as the time elapsed since initial infection, and the possibility of relapse, where recovered individuals may become reinfected after a period of convalescence. Therefore, realistic models should be based on delay differential equations [15,16].

As discussed there, evaluations of large-scale coverage models show that the effect of delays is eliminated due to the uniform distribution of delays throughout the population. This is true for large populations (e.g., pandemics), but at smaller scales, these effects are still observed. The same situation in which delay effects should be modeled applies to models other than epidemiological ones (see Section 5).

Example 1.

Delay models essentially follow the same strategy as SIR; the main difference is that the removal process is modeled with a time shift in the function describing the number of cumulative cases rather than by a separate variable.

To maintain the realistic properties of time-delayed solution models, one possible model is the SIR model with demography (births and deaths), as described in the following system of equation [11,17]

$$\begin{array}{cc}\hfill S^{\prime }\left(t\right)& =A-\mu S\left(t\right)-\beta S\left(t\right)I\left(t\right),\hfill \\ \hfill I^{\prime }\left(t\right)& =\beta S(t-\tau )I(t-\tau )-(\mu +\alpha )I\left(t\right),\hfill \\ \hfill R^{\prime }\left(t\right)& =\alpha I\left(t\right)-\mu R\left(t\right),\hfill \end{array}$$

where A is a recruitment/birth rate, μ a natural death rate, β a transmission rate, α a recovery rate. Everywhere in the paper by τ we denote a time delay. Some realistic initial conditions are also assumed.

Throughout this paper, including here, we use the standard size designations in SIR models, with γ being here a rate of immunity loss (with fixed delay τ). When individuals are subjected to temporary immunity of fixed length τ, the standard Kermack–McKendrick model with delay becomes

$$\begin{array}{cc}\hfill S^{\prime }\left(t\right)& =-\beta S\left(t\right)I\left(t\right)+\gamma I(t-\tau ),\hfill \\ \hfill I^{\prime }\left(t\right)& =\beta S\left(t\right)I\left(t\right)-\gamma I\left(t\right),\hfill \\ \hfill R^{\prime }\left(t\right)& =\gamma I\left(t\right)-\gamma I(t-\tau ).\hfill \end{array}$$

Interestingly, in this form, the equation describing $S\left(t\right)$ does not take into account lags or spikes resulting from vaccinations at specific times. We only consider the delay in infecting the population and its effect on the rest of the model. We will further consider this element of the model and supplement it with the missing effect. Furthermore, we will consider models with discontinuous initial functions and such solutions.

Due to the proposed unified approach to models with continuous and discontinuous solutions, which is applicable to many practical models with different numbers of equations in systems, we will present the entire mathematical apparatus in the terminology of vector differential equations. While we will not repeat this for each model, for the convenience of readers, we will present the vector forms of the problems introduced thus far.

In the classical model, let the state vector be

$$\mathbf{X}\left(t\right)=\left[\begin{array}{c}S\left(t\right)\\ I\left(t\right)\\ R\left(t\right)\end{array}\right].$$

The system can be written as:

$${\mathbf{X}}^{\prime }\left(t\right)=\left[\begin{array}{c}A-\mu S\left(t\right)-\beta S\left(t\right)I\left(t\right)\\ \beta S(t-\tau )I(t-\tau )-(\mu +\alpha )I\left(t\right)\\ \alpha I\left(t\right)-\mu R\left(t\right)\end{array}\right]=f(t,\mathbf{X}\left(t\right)).$$

This can be expressed also more compactly by separating the non-delayed and delayed terms:

$${\mathbf{X}}^{\prime }\left(t\right)=\left[\begin{array}{c}A\\ 0\\ 0\end{array}\right]-\left[\begin{array}{c}\mu S\left(t\right)+\beta S\left(t\right)I\left(t\right)\\ (\mu +\alpha )I\left(t\right)\\ \mu R\left(t\right)-\alpha I\left(t\right)\end{array}\right]+\left[\begin{array}{c}0\\ \beta S(t-\tau )I(t-\tau )\\ 0\end{array}\right].$$

In the second case of the SIRS model with a delay in recovery, let the state vector be

$$\mathbf{Y}\left(t\right)=\left[\begin{array}{c}S\left(t\right)\\ I\left(t\right)\\ R\left(t\right)\end{array}\right].$$

The system can be written as:

$${\mathbf{Y}}^{\prime }\left(t\right)=\left[\begin{array}{c}-\beta S\left(t\right)I\left(t\right)+\gamma I(t-\tau )\\ \beta S\left(t\right)I\left(t\right)-\gamma I\left(t\right)\\ \gamma I\left(t\right)-\gamma I(t-\tau )\end{array}\right]=g(t,\mathbf{Y}(t-\tau )).$$

or in the form

$${\mathbf{Y}}^{\prime }\left(t\right)=\underset{\mathit{Instantaneous} \mathit{Terms}}{\underbrace{\left[\begin{array}{c}-\beta S\left(t\right)I\left(t\right)\\ \beta S\left(t\right)I\left(t\right)-\gamma I\left(t\right)\\ \gamma I\left(t\right)\end{array}\right]}}+\underset{\mathit{Delay} \mathit{Terms}}{\underbrace{\left[\begin{array}{c}\gamma I(t-\tau )\\ 0\\ -\gamma I(t-\tau )\end{array}\right]}}.$$

Note that the functions f and g described above are continuous. In that framework, under biologically reasonable assumptions (bounded, continuous initial functions), the right-hand sides lead to well-posed problems. Recall that our goal is to replace the continuity assumption on the initial function with discontinuous assumptions while maintaining this property.

Now, we will turn our attention to the role of the initial function. As we have pointed out, many studies do not examine this function. They usually assume its continuity or its jump at the point $t=0$. However, its properties should be transferred to the solutions, and any points of discontinuity should have consequences in the future. We will demonstrate this effect, but first, we will explain the problem thus far. In epidemiological models, we should ensure the existence of solutions, uniqueness, and continuous dependence on initial conditions for differential equations with delay, which are infinite-dimensional equations. It is crucial to treat the equation in abstract form as an equation with a condition on the functional space to which the initial function belongs. This is called the phase space, which should meet certain requirements that we will discuss in more detail in Section 3.

We are no longer looking for a function $\mathbf{f}$ such that ${\mathbf{X}}^{\prime }\left(t\right)=\mathbf{f}(t,\mathbf{X}\left(t\right))$ (an ODE), but for a functional $\mathcal{F}$ such that:

$${\mathbf{X}}^{\prime }\left(t\right)=\mathcal{F}(t,{\mathbf{X}}_t)$$

where ${\mathbf{X}}_t$ is the history function defined for $s\in [-\tau ,0]$ as:

$${\mathbf{X}}_t\left(s\right)=\mathbf{X}(t+s)$$

with $\mathbf{X}\left(s\right)=\psi \left(s\right)$ for $s\in [-\tau ,0]$. This means that $\mathcal{F}$ takes the entire recent history of the state (from time $t-\tau$ to time t) as its input. For delay differential equations, we have a special case $\mathcal{F}(t,\psi )=f(t,\psi (0),\psi (-\tau \left)\right)$ for $t\in [0,\tau ]$ (then applying the method of steps).

In classical cases, this means that $\psi \in C([-\tau ,0],{\mathbb{R}}^n)$, where the space is equipped with the supremum norm ${\parallel \psi \parallel }_{\infty }={sup}_{s\in [-\tau ,0]}\parallel \psi \left(s\right)\parallel$. In this paper, we will demonstrate how to study discontinuous initial functions and preserve their discontinuity in solutions for $t>0$. The following lemma (being a special case for a general delay differential problem) forms the basis for studying this problem.

Lemma 1.

Consider the delay differential equation system:

$$\begin{array}{cc}\hfill S^{\prime }\left(t\right)& =A-\mu S\left(t\right)-\beta S\left(t\right)I\left(t\right),\hfill \\ \hfill I^{\prime }\left(t\right)& =\beta S(t-\tau )I(t-\tau )-(\mu +\alpha )I\left(t\right),\hfill \\ \hfill R^{\prime }\left(t\right)& =\alpha I\left(t\right)-\mu R\left(t\right),\hfill \end{array}$$

for $t\ge 0$, with a constant delay $\tau >0$. Let the phase space be $\mathcal{C}=C([-\tau ,0],{\mathbb{R}}^3)$, the Banach space of continuous functions from $[-\tau ,0]$ to ${\mathbb{R}}^3$ equipped with the supremum norm ${\parallel \varphi \parallel }_{\infty }={sup}_{\theta \in [-\tau ,0]}\left|\varphi \left(\theta \right)\right|$.

Given any initial history function $\varphi ={({\varphi }_S,{\varphi }_I,{\varphi }_R)}^T\in \mathcal{C}$, there exists a unique solution $\mathbf{X}\left(t\right)={(S\left(t\right),I\left(t\right),R\left(t\right))}^T$ defined on a maximal interval of existence $[-\tau ,T_{\max })$ such that:

$$\mathbf{X}\left(\theta \right)=\varphi \left(\theta \right)\mathit{for}\mathit{all}\theta \in [-\tau ,0].$$

If $A\ge 0$, $\mu >0$, $\beta >0$, $\alpha \ge 0$, $\tau >0$, and the initial history function is non-negative, i.e., ${\varphi }_S\left(\theta \right)\ge 0$, ${\varphi }_I\left(\theta \right)\ge 0$, ${\varphi }_R\left(\theta \right)\ge 0$ for all $\theta \in [-\tau ,0]$, then the unique solution is defined for all $t\ge 0$ ($T_{\mathit{max}}=\infty$) and satisfies

$$S\left(t\right)\ge 0,I\left(t\right)\ge 0,R\left(t\right)\ge 0\mathit{for}\mathit{all}t\ge 0.$$

Proof. 

The proof of the existence and uniqueness of solutions in this part of the theorem is classical. It is a special case of the result from Theorem 2.3 in [18] or Theorems 2.1 and 2.2 in [19], for instance (see also Corollary 1). The right-hand side defines a functional $F:\mathcal{C}\to {\mathbb{R}}^3$ whose components depend linearly or bilinearly on the values $\mathbf{X}\left(t\right)$ and $\mathbf{X}(t-\tau )$:

$$F\left({\mathbf{X}}_t\right)=\left(\begin{array}{c}A-\mu S\left(t\right)-\beta S\left(t\right)I\left(t\right)\\ \beta S(t-\tau )I(t-\tau )-(\mu +\alpha )I\left(t\right)\\ \alpha I\left(t\right)-\mu R\left(t\right)\end{array}\right),$$

where ${\mathbf{X}}_t\left(\theta \right)=\mathbf{X}(t+\theta )$ for $\theta \in [-\tau ,0]$. Therefore, F is continuous and locally Lipschitz on bounded subsets of $\mathcal{C}$. According to the standard theory of delay differential equations, there is a unique solution $\mathbf{X}\left(t\right)$ with the given history on a maximal interval $[-\tau ,T_{max})$.

Let $N\left(t\right)=S\left(t\right)+I\left(t\right)+R\left(t\right)$. Summing the equations gives

$$N^{\prime }\left(t\right)=A-\mu N\left(t\right)-\alpha I\left(t\right)\le A-\mu N\left(t\right).$$

Comparison with the linear ordinary differential equation $y^{\prime }=A-\mu y$ yields for $t\ge 0$

$$N\left(t\right)\le e^{-\mu t}N\left(0\right)+{\displaystyle \frac{A}{\mu }}\left(1-e^{-\mu t}\right)\le max\{N\left(0\right),A/\mu \},$$

so $N\left(t\right)$ (hence each component) is bounded on $[0,T_{max})$. But solutions of DDEs with locally Lipschitz right-hand side can only blow up if the supremum norm of the segment $\parallel {\mathbf{X}}_t{\parallel }_{\infty }$ blows up. Boundedness of the components prevents blow-up, so $T_{max}=\infty$.

The proof of non-negativity also follow classical lines. Let ${\mathbb{R}}_{+}^3=\{(S,I,R):S,I,R\ge 0\}$. To show forward invariance of ${\mathbb{R}}_{+}^3$ it suffices to check the vector field on the boundary: take any history $\varphi \in \mathcal{C}$ with $\varphi \left(\theta \right)\ge 0$ for $\theta \in [-\tau ,0]$. If $S\left(0\right)=0$ then $S^{\prime }\left(0\right)=A-\mu ·0-\beta ·0·I\left(0\right)=A\ge 0$, if $I\left(0\right)=0$ then $I^{\prime }\left(0\right)=\beta S(-\tau )I(-\tau )\ge 0$ because $S(-\tau ),I(-\tau )\ge 0$. Finally, if $R\left(0\right)=0$ then $R^{\prime }\left(0\right)=\alpha I\left(0\right)\ge 0$.

So whenever a component is zero at the right endpoint of the history and the other components are nonnegative, its derivative is nonnegative; thus, no component can cross into negative values. Therefore $S\left(t\right),I\left(t\right),R\left(t\right)\ge 0$ for all $t\ge 0$. The above remarks can be combined to yield the claimed global, nonnegative solution for all $t\ge 0$. □

This proof emphasizes the importance of the phase space from which the initial functions originate.

2.2. Phase Space

Now, we must consider the role of phase space in this result. In the general case, we replace it with some space Y of discontinuous functions. This requires a change to the Lipschitz condition in the previous lemma with respect to the norm in Y.

Hale and Kato [18,19,20,21,22,23] (and later authors) generalized the phase space to a broader class of function spaces satisfying certain axioms.

Definition 1.

A phase space $\mathcal{B}$ is a normed linear space of functions mapping $[-\tau ,0]$ to ${\mathbb{R}}^n$ with the following properties:

(A1) 

$\mathcal{B}$ is a Banach space with norm ${\parallel ·\parallel }_{\mathcal{B}}$.

(A2) 

For any $\psi \in \mathcal{B}$ and $t\in [-\tau ,0]$, the evaluation map $\psi \mapsto \psi \left(t\right)$ is continuous.

(A3) 

The inclusion $C([-\tau ,0],{\mathbb{R}}^n)\hookrightarrow \mathcal{B}$ is continuous, i.e., there exists $K>0$ such that:

$${\parallel \psi \parallel }_{\mathcal{B}}\le K{\parallel \psi \parallel }_C\mathit{for}\mathit{all}\psi \in C.$$

(A4) 

If $x:(-\infty ,a)\to {\mathbb{R}}^n$ is continuous on $[0,a)$ and $x_0\in \mathcal{B}$, then for $t\in [0,a)$, $x_t\in \mathcal{B}$, and $t\mapsto x_t$ is continuous in $\mathcal{B}$.

If we expect some positivity of functions, we need to assume an additional positivity axiom:

(B) 

The pointwise evaluation maps from $\mathcal{B}$ to ${\mathbb{R}}^n$, i.e., $\psi \mapsto \psi \left(t\right)$ are well-defined and continuous linear functionals. Furthermore, if ψ is non-negative, then ${\parallel \psi \parallel }_{\mathcal{B}}\ge c\parallel \psi \left(\theta \right)\parallel$ for some $c>0$.

The axioms ensure that initial value problems are well-posed. Moreover, the phase space structure guarantees that solutions depend continuously on initial data. Finally, the choice of $\mathcal{B}$ affects the definition of semiflows for autonomous DDEs.

For continuous initial functions the classical phase space is $C([-\tau ,0],{\mathbb{R}}^n)$, but for discontinuous functions we need to consider alternative choices such as $L^p\left([-\tau ,0]\right)$ (integrable functions) or $PC\left(\right[-\tau ,0\left]\right)$ (piecewise continuous function). Unfortunately, spaces $BV\left(\right[-\tau ,0\left]\right)$ (bounded variation functions) or $G\left(\right[-\tau ,0\left]\right)$ (regulated functions) do not meet the key axiom (A4).

Corollary 1.

Let $\mathcal{B}$ be a phase space satisfying the set of axioms from Definition 1. Let the functional $\mathbf{F}:[0,\infty )\times \mathcal{B}\to {\mathbb{R}}^n$ be continuous and locally Lipschitz in its second argument, i.e., for any constant $M>0$, there exists $L_M>0$ such that for all $\varphi ,\psi \in \mathcal{B}$ with ${\left|\right|\varphi \left|\right|}_{\mathcal{B}}\le M$, ${\left|\right|\psi \left|\right|}_{\mathcal{B}}\le M$, we have:

$$|\mathbf{F}(t,\varphi )-\mathbf{F}(t,\psi )|\le L_M\left|\right|\varphi -{\psi \left|\right|}_{\mathcal{B}}.$$

Then, for any initial history $\psi \in \mathcal{B}$, there exists a unique solution $\mathbf{X}\left(t\right)$ on a maximal interval $[-\tau ,T_{\max })$ such that ${\mathbf{X}}_0=\psi$ and the map $t\mapsto {\mathbf{X}}_t$ is continuous in $\mathcal{B}$.

Proof. 

Let us observe, that the contraction mapping is no longer defined on the space $C([0,T],{\mathbb{R}}^n)$ but on the space $C\left(\right[0,T],\mathcal{B})$, or more precisely, on the space of functions $x:[-\tau ,T]\to {\mathbb{R}}^n$ such that $x_0=\psi$ and ${x|}_{[0,T]}$ is continuous and $x_t\in \mathcal{B}$.

However, we must now require the stronger condition that $\mathbf{F}$ is Lipschitz with respect to the abstract seminorm ${\left|\right|·\left|\right|}_{\mathcal{B}}$. This is a nontrivial assumption that depends on the choice of $\mathcal{B}$ and must be verified in the chosen phase space. The axioms of the phase space allow us to show that the integrated version of the DDE defines a contraction on a sufficiently small time interval. □

What about positivity? The positivity proof relied critically on pointwise evaluation of the history function: e.g., $\psi (-\tau )$ and $\psi \left(0\right)$. This is where the abstract theory becomes much more restrictive. We can no longer prove positivity in a general phase space $\mathcal{B}$. Whether positivity holds or not becomes a property of the chosen phase space $\mathcal{B}$ itself. It is the reason to add Axiom (B) to the case of phase spaces studied in epidemiology. For the proof of positivity, we use a contradiction argument. This is still guaranteed if the evaluation maps at the points $t=0$ and at $t=-\tau$ are continuous.

Remark 1.

This abstract framework is powerful because it can handle more general problems (e.g., infinite delays, discontinuous initial data), but it requires correspondingly stronger assumptions to recover the classical results like positivity and uniqueness.

After defining the appropriate phase space in the paper, it is sufficient to verify the axioms and assumptions (e.g., the Lipschitz condition) for the given problem, not only in the aforementioned model, but also in subsequent models, for which discontinuous solutions are justified in practice.

Now, let us consider another observation. A major outbreak only occurs if the initial number of susceptible individuals is high $S\left(0\right)>c$. We can also consider the following SIR model with time delay [15]. Assuming that the force of infection at time t is given by

$$\beta e^{-\mu \tau }S(t-\tau )I(t-\tau ),$$

where $\mu >0$ is the natural death rate and $\tau >0$ is a time delay. This is, of course, still a continuous function that preserves the positivity of solutions and satisfies the Lipschitz condition with respect to the supremum norm. We will study another phase space and its norm later. An infected vector can only transmit the disease to a susceptible human after a certain amount of time has passed. Thus, the infectious period of the disease is represented by $\tau$.

If we suppose that it is more natural to assume $\tau$ is a distributed parameter rather than a fixed time [16], then the force of infection in must be replaced by

$$\beta {\int }_0^{h}f\left(s\right)S(t-s)I(t-s)e^{-\mu s}ds,$$

where $f\left(s\right)$, the fraction of the vector population in which the time to become infectious is s, is a nonnegative function defined on $[0,h]$. Here, some finite positive time h represents the maximum infectious period.

In the original paper it is assumed that $f:[0,h]\to \mathbb{R}$ is square integrable on $[0,h]$ and satisfies

$${\int }_0^{h}f\left(s\right)ds=1,{\int }_0^{h}sf\left(s\right)ds<+\infty .$$

(1)

Note that there is no continuity assumption for this function. This is an interesting and motivating observation for us. The parameter ${\tau }^{*}={\int }_0^{h}sf\left(s\right)ds>0$ represents the average incubation time for the vector to become infectious.

Remark 2.

This model is worth mentioning because it aligns with our approach. It is based on conditions expressed by integrals and the integrability of functions. However, note that in our model, the Lebesgue (or Riemann) integral is replaced by the Stieltjes integral (Henstock–Stieltjes in this model). This allows us to consider discontinuous functions, which is important. While this topic is beyond the scope of the paper, models like the one above suggest an approach to the topic that goes beyond deterministic models. After introducing the new phase space, we will make some observations on this subject (in probabilistic models, these will be measure spaces).

Taking into account natural births, natural deaths, and the force of infection, we arrive at a distributed-time-delay SIR model [13]:

$$\begin{array}{cc}\hfill S^{\prime }\left(t\right)& =\mu -\beta {\int }_0^{h}f\left(s\right)S(t-s)I(t-s)e^{-\mu s}ds-\mu S\left(t\right),\hfill \\ \hfill I^{\prime }\left(t\right)& =\beta {\int }_0^{h}f\left(s\right)S(t-s)I(t-s)e^{-\mu s}ds-\mu I\left(t\right)-\gamma I\left(t\right),\hfill \\ \hfill R^{\prime }\left(t\right)& =\gamma I\left(t\right)-\mu R\left(t\right)\hfill \end{array}$$

with the function $f\left(s\right)$ satisfying the above conditions, and if the integral exists. Here, again, the right-hand side is continuous (due to properties of the Lebesgue integral). Usually, it is assumed that the natural birth rate is equal to the natural death rate, and all newborns are susceptible. Here $\mu >0$ denote both the natural birth rate and death rate, where $1/\mu$ represents the mean life expectancy.

However, descriptions of these models do not particularly focus on initial functions, even though they describe past phenomena. We will use this information when extending the models. More about SIR-based models, including delayed ones, can be found in [11,17,24,25,26,27].

Remark 3.

It is important to note here that if we expect possibly discontinuous solutions, the condition about the existence of the above integrals can be problematic. In the case of continuous functions S and I, the existence is assured by (1).

Moreover, we are interested in some generalization of this problem with the Stieltjes integral, and it may happen that at a point $t^{*}$, both functions h and I, so the Riemann integral may not exist. We solve the problem by replacing the Lebesgue integral above by the Henstock–Stieltjes integrals. Besides the new phase space, we need to propose a new integral in the models with distributed-time delays. This integral will be presented in Section 3.

2.3. Discontinuities, Impulsive Models, Methods

In the next model, we will demonstrate why discontinuous solutions to epidemiological problems should be investigated. The following sections will explain how to do this.

Epidemics can be more effectively controlled by aligning vaccination efforts with outbreak timing. Rather than continuous, uniform vaccination, pulse vaccination involves periodic, targeted campaigns. This leads us to impulsive differential equations. In this interesting context, they are functional-differential equations with impulses. Vaccination is a safe way to move people from the susceptible compartment to the removed compartment, bypassing the infectious compartment and reducing the likelihood of an outbreak.

When the pulse vaccination strategy is included in the SEIR epidemic model, it can be written as follows [28]:

$$\begin{array}{cc}\hfill S^{\prime }\left(t\right)& =m(1-S)-\beta \left(t\right)SI,\hfill \\ \hfill E^{\prime }\left(t\right)& =+\beta \left(t\right)SI-(a+m)E,\hfill \\ \hfill I^{\prime }\left(t\right)& =aE-(g+m)I,\hfill \\ \hfill S\left(n{T}^{+}\right)& =(1-p)S\left(n{T}^{-}\right),n\in {\mathbb{N}}_{+},\hfill \\ \hfill R\left(t\right)& =1-S\left(t\right)-E\left(t\right)-I\left(t\right).\hfill \end{array}$$

In this model, the time period is one year, and T is the time between two consecutive pulse vaccinations. Now, let us consider one limitation of the model that is essential from our point of view. The model considers one impulse of vaccination for a constant population. Furthermore, p is the fraction of the susceptible population inoculated with the vaccine at $t=nT$, where n is a positive integer. The model also considers the following parameters: m is the mortality rate, a is the inverse of the latent period, g is the inverse of the infectious period, and $\beta \left(t\right)$ is constant or given by $\beta (t+1)=\beta \left(t\right)$. The model has two key realistic features: (1) periodic pulse vaccination campaigns that instantly vaccinate a fraction of the susceptible population and (2) the immunity conferred by either infection or vaccination is not permanent, but rather wanes after a certain time. This is modeled using a discrete delay. An interesting case, with a piecewise continuous initial function, is studied in [29].

Remark 4.

We propose a more realistic model by assuming that during one period of time, we can consider a few pulses with partial vaccinations of the population, which implies not only one point of discontinuity in the period of time (a new phase space is necessary). This will be an essential improvement of the model and will be described later, in Section 4.4.

Some earlier research suggests that measles epidemics can be more effectively controlled by aligning vaccination efforts with the natural timing of outbreaks. Instead of uniform, continuous vaccination, pulse vaccination involves periodic, targeted campaigns. Once again, let us stress that the full description of an initial function should contain several impulses. For instance, in one model we can consider large-scale vaccination campaigns, vaccination need not be with a fixed fraction of the susceptible population in one campaign or additional campaigns due to new vaccinations. We can check one period of time, to keep all the information in the initial function, and then apply our new model instead of the presented one.

The SEIR epidemic model presented above can also be generalized ([7,27,28,30], for instance), and an interesting approach allows us to study the discontinuous initial function. Thus, between impulses, i.e., for $t\ne t_k$ we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =\mu N-{\displaystyle \frac{\beta IS}{N}}-\mu S+\gamma R(t-\tau )e^{-\mu \tau }\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta IS}{N}}-(\gamma +\mu )I\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& =-\mu R-\gamma R(t-\tau )e^{-\mu \tau }+\gamma I,\hfill \end{array}$$

(2)

where N is the total constant population ($S+I+R=N$), $\beta$ is the transmission rate, $\gamma$ is the recovery rate, $\mu$ is the birth/death rate (introduced to model population turnover and allow immunity to wane naturally), $\nu$ is the fraction of susceptible vaccinated during each pulse campaign (this models a public health strategy of repeated mass vaccination campaigns every T years (e.g., a yearly flu shot campaign). At these discrete times, the system state jumps). $\tau$ represents the delay, i.e., the period of full immunity. After this time, individuals lose immunity and re-join the susceptible compartment. This introduces a memory or history dependence into the model.

At impulse times $t=t_k$ (e.g., $t_k=k\tau$ for period $\tau$) we have a “hidden” description of the initial function, but with direct condition in impulses times:

$$\begin{array}{cc}\hfill S\left(t_k^{+}\right)& =(1-\nu )S\left(t_k^{-}\right),\hfill \\ \hfill I\left(t_k^{+}\right)& =I\left(t_k^{-}\right),\hfill \\ \hfill R\left(t_k^{+}\right)& =R\left(t_k^{-}\right)+\nu S\left(t_k^{-}\right).\hfill \end{array}$$

(3)

The PVS model is currently undergoing intensive research and development (e.g., see [7,27,28,31,32,33,34]). A discussion of these results is beyond the scope of this work. In Section 3 and Section 4.4, we will focus on showing how this and other models can incorporate the properties of the initial function, particularly points of discontinuity, into their solutions.

For delay differential equations, the initial conditions must specify the state of the system over the history interval $[-\tau ,0]$, not just at a single point. This is because the derivative at $t\ge 0$ depends on past values (e.g., $I(t-\tau )$) of the process. Typically, we consider $S\left(0\right)=S_0$, $I\left(t\right)={\psi }_I\left(t\right)$ for $t\in [-\tau ,0]$, and $R\left(0\right)=\gamma {\int }_{-\tau }^0{\psi }_I\left(s\right)ds$. Alternatively, we can specify the $R\left(t\right)$ history separately. These conditions ensure that the system is well-posed and biologically meaningful (e.g., populations are non-negative).

The key question, from our point of view, is how to choose the function ${\psi }_I\left(t\right)$. This choice depends on the modeling context (e.g., a prior outbreak or a sudden introduction of infection at $t=0$). While it is often continuous, as the paper will clarify, there are no mathematical reasons to restrict our attention to this case only.

A model of vaccination campaigns in which transmission is influenced by previous vaccinations, resulting in discontinuities, can be described in terms of delta Dirac distributions [27]:

$${\displaystyle \frac{dS\left(t\right)}{dt}}=\mu -\beta S\left(t\right)I\left(t\right)-\mu S\left(t\right)-pS\left(t\right)\sum _k\delta (t-t_k^{-}),$$

where $t_k\in (-\tau ,0)$ are past vaccination times. Since $-pS\left(t\right){\sum }_k\delta (t-t_k^{-})$ describes the vaccination pulses at times $t_k$, instantaneously removing $pS\left(t_k^{-}\right)$ susceptible individuals, the initial function $S\left(t\right)$ has jumps at each $t_k$ (discontinuities due to past pulses). These discontinuities represent instantaneous vaccination events within the history window. It is important to note that the model does not incorporate delays and goes beyond the scope of functions and function spaces.

One more important comment is necessary regarding why we propose extending this model. If the vaccination pulses are determined in the past, the solution $S\left(t\right)$ will be continuous for $t>0$. This is justified by the properties of the mathematical model, which we are changing by constructing a different phase space. The only way to account for future jumps is to predetermine them, such that, for some $t_k>0$. After all, the grafting performed at time $t_0$ in the past should have a jumping effect at time $t_0+\tau >0$ after a certain time $\tau$. This is the model we will introduce.

Remark 5

(Fractional models). It is sometimes suggested (cf. [35,36]) that the fractional derivative is highly effective in modeling epidemic transition systems since it takes into account the memory effects and the universal features of the system, which are important for deterministic systems. It is worth mentioning that our proposed approach is particularly effective in fractional differential calculus. The model mentioned below is based on Caputo-type derivatives. However, in many applications, these derivatives are replaced by tempered derivatives. This also makes sense in epidemiology; however, this is a broad topic that is beyond the scope of this paper. We will lay the groundwork for such generalizations by applying Stieltjes-type derivatives (equivalent to the Stieltjes integral problems), which include fractional tempered derivatives [37]. This enables a unified approach to these models using our method.

The fractional operator has a memory effect, making it useful for modeling the future state of a system based on its current state, as in the model for the spread of the Coronavirus. By substituting the Caputo fractional derivative with the first derivative, we can incorporate past historical or hereditary features into the model. The system of time-delay fractional-order differential equations can be generalized as follows [35]:

$$\begin{array}{cc}\hfill D^{a}S\left(t\right)& =-\delta {\displaystyle \frac{S\left(t\right)I(t-\tau )}{N\left(t\right)}}-V_{ac}\nu S\left(t\right),\hfill \\ \hfill D^{a}I\left(t\right)& =\delta {\displaystyle \frac{S\left(t\right)I(t-\tau )}{N\left(t\right)}}-\beta I\left(t\right),\hfill \\ \hfill D^{a}R\left(t\right)& =\beta I\left(t\right)+V_{ac}\nu S\left(t\right).\hfill \end{array}$$

The phase space considered in [35] is the following:

$${\mathcal{C}}_{+}=\left\{\theta \in \mathcal{C}\left([-\tau ,0],{\mathbb{R}}_{0,+}^3\right)|{\theta }_1=S\left(r\right),{\theta }_2=I\left(r\right),{\theta }_3=R\left(r\right)\right\},$$

where $S\left(r\right)>0,I\left(r\right)>0,R\left(r\right)>0,r\in \mathcal{C}[-\tau ,0],{\theta }_1\left(r\right)\ge 0,{\theta }_2\left(r\right)\ge 0,{\theta }_3\left(r\right)\ge 0,{\theta }_1\left(0\right)>0$, ${\theta }_2\left(0\right)>0,{\theta }_3\left(0\right)>0,{\mathcal{C}}_{+}$ is the Banach space of all continuous functions in the interval $[-\tau ,0]$ into ${\mathbb{R}}_{0,+}^3$, where we provide initial history conditions: $\theta =({\theta }_1,{\theta }_2,{\theta }_3)$, and some standard positivity conditions are assumed.

At this point, we should also recommend the paper [38]. The models discussed in the paper regarding the spread of the SARS-CoV-2 virus in Italy are based on systems of equations. The paper includes an element of “tempering” the solutions with the probability $\mathcal{P}$ of remaining infectious at time t after becoming infectious. We will incorporate this idea into our model as well.

3. Mathematical Background

When solving an arbitrary differential or integral equation, the first step is defining a solution. Solutions are typically expected to be continuous, at the very least, meaning the set of solutions forms a subset of the space of continuous functions. Proofs of theorems are based on the properties of this space. However, many types of functional-differential equations have discontinuous solutions (see Chapter 2.5.2 in [39] or [40]). One example is impulsive differential equations. For other types of problems, see [40,41].

Inspired by the papers [1,8], we will examine the problem of the existence of discontinuous solutions to functional differential equations. These papers present some examples and motivations for these types of solutions. The definition and construction of discontinuous solutions differ from those of ordinary differential equations and seem rather complicated.

Here, we present a simple approach that unifies continuous and discontinuous solutions. We demonstrate this approach by examining the functional-differential equation in its abstract form:

$$\begin{array}{ccc}\hfill x^{\prime }\left(t\right)& =& f(t,x(t-\tau \left)\right)\hfill \\ \hfill x\left(t\right)& =& \psi \left(t\right)\mathrm{for}t\in [-\tau ,0].\hfill \end{array}$$

(4)

Such problems arise in the mathematical epidemiology models, as well as in some population dynamics models (e.g., growth of cell modeling: $x^{\prime }\left(t\right)={\displaystyle \frac{1}{\tau }}x(t-\tau )$, cf. also [42,43], with a discontinuous initial function $\psi$ (Section 1.4 in [2], for instance). This allows us to demonstrate all of the ideas.

We focus on two aspects of this theory: solutions and their integral representations, as well as phase space.

The classical theory of functional-differential equations is based on the assumption that the initial function, $\psi \left(x\right)$, is continuous on the interval $[-\tau ,0]$. Consequently, the solutions are also continuous. However, as we observed, this assumption is not always realistic for some mathematical models. Following [1,9], we will assume that the solution can be discontinuous at certain points within the interval $[-\tau ,0]$. Since $x\left(t\right)=\psi (t-\tau )$ for $t\in [0,\tau ]$, the solution should also be discontinuous. Thus, we propose searching for solutions in a larger space, that of regulated functions. Due to certain properties of this space, we can extend the results to it in a unified manner with the continuous case. To maintain this discontinuity property of the initial function, we focus on the integral form of the solution and present its differential form. Therefore, the Riemann–Stieltjes and Henstock–Stieltjes (Kurzweil–Stieltjes) integrals will be useful. Note that integral equations with Kurzweil-type integrals were mainly investigated for their generality (see, for instance, [41]). However, we will show that this is a very natural approach, and that for FDEs with continuous initial functions, it coincides with the classical integral representation (cf. [40]).

Definition 2.

Let $f,g:[a,b]\to \mathbb{R}$. The Riemann–Stieltjes integral of f with respect to g over $[a,b]$ is denoted ${\int }_a^{b}f\left(x\right)dg\left(x\right)$ and is defined to be a number $I\in \mathbb{R}$ such that for every $ϵ>0$, there exists a $\delta >0$ such that for every partition $P=\{x_0,x_1,\dots ,x_n\}$ of $[a,b]$ with mesh norm $\parallel P\parallel ={max}_{1\le i\le n}(x_i-x_{i-1})<\delta$ and for every choice of tags $t_i\in [x_{i-1},x_i]$, the corresponding Riemann–Stieltjes sum satisfies

$$\left|S(P,f,g)-I\right|=\left|\sum _{i=1}^{n}f\left(t_i\right)\left(g\left(x_i\right)-g\left(x_{i-1}\right)\right)-I\right|<ϵ.$$

If such an I exists, we say f is Riemann–Stieltjes integrable with respect to g.

Definition 3.

Let $f,g:[a,b]\to \mathbb{R}$. A function f is called Kurzweil–Stieltjes integrable with respect to g if there exists a number $I\in \mathbb{R}$ such that for every $ϵ>0$, there exists a positive function $\delta :[a,b]\to (0,\infty )$ (called a gauge) such that for every δ-fine tagged partition $P={\left\{(t_i,[x_{i-1},x_i])\right\}}_{i=1}^n$ of $[a,b]$, satisfying

$$[x_{i-1},x_i]\subseteq (t_i-\delta \left(t_i\right),t_i+\delta \left(t_i\right))\mathit{for}\mathit{all}i,$$

the corresponding sum satisfies

$$\left|\sum _{i=1}^{n}f\left(t_i\right)\left(g\left(x_i\right)-g\left(x_{i-1}\right)\right)-I\right|<ϵ.$$

The number I is the Kurzweil–Stieltjes integral, denoted $I=\left(KS\right){\int }_a^{b}fdg$.

The integral can be defined analogously for vector-valued functions (see, for example, [41,44]). The Kurzweil–Stieltjes integral is a generalization of the Riemann–Stieltjes integral. Every Riemann–Stieltjes integrable function is Kurzweil–Stieltjes integrable (use the constant gauge $\delta \left(t\right)=\delta$ from the RS definition). The converse is not true. It can integrate functions like the derivative of Volterra’s function, which are not Riemann integrable. Fundamental theorem of calculus: If g is differentiable on $[a,b]$ and its derivative $g^{\prime }$ is Kurzweil integrable, then

$$\left(KS\right){\int }_a^b{g}^{\prime }\left(t\right)dt=g\left(b\right)-g\left(a\right).$$

This theorem holds under much weaker conditions than those required for the Riemann integral.

3.1. Phase Spaces

In the study of retarded or delay differential equations, the phase space is usually an infinite-dimensional function space because the solution depends on the system’s history over a delay interval. In Section 2, we reviewed the most common set of axioms (see also [20,21]).

A function x is called regulated if one-sided limits $x(t+)$ and $x(t-)$ exist and are finite at every point t. When equipped with the supremum norm, the space of all regulated functions $G\left(\right[a,b\left]\right)$ is a Banach space. Without loss of generality, we will restrict our attention to the subspace $G_{rc}$ of $G\left(\right[a,b\left]\right)$ consisting of right-continuous functions for which the left limits exist. This appears to be a logical assumption given that the solutions to the delayed equations are right-continuous and right-differentiable. Clearly, $C\left(\right[a,b]\subset G([a,b])$.

Lemma 2

([9,40,45,46]). The set of discontinuities of a regulated function is at most countable. Regulated functions are bounded and the space $G\left(\right[0,1],X)$ of regulated functions on $[0,1]$ into the Banach space X is a Banach space too, endowed with the topology of uniform convergence, i.e., with the norm ${\parallel u\parallel }_{\infty }={sup}_{t\in [0,1]}\parallel u\left(t\right)\parallel$.

In fact, a function is regulated if and only if it is a uniform limit of step functions. Clearly, $C\left(\right[0,1],X)\subset G\left(\right[0,1],X)$ and the space of functions with bounded variation $BV\left(\right[0,1],X)\subset G\left(\right[0,1],X)$.

Let us recall some facts about regulated functions [46]. They have at most a countable set of discontinuity points, but it is not a sufficient condition for functions to be regulated. Let $D_x=\{t_k:k\in K\subset \mathbb{N}\}$ denote the set of (left-) discontinuity points of x, then we can define the discrete part of the function x as follows

$$x_d\left(t\right)=\sum _{t_k\le t}\left[(x\left(t_k\right)-x\left(t_k^{-}\right)){\chi }_{[t_k,b]}\left(t\right)\right]$$

(5)

for $t\in [a,b]$, where we set $x\left(a^{-}\right)=x\left(a\right)$ and $x\left(b^{+}\right)=x\left(b\right)$, and define the continuous part of the function x as $x_c=x-x_d$.

We denote the subspace of $G_{rc}\left([a,b]\right)$ consisting of functions that satisfy the following conditions concerning the sum of their jumps at discontinuity points by $Z_G\left([a,b]\right)$ (cf. [9,45]):

$$\sum _{t_k\in D_x}\parallel x\left(t_k\right)-x\left(t_k^{-}\right)\parallel <\infty .$$

If the interval $[a,b]$ is fixed, we will use the notation $Z_G$ instead of $Z_G\left([a,b]\right)$. It is clear that a function with bounded variation belongs to $Z_G$. Moreover, since there are continuous functions whose Jordan variation is not bounded, we have $Z_G\not\subset BV\left([a,b]\right)$, so $Z_G\not\subset G_{\mathrm{rc}}\cap BV$. Now, we can recall the key property that we will use to construct phase space.

Proposition 1

(Section 2 in [45]). Any function $x\in Z_G$ is represented in the form $x=x_c+x_d$, where $x_d$ is the break function defined by (5) and which is of bounded variation, while $x_c=x-x_d$ belongs to $C\left(\right[a,b\left]\right)$.

We call $x_c$ and $x_d$ the continuous and discrete parts of x, respectively. However, for $x\in Z_G^L$, the function $x_c$ need not be of bounded variation. It is obvious that this space is a vector space, and we introduce the following norm

$${\parallel x\parallel }_G={\parallel x_c\parallel }_{\infty }+Var(x_d,[a,b]),$$

which is the norm on $Z_G$. Clearly, ${\parallel x\parallel }_{\infty }\le {\parallel x\parallel }_G$ for any $x\in Z_G$. Although this space seems useful, it does not satisfy Axiom (A4). We need to look for a more useful phase space consisting of regulated functions.

Consider now the subspace $Z_G^L\left([a,b]\right)\subset G\left([a,b]\right)$ equipped with the norm

$${\parallel x\parallel }_L=\parallel x_c{\parallel }_{\infty }+{\parallel x_d\parallel }_1$$

(cf. [45]), where $\parallel x_d{\parallel }_1={\int }_a^b\left|x_d\left(s\right)\right|ds$. This space is interesting because it is unaffected by jump locations. It is important to note that the integral norm is only used to control the discrete parts of functions. The key property that allows us to verify if this space satisfies the phase space axioms (A1)–(A4). This norm satisfies many requirements, including axiom (A4). However, the boundedness of the translation operator at zero requires a certain subspace of $Z_G^L$.

This useful norm has one weakness: the translation operator does not have to be bounded at zero. There are several ways to address this issue. In epidemiological models, changing the space is the most logical solution. The model can treat the initial time, $t=0$, as a point of continuity for the initial function, $\psi$.

Clearly, the map $t\mapsto x_t$ is continuous from $({\mathcal{B}}_{\delta },\parallel ·{\parallel }_L)$ into itself. Consequently,

Lemma 3.

Fix an arbitrary $\delta \in (0,\tau ]$. The space

$$\mathcal{B}={\mathcal{B}}_{\delta }\cap G_{\mathrm{rc}}([-\tau ,0],{\mathbb{R}}^n)$$

satisfies all Axioms (A1)–(A4) from Definition 1. Moreover, if a function $\psi \in \mathcal{B}$ is non-negative (i.e., $\psi \left(\xi \right)\ge 0$ for all $\xi \in [-\tau ,0]$), then for every $\theta \in [-\tau ,0]$ we have

$$\left|\psi \left(\theta \right)\right|\le max\left(1,\frac{1}{\delta }\right){\parallel \psi \parallel }_L.$$

Consequently, $(\mathcal{B},\parallel ·{\parallel }_L)$ satisfies Axiom(B).

Proof. 

Denote by ${\delta }_{\theta }:{\mathcal{B}}_L\to {\mathbb{R}}^n$ the point evaluation functional defined by

$${\delta }_{\theta }\left(\psi \right)=\psi \left(\theta \right).$$

(A1) For any $\psi \in {\mathcal{B}}_L$, the value $\psi \left(\theta \right)$ is well-defined for all $\theta \in [-\tau ,0]$. The linearity of ${\delta }_{\theta }$ follows directly from the linearity of pointwise evaluation:

$${\delta }_{\theta }(a\psi +b\varphi )=(a\psi +b\varphi )\left(\theta \right)=a\psi \left(\theta \right)+b\varphi \left(\theta \right)=a{\delta }_{\theta }\left(\psi \right)+b{\delta }_{\theta }\left(\varphi \right).$$

Thus, ${\delta }_{\theta }$ is a well-defined linear map.

(A2) To prove ${\delta }_{\theta }$ is continuous, we must show it is bounded. That is, we must find a constant $C>0$ such that for all $\psi \in {\mathcal{B}}_L$,

$$|{\delta }_{\theta }{\left(\psi \right)|=|\psi \left(\theta \right)|\le C\parallel \psi \parallel }_L.$$

Let $\psi ={\psi }_c+{\psi }_d$ be the unique decomposition of $\psi$ into its continuous and discrete parts. By the triangle inequality:

$$\left|\psi \left(\theta \right)\right|=|{\psi }_c\left(\theta \right)+{\psi }_d\left(\theta \right)| \le |{\psi }_c\left(\theta \right)|+|{\psi }_d\left(\theta \right)|.$$

Writing ${\psi }_d\left(t\right)={\sum }_k{\Delta }_k{\chi }_{[t_k,0]}\left(t\right)$ with jumps at $t_k\le -\delta$, we obtain ${\int }_{-\tau }^0|{\psi }_d\left(s\right)|ds={\sum }_k|{\Delta }_k|(0-t_k)\ge \delta {\sum }_k\left|{\Delta }_k\right|$. Hence, $|{\psi }_d\left(t\right)|\le {\sum }_k|{\Delta }_k|\le \frac{1}{\delta }{\int }_{-\tau }^0\left|{\psi }_d\left(s\right)\right|ds$. Therefore,

$$\begin{array}{ccc}\hfill \left|\psi \right(\theta \left)\right|& \le & |{\psi }_c\left(\theta \right)|+|{\psi }_d\left(\theta \right)|\le \parallel {\psi }_c{\parallel }_{\infty }+\sum _{t_k\le \theta }\left|a_k\right|\hfill \\ & \le & \parallel {\psi }_c{\parallel }_{\infty }+{\displaystyle \frac{1}{\delta }}\sum _k\left|a_k\right|(-t_k)\hfill \\ & =& \parallel {\psi }_c{\parallel }_{\infty }+{\displaystyle \frac{1}{\delta }}\parallel {\psi }_d{\parallel }_1\le max\left(1,\frac{1}{\delta }\right){\parallel \psi \parallel }_L,\hfill \end{array}$$

so the evaluation map $\psi \mapsto \psi \left(t\right)$ is continuous.

(A3) For $\psi \in C([-\tau ,0],{\mathbb{R}}^n)$ we have ${\psi }_d\equiv 0$, hence ${\parallel \psi \parallel }_L=\parallel {\psi }_c{\parallel }_{\infty }={\parallel \psi \parallel }_{\infty }$. Thus, the inclusion $C\hookrightarrow \mathcal{B}$ is isometric.

(A4) Let $x:(-\infty ,a)\to {\mathbb{R}}^n$ be continuous on $[0,a)$ and $x_0\in \mathcal{B}$. Then, $x_t\left(\theta \right):=x(t+\theta )$ decomposes as $x_{t,c}+x_{t,d}$. The continuous part $x_{t,c}$ depends continuously on t in ${\parallel ·\parallel }_{\infty }$ by uniform continuity of x on compact intervals. The step part $x_{t,d}$ is a finite sum of shifted jumps; the $L^1$–distance between ${\left(x_{t+h}\right)}_d$ and ${\left(x_t\right)}_d$ is bounded by ${\sum }_k|{\Delta }_k\left|\right|h|$, hence is convergent to zero as $h\to 0$. Thus, $t\mapsto x_t$ is continuous in ${\parallel ·\parallel }_L$ and $x_t\in \mathcal{B}$ for all t.

(B) Assume $\psi \in {\mathcal{B}}_L$ is non-negative, meaning $\psi \left(\xi \right)\ge 0$ for all $\xi \in [-\tau ,0]$. We must show that its value at any point $\theta$ is controlled by its norm. Since $\psi$ is non-negative, we have $\left|\psi \right(\theta \left)\right|=\psi \left(\theta \right)$. From the inequality in (A2), we immediately have:

$$\left|\psi \left(\theta \right)\right|=\psi \left(\theta \right)\le {C\parallel \psi \parallel }_L.$$

Therefore, the space $({\mathcal{B}}_L,\parallel ·{\parallel }_L)$ satisfies Axiom (B). □

Corollary 2.

Fix $\delta \in (0,\tau ]$. Let $\mathcal{B}={\mathcal{B}}_{\delta }\cap G_{\mathit{rc}}([-\tau ,0],{\mathbb{R}}^n)$ and define the new scaled phase–space norm

$${\parallel \psi \parallel }_{L,\delta }:=\parallel {\psi }_c{\parallel }_{\infty }+{\displaystyle \frac{1}{\delta }}{\int }_{-\tau }^0\left|{\psi }_d\left(t\right)\right|dt.$$

Then, $(\mathcal{B},\parallel ·{\parallel }_{L,\delta })$ is a Banach space and satisfies Axioms (A1)–(A4). Moreover, if $\psi \in \mathcal{B}$ satisfies $\psi \left(\xi \right)\ge 0$ for all $\xi \in [-\tau ,0]$, then for every $\theta \in [-\tau ,0]$

$$\left|\psi \left(\theta \right)\right|\le {2\parallel \psi \parallel }_{L,\delta }.$$

Consequently, Axiom (B) (pointwise control for non-negative functions) holds uniformly with respect to the parameters δ with a constant 2.

Remark 6.

Although the chosen norm and subspace of $Z_G^L$ are sufficient for the applications under consideration. However, they do not ensure the continuity and boundedness of the translation operator in the most general case. We will address this issue separately. For now, we will only point out the possibility that the space, denoted by ${\mathcal{B}}_{w,L}$, is actually the phase space when equipped with a different norm:

$${\parallel \psi \parallel }_{w,L}:=\parallel {\psi }_c{\parallel }_{\infty }+{\displaystyle \frac{1}{\delta }}{\int }_{-\tau }^{0}w\left(u\right)\left|{\psi }_d\left(u\right)\right|du,$$

where w is a weight (such that $w\left(0\right)=0$ and $w\left(t\right)>0$ for $t\in [-\tau ,0)$). Standard reasoning proves that it is a Banach space. The case of ${\mathcal{B}}_{\delta }$ is covered by the case of the weight function $w\left(x\right)={\chi }_{[-\tau ,\delta ]}\left(x\right)$.

3.2. Solutions for FDE

Let us briefly discuss some notions of solutions for functional differential equations. It is important to relate this definition to the considered hypotheses for $\psi$ and f in (4).

First, consider the case when it should be satisfied in every $t\in [-\tau ,T]$. It is related to the case when both $\psi$ and f are continuous. As a classical solution, we mean a continuously differentiable function x such that its derivative satisfies (4) at each t, so $x\in C^1\left([-\tau ,T]\right)$. Usually it is presented in an integral form (cf. [18,21], for instance):

$$x\left(t\right)=\psi \left(0\right)+{\int }_0^{t}f(s,x(s-\tau ))ds\mathrm{for}t\ge 0.$$

One problem, however, is that the function $f(·,\psi (·\left)\right)$ need not be Riemann (or: Lebesgue) integrable. We need to discuss the new integral form of the problem and the space of solutions.

Let $\psi \in G([-\tau ,0],{\mathbb{R}}^n)$. Recall that we expect that all the discontinuity points of $\psi$ could then be propagated for $t\in [0,T]$.

Definition 4

([9,45]). A function $x:[-\tau ,T]\to {\mathbb{R}}^n$ is called a regulated solution for the problem (4) on $[-\tau ,T]$ provided it is a regulated function, it coincides with ψ on $[-\tau ,0]$, is a.e. differentiable on $[0,T]$ and its derivative satisfies a.e. the equation $x^{\prime }\left(t\right)=f(t,x(t-\tau ))$ on this interval.

If the initial function $\psi$ is continuous, then the regulated solution is a continuous function. If moreover, $N_f\left(x\right)(·)$ is continuous, then it is $C^1$ function, and we obtain a classical solution. However, we still need to expand this definition to indicate a better integral form that allows for discontinuities and is connected to the initial function.

Assume that the initial function, denoted by $\psi$, is a regulated function, and let $D_{\psi }$ be the set of its discontinuity points. According to the properties of regulated functions, this set is at most countable. Consider the following integral equation

$$x\left(t\right)=\psi \left(0\right)+\left(S\right){\int }_0^{t}f(s,x_s)dg\left(s\right),$$

(6)

where $g=g\left(\psi \right)\in Z_G^L$ is continuously dependent on $\psi$, i.e., it is an image of continuous mapping $g:Z_G^L\left([-\tau ,0]\right)\to Z_G^L\left([0,T]\right)$. The integral sign is taken in the Stieltjes sense, which will be described later, and f is of bounded variation.

Now, we can introduce a general definition of solutions to functional differential equations.

Definition 5.

A function $x:[-\tau ,T]\to {\mathbb{R}}^n$ is called a ψ-solution to the problem $x^{\prime }\left(t\right)=f(t,x_t)$ with $x\left(s\right)=\psi \left(s\right)$ for $s\in [-\tau ,0]$ if it satisfies for all t the integral Equation (6) for some function g continuously dependent on ψ.

In the classical approach to solving differential equations with delay, recall that the discontinuity of the initial function only manifests as the propagation of the discontinuity to the derivatives [47]. This results in a series of jump discontinuities in the higher derivatives at times $t=n\tau$ ($n\in \mathbb{N}$). At the same time, the solution becomes smoother between each jump point. The derivatives of the solution become progressively less continuous, but the solution itself does not. We propose keeping all the properties of the initial function in the future.

When $g\left(t\right)=t$, independently of $\psi$, then this notion coincides with the classical one. Our concept of a solution is therefore more general than the classical concept, which is one of its special cases. Selecting an appropriate function g, that depends or does not depend on the function $\psi$ allows for a better fit of the model to actual data, which may differ in each case. This applies not only to the discontinuity points of the initial function $\psi$, but also to model corrections using tempered functions. For example, $g_c\left(t\right)=\mathcal{P}$ in [38].

And how can issues related to impulses be treated as special cases of our approach? Let $\psi \in Z_G^L$ be right-continuous with jump discontinuities in the set $D_{\psi }={\left\{s_i\right\}}_i\subset [-r,0]$ and magnitude $\Delta {\psi }_i=\psi \left(s_i\right)-\psi \left(s_i^{-}\right)$. Define the function $g\left(t\right)$ as follows:

$$g\left(t\right)=t+\sum _i\Delta {\psi }_i·{\chi }_{\{t\ge t_i\}}+\sum _k{\displaystyle \frac{I({\tau }_k,x_{{\tau }_k^{-}})}{f({\tau }_k,x_{{\tau }_k^{-}})}}·{\chi }_{\{t\ge {\tau }_k\}},$$

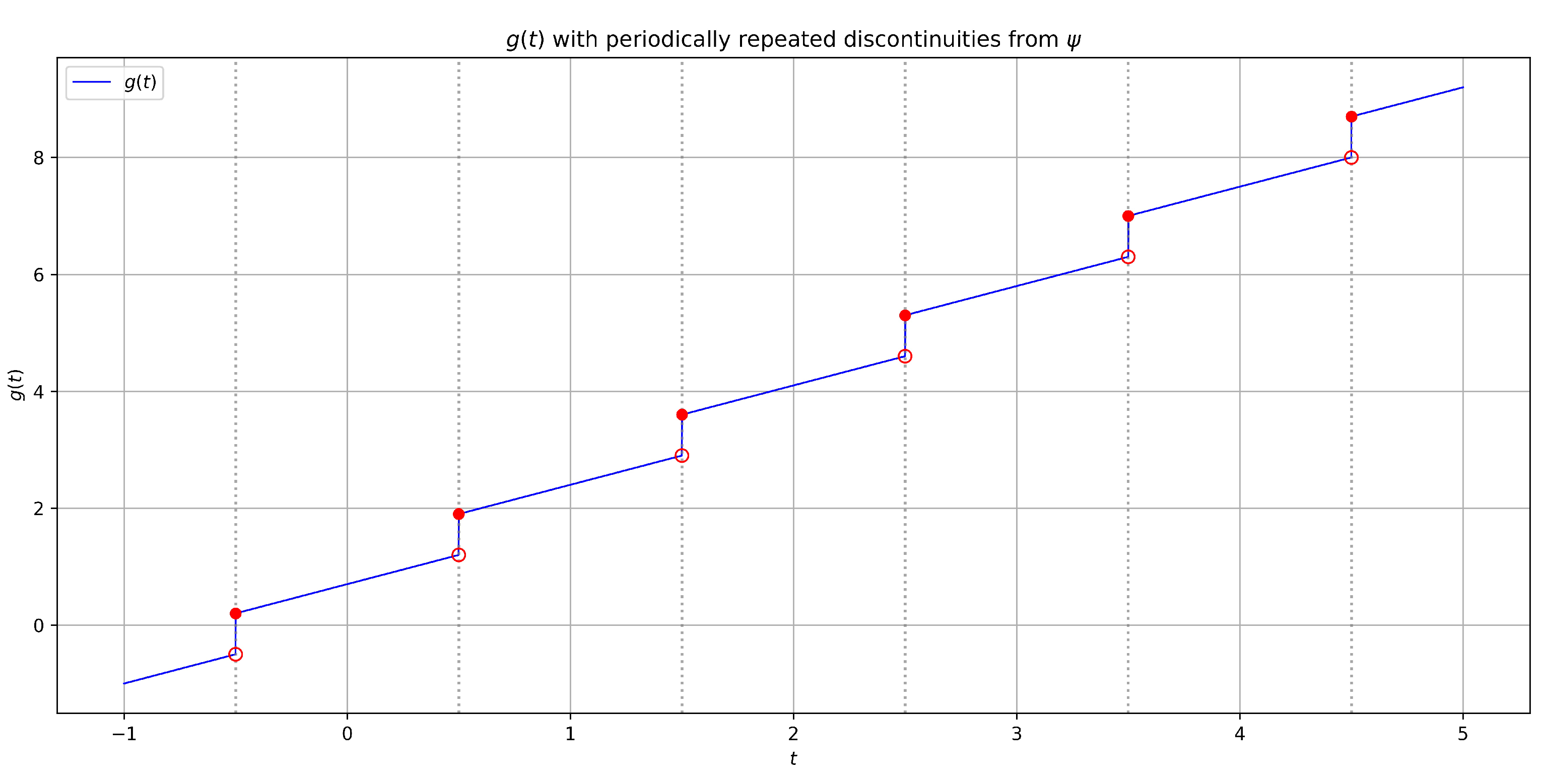
where $t_i=-s_i$. For all impulse times ${\tau }_k$, $f({\tau }_k,x_{{\tau }_k^{-}})\ne 0$. If f is such that the Nemytskii operator $N_f:Z_G^L\to Z_G^L$ generated by f is bounded and continuous, then x is a solution of the impulsive delay differential equation:

$$\begin{array}{ccc}\hfill x^{\prime }\left(t\right)& =& f(t,x_t),t\ne {\tau }_k\left(x\left(t^{-}\right)\right),\hfill \\ \hfill \Delta x\left(t\right)& =& I(t,x_{t^{-}}),t={\tau }_k\left(x\left(t^{-}\right)\right),\hfill \\ \hfill x_{t_0}& =& \psi .\hfill \end{array}$$

(7)

Remark 7.

Clearly, the function g can only retain the information about discontinuities from $\psi \in Z_G^L\left([-\tau ,0]\right)$, i.e., if ${\left(t_k\right)}_{k=1}^{\infty }$ are the points in $[-\tau ,0]$, where ψ has jumps, with jump sizes ${\Delta }_k=\Delta \psi \left(t_k\right)=\psi \left(t_k\right)-\psi \left(t_k^{-}\right)$.

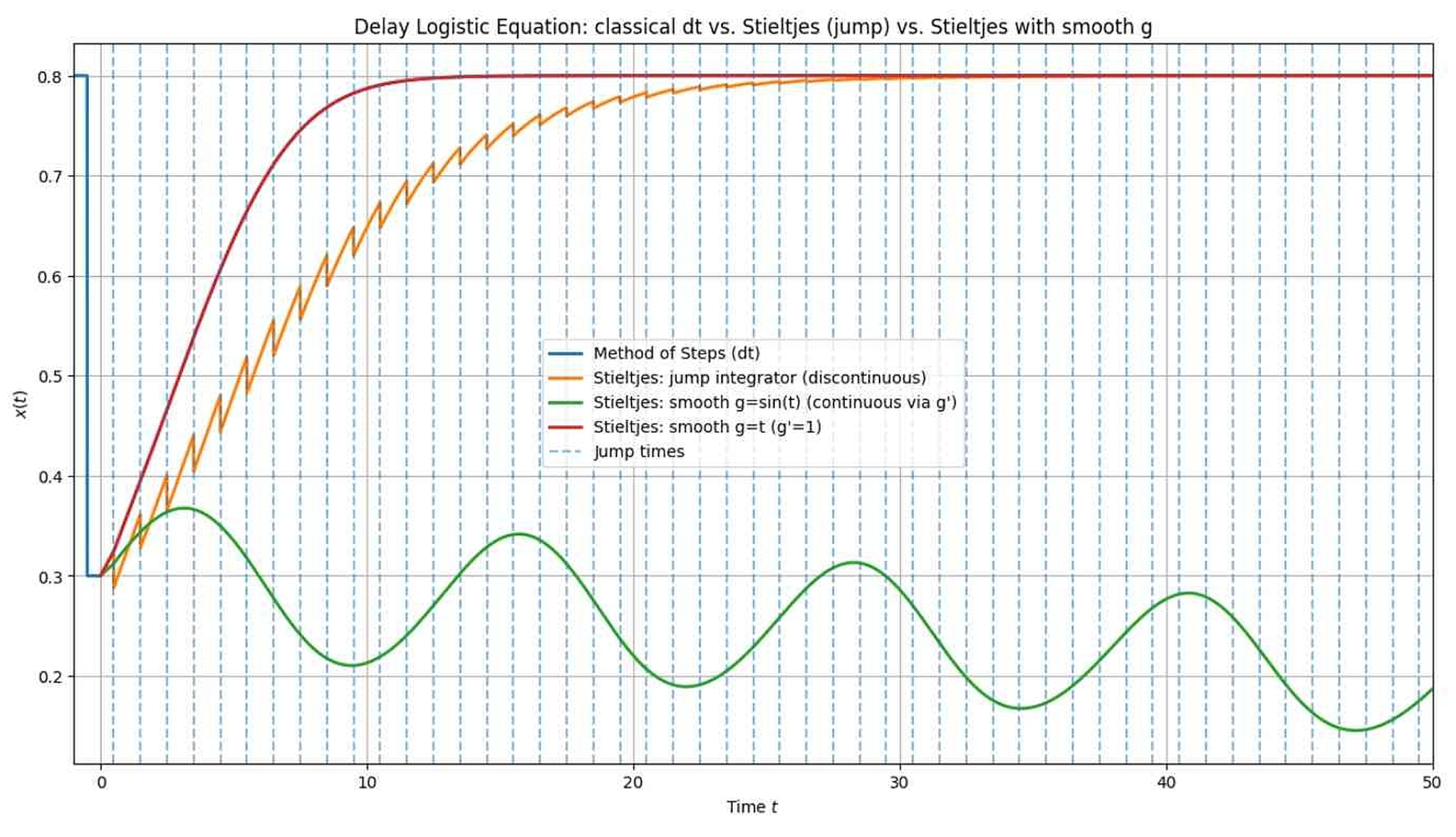
Define $g\left(t\right)$ on $[-\tau ,T]$. We construct $g\left(t\right)$ so that it has jumps of size ${\Delta }_k$ at times:

$$t_{k,n}=t_k+n·\tau ,\mathit{for}n=0,1,2,\dots$$

That is, each discontinuity of ψ at $t_k\in [-\tau ,0]$ is repeated at intervals of length τ. Therefore,

$$g\left(t\right)=t+\sum _{k=1}^m{\Delta }_k·\sum _{n=0}^{\infty }{\chi }_{[t_k+n\tau ,\infty )}\left(t\right),$$

where ${\chi }_{[a,T]}\left(t\right)$ is the characteristic function. More explicitly,

$$g\left(t\right)=t+\sum _{k=1}^m{\Delta }_k·{⌊{\displaystyle \frac{t-t_k}{\tau }}⌋}_{+},$$

where ${\lfloor u\rfloor }_{+}=max(0,\lfloor u\rfloor +1)$ counts the number of full periods after $t_k$ up to t.

The convergence of the series of jumps at every period of time is assured by the assumption that $\psi \in Z_G^L$. What if we expect $T=\infty$? In such a case, we need to add some weights $w_k$ implying convergence of a series:

$$g\left(t\right)=t+\sum _{k=1}^{\infty }{w}_k·{\Delta }_k·\sum _{n=0}^{\infty }{\chi }_{[t_k+nr,\infty )}\left(t\right).$$

Solutions can also be “tempered” by g, as in the case of fractional tempered derivatives (cf. [37]). It is worth mentioning the paper [38] again. The model presented in the paper, which is based on the SIR model and uses the time-tempering function $\mathcal{P}\left(t\right)$. This function is the probability of remaining infectious at time t after becoming infectious. Therefore, it is a monotonic decreasing function. In our terms, $g\left(t\right)=\mathcal{P}\left(t\right)$. Using the Stieltjes integral in our approach preserves the discontinuity of this function. This can help us generalize the proposed model.

Although this is beyond the scope of this work, it is worth noting here that the proposed changes to models based on delay equations obviously apply not only to epidemiology. For those interested in introducing similar changes in other fields, we recommend, for example, the paper [48], where, in application to physics (Sommerfeld–Page equation), delay equations are examined, and the functions considered are only piecewise continuous.

To explicitly show the (possible) dependence of g on ψ, let us rewrite the above function in a direct form. Discrete part of ψ is in the form ${\psi }_d\left(t\right)={\sum }_k{\Delta }_k·{\chi }_{[t_k,0]}\left(t\right)$. We need to extend it periodically (for instance):

$${\tilde{\psi }}_d\left(t\right)=\sum _k{\Delta }_k·{⌊{\displaystyle \frac{t-t_k}{r}}⌋}_{+}.$$

In such a case, we have (see Figure 1):

$$g\left(t\right)=t+{\tilde{\psi }}_d\left(t\right).$$

Remark 8.

This is beyond the scope of our discussion, so we will not go into detail (cf. [38]), but it is worth noting that the continuous part of function g does not have to be trivial (i.e., $g_c\left(t\right)=t$). The Stieltjes integral with respect to $g_c$ is just related to the situation when $x_g^{\prime }\left(t\right)={\displaystyle \frac{dx}{dg}}$ is precisely as the slope of the graph of x after a nonlinear re-scaling of the horizontal axis. If $g_c$ is absolutely continuous, then

$$\left(S\right){\int }_a^{b}f\left(s\right)d{g}_c\left(s\right)={\int }_a^{b}f\left(s\right)g^{\prime }\left(s\right)ds.$$

Therefore, we can highlight certain properties of the solutions and associate them with the function ψ.

Now, let us turn our attention to an important feature of the proposed approach. The function g may contain information from the initial function $\psi$ that we want to preserve in the solution’s properties for $t>0$, which has always been the goal of model research. This includes ensuring the non-negativity, boundedness, and monotonicity of solutions in SIR models. In the proposed approach, these and other properties can be preserved through the function g and the properties of the Stieltjes integral. Different functions g can be defined for specific models based on the initial function $\psi$, but the subject matter will be approached in a unified manner.

Now, we must emphasize the new possibilities afforded by the choice of g. This allows us to maintain the expected properties of the initial function $\psi$ in the future. However, this also means that the uniqueness of solutions depends on the choice of g (see Corollary 1). Consequently,

Theorem 1.

Let $\mathcal{B}$ be a phase space satisfying Axioms (A1)–(A4) from Definition 1, and let $\psi \in \mathcal{B}$ be an initial history. Assume that the functional

$${\mathbf{F}}_g:[0,\infty )\times \mathcal{B}\to {\mathbb{R}}^n$$

satisfies:

1. 

For each $\varphi \in \mathcal{B}$, the map $t\mapsto {\mathbf{F}}_g(t,\varphi )$ is continuous on intervals between jumps of g (or regulated).

2. 

${\mathbf{F}}_g$ is locally Lipschitz in the phase variable uniformly on compact time intervals: for any $R>0$, there exists $L_R>0$ such that

$$|{\mathbf{F}}_g(t,\varphi )-{\mathbf{F}}_g(t,\xi )|\le L_R{\parallel \varphi -\xi \parallel }_{\mathcal{B}},\forall t\ge {0,\parallel \varphi \parallel }_{\mathcal{B}},{\parallel \xi \parallel }_{\mathcal{B}}\le R.$$

Let $g:[0,\infty )\to \mathbb{R}$ be right-continuous with summable jumps and continuous part $g_c$ of bounded variation, i.e.,

$$g\left(t\right)=g_c\left(t\right)+\sum _{s\le t}\Delta g\left(s\right),\mathit{with}\sum _{s\le t}|\Delta g\left(s\right)|<\infty \mathit{and}Var(g_c,[0,T])<\infty .$$

Then, there exists a unique ψ-solution $X:[-\tau ,T_{max})\to {\mathbb{R}}^n$ of the Stieltjes integral equation

$$X\left(t\right)=\psi \left(0\right)+{\int }_0^t{\mathbf{F}}_g(s,X_s)dg\left(s\right),t\ge 0,X_0=\psi ,$$

on a maximal interval $[-\tau ,T_{max})$. The segment map $t\mapsto X_t$ is continuous in $\mathcal{B}$ whenever X is continuous. Moreover, if $T_{max}<\infty$, then

$$\underset{t\to T_{max}^{-}}{lim\; sup}{\parallel X_t\parallel }_{\mathcal{B}}=\infty .$$

Proof. 

Assume that $\psi \in \mathcal{B}$ satisfies the assumptions of our theorem. We consider the integral equation

$$X\left(t\right)=\psi \left(0\right)+{\int }_0^t{\mathbf{F}}_g(s,X_s)dg\left(s\right),t\ge 0,$$

with initial history $X_0=\psi$. Since ${\mathbf{F}}_g$ is continuous, the integrand $s\mapsto {\mathbf{F}}_g(s,X_s)$ is continuous for each continuous X, so the Stieltjes integrals ${\int }_0^t{\mathbf{F}}_g(s,X_s)d{g}_c\left(s\right)$ and ${\int }_0^t{\mathbf{F}}_g(s,X_s)d{g}_d\left(s\right)$ are well defined. The proof follows the classical method of steps with a fixed-point argument, modified to account for the jump part of g.

For sufficiently small $T>0$, i.e.,

$$L_{R}K\left(Var(g_c,[0,T])+\sum _{s\le T}|\Delta g\left(s\right)|\right)<1,$$

define the Banach space

$$\mathcal{X}:=\{X\in C([-\tau ,T],{\mathbb{R}}^n):X_0=\psi ,\parallel X{\parallel }_{\infty }\le R\}$$

with norm ${\parallel X\parallel }_{\infty }:={sup}_{t\in [-\tau ,T]}\left|X\left(t\right)\right|$.

Decompose $g=g_c+g_d$, where $g_c$ is the continuous $BV$ part and $g_d\left(t\right)={\sum }_{s\le t}\Delta g\left(s\right)$ is the discrete part. Define the operator $\mathcal{T}:\mathcal{X}\to \mathcal{X}$ by

$$\left(\mathcal{T}X\right)\left(t\right):=\left\{\begin{array}{cc}\psi \left(t\right),\hfill & t\in [-\tau ,0],\hfill \\ {\displaystyle \psi \left(0\right)+{\int }_0^t{\mathbf{F}}_g(s,X_s)dg\left(s\right),}\hfill & t\in [0,T],\hfill \end{array}\right.$$

where the integral is the Riemann–Stieltjes integral (or KS integral) with respect to the right-continuous function g.

Let $X,Y\in \mathcal{X}$ with ${\parallel X\parallel }_{\infty },{\parallel Y\parallel }_{\infty }\le R$. Using the local Lipschitz property of ${\mathbf{F}}_g$ and axiom (A1), for $t\in [0,T]$, we have

$$\parallel X_s-Y_s{\parallel }_{\mathcal{B}}\le K\underset{\theta \in [-\tau ,0]}{sup}|X(s+\theta )-Y(s+\theta )|\le {K\parallel X-Y\parallel }_{\infty }.$$

Therefore,

$$\begin{array}{ccc}\hfill \left|\right(\mathcal{T}X\left)\right(t)& -& \left(\mathcal{T}Y\right)\left(t\right)|\hfill \\ & & =\left|{\int }_0^t\left({\mathbf{F}}_g(s,X_s)-{\mathbf{F}}_g(s,Y_s)\right)dg\left(s\right)\right|\hfill \\ & & \le {\int }_0^t|{\mathbf{F}}_g(s,X_s)-{\mathbf{F}}_g(s,Y_s)\left|d\right|g_c|\left(s\right)+\sum _{s\le t}|{\mathbf{F}}_g(s,X_s)-{\mathbf{F}}_g(s,Y_s)\left|\right|\Delta g\left(s\right)|\hfill \\ & & \le L_{R}K{\parallel X-Y\parallel }_{\infty }\left(Var(g_c,[0,T])+\sum _{s\le T}|\Delta g\left(s\right)|\right).\hfill \end{array}$$

Define the constant

$$C\left(T\right):=L_{R}K\left(Var(g_c,[0,T])+\sum _{s\le T}|\Delta g\left(s\right)|\right).$$

Since $Var(g_c,[0,T])\to 0$ as $T\to 0$ and ${\sum }_{s\le T}|\Delta g\left(s\right)|\to 0$ as $T\to 0$, we can choose $T>0$ small enough such that $C\left(T\right)<1$. Therefore, $\mathcal{T}$ is a contraction on $\mathcal{X}$, and by the Banach fixed-point theorem, a unique solution X exists on $[0,T]$.

Since X is continuous on $[-\tau ,T]$ and $\mathcal{B}$ satisfies (A2), the map $t\mapsto X_t$ is continuous in $\mathcal{B}$.

Using the method of steps, we can extend the local solution iteratively to the maximal interval $[-\tau ,T_{max})$. Suppose that $T_{max}<\infty$, but ${sup}_{t<T_{max}}{\parallel X_t\parallel }_{\mathcal{B}}<\infty$. Then, for some R larger than this supremum, the contraction argument above produces a local extension beyond $T_{max}$, which contradicts maximality. Therefore, if $T_{max}<\infty$,

$$\underset{t\to T_{max}^{-}}{lim\; sup}{\parallel X_t\parallel }_{\mathcal{B}}=\infty .$$

The uniqueness follows from the same contraction estimate. If X and Y are two solutions on $[-\tau ,T]$, then we can apply the same inequality as above to conclude that

$${\parallel X-Y\parallel }_{\infty }\le {C\left(T\right)\parallel X-Y\parallel }_{\infty }<{\parallel X-Y\parallel }_{\infty },$$

which implies $X\equiv Y$ on $[-\tau ,T]$. By iterating over the maximal interval, uniqueness holds on $[-\tau ,T_{max})$. As an alternative, this part of the proof can be carried out using the Gönwall lemma for the Stieltjes integrals (cf. [40]). However, in epidemiological models, such a generalization is unnecessary. □

The next lemma will allow us to check if discontinuity points for the Kurzweil–Stieltjes integral are preserved (or not). It is also an answer to the question of what we need to assume to keep the continuity or differentiability property at $t=0$ (cf. [47]). Recall that our (KS)-integrals are over closed intervals.

Lemma 4

(Lemma 4.23 and Theorem 2.34 in [49]). Let $f\in G\left(\right[a,b],\mathbb{R})$ and g be a regulated function with bounded variation. Denote by N the set of discontinuity points of F in $(a,b)$ and by $g^C$ the continuous part of g. Then,

$$\left(KS\right){\int }_a^b=\left(KS\right){\int }_a^{b}fd{g}^C+f\left(a\right){\Delta }^{+}g\left(a\right)+\sum _{d\in N}f\left(d\right)\Delta g\left(d\right)+f\left(b\right){\Delta }^{-}g\left(b\right).$$

Remark 9.

Although epidemiological models are based on systems of equations with continuous right-hand sides, we can take advantage of the fact that the proposed approach to solving the problem with the Stieltjes integral also includes the Kurzweil–Stieltjes integral. This allows us to study equations with discontinuous functions. For an extensive discussion of issues related to functions satisfying the Carathéodory condition, along with an interesting discussion of the numerical methods used, see [50]. The problem in this situation lies in the superposition operators generated by such functions in phase space. In our case, phase space is the space of regulated functions, not continuous ones (the necessary and sufficient conditions for this space can be found in [51]).

This is also the reason for adopting the technique of proof based on differential equations in function spaces, which is a methodical approach to proving theorems. Another approach is based on the notion of the Filippov solution (see, for instance applied models in epidemiology, [52,53]). However, this requires research into multivalued superposition operators on the space of regulated functions.

4. Results, Extended Models, Discontinuous Solutions

We will now demonstrate how to modify previous models while retaining their functionality and expanding them with additional capabilities based on their initial functions. This approach can be applied to any of the models discussed, so we will focus on highlighting its possibilities and benefits.

Motivated by a paper (Figure 1 in [27]) in which the jumps are observed and discussed, we propose incorporating this property of solutions into the initial function. Unlike the classical model discussed in the paper [27], discontinuities in derivatives in the initial function imply not only primary discontinuities in derivatives, but also discontinuities in solutions.

4.1. Impulsive Problems

To illustrate how our paper’s findings can be applied, let us consider extending the pulse vaccination strategy problems for the SIR model. Consider the problem (2) and (3). We are given a system with continuous dynamics and impulsive conditions at times $t_k$. The function $g\left(t\right)$ is defined to capture both the continuous flow and the jumps:

$$g\left(t\right)=t+\sum _{k=1}^m{\Delta }_{{\psi }_k}·\sum _{n=0}^{\infty }{\chi }_{[t_k+n\tau ,\infty )}\left(t\right),$$

where $t_k$ are discontinuity points of the initial function $\psi$ (on $[-\tau ,0]$), specifically $t_k=s_k+\tau$ for each discontinuity point $s_k$ of $\psi$. The jumps in $g\left(t\right)$ occur at $t=t_k+n\tau$ for $n=0,1,2,\dots$, with jump size ${\Delta }_{{\psi }_k}$.

Let us consider the initial function $\psi$ defined on $[-\tau ,0]$ as:

$$\psi \left(s\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}},\hfill & s\in [-\tau ,-\tau /2),\hfill \\ {\displaystyle \frac{1}{3}},\hfill & s\in [-\tau /2,0),\hfill \\ 0,\hfill & s=0.\hfill \end{array}\right.$$

This initial function $\psi$ has a discontinuity at $s=-\tau /2$. Therefore, the set of discontinuity points of $\psi$ is a singelton $\left\{s_1\right\}=\{-\tau /2\}$. The impulse times $t_k$ are given by $t_k=s_k+\tau$. So:

$$t_1=-\tau /2+\tau =\tau /2.$$

Thus, the jump points for $g\left(t\right)$ are at $t=t_1+n\tau =\tau /2+n\tau$ for $n=0,1,2,\dots$. The function $g\left(t\right)$ is:

$$g\left(t\right)=t+\sum _{k=1}^m{\Delta }_{{\psi }_k}·\sum _{n=0}^{\infty }{\chi }_{[t_k+n\tau ,\infty )}\left(t\right).$$

With $m=1$, $t_1=\tau /2$, and we set ${\Delta }_{{\psi }_1}=1$:

$$g\left(t\right)=t+\sum _{n=0}^{\infty }{\chi }_{[\tau /2+n\tau ,\infty )}\left(t\right).$$

This means $g\left(t\right)$ increases continuously with slope 1 and has jumps of size 1 at $t=\tau /2,\tau /2+\tau ,\tau /2+2\tau ,\dots$. The set of jump points is:

$$J=\{t_1+n\tau :n=0,1,2,\dots \}=\{\tau /2,\tau /2+\tau ,\tau /2+2\tau ,\dots \}.$$

We have Stieltjes equations:

$$\begin{array}{ccc}\hfill S\left(t\right)& =& S\left(0\right)+{\int }_0^t\left[\left(\mu N-{\displaystyle \frac{\beta I\left(s\right)S\left(s\right)}{N}}-\mu S\left(s\right)+\gamma R(s-\tau )e^{-\mu \tau }\right)(1-{\chi }_J\left(s\right))\right.\hfill \\ & & \left.-\nu S\left(s^{-}\right){\chi }_J\left(s\right)\right]dg\left(s\right),\hfill \\ \hfill I\left(t\right)& =& I\left(0\right)+{\int }_0^t\left[\left({\displaystyle \frac{\beta I\left(s\right)S\left(s\right)}{N}}-(\gamma +\mu )I\left(s\right)\right)(1-{\chi }_J\left(s\right))\right]dg\left(s\right),\hfill \\ \hfill R\left(t\right)& =& R\left(0\right)+{\int }_0^t\left[\left(-\mu R\left(s\right)-\gamma R(s-\tau )e^{-\mu \tau }+\gamma I\left(s\right)\right)(1-{\chi }_J\left(s\right))\right.\hfill \\ & & \left.+\nu S\left(s^{-}\right){\chi }_J\left(s\right)\right]dg\left(s\right).\hfill \end{array}$$

Since $g\left(t\right)$ has jumps only at $s\in J$, we can split the integrals into continuous and jump parts. For any function $F\left(s\right)$:

$${\int }_0^{t}F\left(s\right)dg\left(s\right)={\int }_0^{t}F\left(s\right)ds+\sum _{\begin{array}{c}n=0,\tau /2+n\tau \le t\end{array}}^{\infty }F(\tau /2+n\tau ).$$

This is because $dg\left(s\right)=ds$ for $s\notin J$, and at $s=\tau /2+n\tau$, $dg\left(s\right)$ has a jump of size 1. Therefore, we can write the Stieltjes integral equations:

$$\begin{array}{ccc}\hfill S\left(t\right)& =& S\left(0\right)+{\int }_0^t\left(\mu N-{\displaystyle \frac{\beta I\left(s\right)S\left(s\right)}{N}}-\mu S\left(s\right)+\gamma R(s-\tau )e^{-\mu \tau }\right)(1-{\chi }_J\left(s\right))ds\hfill \\ & & -\nu \sum _{\begin{array}{c}n=0,\tau /2+n\tau \le t\end{array}}^{\infty }S\left({(\tau /2+n\tau )}^{-}\right),\hfill \\ \hfill I\left(t\right)& =& I\left(0\right)+{\int }_0^t\left({\displaystyle \frac{\beta I\left(s\right)S\left(s\right)}{N}}-(\gamma +\mu )I\left(s\right)\right)(1-{\chi }_J\left(s\right))ds,\hfill \\ \hfill R\left(t\right)& =& R\left(0\right)+{\int }_0^t\left(-\mu R\left(s\right)-\gamma R(s-\tau )e^{-\mu \tau }+\gamma I\left(s\right)\right)(1-{\chi }_J\left(s\right))ds\hfill \\ & & +\nu \sum _{\begin{array}{c}n=0,\tau /2+n\tau \le t\end{array}}^{\infty }S\left({(\tau /2+n\tau )}^{-}\right).\hfill \end{array}$$

Note that $1-{\chi }_J\left(s\right)=1$ for $s\notin J$, and 0 for $s\in J$. So the integrals over $ds$ are actually over intervals where $s\notin J$. However, since the integrands are defined continuously, we can extend the integral to all s and subtract the contributions at jump points. But in practice, the integrals are over continuous intervals.

For t in between jumps, the dynamics are given by the ordinary differential equations. At $t=\tau /2+n\tau$, the states jump:

$$\begin{array}{cc}\hfill S\left(t^{+}\right)& =(1-\nu )S\left(t^{-}\right),\hfill \\ \hfill I\left(t^{+}\right)& =I\left(t^{-}\right),\hfill \\ \hfill R\left(t^{+}\right)& =R\left(t^{-}\right)+\nu S\left(t^{-}\right).\hfill \end{array}$$

This example shows how the Stieltjes formulation captures both the continuous dynamics and the impulsive conditions at $t=\tau /2,\tau /2+\tau ,\dots$.

With $\psi$ having a discontinuity at $-\tau /2$, we get $t_1=-\tau /2+\tau =\tau /2$, and the system becomes:

$$\begin{array}{cc}\hfill S\left(t\right)& =S\left(0\right)+{\int }_0^t\left(\mu N-{\displaystyle \frac{\beta I\left(s\right)S\left(s\right)}{N}}-\mu S\left(s\right)+\gamma R(s-\tau )e^{-\mu \tau }\right)(1-{\chi }_J\left(s\right))ds\hfill \\ & -\nu \sum _{\begin{array}{c}n=0,\tau /2+n\tau \le t\end{array}}^{\infty }S\left({(\tau /2+n\tau )}^{-}\right),\hfill \\ \hfill I\left(t\right)& =I\left(0\right)+{\int }_0^t\left({\displaystyle \frac{\beta I\left(s\right)S\left(s\right)}{N}}-(\gamma +\mu )I\left(s\right)\right)(1-{\chi }_J\left(s\right))ds,\hfill \\ \hfill R\left(t\right)& =R\left(0\right)+{\int }_0^t\left(-\mu R\left(s\right)-\gamma R(s-\tau )e^{-\mu \tau }+\gamma I\left(s\right)\right)(1-{\chi }_J\left(s\right))ds\hfill \\ & +\nu \sum _{\begin{array}{c}n=0,\tau /2+n\tau \le t\end{array}}^{\infty }S\left({(\tau /2+n\tau )}^{-}\right),\hfill \end{array}$$

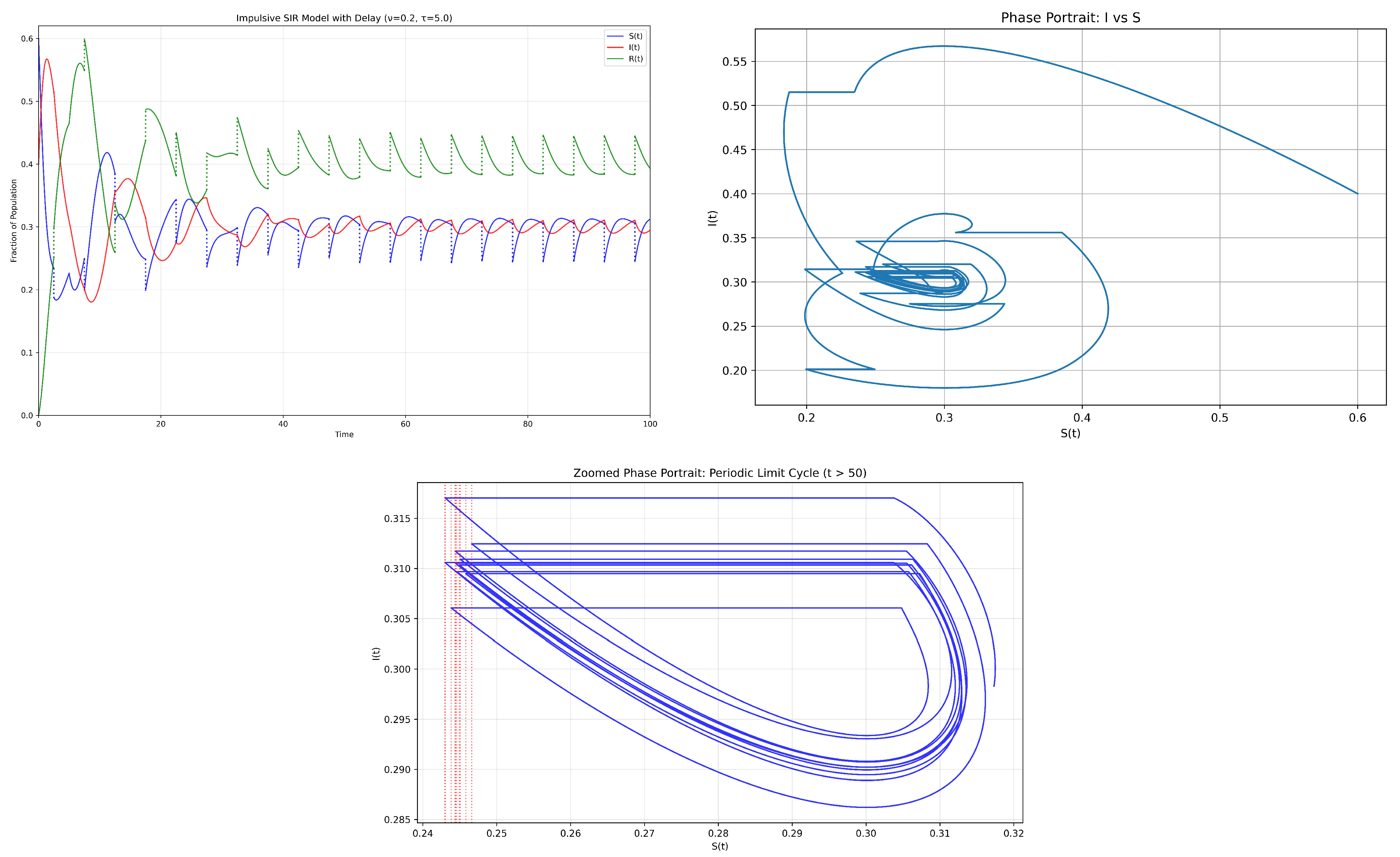
where $J=\{\tau /2+n\tau :n=0,1,2,\dots \}$. This is a simplified form that uses the initial function $\psi$, and the discontinuities follow from the past. Here are some numerical results for the set of parameters: $N=1.0$, $\beta =2.0$, $\gamma =0.5$, $\mu =0.1$, $\tau =5$, and $\nu =0.2$ (see Figure 2).

Simulation of the endemic case: $N=1.0$, $\beta =0.5$, $\gamma =0.2$, $\mu =0.00003$, $\tau =0.5$, $\nu =0.15$. There is a jump in half of the period (see Figure 3).

4.2. Simulations of the SIR Model Using $\psi$-Solutions

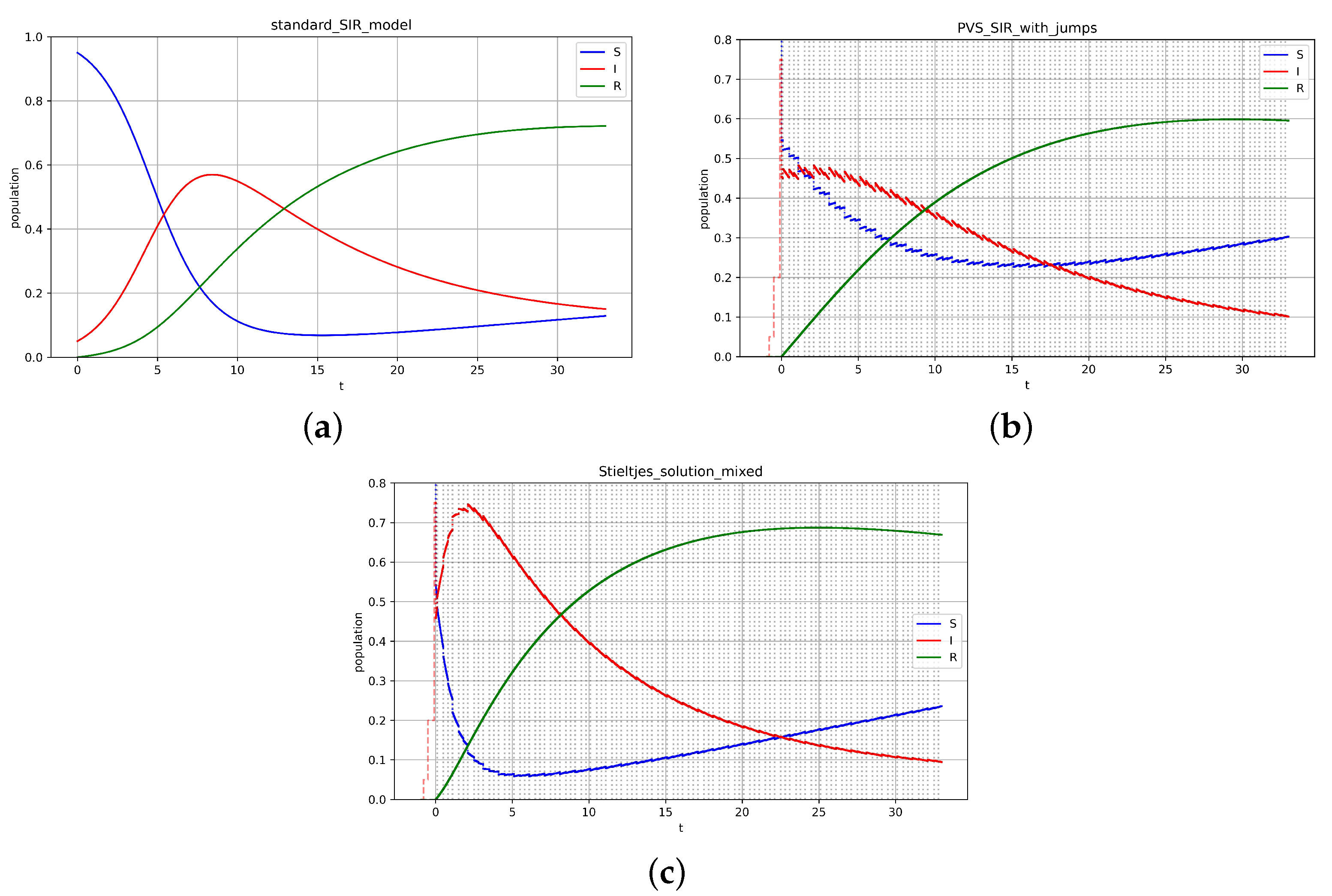
The approach to the topic presented in this paper involves introducing new parameters to epidemiological models and is not intended to replace existing models. However, it can supplement the adjustment of models to actual data, depending on the scale of the data range, for example. Each case requires research, which we leave to the readers interested in specific situations. Using the SIR model as an example, we will demonstrate the impact of incorporating various g functions into the model. First, we will determine the parameters, and then we will illustrate the additional possibilities offered by the proposed model extension. Fix $\beta =0.7$, $\mu =0.02$, $\gamma =0.1$ and $\tau =1$.

Figure 4 illustrates simulations performed using: (a) a classical model; (b) the $\psi$-solution with impulses information preserved from the initial function; and (c) time-scale tempering ($g_c\left(t\right)=2·\sqrt{t}$) together with $g_d\left(t\right)$, based on the impulses of the initial function. Interested readers can perform these simulations on models of interest with delay and their actual data for better fitting.

Although the equilibrium can be calculated in each case, it may vary. For the cases studied, numerical approximations were obtained (after time $t=1000$): (a) $S^{*}=0.1714, I^{*}=0.1381, R^{*}=0.6905$, (b) $S^{*}=0.4759, I^{*}=0.0855, R^{*}=0.4385$, (c) $S^{*}=0.4427, I^{*}=0.0910, R^{*}=0.4663$. An analytical approach requires in-depth, separate studies.

4.3. Notes on Numerical Methods

Although this is not the main topic of this paper, we will present brief comments on numerical solutions to the problem in question. For instance, see [54] for insight into the challenges and approaches when numerically solving equations involving Stieltjes integrals. The application of known or modified numerical methods to equations involving Stieltjes integrals is a broad mathematical topic that will be discussed separately.

In the above numerical simulation, we employed the explicit Euler method for cases without discontinuities. For Stieltjes cases, we applied the Euler method to the continuous part and performed explicit jump calculations using the Euler–Maruyama method with pulses [55] for the jump part. We calculated the delay integral using quadrature with a precomputed Weibull kernel (cf. [54]) over the s-grid and linear interpolation of the history. This is a hybrid scheme: it is an ODE solver with quadrature and impulsive updates. This approach is preferable because it considers the hybrid nature of the problem from the beginning.

Rather than forcing pulses into continuous solvers of ordinary differential equations, we use a customized numerical method that considers the mathematical structure of pulse systems. This results in greater accuracy, preservation of convergence order, and more reliable and efficient algorithms, especially for long-term simulations or problems involving numerous pulses (see Figure 5,

Table 1. Error measurements (S component only) and computation times.

$\Delta \mathit{t}$	Method	Time (s)	S Component
			Max Error	L2 Error
0.050	Standard	0.002	4.800 × ${10}^{-3}$	1.076 × ${10}^{-3}$
	Atomic	0.064	2.046 × ${10}^{-3}$	9.523 × ${10}^{-4}$
	Mixed	0.067	1.720 × ${10}^{-2}$	2.859 × ${10}^{-3}$
0.020	Standard	0.006	1.838 × ${10}^{-3}$	4.133 × ${10}^{-4}$
	Atomic	0.161	8.371 × ${10}^{-4}$	3.784 × ${10}^{-4}$
	Mixed	0.167	1.075 × ${10}^{-2}$	1.873 × ${10}^{-3}$
0.010	Standard	0.011	8.562 × ${10}^{-4}$	1.928 × ${10}^{-4}$
	Atomic	0.329	4.167 × ${10}^{-4}$	1.828 × ${10}^{-4}$
	Mixed	0.393	6.901 × ${10}^{-3}$	1.239 × ${10}^{-3}$

).

However, it is important to note that the focus of this paper is not on new numerical methods and their potential applications. That will be the focus of future research. For now, we will only mention an interesting development of the Euler method, the randomized Euler scheme [50]. This scheme may be useful for studying function discontinuities, especially in combination with [54].

Now, we will compare the Euler and Runge–Kutta fourth-order (RK4) methods for the drift-only part of the delayed SIR-type model with continuous and discontinuous drivers (see

Table 2. Comparison of Euler and RK4 methods: runtime and maximum error.

Method	$\Delta \mathit{t}$	Runtime (s)	Max Error
euler	0.10000	0.0076	2.33 × ${10}^{-2}$
euler	0.05000	0.0140	8.91 × ${10}^{-3}$
euler	0.02500	0.0281	7.25 × ${10}^{-3}$
euler	0.01250	0.0585	5.29 × ${10}^{-3}$
rk4	0.10000	0.0109	2.34 × ${10}^{-2}$
rk4	0.05000	0.0192	8.91 × ${10}^{-3}$
rk4	0.02500	0.0384	7.25 × ${10}^{-3}$
rk4	0.01250	0.0761	5.29 × ${10}^{-3}$

). Both solvers treat jumps and delay-integral contributions the same, but continuous drift (the ODE part) is integrated using either the Euler or RK4 method. Then, we will perform a convergence benchmark by halving the time step ($dt$) and runtime cost.

4.4. Vaccination Model with Delay and Discontinuities

We will return to the model analysis we mentioned earlier. This time, however, we will look for discontinuous solutions and demonstrate how to carry out this process based on the new phase space. It is a new version of the fully discontinuous vaccination model from Example 1.

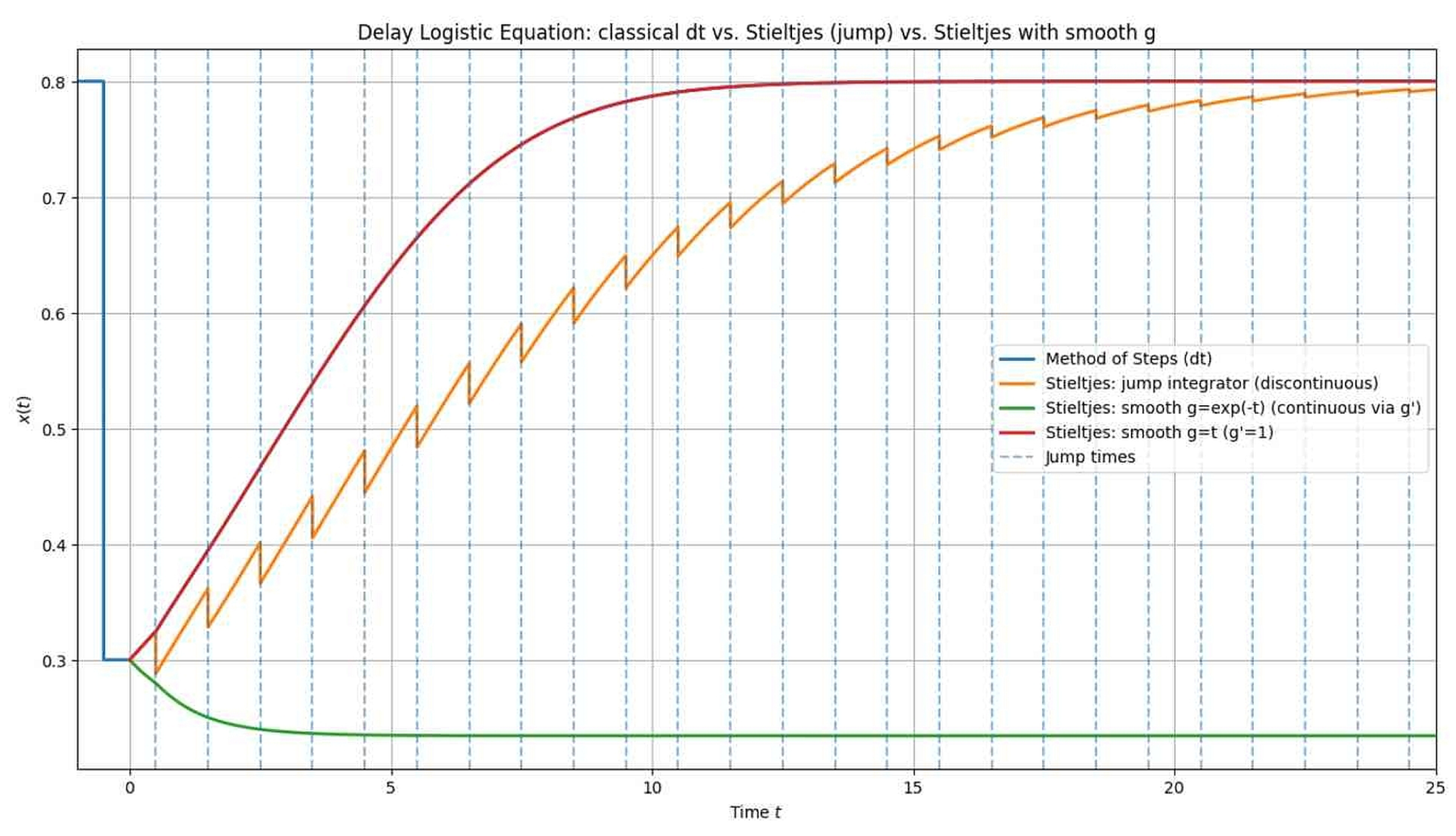
Example 2.

If we are looking for regulated solutions, then $S\left(t\right)=S_c\left(t\right)+S_d\left(t\right)$, where $S_c\left(t\right)$ solves

$${\displaystyle \frac{d{S}_c}{dt}}=\mu -\beta S_c\left(t\right)I\left(t\right)-\mu S_c\left(t\right)$$

(smooth ODE), and $S_d\left(t\right)$ is piecewise constant with jumps $\Delta S_d\left(t_k\right)=-pS\left(t_k^{-}\right)$ at each vaccination time $t_k$. Thus, at each vaccination time $t_k$, the solution instantaneously decreases by $pS\left(t_k^{-}\right)$:

$$S\left(t_k^{+}\right)=S\left(t_k^{-}\right)-pS\left(t_k^{-}\right)=(1-p)S\left(t_k^{-}\right).$$

Between pulses, $S\left(t\right)$ evolves continuously via the ordinary differential equations. In this model, we have:

$$\parallel S\parallel = \parallel S_c{\parallel }_{\infty }+{\int }_a^b\left|S_d\left(s\right)\right|ds,$$

with the bounds of the continuous part $\parallel S_c{\parallel }_{\infty }$ and where $\int |S_d\left(s\right)|ds$ denotes the sum of jumps (weighted by their duration, which is zero for impulses, so this term is effectively a sum of jump heights).

As a single problem, we can define the following Stieltjes differential equation:

$$S\left(t\right)=S\left(0\right)+{\int }_0^t\left[\mu -\beta S\left(s^{-}\right)I\left(s\right)-\mu S\left(s^{-}\right)\right]ds-{\int }_{[0,t]}S\left(s^{-}\right)dV\left(s\right),$$

where $S\left(t^{-}\right)={lim}_{s\uparrow t}S\left(s\right)$, $V\left(t\right)={\sum }_k{\chi }_{\{t_k\le t\}}$ is a step function counting vaccinations, and $dV\left(t\right)$ is the Stieltjes measure (point masses at $t_k$). Here the total vaccinations administered up to time t is $V\left(t\right)=V_c\left(t\right)+V_d\left(t\right)$, with $V_c\left(t\right)={\int }_0^t{v}_c\left(s\right)ds,v_c\left(s\right)\ge 0$, and

$$V_d\left(t\right)=\sum _{k:t_k\le t}{p}_k,p_k\ge 0.$$

Clearly,

$${\int }_{[0,t]}S\left(s^{-}\right)v_c\left(s\right)ds$$

and

$${\int }_{[0,t]}S\left(s^{-}\right)d{V}_d\left(s\right)=\sum _{k:t_k\le t}S\left(t_k^{-}\right)p_k.$$

In particular, for a fixed pulse vaccinations ($v_c=0$, $p_k=p$) we have:

$$S\left(t\right)=S\left(0\right)+{\int }_0^t\left[\mu -\beta S\left(s^{-}\right)I\left(s\right)-\mu S\left(s^{-}\right)\right]ds-p\sum _{k:t_k\le t}S\left(t_k^{-}\right).$$

We will unify such an integral form using the Riemann–Stieltjes integral.

In this approach, we keep the impulsive effect, but there are no distributions, we can consider function spaces. Moreover, when comparing with the stochastic approach, the integral $\int |S_d|ds$ quantifies total vaccination impact (sum of $pS\left(t_k^{-}\right)$ over time), e.g., we have a cumulative vaccination effect. It seems to be more natural for control and optimization (e.g., minimizing vaccination effort $\int |S_d|ds$).

The next natural step is to incorporate a delay into the continuous part of the vaccination model. It is both possible and meaningful to introduce delays into the continuous part of the model. This accounts for real-world scenarios like immune response delays: the time lag between vaccination and effective immunity. Moreover, logistical delays, i.e., time between vaccine administration and population-level effects, and finally incubation periods, i.e., delays in disease progression or symptom onset.

In this case, we can consider the continuous part $S_c\left(t\right)$, to include a time delay $\tau \ge 0$

$${\displaystyle \frac{d{S}_c\left(t\right)}{dt}}=\mu -\beta S_c\left(t\right)I\left(t\right)-\mu S_c\left(t\right)-\gamma S_c(t-\tau ),$$

where $\gamma S_c(t-\tau )$ models delayed effects (e.g., immunity activation after vaccination), and the term $\gamma \ge 0$ scales the delayed impact. The discrete part can be unchanged here. Finally, we can consider the following model:

$$dS\left(t\right)=\left[\mu -\beta S\left(t^{-}\right)I\left(t\right)-\mu S\left(t^{-}\right)-\gamma S(t^{-}-\tau )\right]dt-pS\left(t^{-}\right)d{V}_d\left(t\right),$$

with history described by a regulated function $\psi \left(t\right)={\psi }_c\left(t\right)+{\psi }_d\left(t\right)\in Z_G^L$ on $[-\tau ,0]$, jumps are described explicitly by $S\left(t_k\right)=(1-p)S\left(t_k^{-}\right)$.

Remark 10.

Note that our proposed modeling approach reconciles the previous two approaches. First, the previous approaches did not consider vaccination impulses $t_k$ in the form of their distributions around $t_k$. This eliminates discontinuities and the observed effects (e.g., PVS). Second, rather than considering only point impulses (i.e., treating initial functions as step functions), we can use piecewise continuous functions to model the impulse at time $t_k$ and the short-term increase in “delayed” vaccinations. This allows us to make full use of the information contained in the initial function.

5. Some Other Applications

Many classical treatments of delay differential equations assume the initial function is continuous on $[-\tau ,0]$ (e.g., [3,18,21,39]). However, there are important cases where the initial function is discontinuous on $(-\tau ,0)$, so the phase space must be extended to include such functions. We proposed a new phase space that allows for a unified approach to continuous and discontinuous solutions. Below are some concrete examples where discontinuities in the interval $(-\tau ,0)$ arise naturally.

To indicate the future recommended review of models that can be modified in the manner presented here, let us show a few examples not restricted to epidemiology.

5.1. Models in Biology

In gene regulatory networks, model mRNA production often occurs in stochastic bursts (with the deterministic idealization), leading to discontinuous histories:

$${\displaystyle \frac{dx\left(t\right)}{dt}}=-\gamma x\left(t\right)+\alpha ·x(t-\tau )·{\chi }_{[0,\infty )}(x(t-\tau )$$

where $x\left(t\right)$ = mRNA concentration. This is a specific example of a broader class of models known as delay differential equations with discontinuous right-hand sides. In such cases, we must be careful when defining Stieltjes integrals (see the discussion in [9,45]).

The initial function is discontinuous:

$$x\left(t\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{for}t\in [-\tau ,-\tau /2),\hfill \\ x_0\hfill & \mathrm{for}t\in [-\tau /2,0),\hfill \end{array}\right.$$

(e.g., a transcriptional burst occurred at $t=-\tau /2$). The discontinuous initial condition reflects a sudden activation of transcription in the past, before $t=0$.

5.2. Models in Economics

Inventory management with sudden stock delivery. A delayed inventory system where past stock levels affect reordering, but deliveries arrive at discrete times. Equation:

$${\displaystyle \frac{dI\left(t\right)}{dt}}=-dI\left(t\right)+\beta I(t-\tau )·{\chi }_{\left\{I\right(t-\tau )<s\}},$$

where $I\left(t\right)$ is the inventory level, ${\chi }_{\{·\}}$ is a characteristic function, the initial function $I_0\left(t\right)$ is piecewise constant with jumps at $t=-\tau /3,-2\tau /3$ (past deliveries). Discontinuities represent discrete restocking events in the past.

Example 3.

Let us discuss a delayed logistic growth model in economics (e.g., capital accumulation with a past shock):

$${\displaystyle \frac{dx\left(t\right)}{dt}}=-kx\left(t\right)+\alpha x(t-\tau )\left(1-{\displaystyle \frac{x(t-\tau )}{K}}\right),t\ge 0,$$

with discontinuous initial function:

$$\psi \left(t\right)=\left\{\begin{array}{cc}{x}_0\hfill & \mathit{for}t\in [-\tau ,-\tau /2),\hfill \\ x_1\hfill & \mathit{for}t\in [-\tau /2,0),\hfill \end{array}\right.$$

where $x_0,x_1,K>0$, and $\psi \left(t\right)\in PC[-\tau ,0]$. As the time of discontinuity is fixed, the classical method of steps applies. First, we can recall the classical approach with continuous solutions.

Step 1. For $t\in [0,\tau /2]$, the delay term $x(t-\tau )$ pulls from $[-\tau ,-\tau /2]$, where $x(t-\tau )=x_0$. The DDE reduces to an ODE:

$${\displaystyle \frac{dx\left(t\right)}{dt}}=-kx\left(t\right)+\alpha x_0\left(1-{\displaystyle \frac{x_0}{K}}\right).$$

Thus,

$$x\left(t\right)=\left(x_1-{\displaystyle \frac{\alpha x_0(1-x_0/K)}{k}}\right)e^{-kt}+{\displaystyle \frac{\alpha x_0(1-x_0/K)}{k}}.$$

This is an exponential decay/growth toward a steady state.

Step 2. For $t\in [\tau /2,\tau ]$, the delay term $x(t-\tau )$ pulls from $[-\tau /2,0]$, where $x(t-\tau )=x_1$. The form of our differential equation becomes:

$${\displaystyle \frac{dx\left(t\right)}{dt}}=-kx\left(t\right)+\alpha x_1\left(1-{\displaystyle \frac{x_1}{K}}\right).$$

Use continuity at $t=\tau /2$ (from Step 1):

$$x(\tau /2)=\left(x_1-{\displaystyle \frac{\alpha x_0(1-x_0/K)}{k}}\right)e^{-k\tau /2}+{\displaystyle \frac{\alpha x_0(1-x_0/K)}{k}}.$$

We get a solution on this interval:

$$x\left(t\right)=\left(x(\tau /2)-{\displaystyle \frac{\alpha x_1(1-x_1/K)}{k}}\right)e^{-k(t-\tau /2)}+{\displaystyle \frac{\alpha x_1(1-x_1/K)}{k}}.$$

Step 3. For $t\in [n\tau ,(n+1\left)\tau \right]$, the solution depends on $x(t-\tau )$ from the previous interval. This process repeats, with each solution from an interval patched together using continuity at the endpoints.

In this model, it is observed (in the classical approach) that the discontinuity at the past implies that the initial jump at $t=-\tau /2$ causes a kink in $x\left(t\right)$ at $t=\tau /2$. For $t>\tau$, the solution smooths out if $k>0$ (dissipative effect). Economic Interpretation: $x_0\to x_1$ represents a sudden capital shock (e.g., policy change). The delay τ captures time lags in investment response.

Combining previous steps gives us:

$$x\left(t\right)=\left\{\begin{array}{cc}\left(x_1-C_0\right)e^{-kt}+C_0\hfill & \mathit{for}t\in [0,\tau /2],\hfill \\ \left(x(\tau /2)-C_1\right)e^{-k(t-\tau /2)}+C_1\hfill & \mathit{for}t\in [\tau /2,\tau ],\hfill \end{array}\right.$$

where $C_0={\displaystyle \frac{\alpha x_0(1-x_0/K)}{k}}$, $C_1={\displaystyle \frac{\alpha x_1(1-x_1/K)}{k}}$, $x(\tau /2)=(x_1-C_0)e^{-k\tau /2}+C_0$.

At $t=0$: $x\left(0^{+}\right)=x_1$ (matches $\psi \left(0^{-}\right)$), but ${\displaystyle \frac{dx}{dt}}$ jumps due to discontinuity of ψ at $t=-\tau /2$.

At $t=\tau /2$: $x\left(t\right)$ is continuous, but ${\displaystyle \frac{dx}{dt}}$ has a kink.

What will be changed in the new model with discontinuous ψ-solutions? Recall that in view of Theorem 1, for any fixed g we have a unique solution. However, we can show here that for different properties of ψ preserved in g solutions, they can be different. In the above classical approach, we have (absolutely) continuous solutions. But discontinuous initial function gives us the possibility to keep this property (see Figure 6). Let $\psi \in Z_G^L$ be an initial function with a set of discontinuities $\left(t_k\right)$. Here is a construction of ψ-solutions dependent on

$$g\left(t\right)=t+\sum _{k=1}^{\infty }{w}_k·\Delta {\psi }_k·\sum _{n=0}^{\infty }{\chi }_{[t_k+nr,\infty )}\left(t\right)$$

where $\left(w_k\right)$ is a weight sequence (e.g., ${\displaystyle \frac{1}{{(k+1)}^2}}$, $e^{-\lambda k}$) ensuring convergence (in the case $T=\infty$, ${\tau }_k$ is a delay sequence controlling spacing.

Here we have $t_1=-\tau /2$ and $t_2=0$, so

$$g\left(t\right)=t+{\tilde{\psi }}_d\left(t\right)=t+(x_1-x_0)·\sum _{n=0}^{\infty }{\chi }_{[-\tau /2+n\tau ,\infty )}\left(t\right).$$

Here, the discrete part (jump part) of ψ is:

$${\psi }_d\left(t\right)=\Delta ·{\chi }_{[-\tau /2,0]}\left(t\right)=(x_1-x_0)·{\chi }_{[-\tau /2,0]}\left(t\right).$$

Although these solutions are usually different in both cases, we can better model real data. Figure 7 illustrates the influence of the choice of function g on the solution process.

5.3. Models in Engineering

Reset control systems. A system with delayed feedback and resets at irregular past times:

$${\displaystyle \frac{dy\left(t\right)}{dt}}=-ky\left(t\right)+y(t-\tau )·{\chi }_{\left\{y\right(t-\tau )\notin [a,b\left]\right\}},$$

where the initial function $y\left(t\right)$ has jumps at some points in $(-\tau ,0)$ (e.g., past reset events). The controller “resets” the state when it leaves a band, creating discontinuities.