Effects of Heat on Silicone Breast Implants: In Situ and Modeling Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. In Situ Experiment—Thermal Imaging
2.1.1. The Experimental System
2.1.2. The Experiment Protocol
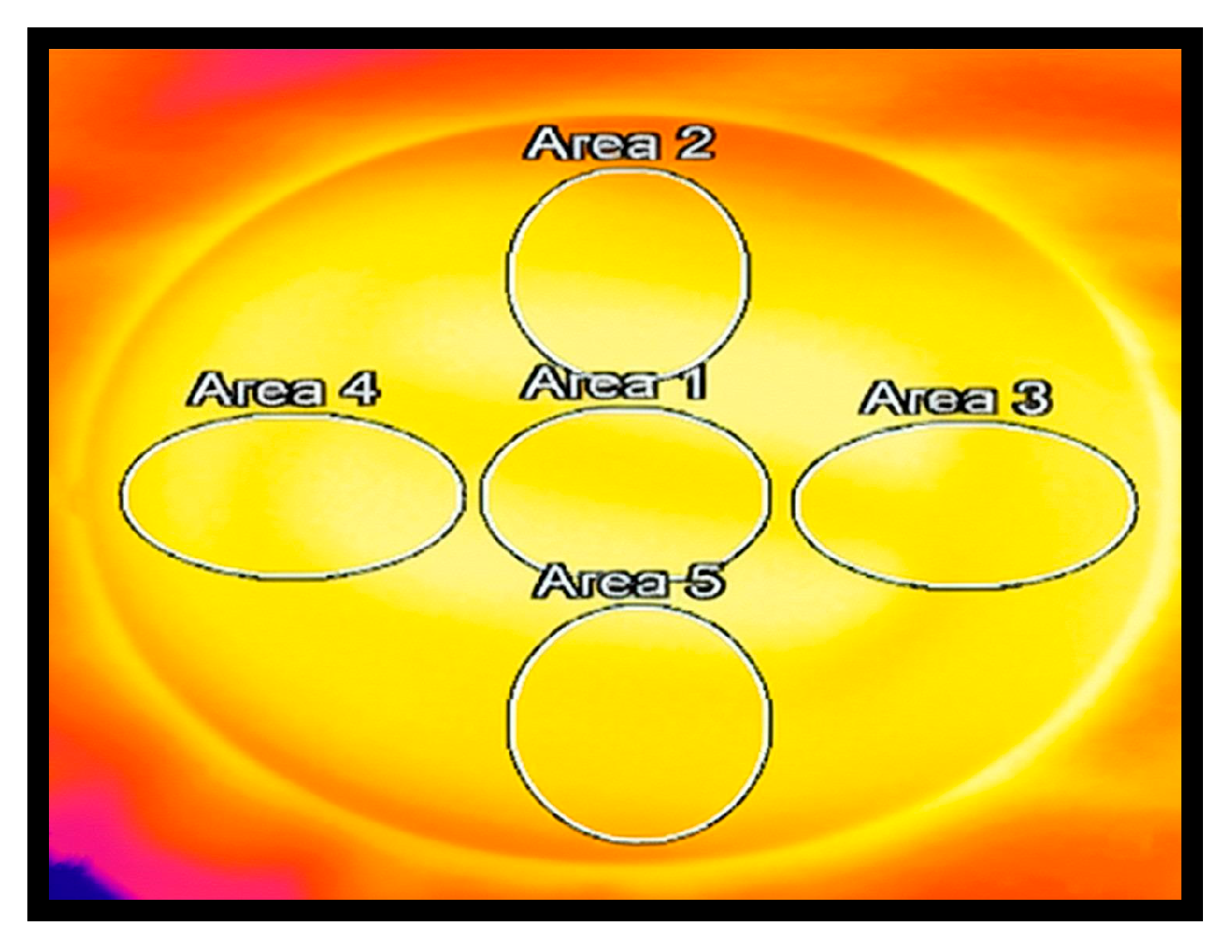
2.1.3. Data Processing
2.1.4. Statistical Analysis
2.2. Numeric Model Simulation
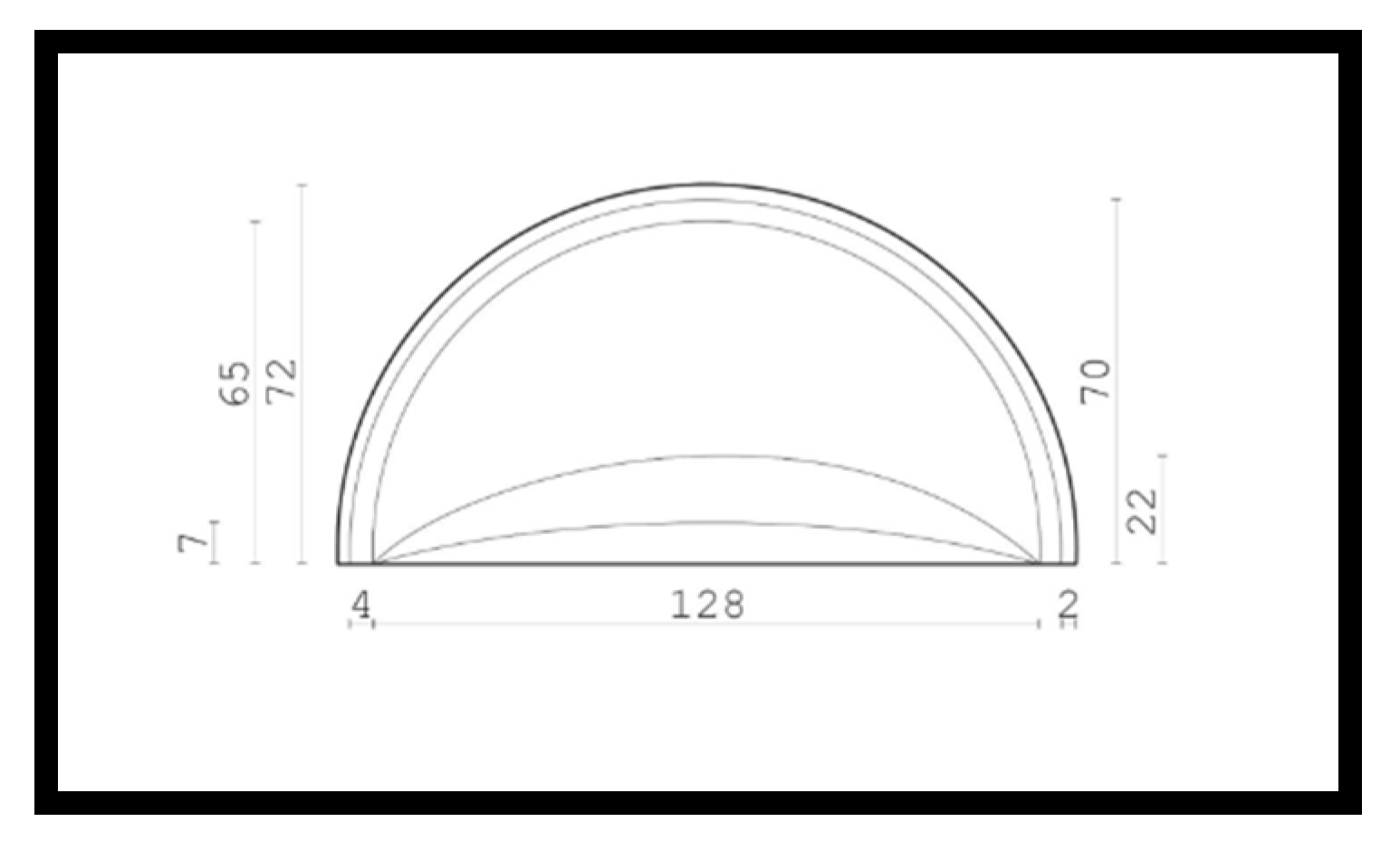
2.2.1. SolidWorks Model
2.2.2. COMSOL Numerical Simulations
2.2.3. Heat Transfer Simulation
3. Results
3.1. In Situ Experiment Baseline Silicone-Gel Implant Temperature Change
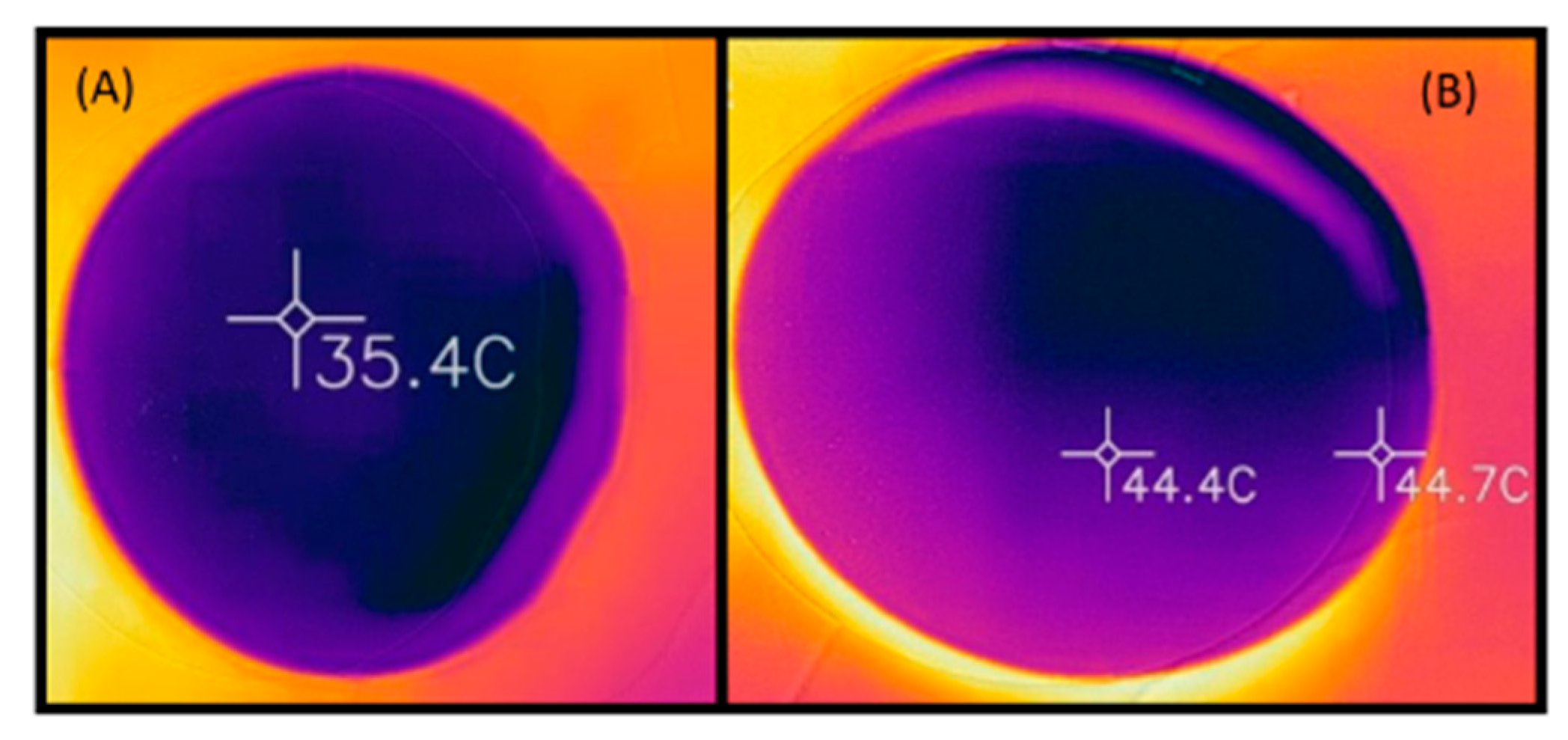
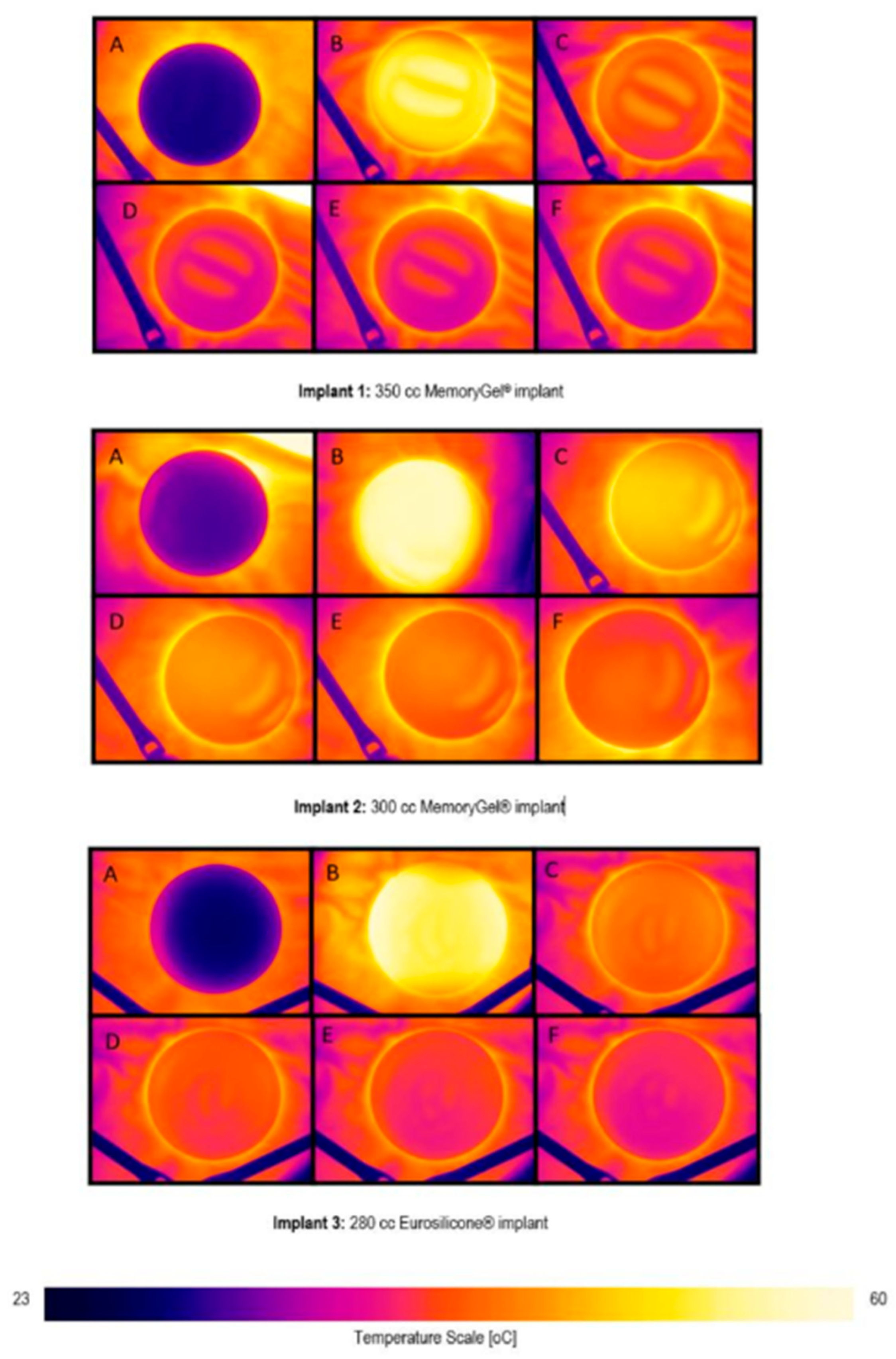
3.2. Thermal Images
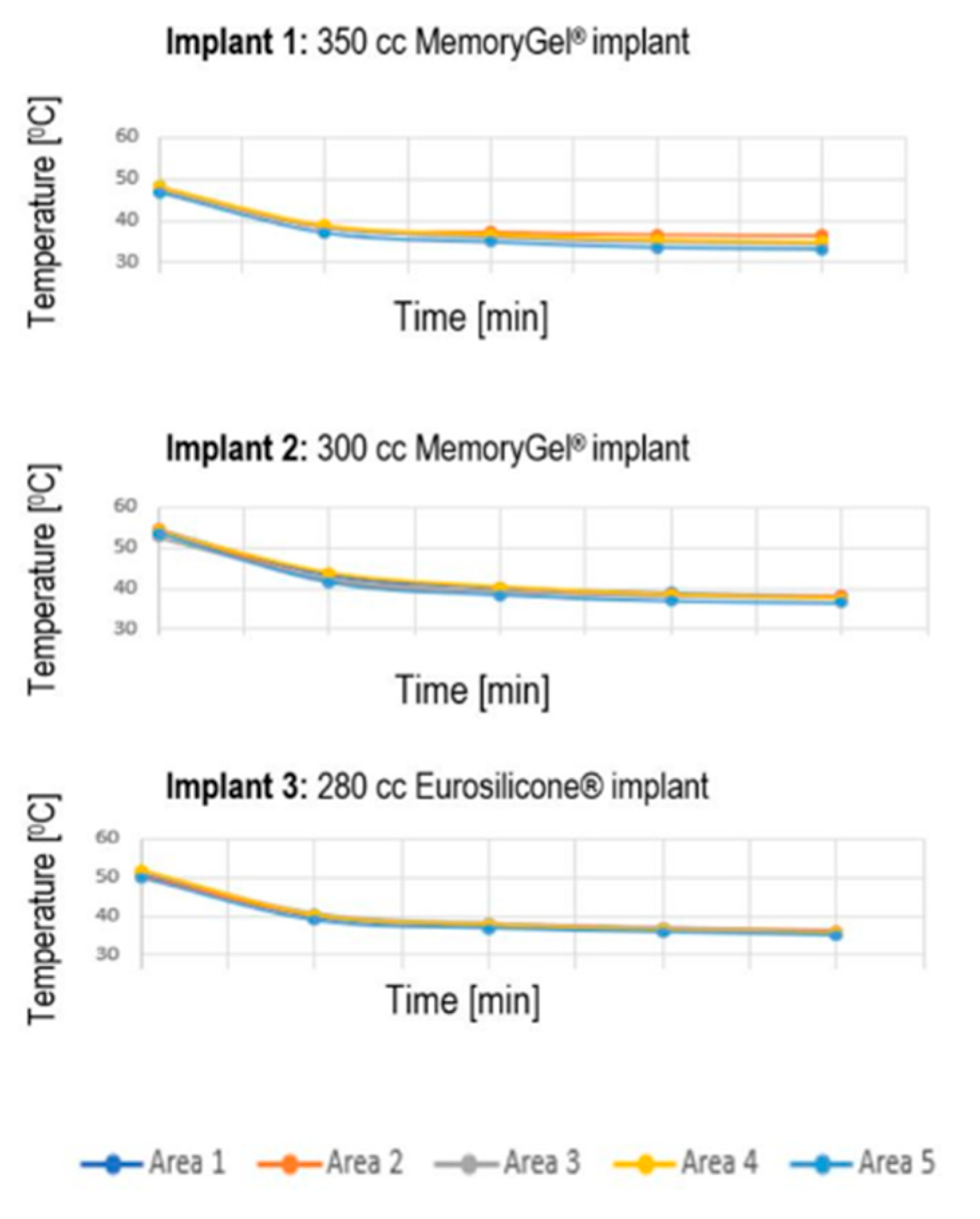
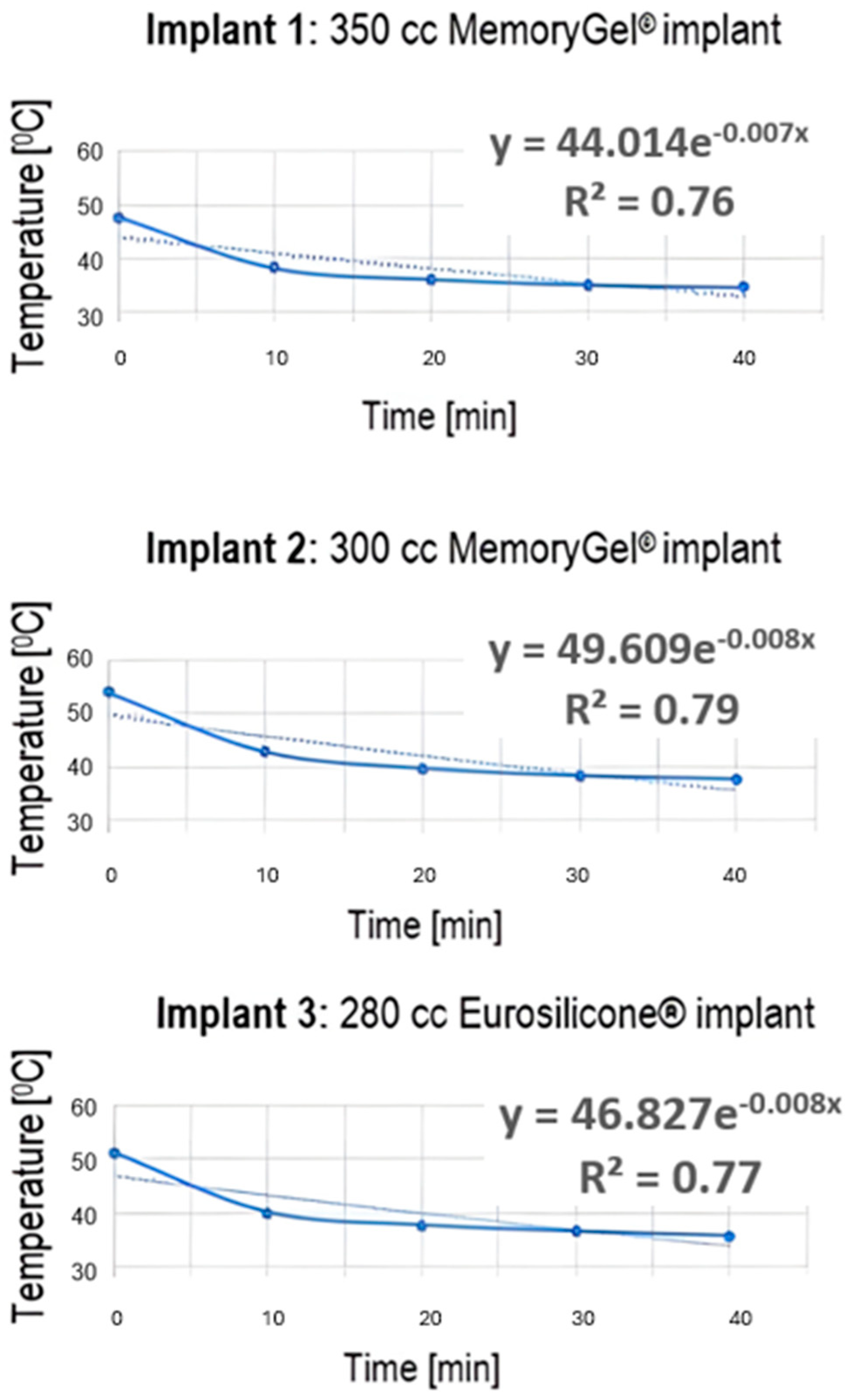
3.3. Temperature Data Extracted from Thermal Images
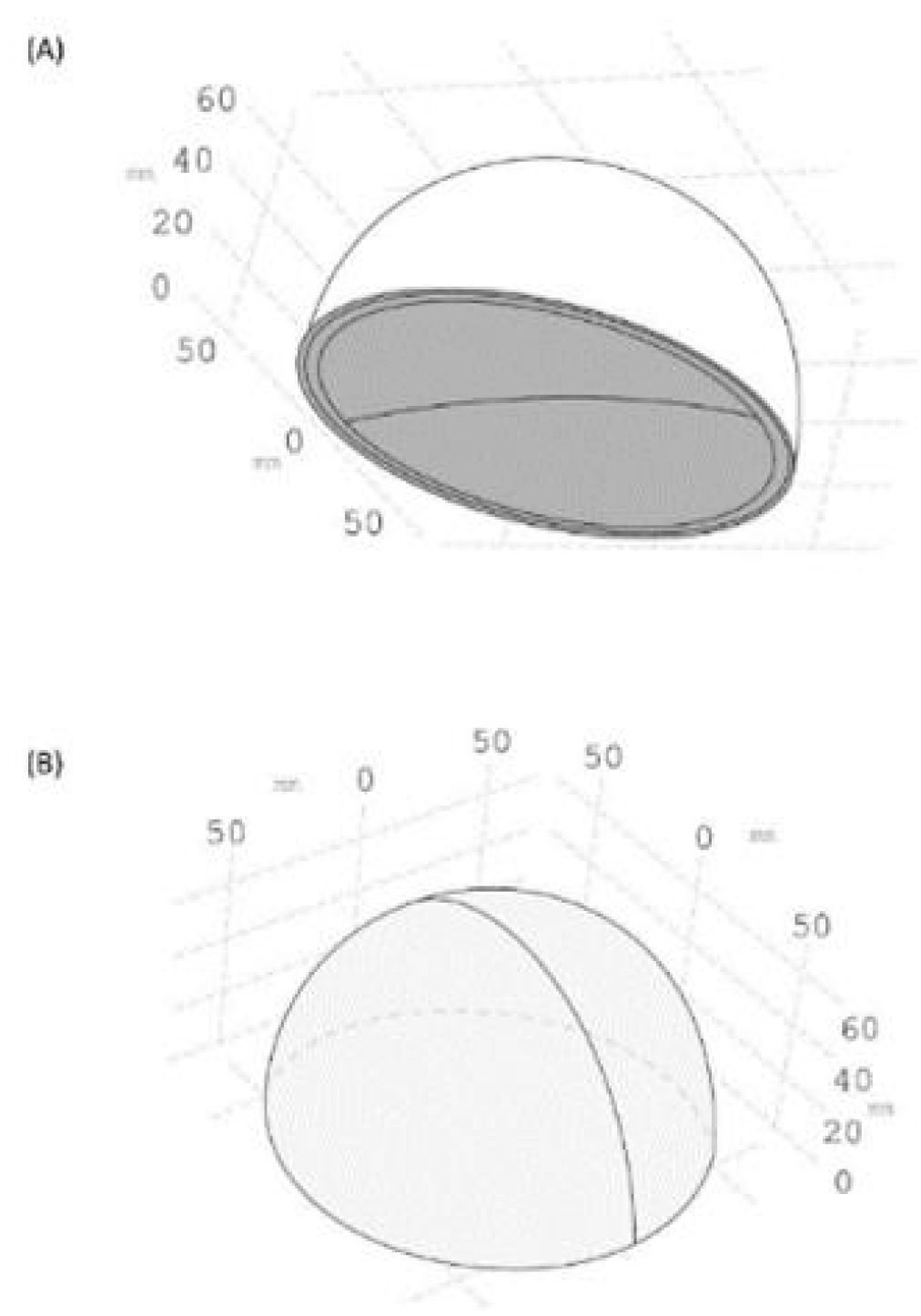
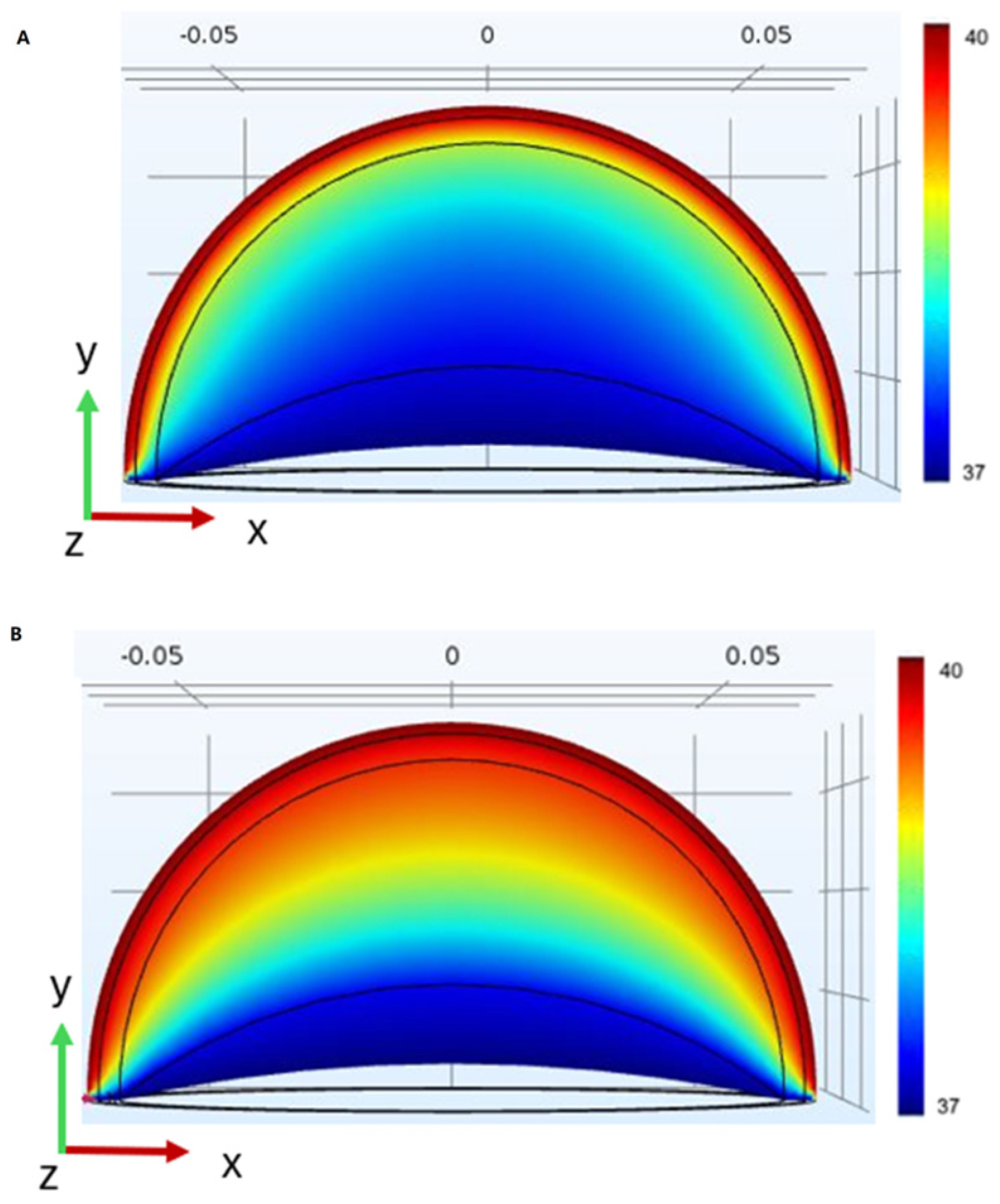
3.4. Numeric Model
3.5. Summary of Experimental and Simulated Data Findings
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gil-Olarte, P.; Gil-Olarte, M.A.; Gómez-Molinero, R.; Guil, R. Psychosocial and sexual well-being in breast cancer survivors undergoing immediate breast reconstruction: The mediating role of breast satisfaction. Eur. J. Cancer Care 2022, 31, e13686. [Google Scholar] [CrossRef]
- Martins Faria, B.; Martins Rodrigues, I.; Verri Marquez, L.; da Silva Pires, U.; Vilges de Oliveira, S. The impact of mastectomy on body image and sexuality in women with breast cancer: A systematic review. Psicooncología 2021, 18, 91–115. [Google Scholar] [CrossRef]
- Meshkin, D.H.; Firriolo, J.M.; Karp, N.S.; Salibian, A.A. Management of complications following implant-based breast reconstruction: A narrative review. Ann. Transl. Med. 2023, 11, 416. [Google Scholar] [CrossRef]
- Jimenez, R.B.; Packowski, K.; Horick, N.; Rosado, N.; Chinta, S.; Koh, D.; Sobti, N.; Specht, M.; Liao, E.C. The timing of acute and late complications following mastectomy and implant-based reconstruction. Ann. Surg. 2023, 278, e203–e208. [Google Scholar] [CrossRef]
- Blok, Y.L.; van Lierop, E.; Plat, V.D.; Corion, L.U.M.; Verduijn, P.S.; Krekel, N.M.A. Implant loss and associated risk factors following implant-based breast reconstructions. Plast. Reconstr. Surg. Glob. Open 2021, 9, e3708. [Google Scholar] [CrossRef]
- Fischer, J.P.; Wes, A.M.; Tuggle, C.T., III; Serletti, J.M.; Wu, L.C. Risk analysis of early implant loss after immediate breast reconstruction: A review of 14,585 patients. J. Am. Coll. Surg. 2013, 217, 983–990. [Google Scholar] [CrossRef] [PubMed]
- Yuen, J.C.; Coleman, C.A.; Erickson, S.W. Obesity-related risk factors in implant-based breast reconstruction using alloderm. Plast. Reconstr. Surg. Glob. Open 2017, 5, e1231. [Google Scholar] [CrossRef] [PubMed]
- Laporta, R.; Longo, B.; Sorotos, M.; Farcomeni, A.; Patti, C.; Mastrangeli, M.R.; Rubino, C.; di Pompeo, F.S. Breast reconstruction following nipple-sparing mastectomy: Clinical outcomes and risk factors related complications. J. Plast. Surg. Hand Surg. 2017, 51, 427–435. [Google Scholar] [CrossRef] [PubMed]
- Mak, J.C.; Kwong, A. Complications in post-mastectomy immediate breast reconstruction: A ten-year analysis of outcomes. Clin. Breast Cancer 2020, 20, 402–407. [Google Scholar] [CrossRef]
- Friedrich, M.; Krämer, S.; Friedrich, D.; Kraft, C.; Maass, N.; Rogmans, C. Difficulties of breast reconstruction–problems that no one likes to face. Anticancer Res. 2021, 41, 5365–5375. [Google Scholar] [CrossRef]
- Osman, F.; Saleh, F.; Jackson, T.D.; Corrigan, M.A.; Cil, T. Increased postoperative complications in bilateral mastectomy patients compared to unilateral mastectomy: An analysis of the NSQIP database. Ann. Surg. Oncol. 2013, 20, 3212–3217. [Google Scholar] [CrossRef] [PubMed]
- Chattha, A.; Bucknor, A.; Kamali, P.; Van Veldhuisen, C.L.; Flecha-Hirsch, R.; Sharma, R.; Tobias, A.M.; Lee, B.T.; Lin, S.J. Comparison of risk factors and complications in patients by stratified mastectomy weight: An institutional review of 1041 consecutive cases. J. Surg. Oncol. 2017, 116, 811–818. [Google Scholar] [CrossRef] [PubMed]
- Bennett, K.G.; Qi, J.; Kim, H.M.; Hamill, J.B.; Pusic, A.L.; Wilkins, E.G. Comparison of 2-Year complication rates among common techniques for postmastectomy breast reconstruction. JAMA Surg. 2018, 153, 901–908. [Google Scholar] [CrossRef]
- MacDonald-Nethercott, M.; Malata, C.M.; Irwin, M.S.; Benyon, S.L.; Wong, K.Y. Analysis of complications following implant-based breast reconstruction in breast cancer patients. Eur. J. Plast. Surg. 2023, 46, 1059–1068. [Google Scholar] [CrossRef]
- Alhindi, N.; Bamakhrama, B.; Alzahrani, A.; Mortada, H.; Ali, N.M.; Alruwaili, A.; Baamir, N.; Aljaaly, H. Risk factors of implant loss and complications post-implant based breast reconstruction: A meta-analysis. Eur. J. Plast. Surg. 2023, 46, 865–874. [Google Scholar] [CrossRef]
- Nickel, K.B.; Fox, I.K.; Margenthaler, J.A.; Wallace, A.E.; Fraser, V.J.; Olsen, M.A. Effect of noninfectious wound complications after mastectomy on subsequent surgical procedures and early implant loss. J. Am. Coll. Surg. 2016, 222, 844–852. [Google Scholar] [CrossRef] [PubMed]
- Olsen, M.A.; Nickel, K.B.; Fox, I.K.; Margenthaler, J.A.; Wallace, A.E.; Fraser, V.J. Comparison of wound complications after immediate, delayed, and secondary breast reconstruction procedures. JAMA Surg. 2017, 152, e172338. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, M.; Wagman, Y.; Liran, A.; Harats, M.; Winkler, E.; Haik, J.; Tessone, A. A literature review of burns in reconstructed breasts after mastectomy. Wounds 2016, 28, 422–428. [Google Scholar]
- Delfino, S.; Brunetti, B.; Toto, V.; Persichetti, P. Burn after breast reconstruction. Burns 2008, 34, 873–877. [Google Scholar] [CrossRef]
- Brzezinski, R.Y.; Levin-Kotler, L.; Rabin, N.; Ovadia-Blechman, Z.; Zimmer, Y.; Sternfeld, A.; Finchelman, J.M.; Unis, R.; Lewis, N.; Tepper-Shaihov, O.; et al. Automated thermal imaging for the detection of fatty liver disease. Sci. Rep. 2020, 10, 15532. [Google Scholar] [CrossRef]
- Ovadia-Blechman, Z.; Hoffer, O.; Halak, M.; Adrai, K.; Zimmer, Y.; Silverberg, D.; Rabin, N. Assessment of blood distribution in response to post-surgical steal syndrome: A novel technique based on Thermo-Anatomical Segmentation. J. Biomech. 2021, 119, 110304. [Google Scholar] [CrossRef]
- Peko Cohen, L.; Ovadia-Blechman, Z.; Hoffer, O.; Gefen, A. Dressings cut to shape alleviate facial tissue loads while using an oxygen mask. Int. Wound J. 2019, 16, 813–826. [Google Scholar] [CrossRef] [PubMed]
- Hoffer, O.; Haik, J.; Nir, R.R.; Beck, Y.; Kofler, B.; Heyman, E.; Golan, O.; Ovadia-Blechman, Z. Effect of External Heating on Silicone Gel Breast Implants: Can Heat Exposure Precipitate Burns and Implant-Related Complications? Plast. Reconstr. Surg. 2023, 151, 529e–530e. [Google Scholar] [CrossRef]
- Erhunmwun, I.; Ikponmwosa, U. Review on finite element method. J. Appl. Sci. Environ. Manag. 2017, 21, 999–1002. [Google Scholar] [CrossRef]
- Sharma, R.; Jadon, V.K.; Singh, B. A review on the finite element methods for heat conduction in functionally graded materials. J. Inst. Eng. (India) Ser. C 2015, 96, 73–81. [Google Scholar] [CrossRef]
- Surana, K.S.; Reddy, J.N. The Finite Element Method for Boundary Value Problems: Mathematics and Computations; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Lone, A.A.; Sheikh, N.A.; Butt, M.M. Coupled thermo-mechanical finite element analysis of cranial implants using micromechanical representative volume element approach. J. Inst. Eng. India C 2024, 105, 483–494. [Google Scholar] [CrossRef]
- Brandon, H.J.; Nichter, L.S.; Back, D.D. New evaluation procedure for multi-dimensional mechanical strains and tangent moduli of breast implants: IDEAL IMPLANT® structured breast implant compared to silicone gel implants. Bioengineering 2019, 6, 43. [Google Scholar] [CrossRef] [PubMed]
- Árpád, I.W.; Kiss, J.T.; Kocsis, D. Role of the volume-specific surface area in heat transfer objects: A critical thinking-based investigation of Newton’s law of cooling. Int. J. Heat. Mass. Transf. 2024, 227, 125535. [Google Scholar] [CrossRef]
- Cramer, M.N.; Gagnon, D.; Laitano, O.; Crandall, C.G. Human temperature regulation under heat stress in health, disease, and injury. Physiol. Rev. 2022, 102, 1907–1989. [Google Scholar] [CrossRef]
- Córdoba, E.E.; Lacunza, E.; Güerci, A.M. Clinical factors affecting the determination of radiotherapy-induced skin toxicity in breast cancer. Radiat. Oncol. J. 2021, 39, 315–323. [Google Scholar] [CrossRef]

| Skin § | Fat | Gland | Muscle | Silicone | |
|---|---|---|---|---|---|
| 1200 | 930 | 1050 | 1100 | 1050 | |
| 3396.3 | 2770 | 3770 | 3800 | 1500 | |
| 0.375 | 0.21 | 0.48 | 0.48 | 0.14 | |
| 0.0005 | - | - | - | - |
| Implant | Area | Baseline (°C) | Post-Heating (°C) | 40 min Post-Cooling (°C) | Post-Heating (Percentage Change, %) | 40 min Post-Cooling (Percentage Change, %) |
|---|---|---|---|---|---|---|
| 1 | 1 | 25.90 | 48.10 | 34.70 | 85.71 | −27.86 |
| 2 | 26.40 | 47.50 | 36.50 | 79.92 | −23.16 | |
| 3 | 26.30 | 47.80 | 34.40 | 81.75 | −28.03 | |
| 4 | 26.20 | 48.20 | 34.80 | 83.97 | −27.80 | |
| 5 | 25.90 | 46.80 | 33.10 | 80.69 | −29.27 | |
| Mean (SD) | 26.14 (0.23) | 47.68 (0.56) | 34.70 (1.21) | 82.41 (2.39) | −27.22 (2.35) | |
| 2 | 1 | 27.50 | 54.50 | 38.20 | 98.18 | −29.91 |
| 2 | 28.20 | 54.60 | 38.10 | 93.62 | −30.22 | |
| 3 | 27.80 | 52.70 | 37.60 | 89.57 | −28.65 | |
| 4 | 28.60 | 54.20 | 37.50 | 89.51 | −30.81 | |
| 5 | 27.80 | 53.60 | 36.40 | 92.81 | −32.09 | |
| Mean (SD) | 27.98 (0.43) | 53.92 (0.79) | 37.56 (0.72) | 92.74 (3.57) | −30.34 (1.26) | |
| 3 | 1 | 26.00 | 50.90 | 35.50 | 95.77 | −30.26 |
| 2 | 26.60 | 50.70 | 36.20 | 90.60 | −28.60 | |
| 3 | 26.80 | 51.60 | 35.90 | 92.54 | −30.43 | |
| 4 | 28.10 | 52.00 | 35.70 | 85.05 | −31.35 | |
| 5 | 26.80 | 50.10 | 35.00 | 86.94 | −30.14 | |
| Mean (SD) | 26.86 (0.77) | 51.06 (0.75) | 35.66 (0.45) | 90.18 (4.30) | −30.16 (0.99) |
| Metric | Experimental Data (In Situ) | Simulated Data (FEM) | Comparison Notes |
|---|---|---|---|
| Baseline Temperature (°C) | 26.14–27.98 (average across implants: 350 cc: 26.14, 300 cc: 27.98, 280 cc: 26.86; Table 2) | 37 °C (bottom boundary condition, simulating body temperature; Section 2.2.3) | The simulated baseline assumes a higher, uniform body temperature; experimental data reflect actual lab conditions (25 °C). |
| Post-Heating Temperature (°C) | 47.68–53.92 (average across implants: 350 cc: 47.68, 300 cc: 53.92, 280 cc: 51.06; Table 2) | 40 °C (external skin surface boundary condition; Section 2.2.3) | Experimental temperatures are higher due to direct heating (65 °C hot water bottle); simulated data use a lower external temperature. |
| 40 Min Post-Cooling Temperature (°C) | 34.70–37.56 (average across implants: 350 cc: 34.70, 300 cc: 37.56, 280 cc: 35.66; Table 2) | Not quantified; implied retention above baseline (Figure 9, Section 3.4) | Experimental data show significant heat retention; simulation suggests prolonged retention but lacks specific values. |
| Post-Heating % Change | 82.41–92.74% (350 cc: 82.41%, 300 cc: 92.74%, 280 cc: 90.18%; Table 2) | Not quantified; qualitative increase due to implant’s thermal properties (Section 3.4) | Experimental data show a significant temperature rise; simulation confirms higher heat accumulation in the implant model. |
| 40 Min Post-Cooling % Change | −27.22 to −30.34% (350 cc: −27.22%, 300 cc: −30.34%, 280 cc: −30.15%; Table 2) | Not quantified; implies slower cooling in implant model (Figure 9, Section 3.4) | Experimental data indicate partial cooling; simulation suggests slower heat dissipation due to a lack of perfusion. |
| Thermal Penetration/Retention | Heat retention above baseline after 40 min (Section 3.3) | Deeper thermal penetration in the implant model vs. the standard breast model (Figure 9, Section 3.4) | Both methods confirm that implants retain heat longer than native tissue, with simulations showing deeper penetration. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffer, O.; Haik, J.; Nir, R.-R.; Beck, Y.; Kofler, B.; Golan, O.; Kornhaber, R.; Cleary, M.; Biros, E.; Ovadia-Blechman, Z. Effects of Heat on Silicone Breast Implants: In Situ and Modeling Analysis. Appl. Sci. 2025, 15, 8831. https://doi.org/10.3390/app15168831
Hoffer O, Haik J, Nir R-R, Beck Y, Kofler B, Golan O, Kornhaber R, Cleary M, Biros E, Ovadia-Blechman Z. Effects of Heat on Silicone Breast Implants: In Situ and Modeling Analysis. Applied Sciences. 2025; 15(16):8831. https://doi.org/10.3390/app15168831
Chicago/Turabian StyleHoffer, Oshrit, Josef Haik, Rony-Reuven Nir, Yuval Beck, Bar Kofler, Oz Golan, Rachel Kornhaber, Michelle Cleary, Erik Biros, and Zehava Ovadia-Blechman. 2025. "Effects of Heat on Silicone Breast Implants: In Situ and Modeling Analysis" Applied Sciences 15, no. 16: 8831. https://doi.org/10.3390/app15168831
APA StyleHoffer, O., Haik, J., Nir, R.-R., Beck, Y., Kofler, B., Golan, O., Kornhaber, R., Cleary, M., Biros, E., & Ovadia-Blechman, Z. (2025). Effects of Heat on Silicone Breast Implants: In Situ and Modeling Analysis. Applied Sciences, 15(16), 8831. https://doi.org/10.3390/app15168831







