Wheeled Permanent Magnet Climbing Robot for Weld Defect Detection on Hydraulic Steel Gates

Abstract

In response to the challenges associated with weld treatment during the on-site corrosion protection of hydraulic steel gates, this paper proposes a method utilizing a magnetic adsorption climbing robot to perform corrosion protection operations. Firstly, a magnetic adsorption climbing robot with a multi-wheel independent drive configuration is proposed as a mobile platform. The robot body consists of six joint modules, with the two middle joints featuring adjustable suspension. The joints are connected in series via an EtherCAT bus communication system. Secondly, the kinematic model of the climbing robot is analyzed and a PID trajectory tracking control method is designed, based on the kinematic model and trajectory deviation information collected by the vision system. Subsequently, the proposed kinematic model and trajectory tracking control method are validated through Python3 simulation and actual operation tests on a curved trajectory, demonstrating the rationality of the designed PID controller and control parameters. Finally, an intelligent software system for weld defect detection based on computer vision is developed. This system is demonstrated to conduct defect detection on images of the current weld position using a trained model.

1. Introduction

Climbing robots capable of maneuvering on vertical steel surfaces are currently in high demand across various industries for performing hazardous operations, such as the maintenance of large steel structures [1,2], storage tanks [3,4], nuclear facilities [5,6], wind turbine towers [7,8], and ships [9,10]. These robots not only replace human workers in conducting dangerous tasks but also eliminate the need for time-consuming and costly scaffolding.

Due to prolonged exposure to atmospheric conditions and water, hydraulic steel gate structures are prone to corrosion, with defects particularly likely to occur at weld joints [11,12]. Owing to their special location and environmental constraints, certain steel gates at hydropower stations are unsuitable for dismantling and lifting. At present, the maintenance of hydraulic steel gates largely relies on manual operations. Considering that large steel gates typically exceed 10 m in length and width, the associated operational risks are considerable. Hydropower stations have an increasingly urgent demand for enhancing the automation level of on-site maintenance, reducing dependence on manual labor, and improving production efficiency [13].

One of the most promising applications of wall-climbing robots lies in the inspection of damage and weldment failure on the surface of hydropower station steel gates. As a major hydropower-producing country, there exists a vast number of in-service steel gates requiring regular inspection to ensure the safe operation of hydropower stations. Accurate localization of damage and weldment failures is crucial for modern manufacturing, providing a basis for precise quality assessment and targeted repair decisions across various products. However, due to complex backgrounds, a low contrast, weak textures, and class imbalances, achieving accurate localization remains a significant challenge. In recent years, convolutional neural networks (CNNs) [14], owing to their powerful feature extraction capabilities, have made substantial progress and have been widely adopted in defect detection tasks [15].

Given the inherent reliability of permanent magnetic adhesion, it is often preferable to use magnetic adsorption to adhere robots to working surfaces where conditions permit, despite the availability of alternative methods. Some robots utilize track-based locomotion [16,17,18], offering good terrain adaptability and limited obstacle-crossing capabilities. However, these designs can cause considerable surface damage during turns. Alternatively, some robots rely on vacuum adsorption [19,20,21], which imposes fewer requirements on the material properties of the working surface. Nevertheless, vacuum-adsorbed robots generally have lower load capacities, posing limitations for operations requiring significant payloads. From a biomimetic perspective, insect-inspired wall-climbing robots have demonstrated excellent climbing ability and flexibility [22,23,24]. However, their complex wheel-leg mechanisms introduce challenges in control and operational stability.

There are two primary limitations for wall-climbing robots used in hydraulic steel gate weld inspection:

• Autonomy: The robot must autonomously navigate along the weld seams on the hydraulic steel gate surface, utilizing sensors to scan and detect potential defects while minimizing human intervention.
• Cabling and Piping: The robot must minimize the number of cables and reduce drag forces that could impede mobility.

This paper presents a robot prototype designed for the inspection of hydraulic steel gates. The prototype is based on a wheeled mobile platform equipped with six permanent magnet wheels for reliable adhesion to magnetic surfaces. An image sensor captures real-time images of the weld areas to correct the robot’s heading. Additionally, the visual system detects the presence of weld defects and classifies their types. By connecting the drive modules via the EtherCAT bus, the design significantly reduces the number of cables, thereby minimizing the risk of cable entanglement.

In the weld inspection task, YOLOv5 and Hough transform are combined for defect location and trajectory extraction. We built a multi-axis control platform based on EtherCAT that supports rapid deployment and module expansion. The robot completes visual recognition and weld tracking closed-loop control on the actual surface of the hydropower station gate, which has good practicality.

The remainder of this paper is organized as follows:

• Section 2 details the overall structure of the mobile robot platform.
• Section 3 presents the visual sensing system and trajectory tracking strategy used to correct the robot’s heading.
• Section 4 describes the design of the weld defect detection system and conducts simulation and experimental tracking tests to validate the control system prototype.
• Section 5 concludes the paper.

2. Mobile Robot System

2.1. Robot Control System Setup

The overall design of the climbing robot control system is illustrated in Figure 1 and is divided into two main components: the robot body and the control cabinet. The robot body consists of several drive modules and additional input/output (I/O) devices. To enhance the stability of the robot and load-bearing capacity during climbing operations, a six-wheel independent drive configuration is employed. Among these, the two drive wheels located at the center of the robot are equipped with independent suspension systems to improve obstacle negotiation capabilities. The robot body is powered by the control cabinet, which also issues control commands to the robot.

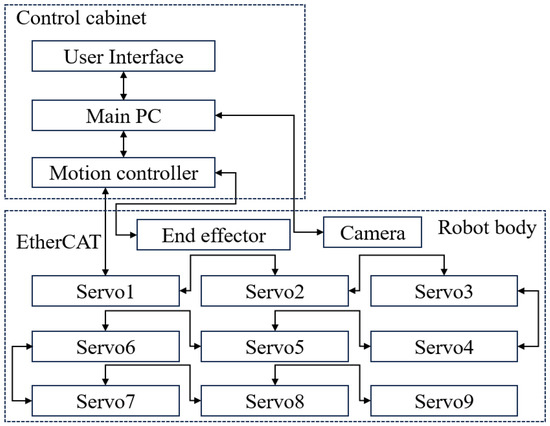
Figure 1. Robot control system setup.

The control cabinet is mainly composed of three parts: the motion controller, the main control PC, and the user interface device. Depending on operational requirements, the user interface can be configured with an industrial touchscreen or a control handle. Unlike smaller robots that typically rely on battery power, this robot is powered via cables, thereby significantly increasing its load-carrying capacity. To minimize the wiring complexity between each servo drive module and the controller, as shown in Figure 2, and to improve system scalability, the climbing robot control system adopts EtherCAT bus architecture. The motion controller acts as the master of the bus system, while the servo drives and other I/O modules function as slaves, communicating with the master via EtherCAT cables.

Figure 2. Servo drive module.

The slave stations, such as servo drive modules, are housed within the robot body. The wiring between the climbing robot body and the control cabinet is simplified to just a single Category 5e Ethernet cable and a set of DC power cables. If additional axes or functionalities need to be integrated, new slave stations can be connected to the existing network by linking them to the last slave station via a network cable and configuring the relevant parameters. This design greatly facilitates the system’s functional expansion.

2.2. Robot Mechanical Structure Setup

The mechanical structure of the entire robot system is depicted in Figure 3 and consists of two main components: the robot body and the end-effector. The end-effector shown in the figure is a grinding head, which can be replaced with other types of working tools based on specific operational requirements. The robot body comprises the frame structure, magnetic wheels, drive system, control system, visual system, and working tools. The robot has a total mass of approximately 47 kg and is equipped with six driving wheels, each powered by a 200 W servo motor. Each magnetic wheel generates an approximate adhesion force of 1250 N. The camera used in this article is an ordinary industrial camera; the camera manufacturer and model are baser-a2A1920-51gcBAS (Basler AG, Ahrensburg, Germany), and they are equipped with a ring LED light source. The motion controller model is trio′s MC4N, and the servo motor and drive use an integrated robot joint module, the model of which is eRob80I (Basler AG, Ahrensburg, Germany). The end effector uses a 2-axis sliding platform, and a separate swing joint is configured at the front end of the robot. The robot body measures 450 mm in length and 400 mm in width, with a mass of approximately 43 kg. The center of gravity is located at a height of about 53 mm. The surface of the hydropower station gate is a large, planar structure, and the contact between the wheeled robot and the gate surface is characterized as line contact. As illustrated in Figure 4, the control cabinet is designed in the form of a trolley case to facilitate rapid transportation and on-site deployment. Operation of the control box is enabled by opening the top cover.

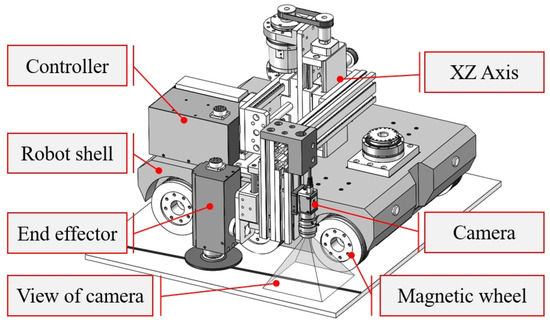
Figure 3. Climbing robot.

Figure 4. Control cabinet.

2.3. Robot Kinematic and Dynamic Model Analysis

The kinematic model of the robot is developed based on the following assumptions:

(1)

The local radius of curvature of the tracked weld at any given point is significantly larger than the minimum turning radius of the robot;

(2)

The front and rear wheels on the same side of the robot maintain identical linear velocities;

(3)

The center of mass of the robot coincides with its center of rotation.

To further investigate the kinematic characteristics of the climbing robot, it is first necessary to establish an appropriate coordinate system. As illustrated in Figure 5, x-o-y denotes the world coordinate system, while x′-o′-y′ represents the robot’s local coordinate system. In the robot coordinate system, O′ corresponds to the geometric center of the climbing robot, b denotes the distance between the left and right wheels, and D is the diameter of the magnetic wheels, v_L, v_R, and v represent the linear velocities of the left wheel, right wheel, and the overall forward velocity of the robot, respectively. ω denotes the angular velocity of the climbing robot about its geometric center.

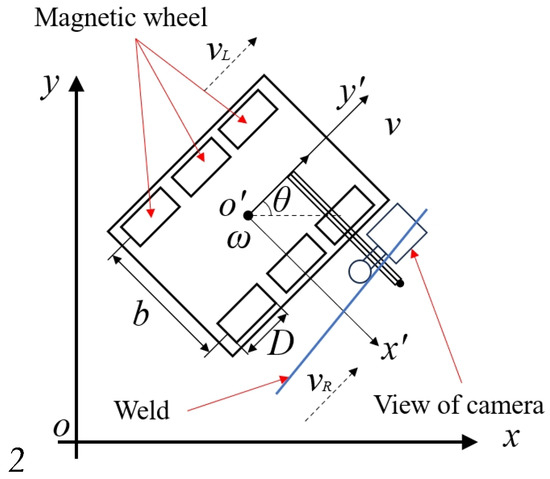
Figure 5. Coordinate system of robot.

The variables and their corresponding meanings are shown in Table 1.

Table 1. Variables and their meanings.

Variable Names	Meanings
$v$	Overall forward velocity
$\omega$	Angular velocity
$v_L$	Left wheel velocity
$v_R$	Right wheel velocity
$D$	Diameter of the magnetic wheels
$b$	Distance between the left and right wheels
$d$	Distance between point B and C
$f$	Distance between point E and D
$l$	Distance between point B and E
$\theta$	Heading angle of the robot
$e_k$	Actual deviation
$M_t$	Driving torque transmitted to the wheels
$M$	Torque of the driving motor
$\eta$	Transmission efficiency
$P$	Power of the motor
$\omega$	Angular velocity of the motor
$m$	Total mass of the robot
$a$	Acceleration of the robot
${\tau }_R$	Driving force of the right wheel
${\tau }_L$	Driving force of the left wheel
$F_f$	Dynamic (kinetic) friction force acting on the robot
$f_m$	Coefficient of kinetic friction
$F_t$	Traction force for upward or downward motion
$G$	Gravitational force acting on the robot
$f_z$	Total resistance force in the vertical direction
$F$	Total magnetic adhesion force of the wheels
$F_j$	Adhesion force of a single magnetic wheel
$N$	Support force acting on the robot in the horizontal plane
$N_i$	Supporting force acting on a single magnetic wheel

The calculation methods for v and ω of the climbing robot in its local coordinate system are presented in Equations (1) and (2):

$$v={\displaystyle \frac{v_L+v_R}{2}},$$

(1)

$$\omega ={\displaystyle \frac{v_L-v_R}{\mathrm{b}}},$$

(2)

The position and posture of the climbing robot are represented by [x, y, θ]^T, where x and y denote the coordinates of the center of the robot, and θ denotes the heading angle of the robot. The kinematic model of the climbing robot can be formulated as follows:

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{cc}cos\theta & 0\\ sin\theta & 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}v\\ \omega \end{array}\right]$$

(3)

Combining Equations (1)–(3), we can get Equation (4) as shown below:

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{c}(v_L+v_R)/2\times cos\theta \\ (v_L+v_R)/2\times sin\theta \\ {(v}_L+v_R)/b\end{array}\right]$$

(4)

Next, we will conduct some dynamic analyses. When the robot is adsorbed onto a vertical steel surface and moves upward in a straight line, let the driving torque of the motor be denoted by M. Considering power losses in the transmission process, and assuming a transmission efficiency of η, the following equation holds:

$$M_t=\eta M=\eta P/\omega$$

(5)

In the above equation, P denotes the power of the driving motor, ω represents the motor′s angular velocity, and M_t is the driving torque transmitted to the wheels. Considering the robot as a whole for force analysis, when it climbs vertically upward, the force balance satisfies the following equation:

$$ma=3({\tau }_R+{\tau }_L)-F_f-G$$

(6)

$$F_f=f_m( F-N)$$

(7)

In the above equation, τ_R and τ_L represent the driving forces of the right and left wheels, respectively; m is the mass of the robot; a is the acceleration in the vertical upward direction; F_f denotes the dynamic friction force acting on the robot; F is the total magnetic adhesion force; f_m denotes the coefficient of kinetic friction and N is the support force acting on the robot in the horizontal direction. Accordingly, the following equation can be established:

$$ma=3({\tau }_R+{\tau }_L)-f_m(\sum _{j=1}^6{F}_j-\sum _{i=1}^6{N}_i)-G$$

(8)

Here, τ_R = τ_L = F_t/6, where F_t is the traction force required for upward motion. The resistance force F_z represents the resultant rolling friction and the gravitational force component in the vertical direction. By combining the above two equations, the following relationship is obtained:

$$F_z=f_m(\sum _{j=1}^6{F}_j-\sum _{i=1}^6{N}_i)+G$$

(9)

The robot′s motion state on the wall surface depends on the relationship between the traction force F_t and the resistive force F_z:

• − If F_t > F_z, the robot undergoes upward acceleration;
• − If F_t = F_z, the robot moves upward at a constant speed;
• − If F_t < F_z, the robot decelerates or remains at rest.

During downward motion along the vertical surface, the wall-climbing robot satisfies the following force balance equation:

$$ma=3\left({\tau }_R+{\tau }_L\right)-f_m\left(\sum _{j=1}^6{F}_j-\sum _{i=1}^6{N}_i\right)+G$$

(10)

At this stage, the dominant resistive force is the rolling friction, whereas gravity contributes to the driving force facilitating the robot′s downward motion.

3. Computer Vision Guided Autonomous Mobility

3.1. Visual System Setup

During weld inspection, the robot is required to move along the direction of the weld. After the visual system captures the weld image, it must simultaneously perform defect detection and extract the weld boundaries from the image. The extracted boundary information is then used to guide the climbing robot to navigate along the weld path. The motion control structure based on the visual system is illustrated in Figure 6 and primarily consists of four components: a visual sensor, an image processing unit, a controller, and an actuator.

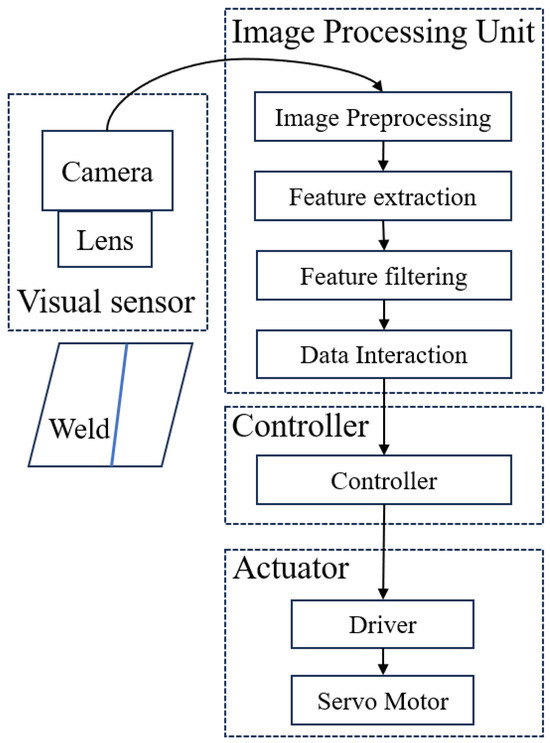
Figure 6. Control system setup.

The visual sensor includes an industrial camera and an industrial lighting device. The output channel of the camera was connected to the controlling PC in the Image Processing Unit that received the digital image data via a Gigabit Ethernet camera interface. The primary function of the industrial camera is to capture images of the weld. In situations where lighting conditions are inadequate, LED lighting equipment is installed in front of the camera to ensure the acquisition of high-quality weld images. The image processing unit performs a series of operations on the captured images, including image preprocessing, feature extraction, and image filtering. Based on the processed image results, the controller coordinates and regulates the motion of the servo motor of the climbing robot, ensuring that the robot consistently follows the weld direction.

3.2. Weld Image Process

After image acquisition, further processing is required to extract the corresponding feature points and feature lines. The raw image in grey-scale pixels was processed by a series of computer vision algorithms using the OpenCV library [25]. The image processing procedure is mainly divided into two stages. First, the weld region is segmented to distinguish the weld area from the non-weld background. Second, the centerline of the weld is extracted from the segmented weld region.

Threshold segmentation is a region-based image segmentation technique that is widely applied in image processing. Given the significant visual differences between the weld and non-weld regions, threshold segmentation can be directly utilized for this task. By selecting an appropriate threshold value, the weld region can be effectively separated from the background, as illustrated in Figure 7. This segmentation provides a foundation for subsequent image processing steps.

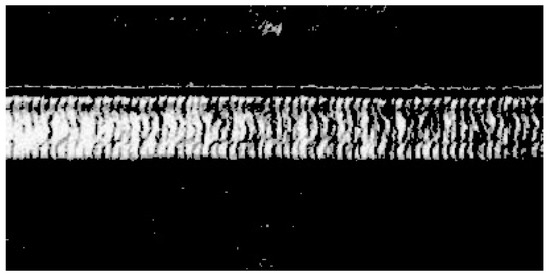
Figure 7. Threshold segmentation.

Based on the previously segmented image regions, the features of the weld area have been obtained. The next step involves extracting the edges of the weld and overlaying them onto the original image to facilitate equipment debugging, as shown in Figure 8. Utilizing the extracted weld edges, the centerline of the weld is subsequently calculated and used as the tracking trajectory for the robot.

Figure 8. Weld edge extraction.

The procedure from initial image acquisition to final deviation calculation is summarized as follows:

• Process the mask image obtained from weld area segmentation to generate a single-channel binary image;
• Extract the weld skeleton by refining the binary weld mask, reducing the weld edge region to a skeleton with a width of several pixels;
• Detect straight lines within the weld skeleton image using the Hough transform;
• Compare the lengths of the detected straight lines and select the best one as the weld edge line;
• Calculate the deviation of the robot relative to the weld path, where the deviation includes both lateral displacement and angular deviation.

3.3. Robot Mobility Based on Weld Center Deviation

Control systems can be categorized into open-loop and closed-loop types based on the presence or absence of a feedback mechanism. Open-loop control, which lacks feedback, generally exhibits low accuracy and is incapable of automatically correcting deviations. To ensure that the climbing robot meets the operational accuracy requirements during task execution, this study adopts a PID-based closed-loop control approach to correct deviations. After the deviation value is obtained, the software system of the robot applies appropriate corrections based on the deviation, thereby ensuring that the robot consistently follows the weld path.

PID stands for Proportional-Integral-Derivative, representing a control algorithm that integrates three control strategies. The fundamental principle of the PID control system is illustrated in Figure 9.

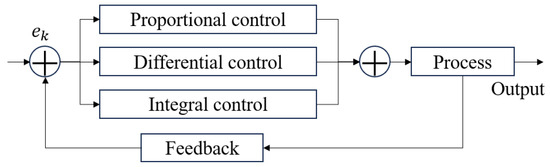
Figure 9. PID control system.

The model of the climbing robot tracking the weld trajectory in this study is illustrated in Figure 10. In the figure, the red line AG represents the weld centerline extracted by the visual system, and the rectangular region enclosed by points HIJK corresponds to the camera’s field of view, with the camera mounted on the right side of the robot. The robot exhibits symmetry about both the dashed lines ST and MN, which intersect at point P. By offsetting the dashed line ST rightward by a distance d1, a virtual robot centerline AF is obtained. When the virtual centerline AF deviates from the weld centerline AG, it indicates that the robot has deviated from the weld trajectory. In response, the robot control system adjusts the differential steering of the left and right wheels to correct the deviation, thereby ensuring that the virtual centerline AF gradually coincides with the weld trajectory line.

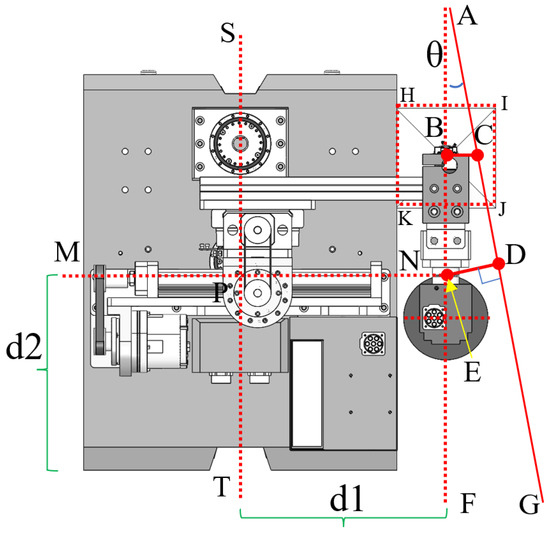
Figure 10. Weld tracking model.

As illustrated in Figure 10, the actual deviation distance BC between the virtual robot centerline AF and the weld centerline AG can be obtained through geometric transformation. Point B denotes the center of the camera lens, and a line parallel to MN is drawn through point B, intersecting the weld centerline at point C. The deflection angle θ is determined by calculating the angle between the weld centerline AG and the vertical axis of the image. The horizontal offset d, corresponding to segment BC, is calculated as the distance between the weld centerline and the vertical axis at the horizontal midline of the image. Based on these parameters, the actual lateral deviation f of the robot chassis relative to the weld, represented by segment DE, can be calculated using the following formula:

$$d={\displaystyle \frac{f}{cos\theta }}-l\times tan\theta ,$$

(11)

In the above formula, d is the offset distance in the weld image; θ is the deflection angle in the weld image; l is the distance from the camera center to the robot offset center, which is represented by BE in the figure.

The actual deviation of the robot relative to the weld is selected as the error value e_k:

$$e_k=f=d\times \mathrm{c}os\theta +l\times sin\theta ,$$

(12)

The PID control equation of the system is expressed as follows:

$$u_k=K_P\left(d_{k}cos{\theta }_k+l_{k}sin{\theta }_k\right)+K_i\sum _{j=0}^k(d_{j}cos{\theta }_j+lsin{\theta }_j)+K_d\left(d_{k}cos{\theta }_k+lsin{\theta }_k-d_{k-1}cos{\theta }_{k-1}-lsin{\theta }_{k-1}\right)$$

(13)

In the above formula, u denotes the differential speed of the active wheels on both sides of the climbing robot. When the weld coincides with the virtual center line AF, the error e is zero, and the proportional term becomes zero. In this case, the system does not perform proportional control. When the weld deviates from the virtual center line AF, the error e is nonzero, and proportional control serves as the primary adjustment mechanism to correct the deviation.

4. Experimental Validation

4.1. Weld Defects Detection

To determine the condition of the current weld position, an image of the weldment under the field view of the camera is captured. The collected images are then processed by a trained defects detection model to assess whether defects are present in the weld at the current location. If defects are detected, the system further identifies the specific type of defect. To enable accurate classification of defect types, the process primarily involves early-stage dataset collection followed by model training and validation.

4.1.1. Dataset Collection

As shown in Figure 11, common types of weld defects on metal surfaces include undercuts, pores, weld bumps, and weld pits. These defects can lead to stress concentration at the weld region, significantly increasing the risk of failure under external loads. Prior to training, a set of images containing representative weld defects was collected.

Figure 11. Common categories of weld defects. (a) Undercuts; (b) Pores; (c) Weld bumps; (d) Weld pits.

Given the challenges associated with obtaining sufficient defect images at an early stage, the sample size was initially limited, making it difficult to train a high-precision classification model. To address this, data augmentation techniques were applied. The dataset was enhanced by adjusting the image structure and introducing artificial noise, thereby improving the robustness and generalization capability of the classification model while mitigating the risk of overfitting. The distribution of various defect types after enhancement is shown in Table 2. After augmentation, the dataset was expanded to 2400 images.

Table 2. Number of defect samples after data augmentation.

Categories of Weld Defects	Number
Undercuts	2236
Pores	1511
Weld bumps	2648
Weld pits	1601

4.1.2. Model Training and Testing

After data augmentation, 1900 images were randomly selected from the weld surface defect dataset as the training set, 400 images were used as the validation set, and the remaining 100 images served as the test set. The neural network classification model was trained based on the YOLOv5 object detection framework. The training parameters were configured as follows: the learning rate was set to 0.001, the batch size was 4, and the number of training epochs was 200. The variation in the loss function value during the model training process is illustrated in Figure 12. The final loss function value converged to approximately 0.02.

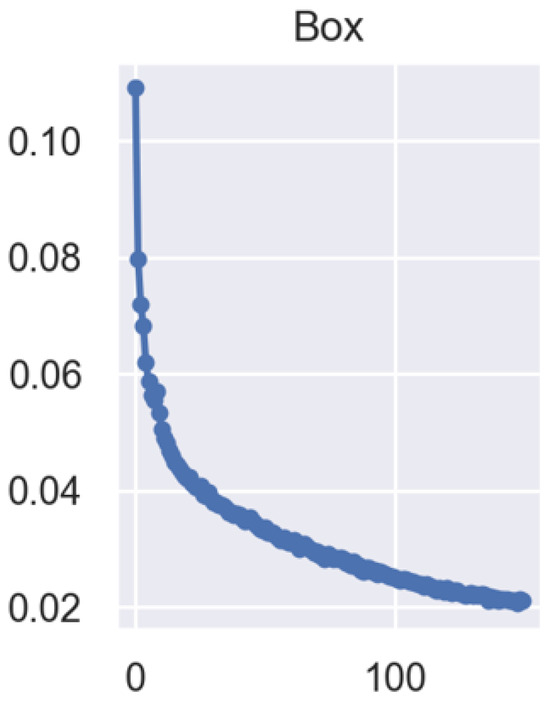
Figure 12. Loss function in the model training process.

The trained model was employed to detect the defect types in the input images, and the detection results are illustrated in Figure 13. The detailed detection performance for various types of weld surface defects is summarized in Table 2.

Figure 13. Image of defect detection test.

As shown in Table 2, the defect type detection model exhibits relatively high accuracy and demonstrates favorable detection performance.

4.2. Tracking Simulation and Experimental Validation

To verify the coordinated control of the robot by the controller and its ability to track the reference trajectory, simulation experiments were conducted in Python3. During the tracking process, the heading angle θ was regulated by adjusting the differential speed between the left and right wheels, ensuring that the robot continuously followed the weld trajectory. When the robot moves precisely along the weld direction, the heading angle θ is zero; when the robot deviates from the weld direction, θ becomes nonzero.

The tracking control parameters for robot motion are as follows: the PID parameters k_p, k_i, and k_d are set to 0.0005, 0.01, and 0, respectively, and the distance b between the left and right wheels is 0.45 m. In the simulation, to further validate the effectiveness of the controller, a curved trajectory was employed instead of a straight path. The equation of the curved trajectory is given by:

$$y=2000\times cos\left(0.0005\times x\right),$$

(14)

As shown in Figure 14, the blue curve represents the simulated weld trajectory, the green curve denotes the ideal robot motion trajectory, and the black solid line indicates the actual tracked trajectory. Figure 15 illustrates the tracking error in the X-direction during the tracking process, while the deviation in the heading angle θ is presented in Figure 16. Based on analysis of the simulation data, it can be concluded that the black curve representing the tracking trajectory closely follows the green curve denoting the ideal motion path of the robot. This result demonstrates the effectiveness of the controller′s strategy and parameter settings within the simulation environment, which warrants further validation through real-world experiments.

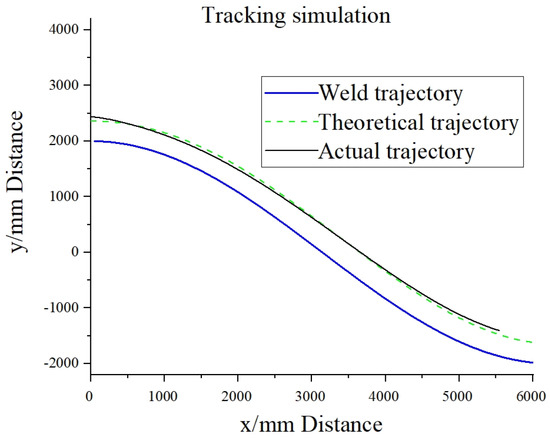
Figure 14. Tracking simulation.

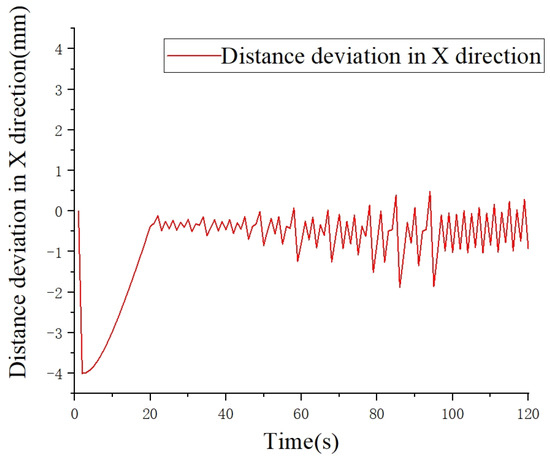
Figure 15. Simulation distance deviation in X direction.

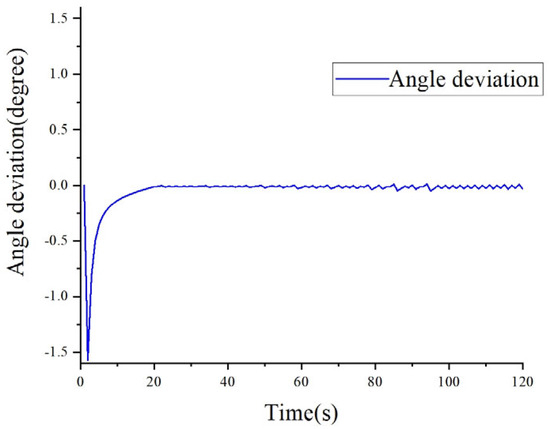
Figure 16. Angle deviation.

A steel-structured experimental site was constructed in the laboratory, utilizing steel plates with a thickness of 8 mm. The site was divided into three areas, designated as A, B, and C. Area A consisted of a vertical steel plate measuring 5 m × 6 m, where the experiments were conducted. Area B featured a curved steel plate designed to facilitate the robot’s transition from the ground to the vertical surface. Area C, mounted on the floor, served as a supporting base for the other two steel plates. The configuration is illustrated in Figure 17. Figure 18 present images of the physical robot.

Figure 17. Steel-structured experimental site.

Figure 18. Actual robot photograph.

A series of experimental results in Figure 19 are presented to validate the effectiveness and accuracy of the proposed algorithm. The total experiment duration is 240 s, and each image corresponds to a 20-s segment of the weld seam. The number after t in the image filename indicates the starting time of that segment. This naming convention clearly shows the timestamp of each image and allows direct alignment with the time axis in the associated charts. The experimental images include not only the actual captured weld seam images but also the weld centerlines identified and extracted by the image processing algorithm. To enhance processing efficiency, all raw images were uniformly converted to single-channel grayscale images prior to processing. In each image, the automatically extracted weld centerline is overlaid as a bold black line, providing an intuitive visualization of the algorithm’s detection performance. These images clearly show the extracted weld centerlines, offering a reliable visual foundation for subsequent robotic control.

Figure 19. Experimental results: (a) img_01_t000s; (b) img_02_t020s; (c) img_03_040s; (d) img_04_t060s; (e) img_05_t080s; (f) img_06_t100s; (g) img_07_t120s; (h) img_08_t140s; (i) img_09_t160s; (j) img_10_t180s; (k) img_11_t200s; (l) img_12_t220s.

During the experiments, several key data points were also extracted, which are of great significance for evaluating system performance and optimizing algorithm parameters. Specifically, these include the lateral offset and angular deviation of the robot relative to the weld centerline. These data not only reflect the stability and robustness of the detection algorithm under various working conditions but also provide a quantitative basis for subsequent system calibration, error compensation, and control strategy design.

The deviation data of the actual robot tracking the straight weld in the X-direction are presented in Figure 20, while the deviation data of the heading angle θ are shown in Figure 21. Based on the experimental data, it can be observed that during the weld-following navigation of the wall-climbing robot, the lateral offset between the robot and the weld remains largely within ±7 mm, while the angular deviation is maintained within ±5°. At the initial position, the robot exhibited a 4 mm deviation from the weld. Upon activation of the autonomous navigation mode, it promptly corrected this positional error. During the autonomous navigation process, external environmental factors, such as vibrations induced by the robot traversing local surface irregularities and variations in lighting conditions on the gate surface, may affect the accuracy of weld detection. These disturbances can lead to fluctuations in the output of the weld recognition model, resulting in minor oscillations in the robot′s trajectory. Nevertheless, the system is capable of maintaining stability within a ±7 mm range, which satisfies the operational requirements for weld-following navigation. These results validate the effectiveness of the proposed navigation system in ensuring stable wall-climbing motion along the weld path.

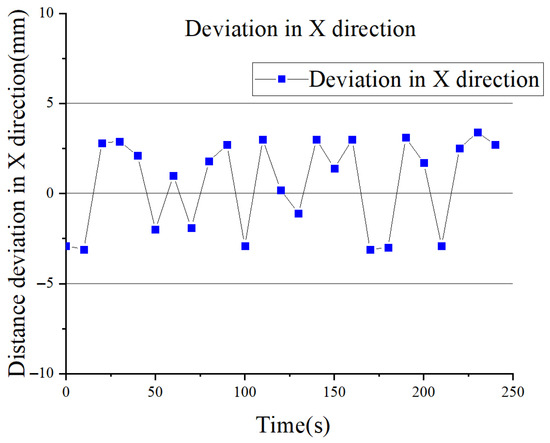
Figure 20. Distance deviation in X direction.

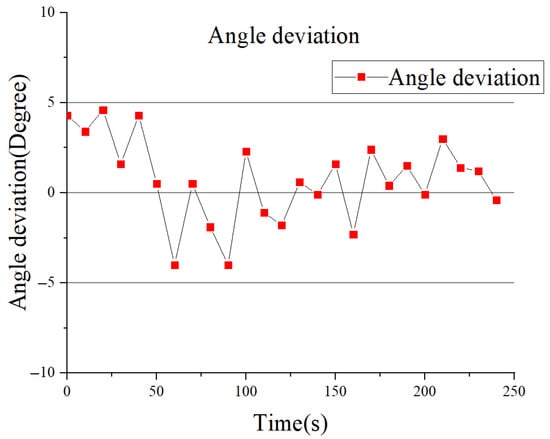
Figure 21. Angle deviation in X direction.

5. Conclusions

In this paper, a wheeled robot performing on-site corrosion-protection operations on the surface of hydraulic steel gates was designed, and a corresponding kinematic model of the climbing robot was established and analyzed. Based on the structural characteristics of the robot, a trajectory tracking controller and control strategy for the magnetically adhered climbing robot were designed. The tracking control method integrates PID control with the kinematic model and computer vision.

The performance of the designed trajectory tracking controller was validated through both simulation and practical experiments. The results indicate that the controller exhibits good control performance and can meet the accuracy requirements of the robot during operation. In order to detect the current state of weld, an intelligent software system for weld defect recognition based on computer vision was developed. The system, utilizing a trained model, demonstrates effective recognition performance for several common types of weld defects. The defect type detection model shows strong accuracy and performs well in identifying different defect types.

Considering the current state of hydraulic steel gate maintenance, the climbing robot proposed in this study can partially substitute for manual labor, thereby reducing the reliance on human intervention and enhancing the overall level of automation in maintenance operations.