Featured Application
Predictive model selection when rare events and data scarcity are involved (credit default, fraud detection, or any other event probability model).
Abstract
Model validation is a challenging Machine Learning task, usually more difficult for consumer credit default models because of the availability of small datasets, the modeling of low-frequency events (imbalanced data), and the bias in the explanatory variables induced by the train/test sets split of the validation techniques (covariate shift). While many methodologies have been developed, cross-validation is perhaps the most widely accepted, often being part of the model development process by optimizing the hyperparameters of predictive algorithms. This experimental research focuses on evaluating existing robust cross-validation variants to address the issues of validating credit default models. In addition, some improvements to those methods are proposed and compared with a wide range of validation techniques, including fuzzy methods. To reach solid and practical conclusions, this work limits its scope to logistic regression, as it is the best-practice modeling technique in real-world applications of this context. It is shown that robust cross-validation algorithms lead to more stable estimates, as expected due to the more homogeneous partitions, which have a positive impact on the selection of credit default models. In addition, the enhancements proposed to existing robust techniques lead to improved results when there are data restrictions.
1. Introduction
Predictive models are widely used in different industry sectors as a basis for decision modeling. They are applied in multiple use cases according to the available data and the modeled event, and examples include fraud detection, targeting marketing campaigns, credit risk assessment, disease diagnosis, predictive asset maintenance, etc.
In all cases, it is necessary to choose the best model in terms of the potential predictive performance in new population samples where decisions should be taken in the future. There is a well-known trade-off between the accuracy of the model in past observations and the model performance in new, unknown samples when the model complexity increases; that is, when a larger number of predictive variables are used to train the model. Then, it is key in any industry sector to identify the optimal model complexity according to the data patterns before using the predictive model for decision making.
Many methods have been investigated and proposed to select the combination of explanatory variables of the final model that maximizes predictive performance or minimizes model error. More simplistic methods like hold-out test samples make a deterministic estimation of error bias, while more advanced methods like cross-validation (CV) and bootstrapping (BTS) are stochastic in nature, considering both bias and variance of the model error [1,2,3,4,5,6,7,8]. The less computational requirements, better practicality, and good results of cross-validation techniques have made CV the most popular stochastic validation methodology for model error estimation, yielding a broad range of CV variants and benchmarking studies over the last decades [6,9,10,11].
The main motivation of this research is that, in the particular case of credit default risk models, there is a simultaneous concurrence of several validation difficulties: the predicted events have low frequency and high severity, while the available data sample is usually small and always imbalanced because the number of defaulters is much smaller than non-defaulters due to the nature of the credit events, leading to a covariate-shift when cross-validation techniques are used. This results in less stable model performance estimations that increase the risk of not selecting the best model. There are studies that address these issues separately [12,13,14], and others propose solutions that are not feasible for all credit default explanatory variables [15], while there are very few robust methods that face all the issues simultaneously [9,16,17].
All the above facts support the motivation basis of this work, in a context where a failure in the prediction of an event could be critical, as happens in credit lending, where the economic impact of a bad loan is many times the profit of any performing loan for the financial institution. In fact, it is even worse for the credit applicant, and it could mean the bankruptcy of any person. In addition, the referenced studies in validation methodologies do not tackle this context specifically, and most of the work conducted specifically for credit lending usually proposes and assesses different modeling techniques without focusing on the validation aspect of the problem. Then, we can pose the questions: Are some existing methods more appropriate than others to validate credit default models? In that case, is it possible to improve those methods even further?
This paper conducts experimental research to test the hypothesis that reducing the volatility of the results of the validation process using more robust cross-validation methods, the estimations should outperform any other validation methodology when tackling all the above issues simultaneously for model selection in the consumer credit default risk context. In addition, some enhancements are proposed and tested to better leverage categorical explanatory variables, leading to the best results in data-scarce situations. In addition, a fuzzy approach to cross-validation has also been proposed and added to the benchmarking.
In order to make this research reproducible and applicable, real-life public credit default datasets from Europe, Asia, Oceania, and America were used together with the most commonly accepted methodologies for the probability of credit default, the logistic regression, and the area under the receiver-operating characteristic curve (ROC). Thus, it has been decided to assess a wide range of validation methodologies and their variants while keeping the models, data, and performance metrics bounded to the consumer credit default context. Presumably, this approach will lead to more conclusive results than testing fewer validation algorithms with more types of models and datasets.
In order to test the performance of each validation methodology, a set of models of very different predefined complexities was used. Then, the validation assessment will cover as many potential situations as possible, ranging from models with a poor predictive performance to the most accurate ones.
All model trainings and validations were made using a random sample of the population of each entire dataset. As the validation results can be compared against the real model performance in the unseen population, both aspects of model validation (selection and assessment) could be tested. Nevertheless, this research has been limited to model selection purposes only, as this is a more realistic application of the validation procedures with limited data availability.
Due to the number of validation algorithms used in the comparison, from now on referred to as “validators”, there are validators with similar performance or efficiency, leading to close results at the end of a set of experiments made on a particular dataset. To make sure that there are statistically significant differences between the performance of the validators before ranking them, non-parametric paired tests have been carried out for comparison among all of them.
Among the main conclusions, it is clear that robust cross-validation algorithms need more data processing to calculate the nearest neighbors of the observations, which allows the homogeneity of the train and test datasets to be increased, therefore reducing the variability of the estimations. The main contribution of this research is that, despite the higher computer resource requirements, these validation techniques outperform the rest of the validation methods for the selection of consumer credit default models in data-scarce situations. As a second contribution, the proposed methodological improvements to better leverage the categorical covariates result in even better model selection capabilities. This is potentially applicable in other statistical data modeling contexts where rare events with a large diversity of explanatory variables and data limitations are present.
2. Credit Default Modeling Use Case
Many times, research papers on model validation experiment with several types of models on a variety of datasets try to draw general conclusions rather than address a particular use case or complex situation. For example, there are publications that compare models such as support vector machines, decision trees, nearest neighbors, linear discriminant analysis, etc., on datasets of different contexts (clinical or medical data, environmental, agricultural, financial products or many others) that do not share common specific problems [9,17].
Given the great diversity of existing datasets and predictive models, it is impossible to include all possible cases in a single study, and any attempt to reach universal conclusions could not be feasible, as stated by the “no free lunch” theorem for any optimization problem. In addition, logistic regressions are by far the most common practice for credit default modeling in real-life applications in financial institutions. As a consequence, only logistic regression models are used in this study to fairly compare the validation techniques in the consumer credit default context. Nevertheless, it has to be clear that the validators used in this research can be used for any algorithm able to make predictive discriminations for binary response variables in other contexts, like fraud detection or anti-money laundering, where less interpretable Machine Learning models can be applied.
2.1. Logistic Regression
Credit default models must be explainable and understandable to make sure that they properly reflect the underlying risks of the lending activities, and they can be used together with different business assumptions to make decisions in other potential scenarios. More importantly, the models must be explainable to banking regulators as part of the legal requirements originated by the Basel Accords set by the Basel Committee on Banking Supervision. Therefore, the models should be flexible and easy to understand, like linear regressions, while taking into consideration that predictions must belong to the (0, 1) interval, as happens with the probability of a credit default. Logistic regressions are very convenient for this task as they link a linear regression model with predictions in the (0, 1) domain via a logit function that is analytically easy to handle. These are the reasons why logistic regression is the only predictive modeling technique underlying the credit scorecards used for rating credit applications for more than 50 years.
Logistic regressions can predict with some degree of accuracy the probability of an event in a specific time horizon. When used for credit default modeling, financial institutions can assess which credit applications could be worthy of lending, considering their probability of default (PD).
Logistic regression is a particular case of generalized linear models commonly used when the outcome variable is dichotomous; that is, the response is a binary random variable that represents the occurrence of an event or otherwise non-event.
In the context of consumer credit default modeling, a data sample consists of a certain number of credit customers (or credit lines), each of which can be assigned to a specific group of credit behavior that is defined by the values taken by certain customer and/or product attributes.
Let N be the number of possible credit behavior groups, then each group is characterized by the probability of default of any of its members or PDi where i = 1, 2, … N. Define ni as the number of observations in group i, and define also the random variable Yi as the number of defaults in group i considering all default events as independent among them. Then, each random variable Yi follows a binomial distribution:
The log-likelihood function of the joint probability distribution of random variables Y1, Y2, … YN is:
Building a probability of default model means representing the dependency between the response or dependent variable PDi of each homogeneous credit default group and some of the customer attributes given by a vector of independent variables X = (X1, X2,… Xp).
Generally, the logit function is used as the link between the probability of default PD and a linear combination of the covariates {Xi}i=1,…p:
The left-hand side of this expression or logit function represents the logarithm of odds, and the p coefficients β in the right-hand side are estimated by maximum likelihood, thus maximizing the log-likelihood function.
In order to include categorical explanatory variables in the above formula, it is very common to transform each categorical variable into a set of dummy or binary variables. When a categorical variable takes K different values, a set of K binary variables can be created, setting the value 1 for one specific value and 0 otherwise. This is usually called variable binarization.
Another possibility is to use the weight of evidence (woe) of the categorical variables as the covariates to include in the model formula. To calculate the woe of a given variable X that takes K different values X = {x1, x2, ….xK}, the following formula is used to substitute each of the values:
where qi is the number of observations with X = xi; qei is the number of defaulted observations with X = xi; NE is the total number of non-defaulted observations in the sample; and E is the total number of defaulted observations or events.
In the case where there are values xi with only a few observations, it would be convenient to aggregate some of the variable values to obtain a new variable X’ with a smaller number of different categories, but more observations in all or some of them. In addition, if K is large, then model interpretation and implementation become quite complex in practice. Therefore, the original variables are usually aggregated to obtain covariates with no more than 10 or 20 different values in real applications. This practice is usually called variable binning.
2.2. Area Under ROC Curve
Predictive model performance metrics, such as accuracy or misclassification error, have been commonly used in many research papers. However, these are not the most convenient metrics to assess the performance of credit default models, and the area under the receiver operating characteristic curve (area under ROC curve or AUR) should be used instead [18,19,20].
The AUR is suitable for imbalanced data [9] because it considers the trade-off between the benefit of right predictions and the cost of errors. Normally, a binary classifier that increases the number of true positives (captured events) will also increase the number of false positives, and this relationship should be taken into consideration in use cases where the cost of a false negative is very different from the cost of a false positive. This is the reason why AUR has been adopted as the best practice in the field when modeling rare events with high severity, as happens in credit defaults.
To calculate the AUR for a particular PD model over a sample dataset, all the observations in the sample must be ranked first according to the predicted PD, from highest to lowest probability of default. Then, a two-way table of the observed versus predicted defaulting events must be created for each different PD value that is considered as a cut-off value to differentiate defaults from non-defaults. For any specific cut-off PD value, correctly predicted defaults are those defaulted observations with a predicted PD greater than or equal to the cut-off PD, while incorrectly predicted defaults are the non-defaulted observations with a predicted PD also above or equal to the cut-off value.
For each PD value, the corresponding ROC curve point (XROC, YROC) is obtained from its two-way table as the pair “sensitivity” vs. “false alarm rate” in the Y-axis and X-axis, respectively. Sensitivity at a specific cut-off PD is calculated as the correctly predicted defaults divided by all the observed defaults of the sample. The false alarm rate is calculated at a particular cut-off PD value as the number of observations incorrectly predicted as defaults divided by all the observed non-defaulters of the sample.
Then, if there are M different PD values predicted by the model PD1 > PD2 > … > PDM, the AUR can be simply calculated as the area under the discrete ROC curve by:
There are several ways to approximate the area under the curve; it is not of great importance which is chosen as long as the formula used is always the same when comparing model performances. In any case, the greater the AUR, the better the model performance. AUR equals 1 in a perfect model with no predicted errors, while the AUR of a pure random model is 0.5, where the response variable is independent from the covariates.
3. Model Validation Methodologies
Model validation has several applications according to the purpose of the overall analysis [10,21]. On one hand, the validation of models to select the best among them is called “model selection”. On the other hand, model validation with the aim of estimating what the performance might be on the underlying population is often called “model assessment”.
To carry out an evaluation of models with certain reliability, some requirements must be fulfilled by the data samples available for both the training and testing to be performed during the validation process. Mainly, the data must be highly representative of the underlying population, as otherwise there will always be an indeterminate bias in the estimated expected model performance in the rest of the population.
In real use cases, the lack of representativeness of the data will usually not allow a trustworthy assessment of the predictive models. So, the uncertainty of the evaluation should also be considered [7,13,14], although it is difficult to evaluate [3]. For this reason, model validation is usually more reliable for model selection purposes.
At the same time, the selection of models can be executed within different scopes that have their own particularities. One may be the comparison of previously trained models to pick which one should be used in a production environment with future data samples. Another framework is the model training process itself [10,21] since many iterations that compare eligible intermediate models are performed before coming up with the final model. In this case, resource consumption during the validation process becomes critical, and this workload could make the use of certain sophisticated methodologies that are computationally intensive unfeasible.
In this research, the validation scope is model selection among a predefined set of models with different combinations of explanatory variables, ranging from a few variables to all variables available in the data sample. The more covariates used by the model, the more complex it is.
There is a trade-off between model complexity and model robustness: too many variables will achieve more precision on the training data but less precision when making predictions on new data [22]. This potential loss of model performance is due to over-fitting to the training data in such a way that they do not correctly reflect the true patterns present in the rest of the population.
Therefore, it is critical to consider this circumstance in the validation process and avoid overestimating the performance of the model by finding a balance between model accuracy and model complexity. This will allow us to select the model with the best expected performance in new samples taken from the underlying population. The different approaches to solving this issue will be described next.
3.1. In-Sample Validation
Under the in-sample approach, the validation procedure is carried out with the same data sample used to train the model. There are many goodness-of-fit tests, like the Chi-squared, Kolmogorov–Smirnov, Anderson–Darling, and Cramér–Von Mises, but maximizing any of these metrics will usually lead to more complex models that overfit to the training data, increasing the generalization error in future samples [4]. This is especially harmful when the sample size is small and not fully representative of the underlying population, making it necessary to account for this potential overfitting when selecting a model to make predictions in new datasets.
In this paper, by “in-sample” validation, we refer to those methods where it is the validation metric that directly penalizes model complexity against model performance. One such metric is the Akaike Information Criterion (AIC) that uses the deviance as a measure of the model error. In this metric, the expected prediction error of a probability of default model PD(.) trained with N observations {xi,yi}i=1,…N is estimated by:
where β is the PD model complexity measured as the number of parameters to fit by maximum likelihood, is the default probability predicted for observation and is the response variable: for defaults and for non-defaults. The deviation error for an observation is calculated as:
Another in-sample validation metric is the Bayesian Information Criterion (BIC), which penalizes complexity more than AIC does, leading to models with a smaller number of parameters. BIC is calculated as:
Between AIC and BIC, it is not clear which metric is better for model selection. In general, BIC outperforms AIC when because AIC usually selects more complex models. On the other hand, for less representative samples, AIC tends to perform better because BIC selects too simplistic models.
In practical modeling applications, AIC and BIC are more commonly used to evaluate the importance of each predictor individually, ranking both of them the independent variables in the same order. For model validation, it is more common to use the approaches described in the following subsections.
3.2. Hold-Out Test Sample
A widely adopted methodology is to separate part of the available data into an independent test set or hold-out test sample (HO sample) that will be used to evaluate the performance of the model after training it with the rest of the available data. This technique can be used with any model performance measure and reduces the bias of the estimation made by the training error [22].
However, when there are few data available, both the bias of the results and their variance (which can become greater than the bias) increase notably, and the use of stochastic methodologies such as bootstrapping (BTS) or repeated cross-validation (CV) becomes necessary [1,12].
3.3. Bootstrapping
This is a general-purpose technique that can be used to estimate a probability distribution for any statistic that can be calculated on a data sample [1,2,4,21,23].
In this technique, an arbitrary number R of subsamples of N observations are generated randomly with replacement from the original available dataset Ω of size N. Then, a PD model is trained in each of the R subsamples, and the model performance is calculated in the rest of the available data not included in each corresponding subsample .
In this way, if L(Y,PD(X)) is the function chosen as the PD model prediction error for any data point (X,Y), the bootstrap error is calculated as:
where is the number of observations in the dataset that only includes the observations (X,Y) not in the subsample used to train the model .
If the model error is taken as 1-AUR—that is, the model performance is measured via the AUR—then it can be written:
where is the AUR calculated in the test set using the PDj model trained in subsample Ωj.
There is an enhanced bootstrap variant called “0.632 bootstrap” aimed at reducing the bias in the bootstrap estimation due to the fact that, on average, around one-third of the observations are not used to train each PDj model. This could lead to poor model performance in situations of limited sample sizes. This variant is a weighted average of the performance AURtrain of the PD model trained in the entire sample Ω and the bootstrap estimation:
An additional refinement is the variant known as the “0.632+ bootstrap” that modifies the weights of the above average to decrease the impact of the training performance when the sample size is small and there is potential overfitting to the training data that could underestimate the real model error [23]. It is calculated as:
where ω = 0.632/(1 − 0.368 ρ) and ρ is the ratio of overfitting defined in terms of the “non-information performance” φ that is the model performance on a population where the response variable Y is independent from the covariates:
3.4. Cross-Validation
Usually, the hold-out test sample technique is used to validate a model when data in excess are available, taking out a large enough independent test set separated from the training data to avoid performance overestimation. For those situations in which there is data scarcity, a smaller validation set should be used to allow for enough training data. However, this can add significant bias to the validation results due to the lower representativeness of the test set. The cross-validation method (CV) was specifically designed to tackle this situation.
The basis of cross-validation is to use all the N observations in the sample Ω to validate the classification model, calculating its performance on all the available data. Then, the k-fold cross-validation method performs a random partition of the data into k subsets of equal size as shown in Figure 1, and uses each subset Ωj of N/k elements (test set) to validate a model that has been previously trained with the remaining N(1 − 1/k) observations of Ω\Ωj (train set).

Figure 1.
Dataset partition into k equally sized subsets .
Thus, all the data are used once each time, either to train the model or to validate it. Finally, the average of the performances obtained in the k test sets is used as an estimation of the model’s performance:
where is the AUR calculated in the dataset using the PDj model trained in Ω\Ωj.
The k-fold cross-validation technique can be applied iteratively by repeating the process r times. That is, once an estimate of the performance has been obtained by cross-validation, a different partition of the available data can be made to estimate again the performance of the predictive model in the same way. Finally, all the results given by the r repetitions are averaged to obtain a more stable final estimate of the predictive model performance:
where is calculated for a particular k-fold partition corresponding to the repetition r.
Given the flexibility to choose the number of partition segments, the number of repetitions, and the method used for partitioning, a significant direct impact of this parameter setting is expected on the CV results [24].
According to several studies, some of the most interesting results obtained may be the following:
- The number of partitions most commonly accepted as the best choice is k = 10 or even k = 5 when compared to other typical values such as k = 2 or k = N [2,25], although this should not be taken as a rigorous rule of universal application [10].
- The iterative repetition of the CV estimates converges as the number of repetitions increases [9] and significantly improves the validation results by reducing their variance [5,8,10,26,27].
- The variance of the CV estimator decreases as the size of the data sample increases [8,26].
- Usually, there is not enough information about the population and the bias of the data samples to calibrate the validation result to the true model performance. For this reason, cross-validation could overestimate or underestimate the actual performance of the predictive model, making it a more appropriate technique for model selection than for model assessment [7,13,14].
The versatility of the CV methodology allows for continuous research on how to leverage this technique to improve the predictions of increasingly sophisticated artificial intelligence algorithms that are applicable in many specialized fields, including credit default risk.
As will be explained in Section 4, many CV variants have been developed from the original methodology described above. Possibly, stratified cross-validation (SCV) is the most popular and commonly used variant among all of them due to its simplicity and potential benefits. SCV is a k-fold cross-validation where the data are partitioned with a random sampling stratified on the target variable [2]. This methodological improvement makes the test sets (and the training sets) more homogeneous among themselves, reducing the volatility of the model performance estimates.
The design of the SCV technique avoids biased distributions of the target variable in the train and test sets, and it could therefore be useful in cases of imbalanced data. Although this technique does not address the problem of covariate shift, it will provide a good basis for comparison against the cross-validation enhancement proposed in Section 5.
3.5. Other Approaches
Some authors have highlighted the limitations of the above stochastic methodologies in situations where there are few data available and suggest giving the results in the form of confidence intervals that conservatively take into account the uncertainty of the estimates [13].
Other researchers prefer to increase the size or the heterogeneity of the samples used [14], but this is not possible in real situations where data availability is limited. Then, the only way to make a better model selection is to optimize the validation technique regarding the issues present in each particular use case, as discussed in the next section.
4. The Partitioning Problem and Cross-Validation Variants
Over the years, various studies have identified cross-validation as generally more convenient than bootstrapping because of both the stability of the results and the computational cost [2,5,6,25]. Numerous studies have been carried out to analyze the variance of cross-validation results using different methods [3,8,26,28].
Given that, this work focuses on experimenting with different cross-validation variants to assess whether there are particular techniques that could present extra benefits for validating credit default models regarding the way they were designed.
Cross-validation methodologies usually differ among them in some parameters that define how the original available data are split into validation and training sets, e.g., how many splits must be performed and how these splits have to be chosen. Consequently, different CV methods do not always select the same set of explanatory variables or even the same number of them for the best predictive model [2]. So it is very difficult or even impossible to select the best CV method and parameterization for any possible dataset because the available dataset size, structure, underlying patterns, and response variable will affect the performance of the chosen CV method.
The researcher must make subjective decisions on the set of parameters to use when applying CV methods to their particular case study. This is the reason why much of the research carried out in the past focused on analyzing the impact of the different parameter settings and CV variants on the results. Ideally, the splitting of the available data should be performed to maximize the representativeness of the test and training sets, avoiding the introduction of additional artificial bias between them.
The main parameters of the k-fold cross-validation are the number of repetitions to perform, the number of segments of the partitions, and the specific partitioning technique. Using different values for the number of test sets and the number of repetitions, several known variants of the CV method can be obtained, such as 5-fold cross-validation repeated twice (5 × 2 CV) or 10-fold cross-validation without repetition (10-fold CV). Other procedural aspects that can be modified are the aggregation level of the results and the chaining of cross-validations.
Regardless of the first two above-mentioned main parameters, the partition technique applied to split the observations into k subsets or segments can be a problem when the data distribution is highly skewed (either in the response variable or in the explanatory variables). In these cases, data partitioning can lead to a shift in the data distribution of the training set compared to the data distribution of the test set. This issue is already known as dataset shift.
This dataset shift may cause additional volatility in the CV results, thus the convergence of the validation algorithm will require more repetitions and, for example, the true predictive model performance may be underestimated if there is a large bias between the training set used to calibrate the model and the test set used to evaluate its performance.
One of the main sources of dataset shift is the availability of a dataset not large enough to have equally representative train and test sets. Another is the existence of anomalous observations that could be present in the test set but not in the training set (or vice versa). Additionally, imbalanced data will favor different proportions of events between the training and test sets.
These three issues are often related since having only a few available data points makes it more likely that any partitioning sampling will result in significant differences between the train and test distributions of any variable. However, many of the studies carried out to date usually analyze each problem separately, while in the context of consumer credit default models, all the issues are simultaneously present: few data available, low frequency events, and very diverse debtors’ attributes due to differences in sociodemographic characteristics, financial information, and delinquency history.
In the following section, several techniques developed during the last decades are discussed. The goal is to identify beforehand if there are CV variants more convenient to be used in a benchmarking study of credit default model validation.
4.1. Monte-Carlo Cross-Validation
Monte-Carlo cross-validation methodology (MC-CV) is not a true cross-validation technique in which all observations are finally used to validate the predictive model. This method basically consists of multiple executions of hold-out test sample validations using a different test sample each time that is drawn randomly without replacement from the available data [11,15].
Some variants could be derived from this basic idea, like the stratified Monte-Carlo cross-validation (SMC-CV), where the hold-out test samples are stratified in the response variable. Going further, a couple of fuzzy variants are proposed here for experimentation by simply considering the size of the hold-out test sample as a random variable distributed uniformly in a predefined interval. Then, a fuzzy Monte-Carlo cross-validation (FMC-CV) and a fuzzy stratified Monte-Carlo cross-validation (FSMC-CV) will be additionally implemented and tested in the present analysis.
The disadvantage of this methodology is that not all the data will be finally used to train and test the model, and not all the training and testing observations will be used to the same extent. The number of times that any data are used for training or testing is left to chance, so it is expected that the results obtained will have some induced volatility. Then, in order to include this technique in the comparison, a larger number of repetitions must be performed compared to true cross-validation methods.
4.2. Leave-One-Out Cross-Validation
One of the most studied techniques in the field of cross-validation is the leave-one-out cross-validation (LOOCV). Fundamentally, this is a k-fold cross-validation where k is equal to the number of observations (k = N). That is, the test sets always contain a single data item [11,12,15,24]. Using LOOCV, there is no need to choose either the value of k (since it is determined by the number of observations of the data sample) or the value of r, since only one repetition is possible.
To combine LOOCV with the AUR metric, it is necessary to perform the cross-validation algorithm in a slightly different way: first, the model predictions of all the individual test observations are computed, and then only one single AUR figure is calculated using all the predicted values. In this case, there is no way to average the performance measure over the test sets.
An important disadvantage is the large computational workload required since N models will have to be trained using N − 1 data. This computational complexity is not compensated for by an improvement in the estimations since unstable results are expected due to the low representativeness of the test sets and because this variance cannot be reduced by repetition [12]. Additionally, the unfeasibility of stratified sampling usually yields a high estimation bias when applied to small data samples. For these reasons, 10-fold cross-validation usually outperforms LOOCV, but this method will also be included as another validator in this study for verification.
4.3. Distribution Balanced Stratified Cross-Validation
An interesting method to cope with the partitioning problem is the Distribution Balanced Stratified Cross-Validation (DB-SCV). This method tries to reduce the deviation in both the target variable and the covariates by making each segment of the partition as intrinsically heterogeneous as possible, and as homogeneous as possible with respect to the rest of the k − 1 segments. That is, it distributes the classes of the response variable as uniformly as possible and, for each of these response classes, it keeps the distribution of the covariates as similar as possible between the test and the train set of each k-fold split.
There are two versions of this validator published by their authors. In the first version [16], from now on referred to as DB-SCV1, for each class, all distances are calculated from an artificial data point taken as a constant reference that is built with the minimum value of each continuous variable and one particular value of each of the categorical variables.
In the second version of this validator [9], referred to as DB-SCV2 from now on, for each class, all the distances are calculated from a reference observation that is selected at random from the data sample at the beginning of the process. The rest of the validation procedure is the same.
4.4. Distribution Optimally Balanced Stratified Cross-Validation
The Distribution Optimally Balanced Stratified Cross-Validation (DOB-SCV) is an enhanced alternative to the DB-SCV. In this case, there is not only one single reference observation for each class. Instead, a new observation of the class is selected at random each time that k observations are going to be evenly distributed through the k segments of the partition. The k − 1 nearest observations to the reference one in terms of the model covariates are chosen each time [9,17].
Since there are only minor differences between DOB-SCV, DB-SCV1, and DB-SCV2, it will be necessary to evaluate with experiments whether there are statistically significant advantages to any of them when selecting the best models in the current experimental context where, according to our knowledge, they have not been compared yet.
4.5. Representative Splitting Cross-Validation
Representative Splitting Cross-Validation (RS-SCV) is another CV variant whose goal is to carry out the cross-validation partitioning in a way that makes both the train and test sets as representative as possible of the available sample data. Thus, sample data should be distributed as evenly as possible in both sets [15].
It has therefore the same aim as the DB-SCV and DOB-SCV techniques, but achieved with an opposite implementation approach: instead of using a clustering algorithm that identifies the nearest observations to distribute them in different segments of each partition, in RS-SCV, the furthest observations are identified to include them in the same segment.
The RS-SCV method uses the DUPLEX algorithm to divide the available dataset into two subsets of equal size, as uniformly as possible between them, identifying the data pairs that are furthest away from each other by means of the Euclidean distance and placing them alternately in the first and the second subset.
There are two main disadvantages to this technique. One is that the DUPLEX algorithm cannot use categorical variables, so this type of variables is not leveraged when distributing the observations uniformly.
The second issue is that applying the DUPLEX algorithm successively yields k-folds that are powers of two: 2, 4, 8, 16, 32…. This makes it more difficult to compare this validation method against the commonly used k-fold values of 5 and 10. For these situations, the solution adopted has been to apply the RS-SCV for k = 4 and 8, respectively, and for other k values using the larger power of two smaller than the original k value as the k-fold parameter. After this, the observations are redistributed evenly among the original number of 5 or 10 folds, keeping the same proportion of observations belonging to the four or eight segments previously made by the DUPLEX algorithm.
This additional random behavior of redistributing the observations when k is not a power of two allows to make several repetitions with different results for averaging. For case k = 2 or any other power of 2, there will be no repetitions as the partitioning technique is deterministic.
4.6. Stochastic Cross-Validation
This technique consists of an ordinary cross-validation with repetition, where a random value for the k parameter is chosen for each repetition [11]. The random distributions originally proposed to select a k value each time are the uniform and the normal distributions.
The result of the estimations could be seen as an average over a mixture of cross-validations with different k-folds. This could be interpreted as a fuzzy approach to cross-validation. The technique was designed to avoid the selection of a particular value for the k parameter because it is usually impossible to know beforehand which one will perform better.
4.7. Fuzzy Cross-Validation
To go deeper into the fuzzy aspect of the stochastic cross-validation previously described, a new fuzzy cross-validation method is proposed in this study to be compared with the rest of the validation methodologies. The aim is to use a truly fuzzy value for the k parameter in each repetition instead of using a particular k value in each repetition.
The basic idea is to make irregular partitions where the size of each segment is fuzzy, meaning that the data sample will be divided into subsets of different numbers of observations. Therefore, there is no proper k-fold parameter, although the number of resulting segments of the irregular partition could be seen as a corresponding fuzzy k parameter.
To choose the size of a particular segment of the partition, a normal distribution or uniform distribution can be used to select a hypothetical k value among a set of possible values that will be used to decide the number of observations of the segment. Then, the observations to be assigned to this segment will be taken randomly from the remaining observations of the data sample not yet belonging to any segment.
The process of selecting the size of the next segment and assigning its observations will continue until the last choice of the segment size is equal to or larger than the remaining observations not yet assigned to any particular segment.
Then, no k parameter needs to be predefined as the number of resulting segments of the partition in each repetition is a consequence of this random process of selecting the size of each segment sequentially.
A simple pseudo-code of this fuzzy cross-validation is given just to state this validation procedure more clearly (Algorithm 1).
| Algorithm 1: Fuzzy cross-validation (Source: own elaboration) |
| For iter = 1 to Total number of repetitions Current fold number = 0 Number of observations not assigned to any fold = Total number of observations While Number of observations not assigned to any fold > 0 Random selection of a k value from a Normal or Uniform distribution Test set size = floor(Total number of observations/k) If Number of observations not assigned to any fold < Test set size then Assign the remaining observations to Current fold number Else Current fold number = Current fold number + 1 Select randomly a test set from the observations without fold assigned Assign the Current fold number to the observations of the test set End if End while Total number of folds = Current fold number For i = 1 to Total number of folds Train a model in the set of observations not belonging to fold number i MP(i) = compute the model performance with the observations of fold number i End for i ModelPerform(iter) = average of the performances MP(i) on the Total number of folds. End for iter Final model performance estimation by averaging all the estimations ModelPerform(iter) on the Total number of repetitions. |
4.8. Maximally Shifted Stratified Cross-Validation
The aim of Maximally Shifted SCV (MS-SCV) is the opposite of making homogeneous partitions, as it tries to maximize the covariate shift, generating the most different possible test and training sets [9]. This method can be seen as the opposite of DB-SCV2, because using the same reference observation per class, MS-SCV assigns the same segment of the partition to the k nearest neighbors instead of distributing them evenly across all k folds. The observation assignment to the same segment continues until the fold is full of observations of that class, and the process continues with the next fold to be filled.
The interest in implementing and testing this method is to verify that it performs very badly for model selection in a credit default context, according to the arguments given in Section 5. MS-SCV could serve as an additional verification of the convenience of homogenous partitioning if its performance as a validator in the current context is finally confirmed as very poor.
4.9. Other Cross-Validation Variants
The flexibility of cross-validation methodology has allowed the introduction of even more variants than the ones discussed above; however, they were finally discarded as potentially useful validators in this study for different reasons. Some of them will be briefly mentioned here.
Leave-p-out cross-validation (LpO-CV) is an exhaustive method where all possible test sets of p observations are used as hold-out test samples. Given the huge number of possible test sets of p elements taken from a population of N elements, where N has a minimum order of magnitude of hundreds or thousands, this variant has been discarded as it is computationally infeasible in real-life applications. Only the special case of p = 1 is considered, as it is the LOOCV technique.
Relevant to mention is Importance Weighted Cross-Validation (IWCV), which was especially designed to address the problem of mitigating the a priori existence of a covariate shift rather than trying to avoid such an induced shift during the data partition [29]. IWCV measures the importance of the covariate deviation and considers it when calculating the model performance to decrease the bias of the estimations as much as possible. For this reason, this technique does not try to reduce the existing deviation in the covariates but rather to correct the deviation afterwards in the calculations. Therefore, this is a complementary technique that could be combined with other CV variants and is, therefore, not a benchmark for direct comparison against any other.
Nested cross-validation is a methodology that chains an additional cross-validation when building the k models within the training datasets. When a regular k-fold cross-validation is carried out to perform a model validation, each of the k times a model is trained in one of the corresponding train sets, another cross-validation with a different k parameter (usually lower) is conducted to make that model training. Then, this additional k-fold cross-validation has the objective of building a better model by means of selecting the most convenient model complexity to avoid overfitting [27]. In the present research, model complexity is already predefined in a set of given models to be compared; therefore, nested cross-validation cannot be used in this experimental design.
4.10. Summary of Validation Methods
To provide a general picture of the main validation techniques previously explained, Figure 2 shows the more relevant features of those methodologies in a hierarchical classification.
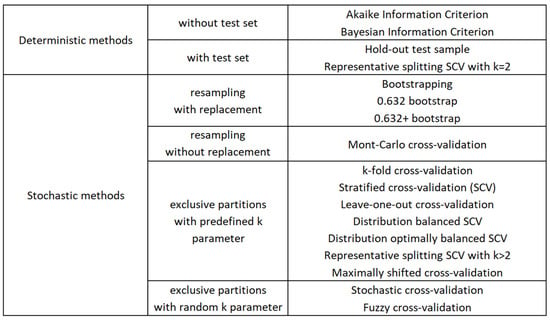
Figure 2.
Classification of validation methods based on fundamental characteristics.
5. Robust Cross-Validation Methods
As stated in the introductory section, the objective of this work is to identify potentially better validation methodologies to be used for credit default data and models. As discussed previously, cross-validation is the most accepted validation method nowadays, so the research methodology is to identify potentially robust cross-validation methods, those with more stable expected estimations, to compare them with the rest of the validation methodologies for model selection purposes. Going further in the research, another goal is to identify new variants of the robust methods by improving the strategy used to reduce the volatility of the estimations.
Among the different methodological variants of cross-validation presented in the previous section, only a few can be considered robust methods because they were designed to make more homogeneous partitioning, potentially resulting in more stable and less volatile estimations. This could be beneficial when validating credit default models, where data scarcity, imbalanced data, and covariate shift are generally present, because these three issues increase the volatility of the results.
Then, robust cross-validation methodologies of interest to be tested and analyzed in this research are DB-SCV and DOB-SCV. Nevertheless, they have some weaknesses that are going to be addressed here to potentially improve their performance for model selection.
The main problem of these methods for validating credit default models is that they rely on Euclidean distances to distribute the sample observations more uniformly. This is a problem when dealing with categorical variables because a Euclidean distance cannot be calculated, and consumer credit models usually have several categorical explanatory variables.
Euclidean distance in several dimensions can only be calculated properly for quantitative attributes that are comparable in their magnitudes. Both DB-SCV and DOB-SCV deal with this issue by using a “binarized” distance for the categorical variables between two observations. This distance is 0 when both observations have the same category and 1 otherwise, considering all possible categories as equidistant from each other. If there are pcateg categorical covariates, the binarized distance between two observations X and Z is calculated similarly to a Euclidean distance as:
To calculate the Euclidean distance between observations using continuous covariates, the values of the covariates must be normalized first to make them comparable. This normalization is made by considering the observed range of values in the sample. Then, the Euclidean distance between two observations X and Z when they have pcont continuous covariates is calculated as:
In case the two observations X and Z have both continuous and categorical variables, the distance between them is calculated following the expression:
In order to enhance the performance of these validators, it is proposed here to use the weight of evidence of the categorical variables to calculate a Euclidean distance for Dcateg. This could lead to better assessing the similarity or the distance between observations when categorical variables are involved, making them more fairly comparable in terms of the same quantitative magnitude.
This does not mean that the woe variables must be used as the model covariates. The covariates in the model could be the woe variables, the binarized dummy variables, or any other transformed variable. However, in order to enhance the process of finding the nearest neighbors, the woe of each categorical covariate will be used to calculate the distance Dcateg. Then, the same Euler’s formula used for Dcont will be used for Dcateg just by means of directly considering the woe of the categorical covariates as if they were continuous variables. This requires the normalization of the woe variables between 0 and 1 using their maximum and minimum values.
This enhancement can be applied to the original DOB-SCV validation methodology, using distances calculated with the weight of evidence for all the categorical covariates in the model being validated. This validator will be referred to as DOB-WOE for the rest of this document, while the same enhancement for DB-SCV will be labelled as DB-WOE2, as it was made for the more recent second version of the DB-SCV algorithm.
In summary, the aim of these robust k-fold cross-validation methods and their proposed enhancements is to make the training and test sets created during the partitioning as similar as possible. Estimating the performance of the model on more homogeneous partitions will yield more robust estimates with less volatility, and, therefore, quicker convergence to a final result when repetitions are made.
It is important to note that these robust methods are going to be tested for model selection, not model assessment, because limiting the possible partitions to a smaller subspace of more homogeneous partitions could introduce additional bias in the validation estimates, probably overestimating the model performance. This is in agreement with the “no free lunch” theorem. An enhancement or optimization made in an algorithm for a specific goal could worsen the performance of the same algorithm for a different goal. In this regard, model selection can be seen as an optimization task that aims to find the best model in a search space of alternative models with different complexities.
6. Experimental Framework
The experiments held in this study try to replicate a real-life validation procedure for model selection in the sense that several predefined models validated in a data sample from a larger population are ranked by each validation algorithm and the resulting rankings are verified using the true performance of the models in the unseen population not used to validate the models. This experiment is conducted multiple times using different data samples taken at random from several populations to perform statistical assessments of the results.
In each experiment, there will be validators giving a model ranking more similar to the true model performance ranking. Then, the validators could also be ranked in each experiment based on their discrimination capability to differentiate between better and worse models. The metric chosen to measure this ability to distinguish good models from bad ones was the Kendall Tau, as will be explained later on.
6.1. Credit Default Datasets
The set of experiments was made with several consumer credit datasets from developed countries of distinct geographical areas to test the validation methodologies with potentially different credit default patterns. These datasets have been used in previous research and are publicly available to make the conclusions comparable with any other future or past studies.
Table 1 shows the datasets used, their size, and bad credit rates, as well as the source repository where they can be found. The event rates of these credit datasets go from 14% to 44%. These high rates are not normally found in credit products; for example, typical rates for credit cards usually vary between 1% and 7% [30], while rates higher than 10% were observed only during the “credit-crunch” of 2007–2008 for some products. However, it is a common practice in predictive modeling of credit defaults to make an oversampling of delinquency events that allows reaching ratios of bad/good credits from 1:1 to 1:5, which facilitates the modeling procedure. So, event rates after oversampling generally vary between 17% and 50%. In this sense, the range of event rates of the credit data used in the experiments aligns very well with those over-sampling conditions given in practice.

Table 1.
Public credit datasets used: name of the dataset, number of observations, number of variables, global default rate, and reference.
We have to make sure that the three issues faced in the validation of consumer credit default models are also present in the current experiments. The imbalanced data issue is already taken into consideration due to the low default rate of most of the datasets, usually making it more difficult to both build and validate predictive models [9,17,35].
To include data scarcity in the experiments, samples of 500 records have been used for the German and Lending Club datasets. The Australian dataset has only 690 records in total, so a sample size of 230 observations was used, representing one-third of the available data. For the Taiwan dataset, 500 observations are probably not representative enough to make modeling exercises, so samples of 10% of the population were used to have sufficient data to build predictive models, but still small enough to be considered as a potential data shortage situation.
The explanatory variables included in the datasets mainly concern socio-demographic, financial, and professional information of the applicant, as well as characteristics related to the credit application (purpose, amount, duration…).
Due to the large number of categorical levels of some variables of the Lending Club 2009 file, the original categorical explanatory variables of this dataset were aggregated in 10 bins when there were more than 10 levels, merging the bins with more similar weight of evidence according to Section 2.1 and using the resulting woe of the merged bin as the new variable value.
Finally, the covariate shift issue will be a result of the data scarcity because the test/train data splits will significantly decrease the representativeness of these datasets. This will lead to partitions with biased covariates if almost all the observations of the experimental sample are needed to fully capture the data patterns of the underlying population.
This means that the hold-out test samples and the partitioning of cross-validation techniques could induce significant deviations between the distributions of the test and training sets, which can cause undesired, unstable results. This situation should be better managed by robust partitioning techniques, which is the hypothesis to be tested in this work.
6.2. Model Set
In consumer credit approval, logistic regressions are the market standard for probability of default models. This makes it possible to reach practical, applicable conclusions without the need to test other types of models, such as neural networks, random forest, SVM, or others not used in this business context.
A set of 63 models was created systematically from different subsets of explanatory variables to diversify the model complexity and the validation results. This allowed us to test the validators for model selection in a wide range of model performances, typically from AURs less than 0.6 to more than 0.8. In addition, as the number of models created was quite large, most of the time there were models with similar performance results, which made the model selection more difficult, resulting in different model performance rankings for similar validation algorithms.
To automate the model set generation, first, an ordered list of all variables was created for each credit dataset. The list order was determined by decreasing variable importance measured with the Akaike Information Criterion AIC. First, the list was divided into three equal parts (top, middle, bottom) or sub-lists; then, four subsets were created from each one of the three sub-lists. These subsets contained all variables, none of them, the variables in even positions of the sub-list, and the variables in odd positions. Taking all possible combinations formed by one subset from each sub-list, a total of 43 − 1 = 63 variable combinations were made, excluding the empty set.
In this way, the models trained in each of the experiments covered a wide range of predictive performance and model complexity, going from a few of the worst explanatory variables to all the variables available in each credit datasets.
For each experiment, each combination of covariates was used on a logistic regression trained with the whole available sample of each credit dataset using the “glm” function of the “Stats” package in R version 4.4.1. Details and syntax of this function can be found on the official R documentation website [36]. In fact, since the underlying population used for sampling was known, it was possible to find out the true performance of each of the models trained by applying them to the remaining observations not included in each sample.
Table A1 in Appendix A shows the expected true AUR performance of each logistic regression considered, calculated by averaging over 150 experiments of each credit dataset, and their corresponding standard deviation. These details give an overview of the large variety of model performances tested in this study, where the averaged true AUR goes from 0.50 to 0.93, allowing us to challenge the model selection capabilities of the validation algorithms in many potential scenarios, thus providing strong support to the conclusions.
The explanatory variables corresponding to each model are shown in Table A1 as a combination of the subsets that correspond to the top, middle, and bottom sub-lists of the variable list ordered by increasing AIC. The subsets of each third of the list have been labelled as follows: “A” = all variables of the corresponding sub-list; “N” = none of the variables; “O” = variables in odd positions of the sub-list; and “E” = variables in even positions.
6.3. Validation Algorithms
A total of 65 validation algorithms have been tested and compared with each other. These validators can be classified into groups according to the methodology used. The acronyms of the validators belonging to each validation methodology are explained to be able to identify their corresponding results, given in Section 7 and Appendix A.
6.3.1. In-Sample Validation
This group is identified as “InSample” and includes the AIC and BIC validation techniques identified as “InSample/AIC” and “InSample/BIC”, respectively.
6.3.2. Hold-Out Test Sample Validation
This is the “HO” validation group, where the acronyms used are MCCV (Monte-Carlo Cross-Validation), SMCCV (stratified MCCV), FMCCV (fuzzy MCCV), and FSMCCV (fuzzy stratified MCCV). In addition to the group prefix, two suffixes were added to these acronyms, indicating the percentage of the data used for testing and the number of repetitions made. For example, “HO:SMCCV/0.2/1000” stands for Stratified Monte-Carlo Cross-Validation with 20% test data and 1000 simulations. For fuzzy methods, the suffix relative to the percentage of test data is 0 because there is no specific test set size, as a random size was taken for each repetition from a uniform distribution between 5% and 50%.
6.3.3. Bootstrap Validation
The bootstrapping validators (BTS) implemented are identified as “boot” (original bootstrap), “sboot” (stratified bootstrap), “b632” (0.632 bootstrap), “sb632” (stratified 0.632 bootstrap), “b632+” (0.632+ bootstrap), and “sb632+” (stratified 0.632+ bootstrap). There is no choice of the test size in these techniques, so only the last suffix with the number of simulations has meaning. Then, “BTS:b632+/0/1000” refers to the 0.632+ bootstrap using 1000 simulations.
6.3.4. Cross-Validation
This is the largest validation group (CV) this study focused on, mainly due to the usual superior performance of this methodology compared to the previous ones, as will be confirmed by the results of the next section, and is aligned with previous studies in more generic contexts.
There are 48 different variants implemented, divided into several subgroups according to the methodology used in the partitioning. In all cases, 50 repetitions [2,27] were conducted to make sure that a stable enough estimate was reached by all the cross-validation techniques.
The original k-fold cross-validation and stratified cross-validation techniques are identified by “CV:kfold/k/r” and “CV:SCV/k/r”, respectively, where the “k” suffix indicates the value of the k-fold parameter and “r” is the number of repetitions made (r = 50). Exceptions are the LOOCV and the RSCV with k = 2 “CV:RSCV/2”, because no repetitions are possible.
Other CV methods have been named in the same way. The representative splitting cross-validation is identified as “CV:RSCV/k/r”; distribution optimally balanced stratified cross-validation as “CV:DOB-SCV/k/r”; the proposed enhancement to this method as “CV:DOB-WOE/k/r”; the distribution balanced cross-validation with algorithm versions 1 and 2 as “CV:DB-SCV1/k/r” and “CV:DB-SCV2/k/r”; and the corresponding enhancement to the latter as “CV:DB-WOE2/k/r”.
Similarly, the acronym chosen for maximally shifted cross-validation was “CV:MS-SCV/k/r”. This partitioning methodology is more heterogeneous by definition and should lead to more volatile results in contrast with the robust methods that are going to be challenged. The MS-SCV has been included in this study to check if its performance is the opposite of the most homogenous partitioning methods in the same situation.
Stochastic cross-validation using a discrete uniform distribution over the integers between 2 and 20 to choose the k-fold value for each repetition has been labelled as “CV:RndCV/0/r”.
Finally, the proposed fuzzy cross-validation methods have been labelled as “CV:FUkfold/0/r” for the uniform distribution version where the integer k-fold parameter was chosen randomly from 2 to 20, while the same method using a normal distribution N(10, 5) capped to minimum and maximum values of 2 and 20, respectively, has been identified as “CV:FNkfold/0/r”.
Except for the stochastic and fuzzy methods, where the k parameter is not specified deterministically, the values tested for the k-fold parameter were k = 2, 5, 10, 15, and 20. The unusual higher values of k = 15 and 20 have been added to the more common values k = 2, 5, and 10 of other researches [2,6,12,25,26] to check if the robust partitioning algorithms decrease the variability of smaller test sets enough to leverage the larger size of the training sets used for calibrating the models.
6.4. Validator Performance Assessment and Comparison
To statistically determine whether a particular validator can be considered better than others at discriminating between good and bad models, the validation algorithms will be considered as if they were classification algorithms whose task is to order a set of predictive models in a ranking according to their estimated performance.
Then, it is necessary to assess how good the ranking provided by a particular validator is compared to the true model ranking that can be built based on the model performance in the population not used to train the models.
To achieve this, the Kendall Tao ranking distance can be used, which counts the number of discrepancies between two ordered lists or rankings. This distance metric can be defined as the number of discordant pairs between two ordered lists L1 and L2, that is, the number of pairs in which the order given by L1 to the two elements of each pair is different from the order given by L2 to the same elements.
Let R1(i) be the rank of element i in list L1 and R2(i) the rank of element i in list L2; then the Kendall Tau distance KT(L1, L2) between the two lists can be calculated using the following expression:
The distance is zero in cases where the two lists have the same order, while the maximum distance is achieved when one list has the reverse ordering of the other. This maximum value is m(m − 1)/2, where m is the number of elements of the lists. Then, a normalized Kendall Tau distance in the interval [0, 1] can be obtained by dividing KT by m(m − 1)/2.
The normalized Kendall Tau distance has been used as a measure of the error that each validator makes when ranking the models by their estimated AUR in comparison with the ranking based on the true AUR of the models. From now on, this metric will be referred to as the “selection error” of the validation algorithm and will be used to assess the validator’s performance for model selection purposes.
This approach allows the assessment of each validator’s performance using a set of models with a wide range of different performances, since in practical applications, there will be situations where the models to be selected will perform well, and others where the AUR of the models will be lower.
In this study, a validator will be considered worse than others for a specific credit default dataset if its selection error is statistically larger when measured on a sufficient number of samples taken randomly from the dataset.
One may think about comparing the selection error of each validator averaged over many samples, but there is no easy way to assess the variance of the selection error to make a proper comparison. Then, the selection error of all the validators needs to be compared in each of the experimental samples one by one, which allows to perform a paired test of the validator performances. Therefore, validation results will differ due to the particular validation method used, avoiding any variability coming from the sample randomness.
To this end, the non-parametric paired Wilcoxon one-sided rank test was used to compare the selection errors with a confidence level of 95% using the R function wilcox.test() over 150 experiments performed in each of the default credit datasets considered. In addition, an overall paired comparison using all the 600 samples was performed, applying a single Wilcoxon test to all the samples of all datasets.
6.5. Overall Experimental Research Methodology
The experimental elements previously described through this Section 6 were performed in subsequent iterations according to the following list of steps that summarizes the overall research methodology:
1. For each credit dataset, the individual importance of each variable is determined using the AIC and generating a variable ranking.
2. Using the variable importance ranking, 63 different combinations of variables were generated in a systematic way.
3. A total of 150 samples of limited size were taken without replacement from each dataset to carry out different experiments in each dataset population.
4. For each experiment, a logistic regression model was trained for each variable combination (model complexity) with all available sample data, and the true model performance was calculated using the remaining population not used to train the model. Therefore, a true model performance ranking could be established in each experiment.
5. Each model was validated by 65 different validation algorithms (validators), and a model ranking was generated for each validator based on its model performance estimations.
6. The model selection error of each validator in each sample was calculated as the normalized Kendall Tau of the comparison of each validator’s model ranking and the true model ranking of the corresponding experiment.
7. A validator performance ranking for model selection was determined for each credit dataset based on the selection error averaged in all the experiments, although non-parametric paired tests were used to determine when the differences in the selection error between validators were statistically significant.
8. Finally, an overall ranking was generated in the same way as step 7, but using all the experiments of all the datasets together.
7. Results and Discussion
The following main results are shown comparing the performance of the validation methods in all the experiments carried out, and other aspects of the validation process. The focus of the analysis is on model selection, and no evaluation of the proper AUR estimation has been made, giving priority to the correct discrimination between better and worse predictive models.
7.1. Model Selection
To make a one-dimensional ranking for the performance of the validators in a given dataset, first, each validator has been ordered in a list according to its average selection error on the 150 experiments from lower to higher values. Then, a minimum rank value has been calculated for each validator, rejecting the null hypothesis that its selection error is equal or lower than the selection error of some previous validator using a one-sided Wilcoxon paired test: if the Wilcoxon test is positive compared to the previous validator in the list, the rank is increased by one. Otherwise, the one-sided Wilcoxon test is evaluated against the following previous validator in the list until a positive paired test is found, supporting the alternative hypothesis that the selection error of the validator is greater at a 95% confidence level. This is considered a minimum rank value for the validator. Then, the rank of the validator is determined as the maximum between the rank of the previous validator in the ordered list and the minimum rank found for it. The resulting ranking in each dataset is shown in Table A2 of Appendix A.
To make a validator performance ranking based on all the credit datasets, an overall rank has been calculated in the same way, performing a single Wilcoxon test in all the experiments of all the datasets, as shown in Table A2 of Appendix A. The validators have been ordered according to this overall rank from best to worst performance for model selection.
In this way, it can be seen in Table A2 that only 20 different ranks were found in a list with 65 different validation techniques. This means that many times the Kendall Tau distance is not different enough to consider one validator better than the next one. Something similar happens with the results of the individual credit datasets shown in the same table.
Table A2 shows that there are more draws in the ranking of the validators in the individual datasets, different from Taiwan, because the samples and populations are smaller, probably with less complex default patterns, which prevents them from easily discriminating among the performances of the validators. This is also the reason why the selection error is larger in these datasets.
Despite some differences found in the performance of the validation methodologies throughout the credit datasets, it was found that the robust cross-validation techniques are usually in the best positions in the rankings. In particular, the enhancement made to the DOB-SCV using the weight of evidence to calculate the distances for categorical variables presents better results than the original method for the same value of the k-fold parameter. In fact, looking at the overall ranking, almost all variants of the robust cross-validation algorithms are in the top positions for any value of the k-fold parameter, making this type of validator very convenient in situations where there is no clue about what k value to choose.
It is remarkable that the robust methods present better performance than the rest of the validation techniques, even for high values of the k parameter, supporting the initial hypothesis that homogeneous partitioning makes more stable test sets, allowing the use of more data for training without harming the results too much.
Of course, it can be seen from Table A2 that there is still an impact of the k parameter, and for this credit default use case, k = 10 and 5 were found to be the more suitable values, aligned with the findings of other research in different contexts.
Roughly speaking, following the more robust cross-validation variants, there is a large group of validators in positions eight and nine of the overall rank, mainly with traditional and fuzzy cross-validation techniques. There are also some robust methods in this group with k = 2, as the negative impact of this parameter is too large to be mitigated by the optimal partitioning. As there is data scarcity in the samples, taking only half of the data for training does not allow for the discovery of enough patterns, decreasing the discriminatory power of any type of cross-validation technique.
Following in position 10, the validation algorithms based on bootstrapping are all close together with the same overall rank, meaning that the methodological variants among them are not quite relevant for model selection purposes in the credit default use case.
The part of the list with the least performing validators with an overall rank greater than 10 is composed of the LOOCV and distinct types of validators due to the less convenient test sizes of 50% and 5% corresponding to the largest and smallest values tried. The disadvantage of taking only 5% of the data for testing (k = 20) is again due to data scarcity, but the problem now is the instability and heterogeneity of smaller test sets that will lead to higher variance of the AUR estimations. More data available for training is better for discovering more data patterns, but only without shortening the test set size too much.
In this respect, fuzzy methods do not use a particular k value, achieving intermediate results between the best and worst choices of the k parameter.
As expected, among the validation approaches that use independent test samples, maximally shifted CV methods are the least performing methods due to the large covariate shift induced by their partitioning technique, as anticipated in Section 4.
Finally, the in-sample methodologies are closing the list, meaning that some kind of independent test set should be used for model selection, at least when there are data restrictions in the available sample.
To better compare the different cross-validation methodologies, the results can be grouped in subsets of the same test set size to eliminate the effect of this factor in the comparison, except for the techniques that use a set of mixed parameter values. The selection of the hold-out test sample size or the k-fold parameter in cross-validation is subject to expert judgement in each practical application and will lead to better or worse validation performance in each particular context, depending on the representativeness of the available sample and the difficulty of modeling the underlying data patterns.
In order to fairly rank the cross-validation methods grouped by the same value of the k-fold parameter, two rankings of k = 5 and 10 have been made again with separate Wilcoxon non-parametric paired tests instead of directly using the ranks provided in the full list in Table A2. The results are shown in Table 2 and Table 3, together with the rest of the CV methods that do not have the need to establish a predefined value for the k parameter.

Table 2.
Average selection error and ranking of CV methods using k = 5 or non-predefined k value for each credit dataset. An overall ranking is calculated using all the experiments made in all credit datasets as the final ranking.

Table 3.
Average selection error and ranking of CV methods using k = 10 or non-predefined k value for each credit dataset. An overall ranking is calculated using all the experiments made in all credit datasets as the final ranking.
It can be seen from Table 2 and Table 3 that the distribution optimally balanced stratified cross-validation is really enhanced by the use of weight of evidence for calculating the distance between observations, being the most robust methodology for model selection in the current context.
However, for distribution balance cross-validation techniques, using the weight of evidence has no improvement, as it can also be verified for the rest of the k values of Table A2. In particular, the first version of this technique tends to perform better than the second version for increasing values of k. This is probably due to the larger randomness of the second version when distributing the observations in the partitions, giving slightly larger variances in the results that are more relevant when the test sets are smaller and more unstable.
In general, the robust CV variants are leading the classification, followed by the traditional and fuzzy methods. The Monte-Carlo hold-out variants have an irregular performance, but the stratification seems to be a disadvantage in these cases.
In particular, LOOCV performs as well as the best validation algorithms for the Australian dataset, probably due to the fact that this dataset has fewer observations and data diversity, leading to less unstable test sets than usual. Then, the more homogeneous and complete training sets that capture all the data patterns are more than enough to compensate for the test set instability in this specific credit dataset.
Closing the lists is MS-SCV, probably because maximally shifting the train/test sets should lead to higher volatility in the estimations, and therefore be more prone to mistakes when deciding between models.
7.2. Sample Size Impact
It is expected that the advantages of using robust validation methods will tend to disappear when increasing the size of the available dataset because the greater representativeness of the training and test sets will increase the homogeneity of the partitions for all kinds of partitioning methods.
To test this hypothesis, the same experiments were carried out with double and triple-sized samples for the Lending Club 2009 dataset, which is the one with larger selection errors. As these samples are more representative of the underlying population patterns, the selection errors are reduced significantly for all validation methods. The full validator comparison for sample sizes of 500, 1000, and 1500 observations is given in Table A3 of Appendix A.
To compare more clearly the effect of sample size for the cross-validation methods, Table 4 and Table 5 show separately the results for two groups corresponding to k = 5 and k = 10, respectively. The methods without a specific k-fold parameter value have also been added to the comparisons.

Table 4.
Impact of the sample size on the selection error and ranking of cross-validation methods with k = 5 or non-predefined k-fold parameter for the Lending Club 2009 credit dataset. Selection error is given by the normalized Kendall Tau averaged over 150 random samples of sizes N = 500, 1000, and 1500.

Table 5.
Impact of the sample size on the selection error and ranking of cross-validation methods with k = 10 or non-predefined k-fold parameter for the Lending Club 2009 credit dataset. Selection error is given by the normalized Kendall Tau averaged over 150 random samples of sizes N = 500, 1000, and 1500.
Table 4 and Table 5 show that there is no significant enhancement using the weight of evidence of the categorical covariates for the distribution optimally balanced stratified cross-validation methods when the sample size is large enough. Nevertheless, the robust validators DOB-SCV and DB-SCV are still at the top of the performance ranking, with some advantage for the DOB variant.
In Table 4, where k = 5, other non-robust methods scale up in the performance list, diluting some of the benefits of the homogeneous partitioning against the random resampling or fuzzy methods. In the case of k = 10, this is not yet clearly seen because the test sets are smaller and therefore more unstable than in the k = 5 case, still giving room for the benefits of homogeneous partitioning.
7.3. Best Model Selection
Apart from analyzing the capability of the validators to rank and discriminate among a wide range of credit default models with different predictive performances in terms of AUR, it is also interesting to check if the same validators have the ability to select the best ones. It could happen that a validator that differentiates well among intermediate models is not able to choose the best one or the top ones.
To check this, the number of times the model selected as the best one was in fact the best model in the unseen population has been counted for each validation technique, as shown in Table 6. In case of any draw in the number of successes, the number of second and third-best models correctly selected was used to break the tie and rank the validators.

Table 6.
Number of times the best model was correctly selected by each validator, summing up the results of all experiments in all credit datasets used.
Again, it is confirmed that the top of the rank is led by robust cross-validation methods, although the representative splitting cross-validation performs surprisingly much better than expected according to the overall selection error shown in Table A2 of Appendix A.
It is also surprising how much the stratified bootstrapping has improved in this rank compared with the results shown in Table A2. Then, to make a more robust assessment about which validators perform better when selecting good predictors, Table 7 shows the total number of times the model selected as the best one by each validator was in fact among the top five performances in the unseen population for all experiments in all datasets. To break any tie in the results, the validator with more second or third-best options in the true top five was preferred.

Table 7.
Number of times the best model selected by each validator was among the true top five models in terms of AUR calculated in the unseen population. The counting sums up the results of all experiments in all credit datasets used.
As shown in Table 7, the robust cross-validation methods are still leading the ranking as the most reliable in general for model selection purposes when the validated models are good predictors. In addition, Monte Carlo cross-validation seems to be a trustworthy alternative when using 20% of the data for testing.
Something important to highlight is that distribution optimally balanced stratified cross-validation, enhanced with the weight of evidence for categorical variables, is usually among the best validators, even for different values of the k-fold parameter. This is an important advantage because the selection of the k parameter is usually subject to expert judgement, and it is not clear when to choose one or another value. The DOB-WOE methodology mitigates the risk of not selecting an optimal value for k because the more homogeneous partitions and more stable results make this technique less sensitive to the train/test split size. This benefit could be potentially useful in other applications, different from the use case of credit default model selection.
7.4. Result Stability
Robust cross-validation methods achieve better results than other techniques in exchange for more computational requirements. This is due to the need to calculate the nearest neighbors of the observations being partitioned, which extends the validation execution time.
Then, more stable results do not necessarily mean any computational saving, but it is possible to measure the stability of the cross-validation estimations in terms of the number of repetitions needed before reaching a final estimate within a certain tolerance level.
Just to confirm this expected behavior, Figure 3 represents the average number of repetitions, after which all changes in the estimated AUR are below 0.001 for each validation technique when validating the model with the best averaged true AUR in each dataset. The validators in Figure 3 on the horizontal axis are in the same order as in Table A2 to visualize that there is a clear trend and therefore a relationship between the validator performance and the stability of its estimations: more stable results correlate with lower selection errors. The main exceptions to this rule are the two fuzzy methods (FNkfold and FUkfold), which need more repetitions than expected by the trend in all the datasets due to their fuzzy nature and therefore more volatile results.
Figure 3.
Number of repetitions needed to stabilize the average AUR under a 0.001 threshold per each validator when validating the best model in each dataset and averaging the experiments. Error bars corresponding to the standard deviation are shown only for Taiwan dataset for clarity of the graph.
Figure 3 shows that the distribution optimally balanced stratified cross-validation gives the more stable estimations of the AUR on average. This is coherent with the performance shown by this type of validation method, which is usually the best choice for model selection, particularly the enhanced algorithm that uses the weight of evidence for the distance between categorical covariates (see Table A2 in Appendix A).
The maximally shifted cross-validation methods need more repetitions than any other cross-validation method tested because their more heterogeneous partitions give place to a larger volatility of the AUR estimations.
The representative splitting cross-validation with k = 2 is not represented because the DUPLEX algorithm always divides the sample into two halves in the same way, and no repetition can be performed in this case.
Another way to check the existing relationship between result stability and model selection capability for any validator is to compare the number of repetitions needed to stabilize the results and the selection error in each dataset. It can be seen that the Taiwan dataset has the lowest selection error in Table 2 and Table 3 for any validator and needs the lowest number of repetitions to stabilize the results in Figure 3. On the other hand, the Lending Club dataset needs more repetitions and has greater selection errors than the rest of the datasets, while the German and Australian datasets behave similarly in both aspects.
7.5. Effect of the Number of Repetitions
If the number of repetitions leads to more stable results, it can be questioned if the same benefits of robust partitioning can be achieved by means of increasing the number of repetitions of more traditional cross-validation methods. In particular, as stratified 10-fold cross-validation is the best non-robust methodology (rank 6 of Table A2), this technique performed with a massive number of repetitions should be the most challenging validator to compare against the best robust cross-validation variant, also for k = 10.
In order to discover which of the two ways of reaching more stable results could be more advantageous for model selection, 120 experiments were used, comparing all the data sets, the original 10-fold cross-validation, its stratified version, and the distribution optimally balanced, enhanced with the weights of evidence for categorical covariates. The hypothesis testing was performed by a Wilcoxon one-sided paired test at a 95% confidence level for the selection error measured by the Kendall Tau, exactly in the same way as in the previous comparisons of Section 7.1 for the whole set of validators.
To make a feasible although intensive traditional cross-validation, a total of 1000 repetitions were performed for the 10-fold CV and SCV, while the most robust validator was repeated only 10 and 50 times. The results are shown in Table 8.

Table 8.
Selection error and ranking of selected validation methods given by the normalized Kendall Tau, averaged over 120 random samples taken from each credit dataset. An overall ranking is calculated using all the experiments made in all credit datasets as the final ranking.
According to the overall ranking of Table 8, better model selection is achieved with the best robust methodology (DOB-WOE) compared to the best non-robust method (SCV), even making 100 times fewer repetitions. In addition, it is also shown that if we make a large number of repetitions, there is no material difference between the original 10-fold cross-validation and its stratified version.
7.6. Limitations of the Analysis
The overall rank of Table A2 in Appendix A could be considered the main contribution of this study because it is the comparison of all validation methods using all the paired tests in all the considered datasets. From the overall rank, it can be stated that there is statistical evidence of the better performance of robust validation methods because the 7 best-ranking positions correspond only to the more robust techniques, and any other robust validator with a rank greater than 8 has less convenient k parameter values different from 5 and 10.
Apart from this qualitative conclusion based on extensive quantitative results, one of the limitations faced in the analysis is that making a pure quantitative assessment of the benefits of a robust validation is not easy or feasible because those benefits depend on many circumstances. For example, the selection error measures, via the normalized Kendall Tau, how many positions each validator has altered the correct order of model performances, but how much the selection of one model instead of another one impacts some final generalization error will depend on the particular models considered, the available data, and the severity of the impact of wrong predictions in each practical application.
To provide a simple visualization of the clear division in model selection performance between robust and non-robust validators when there are data limitations, Figure 4 represents the selection error averaged per each rank for the validators in the first 12 ranks of Table A2. The last validators in the ranking that corresponds to the RSCV with k = 2 (which is deterministic), the maximally shifting cross-validations, and the in-sample methods are not represented in the graph to keep the visualization in a better scale, as the selection error is up to five times larger than the smallest one.
From Figure 4 or Table A2, it can be seen that the variation in the model selection error among the existing validation techniques in ranks 8 to 12, such as stratified CV, bootstrapping, Monte-Carlo CV, leave-one-out CV and even the fuzzy methods tested, is similar in magnitude to the difference found between validators in rank 8 and validators in rank 1 or 2. This means that the improvement in model selection using the best robust validators could be as large as the improvements made when choosing between two different methods from the existing validation methodologies and variants. Then, the benefits of robust model selection are potentially relevant in practice, and at least as relevant as the best improvements found among the methods used as potential validation alternatives.
In fact, previous studies making comparisons between bootstrapping, leave-one-out, cross-validation with different k-fold parameters, and other techniques generally reach qualitative conclusions [5,7,11,12,15,17,24,27] without being able to quantify the potential benefits. Even more, in this type of work, there are usually various methods identified as more convenient, but without concluding which one is the best. Therefore, recommendations are generally given to test several of them in each particular situation, highlighting the importance of making the correct choice of the model selection method, overall, for small sample sizes.
On the contrary, in our research scope, it seems that the gap between the performance of more robust validators and the rest of them makes it clear that a robust validation is better, although difficult to assess quantitatively due to the dependency on the data availability, the models compared for selection, and the severity of the prediction errors.
As the main conclusion, it is important to keep in mind that the more stable the stochastic validation method used is, the more reliable the selection process is expected to be. In this regard, robust cross-validation methods will help in selecting potentially better models of credit default in data-scarce situations.
8. Conclusions
This experimental research tackles the main issues of credit default model selection, where the problems of small data sample, imbalanced datasets, and covariate shift are present simultaneously.
Distribution-balanced and, to a greater extent, optimally balanced stratified cross-validation methods have been identified as robust stochastic methodologies for model selection in the credit default use case when compared against many other validation variants based on hold-out test samples, resampling techniques, and other cross-validation methodologies, including new proposed fuzzy variants.
In particular, the enhancements proposed to those robust CV methods have shown statistically significant improvements in the results, identifying DOB-WOE with k = 5 or 10 as the best robust validators for selecting consumer credit default models in situations of data scarcity when the sample size is large enough to build capable models, but it is quite sensible to set aside test data for validation purposes.
The key aspect to achieve better results in model selection in these situations with imbalanced data and scarce samples is the homogeneity of the train/test splits used to average the cross-validation results, reducing the variability of the AUR estimates in the k-fold partition, regardless of the bias.
The downside of the robust cross-validation methods is the computation required because it is necessary to calculate the nearest neighbors of the observations when distributing them in the partitions. Nevertheless, this could be performed just once for all the observations in the data sample, allowing for quickly performing many repetitions of the validation algorithm if desired. In fact, significantly increasing the number of repetitions instead of the partitioning homogeneity does not seem to be a better strategy, so it is probably better to dedicate some computational resources to distribute the observations more evenly using robust validation methods than focusing only on increasing the number of repetitions of traditional cross-validation.
As expected, when the size of the available data increases, the benefits of robust validation methods decrease because larger data samples directly lead to more homogeneous train/test splits for any splitting technique.
The above conclusions are supported not only by the overall results but also by each individual credit dataset used. Therefore, robust cross-validation methods could be worth leveraging to challenge current production models in lending institutions. Winnings could be assessed through backtesting the new credit default models selected by robust validation and the current ones, using recent historical data to quantify the differences.
In addition, potential future research on these robust validation algorithms could be carried out in other contexts with similar validation problems where the modeling benchmark involves different data patterns and types of predictive algorithms. For example, a use case particularly interesting for the financial industry and sometimes linked to credit defaults is the detection of credit card fraud, which involves more imbalanced datasets and less data availability than the credit default use case. Thus, it is usually more difficult to predict and manage fraudsters than defaulters.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app15105495/s1.
Author Contributions
Conceptualization, Methodology, and Formal Analysis, J.V.A. and L.E.; Investigation, Resources, Software, Writing—Review and Editing, J.V.A.; Review and Supervision, L.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting reported results can be found as Supplementary Materials, and links to the original public datasets analyzed are listed in the reference section.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
This section shows detailed results of the models and validation techniques, averaged over all the samples used in each credit dataset.

Table A1.
True model performance in the unseen population by averaging the model AUR over the 150 experiments in each dataset: “Model” = model number, “var.comb.” = variable combination, “avg.” = AUR average, “sd.” = AUR standard deviation.
Table A1.
True model performance in the unseen population by averaging the model AUR over the 150 experiments in each dataset: “Model” = model number, “var.comb.” = variable combination, “avg.” = AUR average, “sd.” = AUR standard deviation.
| Model | var.comb. | Taiwan | German | Australian | Lending Club | ||||
|---|---|---|---|---|---|---|---|---|---|
| avg. | sd. | avg. | sd. | avg. | sd. | avg. | sd. | ||
| 1 | A|N|N | 0.7164 | 0.0028 | 0.7748 | 0.0181 | 0.9286 | 0.0074 | 0.5965 | 0.0166 |
| 2 | O|N|N | 0.7155 | 0.0018 | 0.7521 | 0.0174 | 0.9104 | 0.0086 | 0.6132 | 0.0214 |
| 3 | E|N|N | 0.6716 | 0.0027 | 0.6870 | 0.0184 | 0.8331 | 0.0102 | 0.6014 | 0.0180 |
| 4 | N|A|N | 0.6058 | 0.0070 | 0.6067 | 0.0185 | 0.7343 | 0.0154 | 0.5908 | 0.0163 |
| 5 | A|A|N | 0.7188 | 0.0034 | 0.7776 | 0.0173 | 0.9266 | 0.0085 | 0.5916 | 0.0169 |
| 6 | O|A|N | 0.7188 | 0.0032 | 0.7611 | 0.0172 | 0.9168 | 0.0093 | 0.5996 | 0.0181 |
| 7 | E|A|N | 0.6815 | 0.0043 | 0.7001 | 0.0167 | 0.8484 | 0.0123 | 0.5925 | 0.0172 |
| 8 | N|O|N | 0.6062 | 0.0062 | 0.5794 | 0.0208 | 0.7088 | 0.0175 | 0.5439 | 0.0139 |
| 9 | A|O|N | 0.7174 | 0.0036 | 0.7779 | 0.0181 | 0.9265 | 0.0085 | 0.5938 | 0.0165 |
| 10 | O|O|N | 0.7175 | 0.0030 | 0.7614 | 0.0180 | 0.9135 | 0.0105 | 0.6045 | 0.0170 |
| 11 | E|O|N | 0.6790 | 0.0043 | 0.6937 | 0.0185 | 0.8451 | 0.0115 | 0.5963 | 0.0171 |
| 12 | N|E|N | 0.5859 | 0.0078 | 0.5690 | 0.0202 | 0.6498 | 0.0148 | 0.5267 | 0.0137 |
| 13 | A|E|N | 0.7175 | 0.0031 | 0.7744 | 0.0173 | 0.9293 | 0.0077 | 0.5927 | 0.0173 |
| 14 | O|E|N | 0.7170 | 0.0026 | 0.7502 | 0.0167 | 0.9188 | 0.0086 | 0.6030 | 0.0193 |
| 15 | E|E|N | 0.6756 | 0.0035 | 0.6929 | 0.0165 | 0.8433 | 0.0114 | 0.5947 | 0.0176 |
| 16 | N|N|A | 0.5217 | 0.0108 | 0.5127 | 0.0188 | 0.5975 | 0.0195 | 0.5681 | 0.0223 |
| 17 | A|N|A | 0.7159 | 0.0031 | 0.7690 | 0.0183 | 0.9243 | 0.0089 | 0.6230 | 0.0168 |
| 18 | O|N|A | 0.7127 | 0.0024 | 0.7441 | 0.0181 | 0.9091 | 0.0101 | 0.6349 | 0.0145 |
| 19 | E|N|A | 0.6727 | 0.0041 | 0.6781 | 0.0196 | 0.8309 | 0.0115 | 0.6238 | 0.0176 |
| 20 | N|A|A | 0.6245 | 0.0093 | 0.5886 | 0.0196 | 0.7319 | 0.0165 | 0.6215 | 0.0151 |
| 21 | A|A|A | 0.7186 | 0.0034 | 0.7724 | 0.0181 | 0.9226 | 0.0096 | 0.6210 | 0.0164 |
| 22 | O|A|A | 0.7174 | 0.0031 | 0.7532 | 0.0184 | 0.9134 | 0.0102 | 0.6303 | 0.0146 |
| 23 | E|A|A | 0.6820 | 0.0047 | 0.6894 | 0.0180 | 0.8407 | 0.0123 | 0.6206 | 0.0170 |
| 24 | N|O|A | 0.6205 | 0.0096 | 0.5561 | 0.0243 | 0.7014 | 0.0208 | 0.5911 | 0.0163 |
| 25 | A|O|A | 0.7177 | 0.0034 | 0.7739 | 0.0187 | 0.9217 | 0.0096 | 0.6224 | 0.0164 |
| 26 | O|O|A | 0.7164 | 0.0031 | 0.7543 | 0.0189 | 0.9085 | 0.0107 | 0.6327 | 0.0143 |
| 27 | E|O|A | 0.6797 | 0.0047 | 0.6879 | 0.0197 | 0.8365 | 0.0123 | 0.6230 | 0.0170 |
| 28 | N|E|A | 0.6000 | 0.0106 | 0.5458 | 0.0209 | 0.6901 | 0.0174 | 0.5872 | 0.0166 |
| 29 | A|E|A | 0.7170 | 0.0031 | 0.7677 | 0.0176 | 0.9250 | 0.0088 | 0.6232 | 0.0168 |
| 30 | O|E|A | 0.7150 | 0.0026 | 0.7419 | 0.0177 | 0.9150 | 0.0096 | 0.6336 | 0.0144 |
| 31 | E|E|A | 0.6771 | 0.0042 | 0.6794 | 0.0175 | 0.8386 | 0.0120 | 0.6238 | 0.0171 |
| 32 | N|N|O | 0.5307 | 0.0146 | 0.5109 | 0.0185 | 0.5855 | 0.0173 | 0.5648 | 0.0241 |
| 33 | A|N|O | 0.7148 | 0.0030 | 0.7720 | 0.0176 | 0.9267 | 0.0081 | 0.6250 | 0.0156 |
| 34 | O|N|O | 0.7130 | 0.0024 | 0.7489 | 0.0178 | 0.9101 | 0.0093 | 0.6394 | 0.0132 |
| 35 | E|N|O | 0.6693 | 0.0031 | 0.6820 | 0.0178 | 0.8362 | 0.0099 | 0.6273 | 0.0168 |
| 36 | N|A|O | 0.6261 | 0.0094 | 0.5958 | 0.0190 | 0.7304 | 0.0156 | 0.6254 | 0.0161 |
| 37 | A|A|O | 0.7186 | 0.0034 | 0.7760 | 0.0172 | 0.9247 | 0.0089 | 0.6225 | 0.0164 |
| 38 | O|A|O | 0.7175 | 0.0031 | 0.7582 | 0.0175 | 0.9147 | 0.0095 | 0.6329 | 0.0149 |
| 39 | E|A|O | 0.6820 | 0.0047 | 0.6946 | 0.0166 | 0.8448 | 0.0121 | 0.6230 | 0.0172 |
| 40 | N|O|O | 0.6229 | 0.0101 | 0.5646 | 0.0214 | 0.6983 | 0.0212 | 0.5922 | 0.0184 |
| 41 | A|O|O | 0.7172 | 0.0036 | 0.7764 | 0.0179 | 0.9238 | 0.0091 | 0.6242 | 0.0156 |
| 42 | O|O|O | 0.7159 | 0.0032 | 0.7587 | 0.0182 | 0.9090 | 0.0103 | 0.6360 | 0.0140 |
| 43 | E|O|O | 0.6795 | 0.0047 | 0.6900 | 0.0181 | 0.8408 | 0.0118 | 0.6260 | 0.0165 |
| 44 | N|E|O | 0.6014 | 0.0102 | 0.5527 | 0.0207 | 0.6882 | 0.0160 | 0.5875 | 0.0172 |
| 45 | A|E|O | 0.7165 | 0.0030 | 0.7718 | 0.0169 | 0.9274 | 0.0080 | 0.6248 | 0.0163 |
| 46 | O|E|O | 0.7153 | 0.0026 | 0.7473 | 0.0170 | 0.9166 | 0.0087 | 0.6368 | 0.0146 |
| 47 | E|E|O | 0.6743 | 0.0036 | 0.6862 | 0.0160 | 0.8439 | 0.0108 | 0.6264 | 0.0167 |
| 48 | N|N|E | 0.5113 | 0.0096 | 0.4989 | 0.0274 | 0.5353 | 0.0218 | 0.5179 | 0.0132 |
| 49 | A|N|E | 0.7149 | 0.0030 | 0.7710 | 0.0187 | 0.9279 | 0.0086 | 0.5973 | 0.0179 |
| 50 | O|N|E | 0.7136 | 0.0024 | 0.7462 | 0.0178 | 0.9140 | 0.0094 | 0.6090 | 0.0203 |
| 51 | E|N|E | 0.6684 | 0.0038 | 0.6836 | 0.0204 | 0.8303 | 0.0115 | 0.5985 | 0.0183 |
| 52 | N|A|E | 0.6220 | 0.0087 | 0.5970 | 0.0195 | 0.7378 | 0.0158 | 0.5881 | 0.0154 |
| 53 | A|A|E | 0.7180 | 0.0034 | 0.7733 | 0.0183 | 0.9257 | 0.0093 | 0.5935 | 0.0172 |
| 54 | O|A|E | 0.7179 | 0.0031 | 0.7553 | 0.0183 | 0.9170 | 0.0102 | 0.5998 | 0.0158 |
| 55 | E|A|E | 0.6800 | 0.0045 | 0.6945 | 0.0186 | 0.8448 | 0.0123 | 0.5928 | 0.0173 |
| 56 | N|O|E | 0.6145 | 0.0087 | 0.5627 | 0.0258 | 0.7133 | 0.0180 | 0.5449 | 0.0176 |
| 57 | A|O|E | 0.7169 | 0.0034 | 0.7747 | 0.0192 | 0.9254 | 0.0094 | 0.5950 | 0.0175 |
| 58 | O|O|E | 0.7166 | 0.0031 | 0.7563 | 0.0188 | 0.9137 | 0.0106 | 0.6031 | 0.0160 |
| 59 | E|O|E | 0.6767 | 0.0046 | 0.6916 | 0.0206 | 0.8414 | 0.0119 | 0.5955 | 0.0177 |
| 60 | N|E|E | 0.5874 | 0.0103 | 0.5561 | 0.0221 | 0.6614 | 0.0155 | 0.5375 | 0.0132 |
| 61 | A|E|E | 0.7162 | 0.0031 | 0.7696 | 0.0179 | 0.9283 | 0.0085 | 0.5948 | 0.0176 |
| 62 | O|E|E | 0.7155 | 0.0027 | 0.7443 | 0.0173 | 0.9191 | 0.0095 | 0.6028 | 0.0163 |
| 63 | E|E|E | 0.6736 | 0.0038 | 0.6855 | 0.0182 | 0.8385 | 0.0118 | 0.5951 | 0.0176 |
| Max. | 0.72 | 0.015 | 0.78 | 0.027 | 0.93 | 0.022 | 0.64 | 0.024 | |
| Min. | 0.51 | 0.002 | 0.50 | 0.016 | 0.54 | 0.007 | 0.52 | 0.013 | |

Table A2.
Selection error and ranking of each validation method given by the normalized Kendall Tau, averaged over 150 random samples taken from each credit dataset. An overall ranking is calculated using all the experiments made in all credit datasets as the final ranking.
Table A2.
Selection error and ranking of each validation method given by the normalized Kendall Tau, averaged over 150 random samples taken from each credit dataset. An overall ranking is calculated using all the experiments made in all credit datasets as the final ranking.
| Validator | All Datasets | Taiwan | German | Australian | Lending Club | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Rank | Error | Rank | Error | Rank | Error | Rank | Error | Rank | |
| CV:DOB-WOE/10/50 | 0.1661 | 1 | 0.1006 | 2 | 0.1120 | 2 | 0.1183 | 1 | 0.3337 | 1 |
| CV:DOB-WOE/5/50 | 0.1664 | 1 | 0.0992 | 1 | 0.1111 | 1 | 0.1192 | 2 | 0.3362 | 2 |
| CV:DOB-WOE/15/50 | 0.1667 | 2 | 0.1018 | 3 | 0.1122 | 2 | 0.1188 | 1 | 0.3342 | 1 |
| CV:DOB-WOE/20/50 | 0.1675 | 3 | 0.1023 | 4 | 0.1126 | 3 | 0.1191 | 2 | 0.3360 | 2 |
| CV:DOB-SCV/5/50 | 0.1677 | 3 | 0.1004 | 2 | 0.1130 | 3 | 0.1189 | 1 | 0.3388 | 2 |
| CV:DOB-SCV/10/50 | 0.1690 | 3 | 0.1022 | 3 | 0.1129 | 3 | 0.1184 | 1 | 0.3424 | 3 |
| CV:DOB-SCV/15/50 | 0.1698 | 4 | 0.1030 | 5 | 0.1128 | 3 | 0.1186 | 1 | 0.3446 | 3 |
| CV:DB-SCV1/15/50 | 0.1706 | 5 | 0.1070 | 8 | 0.1130 | 3 | 0.1195 | 2 | 0.3427 | 3 |
| CV:DB-SCV1/5/50 | 0.1714 | 6 | 0.1083 | 9 | 0.1131 | 3 | 0.1210 | 4 | 0.3430 | 3 |
| CV:DB-SCV1/10/50 | 0.1716 | 6 | 0.1073 | 8 | 0.1127 | 3 | 0.1200 | 3 | 0.3462 | 4 |
| CV:DOB-SCV/20/50 | 0.1716 | 6 | 0.1037 | 6 | 0.1130 | 3 | 0.1187 | 1 | 0.3509 | 5 |
| CV:SCV/10/50 | 0.1721 | 6 | 0.1084 | 9 | 0.1131 | 3 | 0.1203 | 3 | 0.3466 | 4 |
| CV:DB-WOE2/10/50 | 0.1721 | 6 | 0.1068 | 7 | 0.1112 | 1 | 0.1232 | 6 | 0.3473 | 4 |
| CV:DB-SCV2/5/50 | 0.1722 | 7 | 0.1090 | 10 | 0.1126 | 3 | 0.1223 | 5 | 0.3448 | 3 |
| HO:MCCV/0.1/1000 | 0.1724 | 8 | 0.1115 | 12 | 0.1142 | 4 | 0.1218 | 5 | 0.3422 | 2 |
| CV:DB-WOE2/5/50 | 0.1726 | 8 | 0.1081 | 9 | 0.1125 | 3 | 0.1231 | 5 | 0.3468 | 4 |
| CV:RSCV/10/50 | 0.1726 | 8 | 0.1084 | 9 | 0.1131 | 3 | 0.1209 | 4 | 0.3481 | 4 |
| CV:DOB-WOE/2/50 | 0.1727 | 8 | 0.1002 | 2 | 0.1146 | 5 | 0.1273 | 9 | 0.3487 | 4 |
| CV:kfold/10/50 | 0.1729 | 8 | 0.1089 | 10 | 0.1132 | 3 | 0.1204 | 3 | 0.3490 | 4 |
| CV:DB-SCV2/10/50 | 0.1729 | 8 | 0.1075 | 8 | 0.1116 | 2 | 0.1224 | 5 | 0.3500 | 4 |
| CV:DB-WOE2/15/50 | 0.1729 | 8 | 0.1063 | 7 | 0.1109 | 1 | 0.1234 | 6 | 0.3511 | 5 |
| CV:DB-SCV1/20/50 | 0.1729 | 8 | 0.1070 | 8 | 0.1127 | 3 | 0.1204 | 3 | 0.3515 | 5 |
| CV:SCV/5/50 | 0.1730 | 8 | 0.1100 | 11 | 0.1134 | 3 | 0.1206 | 4 | 0.3481 | 4 |
| CV:kfold/5/50 | 0.1731 | 8 | 0.1100 | 11 | 0.1133 | 3 | 0.1207 | 4 | 0.3484 | 4 |
| HO:FMCCV/0/1000 | 0.1732 | 8 | 0.1111 | 12 | 0.1141 | 4 | 0.1207 | 4 | 0.3468 | 4 |
| CV:RSCV/5/50 | 0.1732 | 8 | 0.1099 | 10 | 0.1133 | 3 | 0.1215 | 5 | 0.3481 | 4 |
| CV:FNkfold/0/50 | 0.1732 | 8 | 0.1087 | 9 | 0.1130 | 3 | 0.1207 | 4 | 0.3503 | 4 |
| CV:SCV/15/50 | 0.1733 | 8 | 0.1084 | 9 | 0.1133 | 3 | 0.1200 | 3 | 0.3515 | 5 |
| HO:MCCV/0.2/1000 | 0.1735 | 8 | 0.1116 | 12 | 0.1144 | 5 | 0.1208 | 4 | 0.3474 | 4 |
| CV:RndCV/0/50 | 0.1735 | 9 | 0.1093 | 10 | 0.1137 | 4 | 0.1212 | 4 | 0.3497 | 4 |
| CV:kfold/15/50 | 0.1737 | 9 | 0.1085 | 9 | 0.1129 | 3 | 0.1205 | 3 | 0.3529 | 5 |
| HO:FSMCCV/0/1000 | 0.1739 | 9 | 0.1117 | 12 | 0.1141 | 4 | 0.1216 | 5 | 0.3483 | 4 |
| HO:SMCCV/0.2/1000 | 0.1740 | 9 | 0.1122 | 13 | 0.1142 | 4 | 0.1220 | 5 | 0.3478 | 4 |
| CV:FUkfold/0/50 | 0.1740 | 9 | 0.1095 | 10 | 0.1139 | 4 | 0.1204 | 3 | 0.3521 | 5 |
| CV:DOB-SCV/2/50 | 0.1742 | 9 | 0.1005 | 2 | 0.1168 | 6 | 0.1267 | 9 | 0.3525 | 5 |
| CV:RSCV/15/50 | 0.1745 | 9 | 0.1087 | 9 | 0.1129 | 3 | 0.1234 | 6 | 0.3532 | 5 |
| HO:SMCCV/0.1/1000 | 0.1750 | 9 | 0.1138 | 14 | 0.1152 | 5 | 0.1216 | 5 | 0.3494 | 4 |
| CV:DB-SCV2/15/50 | 0.1750 | 10 | 0.1068 | 7 | 0.1110 | 1 | 0.1230 | 5 | 0.3591 | 6 |
| CV:kfold/20/50 | 0.1752 | 10 | 0.1089 | 10 | 0.1135 | 3 | 0.1205 | 3 | 0.3578 | 6 |
| CV:SCV/20/50 | 0.1754 | 10 | 0.1087 | 9 | 0.1139 | 4 | 0.1208 | 4 | 0.3581 | 6 |
| BTS:sboot/0/1000 | 0.1759 | 10 | 0.1138 | 14 | 0.1158 | 6 | 0.1245 | 7 | 0.3494 | 4 |
| BTS:boot/0/1000 | 0.1761 | 10 | 0.1140 | 14 | 0.1158 | 6 | 0.1248 | 7 | 0.3497 | 4 |
| BTS:sb632/0/1000 | 0.1762 | 10 | 0.1146 | 15 | 0.1157 | 6 | 0.1247 | 7 | 0.3498 | 4 |
| BTS:b632/0/1000 | 0.1762 | 10 | 0.1142 | 14 | 0.1156 | 6 | 0.1248 | 7 | 0.3501 | 4 |
| BTS:sb632+/0/1000 | 0.1762 | 10 | 0.1138 | 14 | 0.1159 | 6 | 0.1245 | 7 | 0.3505 | 4 |
| BTS:b632+/0/1000 | 0.1763 | 10 | 0.1137 | 14 | 0.1159 | 6 | 0.1250 | 8 | 0.3507 | 5 |
| CV:LOOCV | 0.1763 | 11 | 0.1061 | 7 | 0.1204 | 8 | 0.1181 | 1 | 0.3605 | 6 |
| CV:DB-WOE2/20/50 | 0.1763 | 11 | 0.1065 | 7 | 0.1104 | 1 | 0.1243 | 6 | 0.3640 | 6 |
| CV:DB-SCV2/20/50 | 0.1785 | 11 | 0.1072 | 8 | 0.1108 | 1 | 0.1234 | 6 | 0.3724 | 7 |
| CV:DB-WOE2/2/50 | 0.1786 | 12 | 0.1155 | 15 | 0.1187 | 7 | 0.1303 | 10 | 0.3498 | 4 |
| CV:RSCV/20/50 | 0.1790 | 12 | 0.1089 | 10 | 0.1146 | 5 | 0.1195 | 2 | 0.3729 | 7 |
| CV:DB-SCV1/2/50 | 0.1795 | 12 | 0.1155 | 15 | 0.1180 | 7 | 0.1311 | 10 | 0.3534 | 6 |
| CV:DB-SCV2/2/50 | 0.1798 | 12 | 0.1170 | 16 | 0.1175 | 7 | 0.1308 | 10 | 0.3537 | 6 |
| CV:SCV/2/50 | 0.1803 | 12 | 0.1172 | 16 | 0.1180 | 7 | 0.1315 | 11 | 0.3545 | 6 |
| CV:kfold/2/50 | 0.1806 | 12 | 0.1173 | 16 | 0.1197 | 8 | 0.1320 | 11 | 0.3534 | 6 |
| HO:MCCV/0.5/1000 | 0.1806 | 12 | 0.1175 | 16 | 0.1183 | 7 | 0.1313 | 11 | 0.3552 | 6 |
| HO:SMCCV/0.5/1000 | 0.1807 | 12 | 0.1182 | 17 | 0.1187 | 8 | 0.1309 | 10 | 0.3552 | 6 |
| CV:RSCV/2/50 | 0.1984 | 13 | 0.1243 | 18 | 0.1372 | 10 | 0.1447 | 13 | 0.3872 | 8 |
| CV:MS-SCV/20/50 | 0.2161 | 14 | 0.2059 | 19 | 0.1155 | 6 | 0.1212 | 4 | 0.4219 | 9 |
| CV:MS-SCV/15/50 | 0.2180 | 15 | 0.2122 | 20 | 0.1175 | 7 | 0.1194 | 2 | 0.4230 | 9 |
| CV:MS-SCV/10/50 | 0.2219 | 16 | 0.2236 | 21 | 0.1237 | 9 | 0.1229 | 5 | 0.4173 | 9 |
| CV:MS-SCV/5/50 | 0.2470 | 17 | 0.2529 | 22 | 0.1483 | 11 | 0.1324 | 12 | 0.4544 | 10 |
| CV:MS-SCV/2/50 | 0.3885 | 18 | 0.4735 | 23 | 0.3557 | 12 | 0.1867 | 14 | 0.5382 | 11 |
| InSample/BIC/0/0 | 0.7203 | 19 | 0.7797 | 24 | 0.8012 | 13 | 0.8324 | 15 | 0.4678 | 10 |
| InSample/AIC/0/0 | 0.8314 | 20 | 0.8769 | 25 | 0.8893 | 14 | 0.8744 | 16 | 0.6850 | 12 |

Table A3.
Impact of the sample size on the selection error and ranking of each validation method for the Lending Club 2009 credit dataset. Selection error is given by the normalized Kendall Tau averaged over 150 random samples of sizes N = 500, 1000, and 1500.
Table A3.
Impact of the sample size on the selection error and ranking of each validation method for the Lending Club 2009 credit dataset. Selection error is given by the normalized Kendall Tau averaged over 150 random samples of sizes N = 500, 1000, and 1500.
| Validator | Lending Club—N=500 | Lending Club—N=1000 | Lending Club—N=1500 | |||
|---|---|---|---|---|---|---|
| Error | Rank | Error | Rank | Error | Rank | |
| CV:DOB-WOE/10/50 | 0.3337 | 1 | 0.2514 | 2 | 0.2233 | 3 |
| CV:DOB-WOE/15/50 | 0.3342 | 1 | 0.2546 | 3 | 0.2260 | 4 |
| CV:DOB-WOE/20/50 | 0.3360 | 2 | 0.2564 | 5 | 0.2278 | 5 |
| CV:DOB-WOE/5/50 | 0.3362 | 2 | 0.2491 | 1 | 0.2223 | 2 |
| CV:DOB-SCV/5/50 | 0.3388 | 2 | 0.2462 | 1 | 0.2191 | 1 |
| HO:MCCV/0.1/1000 | 0.3422 | 2 | 0.2587 | 6 | 0.2301 | 6 |
| CV:DOB-SCV/10/50 | 0.3424 | 3 | 0.2506 | 2 | 0.2213 | 2 |
| CV:DB-SCV1/15/50 | 0.3427 | 3 | 0.2563 | 4 | 0.2284 | 5 |
| CV:DB-SCV1/5/50 | 0.3430 | 3 | 0.2535 | 3 | 0.2285 | 5 |
| CV:DOB-SCV/15/50 | 0.3446 | 3 | 0.2552 | 4 | 0.2248 | 3 |
| CV:DB-SCV2/5/50 | 0.3448 | 3 | 0.2557 | 4 | 0.2298 | 6 |
| CV:DB-SCV1/10/50 | 0.3462 | 4 | 0.2544 | 3 | 0.2285 | 5 |
| CV:SCV/10/50 | 0.3466 | 4 | 0.2564 | 5 | 0.2300 | 6 |
| CV:DB-WOE2/5/50 | 0.3468 | 4 | 0.2557 | 4 | 0.2309 | 7 |
| HO:FMCCV/0/1000 | 0.3468 | 4 | 0.2557 | 4 | 0.2301 | 6 |
| CV:DB-WOE2/10/50 | 0.3473 | 4 | 0.2569 | 5 | 0.2298 | 6 |
| HO:MCCV/0.2/1000 | 0.3474 | 4 | 0.2550 | 4 | 0.2311 | 7 |
| HO:SMCCV/0.2/1000 | 0.3478 | 4 | 0.2565 | 5 | 0.2314 | 7 |
| CV:RSCV/10/50 | 0.3481 | 4 | 0.2570 | 5 | 0.2295 | 6 |
| CV:RSCV/5/50 | 0.3481 | 4 | 0.2555 | 4 | 0.2309 | 7 |
| CV:SCV/5/50 | 0.3481 | 4 | 0.2558 | 4 | 0.2309 | 7 |
| HO:FSMCCV/0/1000 | 0.3483 | 4 | 0.2563 | 5 | 0.2309 | 7 |
| CV:kfold/5/50 | 0.3484 | 4 | 0.2550 | 4 | 0.2304 | 6 |
| CV:DOB-WOE/2/50 | 0.3487 | 4 | 0.2613 | 7 | 0.2280 | 5 |
| CV:kfold/10/50 | 0.3490 | 4 | 0.2569 | 5 | 0.2309 | 7 |
| HO:SMCCV/0.1/1000 | 0.3494 | 4 | 0.2601 | 7 | 0.2308 | 6 |
| BTS:sboot/0/1000 | 0.3494 | 4 | 0.2594 | 7 | 0.2345 | 8 |
| CV:RndCV/0/50 | 0.3497 | 4 | 0.2574 | 5 | 0.2313 | 7 |
| BTS:boot/0/1000 | 0.3497 | 4 | 0.2592 | 7 | 0.2342 | 8 |
| BTS:sb632/0/1000 | 0.3498 | 4 | 0.2582 | 6 | 0.2344 | 8 |
| CV:DB-WOE2/2/50 | 0.3498 | 4 | 0.2652 | 9 | 0.2370 | 9 |
| CV:DB-SCV2/10/50 | 0.3500 | 4 | 0.2592 | 7 | 0.2292 | 6 |
| BTS:b632/0/1000 | 0.3501 | 4 | 0.2585 | 6 | 0.2347 | 8 |
| CV:FNkfold/0/50 | 0.3503 | 4 | 0.2570 | 5 | 0.2301 | 6 |
| BTS:sb632+/0/1000 | 0.3505 | 4 | 0.2584 | 6 | 0.2342 | 8 |
| BTS:b632+/0/1000 | 0.3507 | 5 | 0.2590 | 7 | 0.2342 | 8 |
| CV:DOB-SCV/20/50 | 0.3509 | 5 | 0.2589 | 6 | 0.2272 | 4 |
| CV:DB-WOE2/15/50 | 0.3511 | 5 | 0.2630 | 8 | 0.2313 | 7 |
| CV:DB-SCV1/20/50 | 0.3515 | 5 | 0.2600 | 7 | 0.2305 | 6 |
| CV:SCV/15/50 | 0.3515 | 5 | 0.2586 | 6 | 0.2303 | 6 |
| CV:FUkfold/0/50 | 0.3521 | 5 | 0.2582 | 5 | 0.2302 | 6 |
| CV:DOB-SCV/2/50 | 0.3525 | 5 | 0.2606 | 7 | 0.2236 | 3 |
| CV:kfold/15/50 | 0.3529 | 5 | 0.2584 | 6 | 0.2313 | 7 |
| CV:RSCV/15/50 | 0.3532 | 5 | 0.2594 | 7 | 0.2310 | 7 |
| CV:DB-SCV1/2/50 | 0.3534 | 6 | 0.2618 | 8 | 0.2361 | 9 |
| CV:kfold/2/50 | 0.3534 | 6 | 0.2673 | 10 | 0.2401 | 10 |
| CV:DB-SCV2/2/50 | 0.3537 | 6 | 0.2637 | 8 | 0.2385 | 9 |
| CV:SCV/2/50 | 0.3545 | 6 | 0.2664 | 9 | 0.2388 | 10 |
| HO:MCCV/0.5/1000 | 0.3552 | 6 | 0.2649 | 9 | 0.2381 | 9 |
| HO:SMCCV/0.5/1000 | 0.3552 | 6 | 0.2649 | 9 | 0.2388 | 10 |
| CV:kfold/20/50 | 0.3578 | 6 | 0.2615 | 7 | 0.2325 | 7 |
| CV:SCV/20/50 | 0.3581 | 6 | 0.2639 | 8 | 0.2324 | 7 |
| CV:DB-SCV2/15/50 | 0.3591 | 6 | 0.2621 | 8 | 0.2304 | 6 |
| CV:LOOCV | 0.3605 | 6 | 0.2713 | 10 | 0.2496 | 11 |
| CV:DB-WOE2/20/50 | 0.3640 | 6 | 0.2656 | 9 | 0.2324 | 7 |
| CV:DB-SCV2/20/50 | 0.3724 | 7 | 0.2663 | 9 | 0.2327 | 7 |
| CV:RSCV/20/50 | 0.3729 | 7 | 0.2633 | 8 | 0.2318 | 7 |
| CV:RSCV/2/50 | 0.3872 | 8 | 0.2996 | 11 | 0.2587 | 12 |
| CV:MS-SCV/10/50 | 0.4173 | 9 | 0.3498 | 12 | 0.3127 | 13 |
| CV:MS-SCV/20/50 | 0.4219 | 9 | 0.3487 | 12 | 0.3189 | 14 |
| CV:MS-SCV/15/50 | 0.4230 | 9 | 0.3463 | 12 | 0.3126 | 13 |
| CV:MS-SCV/5/50 | 0.4544 | 10 | 0.3822 | 13 | 0.3255 | 14 |
| InSample/BIC/0/0 | 0.4678 | 10 | 0.5002 | 14 | 0.5593 | 15 |
| CV:MS-SCV/2/50 | 0.5382 | 11 | 0.5094 | 15 | 0.4924 | 14 |
| InSample/AIC/0/0 | 0.6850 | 12 | 0.7426 | 16 | 0.7402 | 16 |
References
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; Chapman and Hall/CRC Press: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. Int. Jt. Conf. Artif. Intell. 1995, 14, 1137–1145. [Google Scholar]
- Bengio, Y.; Grandvalet, Y. No Unbiased Estimator of the Variance of K-Fold Cross-Validation. J. Mach. Learn. Res. 2004, 5, 1089–1105. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Kim, J. Estimating classification error rate: Repeated cross-validation, repeated hold-out and bootstrap. Comput. Stat. Data Anal. 2009, 53, 3735–3745. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Rodríguez, J.D.; Pérez, A.; Lozano, J.A. A general framework for the statistical analysis of the sources of variance for classification error estimators. Pattern Recognit. 2013, 46, 855–864. [Google Scholar] [CrossRef]
- Jiang, G.; Wang, W. Error estimation based on variance analysis of k-fold cross-validation. Pattern Recognit. 2017, 69, 94–106. [Google Scholar] [CrossRef]
- Moreno-Torres, J.G.; Sáez, J.A.; Herrera, F. Study on the Impact of Partition-Induced Dataset Shift on k-fold Cross-Validation. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1304–1312. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Y. Cross-validation for selecting a model selection procedure. J. Econom. 2015, 187, 95–112. [Google Scholar] [CrossRef]
- Xu, L.; Fu, H.; Goodarzi, M.; Cai, C.; Yin, Q.; Wu, Y.; Tang, B.; She, Y. Stochastic cross validation. Chemom. Intell. Lab. Syst. 2018, 175, 74–81. [Google Scholar] [CrossRef]
- Beleites, C.; Baumgartner, R.; Bowman, C.; Somorjai, R.; Steiner, G.; Salzer, R.; Sowa, M.G. Variance reduction in estimating classification error using sparse datasets. Chemom. Intell. Lab. Syst. 2005, 79, 91–100. [Google Scholar] [CrossRef]
- Isaksson, A.; Wallman, M.; Göransson, H.; Gustafsson, M.G. Cross-validation and bootstrapping are unreliable in small sample classification. Pattern Recognit. Lett. 2008, 29, 1960–1965. [Google Scholar] [CrossRef]
- Varoquaux, G. Cross-validation failure: Small sample sizes lead to large error bars. NeuroImage 2018, 180, 68–77. [Google Scholar] [CrossRef]
- Xu, L.; Hu, O.; Guo, Y.; Zhang, M.; Lu, D.; Cai, C.; Xie, S.; Goodarzi, M.; Fu, H.; She, Y. Representative splitting cross validation. Chemom. Intell. Lab. Syst. 2018, 183, 29–35. [Google Scholar] [CrossRef]
- Zeng, X.; Martinez, T.R. Distribution-balanced stratified cross-validation for accuracy estimation. J. Exp. Theor. Artif. Intell. 2000, 12, 1–12. [Google Scholar] [CrossRef]
- López, V.; Fernández, A.; Herrera, F. On the importance of the validation technique for classification with imbalanced datasets: Addressing covariate shift when data is skewed. Inf. Sci. 2014, 257, 1–13. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Huang, J.; Ling, C.X. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans. Knowl. Data Eng. 2005, 17, 299–310. [Google Scholar] [CrossRef]
- Christodoulakis, G.; Satchell, S. The Analytics of Risk Model Validation, 1st ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Boston, MA, USA, 2008. [Google Scholar]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Larson, S.C. The shrinkage of the coefficient of multiple correlation. J. Educ. Psychol. 1931, 22, 45–55. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Improvements on Cross-Validation: The 0.632+ Bootstrap Method. J. Am. Stat. Assoc. 1997, 92, 548–560. [Google Scholar] [CrossRef]
- Wong, T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Marcot, B.G.; Hanea, A.M. What is an optimal value of k in k-fold cross-validation in discrete Bayesian network analysis? Comput. Stat. 2021, 36, 2009–2031. [Google Scholar] [CrossRef]
- Rodríguez, J.D.; Pérez, A.; Lozano, J.A. Sensitivity Analysis of k-Fold Cross Validation in Prediction Error Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 569–575. [Google Scholar] [CrossRef]
- Krstajic, D.; Buturovic, L.J.; Leahy, D.E.; Thomas, S. Cross-validation pitfalls when selecting and assessing regression and classification models. J. Cheminform. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Markatou, M.; Tian, H.; Biswas, S.; Hripcsak, G. Analysis of Variance of Cross-Validation Estimators of the Generalization Error. J. Mach. Learn. Res. 2005, 6, 1127–1168. [Google Scholar]
- Sugiyama, M.; Krauledat, M.; Müller, K. Covariate Shift Adaptation by Importance Weighted Cross Validation. J. Mach. Learn. Res. 2007, 8, 985–1005. [Google Scholar]
- Delinquency Rate on Credit Card Loans, All Commercial Banks (DRCCLACBS)|FRED|St. Louis Fed. Available online: https://fred.stlouisfed.org/series/DRCCLACBS (accessed on 5 April 2025).
- Default of Credit Card Clients—UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/dataset/350/default+of+credit+card+clients (accessed on 5 April 2025).
- Statlog (German Credit Data)—UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/dataset/144/statlog+german+credit+data (accessed on 5 April 2025).
- Statlog (Australian Credit Approval)—UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/dataset/143/statlog+australian+credit+approval (accessed on 5 April 2025).
- All Lending Club Loan Data. Available online: https://www.kaggle.com/datasets/wordsforthewise/lending-club (accessed on 5 April 2025).
- Sun, Y.; Wong, A.K.C.; Kamel, M.S. Classification of imbalanced data: A review. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 687–719. [Google Scholar] [CrossRef]
- glm Function—RDocumentation. Available online: https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/glm (accessed on 5 April 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).