Pointer Meter Reading Recognition by Joint Detection and Segmentation

Abstract

To handle the task of pointer meter reading recognition, in this paper, we propose a deep network model that can accurately detect the pointer meter dial and segment the pointer as well as the reference points from the located meter dial. Specifically, our proposed model is composed of three stages: meter dial location, reference point segmentation, and dial number reading recognition. In the first stage, we translate the task of meter dial location into a regression task, which aims to separate bounding boxes by an object detection network. This results in the accurate and fast detection of meter dials. In the second stage, the dial region image determined by the bounding box is further processed by using a deep semantic segmentation network. After that, the segmented output is used to calculate the relative position between the pointer and reference points in the third stage, which results in the final output of reading recognition. Some experiments were conducted on our collected dataset, and the experimental results show the effectiveness of our method, with a lower computational burden compared to some existing works.

1. Introduction

Pointer meters are important instruments for monitoring the status of operation devices. They have been widely used in industrial production due to their reliability and low cost [1]. The current way of reading a pointer meter is manual, which leads to issues such as low efficiency, poor accuracy, and high labor costs. In particular, manual meter reading in an unfavorable environment may lead to safety accidents [2]. Therefore, automatic and accurate pointer meter reading recognition is a natural solution, which is very desirable in industry.

With the recent development of deep learning techniques, many methods based on deep learning have been developed in the literature to handle various tasks [3,4,5,6], particularly automatic pointer meter reading. For example, Alexeev et al. [7] presented a deep network model for automatic meter reading detection that employs a convolutional network equipped with a non-linear network-in-network (NiN) kernel [8] and uses global regression to locate the pointer and reference points. The main goal of this model is to accurately detect the pointer position and all symbols of the meter dial. However, in practice, some symbols are not necessary for meter reading recognition, which may have a negative influence on accurate meter reading. In [9], a modified Mask-RCNN [10] with a precise RoI pooling (PrRoIPooling) [11] operation was developed that can identify the type of pointer meter and also fit the binary mask of the pointer and meter dial. Unlike these two methods, Dong et al. [12] focused on detecting the pointers of meters by using a method that takes the pointer as a 2D vector and utilizes a vector detection network to estimate the confidence map of this vector. The resulting vector is then used for the reading calculation by template matching and coordinate projection techniques.

Different from the methods mentioned above that employ object detectors to locate the pointer, some works determine the pointer position by using various deep segmentation networks. For example, Ref. [13] presented an attention U-Net for segmenting the pointer from the meter dial obtained by an object detector. Meanwhile, Yan et al. [14] designed a lightweight semantic segmentation model for fully automatic pointer recognition that leverages a context-guided network and a channel attention mechanism. In addition, in order to further improve the accuracy of reading recognition, various enhancement strategies, such as image skew correction and bilateral filtering for meter images, are discussed in [15]. Even though there have been many deep learning-based pointer meter reading models, the reading accuracy of these models is still unable to meet the requirements of real-world applications.

To overcome this limitation, we present a three-stage method for tackling the pointer meter reading recognition task, which is composed of meter dial location, reference point segmentation, and meter dial reading. The meter dial location stage aims to quickly locate the meter dials and output the corresponding bounding boxes. Different from the task of object location in a complex scene, meter dial location in industrial applications is generally easier to process. Therefore, we adopt a lightweight yet effective object detection network in this stage. In the segmentation stage, the dial region image determined by the bounding box is inputted into a deep semantic segmentation network. Then, the pointer and reference points from this segmentation network are used to compute the dial number in the meter dial reading stage. Due to it being robust to image distortion, we utilize the relative position, not the angle, between the pointer and reference points to obtain the final value of the meter dial. Additionally, we also collected 380 m images from the internet and two manufacturing plants, of which 304 images were used to train the model, and the remaining ones were used for testing.

The remainder of this work is organized as follows. First, we briefly review some related works on object detection and semantic segmentation in Section 2. Then, Section 3 describes the proposed meter reading model in detail. In Section 4, we present some experiments performed on our collected dataset, and the experimental results are reported to verify the effectiveness and efficiency of our model. Finally, we conclude this paper in Section 5.

2. Related Works

2.1. Object Detection

Object detection plays a very important role in the field of machine vision, which aims to detect instances of visual objects of certain classes in images. That is, the purpose of object detection is to accurately locate objects in images by using effective detection algorithms. Currently, most existing object detection approaches are mainly based on various deep network models, and they can be roughly classified into two categories: convolutional neural network (CNN)-based detection approaches and transformer-based detection approaches. In general, the former has a lower computational cost than the latter. In the following, we briefly review some important representative works in deep object detection models based on both CNNs and transformers.

A representative method for object detection is the Fast-RCNN, first proposed by Girshick in [16], which utilizes a deep convolutional neural network (DCNN) [17] with multi-task loss functions to efficiently classify the object proposals and accelerates the detection model by using the classical truncated singular value decomposition strategy. After that, Ren et al. [18] presented the well-known Faster-RCNN by applying a region proposal network to produce several candidate boxes, significantly improving the quality of candidate boxes, as well as showing high detection accuracy. Another representative work is YOLO, presented by Redmon et al. in [19], which is designed with the purpose of completing object detection in a single forward pass, eliminating the computational burden of traditional multi-step detection processes. Due to their simple structure, high accuracy, and low computational costs, YOLO and its variants have been widely used to deal with various detection tasks and achieved excellent detection performance in practical applications. Specifically, YOLOv1 [19] is the first generation of the YOLO series, introducing an end-to-end object detection approach. It divides an input image into a fixed number of grid cells and predicts classes and bounding boxes within each grid cell. YOLOv2 [20] introduces anchor boxes to handle objects of different sizes and adopts deeper network architectures, i.e., Darknet-19 and Darknet-53. Furthermore, YOLOv3 [21] improves the detection performance by using more convolutional layers and reducing the size of the network stride. In particular, it employs three different scales of feature maps to capture features at different levels and also introduces cross-scale connections and multi-scale predictions to enhance detection performance for small objects.

The transformer presented in [22] was originally designed for natural language processing. It works very well in modeling long-term dependencies in time series. Many recent works [23,24,25,26,27] have extended it to deal with various computer vision tasks. Carion et al. [24] innovatively constructed a transformer-based object detection model called DETR by redesigning the object detection network structure. Specifically, it first applies CNNs to capture image features and aggregates these features with positional encodings, and then it passes them to the transformer’s encoder. Next, a set of object queries and the output of this encoder are processed together in the decoder. Finally, each output of the transformer’s decoder is passed through a feedforward network (FFN) to independently decode it into box coordinates and the corresponding class labels. In essence, DETR translates object detection into a prediction problem, which can simplify the overall process of object detection. Based upon the relationship between objects and the global context, it directly produces the final prediction set in parallel. Furthermore, Zhu et al. [28] proposed the deformable DETR, which integrates the advantages of deformable convolution in sparse spatial sampling and the transformer in relationship modeling. In [29], Sun et al. studied the limitations of the DETR model. For instance, the DETR model exhibits slow convergence and a bottleneck in the cross-attention module in the transformer’s decoder. Based upon these observations, an encoder-only variant of DETR was introduced. Inspired by the success of unsupervised pre-training, Dai et al. [30] presented an unsupervised pre-training DETR by introducing random query patch detection, which enables it to work well without any manual annotation. In addition, to address the issue of high computational complexity in DETR, an adaptive clustering transformer was further presented in [31], which is able to significantly reduce the training and inference cost of DETR and obtain a good trade-off between accuracy and speed.

2.2. Semantic Segmentation

The second stage in our model is to segment the pointer and reference points from the meter dial by the semantic segmentation technique, which is also a fundamental task in the fields of image processing and computer vision. Thus, some important deep models for semantic segmentation are reviewed in this subsection.

Two representative semantic segmentation models are the fully convolutional network (FCN) [32] and U-Net [33]. Due to its great success in handling the semantic segmentation task, the FCN has been a popular backbone, in which a skip connection is introduced to combine low-level detail information with high-level semantic information. The skip connection is very beneficial for preserving the boundary information of images and thus improving the segmentation performance. Furthermore, U-Net [33] and its variants [34] use dense skip connections to fuse the features of the encoder and the corresponding features of the decoder and achieve significant performance improvements in medical image segmentation. Different from the FCN and U-Net, the SegNet model, first proposed in [35,36], introduces an index preserving max pooling to compensate for the reduced spatial resolution caused by the max pooling operation used in the encoder. In addition, DeepLab and various improved versions employ dilated convolution to increase the receptive fields of convolution operations and also utilize spatial pyramid pooling to extract multi-scale contextual information, achieving a significant performance gain over previous semantic segmentation models. In order to aggregate the global information and further improve the segmentation performance, ref. [37] proposed a hybrid dilated convolution approach that can effectively increase the encoder’s receptive fields and also mitigate the gridding issue caused by traditional dilated convolution.

Multi-scale feature extraction is also very important for dealing with various semantic segmentation tasks, which can be implemented in different manners. A simple implementation approach is to directly feed multiple input images (i.e., different-resolution versions of an original input image) with different resolutions into one CNN. This method enables the network to extract discriminative multi-scale features [38]. Another way is to first construct a pyramid or steerable pyramid representation of an image [39] and then apply CNNs to process and fuse the feature maps at different scales. In [40], a pyramid pooling module was designed to fuse the local detail information and the global contextual information for effective feature extraction. Similarly, Chen et al. [41] developed atrous spatial pyramid pooling. To better integrate multi-scale feature maps, RefineNet [42] presented a multi-resolution fusion block for accurately producing the segmentation result, in which the feature maps of different resolutions are fused by the skip connection and convolution operations. Unlike the aforementioned segmentation models that use specially designed network structures, a neural architecture search strategy was presented in [43] to adaptively identify and combine multiple branches with different resolutions. Meanwhile, some works attempted to enhance semantic segmentation models using the attention mechanism [44]. For example, a feature pyramid attention module was developed in [45] by combining the feature pyramid representation and attention mechanism, which resulted in more accurate segmentation results. In [46], the self-attention mechanism was introduced to deal with the semantic segmentation task, in which a position attention module is adopted to fuse useful spatial features scattered at different positions, and a channel attention module is also used to focus on interdependent feature maps. In order to capture long-range contextual information, a point-wise network based on spatial attention was proposed in [47], which improves the segmentation performance via bi-directional information propagation. In addition, a criss-cross attention network was introduced in [48] for semantic segmentation, which can effectively extract image contextual information with a low computational cost.

Very recently, transformer-based semantic segmentation models have shown great potential and have outperformed most CNN-based segmentation models. To our best knowledge, ViT [26] is the first work to verify that a pure transformer framework can also obtain state-of-the-art performance in the task of computer vision. The core idea of ViT is to split an input image into patches and consider them a sequence of tokens. These tokens are fed into multiple transformer layers to generate the features of an image, which are used for the task of image classification. Furthermore, PVT [49] equips the standard transformer with a pyramid structure to handle dense prediction tasks. Some experimental results demonstrate that this pyramid transformer has better representation performance than CNN-based network models. Swin [50] introduces the multi-scale feature hierarchical strategy into the transformer, which computes the feature representation with shifted windows. This hierarchical transformer has the flexibility to model at different scales due to the efficiency of the shifted windowing scheme. In fact, the self-attention used in the transformer is a very effective technique for encoding spatial information. Thus, the current best position of semantic segmentation is dominated by transformer-based models. However, self-attention is computationally expensive. To handle this issue, Guo et al. [51] developed a convolutional attention-based segmentation model called SegNeXt. For encoding contextual information, convolutional attention is more efficient and effective than the standard self-attention mechanism. Due to the simplicity and efficiency of cheap convolution operations, this model can significantly improve the segmentation performance with low computational complexity. Despite this, compared to CNN-based models, the inference speed of transformer-based segmentation models is slow, which is undesirable for real-time applications.

3. Proposed Method

As discussed above, CNN-based detection and segmentation models generally have a low computational burden. Therefore, in this work, we focus on CNN-based models for pointer meter dial reading. Figure 1 illustrates the proposed model, which consists of three main components: the meter dial location network, the reference point segmentation network, and the reading dial number module. The location network aims to detect the meter dial, which translates the task of meter dial location into a regression problem that spatially separates bounding boxes by an object detection network. After that, the segmentation network segments the reference points, including pointer and grid points. Once the reference points are obtained, we can read (i.e., recognize) the meter dial number by computing the relative position between the pointer and grid reference points. Even though the structure of each part of our model is very simple, experimental results on our collected dataset demonstrate its efficiency and effectiveness. In the following, we describe the three components of our model in detail.

Figure 1. The architecture of our proposed pointer meter reading model.

3.1. Meter Dial Location Network

In order to achieve real-time meter dial location, we employ a lightweight version of the Darknet-19 framework, first presented in [19], as the backbone of our model. The main motivation is that Darknet-19 has been widely used in the YOLO family, and its effectiveness has been verified in many practical applications. Specifically, this lightweight network has 19 convolutional layers and 5 max pooling layers, the same as the original Darknet-19. The only difference between them is that the number of filters employed in each convolutional layer of our model is half that in Darknet-19. As a result, this lightweight network can locate the meter dial at a fast inference speed with satisfactory location accuracy.

Figure 2 illustrates the architecture of the meter dial location network used in the first stage of our model. This network model first processes the input image via a series of convolution and pooling operations. Then, it applies an average pooling layer followed by a softmax layer to produce the output information about the confidence score, position, and size of each bounding box. At last, a non-maximum suppression operation is performed to further select the bounding box with the highest likelihood and output its coordinate information. After that, according to the coordinates of each bounding box, the input image is cropped to obtain the meter dial and feed it into the next stage to segment the pointer and reference points. Note that, in our model, k1 × 1 and k3 × 3 used in the Con2d layer represent 1 × 1 and 3 × 3 convolution kernels, respectively. In the Maxpool layer, k2 and s1 denote a pooling kernel of size 2 × 2 and a pooling stride of size 1, respectively, and p1 means that the padding size is 1.

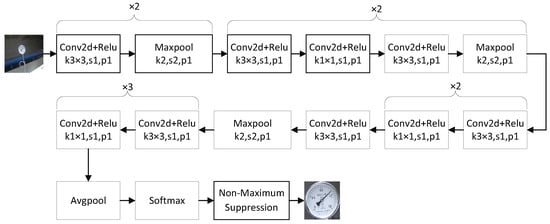
Figure 2. The architectural details of the meter dial location network used in the first stage.

3.2. Reference Point Segmentation Network

After obtaining the meter dial region of the input image, we further segment the pointer and reference points from the meter dial by using a fully convolutional segmentation network. In this reference point segmentation network, we adopt the atrous convolution proposed in [52], which is an efficient and effective way to increase the receptive field of a deep network and also keep the spatial resolution of the resulting feature maps. Due to its fully convolutional framework, the reference point segmentation network is easy to implement and speeds up the inference process on various hardware platforms. This is very important for real-time applications.

Figure 3 shows the architectural details of the reference point segmentation network used in the second stage of our model. This network employs the widely used VGG16 [53] as its backbone but removes the fully connected layers of VGG16 and only retains the convolutional and max pooling layers. In order to capture the global contextual information of an input image, atrous convolution with a stride ratio $r=2$ is utilized to enlarge the model’s receptive field. A Conv2d layer equipped with 1 × 1 convolution is adopted to fuse all the feature maps to output the segmentation result. It is necessary to point out that the segmentation result obtained by the last Conv2d layer is reduced with a downsampling factor of 8x, which is caused by the max pooling layers. Therefore, we apply an upsampler based on the classic bicubic interpolation method to resize the segmentation result to the original image resolution.

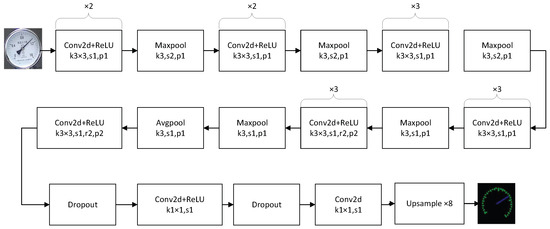
Figure 3. The architectural details of the reference point segmentation network adopted in the second stage.

3.3. Reading Dial Numbers

In this stage, the pointer and grid points segmented from the previous stage are further used to recognize the dial numbers. In general, we need to first determine the center point of the meter dial region that is generated by the meter dial location network. For ease of presentation, let the center point coordinate be $(x,y)$. Based on this coordinate, it is easy to find the pointer by searching similar pixels around the center point. After determining the position and direction of the pointer, a simple method for reading the dial number is to utilize the angle ratio to compute the value, as shown in Figure 4a. This method has been used in some existing works [15,54].

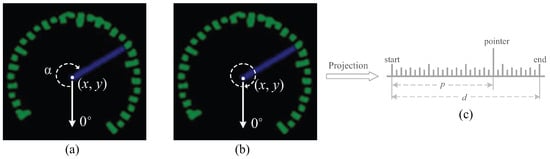
Figure 4. A diagram of different methods for computing the dial number.

Unlike the above method that obtains the dial value of the meter dial by calculating the angle between the pointer direction and the minimum scale direction, we consider the center point $(x,y)$ to be the origin of a polar coordinate system. Based upon the transform relationship between the polar and Cartesian coordinates, circular grid points are projected into uniformly aligned points along with a straight line, which is illustrated in Figure 4b,c. At last, we achieve the final scale value of the meter dial (i.e., reading of dial numbers) by computing the relative position between the pointer and the aligned reference points, which is expressed as

$$value=\frac{p}{d}·scale,$$

(1)

where d denotes the distance between the starting and end points shown in Figure 4c, p is the distance between the starting point and the pointer, and scale represents the largest dial value of the target meter and needs to be known in advance. It is necessary to point out that our distance-based method for reading dial numbers can achieve higher accuracy than the angle-based method. The major reason is that the latter is very sensitive to the distortion of the meter image. Unfortunately, image distortion is inevitable in practical applications.

3.4. Loss Functions

To train our proposed deep model, we apply the widely used Intersection over Union (IoU) loss [55] for the task of bounding box regression and the cross-entropy (CE) loss for the dense prediction task. Specifically, we first optimize the weight parameters of the meter dial location network by minimizing the IoU loss and then train the reference point segmentation network using the CE loss, which is summed up over all the pixels. The IoU loss is defined as

$$IoU(b_1,b_2)=\frac{b_1\cap b_2}{b_1+b_2-b_1\cap b_2},$$

(2)

where $b_1$ and $b_2$, respectively, denote the located bounding box of a meter and the corresponding ground truth, and $b_1\cap b_2$ is the overlapping area of $b_1$ and $b_2$. The CE loss is formulated as follows:

$$CE(p_i,{\widehat{p}}_i)=-p_{i}log{\widehat{p}}_i-(1-p_i)log(1-{\widehat{p}}_i),$$

(3)

where ${\widehat{p}}_i$ represents the predicted label, and $p_i$ refers to the ground truth. Note that, although various loss functions have been designed for detection and segmentation tasks, we found that the IoU and CE loss functions work well for our model.

4. Experiments

4.1. Dataset and Setting

At present, there are no publicly available datasets for the task of pointer meter reading recognition. To address this issue, we collected 380 images with the size 1024 × 1024 from the internet and two manufacturing plants in Shandong, each of which has at least one pointer meter. Figure 5 shows six example cases from this dataset. In order to achieve accurate image labels, two annotators performed the label operation, and their annotations were averaged to produce the final label of each image. The annotation information includes the position, height, and width of each bounding box and the positions of the pointer and different scales. Considering that our pointer meter dataset has a limited number of images, we first pre-trained both the meter dial location network and the reference point segmentation network based on the COCO dataset [56]. Then we further fine-tuned the weight parameters of these two networks based on our meter dataset. All the meter images were randomly sampled and divided into two sets with a ratio of 8:2, namely, one set for model training and the other for model testing. For data augmentation in the training phase, we applied the commonly used random rotation and resizing operations, which can enhance the performance of our model and also alleviate the overfitting problem caused by the small dataset. Note that all the deep models in the experiments were trained with the same data augmentation techniques. In addition, we conducted all experiments on a PC equipped with an Intel Core i7-10700k CPU (Santa Clara, CA, USA), 32GB memory, and an NVIDIA GeForce GTX2080Ti GPU (Santa Clara, CA, USA).

Figure 5. Some examples from our pointer meter dataset.

4.2. Evaluation Metric

Due to our model being composed of three stages, we evaluate the output of each stage to completely quantify the performance of our method. Specifically, for the first stage, the average precision (AP) metric is utilized to measure the location accuracy of the meter dial location network. The AP is measured by computing the area under the precision–recall (P-R) curve, where the definitions of the precision and recall are as follows:

$$Precision=\frac{TP}{TP+FP},$$

(4)

$$Recall=\frac{TP}{TP+FN},$$

(5)

where TP, FP, and FN are, respectively, the number of true positives, false positives, and false negatives. The P-R curve can indicate the relationship between precision and recall for different thresholds. Note that we only consider a bounding box to be correct if its IoU with the ground truth is higher than 0.5. For the second stage, we employ the mean IoU (mIoU) between the segmentation result and its ground truth to assess the performance of the reference point segmentation network, which is formulated as

$$mIoU=\frac{1}{k}\sum _{i=1}^k\frac{p_{ii}}{{\sum }_{j=1}^k{p}_{ij}+{\sum }_{j=1}^k{p}_{ji}-p_{ii}},$$

(6)

where $p_{ij}$ refers to the i-th class being segmented as class j, and k is the total number of all classes. In addition, for the stage of reading dial numbers, the relative error (RE) is used to evaluate the accuracy of dial value estimation, which is defined as

$$RE=\frac{|v_e-v_a|}{v_a},$$

(7)

where $v_e$ and $v_a$ denote the estimated value and the corresponding actual value, respectively. In essence, the RE measures the ratio of the absolute error of the pointer reading value to the actual value, and it is a widely used metric for value estimation.

4.3. Experimental Results

We first used 304 images in our dataset to train the meter dial location network and then used the remaining images (i.e., 76 images) to test our location network. The AP metric and running time are employed to evaluate the detection performance of different methods. Table 1 reports the quantitative results of our method and three widely used deep detection networks, i.e., SSD [57], RetinaNet [58], and YOLOv4 [59]. From this table, it can observed that all detection methods achieve satisfying performance, resulting in very close AP values. This means that meter dial detection is not a very challenging task for existing state-of-the-art generic object detection models. Meanwhile, although YOLOv4 has a slightly higher AP value than our method, the proposed method obtains approximately 3 times the computational efficiency.

Table 1. Quantitative results of different detection methods for meter dial location.

Methods	AP	Time (ms)
Faster R-CNN	94.1	429
SSD	94.7	267
RetinaNet	95.3	302
YOLOv4	95.9	181
Our Method	95.1	64

We further compare the performance of the proposed reference point segmentation model with three representative deep segmentation models, i.e., FCN [32], SegNet [35], and U-Net [33]. The comparison results in terms of mIoU and running time are listed in Table 2. It can be easily found that the proposed segmentation model outperforms the other competing models, while it has a slight degeneration in efficiency. More importantly, a slightly increased computational cost results in a significant gain in the accuracy of dial number reading. Meanwhile, the relative error of the recognized pointer value from our method is approximately 0.011. In most practical applications, this small relative error indicates a high reading accuracy. Specifically, it means that the proposed method can achieve an accuracy of 98.9%. For U-Net, FCN, and SegNet, the relative errors are 0.057, 0.094, and 0.116, respectively. The proposed segmentation method is significantly better than the competing segmentation methods. In addition, Figure 6 shows six meter images and their reading results obtained by our method. It can also be found that the proposed method accurately locates the meter dials and recognizes the values of dial pointers. These results clearly verify the effectiveness of our method.

Table 2. Quantitative results of different methods for dial point segmentation.

Methods	mIoU	Time (ms)
FCN	72.9	105
SegNet	71.0	67
U-Net	75.6	112
RefineNet	77.3	181
Our method	79.2	196

Figure 6. Some meter images and their corresponding reading results obtained by our method.

4.4. Additional Discussion

In Table 1, we observe that the AP values of different detection models have no significant differences. The reason is that the dataset for the task of pointer meter location generally contains one object class, i.e., the meter class. Therefore, the meter detection task is more easy to tackle than the generic object detection task. Generally, most deep models designed for generic object detection are well suited to locate the pointer meter. Meanwhile, the mIoU results listed in Table 2 show that the segmentation models have clear differences in performance. This means that some attention should be paid to developing a more precise method for reference point segmentation. Considering that the reference points are directional and regular, we can design some specific segmentation models by integrating this prior information.

Intuitively, there is a cumulative error from the meter dial location stage and the reference point segmentation stage. It is necessary to point out that meter dial location in industrial applications is generally easier than object location in complex scenes. Therefore, we adopt a lightweight yet effective object detection network to locate meter dials in the first stage. Although it is not perfect, almost all meter dials in the test images can be located with entire bounding boxes. Meanwhile, the segmentation network used in the second stage is able to correct small detection errors using data augmentation techniques in the training phase. In the experiments, we found that this cumulative error can be negligible.

5. Conclusions

For the task of automatic and accurate meter pointer reading, which is very desirable in intelligent factories, this work presents a deep learning-based method. The proposed method first detects the meter dial object, and its bounding box is output by our meter dial location network, which is a lightweight YOLO-like deep convolutional network. Next, the dial region image from the preceding stage is fed into a reference point segmentation network to segment the positions of the dial pointer and reference points. Then, we project the regular points onto uniformly aligned points along with a straight line and calculate the relative position between the pointer and aligned points to achieve the final scale value of the meter dial. Some quantitative evaluation results are provided to demonstrate the good recognition performance of our proposed method.

In addition, this paper focuses on analog meter reading recognition, which is mainly built upon the object detection and segmentation techniques. Different from this task, digital meter reading recognition generally depends on the optical character recognition (OCR) technique. A generic reading approach is desirable to recognize both analog meters and digital ones. Another possible direction is to further compress the number of the model’s parameters, resulting in a more lightweight detection model for platforms with low computational resources. In fact, pointer meters come in several specific shapes, e.g., a circular shape and a square shape. This is very important, and available geometric information is required for designing more efficient and effective pointer meter location models. All these studies could be future work.