Train-Induced Unsteady Airflow in a Metro Tunnel with a Ventilation Shaft

Abstract

To ensure only one train operates in each ventilation section within an extra-long tunnel, a ventilation shaft was typically installed to divide the entire tunnel into multiple sections. Given the crucial role of piston wind in the metro tunnel environment and ventilation, a deeper understanding of train-induced unsteady airflow in a metro tunnel with a ventilation shaft is desirable. This study uses the unsteady flow theory of the Bernoulli equation to mathematically model piston wind in metro tunnels both with and without ventilation shafts. The influence of various shaft parameters on piston wind development is systematically analyzed. The results indicate that the shaft significantly impacts the piston wind. The maximum piston wind speed and ventilation rate in tunnels with ventilation shafts surpass those in tunnels without them. Moreover, shaft location and the cross-sectional area notably affect the maximum piston wind speed, ventilation rate, and airflow in the shaft, whereas shaft height has no significant effect. It is found that a ventilation shaft with a larger cross-sectional area positioned in the middle of the tunnel enhances the performance of piston ventilation.

1. Introduction

With the rapid development of the metro system into the outer suburbs, the distance between stations becomes larger. As a result, the extra-long metro tunnels become more and more common. To reduce the accumulation of passengers at rush hours, the departure interval of metro trains is becoming shorter and shorter. The increase in tunnel length and the decrease in departure intervals will lead to the increasing probability of multiple trains simultaneously travelling in the same tunnel direction. To ensure that there is only one train running in each ventilation section at the same time [1], a ventilation shaft is usually installed in extra-long metro tunnels to divide the entire tunnel into multiple ventilation sections. When a metro train runs in a relatively narrow metro tunnel, the positive pressure formed at the train head will help discharge the harmful air outside the tunnel and the negative pressure induced at the train tail will drag the fresh air inside. This is how the piston wind is generated [2]. Metro tunnels generally use piston wind or additionally equip mechanical ventilation systems to aid in ventilation to eliminate the residual heat [3]. Due to the important role of piston wind in the metro tunnel environment and ventilation [4], it is desirable to have a better understanding of the train-induced unsteady airflow in a metro tunnel with a ventilation shaft.

The characteristics of the unsteady airflow induced by a moving train inside a relatively long narrow space have been studied by many scholars through theoretical analysis [5,6], experiments [7,8], and numerical simulations [9,10,11,12]. For metro tunnels without a ventilation shaft, Kim et al. [13] used a 1/20 scale model tunnel to carry out an experimental analysis related to the unsteady flow of metro trains and obtained the evolution law of pressure and wind speed. According to the Bernoulli equation, associated with the unsteady flow, Wang et al. [14] and Zhang et al. [4] both discussed the influence of relevant parameters on the piston wind by establishing theoretical models for the calculation of piston wind. With the development of computational fluid dynamics (CFD) technology, the CFD technique has become more and more popular with scholars to help analyse the piston wind induced by train motion [15,16]. Huang et al. [17,18] used a CFD simulation to explore piston winds in subway tunnels with natural ventilation ducts. The ventilation performance of various ventilation strategies (with different ventilation duct structures and partition geometries) is compared and analyzed [19]. Aleksander Król et al. [20] conducted numerical simulations to investigate the airflow dynamics induced by train movement in single- or double-track tunnels. Their study revealed that the airflow velocity in narrow single-track tunnels was significantly higher than that in double-track tunnels. Loreline et al. [21] employed a CFD model incorporating dynamic grid technology to numerically simulate the airflow induced by a train in a subway station. The findings indicated that air circulation escalated with the augmentation of both the blockage rate and train speed. Using CFD simulations, Cross et al. [22] found that the ventilation airflow induced by train movement inside the tunnel significantly increased with the increase in the blockage ratio. Furthermore, the effects of piston wind on the environment and energy consumption of subway tunnels [23], the performance of jet fans [24], and smoke propagation characteristics [25,26] are also addressed by some other researchers.

The above studies mainly focus on the piston wind generated by the train in the tunnel without ventilation shafts. Ventilation shafts are usually installed in some long tunnels, which possibly have an important impact on the ventilation performance of the tunnel. With respect to this regard, Lin et al. [27] measured the periodic airflow induced by the piston effect in ventilation shafts of a subway station in Taipei, China. They found that the piston effect causes some air exchanges inside the tunnel through the ventilation shafts. However, the cross-sectional area of the shaft was found to be less important in enhancement of the piston effect and air exchange. Kim et al. [28] used three-dimensional numerical simulation to explore the influence of the shaft position on the ventilation performance of subway tunnels. Through the analysis of the ventilation flow rate through the shaft and the flow field in the tunnel nearby the shaft, the results suggested that the ventilation shaft be installed near the station. Zhang et al. [29] studied the energy-saving effect of natural ventilation by utilizing the newly built shafts in a super-long highway tunnel. They recommend that the natural wind speed and construction cost be determined by the shaft diameter, and the shaft should be installed in the middle of the ventilation section. For an ultra-high-speed elevator hoistway with a tunnel-like structure, Zhang et al. [30] established a theoretical model to analyze the influence of the hoistway structure and ventilation hole on the car-induced unstable airflow.

Previous scholars have conducted extensive investigations into train-induced piston wind and how the ventilation shaft affects the ventilation performance inside tunnels. However, attention has seldom been paid to the influence of the shaft dimensions on the piston wind caused by the train movement. Kim et al. [28] studied the influence of ventilation shaft location on train-induced unstable airflow in subway tunnels, but they did not systematically analyze the influence of other shaft parameters. Knowledge gaps in this field and the need for practical solutions are calling for further investigations into train-induced piston wind in metro tunnels with ventilation shafts.

In summary, the investigation of train-induced unsteady airflow in metro tunnels equipped with ventilation shafts is both significant and valuable. This study is organized as follows: The introductory section reviews the existing literature on unsteady airflow induced by trains and delineates the research objectives of this paper. The following section offers a comprehensive exposition of the theoretical model formulated in this study, along with its validation. Utilizing the established theoretical model, the third section investigates the formation and influencing factors of piston wind in tunnels, considering scenarios both with and without ventilation shafts. It systematically analyzes the impact of various shaft parameters on the maximum piston wind speed and ventilation efficiency. The concluding section summarizes the insights garnered from this research.

2. Theoretical Analysis

2.1. The Premise of Theoretical Analysis

In this study, we consider a long, straight tunnel containing a ventilation shaft, where the tunnel and shaft share the same wall roughness, with no slope or cross-sectional changes, as shown in Figure 1. Correspondingly, tunnels without a ventilation shaft of the same length are also considered for comparison. As the speed of the piston wind caused by the train movement is much less than the speed of sound, and because the Mach number is significantly small, the piston wind flow can be considered to be one-dimensional, unstable, and incompressible [14,30]. Furthermore, when the train passes through the tunnel with a ventilation shaft, the airflow in the shaft is mainly affected by the operation of the train. The air temperature in the tunnel and shaft was considered to be the same as the ambient temperature. The stack effect of the shaft was ignored here, that is, the pressure difference between the shaft bottom and top and the tunnel entrance and exit was assumed to be zero. Based on the above assumptions and Bernoulli’s principle for unsteady flow, the unsteady airflow induced by the metro train was theoretically modeled and analyzed. Table 1 summarizes the physical quantities and their symbols used in the theoretical model. It is important to recognize that the application of the Bernoulli equation in theoretical modeling rests on certain assumptions. Consequently, employing the Bernoulli equation theory is appropriate for scenarios involving relatively simple tunnel structures; however, it becomes challenging to develop a theoretical model for more complex tunnel configurations. To distinguish different scenarios, piston wind (PW) caused by the train in a tunnel with a ventilation shaft is known as PW-WVS. Similarly, piston wind caused by the train in a tunnel without a ventilation shaft is known as PW-NVS.

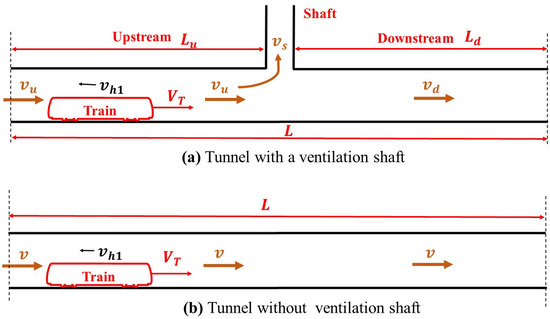
Figure 1. Typical Tunnel Diagram.

Table 1. Physical quantities and their symbols are used in the theoretical model.

Symbol	Physical Meaning
$A_T$	Cross-sectional area of the metro train (${\mathrm{m}}^2$)
$A_L$	Cross-sectional area of the tunnel (${\mathrm{m}}^2$)
$A_s$	Cross-sectional area of the ventilation shaft (${\mathrm{m}}^2$)
$H_s$	Height of the air shaft ($\mathrm{m}$)
$V_T$	Velocity of the train running at a constant speed ($\mathrm{m}/\mathrm{s}$)
$V_t$	Velocity of the train (variable) ($\mathrm{m}/\mathrm{s}$)
$v$	Velocity of the piston wind ($\mathrm{m}/\mathrm{s}$)
$v_u$	Velocity of the piston wind upstream of the tunnel ($\mathrm{m}/\mathrm{s}$)
$v_d$	Velocity of the piston wind downstream of the tunnel ($\mathrm{m}/\mathrm{s}$)
$v_s$	Velocity of airflow in ventilation shaft ($\mathrm{m}/\mathrm{s}$)
$w$	Velocity of airflow relative to the tunnel walls in the annular space ($\mathrm{m}/\mathrm{s}$)
$v_h$	Velocity of airflow relative to the train in the annular space ($\mathrm{m}/\mathrm{s}$)
$v_{h1}$	Velocity of airflow relative to the train in the annular space upstream ($\mathrm{m}/\mathrm{s}$)
$v_{h2}$	Velocity of airflow relative to the train in the annular space downstream ($\mathrm{m}/\mathrm{s}$)
$\alpha$	Blockage ratio of the train to the tunnel
$\beta$	Ratio of shaft cross-sectional area to tunnel cross-sectional
${\lambda }_L$	Frictional resistance coefficient of airflow along the tunnel walls
${\lambda }_h$	Frictional resistance coefficient of airflow along the annular space
${\lambda }_s$	Frictional resistance coefficient of airflow along the ventilation shaft walls
$D_L$	Hydraulic diameter of the tunnel ($\mathrm{m}$)
$D_h$	Hydraulic diameter of the annular space ($\mathrm{m}$)
$D_s$	Hydraulic diameter of the ventilation shaft ($\mathrm{m}$)
$L$	Length of the tunnel ($\mathrm{m}$)
$L_T$	Length of the train ($\mathrm{m}$)
$L_u$	Length of the tunnel upstream ($\mathrm{m}$)
$L_d$	Length of the tunnel downstream ($\mathrm{m}$)
$l_{ij}$	Distance between cross-sections i and j ($\mathrm{m}$)
${\xi }_{in}$	Local drag coefficient at the inlet of the tunnel
${\xi }_{out}$	Local drag coefficient at the outlet of the tunnel
${{\xi }_h}_{in}$	Local drag coefficient at the inlet of the annular space
${{\xi }_h}_{out}$	Local drag coefficient at the outlet of the annular space
${{\xi }_s}_{in}$	Local drag coefficient at the inlet of the ventilation shaft
${{\xi }_s}_{out}$	Local drag coefficient at the outlet of the ventilation shaft
${\xi }_{i-j}$	Local drag coefficient of the airflow from cross-section i to cross-section j

2.2. PW-WVS

According to the Bernoulli equation for unsteady flow, a theoretical model was developed to analyze the piston effect in a metro tunnel with a ventilation shaft [4,14,31]. The Bernoulli equation applied in this study is articulated as Equation (1):

$${\displaystyle \frac{{\rho v}_1^2}{2}}+P_1+\rho g{z}_1={\displaystyle \frac{{\rho v}_2^2}{2}}+P_2+\rho g{z}_2+h_f+\rho \epsilon {\int }_S{\displaystyle \frac{\partial v}{\partial t}}ds$$

(1)

where $\rho$ is the ambient air density (kg/m³), $v_1$ (m/s) and $v_2$ (m/s) are the velocity at cross-section 1 and cross-section 2,$P_1$ (Pa) and $P_2$ (Pa) are the pressure at cross-section 1 and cross-section 2, $z_1$ (m) and $z_2$ (m) are the height of cross-section 1 and cross-section 2,$g$ (m/s²) is the acceleration of gravity, $h_f$ (Pa) represents resistance loss, $\rho \epsilon {\int }_S{\displaystyle \frac{\partial v}{\partial t}}ds$ (Pa) is the inertia head representing the amount of kinetic energy of fluid per unit mass changing over time, and $\epsilon$ is a correction factor of the uneven flow velocity in the tunnel, respectively. Since the cross-sectional area of the tunnel is constant, $\epsilon \approx 1$ is obtained in this study [6,25].

When the metro train travels inside the tunnel, according to the continuity equation [32], Equations (2) and (3) can be obtained:

$$A_T{V}_{t}dt=A_{L}vdt+\left(A_L-A_T\right)wdt$$

(2)

$$v_h=w+V_t={\displaystyle \frac{A_T{V}_T-A_{L}v}{A_L-A_T}}+V_t={\displaystyle \frac{V_t-v}{1-\alpha }}$$

(3)

where $\alpha =A_T/A_L, w$ is the velocity of airflow relative to the tunnel wall in the annular space and $v_h$ is the velocity of airflow relative to the train in the annular space.

In accordance with the aforementioned Bernoulli and continuity equations, the dynamics of unsteady airflow in PW-WVS mode are meticulously analyzed. The section extending from the tunnel entrance to the shaft position is designated as the tunnel’s upstream, while the segment from the shaft position to the tunnel exit is identified as its downstream. As shown in Figure 2, the variation in the piston wind movement covers six patterns: (1) the developing pattern where the train enters the tunnel, namely PPW-TET; (2) the changing pattern where the train moves at a constant speed upstream of the tunnel, known as PPW-TCU; (3) the changing pattern where the train passes by the ventilation shaft at a constant speed, called PPW-TCS; (4) the changing pattern where the train moves at a constant speed downstream of the tunnel, named as PPW-TCD; (5) the changing pattern where the train leaves the tunnel, known as PPW-TLT; and (6) the pattern where the train has left the tunnel, called PPW-ATL. Here, the development of piston wind during the process of a train entering a tunnel (PPW-TET) is used as an example to introduce the establishment process of the theoretical model in detail. The results of the theoretical model for the remaining processes are directly listed.

2.2.1. PPW-TET

When the subway train starts entering the tunnel from outside, as shown in Figure 2a, the following occurs:

(1) The Bernoulli equation for fluid flow between cross-sections 1 and 2 is expressed as Equation (4):

$$P_2=P_a+\left({{\xi }_h}_{in}+{\lambda }_h{\displaystyle \frac{l_{12}}{D_h}}+{{\xi }_h}_{out}\right){\displaystyle \frac{1}{2}}\rho v_{h1}^2+\rho l_{12}{\displaystyle \frac{{dv}_{h1}}{dt}}$$

(4)

where $l_{12}=V_{T}t$, $v_{h1}={\displaystyle \frac{V_T-v_u}{1-\alpha }}$, ${\displaystyle \frac{{dv}_{h1}}{dt}}={\displaystyle \frac{-1}{1-\alpha }}{\displaystyle \frac{d{v}_u}{dt}}$.

(2) The Bernoulli equation for fluid flow between cross-sections 2 and 3 is expressed as Equation (5):

$$P_2=P_3+{\lambda }_L{\displaystyle \frac{l_{23}}{D_L}}{\displaystyle \frac{1}{2}}\rho {v_u}^2+\rho l_{23}{\displaystyle \frac{d{v}_u}{dt}}$$

(5)

(3) The Bernoulli equation for fluid flow between cross-sections 3 and 4 is expressed as Equation (6):

$$P_3+{\displaystyle \frac{1}{2}}\rho {v_u}^2=P_a+\left({\xi }_{3-4}+{\lambda }_L{\displaystyle \frac{l_{34}}{D_L}}+{\xi }_{out}\right){\displaystyle \frac{1}{2}}\rho {v_d}^2+\rho l_{34}{\displaystyle \frac{d{v}_d}{dt}}$$

(6)

(4) The Bernoulli equation for fluid flow between cross-sections 3 and 5 is expressed as Equation (7):

$$P_3+{\displaystyle \frac{1}{2}}\rho {v_u}^2=P_a+\left({\xi }_{3-5}+{\lambda }_s{\displaystyle \frac{H_s}{D_s}}+{{\xi }_s}_{out}\right){\displaystyle \frac{1}{2}}\rho {v_s}^2+\rho H_s{\displaystyle \frac{d{v}_s}{dt}}$$

(7)

As shown in Figure 2a, at the ventilation shaft, the continuity equation is used to obtain the following results, expressed as Equations (8) and (9):

$$A_L{v}_u=A_L{v}_d+A_s{v}_s$$

(8)

$$v_s={\displaystyle \frac{A_L{v}_u-A_L{v}_d}{A_s}}={\displaystyle \frac{v_u-v_d}{\beta }}$$

(9)

where $\beta =A_s/A_L,{\displaystyle \frac{{dv}_s}{dt}}={\displaystyle \frac{1}{\beta }}{\displaystyle \frac{d{v}_u}{dt}}-{\displaystyle \frac{1}{\beta }}{\displaystyle \frac{d{v}_d}{dt}}$;

By combining the above equations, Equation (10) is obtained:

$$\left\{\begin{array}{c}A{\displaystyle \frac{d{v}_u}{dt}}+l_{34}{\displaystyle \frac{d{v}_d}{dt}}=B{v_u}^2-{\displaystyle \frac{k_h}{2}}{v_d}^2+C{v}_u+D\\ {\displaystyle \frac{H_s}{\beta }}{\displaystyle \frac{d{v}_u}{dt}}+E{\displaystyle \frac{d{v}_d}{dt}}=-{\displaystyle \frac{k_s}{2{\beta }^2}}{v_u}^2+F{v_d}^2+{\displaystyle \frac{k_s}{{\beta }^2}}{v}_u{v}_d\end{array}\right. t\in \left[0,{\displaystyle \frac{L_T}{V_T}}\right]$$

(10)

where $A={\displaystyle \frac{l_{12}+l_{23}\left(1-\alpha \right)}{1-\alpha }}$, $B={\displaystyle \frac{\left(1-k_u\right){\left(1-\alpha \right)}^2+k_h}{2{\left(1-\alpha \right)}^2}}$, $C=-{\displaystyle \frac{2k_h{V}_T}{2{\left(1-\alpha \right)}^2}},D={\displaystyle \frac{k_h{V}_T^2}{2{\left(1-\alpha \right)}^2}}$, $E=-{\displaystyle \frac{H_s+{\beta l}_{34}}{\beta }}$, $F={\displaystyle \frac{{\beta }^2{k}_d-k_s}{2{\beta }^2}}$, $k_u={\lambda }_L{\displaystyle \frac{l_{23}}{D_L}}$, $k_h={{\xi }_h}_{in}+{\lambda }_h{\displaystyle \frac{l_{12}}{D_h}}+{{\xi }_h}_{out}$, $k_d={\xi }_{3-4}+{\lambda }_L{\displaystyle \frac{l_{34}}{D_L}}+{\xi }_{out}$, $k_s={\xi }_{3-5}+{\lambda }_s{\displaystyle \frac{H_s}{D_s}}+{{\xi }_s}_{out}$.

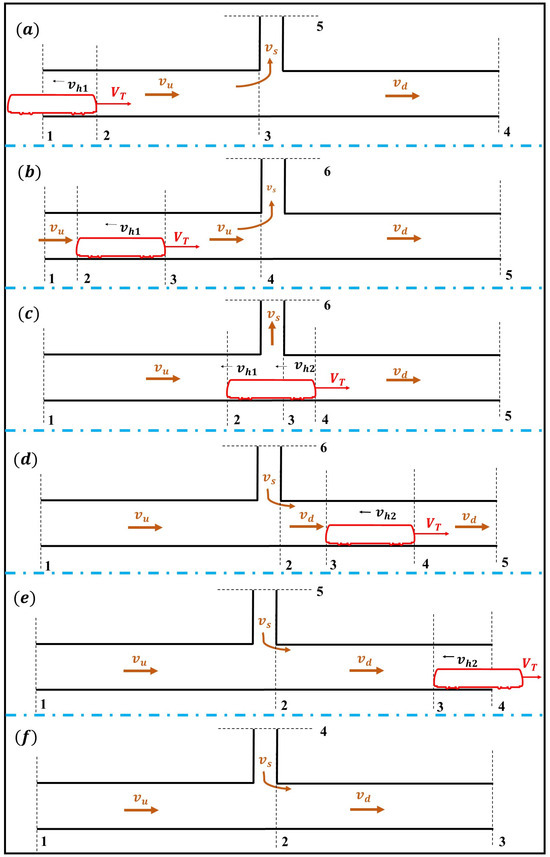
Figure 2. Typical moving patterns of the piston effect in PW-WVS mode (a) PPW-TET; (b) PPW-TCU; (c) PPW-TCS; (d) PPW-TCD; (e) PPW-TCL; (f) PPW-ATL.

2.2.2. PPW-TCU

$$\left\{\begin{array}{c}A{\displaystyle \frac{d{v}_u}{dt}}+l_{45}{\displaystyle \frac{d{v}_d}{dt}}=B{v_u}^2-{\displaystyle \frac{k_h}{2}}{v_d}^2+C{v}_u+D\\ {\displaystyle \frac{H_s}{\beta }}{\displaystyle \frac{d{v}_u}{dt}}+E{\displaystyle \frac{d{v}_d}{dt}}=-{\displaystyle \frac{k_s}{2{\beta }^2}}{v_u}^2+F{v_d}^2+{\displaystyle \frac{k_s}{{\beta }^2}}{v}_u{v}_d\end{array}\right. t\in \left[{\displaystyle \frac{L_T}{V_T}},{\displaystyle \frac{L_u}{V_T}}\right]$$

(11)

where $A={\displaystyle \frac{L_{\mathrm{T}}+\left(l_{12}+l_{34}\right)\left(1-\alpha \right)}{1-\alpha }}$, $B={\displaystyle \frac{k_h-k_u{\left(1-\alpha \right)}^2}{2{\left(1-\alpha \right)}^2}}$, $C=-{\displaystyle \frac{2k_h{V}_T}{2{\left(1-\alpha \right)}^2}},D={\displaystyle \frac{k_h{V}_T^2}{2{\left(1-\alpha \right)}^2}}, E=-{\displaystyle \frac{H_s+{\beta l}_{45}}{\beta }}$, $F={\displaystyle \frac{{\beta }^2{k}_d-k_s}{2{\beta }^2}}$, $k_u={\xi }_{in}+{\lambda }_L{\displaystyle \frac{l_{12}+l_{34}}{D_L}}$, $k_h={{\xi }_h}_{in}+{\lambda }_h{\displaystyle \frac{L_{\mathrm{T}}}{D_h}}+{{\xi }_h}_{out}$, $k_d={\xi }_{4-5}+{\lambda }_L{\displaystyle \frac{l_{45}}{D_L}}+{\xi }_{out}$, $k_s={\xi }_{4-6}+{\lambda }_s{\displaystyle \frac{H_s}{D_s}}+{{\xi }_s}_{out}$.

2.2.3. PPW-TCS

$$\left\{\begin{array}{c}A{\displaystyle \frac{d{v}_u}{dt}}+B{\displaystyle \frac{d{v}_d}{dt}}=C{v_u}^2+D{v_d}^2+E{v}_u+F{v}_d+G\\ M{\displaystyle \frac{d{v}_u}{dt}}-{\displaystyle \frac{H_s}{\beta }}{\displaystyle \frac{d{v}_d}{dt}}=N{v_u}^2-{\displaystyle \frac{k_s}{2{\beta }^2}}{v_d}^2+{\displaystyle \frac{k_s}{{\beta }^2}}{v}_u{v}_d+E{v}_u+Q\end{array}\right.t\in \left[{\displaystyle \frac{L_u}{V_T}},{\displaystyle \frac{L_u+L_T}{V_T}}\right]$$

(12)

where $A={\displaystyle \frac{l_{12}\left(1-\alpha \right)+l_{23}}{1-\alpha }}$, $B={\displaystyle \frac{l_{45}\left(1-\alpha \right)+l_{34}}{1-\alpha }}$, $C={\displaystyle \frac{k_{h1}-\left(1+k_u\right){\left(1-\alpha \right)}^2}{2{\left(1-\alpha \right)}^2}}$, $D={\displaystyle \frac{k_{h2}+\left(1-k_d\right){\left(1-\alpha \right)}^2}{2{\left(1-\alpha \right)}^2}}$, $E=-{\displaystyle \frac{{2k}_{h1}{V}_T}{2{\left(1-\alpha \right)}^2}}$, $F=-{\displaystyle \frac{{2k}_{h2}{V}_T}{2{\left(1-\alpha \right)}^2}}$, $G={\displaystyle \frac{\left(k_{h1}+k_{h2}\right)V_T^2}{2{\left(1-\alpha \right)}^2}},M={\displaystyle \frac{\left(l_{12}\beta +H_s\right)\left(1-\alpha \right)+l_{23}\beta }{\left(1-\alpha \right)\beta }}$, $N={\displaystyle \frac{{k_{h1}{\beta }^2-\left(1-\alpha \right)}^2\left({\beta }^2+k_u{\beta }^2+k_s\right)}{2{{\beta }^2\left(1-\alpha \right)}^2}}$, $Q={\displaystyle \frac{k_{h1}{V}_T^2}{2{\left(1-\alpha \right)}^2}}$, $k_u={\xi }_{in}+{\lambda }_L{\displaystyle \frac{l_{12}}{D_L}}$, $k_{h1}={\xi }_{3-2}+{\lambda }_h{\displaystyle \frac{l_{23}}{D_h}}+{{\xi }_h}_{out}$, $k_{h2}={{\xi }_h}_{in}+{\lambda }_h{\displaystyle \frac{l_{34}}{D_h}}$, $k_d={\lambda }_L{\displaystyle \frac{l_{45}}{D_L}}+{\xi }_{out}$, $k_s={\xi }_{3-6}+{\lambda }_s{\displaystyle \frac{H_s}{D_s}}+{{\xi }_s}_{out}$.

2.2.4. PPW-TCD

$$\left\{\begin{array}{c}{l}_{12}{\displaystyle \frac{d{v}_u}{dt}}+A{\displaystyle \frac{d{v}_d}{dt}}=-{\displaystyle \frac{k_u}{2}}{v_u}^2+B{v_d}^2+C{v}_d+D\\ E{\displaystyle \frac{d{v}_u}{dt}}-{\displaystyle \frac{H_s}{\beta }}{\displaystyle \frac{d{v}_d}{dt}}=F{v_u}^2+{\displaystyle \frac{k_s}{2{\beta }^2}}{v_d}^2-{\displaystyle \frac{k_s}{{\beta }^2}}{v}_u{v}_d\end{array}\right.t\in \left[{\displaystyle \frac{L_u+L_T}{V_T}},{\displaystyle \frac{L}{V_T}}\right]$$

(13)

where $A={\displaystyle \frac{L_{\mathrm{T}}+\left(l_{23}+l_{45}\right)\left(1-\alpha \right)}{1-\alpha }}$, $B={\displaystyle \frac{k_h-k_d{\left(1-\alpha \right)}^2}{2{\left(1-\alpha \right)}^2}}$, $C=-{\displaystyle \frac{2k_h{V}_T}{2{\left(1-\alpha \right)}^2}}$, $D={\displaystyle \frac{k_h{V}_T^2}{2{\left(1-\alpha \right)}^2}}$, $E={\displaystyle \frac{H_s+{\beta l}_{12}}{\beta }}$, $F={\displaystyle \frac{{k_s-\beta }^2{k}_u}{2{\beta }^2}}$, $k_u={\xi }_{in}+{\lambda }_L{\displaystyle \frac{l_{12}}{D_L}}+{\xi }_{1-2}$, $k_h={{\xi }_h}_{in}+{\lambda }_h{\displaystyle \frac{L_T}{D_h}}+{{\xi }_h}_{out}$, $k_d={\lambda }_L{\displaystyle \frac{l_{23}+l_{45}}{D_L}}+{\xi }_{out}$, $k_s={\xi }_{6-2}+{\lambda }_s{\displaystyle \frac{H_s}{D_s}}+{{\xi }_s}_{in}$.

2.2.5. PPW-TCL

$$\left\{\begin{array}{c}{l}_{12}{\displaystyle \frac{d{v}_u}{dt}}+A{\displaystyle \frac{d{v}_d}{dt}}=-{\displaystyle \frac{k_u}{2}}{v_u}^2+B{v_d}^2+C{v}_d+D\\ E{\displaystyle \frac{d{v}_u}{dt}}-{\displaystyle \frac{H_s}{\beta }}{\displaystyle \frac{d{v}_d}{dt}}=F{v_u}^2+{\displaystyle \frac{k_s}{2{\beta }^2}}{v_d}^2-{\displaystyle \frac{k_s}{{\beta }^2}}{v}_u{v}_d\end{array}\right.t\in \left[{\displaystyle \frac{L}{V_T}},{\displaystyle \frac{L+L_T}{V_T}}\right]$$

(14)

where $A={\displaystyle \frac{l_{34}+\left(l_{23}\right)\left(1-\alpha \right)}{1-\alpha }}$, $B={\displaystyle \frac{k_h-\left(1+k_d\right){\left(1-\alpha \right)}^2}{2{\left(1-\alpha \right)}^2}}$, $C=-{\displaystyle \frac{2k_h{V}_T}{2{\left(1-\alpha \right)}^2}}$, $D={\displaystyle \frac{k_h{V}_T^2}{2{\left(1-\alpha \right)}^2}}$, $E={\displaystyle \frac{H_s+{\beta l}_{12}}{\beta }}$, $F={\displaystyle \frac{k_s-{\beta }^2{k}_u}{2{\beta }^2}}$, $k_u={\xi }_{in}+{\lambda }_L{\displaystyle \frac{l_{12}}{D_L}}+{\xi }_{1-2}$, $k_h={{\xi }_h}_{in}+{\lambda }_h{\displaystyle \frac{L_T}{D_h}}+{{\xi }_h}_{out}$, $k_d={\lambda }_L{\displaystyle \frac{l_{23}}{D_L}}$, $k_s={\xi }_{5-2}+{\lambda }_s{\displaystyle \frac{H_s}{D_s}}+{{\xi }_s}_{in}$

2.2.6. PPW-ATL

$$\left\{\begin{array}{c}{l}_{12}{\displaystyle \frac{d{v}_u}{dt}}+l_{23}{\displaystyle \frac{d{v}_d}{dt}}=-{\displaystyle \frac{k_u}{2}}{v_u}^2-{\displaystyle \frac{k_d}{2}}{v_d}^2\\ A{\displaystyle \frac{d{v}_u}{dt}}-{\displaystyle \frac{H_s}{\beta }}{\displaystyle \frac{d{v}_d}{dt}}=B{v_u}^2+{\displaystyle \frac{k_s}{2{\beta }^2}}{v_d}^2-{\displaystyle \frac{k_s}{{\beta }^2}}{v}_u{v}_d\end{array}\right.t\in \left[{\displaystyle \frac{L_u+L_T}{V_T}},{\displaystyle \frac{L}{V_T}}\right]$$

(15)

where $A={\displaystyle \frac{H_s+{\beta l}_{12}}{\beta }}$, $B={\displaystyle \frac{k_s-{\beta }^2{k}_u}{2{\beta }^2}}$, $k_u={\xi }_{in}+{\lambda }_L{\displaystyle \frac{l_{12}}{D_L}}+{\xi }_{1-2}$, $k_d={\lambda }_L{\displaystyle \frac{l_{23}}{D_L}}+{\xi }_{out}$, $k_s={{\xi }_s}_{in}+{\lambda }_s{\displaystyle \frac{H_s}{D_s}}+{\xi }_{4-2}$.

2.3. PW-NVS

When there is no ventilation shaft, as shown in Figure 3, the moving patterns of the piston wind only include four processes: (1) the developing pattern where the train enters the tunnel, named PPW-TET; (2) the changing pattern where the train moves at a constant speed through the tunnel, known as PPW-TCT; (3) the changing pattern where the train leaves the tunnel, called PPW-TCL; and (4) the changing pattern where the train has left the tunnel, named PPW-ATL. The theoretical model of the piston wind in the tunnel without the ventilation shaft is listed in Table 2 [14].

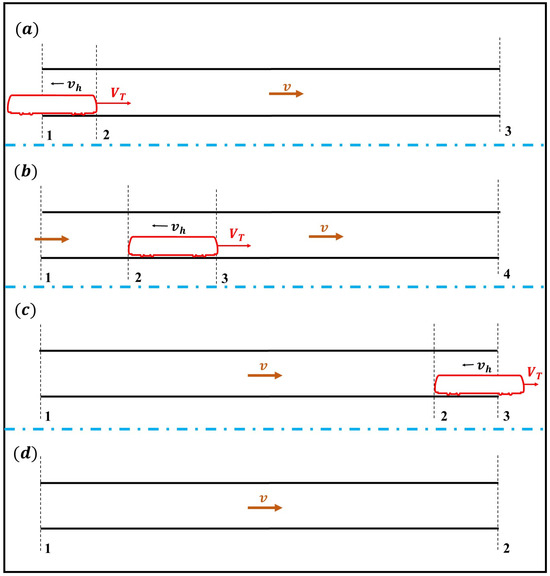
Figure 3. Schematic of the piston effect of a train traveling through a tunnel without ventilation shaft (a) PPW-TET, (b) PPW-TCT, (c) PPW-TCL, and (d) PPW-ATL.

Table 2. Theoretical model of the piston wind without ventilation shaft.

Governing Equation		$\frac{\mathit{d}\mathit{v}}{\mathit{d}\mathit{t}}=\mathit{A}+\mathit{B}\mathit{v}+\mathit{C}{\mathit{v}}^2$
Steps		PPW-TET	PPW-TCT	PPW-TCL	PPW-ATL
Time		$t\in \left[0,{\displaystyle \frac{L_T}{V_T}}\right]$	$t\in \left[{\displaystyle \frac{L_T}{V_T}},{\displaystyle \frac{L}{V_T}}\right]$	$t\in \left[{\displaystyle \frac{L}{V_T}},{\displaystyle \frac{L+L_T}{V_T}}\right]$	$t\in \left[{\displaystyle \frac{L+L_T}{V_T}},\infty \right]$
Equation parameters	A	${\displaystyle \frac{k_2{V}_T^2\left(1-\alpha \right)}{2\left[L\left(1-\alpha \right)+l_{12}\alpha \right]}}$	${\displaystyle \frac{k_2{V}_T^2\left(1-\alpha \right)}{2\left[\left(l_{12}+l_{34}\right)\left(1-\alpha \right)+L_T\right]}}$	${\displaystyle \frac{k_2{V}_T^2\left(1-\alpha \right)}{2\left[l_{12}\left(1-\alpha \right)+l_{23}\right]}}$	0
	B	${\displaystyle \frac{k_2{V}_T\left(1-\alpha \right)}{L\left(1-\alpha \right)+l_{12}\alpha }}$	$-{\displaystyle \frac{k_2{V}_T\left(1-\alpha \right)}{\left(l_{12}+l_{34}\right)\left(1-\alpha \right)+L_T}}$	$-{\displaystyle \frac{k_2{V}_T\left(1-\alpha \right)}{l_{12}\left(1-\alpha \right)+l_{23}}}$	0
	C	${\displaystyle \frac{k_2{V}_T\left(1-\alpha \right)}{L\left(1-\alpha \right)+l_{12}\alpha }}$	${\displaystyle \frac{\left(k_2-k_1\right)\left(1-\alpha \right)}{2\left[\left(l_{12}+l_{34}\right)\left(1-\alpha \right)+L_T\right]}}$	${\displaystyle \frac{\left(k_2-k_1\right)\left(1-\alpha \right)}{2\left[l_{12}\left(1-\alpha \right)+l_{23}\right]}}$	$k_1$
	$k_1$	${\xi }_{out}+{\lambda }_L{\displaystyle \frac{L-l_{12}}{D_L}}-1$	${\xi }_{in}+{\lambda }_L{\displaystyle \frac{l_{12}+l_{34}}{D_L}}+{\xi }_{out}$	${\xi }_{in}+{\lambda }_L{\displaystyle \frac{l_{12}}{D_L}}+1$	$-{\displaystyle \frac{{\xi }_{in}+{\lambda }_L\frac{L}{D_L}+{\xi }_{out}}{2L}}$
	$k_2$	${\displaystyle \frac{{{\xi }_h}_{in}+{\lambda }_h\frac{l_{12}}{D_h}+{{\xi }_h}_{out}}{{\left(1-\alpha \right)}^2}}$	${\displaystyle \frac{{{\xi }_h}_{in}+{\lambda }_h\frac{L_T}{D_h}+{{\xi }_h}_{out}}{{\left(1-\alpha \right)}^2}}$	${\displaystyle \frac{{{\xi }_h}_{in}+{\lambda }_h\frac{l_{23}}{D_h}+{{\xi }_h}_{out}}{{\left(1-\alpha \right)}^2}}$	0
Remark		$l_{12}=V_{T}t$	$l_{12}+l_{34}=L-L_T$	$l_{12}=V_{T}t-L_T$ $l_{23}=L+L_T-V_{T}t$	$/$

2.4. Validation

The validity and practicality of the theoretical model employed in this study have been corroborated by numerous scholarly sources [4,6,31]. Specifically, Zhang et al. [4] established this theoretical model for tunnels without ventilation shafts and performed numerical simulation analyses based on the experiments conducted by Kim et al. [13]. Their findings indicate that the computational results of the model are better than those of three-dimensional and two-dimensional numerical simulations. In our prior research [14], we not only developed but also validated the theoretical model concerning piston wind and examined the impact of various factors influencing the evolution of piston wind. The findings demonstrated that the theoretical results were in good agreement with the experimental results. In the current study, we employed the same methodology to construct a theoretical model of piston wind for metro tunnels both with and without a ventilation shaft. For tunnels equipped with a ventilation shaft, we further confirmed the model’s precision through three-dimensional numerical simulations.

The geometric model was constructed utilizing ICEM based on the dimensions of a typical tunnel, train, and shaft, as specified in Table 3. The numerical domain underwent discretization through structured meshes. To update the volume mesh, the dynamic layering method facilitated by the FLUENT code was implemented. The hexahedral grid features a length of 1 m in the x-direction, with a maximum dimension of 0.2 m in both y and z directions. Consequently, the aggregate mesh count surpasses 4.01 million. The duration of the unsteady simulation extended to 600 s, with a physical time step size set at 0.05 s. For further details on boundary conditions and solver settings used in the numerical simulation, refer to our prior studies [33,34].

Table 3. The detailed dimensions of a typical tunnel, train, and shaft.

Typical Tunnel			Typical Train				Typical Shaft
Length (m)	Width (m)	Height (m)	Length (m)	Width (m)	Height (m)	Speed (km/h)	Length (m)	Width (m)	Height (m)
4000	4.8	6.4	120	2.8	3.8	60	4	4	20

Figure 4 shows the comparison results of the theoretical model and numerical simulation calculation of the airflow velocity through the ventilation shaft. The results show that the theoretical results are in good agreement with the numerical simulation results. Drawing on the research by Zhang et al. [4], our prior studies [14], and the numerical simulations conducted herein, we can substantiate the precision and practicality of the theoretical model. Consequently, all subsequent analyses in this paper will rely exclusively on the outcomes derived from theoretical models.

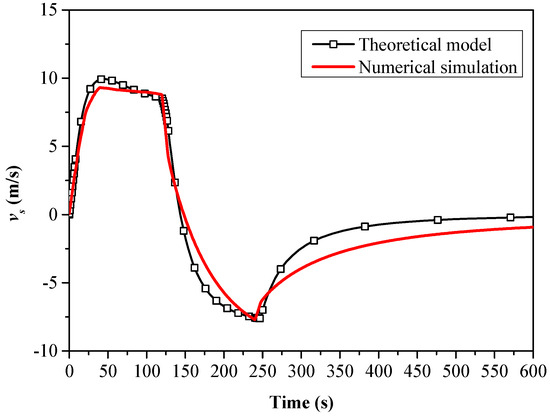
Figure 4. Comparisons between the theoretical model and numerical simulation results.

3. Results and Discussions

3.1. The Development Law of Piston Wind Speed

It is well known that piston wind is affected by many factors, including tunnel parameters [4], train parameters [14], and so on. Since the study at hand focuses on the influence caused by the presence of the ventilation shaft and its dimensions, other factors like the tunnel and train parameters remain unchanged. The influence of the tunnel and train parameters on the piston wind is referred to in our previous research [14]. For a typical tunnel, train, and shaft, the piston effects in full-size tunnels with a ventilation shaft (the shaft was located in the middle of the tunnel, i.e., $L_u=L_d$) are analyzed in detail. Detailed dimensions are shown in Table 3. The frictional resistance coefficient of airflow along the tunnel walls, the shaft walls, and the annular space is 0.02 [14]. Without specification, the following analysis is based on the values shown in Table 3.

3.1.1. PW-WVS

Figure 5a shows the development of the piston wind induced by the metro train in a tunnel with a ventilation shaft. $v_u$ and $v_d$ are the upstream and downstream piston wind speeds of the tunnel, respectively. The area enclosed by the curves in Figure 5a (marked as $Q_{T-in}$ and $Q_{T-out}$) represents the total air volume quantity flowing into (from the tunnel entrance) and out (from the tunnel exit) of the tunnel, respectively. Due to the presence of the ventilation shaft, the development of the piston wind upstream and downstream of the tunnel is significantly different. Both $v_u$ and $v_d$ increase as the train enters the tunnel and then continue to increase until the train is completely running inside. More concretely, $v_u$ increases at a faster rate and reaches its maximum value, $v_{u-max}$, when the train arrives at the shaft position. As the train is passing by the ventilation shaft, $v_u$ starts to decrease and $v_d$ continues to increase. Later, when the metro train travels to the downstream of the tunnel, $v_u$ continues to decrease. On the contrary, $v_d$ continues to increase to its peak value, i.e., $v_{d-max}$, and maintains this speed until the train leaves the tunnel. Both $v_u$ and $v_d$ begin to decrease once the train leaves and finally drop to the same value. The effect of shaft parameters on $v_u$ and $v_d$ will be discussed in Section 3.2.

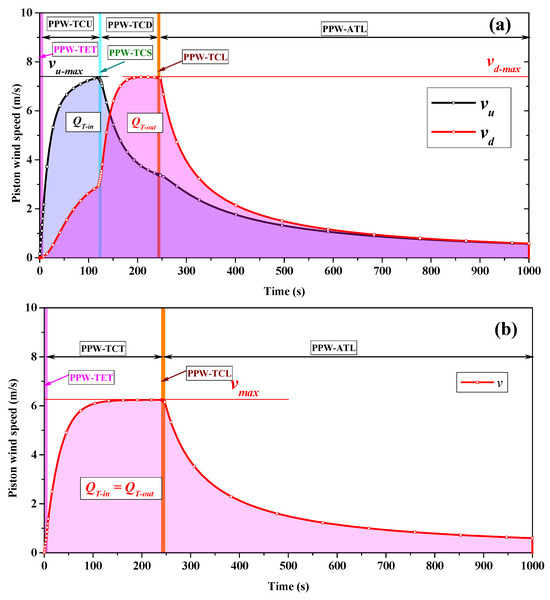
Figure 5. Development law for the piston wind (a) PW-WVS, (b) PW-NVS.

3.1.2. PW-NVS

Figure 5b shows the change in the piston wind speed induced by the metro train in a tunnel without ventilation shaft. When there is no ventilation shaft, the total amount of air flowing into and out of the tunnel is equal ($Q_{T-in}=Q_{T-out}$), as shown in the area enclosed by the curves in Figure 5b. As the train enters the tunnel, the piston wind speed begins to increase. Afterwards, the speed of the piston wind continues to increase until it approaches its peak value, $v_{max}$, and then remains steady until the metro train begins to leave. The piston wind speed begins to decrease as the metro train begins to leave the tunnel.

3.1.3. Comparison of PW-WVS and PW-NVS

A comparison of the piston wind speed in the two typical situations, namely PW-WVS and PW-NVS, is shown in Figure 6. It can be seen that the ventilation shaft has an obvious influence on the piston wind. Both the $v_{u-max}$ and $v_{d-max}$ are larger than the $v_{max}$ and increase by 18.0% and 18.2%, respectively. This is mainly because the drag of the parallel connection between the shaft and the $L_d$ section of the tunnel is generally smaller than that of the $L_d$ section of the tunnel itself. Similarly, the drag of the parallel connection between the shaft and the $L_u$ section of the tunnel is also smaller than that of the $L_u$ section of the tunnel itself.

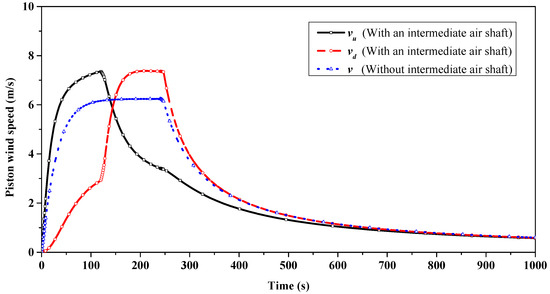
Figure 6. Comparison of piston wind speed development law with and without a ventilation shaft.

3.1.4. Development Law of Airflow in the Ventilation Shaft

Airflow velocity ($v_s$) changes in the PW-WVS mode, as shown in Figure 7. The positive value of $v_s$ indicates that the air flows out of the tunnel through the shaft while the negative value indicates that the air flows into the tunnel through the shaft. $Q_{S-in}$ and $Q_{S-out}$, respectively, represent the total amount of air flowing into and out of the tunnel through the shaft throughout the process. As the train enters the tunnel, $v_s$ begins to increase. When the train travels upstream of the tunnel, $v_s$ first increases to its maximum value, $v_{s-max}$, and then begins to decrease. As the train runs passing by the ventilation shaft, $v_s$ rapidly decreases. After that, the train travels downstream of the tunnel and $v_s$ first rapidly decreases to its minimum value, $v_{s-min}$, then starts to increase until the metro train leaves the tunnel. After the metro train has completely left the tunnel, $v_s$ continues to increase until it gradually approaches zero.

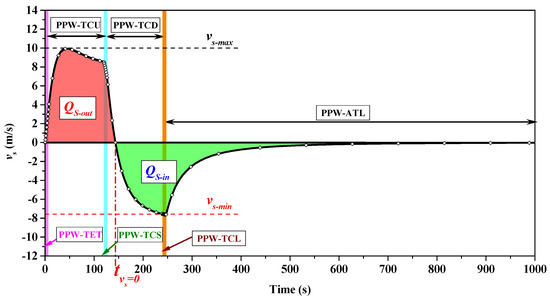
Figure 7. Development law of airflow in the ventilation shaft.

3.2. Influencing Factor

This section focuses on the influence of the shaft and its parameters on the piston wind, including the location of the shaft, the section area of the shaft, and the height of the shaft. Based on the proposed theoretical model, various influencing factors are analyzed.

3.2.1. Location of the Shaft

To characterize the influence of shafts at different locations on the piston wind, the shaft position parameter $\phi$ is proposed, which is defined as Equation (16):

$$\phi =L_u/L$$

(16)

According to the Chinese National Standard, GB 50157-2013 [3]: Code for the design of metro, the ventilation channel should be arranged at 1/2 of the interval tunnel. If it is practically hard, the ventilation channel can be equipped at somewhere no less than 1/3 of a distance to the tunnel portals and no less than 400 m to the station platform. Therefore, five different shaft positions (including $\phi =$ 0.25, 0.375, 0.5, 0.625, 0.75; corresponding distances from the tunnel entrance are 1000, 1500, 2000, 2500 and 3000 m) were selected to analyze their impact on the piston wind.

The effect of the shaft location on the piston wind in the upstream and downstream of the tunnel is shown in Figure 8a,b, respectively. The location of the shaft has a significant influence on $v_u$ and $v_d$. When the shaft is located at different positions, the maximum values of $v_u$ and $v_d$ are greater than the maximum piston wind speed in PW-NVS mode. As $\phi$ increases from 0.25 to 0.75 at intervals of 0.125, the $v_{u-max}$ increases by 25.1%, 21.9%, 18.0%, 13.6.0%, and 8.9% compared to the maximum piston wind speed in PW-NVS mode. Meanwhile, $v_{d-max}$ increases by 7.2%, 12.2%, 18.2%, 25.9%, and 35.9%. The $v_{u-max}$ decreases with the increase in $\phi$, and the $v_{d-max}$ increases with the increase in $\phi$. Their changes versus $\phi$ conform to the law of power functions, as shown in Figure 9a. A larger value of $\phi$ corresponds to a larger value of $L_u$ and a smaller value of $L_d$. The drag of the parallel connection between the shaft and the $L_d$ section of the tunnel is generally smaller than that of the $L_d$ section of the tunnel itself. Thus, if the value of $\phi$ is larger, then it usually leads to a smaller value for $v_{u-max}$. A larger value for $\phi$ then results in a larger value of $v_{d-max}$. As the metro tunnel usually contains the upper and lower lines, with each line running inside an individual tunnel, the ventilation shaft is generally shared by the two metro lines. Therefore, the ventilation shaft is practically reasonable in regard to installation in the middle of the tunnel, which is also consistent with the design code [3].

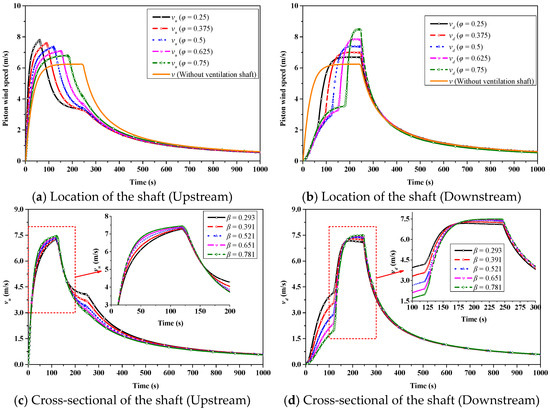
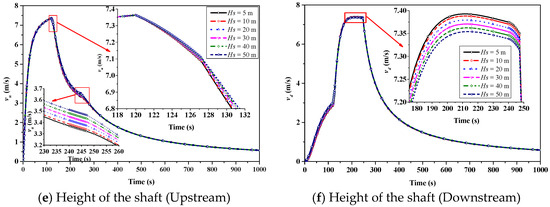
Figure 8. Effect on the piston wind under different influencing factors.

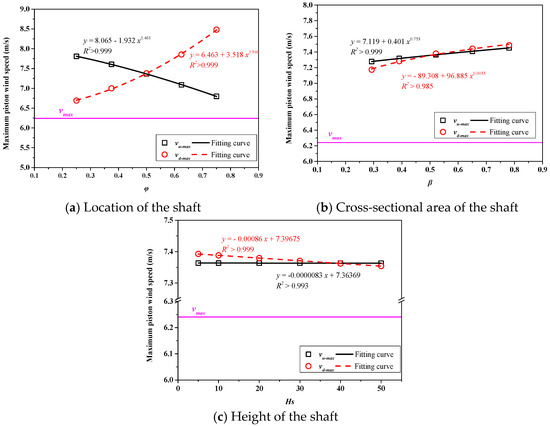
Figure 9. Effect on the maximum piston wind under different influencing factors.

The location of the ventilation shaft also affects the airflow in the shaft. Figure 10a shows the development of the airflow velocity in the ventilation shaft under different shaft positions. The varying trend of $v_s$ is similar when the shaft is located in different positions, but the maximum value and the minimum value are different. As $\phi$ increases, the maximal value of $v_s$ decreases, accompanied by a delay of its attenuation. This is mainly because a larger value for $\phi$ results in a longer traveling distance upstream of the tunnel. Both the $v_{s-max}$ and $v_{s-min}$ linearly decrease with the increase in $\phi$. The fitting formula is given in Figure 10b.

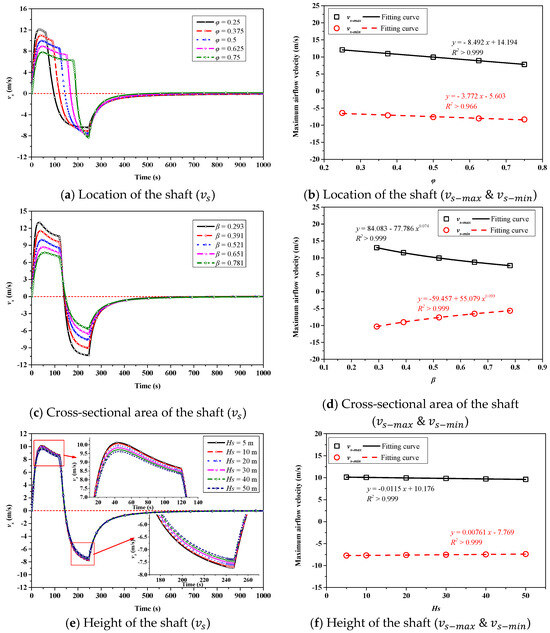
Figure 10. Effect on the airflow in the shaft under different influencing factors.

3.2.2. Cross-Sectional Area of the Shaft

Five different values of $A_s$ of between 9 and 24 m² (the corresponding $\beta$ are 0.293, 391, 0.521, 0.651, and 0.781, respectively) are selected to investigate the influence of the shaft cross-section on the piston wind. Results are shown in Figure 8c,d, respectively.

As shown in Figure 8c, as $\beta$ increases, $v_u$ firstly increases and then rapidly decreases when the train runs from the upstream to the downstream. Meanwhile, $v_d$ first slowly increases when the train runs through the upstream, and the so only increases when the train runs to the downstream, as shown in Figure 8d. After the train completely runs out of the tunnel, the attenuation rate of $v_u$ decreases with the increase in $\beta$, and the decay rate of $v_d$ is only slightly affected by $\beta$. The maximum piston wind speed, $v_{u-max}$, and $v_{d-max}$ all insignificantly increase as the cross-sectional area of the shaft increases. As $\beta$ increases from 0.293 to 0.781, the $v_{u-max}$ increases by 16.6%, 17.2%, 18.0%, 18.7.0%, and 19.4% compared to the maximum piston wind speed in PW-NVS mode. Meanwhile, $v_{d-max}$ increases by 14.9%, 16.7%, 18.2%, 19.3%, and 19.9%, respectively. The varying tendency of the $v_{u-max}$ and $v_{d-max}$ can be well captured with a power function with $\beta$. The fitting results are given in Figure 9b. As shown in Figure 9b, a larger value of $\beta$ corresponds to a larger value for the cross-sectional area of the shaft. As $\beta$ increases, the drag of the parallel passage formed by the shaft and the $L_d$ section of the tunnel is smaller, leading to the increase in the $v_{u-max}$. However, the increase in $\beta$ has little effect on the drag change, so the increase in the $v_{u-max}$ is not obvious, and the reason for the change in the $v_{d-max}$ is similar.

The cross-sectional area of the shaft has a significant influence on the airflow in the shaft, as shown in Figure 10c,d. As the cross-sectional area of the shaft increases, $v_s$ increases and decreases at a slower rate. The $v_{s-max}$ decreases with $\beta$ following the power function, while $v_{s-min}$ increases with $\beta$ in a power function. Fitting results are also given in Figure 10d. It is worth noting that the absolute values of the $v_{s-max}$ and $v_{s-min}$ decrease as $\beta$ increases. This is mainly due to the increase in shaft area, where a smaller air velocity can discharge (or draw in) a sufficient volume of air.

3.2.3. Height of the Shaft

In the following discussion, a shaft height varying between 5 and 50 m is applied while the other parameters of the shaft remain unchanged. Figure 8e,f show that shaft height has a negligible effect on the development of piston wind both in terms of the $v_u$ and $v_d$. Similarly, the impact on the $v_{u-max}$ and $v_{d-max}$ is also very small. The $v_{u-max}$ and $v_{d-max}$ slightly decrease with the increase in $H_s$, which can be almost ignored, as shown in Figure 9c. The main reason is that the drag of the shaft section increases as the shaft height increases, but such an increase is particularly small compared to the tunnel length, and the increase in the drag of the shaft section has little effect on the airflow in the entire tunnel. The stack effect of the shaft is not considered here, which may be another reason. Correspondingly, the airflow in the shaft is also slightly affected by the shaft height, as shown in Figure 10e,f. The absolute values of both the $v_{s-max}$ and $v_{s-min}$ linearly decrease as $H_s$ increases, and the fitting results are given in Figure 10f.

3.3. Ventilation Rate

The previous sections focus on the effect of shaft dimensions and locations on the piston wind speed. To analyze the cumulative effect of unstable airflow caused by trains, the concept of ventilation rate [4,6,31] is introduced. For a metro tunnel without a ventilation shaft, the ventilation rate can be expressed as Equation (17):

$$\eta ={\displaystyle \frac{{\int }_{t=0}^{t=t_t}v{A}_{L}dt}{A_{L}L}}$$

(17)

For the metro tunnel with a shaft investigated here, the ventilation rate can be defined as Equation (18):

$$\eta ={\displaystyle \frac{Q_{T-in}+Q_{s-in}}{A_{L}L+A_s{H}_s}}={\displaystyle \frac{Q_{T-out}+Q_{s-out}}{A_{L}L+A_s{H}_s}}$$

(18)

As shown in Figure 5a, $Q_{T-in}={\int }_{t=0}^{t=t_t}{v}_u{A}_{L}dt$ represents the total volume of air flowing into the tunnel from the entrance of the tunnel, and $Q_{T-out}={\int }_{t=0}^{t=t_t}{v}_d{A}_{L}dt$ represents the total volume of air flowing out of the tunnel from the tunnel exit. Correspondingly, $Q_{s-in}={\int }_{t={\left.t\right|}_{v_s=0}}^{t=t_t}{v}_s{A}_{s}dt$ represents the total volume of air flowing into the tunnel through the shaft, and $Q_{s-out}={\int }_{t=0}^{t={\left.t\right|}_{v_s=0}}{v}_s{A}_{s}dt$ represents the total volume of air flowing out of the tunnel through the shaft, as shown in Figure 7.

Figure 11 shows the ventilation rates with different ventilation shaft parameters, and the ventilation rate without shafts is also shown in the figure. The influence of the shaft location on the ventilation rate is shown in Figure 11a. The ventilation rate firstly increases and then decreases with the increase in $\phi$. As $\phi$ increases from 0.25 to 0.75 at intervals of 0.125, the ventilation rate increases by 10.4%, 11.2%, 11.3%, 10.2%, and 7.4% compared to the ventilation rate in PW-NVS mode. When the shaft is close to the middle of the tunnel, it is practically useful to increase the ventilation rate. A quadratic polynomial fitting is performed to quantify the effect of $\phi$ on the ventilation rate, as shown in Figure 11a. As shown in Figure 11b, the cross-sectional area of the shaft has a significant impact on the ventilation rate. As $\beta$ increases from 0.293 to 0.781, the ventilation rate increases by 8.8%, 10.1.2%, 11.3%, 12.1.0%, and 12.7% compared to the ventilation rate in PW-NVS mode. The relationship between the ventilation rate and $\beta$ can be well correlated by a power function, and the fitting results are given in Figure 11b. The analysis in Section 3.3 shows that the shaft height has little effect on the piston wind. Therefore, the ventilation rate shows a very faint difference with the increase in the shaft height, as shown in Figure 11c.

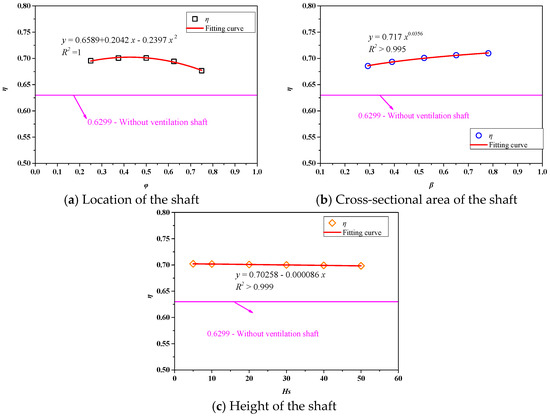
Figure 11. Effect on the ventilation rate under different influencing factors.

4. Conclusions

The Bernoulli equation of the unsteady flow was used to mathematically model the piston effect in a metro tunnel with and without a ventilation shaft. According to the established theoretical model, the influence of the shaft dimension and location on the piston wind and ventilation rate was analyzed. The following conclusions were obtained:

• The ventilation shaft has a significant impact on the piston wind. The maximum piston wind speed in a tunnel with a ventilation shaft is greater than the value in a tunnel without ventilation shaft. Similarly, the presence of a shaft increases the ventilation rate.
• The maximum stable piston wind speed, $v_{u-max},$ decreases with the increase in $\phi$, and $v_{d-max}$ increases with the increase in $\phi$. Changes in the $v_{u-max}$ and $v_{d-max}$ versus $\phi$ can be well represented by power functions. Meanwhile, as $\beta$ increases, the maximum piston wind speed ($v_{u-max}$ and $v_{d-max}$) increases following the power function law. However, the changes in the $v_{u-max}$ and $v_{d-max}$ are negligible with the increase in $H_s$.
• The airflow in the shaft is affected by the shaft location and the shaft cross-section, but shaft height has no obvious effect on it. Both the $v_{s-max}$ and $v_{s-min}$ linearly decrease with the increase in $\phi$. $v_{s-max}$ decreases with $\beta$ in power function, while the $v_{s-min}$ increases with $\beta$ following the power function.
• The location of the shaft and its cross-section have an obvious influence on the ventilation rate, but the influence of the height of the shaft is very small. The ventilation rate first increases and then decreases with the increase in φ. The varying trend in ventilation rates versus φ can be well represented by a quadratic function. Meanwhile, the attenuation of ventilation rates varies in the power function when $\beta$ increases.