Covert Surveillance Video Transmission with QAM Constellations Modulation

Abstract

This study explores the covert transmission of surveillance videos using QAM (quadrature amplitude modulation) constellations. By analyzing transmission strategies used in surveillance video systems, we adopt KL divergence as the constraint for covertness performance and mutual information to characterize transmission rates. Utilizing the Taylor series expansion method, we simplify the complex integral calculations of mutual information and KL divergence into summation operations. This simplification not only reduces computational complexity but also ensures precise calculations. Theoretical derivations establish the necessary conditions for the covert transmission of surveillance videos, optimizing modulation probabilities for constellation points. Experimental results and simulation validations demonstrate the superior performance of our proposed method in terms of both information transfer and precision.

1. Introduction

The widespread deployment of surveillance systems stands as a cornerstone for bolstering public safety, safeguarding property, and systematically monitoring diverse environments [1,2]. As the integration of these systems becomes increasingly pervasive, a paramount concern has emerged regarding the security of surveillance video transmissions, prompting the need for sophisticated and resilient solutions. Surveillance technologies, often shrouded in secrecy for operational efficiency [3], encounter distinct challenges, both in wired and wireless domains. Wired surveillance cameras, despite their discreet nature, are susceptible to exposure through the existence of signal lines [4]. On the other hand, the wireless transmission of surveillance videos confronts intricate challenges related to wireless signal detection and potential interruptions [5].

Considering the fact that the majority of existing video compression standards are tailored for relatively benign, nearly error-free environments, their direct applicability to hostile mobile domains, exemplified by standards such as H.265/HEVC (high-efficiency video coding) [6,7,8] and AV1 (AOMedia Video 1) [9,10], is limited. However, certain effective video compression methods, such as H.264/AVC, exhibit the capability of facilitating the transmission of multimedia services, even over channels with very low bit rates [11,12]. When coupled with advanced modulation schemes in wireless communication, such as Quadrature Amplitude Modulation, the allocation of more bits per transmitted symbol enhances overall transmission capacity [13].

As depicted in Figure 1a, the proposed 16−QAM phase constellation [14] showcases an intricate design strategy, leveraging the sophisticated maximum–minimum distance Gray code methodology presented in [15,16]. This innovative approach inherently gives rise to the establishment of two subchannels, each characterized by distinct integrities and tailored for specific functionalities within the communication system. The high-priority (HP) subchannel plays a pivotal role in the proposed constellation. It is uniquely characterized by the most significant bit (MSB) of both the in-phase (I) and quadrature-phase (Q) bits. This strategic allocation ensures that critical information is embedded in the most robust part of the signal, enhancing the resilience of the communication system to various environmental challenges. In stark contrast, the low-priority (LP) subchannel is formed by the remaining 2 bits of the 4-bit 16−QAM symbol; specifically, the least significant bits (LSBs). While inherently carrying less weight in terms of information content, the LP subchannel contributes to the overall versatility of the communication system by accommodating supplementary data and enhancing overall spectral efficiency. The transmission performance of both the HP and LP subchannels is intricately linked to channel conditions and noise characteristics, as highlighted in previous works [17,18,19]. The robustness and reliability of the communication system, particularly in scenarios with dynamic channel conditions, are contingent upon the optimization and adaptation of these subchannels. Expanding our exploration to the realm of 64−QAM, as illustrated in Figure 1b, the complexity of the phase constellation intensifies with the introduction of three subchannels: HP, medium priority (MP), and LP. This multifaceted design aims to strike a delicate balance between increasing transmission rates and ensuring reliability in the communication system [13]. The HP subchannel continues to serve as the backbone for critical information, while the introduction of the medium priority (MP) subchannel provides an additional tier for accommodating diverse data types, thereby enhancing the system’s adaptability to a variety of communication scenarios. In summary, the proposed phase constellations, whether 16−QAM or 64−QAM, represent a sophisticated amalgamation of innovative design principles, ensuring adaptability, reliability, and efficiency within the ever-evolving landscape of communication systems.

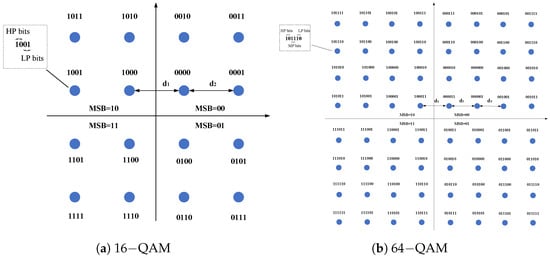
Figure 1. Some QAM constellation sets adopted in surveillance video transmission.

While ensuring the transmission reliability of surveillance systems, the security of the surveillance systems should also be well considered. Besides preventing information content from being eavesdropped, we can even hide the existence of the information transmission process. Both conventional encryption and physical-layer security techniques aim to prevent transmission content from being eavesdropped [20,21]. To enhance the security of wireless surveillance systems, covert communication technologies have attracted substantial attention. Covert communication aims not only to protect the content of surveillance transmission but also hide the very existence of the surveillance transmission. Within the realm of covert communication, the paramount objective extends beyond securing the content of communication from adversarial interception: the imperative to hide the very occurrence of communication activities from potential adversaries is equally crucial to ensure the covertness of these operations [22].

In previous works, covert communication has been a focal point for governmental and military entities aiming to regulate the activities of specific organizations or conceal the intentions of operations within defined geographical areas [23,24]. Early wireless covert channels were predominantly explored through spread spectrum techniques [25]. However, the foundational limits of covert communication within the realm of information theory remained largely unexplored until the investigation of the square root law (SRL) within channels affected by additive white Gaussian noise (AWGN) [26]. Subsequently, the SRL was extended to diverse communication systems, including binary symmetric channels [27,28], discrete memoryless channels [29,30], and multiple access channels [31,32]. It is noteworthy that the SRL posits that if more than $\mathcal{O}\left(\sqrt{n}\right)$ bits are transmitted through n channels, then as n approaches infinity, there is a high probability of the transmitter being detected or the receiver incurring a nonzero probability of decoding error [22]. Furthermore, the covert rate approaches zero as n grows to infinity, i.e., ${lim}_{n\to \infty }\frac{\mathcal{O}\left(\sqrt{n}\right)}{n}=0$. This finding has spurred researchers to investigate methods for achieving positive covert rates [33]. Various strategies have been proposed to attain positive covert rates, including utilizing uniformed jammers [34], introducing noise uncertainty to adversaries, enlisting external friendly helpers, and manipulating the timing of covert communications [24]. However, sustaining the functionality of these energy-intensive communication devices poses a challenge, especially in unsafe environments or complex, sensitive areas that are challenging to access. The presence of communication devices or conspicuous electricity consumption may attract the attention of adversaries, underscoring the intricacies of maintaining covert operations in such contexts [35].

To covertly transmit surveillance videos to a designated recipient, the overall process encompasses the following procedural steps. Surveillance cameras capture monitoring data to generate surveillance videos. Subsequently, these videos are subjected to compression using an appropriate protocol, such as H.264/AVC. The compressed surveillance videos then undergo a covert transmission phase, comprising three steps: (1) adopting an appropriate encoding method, such as 16−QAM, 64−QAM, or 256−QAM, based on channel conditions; (2) configuring suitable transmission power for the covert transmission of the surveillance videos; (3) the receiver decoding the videos according to the selected encoding method. Diverging from the Gaussian codebooks that are prevalent in many theoretical covert communication studies [22,23,33], we adopt QAM codebooks that are commonly employed in video transmission to explore the theoretical bounds of covert transmission. In [36], the authors analyzed the covert transmission performance of phase-shift keying modulation in intelligent reflection surface systems; however, the covertness performance of QAM has not yet been investigated. In this work, we aim to investigate the performance of covert surveillance video transmission with QAM modulation. Leveraging the Taylor series expansion theory, we systematically conduct a comprehensive analysis, encompassing both transmission rates and covert aspects. Our investigation yields theoretical insights into facilitating the derivation of the necessary conditions governing the optimal modulation probability of constellation points under QAM modulation. Following this theoretical groundwork, we conduct a series of experimental simulations to rigorously validate our derived conclusions. Remarkably, our approach demonstrates a commendable performance, exhibiting superior transmission rates and enhanced covertness compared to existing methodologies. This success underscores the efficacy of our optimized strategy in the covert transmission of surveillance videos.

The rest of this paper is organized as follows: Section 2 introduces the surveillance video transmission scheme at the transmitter and receiver, as well as the hypothesis test of covert surveillance video transmission at an adversary, and an optimization problem of constellation transmission probability and amplitude gain is also formulated, aiming to maximize the transmission rate; Section 3.1 analyzes the transmission rates of surveillance videos; Section 3.2 and Section 3.3 present the covertness performance of the surveillance video transmission and the theorem of the optimal conditions of QAM modulation; Section 4 provides the experiments and analysis to verify the performance of our research; Section 5 concludes the paper.

2. Transmission Scheme and Hypothesis Test

2.1. Transmission Scheme

Hierarchical modulations are initially proposed to provide different classes of data for users under different wireless signal reception conditions [37,38]. In Figure 1a,b, 16−QAM and 64−QAM square constellations are provided. In the 16−QAM square constellation, the distance of each constellation point from the boundary of its decision region for the two most significant bits (MSBs) is either “1” or “3” [15]. The 16−QAM coordinates sequence is given as

$$\begin{array}{c}{\mathbf{d}}_{16-QAM}=\left[\begin{array}{cccc}-3& -1& 1& 3\end{array}\right],\hfill \end{array}$$

(1)

and the coordinates of the constellation points of the in-phase (I) and quadrature-phase (Q) bits are selected from that sequence. In conventional coding schemes, constellation points are selected with equal probability [13]. In this work, we optimize the modulation probability of the constellation points. Furthermore, we can provide the general form of the coordinate sequence for QAM as

$$\begin{array}{c}\mathbf{d}=\left[\begin{array}{ccccc}-N+1& -N+3& \cdots & N-3& N-1\end{array}\right]\hfill \end{array}$$

(2)

and the value of the i-th symbol is given by

$$\begin{array}{c}\mathbf{d}\left[i\right]=-N+2i-1,\hfill \end{array}$$

(3)

where N is the number of in-phase (I) and quadrature-phase (Q) coordinate value sets of constellation points. Specifically, when employing 16−QAM, the parameter N is 4; meanwhile, when utilizing 64−QAM, the parameter N is 8. Commonly recognized signal modulation techniques encompass four distinct QAM constellations: 4−QAM (N = 2), 16−QAM (N = 4), 64−QAM (N = 8), and 256−QAM (N = 16).

Assuming that the transmission probability of the constellation point in row j and column k is $p_{j,k}$, the probability density function at the receiver can be expressed as

$$\begin{array}{c}{P}_b=\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k}·q_{j,k,b}(x,y),\hfill \end{array}$$

(4)

where

$$\begin{array}{c}{q}_{j,k,b}(x,y)=\frac{1}{2\pi {\sigma }_b^2}\left[exp\left(-\frac{{(x+g_b\mathbf{d}\left[j\right]\beta )}^2}{2{\sigma }_b^2}-\frac{{(y+g_b\mathbf{d}\left[k\right]\beta )}^2}{2{\sigma }_b^2}\right)\right],\hfill \end{array}$$

(5)

and $g_b$ denotes the channel gain coefficient, ${\sigma }_b$ is the one-sided noise spectral density of the additive white Gaussian noise [15], and $\beta$ denotes the amplitude gain of the transmitted symbols.

When the encoded surveillance videos are transmitted through AWGN channels, they are susceptible to being corrupted by Gaussian noise. In Figure 2, the blue constellation points represent the original constellation, while the red constellation points depict the constellation points that are corrupted by noise.

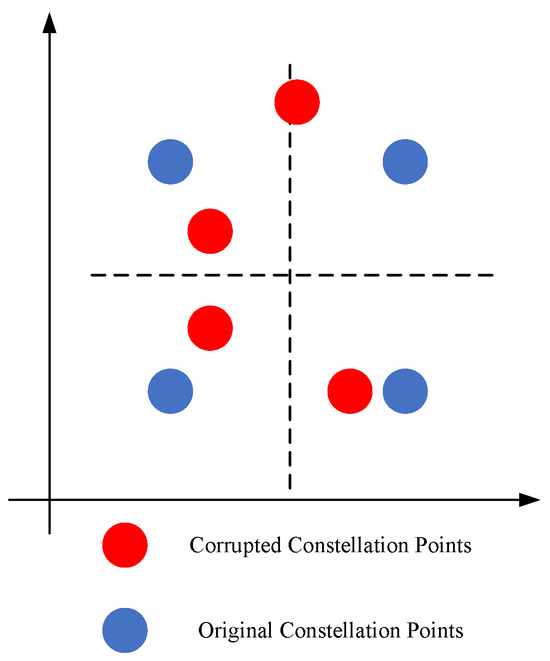
Figure 2. Constellation points corrupted by AWGN channels.

Assuming a surveillance video is transmitted with n symbols, the transmission rate can be measured with mutual information, which is given by

$$\begin{array}{cc}{R}_b\hfill & =\mathbb{I}(Z_b^n;X^n),\hfill \end{array}$$

(6)

where $Z_b$ denotes the symbols received by the receiver and X denotes the symbols sent by the transmitter.

2.2. Hypothesis Test

To determine whether a surveillance video is transmitted, the adversary performs a binary hypothesis test [22] based on n successive observations ${\mathbf{Z}}_w^n=[{\mathbf{Z}}_{w,1},\cdots ,{\mathbf{Z}}_{w,n}]\in {\mathbb{R}}^{K\times n}$. Let ${\mathcal{H}}_0$ denote the null hypothesis and ${\mathcal{H}}_1$ denote the alternative hypothesis. Then, the total detection error probability of the adversary is defined as [39,40,41]

$$\begin{array}{c}\mathrm{Pr}\left(D_1\right|{\mathcal{H}}_0)+\mathrm{Pr}\left(D_0\right|{\mathcal{H}}_1)=1-\mathbb{V}(Q_{1,w}^n\parallel Q_{0,w}^n),\hfill \end{array}$$

(7)

where $\mathrm{Pr}\left(D_1\right|{\mathcal{H}}_0)$ denotes the probability of a false alarm (i.e., rejecting ${\mathcal{H}}_0$ when it is true) and $\mathrm{Pr}\left(D_0\right|{\mathcal{H}}_1)$ denotes the probability of a missed detection (i.e., accepting ${\mathcal{H}}_0$ when it is false). Moreover, $Q_{1,w}^n$ and $Q_{0,w}^n$ denote the likelihood functions of ${\mathbf{Z}}_w^n$ under ${\mathcal{H}}_0$ and ${\mathcal{H}}_1$, while $\mathbb{V}(Q_{1,w}^n\parallel Q_{0,w}^n)$ denotes the total variation distance between $Q_{1,w}^n$ and $Q_{0,w}^n$.

Similar to Equation (4), the probability density functions of $Q_{1,w}^n$ and $Q_{0,w}^n$ at the adversary can be expressed as

$$\begin{array}{c}{Q}_{0,w}=\frac{1}{2\pi {\sigma }_w^2}\left[exp\left(-\frac{x^2+y^2}{2{\sigma }_w^2}\right)\right],\hfill \end{array}$$

(8)

and

$$\begin{array}{c}{Q}_{1,w}=\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k}·q_{j,k,w}(x,y),\hfill \end{array}$$

(9)

where

$$\begin{array}{c}{q}_{j,k,w}(x,y)=\frac{1}{2\pi {\sigma }_w^2}\left[exp\left(-\frac{{(x+g_w\mathbf{d}\left[j\right]\beta )}^2}{2{\sigma }_w^2}-\frac{{(y+g_w\mathbf{d}\left[k\right]\beta )}^2}{2{\sigma }_w^2}\right)\right].\hfill \end{array}$$

(10)

Based on the Pinsker inequality [22,29,42], we can obtain the upper bound of total variation

$$\begin{array}{cc}\mathbb{V}(Q_{1,w}^n\parallel Q_{0,w}^n)\hfill & \le \sqrt{\frac{1}{2}\mathcal{D}(Q_{1,w}^n\parallel Q_{0,w}^n)},\hfill \end{array}$$

(11)

where $\mathcal{D}(Q_{1,w}^n\parallel Q_{0,w}^n)$ is the KL divergence between $Q_{1,w}^n$ and $Q_{0,w}^n$. Let

$$\begin{array}{c}\mathbb{V}(Q_{1,w}^n\parallel Q_{0,w}^n)\le ϵ,\hfill \end{array}$$

(12)

where $ϵ\in [0,1]$ denotes the covertness parameter. With some transformation, the covertness constraint can be expressed as

$$\begin{array}{c}\mathcal{D}(Q_{1,w}^n\parallel Q_{0,w}^n)\le 2{ϵ}^2.\hfill \end{array}$$

(13)

3. Performance Analysis of Covert Surveillance Video Transmission

In previous works [40,43], the performance metrics of covert transmission, i.e., KL divergence and mutual information, have been approximated using intricate integration calculations or less stringent constraints. As depicted in Figure 3, in this section, we introduce a precise approximation method based on the Taylor series expansion theory. This method transforms intricate integration computations into straightforward summations, thereby reducing computational complexity while ensuring the accuracy of results.

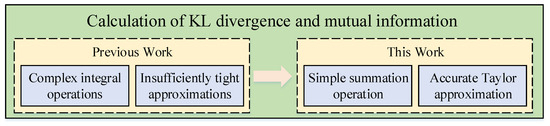
Figure 3. Comparison between previous methods and our proposed covert surveillance video transmission performance analysis method.

3.1. Analysis of Transmission Rates

When a surveillance video is transmitted with QAM modulation, the transmission rate can be measured with mutual information. Recalling the probability density function given in (4), the mutual information can be expressed as

$$\begin{array}{ccc}\hfill & R_b\hfill & =n\mathrm{H}\left(Z_b\right)-n\mathrm{H}\left(Z_b\right|X)\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & =-n\int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,b}(x,y)log\left[\frac{{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}{q}_{j,k,b}(x,y)}{q_{t,s,b}(x,y)}\right]\mathrm{d}x\mathrm{d}y.\hfill \end{array}$$

(15)

Now, we define

$$\begin{array}{cc}\mathbf{F}\left(\beta \right)\hfill & \triangleq log\left[\frac{{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}{q}_{j,k,b}(x,y)}{q_{t,s,b}(x,y)}\right]\hfill \end{array}$$

(16)

$$\begin{array}{c}\triangleq log\left[\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k}exp\left(G_{j,k}\left(\beta \right)\right)\right],\hfill \end{array}$$

(17)

where

$$\begin{array}{cc}{G}_{j,k}\hfill & \triangleq -\frac{2x\beta g_b(\mathbf{d}\left[j\right]-\mathbf{d}\left[t\right])+2y\beta g_b(\mathbf{d}\left[k\right]-\mathbf{d}\left[s\right])}{2{\sigma }_b^2}\hfill \end{array}$$

$$\begin{array}{cc}& -\frac{{\beta }^2{g}_b^2(\mathbf{d}{\left[j\right]}^2-\mathbf{d}{\left[t\right]}^2+\mathbf{d}{\left[k\right]}^2-\mathbf{d}{\left[s\right]}^2)}{2{\sigma }_b^2}.\hfill \end{array}$$

(18)

Taking the derivative of $G_{j,k}$ with respect to $\beta$ and setting $\beta$ to 0, we can obtain

$$\begin{array}{ccc}\hfill & G_{j,k}\left(0\right)\hfill & =0,\hfill \end{array}$$

(19)

$$\begin{array}{cc}{G_{j,k}}^{\prime }\left(0\right)\hfill & =-\frac{x{g}_b(\mathbf{d}\left[j\right]-\mathbf{d}\left[t\right])+y{g}_b(\mathbf{d}\left[k\right]-\mathbf{d}\left[s\right])}{{\sigma }_b^2},\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill & {G_{j,k}}^{″}\left(0\right)\hfill & =-\frac{{g_b}^2(\mathbf{d}{\left[j\right]}^2-\mathbf{d}{\left[t\right]}^2+\mathbf{d}{\left[k\right]}^2-\mathbf{d}{\left[s\right]}^2)}{{\sigma }_b^2}.\hfill \end{array}$$

(21)

Taking the derivative of $\mathbf{F}\left(\beta \right)$ and setting $\beta$ to 0, we can obtain

$$\begin{array}{cc}{\mathbf{F}}^{\prime }\left(0\right)\hfill & =\sum _{j=1}^N\sum _{k=1}^N\left[p_{j,k}{G_{j,k}}^{\prime }\left(0\right)\right],\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill & {\mathbf{F}}^{″}\left(0\right)\hfill & =-{\left[\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k}{G_{j,k}}^{\prime }\left(0\right)\right]}^2+\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k}\left[{\left({G_{j,k}}^{\prime }\left(0\right)\right)}^2+{G_{j,k}}^{″}\left(0\right)\right].\hfill \end{array}$$

(23)

Using the Taylor series expansion, when $\beta \to 0$, we have

$$\begin{array}{cc}\hfill & \int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,b}(x,y)log\left[\frac{{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}{q}_{j,k,b}(x,y)}{q_{t,s,b}(x,y)}\right]\mathrm{d}x\mathrm{d}y\hfill \\ \hfill & =\int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,b}(x,y)\left[\beta {\mathbf{F}}^{\prime }\left(0\right)+\frac{{\beta }^2}{2}{\mathbf{F}}^{″}\left(0\right)+\mathcal{O}\left({\beta }^3\right)\right]\mathrm{d}x\mathrm{d}y.\hfill \end{array}$$

(24)

Then, we can obtain

$$\begin{array}{cc}\hfill & \int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,b}(x,y)\left[\beta {\mathbf{F}}^{\prime }\left(0\right)\right]\mathrm{d}x\mathrm{d}y\hfill \\ \hfill & ={\beta }^2{g_b}^2\frac{{\sum }_{t=1}^N{\sum }_{s=1}^N{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}{p}_{t,s}\left(\mathbf{d}\left[j\right]\mathbf{d}\left[t\right]+\mathbf{d}\left[k\right]\mathbf{d}\left[s\right]-\mathbf{d}{\left[t\right]}^2-\mathbf{d}{\left[s\right]}^2\right)}{{\sigma }_b^2},\hfill \end{array}$$

(25)

and

$$\begin{array}{cc}\hfill & \int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,b}(x,y)\left[\frac{{\beta }^2}{2}{\mathbf{F}}^{″}\left(0\right)\right]\mathrm{d}x\mathrm{d}y\hfill \\ \hfill & ={\beta }^2{g_b}^2\frac{{\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\left(\mathbf{d}{\left[t\right]}^2+\mathbf{d}{\left[s\right]}^2\right)}{2{\sigma }_b^2}\hfill \\ \hfill & -{\beta }^2{g_b}^2\frac{{\left({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}{p}_{j,k}\mathbf{d}\left[t\right]\right)}^2+{\left({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\mathbf{d}\left[s\right]\right)}^2}{2{\sigma }_b^2}.\hfill \end{array}$$

(26)

Combining (15), (23), (25), and (26), the covert transmission rate of a surveillance video can be expressed as

$$\begin{array}{cc}\mathbb{I}(Z_b^n;X^n)\hfill & =n{\beta }^2{g_b}^2\frac{{\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\left(\mathbf{d}{\left[t\right]}^2+\mathbf{d}{\left[s\right]}^2\right)}{2{\sigma }_b^2}\hfill \\ \hfill & -n{\beta }^2{g_b}^2\frac{{\left({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\mathbf{d}\left[t\right]\right)}^2+{\left({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\mathbf{d}\left[s\right]\right)}^2}{2{\sigma }_b^2}.\hfill \end{array}$$

(27)

3.2. Analysis of Covertness Performance

In Equation (13), we measure the covertness performance with KL divergence. For any QAM modulation, the KL divergence can be expressed as

$$\begin{array}{c}\mathcal{D}(Q_{1,w}^n\parallel Q_{0,w}^n)=n\mathcal{D}(Q_{1,w}\parallel Q_{0,w}).\hfill \end{array}$$

(28)

Then, we have

$$\begin{array}{cc}\mathcal{D}(Q_{1,w}\parallel Q_{0,w})\hfill & =\int \int Q_{1,w}(x,y)log\frac{Q_{1,w}(x,y)}{Q_{0,w}(x,y)}\mathrm{d}x\mathrm{d}y\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & =\int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,w}(x,y)log\frac{{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}{q}_{j,k,w}(x,y)}{q_0(x,y)}\mathrm{d}x\mathrm{d}y,\hfill \end{array}$$

(30)

where

$$\begin{array}{cc}{q}_{j,k,w}(x,y)\hfill & =\frac{1}{2\pi {\sigma }_w^2}\left[exp\left(-\frac{{(x+g_w\mathbf{d}\left[j\right]\beta )}^2}{2{\sigma }_w^2}-\frac{{(y+g_w\mathbf{d}\left[k\right]\beta )}^2}{2{\sigma }_w^2}\right)\right],\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill & q_0(x,y)\hfill & =\frac{1}{2\pi {\sigma }_w^2}\left[exp\left(-\frac{x^2+y^2}{2{\sigma }_w^2}\right)\right].\hfill \end{array}$$

(32)

For ease of notation, we define the functions as

$$\begin{array}{cc}\mathbf{T}\left(\beta \right)\hfill & \triangleq log\left[\frac{{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k,w}{q}_{j,k,w}(x,y)}{q_0(x,y)}\right]\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & \triangleq log\left[\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k,w}exp\left(K_{j,k}\left(\beta \right)\right)\right],\hfill \end{array}$$

(34)

where

$$\begin{array}{cc}{K}_{j,k}\hfill & \triangleq -\frac{2x\mathbf{d}\left[j\right]g_w\beta +2y\mathbf{d}\left[k\right]g_w\beta +{\beta }^2{g_w}^2(\mathbf{d}{\left[j\right]}^2+\mathbf{d}{\left[k\right]}^2)}{2{\sigma }_w^2}.\hfill \end{array}$$

(35)

Differentiating with respect to $\beta$ in the function $g\left(\beta \right)$, we can obtain

$$\begin{array}{cc}{\mathbf{T}}^{\prime }\left(\beta \right)\hfill & =\frac{1}{{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k,w}exp\left(K_{j,k}\right)}\sum _{i=1}^N\left[p_{j,k}exp\left(K_{j,k}\right){K_{j,k}}^{\prime }\right],\hfill \\ {\mathbf{T}}^{″}\left(\beta \right)\hfill & =-\frac{1}{{\left[{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k,w}exp\left(K_{j,k}\right)\right]}^2}{\left[\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k,w}exp\left(K_{j,k}\right){K_{j,k}}^{\prime }\right]}^2\hfill \end{array}$$

(36)

$$\begin{array}{c}+\frac{1}{{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k,w}exp\left(K_{j,k}\right)}\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k,w}exp\left(K_{j,k}\right)\left[{\left({K_{j,k}}^{\prime }\right)}^2+{K_{j,k}}^{″}\right].\hfill \end{array}$$

(37)

Given the constraints imposed by space limitations, the nuanced expressions for ${K_{j,k}}^{‴}\left(\beta \right)$ and ${\mathbf{T}}^{⁗}\left(\beta \right)$ concerning the derivative with respect to $\beta$ are regrettably omitted.

Consequently, we proceed to derive the expressions for ${\mathbf{T}}^{\prime }\left(0\right)$, ${\mathbf{T}}^{″}\left(0\right)$, ${\mathbf{T}}^{‴}\left(0\right)$, and ${\mathbf{T}}^{⁗}\left(0\right)$. Leveraging the Taylor series expansion, we arrive at

$$\begin{array}{c}\mathcal{D}(Q_{1,w}\parallel Q_{0,w})\hfill \\ =\int \int Q_{1,w}(x,y)log\frac{Q_{1,w}(x,y)}{Q_{0,w}(x,y)}\mathrm{d}x\mathrm{d}y\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & =\int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,w}(x,y)\left[\beta {\mathbf{T}}^{\prime }\left(0\right)+\frac{{\beta }^2}{2!}{\mathbf{T}}^{″}\left(0\right)+\frac{{\beta }^3}{3!}{\mathbf{T}}^{‴}\left(0\right)+\frac{{\beta }^4}{4!}{\mathbf{T}}^{⁗}\left(0\right)\right]\mathrm{d}x\mathrm{d}y.\hfill \end{array}$$

(39)

Based on (39), we can calculate the first and second terms, which are given by

$$\begin{array}{cc}\hfill & \int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,w}(x,y)\left[\beta {\mathbf{T}}^{\prime }\left(0\right)\right]\mathrm{d}x\mathrm{d}y\hfill \\ \hfill & ={\beta }^2{g_w}^2\left(\frac{{\sum }_{t=1}^N{\sum }_{s=1}^N{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}{p}_{t,s}\mathbf{d}\left[j\right]\mathbf{d}\left[t\right]+\mathbf{d}\left[k\right]\mathbf{d}\left[s\right]}{{\sigma }_w^2}\right),\hfill \end{array}$$

(40)

and

$$\begin{array}{c}\int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,w}(x,y)\left[\frac{{\beta }^2}{2}{\mathbf{T}}^{″}\left(0\right)\right]\mathrm{d}x\mathrm{d}y\hfill \\ =-\frac{{\beta }^2{g_w}^2}{2}\left(\frac{{\sum }_{t=1}^N{\sum }_{s=1}^N{\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}{p}_{t,s}\left(\mathbf{d}\left[j\right]\mathbf{d}\left[t\right]+\mathbf{d}\left[k\right]\mathbf{d}\left[s\right]\right)}{{\sigma }_w^2}\right)\hfill \\ +\frac{{\beta }^4{g_w}^4}{2{\sigma }_w^4}\left(\sum _{t=1}^N\sum _{s=1}^N\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k}{p}_{t,s}\left(\mathbf{d}{\left[j\right]}^2\mathbf{d}{\left[t\right]}^2+\mathbf{d}{\left[k\right]}^2\mathbf{d}{\left[s\right]}^2+2\mathbf{d}\left[t\right]\mathbf{d}\left[s\right]\mathbf{d}\left[j\right]\mathbf{d}\left[k\right]\right)\right).\hfill \end{array}$$

(41)

Then, we consider two cases.

(a) Case 1: If we have ${\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}\mathbf{d}\left[j\right]\ne 0$ and ${\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}\mathbf{d}\left[k\right]\ne 0$, the KL divergence can be expressed as

$$\begin{array}{c}\mathcal{D}(P_{1,w}^n\parallel P_{0,w}^n)=\frac{n{g}_w^2}{2{\sigma }_w^2}\left[{\left(\sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}\mathbf{d}\left[t\right]{)}^2+(\sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}\mathbf{d}\left[s\right]\right)}^2\right]{\beta }^2=\mathcal{O}\left({\beta }^2\right),\hfill \end{array}$$

(42)

and the transmission rate is given by

$$\begin{array}{c}\tilde{\mathbb{I}}({\mathbf{Z}}_b^n;{\mathbf{D}}^n)\hfill \\ =\frac{ϵg_b^2{\sigma }_w^2[{\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\left(\mathbf{d}{\left[t\right]}^2+\mathbf{d}{\left[s\right]}^2\right)-({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}{\mathbf{d}\left[t\right])}^2-\left({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}{\mathbf{d}\left[s\right])}^2\right]}{g_w^2{\sigma }_b^2\left[{\left({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\mathbf{d}\left[t\right]{)}^2+({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\mathbf{d}\left[s\right]\right)}^2\right]}\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & =\mathcal{O}\left(1\right).\hfill \end{array}$$

(44)

It is imperative to emphasize that the mutual information is represented as $\mathcal{O}\left(1\right)$, indicating a fixed value that remains invariant with changes in encoding length. This produces an exceptionally low covert signal transmission rate, typically in the order of $\mathcal{O}\left(n\right)$ in traditional signal transmission scenarios. It is also a significantly low rate within the domain of covert communication, often characterized by $\mathcal{O}\left(\sqrt{n}\right)$. In this case, the covertness of video transmission relies on the adoption of extremely low video signal transmission rates. This implies that within the parameters outlined in Case 1, the scenario falls short of attaining the standard covert communication rate, i.e., $\mathcal{O}\left(\sqrt{n}\right)$.

(b) Case 2: If we have ${\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}\mathbf{d}\left[j\right]=0$ and ${\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}\mathbf{d}\left[k\right]=0$, we can obtain

$$\begin{array}{cc}\hfill & \int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,w}(x,y)\left[\beta {\mathbf{T}}^{\prime }\left(0\right)\right]\mathrm{d}x\mathrm{d}y=0,\hfill \\ \hfill & \int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,w}(x,y)\left[\frac{{\beta }^2}{2!}{\mathbf{T}}^{″}\left(0\right)\right]\mathrm{d}x\mathrm{d}y\hfill \end{array}$$

(45)

$$\begin{array}{c}=\frac{{\beta }^4{g_w}^4}{2{\sigma }_w^4}\left(\sum _{t=1}^N\sum _{s=1}^N\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k}{p}_{t,s}\left(\mathbf{d}{\left[j\right]}^2\mathbf{d}{\left[t\right]}^2+\mathbf{d}{\left[k\right]}^2\mathbf{d}{\left[s\right]}^2+2\mathbf{d}\left[t\right]\mathbf{d}\left[s\right]\mathbf{d}\left[j\right]\mathbf{d}\left[k\right]\right)\right),\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & \int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,w}(x,y)\left[\frac{{\beta }^3}{3!}{\mathbf{T}}^{‴}\left(0\right)\right]\mathrm{d}x\mathrm{d}y=0,\hfill \\ \hfill & \int \int \sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}{q}_{t,s,w}(x,y)\left[\frac{{\beta }^4}{4!}{\mathbf{T}}^{⁗}\left(0\right)\right]\mathrm{d}x\mathrm{d}y\hfill \end{array}$$

(47)

$$\begin{array}{c}=-\frac{{\beta }^4{g_w}^4}{4{\sigma }_w^4}\left(\sum _{t=1}^N\sum _{s=1}^N\sum _{j=1}^N\sum _{k=1}^N{p}_{j,k}{p}_{t,s}\left(\mathbf{d}{\left[j\right]}^2\mathbf{d}{\left[t\right]}^2+\mathbf{d}{\left[k\right]}^2\mathbf{d}{\left[s\right]}^2+2\mathbf{d}\left[t\right]\mathbf{d}\left[s\right]\mathbf{d}\left[j\right]\mathbf{d}\left[k\right]\right)\right).\hfill \end{array}$$

(48)

Combining (39) with (45)–(48), we have

$$\begin{array}{c}\mathcal{D}(Q_{1,w}^n\parallel Q_{0,w}^n)\hfill \\ =\frac{n{\beta }^4{g_w}^4}{4{\sigma }_w^4}\left({\left(\sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}\mathbf{d}{\left[t\right]}^2\right)}^2+{\left(\sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}\mathbf{d}{\left[s\right]}^2\right)}^2+2{\left(\sum _{t=1}^N\sum _{s=1}^N{p}_{t,s}\mathbf{d}\left[t\right]\mathbf{d}\left[s\right]\right)}^2\right)\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill & =\mathcal{O}\left({\beta }^4\right),\hfill \end{array}$$

(50)

and the transmission rate is given by

$$\begin{array}{c}\mathbb{I}({\mathbf{Z}}_b^n;{\mathbf{D}}^n)\hfill \\ =\frac{\sqrt{nϵ}{g}_b^2{\sigma }_w^2{\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\left(\mathbf{d}{\left[t\right]}^2+\mathbf{d}{\left[s\right]}^2\right)}{{\sigma }_b^2{g}_w^2\sqrt{{\left({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\mathbf{d}{\left[t\right]}^2\right)}^2+{\left({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\mathbf{d}{\left[s\right]}^2\right)}^2+2{\left({\sum }_{t=1}^N{\sum }_{s=1}^N{p}_{t,s}\mathbf{d}\left[t\right]\mathbf{d}\left[s\right]\right)}^2}}\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill & =\mathcal{O}\left(\sqrt{n}\right).\hfill \end{array}$$

(52)

As discussed in Case 1, the typical rate for covert communication is characterized by $\mathcal{O}\left(\sqrt{n}\right)$. Building upon the conditions outlined in Case 2, we can ascertain a transmission rate of $\mathcal{O}\left(\sqrt{n}\right)$. This implies that the conditions specified in Case 2 are prerequisite for achieving covert communication.

3.3. Theorem of the Necessary Conditions for Covert Surveillance Video Transmission

In Section 3.1 and Section 3.2, we characterize transmission rates based on mutual information and covertness performance based on KL divergence. Through derivation based on mutual information, we can obtain the maximum theoretical rate of the covert transmission of surveillance videos, providing theoretical support for the selection and setting of transmission protocols. Through derivation based on KL divergence, we can determine the covertness indicator of the covert transmission of surveillance videos, thus characterizing the covertness and security of transmission. The rate, covertness, and security of the covert transmission of surveillance videos are important parameters and necessary conditions for transmission. Specifically, through the optimization of the probability distributions of QAM modulation constellation points, we can achieve optimal covertness performance while maximizing covert transmission rates.

In the preceding subsection, we presented covert transmission rate and covertness analyses for two different cases. It can be seen in (49) and (51) that when the necessary conditions (i.e., ${\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}\mathbf{d}\left[j\right]=0$ and ${\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}\mathbf{d}\left[k\right]=0$) are satisfied, a surveillance video can be transmitted with a rate of $\mathcal{O}\left(\sqrt{n}\right)$ and a covertness parameter of $\mathcal{O}\left({\beta }^4\right)$. As shown in (42) and (43), if the necessary conditions are not satisfied, the transmission rate deteriorates to $\mathcal{O}\left(1\right)$ and covertness deteriorates to $\mathcal{O}\left({\beta }^2\right)$. In previous research, the covert transmission rate is $\mathcal{O}\left(\sqrt{n}\right)$ and the covertness performance measured by KL divergence is $\mathcal{O}\left({\beta }^4\right)$. Thus, we obtain the necessary conditions for surveillance video transmission based on QAM modulation in the following theorem.

Theorem 1.

For any surveillance video transmitted using the QAM modulation method, the prerequisite for achieving optimal covert transmission is that ${\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}\mathbf{d}\left[j\right]=0$ and ${\sum }_{j=1}^N{\sum }_{k=1}^N{p}_{j,k}\mathbf{d}\left[k\right]=0$.

Building upon the theorem presented, we can design the modulation probabilities of QAM constellation points to improve transmission rates and covertness. This optimization facilitates the attainment of accelerated transmission rates while maintaining commensurate levels of covertness. It is imperative to emphasize that these fundamental conditions, anchored in QAM modulation, are not limited to conventional sets, such as 16−QAM, 64−QAM, and 256−QAM. Instead, they establish a broad-reaching conclusion that holds applicability across a diverse spectrum of constellation point modulation methodologies.

4. Experiments and Analysis

In this section, we present simulation results based on test conditions, showcasing the transmission rates of surveillance videos under different transmission powers and the covertness performance metrics corresponding to these power levels. Throughout all subsequent tests, the 16−QAM modulation scheme, as employed in the H.264/AVC protocol, is utilized. Additionally, we conduct comparisons of transmission rates and covertness metric values based on various channel coefficients and receiver noise levels. To assess the effectiveness and superiority of the proposed optimal probability theory, we compare optimization results obtained using the backtracking line method from [40].

To enhance the effectiveness and authenticity of the experimental results, we set the experimental parameters as follows: the covert signal detection channel coefficient $g_w$ is set to 0.4 and 0.8 and the covert communication detection channel noise variance ${\sigma }_w$ is set to 1.5 and 1, respectively; the covert signal receiver channel coefficient $g_b$ is set to 0.4 and 0.8 and the covert signal receiver channel noise variance ${\sigma }_w$ is set to 1.5 and 1, respectively. Additionally, we set the code block length n to $1\times {10}^6$ and the number of symbols in a single-axis constellation set N to 4.

Figure 4a provides a visual comparison of the outcomes obtained using our novel Taylor expansion method and the exact values. The covertness metric $ϵ$, spanning from 0 to 1, serves as an indicator of covertness performance, with smaller values denoting enhanced concealment. As depicted in the visual representation, there is a noticeable decline in transmission rate as the covertness metric diminishes. Remarkably, our proposed Taylor expansion approximation method exhibits a remarkable concordance with the computationally derived exact values. This alignment underscores the high degree of accuracy achieved by our approximation approach. Such close correspondence not only validates the precision of our proposed method but also underscores the efficacy of the theoretical framework derived from this approximation. Figure 4b illustrates the relationship between absolute error and the covertness metric $ϵ$. As the covertness metric decreases, the fitting accuracy exhibits exponential improvement. In the considered scenarios ($ϵ\le 0.01$), the fitting accuracy reaches ${10}^{-5}$, fully satisfying the precision requirements for our experimental objectives. This validation further solidifies the practical applicability and robustness of our proposed approach within the context of covert communication systems.

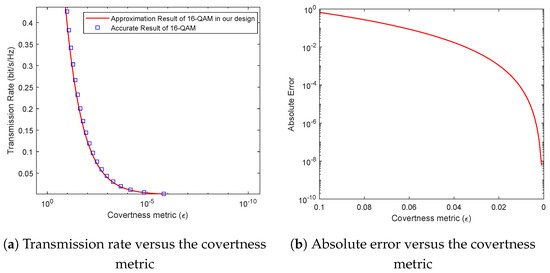
Figure 4. Approximation of our Taylor expansion method.

Figure 5a provides a comprehensive depiction of the intricate trade-off between the covertness metric and transmission power across varying detection channel coefficients. To benchmark the efficacy of our proposed theoretical framework, we systematically contrast its outcomes to optimization results derived using the backtracking line method. Specifically, we investigate covert transmission scenarios for surveillance videos by setting the detection channel coefficient $g_w$ to the values of 0.4 and 0.8. At $g_w$ = 0.4, our proposed methodology reveals a discernible decline in covertness performance with increasing transmission power. Notably, at lower power levels, our approach consistently outshines the comparative backtracking line method, as evidenced by lower covertness metric values. This observation underscores the superiority of our method in achieving enhanced covertness, particularly when confronted with constraints on power levels. Conversely, at higher transmission power levels, both methodologies converge to approximately equal covertness metric values. This convergence suggests that relying solely on the design of QAM constellation probabilities may not be sufficient to ensure the covert transmission of surveillance videos at elevated power levels. However, even in this regime, our proposed method maintains a competitive covertness performance. Furthermore, at $g_w$ = 0.4, our approach showcases superior covertness, indicating a substantial enhancement in performance as the channel gain coefficient decreases. This resilience underscores the effectiveness of our proposed method under diverse channel conditions. In both low- and high-power scenarios, our method consistently outperforms the comparative approach, emphasizing its robust covertness performance under varying operational conditions. This comprehensive analysis reinforces the practical relevance and efficacy of our proposed methodology within the realm of covert communication for surveillance applications.

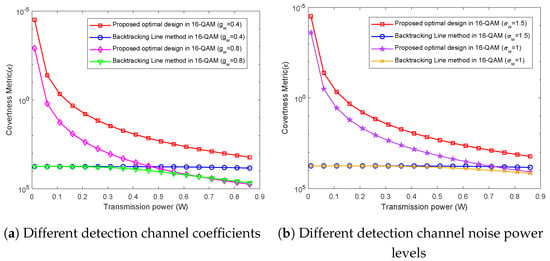
Figure 5. Covertness metric versus transmission power.

Figure 5b depicts the relationship between the covertness metric and transmission power across varying levels of detection channel noise power. Notably, our proposed method consistently surpasses the comparative backtracking line method in terms of covertness performance. This observed superiority is particularly evident as the detection channel noise power escalates, leading to a substantial enhancement in covertness. With a discerning eye on the dynamics of covertness performance, it becomes apparent that at lower power levels, our proposed method demonstrates notable superiority in maintaining effective concealment. The inherent robustness of our approach is especially pronounced in scenarios characterized by limited power availability. However, it is crucial to note that with an increase in transmission power, there is a discernible deterioration in covertness performance. This phenomenon emphasizes the intricate interplay between transmission power and covertness, highlighting the challenges posed by higher power scenarios. Further insights into the trade-offs and optimal strategies under varying conditions can be gleaned from a nuanced examination of the results. Our findings underscore the effectiveness of the proposed methodology in covert surveillance video transmission, showcasing its resilience in the presence of variations in detection channel noise power levels. The observed trends provide valuable insights for practitioners seeking to optimize covertness performance in real-world surveillance applications.

Figure 6a provides a visual representation of the dynamic interplay between transmission rate and transmission power for various receiver channel coefficients. The graph prominently illustrates that with an escalation in transmission power, there is a substantial improvement in transmission rate. This observation underscores the pivotal role of power in influencing the efficiency of covert surveillance video transmission. Whether examining scenarios with a receiver channel coefficient of $g_b$ = 0.4 or $g_b$ = 0.8, our proposed method consistently outperforms the comparative method, yielding higher transmission rates. This consistency across different channel coefficients reaffirms the robustness and versatility of our approach, making it well suited for a spectrum of operational conditions. Furthermore, as the channel coefficient increases, we observe a notable enhancement in transmission rate. This behavior aligns with the expected trend, indicating that a higher channel coefficient contributes to improved communication efficiency. These results illuminate the positive correlation between transmission power and transmission rate, emphasizing the significance of power optimization strategies in enhancing the efficiency of covert surveillance video communication. The insights gained from this analysis provide valuable guidance for practitioners seeking to optimize transmission rates in covert surveillance video communication systems under varying channel conditions.

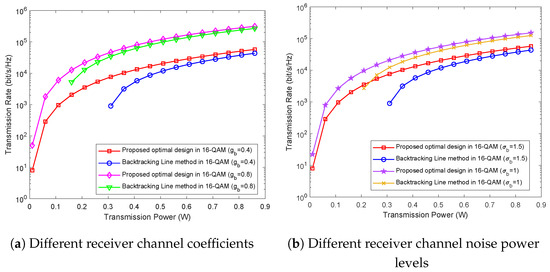
Figure 6. Transmission rate versus transmission power.

Figure 6b provides a detailed portrayal of the nuanced relationship between transmission rate and transmission power for different receiver noise power levels. It is discernible that as channel noise increases, there is a noteworthy reduction in transmission rate. Our proposed method consistently outshines the comparative approach, showcasing higher transmission rates at both low and high power levels. It is also noteworthy that at transmission power levels below 0.2 watts, our proposed method exhibits a higher transmission rate when the noise variance ${\sigma }_b$ is 1.5 compared to existing methods at ${\sigma }_b$=1. This suggests that our proposed method achieves faster transmission rates under low power conditions, with more pronounced improvements in transmission rates compared to high-power scenarios.

Figure 7 illustrates transmission rates under different levels of covertness using our proposed method and the comparative approach. This figure illuminates a trend wherein as covertness increases, both methods experience declines in transmission rates. Notably, our proposed method consistently maintains a superior position compared to the comparative approach, effectively enhancing covertness while sustaining competitive transmission rates. A critical consideration arises from the comparison of results in Figure 5a,b. The substantial divergence in covertness metrics between the proposed method and the comparative approach underscores the challenge of directly comparing transmission rates under equivalent covertness conditions. Our proposed method stands out by simultaneously achieving superior covertness and higher transmission rates, underscoring its effectiveness in optimizing both aspects of covert communication. In summary, our findings demonstrate the intricate interplay between transmission rate, transmission power, and covertness, with our proposed method consistently achieving enhanced covertness and superior transmission rates across diverse operational scenarios.

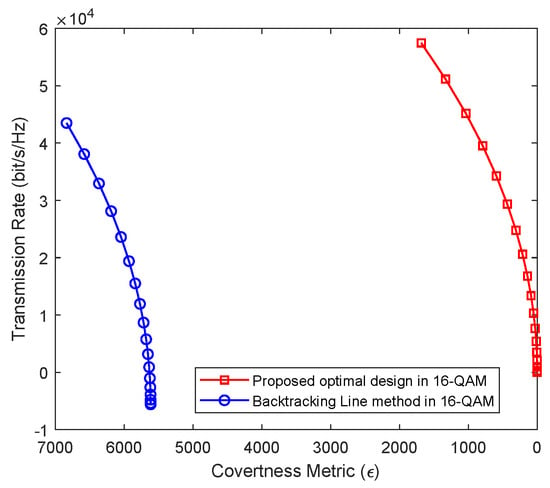
Figure 7. Transmission rates using the different methods.

In this section, we first validated the accuracy of our Taylor series expansion method. Subsequently, we compared existing methods to our proposed optimization method in terms of covertness performance under different channel coefficients and noise conditions for the sender, as well as transmission rates under different channel coefficients and noise conditions for the receiver. Finally, in the same environment, we compared the covertness performance and transmission rate of our proposed method to those of existing methods. Under the same covertness indicator, our proposed method has a higher transmission rate. This implies that surveillance videos can be covertly transmitted at a higher rate, corresponding to higher video clarity and shorter video transmission times.

5. Conclusions

In this paper, we delved into the intricacies of optimization techniques for the covert transmission of surveillance videos. Our primary focus centered on a meticulous exploration of the optimal probability of covert surveillance video transmission within the framework of QAM modulation. We employed mutual information as a metric for assessing covert transmission rate, leveraging its ability to quantify information shared between transmitted signals and the corresponding received signals. Simultaneously, we employed KL divergence as a measure to evaluate the covertness performance of transmitted signals. Based on the Taylor series expansion theory, we systematically conducted a thorough analysis, encompassing both the transmission rate and covertness aspects. In the considered scenarios, the fitting accuracy reached ${10}^{-5}$, fully satisfying the precision requirements for our experimental objectives.

Our investigation resulted in theoretical insights into the requisite conditions governing the optimal modulation probability of constellation points under QAM modulation. The covert transmission rate is $\mathcal{O}\left(\sqrt{n}\right)$ when our proposed theoretical conditions are satisfied; otherwise, it is $\mathcal{O}\left(1\right)$, representing a significant disparity. Subsequent to this theoretical groundwork, we embarked on a series of experimental simulations, which were designed to rigorously validate our derived conclusions. Notably, our approach exhibited a commendable performance, showcasing superior transmission rates and increased covertness compared to existing methodologies. This success underscores the efficacy of our optimized strategy for the covert transmission of surveillance videos.

In future work, our research trajectory includes an expansion of our focus beyond QAM modulation to encompass diverse transmission protocols for surveillance videos. This extension aims to develop additional covert transmission strategies and methodologies, contributing to the broader advancement of covert communication in surveillance scenarios.