A 3D Vision-Based Weld Seam Extraction Method for Arbitrarily Placed Spatial Planar Weldments

Abstract

Vision-based weld seam extraction poses a significant challenge for weldments with complex spatial structures in automated welding. Existing research primarily focuses on identifying weld seams from weldments with given positions and postures, while practical weld path planning requires multiple weld seams identified within arbitrarily placed weldments. This paper proposes a methodology that identifies weld seams from arbitrarily placed spatial planar weldments in a single run. First, by introducing a turntable calibrated with respect to a 3D camera, we perform 3D reconstruction on an arbitrarily placed spatial planar weldment. Second, an improved RANSAC algorithm based on Euclidean clustering is proposed to carry out plane segmentation, focusing on segmentation accuracy. Finally, we present a novel weld seam extraction algorithm leveraging the half-edge data structure to efficiently compute weld seams from the segmented planes. The experiments conducted in this study demonstrate that the average segmentation errors (as an indirect indicator of weld seam extraction error) are reduced by 90.3% to 99.8% over conventional segmentation methods, and the standard deviations are reduced by 64.8% to 97.0%.

1. Introduction

The introduction of visual sensors enables the industrial robot as an actuator to perceive the positional information of the surrounding environment. Therefore, vision-based automatic weld seam extraction (WSE) and weld seam tracking have become an indispensable part of robotic welding, which requires the weldment’s posture and position to be known to the robot.

According to our research on actual production, many welding applications must handle randomly placed weldments with uncertain position information. For these applications, the additional human labor and time cost brought by fixing the weldments with satisfactory accuracy for WSE are unacceptable in terms of efficiency and economy, especially in welding applications with multi-variety and small batches, as exemplified by the samples in Section 4.2. There are two major steps to achieve this goal. The first step is model reconstruction, from which a 2D or 3D model representing the geometric information of the weldment is obtained; the second step is to perform WSE on the model.

Model reconstruction can be straightforward for simple weldments. A common approach is capturing a 2D image using a laser profile sensor and extracting the weld seams through pixel analysis [1,2,3,4,5]. For applications with a more complex weld seam or multiple weld seams to be recognized, a monocular or binocular structured light 3D camera that outputs point clouds is more commonly used [6,7,8,9]. The problem is that when the weldment is too large for the camera’s FOV or when there are occlusions between multiple welds, a single frame of point cloud cannot fully express all the necessary geometric features. In this regard, the studies mentioned above focus on the WSE of a single weld seam or several weld seams in a single frame of a point cloud, referenced as local weld seams in this paper. There are also scholars who work on solving this practical problem and obtaining global weld seams. To perform 3D reconstruction on a large-size tube sheet, Wang et al. [10] collect 2D images and laser rangefinder data simultaneously through the sensors installed on a robot. They perform SIFT feature matching on the 2D images to obtain the positional relationship between different frames of images, which, combined with the depth data, leads to a complete point cloud. Yan et al. [11] first convert the 3D point cloud into a 2D grayscale image and use an edge detection algorithm to detect the pixel set corresponding to the weld seam from the 2D image. The weld seams are then fitted with spline curves. The position errors are within ±0.3 mm, and the standard deviations are less than 0.4 mm. Considering the need to extract geometric features from weldments of complex spatial structures, in this paper, we arbitrarily mount the assembled weldments (One of the factors influencing the quality of welded joints is the appropriate sequence and order of assembly [12]) on a one-axis turntable. By rotating a weldment along with the turntable and capturing multiple frames of point clouds of the weldment using a binocular structured light 3D camera, a point cloud that represents the complete geometric features of the weldment is created through point cloud registration.

WSE can be divided into two types according to the vision sensor used. For research with 2D vision employed, weld seams are mostly obtained by running pixel analysis on 2D images scanned with a laser profile sensor. This approach is particularly suitable for weldments assembled by two workpieces since their geometric features can be expressed in 2D images with decent accuracy. As an example, Guo, Zheng, Lian and Yao [3] perform WSE on V-shaped butt joints by extracting pixels that represent the center line of a weld seam, with an average positional error of 0.147 mm. Chen, Ma, He, Sun and Ren [4] use a neural network to perform semantic segmentation on the 2D image of a narrow butt joint and extract the weld seam with an average position error of 0.207 mm. As for 3D-vision-based applications, most researchers choose to identify geometric elements from the point clouds. Some accomplish it through edge extraction. Zhang, Geng, Tian, Zheng, Jiang and Lai [9] use K-Means clustering to separate boundary points identified by a new feature descriptor. This method’s advantage is its strong adaptability (it can be used for free surfaces). However, its 78.57% corner recognition rate for planar weldments is still insufficient for practical use. More studies choose to segment planes from the point cloud first. Yuankai, Yong, Xincheng, Xiaolong, Yusen and Min [6] study three cases of weldments composed of two parallel planes and use vanilla RANSAC to detect and remove the edge points of the two planes, and then use least squares fitting to calculate the weld seams as the center lines of the two plane point clouds. Yang, Li, Long, Fan and Liang [7] use the least squares method to fit the common plane of the two butted workpieces. The weld seams are calculated by polynomial fitting on the points farthest from the plane. The RMSE error of the fitted weld seams is less than 0.7 mm. Yang et al. [13] apply vanilla RANSAC on the point clouds to fit TEE joints and lap joints in simple weldments. Geng et al. [14] undertake similar work with more complex planar weldments, optimizing RANSAC to enhance the computational efficiency and fitting accuracy compared to vanilla RANSAC. The successful implementation of these methods all has a common prerequisite, that is, either the structure of the weldment is simple enough for the weld seams to be extracted through a single frame of image or the weldments must be fixed with a certain accuracy in advance and the camera must be located (at least roughly) in a position where the weld features can be captured. In addition, since the research objects are all single weld seams or multiple weld seams in a frame of a point cloud, only local weld seams can be obtained in the end rather than all global weld seams. Further research is warranted to address the global welding path planning challenge for spatial planar weldments. Hence, this paper is dedicated to proposing a WSE method for arbitrarily placed spatial planar weldments, i.e., weldments with spatial structures comprised of plate-like materials commonly observed in construction machinery, steel structures, carriage plates, and container plate manufacturing applications [14].

In this paper, we propose a new approach that uses an improved RANSAC algorithm based on Euclidean clustering to carry out plane segmentation, and a novel weld seam extraction algorithm leveraging the half-edge data structure is developed to compute weld seams from the segmented planes efficiently. Due to the difference in weldment sizes and types, equipment types and accuracy levels, and error evaluation methods in the existing literature, we cannot create a unified benchmark for various methods for comparison. However, the process in this paper successfully solves the problem of WSE in a scenario that is more complex than similar articles and greatly improves the accuracy compared to traditional feature extraction methods. It provides an effective reference for applying robot automatic welding of complex planar welded parts without precise clamping.

The structure of this paper is as follows: Section 1 introduces the research background and briefly reviews the literature. Section 2 presents the 3D reconstruction method for point cloud registration and proposes an improved RANSAC algorithm tailored for consecutive plane segmentation. Section 3 introduces a WSE method based on the results of plane segmentation. Section 4 describes several experiments conducted to practice and validate the proposed methods. Finally, Section 5 offers concluding remarks on the study presented in this paper.

2. Improved RANSAC for Plane Segmentation

2.1. Three-Dimensional Reconstruction

To obtain the 3D model that represents the global geometric features of a weldment, we grab multiple point clouds of the weldment, which is randomly fixed on a turntable and rotates with it. Three-dimensional reconstruction is carried out by point cloud registration on all the point clouds. The setup is depicted in Figure 1.

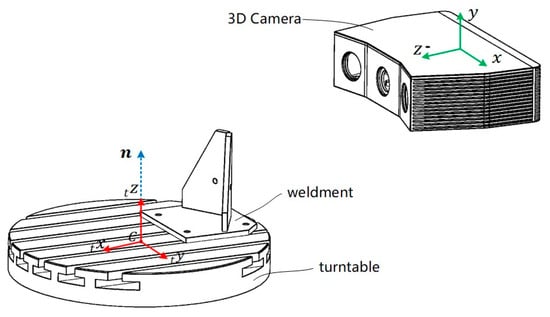
Figure 1. Capturing point clouds of the weldment on a turntable.

For any point fixed on the turntable, the coordinates with respect to the turntable system and the world base system (also the camera system) are ${}_{t}x$ and $x$, which satisfy

$$x=\mathit{P}\left(\mathit{n}\right){}_{t}x+c,$$

(1)

where $\mathit{n}$ is the coordinate of the rotation axis, $\mathit{P}\left(\mathit{n}\right)$ is the angle transform matrix between the two bases and $c$ is the coordinate of the turntable center point with respect to the world base.

After the turntable rotates about its $z$ axis (with respect to the turntable system) with angle $\theta$, the coordinate becomes

$$\begin{array}{cc}\hfill {}_{t}x_{\theta }& =\mathit{R}\left(z,\theta \right){}_{t}x\hfill \\ \hfill \Rightarrow x_{\theta }& =\mathit{P}\left(\mathit{n}\right){}_{t}x_{\theta }+c\hfill \\ & =\mathit{P}\left(\mathit{n}\right)\mathit{R}\left(z,\theta \right){}_{t}x+c\hfill \\ & =\mathit{P}\left(\mathit{n}\right)\mathit{R}\left(z,\theta \right){\mathit{P}}^{-1}\left(\mathit{n}\right)\left(x-c\right)+c\hfill \\ & =R\left(\mathit{n},\theta \right)x+\left(\mathit{I}-\mathit{R}\left(\mathit{n},\theta \right)\right)c,\hfill \end{array}$$

(2)

where

$$\mathit{R}\left(z,\theta \right)=\left(\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right),$$

(3)

and

$$\mathit{R}\left(n,\theta \right)=\mathit{P}\left(\mathit{n}\right)\mathit{R}\left(z,\theta \right){\mathit{P}}^{-1}\left(\mathit{n}\right)$$

(4)

are the rotation matrices with respect to rotation axis $z$ and $\mathit{n}$, respectively.

So, the registered point cloud of multiple frames grabbed on the turntable can be expressed as

$$C_{\theta }=\bigcup _j\bigcup _k\left[\mathit{R}\left(\mathit{n},\theta -{\theta }_j\right)x_k+\left(\mathit{I}-\mathit{R}\left(\mathit{n},\theta -{\theta }_j\right)\right)c\right],$$

(5)

where ${\theta }_j$ is the angular position of the weldment in frame $j$ and $\theta$ is that of the registered point cloud; $x_k$ is the position of the $k$th point in the point cloud.

2.2. Improved RANSAC

Before extracting weld seams from the registered point cloud, we employ RANSAC for single-plane segmentation. As a widely utilized method in geometric feature extraction and shape detection, RANSAC has proved its effectiveness in multiple fields such as SLAM [15], Geographic detection in nature [16] or urban areas [17,18], and so on. As outlined in the algorithm proposed in [19], vanilla RANSAC iteratively fits a plane from a point cloud over $k$ iterations. Each iteration entails four sequential steps (referred to as steps (1) to (4) in Figure 2) to obtain a candidate plane, maximizing the count of inliers—points with distances to the candidate plane smaller than a preset threshold.

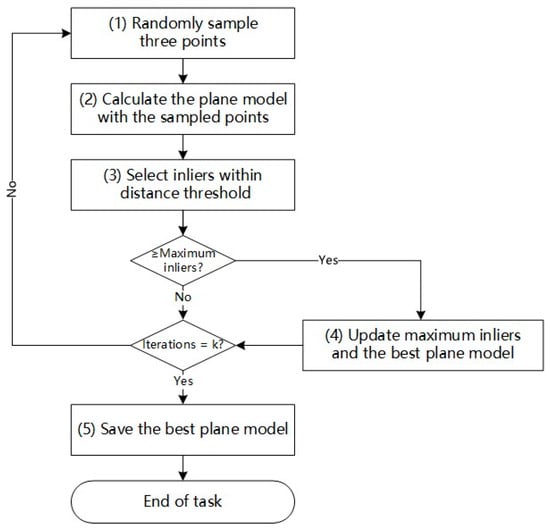
Figure 2. Flowchart of vanilla RANSAC for single plane segmentation.

The iteration number $k$ is defined as

$$k={\displaystyle \frac{\log \left(1-p\right)}{\log \left(1-{\omega }^3\right)}},$$

(6)

where $\omega$ is the inlier ratio, i.e., is the number of inliers divided by the number of points, and the constant variable $p$ is normally set as 0.99 [20].

Despite its effectiveness in various applications, vanilla RANSAC encounters challenges when applied to plane segmentation tasks in spatial planar weldments. To address these issues, we propose several rules tailored to the different steps of the vanilla RANSAC, and the refined algorithm is simply called “improved RANSAC” in this paper.

2.2.1. Optimization for Point Sampling

The initial challenge is “invalid sampling,” as Figure 3a illustrates. This scenario depicts a situation where, instead of extracting the intended candidate plane, $S_1$, an invalid plane, $S_2$, is obtained as it outperforms $S_1$ by including more inliers.

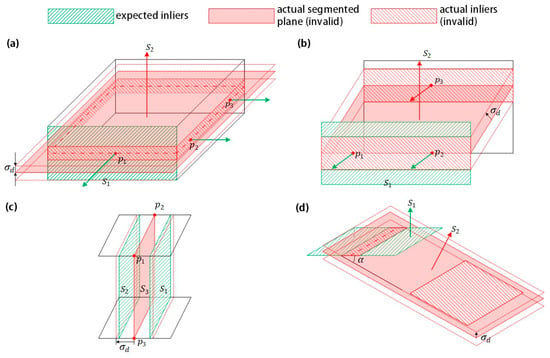
Figure 3. Situations of invalid segmentation: (a) invalid sampling; (b) invalid candidate plane; (c) closely spaced planes; (d) erroneously included inliers.

• Rule 1. Sample validation.

In the sampling step (step 1) of the algorithm in Figure 2, any pair of the three sampled points must have similar normal vectors, which can be estimated with covariance matrices [21]. That is to say, for any three sampled points $p_1,$ $p_2$, and $p_3$, the sample is valid only when

$${\alpha }_{ij}=\arccos \left({\displaystyle \frac{\left|{\mathit{n}}_i·{\mathit{n}}_j\right|}{‖{\mathit{n}}_i‖‖{\mathit{n}}_j‖}}\right)<{\sigma }_a,\hspace{1em}\hspace{1em}i,j\in \left\{1,2,3\right\},i\ne j,$$

(7)

where ${\sigma }_a$ > 0 is the preset angle threshold and ${\mathit{n}}_i$ is the corresponding surface normal vector at $p_i$ in Figure 3a.

By incorporating Rule 1, cases illustrated in Figure 3a are effectively bypassed. This further prevents the generation of unqualified candidate planes, reducing the effort of candidate plane validation.

2.2.2. Optimization for Candidate Plane Validation

The second challenge, termed “invalid candidate plane”, arises after the plane model calculation step (step 2) of the algorithm depicted in Figure 2. Occasionally, invalid candidate planes may emerge despite the sampled points passing Rule 1, as illustrated in Figure 3b. In this scenario, while the sampled points possess similar normal vectors, the candidate plane’s normal vector exhibits a significant disparity.

• Rule 2. Candidate plane validation.

For any candidate plane calculated using the sampled points, its normal vector must be close to those of the sampled points. That is to say, candidate plane $S$ is valid only when

$$\arccos \left({\displaystyle \frac{\left|{\mathit{n}}_i·{\mathit{n}}_S\right|}{‖{\mathit{n}}_i‖‖{\mathit{n}}_S‖}}\right)<{\sigma }_a,\hspace{1em}\hspace{1em}i\in \left\{1,2,3\right\},$$

(8)

where ${\mathit{n}}_S$ is the normal vector of $S$.

2.2.3. Optimization for Inlier Validation and Update Criterion

In the irregular scenario depicted in Figure 3d, a correctly segmented plane erroneously includes inliers belonging to other planes, thereby causing interference with the remaining points to be segmented. This situation underscores the potential for a candidate plane to occupy points intended for other planes.

• Rule 3. Inlier validation.

Besides the distance threshold, the points selected as inliers must have similar normal vectors as the segmented plane. Under this rule, a point $p_i$ is a valid inlier of plane $S$ only if the following conditions are satisfied:

$$\left\{\begin{array}{l}\mathrm{distance}\left(p_i,S\right)<{\sigma }_d,\\ \arccos \left({\displaystyle \frac{\left|{\mathit{n}}_i·{\mathit{n}}_S\right|}{‖{\mathit{n}}_i‖‖{\mathit{n}}_S‖}}\right)<{\sigma }_a.\end{array}\right.\hspace{1em}i\in \left\{1,2,\dots ,l\right\},$$

(9)

where ${\sigma }_d$ is the distance threshold and

$$\mathrm{distance}\left(p_i,S\right)={\displaystyle \frac{\left|A{x}_i+B{y}_i+C{z}_i+D\right|}{\sqrt{A^2+B^2+C^2}}},$$

(10)

for point $p_i=(x_i,y_i,z_i)$ and plane $S$ representing $Ax+By+Cz+D=0$.

Another irregular situation, exemplified in Figure 3c, arises when the distance between two parallel planes is less than the distance threshold ${\sigma }_d$. In this case, the central plane, marked as $S_3$ in Figure 3, is prioritized over $S_1$ and $S_2$ to be chosen as the candidate plane, as per the iteration update in Figure 2, which selects a new candidate plane if it has more inliers than the historical best one. While a straightforward solution would be to use a smaller ${\sigma }_d$, altering such a significant variable in RANSAC could introduce unexpected variability in the output. Hence, there is a need to revise the update criterion accordingly.

To begin with, we introduce variable $\mathit{e}$ as the local segmentation error of a candidate plane:

$$e=\sum _{i=1}^l\left(\gamma \mathrm{distance}\left(p_i,S\right)+\left(1-\gamma \right){\displaystyle \frac{\left|{\mathit{n}}_i·{\mathit{n}}_S\right|}{‖{\mathit{n}}_i‖‖{\mathit{n}}_S‖}}\right),$$

(11)

where $l$ is the number of inliers of the current candidate plane $S$, ${\mathit{n}}_i$ is the normal vector at $p_i$ and $\gamma \in [0,1]$ is the weight to control the significance of distance errors and angle errors.

• Rule 4. Update criterion.

For a new candidate plane $S_j$ in the $j$th iteration, it outperforms the historical best iteration $k$ only when

$${\rho }_j={\displaystyle \frac{l_j}{e_j}}>{\displaystyle \frac{l_k}{e_k}}.$$

(12)

The introduction of the new objective value $\rho$ provides a refined measure of the priority of a candidate plane, considering not only its number of inliers but also the distance and angle errors. This modification substantially mitigates situations akin to Figure 3c, where parallel planes may erroneously interfere with each other.

2.2.4. Optimization for Final Output

Rule 3 and Rule 4 generally perform well for normal situations; however, there are instances where they fall short, particularly when the angle $\alpha$ in Figure 3d is smaller than the ${\sigma }_a$ defined in Rule 3. As illustrated by $S_1$ and $S_2$ in Figure 4, the current RANSAC algorithm would only segment one plane (e.g., plane $S^{\prime }$ in Figure 4b) since the inliers of both $S_1$ and $S_2$ fall within the distance and angle thresholds. This outcome inevitably introduces additional segmentation errors in the resulting fitted planes and weld seams.

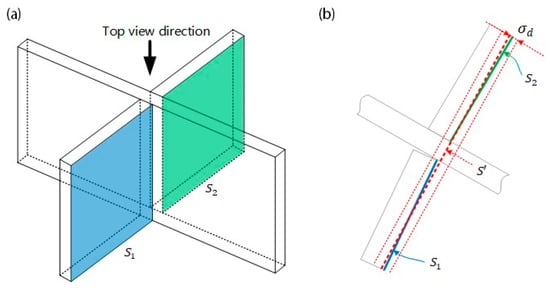
Figure 4. Segmentation error brought by similar planes: (a) 3D view; (b) top view. In the top view, $S_1$ and $S_2$, represented with blue and green solid lines respectively, are the planes to be segmented. In contrast, the mistakenly segmented plane $S^{\prime }$ is represented with a dotted red line. ${\sigma }_d$ is the distance threshold for inlier selection in RANSAC.

The points in $S_1$ and $S_2$ can be easily clustered into two groups using Euclidean clustering: Point sets ${\mathsf{\Phi }}_{\mathrm{i}}$ and ${\mathsf{\Phi }}_j$ are two clusters, if

$$\min \left(\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(p_i,p_j\right)\right)\ge {\sigma }_d$$

(13)

holds for any $i$ and $j$, where ${\sigma }_d$ is the distance threshold [22]. This definition also indicates that for any point $p_i$ in a cluster that has more than one element, there exists at least one point that distanced less than ${\sigma }_d$ to $p_i$.

• Rule 5. Final refinements.

After inlier validation, Euclidean clustering on the inliers is performed, resulting in $m$ clusters of inliers $\left(p_1^1,\dots ,p_{l_1}^1\right),\left(p_1^2,\dots ,p_{l_2}^2\right),\left(p_1^m,\dots ,p_{l_m}^m\right)$. Choose only one cluster as the inliers for the final segmented plane according to the following steps.

(a)

Least-square fitting is performed on each cluster of inliers, leading to a corresponding number of plane models. That is to say,

$$S_j=\mathrm{argmin}\sum _{i=1}^l{‖\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(p_i,S_j\right)‖}^2,$$

(14)

where $p_i$ annotates the $i$th inlier of plane $S_j$.

(b)

Choose a plane as the final output that satisfies

$$S_j=\underset{j}{\mathrm{argmin}}\left(e_j\right),$$

(15)

where $e_j$ is defined as $e$ in (11). The inliers that do not belong in the selected cluster return to the point pool for sampling in the next iteration.

Figure 5 illustrates how Rule 5 affects the segmentation results of the case in Figure 4. Without the refinements in Rule 5, spatially isolated planes with a small angle are recognized as a single plane. Also, the segmented planes may look incomplete if there are points (that should be inliers of the segmented planes) distanced farther than ${\sigma }_d$ to them. Both problems are eliminated with the introduction of Rule 5.

Figure 5. Segmentation before (a) and after (b) using Rule 5, with each segmented plane rendered in a different color.

2.3. Consecutive Plane Segmentation

With the proposed improved RANSAC algorithm for single-plane segmentation, consecutive segmentation becomes achievable. To consecutively segment multiple planes from a point cloud, the fundamental concept involves iteratively executing the algorithm on the point cloud with the inliers of the last segmented plane removed until all valid planes are segmented from the point cloud. Figure 6 illustrates this process. The output of the consecutive plane segmentation comprises a list of plane models segmented from the input point cloud, along with the corresponding inliers of each segmented plane.

Figure 6. The process of consecutive plane segmentation: Each step of the segmentation fits a plane and removes its inliers. The inliers of each plane are rendered in a different color. The color contrast of the inliers belonging to the same plane is caused by the inconsistent density of points in the point cloud (caused by occlusion during point cloud capturing).

In consecutive plane segmentation, two termination conditions can be considered: the number of segmented planes and the number of remaining points. Since the former requires clear user expectations, making automation applications less flexible, the latter termination condition is adopted in this paper.

In the proposed improved RANSAC algorithm, comparisons of normal vectors occur frequently, leading to time-consuming duplication of efforts. Particularly in the sampling process, numerous invalid iterations are spent on sampling points with different normal vectors. This inefficiency could be mitigated by clustering points based on normal vectors. To explore this approach, the normal vectors of the point cloud are visualized in a unit ball (Figure 7a), and the result is rendered into a temperature map representing the probability density of the normal vectors (Figure 7b). It becomes apparent that the points can be clustered based on their normal vectors. This insight inspires us that most points in a point cloud can be divided into several clusters according to their normal vectors.

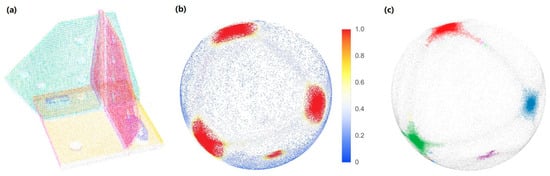
Figure 7. Normal vector clustering: (a) the original point cloud; (b) the temperature map representing the probability density of the normal vectors; (c) normal vector clustering using Euclidean clustering.

To precisely obtain cluster information, Euclidean clustering is applied to the unit ball in Figure 7b. The result (Figure 7c) resembles the probability density result in Figure 7b. The three major clusters in Figure 7c correspond to the three groups of orthogonal planes in Figure 7a.

Normal vector clustering offers two significant merits. Firstly, by clustering points, sampling is performed from a cluster rather than the entire point cloud in each iteration. This not only enhances sampling efficiency by reducing the sample space but also decreases the number of points to be considered in subsequent steps. Secondly, since points with different normal vectors are segregated into distinct clusters, they do not interfere with each other during the selection and counting of inliers, leading to improved segmentation results.

The detailed steps of consecutive plane segmentation based on normal vector clustering are elucidated in the pseudo-code provided in Section 2.4.2.

2.4. Algorithm Implementation

For more clarified elaboration, the algorithm’s pseudo-code is separated into two parts: the first for the improved RANSAC Algorithm and the second for the consecutive plane segmentation.

2.4.1. Implementation for Improved RANSAC Algorithm

The pseudo-code for the improved RANSAC algorithm for a single segmentation is provided in Algorithm 1 in Python style.

Line 5 initiates the main loop (lines 5 to 24) that segments a single plane. Lines 8 to 14 implement Rule 1 (sample validation) in Section 2.2.1, where unqualified samples are bypassed before calculating the candidate plane. Line 15 calculates a candidate plane from the sampled points. Lines 16 to 17 implement Rule 2 (candidate plane validation) in Section 2.2.2. Lines 18 to 20 implement Rule 3 (inlier validation) in Section 2.2.3. Lines 21 and 22 update the current best candidate plane and its inliers by implementing Rule 4 (update criterion) in Section 2.2.3. Lines 23 and 24 check whether the termination condition in Formula (6) is satisfied. Lines 25 and 26 implement Rule 5 in Section 2.2.4, performing Euclidean clustering on the inliers and choosing the best cluster for final segmentation.

Algorithm 1 Improved RANSAC Algorithm
1	Input: the point cloud $points$ and the corresponding normal vectors $normals$;
2	Output: segmented plane model $plane$ and its inliers $inliers$
3	$max\_rho$ = 0
4	$inlier\_indices=\left[\right]$
5	for $i$ in $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}(max\_iteration)$:
6	$inlier\_indices=\left[\right]$
7	$[a,b,c]=[-1,-1,-1]$
8	for $j$ in $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}(max\_sampling)$:
9	$[a1,b1,c1]=\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\_3\_\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}\_\mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s}\_\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{e}\mathrm{s}\left(points\right)$
10	if $\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{d}\_\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}(normals\left[a\right],normals\left[b\right],normals[c]$):
11	$[a,b,c]=[a1,b1,c1]$
12	break
13	if $a<0$:
14	continue
15	$plane=\mathrm{g}\mathrm{e}\mathrm{t}\_\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{e}(points\left[a\right],points\left[b\right],points[c\left]\right)$
16	if not $\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{d}\_\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e}\_\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{e}\left(plane\right)$:
17	continue
18	for $j$ in $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\left(\mathrm{l}\mathrm{e}\mathrm{n}\right(points\left)\right)$:
19	if $\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{d}\_\mathrm{i}\mathrm{n}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{r}\left(\mathrm{j}\right)$:
20	$inlier\_indices.\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}(j$)
21	if $\mathrm{g}\mathrm{e}\mathrm{t}\_\mathrm{r}\mathrm{h}\mathrm{o}(inlier\_indices)>max\_rho$:
22	$max\_rho=\mathrm{g}\mathrm{e}\mathrm{t}\_\mathrm{r}\mathrm{h}\mathrm{o}(inlier\_indices)$
23	if $i>\mathrm{g}\mathrm{e}\mathrm{t}\_\mathrm{k}\left(\mathrm{l}\mathrm{e}\mathrm{n}\right(inlier\_indices\left)\right)$:
24	break
25	$clusters=\mathrm{e}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{n}\_\mathrm{c}\mathrm{l}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}(points,inlier\_indices)$
26	$plane$, $inliers=\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{s}\mathrm{e}\_\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m}\_\mathrm{c}\mathrm{l}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s}(clusters,points,normals)$
27	return $plane$, $inliers$

2.4.2. Implementation for Consecutive Plane Segmentation

The pseudo-code of Consecutive Plane Segmentation is listed in Algorithm 2.

Line 5 performs Euclidean clustering on the normal vectors, which returns a list of clusters containing the point indices. Line 6 begins the main loop, where the biggest cluster is used as the input for single-plane segmentation in each iteration. The improved RANSAC method in line 10 refers to the code block in Algorithm 1.

Algorithm 2 Consecutive Plane Segmentation Algorithm
1	Input: the point cloud $points$ and the corresponding normal vectors $normals$;
2	Output: segmented plane models $planes$ and their corresponding inliers $inliers\_groups$
3	$planes=\left[\right]$
4	$inliers\_groups=\left[\right]$
5	$clusters=\mathrm{e}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{n}\_\mathrm{c}\mathrm{l}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}\left(normals\right)$
6	while $True$:
7	$cluster\_index=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}\left(\right[\mathrm{l}\mathrm{e}\mathrm{n}\left(cluster\right) \mathbf{for} cluster \mathbf{in} clusters\left]\right)$
8	if $\mathrm{l}\mathrm{e}\mathrm{n}\left(clusters[cluster\_index]\right)<least\_points\_for\_segmentation$:
9	break
10	$plane$, $inliers=\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{d}\_\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{S}\mathrm{A}\mathrm{C}($ $points\left[clusters\right[cluster\_index\left]\right]$, $normals\left[clusters\right[cluster\_index\left]\right])$
11	if $\mathrm{l}\mathrm{e}\mathrm{n}\left(inliers\right)==0$:
12	break
13	$clusters[cluster\_index]=[index \mathbf{for} index \mathbf{in} clusters[cluster\_index] \mathbf{if} index \mathbf{not} \mathbf{in} inliers]$
14	$planes.\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\left(plane\right)$
15	$inliers\_groups.\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\left(inliers\right)$
16	return $planes$, $inliers\_groups$

3. Weld Seam Extraction

3.1. Intersection Point Calculation

Consider all the possible topology combinations (Figure 8) of three planes.

Figure 8. The possible topologies of three planes: (a) no intersection lines; (b) one intersection line; (c) two intersection lines; (d) three parallel intersection lines; (e) three intersection lines intersecting at one point. The intersection lines are represented with red lines.

Upon initial observation, situations in Figure 8b–e all appear to potentially produce weld seams. However, considering the physical thickness of any planar object, almost all situations can be expressed as Figure 8e. Consequently, a weld seam can be conceptualized as a set of lines connecting two intersection points, each formed by three planes. This problem can be addressed by solving a simple linear equation with three variables. Since Figure 8e is the only one to be considered, each combination of three planes can be validated using the following criterion:

$${\alpha }_{ij}=\arccos \left({\displaystyle \frac{\left|{\mathit{n}}_i·{\mathit{n}}_j\right|}{‖{\mathit{n}}_i‖‖{\mathit{n}}_j‖}}\right)<{\sigma }_a,\hspace{1em}\hspace{1em}i,j\in \left\{1,2,3\right\},i\ne j,$$

(16)

where ${\mathit{n}}_{\mathit{i}}$ is the normal vector of plane $i$. Formula $\left(16\right)$ looks identical to $\left(7\right)$, but the latter is used to validate sampled points in the RANSAC algorithm.

As noted, “almost” all situations can be simplified to Figure 8e, with one exception: the base plane, where the weldment is mounted on the fixture, is typically obstructed from the camera’s view. Consequently, no points in the point cloud serve as inliers for the base plane. This issue can be readily resolved by manually adding the base plane to the list of segmented planes.

3.2. Vertex Validation

Based on the topology combination analysis described above, every weld seam comprises a line set connecting a starting point and an ending point, both of which are intersected points (vertices) formed by three planes. By iterating through all $C(n, 3)$ combinations of the segmented planes, all possible starting and ending points can be calculated. However, not every vertex is a valid start point or end point of a weld seam. As an illustration, Figure 9 shows a point $p_1$ intersected by planes $S_1$, $S_2$ and $S_3$, which obviously cannot serve as a vertex of a weld seam.

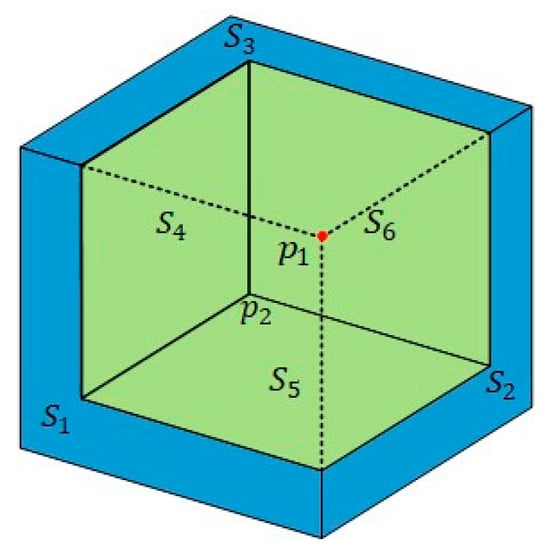
Figure 9. Example of an invalid intersection point ($p_1$).

By comparing $p_1$ with a valid vertex $p_2$ in Figure 9, a quick discovery is that invalid vertices are not located in the inliers of any of the planes intersecting. To rule out invalid intersections for weld seam extraction, each vertex is validated by the following criterion:

$$\min \left(\mathrm{distance}\left(p,P_{S_i}\right)\right)<{\sigma }_d,\hspace{1em}\hspace{1em}i\in \left\{1,2,3\right\}$$

(17)

where $P_{S_i}$ is the cluster of inliers of plane $S_i$. This criterion would likely fail without adopting Rule 5 proposed in Section 2.2.4 because isolated noisy points will be included in the inliers of a segmented plane, making the criterion satisfied even in case of an invalid intersection.

3.3. Edge Convexity Validation

With all the valid vertices obtained, a weld seam can be seen as an edge connecting two vertices that share two intersection planes. However, not all the edges are valid weld seams. A simple example is shown in Figure 10, and except $p_1{p}_2$ (in red color), all the other edges are invalid weld seams.

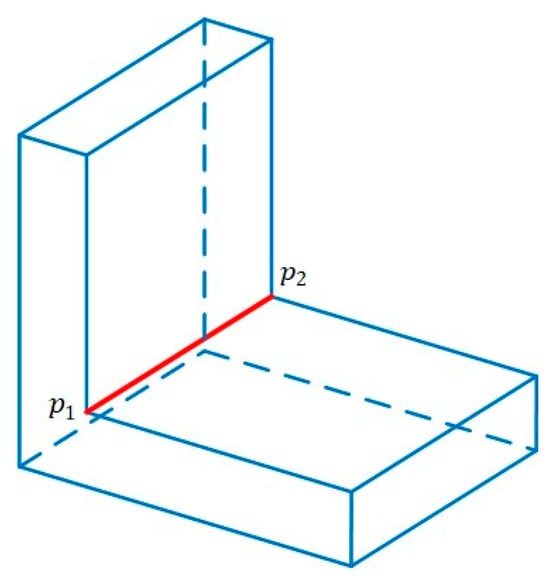
Figure 10. Edges connected by vertices.

By intuition, we recognize that weld seams must represent “concave edges,” while the remaining edges are “convex edges.” A concave edge is formed by two surfaces with an angle between 0° to 180°, and the angle has to be outside of the entity. Through the use of the half-edge data structure, also known as the doubly connected edge list [23], we observe the following pattern. As illustrated in Figure 11, for two adjacent planes, ${\mathit{e}}_1$ and ${\mathit{e}}_2$ are the twin half-edges of their common edge $p_1{p}_2$. ${\mathit{n}}_1$ and ${\mathit{n}}_2$ are the corresponding normal vectors. We introduce variable $\varsigma$ as an indicator of the convexity of an edge:

$$\varsigma =\left({\mathit{n}}_1\times {\mathit{n}}_2\right)·{\mathit{e}}_1.$$

(18)

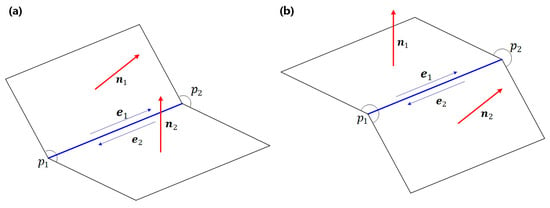
Figure 11. Concave edge (a) and convex edge (b).

The conclusion is as follows: when $\varsigma <0$, edge $p_1{p}_2$ is concave; when $\varsigma >0$, edge $p_1{p}_2$ is convex; when $\varsigma =0$, the two planes forming edge $p_1{p}_2$ are coplanar. With this principle, all the convex edges can be ruled out.

By expressing the intersection points in each plane with the half-edge data structures, all the intersection points and edges constitute a half-edge mesh, where the edge convexity indicator is used to validate concave edges as valid weld seams.

3.4. Algorithm Implementation for WSE

The implementation of WSE is depicted in Algorithm 3. The loop from lines 7 to 18 iterates all the three-plane combinations and calculates the valid vertices, where line 11 implements the criterion $\left(18\right)$. The edges are calculated from line 19 to line 24. Line 25 creates a half-edge mesh from the edges, from which lines 26 to 33 select the valid weld seams from the edges of the half-edge mesh using edge convexity validation in Section 3.3.

Algorithm 3 WSE Algorithm
1	Input: the point cloud $points$; the segmented planes $planes$ and their inliers $inliers\_planes$ (each element in $inliers\_planes$ is a list of point indices representing the inliers of the corresponding plane).
2	Output: list of vertices $vertices$; list of binary tuples $seams$ representing the indices of the points to be connected as weld seams.
3	$vertices=\left[\right]$
4	$edges=\left[\right]$
5	$vertices\_per\_plane=\left[\right[] \mathbf{for}\_\mathbf{in} \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}(\mathrm{l}\mathrm{e}\mathrm{n}\left(planes\right)\left)\right]$
6	$planes\_per\_vertex=\left[\right]$
7	for $comb\_3\_planes$ in $\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}\left(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\right(\mathrm{l}\mathrm{e}\mathrm{n}\left(planes\right)), 3)$:
8	if not $\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{d}\_\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{e}\mathrm{s}\_\mathrm{f}\mathrm{o}\mathrm{r}\_\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(comb\_3\_planes)$:
9	continue
10	$vertex=\mathrm{g}\mathrm{e}\mathrm{t}\_\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\_\mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\left(planes\right[comb\_3\_planes\left[0\right]]$, $planes[comb\_3\_planes[1\left]\right]$, $planes[comb\_3\_planes[2\left]\right])$
11	if not $\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{d}\_\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\_\mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}(vertex, points,inliers\_planes[comb\_3\_planes\left[0\right]], inliers\_planes[comb\_3\_planes\left[1\right]], inliers\_planes[comb\_3\_planes\left[2\right]], sigma\_d)$:
12	continue
13	$vertex\_idx=\mathrm{l}\mathrm{e}\mathrm{n}\left(vertices\right)$
14	$vertices.\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\left(vertex\right)$
15	$vertices\_per\_plane[comb\_3\_planes[0\left]\right].\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}(vertex\_idx)$
16	$vertices\_per\_plane[comb\_3\_planes[1\left]\right].\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}(vertex\_idx)$
17	$vertices\_per\_plane[comb\_3\_planes[2\left]\right].\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}(vertex\_idx)$
18	$planes\_per\_vertex.\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}(comb\_3\_planes)$
19	for $comb\_2\_vertices$ in $\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\left(\mathrm{l}\mathrm{e}\mathrm{n}\left(vertices\right)\right), 2)$:
20	$vertex\_0$, $vertex\_1=comb\_2\_vertices\left[0\right]$, $comb\_2\_vertices\left[1\right]$
21	$planes\_intersected=\mathrm{s}\mathrm{e}\mathrm{t}.\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(\mathrm{s}\mathrm{e}\mathrm{t}\right(planes\_per\_vertex[vertex\_0]), \mathrm{s}\mathrm{e}\mathrm{t}(planes\_per\_vertex[vertex\_1]\left)\right)$
22	if $\mathrm{l}\mathrm{e}\mathrm{n}(planes\_intersected)$ == 2:
23	if $(vertex\_0, vertex\_1)$ not in $edges$ and $(vertex\_1, vertex\_0)$ not in $edges$:
24	$edges.\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\left(\right(vertex\_0, vertex\_1\left)\right)$
25	$mesh=\mathrm{H}\mathrm{a}\mathrm{l}\mathrm{f}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{M}\mathrm{e}\mathrm{s}\mathrm{h}(vertices, edges)$
26	$seams=\left[\right]$
27	for $edge$ in $mesh.edges$:
28	if not $\mathrm{H}\mathrm{a}\mathrm{l}\mathrm{f}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{M}\mathrm{e}\mathrm{s}\mathrm{h}.\mathrm{i}\mathrm{s}\_\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}\left(edge\right)$:
29	$he1,he2=mesh.\mathrm{g}\mathrm{e}\mathrm{t}\_\mathrm{h}\mathrm{a}\mathrm{l}\mathrm{f}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\_\mathrm{t}\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{s}\left(edge\right)$
30	$n1, n2=\mathrm{g}\mathrm{e}\mathrm{t}\_\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}\_\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}(he1.suface),\mathrm{g}\mathrm{e}\mathrm{t}\_\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}\_\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}(he2.surface)$
31	$sigma=\mathrm{d}\mathrm{o}\mathrm{t}\left(\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}\right(n1, n2), he1.vector)$
32	if $sigma$ < 0:
33	$seams.\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\left(edge\right)$
34	return $vertices$, $seams$

4. Experimental Verification

4.1. Experiment Setup

To evaluate the proposed method with weldments, an experimental platform consisting of a turntable and a 3D structured light camera is built, depicted in Figure 12. The 3D camera (DM Series production of Hanchine) has a FOV of $110\times 70 \mathrm{m}\mathrm{m}$ (close end) to $300\times 210 \mathrm{m}\mathrm{m}$ (far end), with a resolution of 2.3 million and an average error of $0.15\%$. The turntable diameter is 250 mm, and the repeatability is ±0.05°.

Figure 12. Experiment setup for 3D reconstruction.

According to Formula $\left(5\right)$, the accurate turntable axis vector $\mathit{n}$ and center point $c$ with respect to the camera coordination are required for 3D reconstruction. We employ the method proposed by Yang et al. [24] to calibrate and verify the parameters in the following steps.

(1)

A standard metal cube (of size $80\times 100\times 120 \mathrm{m}{\mathrm{m}}^3$) is used as the reference object for calibration. The setup is displayed in Figure 13, where 36 frames of point clouds of the cube are captured with the turntable rotating $10°$ for each frame (Figure 14a).

Figure 13. Experiment setup for turntable calibration.

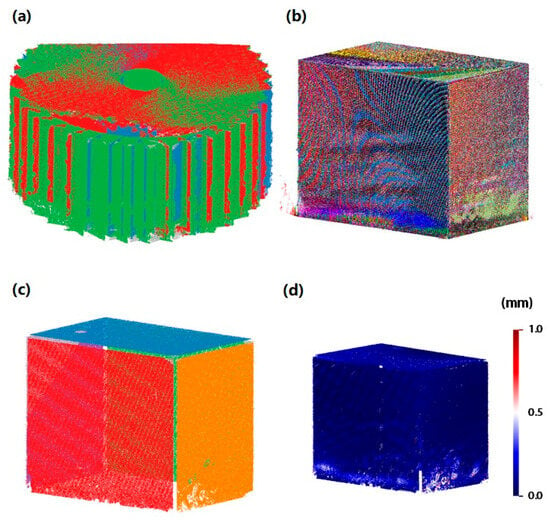
Figure 14. Verification experiments with the calibrated turntable: (a) the multiple point clouds grabbed from the standard cube; (b) the registered point cloud; (c) plane segmentation result of the registered point cloud; (d) temperature map representing segmentation error of the plane segmented planes.

(2)

All frames of point clouds are merged into one with point cloud registration, where $\mathit{n}$ and $c$ are the main parameters. The calculation of $\mathit{n}$ and $c$ is turned into the optimization of the point cloud registration that leads to the minimum registration error, which is further decomposed into axis calibration and center point calibration. The result is recorded in Table 1.

Table 1. Calibration result of the turntable.

Variable	Result
$\mathit{n}$	$[0.0202,-0.681,-0.732]$
$c$ (mm)	$[73.72,-45.10, 466.60]$

Table 1. Calibration result of the turntable.

Variable	Result
$\mathit{n}$	$[0.0202,-0.681,-0.732]$
$c$ (mm)	$[73.72,-45.10, 466.60]$

(3)

Point cloud registration is performed on all the point clouds obtained in step (1) with the parameters calculated in step (2), as depicted in Figure 14b.

(4)

Perform plane segmentation on the registered point cloud in step (3) (Figure 14c). The registration error in step (3) is measured as the plane segmentation error, as visualized in Figure 14d. Since the segmentation error is small, we reasonably infer that the calibration is accurate enough.

4.2. Experiment for 3D Reconstruction

To test the proposed 3D reconstruction and WSE algorithms, we choose some typical spatial planar workpieces from a signal tower base manufacturer as weldments. As displayed in Figure 15, the samples meet the characteristics of “multi-variety and small batches” described in Section 1.

Figure 15. Spatial planar weldments from a signal tower base manufacture.

With the turntable calibrated, point cloud registration with multiple frames of point clouds is possible. To reconstruct the geometric characteristics of the weldment, point cloud registration is applied with Formula $\left(5\right)$. Figure 16 displays the point clouds before and after registration.

Figure 16. Point clouds before (first row) and after (second row) registration, with each point cloud frame rendered in a different color.

4.3. Experiment for Plane Segmentation

Several experiments are conducted to evaluate the performance of the plane segmentation algorithm proposed in Section 3.

The standard cube serves as the experimental object for the initial comparison. Table 2 presents a detailed comparison of segmentation results between vanilla RANSAC, RANSAC without normal vector clustering (non-clustering RANSAC hereafter), and the improved RANSAC. To ensure a fair comparison, all implementations utilize identical configurations for variables such as downsampling, distance threshold, max iteration, etc. No parallel computation, such as AVX, is employed (the same goes for the following comparisons). The reported results are averaged over 20 runs. For vanilla RANSAC, the PCL implementation [25] is utilized.

Table 2. Segmentation result comparison with a standard cube.

Variable	Vanilla RANSAC	Non-Clustering RANSAC		Improved RANSAC (Proposed)
	Value	Value	Comparison *	Value	Comparison *
average error (mm)	$0.28$	0.40	+42.9%	$0.072$	−74.3%
standard deviation	$0.0023$	0.0030	+30.4%	$0.00081$	−64.8%
execution time (s)	$4.85$	$30.46$	+528%	$16.79$	+246%
correct planes segmented	$5/5$	$5/5$	0%	$5/5$	0%
incorrect planes segmented	0	0	0%	0	0%
total points (downsampled)	$\mathrm{140,022}$	$\mathrm{140,022}$	0%	$\mathrm{140,022}$	0%
inliers	$\mathrm{139,003}$	$\mathrm{134,471}$	−3.2%	$\mathrm{134,591}$	−3.17%

* The comparisons are made against Vanilla RANSAC.

Analysis of Table 2 reveals that the improved RANSAC significantly outperforms vanilla RANSAC regarding segmentation accuracy, although this difference may not be readily apparent in Figure 17. Vanilla RANSAC exhibits faster execution compared to the proposed algorithm, as the surface normal estimation and Euclidean clustering utilized in the proposed algorithm are relatively time-consuming. However, compared to non-clustering RANSAC, the improved RANSAC demonstrates superior efficiency.

Figure 17. Segmentation comparison over a standard cube. (a) Vanilla RANSAC; (b) non-clustering RANSAC; (c) improved RANSAC.

In the subsequent experiment, an icosahedral column, serving as a relatively complex standard workpiece, is employed as the experimental object. The comparison results are depicted in Figure 18 and summarized in Table 3. In this set of experiments, both vanilla RANSAC and non-clustering RANSAC exhibit poor performance in accurately segmented planes, with numerous incorrect planes generated. With further tuning in the configuration, the latter may perform better in this experiment. However, we retain this result as, with the same configuration, the improved RANSAC efficiently identifies all the planes.

Figure 18. Segmentation comparison over an icosahedral column. (a) Vanilla RANSAC; (b) non-clustering RANSAC; (c) improved RANSAC.

Table 3. Segmentation result comparison with an icosahedral column.

Variable	Vanilla RANSAC	Non-Clustering RANSAC		Improved RANSAC (Proposed)
	Value	Value	Comparison	Value	Comparison
average error (mm)	$1.02$	$1.26$	+23.5%	$0.0030$	−99.7%
standard deviation	$0.022$	$0.026$	+18.2%	$0.00065$	−97.0%
execution time (s)	$13.42$	$104.93$	+682%	$20.80$	+55.0%
correct planes segmented	$15/21$	$13/21$	−13.3%	$21/21$	+40%
incorrect planes segmented	10	9	−10%	0	−100%
total points (downsampled)	$\mathrm{85,501}$	$\mathrm{85,501}$	0%	$\mathrm{85,501}$	0%
inliers	$\mathrm{84,677}$	$\mathrm{84,395}$	−0.33%	$\mathrm{81,002}$	−4.3%

It is to be noted that in Table 1, Table 2 and Table 3, the total planes to be segmented (displayed as denominators in a row “correct planes segmented”) is not equal to “correct planes segmented” plus “incorrect planes segmented”. As an example, for a given point cloud with three planes to be segmented, if the segmentation mistakenly has two of the planes recognized as one plane and the left one plane recognized as three planes, the number of incorrect planes reaches four, which is bigger than the total planes to be segmented (three). Unreasonable segmentation may output more planes than needed, as actually happens to Vanilla RANSAC and non-clustering RANSAC in Table 3 and Table 4. This phenomenon can be more intuitively observed in Figure 18a,b.

Table 4. Segmentation result comparison with a spatial planar weldment.

Variable	Vanilla RANSAC	Non-Clustering RANSAC		Improved RANSAC (Proposed)
	Value	Value	Comparison	Value	Comparison
average error (mm)	$1.35$	$0.31$	−77.0%	$0.0030$	−99.8%
standard deviation	$0.013$	$0.0023$	−82.3%	$0.00065$	−95%
execution time (s)	$74.77$	$597.63$	+699%	$578.42$	+674%
correct planes segmented	$15/21$	$16/21$	+6.67%	$21/21$	+40%
incorrect planes segmented	7	0	−100%	0	−100%
total points (downsampled)	$\mathrm{394,437}$	$\mathrm{394,437}$	0%	$\mathrm{394,437}$	0%
inliers	$\mathrm{384,093}$	$\mathrm{345,932}$	−9.94%	$\mathrm{354,087}$	−7.81%

In the final comparison group, one of the spatial planar weldments is utilized for weld seam extraction as the object. Table 4 presents the data comparison of the results. The improved RANSAC successfully captures all the planes required. Conversely, vanilla RANSAC fails to segment nearly one-third of the necessary planes and produces several incorrect planes, as demonstrated in Figure 19.

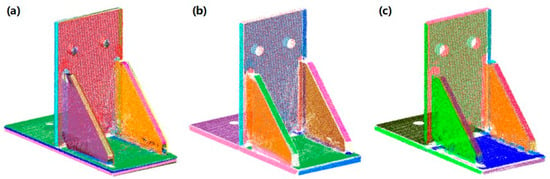
Figure 19. Segmentation comparison over a spatial planar weldment. (a) Vanilla RANSAC; (b) non-clustering RANSAC; (c) improved RANSAC.

By applying the improved RANSAC algorithm, consecutive plane segmentation is performed on the weldments, Figure 20 illustrates the process.

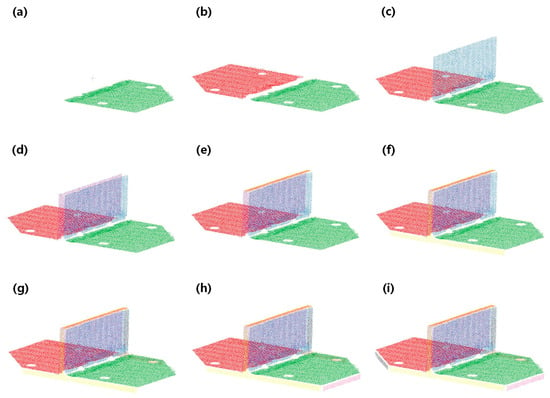
Figure 20. Part of the process of consecutive plane segmentation. One plane is segmented in each stage of (a–i).

The segmentation results of the weldments are displayed in Figure 21, where photographs of the weldments, segmentation results, and the corresponding normal vector clustering results are arranged for comparison.

Figure 21. Plane segmentation for several weldments. (Row one): photos of the physical weldments. (Row two): segmentation results rendering each plane with a different color. (Row three): normal vector clustering results of the corresponding segmentations.

4.4. Experiment for Weld Seam Extraction

After obtaining the segmented planes, the calculation of weld seams can be executed using the WSE algorithm proposed in Section 3. The outcomes, comprising valid weld seams and invalid edges excluded based on the edge convexity criterion, are visualized in Figure 22.

Figure 22. The WSE results: valid weld seams are marked with thick red lines and invalid weld seams are marked with thin blue lines.

4.5. Discussion

The 3D reconstruction for the weldments demonstrates that a point cloud that represents the complete geometric features of a complex spatial planar weldment can be generated by point cloud registration, with the incorporation of a well-calibrated turntable. Notably, this methodology remains effective regardless of the initial position and orientation of the weldments, thus addressing the issue outlined in the introductory section.

Although welding is a relatively low-precision processing process, extracting weld seams from point clouds is still challenging. The reason not only lies in the difficulty of ensuring numerical accuracy when extracting geometric features but also in the fact that conventional feature extraction algorithms such as vanilla RANSAC tend to fail for complex workpieces. Experiments on plane segmentation reveal that conventional RANSAC algorithms exhibit commendable performance and acceptable accuracy solely for objects with rudimentary shapes. When confronted with intricate spatial structures, these algorithms either fail to detect certain planes or return inaccurate results. In contrast, the proposed improved RANSAC algorithm showcases the ability to accurately recognize planes from spatial workpieces, even those characterized by multiple angles and complex intersecting planes.

The improvement of the proposed method over the conventional method varies from case to case. In the experiments conducted in this study, the average errors are reduced by 90.3% to 99.8%, and the standard deviations are reduced by 64.8% to 97.0%. Moreover, thanks to the optimizations introduced in Section 2.2, the improved RANSAC greatly eliminates the problems encountered by conventional RANSAC when dealing with complex workpieces. As shown in the experimental results, the proposed segmentation method ensures the extraction of necessary planes while avoiding the generation of erroneous planes. Since the conventional methods basically fail to generate the weld seams properly, we are unable to provide comparisons on WSE over the proposed method and conventional ones.

5. Conclusions

This paper introduces a global weld seam extraction method tailored for arbitrarily placed spatial planar weldments. The key contributions and outcomes of this research endeavor are summarized as follows:

(1)

By introducing point cloud registration with multiple frames of point clouds captured from a weldment, a three-dimensional reconstruction of the weldment is carried out without knowing the position and posture of the weldment. Due to the universality of this method, it may be applied to most scenarios that require a complete 3D digital twin model.

(2)

We propose an improved RANSAC algorithm designed to execute consecutive plane segmentation with remarkable accuracy. This algorithm is adept at handling the plane segmentation of complex spatial planar weldments, a task challenging for conventional similar algorithms. As demonstrated by the experiments, the average errors are reduced by 90.3% to 99.8% over the traditional RANSAC algorithm, and the standard deviations are reduced by 64.8% to 97.0%. This method can also be used in other processing techniques that require obtaining planar features through point clouds.

(3)

Additionally, we present a weld seam extraction (WSE) algorithm for multiple weld seam extraction, which calculates all the edges from the segmented planes and selects valid weld seams with vertex validation and edge convexity validation utilizing the half-edge data structure.

The proposed methodologies offer an elegant solution for automatically and accurately extracting weld seams from complex weldments without precise fixing. Nevertheless, our approach still has limitations and areas that deserve extension.

(1)

This research uses a single-axis turntable to expand the 3D camera’s FOV. When the workpiece shape is particularly complex, there could still be geometric features that are difficult to capture. To further achieve the 3D reconstruction capability, we consider introducing multi-axis turntables as a replacement. The calibration of multi-axis turntables will become a research focus.

(2)

The WSE method proposed in this paper approximates the weld seams as the intersection lines of adjacent planes in the workpiece. For the case where welding grooves are to be concerned, further microscopic analysis and modeling of the grooves is required before it is used for robot welding path planning. Also, due to the poor performance of RANSAC (even the improved version proposed in the paper) in identifying narrow and long planes, this method only applies to plate structures with a thickness of more than 2 mm.

(3)

To improve the method’s scope of application, our future investigations will center on weldments featuring free surfaces.