Design and Experimental Study of a Down-Drive Piezoelectric High-Frequency Fatigue Testing Machine

Abstract

In order to solve the problem of large dynamic load and low loading accuracy prevailing in traditional fatigue testing machines, and to meet the fatigue test loading demand of alternating small-load microelectromechanical devices and bionic devices, a high-frequency resonant piezoelectric fatigue tester that can apply alternating small loads in the range of 0.1 N~100 N was designed and manufactured, with a piezoelectric oscillator as the driving source of the system. Firstly, the structure of this fatigue testing machine is designed, and a dynamic model is established for the fatigue testing machine to theoretically study the influence of the system mass and stiffness on the change in the resonance frequency of the fatigue testing machine. Then, numerical calculations and experiments are carried out to verify the effect of system mass and stiffness changes on the intrinsic frequency of the fatigue testing machine. Finally, the fatigue testing machine was used to carry out fatigue test on the dog-bone-shaped specimens, and the failure process of specimen fatigue was verified by analysing the load applied to the specimen by the fatigue testing machine, and at the same time, it was proved that the performance of the present fatigue testing machine complied with the requirements. It provides a new technical means to meet the fatigue test loading demand of small-load electromechanical devices and bionic devices.

1. Introduction

In recent years, with the development of microelectromechanical technology and biomimetic technology, products such as microactuators [1,2], microsensors [3], and bionic fish [4] have emerged. The development of technologies for testing the mechanical properties of these products under near-service conditions has become extremely urgent. Fatigue testing is an important method to study the mechanical properties of materials [5,6]. Due to the complexity of the fracture conditions of materials [7], fatigue testers have been designed to test them in bending [8,9], torsion [10], or tension [11,12]. Tensile fatigue studies of products are very helpful in recognizing the safety of steel sheet assemblies, and uniaxial test methods are still widely used compared to the complexity of biaxial bending tests. In the case where uniaxial pure tensile loading is considered, the specimen is clamped in the fixture of a fatigue testing machine, and cyclic tensile stresses at a fixed frequency generated by the fatigue testing system are applied to the specimen in order to fail the specimen and calculate the fatigue life.

The variable load applied to the specimen by the fatigue tester is essentially generating a vibratory load. In the current research, uniaxial fatigue tester drives are mainly categorized into three types, “electromagnetic drive” [13,14], “electro-hydraulic servo drive” [15,16], and “piezoelectric drive” [17]. Among them, the electromagnetically driven type is characterized by fast response and is suitable for routine material testing, and it is also the most commonly used fatigue test equipment; The electro-hydraulic servo-driven type has a larger output power and is suitable for the inspection of large, medium, and heavy loaded parts, but with a low operating frequency and a long testing time, the range of applications is more restricted. Piezoelectric materials are often used as high-speed and -precision actuators due to their fast response, lack of electromagnetic interference, high resolution, and high deformation accuracy [18]. As a result, researchers favour fatigue testing machines that use piezoelectric materials as the drive source. Piezoelectric fatigue testers can be categorized into three types: the first one is piezoelectric ceramic ultrasonic transducer-driven fatigue testers [19,20], the second is piezoelectric stack-driven fatigue testers [21], and the third one is piezoelectric vibrator-driven fatigue testers [22].

Zeng [17] designed a circular piezoelectric vibrator-driven fatigue testing machine, adjusting the frequency of the alternating voltage acting on the piezoelectric vibrator to induce the resonance of the whole system, and the inertial force generated by the mass of the elastic loader in the resonance state is reciprocated on the specimen, thus realizing fatigue testing. Li Kang [23] designed a piezoelectric-driven horizontal fatigue tester, which avoids the interference of the mass of the fixture in the vertical structure for static or dynamic loading. Ma Lei [24] proposed a new type of piezoelectric high-frequency micro load fatigue testing machine; the specimen is only subjected to alternating stress in the horizontal direction, avoiding the influence of other factors on the loading of the specimen, to ensure that the specimen fatigue test results are accurate. Most of the existing fatigue testing machines at home and abroad are designed for macro-scale devices, the dynamic loading is generally more than 500 N; the development of a more mature piezoelectric fatigue testing machine with a dynamic load greater than 100 N, and the development of piezoelectric fatigue testers for the range of less than 100 N, are still in the exploration stage.

Aiming at the problems of large motorised load and low loading accuracy of traditional fatigue test, this paper designs a high-frequency piezoelectric fatigue tester which can apply alternating small loads in the range of 0.1 N~100 N, establishes the kinetic model of its system, and carries out the theoretical and simulation analysis of the system, and finally fabricates the fatigue test prototype and conducts experimental tests on the dog-bone-shaped steel plate specimens. By analysing the load applied to the specimen by the fatigue testing machine, the failure process of specimen fatigue is verified, and at the same time, it is proved that the performance of this fatigue testing machine meets the requirements: to provide test methods for microelectromechanical devices and bionic devices to obtain the dynamic performance parameters under service conditions, and to provide technical means to reveal the related mechanical behaviour, deformation damage mechanism and performance evolution law under small loads.

2. Materials and Methods

2.1. Structural Design

The structure of the piezoelectric fatigue testing machine is shown in Figure 1, which mainly consists of a piezoelectric vibrator, preset load adjusting mechanism, force detecting mechanism, clamping mechanism, specimen, dynamic load adjusting mechanism, and fixing mechanism, as shown in Figure 1a. The piezoelectric vibrator provides the exciting force for the system and consists of a circular substrate and two circular piezoelectric certificates. Among them, the upper and lower circular piezoelectric ceramics are polarized in opposite directions, and under the action of external alternating voltage, the upper and lower circular piezoelectric ceramics will vibrate due to the inverse piezoelectric effect, as shown in Figure 1b. The dynamic load adjustment mechanism is set up to adjust the resonance frequency and force of the resonance system, which mainly consists of a vibration transmitting plate, flexibility loop, lower support plate, vibration transmitting rod, driving and counterweight parts, and each part is connected together by the vibration transmitting rod, as shown in Figure 1c. While the core part of the dynamic load adjustment mechanism is the drive and counterweight part, the piezoelectric actuator is mounted in the lower part of the fatigue tester and transmits the excitation force to the elastic ring through a connecting shaft with a diameter of 5 mm. The piezoelectric actuator consists of a double-layered piezoelectric vibrator with a sandwich, in which the piezoelectric ceramic and metal are bonded together with epoxy resin. The inverse piezoelectric effect of the piezoelectric vibrator generates alternating excitation forces for the actuator, which are amplified by two elastic rings. In addition, in order to vary the driving frequency, two identical semi-cylindrical steel mass blocks were mounted on the upper plate of the piezoelectric actuator and secured with bolts of 3 mm in diameter, as shown in Figure 1d.

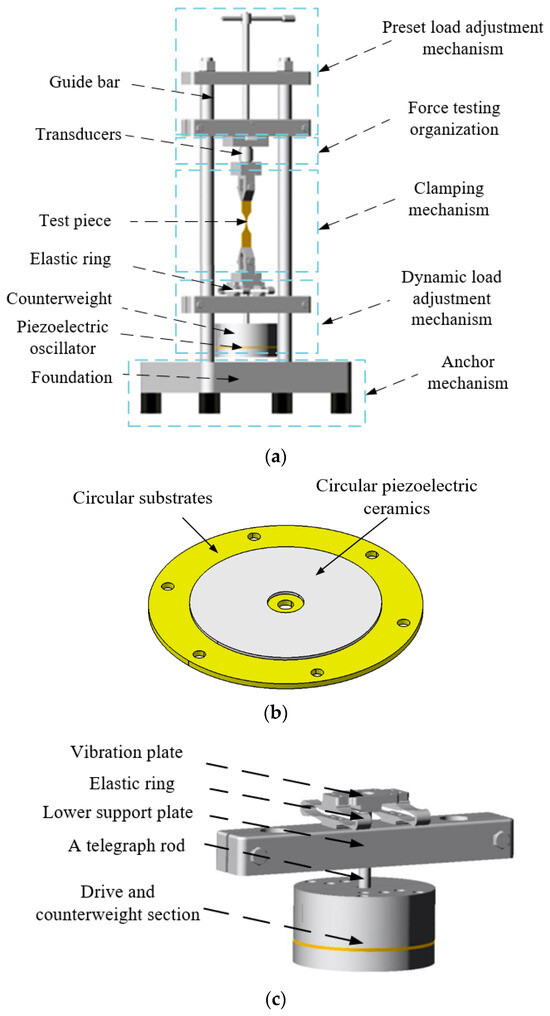
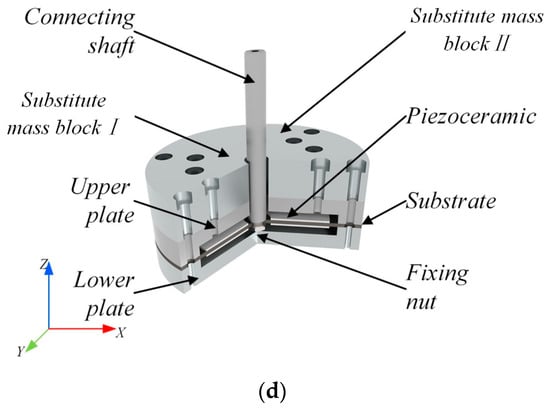
Figure 1. Structure of fatigue testing machine. (a) Fatigue testing machine system structure diagram (200 mm × 45 mm × 600 mm); (b) Three-dimensional schematic of a piezoelectric vibrator; (c) Three-dimensional structure of dynamic load adjustment mechanism; (d) Three-dimensional structure of piezoelectric actuator.

2.2. Working Principle

Although fatigue testing machines have numerous successful applications, they can be traditionally categorized into three types based on the way energy is utilized when loading a specimen. The first type is the excitation energy recovery test system [25], where the specimen is loaded on a rotating eccentric wheel, where the released potential energy from the previous loading cycle is transferred as kinetic energy for the next cycle. The second type is the unincentivized energy recovery test system [26], with constant pressure and rate test loads induced by an electrohydraulic servo control system. Therefore, whether the test system is loaded or not, it still consumes a fixed amount of excitation energy. In contrast to a recycled test system, there is no energy to reuse here, and in addition, continuous testing generates waste heat, which requires additional energy for cooling. The last type is the resonant test system [27], where the driving frequency of the tester is designed to be close to the intrinsic frequency of the test system, which is the intrinsic vibration frequency of the system itself, and whose value is independent of the initial conditions and the magnitude of the external excitation to which it is subjected. In this design, a frequency is applied to the system to excite the resonance of a linear system or the subharmonic oscillations of a nonlinear system, and by applying a small excitation force, the amplitude can be increased so that the energy consumption of the tester is mainly focused on the resonance active damping. This fatigue tester consumes less energy than the first or second previously mentioned test systems.

In this paper, a small-load fatigue tester based on a Type III resonance test system is designed to use a piezoelectric vibrator as the driving force source of the system, which generates vibrations under the action of an applied alternating electric voltage. Adjust the frequency of the alternating voltage applied to the piezoelectric vibrator, prompting the vibration system consisting of the base, guide rod, preset load adjustment mechanism, force detection mechanism, clamping mechanism, specimen, dynamic load adjustment mechanism, and fixing mechanism to resonate. At this time, the inertial force generated by the counterweight mass block in the resonance state reciprocates on the specimen. In addition to this, the inertia force generated by the mass of the counterweight disk, the piezoelectric vibrator, and the lower disk in the status of resonance also acts on the specimen at the same time, thus realizing fatigue testing.

The fatigue testing machine needs to determine the force applied to the specimen in real time during fatigue testing, so it is necessary to build a force testing system as shown in Figure 2, which consists of transducers, boosters, 24VDC power supply, acquisition card, and acquisition software (V190521).

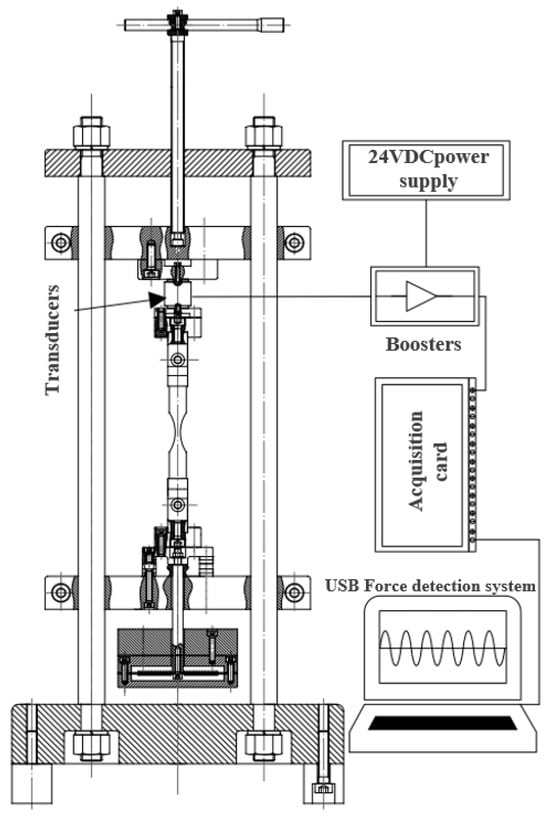
Figure 2. Fatigue testing machine force detection system.

The transducer works on the principle of resistance strain-type, when subjected to external forces, the deformation of its internal elastomer, causing changes in the resistance value of the resistance strain gauges, the transducer’s built-in circuitry will be converted into a change in resistance to voltage changes and output to the booster, which will be converted into a standard voltage signal. The acquisition card is powered by USB and acquires the voltage signal output from the booster and transfers it to the computer via the USB 2.0 bus. The acquisition software displays and records the loads acting on the sensors in real time, as shown in Figure 3 for the interface diagram of the acquisition software.

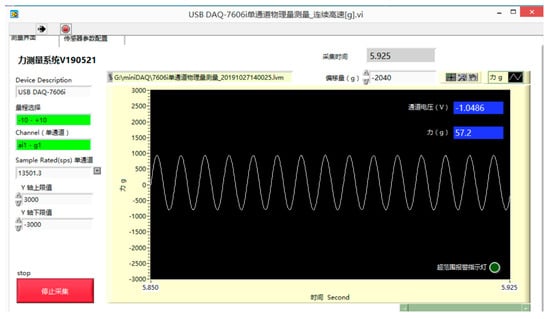
Figure 3. Acquisition Software Interface.

2.3. Material Parameters

2.3.1. Piezoelectric Vibrator

The PZT-8 is often used as a Lanzmann sensor because of its fast response characteristics. In this study, piezoelectric vibrator ceramics were chosen for similar reasons. Figure 4 shows the cross section of the piezoelectric vibrator considering the thickness of the piezoelectric ceramic (Tc) and the thickness of the spring steel substrate (Tm). Table 1 shows its material parameters. Table 2 shows its matrix parameter.

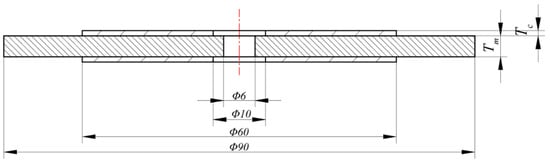
Figure 4. Cutaway view of piezoelectric vibrator.

Table 1. Material parameters of piezoelectric vibrator.

Materials	Densities (kg·m)	Modulus of Elasticity (Pa)	Poisson’s Ratio	Thicknesses (mm)
PZT-8	7600	—	—	Tc
Spring steel	7810	2.1 × 1011	0.288	Tm

Table 2. The three main matrices of the PZT-8.

$\mathbf{Dielectric} \mathbf{Coefficient} \mathbf{Matrix} [{\mathit{\epsilon }}^{\mathit{s}}]$	$\mathbf{Piezoelectric} \mathbf{Matrix} [\mathit{e}]/\mathbf{C}·{\mathbf{m}}^{-2}$	$\mathbf{Matrix} \mathbf{of} \mathbf{Elasticity} \mathbf{Coefficients} [\mathit{c}]/{10}^{10}\mathbf{N}·{\mathbf{m}}^{-2}$
$\begin{array}{cc}& \begin{array}{ccc}x & y & z \end{array}\\ \begin{array}{c}x\\ y\\ z\end{array}& \left[\begin{array}{ccc}900& 0& 0\\ 0& 900& 0\\ 0& 0& 600\end{array}\right]\end{array}$	$\begin{array}{cc}& \begin{array}{ccc}x & y & z \end{array}\\ \begin{array}{c}x\\ y\\ z\\ xy\\ yz\\ xz\end{array}& \left[\begin{array}{lll}0\hfill & 0\hfill & -4.1\hfill \\ 0\hfill & 0\hfill & -4.1\hfill \\ 0\hfill & 0\hfill & 14.0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 10.3\hfill & 0\hfill \\ 10.3\hfill & 0\hfill & 0\hfill \end{array}\right]\end{array}$	$\begin{array}{cc}& \begin{array}{cccccc} x \hfill & y \hfill & z \hfill & xy & yz & xz \end{array}\\ \begin{array}{l}x\hfill \\ y\hfill \\ z\hfill \\ xy\hfill \\ yz\hfill \\ xz\hfill \end{array}& \left[\begin{array}{llllll}14.9\hfill & 8.11\hfill & 8.11\hfill & 0\hfill & 0\hfill & 0\hfill \\ 8.11\hfill & 14.9\hfill & 8.11\hfill & 0\hfill & 0\hfill & 0\hfill \\ 8.11\hfill & 8.11\hfill & 13.2\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 3.4\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 3.13\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 3.13\hfill \end{array}\right]\end{array}$

2.3.2. Mass Block

A semi-cylindrical steel mass block is shown in Figure 5, which is made of 45# steel with thickness dimensions including 10 mm, 20 mm, and 30 mm, and the appropriate thickness is selected according to the need.

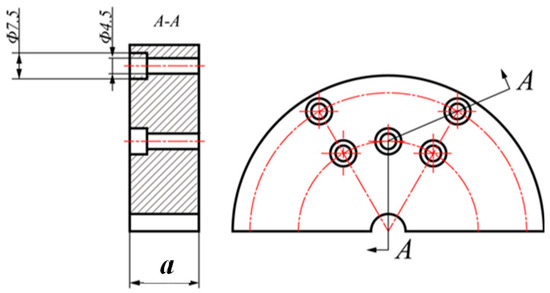
Figure 5. Cutaway view of a mass block.

2.3.3. Elastic Ring

As shown in Figure 6, the elastic ring is divided into three different zones according to its thickness. The middle part is thicker and is used to rigidly connect the other components of the fatigue tester. The left and right ends have thickened arcs designed to prevent damage due to stress concentration on both sides of the elastic ring during operation. In addition to these areas, the part connecting the middle and ends of the elastic ring forms the third part, which is thinner. The stiffness of the elastic ring increases as the thickness of this part increases. By changing the thickness of the elastic ring, the stiffness of the fatigue tester can be adjusted, thus changing the intrinsic frequency of the tester.

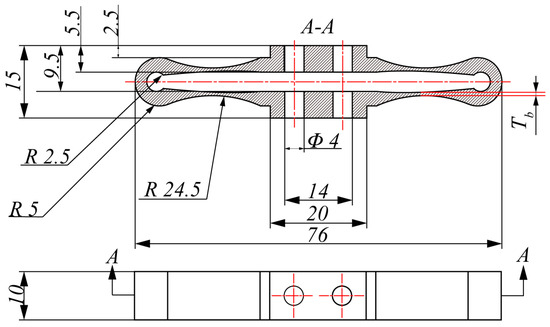
Figure 6. Cutaway view of an elastic ring.

Since the output force of the piezoelectric vibrator is relatively small, the size T_b at the elasticity of the elastic ring should not be too large. Take T_{b min} = 0.1 mm, T_{b max} = 1 mm, with 0.1 mm spacing, and the elastic ring material is 65 Mn spring steel.

2.3.4. Dog-Bone Steel Specimens

As shown in Figure 7 for the dog-bone-shaped steel specimen, since Q235b is a commonly used engineering material and its mechanical properties are very typical, the range of stresses applied to the specimen by the fatigue testing machine and the fatigue performance under alternating stresses are investigated using Q235b as an example. The chemical properties are shown in Table 3. Table 4 shows its mechanical properties.

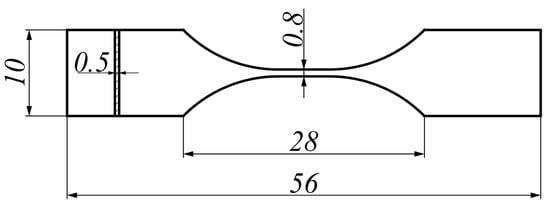
Figure 7. Specimen size.

Table 3. Chemical composition of Q235b.

Chemical Composition of Dog-Bone Specimen (Q235b) (wt%)
C	Si	Mn	S	P
0.12	0.03	0.45	≤0.0045	≤0.0045

Table 4. Mechanical properties of Q235b.

Yield Strength (MPa)	Tensile Strength (MPa)	Elongation min (%)	Density (Kg/m3)
235	375~460	26	7850

3. System Dynamics Modelling and Simulation Analysis

3.1. Structural Design

A fatigue tester is a typical example of a resonant system. In order to simplify the calculation process, the test machine was discretized into several centralized mass cells. According to the actual working conditions, select the parts that transmit more force and displacement as the centralized mass unit, ensure that the stiffness within each unit is consistent or similar, and avoid the appearance of relatively moving parts within the same unit. Therefore, when calculating the vibration characteristics of a fatigue testing machine in terms of a mass–spring–damping system, this method not only ensures the accuracy of the calculation but also reduces the cost of the calculation. Table 5 describes the components of the centralized mass element subsystem. Figure 8 shows the spring-mass-damping system model of the fatigue testing machine.

Table 5. List of discrete chaos models.

Mass Unit	Mass Unit Subunit	Structural Schematic
M1	M1.1 Force sensor
	M1.2 Force sensor substrates
	M1.3 Transfer plate
	M1.4 Upper fixture
M2	M2.1 Specimens
	M2.2 Bottom fixture
	M2.3 Lower fixed support plate
	M2.4 Vibration plate
	M2.5 Elastic ring
M3	M3.1 Connection shaft
	M3.2 Mass block
	M3.3 Circling overhead
	M3.4 Piezoelectric vibrator
	M3.5 Sump

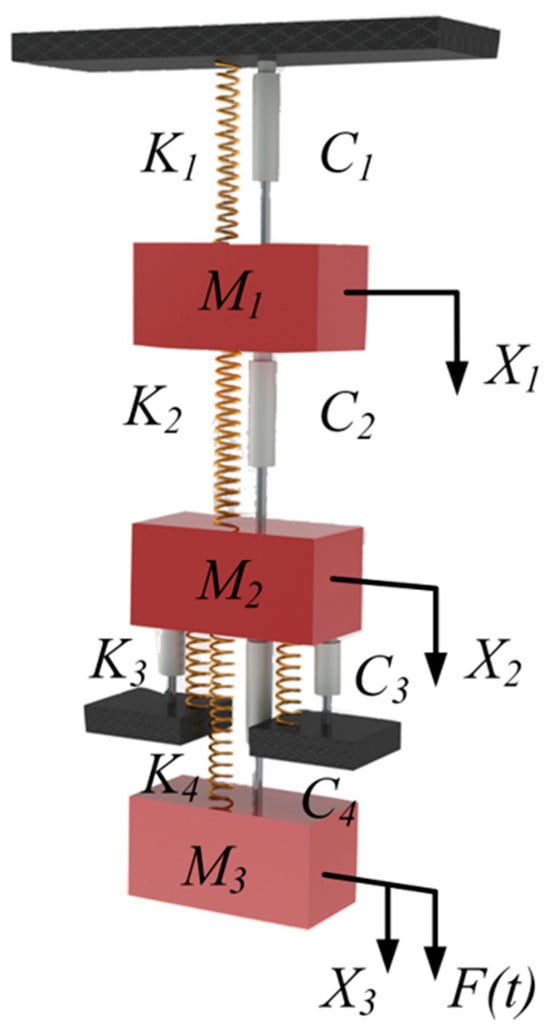
Figure 8. Model of spring–mass–damping system for fatigue testing machine.

Based on the above relationship for each mass unit, the ordinary differential equations are listed:

$$\begin{array}{l}\left[\begin{array}{ccc}{m}_1& & \\ & m_2& \\ & & m_3\end{array}\right]\left\{\begin{array}{c}{\ddot{x}}_1\\ {\ddot{x}}_2\\ {\ddot{x}}_3\end{array}\right\}+\left[\begin{array}{ccc}{c}_1+c_2& -c_2& \\ -c_2& c_2+2c_3-c_4& -c_4\\ & -c_4& c_4\end{array}\right]\left\{\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\end{array}\right\}+\\ \left[\begin{array}{ccc}{k}_1+k_2& -k_2& \\ -k_2& -k_2+2k_3-k_4& -k_4\\ & -k_4& k_4\end{array}\right]\left\{\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\\ F\sin (wt)\end{array}\right\}\end{array}$$

(1)

where k₁ is the transducer stiffness; k₂ is the elastic ring stiffness. K₃ is the sum of the connecting shaft stiffness and the piezoelectric vibrator stiffness.

In fatigue systems, changing the differential equations of a discrete system can be carried out by changing the intrinsic frequency of the system by changing the mass of the mass block, since the mass block is replaceable. Five values were averaged over the 0.999 kg to 3.999 kg range to perform a comprehensive frequency sweep analysis from 0 to 250 Hz. Using this method, it is possible to check the correlation between the mass change and the corresponding intrinsic frequency. The force load–frequency diagrams for the five mass blocks are shown in Figure 9; the greater the mass of the mass blocks, the lower the intrinsic frequency of the system.

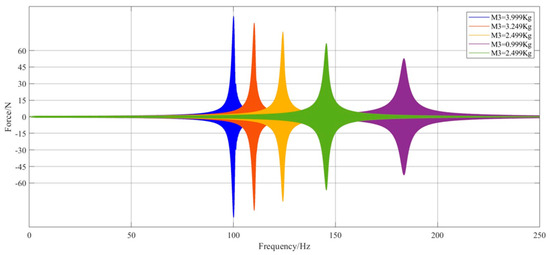
Figure 9. Intrinsic frequency of the system for mass.

Express the piezoelectric vibrator simple harmonic excitation force F(t) as:

$$F(t)=F{e}^{iwt},$$

(2)

Then the steady-state response of this system can be expressed as:

$$x_1(t)=X_1{e}^{iwt},x_2(t)=X_2{e}^{iwt},x_3(t)=X_3{e}^{iwt},$$

(3)

where X₁ and X₂ are complex quantities, taking values related to the system parameters, piezoelectric vibrator simple harmonic excitation force.

Equations (2) and (3) are brought into the vibrational differential Equation (1) and expressed in matrix form:

$$\left[\begin{array}{ccc}{Z}_{11}(w)& Z_{12}(w)& Z_{13}(w)\\ Z_{21}(w)& Z_{22}(w)& Z_{23}(w)\\ Z_{31}(w)& Z_{32}(w)& Z_{33}(w)\end{array}\right]\left\{\begin{array}{c}{X}_1\\ X_2\\ X_3\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\\ F\end{array}\right\},$$

(4)

where

$$\left\{\begin{array}{l}{Z}_{11}(w)=-w^2{m}_1+iw(c_1+c_s(t))+k_1+k_s(t)\hfill \\ Z_{12}(w)=Z_{21}(w)=iw(-c_s(t))-k_s(t)\hfill \\ Z_{13}(w)=Z_{31}(w)=0\hfill \\ Z_{22}(w)=-w^2{m}_2+iw(c_s(t)+2c_2+c_3)+k_s(t)+2k_2+k_3\hfill \\ Z_{23}(w)=Z_{32}(w)=iw(-c_3)-k_3\hfill \\ Z_{33}(w)=-w^2{m}_3+iw(-c_3)+k_3\hfill \end{array}\right.,$$

(5)

If,

$$Z(w)=\left[\begin{array}{ccc}{Z}_{11}(w)& Z_{12}(w)& Z_{13}(w)\\ Z_{21}(w)& Z_{22}(w)& Z_{23}(w)\\ Z_{31}(w)& Z_{32}(w)& Z_{33}(w)\end{array}\right],$$

(6)

then Equation (4) can be expressed as:

$$\left[Z(w)\right]\left\{X\right\}=\left\{F\right\},$$

(7)

where $\left[Z(w)\right]$ is the impedance matrix, $\left\{X\right\}$ is the displacement column vector, and $\left\{F\right\}$ is the excitation amplitude column vector.

$$\left\{X\right\}={\left[Z(w)\right]}^{-1}\left\{F\right\},$$

(8)

where

$${\left[Z(w)\right]}^{-1}={\displaystyle \frac{1}{D}}\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right],$$

(9)

where

$$\left\{\begin{array}{l}D=Z_{11}(w)Z_{22}(w)Z_{33}(w)-Z_{11}(w)Z_{23}^2(w)-Z_{33}(w)Z_{12}^2(w)\hfill \\ a_{11}=Z_{22}(w)Z_{33}(w)-Z_{23}^2(w)\hfill \\ a_{12}=a_{21}=-Z_{12}(w)Z_{33}(w)\hfill \\ a_{13}=a_{31}=Z_{12}(w)Z_{23}(w)\hfill \\ a_{22}=Z_{11}(w)Z_{33}(w)\hfill \\ a_{23}=a_{32}=-Z_{11}(w)Z_{23}(w)\hfill \\ a_{33}=Z_{11}(w)Z_{22}(w)-Z_{12}^2(w)\hfill \end{array}\right.,$$

(10)

Thus, the steady–state response amplitude of the system can be obtained as a function of the excitation frequency w:

$$\left\{\begin{array}{c}{X}_1(w)={\displaystyle \frac{Z_{12}(w)Z_{23}(w)F}{Z_{11}(w)Z_{22}(w)Z_{33}(w)-Z_{11}(w)Z_{23}^2(w)-Z_{33}(w)Z_{12}^2(w)}}\\ X_2(w)={\displaystyle \frac{-Z_{11}(w)Z_{23}(w)F}{Z_{11}(w)Z_{22}(w)Z_{33}(w)-Z_{11}(w)Z_{23}^2(w)-Z_{33}(w)Z_{12}^2(w)}}\\ X_3(w)={\displaystyle \frac{(Z_{11}(w)Z_{22}(w)-Z_{12}^2(w))F}{Z_{11}(w)Z_{22}(w)Z_{33}(w)-Z_{11}(w)Z_{23}^2(w)-Z_{33}(w)Z_{12}^2(w)}}\end{array}\right.,$$

(11)

When the system damping is neglected, the steady-state response of the system can be found with respect to the excitation frequency w:

$$\left\{\begin{array}{l}{x}_1(t)={\displaystyle \frac{k_s(t)k_3\sin wt}{D_n}}\\ x_2(t)={\displaystyle \frac{k_3\sin wt}{D_n}}\left(-w^2{m}_1+k_1+k_s(t)\right)\\ x_3(t)={\displaystyle \frac{\sin wt}{D_n}}[\left(-w^2{m}_1+k_1+k_s(t)\right)\left(-w^2{m}_2+k_s(t)+2k_2+k_3\right)-k_s^2(t)]\end{array}\right.,$$

(12)

where

$$\begin{array}{l}{D}_n=\left(-w^2{m}_1+k_1+k_s(t)\right)\left(-w^2{m}_2+k_s(t)+2k_2+k_3\right)\left(-w^2{m}_3+k_3\right)\\ -\left(-w^2{m}_1+k_1+k_s(t)\right)k_3^2-\left(-w^2{m}_3+k_3\right)k_s^2(t)\end{array}$$

(13)

3.2. Simulation Analysis

In order to further investigate theoretically the influence of the mass M of the counterweight mass block and the stiffness k₂ of the elastic ring on the vibration characteristics of the fatigue tester, the relevant parameters were determined, as shown in Table 6.

Table 6. Detailed list of relevant parameters of the fatigue testing machine.

Mass Unit	Parameter Value/kg	Rigidity Parameter	$\mathbf{Parameter} \mathbf{Value}/(\times {10}^6)(\mathbf{N}/\mathbf{m})$	Damping Parameters	Parameter Value
$M_1$	0.2954	$k_1$	3.33	$c_1$	16.8568
		$k_s(t=0)$	5.43	$c_s(t)$	15.0000
$M_2$	0.3159	$k_2$	0.1: 0.1: 1	$c_2$	17.2519
$M_3$	$0.9990+M(0:0.2:3)$	$k_3$	6.21	$c_3$	20.8610

According to the above Equation (1), the elastic ring stiffness and mass block mass are used as parameters affecting the intrinsic frequency of the fatigue testing machine, by making D_n = 0 in Equation (13), the intrinsic frequency of the system can be solved for different parameters, The relationship is shown in Figure 10.

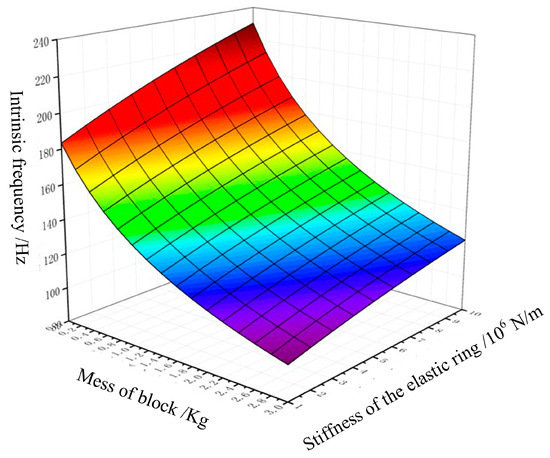
Figure 10. Plot of mass block and elastic ring stiffness versus intrinsic frequency of fatigue tester.

From Figure 10, it can be seen that for the same counterweight mass block mass, increasing the elastic ring stiffness (corresponding to increasing the thickness of the elastic ring at the flexible place Tb in the simulation analysis) gradually increases the system intrinsic frequency; for the same elastic ring stiffness, increasing the mass of the counterweight mass block (which corresponds to increasing the thickness of counterweight mass block a in the simulation analysis) results in a gradual decrease in the intrinsic frequency of the system, which is in accordance with the facts and with the results of the simulation analysis. The overall analysis of the fatigue testing machine was carried out using the finite element method, and the results are shown in Figure 11. The fatigue tester achieved the optimal solution of the modal vibration pattern at an operating frequency of 187 Hz. At this frequency, the piezoelectric actuator vibrates the fatigue tester vertically up and down with no displacement of the rest of the machine, as shown in Figure 12.

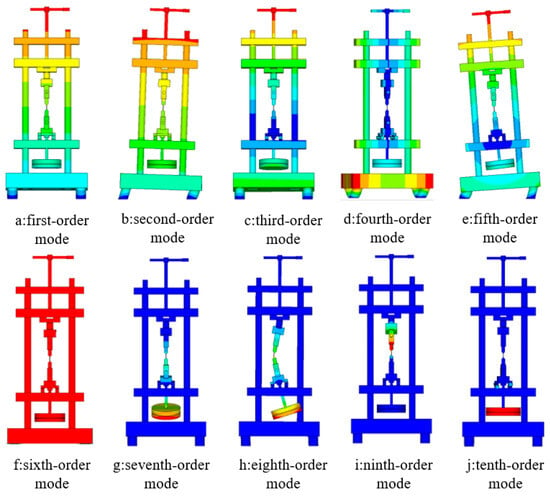
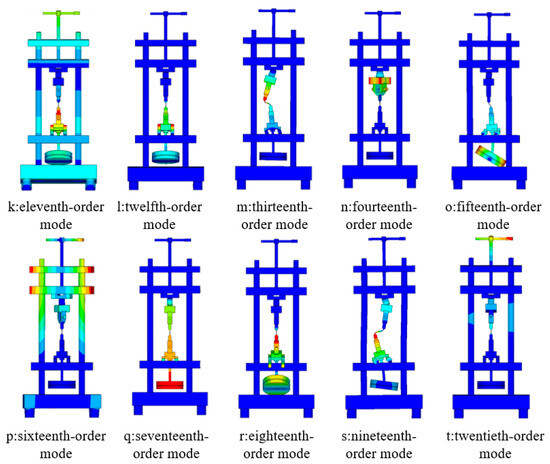
Figure 11. Cloud diagram of the first twenty orders of modal analysis of the fatigue testing machine.

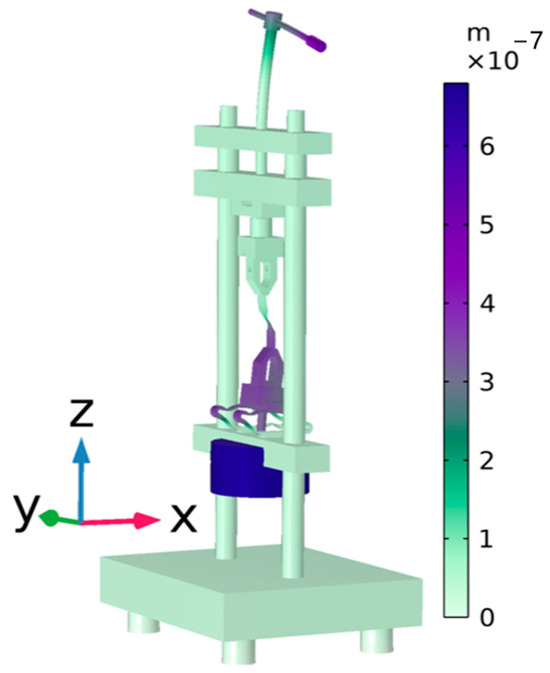
Figure 12. Finite element modal analysis of fatigue testing machine.

According to the above simulation process, the specimen with the central width w = 0.8 mm, the thickness of the counterweight mass block a = 0 mm:2 mm:30 mm, and the thickness of the elastic ring at the flexible place b = 0.1 mm:0.1 mm:1 mm were chosen, and the three-dimensional relationship between the intrinsic frequency of the fatigue testing machine and the thicknesses of the counterweight mass block a, and the thickness of the elastic ring at the flexible place b was obtained, which is shown in Figure 13.

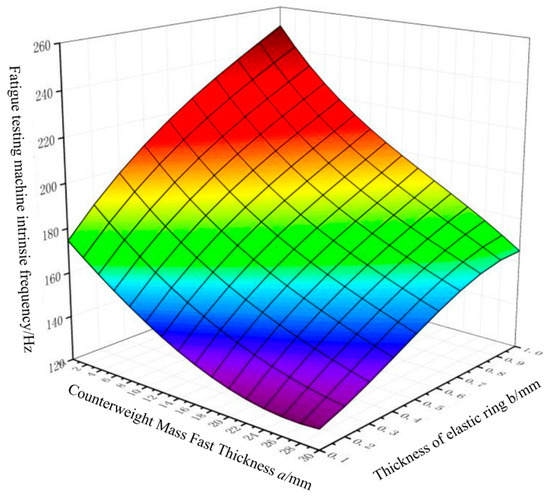
Figure 13. System intrinsic frequency versus thickness of counterweight mass block a, thickness of elastic ring at flexibility b.

From Figure 13 it can be seen that for the same counterweight mass block thickness a, increase the thickness of the elastic ring flexible place b, and fatigue testing machine system intrinsic frequency will gradually increase; for the same elastic ring flexible thickness b, increase the counterweight mass block thickness a, and fatigue testing machine system intrinsic frequency will gradually decrease.

4. Trial Tests

4.1. Test System Construction and Test Methods

Using the developed piezoelectric fatigue testing machine system, several sets of specimens of different sizes were processed on the basis of selected materials, the influence laws of different parameters on the resonance frequency of the system, and the stresses acting on the specimens were investigated, and finally the specimens were subjected to tension–tension fatigue tests. Shown in Figure 14 is the fatigue testing machine performance test system, including fatigue testing machine, signal generator (UTI-T, UTG7052B), phase shifter, power amplifier (SA-PA010), computer, impedance analyser (ZX70A), transducer (FCW-2620), amplifier (T098H), acquisition card (USB DAQ-7606I), and acquisition software (V190521). The characteristics and output performance of the piezoelectric fatigue tester system were investigated by selecting specimens with different stiffnesses, counterweights with different masses, and setting different preset loads and driving voltages. The dimensions of the fatigue testing machine are shown in Table 7.

Figure 14. Fatigue testing machine test system.

Table 7. Main structural dimensions of each part of the fatigue testing machine parts.

Part Number	Part Name	Dimensional Parameters	Parameter Value (mm)
1	Footing	Calibre	$\varphi$30
		High degree	30
2	Foundation	Length	250
		Width	200
		Thickness	45
		Centre distance between two holes in the middle	130
3	Guide bar	Centre Diameter	$\varphi$20
		Diameter on both sides	$\varphi$16
		High degree	488
4	Lower support plate	Length	200
		Width	35
		Thickness	25
5	Load board	Length	200
		Width	35
		Thickness	25
6	Backbone	Length	200
		Width	35
		Thickness	20
7	Screw	Large diameter	M10
8	Load handle	Outer diameter	$\varphi$8
9	Sensor fixing plate	Length	60
		Width	30
		Thickness	15
10	Transducers	Middle diameter	$\varphi$20
		Diameter on both sides	$\varphi$16
		High degree	22
11	Transducer lower connection plate	Length	35
		Width	30
		Thickness	7
12	Fixture fixing plate	Length	35
		Width	30
		Thickness	15
13	Fixture	Width	15
		Specimen clamping range	≤4
14	Specimen	Length	55
		Width on both sides	10
		Middle width	0.8
		Thickness	0.5
15	Vibration plate	Length	53
		Width	30
		Thickness on both sides	7
		Thickness in the middle	13
16	Elastic ring	Length	76
		Width	10
		Thickness	15
		Flex thickness	0.4/0.5/0.6/0.7
17	Telegraph rod	Length	94
		Calibre	8
		Head diameter	5
18	Mass of counterweights	Outer diameter	$\varphi$90
		Inside diameter	$\varphi$10
		Thickness	10/20/30
19	Counterweight	Outer diameter	$\varphi$90
		Inside diameter	$\varphi$70
		Thickness on all sides	13
		Thickness in the middle	8
20	Piezoelectric oscillator	Outer diameter of substrate	$\varphi$90
		Substrate inner diameter	$\varphi$6
		Substrate thickness	2
		Outer diameter of ceramic disc	$\varphi$60
		Ceramic disc inner diameter	$\varphi$10
		Thickness of ceramic disc	1
21	Circling in midstream	Outer diameter	$\varphi$90
		Inside diameter	$\varphi$70
		Thickness on all sides	10
		Thickness at centre	5

Prior to the start of the test, the specimen is clamped between the upper and lower fixtures, a suitable initial static load is applied to the specimen using the preset load adjustment mechanism, and the static load is maintained using the upper locking bolt. A precision impedance analyser is used to determine the intrinsic frequency of the system at this point, and an alternating voltage is applied to the piezoelectric vibrator at the intrinsic frequency. After continuously increasing the RMS value of the driving voltage, the transducer is utilized to determine the alternating load applied to the specimen at different voltages and recorded in real time using the VI acquisition software; The characteristics and output performance of the fatigue testing machine system are investigated by means of specimens of different stiffness.

4.2. System Intrinsic Frequency Impact Factor Testing

The specimen with the width w = 0.8 mm in the middle is selected, and the impedance characterization is carried out under different combinations of counterweight mass block and elastic ring, respectively, and the measured results are compared with the simulation and theoretical results. The test curve graph is shown in Figure 15.

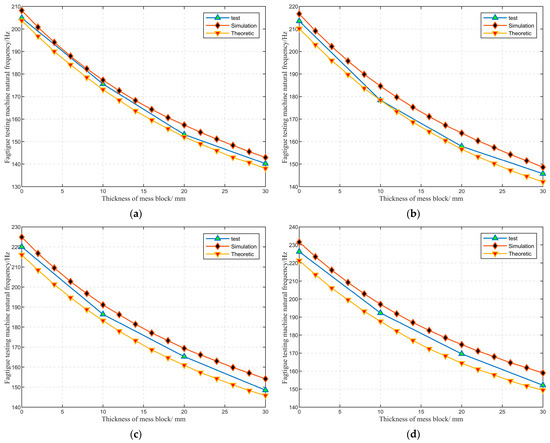
Figure 15. Comparison of simulated, theoretical, and experimental effects of structural parameter on the inherent frequency of the system. (a) T_b = 0.4 mm. (b) T_b = 0.5 mm. (c) T_b = 0.6 mm. (d) T_b = 0.7 mm.

From Figure 15, it can be clearly seen that increasing the thickness a of the counterweight mass block gradually decreases the intrinsic frequency of the system for the same thickness T_b at the elastic ring flexibility. For the same counterweight mass block thickness a, increasing the thickness T_b at the flexible place of the elastic ring, the intrinsic frequency of the system increases gradually, which is consistent with the facts and with the trend of the simulation and theoretical results. Moreover, the measured value of the system’s intrinsic frequency is closer to the simulated and theoretical values, and the maximum error is kept within 10 Hz, which verifies the correctness of the simulation and theoretical analysis.

4.3. Specimen Force Impact Test

In order to study the relationship between the voltage and the stiffness of the specimen on the stresses acting on the specimen, an elastic ring with a thickness T_b = 0.7 mm at the flexible place was selected, and the preset load F₀ = 10 N. The thicknesses a of the counterweight mass block were taken to be 0 mm, 10 mm, 20 mm, and 30 mm, respectively. The relationship of its effect on the stresses acting on the specimen by the fatigue testing machine was tested by selecting different specimens (w = 0.8 mm, 2 mm, and 3 mm) and voltages. The test relationship is shown in Figure 16.

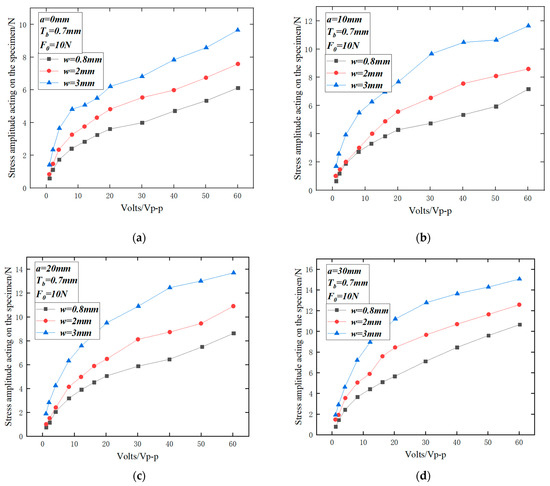
Figure 16. Stress amplitudes acting on the specimen with different counterweight mass blocks as a function of voltage and specimen stiffness. (a) a = 0 mm. (b) a = 10 mm. (c) a = 20 mm. (d) a = 30 mm.

From Figure 16, it can be concluded that the stress amplitude acting on the specimen gradually increases with the increase in driving voltage, At the same counterweight mass block and the same voltage, the amplitude of the stress acting on the specimen gradually increases as the specimen stiffness increases. When the thickness of the specimen w is 3 mm, the thickness of the counterweight mass block a is 30 mm, and the maximum stress acting on the specimen is about 14.8 N at a driving voltage of 60 V peak to peak.

4.4. Tests of the Effect of Preset Loads on Specimen Forces

In order to study the relationship between voltage and preset load on the stress acting on the specimen, based on the elastic ring with thickness T_b = 0.7 mm at the flexible place and the specimen with thickness w = 2 mm in the middle, when the counterweight mass block a was taken as 0 mm, 10 mm, 20 mm, and 30 mm, respectively, the effect of the preset load (F₀ = 20 N, 40 N, and 60 N) and the voltage was tested on the stress acting on the specimen in the fatigue tester by setting up different preset loads. The relationship is shown in Figure 17.

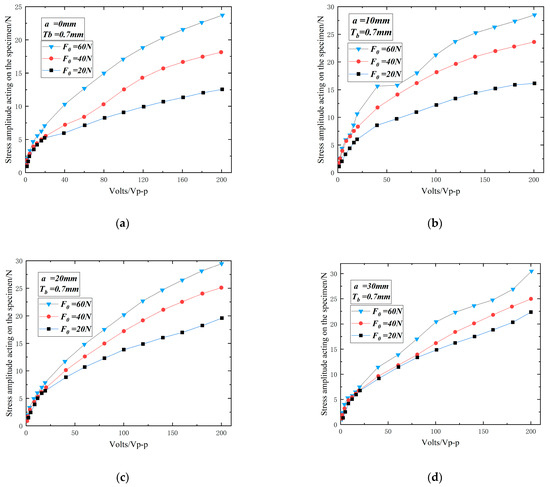
Figure 17. Stress amplitudes acting on the specimen as a function of voltage and preset load for different counterweight mass blocks. (a) a = 0 mm. (b) a = 10 mm. (c) a = 20 mm. (d) a = 30 mm.

As can be seen from Figure 17, the stress amplitude acting on the specimen increases gradually with the increase in driving voltage, and the stress amplitude acting on the specimen increases gradually when the preset load increases at the same counterweight mass block and the same voltage. The stress amplitude acting on the specimen ranges from about 1 N to 32 N within a driving voltage peak-to-peak range of 1 V to 200 V.

4.5. Fatigue Testing Machine Fatigue Testing Performance Verification

Finally, in order to verify the fatigue testing performance of the fatigue testing machine, a specimen with a central width w = 0.8 mm was selected and subjected to tensile–extensional fatigue testing with the following test steps: The load F_b applied to three or more specimens of the same specification at the time of damage is measured in advance and the average value is calculated; A suitable stress ratio R is selected and the maximum, minimum, and average loads applied to the specimen are determined according to the stress levels at each level; Determine the value of the applied preset load based on the average load corresponding to the stress levels at each level; adjust the signal generator to resonate the vibration system; The power supply voltage is adjusted so that the force applied to the specimen meets both the maximum and minimum load requirements; At this time to start timing, to be specimen fatigue rupture time accumulation and driving voltage frequency of the product of the number of cycles of the load. In determining the strength limit F_b of the specimen, limited by the limited test conditions, the specimen was manually tensile-tested using this fatigue testing machine, in which the loading was carried out as slowly and uniformly as possible. The three tensile test curves are shown in Figure 18.

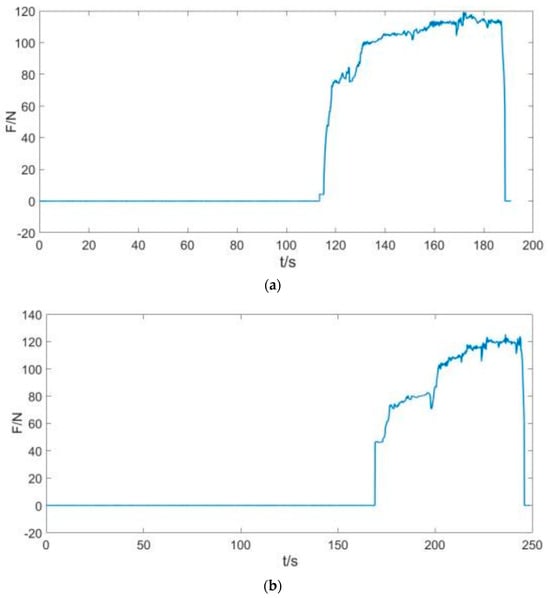
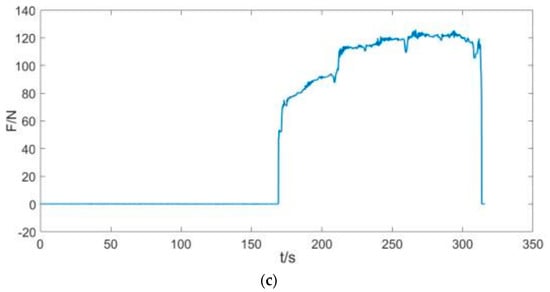
Figure 18. Tensile test diagram. (a) Tensile test I. (b) Tensile test II. (c) Tensile test III.

From Figure 18, it can be seen that the strength of the specimen increases steeply as the specimen is subjected to an increase in tensile time, and after the yielding stage, the fracture strength of the specimen returns to 0. From this, it can be determined that the average strength limit of the specimen is $F_b\approx 120\mathrm{N}$.

In accordance with the maximum load F_max = 0.55, F_b = 66 N load level on the specimen for a set of fatigue tests, and through the acquisition software real-time recording of the dynamic load acting on the specimen, and then after using MATLAB software for the processing of the collected load data, the results of the test results obtained by the curve are shown in Figure 19.

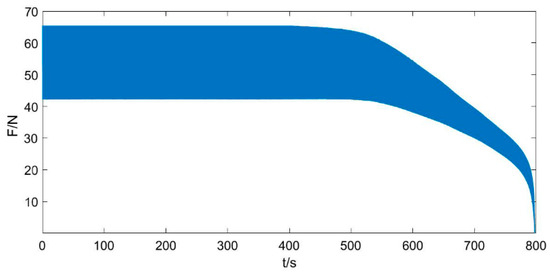
Figure 19. Complete fatigue test load graphs.

As can be seen from Figure 19, the fatigue test load curve can be divided into three more obvious stages. In the first 500 s range, the load acting on the specimen does not change significantly with time. In the range of 500 s~780 s, the static and dynamic loads on the specimen are attenuated more obviously. After 780 s, the static and dynamic loads acting on the specimen change drastically. These three stages correspond to the generally recognized three stages of fatigue fracture: crack initiation, crack extension, and fatigue fracture. This phenomenon is preliminarily analysed due to the change in stiffness parameters of the specimen during the fatigue test. It can also be seen that the designed fatigue testing machine basically meets the demand for fatigue loading of tiny devices and can realize the function of fatigue testing for them.

5. Conclusions

In response to the need for a piezoelectric fatigue tester capable of generating small alternating loads, a down-drive piezoelectric high-frequency fatigue testing machine prototype was developed with a load range of 0.1 N to 100 N. Firstly, the structural composition and working principle of the device were analysed, and a spring–damping system model was established to analyse the effects of mass block mass and spring stiffness on the intrinsic frequency of the fatigue testing machine. Next, the experimental platform was set up, and tensile fatigue tests were performed on steel specimens in the shape of a dog bone. The test results show that the amplitude of the stress acting on the specimen increases gradually with the increase in the driving voltage, the increase in the specimen stiffness, the increase in the preset load, and the increase in the fast mass of the counterweight mass. Through the load change curves during the fatigue test, it was found that both the static and dynamic loads acting on the specimen decayed after 500 s. The designed piezoelectric fatigue testing machine is experimentally verified to be suitable for fatigue testing with small dynamic loads and high loading accuracy. It provides a technical reference for subsequent scholars to study the piezoelectric fatigue testing machine in the range of less than 100 N, which has great application value in the field of fatigue testing technology for reliability and durability determination of microelectromechanical devices and bionic devices products.