A Hybrid Group-Based Food Recommender Framework for Handling Overlapping Memberships

Abstract

Recommender systems (RSs) play a pivotal role in mitigating information overload by aiding individuals or groups in discovering relevant and personalized information. An individual’s food preferences may vary when dining with friends compared to dining with family. Most of the existing group RSs generally assume users to be associated with a single group. However, in real-world scenarios, a user can be part of multiple groups due to overlapping/diverse preferences. This raises several challenges for traditional RSs due to the inherent complexity of group memberships, degrading the effectiveness and accuracy of the recommendations. Computing user to group membership degrees is a complex task, and conventional methods often fall short in accurately capturing the varied preferences of individuals. To address these challenges, we propose an integrated two-stage group recommendation (ITGR) framework that considers users’ simultaneous memberships in multiple groups with conflicting preferences. We employ fuzzy C-means clustering along with collaborative filtering to provide a more flexible and precise approach to membership assignment. Group formation is carried out using similarity thresholds followed by deep neural collaborative filtering (DNCF) to generate the top-k items for each group. Experiments are conducted using a large-scale recipes’ dataset, and the results demonstrate that the proposed model outperforms traditional approaches in terms of group satisfaction, normalized discounted cumulative gain (NDCG), precision, recall, and F1-measure.

1. Introduction

In recent years, the world has witnessed a sudden surge in the consumption of food products. Globally, various food cultures and cuisines are undergoing evolution. There has been a significant increase in food diversity and ingredient combinations, leading to numerous dishes with different tastes being prepared using various ingredients. People typically opt for meals that best align with their preferences when deciding what to eat. However, manually sifting through a vast recipe database to make meal selections can be complicated and time-consuming due to the extensive proliferation of food varieties [1]. Individuals frequently struggle to select foods that align with their personal preferences while also meeting their nutritional needs for maintaining good health.

Despite advancements in search engines aimed at reducing information redundancy, achieving personalized search results and minimizing noise remains a persistent challenge. Recommender systems (RSs) were developed in the late 1990s to generate recommendations closely aligned with user preferences. The emergence of various awards and events organized by prominent tech corporations has sparked significant interest in RSs from both the business and academic realms. The use of RSs has been particularly important on Internet platforms and mobile applications. The rising popularity of these systems can be attributed to the numerous benefits they offer, such as boosting sales for food businesses and aiding individuals in making healthier food choices.

Food recommendation systems have become very useful tools to help people find tasty and suitable food choices [2]. These systems serve a multitude of purposes, spanning from suggesting recipes and meal plans to endorsing restaurants or food delivery services. Through the utilization of user data and machine learning algorithms, these systems continuously learn and adjust to offer precise and relevant recommendations. The ultimate objective is to enhance the dining experience, economize time, and aid users in discovering fresh and enjoyable food alternatives.

Several works have been proposed in the literature to address food the recommendation problem for individuals [3,4,5]. As everyone’s tastes and personal preferences vary, this makes it a complex problem to solve, as it is difficult to generalize RSs for different individuals [6]. The complexity of the recommendation problem increases manifold when we plan to make recommendations for a group of individuals interconnected on the basis of some common features. Most of the existing studies make a simplistic assumption that a user belongs to a single group type [4]. It is common for individuals to be associated with multiple groups concurrently in real-world situations, be it friends, family, or colleagues, where the interests are closely aligned in some cases and while, in others, they are unlikely to converge [2].

Group-based food RSs face a far more challenging scenario since group members may differ greatly from one another with conflicting preferences, such as personality traits, attitude, or behavior [7]. Therefore, a system must appropriately balance each individual’s preferences and provide the group with a list of foods that almost satisfy every member of the group [8]. Rostami et al. [4] introduced a food RS that incorporates community awareness to address the limitations of existing systems. However, the proposed work neglected cold start users, the time factor, food ingredients, and community features. When people negotiate with one another in a group, human personality traits including competition, compromise, avoidance, and accommodation are of the utmost importance and play a significant role in the selection of food products [9]. The purpose of the food RS presented in [10] was to generate custom daily meal plans for the users based on their dietary requirements and historical food preferences.

Although there have been many studies targeted at developing computational tools for food consumption trends, most of them do not manage user preferences and dietary data directly. In [2], the authors presented a food RS that relies on daily personalized meal plans according to users’ previous food preferences and nutritional necessities. The authors proposed an algorithm named analytic hierarchy process sort (AHPS), which is a multi-criteria decision making (MCDM) algorithm used to filter all foods that are not appropriate for a user. Recent works based on optimization approaches focused on maximizing user preferences while fulfilling nutritional requirements for menu generation. In this context, an ant colony optimization technique that implements recommendations based on patients’ dietary needs considering pathology data was proposed in [1]. None of the aforementioned works explicitly addressed the challenges that emerge when an individual functions as a member of a collective group, instead restricting their scopes to the analysis of isolated individuals.

To tackle the challenges inherent in current group-based food recommendation systems (RSs), we proposed an integrated two-stage group recommendation (ITGR) framework. This framework leverages deep neural collaborative filtering (DNCF) networks to efficiently learn from both explicit user preferences, such as ratings and recipe attributes, and implicit preferences, including interactions among group members. A critical challenge in group recommendations is the overlapping of user interests across multiple groups. To address this, the proposed model integrated fuzzy C-means (FCM) clustering with collaborative filtering to enhance intragroup similarity and promote diverse memberships across distinct clusters. Our contributions are summarized as follows:

• We introduced ITGR, a group-based recipe recommendation system employing deep neural networks to effectively incorporate both explicit user ratings and implicit recipe features, thereby facilitating personalized recommendations.
• To address the challenge of intragroup similarity in group-based recipe recommendations, we employed FCM clustering and collaborative filtering, enabling users to belong to multiple groups.
• We proposed a method for generating the top-k recommendations for a group, utilizing an advanced aggregation approach. This method enhances generalization by allowing users to be part of multiple groups.
• We addressed the issue of data sparsity by leveraging latent factors of both users and recipes, thus improving prediction accuracy.
• We demonstrated the effectiveness of our model through simulations, showing that it outperforms existing methods in generating the top-k recommendations.

2. Related Work

2.1. Group Formation

In recent years, several research works have been proposed on food-based RSs, e.g., [6,11,12]. With the evolution of online social networking applications, people are more interested in group-based activities. However, the existing food-related datasets, e.g., allrecipes.com [5], Weibo [7], etc., do not contain information about social interactions and links among users [10]. This motivated some researchers to build datasets with embedded relationship information [2] or to adopt traditional clustering techniques to form groups. Partition-based k-means clustering was widely used in [2,10]; ordered-based clustering, proposed in [13], produced better results than the legacy techniques. Despite their effectiveness in group formation, these models often fail to capture the complex social interactions and preferences among users within the groups and overlook potential multi-group affiliations by assuming each user belongs to only one group.

For instance, k-means is a widely used clustering technique due to its simplicity and relatively low complexity in the cluster selection process. However, k-means tends to form spherical clusters, limiting its applicability in cases where clusters have irregular shapes. Conversely, bottom-up clustering methods, as described in [14], initially treat each data point as an individual cluster. The algorithm iteratively calculates and sums the distances between all clusters, merging them until a single cluster remains. Despite its potential for producing detailed hierarchical structures, bottom-up clustering suffers from high temporal complexity, resulting in reduced efficiency. For clustering data with arbitrary shapes, the DBSCAN (density-based spatial clustering of applications with noise) algorithm is often preferred. The DBSCAN can identify clusters of varying shapes and sizes but has the disadvantage of a higher processing time compared to simpler methods like k-means.

Traditional clustering algorithms typically assign each user to a single group, which may not accurately reflect the user’s diverse interests and associations. To address these limitations, our proposed approach allows for the distribution of users across multiple groups based on their membership scores. This method ensures that users’ specific preferences are adequately represented across different groups, providing a more nuanced and comprehensive clustering solution.

2.2. Single-User-Based Recommendation

Single-user RSs have gained wide popularity and attention due to implementation by technology giants like Facebook, Netflix, Google, Twitter, etc. Asani et al. [15] conducted research on utilizing a natural language processing-based semantic approach to extract user preferences from individuals’ comments, and then a Wu–Palmer-based clustering algorithm was devised to recommend context-aware food and restaurants. Manoharan et al. [16] proposed a model, named gated recurrent units (GRU), to recommend food intake while considering patients’ health conditions. They developed various food parameters, such as calories, fat, sodium, carbohydrates, cholesterol, and fiber, and patient conditions were considered to recommend dietary choices that can effectively manage patients’ blood sugar levels, cholesterol, protein intake, blood pressure, and fat consumption.

In [4], the authors proposed a combination of memory-based and model-based approaches by considering multiple factors, such as food ingredients, cold start users, time factor, and users’ community. The authors performed prediction in two phases, by employing graph clustering in the first phase and deep learning in the second phase, to predict a list of items based on food content and user preferences. Wang et al. [5] proposed a personalized health-aware food recommender scheme where they found correlation between the type of food ingredients and users with allotted health tags. Initially, they employed the VGGNet19, a convolutional neural network (CNN) architecture for image recognition tasks, applied to a video dataset to identify ingredients featured in the given videos. Concurrently, they utilized the bidirectional recurrent neural network (BIRNN), which processes input sequences in both forward and backward directions, to learn user profiles enriched with health-related tags, facilitating the generation of personalized recommendations.

Romadhon et al. [10] proposed memory-based multiple RSs using a collaborative filtering approach that considers the item and genre with cosine similarity and a KNN classification algorithm. The intuition behind this work was to recommend a certain food item or food menu to a group of users. Syed et al. [17] developed an offline multistage model using deep transfer learning. The latent features from images were extracted to solve item cold start issues while implementing multimodel embedding on separate user and item features to address cold start users. Cosine similarity was used to calculate three similarity matrices, given as the input for an online model that generates the top-n relevant items to target users. In [1], the authors proposed an ant colony-based optimization algorithm, ‘diet right’, that takes a patient’s dietary requirements considering the pathological reports. Additionally, the authors in [18] presented a self-organizing map-based food RS that suggests meals based on nutrition data and employs k-means-based clustering to recommend eight essential nutrients for diabetic patients.

Iwendi et al. [19] presented a deep learning framework aimed at enhancing patient diet recommendations using the Internet of Medical Things (IoMT). The study leveraged various machine learning algorithms, including logistic regression, Naive Bayes, and LSTM models, to tailor diet plans based on patient-specific characteristics such as age, gender, weight, and dietary needs. The LSTM model achieved the highest accuracy, at 97.74%, demonstrating its effectiveness in providing precise and personalized dietary recommendations to improve patient health outcomes. In [20], the authors focused on optimizing nutrition by integrating nutrigenetics and genetic data. Their system used a deep learning neural network for automatic product categorization and word embedding for scalability, allowing it to filter and recommend grocery products based on individual genetic profiles and phenotypic information. A case study involving databases from three different sources validated the system’s effectiveness, highlighting its potential for offering personalized dietary recommendations to consumers. Another study, presented in [21], targeted user health by utilizing the random forest (RF) algorithm to recommend ingredients based on users’ body mass index (BMI), allergies, and health status. The system collected data through the Food Express application and demonstrated a precision of 97.74% with the RF algorithm in suggesting appropriate ingredients, surpassing other algorithms like ID3 and random tree.

2.3. Group-Based Recommendation

A group-based RS aims to minimize the disparity among group members and promotes group members’ satisfaction. In the literature as well as in industry, a limited amount of work has been performed on group RSs for food items. Group-based recommendations are usually more challenging than single-user recommendations, as the RS must strike a balance among conflicting preferences of members. Generally, group-based RSs are divided into two categories: (a) memory-based (e.g., [2,7,10,13]) and (b) model-based (e.g., [4,5,9,16]). Memory-based models rely on past or historical data to calculate similarity measures to match similar people or items together. Cosine similarity [10], PCC [7,13], and Jaccard coefficient are the most popular techniques used in memory-based approaches, while model-based techniques use machine learning (ML) models to predict correlation among features. Deep learning [4,5,16], nonparametric, and matrix factorization [9] are examples of model-based techniques. ML-based techniques are highly preferable when we have a sparse dataset.

The authors in [22] offered a customized group-based business model in which users form groups, share products within their communities, and participate in other groups as participants. The authors addressed three key issues: users’ social influence, feedback complexity in group purchases, and situations when a user plays various roles in a group (both as an initiator and participant). They developed a group-based buying graph convolutional network (GBGCN) where they constructed a directed heterogeneous graph of the behavioral data of users and a social network. The authors predicted the top-k items based on initiators’ influence in a social network and the preferences of participants and initiators. The work presented in [23] put forward a personality-aware group-based movie recommendation that aids groups in successfully meeting the expectation of group members. According to this work, items can be efficiently recommended while utilizing the big-five personality traits, such as agreeableness, conscientiousness, openness, emotional stability, and extraversion.

The authors in [24] introduced a food recommendation system for users’ groups, leveraging a deep social community detection approach. By modeling users’ interactions and preferences as a graph, the system detected social communities using deep learning techniques to enhance recommendation accuracy. The proposed model incorporated trust network generation and group rating aggregation, addressing the unique challenges of group-based recommendations. Experimental results demonstrate the model’s effectiveness in providing personalized and health-oriented food suggestions, significantly outperforming traditional single-user recommendation systems. Similarly, the work in [25] proposed a novel group recommender system utilizing genre preferences to reduce clustering costs. By defining a genre preference vector and using it for clustering, the system significantly lowered the time complexity compared to traditional item preference-based methods. Experimental results showed that this genre-based approach not only enhanced clustering efficiency but also improved recommendation accuracy, especially in datasets with fewer users per group. In addition, the work in [26] presented a novel hybrid approach to mitigate the cold start problem in context-aware recommender systems by combining community-created knowledge, ontologies, association rule mining, and an innovative scoring function based on probability metrics. This method aimed to enhance the accuracy and relevance of recommendations for new users by leveraging both predefined domain knowledge and dynamically mined association rules. The approach was designed to improve the performance of location-based services (LBS) by offering more precise and contextualized information to users.

Table 1 presents a summary of the state-of-the-art works in food-based RSs.

Table 1. Comparisons between food recommendation systems in the literature.

Refs.	Considerations	Group Formation	Model	Limitations
[4]	Food ingredients, time stamp, and user community-based food recommendation	Graph clustering	Bidirectional encoder	Interaction is limited to single group only
[5]	Explicit behavior of user, user health profiling, recipe information	RNN, CNN, BI-RNN	WIRCNN	Only consider users explicit feedback
[6]	Similarity-based approach for food recommendation while considering ingredient–ingredient, ingredient–recipe and recipe–user relationships	Bayesian personalized ranking for pairwise learning	Graph convolutional network-based food recommendation	Interaction is limited to single user only
[7]	Group-based purchasing	KNN, PCC	Collaborative filtering	User considered to be part of single group
[11]	Visual aided food recommendation	Hierarchical attention module	Neural network-based hierarchical attention network	Lacks consideration of users’ preferences regarding recipe ingredients
[16]	Personalized food recommendation	Cosine similarity	Gated recurrent network	Only spherical clusters can be formed

3. ITGR Framework

Figure 1 illustrates the holistic architecture of our proposed ITGR framework. The proposed methodology is divided into two key phases: (a) Phase 1: group formation and (b) Phase 2: group recommendation. The group formation phase entails the selection of a suitable similarity metric to facilitate the creation of cohesive groups, serving as an initial step in any group-based RS. Subsequently, the group recommendation phase employs average aggregation techniques to recommend the top-k recipes to users within the group. This two-step process ensures the generation of effective and personalized food recommendations tailored to the preferences and needs of the user groups.

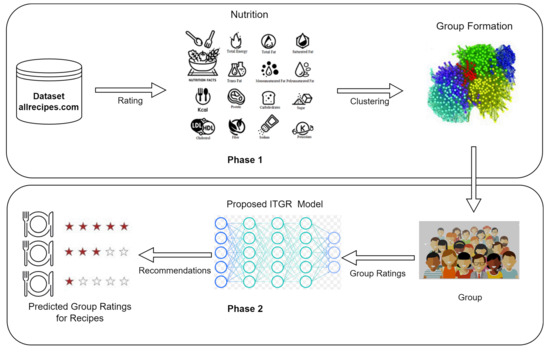
Figure 1. Group recommender system.

In Phase 1, the dataset from allrecipes.com was utilized to gather ratings for various recipes. These recipes were then clustered based on similarities in their ingredients and user ratings, forming distinct groups. Clustering helps in identifying patterns and preferences within the data, enabling the creation of user groups with similar tastes.

In Phase 2, the proposed ITGR model leveraged the group ratings to generate recommendations. The model predicted group ratings for different recipes and suggested the top-k recipes that best matched the group’s preferences. By considering the collective preferences of the group, the ITGR model aimed to provide more accurate and satisfactory food recommendations, enhancing the overall user experience.

This comprehensive approach not only improves the relevance of recommendations but also allows a collaborative environment where users can benefit from shared tastes and preferences within their groups. The ITGR framework’s ability to adapt to group dynamics and deliver personalized recommendations makes it a valuable tool for food recommendation systems.

The following are the steps performed in the proposed framework:

• Phase 1: Group Formation
• Step 1: Dataset Collection: The process began with collecting a dataset from allrecipes.com (accessed on 1 June 2024), which contained user ratings for various recipes.
• Step 2: Rating Extraction: The collected dataset included user ratings for different recipes. These ratings were extracted for further processing.
• Step 3: Nutrition Analysis: The dataset was analyzed for nutritional information, which helped in understanding the ingredients and nutritional value of each recipe.
• Step 4: Group Formation: The clustering results were utilized to form cohesive user groups with similar dietary preferences. Unlike existing food-based group recommender systems, the model exhibited a degree of generalization by allowing a user to be part of multiple groups.
• Phase 2: Group Recommendation
• Step 5: Group Ratings: The formed user groups provided collective ratings for different recipes, reflecting the preferences of the entire group.
• Step 6: ITGR Model Processing: The proposed ITGR model processed the group ratings to generate personalized recommendations for each group.
• Step 7: Recommendation Generation: The ITGR model predicted group ratings for various recipes and recommended the top-k recipes that best matched the group’s preferences.
• Step 8: Predicted Group Ratings for Recipes: The final output consisted of the predicted group ratings for recipes, which were then presented as recommendations to the user groups.

The overall architecture of our proposed HTGF is shown in Figure 2. In the process of forming groups, users may be affiliated with multiple groups, each displaying unique preferences and interests. A user’s food preferences might vary when dining with friends as compared to having a meal with family. To represent user-to-group associations, we employed FCM [27]. Initially, the mean nutrition ratings of users were calculated, followed by the application of FCM to organize users into different groups based on their membership values within each cluster. Subsequently, a Pearson similarity was employed to identify the user u who shared the highest similarity with every other user. The top-k users, exhibiting the most similarity, were selected to form a cohesive group.

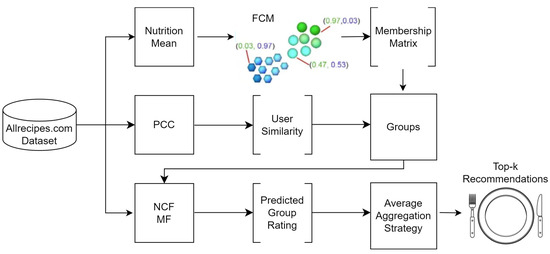
Figure 2. System architecture.

To address the sparsity issue in the group rating matrix, we employed DNCF [28] to predict ratings for unrated recipes. DNCF leveraged the implicit preferences of group members to make accurate rating predictions. As depicted in Figure 2, the average aggregation approach was utilized to calculate the group rating for a specific item i. Based on the calculated average ratings for each recipe, the top-k recipes were recommended to the group. For clarity, Table 2 defines the symbols and their meanings used throughout the text.

Table 2. Notations and their meanings.

Notation	Meaning
DNCF	Deep neural collaborative filtering
PS	Peason similarity
PCC	Pearson correlation coefficient
FCM	Fuzzy C-means
$\mathrm{U}$	Set of users
$\mathrm{I}$	Set of items
$\mathrm{R}$	Rating matrix
$\mathrm{W}$	Set of genres
$\mathrm{C}$	Set of clusters
$\mathrm{Q}$	Set of groups
$\mathrm{X}$	Mean genre ratings
$\mathrm{M}$	Membership matrix
${\mathrm{r}}_{\mathrm{u}\mathrm{i}}$	Rating of user $\mathrm{u}$ on item $\mathrm{i}$
${\mathrm{r}}_{\mathrm{u}}$	Ratings of user $\mathrm{u}$
$\mathrm{W}$	User $\mathrm{u}$’s mean nutrition ratings
$\mathrm{G}$	Group of users

The process started with collecting and processing recipe data from Allrecipes.com. The system then performed various computational steps to ultimately provide the personalized top-K recipe recommendations.

Dataset: The system started with the Allrecipes.com dataset, which contained various recipes along with their nutritional information.

Nutrition Mean: The nutritional means for the recipes were calculated to standardize and summarize the nutritional data.

PCC (Pearson Correlation Coefficient): User similarity was computed using the Pearson correlation coefficient based on the nutritional data.

FCM (Fuzzy C-Means Clustering): This step grouped users into clusters based on their similarity, resulting in a membership matrix that indicated the degree of belonging of each user to each cluster.

Groups: Users were then grouped into distinct clusters based on the membership matrix obtained from the FCM step.

NCF/MF (Neural Collaborative Filtering/Matrix Factorization): This step predicted group ratings for recipes. It used a matrix factorization approach enhanced by neural collaborative filtering techniques.

Predicted Group Rating: The predicted ratings for each group were computed based on the matrix factorization model.

Average Aggregation Strategy: The predicted group ratings were aggregated using an average strategy to derive the final ratings.

Top-K Recommendations: Finally, based on the aggregated ratings, the system generated the top-K recommendations for recipes.

Proposed Model

The existing datasets did not contain the explicit information required to represent groups. The existing research offered a variety of clustering techniques to create groups [29]. FCM, being a well-known and widely used algorithm, yielded superior results compared to k-means due to its ability to handle overlapping clusters and assign degrees of membership to data points rather than strict membership [30]. FCM was used to cluster users into social groupings, such as families or friends. For instance, when dining with friends, a person may have distinct tastes from when eating with family. FCM divided the users into c number of clusters, allowing them to belong to each cluster individually. FCM’s objective function is defined as follows [27]:

$$O=\sum _{i=1}^c\sum _{k=1}^n{\mu }_{ik}^m{d}_{ik}^2.$$

(1)

$$d_{ik}^2={\left|x_k-v_i\right|}^2.$$

(2)

$$\sum _{i=1}^c{\mu }_{ik}=1, \forall k=1,\dots ,n.$$

(3)

Equation (1) represents the objective function of the FCM algorithm, where O is the overall objective value. In this equation, $u_{ik}$ denotes the degree of membership of data point $x_k$ in cluster $i$, $v_i$ represents the centroid of cluster $i$, $d_{ik}^2$ is the squared Euclidean distance between data point $x_k$ and the centroid $v_i$, c represents the overall number of clusters, n represents the overall number of users, and m represents the fuzziness parameter $1.25\le m\le 2$. The squared Euclidean distance $d_{ik}^2$ in (2) is calculated as the square of the difference between data point $x_k$ and centroid $v_i$. According to (3), each user’s overall membership value for each cluster/group corresponds to 1. It is essential to minimize the objective function [27].

$$v_i=\sum _{k=1}^n {\mu }_{ik}^m{x}_k.$$

(4)

$${\mu }_{ik}={ \left[\sum _{i=1}^c {\left(\frac{d_{ik}}{djk}\right)}^{\frac{2}{m-1}}\right]}^{-1}$$

(5)

Equation (4) represents the centroid update step in FCM, where v_i is the center of the i^th cluster and ${\mu }_{ik}\in M$ is the user k’s membership in the cluster i. The degree of membership in (5) is calculated across all the clusters. After forming the clusters, Pearson similarity in (6) is utilized to calculate the similarity among users within each group, to find the intragroup similarity. To assess the similarity between two users, u and v, the PCC computes similarity based on the shared ratings of items by these users. The formula of PCC is as follows [31]:

$${Sim}_{u,v}=\frac{{\Sigma }_{i\in I}(r_{u,i}-\overline{r_u})(r_{v,i}-\overline{r_v})}{\sqrt{{\Sigma }_{i\in I}{(r_{u,i}-\overline{r_u})}^2} \sqrt{{\Sigma }_{i\in I}{(r_{v,i}-\overline{r_v})}^2} }$$

(6)

The range of PCC is [−1, +1], with positive values denoting a significant degree of user similarity, whereas a negative correlation shows a lack of similarity. The following formula computes how similar users u and v are in cluster k:

$${Sim}_{uvc}={Sim}_{u,v}\times {\mu }_{vc}.$$

(7)

where Sim_uvc represents the amount of similarity between users u and v, with v belonging to cluster c. The top-k similar users were chosen to form a group based on (7). We used DNCF [28] to predict the recipes of group members after the group was formed. As shown in Figure 3, the DNCF is a layered model having an input layer, hidden layers, and an output layer. The output layer employs the sigmoid activation function. The input layer has two feature vectors, $v_u^U$ and $v_i^I$, which describe the user u and recipe i, respectively. The following equations were used to determine the parameter ${\widehat{y}}_{ui}$, which was the projected rating of user u on recipe i [28]:

$${\widehat{y}}_{ui}=f\left(P^T v_u^U, Q^T v_i^I \right|P, Q,{\theta }_f).$$

(8)

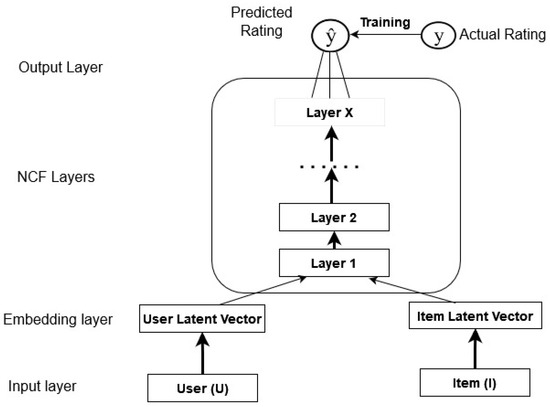
Figure 3. Deep neural collaborative filtering.

Here, $P\in R^{U\times K}$ and $Q\in R^{I\times K}$ stand for the latent factors for users and recipes, respectively. Moreover, $f$ stands for the layered neural network, while ${\theta }_f$ stands for model parameters. The following defines the DNCF loss function:

$$\begin{gathered} L=-\sum _{\left(u,i\right)\in \tilde{y}}log{\widehat{y}}_{ui}-\sum _{\left(u,i\right)\in \widehat{y}}log(1-{\widehat{y}}_j) \\ =-\sum _{\left(u,i\right)\in \widehat{y}\cup \tilde{y}}{y}_{ui}log{\widehat{y}}_{ui}+(1-y_{ui})log(1-{\widehat{y}}_{ui}). \end{gathered}$$

(9)

The unseen interaction between the user and the recipe is represented by $\widehat{y}$ and the observed interaction is represented by $\tilde{y}$. The objective function of DNCF is represented in (9). The stochastic gradient descent (SGD) was employed to minimize the objective function. We used an average aggregation approach on group ratings after predicting the unrated recipe ratings, and then we suggested the top-k recipes to the group.

The average group rating was calculated using the following formula:

$$G_{r_i}=\sum _{a=1}^j{r}_{a,i}.$$

(10)

where j is the total number of users in a group, $r_{ai}$ is the rating of user $a$ on recipe $i$, and $G_{r_i}$ represents the group’s rating of recipe $i$. The group formation procedure is illustrated in Algorithm 1.

Algorithm 1: Group Creation

Input: ratings (R), items (I), k-users. Output: Groups 1: $J\leftarrow \mathrm{s}\mathrm{e}\mathrm{t}\in \mathrm{o}\mathrm{f}\in \mathrm{n}\mathrm{u}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}’\mathrm{s} \left(\mathrm{I}\right)$ 2: $X\leftarrow 0$ 3: $M^{\prime }\leftarrow 0$ 4: $V\leftarrow \mathrm{g}\mathrm{e}\mathrm{t}\mathrm{I}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{C}\mathrm{l}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{C}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\left(\right)$ 5: $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{u}\mathrm{s}\mathrm{e}\mathrm{r} \mathrm{u}\in \mathrm{U} \mathbf{d}\mathbf{o}$ 6:  $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m} \mathrm{i}\in r_u \mathbf{d}\mathbf{o}$ 7: $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{n}\mathrm{u}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{j}\in \mathrm{J} \mathbf{d}\mathbf{o}$ 8:   $\mathbf{i}\mathbf{f} \mathrm{i} \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{s} \mathrm{j} \mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n}$ 9:     $X_{u{j}^{+}}=r_{ui}$ 10:   end if 11: end for 12: $x_u=\frac{x_u}{\left|r_u\right|}$ 13:  end for 14: end for 15: $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{u}\mathrm{s}\mathrm{e}\mathrm{r} \mathrm{u}\in \mathrm{U} \mathbf{d}\mathbf{o}$ 16:  $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{u}\mathrm{s}\mathrm{e}\mathrm{r} \mathrm{v}\in \mathrm{U} \mathbf{d}\mathbf{o}$ 17: ${\mathrm{S}\mathrm{i}\mathrm{m}}_{(\mathrm{u},\mathrm{v})}\leftarrow {\mathrm{P}\mathrm{C}\mathrm{C}}_{(\mathrm{u},\mathrm{v})}$ 18:  end for 19: end for 20: $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{u}\mathrm{s}\mathrm{e}\mathrm{r} \mathrm{u}\in \mathrm{U} \mathbf{d}\mathbf{o}$ 21:  $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{n}\mathrm{u}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{j}\in \mathrm{J}\mathbf{d}\mathbf{o}$ 22:  $\mathbf{i}\mathbf{f} {\mathrm{x}}_{uj}\ne 0 \mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n}$ 23:    $m_{uj}^{\prime }=1$ 24:  end if 25: end for 26: end for 27: $M\leftarrow FCM(V,M^{\prime },X)$ 28: $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{u}\mathrm{s}\mathrm{e}\mathrm{r} \mathrm{u}\in \mathrm{U} \mathbf{d}\mathbf{o}$ 29:  $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{u}\mathrm{s}\mathrm{e}\mathrm{r} \mathrm{v}\in \mathrm{U} \mathbf{d}\mathbf{o}$ 30: $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{c}\mathrm{l}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r} \mathrm{c}\in \mathrm{C} \mathbf{d}\mathbf{o}$ 31:    $S_{(u,v,c)}={Sim}_{(u,v)}\times M_{(v,c)}$ 32: end for 33:  end for 34: end for 35: $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{u}\mathrm{s}\mathrm{e}\mathrm{r} \mathrm{u}\in \mathrm{U} \mathbf{d}\mathbf{o}$ 36:  $\mathbf{f}\mathbf{o}\mathbf{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} \mathrm{c}\mathrm{l}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r} \mathrm{c}\in \mathrm{C} \mathbf{d}\mathbf{o}$ 37:   $G\leftarrow getSorted(S,k-users)$ 38: end for 39: end for 40: return G

Algorithm 1 is explained as follows.

Initializations: The following parameters were provided as input to the algorithm: user ratings and items, which included the title and nutritional information for recipes and k-users, the total number of users in a group. Nutritional information was taken from the recipes in Line 1. We then initialized the mean nutrition matrix X and initial membership matrix M’ to 0 in Lines 2 and 3. The center of the initial clusters were determined by Line 4 using (4).

Lines 5–14 computed the average nutrition ratings, where $r_u$ represents the ratings set of users $u$, $r_{ui}$ denotes the rating of user $u$ on item $i$, and $x_u$ is the mean nutrition ratings of user $u$.

Lines 15–19 calculated the Pearson similarity using (6) to cluster similar users. The initial membership was calculated in Lines 20 to 26. If a user had taken a food item with nutrition $g_j$, then $m_{uj}^{\prime }=1$; otherwise, it was 0. The FCM clustering was used in Line 27 to determine each user’s membership value for each cluster.

The similarity between users in clusters C was calculated (Lines 28–34), according to Equation (7).

Group Formation: After computing the similarity matrix, the top-k similar users were chosen to form a group, which was returned as a final step. The value returned from the algorithm was “groups,” representing the cohesive sets of users with similar dietary preferences identified by the model. This step ensured that each group consisted of users whose preferences were closely aligned, facilitating more accurate and relevant food recommendations.

We present an illustrative example to clarify the methodology proposed in the algorithm.

Illustrative Example

We considered a scenario where Algorithm 1 was utilized to suggest recipes to users. The process is illustrated using Table 3, which showcases a sample dataset containing information for 10 users and 7 recipes.

Table 3. Rating matrix.

	Recipes
Users	i1	i2	i3	i4	i5	i6	i7
u1	5	4	−	5	3	4	−
u2	−	4	5	4	−	5	2
u3	4	3	3	5	3	5	−
u4	4	5	−	3	3	−	−
u5	5	3	−	5	3	4	2
u6	4	2	2	−	2	5	3
u7	−	5	3	4	4	−	3
u8	3	−	−	4	3	3	−
u9	4	5	4	−	5	4	−
u10	4	5	−	4	3	−	4

Table 4 provides a comprehensive overview of the nutritional composition for each recipe, encompassing seven key nutritional factors. Utilizing this data, we could gauge user inclinations towards particular recipes.

Table 4. Nutritional values for recipes.

	Nutrition
Recipes	Calories	Fat	Carbohydrates	Protein	Cholesterol	Sodium	Fiber
i1	6	13	3	5	1	3	1
i2	16	24	11	20	29	25	10
i3	5	5	5	5	3	7	2
i4	15	21	14	7	10	7	6
i5	10	6	11	11	3	4	5
i6	7	4	8	9	6	4	3
i7	11	11	9	15	5	8	4

Table 5 presents the calculated Pearson similarity among users using (6). This table shows the degree of similarity between different users based on their preferences or behaviors. Moreover, Table 6 showcases the user-to-cluster scores computed using the FCM algorithm. This table provides a measure of each user’s association or belongingness to specific clusters based on their characteristics or preferences. Together, these tables were pivotal in our analysis, aiding in understanding user relationships and clustering patterns within the system.

Table 5. Pearson similarity.

	Users
Users	u1	u2	u3	u4	u5	u6	u7	u8	u9	u10
u1	0	−0.14	0.76	0.69	0.91	0	−0.19	0.73	0.17	0.34
u2	−0.14	0	0.28	−0.38	−0.29	−0.11	0.1	−0.26	−0.09	−0.49
u3	0.76	0.28	0	0.26	0.59	−0.00	−0.31	0.73	0.25	−0.27
u4	0.69	−0.38	0.26	0	0.52	−0.31	0.33	0.22	0.31	0.74
u5	0.91	−0.29	0.59	0.52	0	0.08	−0.31	0.8	−0.13	0.42
u6	0	−0.11	−0.00	−0.31	0.08	0	−0.82	−0.02	0.34	−0.37
u7	−0.19	0.1	−0.31	0.33	−0.31	−0.82	0	−0.34	−0.10	0.44
u8	0.73	−0.26	0.73	0.22	0.8	−0.02	−0.34	0	−0.07	−0.00
u9	0.17	−0.09	0.25	0.31	−0.13	0.34	−0.10	−0.07	0	−0.25
u10	0.34	−0.49	−0.27	0.74	0.42	−0.37	0.44	−0.00	−0.25	0

Table 6. FCM.

	Clusters
Users	c1	c2
u1	0.612458	0.387542
u2	0.422801	0.577199
u3	0.575912	0.424088
u4	0.556497	0.443503
u5	0.724817	0.275183
u6	0.516828	0.483172
u7	0.392983	0.607017
u8	0.471901	0.528099
u9	0.418408	0.581592
u10	0.425203	0.574797

Table 7 and Table 8 demonstrate the similarity calculated between users $u$ and $v$ within a given cluster using (7). This equation combines the Pearson similarity between the two users with user $v\prime s$ cluster membership score, providing a comprehensive measure of their similarity. These tables offer valuable insights into user relationships within clusters, aiding in the refinement of our RS by targeting users with similar preferences and characteristics within their respective clusters. This allows the enhancement in precision and relevance of the recommendations, in accordance with the preferences of a user.

Table 7. Similarity cluster 1.

	Users
Users	u1	u2	u3	u4	u5	u6	u7	u8	u9	u10
u1	0	0.06	0.28	0.14	0.17	0.29	0.30	0.10	0.19	0.15
u2	0.06	0	0.04	0.06	0.09	0.06	0.03	0.02	0.015	0.11
u3	0.28	0.036	0	0.13	0.027	0.21	0.20	0.095	0.11	0.17
u4	0.14	0.06	0.13	0	0.23	0.38	0.19	0.066	0.05	0.06
u5	0.17	0.094	0.03	0.23	0	0.17	0.19	0.070	0.02	0.004
u6	0.29	0.06	0.21	0.38	0.17	0	0.22	0.10	0.16	0.11
u7	0.30	0.03	0.20	0.19	0.19	0.22	0	0.08	0.18	0.16
u8	0.10	0.024	0.09	0.07	0.07	0.10	0.08	0	0.072	0.082
u9	0.19	0.015	0.11	0.05	0.02	0.16	0.18	0.072	0	0.017
u10	0.15	0.11	0.17	0.06	0.004	0.11	0.16	0.08	0.017	0

Table 8. Similarity cluster 2.

	Users
Users	u1	u2	u3	u4	u5	u6	u7	u8	u9	u10
u1	0	0.003	0.115	0.077	0.036	0.015	0.054	0.090	0.023	0.006
u2	0.003	0	0.052	0.156	−0.005	0.082	0.110	0.069	0.083	0.089
u3	0.115	0.052	0	0.044	−0.018	−0.013	0.022	−0.023	0.203	−0.011
u4	0.077	0.156	0.044	0	0.068	0.025	0.156	0.203	0.089	0.081
u5	0.036	−0.005	−0.018	0.068	0	0.025	0.182	0.020	0.034	0.034
u6	0.015	0.082	−0.013	0.025	0.025	0	0.142	0.118	0.009	0.009
u7	0.054	0.110	0.022	0.156	0.182	0.142	0	0.007	0.053	0.037
u8	0.090	0.069	−0.023	0.203	0.020	0.118	0.007	0	−0.007	0.111
u9	0.023	0.083	0.203	0.089	0.034	0.009	0.053	−0.007	0	−0.001
u10	0.006	0.089	−0.011	0.081	0.034	0.009	0.037	0.111	−0.001	0

Given a user u₃ and cluster c₁, Table 9 displays the actual ratings of u₃’s top-k comparable users. As shown in Table 10, the DNCF computed similarities, which were utilized to predict the ratings of unrated items once the group was formed. To provide the top-k suggestions, the average aggregation approach was used on the anticipated ratings, as illustrated in Table 10.

Table 9. Actual group members’ ratings.

	Recipes
Users	i1	i2	i3	i4	i5	i6	i7
u1	5	4	-	5	3	4	-
u3	4	-	3	4	3	2	-
u4	4	5	-	3	3	-	-
u5	2	3	-	-	3	4	2
u8	3	-	-	4	3	3	-

Table 10. Predicted group members’ ratings.

	Recipes
Users	i1	i2	i3	i4	i5	i6	i7
u1	5	4	3	5	3	4	3
u3	4	5	3	4	3	2	3
u4	4	5	3	3	3	4	4
u5	2	3	2	5	3	4	2
u8	3	4	2	4	3	3	2

4. Performance Evaluation

This section presents an evaluation of the proposed ITGR’s model. The model’s efficacy was assessed using the allrecipes.com dataset [4]. The collection contained 3900 recipes, 6040 users, and 1,000,200 ratings. In the selected dataset, each user rated at least 20 recipes. The recipes offered seven different nutritional values. Allrecipes.com is a standard dataset that is frequently utilized by researchers in food recommendation systems since it offers a wealth of recipes’ feature information and user ratings to adequately train a machine learning model. To compare our work against existing techniques, we focused particularly on models leveraging matrix factorization and time-aware food recommender-system based on deep learning and graph clustering (TDLGC) for group recommendation scenarios [32]. Matrix factorization methods are widely employed in RSs to uncover latent factors in user–item interactions, facilitating accurate predictions. Moreover, TDLGC is an innovative framework integrating deep learning and graph clustering to address temporal- and community-related considerations [32].

4.1. Performance Metrics

To perform the quantitative comparisons of our proposed scheme, we utilized root mean square error (RMSE), mean absolute error (MAE), precision, and recall [33]. According to [34], evaluating an RS involves considering classification and prediction accuracy. Prediction accuracy refers to the correctness of the model’s rating predictions, which is assessed using metrics like RMSE and MAE. Alternatively, classification accuracy measures the accuracy of recommendations. Additionally, the efficacy of recommendations is evaluated by calculating group satisfaction. The performance measures are listed below.

4.1.1. RMSE

It serves as an error measurement standard, defined as:

$$RMSE=\sqrt{\frac{{\sum }_{i=1}^n{({\widehat{y}}_{ui}-y_{ui})}^2}{N}}.$$

(11)

4.1.2. MAE

It is the absolute difference between the projected rating and the actual rating. It can be modelled as follows:

$$MAE=\frac{{\sum }_{i=1}^n|{\widehat{y}}_{ui}-y_{ui}|}{N}.$$

(12)

4.1.3. Precision

It is used to assess a user’s relevance to the recommended item. It can be defined by the following formula:

$${Precision}_u=\frac{\left|{hits}_u\right|}{\left|{recset}_u\right|}.$$

(13)

where ${recset}_u$ is the collection of the top-k recommended recipes and ${hits}_u$ is the set of accurately recommended recipes that are relevant to user u.

4.1.4. Recall

Recall: This parameter evaluates the ratio of relevant recommendations to the overall fraction of instances. It is defined as follows:

$${Recall}_u=\frac{\left|{hits}_u\right|}{\left|{rel}_u\right|}$$

(14)

4.1.5. F1-Score

It is the harmonic mean of precision and recall, which is used to evaluate the quality of DNCF. It can be calculated as follows:

$$F1-score=\frac{2\times Precisio{n}_u\times {Recall}_u}{Precisio{n}_u+{Recall}_u}$$

(15)

4.1.6. Group Satisfaction

A measure of group satisfaction is used to gauge how well liked the top-k dishes are within the group. Group satisfaction is indicated as follows [35]:

$$Sat\left(g,R\right)=\frac{\sum _{u\in g}Sat\left(u,R\right)}{\left|g\right|}.$$

(16)

Here, average individual user satisfaction within the group is calculated, where g denotes the group and R is the set of recommended recipes. The total number of group members is represented by |g| [35].

$$Sat\left(u,R\right)=\frac{\sum _{i\in R}{\widehat{y}}_{ui}}{\left|R\right|}.$$

(17)

The goal of the proposed system was to maximize group satisfaction, which entailed maximizing the satisfaction of individuals with the recommended recipes.

4.1.7. NDCG

This parameter is frequently employed to evaluate the quality and relevance of ranked recommendations, especially within group-based RSs. It considers both the relevance of the recommended items and their positions in the list [4].

$$NDCG=\frac{DCG}{IDCG}.$$

(18)

4.2. Parameter Settings

The values of the various parameters utilized in the suggested model are listed in Table 11. Early stopping criteria was defined with a batch size of 64 and epoch size 20 to prevent model overfitting. This method penalized incorrectly predicted ratings by combining the RMSprop optimizer, sigmoid [15], and binary cross entropy [8]. The top-10 recipes were suggested to groups with sizes ranging from 5 to 30.

Table 11. Values of parameters in the proposed model.

Parameter	Value
Epoch size	20
Batch size	64
Learning rate	Adjusted to 0.001
Optimizer	RMSprop
Activation function	Sigmoid
Loss function	Binary cross entropy
Group size	(5, 10, 15, 20, 25, 30)
Top-k recommendations	10

4.3. Results and Discussions

The suggested group recommender model’s effectiveness was assessed using a score for group satisfaction. We divided our dataset into 80% and 20% ratings, with 80% of the ratings used to train the model and 20% of the ratings used to assess the model. The suggested model’s performance was evaluated using the group satisfaction metric, NDCG, RMSE, MAE, recall, and precision. While precision and recall were used to assess the generated group recommendations, RMSE and MAE showed the prediction accuracy of the model. By adjusting the group size, we could calculate the impact of group satisfaction. The comparison with existing models is shown in Table 12.

Table 12. Results.

Models	RMSE@10	MAE@10	Precision@10	Recall@10	F1@10	NDCG@10
ITGR	0.2562	0.0656	0.6001	0.0793	0.1402	0.78
MX	0.2569	0.0699	0.4399	0.022	0.0419	0.7296
TDLGC	0.2900	0.0850	0.0721	0.0691	0.0705	0.0497

To aggregate the preferences of the group members, the average aggregation approach was employed. Unlike the most pleasure technique [32], which relies on a veto power-like decision, it is consensus-based and considers the preferences of every group member. Lower RMSE and MAE values suggest that the projected ratings are reasonably close to the actual ratings. More relevant recommendations are indicated by higher precision and recall. It was noted that a user’s tastes vary depending on the group.

In Figure 4a, we compare ITGR with an existing matrix factorization-based overlapping membership (MX) approach for the parameter RMSE, which signifies a higher accuracy level, indicating a closer alignment between the model’s predicted ratings and the actual observed ratings. In the comparison depicted in Figure 4b, the MAE values for ITGR and MX are 0.0656 and 0.0699, respectively. The superior performance of ITGR can be attributed to its training on a broader and more diverse dataset. This extensive training enables ITGR to generalize more effectively to new instances, capturing underlying patterns more accurately. Consequently, ITGR exhibited greater precision in predicting ratings compared to the MX model.

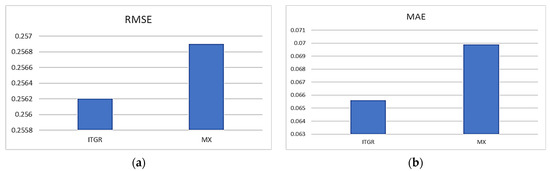
Figure 4. Performance comparison based on: (a) RMSE and (b) MAE.

The comparison in Figure 5a is based on precision, which was 0.6001, 0.4399, and 0.0721 for ITGR, MX, and TDLGC, respectively. Figure 5b details the comparison based on recall. Recall values for ITGR, MX, and TDLGC were 0.0793, 0.022, and 0.0691, respectively. Greater coverage and more pertinent recommendations resulted from a higher recall value. Since their estimation methods were affected by data sparsity, MX and TDLGC showed a low performance in terms of precision and recall. In contrast, since ITGR was trained on the DNCF framework, which made use of the latent variables of users and recipes, it was not greatly impacted by data sparsity.

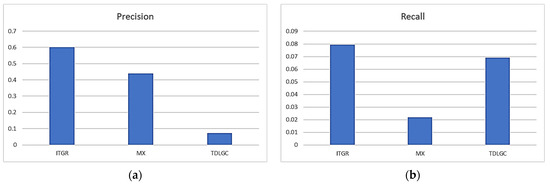
Figure 5. Performance comparison based on (a) precision and (b) recall.

The F1-score comparison for ITGR, MX, and TDLGC is shown in Figure 6a and was 0.1402, 0.0419, and 0.0705 respectively. When k = 10, ITGR’s precision was at its highest. The precision and recall suffered as the group size increased. Figure 6b illustrates how the proposed framework’s precision, recall, and group satisfaction values changed as group size varied. The best performance was achieved with a group size of 10, which conforms to Nawi et al.’s [32] elbow technique calculation. Our scheme’s performance deteriorated above a group size of 10, so the results are not included for group sizes greater than 15. Compared to the other parameters, recall levels were lower. The primary reason for this distinction can be attributed to Equation (14), where the numerator, representing the hits, yields lower values. However, the lack of a significant difference in NDCG values in Figure 6b indicates that the ranking quality of recommendations was consistently high across all group sizes, suggesting a similar effectiveness in presenting the most relevant items to users.

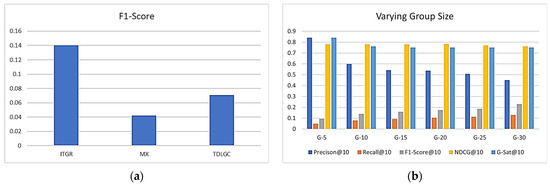
Figure 6. Performance comparison on (a) F1-Score and (b) varying group size.

This occurs because certain items did not appear in any of the top-k recommendations for the group, resulting in relatively fewer hits for individual group members and thus reducing the total value of recall. As evidenced in Table 10, the recall of ITGR surpassed that of existing schemes, underscoring its superiority in effectively capturing relevant items for group recommendations.

The results indicate that the proposed model, ITGR, outperformed existing schemes in terms of rating prediction accuracy. Specifically, when compared to MX, which partitions matrices into three sub-matrices, the accuracy of TDLGC was notably lower. This discrepancy can be attributed to the matrix splitting and estimation process employed by TDLGC, which may introduce additional complexity and a potential loss of information. Moreover, because the MX and TDLGC could not accurately capture the latent preferences of group members, the quality of recommendations suffered [32]. In contrast to MX and TDLGC, our suggested model based on DNCF incorporated the latent feature vectors of users and recipes, thus lowering the error rate.

5. Conclusions

In this study, we introduce an integrated two-stage group recommendation framework (ITGR) and compare its results with existing models. Our proposed framework incorporates clustering techniques such as PCC and FCM to enable users to have memberships in different groups based on preferences. To predict the ratings of unrated items for group members, we employ a DNCF approach that leverages the latent factors of users and items.

Unlike previous approaches, our work takes a novel perspective on group formation by allowing users to be part of multiple groups. We recognize that individuals may have different preferences within different groups, such as varying food preferences when eating with friends versus family. Evaluating our proposed ITGR model using the allrecipes.com dataset demonstrates its improved performance compared to existing schemes.

Despite the positive findings of our study, it is crucial to acknowledge several limitations. The dependence on predefined clustering algorithms limits the system’s ability to adjust to evolving user behaviors or changes in group compositions over time. Moreover, although our approach acknowledges the potential for users to be associated with multiple groups, the methodology used to determine group memberships and interactions among diverse groups may oversimplify complex user behaviors and social dynamics, potentially leading to oversight.

As future work, we plan to explore the use of multi-attention neural networks instead of the average aggregation strategy to recommend the top-k recipes to groups. We will also consider the influence of group members during group formation and investigate its impact on the final recommendations. Additionally, we are interested in exploring transformer-based methods using natural language processing (NLP) approaches for group recommendations. Furthermore, we aim to test our model on multiple datasets to assess its performance across different contexts.