Abstract
Gear pumps are hydraulic machines capable of transferring energy and performing work in pumping fluid. This study presents an analysis of the hydrodynamic model of an external multiple gear pump in order to analyze the fluid flow in combinations of single and different viscosities at the same and different pressures and speeds. Solidworks Flow Simulation 2016 was used to analyze fluid flow. When the radius of the rounding on the collector inner surface is increased from 3 to 15 mm, the pressure drop decreases by 13%. When the radius of the manifold is 3 mm, cavitations are observed. With a liquid distribution system with four input ports and one outlet port in the top cover, the gear pump can handle liquids of viscosity classes 5 to 10. The speed should not exceed 1200 rpm if the liquid has a kinematic viscosity of 10 cSt. The pressure drop and velocity distribution of the liquid in the pressure and suction lines are the same. When the speed changes from 400 to 1200 rpm, the pressure drop increases five times, and the velocity increases three times. At a constant speed of 1000 rpm and an inlet pressure of 10 MPa but with different viscosities, the pressure drop decreases 8 times, and the speed increases 1.5 times. When the inlet pressure is 6 to 24 MPa, with constant speed and the same viscosity, the pressure drop and fluid velocity practically do not change. The dependence of pressure drop on the number of revolutions and radius of the rounding of the inner surface of the collector is statistically significant.
1. Introduction
Gear pumps belong to a separate group of positive displacement pumps [1,2]. The suction and injection of the working fluid into the hydraulic system from the gear pump are provided due to the variable volume in the low- and high-pressure cavities caused by the entrance and exit of the teeth of the meshing during their rotation [3,4]. As the gears rotate and the teeth move out of engagement, the volume of the suction side chamber increases, and fluid is drawn due to the pressure difference between the suction inlet and the low-pressure chamber [4]. The liquid that has filled the cavities between the teeth is then carried along the outer arc by the gears in the direction of rotation. When the teeth engage, the volume of the chamber on the discharge side is reduced. Continuously rotating, the gear teeth displace the liquid into the discharge pipe [5,6]. During the operation, the teeth are tightly adhered to each other, preventing the exit of pumping liquids in the opposite direction [7,8]. But during operation, friction occurs between the gears [9,10,11]. Therefore, gear pumps can only be able to pump products with lubricating properties that do not contain abrasives [12].
To ensure the best suction capacity and to avoid the cavitation of the gear pumps, it is recommended to use underflow gear pumps [13].
Gear pumps are widely used in many industries [3,14,15].
Gear pumps have two, three, or more gears [16,17,18].
Despite the long history of use, there is not much in the literature on gear pump research and developments. The fluid flow pattern in a gear pump with two gears rotating in opposite directions has been well studied [19,20,21,22,23].
There are practically no studies for gear pumps with multiple gears. The design of a multiple-pinion pump construction allows us to solve the problems of increasing productivity, reducing the radial forces acting on the gears, and increasing the uniformity of flow when fluid is displaced into the pressure line.
To achieve these goals, a multi-gear pump was developed with four driven pinions and one drive pinion, as shown in Figure 1 [24].
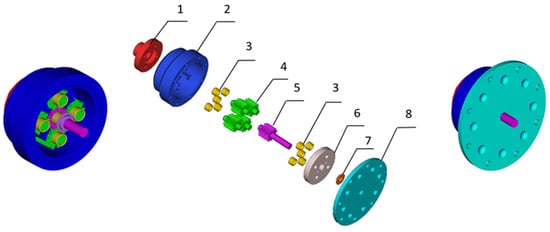
Figure 1.
A design of a multi-gear pump: 1—front cover; 2—housing; 3—bearings; 4—driven pinions; 5—driving pinion; 6—flange; 7—retaining ring; 8—back cover.
The multi-gear pump consists of manifold 1 with several connection openings, representing the fluid distribution system. Front cover 1 has five holes: four suction holes and one outlet hole. The manifold is attached to housing 2 using bolted connections. Housing 2 has five holes in which five bearings 3 are installed. Four idler gears 4, as well as a centered master gear 5 with bearings, are installed, meshing with the idler gears.
The four idler gears 4 arranged in the chambers are arranged relative to each other in such a way that they do not mesh with each other. Attached to housing 2 is a rear cover 8 with a flange 6, which also has holes for bearings 3. Cover 8 has an opening with an O-ring 7 for drive shaft 5.
In this design, due to the four discharge zones, the radial forces acting on the shaft will be balanced. As a result of the fact that the volume of the pump working chamber has increased, the pump capacity will also have higher values. The uniformity of the delivery and the reduction in pressure pulsations are achieved by the fact that the gears engage and disengage with a time offset. In addition, all fluid discharged from the working chambers enters the manifold, where the displaced flows are combined into one.
Focused parameter modeling provides information on the details of localized fluid flow, such as flow jets and cavitation formation sites, in addition to predicting basic pressure and flow characteristics throughout the plant [25,26,27]. Therefore, fluid flow modeling using CFD analysis was applied to the design of the multi-gear pump. Based on this analysis, decisions were made to select the optimal criteria for the fluid distribution system (manifold) of the multi-gear pump, designed to separate the high- and low-pressure regions and direct the fluid flows.
In this regard, the main purpose of the study was to improve the design of the distributor of the prototype of a multi-pinion pump to reduce pressure (energy) losses and increase the efficiency of its operation.
2. Materials and Methods
2.1. Designs of Objects
A special feature of the design of the multi-gear pump is the suction and displacement system. A special feature of the design of a multi-gear pump is the system for the suction and displacement of liquid. The liquid enters through four suction openings 1, is combined into one in chamber 2, and then enters the working chamber through openings 3 in the housing. Having acquired energy, the liquid is forced out of the pump through holes 4 in the housing, and is then combined into one flow in chamber 5 and pumped into the system through pipe 6 (Figure 2).
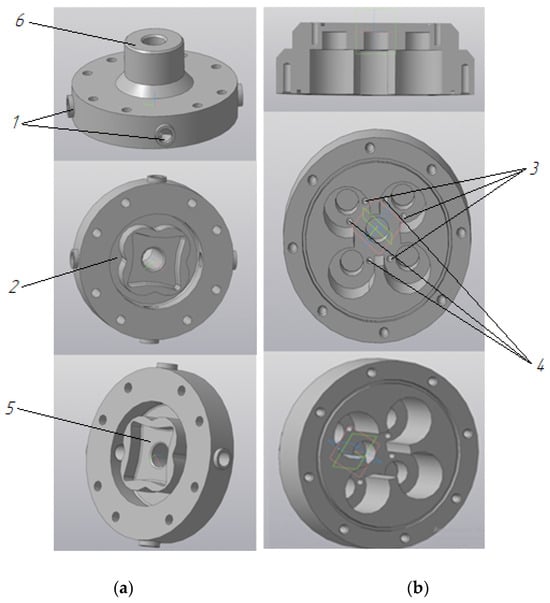
Figure 2.
Elements of a multi-gear pump created in Solidworks: (a) collector; (b) housing: 1—inlets; 2—low pressure chamber (suction); 3—suction line openings; 4—discharge line holes; 5—high pressure chamber (pressure); 6—pressure pipe.
To carry out the study, the SolidWorks program complex was used, which has the application FlowSimulation to calculate the fluid flow. Based on the object under study, the design area was enclosed between the manifold and the pump housing [28].
2.2. Material Properties
The physical and mechanical properties of aluminum were used to model the elements of the multistage pump (Table 1). According to previous studies, this material is the most optimal for the casing of a multi-gear pump [29].

Table 1.
Physical and mechanical properties of the restricted lid space.
When modeling the liquid parameters of the multi-gear pump, the characteristics of the mineral oil VMGZ in the temperature range from −55 to +50 °C were used (Table 2).

Table 2.
Mineral oil parameter VMGZ (GOST 33).
2.3. Grid Construction and Setting of Boundary Conditions in the Distribution System
The distribution system of the multiple-gear pump is a manifold in which the low- and high-pressure areas are hermetically separated. The suction line consists of four inlets 1 with a diameter of 20 mm that direct the liquid to a common cavity 2, from which it is sucked into the working chamber through openings with a diameter of 10 mm due to the pressure difference (Figure 3). The pressure line also has four openings, from which the liquid is pressurized into the common cavity 3 and displaced into the system from nozzle 4 with a diameter of 20 mm.
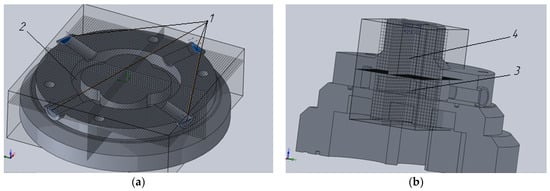
Figure 3.
Construction of a global grid in the areas of fluid flows: (a) the creation of a grid in the calculation of inlet channels; (b) the creation of a grid in the calculation of outlet channels: 1—inlets; 2—low pressure chamber (suction); 3—high pressure chamber (pressure); 4—pressure pipe hole.
Grid construction was carried out in automatic mode [30,31] with the smallest grid cell size (level 7).
The boundary conditions in the study of fluid flow parameters in the suction line [32] included the total input pressure in the range of 0.3 to 1 MPa and the volume flow rate at the outlet in the range of 0.00182 to 0.0055 m3/s; in the pressure line, these included the total outlet pressure from 6 to 24 MPa and the volume flow rate at the input from 0.00182 to 0.0055 m3/s (Figure 4).
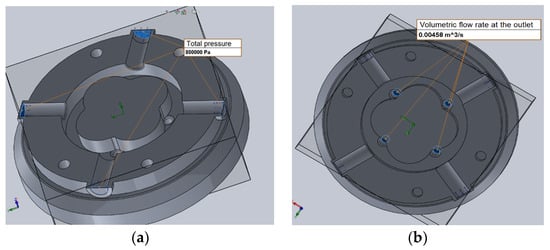
Figure 4.
Example of setting the boundary conditions for the suction line: (a) input pressure; (b) outlet volumetric flow rate.
As an assumption, it was assumed that the structure is airtight and that there are no gaps or narrow slots in the design domain.
3. Results
3.1. Input Data to Estimate Hydraulic Parameters in the Suction and Pressure Lines of the Distribution System
Numerical experiments were performed in SolidWorks Flow Simulation. The main task of the experiments was the study and calculation of the hydraulic parameters of the flow (pressure losses and velocity in the suction and pressure lines) in order to determine the performance of the proposed collector design and operational characteristics of the gear hydraulic machine. The research was carried out in several stages:
- (1)
- The calculation of the suction line of the collector at changes in performance and speed, dynamic viscosity coefficient, and pressure at the inlet of the suction pipe;
- (2)
- The calculation of the collector pressure line at changes in productivity and speed, the coefficient of dynamic viscosity, and pressure at the outlet of the discharge pipe.
Thus, three series of experiments were conducted with a planning matrix of 23.
In the first series of experiments (1–8), the number of revolutions per minute n = var, the dynamic viscosity coefficient µ = const, and the pressures Ps = const and Pp = const. In the second series of experiments (9–16), n = const, µ = var, Ps = const, and Pp = const. In the third series of experiments (17–24), n = const, µ = const, Ps = var, and Pp = var.
The data input to estimate hydraulic parameters in the suction and pressure lines of the distribution system can be expressed as follows:
where m is the gear module; b, the gear tooth width; and z, the number of teeth.
q = 4π ⋅ m2 ⋅ b ⋅ z,
The working volume of the multiple gear pump was q = 275 cm3.
The data from the experiments in the SolidWorks simulation are presented in Table 3.

Table 3.
Variable parameters in modeling fluid flow in the suction line of the distribution system.
The results can be presented in the form of isosurfaces, cross-sectional, and surface patterns, as well as trajectories characterizing changes in the hydraulic parameters of the flow. The results can be most clearly represented by cross-sectional pictures (Figure 5a) or flow trajectories (Figure 5b).
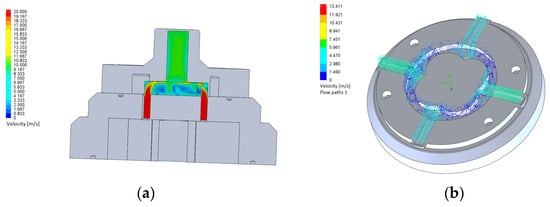
Figure 5.
Options for the presentation of calculation results: (a) velocity change in the pressure line (cross-sectional picture); (b) velocity change in the suction line (flow path).
3.2. Investigation of Changes in the Main Hydraulic Parameters of a Pump System in Suction and Pressure Lines
At the inlet of the suction line, the pressure is at its maximum; then, upon entering the four suction ports, the pressure gradually decreases. The fluid loses energy to overcome resistance at the inlet of the orifices and in the orifices themselves (Figure 6). Figure 7 shows the change in flow velocity.
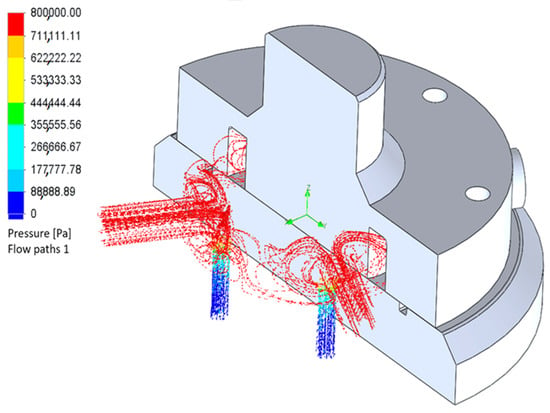
Figure 6.
Schematic of the pressure change in the suction line.
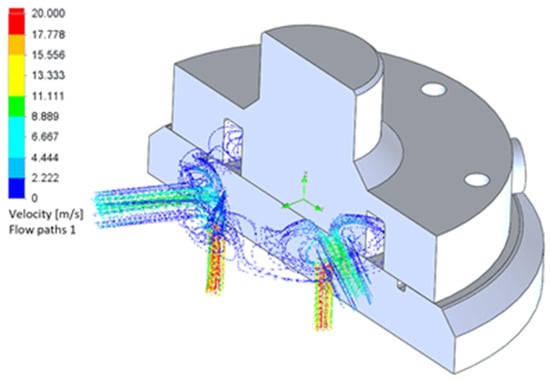
Figure 7.
Schematic of the velocity variation in the suction line.
At the inlet to the suction connections and in the common cavity of the manifold, the velocity values are minimum. As the liquid flows further into the pump working chamber through the 10 mm diameter holes, the velocity increases. From the velocity distribution diagram, it can be observed that in the center of the orifice cross-sections, the velocity is maximum, and as it moves away from the center to the walls, the velocity decreases as a result of friction between the liquid layers.
Figure 6 and Figure 7 show examples of the calculation of liquid flow parameters in the suction line for pressure Ps = 0.8 MPa and liquid flow rate Q = 0.00458 m3/s. At the inlet to the suction line, the pressure value is maximum and equal to 0.8 MPa; then, upon entering the four suction openings, the pressure gradually decreases. The fluid loses energy to overcome the resistance at the inlet of the orifices. Here, the pressure value changes to 0.62 MPa. In the orifices themselves, the pressure decreases to 88 kPa as the fluid moves. Such pressure losses are related to the internal friction of the liquid. Figure 7 shows the change in the fluid flow velocity. At the inlet to the suction connections, the velocity values are minimal and are 6–7 m/s. In the general cavity of the suction line, the presence of low velocities up to 2 m/s and vortex formation zones can be observed. With further movement of liquid into the working chamber of the pump through the holes with a diameter of 10 mm, the speed increases to 17 m/s. According to the velocity distribution diagram, it can be observed that in the center of the cross-sections of the holes, the velocity is maximum and, as it moves away from the center to the walls, the velocity decreases, which is caused by friction between the liquid layers.
Data analysis shows that a minimum suction line pressure of at least 500 kPa is required to maintain continuous flow and prevent cavitation. Liquid viscosity and shaft speed also affect pump performance. Modeling has shown that with this delivery system, the pump can pump liquids of viscosity classes 5–10, with a rotational speed not exceeding 1200 rpm and a kinematic viscosity of 10 cSt.
In the discharge line, the pressure has the highest values when the liquid is displaced, through the four orifices, out of the pumping chamber (Figure 8).
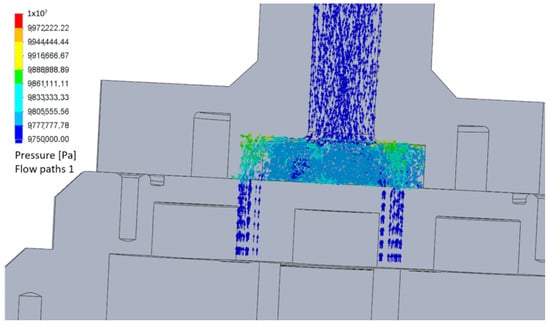
Figure 8.
Schematic of the pressure change in the pressure line.
When the fluid pressure moves through the orifices, the fluid decreases due to internal resistance in the orifices. The fluid then enters the common cavity, where intense mixing and vortexing of fluid particles can be observed, contributing to an additional pressure drop. High-pressure zones, marked in red, arise from the presence of sharp turns and sharp corners. Therefore, one of the tasks of improving the device is to reduce pressure losses in the pressure line and increase the efficiency of operation by rounding its inner edges.
Some liquid particles, moving toward the common cavity and flowing around the inner surface, also have the highest values (marked in red). When entering the common head with a larger diameter, the velocity acquires smaller values. Blue indicates the areas where the particles have velocities close to zero and do not participate in the energy conversion process in any way. This is due to the peculiarities of the collector’s design.
Figure 8 and Figure 9 show the results of the calculation of the liquid flow parameters in the pressure line for the input pressure Pn = 10 MPa and the outlet flow rate Q = 0.00458 m3/s. In the pressure line, at the displacement of liquid through four holes from the working chamber, the pressure has the highest values: 10 MPa. Moving along the orifices, the pressure decreases due to the internal resistance in the orifices and reaches the value of 9.99 MPa.
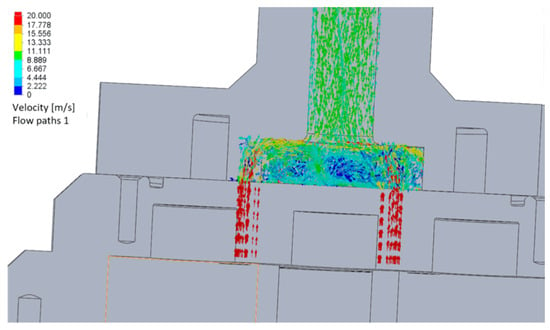
Figure 9.
Schematic of the velocity change in the pressure line.
The fluid then enters the common cavity, where the intense mixing and swirling of fluid particles can be observed, which contributes to an additional pressure drop. High-pressure zones, marked in red, arise due to the presence of sharp turns and sharp corners. Therefore, one of the tasks of improving the device is to reduce pressure losses in the pressure line and increase the efficiency of operation by rounding its inner edges.
Figure 9 shows the variation in velocity. Here, the velocity values have the maximum value at the exit of the working chamber 17–20 m/s. Some liquid particles that move to the common cavity and flow around the inner surface also have the highest values (marked in red). When entering the common pressure tube with a larger diameter, the liquid acquires lower values of the speed of 6–7 m/s. Blue indicates the areas where the particles have velocities close to zero and do not participate in the energy conversion process in any way. This is due to the peculiarities of the collector’s design.
Figure 10 shows the results of the calculation of numerical experiments in SolidWorks according to the initial data of Table 3 and Table 4. The results represent the graphical dependencies of the liquid velocity and pressure drop in the suction lines (Figure 10a) and pressure lines (Figure 10b) of the collector from changes in the liquid flow rate Q in the range from 0.00182 to 0.0055 m3/s, pressure in suction lines Ps (from 0.3 MPa to 1 MPa) and pressure lines Pp (from 6 MPa to 24 MPa), and the dynamic viscosity coefficient µ in the range from 0.00861 to 8.2 Pa·s.
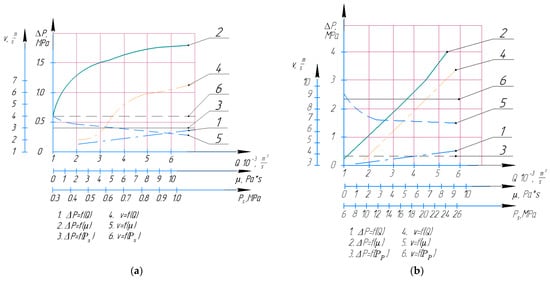
Figure 10.
Velocity υ and pressure drop ∆P in the suction lines (a) and pressure (b) of the distribution system of a multi-gear pump: 1—dependence of pressure drop on fluid flow ∆P = f(Q); 2—dependence of pressure drop on dynamic viscosity coefficient ∆P = f(μ); 3—dependence of pressure drop on suction pressure ∆P = f(Ps)/discharge pressure ∆P = f(Pp); 4—dependence of fluid velocity on flow rate υ = f(Q); 5—dependence of fluid velocity on the coefficient of dynamic viscosity υ = f(μ); 6—dependence of fluid speed on suction pressure υ = f(Ps)/discharge pressure υ = f(Pp).

Table 4.
Variable parameters in the modeling of fluid flow in the pressure line of the distribution system.
An analysis of the obtained data allowed us to reveal some dependencies.
With an increase in the liquid flow rate caused by a change in the driving gear rotation speed, the pressure drop ΔP in the suction line (curve 1, Figure 10a) increases linearly from 0.066 to 0.35 MPa, and liquid velocity (curve 4, Figure 10a) increases with decreasing intensity from 1.67 to 6.03 m/s.
In the header line, an increase in flow rate results in a linear increase in fluid velocity from 3.42 to 9.92 m/s (curve 4, Figure 10b). The pressure drop increases in direct proportion to the flow rate in the range of 0.093 to 0.401 MPa (curve 1, Figure 10b).
The increase in the dynamic viscosity coefficient causes an increase in friction between the liquid layers and the internal walls of the collector, and as a consequence, the pressure drop in the lines increases from 0.42 to 1.65 MPa (curve 2, Figure 10a) and from 0.419 to 3.415 MPa (curve 2, Figure 10b), respectively. The fluid velocity in the suction line decreases from 4.33 to 3.21 m/s (curve 5, Figure 10a), and in the pressure line, it decreases from 9.11 to 6.73 m/s (curve 5, Figure 10b). It should be noted here that it is necessary to increase the pressure in the suction line in the case of liquids with viscosities of 0.0173 Pa·s or more.
Increasing pressure in the suction line has no effect on the investigated parameters of the liquid flow (curves 3 and 6, Figure 10a). The liquid velocity is ~4 m/s, and the pressure drop is ~0.423 MPa. As the calculation results show, to ensure the operability of the multistage pump, the pressure in the suction line should not be less than 0.5 MPa at n = 1000 rpm, which will eliminate the cavitation and violation of the continuity of liquid flow.
The change in pressure in the pressure line has an insignificant influence on the parameters sought. The pressure drop was 0.33 MPa, and the liquid velocity in the outlet pipe was 8.81 m/s (curves 3 and 6, Figure 10b).
3.3. Investigation of Manifold Geometry Variation in Fluid Velocity and Pressure Drop
Since the prototype of a multi-gear pump is a multi-parameter task, another criterion was to obtain the lowest pressure drop when the liquid passes from the ‘inlet’ to ‘outlet’ zone.
In this regard, a geometric optimization of the input space in the top cover manifold was performed. The radius was varied from 3 to 15 mm (Figure 11). The number of rotations was n = 1000 rpm.
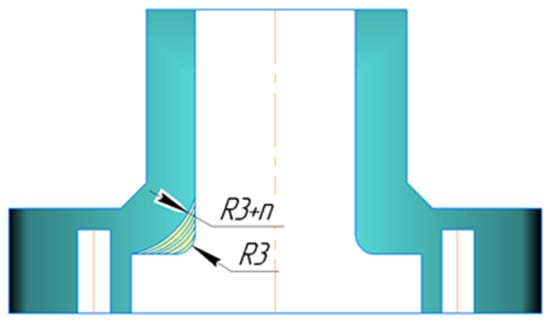
Figure 11.
Profile of the manifold inner cavity with a variable radius.
The fluid velocity and pressure distribution as a function of the radius are shown in Figure 12 and Figure 13.
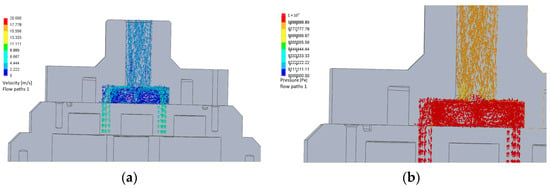
Figure 12.
Fluid velocity (a) and pressure (b) distribution diagrams with a transition radius of 3 mm in the manifold.
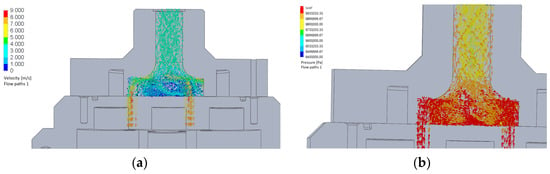
Figure 13.
Fluid velocity (a) and pressure (b) distribution diagrams with a transition radius of 15 mm in the manifold.
The maximum velocity and pressure drop values are shown in Figure 14.
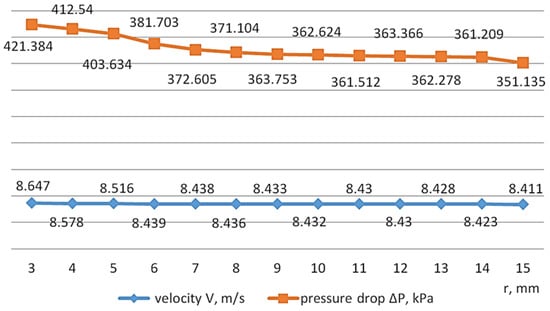
Figure 14.
Distribution of the pressure drop as a function of the radius of the transition in the manifold in the suction line of the distribution system.
As can be seen in Figure 14, the velocity of the fluid flow in the gear pump is almost unchanged depending on the change in radius in the manifold, and the pressure drop decreases from 42.384 kPa to 35.235 kPa when the radius increases from 3 mm to 15 mm.
In the study, it was also hypothesized that the pressure drop across the manifold depends not only on the radius of the transition in the manifold but also on the number of revolutions. For this purpose, the DoE method was used. The input and output data for the DoE are presented in Table 5.

Table 5.
Input and output data for DoE.
Graphically, the dependence of the pressure drop on the transition radius on the inner surface of the collector and the speed is shown in Figure 15.
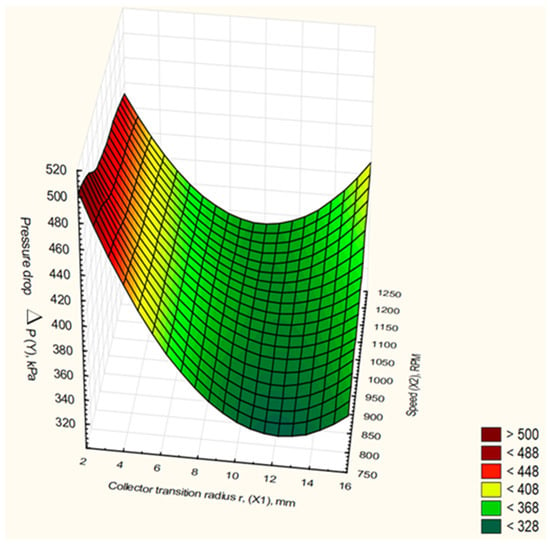
Figure 15.
A 3D diagram of the pressure drop, transition radius, and speed in the collector.
The dependence of the pressure drop ΔP (Y) on the collector transition radius r (X1) and the speed n (X2) can be described using the multiple regression equation [33].
As a result of calculations, the multiple regression equation was obtained:
Y = 431.8137 − 6.6682X1 + 0.00436X2
The constant estimates the aggregate effect of other factors (other than those accounted for in model Xi) on the result Y, and it means that Y, in the absence of Xi, would be 431.8137. The coefficient b1 indicates that as X1 increases by 1, Y decreases by 6.6682. The coefficient b2 indicates that as X2 increases by 1, Y increases by 0.00436.
To assess the reliability of the multiple regression analysis, we calculated the criteria shown in Table 6.

Table 6.
Criteria used to assess the reliability of the obtained multiple regression equation.
The statistical significance of the equation was checked using the coefficient of determination and Fisher’s criterion. In this situation, 76.99% of the total variability of Y (pressure drop) was found to be explained by the change in factor Xi (speed, radius of the rounding of the inner surface of the collector).
4. Conclusions
This paper describes a numerical model that allows the characteristics of fluid motion characteristics in a gear pump, taking into account the viscosity and design characteristics of the inlet orifice system.
The following results were obtained:
- (1)
- Cavitations were observed in the upper cover of the manifold with a transition radius of 3 mm.
- (2)
- Reducing the transition radius in the manifold from 3 to 15 mm in the suction line of the system reduces the pressure drop by 13%.
- (3)
- The liquid flow velocity in the top cover of a multiple gear pump decreases slightly (3%) as a function of changing the radius in the manifold from 3 to 15 mm.
- (4)
- The minimum pressure on the suction line is 500 kPa or more. Smaller pressures contribute to the interruption of the continuity of the liquid flow and the occurrence of cavitation.
- (5)
- Fluid viscosity and drive shaft speed also influence the performance of the multiple gear pump design.
- (6)
- It is established that with this distribution system, taking into account the variable temperature of the liquid in the hydraulic circuits, the multiple gear pump can operate with liquids belonging to a viscosity class of 5–10.
- (7)
- The rotational speed is not greater than 1200 rpm with a kinematic viscosity coefficient of 10 cSt.
- (8)
- The pressure drop depends on the number of revolutions and the radius of the rounding of the manifold.
This study has certain limitations that are related to the sensitivity of the mesh in the modeling process. In future studies, we intend to address these shortcomings by tuning the mesh in manual mode and increasing the number of cells.
Future work is also planned to improve the fluid distribution system in the multistage pump, particularly to consider the possibility of making suction holes in the pump casing. This will reduce suction line losses and increase the range of liquids pumped.
It is expected that this study will be a useful reference for design engineers and developers who will be able to apply the results to obtain different flow parameters for a multi-gear pump.
Author Contributions
Conceptualization, Ł.G. and O.Z.; methodology, O.Z., Ł.G. and T.N.; software, O.R.; validation, Ł.G., O.Z. and A.B. (Alexandra Berg); formal analysis, O.Z. and T.N.; investigation, O.N., A.B. (Alexandra Berg) and A.B. (Andrey Berg); resources, O.Z. and A.B. (Alexandra Berg); data curation, Ł.G. and T.N.; writing—original draft preparation, O.Z., O.R., Ł.G., Ł.W., B.W., W.Ł. and O.N.; writing—review and editing, O.Z., Ł.G., Ł.W. and B.W.; visualization, O.R. and A.B. (Andrey Berg); supervision, O.Z. and Ł.G.; project administration, T.N. and Ł.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant of Young Scientists IRN No. AP19579208 “Creation of a universal prototype of a gear pump for hydraulic systems capable of pumping viscous liquids of various nature”) for the analysis of the design and technological features of gear pumps.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Cieślicki, R.; Karpenko, M. An investigation of the impact of pump deformations on circumferential gap height as a factor influencing volumetric efficiency of external gear pumps. Transport 2022, 37, 373–382. [Google Scholar] [CrossRef]
- Bilalov, R.; Smetannikov, O. Numerical Study of the Hydrodynamics of an External Gear Pump. J. Appl. Mech. Tech. Phys. 2022, 63, 1284–1293. [Google Scholar] [CrossRef]
- Shen, H.; Li, Z.; Qi, L.; Qiao, L. A method for gear fatigue life prediction considering the internal flow field of the gear pump. Mech. Syst. Signal Process. 2018, 99, 921–929. [Google Scholar] [CrossRef]
- Marinaro, G.; Frosina, E.; Senatore, A. A Numerical Analysis of an Innovative Flow Ripple Reduction Method for External Gear Pumps. Energies 2021, 14, 471. [Google Scholar] [CrossRef]
- Rituraj, R.; Vacca, A. Investigation of flow through curved constrictions for leakage flow modelling in hydraulic gear pumps. Mech. Syst. Signal Process. 2021, 153, 107503. [Google Scholar] [CrossRef]
- Șcheaua, F. The use of numerical analysis in order to highlight the fluid dynamics inside a hydraulic gear pump model. J. Ind. Des. Eng. Graph. 2015, 10, 33–36. [Google Scholar]
- Bie, V.; Hulsen, M.; Anderson, P. The effect of non-Newtonian behavior on contact formation in an external gear pump. J. Non-Newton. Fluid Mech. 2022, 306, 104818. [Google Scholar] [CrossRef]
- Yoon, Y.; Park, B.; Shim, J.; Han, Y.; Hong, B.; Yun, S. Numerical simulation of three-dimensional external gear pump using immersed solid method. Appl. Therm. Eng. 2017, 118, 539–550. [Google Scholar] [CrossRef]
- Peng, Z.; Liejiang, W.; Rongmin, L.; Mingyuan, L.; Yan, Q. Flow Field Modeling and Simulation of High-Speed Gear Pump Considering Optimal Radial and End Clearance. IEEE Access 2023, 11, 64725–64737. [Google Scholar] [CrossRef]
- Zardin, B.; Emiliano, N.; Massimo, B. Evaluation of the Hydro—Mechanical Efficiency of External Gear Pumps. Energies 2019, 12, 2468. [Google Scholar] [CrossRef]
- Torrent, M.; Gamez-Montero, P.; Codina, E. Parameterization, Modeling, and Validation in Real Conditions of an External Gear Pump. Sustainability 2021, 13, 3089. [Google Scholar] [CrossRef]
- Michael, P.; Khalid, H.; Wanke, T. An Investigation of External Gear Pump Efficiency and Stribeck Values SAE. Tech. Pap. 2012, 1–8. [Google Scholar] [CrossRef]
- Močilan, M.; Husár, Š.; Labaj, J.; Žmindák, M. Non-Stationary CFD Simulation of a Gear Pump. In Proceedings of the 21st International Polish-Slovak Conference “Machine Modeling and Simulations 2016”, Hucisko, Poland, 8–11 September 2017. [Google Scholar]
- Mithun, M.; Koukouvinis, P.; Karathanassis, I.; Gavaises, M. Numerical simulation of three-phase flow in an external gear pump using immersed boundary approach. Appl. Math. Model. 2019, 72, 682–699. [Google Scholar] [CrossRef]
- Sharma, A.K.; Kumar, M.; Kumar, N.; Das, A.K. Improvement in tribological properties of thrust plate of gear pump through flame spattering in diverse cooling medium. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Zhao, X.; Vacca, A. Theoretical Investigation into the Ripple Source of External Gear Pumps. Energies 2019, 12, 535. [Google Scholar] [CrossRef]
- Egbe, E.A.P. Design Analysis and Testing of a Gear Pump Research Inventy. Int. J. Eng. Sci. 2013, 3, 1–7. [Google Scholar]
- Osinski, P. Modelling and Design of Gear Pumps with Modified Tooth Profile; Lambert Press: Saarbruken, Germany, 2014; 156p. [Google Scholar]
- Rundo, M. Models for Flow Rate Simulation in Gear Pumps: A Review. Energies 2017, 10, 1261. [Google Scholar] [CrossRef]
- Mali, P.; Joshi, G.; Patil, I. CFD Simulation of External Gear Pump using ANSYS CFX. Int. J. Appl. Eng. Res. 2018, 13, 11970–11973. [Google Scholar]
- Mitov, A.; Nikolov, N.; Nedelchev, K.; Kralov, I. CFD Modeling and Experimental Validation of the Flow Processes of an External Gear Pump. Processes 2024, 12, 261. [Google Scholar] [CrossRef]
- Romanenko, I.; Martseniuk Ye Bilohub, O. Modeling the Meshing Procedure of the External Gear Fuel Pump Using a CFD Tool. Computation 2022, 10, 114. [Google Scholar] [CrossRef]
- Ferrari, C.; Morselli, S.; Miccoli, G.; Hamiche, K. Integrated CFD-FEM approach for external gear pump vibroacoustic field prediction. Front. Mech. Eng. 2024, 10, 1298260. [Google Scholar] [CrossRef]
- Gierz, Ł.; Fryczynksi, K.; Łykowski, K.; Wargula, Ł.; Wieczorek, B. Quasi-Planetary Gear Pump. Patent Application of the Patent Office of the Republic of Poland No P.446435, 19 October 2023. [Google Scholar]
- Shoukat, G.; Siddique, K.; Sajid, M. Modeling and CFD Analyses of Gear Pump in OpenFOAM. In Proceedings of the ASME-JSME-KSME 2019 8th Joint Fluids Engineering Conference, San Francisco, CA, USA, 28 July–1 August 2019; Volume 2. Computational Fluid Dynamics. [Google Scholar]
- Adake, D.; Dhote, N.; Khond, M. Experimentation and 2D Fluid Flow Simulation over an External Gear Pump. J. Phys. Conf. Ser. 2023, 2601, 012029. [Google Scholar] [CrossRef]
- Labaj, J.; Husar, S. Analysis of Gear Pump Designed for Manufacturing Processes. Appl. Mech. Mater. 2015, 803, 163–172. [Google Scholar] [CrossRef]
- Kyzyrov, K.B.; Reshetnikova, O.S.; Dosmagambetov, N.G. Modeling and Calculating the Fluid Distribution System Parameters of Hydraulic Hammer VKP.250. Mater. Mech. Eng. Technol. 2021, 2, 3–7. [Google Scholar] [CrossRef]
- Zharkevich, O.; Nikonova, T.; Gierz, Ł.; Berg, A.; Berg, A.; Zhunuspekov, D.; Warguła, Ł.; Łykowski, W.; Fryczyński, K. Parametric Optimization of a New Gear Pump Casing Based on Weight Using a Finite Element Method. Appl. Sci. 2023, 13, 12154. [Google Scholar] [CrossRef]
- Zhetessova, G.; Nikonova, T.; Gierz, Ł.; Berg, A.; Yurchenko, V.; Zharkevich, O.; Kalinin, A. A Comparative Analysis of the Dynamic Strength Properties of the Long Guides of Intelligent Machines for a New Method of the Thermal Spraying of Polymer Concrete. Appl. Sci. 2022, 12, 10376. [Google Scholar] [CrossRef]
- Mussayev, M.M.; Sherov, K.T.; Buzauova, T.M.; Abisheva, N.B.; Ainabekova, S.S. Studying the stress-strain state of a more loaded node of a special device for turn-milling. Metalurgija 2022, 61, 247–249. [Google Scholar]
- Altabey, W.A. Chapter 11—Gears. In Fundamentals of Machine Component Design; Elsevier: Amsterdam, The Netherlands, 2024; pp. 229–279. [Google Scholar]
- Zharkevich, O.; Nurzhanova, O.; Zhunuspekov, D.; Naboko Ye Buzauova, T.; Abdugaliyeva, G.; Mateshov, A.; Bessonov, A. Determination of Optimal Hardfacing Modes for Recovering Electric Motor Shafts. Teh. Vjesn. 2023, 30, 951–957. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).