LWMD: A Comprehensive Compression Platform for End-to-End Automatic Speech Recognition Models

Abstract

Recently end-to-end (E2E) automatic speech recognition (ASR) models have achieved promising performance. However, existing models tend to adopt increasing model sizes and suffer from expensive resource consumption for real-world applications. To compress E2E ASR models and obtain smaller model sizes, we propose a comprehensive compression platform named LWMD (light-weight model designing), which consists of two essential parts: a light-weight architecture search (LWAS) framework and a differentiable structured pruning (DSP) algorithm. On the one hand, the LWAS framework adopts the neural architecture search (NAS) technique to automatically search light-weight architectures for E2E ASR models. By integrating different architecture topologies of existing models together, LWAS designs a topology-fused search space. Furthermore, combined with the E2E ASR training criterion, LWAS develops a resource-aware search algorithm to select light-weight architectures from the search space. On the other hand, given the searched architectures, the DSP algorithm performs structured pruning to reduce parameter numbers further. With a Gumbel re-parameter trick, DSP builds a stronger correlation between the pruning criterion and the model performance than conventional pruning methods. And an attention-similarity loss function is further developed for better performance. On two mandarin datasets, Aishell-1 and HKUST, the compression results are well evaluated and analyzed to demonstrate the effectiveness of the LWMD platform.

1. Introduction

Automatic speech recognition (ASR) transcribes human speech into corresponding transcripts, and it has been widely applied in the real world. After being processed by voice activity detection modules [1,2,3], target speeches will be fed into the ASR systems. Early hybrid ASR systems consist of an acoustic model, a language model and a pronunciation lexicon map, all of which are designed manually and optimized separately. Such hybrid systems result in a cumbersome technique stack and heavily rely on the prior knowledge of the target language, leading to an expensive training cost.

In recent years, end-to-end (E2E) ASR systems have yielded state-of-the-art (SOTA) performance in many ASR tasks, which can integrate the components of hybrid ASR systems into one neural network. And E2E ASR systems have become a more popular alternative to hybrid systems since more simply training pipelines and better performances [4,5,6]. The connectionist temporal classification (CTC) framework [7] and the attention-based encoder-decoder (AED) framework [8] are two popular E2E ASR frameworks in existing works. The CTC framework consists of an acoustic encoder responsible for extracting high-level acoustic representations from the input speeches and a CTC classifier that predicts the output sequence with the CTC criterion. And the AED framework consists of an acoustic encoder and an attention-based decoder that predicts the output sequence in an auto-regressive manner. Based on CTC and AED frameworks, conventional encoders/decoders are usually built by stacking identical blocks, and the multi-headed attention (MHA) based Transformer is the most popular block architecture in existing works [9], which can capture global contextual information effectively with the MHA mechanism. Recently convolution neural network (CNN) also gains increasing attention in building encoders for its advantage in extracting local acoustic information [10].

Even though existing works have achieved promising performance for E2E ASR tasks, most of them tend to adopt large models and ignore resource consumption, which leads to expensive memory and computation costs for real-world applications. There have existed several works that can reduce the resource consumption of neural networks. Refs. [11,12,13] design light-weight architectures on top of Transformer for fewer parameters. Refs. [14,15,16] propose to reduce model parameter numbers with structural pruning based on fixed architectures. Considering the tensor operation is the basic computation in neural networks, several works employ the low-rank decomposition of tensors to reduce the parameter complexity of neural networks [17,18]. And the data low-bit quantization also can reduce model size and computation costs by relieving resource consumption of each parameter, which is widely employ in model compression [19,20,21,22]. Even though these works can indeed reduce model parameter numbers or FLOPs by a certain amount, a non-negligible problem is that most of existing light-weight architectures and structural pruning methods can hardly maintain the same performance with the baseline with a significant parameter reduction.

In order to reduce resource consumption and obtain more light-weight E2E ASR models while maintaining excellent performance, we propose the light-weight model designing (LWMD) platform. LWMD consists of a light-weight architecture searching (LWAS) framework and a differentiable structural pruning (DSP) algorithm. The LWAS framework employs the neural architecture search (NAS) technique to search architectures with small parameter and FLOPs costs, and the DSP framework can further prune searched architectures for fewer resource consumptions. On the one hand, the LWAS framework designs a topology-fused search space to cover many existing human-designed architectures that proved to be effective and develop a resource-aware differentiable search algorithm to select light-weight architectures from the search space based on popular differentiable search algorithms [23,24]. On the other hand, the DSP algorithm proposes a differentiable pruning criterion instead of conventional magnitude-aware criteria to build a stronger correlation between the pruning criterion and the model performance, and an attention-similarity loss function is specially developed for the MHA module of E2E ASR models to get better pruning performance. Moreover, since LWMD only makes modifications to the model architecture, it is orthogonal to some other compression techniques (e.g. quantization) and can be easily combined with them. To summarize, the contributions of this paper can be described as follows:

• LWMD platform. In this paper, we propose the LWMD platform to design light-weight E2E ASR models, which consists of one LWAS framework to search light-weight architectures and one DSP algorithm to prune further searched architectures.
• The LWAS framework. By incorporating different topologies together, LWAS designs one topology-fused search space that can cover many human-designed architectures and develops a resource-aware differentiable search algorithm to select light-weight architectures from the search space.
• The DSP algorithm. With the proposed differentiable pruning criterion, DSP can build a stronger correlation between the pruning criterion and the model performance. An additional attention-similarity loss function is specially developed for MHA modules to get better pruning performance.
• Extensive experiments demonstrate the effectiveness of LWMD in compressing E2E ASR models. More ablation and exploration explain the contributions of the LWAS framework and the DSP algorithm.

The rest of this paper is organized as follows. Section 2 briefly introduces previous works related to this work. Section 3 describes our proposed LWMD platform. Section 4 provides the experiment results and analysis. Section 5 gives the conclusion.

2. Related Works

2.1. E2E ASR Models

There exist two popular types of E2E ASR frameworks: CTC and AED. [7] first proposes the CTC framework, which consists of an acoustic encoder and a CTC classifier. The acoustic encoder is responsible for extracting contextual information from the input speeches and generating a high-level acoustic representation $h^{enc}$ to be fed into the CTC classifier, and the CTC classifier is a softmax network that is trained with the CTC criterion. Even though there have been many improvements on top of the CTC framework [25,26], the conditional independent assumption [7] limits the ability of CTC to capture linguistic information, which results in an unsatisfying performance in applications.

The AED framework is originally proposed for sequence-to-sequence modeling [27]. Considering ASR is also a sequence-to-sequence task, [28,29] propose to apply the AED framework in E2E ASR tasks. The AED framework is composed of an acoustic encoder and an attention-based decoder, where the encoder will feed the high-level acoustic representation $h^{enc}$ into the decoder to generate the output sequence in an auto-regressive (AR) manner. Such an AR decoding manner helps to break the conditional independent assumption in CTC and obtain a more promising performance. However, the AED framework needs more parameters and FLOPs meanwhile.

Based on the CTC and LAS framework, there have existed various encoder and decoder architectures in existing works. Early works tend to employ RNN-based architectures for their sequence modeling capabilities [27,30]. More recently, the Transformer network is introduced for E2E ASR [8,9], which adopts the multi-headed attention (MHA) mechanism. The advantage of Transformer is two-fold: The MHA mechanism allows a more direct way to extract global contextual information across the whole sequence, which results in a better performance than RNN. Also, since most operations in Transformer can be calculated in parallel, Transformer provides a faster training and inference speed than RNN. Therefore, the Transformer encoder and decoder have become the most popular choices in E2E ASR.

Existing Transformer encoders or decoders are built by stacking identical blocks, and each block is composed of the MHA module and the FFN module. Considering CNN has a strong advantage in capturing local information, there have been several works that introduce the CNN module into Transformer and achieve promising performance [10,11,12].

2.2. Model Compression

There have been many works that propose to compress E2E ASR models. In general, existing works can be divided as: light-weight architecture design, model parameter pruning, data quantization and some other methods. And methods of different categories are usually orthogonal, which means they can easily be combined with each other.

Light-weight Architecture Design. Light-weight architecture design aims at creating a base light-weight architecture itself from a pool of candidates. LightConv [11] and LiteTransformer [12] design light-weight Transformer variants, [13] propose to search light-weight encoder architectures with the help of NAS automatically.

Model Pruning. Based on the designed architectures, model pruning can further remove redundant parameters of fixed architectures, and unstructured pruning and structured pruning are two major types of pruning. Even though unstructured pruning can effectively reduce model sizes [14,15], it usually results in a negligible improvement in runtime memory or speed due to irregular pruning results. Structured pruning focuses on pruning unimportant structured blocks of weights [16,31], which are friendly to real-world implementations and can indeed improve runtime memory or speed. And the weight magnitude [14] is the most commonly-used pruning criterion in existing methods.

Data Quantization. Quantization refers to reducing the number of unique values required to represent model weights and activations [19,20,22], which allows to represent them using fewer bits, to reduce the memory footprint, and to lower the precision of the numerical calculations.

Others Besides the above-mentioned pruning methods, there also existed some other ones, e.g., Knowledge Distillation [32] and Tensor Decomposition [17,18,33,34]. These works also can obtain promising compression performance, and they can be incorporated with the above-mentioned ones in general.

3. The Proposed Method

The proposed compression platform consists of one light-weight architecture search framework named LWAS and one structured pruning algorithm named DSP.

3.1. The LWAS Framework

Inspired by the success of NAS methods, we propose the LWAS framework to design light-weight architectures for E2E ASR models. LWAS first designs a topology-fused search space to provide adequate candidate architectures and then develops a resource-aware search algorithm to select light-weight architectures from the search space. Combined with conventional E2E ASR model training, LWAS employs two stages to design light-weight architectures: a search stage and a retraining stage. In the search stage, LWAS search a proper light-weight architecture, and in the retraining stage, the searched architecture is retrained in the same way as training human-design architectures.

3.1.1. Differentiable Architecture Search

Considering the efficiency superiority, LWAS follows the differentiable NAS methods, where the discrete search space is relaxed into continuous with a weighted summation as shown in

$$o\left(x\right)={\sum }_{k=1}^{\left|\mathcal{O}\right|}{c}_k{o}_k\left(x\right)$$

(1)

where $c_k\in (0,1)$ is the weight of the i-th operation $o_k(·)$ in the operation set O and $o_k(·)$ is the mixed operation.

The weight $c_k$ is generated by one re-parameterization trick $c_k=g\left(\mathit{\alpha }\right),\mathit{\alpha }\in {\mathbb{R}}^{\left|O\right|}$ and ${\mathit{\alpha }}_{\mathit{k}}$ is the corresponding architecture parameter for $c_k$. And in this paper, LWAS employ the Gumbel-Softmax [24] re-parameterization trick:

$$\begin{array}{c}\hfill c_k=g\left(\mathit{\alpha }\right)=\frac{\exp ((log{\mathit{\alpha }}_{\mathit{k}}+{\mathit{G}}_{\mathit{k}})/\lambda )}{{\sum }_{k^{\prime }=1}^{\left|\mathcal{O}\right|}\exp ((log{\mathit{\alpha }}_{{\mathit{k}}^{{}^{\prime }}}+{\mathit{G}}_{{\mathit{k}}^{{}^{\prime }}})/\lambda )}\end{array}$$

(2)

where ${\mathit{G}}_{{\mathit{k}}^{{}^{\prime }}}=-log(-log\left(U_i\right))$ is the Gumbel random variant, $U_i$ is a uniform random variant, and $\lambda$ is the temperature of Softmax. After relaxing the search space, the mixed output of candidate architectures and the loss can be obtained, on top of which the gradient descent can be applied to optimize the architecture parameter since the loss is differentiable w.r.t. to $\mathit{\alpha }$. And in this way, light-weight architectures in expectation will be searched by learning $\mathit{\alpha }$.

3.1.2. The Topology-Fused Search Space

Figure 1 illustrates the search space backbone of LWAS, which also contains an acoustic encoder and an attention-based decoder. By adjusting the encoder output target, the search space can support both the architecture search of the CTC and AED frameworks.

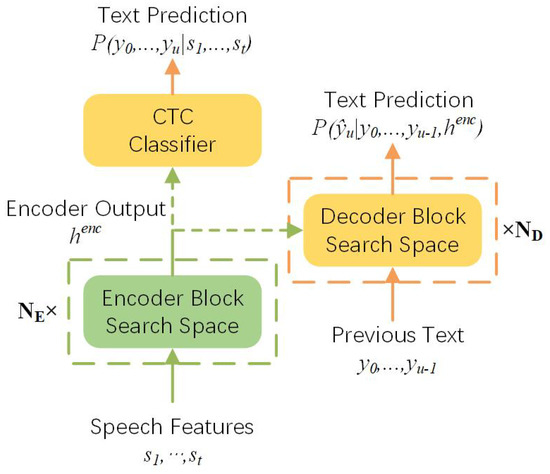
Figure 1. The backbone of our proposed search space. The encoder output can be fed into the CTC classifier or the decoder, and in this way, the search space can support the architecture search of the CTC and AED frameworks meanwhile.

As mentioned above, there have existed several human-designed architectures that have different advantages in performance or resources, as shown in Figure 2a,c. To integrate the advantages of different existing architectures, we propose fusing the topologies of these architectures into the encoder/decoder block search space, i.e., the topology-fused search space, as shown in Figure 2b,d. Drawing on literature methods, we introduce three kinds of edges into the search space, which correspond to MHA, CNN and FFN modules respectively and allow optional topology connections between them. In this way, the architecture topologies of many existing works can be covered in our search space, e.g., in the encoder search space, Transformer $\{x^0\to x^1\to x^3\}$, Conformer $\{x^0\to x^1\to x^2\to x^3\}$, LiteTransformer $\{x^0\to x^1\to x^3,x^0\to x^2\to x^3\}$, and LightConv $\{x^0\to x^2\to x^3\}$ can be obtained. Moreover, apart from these human-designed architectures, more brand-new architecture topologies also can be obtained in the search space. On top of fused topologies, we provide a set of candidate operations for each edge to allow the potential of different operation combinations. The MHA operations own flexible head numbers, e.g., 4, 8, 16, denoted as MHA4, MHA8, and MHA16. A set of CNN operations with diverse kernel sizes are provided, e.g., 7, 15, 31, denoted as CNN7, CNN15, CNN31. The FFN operations have various hidden dimensions, e.g., 512, 1024, 2048, denoted as FFN512, FFN1024, FFN2048.

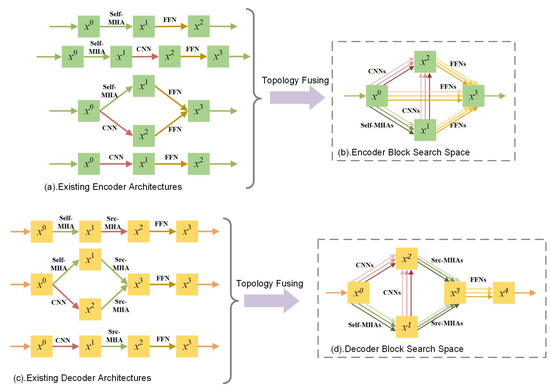
Figure 2. (a) is four human-designed encoder architectures. (b) is our topology-fused encoder search space. (c) is three human-designed decoder architectures. (d) is our topology-fused decoder search space.

Following the paradigm of NAS, the output of each edge $(i,j)$ is the weighted sum of all candidates $o^{(i,j)}\left(x\right)={\sum }_{k=1}^{\left|\mathcal{O}\right|}{c}_k^{(i,j)}{o}_k^{(i,j)}\left(x^i\right)$ and each node can be calculated based on all its predecessors: $x^{\left(j\right)}={\sum }_{i<j}{o}^{(i,j)}\left(x^{\left(i\right)}\right)$. Different from the fixed block number of human-designed architectures, LWAS further makes the block number elastic and determines it based on a block number search module, which is achieved on top of the continuous relaxation of block outputs:

$$\begin{array}{c}\hfill x^{Out}={\sum }_{n=1}^N{c}_n{x}^{L_n}\end{array}$$

(3)

where $x^{Out}$ is the final output of the encoder/decoder, N is the maximum number of the encoder/decoder block, $x^{L_n}$ refers to the output of the n-th block. And then, for each block of the encoder and decoder, the block architecture will be derived from the corresponding search space in a block-wise way.

3.1.3. The Resource-Aware Search Algorithm

To take both the effectiveness and resource consumption into consideration, we propose a resource regularization ${\mathcal{L}}_{\mathrm{Resource}}$ for LWAS. Combined with the training criterion of E2E ASR, the search objective function of NAS-SCAE can be described as:

$$\begin{array}{c}\hfill \mathcal{L}={\mathcal{L}}_{\mathrm{Performance}}+\eta {\mathcal{L}}_{\mathrm{Resource}}\end{array}$$

(4)

where ${\mathcal{L}}_{\mathrm{Performance}}$ refers to the performance-related object, e.g., CTC, or CE, ${\mathcal{L}}_{\mathrm{Resource}}$ is the resource-related regularization, and $\eta$ is a scaling factor. In this paper, we employ parameter numbers and FLOPs of candidate architectures as ${\mathcal{L}}_{\mathrm{Resource}}$, which can be obtained with a table-lookup method.

3.2. The DSP Algorithm

The DSP algorithm is further proposed to prune searched architectures of LWAS. Instead of conventional magnitude-aware criteria (e.g., $l_1$-Norm, $l_2$-Norm), we propose to prune model parameters with a differentiable pruning criterion. An attention-similarity loss function is proposed specifically for pruning MHA modules.

3.2.1. The Differentiable Pruning Criterion

As shown in Figure 3, given a weight matrix $\mathbf{W}\in {\mathbb{R}}^{n\ast d}$, we employ an importance factor $I\in {\mathbb{R}}^d$ to guide the pruning of $\mathbf{W}$, where $\mathbf{I}$ is a one-hot vector, and $I_k=0$ means the k-th dimension is to be pruned and $I_k=1$ means the k-th dimension is to be kept:

$$\begin{array}{c}\hfill {\mathbf{W}}_{pruned}=\mathbf{W}\odot \mathbf{I}=[I_1{\mathbf{w}}_1,\cdots ,I_d{\mathbf{w}}_d]\end{array}$$

(5)

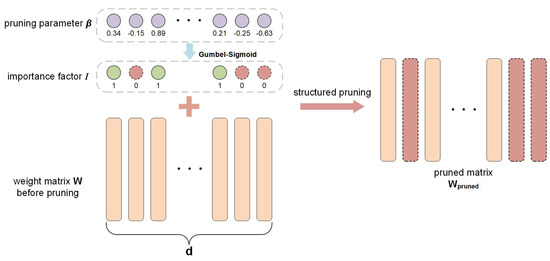
Figure 3. The differentiable structured pruning criterion. With a Gumbel-Sigmoid activation, DSP employs a soften one-hot vector to guide the pruning. 1 corresponds to remained parameters and 0 corresponds to removed parameters.

However, since values of the importance factor $\mathbf{I}$ is discrete, the gradient can not be calculated directly, which makes it hard to optimize with the back propagation algorithm. Considering the sigmoid activation is a special case of the softmax activation:

$$\begin{array}{c}\hfill \mathrm{Sigmoid}\left(x\right)=\frac{1}{1+\exp (-x)}=\frac{\exp \left(x\right)}{\exp \left(x\right)+\exp \left(0\right)}=\mathrm{Softmax}\left([x,0]\right)\end{array}$$

(6)

we propose a Gumbel-Sigmoid activation on top of the Gumbel-Softmax [24] and relax the importance factor I into soften one-hot with Gumbel-Sigmoid:

$$\begin{array}{c}\hfill \mathbf{I}=\mathrm{Gumbel}-\mathrm{Sigmoid}\left(\mathit{\beta }\right)=\frac{\exp ((log\mathit{\beta }+G_1)/\lambda )}{\exp ((log\mathit{\beta }+G_1)/\lambda )+\exp (G_2/\lambda )}\end{array}$$

(7)

where $\mathit{\beta }$ is the corresponding pruning parameter, $G_1$ and $G_2$ are two independent Gumbel random variants, and $\lambda$ is a temperature close to zero.

With such a relaxation, I becomes soften one-hot, and the gradient descent can be directly applied to optimize I since the loss function is differentiable to $\beta$. In other words, the structured pruning is equivalent to learning the pruning parameter $\beta$. Compared with conventional magnitude-aware criterion, a stronger correlation between our pruning criterion and model performance can be built. And we adopt a bi-level optimization manner to optimize $\beta$ [23]. An additional sparse loss ${\mathcal{L}}_{sparse}$ is employed to evaluate the sparsity of the pruned matrix during the bi-level optimization, and it can be calculated by counting the remaining parameter size of W after pruning.

3.2.2. The Attention-Similarity Loss Function

Based on the differentiable pruning criterion, we can directly prune model parameters with the back propagation algorithm by calculating the gradient according to the loss function. Considering the MHA module is an important module in searched architectures that is responsible for extracting global information, we further develop an attention-similarity loss function for MHA modules.

Given Q, K, V as the inputs, each head of the MHA module will calculate an attention weight based on Q and K, and apply the attention weight on V to get a weighted sum as the output. Therefore, the attention weight directly influences the ability to extract global information, and it can be employed to evaluate the quality of the MHA head. In general, a smaller attention weight difference from the well-trained attention head indicates a closer performance of the pruned MHA head. On top of this point, we propose to calculate the attention-similarity loss function as follows:

$$\begin{array}{c}\hfill {\mathcal{L}}_{attn}=Cos\_Sim(Attn,Att{n}_{pruned})\end{array}$$

(8)

where $Cos\_Sim$ refers to the cosine similarity function. $Attn$ refers to the well-trained attention weight and, $Att{n}_{pruned}$ refers to the pruned attention weight.

When pruning CNN and FFN modules, DSP adopts the standard loss function (e.g., CTC or CE). When pruning MHA modules, DSP will replace the standard loss function with the proposed attention-similarity loss function ${\mathcal{L}}_{attn}$. In this way, a more accurate gradient can be calculated to optimize $\beta$.

4. Experiments

4.1. Dataset and Model Implementation

Dataset. In this work, we evaluate the LWMD platform on two widely-used Mandarin datasets: Aishell-1, HKUST and the performance is evaluated by character error rate (CER). We extract acoustic features using 80-dimensional Mel-filterbanks with a 25 ms window and a 10 ms shift and 3-dimensional pitch features are added to the extracted features. We randomly select 5% from the training set as the architecture search evaluation set and the differentiable pruning set.

Baselines. We employ the most commonly-used Transformer and Conformer models as basic baselines. Additionally, LiteTransformer and LightConv are employed as lightweight baselines. It should be noted that Conformer and Transformer only differ in the encoder architectures, while their decoder all follow the Transformer decoder architecture. Further, we employ a random search baseline to compare with LWAS by randomly sampling 5 candidate architectures based on the proposed search space.

Implementation and Testing Details. All the experiments are conducted based on a widely-used E2E ASR toolkit ESPnet [35]. Following the finetuned configuration of ESPnet developers, we set the attention dimension as 256 and the FFN hidden dimension as 2048 with the encoder block number as 12 and the decoder block number as 6 for the Transformer and Conformer baselines. For the LiteTransformer and LightConv encoder, we halve the attention dimension into 128 and the FFN hidden dimension into 1024 with the encoder block number as 18 and the decoder block number as 9. For LWAS, we set $N_E=12$ and $N_D=6$ in Figure 1 with the attention dimension as 256. All the CNN modules follow the same settings in [10].

4.2. Performance Comparisons

To demonstrate the effectiveness of LWMD, we conduct experiments under CTC and AED frameworks, and Table 1 and Table 2 provide experiment results. For the AED framework, we set the beam size as 5 for the beam search and find FLOPs of AED frameworks are obviously larger than CTC frameworks.

Table 1. Experiment results under the CTC framework. FLOPs refer the averages of processing one-second speech. The best results on each framework are in boldface.

	Aishell-1				HKUST
	#Params (M)	FLOPs (G)	Dev CER	Test CER	#Params (M)	FLOPs (G)	Dev CER	Test CER
Transformer	18.3	0.83	5.6	6.2	18.3	0.83	22.1	22.8
Conformer	20.9	0.96	5.4	5.9	20.9	0.96	21.6	22.2
LiteTransformer	14.1	0.60	5.9	6.5	14.1	0.60	22.8	23.3
LightConv	11.0	0.52	6.1	6.8	11.0	0.52	23.0	23.9
Random Search	12.4	0.56	5.7	6.4	11.9	0.54	22.5	23.2
LWAS	11.4	0.51	5.4	5.9	11.8	0.54	21.4	22.2
LWMD (LWAS + DSP)	8.5	0.39	5.4	5.9	9.4	0.44	21.5	22.4

Table 2. Experiment results under the AED framework. FLOPs refer the averages of processing one-second speech. The best results on each framework are in boldface.

	Aishell-1				HKUST
	#Params (M)	FLOPs (G)	Dev CER	Test CER	#Params (M)	FLOPs (G)	Dev CER	Test CER
Transformer	29.9	6.96	5.0	5.4	29.9	7.14	20.3	20.8
Conformer	32.5	7.09	4.7	5.2	32.5	7.27	19.8	20.4
LiteTransformer	25.0	5.72	5.2	5.7	25.0	5.87	20.7	21.3
LightConv	20.8	5.61	5.4	6.0	20.8	5.76	21.0	21.9
Random Search	19.6	3.75	5.1	5.6	19.5	4.50	21.2	22.3
LWAS	17.7	2.81	4.7	5.2	18.1	2.90	20.0	20.4
LWMD (LWAS + DSP)	13.2	2.13	4.7	5.2	14.5	2.41	20.0	20.5

Among the human-designed baselines, Conformer obtains the best performance, which demonstrates the effectiveness of combing the CNN module with the MHA module. Even though LiteTransformer and LightConv can obtain fewer parameters and FLOPs, there existed obvious performance drops compared with Conformer, which indicates they are not the best light-weight architecture choices for E2E ASR.

Different from human-designed baselines, LWMD result in a better performance-speed trade-off. Compared with the best human-designed baseline, the searched architectures by LWAS can obtain much smaller parameter numbers and FLOPs with comparable performance both on CTC and AED frameworks. Compared with the random search results that adopt the same search space as LWAS, the performance gain of LWAS owns to our search algorithm. To be specific, the LWAS framework can obtain at least 1.77×, 1.79× parameter reduction and 2.18×, 2.49× FLOPs reduction under CTC and AED frameworks, respectively, which demonstrates the effectiveness of LWAS in searching light-weight architectures. Moreover, by incorporating LWAS with DSP, the complete LWMD platform can further reduce parameters and FLOPs of searched architecture by around 20% with a negligible performance drop. To sum up, these comparisons illustrate the promising ability of LWMD as a comprehensive E2E ASR model compression platform.

4.3. Ablation Study

4.3.1. The Proposed Search Space

In Table 3, we conduct ablation studies with reduced search spaces on Aishell-1 by fixing block numbers or the operation on certain edges. We observe obvious performance drops after fixing the MHA or CNN operations, which indicates the necessity of diverse candidate operations for the MHA and CNN modules in maintaining performance. Even though there is no performance drop after fixing the block number or fixing the FFN operations, the resource consumption becomes larger than the complete search space since the FFN module and the block number play an important role in adjusting model sizes. Taking all results into consideration, we can see it is essential for LWAS to search light-weight architectures with diverse operation combinations and elastic block number selection, which demonstrates the contribution of the designed search space.

Table 3. Ablation Studies of the search space on Aishell-1. The complete search space is compared with reduced search spaces.

Search Space	#Params (M)	FLOPs (G)	Dev CER	Test CER
Conformer Baseline	32.5	7.09	4.7	5.2
Fix MHA as MHA4	18.2	2.94	5.1	5.6
Fix CNN as CNN15	17.9	2.84	5.2	5.6
Fix FFN as FFN2048	23.4	4.22	4.7	5.2
Fix Block Number	22.3	3.95	4.7	5.2
Complete Search Space	17.7	2.81	4.7	5.2

4.3.2. The DSP Algorithm

To explore the effectiveness of the DSP algorithm, we conducted more ablation studies as shown in Table 4. Besides the result without any pruning, we further provide experiment results with three different pruning algorithms. Random pruning refers to pruning parameters randomly, structured $l_1$-pruning and structured $l_2$-pruning refer to pruning parameters according to the $l_1$-norm or $l_2$-norm magnitude. Among these pruning methods, the worst performance of random pruning indicates the necessity of a proper pruning algorithm. Even though $l_1$-pruning and structured $l_2$-pruning can achieve the same compression ratio with the DSP algorithm, the performance gap demonstrates that the DSP algorithm is a better choice. Further, we compare the results of DSP with/without the attention-similarity loss and observe that the attention-similarity Loss indeed can help to maintain the performance of pruned models. And in Figure 4, we can find the attention-similarity loss results in a more close attention weight with the weight before pruning.

Table 4. The ablation studies of pruning algorithms on Aishell-1. For random pruning, structured $l_1$-pruning and structured $l_2$-pruning, we manually set the pruning ratio to ensure they have close pruning ratios for a fair comparison.

Pruning Methods	#Params (M)	FLOPs (G)	Dev CER	Test CER
w/o pruning	17.7	2.81	4.7	5.2
random pruning	13.2	2.13	5.2	5.8
structured $l_1$-pruning	13.2	2.13	5.0	5.6
structured $l_2$-pruning	13.2	2.15	5.0	5.5
DSP w/o Attention-similarity Loss	13.2	2.13	4.8	5.4
DSP with Attention-similarity Loss (Default)	13.2	2.13	4.7	5.2

Figure 4. Visualized attention weights. (a) is the original attention weight without any pruning, (b) is the attention weight pruned with the attention-similarity loss, and (c) is the attention weight pruned without the attention-similarity loss.

4.4. Low-Bit Quantization

Since LWAS and DSP both focus on designing model architectures, it is orthogonal to the general acceleration techniques, e.g., low-bit quantization. We further employ quantization methods to reduce model sizes without removing parameters. As shown in Table 5, we introduce additional quantization methods into the LWMD platform. With an acceptable performance loss, LWMD can achieve 4.27× parameter reduction with the float16 precision and 8.55× parameter reduction with the int8 precision. In this way, an extreme compression result can be achieved by the LWMD platform.

Table 5. Exploration results of low bit quantization on the LWMD platform. We try to introduce the float16 precision and the int8 precision into LWMD.

Pruning Methods	#Params (M)	Dev CER	Test CER
Conformer Baseline	32.5	4.7	5.2
LWMD (float32)	13.2	4.7	5.2
LWMD + float16	7.6	4.9	5.3
LWMD + int8	3.8	5.2	5.8

5. Conclusions

In this paper, we propose a comprehensive platform named LWMD to compress E2E ASR models and save resource consumption for real-world applications. LWMD first propose an LWAS framework to search light-weight architectures for E2E ASR models and then develop a DSP structured pruning algorithm to remove redundant parameters in searched architectures further. Extensive experiments on Aishell-1 and HKUST demonstrate the effectiveness of LWMD in model compression. By combing the LWAS framework and the DSP algorithm, parameter sizes and FLOPs of E2E ASR systems can be reduced significantly without any performance drops. Moreover, we observe that LWMD is friendly to low-bit quantization methods, which can further reduce model sizes. A slight flaw of the proposed platform is that it cannot integrate all kinds of model compression methods together. Therefore, on top of LWMD, we plan to explore more orthogonal model compression methods for future work. Combining tensor decomposition or knowledge distillation with our existing differentiable methods illustrates a promising point.