Determination of Critical Moisture Content Facing Walnut Shell Breaking and Optimization of Combined Hot Air and Microwave Vacuum Drying Process

Abstract

The conditioning of moisture content is an effective way to improve walnut-crushing performance. In this study, firstly, walnuts with different moisture contents were used to conduct the crushing experiments. The distributions of fragment sizes of shells and kernels with different moisture contents were analyzed by an image processing and sieving method, respectively. The results show that moisture content significantly affects the fragmentation degree of the shell and kernel, as shown by the differences in the fractal dimensions of shell fragments and the average fragment size of kernel fragments. The critical moisture contents of the shells and kernels, corresponding to the specific states of broken shells and whole kernels, were determined. Then, taking the critical moisture content as the target moisture content, the combination of hot air and microwave vacuum drying applied to dry walnuts was presented and the process parameters were optimized. Optimized process parameters include a hot air temperature of 63.23 °C, a moisture content of the transition point of 24.88%, microwave power of 588.24 W and a microwave vacuum thermostatic temperature of 49.01 °C. At this point, the unit time drying rate, unit mass drying energy consumption, mean square error of moisture content and kernel color parameters were 0.215%/min, 3.03 kW·h/kg, 2.93% and 6.42, respectively. It was confirmed that drying the walnuts to a critical moisture content using an optimized process could both maximally improve the crushing performance and significantly reduce the drying time. The findings provide important information for conditioning the crushing state of walnuts and improving crushing performance and have practical value for the improvement of drying systems.

1. Introduction

The walnut is mainly composed of shell and kernel, and it is increasingly used in various fields such as food, medicine, chemistry and materials [1,2]. Shell breaking is essential for the primary post-harvest processing of walnuts to obtain high-quality kernels and their by-products [3,4]. Unfortunately, the quality of walnuts can be reduced by shell-breaking processing. A high rate of crushed kernel is still the main issue for walnut primary processing due to the lower crushing performance of walnut-crushing machines [5]. Therefore, in order to improve the crushing performance, many studies have been carried out to optimize the structural and operating parameters of walnut-crushing machines [6,7,8]. Although crushing performance was improved to some extent, the bottleneck that is kernel over-crushing and shell under-crushing is still not solved [5]. Obviously, it will be difficult to enhance crushing performance until the bottleneck is broken through optimizing and improving walnut-crushing machines. As is well known, the crushing performance is strongly related to the intrinsic properties of the walnut (e.g., hardness and moisture content (MC)), crushing machine configurations (e.g., squeeze plate and shaft) and operational conditions (e.g., shaft rotation speed). Among them, MC has important implications for walnut-crushing performance because it changes the mechanical response and crushing characteristics of the walnut. More importantly, MC is the only material parameter that can be adjusted for walnuts. Thus, some research has focused on the effects that occur at different walnut MCs to explore the crushing characteristics and improve crushing performance.

Research into walnut MC has focused on two main areas. On the one hand, it has been devoted to the study of the influence of MC on crushing performance, with the hope of providing a reference for the rational design of high-quality crushing systems and the optimization of process and product parameters. For example, Wang et al. investigated the effect of walnut moisture content on mechanical properties and optimized the operating parameters of shell-breaking equipment [7]. Altuntas et al. investigated the effect of walnut moisture content on fracture characteristics (i.e., fracture force, fracture energy) [9]. Shahbazi et al. studied the effect of walnut moisture content on crushing state [10]. On the other hand, many scholars have focused on walnut drying, including drying characteristics, mechanisms and technologies that will hopefully develop new drying processes with improved processing and energy efficiency and good product quality. For example, Chen et al. investigated the effect of walnut structure on the hot air (HA) drying characteristics, as well as the effects of water loss, energy consumption, and product quality of walnuts in step-down temperature drying [11,12]. Dolgun et al. studied the heat transfer mechanism of walnuts and designed a novel drying system [13]. Mao et al. showed that radio frequencies systems could substantially shorten the drying time and improve energy efficiency [14]. Although beneficial results have been drawn from the research above, walnuts were commonly treated as a whole. However, it is well known that the walnut has a typical multilayer structure with different chemical compositions and physical properties in the shell and kernel [15,16]. Therefore, the mechanical properties and drying characteristics of walnuts do not usually provide sufficient information to reflect the material properties and moisture transfer characteristics of the shell and kernel. Previous studies have also shown that the variation in drying characteristics and mechanical properties of shells and kernels with regard to MC are usually different, which can be attributed to structural heterogeneity [16,17]. Therefore, research into the relationship between MC and the crushing performances of shell and kernel, as well as a drying process that considers the heterogeneous nature of the walnut structure, are yet to be further developed.

Moreover, these studies revealed the existence of critical MC (CMC) for walnut crushing. For example, Shahbazi determined the walnut-crushing CMC based on the effect of walnut MC on kernel crushing properties [10]. Wang et al. determined the walnut-crushing CMC according to the impact of walnut MC on the shell-breaking rate and high-quality kernel rate [7]. Therefore, determining breaking-property limits of heterogeneous structures and determining the CMC of shells and kernels are important to improve crushing performance, which is the basis of proposing effective drying processes used to obtain walnuts with CMC in the shell and kernel. However, no reports have been published to determine the CMC of shells and kernels separately, or the drying process regarding shell breaking.

In this study, the distributions of fragment sizes of both shells and kernels were analyzed simultaneously with the aim of quantifying the fragmentation degree. On this basis, the relationship between the MC of shells and kernels and the fragmentation degree was systematically investigated, and the CMC of shells and kernels used to break the shells was determined simultaneously. Finally, the optimized parameters of the combination of hot air and microwave vacuum drying (HA-MVD) processes with regard to walnut shell breaking were studied by response surface methodology (RSM). This study provides (i) an improved understanding of the crushing mechanism for the walnut with its heterogeneous structure and (ii) a theoretical reference for applying HA-MVD technology to drying walnuts.

2. Materials and Methods

2.1. Sample

Freshly harvested and dehulled walnuts of Wen-185 variety were collected from the woodland, Wensu County, Aksu, Xinjiang in the 2022 harvest season and used in this study. The samples were previously placed in sealed bags and stored in an air-conditioned room at 60% relative humidity and 21 °C to maintain constant moisture [18]. Since the dimensions of individual fresh walnuts vary naturally, four hundred walnuts were randomly selected to measure their length, width and thickness. Interestingly, the geometric mean diameter (M) distribution of walnuts conforms well to the normal distribution (Figure 1). Hence, walnuts with Ms ranging from 34 to 36 mm were selected for the tests to reduce the variations in the initial dimension and enhance the representativeness of the sample selection. The MC was determined by drying the samples in an air oven at 105 °C for 24 h; the initial MC (IMC) of the walnuts, shells and kernels were 40.73 ± 1.65%, 45.59 ± 1.77% and 33.69 ± 1.28% on a wet basis (w.b.), respectively. For simplicity, the detailed formula for calculating walnut MC has been reported by Chen et al. [19].

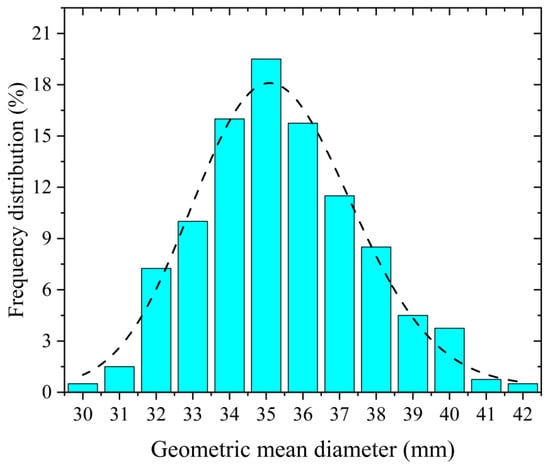
Figure 1. Frequency distribution of geometric mean diameter.

Walnut samples with different MCs in the shells and kernels using hot air drying (HAD) at 45 °C were prepared to conduct the following crushing experiments (See Table 1).

Table 1. Walnut samples with different MCs in the shells and kernels.

Sample Mark	A0	A1	A2	A3	A4	A5	A6	A7	A8	A9	A10	A11	A12
Drying time, h	0	3	6	9	12	15	19	23	28	34	40	48	56
Shell MC, %	45.59	36.89	30.01	26.41	23.39	21.29	18.91	16.83	14.25	11.24	9.41	7.72	5.45
Kernel MC, %	33.69	27.28	23.95	21.40	19.28	16.98	13.66	11.27	9.32	6.95	5.11	2.31	2.23
Walnut MC, %	40.73	33.01	27.17	23.87	21.43	19.21	16.74	14.42	12.43	10.09	8.04	6.58	4.97

2.2. Crushing Experiment

2.2.1. Experimental Equipment and Methods

A pilot-scale walnut-crushing apparatus having dimensions of 1200 mm(L) × 800 mm (W) × 1200 mm(H) was developed to conduct the particle group crushing experiments. The three-dimensional structure and pictorial diagram are shown in Figure 2A,B. It mainly includes a frame, a grading device, a crushing device, a motor, a feed hopper, and a control panel. The crushing device was composed of a rotating crushing roller and an extrusion plate with ‘V’ grooves. In effect, the walnut is primarily cracked in the wedge-shaped space between the rotating crushing rollers and the extrusion plate. In order to ensure the appropriate forces acted on the walnut, several spikes were installed on the surface of the rotating crushing roller and extrusion plate, which is helpful for increasing the area of stress concentration. According to our previous study results, the machine was operated at a crushing angle and roller speed of 0.47° and 108 r/min, respectively [8]. More detailed information on crushing machinery is listed in Table 2. Furthermore, to satisfy requirements for statistical reliability and representative results obtained from the experiments, three replicates of each test were conducted, and a sample of 400 walnuts was used for each test.

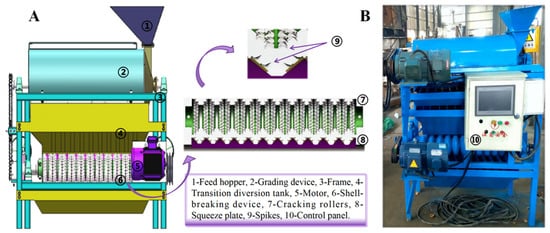
Figure 2. (A) Three-dimensional structure and (B) pictorial diagram of the walnut-crushing apparatus.

Table 2. Parameters of the crushing machine.

Parameters	Size
Grading accuracy/(%)	≥96
Power of cracker/kw	0.75
Cracking angle/(°)	0–1 (0.47)
Overall weight/kg	165
Roller speed/(r/min)	0–210 (108)
Length × width × height/(mm × mm × mm)	1200 × 800 × 1200
Productivity/(kg/h)	1080
Inlet size/(mm × mm)	94 × 45

2.2.2. Quantitative Evaluation Indicators for the Degree of Fragmentation

The fragmentation degree of shells and kernels are important for the quantitative evaluation of crushing quality. Therefore, in order to quantitatively analyze the effect of MC on walnut crushing, the degree of fragmentation of shells and kernels were characterized quantitatively using relevant indicators, respectively.

(1)

Quantitative evaluation indicators for the degree of shell fragmentation

The size distribution of the shell fragments is closely related to the crushing characteristics and mechanism [20]. To determine the size distribution of the shell fragments, and considering the shell fragments with complex morphology, the projected area (PA) was obtained using the image processing function embedded in MATLAB R2018b software. The image processing process of the shell fragments is presented in Figure 3. Note that the threshold value, which is used to distinguish the boundaries of the shell fragments, plays an important role in determining shell fragment PA. Research indicates that, when compared to alternative methods like k-means clustering and the watershed algorithm, the adaptive thresholding technique is extensively utilized in boundary extraction due to its heightened robustness and adaptability [3,21]. Thus, the adaptive threshold was used to determine shell fragments’ PAs.

Figure 3. The image processing process of the shell fragments.

A fractal dimension (D_b) that can reflect the statistical characteristics of material fragmentation has been commonly used to analyze chaotic fragment distributions [22]. Therefore, to quantitatively characterize the fragmentation degree of the shell, the D_b is adopted. In this study, a method proposed by Wu et al. was used to determine D_b from the fragment size distribution [23]. The number of fragments whose equivalent length is greater than or equal to L_eq is:

$$N=N_0{\left(L_{\mathrm{eq}}/L_{\mathrm{eqmax}}\right)}^{{{}_{-D}}_{{}_{\mathrm{b}}}}$$

(1)

$$L_{\mathrm{eq}}=\sqrt{PA}$$

(2)

where N₀ is the number of fragments with the largest equivalent length L_eqmax. Note that the larger D_b is, the larger the fragmentation degree is. The conversion of Equation (1) can be obtained as follows:

$$D_{\mathrm{b}}=\frac{\log \left(N/N_0\right)}{\log \left(L_{\mathrm{eqmax}}/L_{\mathrm{eq}}\right)}$$

(3)

For statistical generality and accuracy, L_eqs > 22 mm were excluded in this study. This is due to the small percentage and poor continuity of distribution in this range, as shown in Figure 4. It should be noted that a similar method was used in Refs. [24,25]. Based on this, the lg(L_eqmax/L_eq) vs. lgN curve of the shell fragments is shown in Figure 5. As shown, the curve has a good correlation with the fitted straight line (R² = 0.95), which indicates that the L_eq distribution of fragments follows the fractal distribution very well. From the fitted straight line, the D_b also can be obtained: D_b = 1.61. In addition, the fitting curve slightly deviates from the initial data points, which is likely due to the decrease in the number of large fragments.

(2)

Quantitative evaluation indicators for the degree of kernel fragmentation

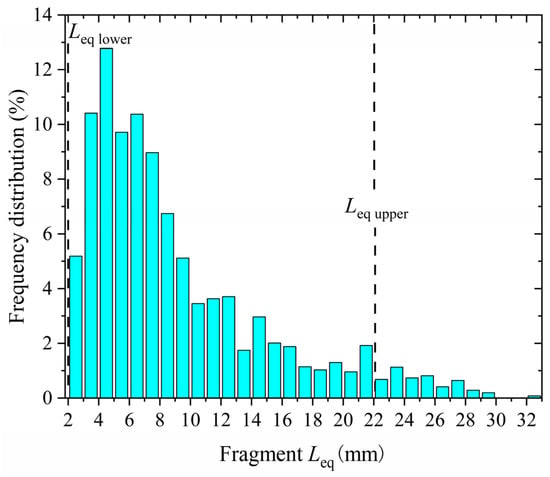
Figure 4. Frequency distribution diagram of L_eqs of the shell fragments at 30.01%.

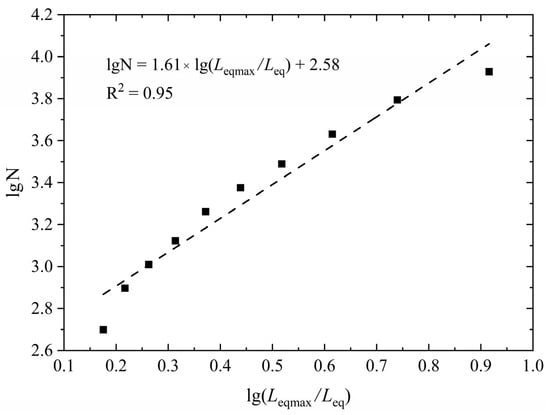
Figure 5. Lg(L_eqmax/L_eq) vs. lgN curve of the shell fragments at 30.01%.

The crushing grade of kernels is important for the evaluation of the quality of walnuts for shell breaking. Crushed kernels were sieved into the six grades using standard sieves of 18, 12, 8, 4 and 2 mm based on a previous study: one-dew kernel, two-dew kernel, three-dew kernel, four-dew kernel, crushed kernel and powder [6], as presented in Table 3.

Table 3. Crushing grade of the kernel.

One-Dew Kernel	Two-Dew Kernel	Three-Dew Kernel	Four-Dew Kernel	Crushed Kernel	Powder
18~26 mm	12~18 mm	8~12 mm	4~8 mm	2~4 mm	0~2 mm

Figure 6 shows the relative mass percentages of various crushed kernels at different MCs. It clearly shows that the relative mass percentages of various crushed kernels have significant differences with the increase in the MC. In this case, the variation in crushed kernel rates with MC for individual grades is unlikely to be a full reflection of the relationship between the MC and the overall fragmentation degree. Therefore, to quantitatively characterize the overall fragmentation degree of kernels, as per Li et al., the average fragment size (d_M) is used [26]. Note that the lower d_M value means a larger degree of fragmentation. The formula of d_M is shown as the following.

$$d_{\mathrm{M}}=\frac{{\displaystyle \sum \left(r_i{d}_i\right)}}{{\displaystyle \sum r_i}}$$

(4)

where d_i is the average fragment size in standard sieves of different grades. r_i is the relative mass percentages of crushed kernels corresponding to d_i.

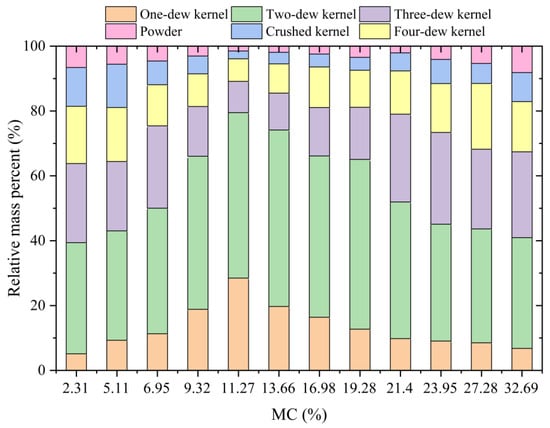
Figure 6. The relative mass percentages of various crushed kernels at different MCs.

2.3. Drying Process Optimization Test

Drying is essential for walnut processing before shell breaking to quickly remove the moisture [27]. Among numerous drying technologies, HA-MVD has been widely used in the drying of foodstuffs due to its high efficiency and good processing quality [28,29,30]. Therefore, in this study, HA-MVD was adopted to dry walnuts, with the aim to develop a drying approach that can be used to obtain the optimal crushing state on the basis of the premises of efficiency, quality and energy consumption.

2.3.1. Experimental Apparatus and Methods

Figure 7 shows the diagram of the HA-MVD system. The experimental apparatus mainly consists of a hot air (HA) dryer (BoXun, GZX-9140MBE, Shanghai, China) and a microwave vacuum (MV) dryer (Huaiteng, HTWB-01, Nanjing, China). Infrared temperature sensors (Opus, RT-350 °C, Fulda, Germany) equipped with the MV dryer were used to monitor the real-time surface temperature of the walnut sample. In order to reduce energy consumption and ensure product quality, a drying strategy was implemented in which the microwave could only operate below the maximum temperature set by the system, and it could be automatically turned off when the temperature exceeded the maximum. Based on the preliminary experiments, the vacuum was set at −0.08 MPa. During the microwave vacuum drying (MVD) operation, the walnuts on the turntable were rotated at a speed of 6 rpm to improve the uniformity of microwave radiation [31,32].

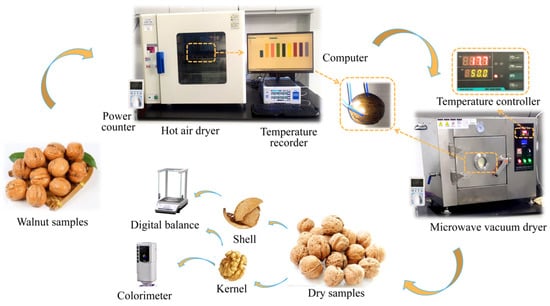
Figure 7. Diagram of the HA-MVD system.

To monitor the change in MC during the drying, the 30 marked walnuts in the dryer were removed and divided into shells and kernels and weighed individually, until a targeted average MC was achieved in the whole dryer. The dried walnut samples were divided into shells and kernels and stored in sealed bags for quality evaluation, respectively. The experiments were performed in triplicate.

2.3.2. Test Index and Measurement Method

In order to optimize a set of drying process parameters that not only approaches CMC (i.e., broken shell and whole kernel), but also applies to achieving high efficiency, low consumption and ensuring quality, unit time drying rate (DR), unit mass drying energy consumption (DQ), mean square error (MSE) of moisture content and kernel color parameter (∆E*) were selected as experimental indicators. DQ and ∆E* were determined using a power counter (LUEABB, DDSY, Jinhua, China) and a colorimeter (3nh, SC-10, Shenzhen, China), respectively. For simplicity, the detailed formula for calculating ∆E* has been reported by Kaveh et al. [33]. Note that the difference between the actual MC (measured value) and theoretical MC (i.e., CMC) of shells and kernels was quantified by MSE and calculated by Equation (5).

$$MSE=\frac{1}{m}{\displaystyle {\sum }_{i=1}^m{\left(y_i{}_s-{\widehat{y}}_i{}_s\right)}^{{}^2}}+{\left(y_i{}_r-{\widehat{y}}_{ir}\right)}^{{}^2}$$

(5)

where y_is and y_ir are the actual MC of shell and kernel, respectively. ${\widehat{y}}_i{}_S$ and ${\widehat{y}}_i{}_r$ are the theoretical MC of shell and kernel, respectively. m is the total number of samples.

2.3.3. Experimental Design, Statistical Analysis and Optimization

The RSM was used to estimate the effects of the process variables on DR, DQ, MSE and ∆E* during the drying of walnuts. HA temperature (x₁), MC of the transition point (x₂), microwave power (x₃) and MV thermostatic temperature (x₄) were selected as independent variables by means of literature survey and preliminary experiments. A central composite rotatable design (CCRD) was arranged in the experimental scheme; coded values corresponding to the natural values of each variable and CCRD are shown in Table 4. The dataset was fitted with the following second-order polynomial model:

$$Y_k={\beta }_{k0}+{\displaystyle \sum _{i=1}^4{\beta }_{ki}}{x}_i+{\displaystyle \sum _{\mathrm{i}=1}^4{\beta }_{kii}}{x}_i^2+{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=i+1}^4{\beta }_{kij}}}{x}_i{x}_j,(k=1, 2, 3, 4)$$

(6)

where β_k0, β_ki, β_kii and β_kij denote constant regression coefficients, and x represents the coded independent variable. Multiple regression analysis was employed to assess the mathematical model for each response variable. The significance of terms within the model for each response was determined using analysis of variance (ANOVA), with significance gauged by the F-statistic within a 95% confidence interval. The model adequacies were checked by R², adjusted-R², predicted-R² and prediction error sum of squares (PRESS). After model fitting, residual analyses were conducted to validate assumptions used in ANOVA. The smaller MSE is the main goal of this study. In addition, minimum DQ, ∆E* and maximum DR should also be guaranteed. Therefore, the desirability function method was performed, and the importance value 5 was specified for the MSE response and the same importance value 3 were appointed to other responses. Note that the Design Expert 10 was used to fit response surfaces and optimize the drying process.

Table 4. Central composite rotatable design with experimental values of response variables (x₁: HA temperature, x₂: MC of the transition point, x₃: microwave power, x₄: MV thermostatic temperature).

Run #	x1 (°C)	x2 (%)	x3 (W)	x4 (°C)	DR (%/min)	DQ (kW·h/kg)	MSE (%)	∆E*
1	55 (−1)	21 (−1)	550 (−1)	45 (−1)	0.141	5.31	2.30	8.46
2	65 (1)	21 (−1)	550 (−1)	45 (−1)	0.160	4.83	2.01	8.74
3	55 (−1)	27 (1)	550 (−1)	45 (−1)	0.175	3.89	4.77	6.84
4	65 (1)	27 (1)	550 (−1)	45 (−1)	0.195	3.03	3.32	7.12
5	55 (−1)	21 (−1)	650 (1)	45 (−1)	0.171	5.00	2.99	8.58
6	65 (1)	21 (−1)	650 (1)	45 (−1)	0.179	4.58	2.33	8.78
7	55 (−1)	27 (1)	650 (1)	45 (−1)	0.203	2.72	6.41	8.04
8	65 (1)	27 (1)	650 (1)	45 (−1)	0.204	2.86	4.38	8.38
9	55 (−1)	21 (−1)	550 (−1)	55 (1)	0.167	5.14	2.81	9.22
10	65 (1)	21 (−1)	550 (−1)	55 (1)	0.188	4.59	2.48	9.62
11	55 (−1)	27 (1)	550 (−1)	55 (1)	0.179	2.83	5.82	8.02
12	65 (1)	27 (1)	550 (−1)	55 (1)	0.218	2.62	4.26	8.38
13	55 (−1)	21 (−1)	650 (1)	55 (1)	0.200	5.01	4.67	9.28
14	65 (1)	21 (−1)	650 (1)	55 (1)	0.214	4.63	3.28	10.24
15	55 (−1)	27 (1)	650 (1)	55 (1)	0.214	2.61	8.42	8.90
16	65 (1)	27 (1)	650 (1)	55 (1)	0.229	2.59	5.92	10.94
17	50 (−2)	24 (0)	600 (0)	50 (0)	0.189	3.61	5.88	8.34
18	70 (2)	24 (0)	600 (0)	50 (0)	0.213	3.23	2.43	8.94
19	60 (0)	18 (−2)	600 (0)	50 (0)	0.153	6.71	1.89	8.90
20	60 (0)	30 (2)	600 (0)	50 (0)	0.217	2.54	7.39	7.52
21	60 (0)	24 (0)	500 (−2)	50 (0)	0.162	3.78	2.51	8.46
22	60 (0)	24 (0)	700 (2)	50 (0)	0.212	3.23	5.67	10.16
23	60 (0)	24 (0)	600 (0)	40 (−2)	0.180	4.04	2.99	7.58
24	60 (0)	24 (0)	600 (0)	60 (2)	0.217	3.31	5.37	9.72
25	60 (0)	24 (0)	600 (0)	50 (0)	0.213	3.67	3.41	6.70
26	60 (0)	24 (0)	600 (0)	50 (0)	0.211	3.29	2.82	6.08
27	60 (0)	24 (0)	600 (0)	50 (0)	0.216	3.17	3.18	6.38
28	60 (0)	24 (0)	600 (0)	50 (0)	0.209	3.22	3.01	6.50
29	60 (0)	24 (0)	600 (0)	50 (0)	0.217	3.19	3.39	6.26
30	60 (0)	24 (0)	600 (0)	50 (0)	0.201	3.20	3.46	6.36
31	60 (0)	24 (0)	600 (0)	50 (0)	0.221	3.41	3.34	6.32
32	60 (0)	24 (0)	600 (0)	50 (0)	0.209	3.29	2.98	6.26
33	60 (0)	24 (0)	600 (0)	50 (0)	0.215	3.17	2.72	5.92
34	60 (0)	24 (0)	600 (0)	50 (0)	0.207	3.25	3.31	6.24
35	60 (0)	24 (0)	600 (0)	50 (0)	0.212	3.24	3.37	6.30
36	60 (0)	24 (0)	600 (0)	50 (0)	0.222	3.39	3.06	5.98

3. Results and Discussion

3.1. Determination of CMC of Shell Breaking

The crushing state that corresponds to the broken shell and whole kernel is a vital objective for the shell-breaking processing of walnuts. Unfortunately, broken shells and whole kernels are in contradiction to each other due to the unique nested structure where the kernel is closed in the shell. To deal with this conflict from the aspect of material properties, the effects of MC on the fragmentation degree of both shell and kernel are explored. Based on this, the CMCs of shells and kernels that correspond to the broken shell and whole kernel are determined, respectively.

3.1.1. Determination of CMC of Shells

To visualize the influence of MC on the degree of shell fragmentation, snapshots of the crushing state of the shells at different MCs are presented in Figure 8. It shows that when the MC decreases from 45.59 to 18.91%, the number of large fragments increases and the large fragment is dominant for the overall size of fragments (Figure 8A,B), which suggests that the degree of fragmentation weakens. Conversely, when the MC further decreases from 18.91 to 9.41%, the number of small fragments increases and the overall size of the fragments decreases significantly (Figure 8B,C), implying the degree of fragmentation strengthens significantly. In contrast, when the MC further decreases from 9.41 to 5.45%, the crushing state appears unchanged (Figure 8C,D). After statistical analysis, the numbers of shell fragments for 45.59%, 18.91%, 9.41% and 5.45% are 10,114, 8973, 10,326 and 10,259, respectively. From the comprehensive analysis above, we guess that compared to the high MC and medium MC, shells with low MC are easy to crush, as shown by the smaller and more numerous shell fragments.

Figure 8. Crushing state of the shells at different MCs (45.59% (A), 18.91% (B), 9.41% (C) and 5.45% (D)).

In order to quantitatively analyze the effect of MC on the fragmentation degree of the shell, Figure 9 shows the variation in D_b with MC. As shown, the D_b decreases rapidly when MC decreases from 45.59 to 18.91% (i.e., stage I). This is because, due to the decrease in the MC, the fiber comprising the shell is hardened mechanically, which allows the shell to resist fragmentation by dissipating energy and limiting crack expansion [34,35]. In contrast, D_b increases rapidly when MC decreases from 18.91 to 9.41% (i.e., stage II). As MC continues to decrease, the properties of the fiber might transform from having a resilient or elastic character to being more and more brittle or fragile in nature [17]. As a result, the shell is more susceptible to fracture due to external loads, resulting in more crack generation and propagation due to multi-point compression, which in turn produces more fracture surfaces and smaller fragments. When MC falls below 9.41%, D_b almost remains constant (i.e., stage III). Obviously, this tendency is consistent with the results of the qualitative analysis mentioned above. In addition, the results show that when MC was 9.41%, D_b reached a maximum value of 1.73, corresponding to the larger fragmentation degree of the shell, which conforms to the objective of walnut shell breaking. Therefore, MC with 9.41% is treated as the CMC of shells in this work.

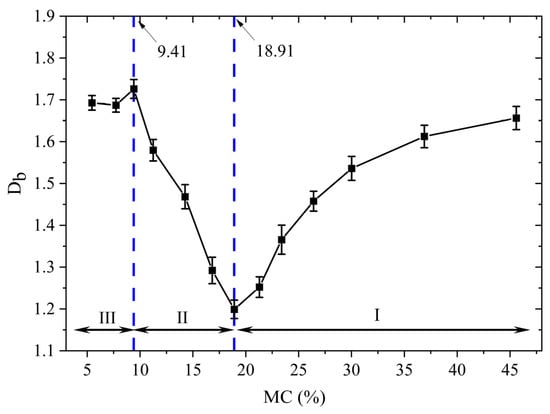
Figure 9. D_b of the shell fragments at different MCs.

3.1.2. Determination of CMC of Kernels

To visualize the effect of MC on the fragmentation degree of kernels, Figure 10 shows snapshots of the crushing state of the kernels at different MCs. It can be seen that when the MC decreased from 32.69 to 11.27%, the number of large fragments increased and the overall size of the fragments increased (Figure 10A,B), which suggests that the degree of fragmentation decreased. Conversely, when the MC was further decreased from 18.91 to 2.31%, the number of small fragments increased and the overall size of the fragments decreased significantly (Figure 10B,C), which implies that the degree of fragmentation increased significantly. Note that although the MC of 32.69% is similar to the MC of 2.31% in terms of crushing state, the latter corresponds to a much more serious fragmentation of the kernel. Therefore, we guess that kernels with too high or too low MC are unsuitable for shell breaking.

Figure 10. Crushing state of the kernels at different MCs (32.69% (A), 11.27% (B) and 2.31% (C)).

In order to quantitatively analyze the effect of MC on the fragmentation degree of the kernels, Figure 11 shows the variation of d_M with MC. As shown, the d_M increased rapidly when the MC decreased from 32.69 to 11.27% (i.e., stage I). This is mainly due to the fact that, as MC decreases, the hardness and mechanical strength of the kernel increases due to its progressively tighter internal tissue structure [17,36]. At the same time, the shell, which is an important structure for moisture retention, creates a warm yet moist environment inside the walnut, thus improving the toughness of the kernels [37]. Hence, the dynamic interactions of self-hardening and external toughening endow kernels with mechanical strength and flexibility, thereby increasing the kernel’s resistance to fragmentation. In contrast, d_M decreased rapidly when MC decreased from 11.27 to 2.31% (i.e., stage II). As MC continued to decrease, more cross-cracks were produced during multi-point extrusion due to the increased brittleness, resulting in a decrease in the size and an increase in the number of broken kernels [26]. Obviously, the change in d_M with MC is consistent with the results of the qualitative analysis mentioned above. In addition, the results show that when MC was 11.27%, d_M reached a maximum value of 15.39, corresponding to the smaller fragmentation degree of the shell, which conforms to the objective of walnut shell breaking. Therefore, an MC of 11.27% is treated as the CMC of kernels in this work.

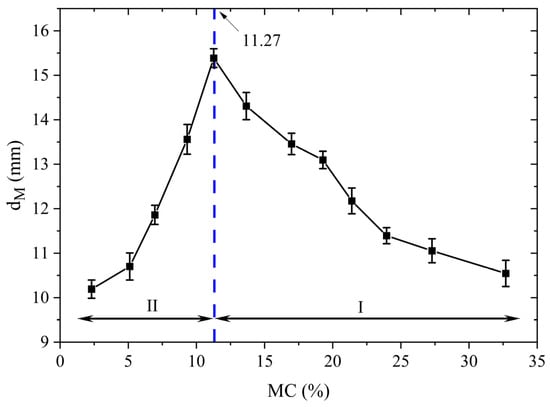
Figure 11. d_M of the kernel fragments at different MCs.

According to the comprehensive analyses above, the CMCs of shells and kernels that correspond to the shell breaking are 9.41% and 11.27%, respectively. Nonetheless, in order to ensure that both shell and kernel have CMC, how to dry walnuts and what is the optimal dry condition still need to be studied and analyzed deeply.

3.2. HA-MVD Process Facing Walnut Shell Breaking

According to the analysis above, the CMC with regard to shell breaking could achieve the desired walnut-crushing state that is broken shell and whole kernel. Accordingly, taking the MSE as the main optimization goal and DR, DQ and ∆E* as the auxiliary optimization goals, the HA-MVD technology was proposed and relevant process parameters were optimized by RSM.

3.2.1. Fitting Models

The results of different runs of drying experiments are shown in Table 5. An ANOVA was conducted to determine the significant effects of process variables on each response. Table 5 shows that all the process variables are found to be statistically significant for DR, DQ, MSE and ∆E*, showing p < 0.01.

Table 5. ANOVA table showing the variables as linear, quadratic and interaction terms on each response variable and coefficients for the prediction models.

Source	DF	Unit Time Drying Rate (DR)			Unit Mass Drying Energy Consumption (DQ)			Mean Square Error of Moisture Content (MSE)			Kernel Color Parameter (∆E*)
		Coefficient	Sum of Squares	p-Value	Coefficient	Sum of Squares	p-Value	Coefficient	Sum of Squares	p-Value	Coefficient	Sum of Squares	p-Value
Model	14	−3.0668	0.017	<0.0001	86.0392	31.11	<0.0001	81.9638	85.6	<0.0001	380.4542	69.04	<0.0001
x1	1	2.0817 × 10−2	1.426 × 10−3	<0.0001	−6.1 × 10−1	0.52	0.0001	−1.2083 × 10−1	12.2	<0.0001	−3.5860	1.53	<0.0001
x2	1	5.8694 × 10−2	4.401 × 10−3	<0.0001	−1.8631	24.56	<0.0001	−1.4133	41.16	<0.0001	−4.7117	3.42	<0.0001
x3	1	4.505 × 10−3	3.528 × 10−3	<0.0001	−6.6583 × 10−2	0.46	0.0002	−1.145 × 10−1	11.97	<0.0001	−4.5990 × 10−1	4.28	<0.0001
x4	1	1.4917 × 10−2	2.709 × 10−3	<0.0001	−6.2350 × 10−1	0.56	<0.0001	−1.2782	8.06	<0.0001	−3.1013	8.10	<0.0001
x1×2	1	5.417 × 10−5	1.056 × 10−5	0.5670	3.6667 × 10−3	0.048	0.1684	−2.0292 × 10−2	1.48	<0.0001	4.9167 × 10−3	0.087	0.2333
x1x3	1	−1.525 × 10−5	2.326 × 10−4	0.0126	3.55 × 10−4	0.13	0.0317	−7.375 × 10−4	0.54	0.0066	5.5500 × 10−4	0.31	0.0312
x1x4	1	1.025 × 10−4	1.051 × 10−4	0.0808	1.15 × 10−3	0.031	0.4641	−3.375 × 10−3	0.11	0.1818	6.6500 × 10−3	0.44	0.0116
x2x3	1	−1.0417 × 10−5	3.906 × 10−5	0.2759	−3.9167 × 10−4	0.055	0.1425	1.3708 × 10−3	0.68	0.0029	2.1083 × 10−3	1.60	<0.0001
x2x4	1	−2.2917 × 10−4	1.891 × 10−4	0.0226	−6.25 × 10−3	0.14	0.0241	8.0417 × 10−3	0.23	0.0617	8.5833 × 10−3	0.27	0.0440
x3x4	1	4.75 × 10−6	2.256 × 10−5	0.4048	3.9 × 10−4	0.15	0.0195	8.025 × 10−4	0.64	0.0035	3.7500 × 10−4	0.14	0.1337
x12	1	−1.3792 × 10−4	3.804 × 10−4	0.0022	1.85 × 10−3	0.068	0.1046	8.9708 × 10−3	1.61	<0.0001	2.3775 × 10−2	11.31	<0.0001
x22	1	−8.275 × 10−4	1.775 × 10−3	<0.0001	3.8611 × 10−2	3.86	<0.0001	3.8391 × 10−2	3.82	<0.0001	5.4097 × 10−2	7.59	<0.0001
x32	1	−2.7792 × 10−6	1.545 × 10−3	<0.0001	2.7 × 10−5	0.15	0.0219	8.3208 × 10−5	1.38	<0.0001	3.0475 × 10−4	18.57	<0.0001
x42	1	−1.6292 × 10−4	5.308 × 10−4	0.0005	4.4 × 10−3	0.39	0.0006	9.2208 × 10−3	1.7	<0.0001	2.3875 × 10−2	11.40	<0.0001
Residual	21		6.555 × 10−4			0.50			1.26			1.21
Lack of fit	10		2.652 × 10−4	0.6729		0.27	0.3160		0.58	0.5372		0.71	0.2435
Pure error	11		3.903 × 10−4			0.22			0.68			0.50
Total	35		0.018			31.61			86.85			70.25
R2		0.9627			0.9842			0.9856			0.9827
Adj-R2		0.9378			0.9737			0.9759			0.9712
Perd-R2		0.8865			0.9415			0.9525			0.9334
Adeq. precision		24.401			42.445			42.177			27.302
PRESS		0.002			1.85			4.13			4.68
CV		2.82			4.20			6.36			3.04

p-Value < 0.05 is significant at a = 0.05. Lack of fit is not significant at p-value > 0.05.

The application of multiple linear regression analyses to the experimental data resulted in second-order polynomial models predicting DR, DQ, MSE and ∆E*. These models align with the initial assumptions made at the outset of the study. Table 5 demonstrates that all regression models exhibit statistical significance at a confidence level of 99%. Statistical significance of all main, linear, and quadratic effects and the interaction of effects calculated for each response can also be seen in Table 5. Non-significant effects (p > 0.05) were systematically removed from the models without disrupting the hierarchical structure of the model. The ANOVA also shows that lack of fit is not significant for all response surface models at a 95% confidence level. On the other hand, a high proportion of variability (R² > 0.96) in the response models can be explained successfully by the models (Table 5). Nevertheless, a high R² value does not always indicate the effectiveness of the regression model. Introducing an additional variable to the model will invariably raise the R² value, irrespective of the statistical significance of the added variable. Therefore, utilizing the adj-R² is recommended for assessing the model’s adequacy. The adj-R² of the DR, DQ, MSE and ∆E* are 0.9378, 0.9737, 0.9759 and 0.9712, respectively, and the PRESS of the DR, DQ, MSE and ∆E* are 0.002, 1.85, 4.13 and 4.68, respectively (Table 5). These low PRESS values and adj-R² values greater than 0.9 suggest that these second-order polynomial models have good accuracy. Moreover, the minor variance between the R² and adj-R² values across the models suggests the exclusion of non-significant terms from the model. The CV of DR, DQ, MSE and ∆E* are 2.82%, 4.20%, 6.36% and 3.04%, respectively.

To visualize the combined effects of the two variables on the response, the response surface and contour plots were obtained for each of the fitted models as functions of two variables, while the other two variables were kept as the central values. Effects of the variables on responses are discussed by evaluation of these plots in the following section.

3.2.2. Unit Time Drying Rate

The DR analysis results are important for tracking moisture transfer. As shown in Table 5, the DR ranged from 0.141 to 0.229%/min. The response surfaces of each variable to DR are shown in Figure 12A and Figure 13A. According to Figure 12A, there is an interaction between the HA temperature and the microwave power. The DR increases with an increase in the HA temperature at low levels of microwave power, while the DR increases and then decreases slightly when microwave power changes from medium to high levels. This is likely due to the fact that the walnuts with the higher IMC were dried at the higher HA temperature, and to the increased humidity difference between the walnuts and their surroundings, which allowed water to migrate outward more rapidly [15,37]. In addition, high temperatures increase the kinetic energy and activity of water molecules in walnuts, thus accelerating the migration of water [16]. However, excessive HA temperatures and microwave power may lead to structural shrinkage and surface hardening of the shell, which will prevent water migration cross-layer within the shell [37,38,39].

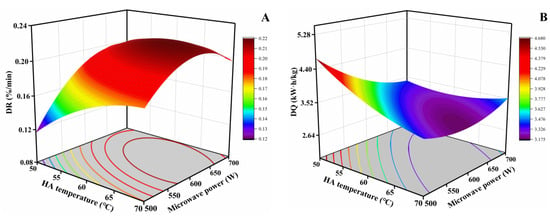
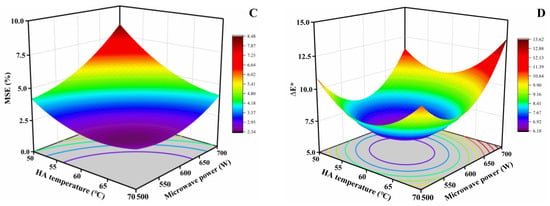
Figure 12. Response surface and contour plots for DR (A), DQ (B), MSE (C) and ∆E* (D) (at constant MC of the transition point (24%) and MV thermostatic temperature (50 °C)).

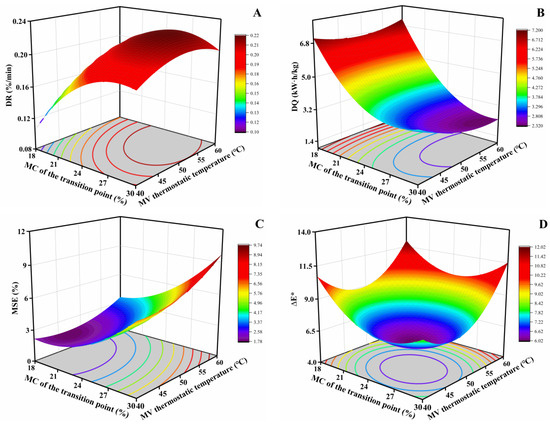
Figure 13. Response surface and contour plots for DR (A), DQ (B), MSE (C) and ∆E* (D) (at constant HA temperature (60 °C) and microwave power (600 W)).

Meanwhile, it can be found that the DR of walnuts dried at higher microwave powers (600–700 W) is faster compared to those dried at lower microwave powers (500–600 W) (Figure 12A). According to the principle of microwave drying, internal heating enables microwaves to directly penetrate the walnut shell, thereby forming a heat source within the walnut based on the aggregation effect that in turn produces a high vapor pressure, which is convenient for the transfer and diffusion of moisture from the kernel to the shell [40,41]. Therefore, high microwave power may result in a more pronounced enhancing effect and cause more increases in the DR of walnuts than low microwave power [42]. Similar results have been noticed for the drying of terebinth, with increasing microwave power increasing DRs [33].

It can be seen from Figure 13A that there is an interaction between the MC of the transition point and the MV thermostatic temperature. The DR will increase when both the MV thermostatic temperature and the MC of the transition point increase. Meanwhile, it was found that the DR of walnuts dried at high MV thermostatic temperatures (50–60 °C) was higher compared to those dried at lower MV thermostatic temperatures (40–50 °C). Similar results have been noticed for the drying of amaranth seeds [43]. In addition, the larger the MC of the transition point, the earlier the MVD stage and the greater the DR is. This can be attributed to the fact that MVD is more efficient, compared to HAD [30].

3.2.3. Unit Mass Drying Energy Consumption

Generally, an efficient drying process uses a minimum amount of energy to dry the products to the desired MC. As summarized in Table 4, DQ ranges from 2.54 to 6.71 kW·h/kg. Figure 12B and Figure 13B display the response surface of each variable to DQ. As shown in Figure 12B, there is an interaction between the HA temperature and the microwave power. The change in DQ with another parameter is not significant at high levels of microwave power or HA temperature. However, DQ decreases rapidly with increasing HA temperature at low levels of microwave power. Increasing the HA temperature will shorten drying times and reduce the DQ. Similarly, the DQ decreases rapidly with increasing microwave power at low levels of HA temperature. The reason is that the increase in the microwave power leads to an increase in the intensity of radiation that the per-unit mass of walnuts receives, and with the increase in the drying rate, the corresponding drying time is significantly shortened, so the DQ decreases [42].

As can be seen from Figure 13B, there is an interaction between the MC of the transition point and the MV thermostatic temperature. The DQ decreases with increasing MV thermostatic temperatures at high levels of MC of the transition point. Meanwhile, the DQ under the different MV thermostatic temperatures had no significant change at low levels of MC of the transition point. In addition, DQ decreased with increasing MC of the transition point. This phenomenon can be elucidated by the interaction between the microwave energy and the absorbing medium. Specifically, considering that the moisture in walnuts is the main radiation-absorbing component, the higher its content, the stronger the absorbing ability is, which further increases the drying rate and shortens the drying time [42,44].

3.2.4. Mean Square Error of Moisture Content

MSE is an indicator to quantify differences in the MC of walnuts and is responsible for their engineering properties. As shown in Table 4, the MSE ranges from 1.89 to 8.42%. Figure 12C and Figure 13C present the response surfaces of each variable to the MSE. It can be observed from Figure 12C that there is an interaction between the HA temperature and the microwave power. The variation in MSE is small in the range of high HA temperatures (60–70 °C) or low microwave power (500–600 W). However, the MSE changes significantly in the range of low HA temperatures (50–60 °C) or high microwave power (600–700 W). The results suggest that there are both sensitive and non-sensitive zones for the effect of HA temperature and microwave power on MSE. In addition, the combination of low HA temperature (50–60 °C) and high microwave power (600–700 W) led to a significant increase in the MSE, which reached a peak of approximately 8.48%.

It can also be seen from Figure 12C that the MSE decreases with increasing HA temperature, whereas it increases with increasing microwave power. This discrepancy is presumably attributable to the variance in heating mechanisms between HA and microwave radiation. The thermal energy is translated from the external shell to the internal kernel through thermal conduction in terms of the HAD, resulting in the fact that the shell is heated rapidly and has a higher temperature compared to the kernel [16]. Hence, the drying rate of shells is obviously faster than that of kernels when the HA temperature increases, which reduces the MC difference between the shell and kernel, thus reducing the MSE. In contrast, microwave heating stands out due to its distinctive aspects of selective and internal heating. Therefore, microwave heating can act directly on the moisture inside the walnut, and through high temperature produce a certain vapor pressure inside the walnut, spreading the moisture from the inner kernel to the surface of the shell [40]. Increasing the power significantly increases the drying rate of the kernels, which increases the MC difference between shell and kernel and thus increases the MSE.

In addition, as summarized in Figure 13C, the MSE is greater at the higher MC of the transition point and MV thermostatic temperature. This suggests that the combination of a higher MC of the transition point and MV thermostatic temperature can increase the difference in the MC of individual walnuts. Meanwhile, we found that the MC of the transition point had a more significant effect on MSE compared to the MV thermostatic temperature, which is consistent with the ANOVA results (Table 5).

3.2.5. Kernel Color Parameter

Color is one of the most important quality indicators of dried products. As summarized in Table 4, ∆E* ranged from 5.92 to 10.94. The response surfaces of each variable to ∆E* are presented in Figure 12D and Figure 13D. The results show that the interaction effects of HA temperature–microwave power and MC of the transition point–MV thermostatic temperature are significant for ∆E* (Table 5). We found that ∆E* decreases and then increases with increasing HA temperature and MV thermostatic temperature (Figure 12D and Figure 13D). The color darkening of food materials during drying might be caused by both enzymatic and non-enzymatic browning reactions [45,46]. Specifically, the low-temperature conditions require a long duration of drying, thus resulting in increasing browning [40]. Also, the heating at the high temperature induced the Maillard reaction of amino acids and reduced sugar inside kernels and caused more non-enzymatic browning [47,48]. Meanwhile, we also found that the ∆E* of walnuts dried at 600 W is lower compared to those dried at higher power (Figure 12D). This is due to the fact that the higher temperature of kernels at higher microwave power levels leads to a higher degree of browning [44].

As can be seen from Figure 12D, the combination of high HA temperatures (65–70 °C) and microwave power (650–700 W) results in a significant increase in the ∆E*. This suggests that the combination of higher HA temperatures and microwave power can exacerbate the browning of kernels during drying. As shown in Figure 13D, the ∆E* is smaller at the higher MC of the transition point and lower MV thermostatic temperature. This implies that earlier access to low-temperature MVD can significantly reduce the color change of kernels. Moreover, a significant negative linear effect between the MC of the transition point and ∆E* confirms that MVD has a smaller effect on kernel color than HAD (Table 5). This is likely due to the lack of oxygen preventing enzymatic oxidation when the MV is applied [49].

3.2.6. Optimization and Validation

Process parameters should be optimized for desired final product characteristics. Optimum conditions for walnut drying using the HA-MVD method were determined to obtain these criteria: minimum DQ, ∆E* and MSE and maximum DR. In order to determine the specified optimum drying condition, second-order polynomial models were established for each response. Note that these regression models are valid only in the selected experimental domain. Solutions are solved for the optimum covering the criteria by using the desirability function method: 63.23 °C for HA temperature, 24.88% for MC of the transition point, 588.24 W for microwave power and 49.01 °C for MV thermostatic temperature. Correspondingly, DR, DQ, MSE and ∆E* are 0.215%/min, 3.03 kW·h/kg, 2.93% and 6.42, respectively. Five runs were conducted at the optimum processing conditions for the verification of the predicted model. The test results are listed in Table 6, where the experimental result is very close to the predicted result, indicating the prediction performance of the regression model is reliable.

Table 6. Validation test of evaluation indexes of walnut drying process.

Index Evaluation	Predicted Value	Test Value
Unit time drying rate (DR), %/min	0.215	0.211 ± 0.01
Unit mass drying energy consumption (DQ), kW·h/kg	3.03	2.99 ± 0.08
Mean square error of moisture content (MSE), %	2.93	2.89 ± 0.65
Kernel color parameter (∆E*)	6.42	6.49 ± 0.31

It was confirmed that, while reducing the MSE by the outside-in heating principle of HAD, the combination of methods improves DR and DQ and reduces ∆E* through the fast, uniform and internal heating characteristics of MVD. The HA-MVD approach amalgamates the merits of both drying methods, enabling high efficiency, reduced energy consumption, and superior drying quality, and is therefore a promising new technology for walnut drying. These findings offer substantial theoretical guidance for the design of combined drying processes applicable to walnuts and analogous multilayer-structured food materials.

3.3. Optimization and Validation

Taking the walnut samples with conventional storage MC (RMC) as a contrast, walnut samples with CMC were crushed using the pilot-scale walnut-crushing apparatus (as seen in Figure 2). The experimental results are shown in Table 7. Compared to the RMC, the CMC could raise the D_b by 0.12 and the d_M by 5.43 mm, indicating a more broken shell and a more whole kernel after walnut crushing. Hence, one can conclude that kernel over-crushing and shell under-crushing can occur for the walnut with RMC during the shell breaking, whereas the desired walnut-crushing state that is broken shells and whole kernels can be obtained through an optimized HA-MVD process. In addition, we found that the difference in crushing performance of walnuts with CMC through either HAD or HA-MVD is small (Table 7, Figure 9 and Figure 11). A similar result was also reported by Lu et al., where there was a slight difference in the mechanical properties of shells and kernels in terms of different drying treatments when the MC of peanuts was in the lower range [37]. Therefore, it is reasonable to ignore the effect of drying process conditions and further optimize a set parameter based on the HA-MVD process with regard to walnut shell breaking in this study.

Table 7. Verification experiments of walnut-crushing performance under different MCs.

Control Groups	Db	dM, mm
RMC (shell: 6.89%, kernel: 2.31%)	1.65 ± 0.04	10.22 ± 0.49
CMC (shell: 9.41%, kernel: 11.27%)	1.77 ± 0.05	15.65 ± 0.53

According to the results of this study, drying the walnuts to CMC using an optimized HA-MVD process could both maximally improve the crushing performance and significantly reduce the drying time. The study proposes an idea of continuous processing of drying and shell breaking from the perspective of improving quality and efficiency, which will provide a new perspective on the processing of walnuts and other nuts. In addition, we found in the walnut-drying experiments that it was difficult for the samples to precisely achieve the target MC (CMC) simultaneously. This may be attributed to uneven drying due to the differences in intrinsic properties (e.g., IMC, structure) of individual walnuts [11,12]. Therefore, to clarify the influence of individual walnut differences on drying characteristics as well as distribution and variation in MC during drying is very important for determining the most suitable drying conditions and then improving drying uniformity.

4. Conclusions

In this study, the distributions of fragment sizes for shells and kernels after walnut crushing were determined simultaneously for the first time, and the fragmentation degree of shells and kernels were quantified using fractal dimensions and the average fragment size, respectively. The fragmentation degrees of shells and kernels have a significant dependence on MC, as shown by the fractal dimension’s decrease, then increase and finally stabilization with decreasing MC, and the average fragment size’s increase and then decrease with decreasing MC. Within the study range, the CMCs of shells and kernels are 9.41% and 11.27%, respectively. The HA temperature, MC of the transition point, microwave power, and MV thermostatic temperature have significant effects on the unit time drying rate, unit mass drying energy consumption, mean square error and kernel color parameter. The HA-MVD process parameters with regard to walnut shell breaking include an HA temperature of 63.23 °C, an MC of the transition point of 24.88%, microwave power of 588.24 W and an MV thermostatic temperature of 49.01 °C. At this point, the unit time drying rate, unit mass drying energy consumption, mean square error of moisture content and kernel color parameter are 0.215%/min, 3.03 kW·h/kg, 2.93% and 6.42, respectively.