Data Collecting and Monitoring for Photovoltaic System: A Deep-Q-Learning-Based Unmanned Aerial Vehicle-Assisted Scheme

Abstract

Nowadays, massive photovoltaic power stations are being integrated into grid networks. However, a large number of photovoltaic facilities are located in special areas, which presents difficulties in management. Unmanned Aerial Vehicle (UAV)-assisted data collection will be a prospective solution for photovoltaic systems. In this paper, based on Deep Reinforcement Learning (DRL), we propose a UAV-assisted scheme, which could be used in scenarios without awareness of sensor nodes’ (SNs) precise locations and has better universality. The optimized data collection work was formulated as a Markov Decision Process (MDP), and the approximate optimal policy was found by Deep Q-Learning (DQN). The simulation results show efficiency and convergence and demonstrate the effectiveness of the proposed scheme compared with other benchmarks.

1. Introduction

Nowadays, massive photovoltaic power stations are integrated into smart power grids. As the coverage area of the grid continues expanding, a large number of facilities are arranged in special areas, such as mountains or hilly terrains, which means management and global monitoring become an urgent problem [1]. Unmanned Aerial Vehicles (UAVs) have become a key enabling technology of interest in recent decades due to their high mobility, low cost, and ease of deployment and have been used in a wide range of scenarios such as natural disaster rescue, cargo delivery, etc. UAVs can be broadly categorized into four types: multi-rotor UAVs, fixed-wing UAVs, single-rotor UAVs, and fixed-wing hybrid vertical takeoff and landing UAVs, which have unique advantages that can be applied to different application scenarios, such as data acquisition [1,2,3], Mobile Edge Computing (MEC) [4,5,6,7], and flight relay [8,9]. In particular, the high maneuverability of UAVs in the air gives them the ability to provide better line-of-sight transmissions, which makes it possible to rapidly deploy communication systems with complex network structures and greatly improves the quality of service to users when UAVs are used as base stations.

Nowadays, research on the application of UAVs in the field of communication has led to a large number of achievements. In particular, UAVs can play an important role in providing timely airborne data services, such as search and rescue and surveillance in emergencies or disasters [10,11], and they can help wireless communication systems recover quickly from paralysis. UAVs can also act as mobile base stations or flying relay stations to provide reliable communications to small and power-limited terrestrial IoT devices or end-users [10,11,12], and their fully controllable maneuverability allows them to get close enough to ground-based devices to establish low-altitude air-to-ground communication links [13]. In situations where the ground-based IoT infrastructure is limited, UAVs can be used to flexibly collect sensing information, thereby saving transmission energy for sensor devices and extending the network lifetime [14]. Due to its unique advantages (mobility, independence, special extreme situation employment, etc.), the UAV is a very potential technique for data collecting in photovoltaic system. Thus, UAV-assisted data collecting and state monitoring will be a prospective solution for photovoltaic system.

While UAVs bring us convenient communication services by virtue of their unique advantages, they still face many challenges. UAVs have difficulty carrying large-capacity batteries due to their small size, resulting in short endurance, and thus insufficient energy has become a major obstacle to the development of UAV communication [15,16,17]. The energy consumption of UAVs mainly consists of the motion energy consumption to overcome gravity and air resistance, and the energy consumed by communication only accounts for a small portion of the total energy consumption of UAVs, so if UAVs perform their tasks under energy constraints, it is very important to make reasonable decisions on their trajectory, design, and optimization. Currently, a large number of researchers have used traditional optimization algorithms to solve the trajectory optimization problem, which requires the acquisition of environmental information such as channel conditions and the positions of other devices before the UAV takes off [16]. However, in practice, the environment of the UAV is complex and dynamic; it is not easy and is even challenging for UAVs to acquire the precise location information of sensor nodes (SNs) in some practical scenarios, such as disaster relief, dangerous areas, and unpredictable scenes. A lot of environmental variables cannot be acquired in advance, including precise position information, so it is research of great practical significance to enable the UAV to make decisions on-the-fly and to learn the optimal flight strategy under the condition that information about the surroundings is not known [17]. Therefore, learning the optimal flight strategy for UAVs to make instant decisions under unknown surrounding environment information is a research direction of practical significance. In ref. [18], the authors investigate the jointly optimal trajectory and time switching allocation design for UAV-secure communication systems with imperfect eavesdropper locations. However, most of the existing UAV data collection schemes are based on the assumption that the position information of SNs is known and fixed and can be provided to UAVs for use. This assumption is valid in some specific scenarios where SNs are fixedly installed at specific locations. In many practical applications, this assumption does not conform to the actual situation. SNs may be randomly deployed in an area and may change their positions due to various reasons, such as wind force, animal interference, human intervention, and so on. In this case, UAVs cannot obtain the precise position information of IoT devices but only the information of the region where they are located. Therefore, how to design an effective UAV-path-planning scheme to minimize the completion time of data collection tasks without knowing the exact position information of SNs becomes a challenging and practical problem.

Reinforcement Learning (RL) is a kind of unsupervised learning, which aims at obtaining an environment model through adaptive learning and adjusting its parameters in order to obtain the optimal action strategy when facing time-varying environments [19]. Deep Reinforcement Learning (DRL) breaks through the limitations of complex environments, and the training speed of neural networks is significantly improved, which has led to its use in a large number of applications. Therefore, DRL has been widely used in complex communication problems in wireless channels. The integration of DRL shows a good application prospect in communication, but there are still some deficiencies in practice. To solve these problems, DeepMind proposes Deep Q-Learning (DQN), which can realize an end-to-end learning policy without increasing empirical knowledge. DQN has played an essential role in communications [20]. In ref. [21], Ding et al., propose a path-planning and spectrum-allocation method for UAVs based on DRL to realize efficient and energy-saving, fair communication. According to all of the above, this paper proposes a DRL approach to minimize the total mission time for UAV-assisted data collection. To resolve the lack of location information, we leverage DQN for trajectory design to minimize the duration of mission completion without precise device location information being known.

The main contributions of this paper are as follows:

• The goal of this paper is to optimize data collection in photovoltaic systems by the minimizing mission completion time of a UAV. Unlike the existing works, we consider this issue in situations where the UAV cannot obtain the precise location information of SNs in a power system. First, a UAV data acquisition system model is established under the condition that the location information of SNs is unknown. The UAV departs from the base station and collects the information sensed by all SNs during its flight time. Due to the lack of positional information, the system senses the changes in signal strength from ground devices to infer the relative positions of the UAV and the ground devices, and then enables the UAV to select a better flight trajectory.
• To make up for the lack of location information, we formulate this problem as a Markov Decision Process (MDP), which proposes a DQN-based algorithm to minimize the flight time under a lack of location information. We train the optimal flight strategy to maximize the cumulative reward through a gradient descent method. The proposed scheme is applicable to more scenarios without repeat training after changing scenarios, which means it has good general applicability.
• To assess the overall performance and convergence of our proposal, we carry out sufficient simulations and training. The simulation results show that with good convergence performance, the efficiency of this scheme reaches 96.1% of the baseline DQN algorithm when the precise device location information is known, which proves that the new scheme proposed in this chapter is still able to minimize the completion time of the data collection task and improve the efficiency of the system in the absence of location information. The simulation results indicate that the proposed approach converges efficiently with adequate training time and achieves comparable performance to location-aware schemes.

The remainder of this paper is organized as follows: We present the system model and problem formulation of a UAV-assisted power sensor network in Section 2. Section 3 illustrates the scheme and overall algorithm of the UAV-assisted method based on DQN. Section 4 gives the simulation results of the proposal and analyzes the scheme performance and algorithm convergence. Lastly, Section 5 concludes the whole paper.

2. System Model and Problem Formulation

2.1. System Model

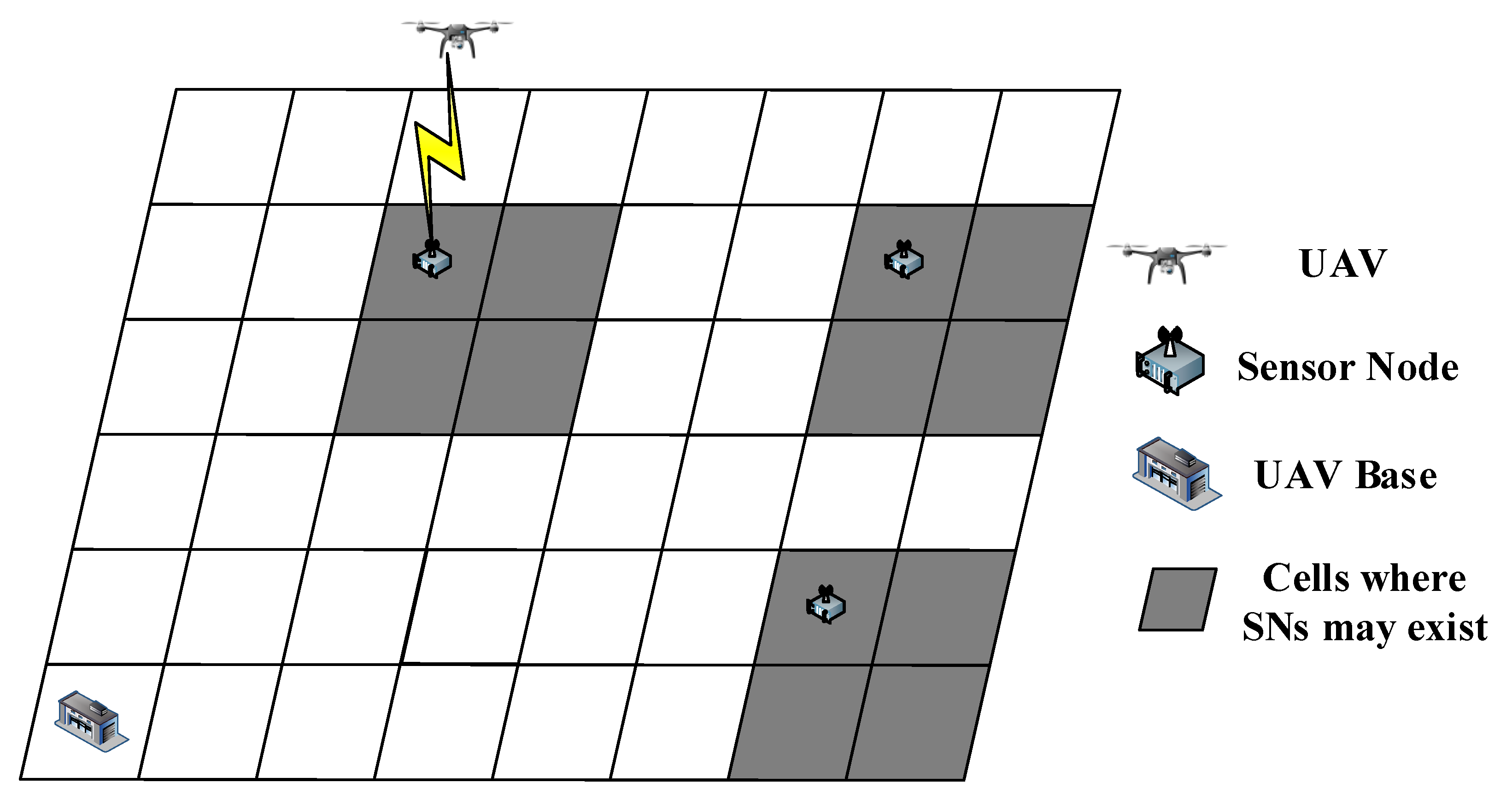
We consider a square grid world composed of $U\times U$ cells with a UAV collecting data from K SNs, as shown in Figure 1. The side length of each cell is l. The UAV only hovers over the center of each cell, transmits broadcast signals, and collects data during the hovering time. The position of the k-th SN at the t-th time slot can be described as

$$u_k\left(t\right)={[x_k\left(t\right),y_k\left(t\right),0]}^T,$$

(1)

where $k\in [1,\cdots ,K]$, and $t\in [1,\cdots ,T]$. In actual scenarios, precise position information may not be easy to obtain and cannot even be reliably predicted through explicit models. Thus, we assume that the UAV is not aware of the precise information about which cell the SN is located in. It is supposed that the UAV flies at a constant altitude, H, so the UAV’s position can be expressed as

$$p\left(t\right)={[x\left(t\right),y\left(t\right),H]}^T.$$

(2)

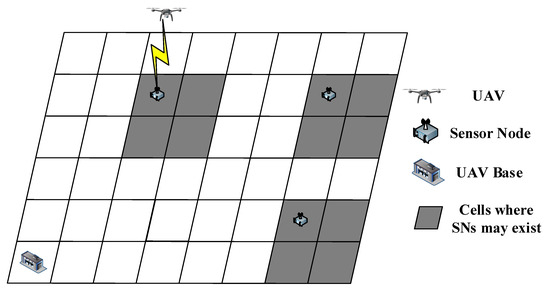
Figure 1. UAV-assisted data collection system without precise location information being known.

The mission time slots are small enough so that the speed of the UAV, $v\left(t\right)$, should be regarded as constant in any time slot. The UAV has two states: hovering or flying at a fixed speed, V, i.e., $v\left(t\right)\in \{0,V\}$ for any $t\in [1,\cdots ,T]$. Each time the UAV moves, it will move to the center of its adjacent cell which is specified as

$$V\times (t-(t-1\left)\right)=V=l.$$

(3)

During the mission time, the UAV needs to collect data from all devices. $p_{k,t}$ represents the uplink transmit power for the k-th SN, $i_k$, when it wakes up to communicate. We assume that only when the UAV wakes up the SNs can they start to upload information or transmit signals in response to the broadcast signal from the UAV, and the device will no longer respond to the UAV after the data are collected. Therefore, $p_{k,t}$ can be expressed as

$$p_{k,t}=\left\{\begin{array}{cc}{p}_{k,upl},\hfill & \mathrm{uploading}\mathrm{data}\hfill \\ p_{k,res},\hfill & \mathrm{responsing}\mathrm{the}\mathrm{UAV}\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(4)

The channel capacity between the UAV and SN, $i_k$, at the t-th slot, measured in bits per second (bps), can be expressed as

$$R_k\left(t\right)=B{log}_2(1+\frac{p_{k,t}{\beta }_0}{{\sigma }^2{\Vert p\left(t\right)-u_k\left(t\right)\Vert }^2}),$$

(5)

where $p\left(t\right)$ denotes the UAV’s position, B is the channel bandwidth, ${\beta }_0$ is the reference channel gain, and ${\sigma }^2$ is the channel noise power.

2.2. Problem Formulation

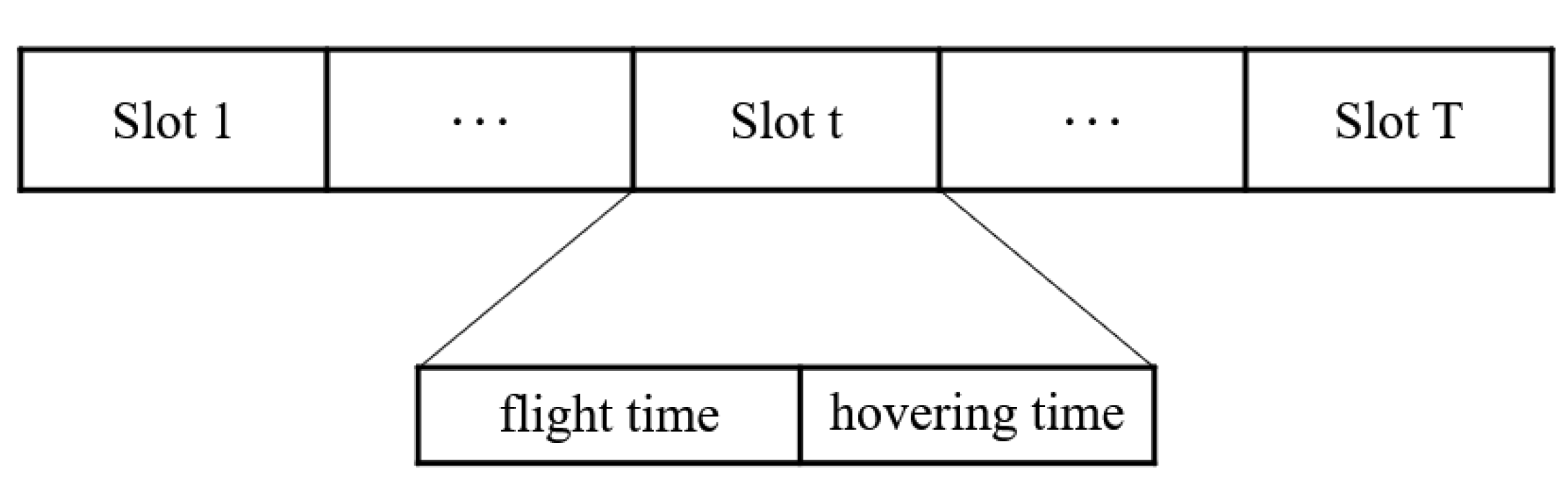
The mission completion time, $T_{all}$, is converted into T time slots with different size durations, ${\delta }_t$, $t\in \{1,2,3,\cdots ,T\}$, as shown in Figure 2. Each time slot, ${\delta }_t$, contains two parts: ${\delta }_{f,t}$ is the flight time, and ${\delta }_{h,t}$ is the hovering time, i.e., ${\delta }_t={\delta }_{f,t}+{\delta }_{h,t}$. During the flight time, ${\delta }_{f,t}$, the UAV flies a fixed distance, l, and chooses the direction of flight according to the policy. The UAV’s position at the $t+1$-th time slot, ${\delta }_{t+1}$, is expressed as

$$\begin{array}{cc}\hfill x(t+1)& =x\left(t\right)+lcos\left({\theta }_t\right),\hfill \\ \hfill y(t+1)& =y\left(t\right)+lsin\left({\theta }_t\right),\hfill \end{array}$$

(6)

where ${\theta }_t\in \{0,\pi /2,\pi ,3\pi /2\}$ represents the angle between the flight direction of the UAV and the x-axis on the XY plane.

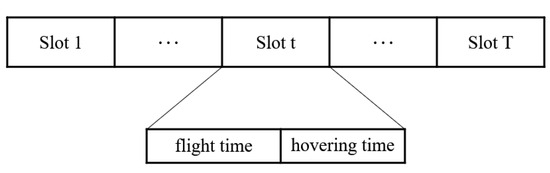
Figure 2. Composition of mission completion time.

The corresponding uplink signal-to-noise ratio, $SN{R}_{k,t}$, between the UAV and the k-th SN at the t-th time slot is denoted as

$$SN{R}_{k,t}=\frac{p_{k,t}{\left|h_{k,t}\right|}^2}{P_N},$$

(7)

where $P_N$ represents the power of additive white Gaussian noise (AWGN) at the UAV receiver, and $|h_{k,t}{|}^2$ is the channel power gain during the hovering time, ${\delta }_{h,t}$. To save the power cost of SNs and ensure service quality during data transmission, we set a pre-defined SNR threshold $SN{R}_{th}$, where the k-th SN can be woken up and served by the UAV only if $SN{R}_{k,t}\ge SN{R}_{th}$. So the binary parameter, $e_{k,t}$, is defined as

$$e_{k,t}=\left\{\begin{array}{cc}1,\hfill & SN{R}_{k,t}\ge SN{R}_{th},\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(8)

We set the side length, l, and $SN{R}_{th}$ so that the UAV can only collect the information carried by the SNs, which are in the same cell as it. Then, the UAV’s hovering time at the t-th time slot is defined as

$${\delta }_{h,t}=\frac{e_{k,t}{D}_{data}}{R_k\left(t\right)}+t_{rec},$$

(9)

where $D_{data}$ denotes the data size of the information carried by k-th SN to be collected, and $t_{rec}$ represents the fixed time for the UAV to receive the response signal from the SNs.

Therefore, the problem of minimizing the mission time, $T_{all}$, is depicted as

$$\begin{array}{cc}\hfill & \underset{{\theta }_t,\{x\left(t\right),y\left(t\right)\},T}{min}\sum _{t=1}^T{\delta }_t=T_{all}\hfill \\ \hfill & \begin{array}{cc}\hfill s.t.& \hfill \sum _{t=1}^T{e}_{k,t}=1,\forall k\\ \hfill & \hfill 0\le x\left(t\right)\le U\times l,\forall t\\ \hfill & \hfill 0\le y\left(t\right)\le U\times l,\forall t\\ \hfill & \hfill {\theta }_t\in \{0,\pi /2,\pi ,3\pi /2\},\forall t\end{array}\hfill \end{array}$$

(10)

2.3. Markov Decision Process

In general, an MDP can be expressed as the tuple $\{S,A,R,P,\gamma \}$, where S is the state space, A is the action space, R is the reward function, P is the state transition probability, and $\gamma$ is the discount factor.

(1) State space, S: Each state, $s_t$, comprises two elements and is expressed as

$$s_t=\{x\left(t\right),y\left(t\right),\frac{R_1(t-1)}{R_1\left(t\right)},\dots ,\frac{R_k(t-1)}{R_k\left(t\right)},\dots ,\frac{R_K(t-1)}{R_K\left(t\right)}\}.$$

(11)

When $t=0$, $s_0=\{x\left(0\right),y\left(0\right),0,\dots ,0\}$, where $\left(x\right(t),y(t\left)\right)$ is the projection of the UAV’s coordinate on the XY plane, and $\frac{R_k(t-1)}{R_k\left(t\right)}$ is the ratio of the signal strength received from the k-th SN at the current time to the previous time. Instead of the instantaneously received signal strength in each time slot, we use its ratio to express the system state because the ratio can implicitly indicate the change in distance from the UAV to each SN.

(2) Action space, A: The UAV has four actions to choose from, $a_t\in \{north,east,south,west\}$. The UAV moves the same distance every time, that is, the side length of the cell is l. We also set some restrictions so that the UAV cannot leave the square grid world. For example, the UAV will not be able to select certain actions at the boundary.

(3) Reward function, R: The reward function maps status action pairs into reward values, which represent task objectives, and the reward function, R, is composed of the following parts:

• $r_{dc}$ is the reward for data collecting. Every time the UAV collects data carried by IoT devices, it will obtain a fixed reward, $r_{dc}$.
• $r_{inc}$ is the constant movement reward, which is applied to actions with increased signal strength from all devices.
• $r_{dec}$ is the constant movement punishment, which is applied to actions with decreased signal strength from all devices.
• $r_b$ is the punishment for the UAV trying to fly away from the region boundary.

(4) State transition probability, P: P is represented by $P(s_{t+1}\mid s_t,a_t)$, expressed as the probability distribution of the next state, $s_{t+1}$, given the current state, $s_t$, and the action, $a_t$, taken and represents the dynamic characteristics of the entire environment.

3. Methodology

3.1. Reinforcement Learning

RL is an extremely valuable research field in machine learning and has been promoting the prosperity of artificial intelligence (AI) for the last 30 years. In the process of RL, the agent makes decisions regularly, observes the results, and adjusts the policy to achieve the optimum policy on its own initiative. Nevertheless, even if this process is proved to be convergent, reaching the optimal policy still requires a long training time because it must explore and acquire the knowledge of the whole scenario, which makes it inapplicable to an extremely complex system. Therefore, the application of RL in practice is minimal [22].

In recent years, DL has become a ground-breaking technology with great significance. It makes up for the shortcomings of RL and brings new development to RL, that is, DRL, which uses the advantages of deep neural networks (DNNs) to train the Q-network, so as to enhance the convergence ability and performance of RL.

3.2. Deep Q-Network Algorithm

When the state space and action space are small, the Q-Learning algorithm can effectively obtain the optimal strategy. However, in practice, for complex system models, these spaces are often large, which is impractical both for maintaining Q-tables and finding state–action values. In this case, the Q-Learning algorithm may not be able to find the optimal strategy. The deep Q-network introduces a deep learning algorithm to overcome this shortcoming. With the excellent performance of deep learning in complex feature extraction, DQN gives up maintaining a Q-table and uses a neural network to fit a function to output the results of different actions in different states. The Q-value solves the problem of the low learning efficiency of the Q-Learning algorithm in a high-dimensional state space and action space. Compared with maintaining Q-tables, using functions to output Q-values only requires storing the network structure and parameters of the neural network and has stronger generalization capabilities.

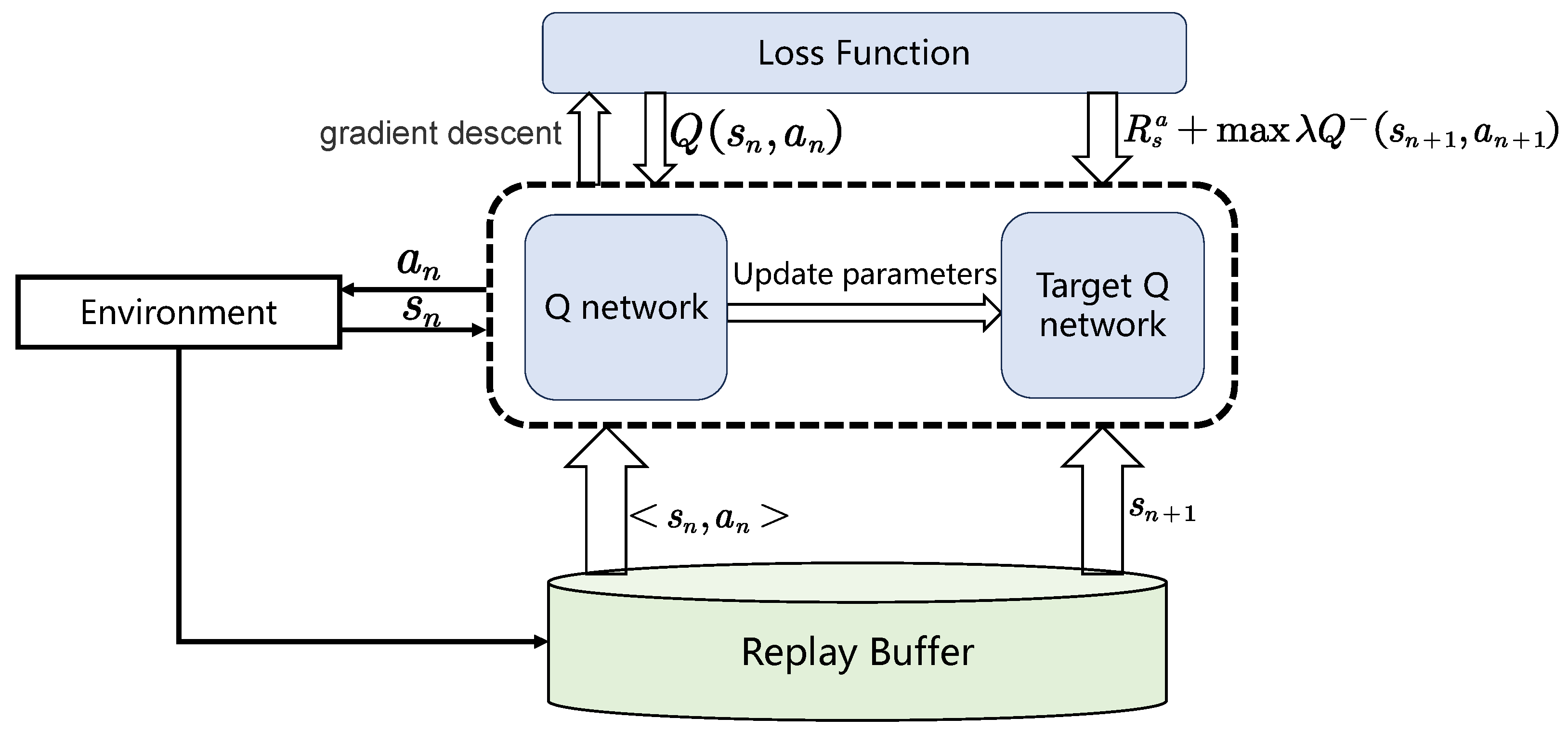
When training the DQN algorithm, the agent will choose to perform the action with the highest value based on the greedy strategy or randomly select an action in the action space. Then, it will receive a reward, $r_n$, given by the environment and move to the next state, $s_{n+1}$. The obtained $<s_n,a_n,r_s^a,s_{n+1}>$ are stored in the experience replay buffer. When the number of samples stored in the experience replay buffer reaches the maximum capacity, a small batch of samples are randomly selected from them to train the estimated Q-network and the target Q-network. Then, the estimated Q-network parameters can be updated using the gradient descent method and periodically update the target Q-network parameters.

Figure 3 shows the structure of the DQN algorithm. The goal is to maximize the discounted accumulated reward, which is denoted as

$$r_t=\sum _{n=o}^{\infty }{\gamma }^n{r}_{t+n}$$

(12)

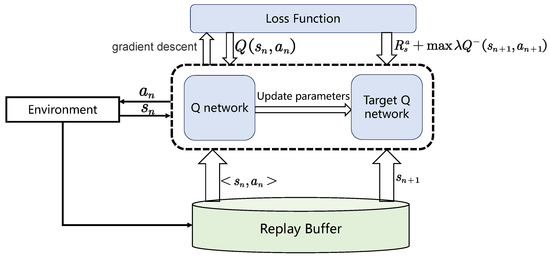
Figure 3. The structure of DQN algorithm.

The RL algorithm uses the state–action value function, $Q_{\pi }(s,a)=E\left[r_t\right|s_t=s,a_t=a]$, to describe the correctness of selecting action a in state s, and the optimal function is denoted as

$$Q^{*}(s,a)=max{Q}^{\pi }(s,a)$$

(13)

The Bellman equation of the optimal Q-function can be denoted as

$$Q^{*}(s,a)=E[r(s,a,s^{\prime })+\gamma \underset{a^{\prime }}{max}{Q}^{\pi }(s^{\prime },a^{\prime })]$$

(14)

where $\pi$ is the policy function, E is the mathematical expectation, and $s^{\prime }$ and $a^{\prime }$ are the state and action of the next moment, respectively. $r(s,a,s^{\prime })$ is the instant reward, ad $\gamma {\displaystyle \underset{\pi }{max}}{Q}^{\pi }(s^{\prime },a^{\prime })$ is the long-term reward.

We take the DNN as the function approximator to fit the Q-function.

$$Q(s,a;\theta )\approx Q^{*}(s,a)$$

(15)

where $\theta$ is the weight parameter of the Q-network.

The DQN is a value-based approach generally used in the context of RL. To alleviate the instability of the non-linear network representation function, DQN introduces an experience replay buffer and the target Q-network.

The experience replay buffer with a fixed capacity has been introduced. The replay buffer stores the status, actions, rewards, and next moment status generated by the interaction between the agent and the environment during the Markov decision process. DQN stores samples in the experience replay buffer and then uniformly samples mini-batch transmission sequences from the experience replay buffer. Through the experience replay buffer, all sample data can be used multiple times, which helps achieve higher data utilization efficiency. The method based on the experience replay buffer can extract arbitrary data, solving the problem of excessive correlation between samples, which reduces the training effect. Furthermore, it can improve the stability of the algorithm. Online learning strategies may affect the performance of the algorithm and lead to local optimization problems. Through experience replay, the offline update strategy can avoid excessive fluctuations in the algorithm and maintain high stability.

Furthermore, a target network and estimation network are introduced. When using a nonlinear function approximator during the training process, the Q-value will always change. However, if a set of changing values are used to update the Q-network, the value estimation may get out of control, which may lead to instability. In order to solve this problem, the estimated Q-network is updated every round through the stochastic gradient descent method, while the parameters of the target Q-network are updated frequently and slowly.

The details of the DQN procedure for the considered problem is presented in Algorithm 1.

Algorithm 1: The Proposed Algorithm

1: Initialize weight parameter $\theta$ for Q-function  2: Initialize weight parameter ${\theta }^{-}=\theta$ for target $\widehat{Q}$-function  3: Initialize experience replay buffer D with capacity N  4: for  $i=1,2,\dots ,M$  do  5:    Initialize the state $s_1$, and pretreat the state ${\phi }_1=\phi \left(s_1\right)$  6:    for $t=1,2,\dots ,T$ do  7:      Select an action $a_t$ with probability $ϵ$ randomly  8:      Otherwise select $a_t=arg\underset{a}{max}Q(\phi \left(s_t\right),a;\theta )$ with probability $1-ϵ$  9:      Adopt action $a_t$ and observe reward $r_t$ and next state $s_{t+1}$ 10:      Pretreat the state ${\phi }_{t+1}=\phi \left(s_{t+1}\right)$ 11:      Store transition $({\phi }_t,a_t,r_t,{\phi }_{t+1})$ in D 12:      Sample minibatch b of transitions $({\phi }_j,a_j,r_j,{\phi }_{j+1})$ from D, $j=1,2,\dots ,T-1$ randomly 13:      Set $y_j=r_j$, if episode terminates at slot j+1 14:      Otherwise, set $y_j=r_j+\gamma \underset{a_{j+1}}{max}\widehat{Q}({\phi }_j,a_{j+1};{\theta }^{-})$ 15:      Perform gradient descent slot on ${(y_j-Q(s_j,a_j;\theta ))}^2$ with respect to the network parameters $\theta$ 16:      Update ${\theta }^{-}=\theta$ every B slots 17:    end for 18: end for

4. Simulations

4.1. Simulation Setup

This section presents the experimental results to test and verify the proposal. We consider a UAV-assisted photovoltaic system with many SNs, which are randomly and evenly distributed in a square area composed of $10\times 10$ cells. The UAV starts from $p\left(0\right)={[50,50,100]}^T$ and flies at a fixed height, $H=100$ m, with a fixed flight distance, $l=100$ m, which is equal to the side length of cells. We regard the total flight time as the completion time of the data collection task because there is an order of magnitude difference between the flight time and hover time. The whole data collection mission lasts T time slots. To learn the flight policy, we use a DQN with five hidden layers and take a rectified linear unit (ReLU) as the activation function in these layers.

4.2. Results

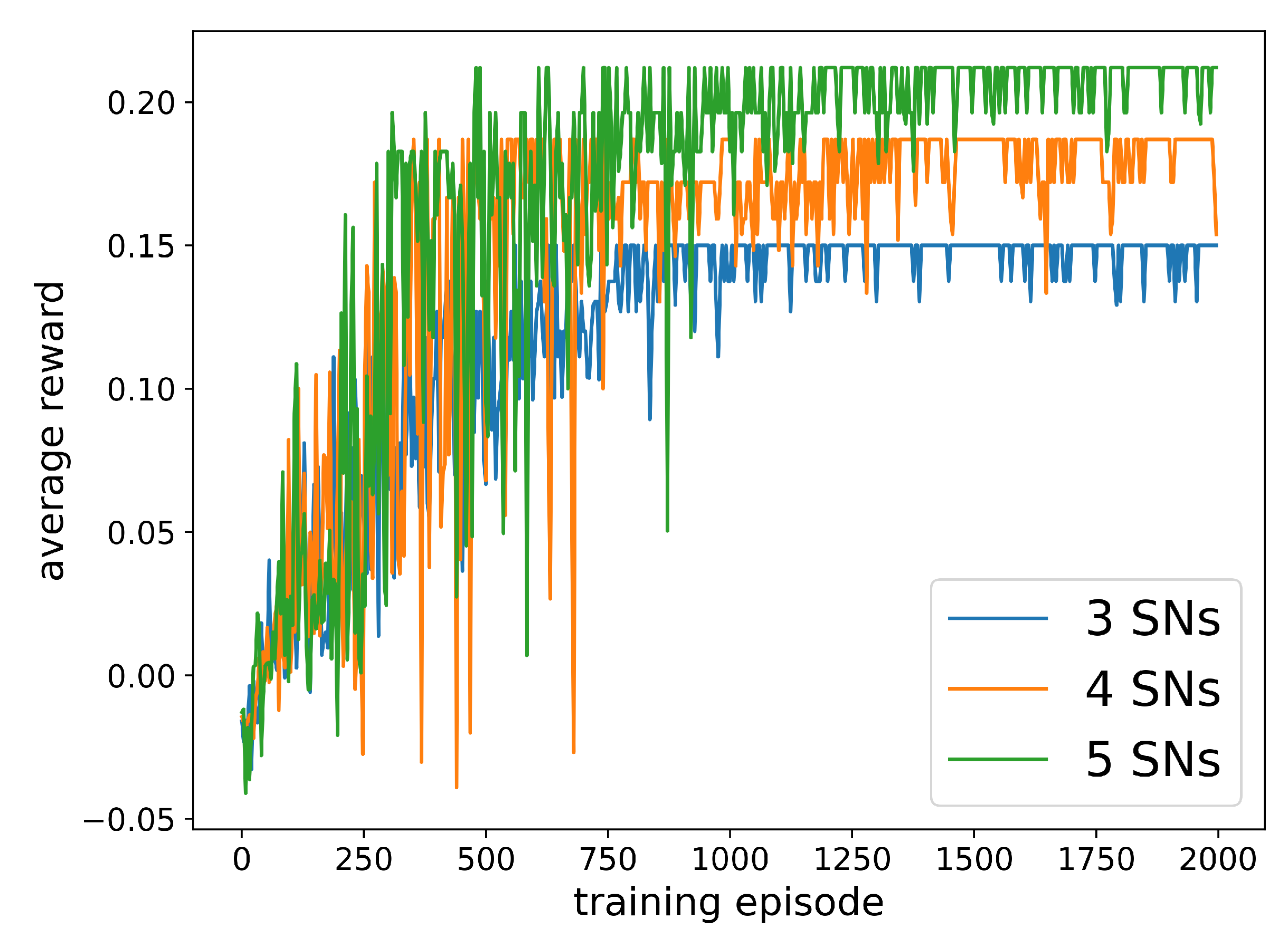
In order to confirm the convergence and scalability of the scheme, this section first conducts simulations in a scenario with 3, 4, or 5 SNs randomly distributed. The simulation results are shown in Figure 4. It can be seen from the resulting diagram that the more SNs in the scene, the more training rounds are required for algorithm convergence. At the same time, the average reward obtained by the UAV agent becomes higher, which shows that the UAV can intelligently plan its trajectory, so that when facing a growth in the number of SNs during the data collection, rewards can be obtained by the UAV with fewer action steps.

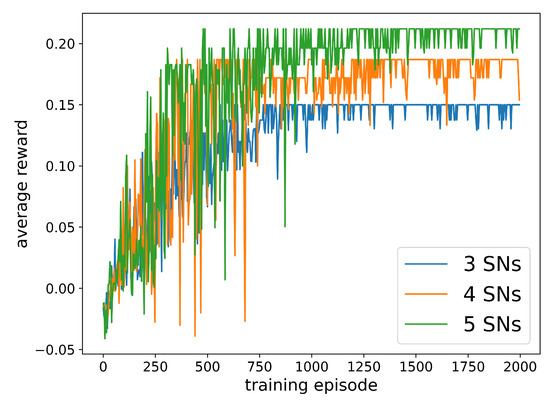
Figure 4. Convergence performance of DQN algorithm under different numbers of SNs.

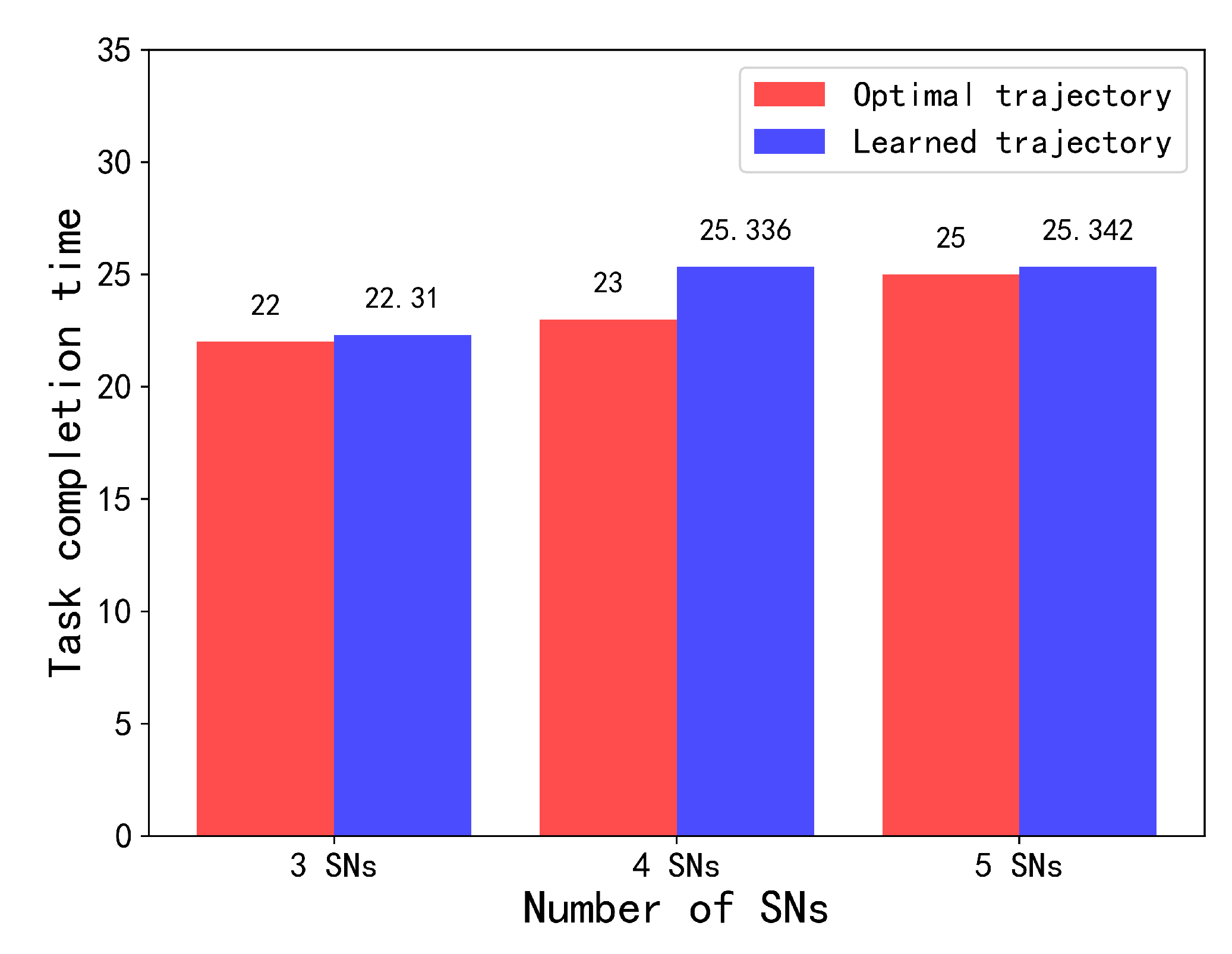
As shown in Figure 5, in the case of four SNs, the algorithm proposed in this chapter can achieve 90% of the performance of the benchmark DQN algorithm under the condition of known and precise location information, even in the presence of three and five SNs. In the scenario of networked devices, it reaches 98% of the performance of the benchmark DQN algorithm. The above shows that an increase in the number of SNs does not necessarily affect the performance of the algorithm.

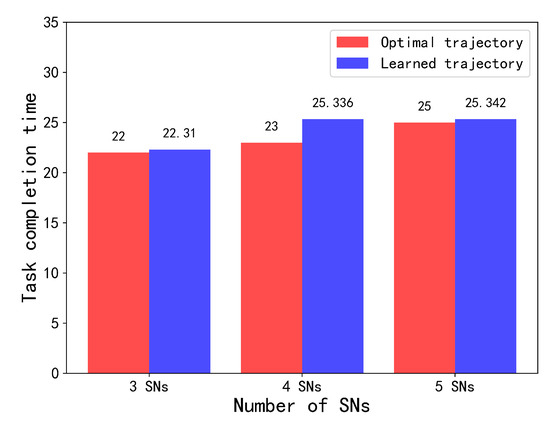
Figure 5. Comparison of the proposed algorithm and the baseline algorithm.

Then, we conduct a simulation experiment on the scenarios with uncertain SN locations. Table 1 sums up the major parameters of the DNN. We only know that each SN is located in an area composed of $2\times 2$ cells, but we cannot obtain its detailed location information. There are three SNs distributed within square areas of {[550, 650], [150, 250]}, {[250, 350], [450, 550]}, {[850, 950], and [850, 950]}, respectively. Specifically, each SN may be located in any of the four cells. To simplify the problem and make the algorithm more universal, we assume that the SNs are always located in the center of the cells. Therefore, we can collect data from the SNs without their precise location information being known.

Table 1. Major DNN parameters.

Simulation Parameters	Value
Learning rate	$\alpha$ = 0.0002
Maximum number of episodes	M = 16,640
Experience replay buffer capacity	$N=8\times {10}^5$
Discount factor	$\gamma$ = 0.9
Minibatch size	b = 128
Greedy index	$ϵ$ = 0.01
Target Q-network update cycle	B = 400
Maximum time slot per episode	$T_{max}$ = 500

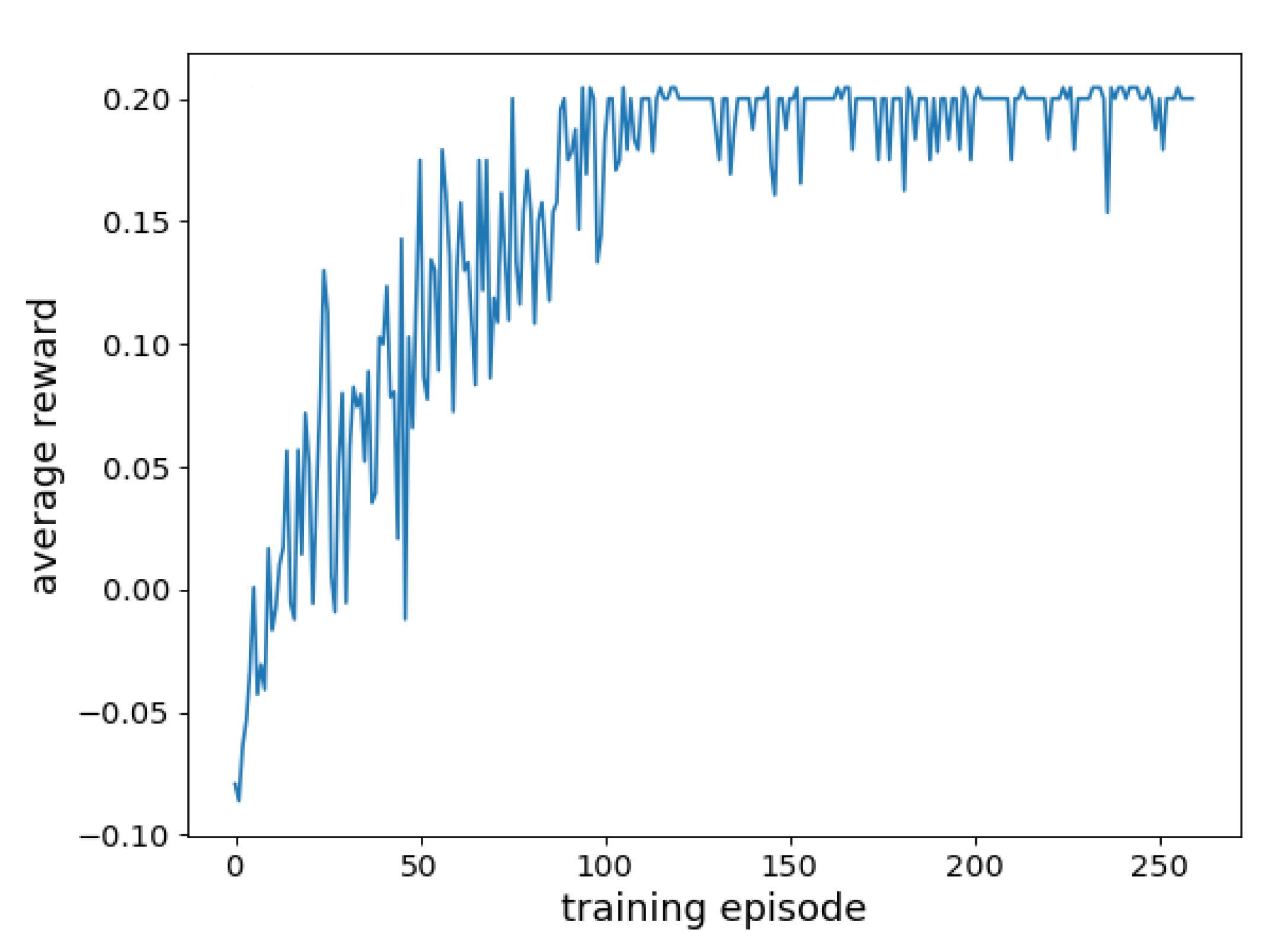
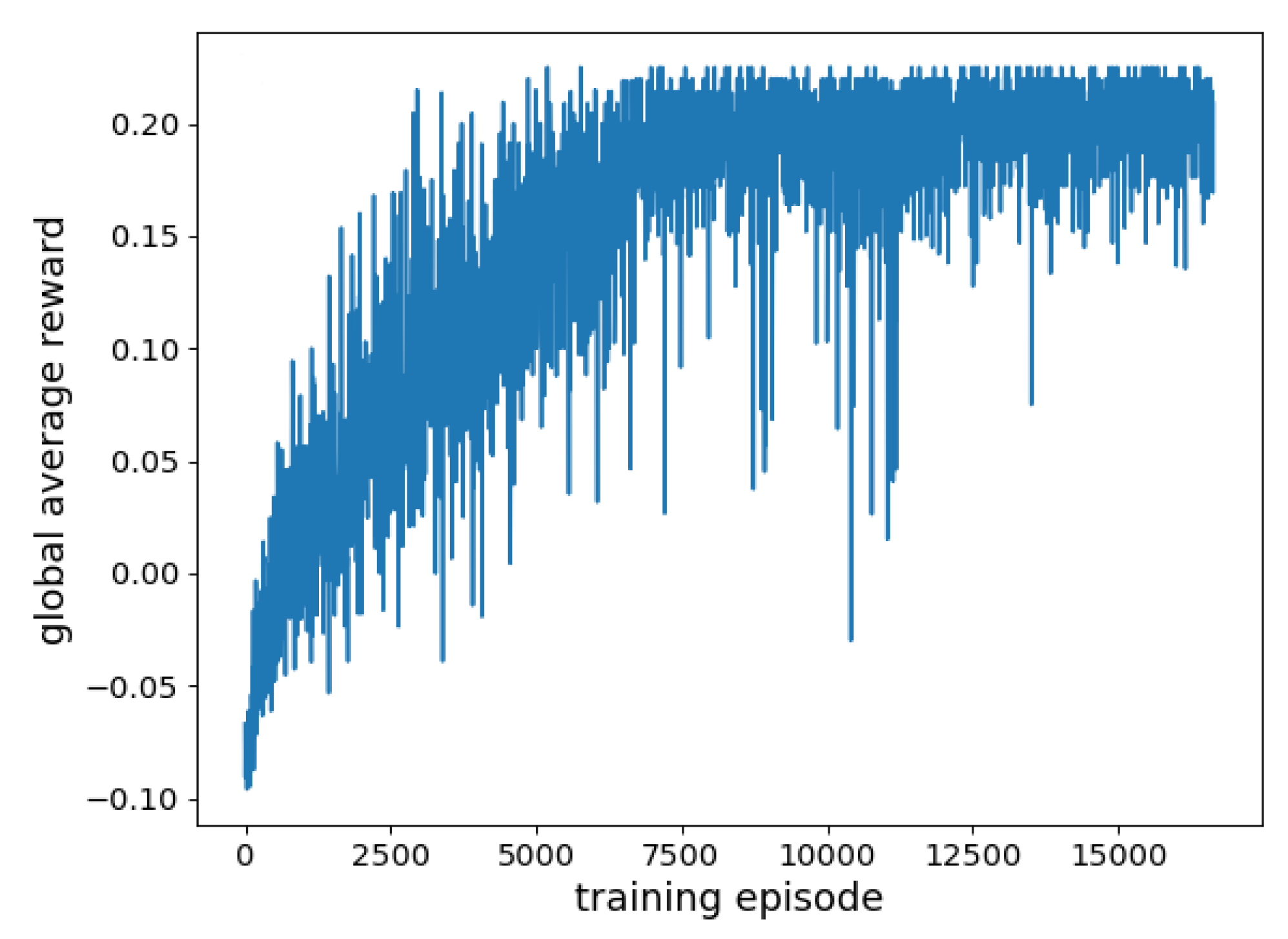
Figure 6 shows the convergence performance in a specific scenario, and the algorithm converges when training 150 episodes. Figure 7 shows the convergence performance in all possible scenarios. Because the proposed algorithm needs to apply to all possible scenarios, the average reward per round is not a specific value but an interval. The algorithm shows signs of convergence when training over 7500 rounds, but there are still fluctuations, and it finally converges at 12,000 episodes.

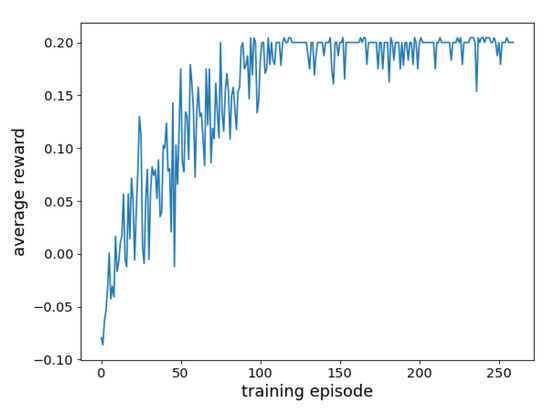
Figure 6. The convergence performance in a particular scenario.

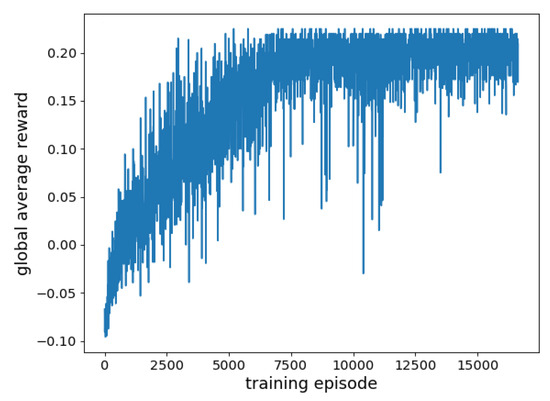
Figure 7. The convergence performance in all scenarios.

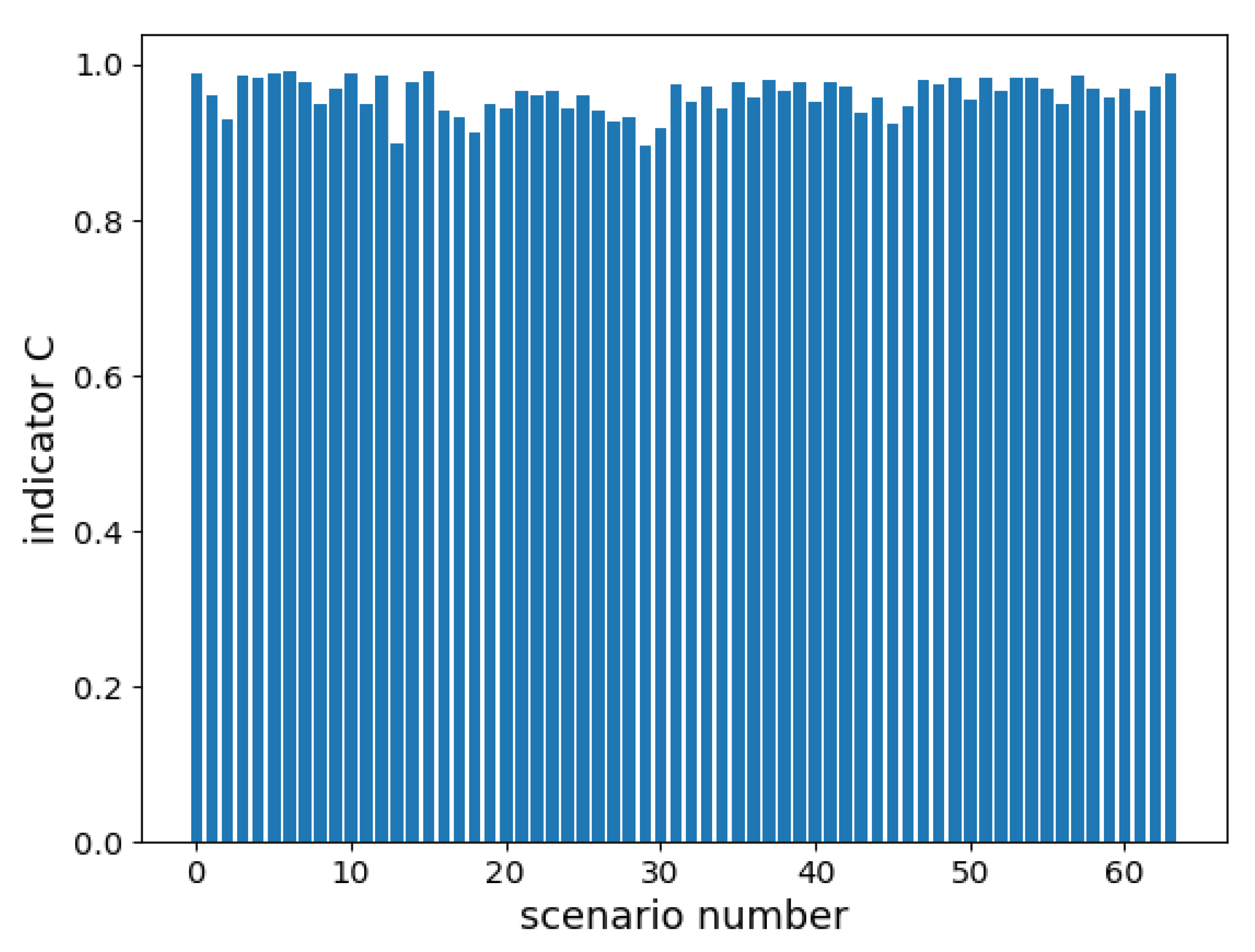
Figure 8 compares the performance of the proposal and benchmark algorithms with the precise position information known. We define the minimum task completion time with the precise position information perfectly known as $T_{min}$ and take the quotient of $T_{min}$ divided by the mission completion time as an indicator, C. The indicator C can be defined as

$$C=\frac{T_{min}}{T}.$$

(16)

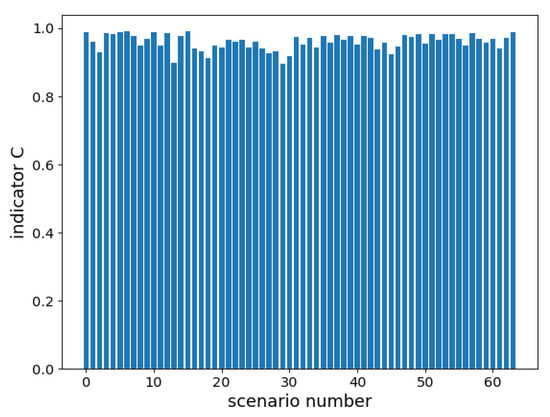
Figure 8. Comparison with the benchmark algorithm.

Obviously, if the performance of the proposed algorithm is satisfactory, C will be very close to 1. We use the data of the last 3200 episodes of the training process to generate this figure and test it 50 times on average in each possible scenario. The proposed algorithm can achieve 96.1% of the efficiency of the benchmark algorithm on average in all possible scenarios and 89.6% even in the worst-performing scenario.

5. Conclusions

Data collection is an essential task in photovoltaic systems as it can provide valuable information for fault detection, power prediction, load balancing, and other applications. In this paper, we investigate data collection in the UAV-assisted photovoltaic system to minimize data collection completion time without precise location information being known. We address the issue by proposing a novel data collection scheme based on DQN to acquire a satisfactory solution for the trajectory optimization. The optimization problem is formulated as an MDP, and the UAV agent interacts with the environment and receives rewards based on its actions. By learning in scenarios with different SN distributions, we demonstrate that the UAV agent can effectively adapt to changes in scenarios without expensive retraining or recollecting training data. We evaluate the proposed scheme in different scenarios with different sensor node distributions and compare it with benchmark algorithms. The performance of the proposal almost matches the performance of the benchmark algorithm with the precise position information known, which achieves 96.1% of the efficiency of the benchmark algorithm on average in all possible scenarios. The simulation results show the satisfactory convergence of the proposal and verify the effectiveness of the DQN-based scheme.