Tunneling Current Variations in Small-Sized Devices Based on a Compact Threshold Voltage Model

Abstract

Accurate modeling of threshold voltage is necessary in the integrated circuit design of strained silicon devices. Thoroughly researching the factors that affect threshold voltage and establishing a more precise threshold voltage model, can provide essential theoretical support for integrated circuit design. By solving a Poisson equation, in this paper, we demonstrate a comprehensive physical model for the threshold voltage of strained Si NMOSFETs using the gradual channel approximation theory and a quasi-two-dimensional analysis. The model investigates the physical effects such as short-channel, narrow-channel, non-uniform doping, and drain-induced barrier lowering effects on the threshold voltage. After substituting the extracted parameters into the model, a comparison was made with experimental results to validate the accuracy and correctness of the established model. Additionally, variations in the tunneling current of small-sized devices were studied. The two models provide essential references for the analysis and design of strained Si large-scale integrated circuits.

1. Introduction

Strained Si materials offer the advantages of high carrier mobility, adjustable band gap, and compatibility with the traditional Si process. They are the preferred alternative in research on high-speed, high-performance, scaled MOSFETs [1,2]. Threshold voltage is the most critical parameter of MOSFETs, and it affects the AC/DC and subthreshold characteristics of the device. Research on the threshold voltage of strained silicon devices is significant, as it determines the devices’ on-off characteristics. Studying the threshold voltage of strained silicon devices helps to understand their operating state and features and can lead to optimized device design and improved performance and reliability. As device dimensions continue to shrink, the influence of short-channel effect becomes more significant. Strained silicon devices can mitigate or suppress short-channel effect through strain engineering techniques, and the threshold voltage is a crucial parameter in studying these effects. Accurate control of the threshold voltage and accurate threshold voltage adjustment are crucial for process optimization and device fabrication. Researching the threshold voltage of strained silicon devices can facilitate the development of improved process methods and technologies, enabling more precise and stable control of threshold voltage, thereby enhancing process controllability and stability. When designing integrated circuits using strained silicon devices, it is necessary to have an accurate threshold voltage model. By delving into the factors that influence threshold voltage, more precise models can provide essential theoretical support for integrated circuit design and for optimizing performance to meet design requirements. So, research on the threshold voltage of strained silicon devices plays a significant role in optimizing device performance, suppressing short-channel effect, optimizing processes, and supporting integrated circuit design. In current state-of-the-art chip designs, to stop short-channel effect, advanced device designs are extensively used, and strained silicon devices are among these designs. Examples include Intel’s Core processor using 32 nm process technology and TSMC’s 7 nm process, where strained silicon technology has been implemented. This research is essential for advancing the development and application of strained silicon technology. There are many studies on the threshold voltage of strained Si NMOSFETs [3,4,5,6,7]. However, the influences of substrate bias, short-channel effect, narrow-channel effect, and drain-induced barrier lowering effect on threshold voltage have still not been fully considered, and therefore the results cannot be fully applied to the design requirements of devices and integrated circuits under realistic process conditions.

In this paper, a threshold voltage model of a long channel is built using the gradual channel approximation theory and the potential of the strain Si MOSFET longitudinal is analyzed. The influence of substrate bias on threshold voltage is fully considered in the model. However, a one-dimension method cannot meet the requirement of threshold voltage accuracy for scaled devices. To improve the threshold voltage accuracy, two-dimensional and quasi-two-dimensional analysis methods are often used [8,9]. When solving a two-dimensional Poisson equation in the depletion region utilizing a two-dimensional method, the physical meaning of model parameters is deficient due to some approximations made on boundary conditions. In this paper, a quasi-two-dimensional method is used to solve a two-dimensional Poisson equation. A threshold voltage model is built fully considering the short-channel effect, DIBL effect, and the narrow-channel effect. To ensure that the simulation results can better match test results, it is necessary to correct the model using process parameters [10]. So, an integrated physical compact model for threshold voltage of a strained Si NMOSFET is built fully considering the physical effects on threshold voltage.

Through experiments, devices of different sizes were fabricated under the same process conditions, and relevant parameters were extracted using parameter extraction software. The calculation results of the model were compared with the simulation results, which further proved the correctness of the threshold voltage intensive physical model of strained Si NMOSFETs established in this paper. The results provide an important reference for the analysis and design of strained Si devices and also provide an essential theoretical basis for further integrated circuit design.

Tunneling current is a crucial parameter in strained silicon devices, as it reflects the electron tunneling through the bandgap or energy barrier in the strained silicon structure. By studying tunneling current, the performance of a device under low-voltage conditions, including conduction capability, energy efficiency, and noise characteristics, can be evaluated. As device dimensions continue to shrink, tunneling current becomes more significant in strained silicon devices. Therefore, research on tunneling current is significant for limiting device size and achieving micro- and nanoscale devices. By understanding and controlling tunneling current, design and process optimization can be conducted to reduce the increase in tunneling current caused by size effects. Tunneling current is also a key factor that affects the reliability of strained silicon devices. Understanding the sources, characteristics, and mechanisms of tunneling current helps to find methods to reduce or suppress tunneling current, thus improving device reliability and reducing the probability of failure. Research on tunneling current in strained silicon devices provides a foundation for developing new technologies and applications. Understanding the characteristics and control methods of tunneling current can provide critical guidance and support for designing novel devices and developing new strained silicon technologies. In conclusion, studying tunneling current in strained silicon devices is important for evaluating performance, limiting device size, enhancing reliability, and advancing strained silicon technology. This research has a significant impact and guiding value in optimizing device design, improving processes, and promoting the application of strained silicon technology in the field of microelectronics.

2. Theoretical Model Derivation

Biaxial strain can significantly increase electron mobility and is widely used in strained Si NMOSFETs [11,12]. Figure 1 shows the sectional structure of a strained Si NMOSFET. A graded $SiGe$ layer with a Ge composition gradient is grown on the Si substrate, which can effectively reduce surface scattering and increase electron mobility. A thick relaxed $SiGe$ layer is grown on the graded $SiGe$ layer, serving as a virtual substrate. Finally, a very thin Si layer is epitaxially grown on the relaxed $SiGe$ layer, introducing tensile strain in the Si layer due to different lattice constants between the Si and $SiGe$ layers. S, G, D, and B represent the source, gate, drain, and substrate contacts, respectively. $T_{SSi}$ and $W_D$ are the thicknesses of the strained Si layer and substrate depletion layer, respectively. $N_{SSi}$ and $N_{SiGe}$ are the doping concentrations of the strained Si layer and relaxed $SiGe$ layer, respectively.

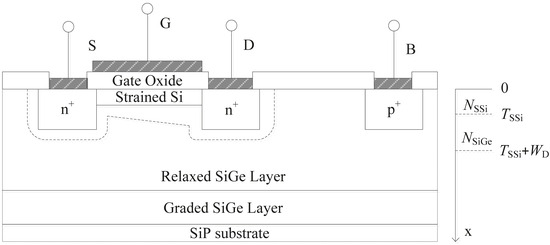
Figure 1. Cross-sectional structure of a strained Si NMOSFET.

2.1. Long-Channel Threshold Voltage Model

Strictly speaking, modeling a MOSFET is a three-dimensional problem. However, from a practical standpoint (unless the channel width W and channel length L are tiny), it can be approximated as a two-dimensional system, which means considering only the y-direction along the channel and the x-direction perpendicular to the channel. Additionally, if the variation in the electric field E_y along the y-direction is much smaller than that in the corresponding electric field E_x along the x-direction, the device can be treated using a one-dimensional approximation method.

2.1.1. Zero Substrate Bias Threshold Voltage Model ($V_{sb}=0$)

The device structure shown in Figure 1 establishes and solves a one-dimensional Poisson’s equation along the x-direction, perpendicular to the channel, when the substrate bias is zero, i.e., $V_{sb}=0$. Therefore, the threshold voltage model for strained Si NMOSFETs can be derived with long channels under zero substrate bias.

In the relaxed $SiGe$ layer, the strain from the $Si/SiGe$ quantum well causes it to relax. In the relaxed $SiGe$ layer, the electron concentration can be disregarded, and the Poisson’s equation can be established as follows:

$$\frac{d^2\varphi }{d{x}^2}=\frac{q{N}_{SiGe}}{{\epsilon }_{SiGe}}, \left(T_{SSi}<x<T_{SSi}+W_d\right),$$

(1)

Among them, $\varphi$ represents the potential with substrate B as the reference point and ${\epsilon }_{SiGe}$ represents the dielectric constant of the relaxed $SiGe$ layer. The boundary conditions are as follows:

$$E=-{\left.\frac{d\varphi }{dx}\right|}_{x=T_{SSi}+W_D}={\left.\varphi \right|}_{x=T_{SSi}+W_D}=0,$$

(2)

where E is the electric field intensity. By integrating Equation (1), we can obtain the electric field and electric potential of the layer as follows:

$$E\left(x\right)=-\frac{d\varphi }{dx}=-\frac{q{N}_{SiGe}}{{\epsilon }_{SiGe}}\left(x-T_{SSi}-W_D\right),$$

(3)

$$\varphi \left(x\right)=\frac{q{N}_{SiGe}}{2{\epsilon }_{SiGe}}{\left(x-T_{SSi}-W_D\right)}^2,$$

(4)

Therefore, when $x=T_{SSi}$, the electric field and electric potential at the surface of the relaxed $SiGe$ layer are, respectively:

$${\left.E\left(x\right)\right|}_{x=T_{SSi}^{+}}=-{\epsilon }_{SiGe}{\left.\frac{d\varphi }{dx}\right|}_{x=T_{SSi}^{+}}=\frac{q{N}_{SiGe}{W}_D}{{\epsilon }_{SiGe}},$$

(5)

$${\varphi }_1={\left.\varphi \right|}_{x=T_{SSi}}=\frac{q{N}_{SiGe}{W}_D^2}{{\epsilon }_{SiGe}},$$

(6)

For the strained Si layer, using the depletion approximation and ignoring the electron concentration, we can establish the one-dimensional Poisson’s equation as:

$$\frac{d^2\varphi }{d{x}^2}=\frac{q{N}_{SSi}}{{\epsilon }_{SSi}}, (0<x<T_{SSi}),$$

(7)

where ${\epsilon }_{SSi}$ is the dielectric constant of the strained Si layer. The boundary conditions are as follows:

$${\epsilon }_{SSi}{\left.\frac{d\varphi }{dx}\right|}_{x=T_{SSi}^{-}}={\epsilon }_{SiGe}{\left.\frac{d\varphi }{dx}\right|}_{x=T_{SSi}^{+}}=-q{N}_{SiGe}{W}_D,$$

(8)

$${\varphi }_1={\left.\varphi \right|}_{x=T_{SSi}}=\frac{q{N}_{SiGe}{W}_D^2}{2{\epsilon }_{SiGe}},$$

(9)

By integrating Equation (7), we can obtain the electric field and electric potential of the strained Si layer as follows:

$${\epsilon }_{SSi}\frac{d\varphi }{dx}=q{N}_{SSi}\left(x-T_{SSi}-\frac{N_{SiGe}}{N_{SSi}}{W}_D\right),$$

(10)

$$\phi \left(x\right)=\frac{q{N}_{SiGe}{W}_D^2}{2{\epsilon }_{SiGe}}+\frac{q{N}_{SSi}}{2{\epsilon }_{SSi}}\left\{{\left[x-\left(T_{SSi}+\frac{N_{SiGe}}{N_{SSi}}{W}_D\right)\right]}^2-{\left(\frac{N_{SiGe}}{N_{SSi}}{W}_D\right)}^2\right\},$$

(11)

The surface electric field and surface potential of the strained Si layer at the Si/SiO₂ interface are determined by the boundary conditions as:

$${\left.{\epsilon }_{SSi}\frac{d\varphi }{dx}\right|}_{x=0^{+}}=-q{N}_{SSi}\left(T_{SSi}+\frac{N_{SiGe}}{N_{SSi}}{W}_D\right),$$

(12)

$${\varphi }_s={\left.\varphi \right|}_{x=0}=\frac{q}{2{\epsilon }_{SSi}{\epsilon }_{SiGe}}\left({\epsilon }_{SSi}{N}_{SiGe}{W}_D^2+2{\epsilon }_{SiGe}{N}_{SiGe}{W}_D{T}_{SSi}+{\epsilon }_{SiGe}{N}_{SSi}{T}_{SSi}^2\right),$$

(13)

The depletion layer thickness in the relaxed $SiGe$ layer can be obtained from Equation (13) as follows:

$$W_D=\sqrt{\frac{2{\epsilon }_{SiGe}}{q{N}_{SiGe}}{\varphi }_s+\frac{{\epsilon }_{SiGe}}{{\epsilon }_{SSi}}\left(\frac{{\epsilon }_{SiGe}}{{\epsilon }_{SSi}}-\frac{N_{SSi}}{N_{SiGe}}\right)T_{SSi}^2}-\frac{{\epsilon }_{SiGe}}{{\epsilon }_{SSi}}{T}_{SSi},$$

(14)

Along the x-direction perpendicular to the channel, the applied gate voltage can be decomposed into the voltage drop across the gate oxide due to the equivalent total depletion charge, surface potential ${\phi }_s$, and flat-band voltage $V_{FB}$ [13]:

$$V_{GB}=V_{FB}+{\phi }_s-\frac{Q_B}{C_{ox}},$$

(15)

The total depletion charge $Q_B$ is the sum of the depletion charges in the strained Si layer and the relaxed SiGe layer, i.e., $Q_B=Q_{si}+Q_{SiGe}$:

$$Q_B=-q{N}_{SSi}{T}_{SSi}-q{N}_{SiGe}{W}_D,$$

(16)

By substituting Equations (14) and (16) into Equation (15), we can simplify and obtain:

$$V_{GB}=V_{FB}+{\phi }_s+{\gamma }_2\left(\sqrt{{\phi }_s+A_1}+A_2\right),$$

(17)

where the values of $A_1$, $A_2$, and ${\gamma }_2$ can be calculated using the following formulas:

$$A_1=\frac{q{N}_{SiGe}}{2{\epsilon }_{SSi}}\left(\frac{{\epsilon }_{SiGe}}{{\epsilon }_{SSi}}-\frac{N_{SSi}}{N_{SiGe}}\right)T_{SSi}^2,A_2=\sqrt{\frac{q}{2}}\left(\sqrt{\frac{N_{SSi}^2}{{\epsilon }_{SiGe}{N}_{SiGe}}}-\sqrt{\frac{{\epsilon }_{SiGe}{N}_{SiGe}}{{\epsilon }_{SSi}^2}}\right)T_{SSi},{\gamma }_2=\frac{\sqrt{2q{\epsilon }_{SiGe}}{N}_{SiGe}}{C_{ox}^{\prime }},$$

When ${\phi }_S$ is equal to the threshold surface potential, $V_{GB}=V_{TH0}$, where $V_{TH0}$ is the threshold voltage at zero substrate bias. Its expression is as follows:

$$V_{TH0}=V_{FB}+{\phi }_s+{\gamma }_2\left(\sqrt{{\phi }_s+A_1}+A_2\right).$$

(18)

2.1.2. The Effect of Substrate Bias on Threshold Voltage

If a reverse bias $V_{bs}$ is applied between the substrate and the source, the surface potential ${\varphi }_S$ with the source as the reference point can be determined as follows:

$${\varphi }_s={\phi }_s=V_{bs},$$

(19)

When the substrate bias is zero, ${\varphi }_s={\phi }_s \mathrm{and} V_{gs}=V_{gb}$. If the substrate bias is not zero, the threshold voltage is defined as the gate-source voltage ($V_{gs}$) at which the surface potential ${\varphi }_s$ equals the threshold surface potential, as obtained from Equation (18):

$$V_{TH}=V_{FB}+{\varphi }_s+{\gamma }_2\left(\sqrt{{\varphi }_s-V_{bs}+A_1}+A_2\right),$$

(20)

Substituting Equation (18) into Equation (20) yields the following result:

$$V_{TH}=V_{TH0}+∆V_{TH},$$

(21)

where $∆V_{TH}={\gamma }_2\left(\sqrt{{\varphi }_s-V_{bs}+A_1}-A_2\sqrt{{\varphi }_s+A_1}\right)$, taking into account the non-uniformity of substrate doping and the influence of substrate voltage [14], and introducing process fitting parameters $K_1$ and $K_2$, the threshold voltage equation for a long-channel strained Si NMOSFET, in this case, is as follows:

$$V_{TH.L}=V_{TH0}+K_1\left(\sqrt{{\varphi }_s-V_{bs}}-\sqrt{{\varphi }_s}\right)+K_2{V}_{bs}.$$

(22)

2.2. The Influences of Short-Channel Effect and Drain-Induced Barrier Lowering Effect on Threshold Voltage

As the device dimensions ($W$ and $L$) continue to decrease, the electric field along the channel direction becomes stronger. The assumption of a gradually varying channel no longer holds, and when L becomes comparable to the depletion region width at the source-drain junctions, the MOSFET is considered to be a short-channel device. In this case, the one-dimensional Poisson’s equation is no longer applicable. For the depleted region in the relaxed $SiGe$ layer, a quasi-two-dimensional analysis method is adopted to establish the threshold voltage model for short-channel strained Si NMOSFETs.

2.2.1. Establishment and Solution of the Quasi-Two-Dimensional Equations

As shown in Figure 2, a Gaussian box is established within the depleted region of $SiGe$, with a thickness of $X_{dep}$. The influence of the free electron concentration is neglected (depletion approximation). By integrating the four surfaces within the plane, the following equations can be obtained:

$${\epsilon }_{ox}\frac{V_{GS}-V_{FB}-V_2-V_S\left(y\right)}{T_{ox}}-{\epsilon }_{SiGe}\frac{X_{dep}}{\eta }\frac{d{E}_s\left(y\right)}{dy}=q{N}_{SiGe}{X}_{dep},$$

(23)

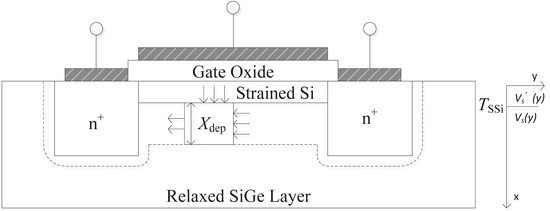
Figure 2. Schematic diagram of the strained $SiGe$ layer depletion region in a Gaussian box.

The first term on the left side of the above equation represents the electric flux entering the Gaussian box from the upper surface, and the second term represents the total electric flux entering the Gaussian box along the y-direction. The whole edge electric flux entering the Gaussian box is equal to the total ionized charge within the Gaussian box, as shown on the right side of the equation. At the bottom of the depleted region, the potential and electric field are both zero due to the connection with the substrate.

Here, $V_2$ is given by $V_2=\frac{q{N}_{SSi}{T}_{SSi}^2}{2{\epsilon }_{SSi}}+\frac{q{N}_{SSi}{T}_{SSi}{T}_{ox}}{{\epsilon }_{ox}}$, where $\eta$ is a fitting parameter related to the process and can be obtained through parameter extraction. The expression for $X_{dep}$ can be obtained by replacing ${\phi }_s$ with ${\varphi }_s-V_{bs}$ Equation (14) as follows:

$$X_{dep}=\sqrt{\frac{2{\epsilon }_{SiGe}}{q{N}_{SiGe}}\left({\varphi }_s-V_{bs}\right)+\frac{{\epsilon }_{SiGe}}{{\epsilon }_{SSi}}\left(\frac{{\epsilon }_{SiGe}}{{\epsilon }_{SSi}}-\frac{N_{SSi}}{N_{SiGe}}\right)T_{SSi}^2}-\frac{{\epsilon }_{SiGe}}{{\epsilon }_{SSi}}{T}_{SSi},$$

(24)

The boundary conditions for Equation (23) are $V_s\left(0\right)=V_{bi} \mathrm{and} V_s\left(L\right)=V_{bi}+V_{DS}$. The solution is given by:

$$V_s\left(y\right)=V_{SL}+\left(V_{bi}+V_{DS}-V_{SL}\right)\frac{\sinh \left(y/l\right)}{\sinh \left(L/l\right)}+\left(V_{bi}-V_{SL}\right)\frac{\sin \mathrm{h}\left(\frac{L-y}{l}\right)}{\sin \mathrm{h}\left(L/l\right)},$$

(25)

The equation $V_{bi}=\frac{kT}{q}\log \left(\frac{N_{SD}{N}_{SiGe}}{n{i}_{SiGe}^2}\right)$ represents the built-in voltage, where $N_{SD}$ is the doping concentration of the source/drain region and $n{i}_{SiGe}$ is the doping concentration of the relaxed $SiGe$ layer. In this equation, $V_{SL}=V_{GS}-V_{FB}-V_2-\frac{q{N}_{SiGe}{X}_{dep}{T}_{ox}}{{\epsilon }_{ox}}$, $k$ represents the Boltzmann constant, $l=\sqrt{\frac{{\epsilon }_{SiGe}{T}_{ox}{X}_{dep}}{{\epsilon }_{ox}\eta }}$, $T$ is the temperature, and $q$ is the charge of an electron. In the strained Si NMOSFET with the strained Si layer, the surface potential is $V_s\left(y\right)$ at the surface of the depletion layer in the relaxed $SiGe$ layer. Assuming the strained Si layer is thin, we can approximately treat it as a one-dimensional structure:

$$V_S^{\prime }\left(y\right)=V_{SL}^{\prime }+\left(V_{bi}+V_{DS}-V_{SL}\right)\frac{\sinh \left(y/l\right)}{\sinh \left(L/l\right)}+\left(V_{bi}-V_{SL}\right)\frac{\sin \mathrm{h}\left(\frac{L-y}{l}\right)}{\sin \mathrm{h}\left(L/l\right)},$$

(26)

where $V_{SL}^{\prime }=V_{GS}-V_{TH0}={\varphi }_s$ represents the surface potential of the long-channel strained Si NMOSFET.

2.2.2. Threshold Voltage

As shown in Equation (26), the surface potential can be minimized along the y-direction. The surface potential at $y=y_0$ is referred to as the threshold surface potential, and the corresponding gate-source voltage is the threshold voltage. By taking the derivative of Equation (26) with respect to y and finding the zero-crossing point, the surface potential at that point will be the minimum surface potential:

$$V_{Smin}=V_{SL}^{\prime }+\left[2\left(V_{bi}-V_{SL}\right)+V_{DS}\right]\frac{\sin \mathrm{h}\left(L/2l\right)}{\sin \mathrm{h}\left(L/l\right)},$$

(27)

When $V_{Smn}={\varphi }_s \mathrm{and}$ $V_{gs}=V_{th}$, substituting this condition into Equation (27) and rearranging, we can obtain:

$$V_{th}=V_{TH0}-\mathsf{\Delta }{V}_{th},$$

(28)

where $\mathsf{\Delta }{V}_{th}=\frac{2\left(V_{bi}-{\phi }_s+V_1\right)+V_{DS}}{2\cosh \left(L/2l\right)-2}$. In the expression for $\mathsf{\Delta }{V}_{th}$, the first term in the numerator can be attributed to the short-channel effect (SCE), which represents the influence of the change in channel length on the threshold voltage when $V_{DS}$ is constant. The second term in the numerator can be attributed to the drain-induced barrier lowering (DIBL) effect, which represents the influence of the change in $V_{DS}$ on the threshold voltage as the channel length varies; then, $\mathsf{\Delta }{V}_{th}=\mathsf{\Delta }{V}_{th}\left(SCE\right)+\mathsf{\Delta }{V}_{th}\left(DIBL\right)$. Considering the impact of the process, we introduce process parameters [14] $K_5$, $K_6$, $K_7$, $K_8$, $K_9$, and $K_{10}$, which are obtained through parameter extraction. Therefore, the influences of the SCE and DIBL effect on the threshold voltage can be expressed as:

$$\mathsf{\Delta }{V}_{th}\left(SCE\right)=-\frac{0.5K_5}{\cosh \left(K_6\frac{L_{eff}}{l_t}\right)-1}\left(V_{bi}-{\varphi }_s+V_1\right),$$

(29)

$$\mathsf{\Delta }{V}_{th}\left(DIBL\right)=-\frac{0.5}{\cosh \left(K_7\frac{L_{eff}}{l_{t0}}\right)-1}\left(K_8+K_9{V}_{bs}\right)V_{ds},$$

(30)

where $X_{dep0}=\sqrt{\frac{2{\epsilon }_{SiGe}}{q{N}_{SiGe}}{\varphi }_s+\frac{{\epsilon }_{SiGe}}{{\epsilon }_{SSi}}\left(\frac{{\epsilon }_{SiGe}}{{\epsilon }_{SSi}}-\frac{N_{SSi}}{N_{SiGe}}\right)T_{SSi}^2}-\frac{{\epsilon }_{SiGe}}{{\epsilon }_{SSi}}{T}_{SSi}$ in Equation (29), $K_6$ is substituted for ${\eta }^{-1/2}$, $l_{t0}=\sqrt{\frac{{\epsilon }_{SiGe}{T}_{ox}{X}_{dep0}}{{\epsilon }_{ox}}}$, and $l_t=\sqrt{\frac{{\epsilon }_{SiGe}{T}_{ox}{X}_{dep}}{{\epsilon }_{ox}}}\left(1+K_{10}{V}_{bs}\right)$.

2.3. The Influence of Narrow-Channel Effect on Threshold Voltage

As shown in Figure 3, in the strained Si NMOSFET device process, there exists a conical oxide transition region between the thin gate oxide layer and the thick field oxide layer, which is referred to as a bird’s beak. When the gate voltage is applied, a gate-controlled depletion region is formed at the edge transition region of the device. The total additional depletion charge caused by the gate voltage at the device edge is $\mathsf{\Delta }{Q}_W$ ($0.5\mathsf{\Delta }{Q}_W$ for each edge). If the channel width W of the device is much larger than the depletion layer width, $X_{dep}$ caused by the gate and the additional depletion charge $\mathsf{\Delta }{Q}_W$ caused by the gate voltage can be neglected compared to the total depletion charge $Q_B$. However, if W is comparable to $X_{dep}$, the extra charge $\mathsf{\Delta }{Q}_W$ cannot be ignored, resulting in an increase in the threshold voltage. The increment of threshold voltage is given by $\mathsf{\Delta }{V}_{th,W}=\mathsf{\Delta }{Q}_W/C_{ox}$, which means that as W decreases, while L remains constant, $V_{th}$ increases. To facilitate circuit simulation, different approximations are made for the shape of the depletion region. It is found that $\mathsf{\Delta }{V}_{th,W}$ is inversely proportional to the device width W and directly proportional to the thickness of the gate oxide layer and the surface potential under strong inversion conditions. Further considerations are given to the substrate bias $V_{bs}$ and the specific process effects, resulting in the development of a semi-empirical $\mathsf{\Delta }{V}_{th,W}$ model:

$$\mathsf{\Delta }{V}_{th,W}=\left(K_3+K_4{V}_{bs}\right)\frac{T_{ox}}{W_{eff}}{\varphi }_s,$$

(31)

$\mathrm{where} K_3$ and $K_4$ are process-fitting parameters, which are obtained through parameter extraction.

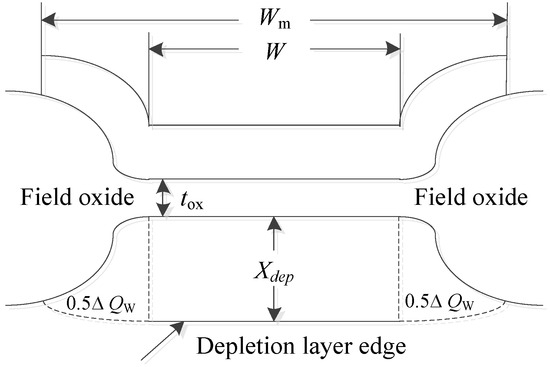
Figure 3. Cross-sectional diagram of a narrow-channel device in the width direction.

2.4. Complete Threshold Voltage Model

Based on the analysis of threshold voltage in long channel devices, the influences of substrate bias, short-channel effect, drain-induced barrier lowering effect, and narrow-channel effect on threshold voltage were studied. Considering all the factors related to threshold voltage, the complete threshold voltage of a strained Si NMOSFET is determined as:

$$V_{TH}=V_{TH,L}+\mathsf{\Delta }{V}_{th}\left(SCE\right)+\mathsf{\Delta }{V}_{th}\left(DIBL\right)+\mathsf{\Delta }{V}_{th,W},$$

(32)

Among them, the expressions for $V_{TH,L}$, $\mathsf{\Delta }{V}_{th}\left(SCE\right)$, $\mathsf{\Delta }{V}_{th}\left(DIBL\right)$, and $\mathsf{\Delta }{V}_{th,W}$ are given by Equations (22) and (29)–(31), respectively. By substituting these expressions into Equation (32), we can obtain the complete expression for the threshold voltage of a strained Si NMOSFET as:

$$\begin{gathered} V_{TH}=V_{TH0}+K_1\left(\sqrt{{\varphi }_s-V_{bs}}-\sqrt{{\varphi }_s}\right)+K_2{V}_{bs}+\left(K_3+K_4{V}_{bs}\right)\frac{T_{ox}}{W_{eff}}{\varphi }_s \\ -0.5\frac{K_5}{\cosh \left(K_6\frac{L_{eff}}{l_t}\right)-1}\left(V_{bi}-{\varphi }_s+V_1\right)-\frac{0.5}{\cosh \left(K_7\frac{L_{eff}}{l_{t0}}\right)-1}\times \left(K_8+K_9·V_{bs}\right)·V_{ds}. \end{gathered}$$

(33)

3. Tunneling Current Model

When MOSFET devices are scaled down proportionally, tunneling current significantly deteriorates the devices’ performances. To illustrate the impact of tunneling current, it is further explained through Figure 4, Figure 5 and Figure 6. Figure 4 depicts the device’s structural model, while Figure 5 and Figure 6 illustrate the principles of tunneling current and the composition of tunneling current, respectively.

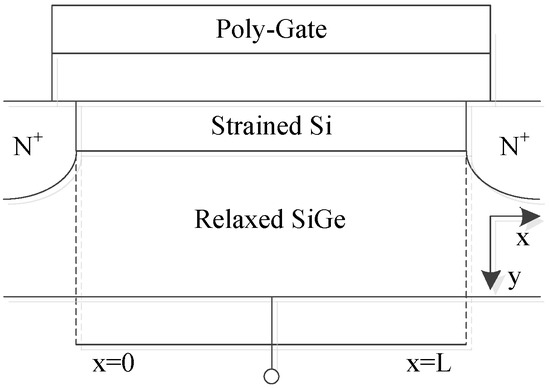
Figure 4. Schematic diagram of a strained Si/SiGe MOSFET’s structure.

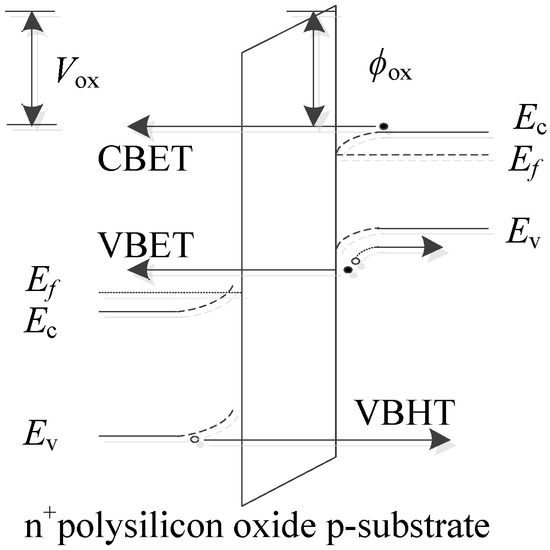
Figure 5. Subthreshold characteristics of tunneling current.

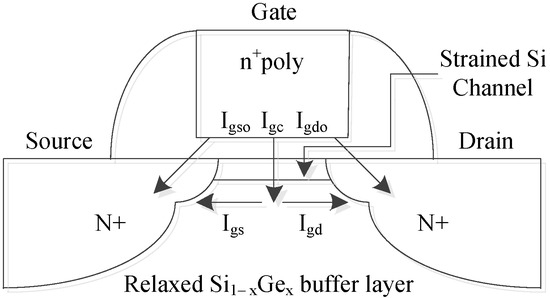
Figure 6. Composition of tunneling current.

There are three direct tunneling mechanisms in strained silicon MOSFET devices: (1) electron tunneling from the strained silicon conduction band to the gate conduction band (CBET), (2) hole tunneling from the strained silicon valence band to the gate valence band (VBET), and (3) hole tunneling from the strained silicon valence band to the gate conduction band (VBHT).

However, in a strained silicon device with a Poly-Si/SiO₂/SSi system, electrons cannot tunnel from the valence band to the conduction band, and holes also cannot tunnel. Therefore, the VBET and VBHT current components are negligible and can be ignored. The gate direct tunneling current in a strained silicon MOSFET device is mainly due to CBET and can be modeled as such [15]:

$$J_{DT}=J_G\approx J_{CBET}=A{\left(\frac{V_{ox}}{T_{ox}}\right)}^2·\exp \left[-B{\left(\frac{V_{ox}}{T_{ox}}\right)}^{-1}\times \left(1-{\left(1-\frac{V_{ox}}{T_{ox}}\right)}^{\frac{3}{2}}\right)\right],$$

(34)

where $J_{DT}$ represents the direct tunneling current density, ${\varphi }_{ox}$ represents the barrier height, $T_{ox}$ represents the oxide layer thickness, and A and B are physical parameters with values of $A=q^3/16\pi \hslash {\varphi }_{ox}$ and $B=\frac{4\sqrt{2m^{*}}{\varphi }_{ox}^{3/2}}{3\hslash q}$, respectively. Here, $\hslash$ represents the Planck constant, and $m^{*}$ represents the effective mass of electrons in the strained silicon conduction band. Therefore, when assuming $1-{(1-\frac{V_{ox}}{{\phi }_{ox}})}^{\frac{3}{2}}\approx 1$, the gate tunneling current at the point can be approximated as:

$$J_G\left(x\right)\approx A{E}_{ox}^2{e}^{-B/E_{ox}}\approx A{E}_{oxs}^2{e}^{-B{T}_{ox}/\left(V_{oxs}-V\left(x\right)\right)}\equiv J_{G0}{e}^{-B^{*}V\left(x\right)},$$

(35)

In the equation, $J_{G0}$ represents the gate tunneling current density at $V_{DS}=0$; $B^{*}=\frac{pB{T}_{ox}}{V_{oxs}^2}$, where $p$ is an adjustment parameter with a default value of 1; $V_{oxs}=V_{GS}$ represents the gate-to-source voltage at $x=0$; $E_{ox}=V_{ox}/T_{ox}$. If the gate leakage current is much smaller than the drain current, then:

$$\begin{gathered} V\left(x\right)=V_{GS}-V_{TH}-\sqrt{{(V_{GS}-V_{TH})}^2-2\left(V_{GS}-V_{TH}-\frac{V_{DS}}{2}\right)V_{DS}·\frac{x}{L}} \\ \approx \left(V_{GS}-V_{TH}-V_{DS}/2\right)·V_{DS}/\left(V_{GS}-V_{TH}\right)L·x, \end{gathered}$$

(36)

In Equation (36), an approximate form is used to describe the characteristics of small-sized devices. This approximation is correct and reasonable when the value is very small or huge.

To more accurately represent tunneling current, the total gate tunneling current can be expressed in integral form as:

$$I_G=W{{\displaystyle \int }}_0^L{J}_G\left(x\right)dx=\left(WL\right)·\frac{{{\displaystyle \int }}_0^L{J}_G\left(x\right)dx}{{{\displaystyle \int }}_0^{L}dx}=\left(WL\right)·⟨J_G\left(x\right)⟩,$$

(37)

According to the mathematical definition of the average value, $⟨x⟩={{\displaystyle \int }}_0^{y}xdx/{{\displaystyle \int }}_0^{y}dx$, the current intensity is equal to the product of current density and area. From Equation (37), we can obtain $I_G=⟨W{{\displaystyle \int }}_0^L{J}_G\left(x\right)dx⟩=⟨I_G\left(x\right)⟩$. For the method of integrating to solve tunneling current, its physical interpretation is that the total current intensity is the product of the gate oxide interface area $\left(W·L\right)$ and the average current density $⟨J_G\left(x\right)⟩$ passing through the interface. Here, $J_G\left(x\right)=J_{G0}{e}^{-B^{*}V\left(x\right)}$ represents the gate tunneling current density at position $x$.

By using Equations (35) and (36) and the integral formula $I_G=W{{\displaystyle \int }}_0^L{J}_G\left(x\right)dx$, if we let $-B^{*}k=p$, where $k=\left(V_{GS}-V_{TH}-V_{DS}/2\right)V_{DS}/\left(V_{GS}-V_{TH}\right)L$, we can obtain the total gate tunneling current as:

$$\begin{gathered} I_G=W{{\displaystyle \int }}_0^L{J}_{G0}{e}^{px}dx=J_{G0}W\frac{1}{p}\left(e^{pL}-1\right)=\frac{J_{G0}W}{p}{e}^{pL}-\frac{J_{G0}W}{p}= \\ \frac{J_{G0}WL\left(V_{TH}-V_{GS}\right)}{B^{*}\left[\left(V_{GS}-V_{TH}\right)V_{DS}-\frac{V_{DS}^2}{2}\right]}\exp \left(\frac{-B^{*}{V}_{DS}\left(V_{GS}-V_{TH}-\frac{V_{DS}}{2}\right)}{V_{GS}-V_{TH}}\right)+\frac{J_{G0}WL\left(V_{GS}-V_{TH}\right)}{B^{*}\left[\left(V_{GS}-V_{TH}\right)V_{DS}-\frac{V_{DS}^2}{2}\right]}, \end{gathered}$$

(38)

Combining Equation (33), we can obtain the complete tunneling current model for strained Si devices under small-size effects.

4. Simulation Experiment

4.1. Experimental Parameters

The comprehensive threshold voltage compact physical model is based on strained Si NMOSFETs, and the relevant process parameters $V_{TH0} \mathrm{and} K_1-K_{10}$ are extracted using the corresponding parameter extraction software. The units and specific parameter values of these process parameters are shown in Table 1.

Table 1. Parameter extraction results.

Process Parameters	Parameter Value
$V_{TH0}/V$	0.701
$K_1/V^{1/2}$	0.438
$K_2$	0.011
$K_3$	2.25
$K_4/V^{-1}$	−0.018
$K_5$	2.28
$K_6$	0.53
$K_7$	0.46
$K_8$	0.069
$K_9/V^{-1}$	−0.021
$K_{10}/V^{-1}$	−0.032

To demonstrate the correctness of the tunneling current model, devices with gate lengths ranging from 40 nm to 90 nm were selected for experimentation. Table 2 shows the physical parameters of these devices.

Table 2. Physical parameters.

Name	Parameters	Values
Gate length	Lmin (nm)	90	75	65	53	45	40
Channel length	Lch (nm)	65	53	45	37	32	28
Overlap dimension length	Lg.ov (nm)	12.5	11.0	10.0	8.0	6.5	6.0
Oxide layer thickness	Tox (nm)	1.3	1.2	1.1	0.9	0.8	0.7
Supply voltage	VDD (V)	1.2	1.1	1.0	1.0	0.9	0.9
Threshold voltage	VTH (V)	0.35	0.33	0.32	0.30	0.28	0.27
Junction depth	Xj (nm)	71.5	58.5	49.5	36.0	35.5	31.5
Substrate dopant concentration	Nsub (1019 cm−3)	0.4	0.6	0.8	1.1	1.4	1.6
Transition depth	Xtr (nm)	35	29	25	18	18	16
Channel dopant concentration	Nch (1018 cm−3)	1.15	1.15	2.0	2.0	2.0	3.0
Gate dopant concentration	Ngate (1020 cm−3)	0.92	0.92	1.14	1.5	1.66	1.66

To comply with the MOSIS deep submicron minimum transistor sizing design rules [16], for a gate length $L_d$ at a technology node, the width of the NMOSFET is set as $W_N=2.5L_d$. In the present study, the width ratio of $W_P/W_N$ is set to 2.20 for all technology nodes and kept constant. Therefore, the width of the PMOSFET is $W_P=5.5L_d$. Table 3 displays the BSIM4 MOSFET model parameters AIGSD, BIGSD, CIGSD, AIGC, BIGC, and CIGC used for calculating the gate tunneling current.

Table 3. The BSIM4 model parameters.

	AIGSD	BIGSD	CIGSD	AIGC	BIGC	CIGC
NMOSFET	0.016	0.002	0.04	0.0164	0.0035	0.08
PMOSFET	0.011	0.001	0.08	0.011	0.0015	0.08

4.2. Experimental Results

Simulations were conducted on the gate and drain currents of an NMOSFET and a PMOSFET under certain bias conditions. The results for the NMOSFET are shown in Figure 7, Figure 8, Figure 9 and Figure 10, while the results for the PMOSFET are shown in Figure 11, Figure 12, Figure 13 and Figure 14. Since the trend of gate tunneling current variation is similar between NMOSFETs and PMOSFETs, in this article, we only used an NMOSFET as an example to illustrate the changes in gate tunneling current for the two different gate states [17].

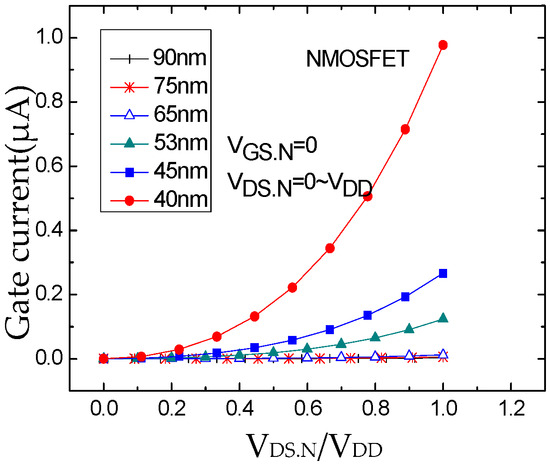
Figure 7. Gate current at V_GS.N = 0.

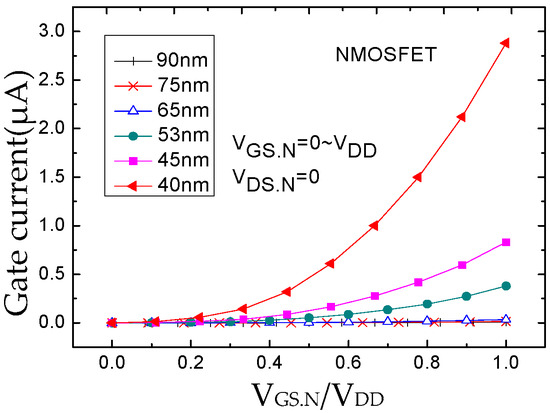
Figure 8. Gate current at V_DS.N = 0.

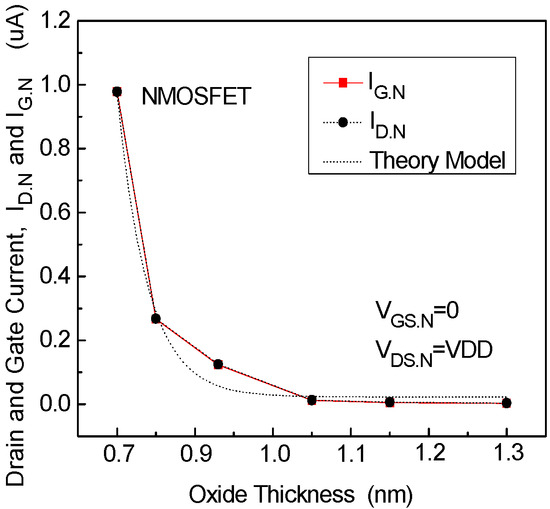
Figure 9. Trends for V_GS.N = 0 and V_DS.N = V_DD.

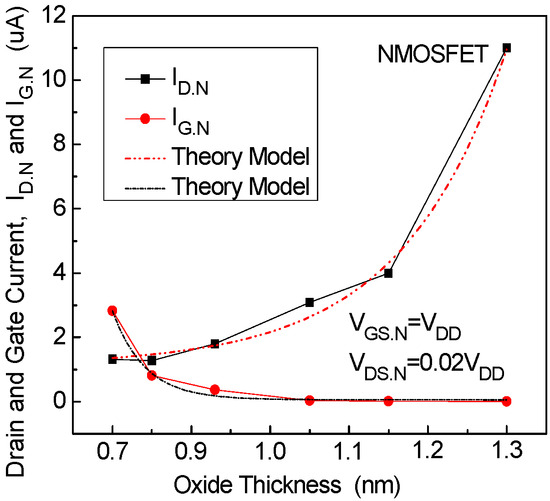
Figure 10. Trends for V_GS.N = V_DD and V_DS.N = 0.02 V_DD.

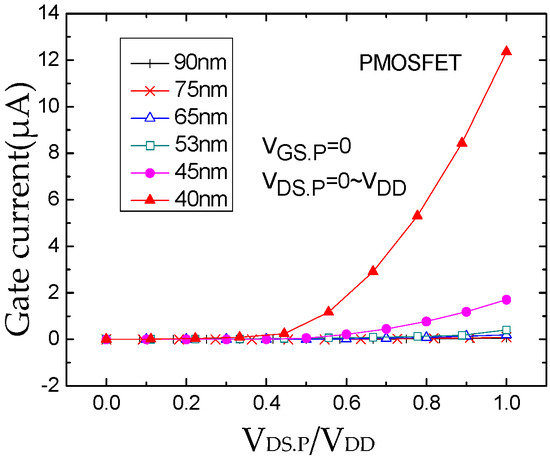
Figure 11. Gate current at V_GS.P = 0.

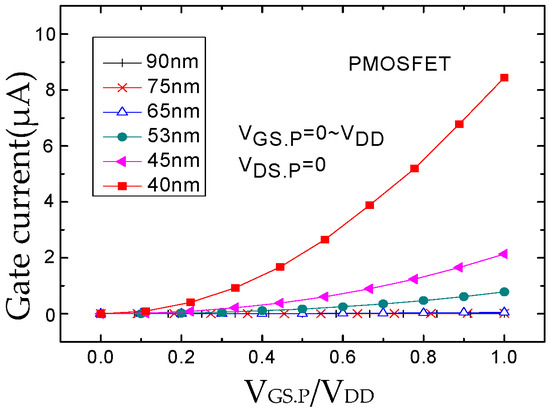
Figure 12. Gate current at V_DS.P = 0.

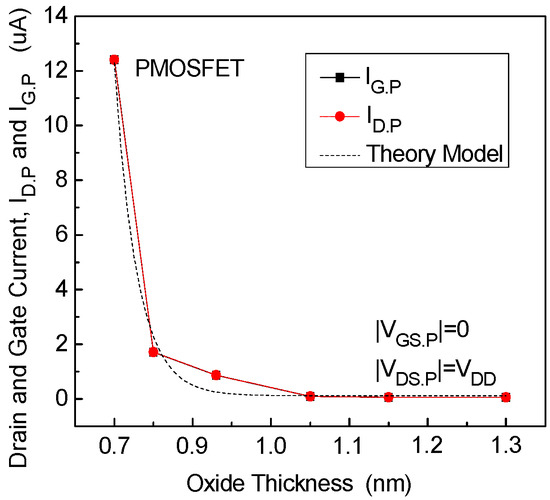
Figure 13. Trends for V_GS.P = 0 and V_DS.P = V_DD.

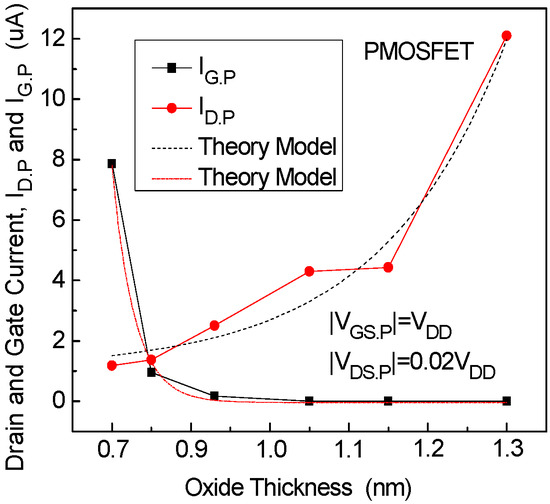
Figure 14. Trends for V_GS.P = V_DD and V_DS.P = 0.02 V_DD.

The simulation results for the NMOSFET and the PMOSFET under two different gate states are shown in Figure 7, Figure 8, Figure 9 and Figure 10. Figure 7 displays the simulation results for the NMOSFET biased in $V_{GS.N}=0$ and $V_{DS.N}=0~V_{DD}$. From the figures, it can be observed that the gate tunneling current for devices with gate lengths ranging from 90 nm to 65 nm remains nearly constant as the normalized drain-source voltage varies from 0 to 1.0 V. However, for devices with gate lengths ranging from 53 nm to 40 nm, the gate tunneling current exhibits an apparent exponential increase. As the gate length decreases, i.e., as the oxide layer thickness becomes thinner, the gate tunneling current increases more rapidly. With a reduction in gate oxide layer thickness, the gate tunneling current increases from 10⁻⁹ A to 10⁻⁶ A, approximately three orders of magnitude, for devices with gate lengths ranging from 90 nm to 40 nm. Figure 8 depicts the simulation results for an NMOSFET under another gate state, $V_{DS.N}=0$ and $V_{GS.N}=0~V_{DD}$, illustrating a similar conclusion. However, the gate tunneling current is greater at $V_{DS.N}=0$ compared to $V_{GS.N}=0$.

Figure 11 depicts the contour plot of gate current ($I_{G.N}$) and drain current ($I_{D.N}$) or the NMOSFET biased at gate state $V_{GS.N}=0$ and drain state $V_{DS.N}=V_{DD}$. For all devices with oxide thickness ranging from 0.7 nm to 1.3 nm under this gate state, both the rectangular-point line representing $I_{G.N}$ and the circular-point line describing $I_{D.N}$ exhibit similar trends. The magnitude of the drain current $I_{D.N}$ is approximately equal to the gate current $I_{G.N}$. The dashed line represents the theoretical variation curve obtained from Equation (38) of the model, which matches the exponential increase observed in the simulation results. This confirms the effectiveness of the proposed model (Equation (38)). The drain current $I_{D.N}$ of devices with gate lengths ranging from 90 nm to 40 nm also increases by approximately three orders of magnitude due to the influence of gate tunneling current, as indicated in Figure 7.

In Figure 12, the NMOSFET is biased at gate state $V_{GS.N}=V_{DD}$ and $V_{DS.N}=0.02V_{DD}$, and is operating in the linear bias region. The simulation results show that, for all devices with oxide thickness ranging from 0.7 nm to 1.3 nm, the circular-point line representing $I_{G.N}$ and the rectangular-point line representing $I_{D.N}$ exhibit inverse variations, consistent with the model (Equation (38)). The two dashed lines in Figure 12 represent the theoretical results obtained from the model. Notably, for gate lengths ranging from 90 nm to 53 nm, the gate current $I_{G.N}$ is significantly smaller than the drain current $I_{D.N}$. For the 45 nm gate length device, the values of $I_{G.N}$ and $I_{D.N}$ are approximately equal, while for the 40 nm gate length device, $I_{G.N}$ is smaller than $I_{D.N}$. These experimental results align with the derived model and support the conclusions drawn from Equation (38). Figure 9, Figure 10, Figure 13 and Figure 14 show the experimental results for the PMOSFET corresponding to the two gate states of the NMOSFET, which are similar to the NMOSFET results and are not further elaborated in the article.

5. Conclusions

In this article, we focus on strained Si NMOSFET devices. We investigate the influences of substrate bias, short-channel effect, and drain-induced barrier lowering effect on threshold voltage, based on the gradual channel approximation and a quasi-two-dimensional Poisson equation. The influence of narrow-channel effect is also studied in detail, and a comprehensive physical model for the threshold voltage is established. The threshold voltage-related parameters are extracted through experiments. Subsequently, the influences of short-channel effect, narrow-channel effect, drain-induced barrier lowering effect, and substrate bias on threshold voltage are discussed in detail. When the drain-source voltage is biased at $V_{ds}=1.2 \mathrm{V}$, the short-channel effect and drain-induced barrier lowering effect cause a threshold voltage shift of 18.57%; a change in channel width results in a threshold voltage shift of 2.75% (as shown in Figure 15); and when the substrate bias is set to $V_{bs}=1.2 \mathrm{V}$, the threshold voltage shifts by 27.22%. Based on the threshold voltage model in this article, we explore the tunneling current in off-state, and provide the experimental results. Future research should involve establishing corresponding models for other structures and smaller-sized devices. The developed physical models for the threshold voltage and tunneling current of strained Si NMOSFETs provide important references for the analysis and design of strained Si large-scale integrated circuits.

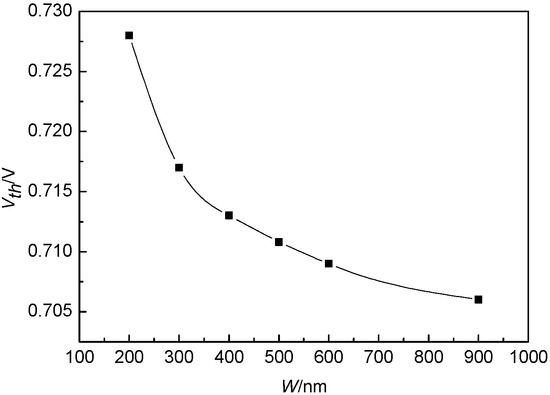
Figure 15. The variation in threshold voltage with channel width.