Abstract
In this paper, we consider a continuous-time differential game of non-renewable resource extraction with n players and assume that the terminal conditions of the game vary. To characterize the gain that the players obtain by using precise information, we use the notion of value of information in relation to the knowledge of terminal conditions. The stated problem is studied for two cases, a linear and a nonlinear one. The obtained results are illustrated for the real values of the parameters.
1. Introduction
In the problems of resource exploitation, information about resource availability plays a key role as it influences the future profit of the company [1,2]. The information about the boundary conditions influences the choice of the control strategy and the amount of the profit gained. To quantify the gain obtained from knowing more precise information, we use the characteristic dubbed value of information (VoI). For more information and examples of the use of the value of information in resource-extraction applications, we refer the interested reader to the papers [3,4]. Despite a substantial number of papers devoted to the concept of value of information, its role in the analysis of specific problems of resource extraction is still insufficiently studied. Thus, there is a clear need for a further investigation of the subject.
In this paper, we further develop the line of research initiated in the papers [5,6] as well as more recent research [7,8], and we consider the problem of determining the value of information in a continuous-time differential game of non-renewable resource extraction with n agents (players). In this particular case, we assume that the terminal conditions on the game vary and study the value of information in relation to the knowledge of terminal conditions. An alternative approach is presented in [9], which studies the same resource-extraction problem but assumes that the distribution of the time-until-failure is known in advance, while the concept of the value of information can be used to measure the inaccuracies in which such an approach incurs. Additionally, note that the problem of resource extraction considered in this paper should not be confused with a related research direction of resource mining in computer applications, such as, e.g., the one described in [10].
The rest of the paper is structured as follows. In Section 2, we describe the problem statement. In Section 3, two classes of model examples are introduced. Section 4 and Section 5 present a detailed analysis of the considered classes of problems. Section 6 presents a numerical illustration of the obtained results for the case of real life parameters. Finally, Section 7 concludes the paper.
2. Problem Formulation
Consider a differential game of n participants (players) [11]. Let be the set n of players. Let the game start at the initial moment from the initial state , which has a prescribed duration . The following assumptions are made:
- The controls are open-loop strategies [12];
- The controls belong to the sets of admissible controls , which consist of all measurable functions on the interval , taking values in the set of admissible control values , which are in turn a convex compact subsets of ;
- The integral payoff iswhere satisfies system (1), and the functions are smooth. Denote , .
3. Model Example
Consider the model example within the framework of differential game formulation presented above. It is assumed that n players (firms or countries) simultaneously exploit a non-renewable natural resource (see, e.g., [11]). The strategy of each player i is to determine the extraction effort from some admissible set . Further, denotes the state corresponding to the resource stock at the time t available to the extraction. Finally, it is assumed that the game is played over a finite time interval .
Consider two theoretical model examples with differing dynamics. In the first case, the dynamics of the stock are given by the following linear differential equation with the initial and terminal conditions :
The second case model has different dynamic constraints and the same boundary conditions:
The objective function of the player i for both cases is defined as:
In the considered differential game, every i player’s goal is to maximize the total profit:
We also consider the situation when the game is played in a cooperative mode and the players cooperate to achieve the maximum total payoff:
The optimal open-loop cooperative strategies of players , are found from solving the optimization problem:
The trajectory that corresponds to the optimal cooperative strategies is called the optimal cooperative trajectory and is denoted by .
The choice of optimal control influences the optimal trajectory and the payoffs of the players. On the other hand, the optimal control is selected in such a way that the boundary conditions are satisfied. Assume that we have imprecise information about the boundary conditions. To characterize the impact of the accuracy of the available information on the amount of the obtained payoff, we introduce the notion of value of information (V).
Definition 1.
The normalized value of information is defined as
where is the total payoff obtained with precise information, while is the payoff obtained with imprecise information.
4. Computations for Model Example with Linear Dynamics
4.1. Cooperative Solution
Consider the model with dynamics (3) and the objective function (5). The optimization problem is solved using the Pontryagin maximum principle (PMP) [12], which is widely recognized as one of the central tools for determining optimal strategies. We mention the papers [13,14] to give an idea of just a couple of applications of this celebrated technique. We define the Hamiltonian function as
The optimal controls are computed from the first-order optimality conditions as
Noting that the adjoint variable is constant according to optimality condition , and, furthermore, has to satisfy . Then, by substituting the expression of optimal control into system (3), we obtain
The optimal cooperative strategies and trajectory is thus
Further, we check the control constraints according to the of the problem, i.e., . For the admissible controls, the following condition should be satisfied:
The optimal value of the total payoff then equals
4.2. Value of Information
Suppose that the information about the initial value of the resource stock is not available to the players and that they have information about the initial stock being instead. In this case, the controls chosen by the players would have the form
and the trajectory corresponding to these controls is
Next, we define an estimated initial value as , where corresponds to the case when the information is overestimated, and to the case when the information is underestimated.
For convenience, we define the value at the final moment of time as , where, according to the problem statement, . In this case, corresponds to the case when the exact initial and final resource stocks coincide, i.e., the actual exploitation of the resource is not carried out with precise information. For this case, define the value of information as the maximum possible value, i.e., 1. Next, consider the cases where . Taking into account this notation, we obtain the value of information
Note that the value of corresponds to the accuracy of resource reserves estimation, which also affects the terminal constraint, i.e., . Thus, we can introduce . We obtain controls for this case and the respective trajectory as
In these notations, the value of information will take the form
4.3. Nash Equilibrium
For the non-cooperative case, we define the Hamiltonian function as:
The optimal controls are obtained from the first-order optimality conditions as:
Noting that the adjoint variable is constant according to optimality condition , and, furthermore, has to satisfy . Thus, we substitute this into (23), then substitute the expression of optimal control into system (3).
Solving this system, we come to the condition
Let us assume that the coefficients are equal to each other, i.e., . Then, the players are symmetrical, which means that their optimal controls should be the same, i.e., . Consider the first equation of the system with respect to one player
Finally, we obtain the solution and the optimal control of the first player:
The same can be done for other players.
Next, we check the control constraints according to the conditions of the problem, i.e., . The controls are admissible if the following condition is satisfied:
Find the payoffs of each i player
As a result, by substituting the optimal control into the objective function, we obtain
Similarly to the calculations from the Section 4.2, we can consider two cases of uncertainty in a non-cooperative scenario separately for each player. As a result, the values of the information coincide with the expressions (18) and (21).
5. Computations for Model Example with Non-Linear Dynamics
5.1. Cooperative Solution
In this section, we consider the model with dynamics (4) and the objective function (5). The optimization problem is solved using the Pontryagin maximum principle [12]. We define the Hamiltonian function as
The optimal controls are computed from the first-order optimality conditions as
Noting that the adjoint variable is constant according to the optimality condition , and, furthermore, has to satisfy . Then, by substituting the expression of optimal control into system (3), we obtain
The optimal cooperative strategies and trajectory is thus
Further, we check the control constraints according to the problem, i.e., . To find admissible controls, we should satisfy the following condition:
The optimal value of the total payoff then equals
5.2. Value of Information
Now, suppose that the information about the initial value of the resource stock is not available to the players and that they have information about the initial stock being instead. In this case, the controls chosen by the players would have the form
and the trajectory corresponding to these controls is
Next, we define an estimated initial value as , where corresponds to the case when the information is overestimated and to the case when the information is underestimated.
For convenience, we define the value at the final moment of time as , where, according to the problem statement, . In this case, corresponds to the case when the exact initial and final resource stocks coincide, i.e., the actual exploitation of the resource is not carried out with precise information. For this case, define the value of information as the maximum possible value, i.e., 1. Next, consider the cases where . Taking into account these designations, we obtain the value of information
Note that the value of corresponds to the accuracy of resource reserves estimation, which also affects the terminal constraint, i.e., . Thus, we can introduce . We obtain controls for this case and the corresponding trajectory as
In these notations, the value of the information will take the form:
5.3. Nash Equilibrium
For the non-cooperative case, we define the Hamiltonian function as
The optimal controls are computed from the first-order optimality conditions as
Note that the adjoint variable is constant according to optimality condition , and, furthermore, has to satisfy . Thus, we substitute this into (44) and then substitute the expression of optimal control into system (4).
Solving this system, we come to the condition
Let us assume that the coefficients are equal to each other, i.e., . Then, the players are symmetrical, which means that their optimal controls should be the same, i.e., . Consider the first equation of the system for one player and solve it with respect to the adjoint variable:
Finally, we obtain the solution and the optimal control of the first player:
The same can be done for other players.
Next, we check the control constraints according to the conditions of the problem, i.e., . The controls are admissible if the following condition is satisfied:
Find the payoffs of each i player
As a result, substituting the optimal control into the objective function, we obtain
Similarly to the calculations from Section 5.2, we can consider two cases of uncertainty in a non-cooperative scenario separately for each player. As a result, the values of the information coincide with the expressions (39) and (42).
6. Numeric Example
This section is devoted to the specific numeric example of non-renewable resource extraction given by the system with linear dynamics. The same can be done for other system with non-linear dynamics.
Consider the coal mining problem [15,16]. The Kuznetsk Basin possesses some of the most extensive coal deposits anywhere in the world. There are a huge number of mining enterprises operating in the Russian coal industry. For example, coal assets in the Kuznetsk basin are owned by three companies: JSC SUEK, which specializes in the power and coal industry; and PJSC MECHEL and LLC EVRAZ, which are engaged in the metallurgical and coke industries. Based on the available data [17,18,19], we formalize the theoretical problem of coal mining in the form of a three-player differential cooperative game, where the players are the following companies: SUEK JSC, PJSC MECHEL, and LLC EVRAZ. The same can be done for non-cooperative games.
To determine the coefficients that determine the payoffs (5), we will use the data on the company’s revenue for 2020. The coefficients will be determined by the following formula:
where is i-company’s revenue and is i-company’s production volume for 2020.

Table 1.
Enterprise data.
Resource extraction is regulated by Russian laws. Particularly, Russian laws divide reserves of minerals according to the degree of geological knowledge into the categories . Moreover, there are categories of predictive resources (), which are subdivided according to the degree of their validity [15]. Table 2 contains information on coal reserves by category in the Kuznetsk Coal Basin [16].

Table 2.
Distribution of coal reserves.
Based on their assessment criteria, assume category to be less credible for the evaluation of the resource reserves level. Reserves of category determine about of all known resources, and predicted resources significantly exceed more accurately estimated resource reserves, which are redundant. Consider this information to set the parameters of the model, such as the initial level of resource reserves and the accuracy of resource reserves estimation. In addition, consider a game to be hold during one year.
Next, consider a case with estimated initial level of resource reserves, and indicate it as case 1. Based on the above-mentioned assumptions, consider the following values of the following parameters:
Assume also that the set of admissible controls corresponds to the interval
For clarity, assume . The obtained optimal controls and optimal trajectories for this case are presented in Figure 1.
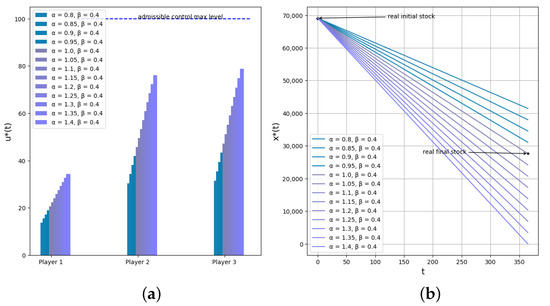
Figure 1.
(a) The optimal controls of three players for the system with linear dynamics with case of uncertainty 1. (b) The optimal trajectories of three players for the system with linear dynamics with case of uncertainty 1.
Next, consider a case with an estimated initial and final level of resource reserves and designate it case 2.
The dependence of the normalized value of information on the accuracy parameter is presented for two cases with different extraction parameters in Figure 2. Since the logarithmic scale shows the relative change of a value, the logarithm of the normalized value of information is also presented in Figure 2.
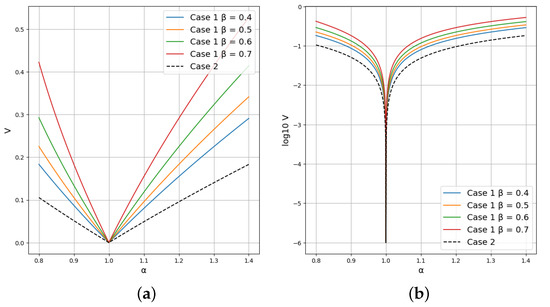
Figure 2.
(a) The normalised value of information for two cases of uncertainty. (b) The logarithm of the normalised value of information for two cases of uncertainty.
7. Conclusions
We considered a continuous-time differential game of non-renewable resource extraction under the assumption that the terminal conditions of the problem are not precisely defined. To characterize the gain that the players obtain by using precise information, we used the notion of value of information. To illustrate the used approach, we considered two cases: a linear and a nonlinear one. Quite remarkably, the obtained results are rather similar: while the value of the payoff function in the Nash equilibrium case are equal, the value of information for both cases differs but has the same structure. The obtained results are illustrated for real values of parameters that characterize three coal mining companies from the Kuznetsk basin, Russia.
Author Contributions
Conceptualization, E.G.; Methodology, E.G.; Software, A.B.; Validation, E.G.; Investigation, A.B.; Resources, E.G.; Data curation, A.B.; Writing—original draft, E.G. and A.B.; Writing—review & editing, E.G.; Visualization, A.B.; Supervision, E.G.; Project administration, E.G.; Funding acquisition, E.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by RFBR and DFG, project number 21-51-12007. A part of this work was performed while the both authors were at Saint Petersburg State University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sadorsky, P.A. Measuring resource scarcity in non-renewable resource with an application to oil and natural gas in Alberta. Appl. Econ. 1991, 23, 975–984. [Google Scholar] [CrossRef]
- Hart, R. Non-renewable resources in the long run. J. Econ. Dyn. Control 2016, 71, 1–20. [Google Scholar] [CrossRef]
- Bratvold, R.B.; Bickel, J.E.; Lohne, H.P. Value of Information in the Oil and Gas Industry: Past, Present, and Future. SPE Reserv. Eval. Eng. 2009, 12, 630–638. [Google Scholar] [CrossRef]
- Peskova, D.; Sizykh, A.; Rukavishnikov, V. Oil and gas exploration planning using VoI technique. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Tomsk, Russia, 23–27 November 2015; IOP Publishing: Bristol, UK, 2016; Volume 33, p. 012032. [Google Scholar]
- Chebotareva, A.; Su, S.; Tretyakova, S.; Gromova, E. On the Value of the Preexisting Knowledge in an Optimal Control of Pollution Emissions. Contrib. Game Theory Manag. 2021, 14, 49–58. [Google Scholar] [CrossRef]
- Tur, A.; Gromova, E.; Gromov, D. On the Estimation of the Initial Stock in the Problem of Resource Extraction. Mathematics 2021, 9, 3099. [Google Scholar] [CrossRef]
- Chebotareva, A.; Su, S.; Voronina, E.; Gromova, E. Value of Cooperation in a Differential Game of Pollution Control. In Mathematical Optimization Theory and Operations Research; Springer: Cham, Switzerland, 2022; pp. 221–234. [Google Scholar] [CrossRef]
- Bolatbek, A. The value of information about boundary conditions in the problem of resource extraction with terminal constraints. Control Process. Stab. 2022, 398–402. [Google Scholar]
- Real-Miranda, R.; López-Barrientos, J.D. A Geologic-Actuarial Approach for Insuring the Extraction Tasks of Non-Renewable Resources by One and Two Agents. Mathematics 2022, 10, 2242. [Google Scholar] [CrossRef]
- Singh, R.; Dwivedi, A.D.; Srivastava, G.; Wiszniewska-Matyszkiel, A.; Cheng, X. A game theoretic analysis of resource mining in blockchain. Clust. Comput. 2020, 23, 2035–2046. [Google Scholar] [CrossRef]
- Dockner, E.J.; Jorgensen, S.; Van Long, N.; Sorger, G. Differential Games in Economics and Management Science; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Pontryagin, L.; Boltyanskii, V.; Gamkrelidze, R.; Mishchenko, E. The Mathematical Theory of Optimal Processes, 2nd ed.; Nauka: Moscow, Russia, 1962. [Google Scholar]
- Forde, J.E.; Ciupe, S.M.; Cintron-Arias, A.; Lenhart, S. Optimal control of drug therapy in a hepatitis B model. Appl. Sci. 2016, 6, 219. [Google Scholar] [CrossRef]
- Majewski, P.; Pawuś, D.; Szurpicki, K.; Hunek, W.P. Toward Optimal Control of a Multivariable Magnetic Levitation System. Appl. Sci. 2022, 12, 674. [Google Scholar] [CrossRef]
- Electronic Fund of Legal and Normative-Technical Documents. Available online: docs.cntd.ru/document/902021575 (accessed on 4 November 2022).
- Ministry of Natural Resources and the Environment of the Russian Federation. Available online: https://www.mnr.gov.ru/docs/gosudarstvennye_doklady/gosudarstvennyy_doklad_o_sostoyanii_i_ispolzovanii_mineralno_syrevykh_resursov_2020/ (accessed on 4 November 2022).
- SUEK. Available online: http://www.suek.com/investors/highlights/#operational (accessed on 4 November 2022).
- Mechel—Global Mining and Steel Company. Available online: https://www.mechel.com/upload/upload/PDF%20%D0%9%D0%B5%D1%87%D0%B5%D0%BB/FY2021__ENG___FV__.pdf (accessed on 4 November 2022).
- Corporate Website—EVRAZ. Available online: https://www.evraz.com/upload/iblock/7a6/Evraz_AR2020_Book.pdf (accessed on 4 November 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).