MONWS: Multi-Objective Normalization Workflow Scheduling for Cloud Computing

Abstract

Cloud computing is a prominent approach for complex scientific and business workflow applications in the pay-as-you-go model. Workflow scheduling poses a challenge in cloud computing due to its widespread applications in physics, astronomy, bioinformatics, and healthcare, etc. Resource allocation for workflow scheduling is problematic due to the computationally intensive nature of the workflow, the interdependence of tasks, and the heterogeneity of cloud resources. During resource allocation, the time and cost of execution are significant issues in the cloud-computing environment, which can potentially degrade the service quality that is provided to end users. This study proposes a method focusing on makespan, average utilization, and cost. The authors propose a task’s dynamic priority for workflow scheduling using MONWS, which uses the min-max algorithm to minimize the finish time and maximize resource utilization by calculating the dynamic threshold value for scheduling tasks on virtual machines. When the experimental results were compared to existing algorithms, MONWS achieved a 35% improvement in makespan, an 8% increase in maximum average cloud utilization, and a 4% decrease in cost.

1. Introduction

Many scientific tasks in the fields of bioinformatics, health care, physics, and astronomy have been observed to require the execution of complex jobs which are, in turn, represented as workflows [1]. Such workflows can be defined as a Direct Acyclic Graph (DAG) [2]. In DAG, nodes are represented as tasks and the edges indicate the data dependency between two nodes. In the aforementioned fields, the workflows are large and complicated in structure [3]. This necessitates more storage and higher computational power. Therefore, various projects are designed in a grid environment such as GrADS, Pegasus, or ASKALON for pre-processing and managing the complex workflows. In recent years, cloud computing has been noted to be the most suitable for executing large workflow applications due to its provision of unlimited resources using the virtualization concept [4].

In cloud computing, users are charged on a pay-per-use model [5,6] because resources are set up dynamically and are based on the need of workflows and their deadlines [7]. This allows for a better management of both the quality and quantity of resources than other distributed systems, such as grids, can achieve [8,9]. However, in order to schedule large scientific-workflow applications, efficient scheduling schemes for processing are deemed essential.

In cloud computing [10], the primary challenge of workflow scheduling [11] lies in assigning each job or task to a virtual machine for execution [12]. Figure 1 illustrates the sample workflow, defined by a set of nine tasks with dependencies between tasks. The output of one task serves as the input for another task.

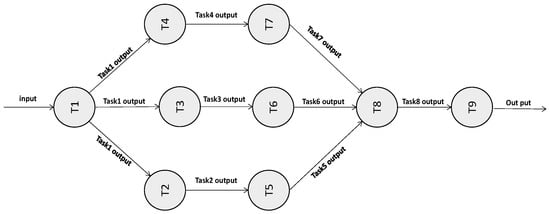
Figure 1. Sample Workflow with nine tasks.

Scheduling plays a vital role in minimizing energy consumption, makespan, and cost while maximizing resource utilization. The existing methods are inadequate for finding optimal solutions. To address this issue, this paper presents a dynamic priority approach for workflow scheduling in cloud computing.

The main contributions of this paper are as follows:

(1)

Identifying the best workflow is a challenging task in scheduling. In this paper, based on the study, we select “Cybershake” as the best workflow;

(2)

Handling dynamic traffic in cloud computing is very difficult. Static thresholds fail to schedule tasks optimally. In our proposed approach, we define a dynamic threshold value based on the task execution time, workflow model, and availability of resources;

(3)

In this paper, we present an extensive literature review for selecting multi-objective parameters for task scheduling;

(4)

We exemplify our proposed work with standard numerical values to prove the efficiency of a framework for cloud computing;

(5)

To make our proposed algorithm more realistic, we include the data transfer time between tasks;

(6)

To calculate the efficiency of proposed algorithm, simulation results are compared with the five existing algorithms.

The article is organized as follows. Section Two discusses the related work in brief. Section Three presents the scheduling problem formation and Section Four elucidates the proposed algorithm. Section Five presents the results of the simulation and performance evaluations and Section Six notes the conclusions derived from the current study.

2. Related Work

Numerous heuristic scheduling algorithms have been proposed in past studies to address the DAG-workflow scheduling problem [13]. Heuristic scheduling algorithms are further classified into list scheduling, cluster scheduling, and group scheduling.

List scheduling is a widely used scheduling algorithm wherein [14] each task and edge is assigned a weight. Based on the assigned weightage, a task list order is then created by prioritizing each task [15]. Following this, tasks are then chosen by their priority to be scheduled on the host, which helps to minimize predetermined cost functions. HEFT [16] and CPOP [17] are two other common list scheduling heuristics used. Group Scheduling is the most popular heuristic scheduling algorithm. In Group Scheduling [18], the tasks are grouped based on their constraints. In DAG, the tasks are partitioned into different levels; therefore, no dependency exists among tasks grouped in the same level. These tasks are then assigned using static scheduling algorithms. Cluster scheduling, on the other hand, is a type of scheduling algorithm that is used for an unbounded number of computing resources.

Zhou et al. [19] proposed a new algorithm, the MW-HBDCS, which is a budget-based scheduling system that works with deadline constraints. The algorithm has two stages: (1) task selection and (2) resource selection. In the first phase, the task-ready pool is formed by assigning each task a rank or priority. In the second phase, the resources are presented with pooled tasks based on their priority or rank. This algorithm outperformed the existing methods in cases of deadline and budget constraints. However, the study did consider important parameters, such as cost and makespan, for making them more efficient.

In another study, Nasr et al. [20] proposed a hybrid algorithm for workflow scheduling based on deadline constraints. The study combined chemical-reaction optimization (CRO) and ant-colony optimization (ACO) as CR-AC for minimizing the workflow scheduling costs for cloud computing. Initially, the study noted that the CRO found the best optimal solutions with low time complexity. In the next phase, ACO was applied to reduce the overall cost and enhance the quality of the solution. The CR-AC outperformed existing algorithms in terms of cost and makespan. However, the study also noted that the time complexity increased energy consumption, and load balancing was not considered for the research.

Verma et al. [21] proposed a cost- and time-constraint-based workflow scheduling for cloud computing to place the trade-off in cost between the cloud consumer and the provider. BDHEFT consists of two phases: service level and task level scheduling. In the service level scheduling, tasks are scheduled in a descending order depending upon rank, whereas in task level scheduling, tasks are scheduled on the best-possible resource available at minimum cost. The experimental results indicated that existing works were efficient in terms of time and cost, whereas a complex workflow process resulted in inefficiency.

A study by Chakravarthi et al. [22] proposed a normalized, budget-aware workflow scheduling (NBWS) algorithm. The algorithm proceeded through a min-max normalization process, which was then followed by calculating an expected reasonable budget for assigning workflow tasks to one of the VMs. The proposed NBWS consisted of the phases of task selection and resource selection. In the task selection phase, tasks were partitioned at different levels of workflow based on the priorities and dependencies of tasks. In the resource selection phase, an estimated reasonable budget was calculated to schedule the task on VMs. This technique outperformed existing methods in terms of budget when executed on standard workflow applications. However, the impact of communication among tasks was not considered in this study.

Zhou et al. [23] presented a new-list workflow scheduling using the fuzzy-based HEFT(FDHEFT), an algorithm that was classified into two phases of task prioritization and instance selection. In the task prioritization phase, tasks were sorted in descending order of high-rank values, i.e., high-rank values were assigned with higher priority. In the second phase, the FDHEFT sorted all the scheduled solutions produced according to their fuzzy dominance values and chose the best K solutions. The main objective of this algorithm was to minimize the makespan and cost of scheduling. However, the study noted that this algorithm increased the computation time.

Overview of workflows:

Cloud computing has recently been used by commercial and scientific applications to access storage and computing infrastructure. These applications are usually created as a workflow.

Depending on the complexity of the problem, workflows in past studies have been grouped as memory-intensive-, CPU-intensive-, or input/output-intensive-based workflows [24].

Montage workflow:

The Montage workflow (Figure 2) is an input/output-intensive astronomy workflow used to construct custom mosaics of the sky depending on the size of the input images. The workflow structure is modified to accommodate for increases in inputs, which then correspond to an increase in the computational jobs.

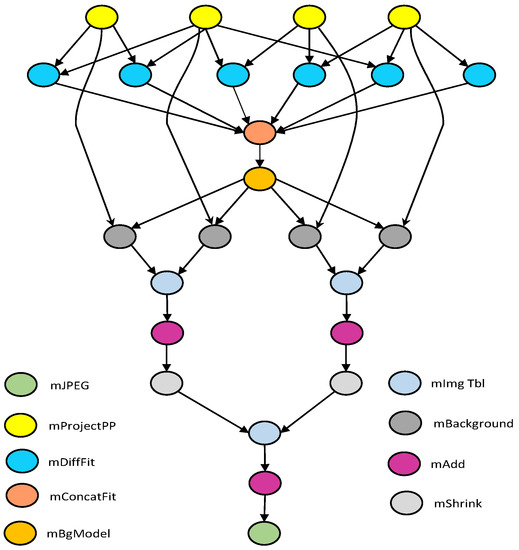
Figure 2. Montage workflow.

Broadband workflow:

The Broadband workflow(Figure 3) was primarily designed to integrate the simulation codes for earthquake motions and their associated calculations. Based on the types of computations performed at each stage, the broadband workflow can be divided into four distinct phases.

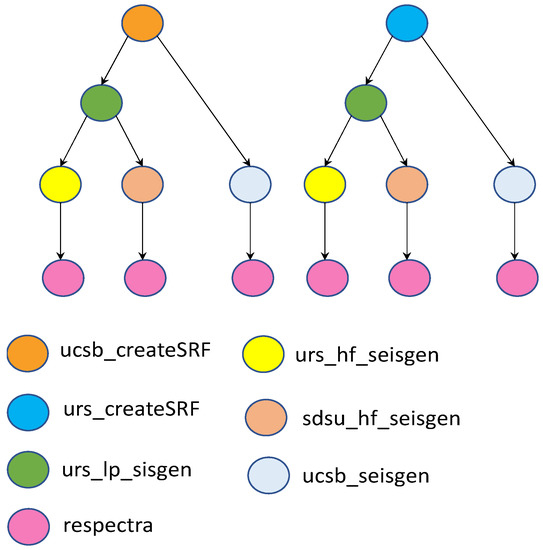
Figure 3. Broadband workflow.

LIGO:

The LIGO (Figure 4) is a memory-intensive application used in the field of physics to detect gravitational waves. This workflow is extremely complex and is made up of several sub-workflows.

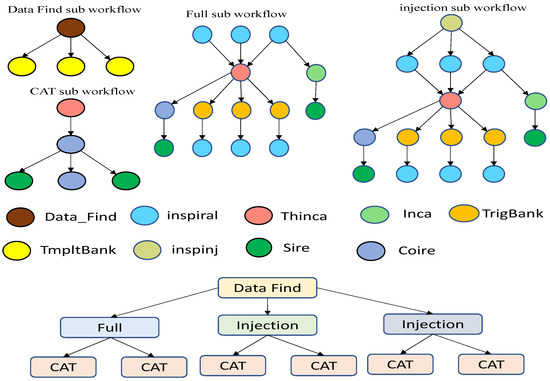
Figure 4. LIGO.

Epigenomics:

Epigenomics (Figure 5) is a largely pipelined application, with multiple pipelines processing independent data chunks in parallel. It begins with FastQSplit jobs and splits the lane into multiple chunks depending on the partition factor. The noise and contaminated data are then filtered from the chunks. The sol2sanger utility then converts each chunk’s data into the Maq DNA sequence-mapping software format. The Fastq2bfq then converts the data into the binary fastQ format for faster processing and reduced disk usage. The map utility then aligns the remaining sequences with the reference genome. Next, mapMerge jobs combine individual map process results. After merging, the maqIndex utility retrieves reads about a specific region from the merged alignment file.

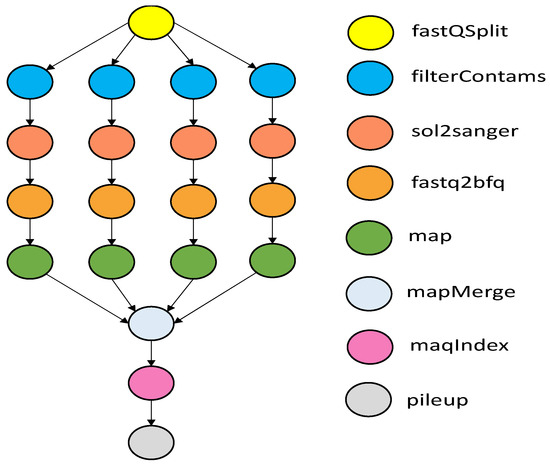
Figure 5. Epigenomics.

Cybershake:

Cybershake workflow (Figure 6) is a data- and memory-intensive workflow application used by the Southern California Earthquake Center. Cybershake can perform computations on particularly large datasets. The workflow starts by generating the strain green tensors (SGT) data from finite simulations derived from the master SGT files. The ExtractSGT job extracts rupture-specific SGT files from the master SGT. Thus, ExtractSGT jobs can be considered to be data partitioning. Seismogram-synthesis jobs generate synthetic seismograms for each rupture variation. Peak intensity values, specifically pertaining to spectral acceleration, are then calculated for each synthetic seismogram by the PeakValueCalcOkaya jobs. The ZipSeismograms and ZipPeakSA jobs collect and compress the synthesized seismograms and peak intensities, which are then staged and archived. These jobs are categorized as simple data collection jobs.

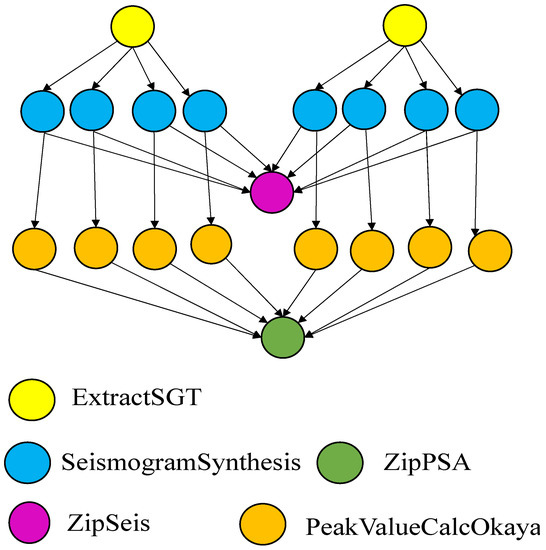
Figure 6. Cybershake.

Table 1 summarizes the existing workflow-scheduling algorithms for cloud computing. This summary also notes where existing algorithms can be improved pertaining to scheduling performance by considering parameters such as cloud utilization, resource utilization, load balancing, and energy consumption. In order to overcome the above unaddressed issues, the current study proposes the MONWS algorithm to enhance the performance of scheduling in cloud computing and Table 2 summarizes the list of notations.

Table 1. Summary of workflow scheduling algorithms for cloud computing.

Ref.	Technique	Objectives										Tools
		Makespan	Energy Consumption	Cost	Budget	Cloud Utilization	Deadline	Execution Time	Response Time	Resource Utilization	Load Balancing
[25]	Modified HEFT	✓	-	-	-	-	-	-	-	-	-	Cloudsim
[26]	BDAS	-	-	-	✓	-	-	✓	-	-	-	Cloudsim
[27]	MinIncreaseInEnergy, NoIdleMachineECTC, MaxUtilECTCandNoIdleMachineMaxUtil	-	✓	-	-	-	-	-	-	✓	-	Cloudsim
[22]	NBWS	-	-	-	✓	-	-	-	-	-	-	Cloudsim
[28]	BHGALO-GOA	✓	-	✓	-	-	-	-	-	-	-	Workflowsim
[13]	DAGMap	-	-	-	-	-	-	✓	-	✓	-	Grid
[29]	NMMWS	✓	-	-	-	✓	-	-	-	-	-	MATLAB
[19]	MW-HBDCS	-	-	-	✓	-	✓	-	-	-	-	SimGrid
[23]	FDHEFT	-	-	✓	✓	-	-	-	-	-	-	Realtime
[21]	BDHEFT	-	-	✓	-	-	-	-	-	-	-	Cloudsim
[30]	Resource ranking and partitioning	-	-	-	-	-	-	-	✓	-	-	Cloudsim
[31]	BB-BC	-	-	✓	-	-	-	✓	-	-	-	Cloudsim
[32]	PEFT	-	-	-	-	-	-	-	-	-	✓	Workflowsim
[33]	MCDM	✓	-	✓	-	-	-	-	-	-	-	Realtime
[34]	HBCWSP	✓	-	-	✓	-	-	-	-	-	-	Realtime
[35]	HEFT-ACO	✓	-	✓	-	-	-	-	-	-	-	Workflowsim
[36]	EM-WOA	-	✓	-	✓	-	-	-	-	-	-	cloudsim
[37]	NRBWS	✓	-	-	✓	-	-	-	-	-	-	Cloudsim

Note: ✓ indicates considered by author and—indicates not considered by authors.

Table 2. List of Notations.

Abbreviations	Definitions
DTT	Data transfer time
DTTp,q	Data transfer time from Tp to Tq
CS	Cloud server
Ect	Estimated computation time
Ms	Makespan
Acu	Average cloud utilization
tp	Predecessor task
ts	Successor task
Est	Early start time
Eft	Early finish time
N_Ect	Normalized estimated computation time
Ptvm	Processing time on VM
Rsame	Same resource
Th(dTi)	A threshold value of each task, Ti
RLi	Ready List of tasks at level 1 of DAG
T_N_Ect	Temporary normalized estimated computation time
T_Ect	Temporary estimated computation time
Act	Actual completion time

3. Scheduling Problem Formation

This section addresses the dynamic workflow scheduling problem of allocating resources for each task in the workflow by minimizing the makespan, cost, and average cloud utilization.

Application Model

The workflow is a directed acyclic graph (DAG) [38] which is represented by D = (T, E), where T = {T₁, T₂,…, T_n} is indicative of a set of tasks and E represents the set of directed edges between the tasks, standing dependencies, or communication between the set of tasks [39]. Each directed edge e_ps = (T_p,T_s) belongs to E, where tasks T_p and T_s are indicative of precedence constraint. This means that the task, T_s, cannot start its execution until task T_p is completed. In workflow applications, a T_p without any predecessors is referred as an entry task, T_entry, and a T_s without any successor task is referred to as an exit task, T_exit. If the workflow application contains multiple instances of T_entry or T_exit, then a virtual edge with zero computation time and zero execution time is to be assumed.

Scheduling Factors:

Data Transfer Time:

$$\begin{array}{l}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\begin{array}{cccc}{\mathrm{T}}_1& { \mathrm{T}}_2& \dots & { \mathrm{T}}_{\mathrm{n}}\end{array}\\ \mathrm{DTT}=\begin{array}{c}{\mathrm{T}}_1\\ {\mathrm{T}}_2\\ ⋮\\ {\mathrm{T}}_{\mathrm{n}}\end{array}\left[\begin{array}{cccc}0& {\mathrm{DTT}}_{1,2}& \dots & {\mathrm{DTT}}_{1,\mathrm{n}}\\ 0& 0& \dots & {\mathrm{DTT}}_{2,\mathrm{n}}\\ ⋮& ⋮& \dots & ⋮\\ 0& 0& \dots & 0\end{array}\right]\end{array}$$

(1)

In Equation (1), DTT refers to the data transfer time and the element DTT_p,q, 1 $\le$ p $\le$ n and 1 $\le$ q $\le$ n indicates the data transfer time between T_p and T_q.

Estimated Computation Time:

The task execution time may vary depending on the VMs. The estimated computation time (E^ct) is calculated according to Equation (2).

$$\begin{gathered} \begin{array}{l}\begin{array}{ccc} {\mathrm{cs}}_1 & \cdots & { \mathrm{cs}}_{\mathrm{m}}\end{array}\\ \begin{array}{ccccc} {\mathrm{vm}}_1& \cdots & {\mathrm{vm}}_{{\mathrm{n}|\mathrm{cs}}_{\mathrm{n}}|}& \cdots & {\mathrm{vm}}_{{\mathrm{n}|\mathrm{cs}}_{\mathrm{m}}|}\end{array}\end{array} \\ {\mathrm{E}}^{\mathrm{ct}}=\begin{array}{c}{\mathrm{T}}_1\\ ⋮\\ {\mathrm{T}}_{\mathrm{n}}\end{array}\left[\begin{array}{ccccc}{\mathrm{Et}}_{1,1}& \cdots & {\mathrm{Et}}_{{1|\mathrm{CS}}_1|}& \cdots & {\mathrm{Et}}_{{1|\mathrm{CS}}_{\mathrm{m}}|}\\ ⋮& \cdots & ⋮& \cdots & ⋮\\ {\mathrm{Et}}_{\mathrm{n},1}& \cdots & {\mathrm{Et}}_{{\mathrm{n}|\mathrm{CS}}_1|}& \cdots & {\mathrm{Et}}_{{1|\mathrm{CS}}_{\mathrm{m}}|}\end{array}\right] \end{gathered}$$

(2)

where Et_p,q, 1 $\le$ p $\le$ n and 1 $\le$ q $\le$ |CS_m| indicates the estimated computation time of T_p on the VM of the cloud server |CS_m|.

Makespan:

Makespan is referred to the time it takes to complete a given task. Minimizing makespan is a popular optimization criterion when scheduling tasks because most users want their applications to run as quickly as possible. Makespan, $M_s$, is calculated as per Equation (3):

$${\mathrm{M}}_{\mathrm{s}}{=\max \left(\mathrm{Makespan}\right(\mathrm{CS}}_{\mathrm{m}}\left)\right),1\le \mathrm{CS}\le \mathrm{m}$$

(3)

where M_s is the overall makespan of tasks on the cloud server, CS_m.

Average Cloud Utilizations:

The optimal utilization [40] of resources on cloud servers is known as average cloud utilization and it is calculated as represented in Equation (4).

$${\mathrm{A}}_{\mathrm{cu}}=\frac{1}{\mathrm{N}}{\displaystyle \sum _{\mathrm{m}=1}^{\mathrm{N}}\mathrm{U}({\mathrm{CS}}_{\mathrm{m}})},1\le \mathrm{m}\le \mathrm{N}$$

(4)

In this equation, ${\mathrm{A}}_{\mathrm{cu}}$ indicates the average cloud utilizations, ${\mathrm{CS}}_{\mathrm{m}}$ indicates cloud servers, and $\mathrm{U}({\mathrm{CS}}_{\mathrm{m}})$ is the utilization of m number of cloud servers, calculated as per Equation (5).

$$\mathrm{U}({\mathrm{CS}}_{\mathrm{m}})=\frac{1}{\left|{\mathrm{CS}}_{\mathrm{m}}\right|}{\displaystyle \sum _{\mathrm{n}=1}^{{\mathrm{CS}}_{\mathrm{m}}}{\mathrm{U}(\mathrm{vm}}_{\mathrm{n}})},1\le \mathrm{n}\le \mathrm{N}$$

(5)

In the above equation, ${\mathrm{U}(\mathrm{vm}}_{\mathrm{n}})$ indicates the utilization of virtual machines and it is calculated as per Equation (6).

$${\mathrm{U}(\mathrm{vm}}_{\mathrm{n}})=\frac{{\mathrm{M}}_{\mathrm{s}}{(\mathrm{vm}}_{\mathrm{n}})}{{\mathrm{M}}_{\mathrm{s}}{(\mathrm{CS}}_{\mathrm{m}})}$$

(6)

The utilization of virtual machines is defined as the overall consumption time taken by virtual machines with respect to the makespan of cloud servers, CS_m.

Early start time:

The early start time of a task, t_i, on virtual machines is calculated using Equation (7).

$${\mathrm{E}}^{\mathrm{st}}{=\max \{\mathrm{access}}_{\mathrm{vm}},\underset{{\mathrm{t}}_{\mathrm{p}}\in {\mathrm{pre}(\mathrm{t}}_{\mathrm{i}})}{\max }{\{\mathrm{AFT}}_{{\mathrm{t}}_{\mathrm{p}}}{+\mathrm{DTT}}_{{\mathrm{t}}_{\mathrm{p}},\mathrm{i}}\text{}}$$

(7)

where access_vm is the minimum access time of the VMs, AFT_tp,i indicates the actual finish time of the predecessor task, t_p, and DTT_tp,i represents the data transfer time of predecessor task, t_p, to the current task, t_i.

Early Finish time:

The early start time of a task t_i on VMs is the summation of the estimated computation time and the early finish time on the VM, which is represented by Equation (8).

$${\mathrm{E}}^{\mathrm{ft}}{=\mathrm{E}}^{\mathrm{ct}}{+\mathrm{E}}^{\mathrm{st}}$$

(8)

Normalized Estimated Computation Time:

$${\mathrm{N}\_\mathrm{E}}^{\mathrm{ct}}=\frac{{\mathrm{E}}^{\mathrm{ct}}{+\min }_{{\mathrm{E}}^{\mathrm{ct}}}}{{\max }_{{\mathrm{E}}^{\mathrm{ct}}}{-\min }_{{\mathrm{E}}^{\mathrm{ct}}}}$$

(9)

By using Equation (9), the N_E^ct is initially calculated at level 1 of the workflow. Following this, the NE^ct is updated as N_T_E^ct because when any task is assigned to the VM the previous E^ct needs to be updated as T_E^ct.

Execution Cost (EC):

$$\mathrm{EC}=\frac{{\mathrm{Pt}}_{\mathrm{vm}}{\ast \mathrm{C}}_{\mathrm{i}}}{{\mathrm{B}}_{\mathrm{i}}}$$

(10)

The execution cost on VMs is calculated as per Equation (10). It is the ratio of the product between the processing time, Pt_vm, and cost per interval C_i to billing intervals B_i, in which the processing time on VMs is calculated according to Equation (11)

$${\mathrm{Pt}}_{\mathrm{vm}}{=\mathrm{E}}^{\mathrm{ct}}+{\displaystyle \sum _1^{\mathrm{d}}{(\mathrm{DTT}}_{{\mathrm{t}}_{\mathrm{i}}}}+\mathrm{Rsame})+\mathrm{delay}$$

(11)

$\mathrm{Rsame}$ is 0 when T_p and T_s are running on the same resource (cloud server). Otherwise, it is considered as 1.

4. Proposed Algorithm

The main objective of this study was to develop an algorithm (Algorithm 1). that could potentially minimize makespan and cost while maximizing cloud utilization.

Initially, all tasks of a given workflow are divided into a bag of tasks at each level. Next, we begin iterating the task schedule with the following first bag of tasks (BoT). Using the min-max algorithm, the estimated computation time value for all tasks in the BoT is normalized. Further, we divide all the tasks of the BoT into b_large and b_small groups by applying a dynamic threshold value. Finally, we schedule each batch using a minimum completion time algorithm. The large batch is processed first, followed by the small batch.

The proposed MONWS algorithm works in two distinct phases viz. the normalize ECT phase and the VM selection phase.

4.1. Normalize ECT

In this phase, the unscheduled tasks from the workflow are moved into the ready list, RLi, in each level. Initially, the b_large and b_small groups will be empty.

In each level of the DAG (workflow), the W,E^ct of each task T_i is normalized using the min-max algorithm to compute N_E^ct. The threshold value for each task is then calculated as follows.

$${\mathrm{Th}(\mathrm{d}}_{{\mathrm{T}}_{\mathrm{i}}})=\frac{{\displaystyle \sum {\max (\mathrm{E}}^{\mathrm{ct}})}}{{\displaystyle \sum {\max (\mathrm{DTT}}_{\mathrm{p},\mathrm{q}})}} \mathrm{if}\mathrm{Task}\mathrm{parent}{\mathrm{T}}_{\mathrm{p}} = !0$$

(12)

$${\mathrm{Th}(\mathrm{d}}_{{\mathrm{T}}_{\mathrm{i}}}) = 1fixed \mathrm{if}\mathrm{Task}\mathrm{parent}{\mathrm{T}}_{\mathrm{p}} = 0$$

(13)

If a task has no parent and no data transfer time, then Threshold Th(d_Ti) is fixed (i.e., 1). If the task has parent, then the above Equations (12) and (13) are calculate and N_E^ct $\ge$ Th(d_Ti) is checked. A move into b_large is then made; otherwise, a move into b_small is made. This is done from top to bottom in the workflow.

4.2. VM Selection

In this phase, tasks are scheduled for VMs by selecting the E^cti,j using the minimum execution time. E^ct is then updated as N_T_E^ct for subsequent tasks. This procedure is repeated until all present tasks have been scheduled.

Algorithm 1: Proposed MONWS Algorithm

Input: workflow with n number of tasks    Output: Scheduling on available VMs on m number of cloud servers

Read Ect and DTT of the given workflow D (T, E)     while        for every task Ti in each level             /*Generate Ready Task List*/             while                  if tasks are unscheduled do b_large is empty                            for every task Ti in each level                            add Ti to Ready List RLi                            end for                     end if             end while          /*Compute Early finish time*/             for every task Ti Ready List RLi do                      if task Ti has no Tp                            Ect= availablevm+Ectvm                      else                            for every vm and Tp of Ti                                if taskvmmap(Tp) =! Vm                                         if Ect<Est                                          Ect=Est                                         endif                                else                                         if Ect<max(availablevm,Act)                                          Ect=max(availablevm,Act)                                         endif                                endif                    endfor                endif        endfor /*Partition of tasks*/               Find min(Ect)              Find max(Ect)              Find N_Ect              Find threshold Th(dt)            if max(N_Ect)>= th(dt)                   add in to b_large            else                 add into b_small            endif    if b_large =! Empty               find min(Eft(i,j)                 taskvmmap(Ti)=vm                 Act = Eft                Est = 1                remove Ti from b_large    else              find min(Eft(i,j)              taskvmmap(Ti) = vm              Act = Eft               Est = 1    endif endfor endwhile

4.3. MONWS Framework

This study considers the Cybershake workflow application as an example, which is illustrated in Figure 7. The design has twenty tasks, T = {T₁, T₂,…..,T₂₀}, with five levels and thirty-two edges between the tasks. The Data Transfer Time matrix, represented as DTTp,s, is highlighted in Table 3 and is representative of the data transfer time among the different tasks.

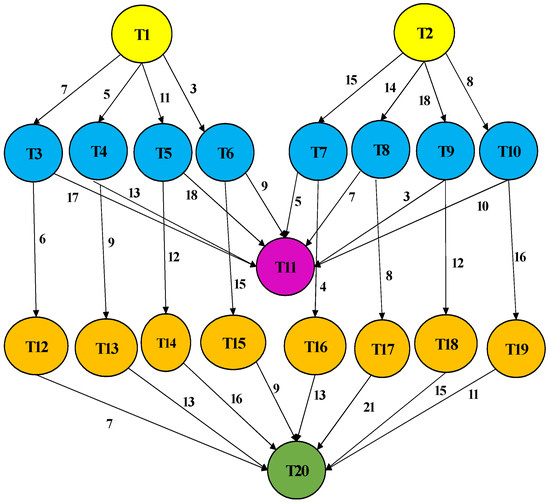
Figure 7. MONWS Workflow application.

Table 3. Data Transfer Time (DTT) between the tasks.

Tasks	T1	T2	T3	T4	T5	T6	T7	T8	T9	T10	T11	T12	T13	T14	T15	T16	T17	T18	T19	T20
T1	-	-	7	5	11	3	-	-	-	-	-	-	-	-	-	-	-	-	-	-
T2	-	-	-	-	-	-	15	14	18	8	-	-	-	-	-	-	-	-	-	-
T3	-	-	-	-	-	-	-	-	-	-	17	6	-	-	-	-	-	-	-	-
T4	-	-	-	-	-	-	-	-	-	-	13	-	9	-	-	-	-	-	-	-
T5	-	-	-	-	-	-	-	-	-	-	18	-	-	12	-	-	-	-	-	-
T6	-	-	-	-	-	-	-	-	-	-	9	-	-	-	15	-	-	-	-	-
T7	-	-	-	-	-	-	-	-	-	-	5	-	-	-	-	4	-	-	-	-
T8	-	-	-	-	-	-	-	-	-	-	7	-	-	-	-	-	8	-	-	-
T9	-	-	-	-	-	-	-	-	-	-	3	-	-	-	-	-	-	12	-	-
T10	-	-	-	-	-	-	-	-	-	-	10	-	-	-	-	-	-	-	16	-
T11	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
T12	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	7
T13	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	13
T14	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	16
T15	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	9
T16	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	13
T17	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	21
T18	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	15
T19	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	11
T20	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-

ECT refers to the estimated computation time for each task and has a different execution time on different virtual machines, illustrated in Table 4. It is defined in the ECT Equation (2).

Table 4. Corresponding computational matrix.

		T1	T2	T3	T4	T5	T6	T7	T8	T9	T10	T11	T12	T13	T14	T15	T16	T17	T18	T19	T20
CS1	vm1	17	14	19	13	19	13	15	19	13	19	13	15	18	20	11	16	22	18	14	19
	vm2	14	17	17	20	20	18	15	20	17	15	22	21	17	18	18	15	18	16	12	17
CS2	Vm3	13	14	16	13	21	13	13	13	13	16	14	22	16	13	21	19	22	11	16	10
	Vm4	22	16	12	14	15	18	14	18	19	13	12	14	14	16	17	12	23	17	19	24

As is illustrated in Figure 7, the workflow has two tasks in level 1 that are in the Ready list, RLi. They are designated as T₁ and T₂, and these tasks can be mapped to any of the four VMs on both cloud servers.

At level 1, T_ECT is represented by the below equation.

$$\begin{array}{l}\begin{array}{cccc}{ \mathrm{vm}}_1& {\mathrm{vm}}_2& {\mathrm{vm}}_3& { \mathrm{vm}}_4\end{array}\\ {\mathrm{T}\_\mathrm{E}}^{\mathrm{ct}}=\begin{array}{c}{\mathrm{T}}_1\\ {\mathrm{T}}_2\end{array}\left(\begin{array}{cccc}17& 14& 13& 22\\ 14& 17& 14& 16\end{array}\right)\end{array}$$

In the workflow example, tasks T₁ and T₂ have no predecessor tasks, which leads to no data transfer time between tasks T₁ and T₂. If DTTp,s is zero, then the threshold value Th(dTi) will be also zero, as seen in Equation (11). In this situation, the Th(dTi) value is fixed as 0.99 and is then compared with the maximum value in N_T_E^ct; wherein the maximum N_T_E^ct is 1. If the threshold Th(dTi) is lesser than the maximum N_T_E^ct i.e.,Th(dTi)< max N_T_E^ct, T₁ is then placed in the b_large. By calculating E^st and E^ft as per Equations (7) and (8), T₁ is then mapped into the VM3 in cloud server2.

$$\begin{array}{l}\begin{array}{cccc} {\mathrm{vm}}_1 & { \mathrm{vm}}_2 & { \mathrm{vm}}_3 & { \mathrm{vm}}_4\end{array}\\ {\mathrm{N}\_\mathrm{T}\_\mathrm{E}}^{\mathrm{ct}}=\begin{array}{c}{\mathrm{T}}_1\\ {\mathrm{T}}_2\end{array}\left(\begin{array}{cccc}0.44444444& 0.11111111& 0& 1\\ 0.11111111& 0.44444444& 0.11111111& 0.33333333\end{array}\right)\end{array}$$

The updated T_E^ct is then calculated as follows.

$$\mathrm{Updated} \mathrm{T}\_{\mathrm{E}}^{\mathrm{ct}} \left(\begin{array}{cccc}14& 17& 27& 16\end{array}\right)$$

The corresponding Normalized N_T_E^ct is calculated as follows:

$$\mathrm{N}\_\mathrm{T}\_{\mathrm{E}}^{\mathrm{ct}}=\begin{array}{c}T2\end{array}\left(\begin{array}{cccc}0& 0.23076923& 1& 0.15384615\end{array}\right)$$

The maximum N_T_E^ct for T₂ is then compared with the Th(dTi), which is fixed at 0.99. In this case as well, the Th(dTi) < maximum N_T_E^ct, therefore leading to T₂ also being placed in the b_large. At this juncture, b_large is now designated as b_large (T₁, T₂). By calculating Est and Eft as per Equations (7) and (8), T₂ is then mapped into VM1 in cloud server1.

In considered workflow level 2

In level 2, there are eight tasks: T₃, T₄, T₅, T₆, T₇, T₈, and T₉ which are placed in the Ready list, RLi. T₁ and T₂ are already slotted in VM3 and VM1, respectively. Therefore, the tasks T₁ and T₂ of level 1 are scheduled (mapped) on VM3 and VM1, respectively. The VM available times, available_vm, for VM1, VM2, VM3, and VM4 are now calculated to be 14, 0, 13, and 0 respectively. However, at this point, T₃ has a predecessor with a DTT (Data transfer time) of 7. Therefore, the T_E^ct matrix for T₃, T₄, T₅, T₆, T₇, T₈, and T₉ would then be updated as follows.

$$\begin{array}{l}\begin{array}{cccc} {\mathrm{vm}}_1& {\mathrm{vm}}_2& {\mathrm{vm}}_3& {\mathrm{vm}}_4\end{array}\\ {\mathrm{T}\_\mathrm{E}}^{\mathrm{ct}}=\begin{array}{c}{\mathrm{T}}_3\\ {\mathrm{T}}_4\\ {\mathrm{T}}_5\\ {\mathrm{T}}_6\\ {\mathrm{T}}_7\\ {\mathrm{T}}_8\\ {\mathrm{T}}_9\\ {\mathrm{T}}_{10}\end{array}\left(\begin{array}{cccc}39& 37& 29& 25\\ 31& 38& 26& 25\\ 43& 44& 34& 28\\ 29& 34& 26& 31\\ 29& 29& 42& 43\\ 33& 34& 45& 50\\ 27& 31& 41& 47\\ 33& 29& 38& 35\end{array}\right)\end{array}$$

The T_E^ct normalization is performed in a stepwise manner according to the threshold Th(dTi). The tasks are then allotted to a suitable virtual machine. These are then moved into either b_large or b_small, similar to the process that was observed at level 1. Table 5 represents the mapping of tasks on the VMs where rows indicate the tasks and the columns indicate the EST, EFT, ACT, and VMID.

Table 5. Tasks allocation and execution description.

Tasks	EST	EFT	ACT	VMID
1	0	13	13	3
2	0	14	14	1
3	13	25	12	4
4	13	26	13	1
5	13	28	15	4
6	13	26	13	1
7	16	29	13	3
8	20	33	13	3
9	14	27	13	1
10	16	29	13	4
11	39	51	12	4
12	25	39	14	1
13	29	43	14	4
14	28	51	13	3
15	26	37	11	1
16	29	41	12	4
17	37	55	18	2
18	32	43	11	3
19	33	45	12	2
20	65	75	10	3

5. Simulation and Performance Evaluations

The current study focuses on evaluating a proposed algorithm by considering the metrics of makespan, average cloud utilization, and cost. The proposed algorithm’s performance was compared against benchmark algorithms min-min [13], max-min [13], NMMWS [29], HEFT [41], and DLS [13]. All the algorithms were implemented in the cloudsim tool. The simulation environment was set up with two data centers and four virtual machines.

To MONWS is evaluated with four different workflows: Montage, Cybershake, LIGO, and Epigenomics.

In this paper, for the purpose of evaluating the results of the MONWS algorithm in terms of performance, simulated experiments are carefully designed and carried out for the considered workflows with a varying number of tasks classified as small (1–25 tasks), average (25–100 tasks), and large (100–1000 tasks). The Pegasus [42] workflow generator is used to generate four representative scientific workflows with the same structure (Montage, Cybershake, Epigenomics, and LIGO).

Makespan:

Makespan was considered the most important evaluation metric for determining the effectiveness of a scheduler. We have inputted small, average, and large tasks to the cloud environment to compare the makespan of the proposed algorithm with existing algorithms such as NMMWS, min-min, max-min, DLS, and HEFT. We observed that our proposed algorithm has a minimum makespan of 82.5 ms when compared with any existing algorithm shown in Figure 8.

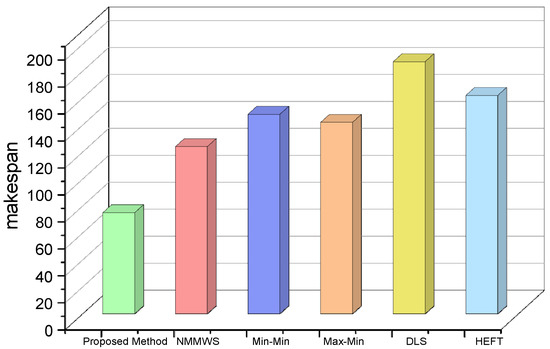
Figure 8. Makespan.

Average cloud utilization:

Average cloud utilization is another crucial metric in cloud computing from the perspective of the cloud provider. The average cloud utilization of the proposed algorithm in comparison to existing algorithms is shown in Figure 9. It can be noted that the proposed algorithm utilized 49% of cloud resources, while existing algorithms utilized 39%, 38%, 33%, and 37%, respectively. It can be inferred from the data that the proposed algorithm outperforms existing algorithms with respect to average cloud utilization.

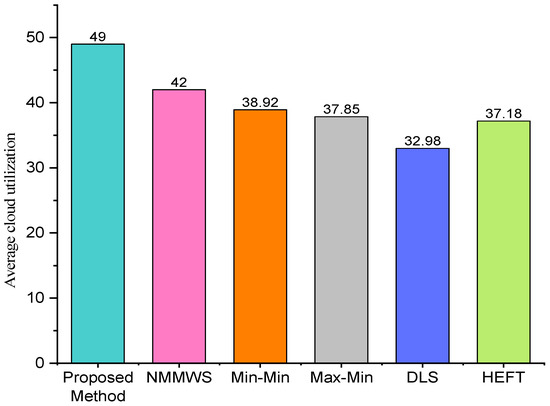
Figure 9. Average cloud utilization.

Cost:

Minimizing cost is another challenging parameter in cloud computing which affects both cloud consumers and providers alike. The cost incurred for the proposed algorithm in comparison to existing algorithms is shown in Figure 10. The costs were calculated using Equation (10), and it is observed that the proposed algorithm incurred costs of 4613.94 ms, which is 8% better than NMMWS and 18% better than min-min.

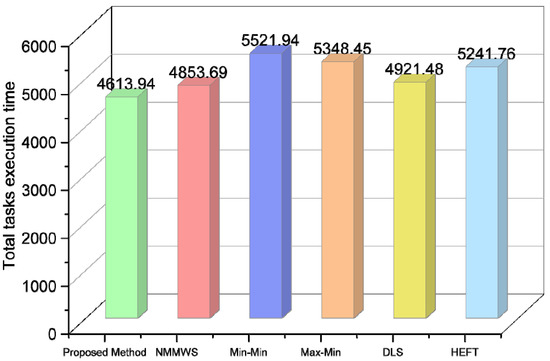
Figure 10. Cost.

VM Actual Working time:

In our proposed work, the actual working time of virtual machines for the given tasks is 130 ms for VM1, 100 ms for VM2, 234 ms for VM3, and 256 ms for VM4, as shown in Figure 11.

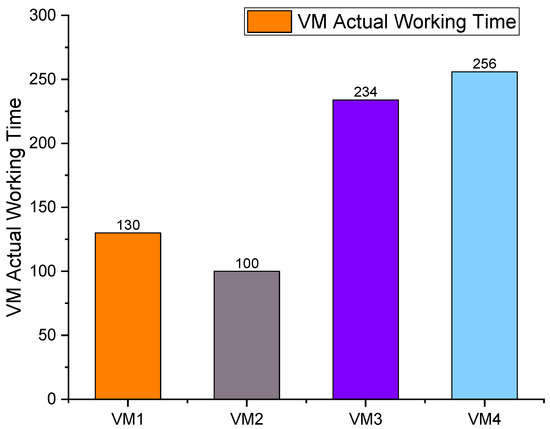
Figure 11. Actual working time of VMs.

Speedup:

The speedup value is the ratio of the minimum sequential execution time to the makespan. The sequential execution time is the total computation cost incurred when mapping all tasks sequentially to a single computing host. The proposed method outperforms the benchmark algorithms in terms of speed. The proposed method achieved a 20% speedup over the existing algorithm, as is shown in Figure 12. We have observed that speed is directly proportional to execution cost.

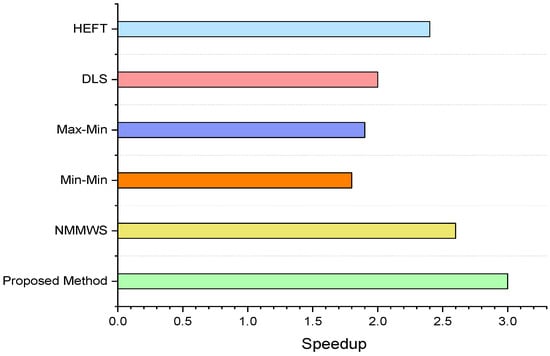
Figure 12. Speedup.

Load balance

Load balance is considered to be the most important metric for cloud service providers in order to maximize resource utilization. When comparing the load balance of the proposed method and the existing algorithms, the proposed method outperformed the benchmark algorithms by 7.23%, as is shown in Figure 13.

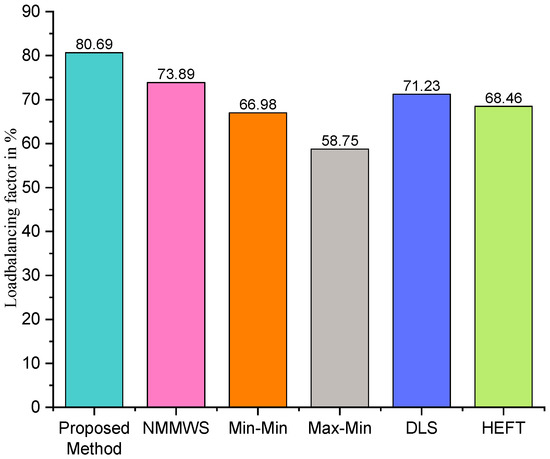
Figure 13. Load balance.

Evaluation of Success Rate:

The success rate, S_rate, is considered to be the ratio of the number of planning workflows and the total number of simulation runs. This rate is indicative of the performance of proposed and existing algorithms.

$${\mathrm{S}}_{\mathrm{rate}}=\frac{\mathrm{No}.\mathrm{of}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{Successful}\hspace{0.17em}\hspace{0.17em}\mathrm{Planning}\hspace{0.17em}\mathrm{Workflows}}{\mathrm{Total}\hspace{0.17em}\mathrm{no}.\mathrm{of}\hspace{0.17em}\mathrm{simulations}}\text{×}100$$

(14)

From Figure 14, Figure 15, Figure 16 and Figure 17, The success rate of the proposed algorithm’s makespan is determined using Montage, Cybershake, Epigenomics, and LIGO, as well as 4, 8, and 12 iterations. We observed that, when the makespan was low, the success rate was consequently higher on the MONWS in comparison to HEFT, DLS, min-min, max-min, and NMMWS. As a result, MONWS chooses the VMs with the earliest possible finish time (EFT) for optimally executing the workflow.

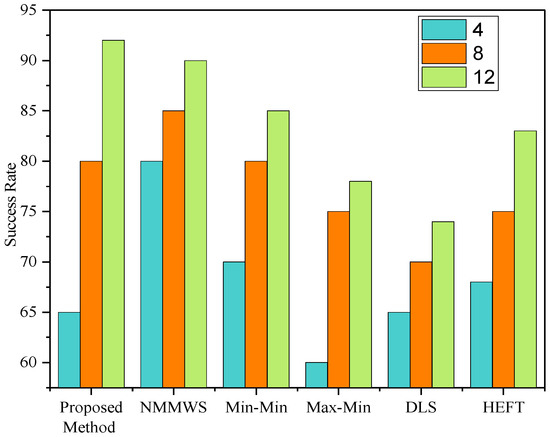
Figure 14. Success rate on the Montage workflow.

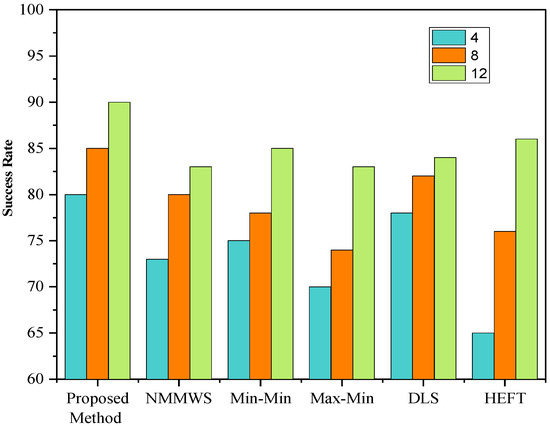
Figure 15. Success rate on the Cybershake workflow.

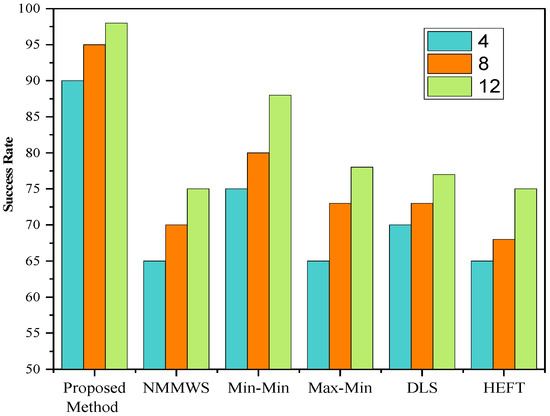
Figure 16. Success rate on the Epigenimics workflow.

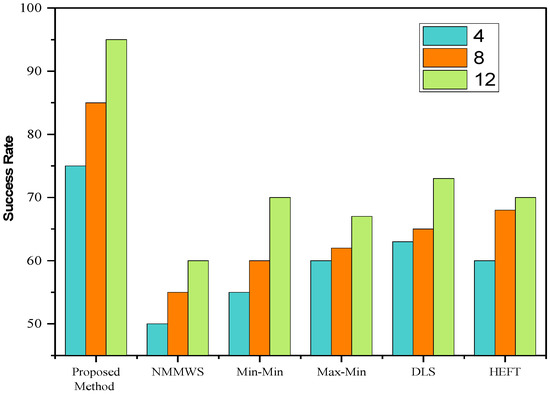
Figure 17. Success rate on the LIGO workflow.

6. Conclusions

This study proposed a novel MONWS algorithm by taking into consideration the dynamic priority of tasks based on min-max in order to minimize makespan and cost and maximize cloud utilization for optimum workflow scheduling. In the proposed algorithm in this study, the tasks were initially moved to the ready list, followed by the calculation of the estimated computation time and early finish time. Finally, the dynamic threshold values were compared in order to divide the tasks into groups (b_large and b_small) for scheduling the tasks on virtual machines. For implementation, the cloudsim simulation tool was utilized, and the results exhibited that the proposed algorithm outperformed the existing algorithms such as HEFT, DLS, min-min, max-min, and NMMWS with respect to real-world scientific workflow applications in terms of makespan, cost, cloud utilization, and load balancing. The MONWS proposed in this study achieved a 35% improvement in makespan, an 8% increase in maximum average cloud utilization, and a 4% decrease in cost.

However, the proposed algorithm needs improvement to handle cases of VM failure and checking energy consumption. The proposed algorithm also did not consider handling multiple workflows dynamically. These could potentially form the basis of future research.