Invariant Feature Encoding for Contact Handprints Using Delaunay Triangulated Graph

Abstract

Contact-based biometric applications primarily use prints from a finger or a palm for a single instance in different applications. For access control, there is an enrollment process using one or more templates which are compared with verification images. In forensics applications, randomly located, partial, and often degraded prints acquired from a crime scene are compared with the images captured from suspects or existing fingerprint databases, like AFIS. In both scenarios, if we need to use handprints which include segments from the finger and palm, what would be the solution? The motivation behind this is the concept of one single algorithm for one hand. Using an algorithm that can incorporate both prints in a common processing framework can be an alternative which will have advantages like scaling to larger existing databases. This work proposes a method that uses minutiae or minutiae-like features, Delaunay triangulation and graph matching with invariant feature representation to overcome the effects of rotation and scaling. Since palm prints have a large surface area with degradation, they tend to have many false minutiae compared to fingerprints, and the existing palm print algorithms fail to tackle this. The proposed algorithm constructs Delaunay triangulated graphs (DTG) using minutiae where Delaunay triangles form from minutiae, and initiate a collection of base triangles for opening the matching process. Several matches may be observed for a single triangle match when two images are compared. Therefore, the set of initially matched triangles may not be a true set of matched triangles. Each matched triangle is then used to extend as a sub-graph, adding more nodes to it until a maximum graph size is reached. When a significant region of the template image is matched with the test image, the highest possible order of this graph will be obtained. To prove the robustness of the algorithm to geometrical variations and working ability with extremely degraded (similar to latent prints) conditions, it is demonstrated with a subset of partial-quality and extremely-low-quality images from the FVC (fingerprint) and the THUPALMLAB (palm print) databases with and without geometrical variations. The algorithm is useful when partial matches between template and test are expected, and alignment or geometrical normalization is not accurately possible in pre-processing. It will also work for cross-comparisons between images that are not known a priori.

1. Introduction

Hand biometrics include multiple modalities such as fingerprint, palm print, finger–knuckle print, and finger vein and palm vein images. Fingerprints have been rising as a popular biometric modality and are extensively used for many applications including access control. They are acquired using contact-based sensors for automated identifications, such as in smart phones, and by transferring from touched surfaces, such as in latent prints for forensic purposes. They can also be acquired in a contactless manner with cameras whose resolution is sufficiently high to show the ridge patterns in images captured at a distance [1].

Palm prints are primarily used in forensic or crime scene analysis [2]. The existing forensic databases consist of images captured using different sensors and are too degraded in parts and often of inadequate quality. Therefore, a large number of spurious minutiae can be generated during feature processing. During matching, they should show some corresponding matches with the counterparts of prints acquired from hands. For automated minutiae matching in these images, they are unable to be pre-processed successfully enough to obtain a satisfactory performance without a manual support because the matching of two prints is performed after they are manually aligned, and key points are manually marked. A handprint system requires modification to process the segments acquired without manual marks or alignment.

Fingerprint images acquired with contact-based sensors are affected by scars on the finger and marks or dirt on the contacting surface, which limits the area of the usable image and hence the number of feature points that can be obtained from them. A handprint system incorporating fingers and palm can provide an increased area and more features, thereby increasing the potential to yield higher accuracy for identity verification. However, such a system has additional challenges in performing part-to-part registration and fusion of features or scores for verification. An increased area will also be accompanied by a larger number of spurious features. Handprint systems are still an ongoing area of research that address these challenges.

In a handprint system, the palm print region shows many more minutiae (×10 times) than fingerprints and is degraded by non-linear distortions. The hand structure and its increased surface area also pose challenges. Palm prints are very different from fingerprints, with additional creases, wrinkles, and palm lines, which tend to generate many spurious minutiae. Conventional fingerprint matching methods are therefore not very useful to implement automated systems that use palm prints. If the images exhibit geometrical transformations (Figure 1), degradation, and partial occlusion (as shown in Figure 2), they can yield large quality variations. A manual and careful examination is often needed for selecting a set of matching prints and features between them. The methods using palm prints are often not the same as those used with fingerprints. It is desirable from an implementation and interpretation of results perspective to have a common framework for processing both fingerprint and palm print images.

Figure 1. Eight instances of hypothenar segments of a palm acquired from a single individual. Note that they show a range of rotational and scale changes for a single individual, and some parts of the segments show quality variation due to the skin–scanner contact pressure, such as thickness and dilution of ridges.

Figure 2. Extremely low-quality hypothenar segments of palm prints acquired from THUPALMLAB database. Images in each row represent four instances of a single palm from one individual. Four rows represent images acquired from four individuals. Note that the data set used in this category shows low-quality prints nearly similar to latent prints. An enlarged portion of the degraded image is shown to illustrate the quality level of the image.

There are several handprint-based recognition systems explored in contactless manner in the recent past [3,4,5]. A method using common feature representation for both finger and palm in contactless images was already presented using ridge information [1,6,7]. High-resolution contactless images were used to acquire ridge orientation information which was then converted into one-dimensional invariant higher order spectral features. However, in contact scenario, acquiring highly visible ridge information without degradation is still difficult unless high-quality prints are acquired, and therefore, alternative feature representation is urged. Further, there is no system (to the best of our knowledge) that accommodates both fingerprints and palm prints in a contact-based hand biometric system which suits both access control and forensic applications. The motivation of this work is one single algorithm for one hand when contact handprints are present in any application. This work is a step towards a common framework in that direction.

In this context, a common framework would be desired to present: (i) a common feature representation; (ii) a common matching algorithm; (iii) robustness via features and matching approach for geometrical variations; and (iv) a strategy to reduce the spurious feature points that will arise from extremely degraded image segments. Minutiae and ridges are generally visible in the segments from a hand, and they can be detected to extract as common features. In the existing literature related to minutiae-based feature representation, one-to-one minutiae match between two fingerprints has been exploited. This approach, however, cannot be applied for geometrically transformed image segments, which will additionally require a manual image alignment before such a match. Therefore, a pair of minutiae, minutiae triangles, and minutiae polygons have been exploited to mitigate the issue of geometrical normalization in the past [8,9,10]. However, one minutiae-based triangle may match with another triangle that is located in a different region of the compared print. To tackle this issue, Delaunay triangles that are formed from the set of minutiae can be extended as a graph and utilized as Delaunay triangulated graph. This can result the matching as a sub-graph to sub-graph instead.

The probability of matching a triangle in one image with a false triangle in another image increases during the triangle match. In contrast, the probability of matching a sub-graph in one image with a false sub-graph in another image reduces because the sub-graph becomes large and comprises multiple Delaunay triangles. Further, the complexity of matching a set of minutiae from one image segment arbitrarily to another similar set in a compared image segment is vastly reduced because of the Delaunay triangulation. This is particularly advantageous because the number of minutiae can be very large in handprint systems which consist of multiple fingers and multiple regions of the palm [11].

This research presents an alternate approach based on a graph incorporated with the Delaunay triangulations. An extended graph with a set of minutiae-based triangles imparts invariance to similarity transformations, such as translation, rotation, and scale changes. This work investigates if the proposed algorithm can be used in handprints and presents an invariant feature representation in a common framework so that the algorithm can be applied for any segment of the hand acquired using touch-based sensors from any surfaces. The proposed algorithm eliminates the effect of geometrical variations in the handprints without any manual pre-alignment process and can be extended to the forensic domain where only parts of handprints are available. The outline of this work is summarized as follows:

• Introducing the algorithm based on new variant of graph matching with triangles using invariant feature representation.
• Evaluating the algorithm using fingerprints with geometrical variations and investigating palm prints with geometrical variation, partial-quality, and extremely degraded impressions that resemble latent prints.
• Comparing the method with the state-of-the-art scale-invariant feature transform (SIFT) features.

The remaining of the article is organized as follows: Section 2 discusses minutiae-based related work in touch-based fingerprints and palm prints; Section 3 illustrates methodology with the algorithm description, data preparation, and experimental setup; Section 4 discusses experimental results. A conclusion and the future direction are provided in Section 5.

2. Related Work

2.1. Fingerprint

Fingerprint recognition systems are categorized into minutiae-based, texture-based, and correlation-based [12]. In the minutiae-based approach, a set of minutiae that correspond to one another between two fingerprint images is used to compute a match score, whereas in the correlation-based approach, the cross-correlation between the two images after geometrical transformations to obtain the best fit provides a match score. On the other hand, selected points and their surrounding areas are passed through texture extraction filters, and the filter outputs are used to obtain a match score in the texture-based approach. Minutiae, as features, have the attributes of simplicity and some tolerance to non-linear distortion [13] and are hence widely used, which leads the minutiae to be accepted as a discriminative feature of choice in fingerprint systems.

Existing minutiae-matching structures are distinguished as: (i) nearest-neighbor-based; (ii) fixed-radius-based; (iii) minutiae-triangle-based; and (iv) texture-based local structures. Nearest-neighbor-based structures use minutiae with their x, y coordinates and orientation information for one-to-one minutiae matching. This leads to non-linear deformation and does not guarantee the best performance in existing systems [14]. Cao and Feng [15] proposed a fixed-radius-based minutiae-star structure, while Cappelli et al. [16] introduced minutiae cylinder code (MCC), where angles between neighboring minutiae and their relative positions are described by Gaussian filters. However, methods that match only using minutiae coordinates and angle are not robust against geometrical variations or distortion.

The work in [17] used a variable distance approach using K-nearest neighbors, the distance between the core points, and the distance between the minutiae. Since the core point is difficult to define in the arch-type fingerprints, and it is not always visible due to the degradation and noise, the work in [18] used a faster region-based convolutional neural network (R-CNN) to find its own reference point. The existing works using neighboring edges and core points are suitable only for images with good quality [19] and will fail if there is an error in detecting the core point.

Since minutiae topological structure provides inadequate information to overcome geometrical transformations of the matching images, many researchers exploited minutiae-related local structures, such as ridge frequency, ridge orientation, relationship and curvature [20,21]. The methods of minutiae-based fingerprint matching represented in the literature involve the use of minutiae pairs, minutiae triplets [9,19], Delaunay triangles [8,10], and minutiae quadruplets where minutiae direction and coordinate information are commonly used for the matching of two fingerprint images. This information, however, is sensitive to geometric transformations which necessitate image alignment before the matching process.

In the minutiae-based polygon approach, pairs of minutiae and surrounding textures were used in the past, which needs an additional alignment step as one minutiae pair can match many pairs of minutiae located on different regions of the compared image. On the other hand, Miguel [9] exploited minutiae triplets where the feature vector consists of angles and distances between minutiae of a triangle. However, one triangle on an image can still possibly match more than one triangle on the counterpart or compared image. Further, using distance between two minutiae as a feature is not always feasible if there is a scale change during image capture.

Deng and Huo [10] exploited Delaunay triangles, where one pair of minutiae was used for alignment of an edge, and then the matching process was performed. In this work, a local structure was formed by the selected concerned minutia and its adjacent minutiae. There are two major computations in this method during the matching of two images, which doubles the computational cost [10]: (i) matching of the pair of minutiae (for alignment) and (ii) matching of minutiae triangles. Again, a pair of minutiae that match may not always be reliable, as one pair of minutiae can match several pairs of minutiae at different locations of a compared image. As the length of the triangle edges is used in the feature vector, the reliability can also be affected by skin stretch and image distortion. This would affect the pair for minutiae matching. The second phase of this matching (triangle matching) started based on the previous minutiae pairs. Further, there is no information about the position of these matching triangles on the two images, and therefore, the located triangles in the match pair apparently can be identified at two different locations of the compared images. The limitation of this approach is its computational cost, as two similar types of computations take place when the surface area is increased from that of a fingerprint to a full hand. The two levels of matching also make this method inefficient. This can be addressed by an alternate approach where image alignment and matching process can be brought under single computation based on a Delaunay triangulation match, and triangle mismatch at different locations can be overcome by graph extension at the same time.

2.2. Palm Prints

Fingerprints are not the only source of identification information used in forensics, and palm prints have also been used for a long time. They are often left on surfaces at a crime scene as latent and transferred as images. The matching of palm prints is more complicated because palms are larger in area, and they have larger numbers of minutiae obtained within smaller regions. Hence, an automated system for storing and comparing large numbers of palm prints has not been pursued in the same manner as for fingerprints. Lately, palm images have also been used in biometric identification for other purposes, and research has been conducted into their processing, alignment, feature extraction, and matching methods [22]. Fingerprint processing methods cannot be directly used with palm images, and they need modifications to address additional challenges.

Existing feature extraction methods in palm prints are categorized as structural-based, statistical-based, sub-space-based, and texture-based approaches. Structure-based methods use minutiae points, ridges, singular points, and creases/lines as prominent attributes, while statistical-based methods use entropy, energy, mean, and variance features. Sub-space-based methods use linear discriminant analysis, independent component analysis, and principal component analysis. Texture- and transform-based methods adopt Fourier transform, wavelet transform, and Gabor wavelet features [23]. The limitation of this approach is its computational cost.

The benefits of statistical-based feature extraction are its lower sensitivity to noise and simple process for feature extraction. However, this approach loses a lot of structural discriminative information. Therefore, the structural approach is mostly preferred over statistical methods [24]. Existing palm print feature representations primarily use minutiae, ridges, and creases, followed by fusion of features or scores using palm segments [24]. Matching of image segments is achieved as full- vs. full-print matches, partial- vs. full-print matches, and partial- vs. latent-print matches.

2.2.1. Match between Full Palm Prints

Most of the existing works in contact-based palm prints use the structural approach. The researchers in [24] proposed a system using the fusion of multiple features, particularly palm lines, ridge density, ridge orientation, and minutiae. The limitations of this work are: (i) images need a manual alignment for geometrical transformations, and (ii) features are not robust to distortions, are time consuming, and have a high complexity as they are still analogous to fingerprinting techniques.

Dai et al. [24] attempted a segment-based approach for a full-palm print system. However, it needs a manual segmentation before processing. Feng et al. [25] addressed a minutiae-based approach for full palm prints. Since the full palm print was crowded with a large number of minutiae and image distortion, region-wise or segment-based palm prints were processed to minimize such issues. Radial triangulation of minutiae was used for feature representation, which can practically be affected by skin stretch. Raymond et al. [26] exploited fingerprint-based methods using minutiae where palm prints were manually segmented into thenar, hypothenar, and interdigital segments. The segments were separately processed as individual prints, and scores from each segment match were fused.

It is outlined in the literature that minutiae-based palm print matches either adopted manual alignment of images before the match or manual segmentation of the full palm prints into distinct regions before processing. Therefore, the existing minutiae-based approaches in such prints have some limitations to overcome the geometrical transformations of the impressions in a real-time scenario. In the work proposed by Liu et al. [27], a general matching process starts with one-to-one minutiae match and followed by their neighboring minutiae recursively. The work in [28] used minutiae quadruplets where four minutiae together worked as a set for the match. In complexity perspective, the orders of complexity for minutiae-triplets, quadruplets and Delaunay triangles are $O\left(n^3\right)$, $O\left(n^4\right)$ and $O\left(n\right)$ respectively (where n = total number of minutiae) [11]. Therefore, minutiae quadruplets have higher complexity.

The majority of the contact-based palm print feature representation is based on minutiae. However, fewer investigations are noted in the literature that experimented with minutiae-based triangles in contact palm prints. It would be advantageous if we used minutiae-triangle-to-triangle matches instead of minutiae quadruplet matches (in the complexity perspective) or one-to-one minutiae matches (alignment perspective). This approach can help to mitigate the issues that arise from the accumulation of spurious minutiae and the process of region-wise palm print segmentation. For instance, one minutiae can match with many spurious minutiae, while one minutiae triangle can match with a smaller number of false triangles compared to minutiae matches. On the other hand, one triangle-based graph can match with a much lower number of false minutiae-based graphs compared to all of the above.

2.2.2. Match between Partial vs. Full Palm Prints

In partial-to-full palm print matching, the live-scan prints are acquired from a high-resolution scanner. The prints have similar geometric and photometric constraints as those in contactless images, and therefore, they need an alignment process before matching. Apart from minutiae-based matching, texture- and transform-based approaches were in practice with contact-based palm prints. However, these approaches have to address the image alignment problem [29]. Since partial palm prints have fewer structural features, image-based (texture) features were exploited in these systems. For an instance, the work in [30] used Gabor filter features by combining multiple regions of the palm features to give a good solution during the application of access control. Similarly, Lucia et al. [22] exploited scale-invariant feature transformation (SIFT) descriptors in high-resolution contact palm prints where the correspondences between key points are estimated by the Euclidean distance of the descriptors. The work in [29] used both iterative closest points (ICP) and palm-line orientation information for the processes of image alignment and matching, respectively. However, because of having noise in the palm line and using orientation features, the ICP algorithm cannot guarantee the accurate alignment of correspondence image pairs.

It is outlined from the literature that several contact-based palm prints used line and orientation-based features in the early days [31]. Line or edge detectors were used to extract such features using differences in Gaussian filters (DoGs) [32], Gabor filters [33], and Radon transform filters [34]. However, they have certain limitations. For instance, the DoG-based method is sensitive to noise and illumination. Since partial palm prints have fewer structural features and are full of lines, textures and orientation-based features have also been exploited using orientation-based descriptors, such as palmcode, competitive code [35], fusion code, the robust line orientation code method (RLOC) [36], and double orientation code (DOC) [37]. However, it is noted that during the process of orientation extraction, none of the filters show the same orientation as the palm print line [38]. Further, the CompCode approach is based on the Gabor features [39,40]. To use the Gabor filters, the images should be aligned or a key point should be detected for the initial alignment of the pair of matching images. The region of interest should already be determined. This can be applied for all the variants of CompCode, such as RLOC, DOC, etc. This is the main issue in the filter-based texture features, along with the computational cost [41].

The work in [30] combined multiple regions of the palm features with Gabor filters. However, this method solely depends on manual segmentation of the palm into several regions and used regional fusion of palm print segments. Further, using Gabor features in a larger surface area can have higher computational cost. Therefore, the feature encoding for handprints needs to be designed to incorporate the automated image alignment (for geometrical transformations) and less computational cost. Further, the feature representation of contactless palm print images cannot be directly used in contact images due to low image quality and low resolution because contactless palm print or handprint approaches use multiview image [42,43] and multiresolution [44] image capture with multimodal approaches [45,46]. These strategies help performance-related issues arising from image quality and low resolution. This leads towards a fair way of adopting minutiae-based invariant representation rather than image-based structural features.

2.2.3. Latent Prints

Minutiae are a common feature used for palm print identification [47], while they played a role in latent prints, and they can be extracted automatically [48]. However, the presence of a load of minutiae is a major issue in latent prints due to the extreme lower image quality similar to Figure 2, which requires a larger processing time for handling them. Another issue is that there may be an overlap between the pair of prints during the match, which can lead to diminishing the system’s efficiency. Further, manual marking of the minutiae is also practiced in latent prints.

In the literature, Wang et al. [18] used radial triangulation of minutiae for alignment of images. This yields estimation of the likelihood ratio of the matching images, rather than providing an actual match decision. Liu et al. [27] used clusters of minutiae-based on ridge period descriptors and orientation of ridges to overcome the issue of an enormous set of minutiae present in the latent prints. However, fake points and print overlap remain in the prints, reducing matching performance. The work in [49] used a triangular sign and a minutiae vicinity descriptor (which is a counter of neighboring minutiae in the extended triangle set) along with the process of manual minutiae marking to overcome the spurious minutiae and noise. A recent work exploited a deep-learning-based method for feature extraction [50]. However, deep learning methods are in early stages in latent domains and need more images for training to avoid over-fitting.

It is summarized that the existing work on the latent prints still holds the alignment issue and practice of manual marking of the minutiae. Since latent prints can be obtained from any part of the hand, it is not clear in the literature how geometrical variations in the images are normalized without any manual support. Further, the use of minutiae triangles or polygon-based minutiae matching is comparatively less practiced with latent prints.

Further, the majority of existing contact-based biometric matches used either fingerprints or palm prints for a single instance or in a separate platform and did not evaluate both types of impressions in a combined single framework. If there is an algorithm to handle any print from a hand, then the civilian applications and the forensic domain will obtain benefit from being able to process the prints from several parts of a hand surface. In a similar way, multiple contact-based prints from a hand also would obtain benefit by using a single algorithm. Since minutiae and ridges are common features for both prints, there is a possibility of utilizing all prints from a hand in a single framework. If an algorithm based on the minutiae is proposed for these prints, it should support (i) geometrical normalization of two images; (ii) elimination of manual marking of minutiae; and (iii) elimination of spurious minutiae. In this context, the Delaunay triangulation and graph-based algorithm are proposed in this paper as it would be advantageous in contact prints when there is no information about where the prints from a hand are obtained. Delaunay triangles have lower computational complexity compared to the other minutiae triangles and quadruplets during matching, which is proportional to the time complexity.

Combining different impressions from a hand using a single framework and introducing a new algorithm using minutiae or minutiae-like key points can be a new approach. When severe distortion in contact prints affects the presence of minutiae, minutiae-like points, such as pores and palm-line intersection points, can also be utilized in high-resolution partial and latent prints during cross-matching modality.

Since lines, wrinkles, and distortion generate a large number of spurious minutiae, the algorithm should carefully handle them and automatically align the prints before matching. Further, it should preserve the invariant nature for geometrical variations. The proposed approach is summarized with three alternative strategies below:

• Defining a feature vector to show invariant properties. To eliminate scale and rotation variations of matching images, the feature vector consists of triangle features except the length of the triangle. This can help to tolerate scale and small angle changes due to the spurious minutiae (when forming triangles).
• Introducing the graph-based Delaunay triangulation match, where all triangles in an image are compared with the triangles in a counter image, and the triangles are allowed to grow further by adding more nodes/minutiae to a certain extent.
• If we perform only triangle-to-triangle matches, then there is a possibility of having one triangle match with many false triangles at several locations in the counter image. To systematically check the true match, an additional validation process of the previously matched triangle-based graphs is introduced. The probability of a sub-graph (formed from the matched triangles) matching with false sub-graphs in the counter image due to the false minutiae would be comparatively lower than the triangle match. This eliminates spurious minutiae-related graphs in the larger hand surface area, and then the validated graphs are merged.

3. Proposed Method

In this section, the proposed algorithm is briefly explained. When there is a triangle match between a pair of images, there is a possibility of having a match between neighboring triangles of the initially matched. These all-matched triangle sets are known as sub-graphs. The sub-graph is formed by connecting minutiae with the initial triangle and extended until there is a match among the neighboring triangles. At a point, the sub-graph may stop without growing due to the presence of partial occlusion or degradation.

Now, if one triangle on an image matches with two triangles on another image due to the spurious minutiae, then there would be a possibility of forming many distinct independent sub-graphs in different locations of the counterpart of the image. Further, in a handprint, one minutiae- -triangle-based sub-graph may be formed in finger segment, while the other sub-graph may be in palm segment. The region between these two sub-graphs could be distorted or not clear due to the degradation. Therefore, there would be a problem to extend such sub-graphs further. In the end, there would be many sub-graphs, and all of these sub-graphs may not be reliable. That means, one sub-graph can match with two or more sub-graphs in different locations of the counter image due to the bombardment of spurious minutiae. Then, there should be a mechanism to make such sub-graphs grow further and select the best reliable sub-graphs among them to form an authentic minutia-based graph. This is the base idea of the proposed algorithm.

In the literature, Jose et al. [51] worked with latent palm prints using a single graph which is connected from a set of neighboring triangles. But the graph can be extended until there is a match among the neighboring triangles. And it is noted that the work used manually marked minutiae information for the image alignment process. There are a few questions left in this work: (i) What if the graph stops at a certain point without growing due to the presence of occlusion or degradation? (ii) How would the bombardment of spurious minutiae be eliminated? (iii) How would geometrical alignment of the images be achieved? (iv) How would the matched triangles and graph be validated? (v) How could the computational complexity be compromised (due to the spurious minutiae present on image)? These questions highlight the gaps, and the work in [51] concluded without addressing these issues. Further, their feature vector used the distance of a triangle side that can be affected by skin stretch.

In this context, the following aspects are introduced in the proposed method:

• Invariant feature representation—a feature vector of a triangle is proposed to tolerate scale and rotation variations of images (distance of a triangle side or ridge count are eliminated in feature vector).
• Geometrical alignment—image alignment is achieved using initial triangle matching and the matched triangles are used as reference locations. This process helps to automatically align the images.
• Computational complexity in processing a larger surface area—Delaunay triangulation is used to lower the computational complexity of the minutiae-based triangles in an increased hand size with a large number of spurious minutiae.
• Elimination of spurious minutiae—this is achieved by verification of independent matched triangles and validation of sub-graphs. Since spurious minutiae can generate false triangles on handprints, we can discard some of the sub-graphs formed from the false triangle match after validity checking. The sub-graphs are validated based on the number of minutiae each graph holds (threshold).

3.1. Delaunay-Triangle-Graph (DTG) Algorithm

The algorithm namely, the Delaunay triangulation graph (DTG) is introduced for handprints using minutiae or minutiae-like key points, and it focuses on an automated alignment of geometrically transformed images. Minutia-based triangles are generated from Delaunay triangulation. Now, this preliminary process estimates the possible set of matched triangles (likelihood) using a simple minutiae-based feature set as shown in Figure 3. By observing the figure, these sets of matched triangles cannot be the final matched triangles. However, existing past work considered these triangle sets as final matched triangles.

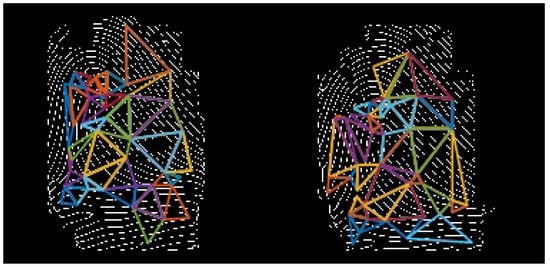
Figure 3. Phase 1: Initial output of the matched triangles in test and template images. They are called base triangles and act as reference triangles for further processing. Note that different colors indicate matched triangle pairs. One triangle can match more triangles at a time, and they do not show exact matches (i.e., false matches are possible here). This process shows only the possible matched triangles and provides landmarks for the next phase of the algorithm.

Therefore, they can be checked further in the subsequent step by accepting or discarding the triangles using a validation mechanism because, in latent and contact-based hand prints, the triangles matched in the initial step may not be reliable due to the dispersion of minutiae. Therefore, this process requires further extension. The algorithm consists of following phases: (i) base triangle generation; (ii) extension of sub-graph; (iii) elimination of sub-graph; and (iv) merging of sub-graphs to form the DTG. The overall process of the DTG algorithm is illustrated in Figure 4.

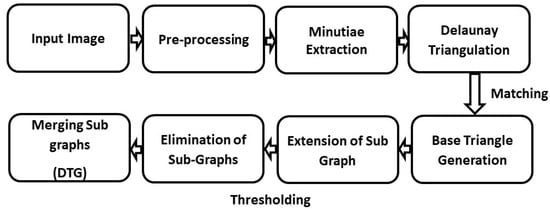
Figure 4. Overall flow of the Delaunay triangulated graph (DTG) algorithm.

3.1.1. Base-Triangle Generation

The algorithm initially searches a set of a possible number of matching triangles $\left(N\right)$ from Delaunay triangulation. A collection of reference locations is initially identified from a set of matched minutia-based triangles, namely, base-triangles, as shown in Figure 3. These triplets are a set of possible matched or similar triangles which are then identified as reference locations for further extension and used for image alignment as well. The feature vector for the triangle match is stated in Equation (1).

$$fv=\{{\theta }_p,t_p,o_p,o{d}_p,{\theta }_q,t_q,o_q,o{d}_q,{\theta }_r,t_r,o_r,o{d}_r\}$$

(1)

where

• p, q and r—minutiae right to left order;
• $\theta$—triangle angle;
• t—minutiae type;
• o—orientation of a minutiae from right to left;
• od—orientation difference between adjacent minutiae.

3.1.2. Extension of Sub-Graph

In this phase, the matched triplets in two images are chosen as base triangle pairs and located as reference triangles. Each base triangle is then expanded by adding neighboring triangles by comparing the neighboring triangles’ spatial locality information with the previous matched triplets. This process formed a certain number of sub-graphs in a disjoint manner. Here the triangles may or may not share a pair of edges or pair of minutiae for the alignment of images. This is a validation process of the previously matched triangles. At the beginning, the first base-triangle pair is selected as an initial reference location to proceed as follows:

• Task A—Computation of orientation and distance information between the pair of base-triangles.

Initial reference location is identified by selecting the base-triangles in template and test images. The features of three minutiae between first and second base triangles are computed as shown in Equation (2). A similar process is followed in test image as well.

$$\begin{array}{c}{\varphi }_n=o{r}_n-o{r}_m\mathrm{and}{\varphi }_n^{\prime }=o{r}_n^{\prime }-o{r}_m^{\prime }\end{array}$$

(2)

• $o{r}_n$—orientation of nth minutiae in the first base triplet in template (n = 1, 2, 3).
• $o{r}_m$—orientation of mth minutiae in the second base triplet in template (m = 1, 2, 3).
• $o{r}_n^{\prime }$—orientation of nth minutiae in the first base triplet in query image.
• $o{r}_m^{\prime }$—orientation of mth minutiae in the second base triplet in query image.

A distance between nth and mth minutiae (where m = n) in the first and second base triangles in template image is computed as $Di{s}_n$. A similar process is followed in the query image and the distance is ${Dis}_n^{\prime }$. Since distance feature can be affected by skin stretch, a distance ratio is used for further computation.

• Task B—Computation of distance ratio and orientation difference between template and probe.

$$\begin{array}{c}DRa{t}_n=Di{s}_n/{Dis}_n^{\prime }\\ {\varphi }_{D}i{f}_n={\varphi }_n-{\varphi }_n^{\prime }\end{array}$$

(3)

$\left(DRa{t}_n\right)$—Ratio of two distances between the base triangles acquired from template and test images.

$\left({\varphi }_{D}i{f}_n\right)$—Orientation difference between the base triangles acquired from template and test images.

To form a sub-graph, a minutia node in the second base triangle was added to the nodes of the first base triangle if ${\varphi }_{D}i{f}_n<\theta$, $DRa{t}_n<d$. Trial and error experiments were used to empirically determine the values for d and $\theta$.

The above two steps are significantly different from the existing past minutiae-triangle-based work. The majority of them used distance and orientation of minutiae in a triangle as features. The triangle matching was one–one or one–one graph matching with a centralized minutiae. The validation of those final matched triangles is completely ignored. The relative information about the neighboring triangles of a previously matched triangle is comparatively ignored. Here, we have used such information and utilized the distance ratio between two base triangles in order to overcome the scale change and distortion.

• Iteration of Tasks A and B

The processes of A and B were repeated until computing the relational information between the first base triangle and the remaining $(N-1)$ triangles. This process generates a sub-graph with fewer or more triangles based on the matching images from different individuals or the same individual.

• Iteration of Tasks A, B, and C

For the continuation of the above process, the second base triangle was located as initial reference point. The process was repeated to finalize that the Nth base triangle was referenced. Sub-graphs were generated through this process, as shown in Figure 5, where one triplet is the base triangle or reference location and the other triangles are related triangles with the base in each graph, and they match with their counter part.

Figure 5. Phase 2: graphs generated in template image and their matching counterparts in test image are shown. Each sub-graph is started from initial base triangle (initial matched triangle) and extended with other triangles if there is spatial connectivity among other matched triangles. Any sub-graph which consists of a threshold number of minutiae is selected as a reliable sub-graph and the remaining sub-graphs (with fewer minutiae) are discarded.

3.1.3. Elimination of Sub-Graphs

There is a possibility for obtaining largely extended or shorter sub-graphs depending on the match between two images acquired from the same or different individuals, respectively. Therefore, a threshold value for the number of minutiae present in a sub-graph was used to extract the reliable sub-graphs at the end. The threshold value was determined by trial and error experiments, and it completely depends on the nature of prints.

3.1.4. Merging of Sub Graphs

The validated sub-graphs were then merged, which formed the DTG. The minutiae belonging to this DTG graph were considered as reliable minutiae, and they have been used for score computation.

3.2. Data Set

The focus of this work is an investigation for a method that can suit touch-based impressions acquired from a hand using a common key-invariant feature representation. It needs to tolerate geometrical variations in compared images and eliminate any pre-alignment process. To obtain many sub-graphs, we need partial prints with sufficient minutiae, and they should show enough geometrical variations. The prints are selected based on the number of minutiae each holds. If a print holds a lower number of minutiae that is not sufficient to form a minimal graph, that print is discarded. The algorithm should be validated in each of the above-mentioned specific experimental criteria.

We have used fingerprints and palm prints for the experiments. The fingerprints were acquired from publicly available FVC2002 DB1 [52] data set. which consists of sufficient minutiae to form multiple sub-graphs. The data set is further split into two sets:

• Fingerprints without geometrical variations (without rotational changes). Fingerprints from 35 users –> 2–4 images from each users were used.
• Fingerprints with geometrical variations (with rotation and scale changes). Fingerprint images from 67 users were used for this evaluation.

We have used palm print image segments from the publicly available THUPALMLAB database [53], which consists of palm prints acquired from 80 users captured from commercial scanner with a range of quality variations. They are high-resolution images with 2040 × 2040 pixels. This data set was evaluated in several contact-based palm print applications in the existing literature [26,54]. We have selected the hypothenar region of the palm. The work in [26] experimentally proved that this region comparatively performed better than the other regions. The segments show sufficient geometrical variations for the evaluation, as shown in Figure 1 (eight segments of prints from a single individual). It is noted that the data set with extremely-low-quality prints generated a large number of spurious minutiae. To categorize the images into different categories, such as partial-quality and low quality, we experimentally counted the number of minutiae each print holds. If the count is exceptionally large and shows a great deviation from the average number of the minutiae range each print holds, then the image is considered as extremely degraded and cluttered with a large number of false minutiae. To confirm this process, we manually checked each print. The data set was split into two categories as follows:

• Partially degraded images acquired from 35 users (Figure 1).
• Extremely low-quality impressions acquired from 40 users (Figure 2).

The evaluations were processed using partial-quality images with geometrical variations and extremely-low-quality impressions with geometrical variations.

4. Experiments

The overall experimental procedure of the hand-based system includes the process of pre-processing, feature extraction, matching, and score computation, as shown in Figure 6.

Figure 6. Overall procedural flow of the hand-based recognition system for full-hand biometrics.

4.1. Pre-Processing

Since the images acquired from fingers and palm were touch-based, an enhancement of the prints is applied where ridge orientation and ridge frequency estimation processes are performed. The enhancement is followed by the Gabor filter proposed in [51] with the impressions to improve and preserve highly-curved ridges.

4.2. Feature Extraction

The feature extraction phase followed a set of processes to localize minutiae-based triangles.

• Binarization

A binary transformation is performed on enhanced greyscale image using an adaptive threshold. In binarization, each pixel is assigned as ‘0’ and ‘1’ based on the small and large intensity mean in the local neighborhood within a block respectively.

• Thinning

To locate the feature points in the binary image, the thickness of the ridges was minimized to a single pixel through the skeletonization process.

• Feature-point localization

The ridges show endings and some branches which were then localized as end-points and bifurcations, respectively.

• Delaunay triangulation

In this algorithm, the Delaunay triangulation concept was applied to form a connected graph from a set of identified minutiae. The feature vector, fv, is stated in Equation (2). The overall feature extraction process is illustrated in Figure 6.

Since the Delaunay triangles are sensitive to false minutiae, these need to be eliminated from the pool of minutiae set. The work in the literature [55] supports handling false minutiae in fingerprints. However, palm prints are too degraded and have a tremendous number of minutiae, as shown in Figure 7b. Further, removing false minutiae is not a simple process in this case, and the existing false minutiae removal algorithm cannot support this as it was designed for fingerprints with a lower number of minutiae within a smaller area. Therefore, the proposed algorithm works itself to eliminate false minutiae-related issues in the handprints. This process was ensured by triangle-to-triangle matching that leads to graph-to-graph matching. It is obvious that the probability of matching a graph with false graphs is lower than the minutia–minutia match or triangle–triangle match. Any false graphs formed from the false minutiae are automatically discarded when selecting reliable graphs using a threshold value which is generated based on the number of minutiae each graph holds.

Figure 7. Minutia localization of a palm print image: Subfigures (a,b) illustrate enhanced image and localized minutiae set, respectively. Note that the minutiae set in subfigure (b) consists of genuine and spurious minutiae. The yellow spots highlight endpoints, while red spots indicate bifurcation of ridges. To evaluate the algorithm’s applicability with the palm, a hypothenar segment of a palm print was used to minimize the overloaded minutiae.

4.2.1. Matching

It is noted that contact fingerprint state-of-the-art methods primarily focus on minutiae-based triplets, quadruplets, and minutiae-pair matching. However, there is a possibility for matching two triangles/quadruplets in different locations of the images with the same features. The work based on the Delaunay triangulation matching in the past work performed triangle–triangle matching, and the scores were computed using only initial matched triangles. There is no mechanism for checking reliability of the initial matched triangles. Further, the existing matching strategies cannot directly support both partial prints and latent prints.

The work in this paper has performed a few further steps to (i) check the reliability of such initially matched triangles; (ii) extend the triangles form several sub-graphs; (iii) eliminate unreliable sub-graphs; and (iv) fuse the disjoint sub-graphs based on a validation threshold. The threshold value is generated based on the number of minutiae each graph holds.

The assumption made here is that if there is a match between two triangles in two images captured from the same individual, then the related information around that particular triangle with all the other neighboring triangles will also be matched. Then, the initial matched triangles can grow further, and there is a possibility for the formation of several sub-graphs based on the initial triangles, and these sub-graphs can be identified in different hand locations.

In contrast, if there is a triangle match between two images captured from two different individuals, there would be a possibility of having less extension of the initial triangle, and it would form fewer sub-graphs. It is obvious that the volume of sub-graph growth would be small and it would stop early in the process. In this point of view, the minutia-based matching triplets obtained from the initial phase were checked.

In the first phase of the algorithm, base triangles (initially matched triangles) were formed by matching Delaunay triangles between the template and probe pairs. An illustration of the phase 1 of the algorithm with a set of matched triangles is shown in Figure 3. It can be observed that some of these triangles do not actually match the other triangles in the counter part, and the matched triangles may or may not be reliable, as spurious minutiae can have significant effects in the process of initial triangle formation. Therefore, there is a need for another step to check the reliability of the initially matched triangles in Figure 3. They were validated in the second phase of the method. At the end, a collection of sub-graphs is generated, as illustrated in Figure 5. False sub-graphs were eliminated using the threshold number of minutiae each graph holds. The extracted sub-graphs were then merged, and DTG was formed.

4.2.2. Score Computation

Since we have used the number of triangles based on the minutiae, the matching of two images was processed based on the number of matched triangles in the final stage of the algorithm. A ratio between the total Delaunay triangles and the number of matched triangles in the final graph (combination of sub-graphs) was used to compute the score (s), as shown in Equation (4), where p is a set of minutiae used to generate matched triangles and q is the total number of minutiae used to generate Delaunay triangulation at the initial state. We have computed the number of the genuine-accept rate (the match between the images from the same individual) and the number of the false-accept rate (the match between the images acquired from different individuals) based on the different threshold values of scores.

$$\begin{array}{c}a=\frac{p!}{3!(p-3)!},b=\frac{q!}{3!(q-3)!},s=a/b\end{array}$$

(4)

5. Results

5.1. Handprint Segments from Finger Region

Experiments for fingerprints have been performed using partial-quality images which contain sufficient minutiae to form a graph in a print. The images have been divided into two different data sets with geometrical variations and without geometrical variations. From the images with geometrical variations, particularly with the scaled and rotated images, the following results are obtained as illustrated in Table 1. For the former experiment using 200 genuine and 8538 impostor matches, an equal error rate (EER) of 1.87% is obtained with a 97% genuine-accept rate (GAR) at a rate of 1% false-accept rate (FAR). For the later experiment using 962 genuine and 67,944 impostor matches, an EER of 1.97% was obtained with 94.25% GAR at a rate of 1% FAR.

Table 1. Performance evaluation of fingerprint matching using the algorithm based on Delaunay triangulation and graphs.

Fingerprint Quality and Geometrical Variations	No. of Genuine Tests	No. of Impostor Tests	GAR	FAR	EER
Partial-quality images without geometrical variations (35 users)	200	8538	97.3%	1%	1.87%
Partial-quality images with geometrical variations (67 users)	962	67,944	94.2%	1%	1.97%

It is observed in the graph illustrated in Figure 8 that the algorithm performed well with the fingerprints that show geometrical variations. The algorithm proves its invariant nature for the images and opens a path to investigate other properties of the prints. It strongly gives a recommendation that if a hand segment is acquired from a finger region that can show sufficient minutiae, the algorithm would definitely support it. The next experiment has been planned to investigate the robustness with degradation present in the images.

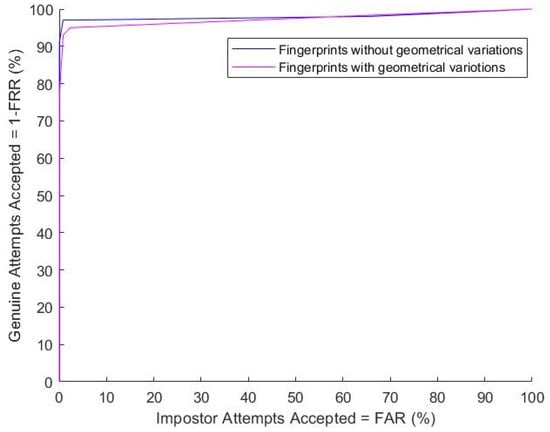
Figure 8. The comparison between FAR vs. GAR in fingerprint images with and without geometrical variations.

5.2. Handprint Segments from Palm Region

An experiment has been exploited to investigate how the algorithm can be incorporated with the handprints acquired from the palm region. We need partial-quality and extremely-low-quality (with severe degradation) handprints for separate evaluation. The THUPALMLAB database consists of a range of image degradation. Since the algorithm is not much affected by geometrical variations, we have used palm segments that show sufficient geometrical variations (Figure 1). The THUPALMLAB database has been split into two sets: (i) partial-quality images with geometrical variations and (ii) extremely-low-quality (severe degradation) images with geometrical variations. We have used the hypothenar region of the palm prints as this segment comparatively performed better than other regions for the state-of-the-art algorithm [26].

The THUPALMLAB database (left) consists of 600 images from 75 users, and it has been divided into two sets. Partial-quality images from 35 users and extremely-low-quality images from 40 users were divided. To differentiate the images into different categories such as partial-quality and low-quality images, we experimentally counted the number of minutiae each print holds. If the count is exceptionally higher than others and shows a great deviation from the average number of minutiae range each print holds, then the image is considered as extremely degraded and it is assumed it is cluttered with a large number of false minutiae. To confirm this process, we manually checked each print and compared them. The performed experiments are as follows:

• Experiment using partial degraded images with geometrical variations.
• Experiment using extremely degraded images with geometrical variations.

5.2.1. Experiment Using Partial Degraded Images with Geometrical Variations

The experiment has been performed using 200 segments acquired from 25 users where 1400 genuine and 38,400 impostor scores have been generated. The data set shows a performance of 88.5% GAR at a point of 5%, and an EER of 5.76% is reported with this data set. In another experiment, a set of 280 segments from 35 users has been used as templates and probes, which generated 1960 genuine and 76,160 impostor matches. A performance metric of 90% GAR at a point of 5% FAR is observed, and an EER of 5.69% is reported with this data set. It is observed from the results that the increased size of the data set slightly increases the genuine-accept rate of the system and reduces the EER.

5.2.2. Experiment Using Extremely Degraded Images with Geometrical Variations

In practice, the image degradation in contact-based impressions is large in scale. Particularly, in forensic scenarios, the image quality will be worse than the other contact prints. Therefore, we have conducted a separate experiment using low-quality images that are similar to forensic impressions, as illustrated in Figure 2. Extremely-low-quality and degraded palm print segments have been used in this experiment.

For this experiment, a set of images from THUPALMLAB database with 320 templates and probes from 40 users has been used. This generated the scores of 2233 genuine and 99,525 impostor matches. A performance metric of 80% GAR at a point of 5% FAR is observed, and an EER of 6.94% is reported with this data set. Figure 9 illustrates the comparison of the above performance. Table 2 summarizes the results acquired from palmprint recognition for all three different conditions.

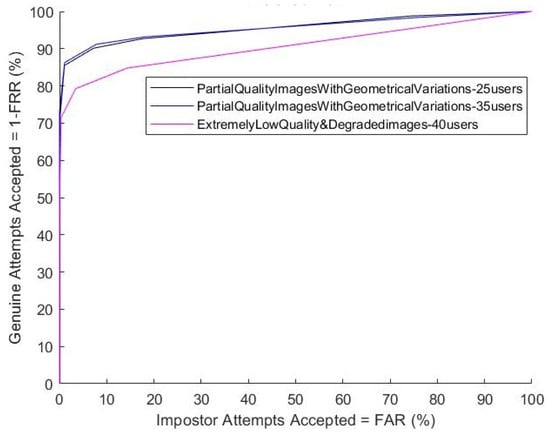
Figure 9. Receiver operating characteristic curve (ROC): The comparison between FAR and GAR in palm print segments images with partial-quality and extremely degraded images with geometrical variations. Note that the extremely degraded images are categorized by applying a criteria of having an exceptionally large number of minutiae beyond a range.

Table 2. Matching performance on different levels in palm print degradation with geometrical variations at 5% of FAR.

Palmprint Quality	No. of Genuine Tests	No. of Impostor Tests	GAR
Partially degraded impressions with geometrical variations (25 users)	1400	38,400	88.5%
Partially degraded impressions with geometrical variations (35 users)	1960	76,160	90%
Extremely degraded impressions with geometrical variations (40 users)	2233	99,525	80.33%

It is observed that when there is an increased number of partial-quality images, the GAR is slightly increased. Even though the impressions from the extremely-low-quality and degraded data set shows comparatively lower performance in term of EER, there is potential to use the algorithm with degraded prints and extend it to the forensic domain in future. Since our focus is to investigate how well the proposed approach can work with extreme cases in contact prints that resemble latent prints, the method still gives a positive motive to propose it towards general and forensic applications. It is obvious that the extreme cases are not always the majority in these applications. Therefore, the results indicate that the algorithm can cope with that scenario as well. Further, the comparison result of the algorithm outperformed the state-of-the-art SIFT features as outlined in Table 3. In that perspective, the proposed method can be acceptable to a certain level.

Table 3. Comparison of performance between the DTG algorithm and the state-of-the-art SIFT features [16].

Palm Print Quality Type	EER Using DTG	EER Using SIFT [16]
Partially degraded impressions with geometrical variations (25 users)	5.76%	7.60%
Partially degraded impressions with geometrical variations (35 users)	5.69%	6.44%
Extremely degraded (low-quality) impressions with geometrical variations (40 users)	6.94%	10.85%

It is noted that the state-of-the-art matching algorithms for the contact prints (fingerprint or palm print) were specifically implemented for full or partial prints in a single platform, which focuses on achieving best performance using full data set at any cost. On the other hand, the contactless domain explores Convolutional Neural Network (CNN)-based methods in addition to multi-view, multi-modal and multi-resolution strategies to achieve the best performance at any cost. The CNN-based methods need a larger size of data to overcome the over-fitting issue during training the model. Since our focus is not proposing an algorithm for fingerprints or palm prints only but investigating a common approach for contact handprints, the existing work in contact-based approaches is only considered for the comparison investigation.

Minutia-based and texture-based techniques are the majority of the existing work. The Gabor, SIFT, CompCode and its variants (RLOC, binary orientation co-occurrence vector (BOCV)) algorithms used the orientation of palm lines as the palm print features by using the Gabor filter. To extract the Gabor features, the ROI should have been already defined, and the images should be aligned based on any key points. This is the main issue in the majority of the filter-based methods, along with the computational cost [39,40,41].

It is not evidenced whether those algorithms can be applied to other regions of the contact prints of the hand in both civilian and forensic domains using a common framework. The goal of this work is to design an algorithm that suits any region of the handprint without any manual intervention or geometrical normalization of the images in contact prints. This will be evaluated using prints acquired from forensic domains in future. There is no such experiment in contact prints of hands that works under a common framework to compare our work.

Since this algorithm targets contact-based handprints, comparison of the state-of-the art methods for all combined prints is not mentioned due to the non-availability of the common algorithm. However, scale-invariant feature transform (SIFT) features have been investigated in both contact palm prints, fingerprints, and latent prints, and they do not need ROI estimation and manual alignment [56,57]. Therefore, the proposed algorithm was compared with the state-of-the-art [22] feature representation of palm prints using SIFT features. The CompCode and Gabor filter-based existing approaches have severe computational costs due the complexity and large palm print surface area, and therefore, the SIFT features were compared with minutia features.

From the analysis of results illustrated in Table 3, the DTG algorithm comparatively outperformed the SIFT features in term of EER in the two categories of the data set. It can be claimed that the DTG can perform in an automated way without any manual intervention or complex computational process for any handprints.

6. Conclusions

The investigation on the DTG algorithm gives a rationale for the methodology and validates the claims using impressions from handprints with a range of image quality and geometrical variations. It works well for fingerprint segments with geometrical variations. For the palm print segments, it demonstrates how far it works well with partial-quality and extremely-low-quality handprints while using only simple minutiae features. The handprint segments completely show geometrical variations, and the DTG is not very sensitive to similarity transformations present in the database. They resulted in comparatively better performance than the state-of-the-art method as well. Even though the performance with extremely degraded prints is comparatively less than the partial-quality prints, there is potential to use the DTG in extreme cases of the contact prints because extreme degradation is not always the majority case for contact prints. Further, it has an advantage to leverage the method in multiple regions of the handprints where poor quality regions would be merged with good quality regions of the hand. Therefore, the algorithm can be acceptable in algorithmic and application contexts.

In the algorithmic context, the proposed method uses only minutiae. However, there is a possibility for fusing other features if the quality of the images is good enough to show ridge information clearly. The processes of one-to-one minutiae match and false minutiae removal are replaced by graph match and graph validation that eliminate unnecessary computations for false minutia removal. In the application context, if any prints that show not only minutiae but any minutiae-like point-related information, that can benefit from the algorithm. As the method is invariant to geometrical transformations, any segment of the hand can be treated without manual alignment of the compared images.

The significance of the DTG is that it would be advantageous to adopt contact-based handprint system in access control and other civilian applications. On the other hand, the similar procedure can be adopted in forensic environment as it generally shows extremely-low-quality prints and forensic experts do not know which part of the hand the prints are obtained from. In that scene, the algorithm can produce some likelihood similarity for the matching images if they are too far degraded. In an overall context, the DTG is the output for the concept of one single algorithm for one hand.