Abstract
The present study was designed to determine the contribution of the cross-sectional area of the ski poles (Sp) to the total aerodynamic drag during alpine skiing. At three different wind speeds in a wind tunnel, 10 skiers assumed typical alpine skiing postures (high, middle, and tuck), and their frontal aerodynamic drag was assessed with a force plate and their cross-sectional area, along with that of their ski poles, determined by interactive image segmentation. The data collected were utilized to examine intra-subject variation in Sp, the effects of Sp on the coefficient of aerodynamic drag (Cd), and the product of Cd and total cross-sectional area (Cd∙S. The major findings were as follows: (i) Sp ranged from 0.0067 (tuck position) to 0.0262 m2 (middle position), contributing 2.2–4.8% of the total cross-sectional area, respectively; (ii) Sp was dependent on wind speed in the high and middle positions; (iii) intra-subject variations ranged from 0.0018 m2 (27.6%) in the tuck position to 0.0072 m2 (30.5%) in the high position; (iv) Sp exerted a likely effect on Cd and Cd∙S. The extensive intra- and inter-skier variability in Sp can account for as much as ~5% of the total frontal cross-sectional area and future investigations on how elite skiers optimize their positioning of the poles in a manner that reduces aerodynamic drag are warranted.
1. Introduction
Alpine ski racing, with its varying terrain and slope, gate set-up, and snow conditions, is extraordinarily challenging, requiring a high degree of technical skill and motor control [1]. These demands are compounded by the high average speeds involved: 54 km/h for Slalom, 65 km/h for Giant Slalom, 86 km/h for Super-G, and 94 km/h for Downhill [2]. Despite this complexity, which demands sophisticated biomechanical analysis [3], the only two forces acting that can slow down skiers are friction between the skis and the snow and aerodynamic drag [4,5,6,7] and skiing performance is improved by virtually any lessening of the former [8].
The skier’s posture, i.e., his/her area of frontal exposure, is the major factor determinant of aerodynamic drag, with less exposure resulting in higher speed and reduced overall race time [3]. Indeed, in connection with downhill competitions, differences in aerodynamic drag account for almost half of the difference in the finishing times of slower and faster skiers [9]. However, in giant slaloms, aerodynamic drag is not thought to be a major concern, accounting for only 15% of the total energy loss per turn [6]. At the same time, Meyer and colleagues [5] found that a giant slalom skier can reduce his/her energy dissipation due to aerodynamic drag by altering posture from dynamic to compact and, indeed, in this discipline aerodynamic drag accounts for 5–28% of all energy losses [6]. Clearly, the downhill and super-giant slalom, with their considerably higher speeds, involve more aerodynamic drag than slalom and giant slalom [10,11]. In light of the fact that the difference between the finishing times of elite alpine skiers competing for medals is often on the order of hundredths of a second [12], even very minor optimization of aerodynamic drag can be decisive.
To measure aerodynamic drag in connection with alpine ski racing, several experimental approaches have been developed for both speed [13,14,15] and technical disciplines [5,6,16]. Assessment of the coefficient of aerodynamic drag (Cd) and cross-sectional area (S), as well as Cd∙S, the product of these two, in wind tunnels have attempted to optimize body posture, showing that height, joint angles, and positioning of the arms and head all influence the aerodynamic drag [5,6,16]. Moreover, Cd∙S for the technical disciplines ranged from 0.63–0.66 in the high, 0.51–0.55 in the middle, and 0.23–0.24 in the tuck positions, which is generally lower than the corresponding values reported for the speed disciplines (0.15–0.4) [8,13].
Investigation of different body postures in a wind tunnel demonstrated that aerodynamic drag was 41% less with the arms in a tuck position than stretched out (as when jumping) [17]. Although the ski poles are positioned more or less transverse to the wind flow during the performance of all of the technical disciplines, including during the intensive turning involved in the speed disciplines (see, for example, Figure 1) and the poles (typically 120–135 cm in length for male skiers) are considerably longer than the arms and have baskets, their impact on aerodynamic drag remains largely unexplored. Accordingly, the contribution of the ski poles to total aerodynamic drag in connection with various postures during alpine skiing at different speeds was assessed here in a wind tunnel. More specifically, we evaluated (i) the contribution of the cross-sectional area of the poles (Sp) to the skier’s total cross-sectional frontal area (S); (ii) intra-subject variation in this respect; and (iii) the influence of Sp on the coefficient of aerodynamic drag (Cd) and the product Cd∙S.

Figure 1.
The coronal plane of a skier in the wind tunnel (right) and the corresponding interactive segmentation (left).
2. Materials and Methods
The data analyzed in the present study were taken from two previous investigations, where the collection of these data is described in detail [6,16]. Therefore, below we describe only essential aspects of our methodology, concentrating on details of data processing that differ from those of earlier reports.
2.1. Participants
The 10 male skiers (body mass: 80.8 ± 7.0 kg; height: 1.81 ± 0.05 m, means ± standard deviations) involved in this study were all members of the Swedish alpine ski team and signed their written informed consent prior to participation. The current study involving the reuse of some data was approved by the Commission for Ethical Issues in Sports in Ljubljana, Slovenia (Ref. No. 4/2023).
2.2. Instruments, the Experimental Design and Data Collection
Data were collected while the subjects were standing inside a closed-loop wind tunnel (12.5 m long, 2.7 m wide, 1.8 m high, contraction ratio 1:4.23) equipped with a 220 kW centrifugal blower that can produce wind speeds up to 30 m/s. The standard deviations associated with the measurements were 0.14 m/s and 1.8 N for wind speed and aerodynamic drag force, respectively. Aerodynamic drag was measured with a force platform (model 9286AA, Kistler Instrument Corp., Winterthur, Switzerland), which was set to zero prior to each test under windless conditions. The cross-sectional area of the poles (Sp) and the total cross-sectional area of the skier (S) were assessed by application of click-based interactive segmentation [18] to the images taken in the coronal plane from behind with an HDR-HC7 camcorder purchased from the Sony Corporation (Tokyo, Japan) (Figure 1). Fifteen images (5 in each of the three positions) were re-processed to determine the reproducibility of the measurement of cross-sectional area, resulting in a difference of 0.31 ± 0.24% (mean ± SD).
During the wind tunnel test, the participants wore their own suitably sized giant slalom alpine ski racing gear, i.e., racing suit, gloves, helmet, goggles, ski boots, and poles, enabling them to familiarize themselves with the positioning. The conical poles were round in cross-section and had round baskets. The stance width (i.e., the fixed distance between the ski bindings) was adjusted individually. Upon receiving a given visual signal, participants assumed one of three different typical positions (tuck, middle, high) five times in a randomized order at the respective wind speeds: 40, 60, and 80 km/h. Prior to this testing, these three typical positions were recorded while two of our subjects adopted them when skiing down a training course for Giant Slalom. The aerodynamic drag (Fd) was considered to be the 5-s average of the force in the direction in which the wind was blowing, once this signal had stabilized completely.
2.3. Calculations
As is standard practice in studies involving wind tunnels, the skier’s cross-sectional area (S) multiplied by the coefficient of aerodynamic drag (Cd) was obtained from the Rayleigh drag equation Cd∙S = 2∙Fd/(ρ·V2). In this equation, Fd represents the aerodynamic drag, V the wind speed, and ρ the density of the air. The cross-sectional areas, both total (S) and of the ski poles (Sp) alone, were derived from image processing as described above. The value of S obtained by interactive segmentation was in pixels and special calibration marks in the wind tunnel were utilized to convert these pixels into square meters. Division of Cd∙S by S provided Cd. Since in the combined tuck and high positions, the skier obstructed roughly 6–12% of the airflow in the wind tunnel, Cd was corrected for blockage as proposed by Elfmark and colleagues [19].
2.4. Statistical Analyses
The cross-sectional areas S and Sp are presented as means and standard deviations, as well as the percentage of S accounted for by Sp (i.e., (Sp/S)∙100). The individual variation in Sp for each skier was expressed as the difference between the maximal and minimal measured values of Sp and Sp/S (min–max range), together with the coefficient of variance (CV) for Sp.
To compare the cross-sectional area with the different positions and speeds, three Bayesian linear multilevel models were applied to S, Sp and Sp/S, respectively. In these models, the speed and position were fixed factors, and a random intercept was utilized for each athlete. To examine the effect of Sp on Cd and Cd∙S, linear Bayesian multilevel models were fitted for each position, Sp, and body cross-sectional area, again employing a random intercept for each skier. Weakly informative priors were included on standardized values in each model, with intercept and coefficients of ~N(0, 2.5) and residuals of ~exp(1). With each model, 4 chains of 4000 warm-up and 4000 sampling iterations were performed, for a total of 16,000 sampling iterations. There were no diverging transitions, the minimal effective sample size to total sample size ratio of >0.26, and maximal Rhat value < 1.0016.
The highest-density intervals were utilized to calculate the confidence intervals (CI). In addition, the probabilities of direction (pd) (values from 0.5–1), which indicate how probable it is that a positive effect is actually positive and a negative effect actually negative, were determined. The pd can be interpreted as pd < 0.95 unclear, pd > 0.95 possibly existing, pd > 0.97 likely existing, pd > 0.99 probably existing, and pd > 0.999 certainly [20]. The R 4.2.2 software [21] was employed to carry out all analyses and rstanarm 2.21.3 [22] for fitting models.
3. Results
The cross-sectional areas of the skiers’ bodies (S) and of their poles (Sp) in the different positions and at different wind speeds are shown in Table 1, together with the intra-skier variation between trials. Figure 2 illustrates the cross-sectional area of the poles for each skier during all of the trials and the images of Skier 8 presented in Figure 3 highlight the extent to which the positioning of the poles and corresponding Sp obtained at 40, 60, and 80 km/h varied. Also noteworthy is the asymmetric positioning of the left and right poles (which was common for this particular skier), as well as the variation in the height of the shoulders and head.

Table 1.
The cross-sectional area of the skiers and poles at different wind speeds and body positions.
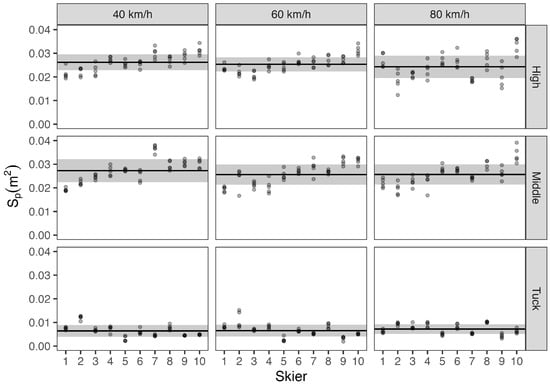
Figure 2.
The cross-sectional area of the ski poles (Sp) with different wind speeds and positions for each individual skier. The means for all 10 athletes are represented by the black lines and the standard deviations for these means by the grey shaded areas.

Figure 3.
The middle position was taken by “Skier 8” during one of the tests at 40 (left), 60 (middle), and 80 km/h (right). At the top is the posterior view and at the bottom is the sagittal view. Sp—cross-sectional area of the poles.
3.1. The Cross-Sectional Area of the Ski Poles
The skiers demonstrated a somewhat smaller Sp in the high and middle positions compared to the tuck position, as well as in the middle versus high position (High–Middle = −0.0009 m2, 95% CI [−0.0017, −0.0001 m2], pd = 0.987; High–Tuck = 0.0186 m2, 95% CI [0.0178, 0.0194 m2], pd = 1.000; Middle–Tuck = 0.0195 m2, 95% CI [0.0186, 0.0202 m2], pd = 1.000). The percentage of the total cross-sectional area occupied by the poles differed between the positions, being greatest in the middle position, followed by the high position (High–Middle = −0.5%, 95% CI [−0.7, −0.3%], pd = 1.000; High–Tuck = 2.1%, 95% CI [1.9, 2.3%], pd = 1.000; Middle–Tuck = 2.6%, 95% CI [2.4, 2.7%], pd = 1.000).
In the high and middle positions, Sp at a wind speed of 40 km/h was probably higher than at 60 km/h and was certainly higher than at 80 km/h (40–60 km/h = 0.0013 m2, 95% CI [0.0003, 0.0022 m2], pd = 0.994; 40–80 km/h = 0.0018 m2, 95% CI [0.0008, 0.0028 m2], pd = 1.000; 60–80 km/h = 0.0005 m2, 95% CI [−0.0005, 0.0015 m2], pd = 0.849). At the same time, in the tuck position, it was unclear whether wind speed influenced Sp (40–60 km/h = −0.0001 m2, 95% CI [−0.0015, 0.0013 m2], pd = 0.561; 40–80 km/h = −0.0008 m2, 95% CI [−0.0021, 0.0006 m2], pd = 0.863; 60–80 km/h = −0.0007 m2, 95% CI [−0.0020, 0.0007 m2], pd = 0.830).
In the high and middle positions, the cross-sectional area of the poles comprised a somewhat higher percentage of S at a wind speed of 40 km/h than at the two higher speeds (40–60 km/h = 0.3%, 95% CI [0.1, 0.5%], pd = 0.999; 40–80 km/h = 0.4%, 95% CI [0.2, 0.6%], pd = 1.000; 60–80 km/h = 0.0%, 95% CI [−0.2, 0.2%], pd = 0.667). At the same time, the influence of wind speed on the Sp in the tuck position was again unclear (40–60 km/h = 0.0%, 95% CI [−0.3, 0.2%], pd = 0.587; 40–80 km/h = −0.2%, 95% CI [−0.5, 0.1%], pd = 0.928; 60–80 km/h = −0.2%, 95% CI [−0.5, 0.1%], pd = 0.894).
3.2. Effects of the Cross-Sectional Area of the Poles on Cd and Cd·S
The intra-athlete influence of a 0.01 m2 increase in the cross-sectional area of the ski poles on the Cd and Cd · S with all wind speeds (controlling for S) can be seen in Table 2. In the case of the high position, Sp had an unclear effect on Cd, while exerting a likely positive effect on Cd·S. With the middle position, there were likely positive effects on both Cd and Cd·S. Finally, in the tuck position, there was a probable negative effect on Cd and possible negative effect on Cd·S. The general relationship between the cross-sectional area of the ski poles and Cd and Cd·S is illustrated in Figure 4.

Table 2.
Relationship between the cross-sectional area of the ski poles and Cd and Cd·S.
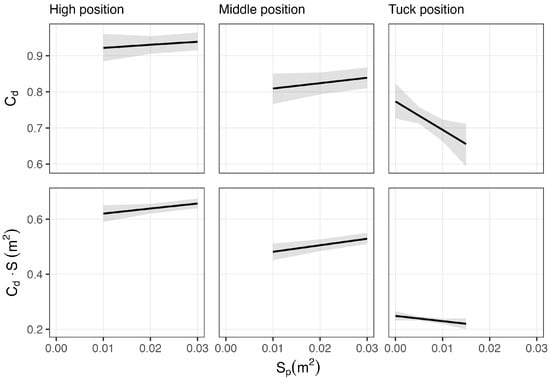
Figure 4.
The values of Cd (coefficient of drag) and Cd·S (product of coefficient of drag and total cross-sectional area) are predicted by the cross-sectional areas of the ski poles (Sp). Gray shaded areas represent a 95% confidence interval.
Table 3 documents the effects of increasing Sp by the average range for all the skiers combined at each position on Cd and Cd·S (m2).

Table 3.
Effect of increasing the cross-sectional area of the ski poles by the average range of all of the skiers combined on Cd and Cd·S (m2).
4. Discussion
The major findings from this investigation on the contribution of the ski poles to total aerodynamic drag during alpine skiing were as follows: (i) the average cross-sectional area of the ski poles (Sp) ranged from 0.0067 in the tuck position to 0.0262 m2 in the middle position; (ii) these areas accounted for 2.2–4.8% of the total cross-sectional area; (iii) the contribution of the ski poles to the total cross-sectional area was dependent on wind speed in the high and middle positions; (iv) at 80 km/h, the inter-subject variations in this contribution ranged from 0.0018 m2 (27.6%) in the tuck position to 0.0072 m2 (30.5%) in the high position; and, finally, (v) Sp exerted a likely effect on the coefficient of drag (Cd) and Cd∙S (product of coefficient of drag and total cross-sectional area).
This study involved 10 elite skiers who assumed three different standard positions five times at each of three different wind speeds in a wind tunnel. We did not standardize these conditions, as was done in certain previous studies [8,13,15], because the variations in the positions of the skiers and their poles, as well as in the wind speed, allowed us to examine the influence of these different conditions on the impact of the poles of aerodynamic drag. Moreover, the posture of a skier during a race varies considerably, often deviating from the basic positions, as he/she adapts to the varying terrain, snow conditions, and gate positions [23].
Our current findings reveal that the Sp could account for as much as 5.0 ± 0.8% of the total frontal cross-sectional area (Table 1), making the greatest absolute contribution in the high position and the most pronounced relative contribution in the middle position. Furthermore, the intra-skier variations in Sp were relatively extensive (17.1–34.8%), more so apparently at the two highest speeds examined. This variation for all of the skiers combined was even more pronounced (35.6–63.0%), as were the absolute differences between skiers (Figure 2). Knowing that aerodynamic drag is one of the two resistive forces in alpine skiing [4,7,24,25] contributing to energy dissipation [6,26], these observations indicate that the ski poles may be responsible for variations in total energy loss as great as 1% (considering that maximally 28% of the energy loss during giant slalom is due to aerodynamic drag [Supej et al., 2013] [6], a 5.8% relative cross-sectional area of the poles, and 63% variation), with an average of approximately 0.3% (considering that, on average, 15% of the energy loss during giant slalom is due to aerodynamic drag [Supej et al., 2013] [6], a 4.5% relative cross-sectional area of the poles and 40% variation (the latter two values being approximately the mean values for the middle and high positions). No more than a fraction of a second often separates the finishing times of the gold and silver medallists [12], e.g., 0.01 s or 0.015% in the case of the Super Giant Slalom for men in the recent 2023 Alpine Skiing World Championships.
As illustrated in Figure 3, the position in which the skiers held their poles varied considerably, which, since there is an obvious geometrical relationship between the cross-sectional area and inclination of the poles in the airstream, influenced the values of the cross-sectional area obtained. It should be noted that in the example shown in this figure the Sp for the poles declined with increasing wind speed, whereas the graph in Figure 2 shows that the opposite was more often observed for this particular Skier 8. The variation in the positioning of the poles between skiers was even greater than this variation for one and the same subject (Table 1) and it would be worthwhile investigating further the pole position (for example, more or less parallel to the direction of skiing, i.e., to the wind flow) that minimizes drag optimally. However, this potential improvement in performance indicated here is considerably lower than the ~40% reduction in aerodynamic drag that could be achieved by training the arms according to previous reports [17,24] and future investigation should take both the arms and poles into consideration.
The smallest relative contribution of Sp to aerodynamic drag was associated with the tuck position, even though this is the position where the total frontal cross-sectional area of the skier is by far the smallest (Table 1). Perhaps the fact that the poles are held much more parallel to the ground in the tuck position reduces their cross-sectional area to approximately one-quarter of that in the high and middle positions. To further reduce drag, some skiers who specialize in the speed disciplines use folded poles that allow them to align the shape of their poles to that of their bodies. However, even in such a situation, the poles can give rise to strong vortices that increase aerodynamic drag [27].
As might be expected, we observed a probable positive effect of Sp on Cd in both the middle and high positions and on Cd∙S in the high position, such that a change in Sp of 0.01 m2 might alter Cd and Cd∙S by as much as 0.02 m2 (Table 2). More surprising were the negative effects of Sp on Cd and Cd∙S in the tuck position, implying that these values both decrease with increasing Sp. The finding is probably due to the fact that the less favorable positioning of the poles (larger Sp) allows more favorable aerodynamic positioning of the skier. For example, if the skier inclines the poles slightly more forwards (tips higher than the grips), this would allow a lower, more aerodynamic positioning of the head and torso, which contribute strongly to the total aerodynamic drag [8,28].
Another interesting observation here was that both Sp and its relative contribution to the total aerodynamic drag were on average higher in the middle and high positions at 40 km/h than at 60 and 80 km/h, even though the skiers were instructed to assume the same position at all three wind speeds. Whether the skiers instinctively changed their position somewhat to reduce the aerodynamic drag (i.e., by positioning the poles in a manner that reduced their cross-sectional area) and/or whether this was a consequence of the drag on the poles forcing them into a more inclined position is not possible to know and it is difficult to predict whether similar behavior would occur during actual skiing.
The limitations of the current investigation are similar to those associated with a previous study based on the same measurements [16], as well as other experiments conducted in a wind tunnel [5,8,13]. In short, despite their familiarity with skiing positions which they assume almost automatically, elite skiers may not adopt exactly the same positions in a wind tunnel as on snow. Moreover, to maintain balance and/or adapt to the prevailing terrain and snow conditions, elite skiers switch between many different positions during a race, whereas here only the three most typical positions were considered. The lower shell of the ski boots was elevated approximately 30 mm by the ski binding and was probably affected by the boundary layer of air near the surfaces of the tunnel, due to friction between the moving air stream and solid surfaces. However, most importantly, the poles with their baskets were high enough to assume they were in the free air stream as shown by an additional 2D kinematic analysis of the positions of the pole baskets, which revealed that their heights (left and right combined) were 28.4 ± 13.4, 17.1 ± 11.2, and 93.0 ± 12.1 cm (mean ± SD) for the high, middle, and tuck positions, respectively. To minimize the error of the drag coefficient, we employed a blocking correction with an error of 2.2%, obtained for alpine skiers tested in the same wind tunnel [19].
Last, but not least, derivation of the cross-sectional areas of the skier and poles through click-based interactive segmentation of the video recordings may not be entirely accurate. In the case of the poles in particular, the pixel size of the video recordings plays an important role. Thus, since the diameters of the conical poles ranged from ~10 to ~19 mm, the use of a pixel size of appropriately 1 mm could introduce an error of ~10%, even though the reproducibility of the determination of the cross-sectional area by image processing was only 0.31%. Since this error can be assumed to be of the same proportion in connection with all measurements, measurements of the absolute values of the cross-sectional area of the poles and their contribution to the total cross-sectional area will be affected most.
5. Conclusions
In summary, we examined the contribution of ski poles to the aerodynamic drag associated with alpine skiing using a wind tunnel. There was extensive intra- and inter-subject variability in the cross-sectional area of the poles (Sp) and Sp was found to account for as much as ~5% of the total frontal cross-sectional area, with estimated inter-skier differences in total energy loss being as much as 1%. Since the finishing differences between elite skiers in competitions are extremely small, sometimes no more than 0.015% between the gold and silver medallists, further investigation of the pole position that reduces aerodynamic drag maximally is clearly motivated.
Moreover, our current observations on the effects of Sp on Cd and Cd∙S reveal clearly that it is necessary to differentiate between the effect of the poles during more intense turns (involving high and middle positions) and during less intense turns or on flat terrain (tuck position). With higher postures, the poles may increase drag directly, whereas the less favorable pole positioning in a tuck position may reduce overall aerodynamic drag. Although our present work has focused on the technical disciplines, our findings concerning the middle and high positions are likely to be even more relevant to the speed disciplines as well, where skiers adopt positions similar to those utilized in the technical disciplines during more intensive turns on challenging terrain. To make the best use of this knowledge in practice, we recommend that elite skiers train in a wind tunnel with real-time feedback during annual pre-season training to hold their ski poles in a manner that reduces aerodynamic drag, and then apply this when training on snow.
Author Contributions
Conceptualization, M.S.; Methodology, M.S. and H.-C.H.; Formal analysis, M.S., A.K., N.V. and J.O.; Data curation, M.S., J.O. and H.-C.H.; Writing–original draft, M.S.; Writing–review & editing, M.S., A.K., N.V., J.O. and H.-C.H.; Visualization, A.K.; Supervision, M.S.; Project administration, M.S.; Funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Slovenian Research Agency (P5-0147).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Commission for Ethical Issues in Sports in Ljubljana, Slovenia (Ref. No. 4/2023; date of approval: 20 February 2023).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data are available upon reasonable request. Raw wind tunnel data (anonymized transcripts) are available from the corresponding author (M.S.).
Acknowledgments
The authors sincerely thank Lars Saetran and Luca Oggiano for their help in the original data collection and skiers and their coaches for their cooperation.
Conflicts of Interest
The authors have no conflict of interest to declare.
References
- Raschner, C.; Hildebrandt, C.; Mohr, J.; Müller, L. Sex Differences in Balance Among Alpine Ski Racers: Cross-Sectional Age Comparisons. Percept. Mot. Ski. 2017, 124, 1134–1150. [Google Scholar] [CrossRef] [PubMed]
- Gilgien, M.; Reid, R.; Raschner, C.; Supej, M.; Holmberg, H.C. The Training of Olympic Alpine Ski Racers. Front. Physiol. 2018, 9, 1772. [Google Scholar] [CrossRef] [PubMed]
- Supej, M.; Holmberg, H.C. Recent Kinematic and Kinetic Advances in Olympic Alpine Skiing: Pyeongchang and Beyond. Front. Physiol. 2019, 10, 111. [Google Scholar] [CrossRef]
- Federolf, P.; Scheiber, P.; Rauscher, E.; Schwameder, H.; Lüthi, A.; Rhyner, H.U.; Müller, E. Impact of skier actions on the gliding times in alpine skiing. Scand. J. Med. Sci. Sports 2008, 18, 790–797. [Google Scholar] [CrossRef]
- Meyer, F.; Le Pelley, D.; Borrani, F. Aerodynamic drag modeling of alpine skiers performing giant slalom turns. Med. Sci. Sports Exerc. 2012, 44, 1109–1115. [Google Scholar] [CrossRef]
- Supej, M.; Sætran, L.; Oggiano, L.; Ettema, G.; Šarabon, N.; Nemec, B.; Holmberg, H.C. Aerodynamic drag is not the major determinant of performance during giant slalom skiing at the elite level. Scand. J. Med. Sci. Sports 2013, 23, e38–e47. [Google Scholar] [CrossRef] [PubMed]
- von Hertzen, R.; Holmlund, U.; Ranta, M.A. On the velocity maximization in downhill skiing. J. Biomech. 1997, 30, 525–529. [Google Scholar] [CrossRef]
- Elfmark, O.; Teigen Giljarhus, K.E.; Liland, F.F.; Oggiano, L.; Reid, R. Aerodynamic investigation of tucked positions in alpine skiing. J. Biomech. 2021, 119, 110327. [Google Scholar] [CrossRef]
- Luethi, S.M.; Denoth, J. The influence of aerodynamic and anthropometric factors on speed in skiing. Int. J. Sport Biomech. 1987, 3, 345–352. [Google Scholar] [CrossRef]
- Gilgien, M.; Kröll, J.; Spörri, J.; Crivelli, P.; Müller, E. Application of dGNSS in alpine ski racing: Basis for evaluating physical demands and safety. Front. Physiol. 2018, 9, 145. [Google Scholar] [CrossRef]
- Gilgien, M.; Spörri, J.; Chardonnens, J.; Kröll, J.; Müller, E. Determination of external forces in alpine skiing using a Differential Global Navigation Satellite System. Sensors 2013, 13, 9821–9835. [Google Scholar] [CrossRef] [PubMed]
- Supej, M.; Cernigoj, M. Relations between different technical and tactical approaches and overall time at men’s world cup giant slalom races. Kinesiol. Slov. 2006, 12, 63–69. [Google Scholar]
- Barelle, C.; Ruby, A.; Tavernier, M. Experimental model of the aerodynamic drag coefficient in alpine skiing. J. Appl. Biomech. 2004, 20, 167–176. [Google Scholar] [CrossRef]
- Thompson, B.E.; Friess, W.A.; Knapp, K.N. Aerodynamics of speed skiers. Sports Eng. 2001, 4, 103–112. [Google Scholar] [CrossRef]
- Elfmark, O.; Bardal, L.M. An empirical model of aerodynamic drag in alpine skiing. Proceedings 2018, 2, 310. [Google Scholar]
- Majeric, M.; Verdel, N.; Ogrin, J.; Holmberg, H.C.; Supej, M. Application of Experimental Measurements in a Wind Tunnel to the Development of a Model for Aerodynamic Drag on Elite Slalom and Giant Slalom Alpine Skiers. Appl. Sci. 2022, 12, 902. [Google Scholar] [CrossRef]
- Brownlie, L.; Larose, G.; D’Auteuil, A.; Allinger, T.; Meinert, F.; Kristofic, P.; Dugas, S.; Boyd, R.D.; Stephens, D. Factors affecting the aerodynamic drag of alpine skiers. Procedia Eng. 2010, 2, 2375–2380. [Google Scholar] [CrossRef]
- Sofiiuk, K.; Petrov, I.A.; Konushin, A. Reviving Iterative Training with Mask Guidance for Interactive Segmentation. arXiv 2021, arXiv:2102.06583. [Google Scholar]
- Elfmark, O.; Reid, R.C.; Bardal, L.M. Blockage Correction and Reynolds Number Dependency of an Alpine Skier: A Comparison between Two Closed-Section Wind Tunnels. Proceedings 2020, 49, 19. [Google Scholar]
- Makowski, D.; Ben-Shachar, M.S.; Chen, S.H.A.; Lüdecke, D. Indices of Effect Existence and Significance in the Bayesian Framework. Front. Psychol. 2019, 10, 2767. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. 2021. Available online: https://www.R-project.org/ (accessed on 12 December 2022).
- Goodrich, B.; Gabry, J.; Ali, I.; Brilleman, S. rstanarm: Bayesian Applied Regression Modeling via Stan. R Package Version 2.21.4. 2023. Available online: https://mc-stan.org/rstanarm (accessed on 2 May 2023).
- Supej, M.; Spörri, J.; Holmberg, H.C. Methodological and practical considerations associated with assessment of alpine skiing performance using global navigation satellite systems. Front. Sports Act. Living 2020, 1, 74. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, K.; Ohtsuki, T. Postural Changes and Aerodynamic Forces in Alpine Skiing. Ergonomics 1977, 20, 121–131. [Google Scholar] [CrossRef]
- Leino, M.A.H.; Spring, E.; Suominen, H. Methods for the simultaneous determination of air resistance to a skier and the coefficient of friction of his skis on the snow. Wear 1983, 86, 101–104. [Google Scholar] [CrossRef]
- Hébert-Losier, K.; Supej, M.; Holmberg, H.C. Biomechanical factors influencing the performance of elite alpine ski racers. Sports Med. 2014, 44, 519–533. [Google Scholar] [CrossRef]
- Asai, T.; Hong, S.; Ijuin, K. Flow Visualization of Downhill Ski Racers Using Computational Fluid Dynamics. Procedia Eng. 2016, 147, 44–49. [Google Scholar] [CrossRef]
- Asai, T.; Hong, S.; Ijuin, K. Flow visualisation of downhill skiers using the lattice Boltzmann method. Eur. J. Phys. 2017, 38, 024002. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).