Featured Application
We believe the paper may be of particular interest to the readers of your journal because in this paper, a simple but high-precision geomagnetic field modeling method is proposed. We also present Chinese Geomagnetic Reference Field 2020 (CGRF2020) as an example of this modeling method. Using CGRF2020, one can calculate high-precision geomagnetic field values in most of China and surrounding areas.
Abstract
We improved the surface spline method to make the centers of the base functions fixed. This improvement makes it meaningful to analyze the time series of coefficients. Based on the revised surface spline (RSS) method and 2382 geomagnetic data measured in mainland China, we built Chinese Geomagnetic Reference Field 2020 (CGRF2020) to describe the spatial distribution of the geomagnetic field in most of China and surrounding areas. The root mean square residual is 0.1318 degrees for D, 0.0857 degrees for I, 93.70 nT for F, 73.94 nT for X, 65.02 nT for Y, and 97.82 nT for Z. The values of F, X, Y, and Z are about 20 nT less than those by the SCH method and IGRF13. We also preliminarily analyzed the correlation between geomagnetic anomalies and geological structures.
1. Introduction
As a standard geomagnetic product, the geomagnetic reference field provides a higher-precision geomagnetic description field of the region. A geomagnetic reference field can easily provide the geomagnetic normal reference value of the target location so as to help identify whether the measurement data are abnormal and the magnitude of the anomaly. Therefore, in the field of energy and mineral resources, geomagnetic reference fields are needed to provide the normal distribution of the geomagnetic field so as to help accurately estimate the geomagnetic anomaly morphology and predict the mineral locations and reserves. By analyzing the precise geomagnetic field distribution provided by the geomagnetic reference field itself, the structure distribution of underground materials can be inferred, thus providing help in tectonic-geodynamic studies. The high-precision geomagnetic reference field also provides accurate and undisturbed navigation information for archaeological and environment investigations, military aviation, and other fields [1,2,3,4,5].
One important research problem with geomagnetism is how to describe the spatial and temporal distribution of the geomagnetic field as accurately as possible. To describe the global geomagnetic field and its secular variation, the International Association of Geomagnetism and Aeronomy (IAGA) has issued the International Geomagnetic Reference Field (IGRF) once every 5 years since 1968, with few exceptions [6]. The latest model, the thirteenth generation of IGRF, IGRF13, was issued in December 2019 [7]. While the IGRF is intended to describe the global geomagnetic field, its usefulness in characterizing the geomagnetic field over a regional area is limited due to its higher errors. Various countries, therefore, establish national geomagnetic charts or models according to the needs of the scientific community [8,9,10]. National geomagnetic charts, which describe the spatial–temporal variation in the regional geomagnetic field, tend to be country wide and are established or published every 5~10 years usually [11,12,13,14,15,16,17]. These charts or models describe the spatial distribution of the geomagnetic field of a region and are based on some absolute geomagnetic data. Efforts to develop such charts are faced with the technical challenge of describing the spatial distribution of the geomagnetic field with accuracy and proper resolution based on a large amount of spatially discrete data. Building a model and then calculating the regional geomagnetic field is an efficient method to resolve this technical problem. The first generation of the Chinese geomagnetic charts, i.e., China geomagnetic chart for 1950.0, was established in the 1950s. Seven generations of China geomagnetic charts were published during 1960~2000 (every 10 years). These charts were generated mainly using the Taylor polynomial method [18,19,20]. After that, China geomagnetic charts have been made using the spherical cap harmonic (SCH) method [21,22,23,24,25,26,27,28,29]. The SCH method is derived from the spherical harmonic method used in the International Geomagnetic Reference Field (IGRF) and meets the potential theory of the geomagnetic field while providing the three-dimensional structure of the field.
Despite the advantages of the SCH method, it has its own disadvantages. In addition to its being a little complex to calculate the non-integer-order Schmitt-Legendre functions, we find the non-integral-order Schmitt-Legendre function divergent oscillation when we increase the truncation order to improve the description precision. Qiu tried to use three sets of low-order spherical cap harmonic coefficients to describe the geomagnetic field in China to solve this problem [30]. However, it is necessary to first determine which set of coefficients should be chosen, according to the locations, and there are some complex steps to determine the geomagnetic field where the three models overlap.
Many kinds of modeling method are used to discuss various complex geophysical phenomena and processes [31,32,33]. The purpose of this paper is to propose a more convenient modeling method to express the regional geomagnetic field in most of China and surrounding areas. This method should have the following advantages: one formula and its coefficients for the whole target region; higher fitting accuracy; and a relatively independent form of basis function, which facilitates time series analysis. In this case, we propose a revised surface spline method to describe the regional geomagnetic field. This theory can be used to calculate the geomagnetic field distribution with a high spatial resolution by one easy-to-use formula and one set of coefficients.
2. Materials and Methods
2.1. Revised Surface Spline Method
The surface spline method was first applied in 1987 [34]. It can be expressed by Equation (1).
Here, x and y are the geographical longitude and latitude of the calculated position, respectively; xi and yi are the geographic longitude and latitude of the ith spatial position, respectively; P(x, y) is the value of an element of the geomagnetic field at position (x, y); a0, a1, a2, and Ai are the fitting coefficients of the surface spline function; N is the amount of original data; ri is the distance between the calculated position and the ith spatial position; and ε is the curvature factor and is usually 10−7.
From Equation (1), the traditional surface spline fitting formula consists of two parts. The first part is 1-order polynomials, and the second part includes some U-shaped waves centered on the base points. Because the base points are the field repeat stations in the traditional surface spline method, the geographical longitudes and latitudes of field repeat stations should be input when calculating geomagnetic data. Therefore, in practical use, we should not only know the fitting coefficients but also know the longitudes and latitudes of the repeat stations. In addition, the temporal characteristics of the geomagnetic field cannot be obtained by analyzing the time series of coefficients, due to the different centers of the basis function corresponding to the coefficients. This makes it inconvenient to extend and apply the surface spline method.
So, we redefine the centers of the U-shaped waves as a grid lattice distribution position in the second part. In addition, we increase the truncation order of polynomials in the first part to describe a more complex trend distribution of the geomagnetic field. Then the revised surface spline method can be expressed as:
Here, K is the truncation order of polynomials; aij and Ai are the fitting coefficients of the revised surface spline function; x and y are the geographical longitude and latitude of the calculated position, respectively; xi and yi are the geographic longitude and latitude of the ith grid lattice distribution position, respectively; P(x, y) is the value of an element of the geomagnetic field at position (x, y); N is the number of the grid lattice distribution positions; ri is the distance between the calculated position and the ith grid position; and ε is the curvature factor and usually is also 10−7.
2.2. Source and Processing of the Geomagnetic Data
We collected three-component geomagnetic data for 2832 repeat stations, 1447 of them measured in 2019 and 1385 of them measured in 2020. The mean separation between two adjacent stations is about 70 km in most areas of China and is about 150 km in Tibet, China. All of the stations are located in a weak magnetic interference environment (e.g., far from man-made magnetic sources and with lower magnetic field gradients (less than 5 nT/m)). The measured geomagnetic elements are the geomagnetic declination (D), the inclination (I), and the total intensity (F). A GSM-19T proton magnetometer with a sensitivity of 0.05 nT and an accuracy of 0.2 nT was used to measure F. A CTM-DI magnetometer was used to measure D and I with a sensitivity of 0.1′ and an accuracy of 0.2′ [35]. A PM-100 GNSS system was used to measure the longitudes, latitudes, and elevations of stations and also provide the direction of geographical north, which is needed to determine the geomagnetic declination [36]. All geomagnetic elements (F, D, and I) of each station were measured in 6 sets. In each set, F was measure 10 times, D was measure 4 times, and I was measure 4 times to avoid operational mistakes.
All geomagnetic data of the three elements were calculated to 00:00~03:00 Beijing time on 1 January 2020 after reduction of the diurnal and secular variations. The reference data used in the reduction of the diurnal variations were the minute mean values of the nearest geomagnetic observatory to repeat stations [37]. The reference data used in the reduction of the secular variation were from a 6-order natural orthogonal component (NOC) model of the geomagnetic secular variation in China [38,39].
Then, we averaged the results of the same repeat stations in 2019 and 2020 with the preceding data, processing to further reduce the error and removing some data that were too close. In all, 1120 repeat stations remained for building the Chinese geomagnetic reference field. The spatial distribution of these repeat stations is shown in Figure 1. We also collected geomagnetic data at 45 geomagnetic observatories and at 118 stations in neighboring countries and calculated geomagnetic data by the enhanced magnetic model [40] for 419 positions. The spatial distribution of all four parts of these positions is shown in Figure 1.
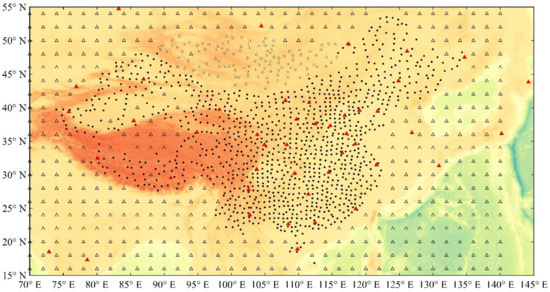
Figure 1.
Site distribution for CGRF2020. ● repeat stations, ○ stations in neighboring countries, ▲ geomagnetic observatories, and Δ positions where geomagnetic data were calculated from EMM.
3. Results
3.1. Parameter Determination
According to Equation (2), the main parameters that determine the accuracy of the revised surface spline model include the truncation order K and the number of grid lattice distribution positions N. Because the total number of grid positions is inversely proportional to the square of the grid interval (R; unit is degree), we calculated root mean square residuals, RMS σ, using several different truncation orders K and the grid interval R. Three elements, D, I, and F, are fitted; and X, Y, and Z are calculated by D, I, and F to compare with the results of previous studies. Although we obtained the fitting coefficients using the ordinary least squares method based on all four parts of the geomagnetic data, we focused on the geomagnetic field distribution in China. So we calculated the RMS σ based on the first two parts of the geomagnetic data and the data of 1120 repeat stations; the results are displayed in Table 1.

Table 1.
RMS of some elements with different K and R.
When K > 4, the RMS sharply increased when R < 3 degrees; so this situation was not included in the consideration, and the values in this situation are not shown in Table 1. From Table 1, we can also see the advantages of the revised surface spline method. The lowest RMS values are 73.94 nT for X, 65.01 nT for Y, and 97.82 nT for Z. As a comparison, we also calculated the RMS residual of IGRF13; the results are 0.1858 degrees for D, 0.1089 degrees for I, and 117.48 nT for F. Usually, the estimated RMS errors of IGRF and WMM are 140–300 and 50–150 nT higher, respectively, in China [7,41,42]. In comparison, CGRF2010 by the spheric cap harmonic method has a higher value and a lower convergence rate of the RMS residual. The RMS values are about 101 nT for X, 80.5 nT for Y, and 122 nT for Z when the truncation order is 11, and the convergence rates are about 4 nT for X, 0.2 nT for Y, and 4 nT for Z when the order increases from 1 to 11 [29]. The errors will still increase to about 150 nT for X, 80 nT for Y, 180 nT for Z, and 250 nT for F when using the spheric cap harmonic method to build a 3D geomagnetic model [43]. We also calculated the RMS using the Taylor polynomial method, which can also be used to describe the geomagnetic field in the same area when the truncation order is 8. The RMS is 0.16 degrees for D, 0.10 degrees for I, and 111.31 nT for F. We chose a higher truncation order and a lower grid interval to describe the more complex geomagnetic field spatial structure. So K = 3 and R = 2 degrees were determined as the model parameters.
3.2. Maps and Coefficients of CGRF2020
Figure 2 shows the spatial distribution of the geomagnetic field described by CGRF2020-RSS and its difference from IGRF13. In most of China, the magnitude of geomagnetic anomalies can be up to 5′ for D and I; 100 nT for F, H, X, and Z; and 50 nT for Y.
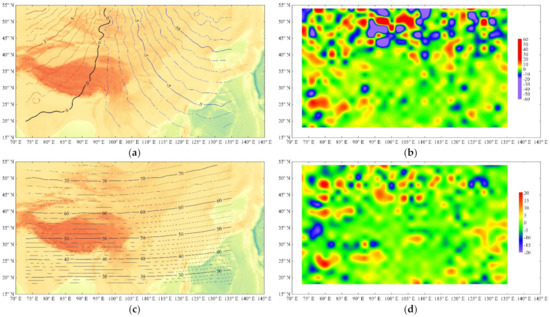
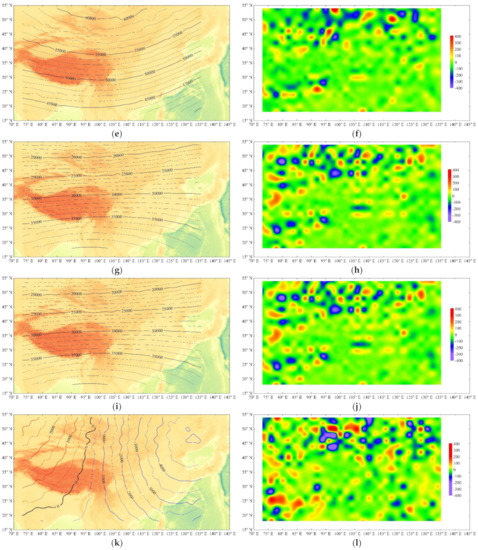
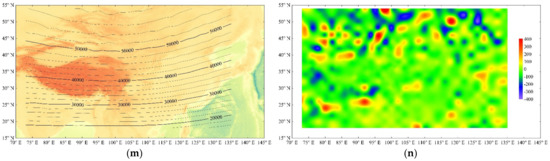
Figure 2.
Spatial distribution of the geomagnetic field (left side) and the difference from IGRF13 (right side) in most of China and adjacent areas for 2020 by the RSS method. For D and I, the red lines denote positive values and the blue lines denote negative values. The unit of F, H, X, Y, and Z and the unit of the differences in F, H, X, Y, and Z is nT; the unit of D and I is degree; and the unit of the differences in D or I is arcminute. (a) D; (b) difference in D; (c) I; (d) difference in I; (e) F; (f) difference in F; (g) H; (h) difference in H; (i) X; (j) difference in X; (k) Y; (l) difference in Y; (m) Z; (n) difference in Z.
After studying the right half of Figure 2 (the spatial distribution of seven elements of geomagnetic anomalies), we find the following:
- The anomalies in the declination D and the east component Y are positive in most of North China and East China and are negative in most of West China. There are several positive anomalies located at (42° N, 118° E), (40° N, 107° E), (40° N, 83° E), and (35° N, 118° E), with the amplitude up to 10′ for D and up to 100 nT for Y; there are several negative anomalies centered near (42° N, 122° E), (40° N, 110° E), and (40° N, 80° E), with the amplitude up to −10′ for D and 100 nT for Y.
- The anomalies in the total intensity F and the vertical component Z are negative in most of China. Several old hard blocks correspond to the distribution of positive anomalies. For example, the anomaly over Sichuan Basin is a positive anomaly located at 28–33° N, 103–112° E, with the amplitude up to 100 nT for F and Z. There is also a positive anomaly (35–42° N, 75–88° E) near Tarim Basin, with the amplitude up to 150 nT for F and 200 nT for Z. There are three significant negative anomalies, the first one located in Qinling Mountains (30–35° N, 103–115° E), the second one located in Tianshan Mountains (38–42° N, 75–90° E), and the last one located in the south of Tibet (27–30° N, 78–100° E). Their amplitudes can be up to −100, 150, and −150 nT for F and Z, respectively.
- The spatial distributions of the anomalies in the horizontal component H and the north component X are almost the same. The amplitude of the anomalies is relatively weak in most areas of China, except for the three pairs of positive–negative anomalies. The first of them is located near Sichuan Basin and the west part of Qinling Mountains (27–33° N, 103–112° E), with the amplitude up to ±100 nT; the second pair is located near Tarim Basin and Tianshan Mountains (37–47° N, 73–87° E), with the amplitude up to ±150 nT; and the third is located near Southern Tibet or the Himalayas (25–32° N, 80–95° E), with the amplitude up to ±150 nT.
- The anomalies in the inclination I are negative in most parts of China. The centers of the negative anomalies are located in North China (37–45° N, 118–121° E) and Southeast China (23–32° N, 116–123° E), with the amplitude up to −8′. The centers of the positive anomalies are located in Sichuan Basin and Tarim Basin, with the amplitude up to 10′.
We have provided all the coefficients in Appendix A. Insert these coefficients into Equation (2) to calculate the geomagnetic fields of D, I, and F. The coefficients of the first part of Equation (2) are shown in Table A1, Table A2, Table A3 and Table A4 lists the coefficients of the second part of Equation (2) for D. The first column provides the longitude of the ith position xi in grid lattice distribution, the first action is the latitude yi, and the data where the column and the action meet are the coefficient of Ai. Then we can calculate D on positions x and y using Equation (2). The coefficients for I and F can be used in the same way.
4. Discussion
We tried to use a simple method to achieve a high-precision spatial description of a regional geomagnetic field. The choice of the theoretical method for modeling is the first problem to be considered. The candidate modeling methods include the spherical cap harmonic method, the Taylor polynomial method, and the surface spline method. Because compared with the other two methods, the surface spline method can greatly improve the ability of model description [44], this theory is considered as an alternative to describe the detailed spatial structure of the geomagnetic field without boundary distortion. However, in practice, the theory needs to give not only the fitting coefficient but also the central position of the fundamental wave. We solved the problem by improving the surface spline method. The geomagnetic field of most of China and its surrounding areas can be calculated with a higher precision by a simple method based on the fitting coefficients.
The fundamental wave morphologies of three methods, the spherical cap harmonic method, the Taylor polynomial method, and the surface spline method, are compared. The fluctuations in the fundamental wave of the revised surface spline method on the calculated region boundary are less than the fluctuations in the spherical cap harmonic method and the Taylor polynomial method. So the expected boundary distortion by the surface spline method is smaller, with the same accuracy. This means that the revised surface spline method will be a convenient and useful theory for describing fields.
However, the revised surface spline method can be further improved in the future. For example, there are too many coefficients in the current model. We hope to unify the coefficients of the three elements by combining the surface spline fitting of the geomagnetic potential with spherical expansion in the future.
However, we find that the distribution of geomagnetic anomalies in Mongolia is complex. This may require testing of the geomagnetic field measurements we have collected in the area.
5. Conclusions
After improving the surface spline method, we propose the revised surface spline method based on grid lattice distribution positions. Because fundamental wave centers are fixed, it is possible to determine the time variation characteristics of a geomagnetic field by analyzing the time series of coefficients.
Based on geomagnetic field measurements in mainland China during 2019–2020, we set up Chinese Geomagnetic Reference Field 2020 to describe the geomagnetic field in most of China and surrounding areas. The RMS residual fitted by the RSS values are 0.1318 degrees for D, 0.0857 degrees for I, 93.70 nT for F, 73.94 nT for X, 65.02 nT for Y, and 97.82 nT for Z. The values of F, X, Y, and Z are about 20 nT less than those by the SCH method and IGRF13. So RSS can better reflect the spatial distribution of the geomagnetic field.
The spatial distribution of the geomagnetic field described by RSS shows that geomagnetic anomalies are spatially related to geological structures. Sichuan Basin and Tarim Basin are with positive geomagnetic anomalies for F, H, X, and Z. Qinling Mountains, Tianshan Mountains, and the south of Tibet are with negative geomagnetic anomalies for F, H, X, and Z.
Author Contributions
Methodology, B.C.; software, B.C.; validation, B.C., J.Y. and Z.N.; data processing, B.C., J.Y. and C.W.; writing—original draft preparation, B.C.; writing—review and editing, B.C. and Z.N.; visualization, B.C.; funding acquisition, B.C. and C.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Special Fund of Institute of Geophysics, China Earthquake Administration, “Study on the lithospheric magnetic field model and its variation based on SWARM satellite and ground magnetic data” (DQJB20B25), and the monitoring and maintenance project of China Earthquake Administration “Organization and quality assessment of roving geomagnetic monitoring” (202006235445).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
You can contact us or the Institute of Geophysics of China Earthquake Administration (https://www.cea-igp.ac.cn/, 16 December 2021) to apply for relevant research data.
Acknowledgments
We wish to acknowledge the Geomagnetic Network of China for providing geomagnetic data on geomagnetic observatories. We thank the geomagnetic survey group of China Earthquake Administration for their field and data support. We are also grateful for supporting geomagnetic data and models from the International Association of Geomagnetism and Aeronomy, the International Real-time Magnetic Observatory Network, and National Oceanic and Atmospheric Administration.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The first part of the coefficients of the CGRF2020-RSS.
Table A1.
The first part of the coefficients of the CGRF2020-RSS.
| a00 | a10 | a11 | a20 | a21 | a22 | a30 | a31 | a32 | a33 | |
|---|---|---|---|---|---|---|---|---|---|---|
| D | −51.2926 | 1.5265 | 0.7781 | −0.0144 | −0.0134 | 0.0055 | 0.0000 | 0.0001 | −0.0001 | 0.0001 |
| I | −19.2891 | 0.2362 | 2.1605 | −0.0056 | 0.0168 | −0.0287 | 0.0000 | −0.0001 | 0.0000 | 0.0001 |
| F | 56940.51 | −514.85 | −735.75 | 5.19 | 9.75 | 22.58 | −0.01 | −0.05 | 0.04 | −0.23 |

Table A1.
The second part of the coefficients of D.
Table A1.
The second part of the coefficients of D.
| Ai | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 |
|---|---|---|---|---|---|---|---|---|---|---|
| 72 | 0.0043 | −0.0037 | 0.0183 | −0.0074 | −0.0233 | 0.0499 | −0.0271 | 0.0064 | 0.0127 | −0.0126 |
| 74 | 0.0136 | −0.0417 | 0.0199 | −0.0160 | 0.0056 | −0.0303 | 0.0072 | 0.0191 | −0.0445 | 0.0148 |
| 76 | −0.0278 | 0.0576 | −0.0261 | 0.0254 | −0.0037 | 0.0533 | −0.0591 | 0.0043 | 0.0517 | −0.0140 |
| 78 | 0.0122 | −0.0163 | 0.0071 | −0.0384 | 0.0018 | −0.0085 | 0.0125 | 0.0140 | −0.0573 | 0.0325 |
| 80 | 0.0025 | −0.0240 | 0.0235 | 0.0019 | 0.0103 | 0.0155 | −0.0077 | −0.0195 | 0.0466 | −0.0188 |
| 82 | 0.0050 | 0.0010 | 0.0183 | −0.0252 | 0.0022 | −0.0134 | −0.0003 | 0.0196 | −0.0234 | −0.0058 |
| 84 | −0.0055 | −0.0020 | −0.0100 | 0.0203 | 0.0022 | −0.0133 | 0.0112 | −0.0060 | −0.0108 | 0.0225 |
| 86 | 0.0009 | 0.0051 | 0.0008 | −0.0281 | 0.0275 | 0.0096 | −0.0113 | 0.0055 | 0.0060 | −0.0050 |
| 88 | −0.0039 | 0.0024 | 0.0020 | 0.0032 | −0.0010 | −0.0278 | 0.0129 | −0.0047 | −0.0077 | −0.0017 |
| 90 | 0.0037 | −0.0046 | 0.0092 | −0.0159 | 0.0150 | −0.0001 | −0.0023 | 0.0224 | −0.0011 | 0.0066 |
| 92 | −0.0003 | −0.0037 | 0.0001 | 0.0107 | −0.0245 | 0.0313 | −0.0070 | −0.0501 | 0.0325 | −0.0355 |
| 94 | 0.0003 | 0.0020 | −0.0027 | −0.0018 | 0.0204 | −0.0345 | 0.0250 | 0.0097 | 0.0025 | 0.0013 |
| 96 | 0.0005 | 0.0056 | −0.0051 | 0.0013 | −0.0148 | 0.0341 | −0.0263 | −0.0005 | 0.0048 | −0.0078 |
| 98 | −0.0064 | −0.0044 | 0.0009 | 0.0080 | −0.0080 | −0.0178 | 0.0126 | 0.0095 | −0.0129 | 0.0103 |
| 100 | 0.0120 | 0.0001 | 0.0015 | −0.0014 | 0.0014 | 0.0257 | −0.0303 | 0.0044 | 0.0060 | −0.0045 |
| 102 | −0.0105 | 0.0025 | −0.0048 | 0.0056 | −0.0085 | −0.0062 | 0.0243 | 0.0002 | −0.0153 | 0.0159 |
| 104 | 0.0059 | −0.0044 | 0.0105 | −0.0187 | 0.0262 | −0.0271 | −0.0049 | −0.0021 | 0.0103 | −0.0169 |
| 106 | 0.0007 | −0.0096 | 0.0075 | 0.0019 | −0.0093 | 0.0194 | 0.0059 | −0.0041 | 0.0107 | −0.0016 |
| 108 | 0.0004 | 0.0175 | −0.0124 | 0.0038 | 0.0038 | −0.0190 | 0.0007 | −0.0035 | 0.0027 | −0.0133 |
| 110 | −0.0165 | 0.0006 | −0.0058 | 0.0034 | −0.0083 | 0.0282 | −0.0096 | 0.0080 | −0.0234 | 0.0395 |
| 112 | 0.0247 | −0.0010 | −0.0033 | −0.0012 | 0.0081 | −0.0224 | 0.0108 | −0.0109 | 0.0183 | −0.0192 |
| 114 | −0.0149 | −0.0074 | 0.0171 | −0.0050 | −0.0111 | 0.0217 | −0.0159 | 0.0187 | −0.0192 | 0.0033 |
| 116 | 0.0089 | 0.0053 | −0.0086 | 0.0042 | 0.0129 | −0.0218 | 0.0110 | −0.0142 | 0.0305 | −0.0049 |
| 118 | −0.0103 | −0.0084 | −0.0068 | 0.0097 | −0.0230 | 0.0369 | −0.0138 | 0.0016 | −0.0206 | −0.0192 |
| 120 | 0.0208 | −0.0014 | 0.0134 | 0.0112 | −0.0139 | −0.0144 | 0.0052 | 0.0068 | 0.0228 | −0.0044 |
| 122 | −0.0288 | 0.0171 | −0.0286 | −0.0034 | 0.0031 | 0.0088 | 0.0197 | −0.0457 | 0.0114 | −0.0048 |
| 124 | 0.0272 | −0.0092 | −0.0005 | 0.0299 | −0.0092 | −0.0113 | 0.0004 | 0.0187 | 0.0030 | −0.0061 |
| 126 | −0.0141 | −0.0019 | 0.0043 | −0.0126 | 0.0047 | 0.0030 | −0.0075 | −0.0089 | 0.0069 | −0.0052 |
| 128 | −0.0071 | 0.0121 | −0.0004 | −0.0035 | −0.0021 | −0.0010 | 0.0067 | 0.0077 | −0.0119 | 0.0058 |
| 130 | 0.0183 | −0.0095 | 0.0011 | −0.0141 | 0.0363 | −0.0143 | −0.0010 | −0.0022 | 0.0079 | 0.0049 |
| 132 | −0.0087 | −0.0155 | 0.0113 | 0.0164 | −0.0506 | 0.0180 | 0.0018 | −0.0080 | −0.0002 | −0.0060 |
| 134 | −0.0031 | 0.0255 | −0.0224 | 0.0085 | 0.0132 | 0.0084 | −0.0191 | 0.0246 | −0.0064 | −0.0077 |
| 136 | 0.0068 | −0.0185 | 0.0207 | −0.0171 | 0.0083 | −0.0141 | 0.0173 | −0.0192 | 0.0087 | −0.0036 |
| Ai | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 | 52 | 54 |
| 72 | 0.0125 | −0.0127 | −0.0084 | 0.0408 | −0.0355 | −0.0135 | 0.0129 | 0.0026 | −0.0198 | 0.0136 |
| 74 | 0.0035 | −0.0110 | 0.0096 | −0.0050 | −0.0208 | 0.0493 | 0.0383 | −0.0404 | 0.0065 | 0.0059 |
| 76 | −0.0046 | −0.0004 | 0.0217 | −0.0499 | 0.0747 | −0.0726 | −0.0586 | 0.0557 | 0.0250 | −0.0757 |
| 78 | −0.0172 | 0.0188 | −0.0136 | 0.0427 | −0.0376 | 0.0092 | 0.0744 | −0.0369 | −0.0590 | 0.1285 |
| 80 | −0.0108 | 0.0353 | −0.0584 | −0.0133 | 0.0270 | −0.0042 | −0.0375 | 0.0139 | 0.0129 | −0.0582 |
| 82 | 0.0294 | −0.0702 | 0.0947 | 0.0107 | −0.0597 | 0.0613 | −0.0265 | 0.0156 | 0.0335 | −0.0164 |
| 84 | −0.0163 | 0.0463 | −0.0602 | −0.0266 | 0.0448 | −0.0580 | 0.0460 | −0.0481 | −0.0199 | 0.0069 |
| 86 | 0.0099 | −0.0510 | 0.0592 | 0.0071 | 0.0024 | 0.0297 | −0.0466 | 0.0727 | −0.0452 | 0.0635 |
| 88 | 0.0013 | 0.0225 | −0.0377 | 0.0193 | −0.0406 | −0.0168 | 0.0589 | −0.0565 | 0.0720 | −0.1049 |
| 90 | −0.0063 | −0.0003 | 0.0068 | −0.0156 | 0.0555 | −0.0219 | −0.0532 | 0.0250 | −0.0608 | 0.0745 |
| 92 | 0.0260 | −0.0073 | 0.0074 | −0.0061 | −0.0350 | 0.0420 | 0.0164 | 0.0947 | −0.0708 | 0.0390 |
| 94 | 0.0046 | −0.0129 | 0.0164 | −0.0619 | 0.1380 | −0.1504 | 0.0512 | −0.1462 | 0.1112 | −0.0701 |
| 96 | 0.0044 | −0.0064 | 0.0072 | 0.0413 | −0.1056 | 0.1712 | −0.0955 | 0.1155 | −0.0505 | 0.0244 |
| 98 | −0.0053 | 0.0044 | −0.0112 | 0.0265 | −0.0796 | 0.0864 | −0.2332 | 0.2231 | −0.1287 | 0.0095 |
| 100 | −0.0027 | 0.0048 | −0.0103 | −0.0032 | 0.0558 | −0.0773 | 0.2071 | −0.1435 | 0.0269 | 0.0512 |
| 102 | −0.0042 | 0.0003 | 0.0102 | 0.0133 | −0.0389 | 0.0505 | −0.1525 | 0.1101 | −0.0306 | −0.0431 |
| 104 | 0.0027 | 0.0091 | −0.0406 | 0.0472 | −0.0621 | 0.0797 | −0.0360 | −0.0147 | 0.0223 | 0.0367 |
| 106 | 0.0155 | −0.0338 | 0.0555 | −0.0661 | 0.0468 | −0.0241 | 0.0021 | 0.0873 | −0.0554 | −0.0478 |
| 108 | −0.0108 | 0.0238 | 0.0044 | −0.0007 | 0.0603 | −0.1007 | 0.0863 | −0.1403 | 0.1088 | 0.0375 |
| 110 | −0.0054 | 0.0015 | −0.0515 | 0.0318 | −0.0650 | 0.0749 | −0.0548 | 0.0614 | −0.0627 | −0.0619 |
| 112 | −0.0158 | 0.0174 | 0.0093 | 0.0017 | 0.0194 | −0.0219 | 0.0287 | −0.0017 | 0.0253 | 0.0397 |
| 114 | 0.0132 | −0.0121 | 0.0234 | −0.0228 | 0.0257 | −0.0609 | 0.0317 | −0.0541 | 0.0254 | −0.0303 |
| 116 | −0.0024 | −0.0051 | −0.0254 | 0.0133 | −0.0398 | 0.0934 | −0.0607 | 0.1106 | −0.0902 | 0.0528 |
| 118 | 0.0301 | −0.0038 | 0.0214 | 0.0224 | 0.0182 | −0.0694 | 0.0293 | −0.0867 | 0.0830 | −0.0455 |
| 120 | −0.0027 | −0.0266 | 0.0093 | −0.0615 | 0.0430 | 0.0020 | 0.0176 | 0.0182 | −0.0520 | 0.0310 |
| 122 | 0.0178 | −0.0001 | 0.0289 | −0.0154 | −0.0046 | −0.0133 | 0.0060 | −0.0182 | 0.1013 | −0.0730 |
| 124 | −0.0168 | −0.0021 | −0.0171 | 0.0483 | −0.0193 | 0.0535 | −0.0782 | 0.1060 | −0.1709 | 0.1076 |
| 126 | 0.0107 | 0.0183 | −0.0201 | −0.0318 | −0.0014 | −0.0381 | 0.0537 | −0.1043 | 0.1000 | −0.0547 |
| 128 | −0.0086 | 0.0086 | −0.0208 | 0.0891 | −0.0551 | 0.0864 | −0.0994 | 0.1962 | −0.1374 | 0.0512 |
| 130 | −0.0038 | 0.0008 | −0.0038 | −0.0503 | 0.0250 | −0.0658 | 0.0907 | −0.1544 | 0.0855 | −0.0341 |
| 132 | −0.0039 | −0.0028 | 0.0347 | −0.0282 | 0.0580 | −0.0238 | −0.0109 | 0.0396 | −0.0062 | 0.0187 |
| 134 | 0.0200 | −0.0044 | −0.0219 | 0.0251 | −0.0237 | −0.0098 | 0.0298 | −0.0395 | 0.0302 | −0.0453 |
| 136 | 0.0064 | −0.0155 | 0.0196 | −0.0215 | 0.0191 | −0.0094 | 0.0040 | 0.0114 | −0.0266 | 0.0339 |

Table A3.
The second part of the coefficients of I.
Table A3.
The second part of the coefficients of I.
| Ai | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 |
|---|---|---|---|---|---|---|---|---|---|---|
| 72 | −0.0117 | 0.0249 | −0.0167 | 0.0158 | −0.0291 | 0.0126 | 0.0140 | −0.0191 | 0.0093 | −0.0036 |
| 74 | −0.0152 | 0.0084 | −0.0105 | 0.0068 | 0.0220 | −0.0101 | 0.0154 | −0.0288 | 0.0408 | −0.0260 |
| 76 | 0.0133 | −0.0103 | 0.0147 | −0.0150 | −0.0126 | −0.0126 | −0.0060 | 0.0166 | −0.0266 | 0.0046 |
| 78 | 0.0188 | −0.0402 | 0.0448 | −0.0277 | 0.0065 | 0.0320 | −0.0058 | −0.0050 | 0.0218 | −0.0205 |
| 80 | −0.0103 | 0.0114 | −0.0084 | −0.0114 | 0.0478 | −0.0448 | 0.0020 | 0.0130 | −0.0124 | 0.0088 |
| 82 | 0.0029 | 0.0040 | 0.0058 | −0.0220 | −0.0026 | 0.0029 | 0.0186 | −0.0436 | 0.0252 | 0.0034 |
| 84 | −0.0091 | 0.0045 | 0.0050 | 0.0090 | −0.0049 | 0.0163 | −0.0110 | 0.0299 | −0.0192 | 0.0030 |
| 86 | −0.0036 | 0.0134 | −0.0332 | 0.0160 | 0.0018 | −0.0213 | 0.0093 | −0.0276 | 0.0213 | −0.0075 |
| 88 | 0.0010 | 0.0033 | 0.0093 | −0.0014 | −0.0130 | 0.0221 | −0.0101 | 0.0167 | −0.0001 | −0.0034 |
| 90 | 0.0007 | −0.0100 | −0.0033 | 0.0112 | −0.0103 | 0.0085 | 0.0036 | −0.0336 | 0.0064 | −0.0001 |
| 92 | 0.0095 | −0.0041 | 0.0092 | −0.0066 | −0.0118 | 0.0311 | −0.0470 | 0.0751 | −0.0314 | 0.0139 |
| 94 | −0.0145 | 0.0032 | 0.0007 | 0.0047 | 0.0002 | −0.0134 | 0.0212 | −0.0460 | 0.0112 | 0.0035 |
| 96 | 0.0174 | −0.0118 | 0.0069 | −0.0092 | 0.0065 | −0.0007 | 0.0187 | −0.0127 | 0.0168 | −0.0081 |
| 98 | −0.0145 | 0.0116 | −0.0096 | 0.0123 | −0.0186 | 0.0166 | −0.0184 | 0.0098 | −0.0095 | 0.0077 |
| 100 | 0.0060 | −0.0050 | 0.0062 | −0.0044 | 0.0089 | −0.0117 | −0.0010 | 0.0053 | 0.0035 | −0.0029 |
| 102 | −0.0094 | 0.0112 | −0.0107 | 0.0092 | −0.0090 | 0.0134 | 0.0048 | −0.0076 | −0.0057 | 0.0024 |
| 104 | 0.0143 | −0.0125 | 0.0069 | −0.0087 | 0.0031 | −0.0043 | −0.0092 | 0.0133 | 0.0002 | −0.0008 |
| 106 | −0.0051 | −0.0079 | 0.0056 | 0.0009 | 0.0041 | −0.0005 | 0.0067 | −0.0193 | 0.0171 | −0.0226 |
| 108 | −0.0159 | 0.0392 | −0.0154 | −0.0007 | −0.0057 | 0.0047 | −0.0058 | 0.0036 | 0.0182 | −0.0143 |
| 110 | 0.0307 | −0.0377 | 0.0130 | −0.0021 | 0.0075 | −0.0043 | 0.0083 | −0.0178 | 0.0146 | −0.0159 |
| 112 | −0.0326 | 0.0072 | 0.0036 | −0.0016 | −0.0003 | −0.0018 | −0.0033 | 0.0113 | −0.0156 | 0.0022 |
| 114 | 0.0243 | 0.0084 | −0.0047 | −0.0047 | 0.0021 | 0.0021 | −0.0026 | −0.0015 | 0.0205 | −0.0106 |
| 116 | −0.0154 | −0.0022 | 0.0001 | 0.0007 | −0.0014 | 0.0057 | 0.0017 | −0.0078 | −0.0094 | 0.0050 |
| 118 | 0.0128 | 0.0003 | −0.0133 | 0.0294 | −0.0201 | −0.0106 | 0.0146 | −0.0055 | 0.0076 | −0.0057 |
| 120 | −0.0109 | −0.0108 | 0.0025 | −0.0022 | −0.0056 | 0.0278 | −0.0257 | 0.0116 | 0.0088 | −0.0172 |
| 122 | 0.0187 | 0.0201 | −0.0001 | −0.0087 | 0.0159 | −0.0165 | 0.0113 | −0.0135 | −0.0065 | 0.0190 |
| 124 | −0.0234 | −0.0220 | 0.0094 | −0.0149 | −0.0034 | 0.0051 | −0.0057 | 0.0122 | 0.0023 | 0.0007 |
| 126 | 0.0509 | −0.0272 | 0.0317 | −0.0044 | 0.0205 | −0.0149 | 0.0155 | −0.0138 | −0.0210 | 0.0211 |
| 128 | −0.0543 | 0.0351 | −0.0381 | 0.0147 | −0.0341 | 0.0246 | −0.0132 | 0.0126 | 0.0172 | −0.0027 |
| 130 | 0.0326 | −0.0221 | 0.0139 | −0.0051 | 0.0333 | −0.0341 | 0.0134 | −0.0117 | −0.0159 | 0.0032 |
| 132 | −0.0144 | 0.0047 | 0.0176 | −0.0218 | 0.0100 | −0.0125 | 0.0206 | 0.0041 | 0.0113 | −0.0189 |
| 134 | 0.0262 | −0.0341 | 0.0199 | −0.0127 | 0.0097 | −0.0026 | 0.0008 | −0.0292 | 0.0275 | −0.0153 |
| 136 | −0.0149 | 0.0209 | −0.0216 | 0.0208 | −0.0196 | 0.0159 | −0.0118 | 0.0179 | −0.0147 | 0.0028 |
| Ai | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 | 52 | 54 |
| 72 | 0.0011 | 0.0022 | −0.0086 | 0.0045 | 0.0070 | −0.0040 | −0.0299 | 0.0456 | −0.0213 | 0.0005 |
| 74 | 0.0144 | −0.0015 | −0.0070 | 0.0082 | −0.0113 | 0.0098 | 0.0175 | −0.0138 | 0.0027 | 0.0042 |
| 76 | 0.0176 | −0.0274 | 0.0370 | −0.0146 | −0.0053 | 0.0185 | −0.0193 | −0.0178 | 0.0140 | −0.0053 |
| 78 | −0.0093 | −0.0022 | 0.0128 | −0.0491 | 0.0299 | −0.0261 | 0.0071 | 0.0028 | 0.0002 | 0.0071 |
| 80 | 0.0100 | −0.0040 | 0.0393 | −0.0347 | 0.0746 | −0.0665 | 0.0778 | −0.0194 | −0.0049 | −0.0112 |
| 82 | −0.0102 | −0.0149 | −0.0092 | 0.0090 | −0.0479 | 0.0427 | −0.0491 | −0.0065 | 0.0069 | 0.0113 |
| 84 | −0.0083 | 0.0261 | 0.0066 | −0.0166 | 0.0501 | −0.0616 | 0.0511 | 0.0019 | −0.0071 | 0.0047 |
| 86 | 0.0097 | −0.0285 | 0.0098 | −0.0039 | −0.0283 | 0.0363 | −0.0030 | −0.0119 | 0.0027 | −0.0247 |
| 88 | 0.0080 | −0.0171 | 0.0376 | −0.0053 | −0.0018 | 0.0137 | −0.0670 | 0.0543 | −0.0107 | 0.0299 |
| 90 | 0.0004 | 0.0058 | −0.0212 | −0.0148 | 0.0270 | −0.0351 | 0.0868 | −0.0716 | 0.0114 | −0.0092 |
| 92 | −0.0092 | 0.0108 | −0.0065 | 0.0254 | −0.0271 | 0.0318 | −0.0581 | 0.0498 | −0.0131 | −0.0105 |
| 94 | −0.0030 | −0.0127 | 0.0158 | −0.0105 | −0.0069 | −0.0063 | 0.0205 | −0.0275 | 0.0211 | 0.0136 |
| 96 | −0.0013 | 0.0183 | −0.0143 | −0.0029 | 0.0122 | 0.0162 | −0.0378 | 0.0498 | −0.0372 | −0.0132 |
| 98 | −0.0082 | −0.0025 | 0.0050 | 0.0042 | −0.0075 | −0.0074 | 0.0464 | −0.0450 | −0.0018 | 0.0440 |
| 100 | 0.0024 | 0.0045 | −0.0069 | −0.0185 | 0.0321 | −0.0032 | −0.0590 | 0.0491 | 0.0022 | −0.0348 |
| 102 | 0.0079 | −0.0209 | 0.0305 | −0.0017 | −0.0291 | 0.0004 | 0.0290 | −0.0286 | 0.0255 | −0.0067 |
| 104 | −0.0068 | 0.0159 | −0.0168 | −0.0171 | 0.0762 | −0.0455 | 0.0380 | −0.0024 | −0.0532 | 0.0350 |
| 106 | 0.0255 | −0.0310 | 0.0206 | 0.0079 | −0.0752 | 0.0517 | −0.0724 | 0.0449 | 0.0200 | −0.0148 |
| 108 | 0.0067 | 0.0058 | 0.0032 | −0.0259 | 0.0754 | −0.0539 | 0.0677 | −0.0419 | 0.0093 | −0.0105 |
| 110 | 0.0140 | −0.0221 | 0.0281 | −0.0205 | −0.0068 | 0.0153 | −0.0284 | −0.0038 | 0.0068 | 0.0054 |
| 112 | 0.0038 | 0.0026 | −0.0135 | 0.0091 | 0.0000 | −0.0288 | 0.0453 | −0.0301 | 0.0267 | −0.0145 |
| 114 | 0.0037 | −0.0025 | 0.0131 | −0.0130 | 0.0097 | 0.0164 | −0.0285 | 0.0519 | −0.0431 | 0.0146 |
| 116 | 0.0031 | −0.0048 | −0.0214 | 0.0300 | −0.0192 | 0.0049 | −0.0084 | −0.0337 | 0.0207 | −0.0001 |
| 118 | −0.0089 | 0.0246 | 0.0040 | −0.0013 | −0.0183 | 0.0253 | −0.0134 | 0.0577 | −0.0340 | 0.0044 |
| 120 | 0.0307 | −0.0370 | −0.0012 | −0.0117 | 0.0310 | −0.0332 | 0.0111 | −0.0526 | 0.0341 | −0.0087 |
| 122 | −0.0304 | 0.0258 | 0.0136 | −0.0081 | 0.0030 | −0.0201 | 0.0488 | 0.0089 | −0.0075 | −0.0008 |
| 124 | −0.0035 | 0.0057 | −0.0226 | 0.0141 | −0.0082 | 0.0414 | −0.0734 | 0.0179 | −0.0180 | 0.0109 |
| 126 | −0.0103 | 0.0037 | 0.0118 | −0.0103 | 0.0064 | −0.0437 | 0.0687 | −0.0304 | 0.0321 | −0.0084 |
| 128 | −0.0064 | −0.0024 | −0.0042 | 0.0012 | −0.0133 | 0.0579 | −0.0557 | 0.0057 | −0.0106 | −0.0008 |
| 130 | 0.0079 | 0.0076 | −0.0022 | 0.0067 | 0.0061 | −0.0374 | 0.0240 | 0.0021 | 0.0136 | −0.0061 |
| 132 | 0.0103 | −0.0192 | 0.0018 | 0.0005 | −0.0075 | 0.0220 | −0.0046 | −0.0068 | 0.0006 | −0.0029 |
| 134 | 0.0163 | 0.0040 | −0.0078 | 0.0168 | −0.0098 | −0.0047 | −0.0062 | 0.0080 | 0.0008 | −0.0014 |
| 136 | 0.0033 | −0.0132 | 0.0162 | −0.0260 | 0.0252 | −0.0124 | 0.0054 | 0.0027 | −0.0120 | 0.0094 |

Table A4.
The second part of the coefficients of F.
Table A4.
The second part of the coefficients of F.
| Ai | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 |
|---|---|---|---|---|---|---|---|---|---|---|
| 72 | −14.6349 | 13.7592 | −7.2368 | 16.7847 | −51.4039 | 64.9940 | −37.1171 | −0.1891 | 11.4560 | −9.3127 |
| 74 | 10.6347 | −1.9384 | 1.2586 | −12.5948 | 34.6707 | −27.8421 | 13.1336 | 4.5755 | −1.4905 | −5.5042 |
| 76 | −1.2869 | −15.1666 | 1.5082 | −2.7027 | 19.3015 | −26.7798 | 17.4671 | −8.9993 | −5.6847 | 14.9245 |
| 78 | −6.6708 | 42.5043 | −20.1758 | 23.4548 | −58.2267 | 32.8239 | −11.1312 | 0.1198 | 2.0167 | 1.7611 |
| 80 | 5.1969 | −37.1238 | 10.4947 | −10.2332 | 41.1358 | −7.4607 | −9.6125 | 24.0920 | −10.5866 | −11.9769 |
| 82 | 2.9112 | 5.8836 | 18.1010 | −23.0959 | 7.5271 | −22.0457 | 12.3434 | −9.9386 | −14.1503 | 30.8439 |
| 84 | −2.9171 | 3.5657 | −3.4691 | −16.4864 | 42.6278 | −24.4700 | 17.9801 | −3.1890 | 13.3405 | −15.6858 |
| 86 | 6.2943 | −20.8039 | 22.6271 | −0.6962 | −32.8713 | 19.5658 | −21.0528 | 6.4805 | −13.9210 | 12.8213 |
| 88 | −3.4032 | 10.1920 | −5.5591 | −8.7708 | 21.6194 | 5.6233 | 4.1947 | 3.9910 | −1.1427 | 2.2928 |
| 90 | 0.7563 | −4.2991 | −1.6159 | 8.6991 | −14.9230 | 4.1343 | −42.7192 | 27.7681 | −16.7673 | 7.7860 |
| 92 | 4.8735 | −4.7560 | 7.0941 | −0.4393 | −23.9449 | 62.8203 | −19.5332 | 28.4429 | −16.5018 | −4.0118 |
| 94 | −6.2815 | 5.4927 | −4.9520 | 7.9354 | −13.9294 | 8.1646 | −45.2812 | 11.0199 | −5.8203 | 13.9166 |
| 96 | 6.2837 | −6.2564 | 2.9430 | −4.2688 | 13.6180 | −9.1942 | 28.9355 | −14.6804 | 18.7779 | −21.0134 |
| 98 | −4.2468 | 5.1656 | −7.0385 | 6.2189 | −14.7397 | 12.1954 | −5.5613 | −5.8178 | −0.0426 | 4.8654 |
| 100 | 6.1354 | −6.1413 | 8.1017 | −4.0519 | 15.1407 | −19.9295 | 1.0231 | 6.0794 | 3.5981 | −6.6333 |
| 102 | −8.2728 | 6.8407 | −7.9535 | 5.5245 | −19.1472 | 26.6431 | 0.6804 | −13.2343 | 2.9787 | −2.1152 |
| 104 | 10.8701 | −10.9272 | 15.1468 | −10.5687 | 10.4264 | −10.0029 | −14.8287 | 28.4519 | −17.8533 | 6.9129 |
| 106 | −2.8819 | −10.4081 | −3.4031 | 6.3000 | −5.1743 | 8.1854 | −9.2933 | 15.5077 | −22.0842 | 22.5702 |
| 108 | −13.5480 | 46.0477 | −18.0280 | 3.7190 | −3.6025 | 8.9688 | −14.9151 | 14.6006 | 1.2973 | −15.6363 |
| 110 | 13.8667 | −31.2848 | 4.2254 | −0.0766 | −2.0574 | −0.5575 | 0.3229 | 5.2300 | −16.4278 | 23.2953 |
| 112 | −11.5528 | 11.0092 | 2.3718 | 7.9406 | 0.2783 | −0.5420 | −2.5247 | 1.5259 | −4.1484 | −5.1059 |
| 114 | −1.1618 | 11.5883 | −13.0790 | −5.0932 | 2.5293 | −2.3888 | 3.5583 | 1.2971 | 8.4702 | 3.7272 |
| 116 | 1.7154 | −9.4996 | 17.7469 | −18.7953 | 11.4076 | −0.6741 | −7.7922 | 5.8191 | −19.7159 | 10.1240 |
| 118 | 5.7027 | 1.1162 | −12.2477 | 25.7830 | −12.6469 | −6.8059 | 8.8340 | 8.9776 | −2.1026 | 4.5643 |
| 120 | −10.0626 | −0.3263 | 3.0639 | −10.0471 | −0.2518 | 23.0213 | −24.4916 | −3.5038 | 7.1407 | 1.6889 |
| 122 | 10.9964 | −2.1712 | 4.0445 | 2.5280 | −2.2493 | −5.3337 | 2.4238 | 18.2616 | −21.6725 | 0.8413 |
| 124 | 0.8605 | −18.7314 | 15.4017 | −15.5972 | 6.6312 | 5.3215 | −9.9649 | 1.1456 | 13.3540 | −5.6655 |
| 126 | 9.4586 | −1.7134 | 0.1001 | 8.0642 | −7.3272 | 2.4939 | 7.4439 | −13.6202 | −10.7725 | 15.6161 |
| 128 | −13.6334 | 12.7715 | −5.8955 | −2.1874 | −3.3535 | 3.3510 | −11.7776 | 22.4687 | −5.1762 | 21.2140 |
| 130 | 7.2579 | −12.1961 | 3.9581 | −4.5075 | 15.3084 | −2.6174 | 4.8517 | −9.0343 | −3.7837 | −17.9162 |
| 132 | 0.3425 | 3.7098 | 0.8993 | 8.3591 | −10.5178 | −9.9437 | 1.5077 | 1.0401 | 5.4419 | 0.8753 |
| 134 | −1.6012 | −3.6495 | 0.3836 | −3.4033 | 0.3153 | 11.5465 | −0.7363 | −4.8852 | 8.5154 | −5.5271 |
| 136 | 2.1789 | −0.6194 | 4.0557 | −6.6561 | 7.6590 | −10.7368 | 5.5924 | −2.6753 | 3.5481 | −9.9871 |
| Ai | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 | 52 | 54 |
| 72 | 0.0011 | 0.0022 | −0.0086 | 0.0045 | 0.0070 | −0.0040 | −0.0299 | 0.0456 | −0.0213 | 0.0005 |
| 74 | 0.0144 | −0.0015 | −0.0070 | 0.0082 | −0.0113 | 0.0098 | 0.0175 | −0.0138 | 0.0027 | 0.0042 |
| 76 | 0.0176 | −0.0274 | 0.0370 | −0.0146 | −0.0053 | 0.0185 | −0.0193 | −0.0178 | 0.0140 | −0.0053 |
| 78 | −0.0093 | −0.0022 | 0.0128 | −0.0491 | 0.0299 | −0.0261 | 0.0071 | 0.0028 | 0.0002 | 0.0071 |
| 80 | 0.0100 | −0.0040 | 0.0393 | −0.0347 | 0.0746 | −0.0665 | 0.0778 | −0.0194 | −0.0049 | −0.0112 |
| 82 | −0.0102 | −0.0149 | −0.0092 | 0.0090 | −0.0479 | 0.0427 | −0.0491 | −0.0065 | 0.0069 | 0.0113 |
| 84 | −0.0083 | 0.0261 | 0.0066 | −0.0166 | 0.0501 | −0.0616 | 0.0511 | 0.0019 | −0.0071 | 0.0047 |
| 86 | 0.0097 | −0.0285 | 0.0098 | −0.0039 | −0.0283 | 0.0363 | −0.0030 | −0.0119 | 0.0027 | −0.0247 |
| 88 | 0.0080 | −0.0171 | 0.0376 | −0.0053 | −0.0018 | 0.0137 | −0.0670 | 0.0543 | −0.0107 | 0.0299 |
| 90 | 0.0004 | 0.0058 | −0.0212 | −0.0148 | 0.0270 | −0.0351 | 0.0868 | −0.0716 | 0.0114 | −0.0092 |
| 92 | −0.0092 | 0.0108 | −0.0065 | 0.0254 | −0.0271 | 0.0318 | −0.0581 | 0.0498 | −0.0131 | −0.0105 |
| 94 | −0.0030 | −0.0127 | 0.0158 | −0.0105 | −0.0069 | −0.0063 | 0.0205 | −0.0275 | 0.0211 | 0.0136 |
| 96 | −0.0013 | 0.0183 | −0.0143 | −0.0029 | 0.0122 | 0.0162 | −0.0378 | 0.0498 | −0.0372 | −0.0132 |
| 98 | −0.0082 | −0.0025 | 0.0050 | 0.0042 | −0.0075 | −0.0074 | 0.0464 | −0.0450 | −0.0018 | 0.0440 |
| 100 | 0.0024 | 0.0045 | −0.0069 | −0.0185 | 0.0321 | −0.0032 | −0.0590 | 0.0491 | 0.0022 | −0.0348 |
| 102 | 0.0079 | −0.0209 | 0.0305 | −0.0017 | −0.0291 | 0.0004 | 0.0290 | −0.0286 | 0.0255 | −0.0067 |
| 104 | −0.0068 | 0.0159 | −0.0168 | −0.0171 | 0.0762 | −0.0455 | 0.0380 | −0.0024 | −0.0532 | 0.0350 |
| 106 | 0.0255 | −0.0310 | 0.0206 | 0.0079 | −0.0752 | 0.0517 | −0.0724 | 0.0449 | 0.0200 | −0.0148 |
| 108 | 0.0067 | 0.0058 | 0.0032 | −0.0259 | 0.0754 | −0.0539 | 0.0677 | −0.0419 | 0.0093 | −0.0105 |
| 110 | 0.0140 | −0.0221 | 0.0281 | −0.0205 | −0.0068 | 0.0153 | −0.0284 | −0.0038 | 0.0068 | 0.0054 |
| 112 | 0.0038 | 0.0026 | −0.0135 | 0.0091 | 0.0000 | −0.0288 | 0.0453 | −0.0301 | 0.0267 | −0.0145 |
| 114 | 0.0037 | −0.0025 | 0.0131 | −0.0130 | 0.0097 | 0.0164 | −0.0285 | 0.0519 | −0.0431 | 0.0146 |
| 116 | 0.0031 | −0.0048 | −0.0214 | 0.0300 | −0.0192 | 0.0049 | −0.0084 | −0.0337 | 0.0207 | −0.0001 |
| 118 | −0.0089 | 0.0246 | 0.0040 | −0.0013 | −0.0183 | 0.0253 | −0.0134 | 0.0577 | −0.0340 | 0.0044 |
| 120 | 0.0307 | −0.0370 | −0.0012 | −0.0117 | 0.0310 | −0.0332 | 0.0111 | −0.0526 | 0.0341 | −0.0087 |
| 122 | −0.0304 | 0.0258 | 0.0136 | −0.0081 | 0.0030 | −0.0201 | 0.0488 | 0.0089 | −0.0075 | −0.0008 |
| 124 | −0.0035 | 0.0057 | −0.0226 | 0.0141 | −0.0082 | 0.0414 | −0.0734 | 0.0179 | −0.0180 | 0.0109 |
| 126 | −0.0103 | 0.0037 | 0.0118 | −0.0103 | 0.0064 | −0.0437 | 0.0687 | −0.0304 | 0.0321 | −0.0084 |
| 128 | −0.0064 | −0.0024 | −0.0042 | 0.0012 | −0.0133 | 0.0579 | −0.0557 | 0.0057 | −0.0106 | −0.0008 |
| 130 | 0.0079 | 0.0076 | −0.0022 | 0.0067 | 0.0061 | −0.0374 | 0.0240 | 0.0021 | 0.0136 | −0.0061 |
| 132 | 0.0103 | −0.0192 | 0.0018 | 0.0005 | −0.0075 | 0.0220 | −0.0046 | −0.0068 | 0.0006 | −0.0029 |
| 134 | 0.0163 | 0.0040 | −0.0078 | 0.0168 | −0.0098 | −0.0047 | −0.0062 | 0.0080 | 0.0008 | −0.0014 |
| 136 | 0.0033 | −0.0132 | 0.0162 | −0.0260 | 0.0252 | −0.0124 | 0.0054 | 0.0027 | −0.0120 | 0.0094 |
References
- Kaufman, A.A.; Hansen, R.O.; Kleinberg, R.L.K. Principles of the Magnetic Methods in Geophysics; Elsevier: Oxford, UK, 2009; p. 301. [Google Scholar]
- Gvishiani, A.; Soloviev, A. Observations, Modeling and Systems Analysis in Geomagnetic Data Interpretation; Springer: Cham, Switzerland, 2020; p. 311. [Google Scholar]
- Eppelbaum, L.V. Geophysical Potential Fields: Geological and Environmental Applications; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Fu, C.Y.; Chen, Y.T.; Qi, G.Z. Fundamentals of Geophysics; Science Press: Beijing, China, 1985. (In Chinese) [Google Scholar]
- Xu, W.Y. Geomagnetism; Seismological Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- Witze, A. Earth’s magnetic field is acting up and geologists don’t know why. Nature 2019, 565, 143–144. [Google Scholar] [CrossRef] [PubMed]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.N.; Brown, W.J.; Califf, S.; Chambodut, A.; et al. International Geomagnetic Reference Field: The thirteenth generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- Alldredge, L.R. Geomagnetic local and regional harmonic analysis. J. Geophys. Res. 1982, 87, 1921–1926. [Google Scholar] [CrossRef]
- Alldredge, L.R. On regional magnetic charts. J. Geomag. Geoelectr. 1987, 39, 723–738. [Google Scholar] [CrossRef]
- Haines, G.V. Regional magnetic field modeling: A review. J. Geomag. Geoelectr. 1990, 42, 1001–1018. [Google Scholar] [CrossRef][Green Version]
- Haines, G.V.; Newitt, L.R. Canadian geomagnetic reference field 1985. J. Geomag. Geoelectr. 1986, 38, 895–921. [Google Scholar] [CrossRef]
- Barton, C.E. Global and regional geomagnetic reference fields. Explor. Geophys. 1988, 19, 401–416. [Google Scholar] [CrossRef]
- Newitt, L.R.; Haines, G.V. A Canadian geomagnetic reference field for epoch 1987.5. J. Geomag. Geoelectr. 1989, 41, 249–260. [Google Scholar] [CrossRef][Green Version]
- Ates, A.; Kearey, P.; Tufan, S. New gravity and magnetic anomaly maps of Turkey. Geophys. J. Int. 1999, 116, 499–502. [Google Scholar] [CrossRef]
- Kote, M.; Haok, V. Modeling European magnetic repeat station and survey data by SCHA in search of time-variation anomalies. Phys. Earth Planet Inter. 2000, 122, 205–220. [Google Scholar]
- Buyuksarac, A.; Jordanova, D.; Ates, A.; Karloukovski, V. Interpretation of the gravity and magnetic anomalies of the Cappadocia region, central Turkey. Pure Appl. Geophys. 2005, 162, 2197–2213. [Google Scholar] [CrossRef]
- Di, C.-Z.; Gu, Z.-W.; Soriano, B.M.; Chen, B.; Lao, C.G.; Zhang, Y.; Xin, C.-J.; Gao, J.-T. The study of magnetic field models for Philippines and its neighboring regions. Chin. J. Geophys. 2011, 54, 1061–1074. (in Chinese). [Google Scholar] [CrossRef]
- Xia, G.H.; Cheng, S.L.; Wu, L.L. The geomagnetic field chart of China in 1980.0 and the mathematical model. Chin. J. Geophys. 1988, 31, 82–89. (In Chinese) [Google Scholar]
- Xu, W.Y.; Xia, G.H.; An, Z.C. Magnetic survey and China GRF2000. Earth Planet Space 2003, 55, 215–217. [Google Scholar] [CrossRef]
- Xu, W.Y.; Wei, Z.G.; Xia, G.H. Regional features of the secular variations of the geomagnetic field in China for 2000. Chin. J. Geophys. 2005, 48, 551–560. (In Chinese) [Google Scholar] [CrossRef]
- An, Z.C. Spherical cap harmonic analysis of geomagnetic field for China. Chin. J. Geophys. 1993, 36, 753–764. (In Chinese) [Google Scholar]
- An, Z.C. Spherical cap harmonic analysis of the geomagnetic field and its secular variation in China for 2000. Chin. J. Geophys. 2003, 46, 68–77. (In Chinese) [Google Scholar] [CrossRef]
- An, Z.C. Spherical cap harmonic model of the Chinese geomagnetic reference field for 1936. Chin. J. Geophys. 2003, 46, 624–627. (In Chinese) [Google Scholar] [CrossRef]
- An, Z.C. Spherical cap harmonic analysis of the geomagnetic residual field in China for 1950~1990. Chin. J. Geophys. 2003, 46, 767–771. (In Chinese) [Google Scholar] [CrossRef]
- An, Z.-C.; Tang, D.-H.; Wang, Y.-H.; Yuan-Fang, X.; Golovkov, V.P.; Rotanova, N.M.; Kharitonov, A.L. MAGSAT magnetic anomaly maps for Asia. Chin. J. Geophys. 1996, 39, 461–469. (In Chinese) [Google Scholar]
- An, Z.C.; Tang, D.H.; Rotanova, N.M.; Golovkov, V.P. Spherical cap Harmonic analysis of MAGSAT magnetic anomalies over Asia. Chin. J. Geophys. 1998, 41, 168–173. (In Chinese) [Google Scholar]
- Gao, J.-T.; An, Z.-C.; Gu, Z.-W.; Han, W.; Zhan, Z.-J.; Yao, T.-Q. Selection of geomagnetic normal field and calculation of geomagnetic anomalous field. Chin. J. Geophys. 2005, 48, 66–73. (In Chinese) [Google Scholar] [CrossRef]
- Gu, Z.-W.; An, Z.-C.; Gao, J.-T.; Han, W. Spherical cap harmonic analysis of the geomagnetic field in the Beijing-Tianjin-Hebei region. Chin. J. Geophys. 2004, 47, 1128–1134. (In Chinese) [Google Scholar] [CrossRef]
- Chen, B.; Ni, Z.; Ru-Gang, X.; Zuo-Wen, G.; Jie-Hao, Y.; Lei, W. The Geomagnetic field in China and neighboring regions for the 2010.0 epoch. Chin. J. Geophys. 2016, 59, 1446–1456. (In Chinese) [Google Scholar] [CrossRef]
- Qiu, Y.D. Inversion of lithospheric magnetic field in China mainland with CHAMP and Swarm satellite magnetic survey data. Ph.D. Thesis, Wuhan University, Wuhan, China, 2017. [Google Scholar]
- Chattopadhyay, G.; Chattopadhyay, C. A probe into the chaotic nature of total ozone time series by correlation dimension method. Soft Comput. 2008, 12, 1007–1012. [Google Scholar] [CrossRef]
- Aldebert, C.; Koenig, G.; Baklouti, M.; Fraunié, P.; Devenon, J.-L. A Fast and Generic Method to Identify Parameters in Complex and Embedded Geophysical Models: The Example of Turbulent Mixing in the Ocean. J. Adv. Modeling Earth Syst. 2021, 13, e2020MS002245. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Chattopadhyay, G. Modeling and Prediction of Monthly Total Ozone Concentrations by Use of an Artificial Neural Network Based on Principal Component Analysis. Pure Appl. Geophys. 2012, 169, 1891–1908. [Google Scholar] [CrossRef]
- Yu, Z.W. A new interpolation method for geological surface. J. China Univ. Min. Technol. 1987, 4, 69–76. [Google Scholar]
- Gu, Z.; Zhan, Z.; Gao, J.; Han, W.; An, Z.; Yao, T.; Chen, B. Geomagnetic Survey and Geomagnetic Model research in China. Earth Planets Space 2006, 58, 741–750. [Google Scholar] [CrossRef]
- Gu, Z.; Zhan, Z.; Gao, J.; Yao, T.; Han, W. Application of GPS in Geomagnetic Survey. Earth Planets Space 2006, 58, 723–729. [Google Scholar] [CrossRef][Green Version]
- Wu, Y.; Liu, L.; Ren, Z. Equinoctial asymmetry in solar quiet fields along the 120° E meridian chain. Appl. Sci. 2021, 11, 9150. [Google Scholar] [CrossRef]
- Gu, Z.-W.; Bin, C.; Jin-Tian, G.; Chang-Jiang, X.; Jie-Hao, Y.; Chuan-Zhi, D. Research of geomagnetic spatial-temporal variations in China by NOC method. Chin. J. Geophys. 2009, 52, 2602–2612. (In Chinese) [Google Scholar] [CrossRef]
- Chen, B.; Yuan, J.; Wang, C.; Rugang, X.U.; Wang, Z.; China Earthquake Administration; AE Agency. Data processing flowchart of Chinese mobile geomagnetic monitoring array. J. Seismo. Res. 2017, 40, 335–339. (In Chinese) [Google Scholar]
- Maus, S. An ellipsoidal harmonic representation of Earth’s lithospheric magnetic field to degree and order 720. Geochem. Geophys. Geosystems 2010, 11, 1–12. [Google Scholar] [CrossRef]
- Chulliat, A. The US/UK World Magnetic Model for 2015–2020. In Technical Report; National Geophysical Data Center: Boulder, CO, USA, 2015. [Google Scholar]
- Linjuan, N.; Yaodong, Q.; Wenbin, S.; Suqin, Z.; Bingbing, Z. Accuracy evaluation and applicability of IGRF12 and WMM2015 model in Chinese Mainland. Geomat. Inf. Sci. Wuhan Univ. 2017, 42, 1229–1235. (In Chinese) [Google Scholar] [CrossRef]
- Mao, F. Three-Dimensional Spherical Cap Harmonic Analysis of China Geomagnetic Field at 2015.0. Master’s Thesis, Institute of Geophysics, China Earthquake Administration, Beijing, China, 2019. [Google Scholar]
- Yan, F.; Huang, Y.; Liu, S.; Li, Y.-J.; Jiang, Y. Modeling of CHAMP satellite data according to the 3D surface spline model of geomagnetic fields. Appl. Geophys. 2021, 17, 616–623. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).