UAV-Cooperative Penetration Dynamic-Tracking Interceptor Method Based on DDPG

Abstract

The multi-UAV system has stronger robustness and better stability in combat. Therefore, the collaborative penetration of UAVs has been extensively studied in recent years. Compared with general static combat scenes, the dynamic tracking and interception of equipment penetration are more difficult to achieve. To realize the coordinated penetration of the dynamic-tracking interceptor by the multi-UAV system, the intelligent UAV model is established by using the deep deterministic policy-gradient algorithm, and the reward function is constructed using the cooperative parameters of multiple UAVs to guide the UAV to proceed with collaborative penetration. The simulation experiment proved that the UAV finally evaded the dynamic-tracking interceptor, and multiple UAVs reached the target at the same time, realizing the time coordination of the multi-UAV system.

1. Introduction

Compared with traditional manned aerial vehicles, unmanned aerial vehicles (UAVs) can be autonomously controlled or remotely controlled, which have the advantages of low requirements on the combat environment and strong battlefield survivability, and they can be used to perform a variety of complex tasks [1,2]. Therefore, UAVs have been widely studied and applied [3]. With the continuous application of UAVs in the military field, the system composed of a single UAV has gradually revealed the problems of poor flexibility and low stability [4,5]. The cooperative combat method of using a multi-UAV system composed of multiple UAVs has become a new main research direction [6,7]. Under the conditions of the modernized and networked battlefield, the air cluster composed of multiple UAVs has the air power to continuously launch the required strikes, forcing the enemy to spend more resources and deal with more fighters, thereby enhancing the overall capability and overall performance of military combat confrontation.

Multi-UAV-cooperative penetration is one of the key issues to achieve multi-UAV-cooperative combat. Multiple UAVs start from the same location or different locations, and finally arrive at the same place. At present, UAVs’ penetration-trajectory-planning methods mainly include the A* algorithm [8], the artificial potential field method [9,10], and the RRT algorithm [11]. Most of the application scenarios of these methods are environments with static no-fly zones and rarely consider dynamic threats. The A* algorithm is a typical grid method. This type of method rasterizes the map for planning, but the size of the grid will have a greater impact on the result and is difficult to determine. Based on the artificial potential field law, it is easy to fall into the local optimum, leading to the unreachable target. When there is a dynamic-tracking interceptor in the environment, the environment information becomes complicated, and real-time planning requirements are put forward for UAVs. Therefore, traditional algorithms cannot meet the requirements.

Multi-UAV-cooperative penetration generally requires that multiple UAVs achieve time coordination to penetrate defenses according to different trajectories and finally reach the target area at the same time or according to a certain time sequence. When the UAVs depart from different locations, it will greatly increase the difficulty of collaboration. The multi-UAV-coordination algorithm can be improved based on the traditional single-UAV-penetration algorithm adapted to the multi-UAV environment. Chen uses the optimal-control method to improve the artificial potential-field method to achieve multi-UAV coordination [11,12], and Kothari improves the RRT algorithm to achieve multi-UAV coordination [13]. At the same time, there are a large number of methods for cooperative control of UAVs based on the graph theory [3]. Li proposed a multi-UAV-collaboration method based on the graph theory [14]. Ruan proposed a multi-UAV-coordination method based on multi objective optimization [15]. The above methods all realize the coordination of multiple UAVs, but their algorithms lack the research on dynamic environments and cannot adapt to the complex and dynamic battlefield environment. Aimed at the environment with dynamic threats, this paper proposes a method based on deep reinforcement learning to achieve multi-UAV-cooperative penetration.

Reinforcement learning is an important branch of machine learning. Its main feature is to evaluate the action policy of the agent based on the final rewards and through the interaction and trial and error between the agent and the environment. Reinforcement learning is a far-sighted machine-learning method that considers long-term rewards [16,17]. It is often used to solve sequential decision-making problems. Reinforcement learning can not only be applied in a static environment but also when the parameters of the environment are constantly changing, and the agent can also be applied in a dynamic environment [16,17,18]. The research of reinforcement learning is mostly concentrated in the field of a single agent, but there is also a large body of research on reinforcement-learning algorithms for multiagent systems. There is also much research on applying reinforcement learning to UAVs. Pham successfully applied deep reinforcement learning to UAVs to realize autonomous navigation of UAVs [19]. Wang also studied the autonomous navigation of UAVs in large, unknown, and complex environments based on deep reinforcement learning [20]. Wang applied reinforcement learning to the target search and tracking of UAVs [21]. Based on deep reinforcement learning, Yang studied the task scheduling problem of UAV clusters and solved the application problem of reinforcement learning in multi-UAV systems [22]. Through the investigation of relevant literature, it can be found that the application of deep reinforcement learning to multi-UAV systems is a feasible method, which can be used to achieve complex multi-UAV-system tasks and has great research potential.

The main work of this paper uses the multi-UAV-cooperative penetration dynamic-tracking interceptor as the scenario. Based on the deep reinforcement-learning DDPG algorithm, we establish the intelligent UAV model and realize the multi-UAV-cooperative penetration dynamic-tracking interceptor by designing the reward function related to coordination and penetration. The simulation experiment results show that the trained multi-UAV system can achieve cooperative attack tasks from different initial locations, which proves the application potential of artificial intelligence methods, such as reinforcement learning in the implementation of coordinated tasks in UAV clusters.

2. Problem Statement

2.1. Motion Scene

This paper solves the problem of multi-UAV-cooperative penetration of dynamic interceptors. We assume multiple UAVs are respectively numbered as $L=\left\{1,2,\dots ,n\right\}$. The scene is set as a two-dimensional engagement plane. Figure 1 is the schematic diagram of the motion scene of the multi-UAVs.

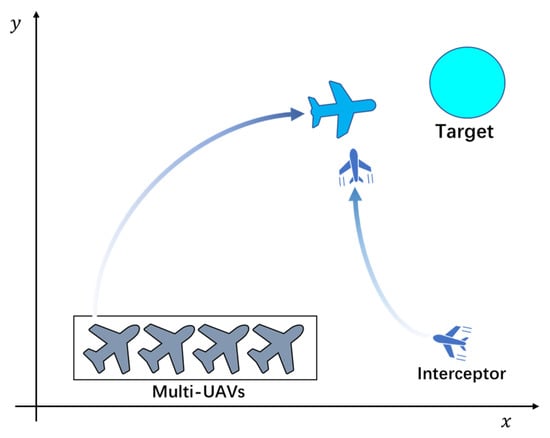
Figure 1. The motion scene of the multi-UAVs.

Based on reinforcement learning algorithms, the following are the requirements:

• The UAV is not intercepted by interceptors when it is moving;
• Multi-UAVs finally reach the target area at the same time.

2.2. UAV Movement Model

First, a two-dimensional movement model of the UAV is established. Figure 2 is the schematic diagram of the movement of the UAV. It is assumed that the linear velocity of the UAV is constant, and the angular velocity, $\omega$, is a continuously variable value. It is assumed that the angle between the movement direction of the UAV and the x-axis is the azimuth angle, $\theta$.

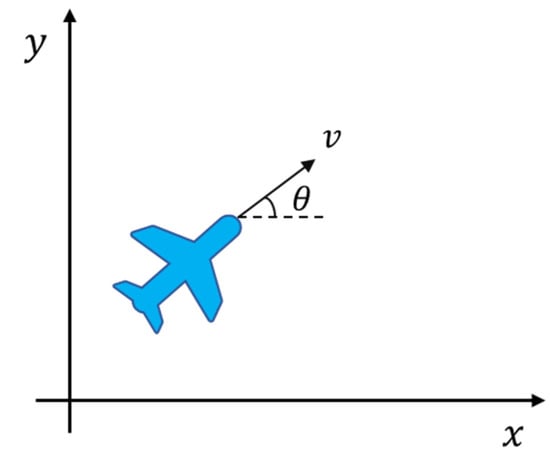
Figure 2. Schematic diagram of UAV movement.

The movement of the UAV is divided into x and y directions. First, the current azimuth angle is obtained by integrating the angular velocity of the UAV, and then the velocity is decomposed on the coordinate axis by the azimuth angle, $\theta$, and finally, the position information of the UAV is obtained through integration. The mathematical model is shown in (1):

$$\left\{\begin{array}{c}\theta ={\theta }_0+{{\displaystyle \int }}_0^t\omega dt\\ v_x=v \sin \theta \\ v_y=v\cos \theta \\ x=x_0+{{\displaystyle \int }}_0^t{v}_{x}dt\\ y=y_0+{{\displaystyle \int }}_0^t{v}_{y}dt\end{array}\right.$$

(1)

2.3. Dynamic-Interceptor Design

Compared with the static environment, the position of the dynamic-interceptor changes in real time in the environment, so the UAV is required to be able to perform real-time planning. In this paper, the dynamic interceptor is defined as a tracking interceptor according to the proportional-guided pursuit law. Compared with most common dynamic interceptors with simple motion rules, such as interceptors that cycle in a uniform linear motion or circular motion, the tracking interceptor has stronger uncertainty, and it is difficult to evade by predicting the motion. The movement requirements of the multi-UAV system are much higher. In this paper, it is assumed that the linear velocity of the tracking interceptor is constant, and the angular velocity is calculated by proportional guidance. The schematic diagram of its movement is shown in Figure 3.

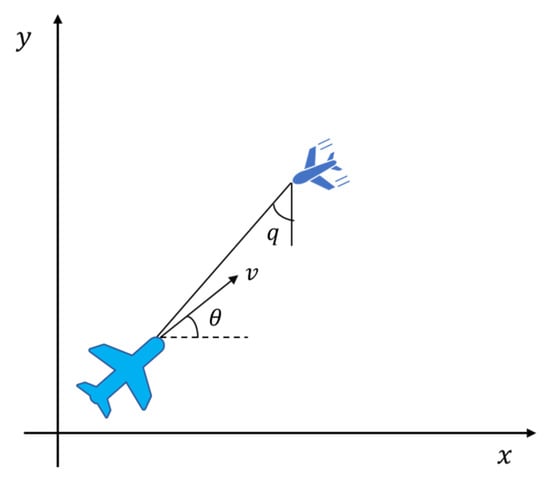
Figure 3. Schematic diagram of interceptor’s movement.

The basic principle of the proportional-guidance method is to make the interceptor’s rotational angular velocity proportional to the line-of-sight angular velocity. Next, the proportional-guidance mathematical model of the interceptor is introduced.

Assuming that the position of the interceptor is $x_b,y_b,$ the speed is $v_{x_b},v_{y_b}$, the position of the UAV is $x,y$, and the speed is $v_x,v_y$, and the relative position and speed of the interceptor to the UAV are shown in (2):

$$\left\{\begin{array}{c}{x}_r=x_b-x\\ y_r=y_b-x\\ v_{x_r}=v_{x_b}-v_x\\ v_{y_r}=v_{y_b}-v_y\end{array}\right.$$

(2)

The interceptor’s line of sight angle to the UAV can be obtained as:

$$q=\arctan \left(\frac{x_r}{y_r}\right)$$

(3)

To obtain the line-of-sight angular velocity, (3) is derived, as shown in (4):

$$\dot{q}=\frac{v_{y_r}{x}_r-v_{x_r}{y}_r}{x_r^2+y_r^2}$$

(4)

The rotational angular velocity of the dynamic-tracking interceptor can be obtained by (5):

$${\omega }_b=K\dot{q}$$

(5)

K is the proportional guidance coefficient, taking K = 2.

Based on the angular velocity of rotation calculated by the proportional guidance, the interceptor performs a two-dimensional movement according to the angular velocity of the rotation obtained by the proportional guidance. The movement model is similar to that of a UAV:

$$\left\{\begin{array}{c}{\theta }_b={\theta }_{\mathrm{b}0}+{{\displaystyle \int }}_0^t{\omega }_{b}dt\\ v_{bx}=v_b\sin {\theta }_b\\ v_{by}=v_b\cos {\theta }_b\\ x_b=x_{b0}+{{\displaystyle \int }}_0^t{v}_{bx}dt\\ y_b=y_{b0}+{{\displaystyle \int }}_0^t{v}_{by}dt\end{array}\right.$$

(6)

3. Deep Deterministic Policy-Gradient Algorithm

The DDPG algorithm is a branch of reinforcement learning [5]. The basic process of reinforcement-learning training is that the agent performs an action based on the current observation state. This action acts on the agent’s training environment and returns a reward and a new state observation. The goal of training is to maximize the final reward. Reinforcement learning does not need to give any artificial strategies and guidance during training but only needs to give the reward function when the environment is in various states. This is also the only part of training that can be adjusted artificially. Figure 4 shows the basic process of reinforcement learning.

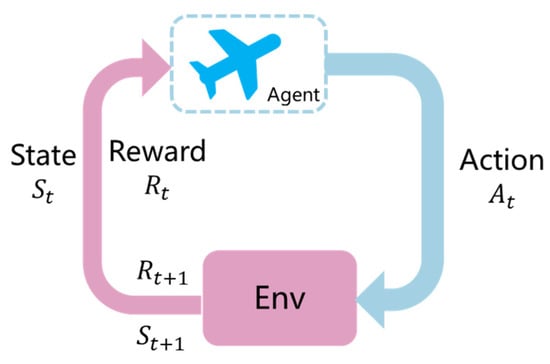
Figure 4. The basic process of reinforcement learning.

The DDPG algorithm is an actor-critic framework algorithm that solves the problem of applying reinforcement learning in continuous space. There are two networks in the DDPG algorithm, namely, the state-action value function network $Q(s,a|{\theta }^Q)$ using ${\theta }^Q$ parameters and the policy network $\mu (s|{\theta }^{\mu })$ using ${\theta }^{\mu }$ parameters. At the same time, two concepts are introduced, target network and experience replay. When the value function network is updated, the current value function is used to fit the future state-action value function. If both state-action value functions use the same network, it is difficult to fit during training. Therefore, the concept of the target network is introduced. The target network is used as the future state-action value function, which is the same as the state-action value function network to be updated, except that it is not updated in real time but is updated according to the state-action value function network when the state-action value function network is updated to a certain extent. The policy network also adopts the same training method in DDPG. The experience replay is a function of storing state transfer $\left(s_t,a_t,r_t,s_{t+1}\right)$, and it will be stored in the experience replay pool every time the agent performs an action that causes the state to transfer. When the value function is updated, it will not be updated directly according to the action of the current policy, but the state transition value will be extracted from the experience playback pool for updating. The advantage of such an update is that the training and learning of the network is more efficient.

Before training, the value function network, $Q(s,a|{\theta }^Q)$, and the policy network, $\mu \left(s|{\theta }^{\mu }\right)$, are first randomly initialized, and then the target network, $Q^{\prime }$ and ${\mu }^{\prime }$, are initialized. It is also necessary to initialize an action random noise, $\mathcal{N}$, which is conducive to the agent’s exploration. During training, the agent selects and executes actions, $a_t=\mu \left(s_t\mid {\theta }^{\mu }\right)+{\mathcal{N}}_t$, based on the current policy network and action noise and receives rewards, $r_t$, and new state observations, $s_{t+1}$, based on environment feedback. The state transition $\left(s_t,a_t,r_t,s_{t+1}\right)$ is stored in the experience replay pool. After that, N state transitions $\left(s_i,a_i,r_i,s_{i+1}\right)$ are randomly selected to update the value function network. The principle of updating the value function network is to minimize the loss function. The mathematical expression of the loss function is as follows:

$$L=\frac{1}{N}{{\displaystyle \sum }}_i{\left(y_i-Q\left(s_i,a_i\mid {\theta }^Q\right)\right)}^2$$

(7)

where $y_i=r_i+\gamma Q^{\prime }\left(s_{i+1},{\mu }^{\prime }\left(s_{i+1}\mid {\theta }^{{\mu }^{\prime }}\right)\mid {\theta }^{Q^{\prime }}\right)$, $y_i$ is only related to ${\theta }^Q$.

Assuming the objective function of training is the following:

$$J\left({\theta }^{\mu }\right) =E_{{\theta }^{\mu }}\left[r_1+\gamma r_2+{\gamma }^2{r}_3+\dots {\gamma }^N{r}_N\right]$$

(8)

where $\gamma$ is the discount factor. The policy network is updated according to the gradient of the objective function, and its mathematical expression is as follows:

$${\left.{\left.{\nabla }_{{\theta }^{\mu }}J\approx \frac{1}{N}{{\displaystyle \sum }}_i{\nabla }_{a}Q\left(s,a\mid {\theta }^Q\right)\right|}_{s=s_i,a=\mu \left(s_i\right)}{\nabla }_{{\theta }^{\mu }}\mu \left(s\mid {\theta }^{\mu }\right)\right|}_{s_i}$$

(9)

After training and finally updating the target network, the mathematical expression is as follows:

$$\left\{\begin{array}{c}{\theta }^{Q^{\prime }}\leftarrow \tau {\theta }^Q+\left(1-\tau \right){\theta }^{Q^{\prime }}\\ {\theta }^{{\mu }^{\prime }}\leftarrow \tau {\theta }^{\mu }+\left(1-\tau \right){\theta }^{{\mu }^{\prime }}\end{array}\right.$$

(10)

To extend DDPG to a multi-UAV system, multiple actors and a critic must exist in the system. During each training, the value function network evaluates the policies of all UAVs in the environment, and the UAVs update their respective policy networks based on the evaluation and independently choose to execute actions. Figure 5 shows the structure of the multi-UAV DDPG algorithm.

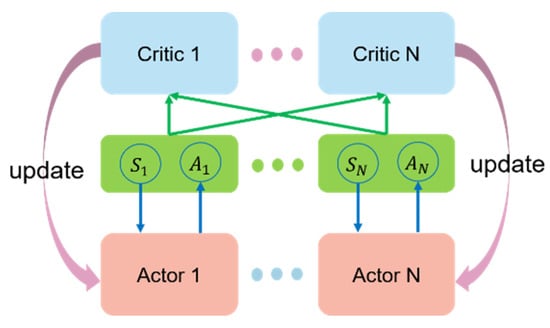
Figure 5. Multi-UAV DDPG algorithm.

The algorithm design also needs to construct the UAV’s action space, state space, reward function, and termination conditions. In this paper, all UAVs are tested and simulated using small UAV models for the purpose of preliminary verification of the algorithm.

3.1. Action-Space Design

It can be seen from the motion model of the UAV that the action the UAV can perform is to change the angular velocity so the action space of multiple UAVs is designed as $A=\left\{{\omega }_1,{\omega }_2,\dots ,{\omega }_n\right\}$, which is the collection of the angular velocity of multiple UAVs.

3.2. State-Space Design

To realize the coordinated penetration of UAVs, the design of the state space should include the UAVs’ positions, $x_i,y_i$, speed, $v_{x_i},v_{y_i}$, and the central position of the target area, $x_t,y_t$. At the same time, it is necessary to introduce the state observation of the interceptor position, $x_b,y_b$. Therefore, the state space is set to $S=\left\{x_i,y_i,v_{x_i},v_{y_i},x_t,y_t,x_b,y_b\right\},i\in L$.

3.3. Termination Conditions Design

The termination conditions are divided into four items, namely, out of bounds, collision, timeout, and successful arrival.

a)

Out of bounds: When the movement of the UAV exceeds the environmental boundary, it will be regarded as a mission failure; an end signal and a failure signal will be given.

b)

Collision: When the UAV is captured by the interceptor, that is, the distance between the two, $d_b=\sqrt{{(x-x_b)}^2+{(y-y_b)}^2}\le d_{collision}$, it is regarded as a mission failure; an end signal and a failure signal are given.

c)

Timeout: When the training time exceeds the maximum exercise time, the task will be regarded as a failure; an end signal and a failure signal will be given.

d)

Successful arrival: When the UAV successfully reaches the target area, the mission is successful; an end signal and a success signal are given.

When any UAV in the environment finishes training, all UAVs finish training and give a failure or success signal according to the distance from the target point.

3.4. Reward-Function Design

The sparse reward problem is a common problem when designing the reward function. This problem will affect the training process of the UAV, prolong the training time of the UAV and even fail to achieve the training goal. To better achieve collaborative tasks and solve the problem of sparse reward, the reward-function design is divided into four parts, namely, the distance-reward function, $R_d$, which is related to the distance between the UAV and the target, the cooperative reward, $R_{co}$, which is used to constrain the position of the UAV, the mission success reward, $R_s$, and the mission failure reward, $R_{fail}$. The reward function is linearized to improve the efficiency of UAV cluster training. One of the UAVs is an example to introduce the design of the reward function.

Assume $d_i=\sqrt{{(x_i-x_t)}^2+{(y_i-y_t)}^2},i\in L$ represents the distance between one UAV and the target area, $d_{target}$, representing the distance between the UAV’s initial location and the target area.

The distance reward, $R_d$, is related to the distance from the UAV to the target area. The closer the distance, the greater the distance-reward value. This type of reward is the key reward on whether the UAV can reach the target area. The specific form is shown in (11):

$$R_d=0.6-d_i/d_{target}$$

(11)

The cooperative reward is related to the cooperative parameters in the UAV cluster. Here, the difference between the farthest and closest distance between the UAV and the target area is selected as the coordination parameter. Its specific expression is shown in (12). When there are two UAVs in the cluster, the distribution diagram is shown in Figure 6.

$$R_{co}=R_d\times \left(1-\left(d_{max}-d_{min}\right)/d_{target}\right)$$

(12)

where $d_{max}={\{d_1,d_2,\dots ,d_n\}}_{max}$, $d_{min}={\{d_1,d_2,\dots ,d_n\}}_{min}$, respectively, represent the maximum and minimum distances between the UAV and the target area in the environment. It can be seen from the mathematical expression and distribution diagram that there are two major distribution trends for synergistic rewards. When the maximum-distance difference of the UAV cluster is smaller, its value is larger, which will lead the UAVs to move towards time coordination. When the UAV is closer to the target area, its value is larger, and the UAV will be guided to reach the target area.

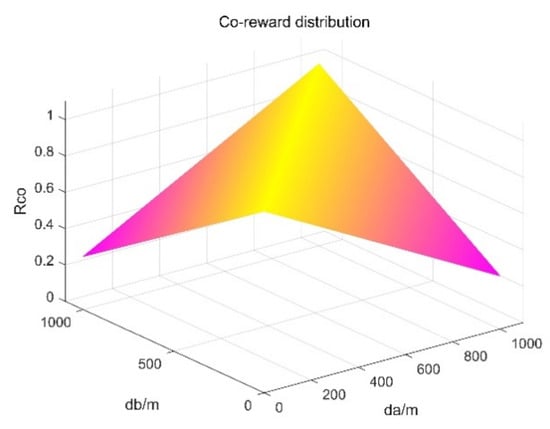
Figure 6. Co-reward distribution.

When the UAV receives the success signal and finally reaches the target area, the mission is successful, and it will give a success reward. The success reward is also related to the farthest distance between the UAV cluster and the target point. The closer the distance, the greater the success reward, as shown in (13).

$$R_{fail}=-1000$$

(13)

When the final mission of the UAV fails, that is, when it is intercepted by an interceptor and fails to reach the target area, it will give a negative reward of failure, as shown in (14).

$$R_s=250+2500/d_{max}$$

(14)

By linearly superimposing the above multiple reward functions, the final reward function can be obtained. The reward function, R, of the UAV is shown in (15).

$$R={\beta }_1{R}_d+{\beta }_2{R}_{co}+{\beta }_3{R}_s+{\beta }_4{R}_{fail}$$

(15)

where ${\beta }_1+{\beta }_2+{\beta }_3+{\beta }_4=1$.

4. Experimental-Simulation Analysis

4.1. Simulation-Scene Settings

Based on environment modeling, a simulation experiment of multi-UAV-cooperative penetration was carried out. To simplify the training, the scene and the speed of the UAV are all set to smaller values. The number of UAVs in the cluster is set to two. In the environment, there are as many dynamic interceptors as there are UAVs. Each dynamic interceptor is responsible for the tracking of an unmanned aerial vehicle, that is, each interceptor calculates the angular velocity of the proportional guidance rotation for an unmanned aerial vehicle. The initial positions of the two interceptors are at the center of the target point, and the radius of the target area is set to 60 m. Table 1 shows the simulation parameters during training.

Table 1. Simulation Parameters.

	Parameters	Value
UAV	Linear velocity $v$	$20 \mathrm{m}/\mathrm{s}$
	Angular velocity $\omega$	$-0.5 \mathrm{rad}/\mathrm{s}~0.5 \mathrm{rad}/\mathrm{s}$
	Initial azimuth $\theta$	$\frac{\pi }{4}$
	Initial position $\left(x,y\right)$	$x_A,y_A= \left[50 \mathrm{m},50 \mathrm{m}\right]$ $x_B,y_B= \left[50 \mathrm{m},500 \mathrm{m}\right]$
Interceptor	Linear velocity $v$	$22 \mathrm{m}/\mathrm{s}$
	Initial azimuth $\omega$	$\frac{5\pi }{4}$
	Angular velocity $\theta$	$-0.5 \mathrm{rad}/\mathrm{s}$$~0.5 \mathrm{rad}/\mathrm{s}$
	Initial position $\left(x,y\right)$	Same as target
Target	Position $\left(x,y\right)$	$x_t,y_t= \left[850 \mathrm{m},850 \mathrm{m}\right]$
	Simulation step $\mathrm{d}t$	$1 \mathrm{s}$

During the training process, the learning rate of the actor network and the critic network are set to ${\alpha }_1=0.0001,{\alpha }_2=0.001$, the discount factor is set to $\gamma =0.9$, and the action noise is set to 0.3.

4.2. Simulation Results and Analysis

After 10,000 trainings, the simulation results are shown in Figure 7.

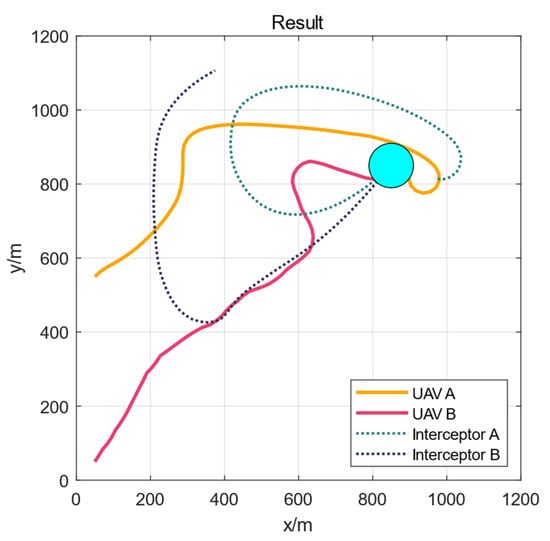
Figure 7. Experiment Result.

Two UAVs can pass enough to bypass the dynamic interceptor and finally reach the target area at the same time, and the time to reach the target area will not exceed the simulation step (1 s).

Figure 8 and Figure 9 shows the angular velocity change curves of UAVs and interceptors and the line-of-sight change curves of the interceptors.

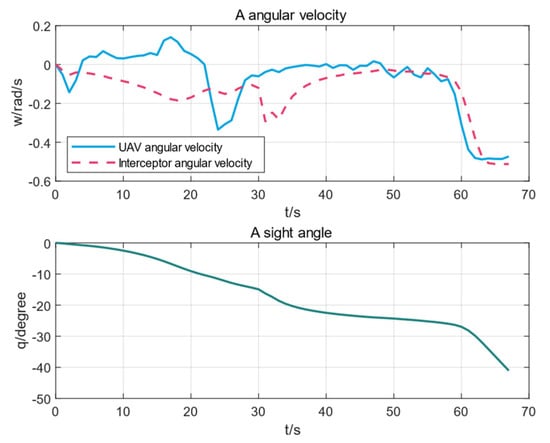
Figure 8. The parameter change curve of UAV A and Interceptor A during training.

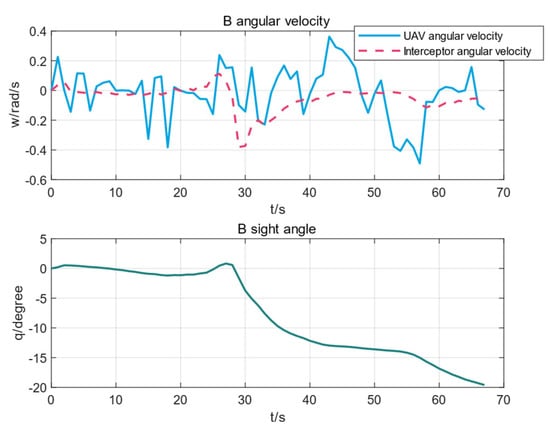
Figure 9. The parameter change curve of UAV B and Interceptor B during training.

It can be seen from the figure that the UAVs carried out a wide-angle exercise, the interceptor’s line of sight to the UAVs continued to increase, and the interception failed.

Figure 10 shows the distance curve between the two UAVs and the interceptor. The black line at the bottom of the figure represents the distance captured by the interceptor.

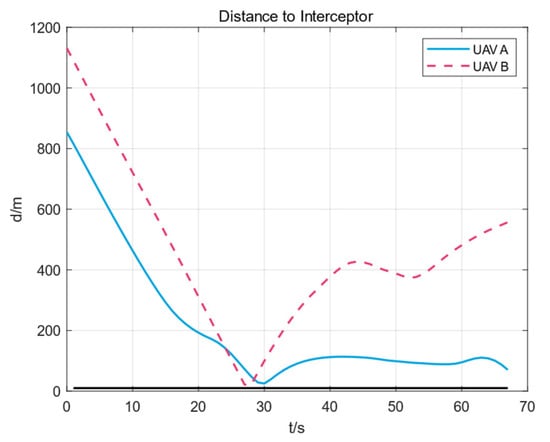
Figure 10. The distance between the UAV and the interceptor.

It can be seen from the figure that the minimum distance between the two UAVs and the interceptors is above the black line, that is, they are not captured by the interceptors.

Figure 11 is the distance between the two UAVs and the target point. In the figure, there is a certain gap between the initial distance between the two UAVs and the target area, which is about 10 m.

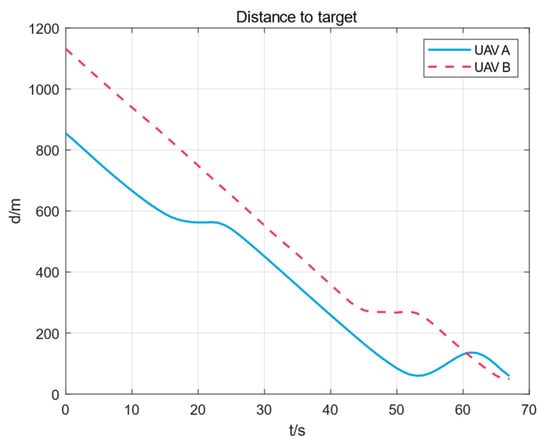
Figure 11. The distance curve between the UAV and the target.

It can be seen from the figure that the final distance difference between the two UAVs and the target point is almost zero. At the beginning of the movement, the distance between the two UAVs and the target point is about 3 m. UAV A will deliberately go around to ensure that it is moving. Finally, the target point can be reached at the same time.

The simulation experiment shows that the DDPG algorithm can complete the cooperative penetration of the dynamic-tracking interceptor through the training of the UAV cluster, which meets the high-performance requirements of the multi-UAV system and is a method with huge application potential.

5. Conclusions

Based on the deep reinforcement-learning DDPG algorithm, this paper studies the UAV-cooperative penetration. Based on the mission scenario model, the UAV’s action space, state space, termination conditions, and reward functions are designed. Through the training of the UAV, the coordinated penetration of multiple aircraft was realized. The main conclusions of this paper are as follows:

The collaborative method based on the DDPG algorithm designed in this paper can achieve coordinated penetration between UAVs. After UAVs are trained, they can coordinate to evade interceptors without being intercepted by them. Compared with traditional algorithms, the UAV’s penetration performance is stronger, the applicable environment is more complex, and it has great application prospects.

The reinforcement learning collaboration method in this paper realizes the time collaboration between UAVs on the premise of exchanging state information between multiple aircrafts, and the movement of UAVs finally reaches the target area at the same time from different initial locations, achieving time coordination. However, this paper doesn’t consider factors such as communication delays or failures between UAVs, which causes the UAV to receive the wrong information. This problem may be solved by predicting UAVs’ states and information fusion. Further research can be carried out in the follow-up work.

This paper only considers the movement of the engagement plane. In the follow-up work, the movement can be expanded to three dimensions, and multi-UAV-cooperative penetration in a 3D environment will put forward higher requirements on the algorithm.