Clustering-Based Channel Allocation Method for Mitigating Inter-WBAN Interference

Abstract

In this paper, we propose a channel assignment method that can mitigate the inter-WBAN interference when the density of WBANs is high. To achieve the goal, we group the coexisting WBANs into a set of clusters by using the Louvain algorithm and allocate different channels to the WBANs in the same cluster by using a graph coloring method. By increasing the distance between the WBANs using the same channel, our method reduces the inter-WBAN interference. As a result, compared with the conventional centralized channel allocation method, our method increases the average data rate of a WBAN more than twice even when the number of coexisting WBANs is larger than the number of available channels. Compared with a distributed method involving an iterative process, our method reduces the channel decision time by $94.6\%$. Furthermore, since our method self-configures the algorithm parameters dynamically according to the topology changes, it can be used without human intervention even when the topology changes.

1. Introduction

As wearable devices become popular, a wireless body area network (WBAN) is attracting a lot of interest not only from academia but also from industry [1,2]. Especially, as the population of the world older than 65 years old keeps increasing sharply [3], a WBAN is expected to play a pivotal role in supporting customized healthcare services and wellness services [4,5]. A WBAN is composed of a coordinator node and a set of sensor nodes. Sensor nodes measure the body or environment status and report the measured data to a coordinator. A coordinator processes the data from sensor nodes or sends them to a remote server. A coordinator also orchestrates the packet transmissions within a WBAN. To facilitate the wireless communications between a coordinator and sensor nodes within a WBAN, IEEE has released IEEE 802.15.6 standard [6] and ETSI has released the SmartBAN specifications [7,8]. These standards specify the frequency bands for a WBAN and allow the sensor nodes to operate in and on a human body with low power and low complexity.

The key benefit of a WBAN comes from its ability to support real-time continuous monitoring function without obstructing a user [9,10]. However, the density of WBANs increases with the popularity of WBANs and the number of channels available for WBANs is limited. Thus, as the number of coexisting WBANs in an area increases, it becomes more likely that multiple WBANs use the same channel at the same time. If more than two WBANs simultaneously send data using the same channel, they interfere with each other’s data transmissions. Since the interference between WBANs hinders the data transmission within a WBAN, it may fail the continuous monitoring function of a WBAN. For example, in [11], it is noted that the interference among the coexisting WBANs decreases the data transmission rate within a WBAN by 35%. Therefore, the inter-WBAN interference management problem becomes crucial for a WBAN to function properly even in a highly populated area.

The root cause of the inter-WBAN interference is that multiple WBANs within the transmission ranges of each other send data by using the same channel at the same time. To alleviate the amount of inter-WBAN interference, power control methods have been proposed [12,13]. They attempt to minimize the amount of interference that a WBAN imposes on the other WBANs by controlling the transmission power of each WBAN. Medium access control methods have also been proposed to resolve the inter-WBAN interference problem [14,15]. They manipulate the transmission opportunities of the coexisting WBANs to avoid the situation where their data transmission times overlap with each other. These methods try to alleviate the interference among the coexisting WBANs that use the same channel. However, as the number of coexisting WBANs increases, these methods decrease the data transmission rate within a WBAN and increase the data transmission delay. The performance of these methods can be improved if the number of coexisting WBANs using the same channel decreases. Inter-WBAN interference can be avoided if the channel used by a WBAN is not the same as those used by its neighboring WBANs.

Channel allocation methods have been proposed to assign different channels to the coexisting WBANs [16,17]. By noting that the amount of interference between two WBANs decreases as the distance between them increases [18], these methods attempt to separate the WBANs using the same channel as far away as possible. Usually, each WBAN determines a channel to use in a distributed manner by exploiting the information received from its neighbors. However, it is difficult to assume that a WBAN exchanges its state information with unidentified WBANs willingly. In addition, a common signaling channel between WBANs can be easily congested as the number of coexisting WBANs increases, which hinders a WBAN from acquiring necessary information in time. In terms of implementation, it is difficult to use a complex algorithm because a coordinator in a WBAN is usually limited in the computation power, storage, and energy. Therefore, a WBAN performs a relatively simple operation repeatedly to determine a channel to use. However, it takes time for the iterative process to converge to a stable point. Therefore, the inter-WBAN interference during the transient time degrades the data transmission quality within a WBAN.

To resolve these issues, we take a machine learning approach and propose a dynamic channel allocation method operating in a centralized manner. We aim to increase the data rate of a WBAN by assigning channels in a way that the distance between WBANs using the same channel increases as much as possible. We model this problem as a combination of a graph partitioning problem and a graph coloring problem. To solve the problem, we devise two modules: a base module and an adaptive module. In the base module, a server collects the information from the WBANs and constructs an interference relationship graph among them. Then, a server partitions the graph by using the Louvain graph partitioning algorithm [19] so that its modularity is maximized. Then, for each cluster, the Welsh Powell graph coloring method is applied to the subgraph formed by the WBANs in the same cluster [20] to determine the channels for them. The adaptive module is designed to adjust to the gradual topology changes fast. It reuses the cluster information made by the base module to avoid the graph partitioning procedure. In contrast to the distributed method where messages are exchanged among WBANs through a narrow band channel, a cellular network providing high data transmission rate (such as LTE, 5G, etc.) is used for message exchanges between a server and WBANs. Therefore, a server acquires necessary information in time regardless of the density of the coexisting WBANs. We summarize our main contributions as follows.

• We address the inter-WBAN interference problem and propose a centralized channel allocation algorithm, which resolves the problem by using both a graph partitioning method and a graph coloring method. Our method is practical and adaptable to dynamic environments because it operates in a self-configurable manner without human intervention.
• We address the problem of topology changes caused by the mobility of a WBAN and propose an adaptive module. The adaptive module replaces the graph partitioning process with simple comparison operations. The performance of the adaptive module is comparable to that of our base module when the graph topology changes gradually.
• We conduct extensive simulation studies to assess the performance of our method. Compared with the recent centralized channel allocation method, our method increases the average data rate of a WBAN by $2.2$ times when the density of the WBANs is 0.5 WBANs per square meter. When the density of the coexisting WBANs increases to 2 WBANs per square meter, our method increases the average data rate by $5.4$ times. In addition, compared with a distributed method involving an iterative process, our method reduces the channel decision time by $94.6\%$.

The rest of the paper is organized as follows. In Section 2, we discuss the related works. After describing a system model in Section 3, we detail our channel allocation method in Section 4. We evaluate the performance of the proposed method through extensive simulation studies in Section 5. We conclude the paper in Section 6 with future research directions.

2. Related Works

To resolve the inter-WBAN interference problem, IEEE 802.15.6 standard specifies three coexistence strategies: a beacon shifting, an active superframe interleaving, and a channel hopping [6]. For the beacon shifting, a WBAN schedules the beacon frame transmission during an idle period. However, since the idle period approaches to zero as the number of coexisting WBANs increases, a beacon shifting is not appropriate when the density of the coexisting WBANs is high [10]. For the active superframe interleaving, each WBAN adjusts its superframe length and inactive duration so that the coexisting WBANs take turns in sending data in an active period. However, the transmission opportunity of a WBAN decreases with the number of coexisting WBANs. Therefore, the active superframe interleaving increases the transmission delay as the number of coexisting WBANs increases [21]. In case of the channel hopping, a coordinator in each WBAN determines the channel hopping sequence. However, since WBANs can move around, an optimal channel hopping sequence must be selected adaptively according to the changes in the set of coexisting WBANs. In addition, a specific mechanism to implement these strategies is left as an open issue in the standard. Thus, a proper algorithm must be devised to overcome the shortcomings of these methods.

2.1. Channel Allocation Methods

Various channel allocation methods have been proposed to mitigate the inter-WBAN interference. According to the operation mode, they can be categorized into the distributed methods [10,16,17,22,23], the centralized methods [24,25,26], and the hybrid methods [27]. In the distributed method, a coordinator in a WBAN decides the channel to use, while a remote server determines the channels for WBANs in the centralized method. In the hybrid method, both WBANs and a server decide the channels interactively.

The distributed methods can be classified further according to whether the message exchanges among neighboring WBANs are required or not. In the distributed methods proposed in [16,17,22], each coordinator in a WBAN communicates with the coordinators in its neighboring WBANs to collect their state information. Then, by exploiting the collected data, each coordinator determines a channel to use. Since a channel is determined in an iterative manner, it takes time for a coordinator to determine the least congested channel. In addition, the signaling overhead increases sharply as the density of WBANs in an area increases. For example, if a WBAN needs to exchange the message $n_s$ times and the size of a time slot is $t_s$, it takes $n_s{t}_s$ time for a WBAN to determine the least congested channel. In addition, if the message size is $m_s$ and the number of neighboring WBANs of a WBAN is $n_n$, the signaling overhead of a WBAN becomes $m_s{n}_n{n}_s$. Therefore, as the number of WBANs in an area increases, the signaling channel among WBANs becomes congested, which increases the probability that a WBAN is unable to collect necessary messages in time. As a result, the channel selection process may not select the least congested channel. In terms of implementation, the coordinators must be synchronized in a time slot level, which is not easy among autonomous systems such as WBANs. In addition, since a WBAN has to exchange messages with unidentified WBANs, it may cause a security issue. Compared with these methods, our method has the following advantages. In our method, a server determines the channels for the coexisting WBANs. Since a server can determine channels without iteration, our method reduces the channel decision time. In our method, messages are sent from WBANs to a server through a cellular link. Therefore, our method prevents a WBAN from exchanging messages with unidentified WBANs. In addition, since a cellular link is faster and more reliable than an inter-WBAN signaling link, our method is more reliable in that a server can obtain necessary information in time regardless of the number of coexisting WBANs.

The methods proposed in [10,23] operate in a distributed manner without message exchanges among WBANs. In these methods, each WBAN keeps evaluating the quality of a channel by passively monitoring the performance it receives while using the channel. Then, by exploiting a learning process or a pre-configured channel hopping sequences determined by a Latin square, each WBAN selects a channel which is expected to be the best. However, the learning process inevitably involves an exploration phase to find the best channel. Therefore, it takes time for the learning process to find the best channel [10]. During the exploration phase, a WBAN may experience severe interference. In addition, when the environment around a WBAN changes, the exploration phase has to be repeated. In [23], a set of K-order Latin squares is assumed, and each WBAN randomly selects a Latin square from the set to determine its channel hopping sequence. Since each WBAN is assumed to be composed of the same number of sensor nodes (i.e., K), their method cannot be applied when WBANs have the different number of sensor nodes, which is common in practice. In addition, since K is fixed, it cannot easily adapt to the topology changes. Our method is different from these methods in the following aspects. Our method does not require an exploration phase to determine channels. Thus, our method can determine channels faster than the method proposed in [10]. Compared with the method in [23], our method is more adaptive to the dynamic environment because our method does not have a hyperparameter such as K in [23] that needs to be determined before an algorithm is applied.

In [27], a hybrid method is introduced. They formulate the channel selection problem as a Stackelberg game with pricing. An AP acts as a leader in the game and configures the price of the resources to limit the interference caused by WBANs. WBANs act as followers in the game and try to maximize the utility by using the resource price determined by an AP. However, they consider a static environment, and it is not clear how to systematically configure hyperparameters that lead to an optimal result in the situation where both the number and the positions of WBANs change. Our method differs with the hybrid method in that our method does not require both a pre-configured hyperparameter and the competition among the WBANs. In [27], WBANs play a game given the resource price configured by an AP. Therefore, it takes multiple iterations for the WBANs to reach an equilibrium state. Since our method does not involve such an iteration, it can determine channels faster than the method in [27].

On behalf of WBANs, a server determines the channels in the centralized channel allocation method. A server is supposed to have much higher computing capability than a coordinator in a WBAN. Therefore, a server is expected to determine the channels faster than a coordinator even in the case where the time complexity of the channel allocation algorithm in a server is bigger than that running in a coordinator. A server exploits the information obtained from WBANs to determine the channels. In other words, in contrast to the distributed method where messages are exchanged among WBANs, messages are exchanged between a server and WBANs in the centralized method. Generally, a coordinator in a WBAN uses a cellular network such as LTE and 5G to send messages to a server. Since a cellular link is more reliable than the signaling link among WBANs, a server is able to collect necessary information reliably and determine channels without iteration even when the density of WBANs is high.

In [24], a server constructs an interference matrix by using the information gathered from WBANs and determines channels by exploiting the matrix. However, they do not consider the situation where the number of available channels is less than the number of interfering WBANs. In contrast, we consider the situation where the number of the coexisting WBANs is larger than the number of available channels. In this environment, we aim to maximize the total data rate. The authors in [25] propose a channel hopping method by exploiting the spatial and temporal regularity in human trajectories. A server measures both the trajectory and the channel hopping sequence of each WBAN in an area. Then, a server allocates a channel hopping sequence to a WBAN according to the human trajectory similarities and the channel hopping sequence similarities in the area. Since the channel assignment method is based on the regularity in human trajectory, it may not be applicable when a set of humans in an area changes. In contrast, we consider an environment where a set of WBANs in an area changes over time. Since we do not rely on the regularity in human trajectory, our method can adjust to the dynamic changes in the set of WBANs in an area. The authors in [26] propose a machine learning approach to resolve the channel allocation problem. They cluster the coexisting WBANs by using the K-nearest neighbor (KNN) method. After formulating clusters, they assign a channel to each cluster by using a graph coloring method. The WBANs in the same cluster share the bandwidth of the channel allocated to the cluster in an FDMA manner. Since the data rate depends on the amount of bandwidth, the data rate achievable by a WBAN in a cluster decreases as the number of WBANs in a cluster increases. Our work is the most relevant to [26] in that both methods group the WBANs into a set of clusters before allocating the channels. However, in [26], a channel is not allocated directly to a WBAN. They assign a channel to a cluster, and the WBANs in the same cluster share the bandwidth of the channel allocated to the cluster in an FDMA manner. In contrast, we allocate a channel to a WBAN directly to increase the data rate provided to a WBAN. In addition, the authors in [26] recommend the number of clusters needed to partition an interference relationship graph through the simulation studies in a specific network topology. However, our method self-configures the number of optimal clusters by adopting the modularity-based clustering method. We also propose an adaptive module to quickly adjust to the gradual topology changes.

2.2. Research Gap

In Table 1, we compare the channel allocation methods in a qualitative manner. We observe in the table that we still need an inter-WBAN coexistence strategy that has the following properties. The inter-WBAN coexistence method should be able to determine channels quicklyso that the total data rate of the coexisting WBANs are maximized. In addition, it should be adaptive to topology changes even when the number of coexisting WBANs is larger than the number of available channels. To increase the channel decision time, we take a centralized approach where a server collects necessary information from WBANs and determines the channels for them without iteration. To increase the adaptability, the parameters used in a channel allocation method need to be self-configured according to the topology changes. To tackle the issue, we adopt the modularity-based graph partitioning approach. Since an interference relationship graph formed by the coexisting WBANs is partitioned in a way that the modularity of the graph is maximized, the number of clusters is determined automatically regardless of the locations and the number of the WBANs in an area. In addition, we devise an adaptive module that can quicklyadjust to the changes in the topology of an interference relationship graph.

Table 1. Comparison of the channel allocation methods (GC represents a graph coloring and DT represents decision time).

Method	Operation	Signaling	Overhead	Adaptability	DT	Approach
[16,17]	distributed	inter-WBAN	high	moderate	moderate	GC
[22]	distributed	inter-WBAN	high	moderate	slow	heuristic, FDMA
[10]	distributed	not required	low	low	slow	stochastic learning
[23]	distributed	not required	low	low	fast	latin square
[24]	centralized	WBAN-Server	moderate	low	fast	heuristic
[25]	centralized	WBAN-Server	moderate	low	fast	greedy
[26]	centralized	WBAN-Server	moderate	low	fast	KNN, FDMA
[27]	hybrid	WBAN-Server	high	low	slow	Stackelberg game
proposed	centralized	WBAN-Server	moderate	high	fast	clustering, GC

3. System Model

We consider a set of WBANs in an area $S$. A cloud server coordinates the channels for the WBANs in $S$ so that the amount of interference experienced by the WBANs can be mitigated. We assume that within each WBAN, there is always data to be exchanged between a coordinator and the sensor nodes. Similar to other works [23], we also assume that the unsuccessful data transmission within a WBAN is caused only by the interference among the WBANs. We assume that the control time is divided into discrete time slots of equal size ${\tau }_c$. At every ${\tau }_c$, the coordinators of the WBANs send their location information to a cloud server through a cellular link such as an LTE and 5G. Therefore, we assume that a server can receive the messages from the coordinators reliably and in time regardless of the density of the coexisting WBANs. A cloud server performs a channel allocation task with the position information. We denote the set of WBANs in $S$ at the t-th time slot as $N\left(t\right)$.

We denote the set of channels that can be assigned to a WBAN as $K=\{1,2,\cdots ,|K\left|\right\}$, where $\left|K\right|$ is the cardinarity of the set K. The channel allocated to a WBAN i during the t-th time slot is denoted as $k_i\left(t\right)\in K$. We also denote by $N_i\left(t\right)$ the set of WBANs within the interference range of a WBAN i. In other words, if a WBAN $j\in N_i\left(t\right)$ uses the same channel as that of i during the t-th time slot, j interferes i. To focus on the influence of the channel allocation method, we assume that each WBAN does not control the data transmission power and denote the transmission power of each sensor node in a WBAN i as $p_i$. Then, the amount of interference experienced by a WBAN i during the t-th time slot is given as

$$I_i\left(t\right)=\sum _{j\in N_i\left(t\right)}{p}_j{h}_{i,j}\left(t\right){\delta }_{i,j}\left(t\right),$$

(1)

where $h_{i,j}\left(t\right)$ is the channel gain between a WBAN i and a WBAN j. Since we consider a relatively long time slot, we assume that the small time scale fading averages out and only the path loss influences on $h_{i,j}\left(t\right)$. The function ${\delta }_{i,j}\left(t\right)$ is used to represent whether WBANs i and j are using the same channel or not. In other words, ${\delta }_{i,j}\left(t\right)=1$ if $k_i\left(t\right)=k_j\left(t\right)$. Otherwise, ${\delta }_{i,j}\left(t\right)=0$. From the Shannon’s capacity formula [18], the data rate per Hertz obtained by a WBAN i during the time slot t is given as

$${\gamma }_i\left(t\right)={log}_2(1+\frac{p_i{h}_{i,i}\left(t\right)}{I_i\left(t\right)+N_0}),$$

(2)

where $N_0$ is the noise power, which is assumed to be a stationary random process. Accordingly, the total data rates of the WBANs in $N\left(t\right)$ is obtained as

$$\gamma \left(t\right)=\sum _{i\in N\left(t\right)}{\gamma }_i\left(t\right)$$

(3)

Our goal is to maximize $\gamma \left(t\right)$. From Equations (1) and (2), we observe that we can control $\gamma \left(t\right)$ by manipulating the channel allocation profile $(k_1\left(t\right),\cdots ,k_{\left|N\right(t\left)\right|}\left(t\right))$. Thus, our goal becomes selecting an optimal channel allocation profile that can maximize the total data rates $\gamma \left(t\right)$. However, this is an NP-complete combinatorial problem. Thus, to resolve the problem, we propose a heuristic algorithm by using both a graph partitioning method and a graph coloring method.

If the number of available channels (i.e., $\left|K\right|$) is less than $\left|N\right(t\left)\right|$, some WBANs in $S$ inevitably use the same channel. The amount of interference between the WBANs using the same channel increases as the distance between them decreases. Therefore, to mitigate the inter-WBAN interference, the WBANs using the same channel have to be separated as far away as possible.

To design a channel allocation algorithm, we represent the interference relationship among the WBANs in $S$ at the t-th time slot as an undirected graph $G\left(t\right)=\left(N\right(t),E(t),W(t\left)\right)$, where $E\left(t\right)$ is the set of edges, and $W\left(t\right)$ is the set of edge weights. The path loss increases as the distance from a sender to a receiver increases [18]. Thus, the amount of interference that a WBAN j imposes on a WBAN i is inversely proportional to the distance between i and j. Thus, we define an edge between two WBANs according to the severity of the interference between them. In other words, if there is an edge $e_{i,j}\left(t\right)\in E\left(t\right)$ between a WBAN i and a WBAN j, it means that i and j will interfere with each other considerably when they use the same channel during the t-th time slot. Specifically, we define $e_{i,j}\left(t\right)$ as follows.

$$e_{i,j}\left(t\right)=\left\{\begin{array}{cc}1,\hfill & d_{i,j}\left(t\right)<{\delta }_d\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right.,$$

(4)

where $d_{i,j}\left(t\right)$ is the distance between a WBAN i and j, and ${\delta }_d$ is the distance over which the amount of interference between two WBANs can be considered marginal. To reflect the influence of the distance on the amount of interference, we also impose an weight on an edge $e_{i,j}\left(t\right)$ as follows.

$$w_{i,j}\left(t\right)=\left\{\begin{array}{cc}\frac{1}{d_{i,j}\left(t\right)},\hfill & e_{i,j}\left(t\right)=1.\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

(5)

The inter-WBAN interference among the WBANs in $S$ can be reduced if we group the WBANs based on the severity of the interference among them if they use the same channel and allocate different channels to the WBANs in the same cluster. Let us assume that the interference relationship graph $G\left(t\right)$ is partitioned into a set of clusters $C\left(t\right)=\{C_1\left(t\right),\cdots ,C_{\left|C\right|}\left(t\right)\}$ and denote a WBAN j in a cluster $C_i\left(t\right)$ as $v_{i,j}\left(t\right)$. Then, the total interference imposed on $v_{i,j}\left(t\right)$ by the WBANs in the same cluster $C_i$ is given as.

$$I_{i,j}\left(t\right)=\sum _{k\in N_j\left(t\right)\wedge C_i\left(t\right)}{I}_j\left(t\right)$$

(6)

Thus, to mitigate the inter-WBAN interference among the WBANs in $S$, we need to reduce ${\sum }_{C_i\left(t\right)\in C\left(t\right)}{\sum }_{j\in C_i\left(t\right)}{I}_{i,j}\left(t\right)$. To achieve the goal, we propose the WBAN clustering process and the channel assignment process, which will be detailed in the next section.

4. Cluster-Based Channel Allocation Method

The proposed channel allocation method is composed of two modules. One is called a base module and the other is named an adaptive module. When an interference relationship graph $G=(N,E,W)$ is given, the base module partitions the graph into a set of clusters so that the modularity of the graph is maximized. Then, it allocates different channels to the WBANs in the same cluster. The adaptive module is devised to adjust the channel allocation process to the gradual changes in the topology of an interference relationship graph. The adaptive module uses the cluster information resulting from the base module. By avoiding the graph partitioning process, the adaptive module can reduce the time complexity for the channel allocation.

4.1. Base Module

The number of channels available for a WBAN is limited. Therefore, to reduce the total interference among WBANs, we should allocate channels in a way that the WBANs using the same channel are located as far away as possible. To achieve the goal, in the base module, a cloud server constructs an interference relationship graph G using the location information reported by the WBANs in $S$. Then, the cloud server partitions the graph using the Louvain algorithm to maximize the modularity of the graph. We denote the resulting set of clusters for a graph $G=(N,E,W)$ as $C=\{C_1,\cdots ,C_{\left|C\right|}\}$. A cluster $C_i$ is composed of the WBANs $C_i=\{{\nu }_{i,1},\cdots ,{\nu }_{i,|C_i|}\}$, where ${\nu }_{i,j}$ represents a WBAN j belonging to a cluster i.

To determine a channel for each WBAN in each cluster $C_i$, we consider the interference relationship subgraph $G_{C_i}$ induced by the WBANs in $C_i$. We assign a color to each WBAN ${\nu }_{i,j}$ in $C_i$ by applying a graph coloring algorithm to $G_{C_i}$. We denote the minimum number of colors required to color the WBANs in $C_i$ as $n_c^i$. We also denote the set of required colors for $G_{C_i}$ as $O_i=\{1,\cdots ,n_c^i\}$ and assume that colors are assigned from one sequentially. If the number of required colors is not larger than the number of available channels (i.e., $n_c^i\le \left|K\right|$) and a color q is assigned to a WBAN ${\nu }_{i,j}$, q becomes the channel number allocated to ${\nu }_{i,j}$. However, if $n_c^i>\left|K\right|$, the same channel is inevitably assigned to multiple WBANs in $C_i$. In this case, a cloud server allocates a channel to ${\nu }_{i,j}\in C_i$ as follows. If a color q is assigned to a WBAN $v_{i,j}$ and $q\le \left|K\right|$, a cloud server assigns the channel q to $v_{i,j}$. In contrast, if $\left|K\right|<q\le n_c^i$, the channel number to be allocated to the WBAN whose color is q is randomly determined from $[1,|K\left|\right]$ according to the Uniform distribution.

After assigning channels to the WBANs in $C_i$, the base module determines a center position of the cluster as follows.

$$\overrightarrow{p}\left(C_i\right)=\frac{1}{|C_i|}\sum _{{\nu }_{i,j}\in C_i}\overrightarrow{p}\left({\nu }_{i,j}\right),$$

(7)

where $\overrightarrow{p}\left({\nu }_{i,j}\right)$ is the vector that represents the location of a WBAN ${\nu }_{i,j}$, and $\overrightarrow{p}\left(C_i\right)$ represents the position of the center point in $C_i$. We summarize the base module in Algorithm  1.

Algorithm 1 Base Module

1: Input: a graph $G=(N,E,W)$ 2: Output: a channel allocation vector $\alpha$ 3: Given a graph $G=(N,E,W)$: 4:   Make clusters using Louvain algorithm and get $C=\{C_1,\cdots ,C_{\left|C\right|}\}$. 5: $i=0$ 6: while $i\le \left|C\right|$do 7:     Color the WBANs in $G_{C_i}$ by using a graph coloring algorithm. 8:     Get the number $n_c^i$ of colors required to color all the WBANs in $C_i$. 9:     $j=0$ 10:     while $j\le |C_i|$ do 11:         Get the color q assigned to ${\nu }_{i,j}$. 12:         if $q\le \left|K\right|$ then 13:            Allocate the channel q to a WBAN ${\nu }_{i,j}$. 14:         else 15:            Randomly select a channel $q^{\prime }$ from $[1,|K\left|\right]$ 16:            Allocate $q^{\prime }$ to ${\nu }_{i,j}$. 17:         $j++$ 18:     Get a center point of $C_i$: $\overrightarrow{p}\left(C_i\right)=\frac{1}{|C_i|}{\sum }_{{\nu }_{i,j}\in C_i}\overrightarrow{p}\left({\nu }_{i,j}\right)$ 19:     $i++$

The edge between two WBANs i and j exists only when $d_{i,j}<{\delta }_d$. Our base module clusters the WBANs according to the concentration level of the edges within the clusters. Thus, the WBANs in the same cluster will interfere with each other if they use the same channel. Therefore, by allocating different channels to the WBANs in the same cluster as much as possible, the base module mitigates the inter-WBAN interference.

4.2. Adaptive Module

The WBANs in $S$ may change their locations according to their mobility characteristics during a time slot. In addition, new WBANs may enter into $S$, and some WBANs may move out of the area. The base module may be invoked at every time slot to resolve the issue. However, since the time complexity of a graph partitioning algorithm increases with the number of edges in the graph, the base module may not be fast enough for allocating channels in a dynamic environment where WBANs move around. To address the issue, we design the adaptive module to enable a channel allocation process to adjust to the gradual changes of the interference relationship graph fast. The adaptive module is invoked at the beginning of each time slot t. It uses not only $N\left(t\right)$ and $\overrightarrow{p}\left(\nu \right)$s $(\forall \nu \in N(t\left)\right)$ but also the cluster information of the previous time slot $C(t-1)=\{C_1(t-1),\cdots ,C_{\left|C\right(t-1\left)\right|}(t-1)\}$ and $\overrightarrow{p}\left(C_i(t-1)\right)$s $(\forall C_i(t-1)\in C(t-1))$. If a WBAN ${\nu }_{new}$ newly moves into the region $S$ during the previous time slot $t-1$, it does not belong to any cluster in $C(t-1)$. The adaptive module determines the cluster that ${\nu }_{new}$ belongs to by using the distance between ${\nu }_{new}$ and $\overrightarrow{p}\left(C_i(t-1)\right)$, $\forall C_i(t-1)\in C(t-1)$. Specifically, ${\nu }_{new}$ becomes the member of the closest cluster $C_x(t-1)$, where

$$C_x(t-1)={\mathrm{argmin}}_{C_i(t-1)\in C(t-1)}\left|\right|\overrightarrow{p}\left({\nu }_{new}\right)-\overrightarrow{p}\left(C_i(t-1)\right){\left|\right|}_2.$$

(8)

If a WBAN ${\nu }_{i,j}\in C_i(t-1)$ moves during the time slot, it may be closer to the centroid of the other cluster than $\overrightarrow{p}\left(C_i(t-1)\right)$. In this case, the adaptive module changes the cluster membership of the WBAN ${\nu }_{i,j}$ from $C_i(t-1)$ to the cluster $C_y(t-1)$ whose centroid is the closest to the current location of the WBAN ${\nu }_{i,j}$.

After determining the cluster membership of all the WBANs in $N\left(t\right)$, the adaptive module obtains the updated cluster information $C^{\prime }\left(t\right)=\{C_1^{\prime }\left(t\right),\cdots ,C_{\left|C\right(t-1\left)\right|}^{\prime }\left(t\right)\}$ at the start of the t-th time slot. Then, the adaptive module calculates the modularity of $C^{\prime }\left(t\right)$ to inspect the quality of the fast adaptation. If the modularity of $C^{\prime }\left(t\right)$ is larger than a threshold value ${\delta }_m$, the adaptive module regards the situation as the graph structure is not changed abruptly. Therefore, the adaptive module adjusts quickly to the gradual change by reassigning only the channels of a subset of WBANs. Specifically, for each cluster $C_i^{\prime }\left(t\right)\in C^{\prime }\left(t\right)$, a cloud server compares the members in $C_i(t-1)$ and those in $C_i^{\prime }\left(t\right)$. If $C_i(t-1)$ is identical to $C_i^{\prime }\left(t\right)$ or $C_i^{\prime }\left(t\right)\subset C_i(t-1)$, each WBAN in $C_i^{\prime }\left(t\right)$ uses the same channel that it used in the previous time slot. However, when the cluster members are changed during a time slot (i.e., $C_i(t-1)\ne C_i^{\prime }\left(t\right)$ and $C_i^{\prime }\left(t\right)$ is not a subset of $C_i(t-1)$), the adaptive module allocates channels to the WBANs in $C_i^{\prime }\left(t\right)$ by applying the same channel allocation procedure in Algorithm  1 (from line 7 to line 17). After determining the channels for all the WBANs in $C_i^{\prime }\left(t\right)$, the adaptive module updates the center point of the cluster $C_i^{\prime }\left(t\right)$.

On the other hand, if the modularity is less than a threshold value ${\delta }_m$, the adaptive module regards that the topology of an interference relationship graph changed a lot during a time slot. Thus, the adaptive module determines that the total interference in the system needs to be improved by partitioning the current graph again. Therefore, in this case, a cloud server constructs a graph $G\left(t\right)=\left(N\right(t),E(t),W(t\left)\right)$ by using the locations of the WBANs in $N\left(t\right)$ and calls the base module to determine the set $C\left(t\right)=\{C_1\left(t\right),\cdots ,C_{\left|C\right(t\left)\right|}\left(t\right)\}$ of clusters and the channels for the WBANs in each cluster $C_i\left(t\right)$. The adaptive module is summarized in Algorithm  2.

Algorithm 2: Adaptive Module

1: Input: 2:    $C(t-1)=\{C_1(t-1),\cdots ,C_{\left|C\right(t-1\left)\right|}(t-1)\}$, $\overrightarrow{p}\left(C_i(t-1)\right)$, $\forall C_i(t-1)\in C(t-1)$, 3:    $N\left(t\right)$, and $\overrightarrow{p}\left(\nu \right)$, $\forall \nu \in N\left(t\right)$ 4: Output: a channel allocation vector $\alpha \left(t\right)$ 5: $i=0$ 6: while $i\le \left|C\right(t-1\left)\right|$do 7:     $Y=C_i(t-1)$ 8:     while ${\nu }_{i,j}\in Y\wedge Y\ne \varnothing$ do 9:         if ${\nu }_{i,j}\notin N\left(t\right)$ then 10:            $$\begin{gathered} C_i(t-1)=C_i(t-1)-\left\{{\nu }_{i,j}\right\} \\ Y=Y-\left\{{\nu }_{i,j}\right\} \end{gathered}$$ 11:     $C_i^{\prime }\left(t\right)=C_i(t-1)$ 12:     $i++$ 13: $Z=N\left(t\right)$ 14: while $\nu \in Z\wedge Z\ne \varnothing$do 15:     $C_x^{\prime }\left(t\right)={\mathrm{argmin}}_{C_i(t-1)\in C(t-1)}\left|\right|\overrightarrow{p}\left(\nu \right)-\overrightarrow{p}\left(C_i(t-1)\right){\left|\right|}_2$ 16:     if $\nu \notin N(t-1)$ then 17:         $C_x^{\prime }\left(t\right)=C_x^{\prime }\left(t\right)\cup \left\{\nu \right\}$ 18:     else 19:         if $\nu \in C_i(t-1)\wedge C_i(t-1)\ne C_x^{\prime }\left(t\right)$ then 20:            $C_x^{\prime }\left(t\right)=C_x^{\prime }\left(t\right)\cup \left\{\nu \right\}$ 21:     $Z=Z-\left\{\nu \right\}$ 22: if modularity of $C^{\prime }\left(t\right)=\{C_1^{\prime }\left(t\right),\cdots ,C_{\left|C\right(t-1\left)\right|}^{\prime }\left(t\right)\}<{\delta }_m$ then 23:     call Base Module 24: else 25:     $i=0$ 26:     while $i\le \left|C\right(t-1\left)\right|$ do 27:         if $C_i^{\prime }\left(t\right)⊈C_i(t-1)$ then 28:              allocate a channel for each WBAN in $C_i^{\prime }\left(t\right)$ (line 7 ∼ line 17 in Algorithm  1) 29:         update center point of each cluster $C_i^{\prime }\left(t\right)$ 30:         $i++$

4.3. Computational Complexity

Our base module is composed of two parts. In the first part, an interference relationship graph is partitioned into clusters by the Louvain algorithm. In the second part, a channel is allocated to each WBAN in a cluster by the Welsh Powell graph coloring method. The time complexity of the Louvain algorithm is known to be $O\left(\right|E|$) [28], where E is the set of edges in a graph. Therefore, the computational complexity of the first part in our base module is $O\left(\right|E|$). The computational complexity of the Welsh Powell graph coloring method is $O\left(\right|N{|}^2)$, where N is the set of vertices in a graph. However, in the second part of our base module, a graph coloring is applied not to the graph $G=(N,E,W)$ but to the subgraph formed by the WBANs in a cluster. The set of clusters made by the first part of our base module is denoted as C. If we assume that WBANs are uniformly distributed in an area, the average number of WBANs in a cluster is expected to be $m=\left|N\right|/\left|C\right|$. Therefore, the computational complexity of the second part in the base module is $O(m^2\left|C\right|)={O\left(\right|N|}^2/\left|C\right|)$. Therefore, compared with the method that does not group the coexisting WBANs, our base module reduces the computational complexity from $O\left(\right|N{|}^2)$ to $O\left(\right|N{|}^2/\left|C\right|)$.

Instead of partitioning an interference relationship graph, our adaptive module exploits the cluster information made by the base module. However, the adaptive module rearranges the cluster membership of each WBAN by comparing the current location of a WBAN and the center point of each cluster. Therefore, at the time slot t, the time complexity of updating the cluster information becomes $O\left(\right|N\left(t\right)\left|\right|C(t-1)\left|\right)$. Therefore, compared with the base module, the adaptive module reduces the time complexity for constructing a set of clusters from $O\left(\right|E\left(t\right)\left|\right)$ to $O\left(\right|N\left(t\right)\left|\right|C(t-1)\left|\right)$.

5. Performance Evaluation

In this section, we evaluate the proposed method through extensive simulation studies. We randomly deploy a set of WBANs in a 10 m × 10 m area $S$. Specifically, we select both the x-coordinate and the y-coordinate of each WBAN from [0,10 m] according to the uniform distribution. By considering the width of a human body [29], we make the distance between any two WBANs be larger than 0.5 m. We set the number of channels available for WBANs to 13. We also set ${\delta }_m=0.3$ and ${\delta }_d=3$ m. The transmission power of sensor nodes in each WBAN is set to $p_i=p=1$ mW. The length of a time slot is set to 10 s.

We evaluate the performance of the proposed method in terms of the data rate per Hertz (i.e., ${\gamma }_i$) by quantitatively comparing it with those obtained by two alternatives. The first alternative is proposed in [26] where a graph is partitioned into a set of clusters by the KNN method, and a channel is allocated to each cluster by the graph coloring method. Once a channel is assigned to a cluster, the WBANs belonging to the same cluster share the same channel in an FDMA manner. Hereafter, we will call the first alternative KNN. In the second alternative, each WBAN randomly selects a channel from $[1,|K\left|\right]$ regardless of the other WBANs. Henceforth, we will call the second alternative RAND.

In Figure 1, we show how each method allocates a channel to a WBAN when $\left|N\right|=100$. Each dot represents a location of a WBAN. Except Figure 1c, each color of a dot in Figure 1 represents the channel allocated to a WBAN. The color of a dot in Figure 1c represents the cluster that a WBAN belongs to. In other words, if two WBANs are painted with the same color, they belong to the same cluster. When RAND is used, WBANs randomly select a channel to use independently of the other WBANs. Thus, RAND distributes the channels uniformly over $S$. KNN allocates a channel not to a WBAN but to a cluster formed by the K-nearest neighbor method. Thus, the WBANs belonging to the same cluster share the same channel in an FDMA manner. In contrast, our method allocates different channels to the WBANs in the same cluster to reduce the interference among the WBANs using the same channel. The differences in the way of allocating channels result in the differences in the total interference and the total data rates.

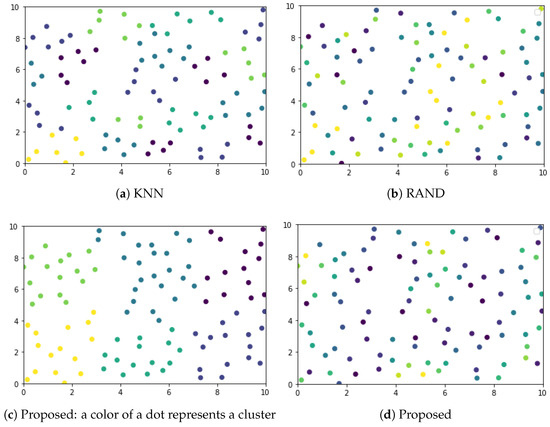
Figure 1. Comparison of the channel allocation behavior. Each dot represents a location of a WBAN. Except (c), where a color of a dot represents a channel allocated to a WBAN. The color of a dot in (c) represents a cluster. Thus, in (c), the WBANs having the same color belong to the same cluster.

In Figure 2, we show how the average SIR experienced by the WBANs in $S$ varies according to the number of WBANs in the area. The number of available channels is limited. Therefore, SIR decreases as the number of WBANs increases. KNN avoids the inter-cluster interference by allocating different channels to different clusters. Therefore, a WBAN achieves the largest SIR when KNN is used. However, the data rate obtained by a WBAN is influenced not only by the SIR but also by the amount of bandwidth used by the WBAN.

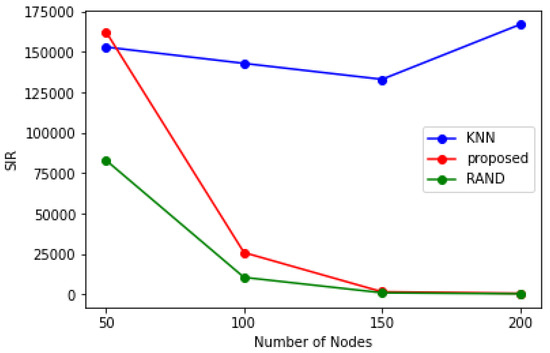
Figure 2. Comparison of the average SIR obtained by each method.

To inspect the effect of the channel sharing, we compare the data rate obtained by a WBAN in Figure 3. The number of WBANs in a cluster increases with the number of coexisting WBANs $\left|N\right|$. Correspondingly, in the case of KNN, the amount of a channel bandwidth that a WBAN in a cluster can use decreases as $\left|N\right|$ increases. Therefore, we can observe in Figure 3 that the data rates achieved by KNN are the smallest for all $\left|N\right|$. This is attributed to the fact that as the number of WBANs increases, the gain obtained by increasing the SIR is outweighed by the loss caused by sharing a channel in an FDMA manner. When RAND is used, each WBAN chooses a channel randomly irrespective of the other WBANs. Therefore, among the WBANs in $N_i$, the number of WBANs that select the same channel as the one chosen by a WBAN i increases with $|N_i|$. Since $|N_i|$ also increases with $\left|N\right|$, the data rates achieved by RAND decrease with $\left|N\right|$. In contrast, our method groups the WBANs that will interfere with each other when they use the same channel. After making a set of clusters, our method allocates different channels to the WBANs in the same cluster to mitigate the total interference. Thus, our method achieves higher data rates than the other methods. For example, compared with KNN, our method increases the average data rate provided to a WBAN by $2.2$ times when $\left|N\right|=50$. Our method further increases the average data rate by $5.4$ times when $\left|N\right|=200$. When compared with RAND, our method increases the average data rate by $1.2$ times for all $\left|N\right|$.

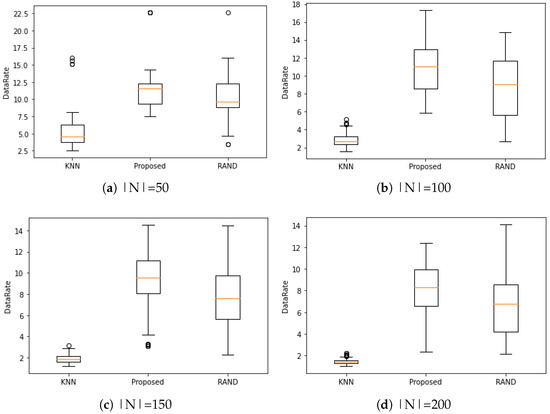
Figure 3. Comparison of the data rate provided to a WBAN.

When $\left|N\right|=200$, RAND and our method seem to produce similar results. To examine the differences between these methods, we inspect the distribution of the data rate of a WBAN (${\gamma }_i$) when $\left|N\right|=200$, which we show in Figure 4. In this figure, we can observe that the proportion of WBANs whose data rates range from 6 to 12 is $61.5\%$ when RAND is used. When our method is used, the proportion of WBANs whose data rates are within the same range increases to $79.5\%$. In addition, the variance of the data rate achieved by our method is 5.84 which is smaller than 6.58 obtained by RAND.

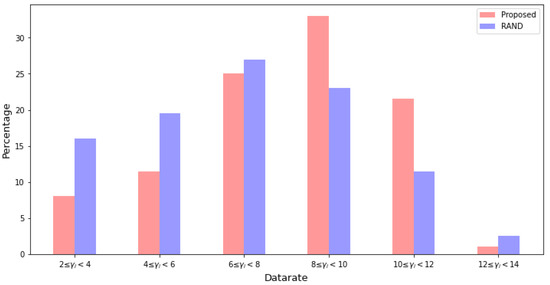
Figure 4. Comparison of the distribution of ${\gamma }_i$ when $\left|N\right|=200$.

To scrutinize the influence of the channel allocation method, in Figure 5, we compare our method and RAND in terms of the interference imposed on a WBAN when $\left|N\right|=100$. Specifically, for each WBAN i in a cluster j, we inspect $D_i\left(t\right)={\sum }_{k\in C_j\left(t\right)\wedge N_i\left(t\right)}{I}_i\left(t\right)-{\sum }_{k\in C\left(t\right)-C_j\left(t\right)\wedge N_i\left(t\right)}{I}_i\left(t\right)$. The first term ${\sum }_{k\in C_j\left(t\right)\wedge N_i\left(t\right)}{I}_i\left(t\right)$ represents the interference imposed on a WBAN i in $C_j$ by the other WBANs in the same cluster, while the second term in $D_i\left(t\right)$ is the interference imposed on i by the WBANs in the other clusters. RAND does not construct a set of clusters. Thus, to compare our method with RAND under the same condition, we use the same set of clusters constructed by our method and apply RAND to each cluster. In Figure 5, we can observe that $D_i\left(t\right)\le 0$ when our method is used, while RAND $D_i\left(t\right)\ge 0$ for all $i\in N\left(t\right)$. It indicates that since inter-WBAN interference is affected by the distance between the WBANs using the same channel, we can alleviate the inter-WBAN interference imposed on a WBAN by allocating different channels to the WBANs in the same cluster after partitioning a graph into a set of clusters so that the modularity of the graph is maximized.

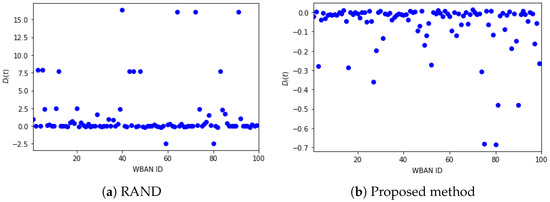
Figure 5. Comparison of the interference experienced by a WBAN ($\left|N\right|=100$).

In Figure 6, we compare our method and RAND in terms of $Z_j\left(t\right)=\frac{1}{|C_j\left(t\right)|}{\sum }_{i\in C_j\left(t\right)}{D}_i\left(t\right)$. When RAND is used, the total interference among the WBANs in the same cluster $C_j\left(t\right)$ is larger than the total interference imposed on all the WBANs in $C_j\left(t\right)$ from the WBANs in $C\left(t\right)-C_j\left(t\right)$. In contrast, when our method is used, $Z_j\left(t\right)<0$ for all the clusters. Thus, our method increases the data rate by reducing the interference among the WBANs in the same cluster.

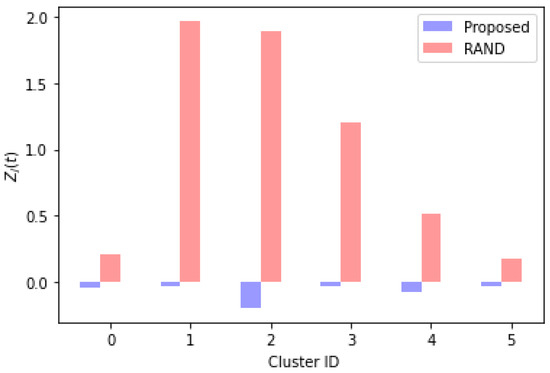
Figure 6. Comparison of $Z_j\left(t\right)=\frac{1}{|C_j\left(t\right)|}{\sum }_{i\in C_j\left(t\right)}{D}_i\left(t\right)$ when $\left|N\right|=100$.

In Figure 7, we depict the distribution of the data rate of a WBAN in each cluster when $\left|N\right|=100$. We observe that in terms of the average data rate in a cluster, the differences among the clusters are marginal. We also observe that our channel allocation method does not penalize clusters in terms of the data rates provided to the WBANs in the clusters.

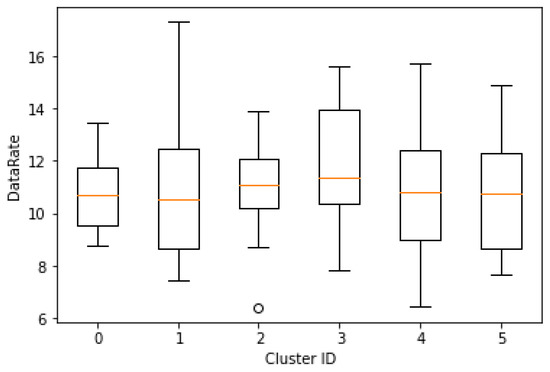
Figure 7. Comparison of the data rate among the clusters when $\left|N\right|=100$.

To evaluate the performance of our method in a dynamic environment, we enable each WBAN to move during each time slot. Specifically, a WBAN randomly chooses both a movement direction from $[0,{360}^{\circ }]$ and a movement speed from [0, 3.6 km/h] according to the Uniform distribution. If a WBAN moves out of the area $S$, a new WBAN is added so that the number of WBANs in $S$ is the same all the time. When a new node is added to $S$, its location is randomly selected in $S$.

In Figure 8, we depict the variations of the modularity of the interference relationship graph over time. The term ‘now’ in this figure represents the modularity of a graph at the start of a time slot t, and the term ‘move’ represents the modulartiy of a graph formed by the WBANs at the end of the time slot t. The results shown as ‘’recluster’ in this figure are obtained when our adaptive module is applied right after ‘move’.

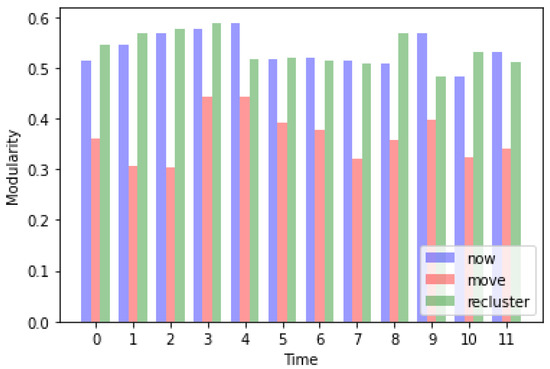
Figure 8. Variations of the graph modularity over time. The term ‘now’ represents the modularity at the start of a time slot t; ‘move’ represents the modularity of the graph at the end of the time slot t. The results shown as ‘recluster’ are obtained when our adaptive module is used right after ‘move’.

Since WBANs can randomly move around, their locations change over time. Thus, the cluster membership made based on the set of WBANs at the beginning of a time slot may not faithfully reflect the interference relationship graph formed by the set of WBANs at the end of the time slot. Therefore, the modularity of a graph reduces at the end of a time slot. Since our adaptive module rectifies the cluster membership of each WBAN distorted by its movement, it increases the modularity of the graph constructed based on the set of WBANs at the end of the time slot.

To examine the effectiveness of the adaptive module, in Figure 9, we compare the distributions of ${\gamma }_i\left(t\right)$s obtained when only the base module is used with those obtained when both the base module and the adaptive module is used over time. When both modules are used, the base module is called at the time slots 7, 8, 10, and 11 when $\left|N\right|=100$. When $\left|N\right|=200$, the base module is called at the time slots 1, 3, 4, 5, 8, and 9. We can observe that the differences between these two cases are marginal for all the time slots.

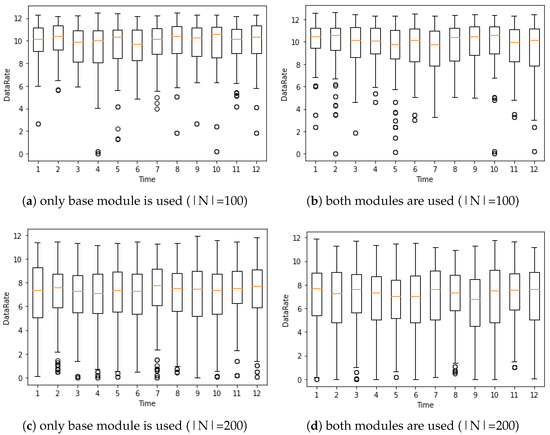
Figure 9. Validity of the adaptive module.

To further investigate the validity of our method, we compare the average data rate achieved by our method with those obtained by the stochastic learning algorithm (SLA) proposed in [10]. We show the result in Figure 10. We can observe that the data rate increases gradually when SLA is used. This is attributed to the manner that SLA determines a channel to use. When SLA is used, each WBAN learns a channel selection probability distribution and exploits it to select a channel to use in a stochastic manner. Whenever a WBAN uses a channel, it measures the data rate of the intra-WBAN communication. Using the measured data rate, the WBAN modifies its channel selection probability distribution. Since the learning process inevitably involves an exploration phase, it takes time for a WBAN to predict the best channel in a given network topology. Therefore, during the exploration phase, the data rate of a WBAN is low because a WBAN does not select the channel that gives it the maximum data rate. When our method is used, a server collects necessary information from the WBANs and allocates channels for them without an iterative process. We note that the performance of our method is comparable to that of SLA in a stable state. When we inspect the differences between the data rates obtained by our method and those obtained by SLA in a converged state, the differences are less than 8.1% for all $\left|N\right|$s. We evaluate the channel decision time with a computer that is equipped with an AMD Ryzen 3700x whose CPU clock is 36 GHz. The size of a RAM is 16 GB, and Python version 3.10.3 is used to measure the channel decision time. When $\left|N\right|=100$, it takes 49.78 s for SLA to converge to a stable point. Our base module decreases the channel decision time to 2.69 s (i.e., 94.6 % reduction). Considering the average walking speed of a pedestrian is 3∼4 km/h, it is likely that the topology of the coexisting WBANs changes before SLA converges. If a topology changes before SLA converges, SLA has to learn the best channel through the exploration phase again, which prevents SLA from obtaining the maximum performance.

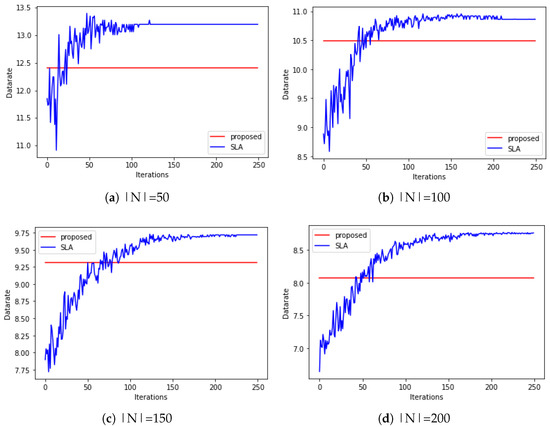
Figure 10. Comparison with the SLA in terms of the average data rate of the coexisting WBANs.

6. Conclusions and Future Works

In this paper, we proposed a dynamic channel allocation method which is composed of a base module and an adaptive module. The base module consists of two parts. The first part of the base module groups a set of WBANs that will severely interfere with each other if they use the same channel. Then, for each cluster, the second part of the base module allocates different channels to the WBANs in the same cluster. An adaptive module is designed to adjust to the gradual topology changes quickly by avoiding the graph partitioning process. We compare the performance of our method with those of the conventional methods through extensive simulation studies. We show that our method outperforms the conventional centralized method by 2.2 times in terms of the average data rate of a WBAN when the density of the coexisting WBANs is 0.5 WBANs per square meter. Our method further increases the average data rate by 5.4 times when the density of the coexisting WBANs is 2 WBANs per square meter. Compared with a distributed method involving an iterative process, our method reduces the channel decision time by 94.6%.

As future work, we will optimize the channel allocation method when the number of colors required to color the WBANs in a cluster is larger than the number of channels available for WBANs. The data rate obtained by a WBAN located at the edge of cluster is relatively smaller than that of a WBAN close to the center of a cluster. To reduce the edge effect, we are working on developing a deep learning model that uses not only the location information of a WBAN, but also other information related with the received signal strength. When the number of coexisting WBANs becomes larger than some point, the data rate of a WBAN cannot be improved by a single channel allocation strategy. Overcoming such a limit by jointly using the channel allocation strategy, transmission power control, and transmission time control is one of our important future works.