Optimal Design of Droplet Ejection for PZT Printhead Based on Surrogate Model

Abstract

Droplet ejection technology is widely used in green and intelligent manufacturing. A stable jetting can be defined as no obvious satellite droplets during the whole ejection process, which is of great importance to ensure the quality and efficiency of the printed products; However, due to the multi-parameter features and the interaction between different physics, using traditional analytical-based approaches to analyze and/or optimize is usually difficult and even unfeasible. Experimental tests using a PZT printhead design-optimization method based on surrogate modeling are proposed in this paper to overcome this challenge, which can synthesize the advantages of numerical simulation. The basic data for surrogate model construction was obtained by the Computational Fluid Dynamics (CFD) numerical-based model, which was developed to predict the flow characteristic under different parameter settings of the printhead. The accuracy of the developed numerical model was validated by performing experimental tests; thereby, the predictive ability of the numerical model in droplet ejection was verified. With the validated numerical model, the Design of Experiments (DoE) was performed to generate the necessary training and validation sample dataset required by the surrogate modeling. Thereafter, four surrogate modeling methods were adopted to construct the relationship between the design parameters and flow features, where the Kriging (KRG) was identified as the optimal modeling method. Based on the developed KRG model, global sensitivity analysis (GSA) of the parameters was carried out with Sobol’s method; thereby, the influence of different parameters can be quantified. Finally, a genetic algorithm (GA) was used to optimize the structure of the droplet printhead. Through validation, the optimized design model increases the droplet ejection speed by 20.84% while keeping no satellite droplet formation, confirming the efficient and stable printhead ejection, and verifying the feasibility and effectiveness of the analysis/optimization method proposed in this paper.

1. Introduction

Microdroplet ejection technology has the ability to deposit materials at the micron level [1], which makes the technology widely used in industrial production, such as electronic printing, bioengineering, display devices and sand mold production [2,3,4,5]. In the microdroplet ejection technology, the printhead is the key structure, and the piezoelectric (PZT) on-demand printhead is the most commonly used [6,7]. Depending on the printing requirements, the PZT printhead can spray droplet deposits to produce the product. However, in droplet ejection technology, the generation of satellite droplets can easily cause surface defects such as model pores and sand inclusion. Some scholars have shown that through the optimization design of printing parameters, such as droplet characteristics or droplet speed, the generation of satellite droplets can be effectively reduced, and the molding accuracy of the model can be fundamentally controlled [8,9,10]. The essence of the optimized design to reduce satellite droplets is to improve the stability of the droplet ejection. Therefore, many scholars take stable ejection (that is, no obvious satellite droplets are generated) as the research objective to optimize and study the ejection process and to set the parameters of the droplets [11,12,13]. However, the PZT printhead droplet ejection process is a complex fluid-structure interaction process, which is affected by many parameters, such as the frequency of the driving waveform, the physical properties of the ink and the size of the nozzle. It is very difficult to use or achieve traditional modeling methods to optimize the above parameters and obtain the optimal solution. Therefore, seeking a method that can replace the traditional model and accurately express the relationship between the influencing parameters (driving waveform, ink characteristics, etc.) and the ejection droplet is a prerequisite for designing optimized printing parameters, which is also a difficult problem to be solved.

In recent years, the optimization design of printing parameters was mainly based on the simulation of the CFD numerical model, and the simulation results were used to optimize the design of individual parameters. For example, Sim et al. [14] established a one-dimensional (1D) digital model between the deformation characteristics of the PZT membrane and the ejected droplets according to the working principle of the PZT printhead, which helped optimize the design of the PZT printhead and greatly improved the simulation speed. However, the study focused only on the kinetic effects of the PZT membrane, ignoring the effects of fluid dynamics on the jetting droplets. In order to improve the injection quality of droplets, Zhong et al. [15] established a two-dimensional (2D) CFD model of the PZT printhead to study the effects of operating parameters such as ejection aperture, driving waveform and fluid characteristics on the injection results and verified that high-quality droplets could be obtained by setting reasonable operating parameters. In order to improve the dynamic accuracy of the single droplet injection process of PZT, Liou et al. [16] established a three-dimensional (3D) simulation model to study and analyze the relationship between the driving pulse, ink characteristics, nozzle diameter and spray droplet speed, volume and shape through the simulation results, and explained the influencing mechanism of process parameters on droplet injection. In studies of droplet injection, many scholars advocate that the characteristics of droplet injection are mainly determined by the driving pulse, so they are committed to optimizing the driving pulse to improve its stability. For example, Wu et al. [11] designed three different driving waveforms and verified the effect of driving waveforms on droplet morphology through the volume of fluid (VOF) simulation model. To determine the optimal duration of the waveform and improve the droplet ejection accuracy, Kwon et al. [17] proposed a method to design the driving pulse waveform based on the motion of the meniscus of the PZT printhead. For obtaining high-quality injection droplets, Wei et al. [18] established a laminar flow simulation model in COMSOL software and optimized the different parameters of the driving waveform. In order to accurately control the deformation of the PZT printhead membrane, Wang et al. [19] proposed a self-perception method for the deformation of the printhead membrane and iterated a new driving waveform according to this method. Experimental results showed that the control accuracy of the optimized waveform parameters was significantly higher than that of the unoptimized waveform. In order to improve the effect of residual damping of oscillation inside the ink chamber of the printhead, Khalate [20] proposed an input-driven waveform design method based on robust optimization, and the experimental results proved the effectiveness of the method and the consistency of the droplet ejection process. For the above studies on optimizing the driving waveform, the combined influence of other parameters (such as ink viscosity, density and surface tension) on the ejection droplet is ignored (that is, the modeled relationship between the printing parameters and droplet ejection established in the above studies are imperfect).

Based on the above analysis, it can be seen that researchers have proposed different methods to achieve and find the optimized target ejection parameters, and CFD numerical simulation models or experiments are needed to verify these new methods. However, due to the experimental conditions and the large-scale calculation of the numerical model, scholars cannot easily find the optimal solution for the ejection parameters for the high-quality droplet. On the other hand, the existing optimization design is mainly based on the optimization of individual parameters, and the comprehensive effect of these influencing parameters is not mentioned. In order to solve the above problem, this paper proposed a new method, that is, utilizing the surrogate model instead of the original numerical model for calculation. In addition, for expressing the numerical relationship between the optimization goal of the ejection droplet and different optimization parameters (such as driving pulse frequency, physical ink characteristics, etc.), the surrogate model will be established on the basis of the CFD simulation model, and the optimal solution will be obtained through the continuous optimization calculation of the surrogate model.

The rest of this paper is summarized as follows: Firstly, the sand-printer PZT printhead was adopted as the study object to introduce its working principle and the influencing parameters of the ejection droplet for the optimization objective of this study. On this basis, we established the CFD numerical simulation model of the single droplet injection process and verified the effectiveness of this model, which provided a basis for the surrogate model construction. Secondly, sensitivity analysis and uncertainty optimization were carried out for the influence parameters of the droplet ejection process, and we utilized the surrogate model to optimize the influencing parameters. Finally, the optimization results of the surrogate model were discussed and summarized with relevant conclusions.

2. Description of the PZT Printhead

Figure 1 is a single ejection unit of the PZT printhead used in this study. Each ejection unit has the same structure and working principle, and the nozzle can be controlled for independent ejection. The ejection units are arranged in a straight line and are driven by piezoelectric ceramic sheets. Each printing unit has an independent driving mode and a switching mode so that each nozzle will not affect the other in the process of working. Each individual nozzle unit contains an ink reservoir, an ink chamber that absorbs ink from an ink box, a nozzle, a PZT film and a pair of positive and negative electrodes that control the movement of the PZT membrane. When the excitation pulse voltage with a certain edge slope (as shown in Figure 2) is loaded to the PZT membrane, the excited membrane will bend and deform to squeeze the ink chamber; thereby, the volume of the ink chamber will decrease, and the ink will be ejected from the nozzle. After experiencing a pulse voltage signal, the excitation pulse voltage will be removed with a certain edge slope, and the PZT membrane will return to its original state. Negative pressure will be generated in the chamber to pull the neck of the droplet off, forming an independent droplet.

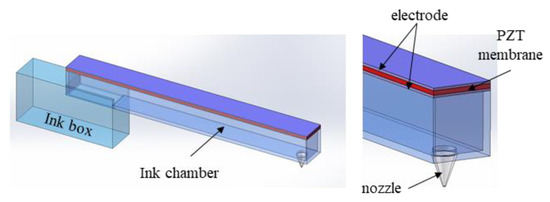
Figure 1. PZT printhead ejection unit.

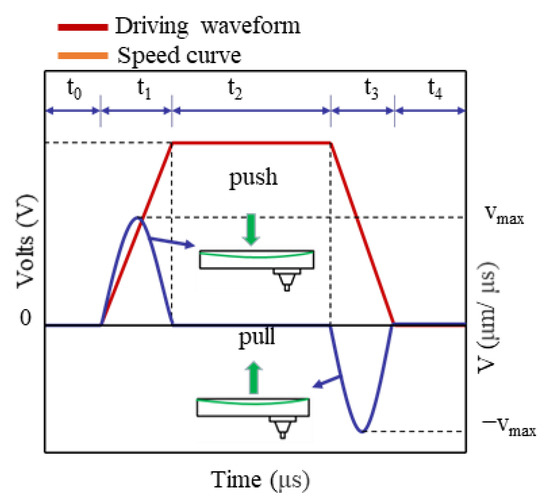
Figure 2. Driving pulse signal.

In this study, to verify the effectiveness of the models, a droplet ejection observation experimental platform was built, as shown in Figure 3. The experimental bench mainly includes droplet ejection, observer and drive control modules. In the droplet ejection module, droplet jetting is performed using a Fujifilm Sapphire QS256/80 AAA model printhead, which has 36 independent array prints and uses furan resin as the ejection material. The droplet observer module contains a video recorder, a flash and a display device. High-strength, well-aimed infrared light-emitting diodes are used to illuminate the trajectory of the droplet movement and to help record the video and pictures of the droplet. The aiming direction of the camera and the LED light line are needed to form a certain obtuse angle during placement so as to achieve a better shooting effect in the case of fewer hot spots. The ignition signal that drives the printhead can be transmitted to the video recorder and flash at the same time, allowing the two modules to work simultaneously to record the complete movement of the droplet. The setting parameters of the test bench are shown in Table 1.

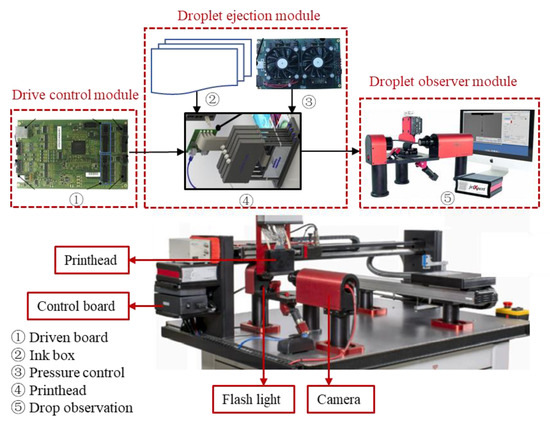
Figure 3. Experimental platform.

Table 1. Experimental parameters.

Observation Module		Droplet Generation
Pixel	1032 × 778	Printhead type	QS256/80 AAA
Voltage amplitude	5 V (TTL)	Voltage amplitude	100 V
Frequency	80 kHz	Frequency	8 kHz
Focal length	6:1	Ink type	Furan resin
Pulse width	0.25 μs
Supply voltage	220 V

3. PZT Printhead CFD Modeling

In order to build the base model of the surrogate model, a CFD simulation model of the PZT printhead was established before iterative optimization.

3.1. Droplet Ejection Process Model of PZT Printhead

The mathematical model of the droplet forms the basis and research foundation for the accurate construction of the CFD numerical model of the printhead. In this type of printhead, the PZT membrane is attached to the top of the ink chamber, and under the action of the driving pulse electrical signal, the membrane will be deformed by a small amount of bending. This deformation transmits pressure into the ink chamber to form a pressure wave, causing the liquid to be ejected from the nozzle as droplets. According to the above-mentioned working state of the printhead, this process can be simplified into a physical model for analysis.

Firstly, according to the piezoelectric material characteristic formula:

$$\begin{array}{l}{S}_1=S_{11}^E{T}_1+d_{31}{E}_3\\ D_3=d_{31}{T}_1+{\epsilon }_{33}^T{E}_3\end{array}\}$$

(1)

where $S_1$ and $T$ are the strain and stress in the transverse direction, respectively; $D_3$ and $E_3$ are the electric field and stress in the longitudinal direction, respectively; ${\epsilon }_{33}^T$ is the dielectric constant when the external stress is zero or constant, and $d_{31}$ is the PZT constant and the elastic compliance coefficient when the electric field is either constant or equal to zero.

Wei [21] proposed that if the electric field applied to the PZT membrane is uniform, then $E_3$ is a linear function of the voltage, $U$, that is loaded on the PZT membrane. If the maximum displacement of the PZT membrane in the deformation direction is denoted as h, then the relationship between the force and the displacement of the PZT driver can be expressed as:

$$h=\alpha U-\beta F$$

(2)

where $\alpha$ and $\beta$ are constants, $U$ is the driving voltage value, and $F$ is the external force.

As shown in Figure 4, the electric field and displacement movement changes of the PZT membrane are simplified into an elastic model. When the pulse signal is applied to the PZT membrane, the membrane bends and squeezes the ink chamber with a certain acceleration under the action of the electric field’s force, and the liquid in the ink chamber also exerts a certain pressure, $P(t)$, on the PZT membrane. According to Newton’s laws:

$$m\frac{d^{2}h}{d{t}^2}=F(t)-P(t)A-kh$$

(3)

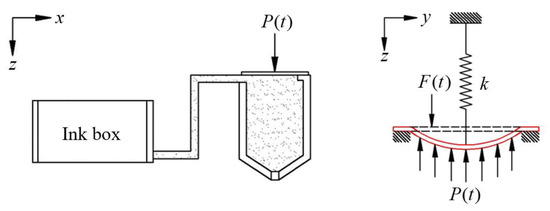
Figure 4. Simplified model of the droplet injection process.

Among them, A, k and m are divided into the area, elastic coefficient and mass of the PZT membrane, and $F(t)$ is the force generated by the accelerated motion and deformation of the membrane.

Substituting the above formula into Equation (2), the force equation of the PZT membrane can be obtained by:

$$m\frac{d^{2}h}{d{t}^2}+(k+\frac{1}{\beta })h=\frac{\alpha }{\beta }\varphi -PA$$

(4)

In the process of droplet injection and observing the principle of energy conservation, the Naiver-Stokes equations are established as follows:

$$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho v)=0$$

(5)

$$\frac{\partial }{\partial t}(\rho v)+\nabla \cdot (\rho vv)=-\nabla p+\nabla \cdot [\eta (\nabla v+\nabla v^T)]+\rho g+F$$

(6)

where $\rho$ is the density, $v$ is the speed, $p$ is the pressure, $\eta$ is the viscosity and $F$ is the volume force.

Through the combined expression of Equations (4) and (6), the complete process from droplet generation to injection in the working process of the PZT printhead can be described. Through the above theoretical analysis, it can be found that the pulse width of the driving pulse signal and parameters, such as droplet density, viscosity and surface tension, are important factors that affect the droplet ejection results and especially the speed. Therefore, this paper mainly carried out the optimization design with the above parameters.

3.2. Modeling of the PZT Printhead CFD Numerical Model

In order to obtain the basic data of the surrogate model and optimization design process, a CFD numerical model of the PZT printhead was established to simulate the ejection process of droplets [22]. Different from the previous 3D or 2D printhead simulation models, this study adopted a modeling method that simplified the calculation of the 3D model of the PZT printhead by dividing it into two: a 3D chamber model and a 2D nozzle-air domain model. The bending deformation of the PZT membrane was simulated by using a dynamic mesh technique, and the change in the cross-sectional area of the chamber was recorded in real-time. The recorded cross-sectional area was fitted into a fifth-order function as the input boundary condition of the nozzle-air domain model to simulate the droplet ejection process. For the 2D nozzle-air domain model, in addition to establishing its input boundary conditions, it is also necessary to verify the mesh independence of the model to prove its accuracy and validity. The modeling process and boundary condition settings of the PZT printhead numerical model are shown in Figure 5. In this study, the ANSYS Fluent 19.2 commercial software was used to perform computational simulation, with only the fluid dynamics behavior considered during the simulation.

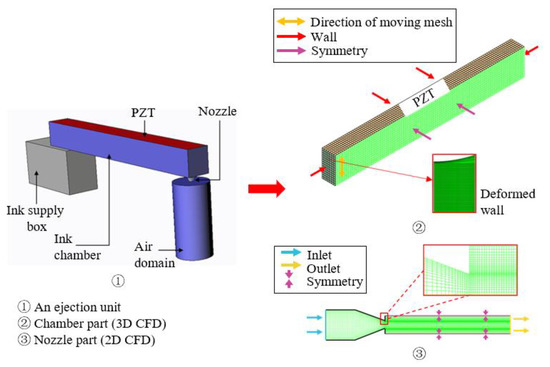
Figure 5. Schematic diagram of CFD model development for the droplet injection process.

The 3D chamber model’s main function is to simulate the process of deformation movement of the PZT membrane and obtain the ink mass-flow curve in the chamber, which is used as the boundary input condition of the 2D nozzle-air domain model. When the numerical simulation model was established, the PZT membrane was set as the moving mesh. The DEFINE_GRID_MOTION macro function of the UDF method was used to drive the motion deformation of the membrane. The DEFINE_ADJUST macro was used to record the change in the cross-sectional area of the chamber, and the mass-flow curve of the flowing ink was calculated by the DEFINE_EXECUTE_AT_END macro. The other boundary conditions were set as WALL. During this simulation, the ink mass-change value in the chamber was recorded, and a mass-flow curve using Equation (7) was obtained.

$$mass\_flow\_rate(t)=\{\begin{array}{cc}a{t}^5+b{t}^4-c{t}^3-d{t}^2+et,\hfill & 0\le t<t_1\\ \hfill 0,\hfill & t_1\le t<t_2\\ a[t-(t_2-t_1){]}^5+b[t-(t_2-t_1){]}^4-c[t-(t_2-t_1){]}^3\hfill & \\ -d[t-(t_2-t_1){]}^2+e[t-(t_2-t_1)],\hfill & \hfill t_2\le t<t_3\hfill \\ 0,& t>t_3\end{array}$$

(7)

For the 2D nozzle-air domain CFD model, the validity and correctness needed to be verified, including the verification of the independence of the mesh. In the microdroplet ejection technology, the criterion of stable ejection is mainly based on the number of satellite droplets. Therefore, in this study, the ejection process in which there are no more than two satellite droplets, and the satellite droplets can join the main droplet before the collision with the bottom plate, is considered a stable ejection. Before the simulation calculation, a convergence model that can stably eject droplets and include mesh independence verification was selected first to verify the validity of the model. The relevant parameters set are shown in Table 2.

Table 2. Parameter settings for simulations.

Parameter	Values
Fluid	Newtonian fluid
Analytical model	Turbulence model
Solution method	PISO scheme
	Second-order
Viscosity	12.5 cp (20 °C)
Density	1500 kg/m3
Surface tension	0.065 N/m (20 °C)
Maximum iteration steps	200

The comparison between the experimental and the CFD numerical simulation results are shown in Figure 6, and the ejection process of the two has a good consistency. It can be obtained from the evolution process of the droplet flow contours that the driving voltage signal increased from 0 to 100 V during the period of 0–3.85 µs, and the PZT membrane moved to the maximum displacement to squeeze the ink in the chamber. Under the influence of pressure waves in the chamber, the ink formed a half-moon liquid column at the nozzle. During the period of 3.85–14.4 µs, the voltage signal remained unchanged at 100 V, and the ink continued to be ejected from the nozzle and formed a long liquid column under the liquid tension. During 14.4–16.2 µs, the driving signal was reduced from 100 to 0 V, the PZT membrane returned to the horizontal position, and the liquid column at the nozzle was pulled by the reverse pressure wave in the ink chamber. The pulled liquid column followed the main droplet and finally formed a complete spherical droplet that was ejected into the air. Meanwhile, according to the above results, the new ejection cycle did not affect the ejection results of the previous round, and the established CFD model also maintained good consistency with the experimental results in the second round of droplet ejection.

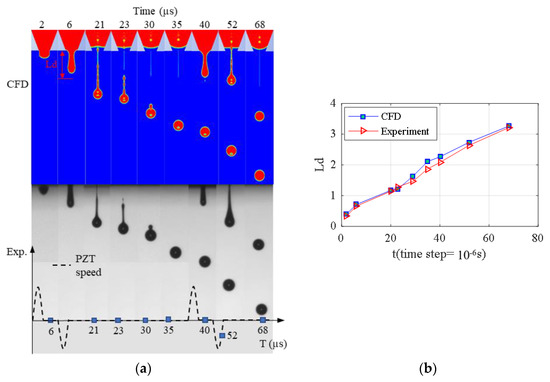
Figure 6. Comparison of CFD model and experimental results. (a) Comparison of droplet morphology between CFD model and experiment. (b) Comparison of the droplet length (which is normalized to the range from 0–1) between the CFD simulations and the experimental tests.

In order to verify the effectiveness of the CFD model, the comparison between the simulation model and experimental results at various time periods under the conditions of 12 cp viscosity, 1350 kg/m³ density and 0.07 N/m surface tension was also selected in this study, as shown in Figure 7. According to the comparison results, it can be seen that both the variation process of droplet stretching and the formation of satellite droplets have very good consistency, which confirms the reliability of the established CFD model.

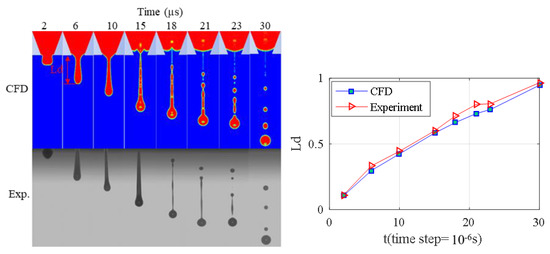
Figure 7. CFD model experiment verification.

4. Optimization of the PZT Printhead Based on the Surrogate Model

From the above content, it can be seen that there are many factors affecting the stable ejection of the PZT printhead, and the coupling relationship between important parameters in the ejection process is complicated. For the PZT printhead with complex ejection mechanisms, traditional parameter optimization is mostly based on discrete analysis, which requires a lot of iterative analyses and calculations. In order to solve the problem of heavy computation, this study adopted the surrogate model, which was established based on the CFD simulation model instead of the decentralized numerical model. The surrogate model designing process is as follows (Figure 8).

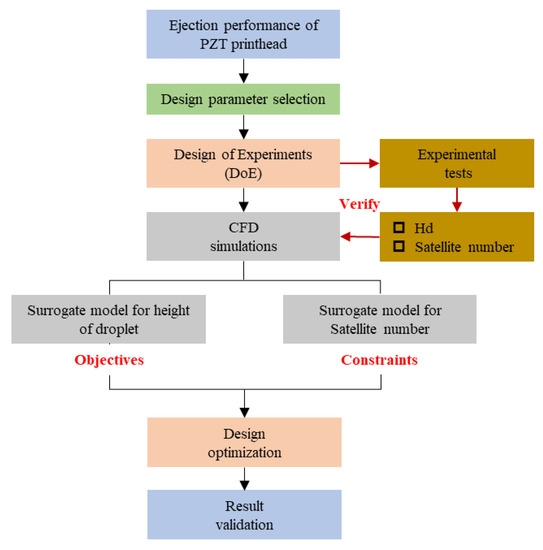
Figure 8. The process of surrogate modeling-based optimization.

4.1. Definition of the Optimization Problem

In this study, the ultimate goal of optimization is to achieve stable and effective ejection (without satellite droplets) at a fast ejection velocity. It is found that the stable ejection of droplets can be directly reflected by the droplet’s flow contours. Second, the droplet’s ejection speed should be as fast as possible without producing satellite droplets to ensure the efficiency of the printhead. Therefore, the height value, H_d, when the complete droplet is formed (the larger the value of H_d, the faster the droplet velocity) was used as the parameter to quantify the droplet ejection performance of the PZT printhead, and the liquid density ρ, viscosity η, surface tension σ and the period T driving the waveform could be used as design variables. The method of variable normalization and weight setting is as follows:

$$V_{flux}=(flux-flu{x}_{\min })/(flu{x}_{\max }-flu{x}_{\min })$$

(8)

where $V_{flux}$ represents the normalized value of each parameter variable, $flux$ is the parameter variable value used in numerical simulation. $flu{x}_{\min }$ and $flu{x}_{\max }$ are the minimum and maximum values of the parameter variable’s range, respectively.

The value range of parameter variables is as follows:

$$\{\begin{array}{l}0\le \mathrm{Hd}\le 1\\ 500\le \rho \le 1650{\mathrm{kg}/\mathrm{m}}^3\\ 5\le \eta \le 25\mathrm{cp}\\ 0.004\le \sigma \le 0.008\mathrm{mN}/\mathrm{m}\\ 9.7\le \mathrm{T}\le 15.7\mathsf{\mu }\mathrm{s}\end{array}$$

(9)

4.2. Design of Experiments

The Design of Experiments (DoE) usually refers to the sample point generation strategy, which is one of the key steps in designing suitable experimental sample points that are necessary to ensure the accuracy of the surrogate model [23]. The Latin hypercube sampling method (LHS) was selected among the methods to generate sample points based on the comparison of different experimental designs. This method is considered to be one of the most effective in reducing computational costs [24], so it is also used in this study to obtain the sample points for the surrogate model. When taking the ejection liquid density ρ, viscosity η, surface tension σ and the drive pulse period T as the design variables, we generated 40 sample points as the basis for sample point construction and 16 verification points to verify the accuracy of the surrogate model. The distribution of the 40 sample points and 16 validation points is shown in Figure 9. For ease of observation, only the design variables of the distributions of ink viscosity, density and surface tension are plotted corresponding to the X-, Y- and Z-axis, respectively. All the parameters were normalized to a range from 0–1. According to the normalized distribution map of discrete points, the generated sample and verification points fill the three-dimensional space completely and basically cover the range of droplet ejection settings. Based on the above sample and verification points, the CFD model designed in Section 3 was used for transient simulation to calculate the dynamic performance of the droplet ejection process, and the simulation results were used to construct the surrogate model.

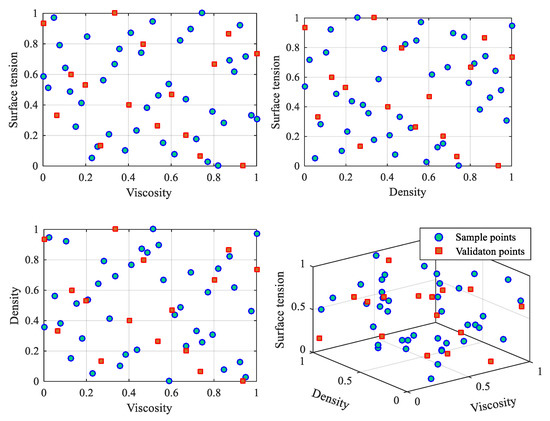
Figure 9. Sample points for surrogate modeling.

4.3. Surrogate Model

The fast calculation of the surrogate model can be used as an alternative method for high-cost simulation models, which can provide a new arithmetic operation method for the expression of the relationship between input parameters and output response, as well as greatly reduce the problem of large computational volume in the iterative optimization of numerical models [25]. In recent years, the agent model developed by researchers has been successfully applied to different engineering problems due to its high efficiency and low cost, such as the polynomial regression surface (PRS), radial basis function (RBF), Kriging (KRG) and support vector regression (SVR) model. The PRS function is based on the principle of multiple regression analysis and uses the resulting set of input-output relationships to establish a polynomial regression equation with the functioning mean and the remaining standard deviation. The RBF uses its interpolation to calculate the next point of the objective function and achieve convergence without further assumptions about the objective function, which is very effective for problems where the calculation results are extremely complex. The KRG method is based on a spatial interpolation algorithm, which combines the information of known points in space and outputs predictions of unknown point information by establishing an approximate function map. The SVR model mainly uses a nonlinear mapping function to map sample points to a high-dimensional feature space to obtain an input-output fitting relationship, which is very suitable for the case of limited training points. The main functions of the above two surrogate models are shown in in Table 3.

Table 3. Surrogate model details.

Surrogate Model	$\widehat{\mathit{y}}(\mathit{x})$	Correlation Function
KRG	$\widehat{\beta }+r^T(x)R^{-1}(y-f\widehat{\beta })$	$R(x^i,x^j)=\exp (-{\displaystyle \sum _{k=1}^{n_{dv}}{\theta }_k|x_k^i-x_k^j{|}^2)}$
SVR	${\displaystyle \sum _{i=1}^{n_s}(a_i-a_i^{*})}k(x_i\cdot x)+b$	$k\left(x,x^{\prime }\right)=\mathit{exp}(-\frac{|\left|x-x^{\prime }\right|{|}^2}{2{\sigma }^2})$
PRS	$b_0+{\displaystyle \sum _{i=1}^n{b}_i{x}_i}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{b}_{ij}{x}_i}{x}_j}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\displaystyle \sum _{k=1}^n{b}_{ijk}}{x}_i}{x}_j{x}_k}$	-
RBF	${\displaystyle \sum _{i=1}^{n_s}{\lambda }_i\phi (r(x_i,x))}$	$\phi (r(x_i,x))=\sqrt{\left|\right|x-x_i|{|}^2+c^2}$

In order to verify and evaluate the accuracy of the above four surrogate models, the LHS method was used to generate 16 verification points. In this study, in order to evaluate the computational performance of the surrogate model more intuitively, the parameter R is used to express it. The closer the value of R² is to 1, the higher the accuracy of the surrogate model. The estimation method is as follows:

$$R^2=1-\frac{{\displaystyle {\sum }_{i=1}^m{(y_i-{\widehat{y}}_i)}^2}}{{\displaystyle {\sum }_{i-1}^m{(y_i-{\overline{y}}_i)}^2}}$$

(10)

where m = 16 is the number of verification points of the evaluation agent model, $y_i$ is the true value after the CFD model simulation, and ${\widehat{y}}_i$ is the predicted value calculated by the surrogate model.

The verification results of the four surrogate models are shown in Table 4, and the corresponding accuracies are shown in Figure 10. Due to the different calculation methods of the four surrogate models, the corresponding accuracy is also different. The results show that KRG model has the highest R² value among the four individual models, indicating that this model has the highest calculation accuracy under this application. Therefore, this paper used KRG as the surrogate model to replace the original numerical simulation model for ejection control parameter optimization. Figure 11 shows the direct accuracy verification of the KRG model, where the X- and Y-axis represent the results obtained from CFD simulations and surrogate model predictions, respectively. The closer the point is to the line, the more consistent the results of the verification point and the surrogate model are [26]. It can be found that the point distribution produced by the KRG model is better when compared with others, so it is reasonable to choose the KRG model for result predictions.

Table 4. R² of different surrogate models.

Model	PRS	RBF	KRG	SRV
Satellite number	0.4919	0.8663	0.8966	0.8129
Hd	0.8804	0.7265	0.8911	0.4956

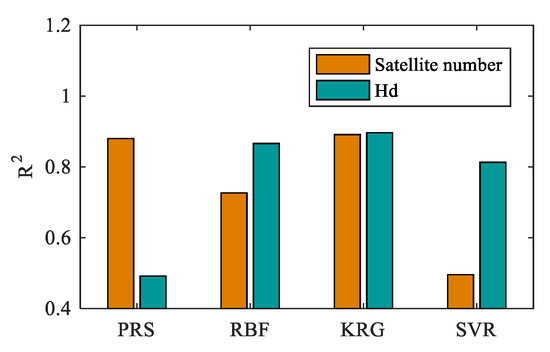
Figure 10. Errors of different surrogate models.

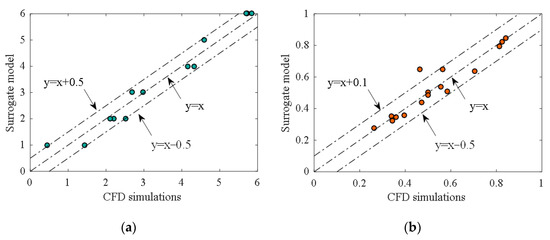
Figure 11. Direct validations of the KRG model. (a) Satellite droplet number prediction. (b) Droplet length prediction.

4.4. Sensitivity Analysis and Parameter Optimization

The formation of the injection droplets in the working process of the PZT printhead involves the interaction of multiple parameters and physical fields. Therefore, in the early parameter optimization design, the main parameters affecting the droplet ejection results should be found for optimization. In this study, the Sobol method in the Global Sensitivity Analysis (GSA) algorithm is mainly used to complete the selection of the main parameters. The Sobol calculation method is mainly based on the Monte Carlo method of variance [27], and the combination of individual and other parameters can be expressed through different simulations. The process of estimating the sensitivity of the ejection parameters using the Sobol algorithm is as follows:

(1)

Generate two groups of sample values, which can be expressed as;

$$A=\left[\begin{array}{c}{x}_{11}\cdots x_{1i}\cdots x_{1d}\\ x_{21}\cdots x_{2i}\cdots x_{2d}\\ ⋮\\ x_{n1}\cdots x_{ni}\cdots x_{nd}\end{array}\right]B=\left[\begin{array}{c}{x}_{11}^{\prime }\cdots x_{1i}^{\prime }\cdots x_{1d}^{\prime }\\ x_{21}^{\prime }\cdots x_{2i}^{\prime }\cdots x_{2d}^{\prime }\\ ⋮\\ x_{n1}^{\prime }\cdots x_{ni}^{\prime }\cdots x_{nd}^{\prime }\end{array}\right]$$

(2)

Switch the ith line parameters of matrix A and B to get the new matrix A and B;

$$A_i=\left[\begin{array}{c}{x}_{11}\cdots x_{1i}^{\prime }\cdots x_{1k}\\ x_{21}\cdots x_{2i}^{\prime }\cdots x_{2k}\\ ⋮\\ x_{n1}\cdots x_{ni}^{\prime }\cdots x_{nk}\end{array}\right]B_i=\left[\begin{array}{c}{x}_{11}^{\prime }\cdots x_{1i}\cdots x_{1k}^{\prime }\\ x_{21}^{\prime }\cdots x_{2i}\cdots x_{2k}^{\prime }\\ ⋮\\ x_{n1}^{\prime }\cdots x_{ni}\cdots x_{nk}^{\prime }\end{array}\right]$$

(3)

Substitute the values of each row in the new matrices A and B into the regression model as the input to obtain the corresponding response results;

(4)

Utilize the Formulas (13)–(16) to calculate the response of the vibration prediction;

$${{\widehat{f}}_0}^2=\frac{1}{n}{\displaystyle \sum _{r=1}^{n}f(x_{r1},x_{r2},\cdots ,x_{rd})f}(x_{r1}^{\prime },x_{r2}^{\prime },\cdots ,x_{rd}^{\prime })$$

(11)

$$\widehat{V}(y)=\frac{1}{n}{\displaystyle \sum _{r=1}^n{f}^2(x_{r1},x_{r2},\cdots ,x_{rd})-{{\widehat{f}}_0}^2}$$

(12)

$${\widehat{U}}_i=\frac{1}{n}{\displaystyle \sum _{r=1}^{n}f(x_{r1},\cdots ,x_{rd})f(x_{r1}^{\prime },\cdots x_{r(i-1)}^{\prime },x_{ri},x_{r(i+1)}^{\prime },\cdots ,x_{rd}^{\prime })}$$

(13)

$${\widehat{U}}_{-i}=\frac{1}{n}{\displaystyle \sum _{r=1}^{n}f(x_{r1},\cdots ,x_{rd})f(x_{r1},\cdots x_{r(i-1)},x_{ri}^{\prime },x_{r(i+1)},\cdots ,x_{rd})}$$

(14)

(5)

Calculate individual effect values $x_i({\widehat{S}}_{xi})$ and overall influence effect values $x_i({\widehat{S}}_{xi}^T)$ of parameters, the process of which is as follows;

$${\widehat{S}}_{xi}=\frac{{\widehat{U}}_i-{{\widehat{f}}_0}^2}{\widehat{V}(y)}$$

(15)

$${\widehat{S}}_{xi}^T=1-\frac{{\widehat{U}}_{-i}-{{\widehat{f}}_0}^2}{\widehat{V}(y)}$$

(16)

where the sum ${\widehat{S}}_{xi}^T$ of all input parameters is 1. The higher the ${\widehat{S}}_{xi}^T$, the higher effect of the input parameter.

In this study, ink density $\rho$, viscosity $\eta$, surface tension $\sigma$ and driving pulse period T values were selected for sensitivity analysis, and the results are shown in Figure 12. According to the calculation results, the individual and global sensitivity index of the ink density value is the highest, which means that the density value has the greatest influence on the liquid column length and satellite droplet. The second is the ink surface tension and viscosity values, which have the same effect on droplet stability. The last is the driving pulse period value, which has the smallest influence. The four above parameters are the main parameters that have been confirmed to affect the accuracy of droplet injection, but why the density value affects the proportion the most needs further research and judgment. The stable ejection of droplets along the density and viscosity directions is plotted to verify this, as shown in Figure 13.

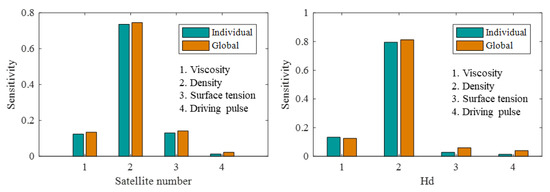
Figure 12. Results of the sensitivity analysis.

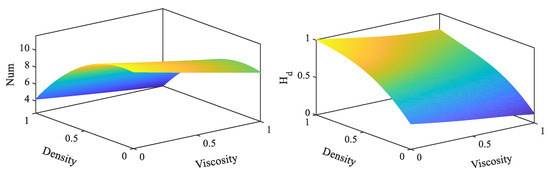
Figure 13. Surface plot of droplet ejection for density and viscosity settings.

Figure 14 shows the trend diagram of the influence of design parameters $\eta$, $\rho$, $\sigma$ and T on the number of satellite droplets and droplet height Hd. The results are the same as the sensitivity analysis of the design parameters above; the value $\rho$ has the greatest influence on the stability of droplet ejection, followed by the value $\eta$. In the range of 500–1650 kg/m³, the larger the $\rho$ value, the larger the mass of a single droplet, the fewer the number of satellite droplets, and the larger the height reflected in the Hd value. Within the range of viscosity value between 5–25 cp, the larger the value $\eta$ is, the smaller the number of satellite droplets, and the smaller the Hd value is due to the increase of cohesion between molecules inside the liquid. In the range of 0.004–0.008 mN/m, the influence of $\sigma$ value on the number of satellite droplets presents a nonlinear change, and in the range of 9.7–15.7 µs of T, the larger the T value, the more satellite droplets. At the same time, the results show that $\sigma$ and T values have little effect on the droplet column length, Hd, within the design range in this paper. Therefore, in the application of the droplet ejection technology, the pulse width can be reduced, and the fluid density and viscosity values can be appropriately increased to increase the stability of droplet ejection.

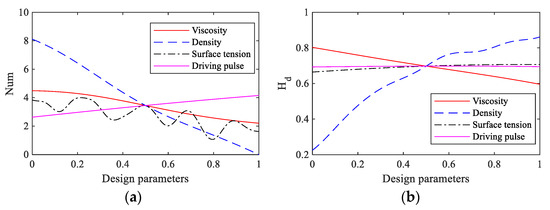
Figure 14. The design parameters influence trend. (a) Effect of design parameters on Hd. (b) Effect of design parameters on the number of satellite droplets.

5. Results

In this study, the result objective of the optimization is to achieve stable droplet ejection. Therefore, during optimization, the length of the liquid column, Hd, was taken as the optimization target value, and the KRG model was taken as the adaptive function model. According to the forty generated samples, utilizing the genetic algorithm (GA) was used for data optimization.

After optimization convergence, the optimal value of Hd = 0.968 was obtained, and the corresponding optimization parameters were: liquid density ρ was 1500 kg/m³, viscosity η was 11.73 cp, surface tension σ was 0.058 N/m and driving waveform period T was 10.92 µs. In order to verify the optimization results, the obtained optimization parameters were substituted into the CFD model for simulation calculation again. The simulation results of optimized parameters and initial parameters are shown in Figure 15. Compared with the original Model 1 (ρ, η, σ and T are 1350 kg/m³, 12 cp, 0.07 N/m and 8 µs, respectively), the droplet velocity was basically unchanged, and it can be obviously observed that there were no satellite droplets in the optimized model, which achieved the objective of stable droplet ejection. Compared with the original Model 2 (ρ, η, σ and T are 1500 kg/m³, 12.5 cp, 0.065 N/m and 8 µs, respectively), the droplet velocity of the optimized model was increased by 20.84%. From the above comparison results, it can also be found that the ink characteristics, such as viscosity, density and surface tension, directly affect the droplet stability ejection state, which is consistent with the previous parameter sensitivity analysis results and verifies the feasibility of this study.

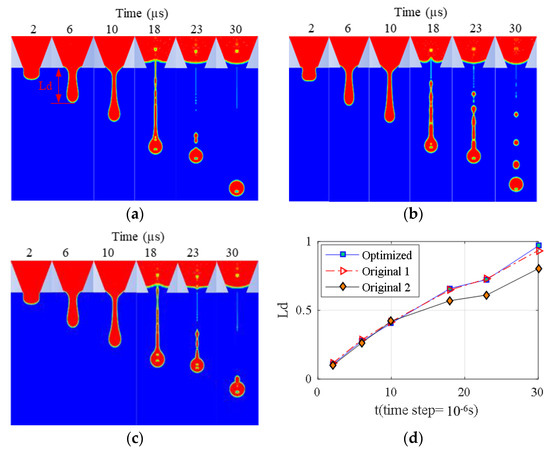
Figure 15. Comparison between the optimized model and the original model. (a) Droplet ejection counters of the optimized model. (b) Droplet ejection counters of the original Model 1. (c) Droplet ejection counters of the original Model 2. (d) Comparison of the droplet length.

6. Summary

In this study, the stability ejection of droplets of the PZT printhead was the purpose, and the design and optimization of the droplet ejection process were optimized. Specifically, we focused on the establishment of the CFD and surrogate model of the droplet ejection process, the sensitivity analysis of the influencing droplet ejection parameters and the optimization process analysis. The summary is as follows:

(1) The working principle of the droplet ejection process of the PZT printhead and the influencing factors of the ejection parameters were explained. We established the CFD numerical simulation model of a single droplet ejection process, and the feasibility of the proposed CFD model was verified by comparing the experimental results. Our results provide a basis for building the surrogate model.

(2) Based on the LHS method, the CFD simulation results were used to proceed to conduct DoE, and the accuracy of the four surrogate models of PRS, RBF, KRG and SRV was verified by using the generated verification points. The validation results show that the KRG model has the largest R² value, indicating that the KRG model in this study was more suitable for the study of the droplet ejection process.

(3) According to the KRG surrogate model established, the sensitivity analysis of the four parameters of ink density, viscosity, surface tension and driving pulse period was carried out by the Sobol method, and the influence of the above parameters on droplet ejection was determined. The results showed that the influence of ink density on droplet stability ejection was the largest, followed by ink viscosity and surface tension, and finally, the driving pulse period value.

(4) Based on the GA algorithm, the surrogate model design parameters were optimized. The optimization process took the droplet column length, Hd, as the objective and with no satellite droplets as the constraint condition. The optimized liquid column length was reduced compared with the original length, which verified the feasibility and effectiveness of the optimization method proposed in this paper.

This study aimed to propose a method to optimize the droplet ejection parameters more efficiently and directly so as to provide a reference for the optimization and design of the droplet ejection technology. At the same time, this study also has some limitations: In this paper, only four influencing parameters were selected for optimization and sensitivity analysis. Other influencing parameters, such as nozzle structure size and driving signal amplitude, need to be studied further. The sensitivity analysis of the influencing parameters showed that the ink density had the greatest influence, but under the comprehensive influence mechanism, the emergence of this result also needs further verification and analysis. The limitations listed above will be further addressed in future studies.