Optimized-Based Fault-Tolerant Control of an Electro-Hydraulic System with Disturbance Rejection

Abstract

In this article, the design and implementation of a fault-tolerant controller are proposed for an electro-hydraulic actuator (EHA) in the presence of disturbances and actuator faults. The existence of nonlinearities, uncertainties, and a bias fault (i.e., internal leakage fault) in the system dynamics significantly decreases the desired performance. The nonlinear disturbance observers (NDO) are constructed to handle the adverse influences caused by the above disadvantages. The whole fault-tolerant control (FTC) scheme consists of two design loops: an inner force control loop and an outer position control loop. The inner loop is based on an optimized backstepping framework to achieve the optimal performance, whilst the problem of uncertainties and disturbances is dealt with using a terminal sliding mode directly designed from the position tracking error. It is shown by theoretical analysis that system stability is ensured under faulty conditions. Finally, simulation results and comparison studies are conducted to further verify the effectiveness of the proposed approach.

1. Introduction

Over the past few decades, electro-hydraulic systems have been extensively used in various civilian and industrial applications due to many outstanding achievements [1,2,3,4]. There exist different research studies, and many results have been introduced to obtain the force or position control requirements, including model-based feedback control [5], sliding-mode control [6], backstepping control [7], adaptive robust control [8], and so on. However, in the abovementioned works, many simultaneous problems of EHAs, such as uncertainties, disturbances, faults, and optimal performance, have not been well investigated. It is noted that the uncertainties include parametric uncertainties (i.e., parameter deviation, modeling errors, etc.) and uncertain nonlinearities (i.e., nonlinear friction force, and external load) [5,6,7,8]. Meanwhile, the most popular fault in the EHA is the internal leakage fault that comes from the piston seal and/or internal flow loss [9,10]. Such problems may degrade tracking performance or even cause instability of the whole EHA system if they are not tackled in a timely manner. Thus, the fault-tolerant capability is vital for guaranteeing the reliable control system and obtaining optimal performance of the EHA system.

To overcome the adverse effects of disturbance and uncertainty, the actuator fault issue, many effective FTC methods have been suggested to ensure system stability at an acceptable level [11]. Most notably, observers or an intelligent approximator-based FTC approach are widely adopted to react to faults, i.e., disturbance observer (DO) [12], state-dependent delay (SDD) [13], fixed-time observer [14], extended state observer [15,16], neural networks (NN) [17,18], fuzzy logic system (FLS) [19,20], and so on. It is noted that the effect of fault is significantly larger than lumped disturbance; many works merged the disturbance and bias fault into lumped disturbance. To deal with this issue, a designed compensator is then presented in Refs. [12,13,14,15,16,17,18,19,20]. In Ref. [21], by using the time delay estimation-based FTC control approach, the effects of disturbances and an internal leakage fault are compensated as lumped uncertainties. The authors in Ref. [22] proposed an adaptive NN actuator failure compensation control scheme for the vehicle active suspension systems. In Ref. [23], the fault estimation and FTC scheme were suggested for the hydraulic manipulator in the presence of the internal leakage fault and lumped disturbance, by using two DOs and a control reconfiguration law. In Ref. [24], the combination of an adaptive law and the DO was adopted to cope with the internal leakage fault. However, in the existing literature, the FTC approach based on optimal performance for the nonlinear system has not been well addressed, especially for EHA systems. How to obtain reliable control of the EHA whilst ensuring optimal performance is still challenging in the control field.

In most industrial fields, certain optimal performance of the EHA is required. Thus, the optimal control emerges as an effective method and there has been more attention paid to not only handle the control issue but also guarantee the optimal performance for the nonlinear system. To obtain the optimal control performance, solving the solution of the Hamilton–Jacobi–Bellman (HJB) equation is necessary [25,26,27,28]. Nonetheless, the HJB equation is solved complexity due to the inherent nonlinearity and intractability, which results in reducing its feasibility and applicability. Then, NN-based reinforcement learning (RL) is an effective tool to overcome the above challenge. A typical structure, namely actor–critic architecture, was used to implement the RL algorithm [29,30]. In Ref. [31], the optimal tracking control problems for an unknown unmanned surface vehicle have been investigated via using an actor–critic reinforcement learning framework. In Ref. [32], actor–critic RL has been successfully applied for the EHA. Moreover, a reinforcement learning (RL) control strategy for a flexible two-link manipulator to enable vibration suppression was developed in Ref. [33], while retaining trajectory tracking. Although some published papers applied the RL for control issues, the achievement of FTC to solve tracking control problems using powerful learning algorithms and tackling both disturbance and actuator fault for the EHA systems has not been investigated. Therefore, the development of the FTC scheme with optimal performance for related EHA applications subject to actuator faults and disturbances motivates this paper.

Through the above analysis, it is revealed that most EHA systems have the requirement of optimal performance, while simultaneously suffering from disturbances/uncertainties and the internal leakage fault, which need to be addressed. Inspired by the abovementioned reasons, the proposed FTC scheme in this article for the EHA is investigated by using a cascade control technique, including the two control loops (position and force controls) and two DOs that warrant the system stability and the optimal control performance subject to the above disadvantages. The main contributions of this paper can be summarized in the following.

• Compared with Refs. [34,35], this work firstly investigates the FTC problem for the EHA system to simultaneously solve the lumped disturbances, bias fault, so that the force control of the EHA system is optimized.
• To effectively attenuate the influences of the disturbances and the fault in the EHA system, the combination of DOs, a nonsingular terminal sliding-mode (NTSMC) scheme for the position tracking control loop, and an optimized force control method is developed.
• The system stability and asymptotic tracking error convergence is warranted by Lyapunov theory, and the effectiveness and feasibility of the suggested methodology are verified based on the simulation results.

The rest of this article is arranged as follows: In Section 2, the mathematical model with the actuator fault model of the EHA is described. The proposed cascade FTC comprises of the two loops (position and force controls) and two DOs, which is designed in Section 3. Section 4 presents the numerical simulation and comparison studies, respectively. Finally, the brief conclusions and future works are drawn in Section 5.

2. System Descriptions and Preliminaries

The schematic diagram of the EHA with actuator faults is shown in Figure 1. The internal leakage fault of the hydraulic driven actuator is studied.

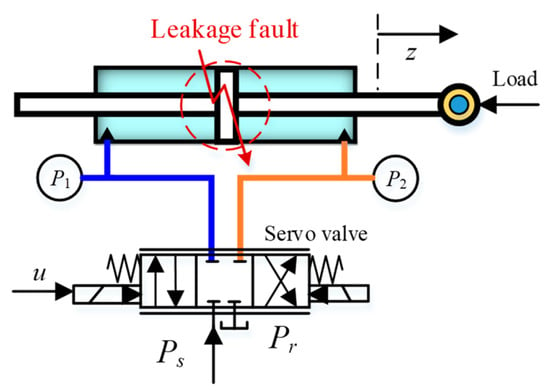
Figure 1. Schematic of hydraulic system with faults.

The dynamics of the actuator’s moving part can be derived by Newton’s second law

$$m\ddot{z}=P_{L}A-k_b\dot{z}+\Delta \left(t,z,\dot{z}\right)$$

(1)

where z is the piston’s displacement; $\Delta (•)$ represents the disturbance terms, i.e., load’s force, friction; $P_L=P_1–P_2$ is the load pressure, with $P_1,P_2$ being the pressure inside the extend and retract chambers; and m and $k_b$ describe the mass of the moving part and the equivalent viscous damping coefficient.

We suppose that the valve’s voltage input is related to the spool valve displacement by the directly proportional. Then, the load flow rate $Q_L$ is related to the control signal u by

$$Q_L=k_{s}u\sqrt{P_s-sign\left(u\right)P_L}$$

(2)

where P_s is the supply pressure, $k_s$ is a servo-valve’s proportional gain, and sign(•) is the standard signum function.

The fluid flow distribution into the two chambers of the cylinder is given by Refs. [8,36]:

$$Q_L=A\dot{z}+\frac{V_c}{4{\beta }_e}{\dot{P}}_L+Q_l-q_{Le}$$

(3)

where ${\beta }_e, A$ are the Bulk modulus, a piston effective area, and $Q_l$ is the internal leakage. $V_c$ is a fixed control volume of the cylinder. $q_{Le}$ denotes the time-varying disturbances (i.e., external flow leakage, lumped modeling error).

Considering the system suffering from an internal leakage fault, the $Q_l$ can be represented as follows:

$$Q_l=C_0{P}_L+\upsilon$$

(4)

where $C_0$ is the nominal coefficient, and the time-varying bias fault signal υ is leakage at the piston seal or internal flow loss. It can be formulated as follows in Refs. [37,38]

$$\upsilon =-C_f\sqrt{\frac{1}{A}}\sqrt{\left|A{P}_L\right|}sign\left(A{P}_L\right)$$

(5)

where the time-varying internal leakage fault $C_f$ is considered with time profiles modeled by

$$C_f=\{\begin{array}{l}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{if}\hspace{0.17em}t<T_0\\ (1-e^{-\alpha (t-T_0)})C_{f0}\hspace{0.17em}\mathrm{otherwise}\end{array}$$

(6)

where $T_0,\alpha ,C_f{}_0$ denote, in turn, the unknown time that a fault occurs, the unknown fault evolution rate, and the leakage fault coefficient.

Choosing $\zeta ={[{\zeta }_1,{\zeta }_2,{\zeta }_3]}^T\triangleq {[z,\dot{z},A{P}_L]}^T$ as the state variables, from (3)–(6), the system with actuator faults modeled can then be written as:

$$\{\begin{array}{l}{\dot{\zeta }}_1={\zeta }_2\\ m{\dot{\zeta }}_2=f_2\left({\zeta }_2\right)+{\zeta }_3+{\sigma }_1\left({\zeta }_1,{\zeta }_2,t\right)\\ {\dot{\zeta }}_3=f_3\left({\zeta }_2,{\zeta }_3\right)+g_3\left({\zeta }_3,u\right)u+{\sigma }_2\left({\zeta }_3,t\right)\end{array}$$

(7)

where

$$f_2=-k_b{\zeta }_2,{\sigma }_1=\Delta ,{\sigma }_2=\frac{4A{\beta }_e}{V_c}\left(q_{Li}+\frac{C_f}{\sqrt{A}}\sqrt{{\zeta }_3}sign\left({\zeta }_3\right)\right),$$

$$f_3=-\frac{4A{\beta }_e{C}_0}{V_c}{\zeta }_3-\frac{4{\beta }_e{A}^2}{V_c}{\zeta }_2,g_3=\frac{4A{\beta }_e{k}_t}{V_c}\sqrt{P_s-\frac{1}{A}{\zeta }_{3}sign\left(u\right)}.$$

Assumption 1.

a. 

The tracking reference signal${\zeta }_{1d}$, its derivative${\dot{\zeta }}_{1d}$, and all states are bounded.

b. 

Under normal working conditions, the pressures$P_1,P_2$, and$\left|P_L\right|$are sufficiently smaller than$P_s$.

c. 

There exist upper bounds for${\sigma }_1,{\sigma }_2$and their derivatives${\dot{\sigma }}_1,{\dot{\sigma }}_2$, such that they satisfy$\left|{\sigma }_i\right|\le d_{im},\left|{\dot{\sigma }}_i\right|\le D_i;i=1,2$, where$d_{im}, D_i$,are positive constants.

Remark 1.

For assumptions 1a and c: These are popular assumptions that have been used in previous works, for instance Refs. [1,7,38],to facilitate validating the stability problem of the closed-loop system. For assumption 1b: The pressures$P_1,P_2$originate from$P_s$, whilst$P_L=P_1–P_2$also does not exceed$P_s$. Therefore, Assumption 1 is reasonable and feasible.

Lemma 1

([39]). For a time-varying positive function $L_1\left(t\right)\ge 0$, ∀t ∈ [0, ∞] and $L_1\left(0\right)$ is bounded. If the following inequality holds

$${\dot{L}}_1\le -a_0{L}_1+b_0$$

(8)

where $a_0$ and $b_0$ are two positive constants, then it can be implied that $L_1\left(t\right)$ is bounded.

Remark 2.

The control objective is to synthesize a control signalusuch that the output position${\zeta }_1$tracks the desired trajectory${\zeta }_{1d}$to a bounded compact set, in the face of the lumped disturbances and actuator faults. Inspired by the combination of NTSMC, NDO, and optimal force control, the proposed FTC is developed to obtain the system stability and have an optimal performance for the nonlinear system (7).

3. Proposed Control Scheme

The control structure for the EHA system is illustrated in Figure 2. The cascade FTC control scheme comprises of outer-loop position tracking control and inner-loop force tracking control designs. By considering the lumped disturbances and the bias fault as lumped uncertainties, the two DOs are designed to handle the impacts of them. To obtain a high-accuracy tracking performance, a NTSMC scheme is elaborated for the position tracking control loop. Meanwhile, an optimal force controller is firstly constructed to guarantee the actual torque signals tracking the desired virtual torque signals. Optimization force control is implemented based on the RL strategy of actor–critic architecture. The suggested FTC strategy is proposed by combining the DOs, cascade control scheme including position control and optimal force control, which can not only minimize the selected cost functions to achieve the good tracking performance, but also ensure the boundness of all signal states in the face of the actuator fault and disturbances.

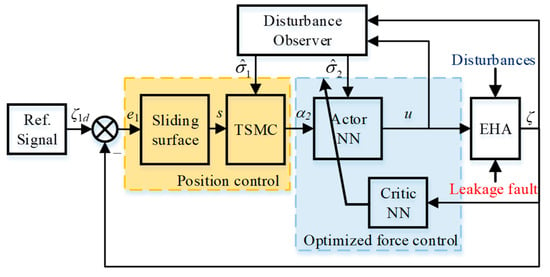
Figure 2. Sketch of the proposed control approach.

3.1. Disturbance Observer-Based NTSMC Design

The nonlinear system (7) with lumped disturbances and the bias fault is first considered. Consequently, the position control design procedure for the suggested FTC is presented in this subsection.

The error states are defined as follows:

$$e_1={\zeta }_1-{\zeta }_{1d}$$

(9)

where ${\zeta }_{1d}$ is the desired signal.

The derivative of e₁ can be expressed as

$${\dot{e}}_1={\zeta }_2-{\dot{\zeta }}_{1d}$$

(10)

A terminal sliding manifold is given by

$$s=m{\dot{e}}_1+\eta e_1^{\lambda }$$

(11)

where $m,\eta$ are positive terms, $\lambda ={\lambda }_1/{\lambda }_2,{\lambda }_1$ and ${\lambda }_2$ are positive odd integers satisfying ${\lambda }_1<{\lambda }_2$.

The time derivative of (11) is computed as

$$\dot{s}=m{\ddot{e}}_1+\eta \lambda e_1^{\lambda -1}{\dot{e}}_1=f_2+{\zeta }_3+{\sigma }_1-m{\dot{\zeta }}_{1d}+\eta \lambda e_1^{\lambda -1}{\dot{e}}_1$$

(12)

Let us denote the estimations of the disturbances ${\widehat{\sigma }}_1,{\widehat{\sigma }}_2$. The DO for mismatched disturbance ${\sigma }_1$ is elaborated as

$$\begin{array}{l}{\widehat{\sigma }}_1={\chi }_1+{\kappa }_1{\zeta }_2\\ {\dot{\chi }}_1=-{\kappa }_1{\chi }_1+s-{\kappa }_1\left(f_2+g_2{\zeta }_3+{\kappa }_1{\zeta }_2\right)\end{array}$$

(13)

where ${\chi }_1$ is internal states, ${\kappa }_1$ denotes the observer gain of the mismatched DO.

Define the mismatched disturbance error ${\tilde{\sigma }}_1={\sigma }_1-{\widehat{\sigma }}_1$. Taking the derivative of ${\tilde{\sigma }}_1$, one yields

$$\begin{array}{l}{\dot{\tilde{\sigma }}}_1={\dot{\sigma }}_1-{\dot{\widehat{\sigma }}}_1={\dot{\sigma }}_1-{\dot{\chi }}_1-{\kappa }_1{\dot{\zeta }}_2\\ ={\dot{\sigma }}_1+{\kappa }_1{\chi }_1-s+{\kappa }_1\left(f_2+g_2{\zeta }_3+{\kappa }_1{\zeta }_2\right)-{\kappa }_1\left(f_2+g_2{\zeta }_3+{\sigma }_1\right)\\ ={\dot{\sigma }}_1-{\kappa }_1{\tilde{\sigma }}_1-s\end{array}$$

(14)

The exponential approach rate is used. Hence, the desired force for the mechanical subsystem is constructed as follows:

$${\alpha }_2=-f_2-{\widehat{\sigma }}_1+m{\dot{\zeta }}_{1d}-\eta \lambda e_1^{\lambda -1}{\dot{e}}_1-{\gamma }_{1}s-{\gamma }_2{s}^{\vartheta }-k_{1}sign\left(s\right)$$

(15)

where ${\gamma }_1,{\gamma }_2,k_1$ are control gains and positive constants, and $0<\vartheta <1$.

Let the torque error be determined as follows:

$$e_3={\zeta }_3-{\alpha }_2$$

(16)

The Lyapunov function candidate $V_1$ is adopted as

$$V_1=\frac{1}{2}{s}^2+\frac{1}{2}{\tilde{\sigma }}_1^2$$

(17)

Taking the derivative of V₁ and noting (12), (14), we obtain:

$$\begin{array}{l}{\dot{V}}_1=s\left(-{\gamma }_{1}s-{\gamma }_2{s}^{\vartheta }-k_{1}sign\left(s\right)+{\tilde{\sigma }}_1+e_3\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\tilde{\sigma }}_1\left({\dot{\sigma }}_1-{\kappa }_1{\tilde{\sigma }}_1-s\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=-k_1\left|s\right|-{\gamma }_1{s}^2-{\gamma }_2{s}^{\vartheta +1}+s{e}_3-{\kappa }_1{\tilde{\sigma }}_1^2+{\tilde{\sigma }}_1{\dot{\sigma }}_1\end{array}$$

(18)

Differentiating e₃ with respect to time yields that

$${\dot{e}}_3=f_3+g_{3}u+{\sigma }_2-{\dot{\alpha }}_2$$

(19)

The matched DO is constructed to approximate both matched disturbance and the bias fault ${\sigma }_2$ as

$$\begin{array}{l}{\widehat{\sigma }}_2={\chi }_2+{\kappa }_2{\zeta }_3\\ {\dot{\chi }}_2=-{\kappa }_2{\chi }_2-{\kappa }_2\left(f_3+g_{3}u+{\kappa }_2{\zeta }_3\right)\end{array}$$

(20)

where ${\chi }_2$ is internal states, ${\kappa }_2$ denotes the observer gain of the matched DO.

The matched disturbance error is calculated by ${\tilde{\sigma }}_2={\sigma }_2-{\widehat{\sigma }}_2$. Taking the derivative of ${\tilde{\sigma }}_2$, one obtains

$$\begin{array}{l}{\dot{\tilde{\sigma }}}_2={\dot{\sigma }}_2-{\dot{\widehat{\sigma }}}_2={\dot{\sigma }}_2-{\dot{\chi }}_2-{\kappa }_2{\dot{\zeta }}_3\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\dot{\sigma }}_2-{\kappa }_2{\tilde{\sigma }}_2\end{array}$$

(21)

Remark 3.

The singular problem in (15) can be overcome by using the modified terminal sliding manifold as Ref. [40]:

$$s=m{\dot{e}}_1+\phi \left(e_1\right)$$

(22)

where

$$\phi \left(e_1\right)=\{\begin{array}{l}\eta e_1^{\lambda }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\overline{s}=0\hspace{0.17em}or\hspace{0.17em}\overline{s}\ne 0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\left|e_1\right|>{\eta }_s\\ k_{1s}{e}_1+k_{2s}{e}_1^{2}sign\left(e_1\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\overline{s}\ne 0\hspace{0.17em}and\hspace{0.17em}\left|e_1\right|\le {\eta }_s\end{array}$$

(23)

where$k_{1s}=\left(2-\nu \right){\eta }_s^{\nu -1},k_{2s}=\left(\nu -1\right){\eta }_s^{\nu -2}$, ${\eta }_s$is a positive scalar, and$\overline{s}=m{\dot{e}}_1+\eta e_1^{\lambda }$.

3.2. Optimal Force Control Design

In this subsection, the final control law u is constructed to ensure the optimized solutions of inner-loop force tracking control designs. The system stability and acceptable performance of the whole closed-loop system can be preserved. The control design procedure is presented as follows:

Let us introduce the following cost function as

$$J={\displaystyle \underset{t}{\overset{\infty }{\int }}\left(e_3^2+u^2\right)d\tau }$$

(24)

The HJB equation is elaborated as

$$H=e_3^2+u^2+\frac{\partial J}{\partial e_3}{\dot{e}}_3=e_3^2+u^2+J_{e_3}\left(f_3+g_{3}u+{\sigma }_2-{\dot{\alpha }}_2\right)$$

(25)

where $J_{e_3}=\frac{\partial J}{\partial e_3}$ denotes the gradient of $J$.

The optimal control u^∗ can be calculated if the derivative of the HJB function with respect to u^∗ obtains:

$$\frac{\partial H}{\partial u^{*}}=0\leftrightarrow u^{*}=-\frac{1}{2}{g}_3{J}_{e_3}^{*}$$

(26)

The $J_{e_3}^{*}$ function can be presented as

$$J_{e_3}^{*}=2k_3{e}_3+2f_3+2{\widehat{\sigma }}_2+J_{e_3}^0$$

(27)

where $J_{e_3}^0=J_{e_3}^{*}-2k_3{e}_3-2f_3-2{\widehat{\sigma }}_2$, $k_3$ is a positive scalar.

By using NN approximation to construct the critic network, an unknown continuous vector function $J_{e_3}^0$ can be estimated; it follows that:

$$J_{e_3}^0={\varphi }^{*T}h\left({\zeta }_1,{\zeta }_2,e_3\right)+\varsigma$$

(28)

where ${\varphi }^{*}$ is the ideal weight of the NN, $\varsigma$ is the error of NN approximation, $h\left({\zeta }_1,{\zeta }_2,e_3\right)$ is the basis function. Throughout this paper, for the simplicity of expression, we abbreviate $h\left({\zeta }_1,{\zeta }_2,e_3\right)$ by h. In general, the most popularly used Gaussian radial basis functions are employed as follows:

$$h=\exp \left[\frac{-{\left({\zeta }_{in}-{\mu }_i\right)}^T\left({\zeta }_{in}-{\mu }_i\right)}{b_i^2}\right]$$

(29)

where ${\zeta }_{in}={\left[\begin{array}{ccc}{\zeta }_1& {\zeta }_2& e_3\end{array}\right]}^T$ is the NN inputs vector, and ${\mu }_i,b_i$ denote the center of the neural, the Gaussian function’s width, respectively.

Assumption 2.

There exists an ideal weight vector${\varphi }^{\ast }$such that |ς| < ς^∗ with constant ς^∗ > 0 for all ${\zeta }_{in}$ ∈ Ω_ζ ⊂ ${\Re }^3$.

Substituting (27) and (28) to (26), one obtains

$$u^{*}=-g_3\left(k_3{e}_3+f_3+{\widehat{\sigma }}_2+\frac{1}{2}{\varphi }^{*T}h+\frac{1}{2}\varsigma \right)$$

(30)

Due to the unavailable ideal weight vector ϕ^∗, the optimal controller (30) cannot be implemented. Hence, the RL algorithm is introduced by utilizing the following both critic and actor NNs. The critic NN is used to evaluate the controlling performance, whilst the actor NN generates the final control law. The critic NN for evaluating the control performance is further derived as

$${\widehat{J}}_{e_3}^{*}=2k_3{e}_3+2f_3+2{\widehat{\sigma }}_2+{\widehat{\varphi }}_c^{T}h$$

(31)

where ${\widehat{\varphi }}_c$ is the estimation of NN optimal weight ϕ^∗.

The critic NN weight is updated by the following law as

$${\dot{\widehat{\varphi }}}_c=-{\beta }_{c}h{h}^T{\widehat{\varphi }}_c$$

(32)

where ${\beta }_c$ is a positive constant.

The final control law of the optimal force controller can be constructed as follows:

$${\widehat{u}}^{*}=g_3\left(-k_3{e}_3-f_3-{\widehat{\sigma }}_2-\frac{1}{2}{\widehat{\varphi }}_a^{T}h\right)$$

(33)

where ${\widehat{\varphi }}_a$ is the estimation of actor NN optimal weight ϕ^∗, and the adaptive law of the actor NN weight is determined as Ref. [34]:

$${\dot{\widehat{\varphi }}}_a=-h{h}^T\left({\beta }_a\left({\widehat{\varphi }}_a-{\widehat{\varphi }}_c\right)+{\beta }_c{\widehat{\varphi }}_c\right)$$

(34)

where ${\beta }_a$ is a positive constant.

Applying ${\widehat{u}}^{*}$ and ${\widehat{J}}_{e_3}^{*}$ to (25), the approximation of the HJB equation yields

$$\begin{array}{l}H\left(e_3,{\widehat{u}}^{*},{\widehat{J}}_{e_3}^{*}\right)=e_3^2+g_3^2{\left(k_3{e}_3+f_3+{\widehat{\sigma }}_2+\frac{1}{2}{\widehat{\varphi }}_a^{T}h\right)}^2\\ +\left(2k_3{e}_3+2f_3+2{\widehat{\sigma }}_2+{\widehat{\varphi }}_c^{T}h\right)\\ \times \left(f_3-g_3^2\left(k_3{e}_3+f_3+{\widehat{\sigma }}_2+\frac{1}{2}{\widehat{\varphi }}_a^{T}h\right)+{\sigma }_2-{\dot{\alpha }}_2\right)\end{array}$$

(35)

Defining the residual error between the HJB and its approximation, we have

$$\epsilon =H\left(e_3,{\widehat{u}}^{*},{\widehat{J}}_{e_3}^{*}\right)-H\left(e_3,u^{*},J_{e_3}^{*}\right)=H\left(e_3,{\widehat{u}}^{*},{\widehat{J}}_{e_3}^{*}\right)$$

(36)

and considering the optimized solution ${\widehat{u}}^{*}$ is expected to satisfy, the following equality is derived:

$$\frac{\partial H}{\partial {\widehat{\varphi }}_a}=g_3^{2}h{h}^T\left({\widehat{\varphi }}_a-{\widehat{\varphi }}_c\right)=0$$

(37)

Under the premise that (37) is warranted, the RL updating laws are given by the establishment of a non-negative function, as follows:

$$Q={\left({\widehat{\varphi }}_a-{\widehat{\varphi }}_c\right)}^T\left({\widehat{\varphi }}_a-{\widehat{\varphi }}_c\right)$$

(38)

With the differentiation of (38) with respect to time, one obtains

$$\begin{array}{l}\frac{dQ}{dt}=\frac{\partial Q}{\partial {\widehat{\varphi }}_c}{\dot{\widehat{\varphi }}}_c+\frac{\partial Q}{\partial {\widehat{\varphi }}_a}{\dot{\widehat{\varphi }}}_a=-2\left({\widehat{\varphi }}_a-{\widehat{\varphi }}_c\right)\left(-{\beta }_{c}h{h}^T{\widehat{\varphi }}_c\right)\\ +2\left({\widehat{\varphi }}_a-{\widehat{\varphi }}_c\right)\left(-h{h}^T\left({\beta }_a\left({\widehat{\varphi }}_a-{\widehat{\varphi }}_c\right)+{\beta }_c{\widehat{\varphi }}_c\right)\right)\\ =-2{\beta }_a\left({\widehat{\varphi }}_a-{\widehat{\varphi }}_c\right)h{h}^T\left({\widehat{\varphi }}_a-{\widehat{\varphi }}_c\right)\le 0\end{array}$$

(39)

From (38), (39), it is concluded that $Q=0$ can be obtained by using the updating laws (32) and (34), and then (37) can be satisfied as well.

Choose the overall Lyapunov function candidate for the system as

$$V=V_1+\frac{1}{2}{e}_3^2+\frac{1}{2}{\tilde{\varphi }}_a^T{\tilde{\varphi }}_a+\frac{1}{2}{\tilde{\varphi }}_c^T{\tilde{\varphi }}_c+\frac{1}{2}{\tilde{\sigma }}_2^2$$

(40)

where ${\tilde{\varphi }}_a={\widehat{\varphi }}_a-{\varphi }^{*},{\tilde{\varphi }}_c={\widehat{\varphi }}_c-{\varphi }^{*}$ are the NN weight errors.

The time derivative of V is derived by

$$\begin{array}{l}\dot{V}={\dot{V}}_1+e_3{\dot{e}}_3+{\tilde{\varphi }}_a^T{\dot{\tilde{\varphi }}}_a+{\tilde{\varphi }}_c^T{\dot{\tilde{\varphi }}}_c+{\tilde{\sigma }}_2{\dot{\tilde{\sigma }}}_2\\ =-k_1\left|s\right|-{\gamma }_1{s}^2-{\gamma }_2{s}^{\vartheta +1}+s{e}_3-L_1{\tilde{\sigma }}_1^2+{\tilde{\sigma }}_1{\dot{\sigma }}_1\\ +e_3\left({\phi }_3+g_3^2\left(-k_3{e}_3-f_3-{\widehat{\sigma }}_2-\frac{1}{2}{\widehat{\varphi }}_a^{T}h\right)+{\sigma }_2-{\dot{\alpha }}_2\right)\\ -{\tilde{\varphi }}_a^{T}h{h}^T\left({\beta }_a\left({\widehat{\varphi }}_a-{\widehat{\varphi }}_c\right)+{\beta }_c{\widehat{\varphi }}_c\right)-{\beta }_c{\tilde{\varphi }}_c^{T}h{h}^T{\widehat{\varphi }}_c+{\tilde{\sigma }}_2\left({\dot{\sigma }}_2-L_2{\tilde{\sigma }}_2\right)\end{array}$$

(41)

Using Young’s inequality, one obtains

$$\begin{array}{l}s{e}_3\le \frac{1}{2}{s}^2+\frac{1}{2}{e}_3^2\\ {\tilde{\sigma }}_1{\dot{\sigma }}_1\le \frac{1}{2}{\tilde{\sigma }}_1^2+\frac{1}{2}{\dot{\sigma }}_1^2\\ e_3{f}_3\le \frac{1}{2}{e}_3^2+\frac{1}{2}{f}_3^2\\ e_3{\sigma }_2\le \frac{1}{2}{e}_3^2+\frac{1}{2}{\sigma }_2^2\\ e_3{\dot{\alpha }}_2\le \frac{1}{2}{e}_3^2+\frac{1}{2}{\dot{\alpha }}_2^2\\ -e_3{g}_3^2{f}_3\le \frac{1}{2}{g}_3^4{e}_3^2+\frac{1}{2}{f}_3^2\\ -e_3{g}_3^2{\widehat{\sigma }}_2=-e_3{g}_3^2\left({\sigma }_2-{\tilde{\sigma }}_2\right)\le g_3^4{e}_3^2+\frac{1}{2}{\sigma }_2^2+\frac{1}{2}{\tilde{\sigma }}_2^2\\ -\frac{1}{2}{e}_3{g}_3^2{\widehat{\varphi }}_a^{T}h\le \frac{1}{4}{g}_3^4{e}_3^2+\frac{1}{4}{\widehat{\varphi }}_a^{T}h{h}^T{\widehat{\varphi }}_a\end{array}$$

(42)

Substituting (42) to (41) yields

$$\begin{array}{l}\dot{V}\le -\left({\gamma }_1-\frac{1}{2}\right)s^2-\left(k_3{g}_3^2-2-\frac{7}{4}{g}_3^4\right)e_3^2\\ -{\displaystyle \sum _{i=1}^2\left({\kappa }_i-\frac{1}{2}\right){\tilde{\sigma }}_i^2}+\frac{1}{2}{\dot{\sigma }}_1^2+f_3^2+{\sigma }_2^2+\frac{1}{2}{\dot{\alpha }}_2^2+\frac{1}{4}{\widehat{\varphi }}_a^{T}h{h}^T{\widehat{\varphi }}_a\\ -{\beta }_a{\tilde{\varphi }}_a^{T}h{h}^T{\widehat{\varphi }}_a+\left({\beta }_a-{\beta }_c\right){\tilde{\varphi }}_a^{T}h{h}^T{\widehat{\varphi }}_c-{\beta }_c{\tilde{\varphi }}_c^{T}h{h}^T{\widehat{\varphi }}_c\end{array}$$

(43)

Applying Young’s inequality and according to the equivalent transformation (i.e., ${\tilde{\varphi }}_a^{T}h{h}^T{\tilde{\varphi }}_a+2{\tilde{\varphi }}_a^{T}h{h}^T{\varphi }^{*}+{\varphi }^{*}h{h}^T{\varphi }^{*}={\widehat{\varphi }}_a^{T}h{h}^T{\widehat{\varphi }}_a$), one obtains

$$\begin{array}{l}{\tilde{\varphi }}_a^{T}h{h}^T{\widehat{\varphi }}_a=\frac{1}{2}{\tilde{\varphi }}_a^{T}h{h}^T{\tilde{\varphi }}_a+\frac{1}{2}{\widehat{\varphi }}_a^{T}h{h}^T{\widehat{\varphi }}_a-\frac{1}{2}{\varphi }^{*}h{h}^T{\varphi }^{*}\\ {\tilde{\varphi }}_c^{T}h{h}^T{\widehat{\varphi }}_c=\frac{1}{2}{\tilde{\varphi }}_c^{T}h{h}^T{\tilde{\varphi }}_c+\frac{1}{2}{\widehat{\varphi }}_c^{T}h{h}^T{\widehat{\varphi }}_c-\frac{1}{2}{\varphi }^{*}h{h}^T{\varphi }^{*}\\ {\tilde{\varphi }}_a^{T}h{h}^T{\widehat{\varphi }}_c\le \frac{1}{2}{\tilde{\varphi }}_a^{T}h{h}^T{\tilde{\varphi }}_a+\frac{1}{2}{\widehat{\varphi }}_c^{T}h{h}^T{\widehat{\varphi }}_c\end{array}$$

(44)

Combined with (43) and (44), we obtain

$$\begin{array}{l}\dot{V}\le -\left({\gamma }_1-\frac{1}{2}\right)s^2-\left(k_3{g}_3^2-2-\frac{7}{4}{g}_3^4\right)e_3^2\\ -{\displaystyle \sum _{i=1}^2\left({\kappa }_i-\frac{1}{2}\right){\tilde{\sigma }}_i^2}-\frac{{\beta }_c}{2}{\tilde{\varphi }}_a^{T}h{h}^T{\tilde{\varphi }}_a-\frac{{\beta }_c}{2}{\tilde{\varphi }}_c^{T}h{h}^T{\tilde{\varphi }}_c\\ +\frac{1}{2}{\dot{\sigma }}_1^2+{\phi }_3^2+{\sigma }_2^2+\frac{1}{2}{\dot{\alpha }}_2^2+\frac{\left({\beta }_a+{\beta }_c\right)}{2}{\varphi }^{*}h{h}^T{\varphi }^{*}\\ -\left(\frac{{\beta }_a}{2}-\frac{1}{4}\right){\widehat{\varphi }}_a^{T}h{h}^T{\widehat{\varphi }}_a-\frac{\left(-{\beta }_a+2{\beta }_c\right)}{2}{\widehat{\varphi }}_c^{T}h{h}^T{\widehat{\varphi }}_c\end{array}$$

(45)

If the inequality $\frac{1}{2}<{\beta }_a<\frac{1}{2}{\beta }_c,$ holds, there exist the upper bounds of the nonlinear function $g_3,f_3,{\dot{\alpha }}_2$ (i.e., $g_3<{\mathrm{\Lambda }}_3,f_3\le {\phi }_{3m},{\dot{\alpha }}_2\le {\alpha }_{2m}$) [25,35], and ${\sigma }_2\le d_{2m},{\dot{\sigma }}_1\le D_{1m}$ under Assumption 1. Thus, the time derivative of V can be given as

$$\dot{V}\le -\Gamma V+\psi$$

(46)

where

$$\mathrm{\Gamma }=\min \left(\begin{array}{l}{\lambda }_{\min }\left(2{\gamma }_1-1\right),{\lambda }_{\min }\left(2k_3{\Lambda }_3^2-4-\frac{7}{4}{\Lambda }_3^4\right),\\ {\lambda }_{\min }\left(2{\kappa }_1-1\right),{\lambda }_{\min }\left(2{\kappa }_2-1\right),{\lambda }_{\min }\left({\beta }_{c}h{h}^T\right)\end{array}\right)$$

$$\psi =\frac{1}{2}{D}_{1m}^2+{\phi }_{3m}^2+d_{2m}^2+\frac{1}{2}{\alpha }_{2m}^2+\frac{\left({\beta }_a+{\beta }_c\right)}{2}{\varphi }^{*}h{h}^T{\varphi }^{*}$$

Theorem 1.

With the EHA system (7), if the two DOs are designed as (13), (20), the position control law is presented in (15), the optimal force controller is indicated by (33). The adaptive law of the critic and actor NN weights is determined by (32) and (34). Then, all closed-loop signals, i.e., tracking errors, disturbance errors, and critic and actor NN weight errors are uniformly ultimately bounded (UUB) in the face of actuator failures and lumped disturbances.

Proof. 

From (46), we can obtain

$$\dot{V}\left(t\right)\le V\left(t_0\right)e^{-\mathrm{\Gamma }\left(t-t_0\right)}+\frac{\mathrm{\psi }}{\mathrm{\Gamma }}$$

(47)

From Lemma 1, it is indicated that $\underset{t\mathrm{\to }\mathrm{\infty }}{\lim }V=\raisebox{1ex}{$\mathrm{\psi }$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\Gamma }$}\right.$, which means that the Lyapunov function V in (46) is convergent, all signals are bounded and will tend to a small compact set defined by $\mathrm{\Omega }=\left\{s,e_3,{\tilde{\sigma }}_1,{\tilde{\sigma }}_2,{\tilde{\varphi }}_a,{\tilde{\varphi }}_c|\left|s\right|,\left|e_3\right|,\left|{\tilde{\sigma }}_1\right|,\left|{\tilde{\sigma }}_2\right|,\left|{\tilde{\varphi }}_a\right|,\left|{\tilde{\varphi }}_c\right|\le \sqrt{2\mathrm{\psi }/\mathrm{\Gamma }}\right\}$. □

4. Simulation Results

4.1. Simulation Setup

To verify the improved performance of the proposed FTC, the simulation results are conducted in the EHA system by using MATLAB/Simulink. Two desired trajectories, i.e., the variable frequency sinusoidal (VFS) signals and a ramp signal, are described as

$$\begin{array}{l}{\zeta }_{1d}=10+10\left(sin(\pi t-\pi /2)+cos\left(0.5\pi t\right)\right)\left(\mathrm{mm}\right)\\ {\zeta }_{1d}=10t\left(\mathrm{mm}\right)\end{array}$$

(48)

The values of the EHA system parameters are given on the basis of data reported in Ref. [21], as listed in Table 1.

Table 1. EHA parameters.

System Parameter	Value	Unit
βe	1.25 × 103	MPa
ks	3.2 × 10−8	m3/s/V/Pa−1/2
kb	450	Ns/m
m	4.5	kg
A	4 × 10−4	m2
$P_s$	16	MPa
Vc	6 × 10−5	m3
$P_r$	0.1	MPa

For comparison, other control strategies are given to validate the advantages of the proposed FTC method in the simulation.

(1) DBC: This is the direct backstepping controller without two DOs. The control law is designed by Ref. [41]:

$$\begin{array}{l}{e}_1={\zeta }_1-{\zeta }_{1d};{\zeta }_{2d}={\dot{\zeta }}_{1d}-k_1{e}_1;\\ e_2={\zeta }_2-{\zeta }_{2d};{\zeta }_{3d}=m{\dot{x}}_{2d}-f_2-e_1-k_2{e}_2;\\ e_3={\zeta }_3-{\zeta }_{3d};u=\frac{1}{g_3}({\dot{\zeta }}_{3d}-f_3-k_3{e}_3-e_2);\end{array}$$

(49)

where $k_1, k_2, and k_3$ represent the positive gain parameters.

(2) BSMCDO: This is the traditional backstepping sliding-mode controller with two DOs [42]. The control law is described by:

$$\begin{array}{l}\hspace{0.17em}s=m{\dot{e}}_1+\eta e_1\\ {\zeta }_{3d}=-k_1{\dot{e}}_1+m{\ddot{\zeta }}_{1d}-f_2-k_{2}s-{\widehat{\sigma }}_1\\ e_3={\zeta }_3-{\zeta }_{3d}\\ u=-\frac{1}{g_3}\left(f_3-{\dot{\zeta }}_{3d}+{\widehat{\sigma }}_2+k_3{e}_3+s\right)\end{array}$$

(50)

where k_i, i = 1, 2, 3 are the positive constant.

(3) Proposed controller: This strategy is a nonsingular terminal sliding-mode optimized backstepping control (NTSMOBC) with two DOs.

The following control gains are carefully regulated and tuned via the trial and error method and chosen as: $k_1=50;{\gamma }_1=20;{\gamma }_2=1.5$; λ₁ = 3; λ₂ = 5; η = 10. Meanwhile, the parameters of the optimal force controller are chosen as $k_3=25;{\beta }_a=5.5;{\beta }_c=23$. There exist two RBF NNs in the control EHA system. The critic NN part contains 65 nodes with a width equal to 0.5 and centers μ_i = 2.5 + 0.4i (i = 1 ÷ 65) evenly spaced in the interval [−2.5, 2.5]. The actor NN part contains 25 nodes with a width equal to 0.5 and centers μ_i = 2.5 + 0.4i (i = 1 ÷ 25) evenly spaced in the interval [−2.5, 2.5]. The initial conditions of the critic NN, actor NN are selected as ${\widehat{\varphi }}_c\left(0\right)$ = [0.04 … 0.04]^T, ${\widehat{\varphi }}_a\left(0\right)$ = [4 … 4]^T, respectively. The parameters for the DO gains are set as κ₁ = 60; κ₂ = 5.5.

In fair comparison, the control parameters of DBC, BSMCDO controller are the same as the corresponding parameters in the proposed controller, e.g., same value of k₁; k₂ = γ₁; k₃; η; κ₁; κ₂.

To assess the qualification of the proposed control algorithm in the face of the actuator fault, the various operational conditions are provided during 30 s. In the first condition, the system operates in normal condition with lumped disturbances. In the second condition, the internal leakage fault occurs after 10 s.

4.2. Evaluation Result

Two case studies were executed to appraise the effectiveness of the suggested FTC scheme. Case study 1 considered only the lumped uncertainty, while both the internal leakage fault and lumped uncertainty were tested in Case study 2. The simulation results are described as follows.

Case study 1: In this case study, the electro-hydraulic system operates in normal condition with inherent lumped disturbances. Figure 3 depicts the simulation results with a ramp and a sinewave response. From Figure 3a,b, the output position of three control algorithms exhibits good tracking capability. Nevertheless, the peak value of the position tracking error using the proposed controller and BSMCDO is smaller than that of usually applied DBC, as seen in Figure 3c,d, because the DOs effectively suppress lumped disturbances, which can be achieved by Figure 4. It can be known that the combination of NTSMC and the optimized-based BC scheme can not only obtain the purpose of optimization, but also guarantee the high-accuracy tracking performance in hydraulic servosystems; then, the suggested controller outperforms the BSMCDO controllers in terms of transient and final tracking errors. To ensure the ORC’s optimal performance, the critic and actor NN weight estimations ${\widehat{\varphi }}_c,{\widehat{\varphi }}_a$ of the ORC converge to the corresponding steady-state value, as shown in Figure 5. The effectiveness of comparative controllers is assessed through three performance indices and expressed in Table 2. From Table 2, the root mean square error (e_RMS), average tracking error (e_a), and maximum error (e_max) [7,43] of the proposed controller are, in turn, 0.0351, 0.0298, and 0.1954 mm with the desired sinewave signal, and 0.0278, 0.0201, and 0.0980 mm with the desired ramp signal, which is the smallest in comparison with other controllers. This reconfirms the perfect control performance of the proposed FTC strategy.

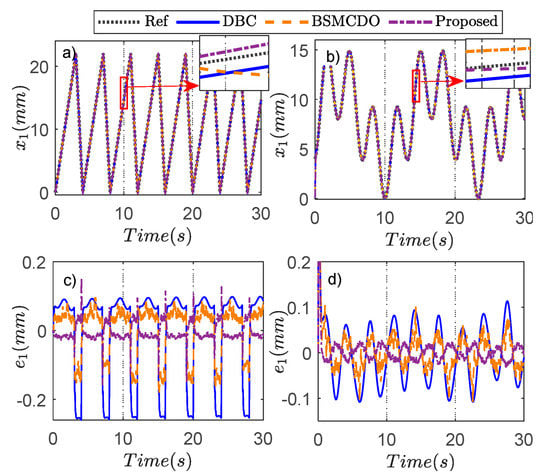
Figure 3. Comparison of three control methods in Case study 1: (a) Ramp response. (b) VFS response. (c) Tracking error for ramp demand. (d) Tracking error for VFS demand.

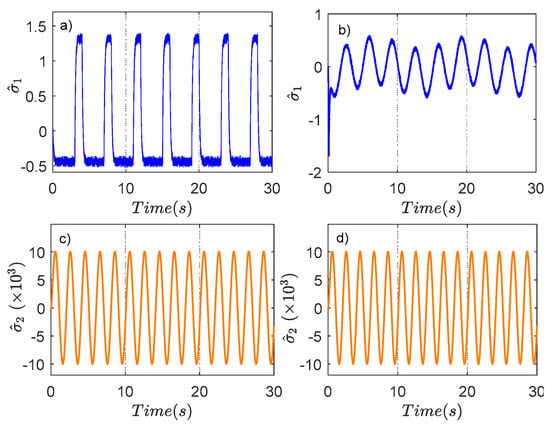
Figure 4. Lumped disturbances estimation of the proposed method in Case study 1: (a) ${\widehat{\sigma }}_1$ for ramp demand. (b) ${\widehat{\sigma }}_1$ for VFS demand. (c) ${\widehat{\sigma }}_2$ for ramp demand. (d) ${\widehat{\sigma }}_2$ for VFS demand.

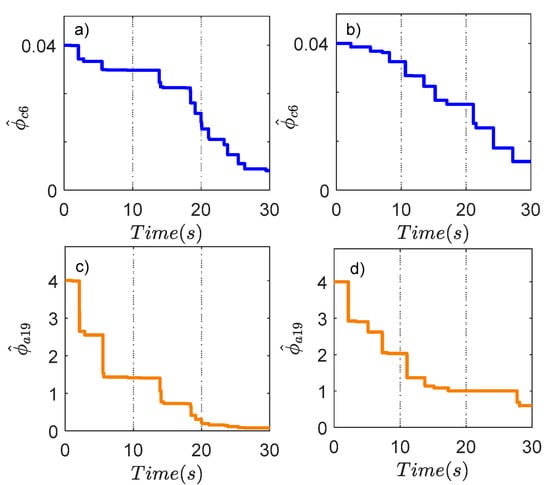
Figure 5. Critic and actor NN weight estimations of the proposed method in Case study 1: (a) ${\widehat{\varphi }}_{c6}$ for ramp demand. (b) ${\widehat{\varphi }}_{c6}$ for VFS demand. (c) ${\widehat{\varphi }}_{a19}$ for ramp demand. (d) ${\widehat{\varphi }}_{a19}$ for VFS demand.

Table 2. Performance indices of three controllers in simulation, Case study 1.

	Controller	DBC	BSMCDO	Proposed
Ramp	eRMS	0.1027	0.0637	0.0351
	ea	0.1103	0.0726	0.0298
	emax	0.2644	0.2381	0.1954
VPS	eRMS	0.0986	0.0727	0.0278
	ea	0.1009	0.0869	0.0201
	emax	0.1542	0.1194	0.0980

Case study 2: In this scenario, the internal leakage fault in simulation is generated after $T_0=10s$ with internal leakage coefficient $C_f{}_0=3.5\times {10}^{-8}{m}^4/\left(N^{1/2}s\right)$, and the fault evolution rate $\alpha =10$. The simulation results are displayed in Figure 6, which indicates that the position errors of the DBC, BSMCDO, and the FTC proposed method are affected by the appearance of leakage fault. However, in comparison with DBC, the tracking error of the other methods is smaller due to a disturbance compensation system of two DOs. The accurate estimation of the matched, mismatched disturbances, and the bias fault using two Dos, are shown in Figure 7. Meanwhile, compared with the BSMCDO control method, the proposed controller combines the robustness properties of the NTSMC and the optimal performance of the optimized force controller. Therefore, the FTC proposed approach obtained the better performance and stronger robustness even though the bias fault appears. Figure 8 illustrates the norms of critic and actor NN weight estimations, respectively, and the ${\widehat{\varphi }}_c,{\widehat{\varphi }}_a$ converge eventually. Table 3 presents the results of three performance indices of three controllers. It indicates that the e_RMS of the proposed controller is reduced by 73.9%, and 48.4%; the e_a of the proposed controller is reduced by 79.8%, and 60.8%, in comparison with DBC, BSMCDO for VFS demand, respectively. The performance indices for ramp demand also reflect similar results in Table 3. This clearly validates the effectiveness of the proposed method.

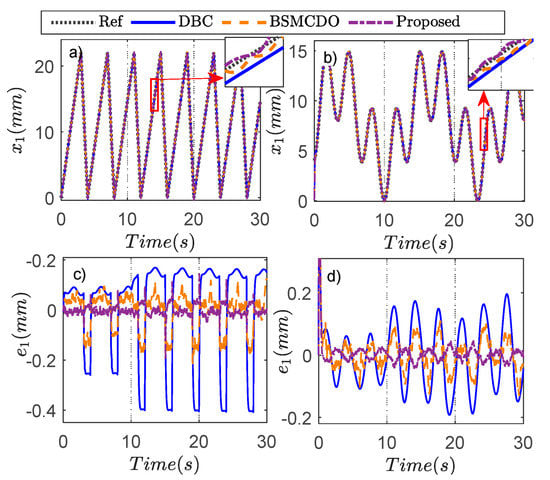
Figure 6. Comparison of three control methods in Case study 2: (a) Ramp response. (b) VFS response. (c) Tracking error for ramp demand. (d) Tracking error for VFS demand.

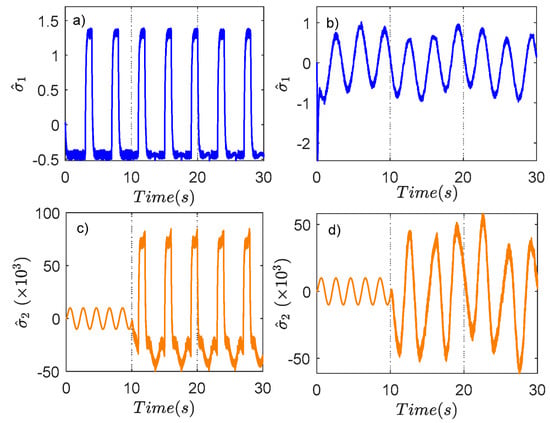
Figure 7. Lumped disturbances estimation of the proposed method in Case study 2: (a) ${\widehat{\sigma }}_1$ for ramp demand. (b) ${\widehat{\sigma }}_1$ for VFS demand. (c) ${\widehat{\sigma }}_2$ for ramp demand. (d) ${\widehat{\sigma }}_2$ for VFS demand.

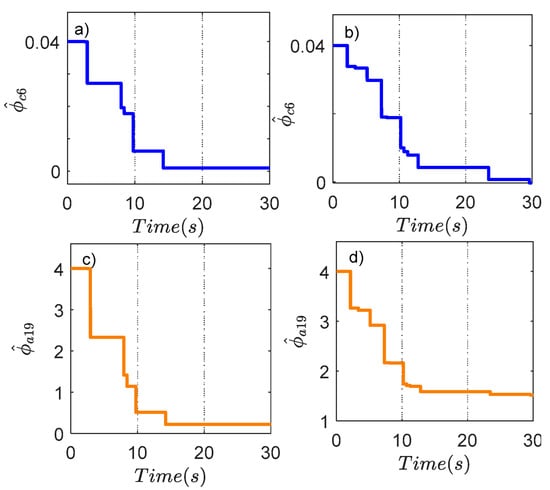
Figure 8. Critic and actor NN weight estimations of the proposed method in Case study 2: (a) ${\widehat{\varphi }}_{c6}$ for ramp demand. (b) ${\widehat{\varphi }}_{c6}$ for VFS demand. (c) ${\widehat{\varphi }}_{a19}$ for ramp demand. (d) ${\widehat{\varphi }}_{a19}$ for VFS demand.

Table 3. Performance indices of three controllers in simulation, Case study 2.

	Controller	DBC	BSMCDO	Proposed
Ramp	eRMS	0.1190	0.1024	0.0838
	ea	0.1201	0.1106	0.0778
	emax	0.4198	0.2684	0.2106
VPS	eRMS	0.1595	0.0857	0.0442
	ea	0.1768	0.0912	0.0357
	emax	0.1986	0.1458	0.1260

According to the comparative simulation studies in Figure 3 above, it is verified that the proposed FTC can obtain the desired control goal. Moreover, it provides the excellent tracking performance in the face of the matched, mismatched disturbances, the internal leakage fault, among three controllers.

5. Conclusions

The optimal FTC strategy was successfully applied to the EHA system with lumped disturbances and internal leakage faults via the cascade control using NTMSC and a simplified RL algorithm based on the optimized technology. The lumped uncertainties including matched, mismatched disturbances and the internal leakage fault are catered for simultaneously. Two DOs were deployed for estimations of them. A novel controller-based NTSMC, and an optimal force tracking control approach is further constructed for the EHA system, which can not only obtain the purpose of optimization, but also guarantee the high-accuracy tracking performance in hydraulic servosystems. The simulation results were implemented to verify the superior performance and system stability of the suggested strategy, even in faulty conditions.

Nevertheless, the presented strategy still has some disadvantages. First, the loss of effectiveness fault was ignored in this work. Second, verifying the proposed algorithm in actual experiments has not yet been performed. In future works, we will tend to develop the FTC scheme for practical EHAs with some types of actuator faults, including bias fault and loss of effectiveness fault.